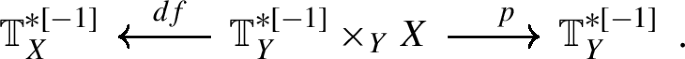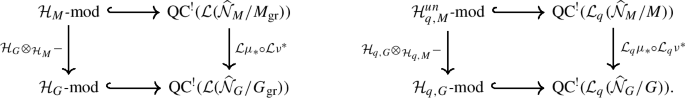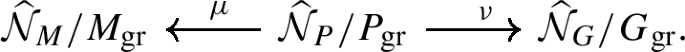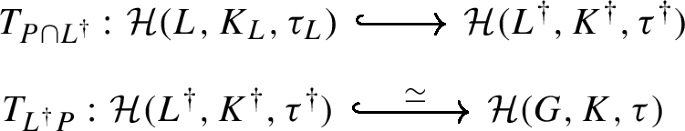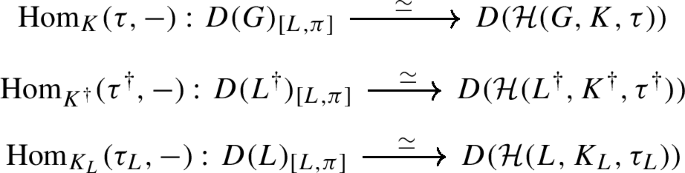Abstract
Kazhdan and Lusztig identified the affine Hecke algebra ℋ with an equivariant \(K\)-group of the Steinberg variety, and applied this to prove the Deligne-Langlands conjecture, i.e., the local Langlands parametrization of irreducible representations of reductive groups over nonarchimedean local fields \(F\) with an Iwahori-fixed vector. We apply techniques from derived algebraic geometry to pass from \(K\)-theory to Hochschild homology and thereby identify ℋ with the endomorphisms of a coherent sheaf on the stack of unipotent Langlands parameters, the coherent Springer sheaf. As a result the derived category of ℋ-modules is realized as a full subcategory of coherent sheaves on this stack, confirming expectations from strong forms of the local Langlands correspondence (including recent conjectures of Fargues-Scholze, Hellmann and Zhu).
In the case of the general linear group our result allows us to lift the local Langlands classification of irreducible representations to a categorical statement: we construct a full embedding of the derived category of smooth representations of \(\mathrm{GL}_{n}(F)\) into coherent sheaves on the stack of Langlands parameters.
Similar content being viewed by others
1 Introduction
Our goals in this paper are to provide a spectral description of the category of representations of the affine Hecke algebra and deduce applications to the local Langlands correspondence. We begin with a quick review of Springer theory and then discuss our main results starting in Sect. 1.3.
We will work in the setting of derived algebraic geometry over a field \(k\) of characteristic zero, as presented in [45]. In particular all operations, sheaves, categories etc will be derived unless otherwise noted.
1.1 Springer theory and Hecke algebras
We first review some key points of Springer theory, largely following the perspective of [34, 48]. Let \(G\) denote a complex reductive group with Lie algebra \(\mathfrak {g}\) and Borel \(B\subset G\). We denote by \({\mathcal {B}}\simeq G/B\) the flag variety, \({\mathcal {N}}\) the nilpotent cone, \(\mu :\widetilde {\mathcal {N}}=T^{\ast} {\mathcal {B}}\to {\mathcal {N}}\) the Springer resolution, and \({\mathcal {Z}}=\widetilde {\mathcal {N}}\times _{{\mathcal {N}}}\widetilde {\mathcal {N}}\) the Steinberg variety.
The Springer correspondence provides a geometric realization of representations of the Weyl group \(W\) of \(G\). The Weyl group is in bijection with the Bruhat double cosets \(B\backslash G/B=G\backslash ({\mathcal {B}}\times {\mathcal {B}})\), and hence with the conormals to the Schubert varieties, which form the irreducible components of the Steinberg variety \({\mathcal {Z}}\). In fact the group algebra of the Weyl group can be identified with the top Borel-Moore homology of \({\mathcal {Z}}\) under the convolution product
where \(d = \dim ({\mathcal {N}}) = \dim (\widetilde {{\mathcal {N}}}) = \dim ({\mathcal {Z}})\). This realization of \(W\) can be converted into a sheaf-theoretic statement. The Springer sheaf
is the equivariant perverse sheaf on the nilpotent cone given by the pushforward of the (shifted) constant sheaf on the Springer resolution. Thanks to the definition of \({\mathcal {Z}}\) as the self-fiber-product \({\mathcal {Z}}=\widetilde {\mathcal {N}}\times _{{\mathcal {N}}}\widetilde {\mathcal {N}}\), a simple base-change calculation provides an isomorphism
between the endomorphisms of \({\mathbf {S}}\) and the top homology of \({\mathcal {Z}}\), i.e., the group algebra \({\mathbb{C}}W\). By Lusztig’s generalized Springer correspondence [67, Theorem 6.5] the abelian category \(\operatorname {Perv}({\mathcal {N}}/G)\) is semisimple, thus all objects are projective and we may interpret this isomorphism as a full embedding of the abelian category of representations of \(W\) into equivariant perverse sheaves on the nilpotent cone,
One important role for this embedding is provided by the representation theory of Chevalley groups. The universal unipotent principal series representationFootnote 1
has as endomorphism algebra the finite Hecke algebra
which (after choosing a square root of \(q\)) may be identified with \({\mathbb{C}}W\). Thus Springer theory provides a full embedding
where we say a representation of \(G(\mathbb{F}_{q})\) is in the unipotent principal series if it is generated by its \(B(\mathbb{F}_{q})\)-invariants.
1.2 Affine Hecke algebras
We now let \(G\) be a reductive group, Langlands dual to a split group \(G^{\vee}(F)\) over a nonarchimedean local field \(F\) with ring of integers \(O\) and residue field \(\mathbb{F}_{q}\). We write \(G_{\mathrm {gr}}=G\times {\mathbb{G}}_{m}\) as shorthand, which acts on \({\mathcal {Z}}\) by \((g, z) \cdot (x, B, B') = (z^{-1}gxg^{-1}, gB, gB')\).
Definition 1.1
Let \(G\) be a reductive group with maximal torus \(T\). The (extended) affine Weyl group of the dual group \(G^{\vee}\) is the semidirect product \(W_{a} = W \ltimes X_{\bullet}(T^{\vee}) = W \ltimes X^{\bullet}(T)\) of the finite Weyl group with the cocharacter lattice of \(T^{\vee}\). The affine Hecke algebra ℋ is a certain \(q\)-deformation of the group ring \({\mathbb{C}}{W}_{a}\) such that specializing \(q\) at a prime power gives the Iwahori-Hecke algebra:
where \(I \subset G^{\vee}(F)\) is an Iwahori subgroup. Explicit presentations of the affine Hecke algebra can be found, for example, in Sect. 7.1 of [34]. Unlike the finite Hecke algebra, \({\mathcal {H}}_{q} \not\simeq {\mathbb{C}}W_{a}\).
Our starting point is the celebrated theorem of Kazhdan-Lusztig [58] (as later extended and modified by Ginzburg, see [34] and Lusztig [72]), providing a geometric realization of the affine Hecke algebra in terms of the Steinberg variety.
Theorem 1.2
[34, 58, 72] Suppose that \(G\) has simply connected derived subgroup. There is an isomorphism of algebras \(\mathcal {H}\simeq K_{0}({\mathcal {Z}}/G_{\mathrm {gr}}) \otimes _{{\mathbb{Z}}} {\mathbb{C}}\), compatible with the Bernstein isomorphism \(Z(\mathcal {H})\simeq {\mathbb{C}}[G_{\mathrm {gr}}]^{G_{\mathrm {gr}}} \simeq K_{0}^{G_{\mathrm {gr}}}(\operatorname {pt}) \otimes _{ {\mathbb{Z}}} {\mathbb{C}}\) between the center of ℋ and the ring of equivariant parameters.
Kazhdan and Lusztig famously applied Theorem 1.2 to prove the Deligne-Langlands conjecture, as refined by Lusztig. The category of representations of \(\mathcal {H}_{q}\) is identified with the “Iwahori block”, the (smooth) representations of \(G^{\vee}(F)\) that are generated by their \(I\)-invariants (i.e., “appear in the decomposition of \(C^{\infty}_{c}(G^{\vee}(F)/I; \overline {\mathbb{Q}}_{\ell})\)”). Equivalently this is the unramified principal series, the representations of \(G^{\vee}(F)\) appearing in the parabolic induction of unramified characters of a split torus (i.e., “appear in the decomposition of \(C^{\infty}(G^{\vee}(F)/N^{\vee}(F)T^{\vee}(O); \overline {\mathbb{Q}}_{\ell})\)”). The Deligne-Langlands conjecture provides a classification of irreducible representations in the Iwahori block (i.e. with an Iwahori fixed vector), or equivalently irreducible \(\mathcal {H}_{q}\) modules, in terms of Langlands parameters:
Theorem 1.3
[58, 76] The irreducible representations of \(\mathcal {H}_{q}\) are in bijection with \(G\)-conjugacy classes of \(q\)-commuting pairs of semisimple and nilpotent elements in \(G\)
together with a \(G\)-equivariant local system on the orbit of \((s,n)\) which appears in the decomposition of a corresponding Springer sheaf.
For fixed \((s, q)\) the variety \({\mathcal {N}}^{(s,q)}\) of \((s,q)\)-fixed points on the nilpotent cone can be interpreted as a variety of Langlands parameters. Representations with a fixed Langlands parameter \((s, n)\) form an L-packet, and are described in terms of irreducible representations of the component group of the stabilizer. These representations can then be interpreted as equivariant local systems on the orbit of the Langlands parameter. Indeed general conjectures going back to work of Lusztig [66], Zelevinsky [83] and Vogan [82] describe the representation theory of \(G^{\vee}(F)\) at a fixed central character with the geometry of equivariant perverse sheaves on suitable spaces of Langlands parameters, generalizing the appearance of \({\mathcal {N}}^{(s,q)}\) above.
However, unlike the classical Springer theory story for \(\mathcal {H}^{f}_{q} \simeq {\mathbb{C}}W\), the realization of ℋ by equivariant \(K\)-theory in Theorem 1.2 does not immediately lead to a realization of ℋ as endomorphisms of a sheaf, and therefore to a sheaf-theoretic description of the entire category of ℋ-modules. Rather, in applications equivariant \(K\)-theory is used as an intermediate step on the way to equivariant Borel-Moore homology, which leads back to variants of the Springer correspondence. Namely, by fixing a central character for ℋ, i.e. a Weyl group orbit of \((s,q)\in T \times {\mathbb{G}}_{m}\), the central completions of equivariant \(K\)-theory are identified by Lusztig [68, 69] with graded Hecke algebras, which have a geometric description where we replace the nilpotent cone \({\mathcal {N}}\), Springer resolution \(\widetilde {{\mathcal {N}}}\) and Steinberg variety \({\mathcal {Z}}\) by their \((s,q)\)-fixed points. For example, the Chern character identifies the completion of ℋ at the trivial central character with the \(G_{\mathrm {gr}}= G \times {\mathbb{G}}_{m}\)-equivariant homology of the Steinberg variety \({\mathcal {Z}}\). This algebra is identified via Theorem 8.11 of [70] with the full Ext-algebra of the Springer sheaf in the equivariant derived category
Moreover, by a theorem of Rider [77] this Ext algebra is formal, hence we obtain a full embedding
of representations of \({\mathcal {H}}^{gr}\) into the equivariant derived category of the nilpotent cone. More generally, for \((s,q)\in T \times {\mathbb{G}}_{m}\), we have an identification
of the corresponding graded Hecke algebra in terms of an \((s,q)\)-variant of the Springer sheaf. This provides a geometric approach to constructing and studying modulesFootnote 2 of ℋ, see [34].
These developments give satisfying descriptions of the representation theory of ℋ at a fixed central character. However there are numerous motivations to seek a description of families of representations of varying central character, including classical harmonic analysis (for example in the setting of spherical varieties [78]), \(K\)-theory and the Baum-Connes conjecture [3], and modular and integral representation theory [39, 51, 52].
1.3 Coherent Springer theory
In this paper we apply ideas from derived algebraic geometry to deduce from Theorem 1.2 a different, and in some sense simpler, geometric realization of the affine Hecke algebra, in which we first replace \(K\)-theory by Hochschild homology, and then derive a description of its entire category of representations as a category of coherent sheaves (without the need for specifying central characters). For technical reasons, we will need to replace the nilpotent cone \({\mathcal {N}}\) with its formal completion \(\widehat {{\mathcal {N}}} \subset \mathfrak {g}\), and likewise the Steinberg variety \({\mathcal {Z}}= \widetilde {{\mathcal {N}}} \times _{\mathfrak {g}} \widetilde {{\mathcal {N}}}\) will be defined via a derived fiber product. For precise definitions of objects in this context, see Sect. 1.6.3.
Theorem 1.4
Let \(k = \overline {\mathbb{Q}}_{\ell}\) or ℂ, and \(G\) a reductive algebraic group over \(k\). The trace map from connective \(K\)-theory to Hochschild homology on \({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})\) factors through an isomorphism of \(K_{0}\) and \(HH_{\bullet}\) (which is concentrated in cohomological degree zero):

Remark 1.5
Our results also allow for an identification of monodromic variants of the affine Hecke category. See Remark 2.34 for details.
The Hochschild homology of categories of coherent sheaves admits a description in the derived algebraic geometry of loop spaces. In particular, we deduce an isomorphism of the affine Hecke algebra with volume forms on the derived loop space to the Steinberg stack,
More significantly, the geometry of derived loop spaces provides a natural home for the entire category of ℋ-modules, without fixing central characters.
Definition 1.6
Let \(\widehat {{\mathcal {N}}} \subset \mathfrak {g}\) be the formal completionFootnote 3 of the nilpotent cone, \(\widetilde {{\mathcal {N}}}\) the usual (reduced) Springer resolution and \(\mu : \widetilde {{\mathcal {N}}} \rightarrow {\mathcal {N}}\hookrightarrow \widehat {{\mathcal {N}}}\) the composition of the Springer resolution with the inclusion. The coherent Springer sheaf \({\mathcal {S}}_{G} \in {\operatorname {Coh}}({\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}}))\) (or simply \({\mathcal {S}}\)) is the pushforward of the structure sheaf under the loop map \({\mathcal {L}}\mu :{\mathcal {L}}(\widetilde {\mathcal {N}}/G_{\mathrm {gr}})\to {\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})\):
Equivalently, \({\mathcal {S}}_{G}\) is given by applying the parabolic induction correspondence

to the (reduced) structure sheaf of \({\mathcal {L}}({\{0\}}/T)\).
A priori the coherent Springer sheaf is only a complex of sheaves. However we show, using the theory of traces for monoidal categories in higher algebra, that its Ext algebra is concentrated in degree zero, and is identified with the affine Hecke algebra. This provides the following “coherent Springer correspondence”, realizing the representations of the affine Hecke algebra as coherent sheaves.
Theorem 1.7
Theorem 4.12
Let \(G\) be a reductive algebraic group over \(k = \overline {\mathbb{Q}}_{\ell}\) or ℂ.
-
(1)
There is an isomorphism of algebras \(\mathcal {H}_{G}\simeq \operatorname {End}_{{\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})}({\mathcal {S}}_{G})\) and all other self-\(\operatorname{Ext}\) groups of \({\mathcal {S}}_{G}\) vanish.
-
(2)
There is an embedding of dg derived categories
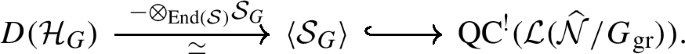
-
(3)
The embedding takes the anti-spherical module to the projection of the dualizing sheaf to the Springer subcategory
$$ D(\mathcal {H}_{G}) \ni \operatorname{Ind}_{{\mathcal {H}}^{f}}^{{\mathcal {H}}}(\mathrm{sgn}) \longmapsto \mathrm{pr}_{{\mathcal {S}}_{G}}(\omega _{{\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})}) \in \operatorname {QC}^{!}( {\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})). $$ -
(4)
The embedding is compatible with parabolic induction of affine Hecke algebras, i.e. if \(P\) is a parabolic subgroup of \(G\) with Levi quotient \(M\), then there is a commuting diagram
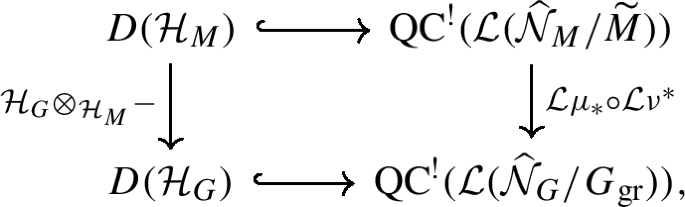
where \({\mathcal {L}}\mu _{*} \circ {\mathcal {L}}\nu ^{*}\) is the pull-push along the correspondence obtained by applying ℒ to the usual parabolic induction correspondence
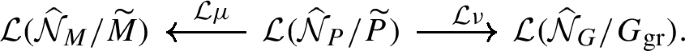
In particular, \({\mathcal {L}}\mu _{*} {\mathcal {L}}\nu ^{*} {\mathcal {S}}_{M} \simeq {\mathcal {S}}_{G}\).
One consequence of the theorem is an interpretation of the coherent Springer sheaf as a universal family of ℋ-modules.
We also conjecture (Conjecture 4.15) – and check for \(SL_{2}\) – that \({\mathcal {S}}\) is actually a coherent sheaf (i.e., lives in the heart of the standard t-structure on coherent sheaves). The vanishing of all nonzero Ext groups of \({\mathcal {S}}\) suggests the existence of a natural “exotic” t-structure for which \({\mathcal {S}}\) is a compact projective object in the heart. For such a t-structure we would then automatically obtain a full embedding of the abelian category \(\mathcal {H}{\operatorname {-mod}}\) into “exotic” coherent sheaves, where one could expect a geometric description of simple objects.
In [13] we will explain how equivariant localization and Koszul duality patterns in derived algebraic geometry (as developed in [6, 31, 32]) provide the precise compatibility between this coherent Springer theory and the usual perverse Springer theory, one parameter at a time.
1.4 Applications to the local Langlands correspondence
We will consider a derived stack \({\mathbb{L}}_{q,G}^{u}\) of unipotent Langlands parameters, which parametrizes the unipotent Weil-Deligne representations for a local field \(F\) with residue field \(\mathbb{F}_{q}\), and whose set of \(k\)-points is a variant of the set of Deligne-Langlands parameters in Theorem 1.3 (with semisimplicity of \(s\) dropped). Note that the following notions make sense for any \(q \in \mathbb{C}\), with applications to local Langlands when \(q\) is a prime power, and that, in line with expectations, the stack of unipotent Langlands parameters depends only on the order of the residue field of \(F\).
Definition 1.8
Let \(q = p^{r}\) be a prime power.
-
(1)
The stack of unipotent Langlands parameters \({\mathbb{L}}_{q,G}^{u}= {\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)\) (or simply \({\mathbb{L}}_{q}^{u}\)) is the derived fixed point stack of multiplication by \(q\in {\mathbb{G}}_{m}\) on \(\widehat {{\mathcal {N}}}/G\). Equivalently, it is the fiber of the loop (or derived inertia) stack of the nilpotent cone over \(q\in {\mathbb{G}}_{m}\),

By Proposition 4.3, the derived inf-stack \({\mathbb{L}}_{q,G}^{u}\) has no derived nor infinitesimal structure, i.e. \({\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G) = {\mathcal {L}}_{q}(\mathfrak {g}/G)\), and by [35] it is reduced, so we may equivalently define \({\mathbb{L}}_{q,G}^{u}\) using the classical fiber product of the reduced nilpotent cone \({\mathcal {N}}\), i.e.
$$ {\mathbb{L}}_{q,G}^{u} \simeq \{g\in G, n\in {\mathcal {N}}: gng^{-1}=qn\}/G. $$ -
(2)
The \(q\)-coherent Springer sheaf \({\mathcal {S}}_{q,G}\in {\operatorname {Coh}}({\mathbb{L}}_{q}^{u})\) (or simply \({\mathcal {S}}_{q}\)) is the ∗-specialization of \({\mathcal {S}}_{G}\) to the fiber \({\mathbb{L}}_{q}^{u}\) over \(q\). Equivalently, \({\mathcal {S}}_{q,G}\) is given by applying the parabolic induction correspondence

to the structure sheaf of \({\mathbb{L}}_{q,T}^{u} \simeq T \times BT\).
Specializing Theorem 1.7 to \(q\in {\mathbb{G}}_{m}\) we obtain the following. Note that Theorem 2.2, Proposition 2.4 and Corollary 2.5 of [75] apply in the case where \(q\) is specialized away from roots of unity; in particular, \({\mathcal {H}}_{q,G}\) has finite cohomological dimension if \(q\) is not a root of unity. Thus in the following statement we implicitly identify the compact objects \(D_{perf}(\mathcal {H}_{G}) \subset D(\mathcal {H}_{G})\) (i.e. the subcategory of perfect complexes) with the bounded derived category of coherent complexes.
Theorem 1.9
Theorem 4.12
Suppose that \(q = p^{r}\) is a prime power (or more generally, \(q \in {\mathbb{G}}_{m}\) is not a root of unity), and let \(G\) be a reductive algebraic group over \(k = \overline {\mathbb{Q}}_{\ell}\) or ℂ.
-
(1)
There an isomorphism of algebras \({\mathcal {H}}_{q,G} \simeq \operatorname {End}_{{\mathbb{L}}_{q,G}}({\mathcal {S}}_{q,G})\) and a full embedding
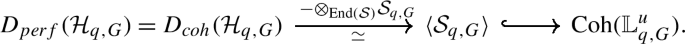
In particular, this gives a full embedding of the principal block of \(G^{\vee}(F)\) into coherent sheaves on the stack of unipotent Langlands parameters.
-
(2)
The embedding takes the anti-spherical module to the structure sheaf \({\mathcal {O}}_{{\mathbb{L}}_{q,G}^{u}} \in {\operatorname {Coh}}({\mathbb{L}}_{q,G}^{u})\).
-
(3)
The embedding is compatible with parabolic induction, i.e. if \(P^{\vee} \subset G^{\vee}\) is a parabolic with quotient Levi \(M^{\vee}\), then we have a commutative diagram
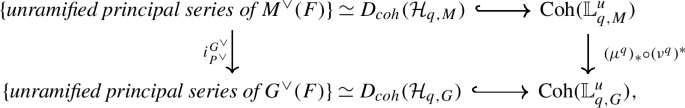
where \(i_{P^{\vee}}^{G^{\vee}}: \operatorname {Rep}^{sm}_{f.g.}(M^{\vee}(F)) \rightarrow \operatorname {Rep}^{sm}_{f.g.}(G^{\vee}(F))\) is the parabolic induction functor from smooth finitely-generatedFootnote 4reprentations of \(M^{\vee}(F)\) to \(G^{\vee}(F)\) restricted to the unramified principal series, and the map \((\mu ^{q})_{*} \circ (\nu ^{q})^{*}\) is the pull-push along the correspondence obtained by applying taking derived \(q\)-invariants of the usual parabolic induction correspondence
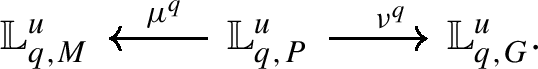
In particular, \((\mu ^{q})_{*} (\nu ^{q})^{*} {\mathcal {S}}_{q,M} \simeq {\mathcal {S}}_{q,G}\).
Note that due to Proposition 4.3, in the \(q\)-specialized setting of the above theorem the stack of parameters has no infinitesimal structure, i.e. \({\mathcal {L}}_{q}(\mathfrak {g}/G) = {\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)\). This has two consequences: first, due to Proposition 3.12, which does not apply in the context of Theorem 1.7, we may identify the anti-spherical sheaf at specialized \(q\) with the structure sheaf, which is equivalent to the dualizing sheaf. Second, the anti-spherical sheaf at specialized \(q\) is a compact object in the category, i.e. a coherent sheaf, whereas the sheaf appearing in Theorem 1.7 is not.
The existence of such an equivalence was conjectured independently by Hellmann in [50], whose work we learned of at a late stage in the preparation of his paper. Indeed, the above result resolves Conjecture 3.2 of [50]. Hellmann’s work also gives an alternative characterization of the (\(q\)-specialized) coherent Springer sheaf as the Iwahori invariants of a certain family of admissible representations on \({\mathbb{L}}_{q,G}^{u}\) constructed by Emerton and the third author in [39].
A much more general categorical form of the local Langlands correspondence is formulated by Fargues-Scholze [41] and Zhu [86], as well as compatibility with a categorical global Langlands correspondence. In loc. cit. a forthcoming proof by Hemo and Zhu [53] of a result closely parallel to ours is also announced.
Remark 1.10
The local Langlands correspondence depends on a choice of Whittaker normalization; that is, a choice of a pair \((U,\psi )\), where \(U\) is the unipotent radical of a Borel subgroup of \(G^{\vee}\) and \(\psi \) is a generic character of \(U(F)\), up to \(G^{\vee}(F)\)-conjugacy, and indeed, the conjecture in [50] and the announced result in [53] depend on such a choice. In the formulation of Theorem 1.9 no such choice appears explicitly, but instead comes from the integral structure on \(G^{\vee}\), which in particular gives us a distinguished hyperspecial subgroup \(G^{\vee}(O)\) of \(G^{\vee}(F)\).
Indeed, for any unramified group \(G^{\vee}\) over \(F\) there is a natural bijection between \(G^{\vee}(F)\)-conjugacy classes of Whittaker data \((U,\psi )\) for \(G^{\vee}\) and \(G^{\vee}(F)\)-conjugacy classes of triples \((K_{x}, U_{x}, \psi _{x})\), where \(K_{x}\) is a hyperspecial subgroup of \(G^{\vee}(F)\), \(U_{x}\) is the unipotent radical of a Borel subgroup of the reductive quotient \(G^{\vee}_{x}\) of \(K_{x}\), and \(\psi _{x}\) is a generic character of \(U_{x}\). This bijection has the property that if \((U,\psi )\) corresponds to \((K_{x},U_{x},\psi _{x})\), then the summand of the compact induction \(\operatorname {cInd}_{U(F)}^{G^{\vee}(F)} \psi \) corresponding to the unipotent principal series block is isomorphic to \(\operatorname {cInd}_{K_{x}}^{G^{\vee}(F)} \operatorname{St}_{x}\), where \(\operatorname{St}_{x}\) denotes the inflation to \(K_{x}\) of the Steinberg representation of the reductive quotient \(G^{\vee}_{x}\). In particular the “unipotent principal series part” of \(\operatorname {cInd}_{U(F)}^{G^{\vee}(F)} \psi \) depends only on the conjugacy class of hyperspecial subgroup associated to \((U,\psi )\), and not the whole tuple \((K_{x}, U_{x}, \psi _{x})\). This means that the restriction of the local Langlands correspondence to the unramified principal series depends only on a choice of hyperspecial subgroup (which we have fixed).
Note in particular that for any choice of Whittaker datum \((U,\psi )\) compatible with our hyperspecial subgroup \(G^{\vee}(O)\), the \(\mathcal {H}_{q,G}\)-module associated to the compact induction \(\operatorname {cInd}_{U(F)}^{G^{\vee}(F)} \psi \) is precisely the antispherical module, so property (2) of Theorem 1.9 is consistent with (and indeed, equivalent to) the Whittaker normalization appearing in [50].
In the case of the general linear group and its Levi subgroups, one can go much further. Namely, in Sect. 5 we combine the local Langlands classification of irreducible representations due to Harris-Taylor and Henniart with the Bushnell-Kutzko theory of types and the ensuing inductive reduction of all representations to the principal block. The result is a spectral description of the entire category of smooth \(\operatorname {GL}_{n}(F)\) representations. To do so it is imperative to first have a suitable stack of Langlands parameters. These have been studied extensively in mixed characteristic, for instance in [51] in the case of \(\operatorname {GL}_{n}\), or more recently in [4, 24], and [35] for more general groups. Since in our present context we work over ℂ, the results we need are in general simpler than the results of the above papers, and have not appeared explicitly in the literature in the form we need.
Theorem 1.11
[51]
Let \(F\) be a local field with residue field \(\mathbb{F}_{q}\). There is a classical Artin stack locally of finite type \(\mathbb{L}_{F,\operatorname {GL}_{n}}\), with the following properties:
-
(1)
The \(k\)-points of \(\mathbb{L}_{F,\operatorname {GL}_{n}}\) are identified with the groupoid of continuous \(n\)-dimensional representations of the Weil-Deligne group of \(F\).
-
(2)
The formal deformation spaces of Weil-Deligne representations are identified with the formal completions of \(\mathbb{L}_{F,\operatorname {GL}_{n}}\).
-
(3)
The stack \({\mathbb{L}}_{q,\operatorname {GL}_{n}}^{u}\) of unipotent Langlands parameters is a connected component of \(\mathbb{L}_{F,\operatorname {GL}_{n}}\).
We then deduce a categorical local Langlands correspondence for \(\operatorname {GL}_{n}\) and its Levi subgroups as follows:
Theorem 1.12
For each Levi subgroup \(M\) of \(\operatorname {GL}_{n}(F)\), there is a full embedding
of the derived category of smooth \(M\)-representations into ind-coherent sheaves on the stack of Langlands parameters, uniquely characterized by the following properties.
-
(1)
If \(\pi \) is an irreducible cuspidal representation of \(M\), then the image of \(\pi \) under this embedding is the skyscraper sheaf supported at the Langlands parameter associated to \(\pi \).
-
(2)
Let \(M'\) be a Levi subgroup of \(G\), and let \(P\) be a parabolic subgroup of \(M'\) with Levi subgroup \(M\). There is a commutative diagram of functors:
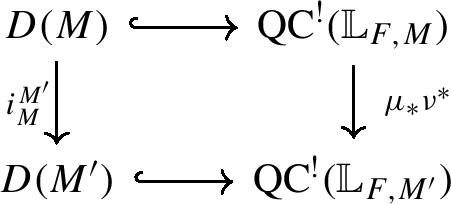
in which \(i_{M}^{M'}\) is the parabolic induction functor and the right-hand map is obtained by applying the correspondence
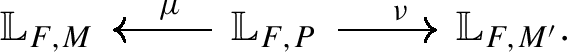
Note that the local Langlands correspondence for cuspidal representations of \(\operatorname {GL}_{n}\) and its Levis, is an input to the above result. We do not expect the functor to be an equivalence, see Remark 4.13.
As with Theorem 1.9 our results here were independently conjectured by Hellmann (see in particular Conjecture 3.2 of [50]) for more general groups \(G\); these results also fit the general categorical form of the local Langlands correspondence formulated by Fargues-Scholze [41] and Zhu [86].
1.4.1 Discussion: categorical Langlands correspondence
Theorems 1.9 and 1.12 match the expectation in the Langlands program that has emerged in the last couple of years for a strong form of the local Langlands correspondence, in which categories of representations of groups over local fields are identified with categories of coherent sheaves on stacks of Langlands parameters. Such a coherent formulation of the real local Langlands correspondence was discovered in [6], while the current paper finds a closely analogous picture in the Deligne-Langlands setting. As this paper was being completed Xinwen Zhu shared the excellent overview [86] on this topic and Laurent Fargues and Peter Scholze completed the manuscript [41], to which we refer the reader for more details. We only briefly mention three deep recent developments in this general spirit.
The first derives from the work of V. Lafforgue on the global Langlands correspondence over function fields [60, 61]. Lafforgue’s construction in Drinfeld’s interpretation (cf. [62, Sect. 6], [61, Remark 8.5] and [44]) predicts the existence of a universal quasicoherent sheaf \({\mathfrak {A}}_{X}\) on the stack of representations of \(\pi _{1}(X)\) into \(G\) corresponding to the cohomology of moduli spaces of shtukas. The theorem of Genestier-Lafforgue [47] implies that the category of smooth \(G^{\vee}(F)\) representations sheafifies over a stack of local Langlands parameters, and the local version \({\mathfrak {A}}\) of the Drinfeld-Lafforgue sheaf is expected [86] to be a universal \(G^{\vee}(F)\)-module over the stack of local Langlands parameters. In other words, the fibers \({\mathfrak {A}}_{\sigma}\) are built out of the \(G^{\vee}(F)\)-representations in the L-packet labelled by \(\sigma \). The expectation is that the coherent Springer sheaf, which by our results is naturally enriched in \(\mathcal {H}_{q}\)-modules, is identified with the Iwahori invariants of the local Lafforgue sheaf \({\mathcal {S}}_{q}\simeq {\mathfrak {A}}^{I}\).
The second is the theory of categorical traces of Frobenius as developed in [44, 46, 85]. When applied to a suitably formulated local geometric Langlands correspondence, we obtain an expected equivalence between an automorphic and spectral category. The automorphic category is \(\operatorname {Sh}(G^{\vee}(F)/^{\operatorname {Fr}} G^{\vee}(F))\), the category of Frobenius-twisted adjoint equivariant sheaves on \(G^{\vee}(F)\), with orbits given by the Kottwitz set \(B(G^{\vee})\) of isomorphism classes of \(G^{\vee}\)-isocrystals. The spectral category is expected to be a variant of a category \(\operatorname {QC}^{!}({\mathbb{L}}_{F,G})\) of ind-coherent sheaves over the stack \({\mathbb{L}}_{F,G}\) of Langlands parameters into \(G\). The former category contains the categories of representations of \(G^{\vee}(F)\) and its inner forms as full subcategories, hence we expect a spectral realization in the spirit of Theorems 1.9 and 1.12.
The last of these developments is the program of Fargues-Scholze [40, 41] in the context of \(p\)-adic groups, which interprets the local Langlands correspondence as a geometric Langlands correspondence. On the automorphic side one considers sheaves on the stack \(\operatorname {Bun}_{G^{\vee}}\) of bundles on the Fargues-Fontaine curve, whose isomorphism classes \(|\operatorname {Bun}_{G^{\vee}}|=B(G^{\vee})\) are given as before by the Kottwitz set of \(G^{\vee}\)-isocrystals. This category of sheaves admits a semiorthogonal decomposition indexed by \(B(G^{\vee})\), in which the factor corresponding to \(b \in B(G^{\vee})\) is naturally equivalent to the category of smooth representations of the inner form \(G^{\vee}_{b}(F)\) arising from \(b\). On the spectral side of the picture is the same category of ind-coherent sheaves on the moduli stack of Langlands parameter that we study. Fargues-Scholze construct a spectral action of the category of perfect complexes on this moduli stack on the category of \(\ell \)-adic sheaves on \(\operatorname {Bun}_{G^{\vee}}\), and conjecture that there is an equivalence of this category with the category of ind-coherent sheaves on the moduli stack of Langlands parameters compatible with this spectral action. Such an equivalence necessarily has the properties given in Theorem 1.12, although we do not attempt to verify that our construction is compatible with that of Fargues-Scholze.
1.5 Methods
We now discuss the techniques underlying the proofs of Theorems 1.4 and 1.7 – namely, Bezrukavnikov’s Langlands duality for the affine Hecke category and the theory of traces of monoidal dg categories.
1.5.1 Bezrukavnikov’s theorem
The Kazhdan-Lusztig theorem (Theorem 1.2) has been famously categorified in the work of Bezrukavnikov [17, 18], with numerous applications in representation theory and the local geometric Langlands correspondence (see Theorem 2.17).
Theorem 1.13
Let \(\mathbf{G} := G^{\vee}(\overline{{\mathbb{F}}}_{q}((t)))\) denote the loop group viewed as an ind-scheme, and \(\mathbf{I} \subset \mathbf{G}\) denote the corresponding Iwahori subgroup. We define the (derived) Steinberg stack \({\mathcal {Z}}/G\) over \(\overline {\mathbb{Q}}_{\ell}\). There is a monoidal equivalence on homotopy categories
intertwining the pullback by geometric Frobenius and pushforward by multiplication by \(q\) automorphisms.
Remark 1.14
In view of Theorem 1.13, we define the affine Hecke category to be \(\mathbf {H}:= {\operatorname {Coh}}({\mathcal {Z}}/G)\). It is natural to expect a mixed version, identifying the mixed affine Hecke category \(\mathbf {H}^{{\mathrm {m}}}:= {\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})\) with the mixed Iwahori-equivariant sheaves on the affine flag variety (as studied in [19]). Indeed such a version is needed to directly imply the Kazhdan-Lusztig Theorem 1.2 by passing to Grothendieck groups, rather than its specialization at \(q=1\).
Theorem 1.13 establishes the “principal block” part of the local geometric Langlands correspondence. Namely, it implies a spectral description of module categories for the affine Hecke category (the geometric counterpart of unramified principal series representations) as suitable sheaves of categories on stacks of Langlands parameters.
We apply Theorem 1.13 in Sect. 2 to construct a semiorthogonal decomposition of the affine Hecke category. This allows us to calculate its Hochschild homology and to establish the comparison with algebraic K-theory.
1.5.2 Trace decategorifications
To prove Theorem 1.7 we use the relation between the “horizontal” and “vertical” trace decategorifications of a monoidal category, and the calculation of the subtler horizontal trace of the affine Hecke category in [12].
Let \((\mathbf {C},\ast )\) denote a monoidal dg category. Then we can take the trace (or Hochschild homology) \(\mathrm{tr}(\mathbf {C})=HH(\mathbf {C})\) of the underlying (i.e. ignoring the monoidal structure) dg category \(\mathbf {C}\), which forms an associative (or \(A_{\infty}\)-)algebra \((\mathrm{tr}(\mathbf {C}),\ast )\) thanks to the functoriality (specifically the symmetric monoidal structure) of Hochschild homology, as developed in [30, 46, 55, 79]. This is the naive or “vertical” trace of \(\mathbf {C}\). On the other hand, a monoidal dg category has another trace or Hochschild homology \({\mathbf {Tr}}(\mathbf {C},\ast )\) using the monoidal structure which is itself a dg category – the categorical or “horizontal” trace of \((\mathbf {C},\ast )\). This is the dg category which is the universal receptacle of a trace functor out of the monoidal category \(\mathbf {C}\). In particular, the trace of the monoidal unit of \(\mathbf {C}\) defines an object \([1_{\mathbf {C}}]\in {\mathbf {Tr}}(\mathbf {C},\ast )\) – i.e., \({\mathbf {Tr}}(\mathbf {C},\ast )\) is a pointed (or \(E_{0}\)-)category.Footnote 5 Moreover, as developed in [30, 46] the categorical trace provides a “delooping” of the naive trace: we have an isomorphism of associative algebras
In particular taking Hom from \([1_{\mathbf {C}}]\) defines a functor
Under suitable compactness assumptions the left adjoint to this functor embeds the “naive” decategorification (the right hand side) as a full subcategory of the “smart” decategorification (the left hand side).
More generally, given a monoidal endofunctor \(F\) of \((\mathbf {C},\ast )\), we can replace Hochschild homology (trace of the identity) by trace of the functor \(F\), obtaining two decategorifications (vertical and horizontal) with a similar relation
Remark 1.15
Trace of Frobenius
When \(\mathbf {C}\) is a category of \(\ell \)-adic sheaves on a stack defined over \({\mathbb{F}}_{q}\) extended to \(\overline{{\mathbb{F}}}_{q}\) and \(\operatorname {Fr}\) is the corresponding geometric Frobenius morphism, a formalism of categorical traces realizing the function-sheaf correspondence – i.e. \(\mathrm{tr}(\operatorname {Sh}(X), \operatorname {Fr}^{*})\) should be the space of functions on \(X({\mathbb{F}}_{q})\) – was recently established in [1]. The monoidal version of trace decategorification would then allow us to pass from Hecke categories to categories of representations directly. Zhu [85] explains some of the rich consequences of this formalism that can already be proved directly.
Example 1.16
Finite Hecke Categories and unipotent representations
For the finite Hecke category \(\mathbf {C}=\operatorname {Sh}(B\backslash G/B)\), the main theorem of [7] identifies \({\mathbf {Tr}}(\mathbf {C},\ast )\) with the full category of Lusztig unipotent character sheaves on \(G\). The object \([1_{\mathbf {C}}]\) is the Springer sheaf itself, and modules for the naive decategorification \((\mathrm{tr}(\mathbf {C}, \mathrm{id}_{\mathbf {C}}), \ast )\) gives the Springer block, or unipotent principal series character sheaves, as modules for the graded Hecke algebra. Likewise the trace of Frobenius on \((\mathbf {C},\ast )\) is studied in [85, Sect. 3.2] (see also [44, Sect. 3.2]), where the categorical trace is the category of all unipotent representations of \(G({\mathbb{F}}_{q})\), and the coherent Springer sheaf \([1_{\mathbf {C}}]\) generates the full subcategory consisting of the unipotent principal series, equivalent to modules for the naive decategorification \((\mathrm{tr}(\mathbf {C}, \operatorname {Fr}), \ast )\).
1.5.3 Trace of the affine Hecke category
We now consider the two kinds of trace decategorification for the affine Hecke category \(\mathbf {H}\). First our description of the Hochschild homology of the Steinberg stack provides a precise sense in which the affine Hecke category categorifies the affine Hecke algebra. The following Corollary is a result of Theorems 1.13 and 1.4.
Corollary 1.17
The (vertical/naive) trace of Frobenius on the affine Hecke category is identified with the affine Hecke algebra \({\mathcal {H}}_{q} \simeq \mathrm{tr}(\mathbf {H}, \operatorname {Fr}^{*})\). Hence the naive decategorification of \(\mathbf {H}{\operatorname {-mod}}\) is the category of unramified principal series representations of \(G^{\vee}(F)\).
Remark 1.18
Note that this corollary would follow directly from Theorem 1.13 if we had available the hoped-for function-sheaf dictionary for traces of Frobenius on categories of \(\ell \)-adic sheaves (Remark 1.15). After this paper was complete Xinwen Zhu informed us that Hemo and he have a direct argument for this corollary, see the forthcoming [53]. Combined with Bezrukavnikov’s theorem and Theorem 1.19 this gives an alternative argument for the identification of \(\mathcal {H}_{q}\) with the Ext algebra of the coherent Springer sheaf.
The results of [12] (based on the technical results of [11]) provide an affine analog of the results of [7, 20] for finite Hecke categories and (thanks to Theorem 1.13) a spectral description of the full decategorification of \(\mathbf {H}\). Statement (1) is directly taken from Theorem 4.4.1 in [12], statements (2)-(3) follow immediately from the same techniques and Theorem 3.8.5 of [46] (see Theorems 3.4 and 3.23 and Lemma 3.24), and the absence of a singular support condition is discussed in Remark 4.14.
Theorem 1.19
[12]
Let \(G\) be a reductive group over \(k = \overline {\mathbb{Q}}_{\ell}\) or ℂ.
-
(1)
The (horizontal/categorical) trace of the monoidal category \(({\operatorname {Coh}}({\mathcal {Z}}/G),\ast )\) is identified as
$$ {\mathbf {Tr}}({\operatorname {Coh}}({\mathcal {Z}}/G),*) = {\operatorname {Coh}}({\mathcal {L}}(\widehat {{\mathcal {N}}}/G)). $$The same assertion holds with \(G\) replaced by \(G_{\mathrm {gr}}=G\times {\mathbb{G}}_{m}\).
-
(2)
The trace of multiplication by \(q \in {\mathbb{G}}_{m}\) acting on the monoidal category \(({\operatorname {Coh}}({\mathcal {Z}}/G),\ast )\) is identified as
$$ {\mathbf {Tr}}(({\operatorname {Coh}}({\mathcal {Z}}/G),*), q_{*}) = {\operatorname {Coh}}({\mathbb{L}}_{q}^{u}). $$ -
(3)
The distinguished object \([1_{\mathbf {C}}]\) in each of these trace decategorifications is given by the coherent Springer sheaf \({\mathcal {S}}\) (or its \(q\)-specialized version \({\mathcal {S}}_{q}\)). Hence the endomorphisms of the coherent Springer sheaf recover the affine Hecke algebra (the vertical trace, as in Theorem 1.7), and the natural functor in Theorem 3.4is identified with
$$ \operatorname{Hom}({\mathcal {S}}_{q},-): {\operatorname {Coh}}({\mathbb{L}}_{q}^{u})\longrightarrow \mathcal {H}_{q} {\operatorname {-mod}}. $$
In other words, we identify the entire category of coherent sheaves on the stack of unipotent Langlands parameters as the categorical trace of the affine Hecke category. Inside we find the unramified principal series as modules for the naive trace (the Springer block). Just as the decategorification of the finite Hecke category (Example 1.16) knows all unipotent representations of Chevalley groups, the horizontal trace \({\operatorname {Coh}}({\mathbb{L}}_{q}^{u})\) of the affine Hecke category contains in particular all unipotent representations of \(G^{\vee}(F)\) – i.e., the complete L-packets of unramified principal series representations – thanks to Lusztig’s remarkable Langlands duality for unipotent representations:
Theorem 1.20
[71]
The irreducible unipotent representations of \(G^{\vee}(F)\) are in bijection with \(G\)-conjugacy classes of triples \((s,n,\chi )\) with \(s\), \(n\) \(q\)-commuting as in Theorem 1.3and \(\chi \) an arbitrary \(G\)-equivariant local system on the orbit of \((s,n)\).
It would be extremely interesting to understand Theorem 1.20 using trace decategorification of Bezrukavnikov’s Theorem 1.13. In particular we expect the full category of unipotent representations to be embedded in \(\operatorname {QC}^{!}({\mathbb{L}}_{q}^{u})\).
1.6 Assumptions and notation
We work throughout over a field \(k\) of characteristic zero. Our results on traces hold in this general setting, though most representation theoretic applications will be in the specific case of \(k = \overline {\mathbb{Q}}_{\ell}\) or ℂ (e.g. in Sect. 2.2). All functors and categories are dg derived unless noted otherwise.
1.6.1 Categories
We work in the setting of \(k\)-linear stable \(\infty \)-categories, which for us will arise via applying the dg nerve construction (Construction 1.3.1.6 of [65]) to a pre-triangulated dg category. These come in two primary flavors, “big” and “small”: \(\mathbf {dgCat}_{k}\) is the \(\infty \)-category of presentable stable \(k\)-linear \(\infty \)-categories (with colimit-preserving functors), and \(\mathbf {dgcat}_{k}\) is the \(\infty \)-category of small idempotent-complete stable \(k\)-linear \(\infty \)-categories (with exact functors). We denote the compact objects in a stable \(\infty \)-category \(\mathbf {C}\) by \(\mathbf {C}^{\omega}\), i.e. the objects \(X \in \mathbf {C}\) for which \(\operatorname{Hom}_{\mathbf {C}}(X, -)\) commutes with all infinite direct sums. Both \(\mathbf {dgCat}_{k}\) and \(\mathbf {dgcat}_{k}\) are symmetric monoidal \(\infty \)-categories under the Lurie tensor product, with units \(\mathbf {Vect}_{k} = k\text{-}\mathrm {mod}\in \mathbf {dgCat}_{k}\) and \(\mathbf {Perf}_{k} = k\text{-}\mathrm {perf}\in \mathbf {dgcat}_{k}\) the dg categories of chain complexes of \(k\)-vector spaces and perfect chain complexes, respectively. We have a symmetric monoidal ind-completion functor:
It defines an equivalence between \(\mathbf {dgcat}_{k}\) and the subcategory of \(\mathbf {dgCat}_{k}\) defined by compactly generated categories and compact functors (functors preserving compact objects, or equivalently, possessing colimit preserving right adjoints).
Let \(A\) be a Noetherian dg algebra. We let \(A\text{-}\mathrm {mod}= D(A) \in \mathbf {dgCat}_{k}\) denote the dg derived category of \(A\)-modules, \(A\text{-}\mathrm {perf}= D_{perf}(A) \in \mathbf {dgcat}_{k}\) denote the full subcategory of perfect complexes, and \(A\text{-}\mathrm {coh}= D_{coh}(A)\) denote the full subcategory of cohomologically bounded complexes with coherent (i.e. finitely generated) cohomology. Let \(\mathbf {C}\) denote a symmetric monoidal dg category, and \(A \in \mathrm{Alg}(\mathbf {C})\) an algebra object. We denote by \(A\text{-}\mathrm {mod}_{\mathbf {C}}\) (resp. \(A\text{-}\mathrm {perf}_{\mathbf {C}}\)) the category of \(A\)-module (resp. \(A\)-perfect) objects in \(\mathbf {C}\); the category \(A\text{-}\mathrm {mod}_{\mathbf {C}}\) is compactly generated by \(A\text{-}\mathrm {perf}_{\mathbf {C}}\). When \(\mathbf {A} \in \mathbf {dgCat}_{k}\) is a cocomplete monoidal category, we denote by \(\mathbf {A}\text{-}\mathbf {mod}\) the \((\infty , 2)\)-category of \(\mathbf {A}\)-modules in \(\mathbf {dgCat}_{k}\), i.e. cocomplete \(\mathbf {A}\)-module categories (see Sect. 3.6 of [46] for a definition).
Assume that \(\mathbf {C}\) is either small or that it is compactly generated, and let \(X \in \mathbf {C}\) be an object, which we require to be compact in the latter case. The notation \(\langle X \rangle \) denotes the subcategory classically generated by \(X\) when \(\mathbf {C}\) is small (i.e. the smallest pretriangulated idempotent-complete subcategory containing \(X\)), and weakly generated by \(X\) when \(\mathbf {C}\) is cocomplete and compactly generated (i.e. the essential image of the left adjoint of \(\operatorname{Hom}_{\mathbf {C}}(X, -)\)).
1.6.2 Algebraic geometry
In Sect. 3, we work in the setting of derived algebraic geometry over an arbitrary field \(k\) of characteristic zero as in [45]. Namely, this is a version of algebraic geometry in which functors of (discrete) categories from rings to sets are replaced by prestacks, functors of (\(\infty \)-)categories from connective commutative dg \(k\)-algebras to simplicial sets. Examples of prestacks are given by both classical schemes and stacks and topological spaces (or rather the corresponding simplicial sets of singular chains) such as \(S^{1}\), considered as constant functors.
We will only be concerned with QCA (derived) stacks (or their formal completions along closed substacks) as in [38], i.e., quasi-compact stacks of finite presentation with affineFootnote 6 finitely-presented diagonal (in fact only with quotients of schemes by affine group-schemes and their formal completions along closed substacks), and use the term stack to refer to such an object.
A stack \(X\) carries a symmetric monoidal \(\infty \)-category \(\operatorname {QC}(X) \in \mathbf {dgCat}_{k}\) of quasicoherent sheaves, defined by right Kan extension from the case of representable functors \(X=\operatorname {Spec}(R)\) which are assigned \(\operatorname {QC}(\operatorname {Spec}R)=R{\operatorname {-mod}}\). For all stacks we will encounter (and more generally for perfect stacks in the sense of [9]), we have \(\operatorname {QC}(X)\simeq \operatorname{Ind}(\operatorname {Perf}(X))\), i.e., quasicoherent sheaves are compactly generated and the compact objects are perfect complexes.
We can also consider the category \(\operatorname {QC}^{!}(X) \in \mathbf {dgCat}_{k}\) of ind-coherent sheaves, whose theory is developed in detail in the book [45] (see also the earlier [43]). The category \(\operatorname {QC}^{!}(X)\) (under our assumption that \(X\) is QCA) is compactly generated by \({\operatorname {Coh}}(X)\), the objects which are coherent after smooth pullback to a scheme (see Theorem 3.3.5 of [38]). For smooth \(X\), the notions of coherent and perfect, hence ind-coherent and quasicoherent, sheaves are equivalent.
A crucial formalism developed in detail in [45] is the functoriality of \(\operatorname {QC}^{!}\). Namely for an almost finite-type map \(p:X\to Y\) of stacks, we have colimit-preserving functors of pushforward \(p_{*}:\operatorname {QC}^{!}(X)\to \operatorname {QC}^{!}(Y)\) and exceptional pullback \(p^{!}:\operatorname {QC}^{!}(Y)\to \operatorname {QC}^{!}(X)\), which form an adjoint pair \((p_{*},p^{!})\) for \(p\) proper. These functors satisfy a strong form of base change, which makes \(\operatorname {QC}^{!}\) a functor – in fact a symmetric monoidal functorFootnote 7 – out of the category of correspondences of stacks (the strongest form of this result is [45, Theorem III.3.5.4.3, III.3.6.3]).
We note that for a closed substack \(Z \subset X\), the category of quasicoherent (or ind-coherent, or perfect, et cetera) sheaves \(\operatorname {QC}(\widehat {Z})\) on the formal completion \(\widehat {Z}\) is canonically equivalent to the category \(\operatorname {QC}_{Z}(X)\) of sheaves on \(X\) set-theoretically supported on \(Z\).
See Definition 2.3.1 of [31] for a definition of the derived loop space \({\mathcal {L}}(-)\). For a stack \(X\) with a self-map \(f\), we define \({\mathcal {L}}_{f}(X)\) to be the derived fixed points of \(f\), i.e. the derived fiber product

When \(f = \mathrm{id}_{X}\), we have \({\mathcal {L}}_{f} X = {\mathcal {L}}X\). Given a group action \(G\) on a scheme \(X\), and \(f: X \rightarrow X\) commuting with the \(G\)-action, we have via Proposition 2.1.8 of [31] a Cartesian diagram:

where \(\alpha \) is the action map.
1.6.3 Representation theory
In Sects. 2, 4 and 5, unless otherwise noted, \(G\) denotes a split reductive group over a field \(k = \overline {\mathbb{Q}}_{\ell}\) or ℂ) with a choice of Borel \(B\) and torus \(T \subset B\) with universal Cartan \(H\) and (finite) universal Weyl group \(W_{f}\). The extended affine Weyl group is denoted \(W_{a} := X^{\bullet}(H) \rtimes W_{f}\). We denote by \(\operatorname {Rep}(G) = \operatorname {QC}(BG)\) the derived category of rational representations of \(G\). Likewise, \(\mathfrak{g} = \operatorname {Lie}(G)\), \(\mathfrak{b} = \operatorname {Lie}(B)\), et cetera.
Morally, we view \(G\) as a group on the spectral side of Langlands duality. On the automorphic side, one is interested in representations of the split group \(G^{\vee}(F)\), where we let \(F\) denote a non-archimedian local field with ring of integers \(O\). We denote by \(I\) the Iwahori subgroup with pro-unipotent radical \(I^{\circ}\), defined by the fixed Borel subgroup \(B^{\vee }\subset G^{\vee}\) and maximal hyperspecial \(G^{\vee}(O) \subset G^{\vee}(F)\). In Sect. 5.1, we will reverse this convention for ease of reading, and \(G\) will denote a split reductive group over \(F\).
We will often be interested in equivariance with respect to the trivial extension of \(G\) by \(\mathbb{G}_{m}\) which we denote \(G_{\mathrm {gr}}=G\times {\mathbb{G}}_{m}\); this amounts to additional weight grading on coherent sheaves. We fix once and for all a coordinate \(z \in {\mathbb{G}}_{m}\). For any geometric vector space or bundle \(V\) (e.g. a Lie algebra \(\mathfrak {g}\) or the Springer resolution \(\widetilde {{\mathcal {N}}}_{G}\) introduced below), by convention the coordinate will act on geometric fibers by weight −1, i.e. \(z \cdot x = z^{-1} x\) for \(x \in V\), and therefore on functions by weight 1 (i.e. \(z \cdot f(-) = zf(-)\) for \(f \in V^{*}\)). This negative sign convention corresponds to the convention that the \(z=q\) fixed points of \({\mathcal {N}}/G_{\mathrm {gr}}\) correspond to unipotent Langlands parameters \((s, N)\) for a local field with residue \(\mathbb{F}_{q}\), i.e. \((s, N, q) \cdot N = sNs^{-1}q^{-1} = N\).Footnote 8
Let \({\mathcal {B}}_{G} = G/B\) denote the flag variety, \({\mathcal {N}}_{G}\) denote the nilpotent cone, and \(\widehat {{\mathcal {N}}}_{G}\) its formal neighborhood inside \(\mathfrak {g}\). We let \(\widetilde {{\mathcal {N}}}_{G}\) denote the (reduced) Springer resolution, and denote by \(\mu : \widetilde {{\mathcal {N}}}_{G} = T^{*}({\mathcal {B}}_{G}) \rightarrow {\mathcal {N}}_{G} \hookrightarrow \widehat {{\mathcal {N}}}_{G}\) the composition of the Springer resolution with the inclusion, and \(\widetilde{\mathfrak{g}}\) the Grothendieck-Springer resolution, which is \(G_{\mathrm {gr}}\)-equivariant. Sometimes, we take the codomain of \(\mu \) to be all of \(\mathfrak {g}\). Let \({\mathcal {Z}}_{G}= \widetilde {\mathcal {N}}_{G} \times _{\mathfrak{g}} \widetilde {\mathcal {N}}_{G}\) denote the derived Steinberg scheme, \({\mathcal {Z}}'_{G} = \widetilde {\mathcal {N}}_{G} \times _{\mathfrak{g}} \widetilde{\mathfrak{g}}\) denote the non-reduced Steinberg scheme, and \({\mathcal {Z}}^{\wedge}_{G} = (\widetilde {\mathfrak {g}} \times _{\mathfrak {g}} \widetilde {\mathfrak {g}})^{ \wedge}\) denote the formal Steinberg scheme via completing along the nilpotent elements. We denote by \(\pi _{0}({\mathcal {Z}}_{G})\) the classical Steinberg variety, which coincides with \(({\mathcal {Z}}'_{G})^{red} = ({\mathcal {Z}}^{\wedge}_{G})^{red}\). We will drop the subscript if there is no ambiguity regarding the group \(G\) in discussion.
We denote the affine Hecke algebra by \(\mathcal {H}_{G}\); we use a Coxeter presentation, i.e. a definition on the spectral side, which can be found e.g. in Definition 7.1.9 of [34]. It is a \(k[q, q^{-1}]\)-algebra whose specializations at prime powers \(q = p^{r}\) are isomorphic to the Iwahori-Hecke algebras \(\mathcal {H}_{q,G} \simeq {\mathcal {H}}(G^{\vee}(F), I) := C^{\infty}_{c}(I \backslash G^{ \vee}(F)/I; k)\) of compactly supported Iwahori-biequivariant functions on a loop group (or \(p\)-adic group). More generally, for a locally compact totally disconnected group \(G\) (now viewed on the automorphic side), a compact open subgroup \(K \subset G\) and a representation \(\tau \) of \(K\), we denote its Hecke algebra by \({\mathcal {H}}(G, K, \tau ) := \operatorname {End}_{G}(\operatorname {cInd}_{K}^{G} \tau )\) (these appear in Sect. 5).
The mixed affine Hecke category is defined by \(\mathbf {H}^{{\mathrm {m}}}_{G} := {\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})\), while the affine Hecke category is defined to be \(\mathbf {H}_{G} := {\operatorname {Coh}}({\mathcal {Z}}/G)\). Note that we define these categories directly on the spectral side of Langlands duality, while they are usually defined on the automorphic side. That is, we implicitly pass through Bezrukavnikov’s theorem (Theorem 1.13).
We define the coherent Springer sheaf and the coherent \(q\)-Springer sheaf by:
The coherent \(q\)-Springer sheaf is a coherent sheaf on the stack of unipotent Langlands parameters:
Note that this definition is functorial and makes sense for any affine algebraic group \(G\) (still completing along nilpotents), and thus the coherent \(q\)-Springer sheaf may be realized by applying parabolic induction

to the structure sheaf of \(\mathbb{L}^{u}_{q,T}\), i.e. \({\mathcal {S}}_{q,G} = \mu _{*}\nu ^{*} {\mathcal {O}}_{\mathbb{L}^{u}_{q,T}}\) (where \(T\) is the quotient torus of \(B\), and does not depend on a choice of lift). By Proposition 4.3, if \(G\) is reductive then \(\mathbb{L}^{u}_{q,G}\) is a classical stack (i.e. no derived and no infinitesimal structure) when \(q\) is not a root of unity. Note that other authors [4, 24, 35, 51, 86] have defined a moduli stack of Langlands parameters \(X_{F, G}\) for a given local field \(F\) and a reductive group \(G^{\vee}\) with coefficients in \(F\). Our stack embeds as a connected component of tame Langlands parameters.
2 Hochschild homology of the affine Hecke category
In this section we calculate the Hochschild homology of the affine Hecke category. In particular in Corollary 2.26 we prove that the Chern character from \(K\)-theory factors through an isomorphism between \(K_{0}\) and Hochschild homology. For this we use Bezrukavnikov’s Langlands duality for the affine Hecke category to construct a semiorthogonal decomposition on the equivariant derived category of the Steinberg stack with simple components, from which the calculation of localizing invariants is immediate.
2.1 Background
We first review some standard notions regarding Hochschild homology and equivariant \(\ell \)-adic sheaves that we need for our arguments. In this subsection we take \(k\) to be any field of characteristic 0.
2.1.1 Trace decategorifications and Hochschild homology
An extended discussion of the notions in this subsection can be found in [8, 31, 46, 79]. We recall the notion of a dualizable object \(X\) of a symmetric monoidal \((\infty , 2)\)-category \(\mathbf {C}_{\otimes}\) with monoidal unit \(1_{\otimes}\) (see the Appendix of [45] for a definition).
Definition 2.1
The object \(X\) is dualizable if there exists an object \(X^{\vee}\) and coevaluation and evaluation morphisms
satisfying a standard identity. Dualizability is a property rather than an additional structure on \(X\) (see Proposition 4.6.1.10 in [65]). The trace of an endomorphism \(f\in \operatorname {End}_{\mathbf {C}}(X)\) of a dualizable object is defined by
Remark 2.2
Note that \(\operatorname {End}(1_{\otimes})\) is naturally enriched as an object of \(\mathbf {C}_{\otimes}\) which is universal amongst objects tensored over \(1_{\otimes}\), i.e. there is a natural equivalence of algebras \(\operatorname {End}(1_{\otimes}) \simeq 1_{\otimes}\). In particular, \(\operatorname {End}(1_{\otimes})\), which is a priori only an \(A_{\infty}\)-algebra, is an \(E_{\infty}\)-algebra (see the discussion in Sect. 4.7.1 of [65] for details).
The notion of dualizability depends only on the 1-categorical structure of \(\mathbf {C}_{\otimes}\). However, in our applications, we are interested in the case when \(X\) is an algebra object in the symmetric monoidal \(\infty \)-category \(\mathbf {C}_{\otimes}\), and the resulting algebra structure on traces. To formulate this, we require a functoriality on traces involving (right-)dualizable 2-morphisms in \(\mathbf {C}_{\otimes}\); this discussion requires the presence of non-invertible 2-morphisms in \(\mathbf {C}_{\otimes}\).
Since \(\mathbf {C}_{\otimes}\) is a monoidal \((\infty , 2)\)-category, the endomorphisms of the monoidal unit \(\mathbf {End}_{\mathbf {C}_{\otimes}}(1_{\otimes})\) in fact form an \((\infty , 1)\)-category. We have the following natural functoriality enjoyed by the abstract construction of traces in the higher-categorical setting; see [46, 55, 79] (and [8] for an informal discussion). Namely the trace of an object is covariantly functorial under right dualizable morphisms.
Definition 2.3
A morphism of pairs \((F, \psi ): (X, f) \rightarrow (Y, g)\) is a right dualizable morphism \(F: X \rightarrow Y\) (i.e. has a right adjoint \(G\)) between dualizable objects along with a commuting structure \(\psi : F \circ f \rightarrow g \circ F\). Given a morphism of pairs \((F, \psi )\), it defines a map \(\mathrm{tr}(F, \psi )\) on traces via the composition

where \(\eta _{F}\) and \(\epsilon _{F}\) are the unit and counit of the adjunction \((F, G)\), and the equivalence in the middle is via cyclic symmetry of traces (see also Definition 3.24 of [8]).
Note that taking the trace is canonically symmetric monoidal with respect to the monoidal structure in \(\mathbf {C}_{\otimes}\) and composition in \(\mathbf {End}_{\mathbf {C}_{\otimes}}(1_{\otimes})\) (or equivalently, tensoring in \(1_{\otimes}\)). The trace construction enhances to a symmetric monoidal functor from the \(\infty \)-category of endomorphisms of dualizable objects in \(\mathbf {C}_{\otimes}\) to the category \(\mathbf {End}_{\mathbf {C}_{\otimes}}(1_{\otimes}) \simeq 1_{\otimes}\), see [79, 2.5], [55, 2], and [46, 3] for details. In particular, if \(X\) is an algebra object in \(\mathbf {C}_{\otimes}\) with right dualizable unit and multiplication, and \(f: X \rightarrow X\) is a map of algebra objects, then \(\mathrm{tr}(X, f)\) is an algebra object in \(\mathbf {End}_{\mathbf {C}_{\otimes}}(1_{\otimes})\).
In this paper, we consider the \(\infty \)-category \(\mathbf {C}_{\otimes }= \mathbf {dgCat}_{k}\) of presentable (i.e. cocomplete) \(k\)-linear dg categories, with morphisms given by colimit-preserving (i.e. continuous, or left adjoint) functors, with monoidal product the Lurie tensor product. We now specialize to this setting.
Example 2.4
Any presentable compactly generated dg category \(\mathbf {C}=\operatorname{Ind}(\mathbf {C}^{\omega})\in \mathbf {dgCat}_{k}\) is dualizable, with dual given by taking the ind-completion of the opposite of compact objects \(\mathbf {C}^{\vee}=\operatorname{Ind}(\mathbf {C}^{\omega ,op})\). Thus we may speak of traces of its endofunctors, which are endomorphisms of the unit, i.e. chain complexes
Furthermore, note that a right dualizable morphism of presentable compactly generated dg categories must have a colimit-preserving right adjoint, or equivalently is a functor which preserves compact objects.
Definition 2.5
The Hochschild homology of a dualizable (for instance, compactly generated) presentable \(k\)-linear dg category \(\mathbf {C} \in \mathbf {dgCat}_{k}\) is the trace of the identity functor
We often omit \(k\) from the notation above. More generally, the Hochschild homology of \(\mathbf {C}\) with coefficients in a colimit-preserving endofunctor \(F\) is \(HH(\mathbf {C},F)=\mathrm{tr}(\mathbf {C},F)\in \mathbf {Vect}_{k}\).
Remark 2.6
Large vs. small categories
The above definition is formulated in terms of large categories, but can be defined for small categories by taking ind-completions. Since every compactly generated category is dualizable but not conversely, the notion of Hochschild homology for large categories is more general. We will often not distinguish between the two.
We have a notion of characters of compact objects in categories, defined via functoriality of traces.
Definition 2.7
Let \(\mathbf {C} \in \mathbf {dgCat}_{k}\) be dualizable, and \(F: \mathbf {C} \rightarrow \mathbf {C}\) an endofunctor. Any object \(c \in \mathrm{Ob}(\mathbf {C})\) defines a functor \(\alpha _{c}: \mathbf {Vect}_{k} \rightarrow \mathbf {C}\) by action on the object \(c\), and a map \(\psi : c \rightarrow F(c)\) defines a commuting structure. If \(c\) is a compact object, then \(\alpha _{c}\) is right dualizable. Thus, by functoriality of traces, we have a map
and the characterFootnote 9\([c] = \mathrm{tr}(\alpha _{c}, \psi )(1)\) of \(c\) is the image of \(1 \in k\) under this map.
Remark 2.8
We highlight a few properties of Hochschild homology which we use in our arguments:
-
(1)
Hochschild homology is a localizing invariant in the sense of [22] by Theorem 5.2 of [59], and in particular in the explicit algebraic model of Definition 2.12 one can replace \(\mathrm{Ob}(\mathbf {C})\) with any set of generating objects.
-
(2)
Hochschild homology takes (possibly infinite) \(F\)-stable semiorthogonal decompositions (see Sect. 2.3) of \(\mathbf {C}\) to direct sums. This is a consequence of (1) since semiorthogonal decompositions give rise to exact sequences of categories.
-
(3)
Let \(A\) be a dg algebra, \(M\) an dg \(A\)-bimodule, and define \(F_{M}(-) = M \otimes _{A} -\). Then, \(HH(A\text{-}\mathrm {mod}, F_{M}) = A \otimes _{A \otimes _{k} A^{op}} M\). This derived tensor product can be computed via a bar resolution or otherwise.
-
(4)
The Hochschild homology receives a Chern character map from the connective \(K\)-theory spectrum (see Definition 2.14).
Example 2.9
We give a toy example to illustrate a canonical identification of two calculations of Hochschild homology. Let \(\mathbf {C} = {\operatorname {Coh}}(\mathbb{P}^{1})\). It is well-known that \({\mathcal {O}}(-1) \oplus {\mathcal {O}}\) generates the category, with endomorphism algebra represented by the Kronecker quiver. Since the Kronecker quiver has no cycles, we have an identification \(HH({\operatorname {Coh}}(\mathbb{P}^{1})) \simeq k^{2}\). The character map is the (twisted) algebraic Euler characteristic: \([{\mathcal {L}}] = (\chi (\mathbb{P}^{1}, {\mathcal {L}}(1)), \chi (\mathbb{P}^{1}, {\mathcal {L}}))\).
On the other hand, the Hochschild-Kostant-Rosenberg isomorphism (see Theorem 4.1 of [29]) identifies the Hochschild homology of a smooth variety with the global sections of its negatively-shifted algebra of differential forms, which in this example produces an identification \(HH({\operatorname {Coh}}(\mathbb{P}^{1})) \simeq H^{0}(\mathbb{P}^{1}, {\mathcal {O}}_{ \mathbb{P}^{1}}) \oplus H^{1}(\mathbb{P}^{1}, \Omega ^{1}_{\mathbb{P}^{1}}) \simeq k^{2}\). The character map is the Chern character, i.e. \([{\mathcal {O}}(n)] = (1, n)\); compatibility of traces forces a particular identification \(H^{0,0}(\mathbb{P}^{1}) \oplus H^{1,1}(\mathbb{P}^{1}) \simeq \operatorname {End}( {\mathcal {O}}(-1)) \oplus \operatorname {End}({\mathcal {O}})\).
2.1.2 The cyclic bar and Block-Getzler complex
The Hochschild homology of compactly generated (or equivalently, small) categories has an algebraic realization via the cyclic bar complex, which we briefly recall; see Sect. 5.3 in [59] for further discussion. In the below definition, we relax the condition that \(\mathbf {C}\) is pretriangulated; morally it should be thought of as a full subcategory of \(F\)-fixed compact generators of a cocomplete dg category.
Definition 2.10
The cyclic bar complex of a small \(k\)-linear dg category \(\mathbf {C}\), equipped with a dg-endofunctor \(F\), is defined to be the sum totalization of the simplicial chain complexes withFootnote 10
where the face maps \(d_{i}: {\mathcal {C}}^{-n} \rightarrow {\mathcal {C}}^{-(n-1)}\) (for \(i = 0, \ldots , n\)) compose morphisms, i.e.
If \(\mathbf {C}\) is a monoidal dg category, and \(F\) has the structure of a monoidal functor, then \(HH(\mathbf {C}, F)\) is an (associative) dg algebra via functoriality and the shuffle or Eilenberg-Zilber map.
Now, let \(k\) be a field of characteristic 0, and \(G\) a reductive group over \(k\). For dg categories with a \(\operatorname {Rep}(G)\)-action, there is an explicit algebraic model for the Hochschild homology due to Block and Getzler [21]. We define a \(\operatorname {Rep}(G)\)-internal \(\operatorname{Hom}\) for \(\operatorname {Rep}(G)\)-module categories in the following standard lemma.
Lemma 2.11
Let \(\mathbf {C}\) be a \(\operatorname {Rep}(G)\)-module category. The \(\operatorname{Hom}\)-sets of \(\mathbf {C}\) are canonically enriched in \(\operatorname {Rep}(G)\) such that
where \(\underline{\operatorname{Hom}}\) denotes the \(\operatorname {Rep}(G)\)-internal Hom. In particular, if \(E \in \mathbf {C}\) is a compact \(\operatorname {Rep}(G)\)-generator for \(\mathbf {C}\), then \(\mathbf {C}\) is equivalent to modules in \(\operatorname {Rep}(G)\) for the internal endomorphism algebra
Proof
The lemma is an application of the rigidity of \(\operatorname {Rep}(G)\) and the Barr-Beck-Lurie monadicity theorem. The internal \(\operatorname{Hom}\) is defined in the following way. For any \(X \in \mathbf {C}\), the functor \(\mathrm{act}_{X}:\operatorname {Rep}(G)\to \mathbf {C}\) given by action on \(X\) has a \(\operatorname {Rep}(G)\)-linear colimit-preserving right adjoint \(\Psi _{X}(-)=\underline{\operatorname{Hom}}_{\operatorname {Rep}(G)}(X,-)\). We define \(\underline{\operatorname{Hom}}_{\mathbf {C}}(X, Y) = \Psi _{X}(Y)\). More explicitly, we have
where \(G\) acts on \({\mathcal {O}}(G)\) by conjugation. Note that \(\Psi _{E}\) takes \(E\) to the internal endomorphism algebra, which represents the corresponding monad \(\Psi _{E} \circ \mathrm{act}_{E}\) on \(\operatorname {Rep}(G)\). By rigidity, this monad is \(\operatorname {Rep}(G)\)-linear, thus is given by tensoring with \(\underline{A} = \underline{\operatorname {End}}_{\mathbf {C}}(E)^{op}\), its value on the monoidal unit. The functor \(\Psi _{X}\) is monadic; it preserves colimits since its left adjoint preserves compactness, and it is conservative since \(E\) is a \(\operatorname {Rep}(G)\)-generator, thus the claim follows by Barr-Beck. □
Block and Getzler defined a chain complex in [21] associated to any dg category \(\mathbf {C}\) enriched in \(\operatorname {Rep}(G)\). We review this notion here. We often do not take the entire category \(\mathbf {C}\), but a full subcategory which generates under the \(\operatorname {Rep}(G)\)-action (but is not closed under it).
Definition 2.12
Let \(G\) be a reductive group, and let \(\mathbf {C}\) be a small dg category enriched in \(\operatorname {Rep}(G)\) equipped with an \(\operatorname {Rep}(G)\)-enriched dg-endofunctor \(F\). For any \(V \in \operatorname {Rep}(G)\), we abusively denote by \(\gamma : V \rightarrow V \otimes k[G]\) the coaction map. The Block-Getzler complex (over \(k\)) \({\mathcal {C}}_{G}^{\bullet}(\mathbf {C}, F)\) is defined to be the sum totalization of the simplicial object in chain complexes with
where \(G\) acts on \(k[G]\) by conjugation, and the face maps \(d_{i}: {\mathcal {C}}_{G}^{-n} \rightarrow {\mathcal {C}}_{G}^{-(n-1)}\) (for \(i = 0, \ldots , n\)) compose morphisms, i.e.
We define the enhanced Block-Getzler complex to \(\underline{{\mathcal {C}}}_{G}^{\bullet}(\mathbf {C}, F)\) to be the complex above, but without taking \(G\)-invariants.Footnote 11 Finally, for a specified \(g \in G(k)\) we define
where \(k_{g}\) is the skyscraper module at \(g \in G\). Note that there are canonical maps
We now wish to show that the Block-Getzler complex computes Hochschild homology for \(\operatorname {Rep}(G)\)-module categories. Letting \((-)^{{\mathrm {dq}}} := - \otimes _{\operatorname {Rep}(G)} \mathbf {Vect}_{k}\) denote the de-equivariantization, since \(\mathbf {Vect}_{k}^{{\mathrm {dq}}}\simeq \operatorname {QC}(G)\) for any \(g \in G(k)\) we have an automorphism \(g_{*}\) of the category \(\mathbf {C}^{{\mathrm {dq}}}\) induced by the action of the skyscraper sheaf \(k_{g}\) at \(g \in G(k)\). For any \(\operatorname {Rep}(G)\)-linear endofunctor \(F: \mathbf {C} \rightarrow \mathbf {C}\), consider the squares

The left square is equipped with a canonical commuting structure coming from the \(\operatorname {Rep}(G)\)-linear structure of \(F\), and the right square is equipped with a canonical commuting structure since \(F^{{\mathrm {dq}}}\) acquires a natural \(\operatorname {QC}(G) \simeq \mathbf {Vect}_{k}^{{\mathrm {dq}}}\)-linear structure. We denote by \(F^{{\mathrm {dq}}}_{g} := F^{{\mathrm {dq}}}\circ g_{*} \simeq g_{*} \circ F^{{\mathrm {dq}}}\), and consider the map of pairs \(\Psi : (\mathbf {C}, F) \rightarrow (\mathbf {C}^{{\mathrm {dq}}}, F_{g}^{{\mathrm {dq}}})\).
Proposition 2.13
Let \(G\) be a reductive group (over \(k\)), \(\mathbf {C}\) be a small dg category with a \(\operatorname {Rep}(G)\)-action, and \(F\) a \(\operatorname {Rep}(G)\)-linear endofunctor. Let \(\mathbf {C}_{0} \subset \mathbf {C}\) be a full subcategory, closed under \(F\), which generates \(\mathbf {C}\) over \(\operatorname {Rep}(G)\). Then, the map \({\mathcal {C}}_{G}^{\bullet}(\mathbf {C}_{0}, F) \rightarrow {\mathcal {C}}^{\bullet}_{G,g}( \mathbf {C}_{0}, F)\) computes the map in Hochschild homology \(HH(\Psi ): HH(\mathbf {C}, F) \rightarrow HH(\mathbf {C}^{{\mathrm {dq}}}, F_{g}^{ {\mathrm {dq}}})\).
Proof
The claim that \({\mathcal {C}}_{G}^{\bullet}(\mathbf {C}_{0}, F)\) computes \(HH(\mathbf {C}, F)\) is similar to Proposition 2.3.6 of [31]. Since \(\mathbf {C}_{0}\) (compactly) generates \(\mathbf {C}\) under the \(\operatorname {Rep}(G)\)-action, to compute Hochschild homology we may use the cyclic bar complex with \(n\)th term
By Proposition 2.3.2 of op. cit. we have
By Peter-Weyl, we have
These identifications are compatible with the face maps by a straightforward diagram chase.
The claim that \({\mathcal {C}}_{G,g}^{\bullet}(\mathbf {C}_{0}, F)\) computes \(HH(\mathbf {C}^{{\mathrm {dq}}}, F_{g}^{{\mathrm {dq}}})\) follows from the observation that if \(\mathbf {C}_{0}\) (compactly) generates \(\mathbf {C}\) over \(\operatorname {Rep}(G)\), then its image in the de-equivariantization (compactly) generates \(\mathbf {C}^{{\mathrm {dq}}}\), and that the \(\operatorname{Hom}\)-spaces in \(\mathbf {C}^{{\mathrm {dq}}}\) are obtained from the \(\operatorname {Rep}(G)\)-internal \(\operatorname{Hom}\)-spaces of \(\mathbf {C}\) after forgetting the \(G\)-module structure. Thus \({\mathcal {C}}^{\bullet}_{G,g}(\mathbf {C}_{0}, F)\) is just the cyclic bar complex via the identification of the last tensor factor (implicitly using the commuting structure):
Verification that the identifications are compatible under \(\Psi \) is a straightforward diagram chase. □
2.1.3 Chern character from \(K\)-theory to Hochschild homology
Finally, we will use the universal trace map from connective \(K\)-theory to Hochschild homology constructed in [22].
Definition 2.14
For any small \(k\)-linear dg-category \(\mathbf {C}\), the connective \(K\)-theory spectrum \(K(\mathbf {C})\) is the connective \(K\)-theory of the corresponding Waldhausen category defined in Sect. 5.2 of [59]. Since Hochschild homology is a localizing invariant, by Theorems 1.1 and 1.3 of [22] it receives a canonical and functorial map from the connective \(K\)-theory spectrum which we call the Chern character:Footnote 12
Remark 2.15
We note two important properties of the Chern character that we use. Note that unlike in the definition of Hochschild homology, in this discussion we restrict ourselves to small categories \(\mathbf {C}\) (i.e. the compact objects of a compactly generated cocomplete category).
-
(1)
Via functoriality of the Chern character, for any object \(X \in \mathrm{Ob}(\mathbf {C})\), the Chern character sends \([X] \in K_{0}(\mathbf {C}) \mapsto [X] \in HH_{0}(\mathbf {C})\), i.e. equivalence classes in the Grothendieck group to their characters in Hochschild homology in the sense of Definition 2.7.
-
(2)
Using the lax monoidal structure of \(K\)-theory, we see that for a monoidal category \(\mathbf {C}\) the Chern character defines a map of algebras (see also Theorem 1.10 of [23]).
Often in applications to geometric representation theory, we are only interested in (or able to compute) the Grothendieck group \(K_{0}\). However, note that the map \(K_{0}(\mathbf {C}) \rightarrow HH_{0}(\mathbf {C})\) does not automatically induce a map of algebras \(K_{0}(\mathbf {C}) \rightarrow HH(\mathbf {C})\) at the chain level. In order to compare \(K_{0}\) with Hochschild homology, we require certain vanishing conditions to hold. Namely, if \(HH(\mathbf {C})\) is concentrated in degrees \(\geq 0\), then the Chern character canonically factors through the truncation of \(K(\mathbf {C})\) to degrees \(\geq 0\), i.e. \(K_{0}(\mathbf {C})\) since \(K(\mathbf {C})\) is connective:

and we may ask whether this map is an equivalence. In particular, given this vanishing, when \(\mathbf {C}\) is a monoidal category the induced map from \(K_{0}(\mathbf {C}) \rightarrow HH(\mathbf {C})\) is automatically a map of dg algebras at the chain level.
2.1.4 Equivariant \(\ell \)-adic sheaves, weights, and Tate type
In this subsection we review some standard notions concerning weights and the \(\ell \)-adic cohomology of \(BG\). In this section and the following one, we fix a prime power \(q = p^{r}\) and a prime \(\ell \ne p\), and will work with \(\ell \)-adic sheaves ℱ on \(\overline {\mathbb{F}}_{q}\)-schemes \(X\). All schemes and sheaves on them that arise are defined over \({\mathbb{F}_{q}}\), i.e., \(X\) will come with a geometric Frobenius automorphism \(\operatorname {Fr}\) and ℱ with a \(\operatorname {Fr}\)-equivariant (Weil) structure, which will be left implicit.
Fix a square root of \(q\) in \(\overline {\mathbb{Q}}_{\ell}\), thereby defining a notion of half Tate twist (this choice can be avoided by judicious use of extended groups as in [15, 28, 84]). For \(\mathcal{F} \in \operatorname {Sh}(X)\) where \(X\) is over \({\mathbb{F}_{q}}\), we will denote the Tate twist by \(\mathcal{F}(n/2)\) for \(n \in {\mathbb{Z}}\). For a scheme \(X\) with an action by a smooth group scheme \(G\), we denote by \(\operatorname {Sh}(X/G) = \operatorname {Sh}^{G}(X)\) the bounded derived category of \(G\)-equivariant \(\overline {\mathbb{Q}}_{\ell}\)-sheaves on \(X\) with constructible cohomology (see Sect. 1.3 of [19] and [16]). In this context, the cohomology of a sheaf \(H^{\bullet}(X, -)\) will be understood to mean étale cohomology.
Following the Appendix of [42], this notion can be extended to \(G\)-equivariant ind-schemes (i.e. a functor which is representable by a directed colimit of schemes with transition maps closed embeddings), where \(G\) is a pro-affine algebraic group (i.e. an inverse limit of finite-type affine algebraic groups in the category of schemes) acting in a sufficiently finite way. We say a \(G\)-action on \(X\) is nice if the following two properties hold: (1) every closed subscheme \(Z \subset X\) is contained in a closed \(G\)-stable subscheme \(Z' \subset X\) such that the action of \(G\) on \(Z'\) factors through a quotient of \(G\) which is affine algebraic, and (2) \(G\) contains a pro-unipotent subgroup of finite codimension, i.e. if \(G = \displaystyle \lim _{\longleftarrow} G_{n}\), then there is an \(n\) such that \(\ker (G \rightarrow G_{n})\) is a projective limit of unipotent affine algebraic groups. If \(G\) is a pro-affine group scheme acting nicely on \(X\), and \(X = \displaystyle \operatorname*{colim}_{\longrightarrow} X_{i}\) with affine quotient \(G_{i}\) acting on \(X_{i}\), then we defineFootnote 13\(\operatorname {Sh}^{G}(X) = \displaystyle \operatorname*{colim}_{\longrightarrow} \operatorname {Sh}^{G_{i}}(X_{i})\).
We recall the well-known calculation of the \(\ell \)-adic cohomology ring of \(BG\), whose description we repeat for convenience following [80] (in the Hodge-theory context).
Proposition 2.16
Let \(G\) be a pro-affine group scheme with split reductive quotient over \(\overline{{\mathbb{F}}}_{q}\). Then, \(H^{\bullet}(BG; \overline {\mathbb{Q}}_{\ell})\) is polynomial, generated in even degrees, and \(H^{2k}(BG; \overline {\mathbb{Q}}_{\ell})\) is a Frobenius eigenspace with eigenvalue \(q^{k}\). Furthermore the dg algebra \(C^{\bullet}(BG; \overline {\mathbb{Q}}_{\ell})\) under the cup product is formal, i.e. there is an algebra quasi-isomorphism \(C^{\bullet}(BG; \overline {\mathbb{Q}}_{\ell}) \simeq H^{\bullet}(BG; \overline {\mathbb{Q}}_{\ell})\).
Proof
First, since \(G\) is pro-affine, there is a reductive (finite type) algebraic group \(G_{0}\) such that the kernel \(\ker (G \rightarrow G_{0})\) is pro-unipotent. By Theorem 3.4.1(ii) in [16] we may assume that \(G\) is reductive (and finite type).
We first establish the claim that \(H^{\bullet}(BG; \overline {\mathbb{Q}}_{\ell})\) is polynomial in even degrees and compute the action of Frobenius. It is a standard calculation that \(H^{\bullet}({\mathbb{G}}_{m}, \overline {\mathbb{Q}}_{\ell}) = H^{0}({\mathbb{G}}_{m}, \overline {\mathbb{Q}}_{\ell}) \oplus H^{1}({\mathbb{G}}_{m}, \overline {\mathbb{Q}}_{\ell})\), where \(H^{0}\) is a 1-eigenspace for the Frobenius and \(H^{1}\) is a \(q\)-eigenspace. By Corollary 10.4 of [63], it follows that \(H^{\bullet}(B{\mathbb{G}}_{m}, \overline {\mathbb{Q}}_{\ell}) \simeq \overline {\mathbb{Q}}_{\ell}[u]\) where \(u\) has cohomological degree \(|u| = 2\), and is a \(q\)-eigenvector for Frobenius. In particular, by the Künneth formula (Theorem 11.4 in op. cit.) we have that for a split torus \(T\), \(H^{\bullet}(BT; \overline {\mathbb{Q}}_{\ell})\) is polynomial in even degrees, and \(H^{2k}\) is a Frobenius-eigenspace with eigenvalue \(q^{k}\). Thus, the claim is true when \(G = T\) is a torus. Now, assume \(T\) is a split torus inside a reductive group \(G\), and \(B\) is a Borel subgroup with \(T \subset B \subset G\). Applying Theorem 3.4.1(ii) of [16] again, we have \(H^{\bullet}(BB; \overline {\mathbb{Q}}_{\ell}) \simeq H^{\bullet}(BT; \overline {\mathbb{Q}}_{\ell})\). By Theorem 1.1 of [81], \(H^{\bullet}(BG; \overline {\mathbb{Q}}_{\ell})\) is a polynomial subring of \(H^{\bullet}(BB; \overline {\mathbb{Q}}_{\ell}) \simeq H^{\bullet}(BT; \overline {\mathbb{Q}}_{\ell})\), completing the claim. Formality follows by a standard weight-degree argument. □
2.2 Automorphic and spectral realizations of the affine Hecke category
We follow the set-up of Bezrukavnikov in [18], except that we view the group on the automorphic side as dual to a chosen group on the spectral side for ease of notation. Let \(G\) be a fixed reductive algebraic group over \(\overline {\mathbb{Q}}_{\ell}\) on the spectral side of Langlands duality, and let \(G^{\vee}\) be the extension of scalars to \(\overline {\mathbb{F}}_{q}\) of its dual group split form over \(\mathbb{F}_{q}\) (equipped with corresponding Frobenius automorphism).
Let \(F = \overline {\mathbb{F}}_{q}((t))\) and \(O = \overline {\mathbb{F}}_{q}[[t]]\). We denote by  the loop group, i.e. the group ind-scheme over \(\overline {\mathbb{F}}_{q}\) with
the loop group, i.e. the group ind-scheme over \(\overline {\mathbb{F}}_{q}\) with  defined in Sect. 0.2 of [42]. We denote by
defined in Sect. 0.2 of [42]. We denote by  the arc group, which is a pro-affine group scheme with
the arc group, which is a pro-affine group scheme with  . There is a group scheme homomorphism
. There is a group scheme homomorphism  , and the Iwahori subgroup of
, and the Iwahori subgroup of  is defined
is defined  , which inherits its structure as a closed subgroup and is therefore also a pro-affine group. We let
, which inherits its structure as a closed subgroup and is therefore also a pro-affine group. We let  denote its pro-unipotent radical.
denote its pro-unipotent radical.
On the automorphic side, we are interested in equivariant \(\overline {\mathbb{Q}}_{\ell}\)-sheaves on the affine flag variety  , an ind-proper ind-scheme constructed in the Appendix of [42]. It carries a left action of
, an ind-proper ind-scheme constructed in the Appendix of [42]. It carries a left action of  whose orbits are of finite type and naturally indexed the affine Weyl group \(W_{a}\) for the group \(G^{\vee}\). For \(w \in W\), we denote by \({\mathfrak {F}l}^{w}\) the corresponding orbit. Denote by \(j_{w}: {\mathfrak {F}l}^{w} \hookrightarrow {\mathfrak {F}l}\) the inclusion of the corresponding
whose orbits are of finite type and naturally indexed the affine Weyl group \(W_{a}\) for the group \(G^{\vee}\). For \(w \in W\), we denote by \({\mathfrak {F}l}^{w}\) the corresponding orbit. Denote by \(j_{w}: {\mathfrak {F}l}^{w} \hookrightarrow {\mathfrak {F}l}\) the inclusion of the corresponding  -orbit. Let \(\ell : W_{a} \rightarrow \mathbb{Z}^{\geq 0}\) denote the length function on the affine Weyl group.
-orbit. Let \(\ell : W_{a} \rightarrow \mathbb{Z}^{\geq 0}\) denote the length function on the affine Weyl group.
On the spectral side, the stacks that appear are defined over \(\overline {\mathbb{Q}}_{\ell}\). Recall the derived Steinberg variety \({\mathcal {Z}}= \widetilde {{\mathcal {N}}} \times _{\mathfrak {g}} \widetilde {{\mathcal {N}}}\) and the classical non-reduced Steinberg variety \({\mathcal {Z}}' = \widetilde {\mathfrak {g}} \times _{\mathfrak {g}} \widetilde {{\mathcal {N}}}\) (see Sect. 1.6.3). Each of these (derived) schemes has a natural \(G\)-action, as well as a commuting \({\mathbb{G}}_{m}\)-action which by our convention acts by scaling on the points of \(\mathfrak {g}\), \(\widetilde {{\mathcal {N}}}\), and \(\widetilde {\mathfrak {g}}\) by weight −1 (thus on linear functionals by weight 1). Recall the notation \(G_{\mathrm {gr}}= G \times {\mathbb{G}}_{m}\).
The following is Theorem 1 of [18], while the Frobenius property of \(\Phi \) appears as Proposition 53.
Theorem 2.17
Bezrukavnikov
At the level of homotopy categories, there are equivalences of categories \(\Phi \) and \(\Phi '\) and a commutative diagram

where  is the quotient map and \(i: {\mathcal {Z}}/G \hookrightarrow {\mathcal {Z}}'/G\) is the inclusion. Moreover the functors admits the following natural structures:
is the quotient map and \(i: {\mathcal {Z}}/G \hookrightarrow {\mathcal {Z}}'/G\) is the inclusion. Moreover the functors admits the following natural structures:
-
\(\Phi \) is naturally an equivalence of monoidal categories, and
-
\(\Phi \) and \(\Phi '\) intertwine the action of Frobenius on
 (resp.
(resp.  ) with the action of \(q\in {\mathbb{G}}_{m}\) on \({\operatorname {Coh}}({\mathcal {Z}}/G)\) (resp. \({\operatorname {Coh}}({\mathcal {Z}}'/G)\)).
) with the action of \(q\in {\mathbb{G}}_{m}\) on \({\operatorname {Coh}}({\mathcal {Z}}/G)\) (resp. \({\operatorname {Coh}}({\mathcal {Z}}'/G)\)).
Remark 2.18
We note that while it is expected that the above equivalences lift to \(\infty \)-categorical enhancements, it is not currently written in the literature explicitly. In our arguments (e.g. in Proposition 2.19) we do not need this stronger version; we use the equivalence to produce graded lifts of certain standard objects in the spectral affine Hecke category which may be done at the level of homotopy categories.
We point out certain distinguished sheaves in  and
and  (computed explicitly for \(G = SL_{2}, PGL_{2}\) in Examples 2.2.3-5 in [74]).
(computed explicitly for \(G = SL_{2}, PGL_{2}\) in Examples 2.2.3-5 in [74]).
-
(a)
Let \(\lambda \in X_{*}(T^{\vee}) = X^{*}(T) \subset W_{a}\) be a character of the maximal torus of \(G\), considered as an element of the affine Weyl group of the dual group. The Wakimoto sheaves \(J_{\lambda}\) are defined as follows. When \(\lambda \) is dominant, we take \(J_{\lambda }= j_{\lambda , *} \underline{\overline {\mathbb{Q}}_{\ell}}_{{\mathfrak {F}l}^{\lambda}}[ \langle 2\rho , \lambda \rangle ]\). When \(\lambda \) is antidominant, we take \(J_{\lambda }= j_{\lambda ,!} \underline{\overline {\mathbb{Q}}_{\ell}}_{{\mathfrak {F}l}^{\lambda}}[ \langle 2\rho , -\lambda \rangle ]\). In general, writing \(\lambda = \lambda _{1} - \lambda _{2}\), we define \(J_{\lambda }= J_{\lambda _{1}} * J_{-\lambda _{2}}\), which is independent of choices due to Corollary 1 in Sect. 3.2 of [2].
-
(b)
For any \(w \in W_{a}\), we define the corresponding costandard (resp. standard) object by \(\nabla _{w} := j_{w,*} \underline{\overline {\mathbb{Q}}_{\ell}}_{{\mathfrak {F}l}^{w}}[\ell (w)]\) (resp. \(\Delta _{w} := j_{w,!} \underline{\overline {\mathbb{Q}}_{\ell}}_{{\mathfrak {F}l}^{w}}[\ell (w)]\)). They are monoidal inverses by Lemma 8 in Sect. 3.2 of [2]. By Lemma 4 of [18], we have \(\nabla _{w} * \nabla _{w'} = \nabla _{ww'}\) (and likewise for standard objects) when \(\ell (w) + \ell (w') = \ell (ww')\). If \(\lambda \in X_{*}(T^{\vee}) = X^{*}(T)\) is dominant, then the Wakimoto is costandard \(J_{\lambda }= \nabla _{\lambda}\); if \(\lambda \) is antidominant, the Wakimoto is standard \(J_{\lambda }= \Delta _{\lambda}\).
-
(c)
Let \(w_{0} \in W_{f} \subset W_{a}\) be the longest element of the finite Weyl group. The antispherical projector or big tilting sheaf
 is defined to be the tilting extension of the constant sheaf \(\underline{\overline {\mathbb{Q}}_{\ell}}_{{\mathfrak {F}l}^{w_{0}}}\) of \({\mathfrak {F}l}^{w_{0}}\) to \({\mathfrak {F}l}\), as in Proposition 11 and Sect. 5 of [18]. Note that this object does not descend to
is defined to be the tilting extension of the constant sheaf \(\underline{\overline {\mathbb{Q}}_{\ell}}_{{\mathfrak {F}l}^{w_{0}}}\) of \({\mathfrak {F}l}^{w_{0}}\) to \({\mathfrak {F}l}\), as in Proposition 11 and Sect. 5 of [18]. Note that this object does not descend to  .
.
We abusively use the same notation to denote sheaves in  ; note that \(\pi ^{*} \Delta _{w} \simeq \Delta _{w}\) and \(\pi ^{*} \nabla _{w} \simeq \nabla _{w}\) by base change. All sheaves above are perverse sheaves, since the inclusion of strata are affine.
; note that \(\pi ^{*} \Delta _{w} \simeq \Delta _{w}\) and \(\pi ^{*} \nabla _{w} \simeq \nabla _{w}\) by base change. All sheaves above are perverse sheaves, since the inclusion of strata are affine.
For our applications, we need to work not with \({\mathcal {Z}}/G\) but with \({\mathcal {Z}}/G_{\mathrm {gr}}\) (recall that \(G_{\mathrm {gr}}= G \times {\mathbb{G}}_{m}\)). The following proposition is the key technical argument we need to construct the semiorthogonal decomposition of \({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})\) and hence deduce results on its homological invariants – a graded lift of standards and costandards under Bezrukavnikov’s theorem. It is conjectured in [18] (and announced in [54]) that the equivalences in Theorem 2.17 should have mixed versions, relating a mixed form of the Iwahori-equivariant category of \({\mathfrak {F}l}\) with a \({\mathbb{G}}_{m}\)-equivariant version of \({\operatorname {Coh}}({\mathcal {Z}}/G)\), i.e. \({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})\), which would immediately give us the desired result. In particular, see Example 57 in [18] for an expectation of what the sheaves \(\Phi (\Delta _{w})\) are explicitly and note that they have \({\mathbb{G}}_{m}\)-equivariant lifts.
Proposition 2.19
The objects \(\Phi (\nabla _{w}), \Phi (\Delta _{w}) \in {\operatorname {Coh}}({\mathcal {Z}}/G)\) have lifts to objects in \({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})\) for all \(w \in W_{a}\), compatible with the action of Frobenius under the equivalence in Theorem 2.17.
Proof
We will prove the statements for the standard objects; the statements for costandards follows similarly. Wakimoto sheaves are sent to twists of the diagonal \(\Phi (J_{\lambda}) \simeq {\mathcal {O}}_{\Delta}(\lambda )\) by Sect. 4.1.1 of [18], which evidently have \({\mathbb{G}}_{m}\)-equivariant lifts. Convolution is evidently \({\mathbb{G}}_{m}\)-equivariant, so the convolution of two sheaves with \({\mathbb{G}}_{m}\)-lifts also has a \({\mathbb{G}}_{m}\)-lift. Assuming that the standard objects corresponding to finite reflections have \({\mathbb{G}}_{m}\)-lifts, by Lemma 4 of [18] we can write the standard for the affine reflection as a convolution of Wakimoto sheaves and standard objects for finite reflections. Thus, we have reduced to showing that all standard objects \(\Phi (\Delta _{w})\) have \({\mathbb{G}}_{m}\)-lifts for \(w\) a simple finite reflection.
By Corollary 42 of [18] \(\Phi '\) has the favorable property that \({\mathcal {Z}}'\) is a classical (non-reduced) scheme, and that it restricts to a map on abelian categories on  taking values in \({\operatorname {Coh}}({\mathcal {Z}}'/G)^{\heartsuit}\) (though it is not essentially surjective). In particular, by Proposition 26 and Lemma 28 in [18] it takes the tilting sheaf \(\Xi \) to \({\mathcal {O}}_{{\mathcal {Z}}'/G}\), which manifestly has a \({\mathbb{G}}_{m}\)-lift.
taking values in \({\operatorname {Coh}}({\mathcal {Z}}'/G)^{\heartsuit}\) (though it is not essentially surjective). In particular, by Proposition 26 and Lemma 28 in [18] it takes the tilting sheaf \(\Xi \) to \({\mathcal {O}}_{{\mathcal {Z}}'/G}\), which manifestly has a \({\mathbb{G}}_{m}\)-lift.
We claim that \({\mathbb{G}}_{m}\)-lifts for the \(\Phi '(\Delta _{w}) \in {\operatorname {Coh}}({\mathcal {Z}}'/G)\) for \(w \in W_{f}\) induce \({\mathbb{G}}_{m}\)-lifts for the \(\Phi (\Delta _{w}) \in {\operatorname {Coh}}({\mathcal {Z}}/G)\). Since \({\mathcal {Z}}\) is a derived scheme, the functor \(i_{*}: {\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}}) \rightarrow {\operatorname {Coh}}({\mathcal {Z}}'/G_{\mathrm {gr}})\) is not fully faithful (i.e. objects on the left may have additional structure). But since \(\Phi '(\Delta _{w}) \simeq i_{*} \Phi (\Delta _{w})\) are in the heart and \(i_{*}\) is \(t\)-exact (for the standard \(t\)-structures) and conservative, we have that \(\Phi (\Delta _{w}) \in {\operatorname {Coh}}({\mathcal {Z}}/G)^{\heartsuit}\). Moreover, the restriction of \(i_{*}\) to \({\operatorname {Coh}}({\mathcal {Z}}/G)^{\heartsuit}\) is fully faithful, proving the claim. Thus, we have reduced to showing that the finite simple standard objects \(\Phi '(\Delta _{w}) \in {\operatorname {Coh}}({\mathcal {Z}}'/G)^{\heartsuit}\) have \({\mathbb{G}}_{m}\)-lifts; in particular these are objects in the abelian category of coherent sheaves.
By Lemma 4.4.11 in [19], \(\Xi \) is a successive extension of standard objects \(\Delta _{w}(\ell (w)/2)\) for \(w \in W_{f}\). Thus, there is a standard object \(\Delta _{w}(\ell (w)/2)\) and a surjection \(\Xi \twoheadrightarrow \Delta _{w}(\ell (w)/2)\), which is Frobenius-equivariant as it arises as a morphism in the mixed category. This implies that the kernel \(K = \ker (\Xi \twoheadrightarrow \Delta _{w}(\ell (w)/2))\) is a Frobenius-equivariant subobject of \(K\). On the spectral side, using Proposition 53 in op. cit., this means that \(\Phi '(K) \subset \Phi '(\Xi ) \simeq {\mathcal {O}}_{/{\mathcal {Z}}'/G}\) is a \(q\)-equivariant subobject with quotient \(\Phi '(\Delta _{w}(\ell (w)/2))\). We wish to show that the quotient has a \({\mathbb{G}}_{m}\)-equivariant lift, which amounts to showing that \(\Phi '(K)\) is a \({\mathbb{G}}_{m}\)-equivariant subobject.
Since \(\Phi (K)\) is already endowed with a \({\mathbb{G}}_{m}\)-equivariant structure, \(q\)-equivariance for a subobject of a \({\mathbb{G}}_{m}\)-equivariant object is property, not an additional structure. We claim that for \(q\) not a root of unity, any \(q\)-closed subsheaf of a \({\mathbb{G}}_{m}\)-equivariant sheaf on a quotient stack must be \({\mathbb{G}}_{m}\)-closed as well (i.e. the isomorphism defining the \({\mathbb{G}}_{m}\)-equivariant structure restricts to the subsheaf). Assuming this claim, and iterating the above argument replacing \(\Xi \) with the kernel \(K\), we find that \(\Phi '(\Delta _{w})\) has a \({\mathbb{G}}_{m}\)-equivariant lift for every \(w \in W_{f}\) (since the big tilting object contains every \(\Delta _{w}\) as a subquotient), completing the proof.
We now justify the claim. First, if ℱ is a sheaf on a quotient stack \(X/G\) with a \({\mathbb{G}}_{m}\)-action, we can forget the \(G\)-equivariance (i.e. base change to the standard atlas \(X \rightarrow X/G\)). Now, by reducing to an open affine \({\mathbb{G}}_{m}\)-closed cover of \(X\), we can assume \(X\) is affine. On an affine scheme \(X = \operatorname {Spec}(A)\), the \({\mathbb{G}}_{m}\)-action gives the structure of a ℤ-grading on \(A\), and a submodule of a graded \(A\)-module \(M' \subset M\) is \(q\)-equivariant if it is a sum of \(q\)-eigenspaces, and \({\mathbb{G}}_{m}\)-equivariant if it is a sum of homogeneous submodules. The claim follows from the observation that any \(m \in M'\) can only have eigenvalues \(q^{n}\) for \(n \in {\mathbb{Z}}\), which are distinct, so the \(q\)-eigenspaces entirely determine the \({\mathbb{G}}_{m}\)-weights. □
2.3 A semiorthogonal decomposition
In this section, we describe an “Iwahori-Matsumoto” semiorthogonal decomposition of the mixed affine Hecke category \(\mathbf {H}^{{\mathrm {m}}}:= {\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})\), arising from the stratification of the affine flag variety \({\mathfrak {F}l}\) on the automorphic side of Bezrukavnikov’s equivalence Theorem 2.17 and the lifting result in Proposition 2.19. This will, in turn, induce a direct sum decomposition on Hochschild homology. First, let us establish terminology.
Definition 2.20
Let \(\{ \mathbf {S}_{n} \}_{n\in \mathbb{N}}\) denote a collection of full subcategories of a small dg category \(\mathbf {C}\). We say that \(\{ \mathbf {S}_{n} \}\) defines a semiorthogonal decomposition of \(\mathbf {C}\) if there is an exhaustive left admissible filtration \(F_{n}\mathbf {C}\) of \(\mathbf {C}\) such that \(\mathbf {S}_{n}\) is the left orthogonal of \(F_{n-1}\mathbf {C}\) inside \(F_{n}\mathbf {C}\). In particular, in this case \(\operatorname{Hom}^{\bullet}_{\mathbf {C}}(X_{n}, X_{m}) \simeq 0\) for \(X_{i} \in \mathbf {S}_{i}\) and \(n > m\).
The following result is standard.
Proposition 2.21
Let \(G\) be a pro-affine group scheme acting nicely on an ind-scheme \(X\). Assume that the stabilizer of each orbit is connected, and that every \(G\)-closed subscheme of \(X\) is a union of finitely many \(G\)-orbits. Let \(I\) be an indexing set for the \(G\)-orbits \(X_{i}\) under the (partial) closure relation, i.e. \(X_{n} \subset \overline{X_{m}}\) implies \(m \geq n\), and let \(j_{n}: X_{n} \hookrightarrow X\) denote the inclusion. Then, \(\langle j_{n!} {\overline {\mathbb{Q}}_{\ell}}_{X_{n}}\rangle \) defines a semiorthogonal decomposition of \(\operatorname {Sh}^{G}(X)\), where the ordering is given by any choice of extension of the partial order to a total order.
Proof
It is standard that stratifications of stacks give rise to semi-orthogonal decompositions on categories of \(\ell \)-adic sheaves. We note that each orbit is equivariantly equivalent \(BH\) where \(H\) is the stabilizer (connected by assumption), and \(\operatorname {Sh}(BH)\) is generated by the constant sheaf \(\overline {\mathbb{Q}}_{\ell}\) when \(H\) is connected. □
Corollary 2.22
Fix a Bruhat ordering of the affine Weyl group \(W_{a}\). The standard objects \(\langle \nabla _{w} = j_{n!} {\overline {\mathbb{Q}}_{\ell}}_{X_{n}}\rangle \) give a semiorthogonal decomposition of \(\operatorname {Sh}^{\mathbf{I}}({\mathfrak {F}l})\).
Remark 2.23
The costandard objects \(\Delta _{w} = j_{n*} {\overline {\mathbb{Q}}_{\ell}}_{X_{n}}\) define a semiorthogonal decomposition in the reverse order.
We would like to lift the above semiorthogonal decomposition of \({\operatorname {Coh}}({\mathcal {Z}}/G)\) to \({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})\). We do so by applying Lemma 2.11 to the \({\mathbb{G}}_{m}\)-equivariant lifts of the objects \(\Phi (\Delta _{w})\) from Proposition 2.19. We will apply the following result to the setting:
recalling the de-equivariantization functor \((-)^{{\mathrm {dq}}}: \mathbf {C} \rightarrow \mathbf {C}^{{\mathrm {dq}}}= \mathbf {C} \otimes _{ \operatorname {Rep}(H)} \mathbf {Vect}_{k}\) from Sect. 2.1.1.
Corollary 2.24
Let \(H\) be a group-scheme over a field \(k\) of characteristic 0, and \(\mathbf {C}\) a compactly generated cocomplete \(\operatorname {Rep}(H)\)-module dg category. Let \(\{E_{n} \in \mathbf {C} \mid n \in \mathbb{N}\}\) be a linearly ordered set of objects such that \(\langle E_{n}^{{\mathrm {dq}}}\rangle \) defines a semiorthogonal decomposition of \(\mathbf {C}^{{\mathrm {dq}}}\). Denote by \(A_{n} = \underline{\operatorname {End}}_{\mathbf {C}}(E_{n})^{op}\) the \(\operatorname {Rep}(H)\)-algebras from Lemma 2.11. Then, we have an equivalence
Proof
Let \(\mathbf {C}^{{\mathrm {dq}}}_{n} := \langle E_{n}^{{\mathrm {dq}}}\rangle \) be the category generated by \(E_{n}^{{\mathrm {dq}}}\), and let \(\mathbf {C}_{n}\) be the preimage under \((-)^{{\mathrm {dq}}}\). The categories \(\mathbf {C}_{n}\) form a semiorthogonal decomposition of \(\mathbf {C}\), since \(\operatorname{Hom}_{\mathbf {C}}(X, Y) = \underline {\operatorname {Hom}}_{\mathbf {C}}(X, Y)^{G}\) by Lemma 2.11, and since \(\underline {\operatorname {Hom}}_{\mathbf {C}}(X, Y) = \operatorname{Hom}_{\mathbf {C}^{{\mathrm {dq}}}}(X^{{\mathrm {dq}}}, Y^{{\mathrm {dq}}})\) after forgetting the \(\operatorname {Rep}(G)\)-enriched structure on the left. Hochschild homology is a localizing invariant in the sense of [22], and in particular takes semiorthogonal decompositions to direct sums. Thus we have an equivalence \(HH(\mathbf {C}) \simeq \displaystyle \bigoplus _{n \in \mathbb{Z}} HH(\mathbf {C}_{n})\). Applying Lemma 2.11, we find \(\displaystyle HH(\mathbf {C}) \simeq \bigoplus _{n \in \mathbb{Z}} HH(A_{n}\text{-}\mathrm {mod}_{\operatorname {Rep}({\mathbb{G}}_{m})})\). □
We now compute the endomorphism algebras \(A_{w}\) as algebras in \(\operatorname {Rep}({\mathbb{G}}_{m})\), using the graded lifts from Proposition 2.19 and the semiorthogonal decomposition in Corollary 2.22.
Proposition 2.25
Let \(E_{w}\) denote the \({\mathbb{G}}_{m}\)-lifts of \(\Phi (\Delta _{w})\) constructed in Proposition 2.19, and \(A_{w} = \underline{\operatorname {End}}_{{\mathcal {Z}}/G_{\mathrm {gr}}}(E_{w}^{{\mathrm {dq}}})\). We have quasi-isomorphisms \(A_{w} \simeq \operatorname {Sym}_{\overline {\mathbb{Q}}_{\ell}} \mathfrak {h}[-2]\) where \(\mathfrak{h}[-2]\) is the universal dual Cartan shifted into cohomological degree 2 with \({\mathbb{G}}_{m}\)-weight 1. In particular, \(A_{w}\) is formal.
Proof
Since \(\Phi \) is an equivalence of categories we can compute \(A_{w}\) on the automorphic side. The unit map \(\mathcal{F} \rightarrow j^{!} j_{!} \mathcal{F}\) is an equivalence for \(j\) a locally closed immersion, so that

Since \({\mathfrak {F}l}^{w}\) is an  -orbit, letting
-orbit, letting  denote its stabilizer for a choice of base point in \({\mathfrak {F}l}^{w}\), we find that
denote its stabilizer for a choice of base point in \({\mathfrak {F}l}^{w}\), we find that  is the equivariant cohomology chain complex for
is the equivariant cohomology chain complex for  with \(\overline {\mathbb{Q}}_{\ell}\)-coefficients under the cup product. The reductive quotient (i.e. by the pro-unipotent radical) of
with \(\overline {\mathbb{Q}}_{\ell}\)-coefficients under the cup product. The reductive quotient (i.e. by the pro-unipotent radical) of  is the quotient torus \(H^{\vee}\), so \(A_{w} \simeq C^{\bullet}(BH^{\vee}; \overline {\mathbb{Q}}_{\ell})\). By Proposition 2.16, this algebra is formal and isomorphic to \(H^{\bullet}(BH^{\vee}; \overline {\mathbb{Q}}_{\ell}) \simeq \operatorname {Sym}_{\overline {\mathbb{Q}}_{\ell}} \mathfrak {h}[-2]\).
is the quotient torus \(H^{\vee}\), so \(A_{w} \simeq C^{\bullet}(BH^{\vee}; \overline {\mathbb{Q}}_{\ell})\). By Proposition 2.16, this algebra is formal and isomorphic to \(H^{\bullet}(BH^{\vee}; \overline {\mathbb{Q}}_{\ell}) \simeq \operatorname {Sym}_{\overline {\mathbb{Q}}_{\ell}} \mathfrak {h}[-2]\).
For the \({\mathbb{G}}_{m}\)-weight, recall that the pullback along multiplication by \(q\) corresponds under \(\Phi \) to the Frobenius automorphism. Thus, for \(q\) not a root of unity, the \(q^{n}\)-eigenspace and the homogeneous \({\mathbb{G}}_{m}\)-weight \(n\) part coincide, and the claim follows by Proposition 2.16. □
We now apply Corollary 2.24 to the set-up in the above proposition.
Corollary 2.26
Letting \(k = \overline {\mathbb{Q}}_{\ell}\) or ℂ, we have an isomorphism of \(k[z,z^{-1}]\)-modules
In particular, we have that
-
(1)
the Hochschild homology \(HH(\mathbf {H}^{{\mathrm {m}}})\) is cohomologically concentrated in degree zero,
-
(2)
the Chern character \(K(\mathbf {H}^{{\mathrm {m}}}) \rightarrow HH(\mathbf {H}^{{\mathrm {m}}})\) factors through \(K_{0}(\mathbf {H}^{{\mathrm {m}}})\), and
-
(3)
the map \(K_{0}(\mathbf {H}^{{\mathrm {m}}}) \otimes _{{\mathbb{Z}}} k \rightarrow HH(\mathbf {H}^{{\mathrm {m}}})\) is an equivalence.
Proof
The claim for ℂ follows from \(\overline {\mathbb{Q}}_{\ell}\) by fixing an isomorphism. Fix a Bruhat order on \(W_{a}\), extended to a total order. Applying Corollary 2.24 in the case \(\mathbf {C} = \mathbf {H}^{{\mathrm {m}}}= {\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})\), \(\mathbf {C} = \mathbf {H}= {\operatorname {Coh}}({\mathcal {Z}}/G)\), and \(H = {\mathbb{G}}_{m}\), we have a canonical equivalence
where \(A = \operatorname {Sym}^{\bullet }_{\overline {\mathbb{Q}}_{\ell}} \mathfrak {h}[-2] \simeq A_{w}\) is the algebra from Proposition 2.25 (which does not depend on \(w \in W_{a}\)). The Hochschild homology of \(A\text{-}\mathrm {perf}_{\operatorname {Rep}({\mathbb{G}}_{m})}\) is computed by the Block-Getzler complex of Definition 2.12, which we can compute explicitly. Its terms are \((A^{\otimes n+1} \otimes \overline {\mathbb{Q}}_{\ell}[z,z^{-1}])^{{\mathbb{G}}_{m}}\), and since \(z\) has \({\mathbb{G}}_{m}\)-weight 0, there is an isomorphism \((A^{\otimes n+1} \otimes \overline {\mathbb{Q}}_{\ell}[z,z^{-1}])^{{\mathbb{G}}_{m}} \simeq (A^{ \otimes n+1})^{{\mathbb{G}}_{m}} \otimes \overline {\mathbb{Q}}_{\ell}[z,z^{-1}]\) and we observe that \((A^{\otimes n+1})^{{\mathbb{G}}_{m}} = \overline {\mathbb{Q}}_{\ell}\) since each \(A\) is generated over \(\overline {\mathbb{Q}}_{\ell}\) by positive weights. Thus, the natural map \({\mathcal {C}}^{\bullet}_{{\mathbb{G}}_{m}}(\overline {\mathbb{Q}}_{\ell}) \rightarrow {\mathcal {C}}^{\bullet}_{{\mathbb{G}}_{m}}(A)\) is a quasi-isomorphism, so the first claim follows. Factorization through \(K_{0}\) follows since the Hochschild homology is coconnective.
To show that the map \(K_{0}(A\text{-}\mathrm {mod}_{\operatorname {Rep}({\mathbb{G}}_{m})}) \otimes _{{\mathbb{Z}}} \overline {\mathbb{Q}}_{\ell}\rightarrow HH(A \text{-}\mathrm {mod}_{\operatorname {Rep}({\mathbb{G}}_{m})}/\overline {\mathbb{Q}}_{\ell})\) is an equivalence, first note that since \(HH(A\text{-}\mathrm {mod}_{\operatorname {Rep}({\mathbb{G}}_{m})}/\overline {\mathbb{Q}}_{\ell})\) is concentrated in degree zero, the Chern character factors through \(K_{0}\), i.e. we have a commuting diagram for each summand

By Remark 2.15, the map \(K_{0}(\operatorname {Rep}({\mathbb{G}}_{m})) \rightarrow K_{0}(A\text{-}\mathrm {perf}_{\operatorname {Rep}({\mathbb{G}}_{m})})\) is an equivalence, since both sides are freely generated by \(K_{0}(\operatorname {Rep}({\mathbb{G}}_{m})) = HH(\operatorname {Rep}({\mathbb{G}}_{m}))\) by the character of a single object \([A]\), i.e. the free object. Using the semiorthogonal decomposition, these equivalences induce an equivalence \(K_{0}(\mathbf {H}^{{\mathrm {m}}}) \otimes _{\mathbb{Z}} \overline {\mathbb{Q}}_{\ell}\simeq HH(\mathbf {H}^{{\mathrm {m}}}/ \overline {\mathbb{Q}}_{\ell})\), which is an equivalence of algebras by Remark 2.15. □
We also have the following result for the non-\({\mathbb{G}}_{m}\)-equivariant version.
Corollary 2.27
Let \(k = \overline {\mathbb{Q}}_{\ell}\) or ℂ. The map of algebras \(K({\operatorname {Coh}}({\mathcal {Z}}/G)) \rightarrow HH({\operatorname {Coh}}({\mathcal {Z}}/G))\) factors through \(K_{0}\) and we have an isomorphism as dg \(k\)-modules
Proof
Essentially the same as the previous corollary, along with a direct calculation of the Hochschild homology of the formal dg ring \(HH(\operatorname {Sh}(BH^{\vee})) = HH(\operatorname {Sym}^{\bullet }_{k}(\mathfrak {h}[-2])\text{-}\mathrm {mod})\). □
2.4 Hochschild homology of the affine Hecke category
In this section, we will show that the trace decategorification of the mixed affine Hecke category \(\mathbf {H}^{{\mathrm {m}}}\) is the affine Hecke algebra ℋ, while the trace decategorification of the affine Hecke category \(\mathbf {H}\) is a derived variant of the group algebra of the extended affine Weyl group \(kW_{a}\). We assume that \(G\) has simply connected derived subgroup until Sect. 2.4.2, where we remove the assumption.
We begin by quoting the following celebrated theorem by Ginzburg, Kazhdan and Lusztig.
Theorem 2.28
Ginzburg-Kazhdan-Lusztig
Let \(k = \overline {\mathbb{Q}}_{\ell}\) or ℂ, and assume that \(G\) has simply connected derived subgroup. Then there is an equivalence of associative algebras \(\mathcal {H}\rightarrow K_{0}(\mathbf {H}^{{\mathrm {m}}}) \otimes _{{\mathbb{Z}}} k\), compatibly with an identification of the center with \(K_{0}(\operatorname {Rep}(G_{\mathrm {gr}})) \otimes _{{\mathbb{Z}}} k\). Likewise, there is an equivalence of associative algebras \(kW_{a} \simeq K_{0}(\mathbf {H}) \otimes _{{\mathbb{Z}}} k\) with center \(K_{0}(\operatorname {Rep}(G))\).
Proof
The only difference between our statement and that in [58] [34] is their Steinberg stack is the classical stack \(\pi _{0}({\mathcal {Z}})/G_{\mathrm {gr}}\), which has no derived structure. On the other hand, we are interested in \({\mathcal {Z}}/G_{\mathrm {gr}}\) which has better formal properties. The statement follows from the fact that the Grothendieck group is insensitive to derived structure, i.e. the ideal sheaf for the embedding \(\pi _{0}({\mathcal {Z}})/G_{\mathrm {gr}}\hookrightarrow {\mathcal {Z}}/G_{\mathrm {gr}}\) acts nilpotently on any coherent complex. Finally, note that while the statement of Theorem 3.5 of [58] and Theorem 7.2.5 in [34] are made for \(k = {\mathbb{C}}\), the proofs do not employ topological methods and apply to the isomorphic field \(\overline {\mathbb{Q}}_{\ell}\). □
For the remainder of the section, we let \(k = \overline {\mathbb{Q}}_{\ell}\) or ℂ. We combine the above theorem with Corollary 2.26 to arrive at the following main theorem. We will remove the simply connectedness assumption in Sect. 2.4.2.
Theorem 2.29
Assume that \(G\) has simply connected derived subgroup. There is an equivalence of algebras, and an identification of the center:

Proof
That the map is an isomorphism is a combination of Theorem 1.2 and Corollary 2.26. □
The following non-mixed variant may also be of interest, and is the analogue to Corollary 2.27. In this case, the map to Hochschild homology is not an equivalence, though it does induce an equivalence on \(HH_{0}\). We note that the dg algebra \(\operatorname {Sym}^{\bullet }_{k}(\mathfrak {h}[-1] \oplus \mathfrak {h}[-2])\) appearing in the statement is equivalent to \(C^{\bullet}(H^{\vee }\times BH^{\vee})\).
Corollary 2.30
With the assumptions above, there is a commuting diagram of algebras:

Proof
By Corollary 2.27, the Hochschild homology \(HH({\operatorname {Coh}}({\mathcal {Z}}/G))\) is coconnective, so the Chern character from \(K({\operatorname {Coh}}({\mathcal {Z}}/G))\) factors through \(K_{0}({\operatorname {Coh}}({\mathcal {Z}}/G)) \otimes _{{\mathbb{Z}}} k = kW_{a}\). Thus we have a map of algebras \(kW_{a} \rightarrow HH({\operatorname {Coh}}({\mathcal {Z}}/G))\) which induces an equivalence on \(H^{0}\). Next, note that the subcategory  generated by the monoidal unit (i.e. the skyscraper sheaf \(\delta _{e}\)), which is closed under the monoidal structure, is in the center of \({\operatorname {Coh}}({\mathcal {Z}}/G)\), so that the subalgebra \(HH(\langle \delta _{e} \rangle ) \simeq \operatorname {Sym}^{\bullet }_{k}(\mathfrak {h}[-1] \oplus \mathfrak {h}[-2]) \subset HH({\operatorname {Coh}}({\mathcal {Z}}/G))\) is central. This defines a map of algebras \(HH(\langle \delta _{e} \rangle )\text{-}\mathrm {mod}\rightarrow HH({\operatorname {Coh}}({\mathcal {Z}}/G))\), which defines a map of algebras out of the tensor product \(HH(\langle \delta _{e} \rangle ) \otimes _{k} kW_{a} \rightarrow HH({\operatorname {Coh}}({\mathcal {Z}}/G))\) which is an equivalence when restricted to each tensor factor; thus it is an equivalence. □
generated by the monoidal unit (i.e. the skyscraper sheaf \(\delta _{e}\)), which is closed under the monoidal structure, is in the center of \({\operatorname {Coh}}({\mathcal {Z}}/G)\), so that the subalgebra \(HH(\langle \delta _{e} \rangle ) \simeq \operatorname {Sym}^{\bullet }_{k}(\mathfrak {h}[-1] \oplus \mathfrak {h}[-2]) \subset HH({\operatorname {Coh}}({\mathcal {Z}}/G))\) is central. This defines a map of algebras \(HH(\langle \delta _{e} \rangle )\text{-}\mathrm {mod}\rightarrow HH({\operatorname {Coh}}({\mathcal {Z}}/G))\), which defines a map of algebras out of the tensor product \(HH(\langle \delta _{e} \rangle ) \otimes _{k} kW_{a} \rightarrow HH({\operatorname {Coh}}({\mathcal {Z}}/G))\) which is an equivalence when restricted to each tensor factor; thus it is an equivalence. □
2.4.1 \(q\)-Specializations of the affine Hecke algebra
Let \(q: {\mathcal {Z}}/G \rightarrow {\mathcal {Z}}/G\) be the action by \(q \in {\mathbb{G}}_{m}\) under our conventions, i.e. multiplying by \(q^{-1}\). In this section we compute the trace of the functorFootnote 14\(q_{*}\) on the category \(\mathbf {H}= {\operatorname {Coh}}({\mathcal {Z}}/G)\). First, we make the general observation that if \(F\) is an automorphism of a small dg category \(\mathbf {C}\) and \({\mathcal {E}}\in \mathbf {C}\), then an \(F\)-equivariant structure on ℰ induces an automorphism of the dg algebra \(A = \operatorname {End}_{\mathbf {C}}({\mathcal {E}})\), and thus an automorphism of the category \(A\text{-}\mathrm {perf}\) which we denote \(F_{A}\). This \(F\)-equivariant structure on ℰ defines a commuting structure for an equivalence of pairs \((A\text{-}\mathrm {perf}, F_{A}) \rightarrow (\langle {\mathcal {E}}\rangle , F)\).
Proposition 2.31
Let \(q \ne 1\) and let \(A_{w}\) denote the algebras from Proposition 2.25. Then, \(HH(A_{w}, q_{*}) \simeq k\).
Proof
First, observe that the functor \(q_{*}\) induces the automorphism on the algebra \(A_{w} \simeq \operatorname {Sym}_{k} \mathfrak {h}^{*}[-2]\) arising via the \(q\)-scaling map on \(\mathfrak {h}\) (in particular, \(\mathfrak {h}^{*}\) has weight −1). The claim is a direct calculation using the complex \(C_{q}(A_{w}, {\mathbb{G}}_{m})\) from Definition 2.12 via Koszul resolutions: \(C_{q}(A_{w}, {\mathbb{G}}_{m})\) is the derived tensor product \(A_{w} \otimes _{A_{w} \otimes A_{w}}^{L} A_{w}\) where \(A_{w}\) is the diagonal bimodule for one factor and is twisted by \(q_{*}\) on the other factor.
Rather than a direct calculation, we give a geometric argument. First, note that \(q_{*}\) preserves the \({\mathbb{G}}_{m}\)-weights of \(A_{w} \simeq \operatorname {Sym}^{\bullet }_{k} \mathfrak {h}^{*}[-2]\) (i.e. since \(q \in {\mathbb{G}}_{m}\) is central). We apply a Tate shearing (i.e. sending cohomological-weight bidegree \((a, b)\) to \((a - 2b, b)\)) to the algebra \(\operatorname {Sym}_{k} \mathfrak {h}^{*}[-2]\) to obtain the algebra \({\mathcal {O}}(\mathfrak {h}) = \operatorname {Sym}^{\bullet }_{k} \mathfrak {h}^{*}\). Note that \(HH(\operatorname {Perf}({\mathfrak {h}}), q_{*}) = {\mathcal {O}}({\mathfrak {h}}^{q})\), i.e. functions on the derived fixed points of action by \(q\). When \(q \ne 1\) we have \({\mathfrak {h}}^{q} = \{0\}\), so \(HH(\operatorname {Perf}({\mathfrak {h}}), q_{*}) = k\). Undoing the shearing, we find that the natural map \(HH(A_{w}, q_{*}) \rightarrow HH(k, q_{*})\) is an equivalence. □
Corollary 2.32
Let \({\mathcal {H}}_{q}\) denote the specialization of the affine Hecke algebra at \(q \in {\mathbb{G}}_{m}\). If \(q \ne 1\), we have an equivalence of algebras
Proof
The calculation in Proposition 2.31 shows that specialization at \(q \in {\mathbb{G}}_{m}\) induces an equivalence on Block-Getzler complexes (viewing \(A_{w}\) as an algebra in \(\operatorname {Rep}({\mathbb{G}}_{m})\)):
inducing an equivalence \(HH({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})) \otimes _{k[z,z^{-1}]} k_{q} \simeq HH( {\operatorname {Coh}}({\mathcal {Z}}/G), q_{*})\), since the trace of an endofunctor \(F\) on a category \(\mathbf {C}\) takes semiorthogonal decompositions preserved by \(F\) to direct sums. Consequently, under the identification of algebras \(HH({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})) \simeq \mathcal {H}\), specialization at \(q\) defines an equivalence \(HH({\operatorname {Coh}}({\mathcal {Z}}/G), q_{*}) \simeq \mathcal {H}_{q}\). □
Remark 2.33
The above corollary is evidently untrue for \(q=1\), since ℋ is flat over \(k[z,z^{-1}]\) but \(HH(\mathbf {H})\) has derived structure by Corollary 2.30.
Remark 2.34
Our methods also allow for an identification of the following monodromic variants of the affine Hecke category introduced in [18] (where \({\mathcal {Z}}' = \widetilde {\mathfrak {g}} \times _{\mathfrak {g}} \widetilde {{\mathcal {N}}}\) and \({\mathcal {Z}}^{\wedge}\) is the formal completion of \(\widetilde {\mathfrak {g}} \times _{\mathfrak {g}} \widetilde {\mathfrak {g}}\) along \({\mathcal {Z}}\)):
The category \({\operatorname {Coh}}({\mathcal {Z}}'/G_{\mathrm {gr}})\) is not monoidal, so it does not make sense to ask that it is identified with ℋ as an algebra. However, it is equivalent to ℋ as a (right) module for \(HH({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})) \simeq {\mathcal {H}}\). The category \({\operatorname {Coh}}({\mathcal {Z}}^{\wedge}\!/G_{\mathrm {gr}})\) does not have a monoidal unit, and its monoid structure is trivial; in [33] an enlargement of \({\operatorname {Coh}}({\mathcal {Z}}^{\wedge}\!/G_{\mathrm {gr}})\) will be defined to resolve these issues (see also [19]) but we will not address it here.
In these cases the generating object \(E_{w} = \underline{\overline {\mathbb{Q}}_{\ell}}_{{\mathfrak {F}l}^{w}}\) for each stratum on the automorphic side live in different categories, resulting in different endomorphism algebras (see Proposition 2.25). Recall that for \({\mathcal {Z}}\), the category appearing is \(D(BH^{\vee})\) so we had \(A_{w} = C^{\bullet}(BH^{\vee}; \overline {\mathbb{Q}}_{\ell}) \simeq \operatorname {Sym}^{\bullet }_{\overline {\mathbb{Q}}_{\ell}} \mathfrak {h}[-2]\). For \({\mathcal {Z}}'\), the category is \(D(\operatorname {pt})\), so \(A'_{w} = \overline {\mathbb{Q}}_{\ell}\). For \({\mathcal {Z}}^{\wedge}\!\), the category is  , the full subcategory of sheaves with unipotent monodromy, and \(A^{\wedge}_{w} \simeq C^{\bullet}(H^{\vee}; \overline {\mathbb{Q}}_{\ell}) \simeq \operatorname {Sym}^{\bullet }_{ \overline {\mathbb{Q}}_{\ell}} \mathfrak {h}[-1]\).
, the full subcategory of sheaves with unipotent monodromy, and \(A^{\wedge}_{w} \simeq C^{\bullet}(H^{\vee}; \overline {\mathbb{Q}}_{\ell}) \simeq \operatorname {Sym}^{\bullet }_{ \overline {\mathbb{Q}}_{\ell}} \mathfrak {h}[-1]\).
For the enlargement of \({\operatorname {Coh}}({\mathcal {Z}}^{\wedge}\!)\) from [33], the constant sheaf does not generate on each stratum, and instead one should take a “cofree monodromic” sheaf (defined in op. cit.) whose endomorphisms \(\widehat {\operatorname {Sym}}^{\bullet}_{\overline {\mathbb{Q}}_{\ell}} \mathfrak {h}^{*}\) are Koszul dual to \(A^{\wedge}_{w} = \operatorname {Sym}^{\bullet }\mathfrak {h}[-1]\). Likewise, for \({\operatorname {Coh}}({\mathcal {Z}})\) the constant sheaf is not compact, and rather than coherent sheaves one could have considered the smaller category of compact sheaves. The generator then is the induced sheaf, which has endomorphisms \(C_{\bullet}(H^{\vee}; \overline {\mathbb{Q}}_{\ell}) \simeq \operatorname {Sym}^{\bullet }_{\overline {\mathbb{Q}}_{\ell}} \mathfrak {h}^{*}[1]\), which is Koszul dual to \(A_{w} = \operatorname {Sym}^{\bullet }_{\overline {\mathbb{Q}}_{\ell}} \mathfrak {h}[-2]\).
2.4.2 Groups of non-simply connected type
In this section we will remove the simply connectedness assumptions from earlier theorems. We work in the following set-up. Let \(G\) be a reductive algebraic group with simply connected derived subgroup, and \(\phi : G \rightarrow G'\) a central isogeny with kernel \(Z\) (i.e. a quotient by a finite subgroup \(Z\) of the center). Following Sect. 1.5 of [76], this induces a \(Z\)-action on \({\mathcal {H}}_{G}\) via the formula
Equivalently, the affine Hecke algebra has a multiplicative grading by characters of \(Z\), i.e.
and we have an identification of \({\mathcal {H}}_{G'}\) with the trivial graded part or \(Z\)-invariants
Our goal will be to prove a similar formula in Hochschild homology, which arises when the category is equipped with a \(Z\)-trivialization in the following sense.
Definition 2.35
Let \(G\) be an affine algebraic group with central subgroup \(Z \subset G\), and \(\mathbf {C}\) be a \(\operatorname {Rep}(G)\)-module category. A \(Z\)-trivialization of \(\mathbf {C}\) is a \(\operatorname {Rep}(G/Z)\)-linear category \(\mathbf {C}'\) and an equivalence \(\mathbf {C} \simeq \mathbf {C}' \otimes _{\operatorname {Rep}(G/Z)} \operatorname {Rep}(G)\).
Remark 2.36
If \(G\) is reductive (thus \(Z\) is semisimple), then we have a decomposition of \(\operatorname {Rep}(G)\) into \(\operatorname {Rep}(G/Z)\)-module categories by \(Z\)-characters. Via the \(Z\)-trivialization, this gives a decomposition of \(\mathbf {C}\) into \(\operatorname {Rep}(G)\)-module categories
where the natural functor \(\mathbf {C}' \rightarrow \mathbf {C}\) induces an equivalence \(\mathbf {C}' \simeq \mathbf {C}_{\mathrm{triv}}\) with the trivial block. In this setting, the direct sum decomposition of \(\mathbf {C}\) induces a \(X^{\bullet}(Z)\)-grading in Hochschild homology
such that \(HH(\mathbf {C}_{\mathrm{triv}}) \simeq HH(\mathbf {C}')\). Since the sum decomposition is evidently functorial for \(\operatorname {Rep}(G)\)-functors compatible with trivializations, so is the grading on Hochschild homology.
It remains to show that these \(X^{\bullet}(Z)\)-gradings agree via the identifications in Theorem 2.29.
Proposition 2.37
The identification \({\mathcal {H}}\simeq HH(\mathbf {H}^{{\mathrm {m}}})\) of Theorem 2.29are compatible with the \(X^{\bullet}(Z)\)-gradings defined in Equation (2.1) and Remark 2.36.
Proof
We claim that the \(Z\)-action on ℋ defined in [76] induces a decomposition of ℋ into eigenspaces indexed by \(W_{f}\) double cosets \(W_{f} \lambda W_{f} \subset W_{a}\) for \(\lambda \in X^{\bullet}(T)\), spanned by Iwahori-Matsumoto basis elements \(T_{w}\) for \(w \in W_{f} \lambda W_{f}\), with eigenvalue \(\lambda |_{Z}\). This claim can be directly verified, e.g. using the Bernstein relations in Sect. 7.1 of [34]. This \(X^{\bullet}(Z)\)-eigenbasis of ℋ corresponds under Theorem 2.29 to the basis \(\{[\mathrm{id}_{\Phi (\Delta _{w})}] \mid w \in W_{a}\} \subset HH( \mathbf {H}^{{\mathrm {m}}})\), i.e. identity maps for the spectral-side standard objects \(\Phi (\Delta _{w})\) described in Sect. 2.2, which we need to verify is an eigenbasis with corresponding eigenvalues.
By functoriality, for any functor \(F: \mathbf {C} \rightarrow \mathbf {D}\) of categories in our set-up, if \([\mathrm{id}_{X}] \in HH_{0}(\mathbf {C})\) is a \(\lambda \)-eigenvector for \(Z\), then \([\mathrm{id}_{F(X)}] \in HH_{0}(\mathbf {D})\) is as well; the converse is true if \(F\) is faithful on the homotopy category (i.e. \(H^{0}(\operatorname{Hom}^{\bullet}(X, X)) \rightarrow H^{0}(\operatorname{Hom}^{\bullet}(F(X),F(X)))\) is injective). We will use this fact repeatedly. In particular, since the forgetful functor \({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}}) \rightarrow {\operatorname {Coh}}({\mathcal {Z}}/G)\) is faithful, we can forget \({\mathbb{G}}_{m}\)-equivariance, and since the \(Z\)-action is compatible with convolution, it suffices to check our statement for finite reflections and the lattice.
For the lattice, we have \(\Phi (\Delta _{\lambda}) \simeq \Delta _{*} {\mathcal {O}}_{\widetilde {{\mathcal {N}}}}(\lambda ) = \Delta _{*} p^{*} V_{\lambda }\in {\operatorname {Coh}}({\mathcal {Z}}/G)\), where \(p: \widetilde {{\mathcal {N}}}/G \rightarrow BB\) is the projection. The eigenvalue for the identity map of \(V_{\lambda }\in {\operatorname {Coh}}(BB)\) is evidently \(\lambda |_{Z}\). For finite simple reflections, since \(i_{*}\) is fully faithful on the homotopy category we may instead consider the equivalence \(\Phi '\). Here, the spectral-side object corresponding to the automorphic big tilting object is \({\mathcal {O}}_{{\mathcal {Z}}'/G}\). By applying functoriality to the pullback from a point we see that the identity on any structure sheaf has trivial \(Z\)-eigenvalue, and therefore any subquotient does, thus \(\Phi '(\Delta _{w})\) and \(\Phi (\Delta _{w})\) do. □
Corollary 2.38
The statements of Theorem 2.29, Corollary 2.30and Corollary 2.32hold without the assumption that \(G\) has simply connected derived subgroup.
Proof
By Theorem 2.29, we have an identification \(HH(\mathbf {H}^{{\mathrm {m}}}_{G}) \simeq {\mathcal {H}}_{G}\). Since the center \(Z\) acts on \({\mathcal {Z}}\) and \({\mathcal {Z}}'\) trivially, the categories \({\operatorname {Coh}}({\mathcal {Z}}/G)\) and \({\operatorname {Coh}}({\mathcal {Z}}'/G)\) come equipped with natural \(Z\)-trivializations, and thus their Hochschild homologies have \(X^{\bullet}(Z)\)-gradings. By Proposition 2.37 the two gradings coincide under our equivalence, proving the claim. □
3 Traces of representations of convolution categories
We have seen in Theorem 2.29 that the affine Hecke algebra ℋ is identified with the Hochschild homology of the (mixed) affine Hecke category \(\mathbf {H}^{{\mathrm {m}}}={\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})\). In this section we describe a general theory of categorical traces in derived algebraic geometry to explain why this is a useful realization. Namely, as an application we will see in Sect. 4 that the geometric realization of Hochschild homology via derived loop spaces implies a realization of the affine Hecke algebra as endomorphisms of the coherent Springer sheaf, a certain coherent sheaf on the loop space of the stacky nilpotent cone. Hence, we deduce a localization description of the category of modules for the affine Hecke algebra as the category of coherent sheaves generated by the coherent Springer sheaf.
3.1 Traces of monoidal categories
In this section we present the two different trace decategorifications for a monoidal category and their relation. See [8, 9, 30, 46, 55] for detailed exposition.
Definition 3.1
Let \((\mathbf {A},\ast )\) denote an \(E_{1}\)-monoidal compactly generated cocomplete \(k\)-linear dg category and \(F\) a monoidal endofunctor. There are two notions of its Hochschild homology or trace. See definitions in Sect. 2.1.1.
-
(1)
The naive or vertical trace (or Hochschild homology) is a chain complex \(\mathrm{tr}(\mathbf {A}, F)=HH(\mathbf {A}, F)\). Via functoriality of traces, and under the assumptions that the multiplication functor \(\ast : \mathbf {A} \otimes \mathbf {A} \rightarrow \mathbf {A}\) preserves compact objects and that the monoidal unit is compact, it has the additional structure of an associative (or \(E_{1}\)-)algebra \((HH(\mathbf {A}),\ast )\).
-
(2)
The 2-categorical or horizontal trace (or monoidal/categorical Hochschild homology) is a dg categoryFootnote 15\({\mathbf {Tr}}((\mathbf {A}, \ast ), F) = \mathbf {A} \otimes _{\mathbf {A} \otimes \mathbf {A}^{rv}} \mathbf {A}_{F}\) where \(\mathbf {A}_{F}\) is the (\(E_{1}\)-)monoidal category whose left action is twisted by \(F\).Footnote 16 Via functoriality of traces, the horizontal trace is the tautological receptacle for characters in \(\mathbf {A}\):
$$ [-]: \mathbf {A} \rightarrow {\mathbf {Tr}}((\mathbf {A}, \ast ), F). $$The monoidal unit \(1_{\mathbf {A}}\) itself defines an object \([1_{\mathbf {A}}]\in \mathbf {Tr}((\mathbf {A},\ast ),F)\), i.e. \(\mathbf {Tr}((\mathbf {A},\ast ), F)\) is a pointed (or \(E_{0}\)-)category.
We sometimes omit the monoidal product ∗ from the notation, and when \(F = \mathrm{id}_{\mathbf {C}}\) we also sometimes omit it from the notation.
We define the notion of characters in horizontal traces more precisely and generally below. These more general notions are used primarily in Sect. 3.4.
Definition 3.2
One can view the horizontal trace as a trace decategorification in the sense of Definition 2.1 in the following way, following Sect. 3.6 of [46]. We consider the symmetric monoidal “Morita” category \(\mathbf {Mor}_{k}\), whose objects are the \((\infty , 2)\)-categories \(\mathbf {A}\text{-}\mathbf {mod}\), i.e. left-module categories for a monoidal category \(\mathbf {A}\), and whose 1-morphisms
are \((\mathbf {B}, \mathbf {A})\)-bimodule categories, and 2-morphisms are functors of bimodule categories.Footnote 17 Then, for a monoidal endofunctor \(F: \mathbf {A} \rightarrow \mathbf {A}\), we have \(\mathrm{tr}(\mathbf {A}\text{-}\mathbf {mod}, F) = {\mathbf {Tr}}(\mathbf {A}, \mathbf {A}_{F})\).
We can apply Definition 2.7 to obtain the following more general notion of character map for the horizontal trace (see Sect. 3.8.2 in [46]). That is, the horizontal trace \({\mathbf {Tr}}(\mathbf {A}, F)\) can be viewed as the tautological receptacle for characters \([(\mathbf {M}, F_{\mathbf {M}})]\) of left \(\mathbf {A}\)-module categories \(\mathbf {M}\) equipped with an \(F\)-semilinear endofunctor \(F_{\mathbf {M}}\), i.e. a map of \(\mathbf {A}\)-module categories \(F_{\mathbf {M}}: \mathbf {M} \rightarrow \mathbf {M}_{F} := \mathbf {A}_{F} \otimes _{ \mathbf {A}} \mathbf {M}\).Footnote 18
The trace \([A]\) of objects \(A \in \mathbf {A}\) in Definition 3.1 above is a special case in the following way: consider \(\mathbf {M} := \mathbf {A}\) as the usual (left) regular \(\mathbf {A}\)-module category; for \(A \in \mathrm{Ob}(\mathbf {A})\), we define \(F_{A}(-) := F(-) \ast A\). In this case, we have \([A] = [\mathbf {A}, F_{A}]\). In particular, the trace of the monoidal unitFootnote 19 is \([1_{\mathbf {A}}] = [\mathbf {A}, F]\), i.e. the trace of the regular representation.
Moreover, the categorical trace provides a “delooping” of the naive trace. To make the relationship between the two traces precise, we first recall the notion of a rigid monoidal category (see Definition 9.1.2 and Lemma 9.1.5 in [45]).
Definition 3.3
Let \(\mathbf {A}\) be a compactly generated stable monoidal \(\infty \)-category, with multiplication \(\mu : \mathbf {A} \otimes \mathbf {A} \rightarrow \mathbf {A}\). We say \(\mathbf {A}\) is rigid if the monoidal unit is compact, \(\mu \) preserves compact objects, and if every compact object of \(\mathbf {A}\) admits a left and right (monoidal) dual.
We have the following relationship between vertical and horizontal traces of [46], which may be interpreted via Theorem 1.1 of [30] as a compatibility of iterated traces. Let \(\mathbf {A}\) be a monoidal category, and \(F\) a monoidal endofunctor. We denote by \((\mathbf {A}, F)\text{-}\mathbf {mod}\) the 1-category (i.e. forget the 2-morphisms) of \(\mathbf {A}\)-module categories with \(F\)-semilinear endofunctors as in Definition 3.2.
Theorem 3.4
Theorem 3.8.5 [46], Theorem 1.1 [30]
Assume that \(\mathbf {A}\) is compactly generated and rigid monoidal, and \(F\) a monoidal endofunctor. Then, there is an equivalence of algebrasFootnote 20
More generally, there is an equivalence of functors from the category of \(F\)-equivariant module categories:
In particular, assuming that \([\mathbf {A}, F]\) is a compact object, then the left adjoint to the functor \(\operatorname{Hom}_{{\mathbf {Tr}}(\mathbf {A}, F)}([\mathbf {A},F], -)\) defines a fully faithful embedding which preserves compact objects, whose essential image is the category generated by \([\mathbf {A}, F]\):

3.2 Traces in geometric settings
The geometric avatar for Hochschild homology is the derived loop space (or more generally, the derived fixed points of a self-map), see [5, 8] for extended discussions.
Definition 3.5
Let \(X\) be a derived stack.
-
(1)
We define the derived loop space \({\mathcal {L}}X\) (or derived inertia stack) to be
$$ {\mathcal {L}}X = \operatorname {Map}_{\mathbf {DSt}_{k}}(S^{1}, X) \simeq X \mathbin {\mathop {\times }\limits _{X \times X}} X $$i.e. the derived mapping stack from a circle, or more concretely the derived self-intersection of the diagonal.
-
(2)
More generally, if \(\phi : X \rightarrow X\) is a self-map, we define the derived fixed points or \(\phi \)-twisted loop space \({\mathcal {L}}_{\phi }X\) to be the fiber product
i.e. the derived intersection of the diagonal with the graph \(\Gamma _{\phi }= \mathrm{id}_{X} \times \phi \) of \(\phi \). Note that the derived fixed points of the identity is the derived loop space, i.e. \({\mathcal {L}}_{\mathrm{id}_{X}} X = {\mathcal {L}}X\).
-
(3)
The formation of derived loop spaces and derived fixed points are functorial, i.e. if \(f: X \rightarrow Y\) is map of derived stacks, and \(\phi _{X}\), \(\phi _{Y}\) are compatible self-maps, then we have a map of derived stacks \({\mathcal {L}}_{\phi} f: {\mathcal {L}}_{\phi _{X}} X \rightarrow {\mathcal {L}}_{\phi _{Y}} Y\).
Example 3.6
For \(X\) a scheme over a characteristic 0 field \(k\) we have that the derived loop space \({\mathcal {L}}X\simeq \mathbb{T}_{X}[-1]\) is the total space of the shifted tangent complex to \(X\) (see Proposition 4.4 in [5]), while for \(X=\operatorname {pt}/G\) we have \({\mathcal {L}}X=G/G\simeq \mathrm{Loc}_{G}(S^{1})\), i.e. the classical inertia stack (see Proposition 2.1.8 in [31]). For a general stack the loop space is a combination of the shifted tangent complex with the inertia stack.
Example 3.7
For us, the self-maps above will arise via a action of a group \(G\) on \(X\), i.e. for \(g \in G(k)\) we obtain a map \(g: X \rightarrow X\). Then, we have the relationship \({\mathcal {L}}_{g} X = {\mathcal {L}}(X/G) \times _{{\mathcal {L}}(BG)} \{g\}\).
Note the parallel between the loop space, which is the self-intersection of the diagonal (the identity self-correspondence from \(X\)) and Hochschild homology (the trace of the identity on a category). As a result the push-pull functoriality of categories of sheaves under correspondences implies an immediate relation between their Hochschild homology and loop spaces. Since \(\operatorname {QC}\) is functorial under ∗-pullbacks and \(\operatorname {QC}^{!}\) under !-pullbacks, this produces the following answers, both of which hold in particular for QCA stacks (see Corollary 4.2.2 of [8, 38], and Example 2.2.10 in [31]):
In other words, taking \(\phi = \mathrm{id}_{X}\), the Hochschild homology of \(\operatorname {QC}(X)\) (respectively \(\operatorname {QC}^{!}(X)\)) is given by functions (respectively volume forms) on the derived loop space. For \(X=\operatorname {Spec}(R)\) a smooth affine scheme, along with Example 3.6 this recovers the Hochschild-Kostant-Rosenberg identification of Hochschild homology of \(R{\operatorname {-mod}}\) with differentials on \(R\),
Example 3.8
Quasicoherent sheaves under tensor product
Let \(X\) be a perfect stack in the sense of [9]. Then, the symmetric monoidal structure on \(\operatorname {QC}(X)\) via tensor product has compact unit and multiplication. We have that \(HH(\operatorname {QC}(X)) = {\mathcal {O}}({\mathcal {L}}X)\) is an algebra object (with the multiplication given by the shuffle product after passing through HKR as in Example 3.6; see Sect. 4.2 of [64] for a discussion of this structure), and the universal trace \(\operatorname {QC}(X) \rightarrow {\mathbf {Tr}}(\operatorname {QC}(X)) = \operatorname {QC}({\mathcal {L}}X)\) given by pullback along evaluation at the identity. Furthermore, the monoidal unit is \({\mathcal {O}}_{X} \in \operatorname {QC}(X)\) with trace \([{\mathcal {O}}_{X}] = {\mathcal {O}}_{{\mathcal {L}}X} \in \operatorname {QC}({\mathcal {L}}X)\). Finally, we have
where the fully faithful inclusion is an equivalence if \(X\) is affine.
We now establish a certain Calabi-Yau property of derived fixed points of smooth stacks (or more generally, smooth maps). In our arguments it will be useful to factor the loop space of a map \({\mathcal {L}}f: {\mathcal {L}}X \rightarrow {\mathcal {L}}Y\) through the following intermediate derived stack, which we define in three equivalent ways.
Definition 3.9
Let \(f: X \rightarrow Y\) be a map of derived stacks with compatible self-maps \(\phi _{X}\), \(\phi _{Y}\), and define \(Z := X \times _{Y} X\). We define \({\mathcal {L}}_{\phi }Y_{X}\) via the pullback diagrams:

Roughly, this is the derived moduli stack of paths in \(X\) mapping to loops in \(Y\).
The following lemma is a straightforward verification of the depicted diagrams, which we leave to the reader.
Lemma 3.10
The above three presentations are canonically equivalent, and we have a canonical factorization

where the maps are realized via the base change

i.e. \(\delta \) is a base change of the relative diagonal for \(f\), and \(\pi \) is a base change of \(f\) itself.
Example 3.11
When \(\phi \) is the identity and \(Y = \operatorname {pt}\), the factorization above is just \({\mathcal {L}}X \rightarrow X \rightarrow \operatorname {pt}\).
When \(X\) is a smooth stack, there is an equivalence of categories \(\operatorname {Perf}(X) = {\operatorname {Coh}}(X)\), thus by (3.1) we expect that \({\mathcal {O}}({\mathcal {L}}X) \simeq \omega ({\mathcal {L}}X)\). It turns out that this equivalence on global sections comes from a map on the underlying sheaves themselves. We now establish the following Calabi-Yau property of derived fixed points of smooth stacks, which we will use repeatedly in our arguments. We refer the reader to Sect. 8 of [37] for discussion of quasi-smoothness for derived Artin stacks.
Lemma 3.12
Let \(X\), \(Y\) be derived Artin stacks equipped with proper self-maps \(\phi _{X}\), \(\phi _{Y}\), and let \(f: X \rightarrow Y\) be a smooth relative Artin 1-stackFootnote 21commuting with \(\phi _{X}\), \(\phi _{Y}\). Then, there is a canonical equivalence of functors
In particular, if \(X\) is a smooth Artin 1-stack with a proper self-map \(\phi \), then \(\omega _{{\mathcal {L}}_{\phi }X} \simeq {\mathcal {O}}_{{\mathcal {L}}_{\phi }X}\), and if \(f\) is proper then \({\mathcal {L}}_{\phi }f^{*}\) is biadjoint to \({\mathcal {L}}_{\phi} f_{*}\).
Proof
Following the notation and factorization in Lemma 3.10, we have canonical identifications:
Furthermore, after choosingFootnote 22 one of the projections \(Z = X \times _{Y} X \rightarrow X\), the usual exact triangle for cotangent complexes for the composition \(X \rightarrow Z \rightarrow X\) gives a canonical equivalence
Thus, we have a canonical equivalence
By assumption the cotangent complex \(\mathbb{L}_{f}\) is perfect in degrees \([0, 1]\), so the relative cotangent complex \(\mathbb{L}_{\Delta _{X/Y}}\) is perfect in degrees \([-1, 0]\); in particular, \(\Delta _{X/Y}\) is representable by schemes and quasi-smooth and thus we have a canonical equivalence (see Proposition 7.3.8 of [43]) \({\mathcal {L}}_{\phi }f^{!} \simeq {\mathcal {L}}_{\phi }f^{*} \otimes \omega _{{\mathcal {L}}_{ \phi }X/{\mathcal {L}}_{\phi }Y} \simeq {\mathcal {L}}_{\phi }f^{*}\) as desired. □
Furthermore, by functoriality of Hochschild homology, for a map of stacks \(f: X \rightarrow Y\) we expect that the pullback and pushforward functors define maps of global functions or volume forms \(HH(f^{*}): {\mathcal {O}}({\mathcal {L}}Y) \rightarrow {\mathcal {O}}({\mathcal {L}}X)\) and (if \(f\) is proper) \(HH(f_{*}): \omega ({\mathcal {L}}X) \rightarrow \omega ({\mathcal {L}}Y)\). We identify this map with the global sections of a natural map on the underlying sheaves in two cases of concern (see Appendix A.1 for the proof).
Definition 3.13
Let \(f: X \rightarrow Y\) be a map of QCA stacks, and \(\phi _{X}\), \(\phi _{Y}\) compatible proper self-maps.
-
(1)
If \(f\) is proper, then we have a pushforward map \(\omega ({\mathcal {L}}_{\phi }f_{*}): \omega ({\mathcal {L}}_{\phi }X) \rightarrow \omega ({\mathcal {L}}_{\phi }Y)\) of global volume forms. That is, by Remark 4.6 in [8], since \(f\) is proper, \({\mathcal {L}}_{\phi }f: {\mathcal {L}}_{\phi }X \rightarrow {\mathcal {L}}_{\phi }Y\) is proper; \(\omega ({\mathcal {L}}_{\phi }f_{*})\) is the global sections of the counit of the adjunction \(({\mathcal {L}}_{\phi }f_{*}, {\mathcal {L}}_{\phi }f^{!})\) applied to \(\omega _{{\mathcal {L}}_{\phi }Y}\).
-
(2)
If \(f\) is smooth, then we have a “Gysin” pullback \(\omega ({\mathcal {L}}_{\phi }f^{*}): \omega ({\mathcal {L}}_{\phi }Y) \rightarrow \omega ({\mathcal {L}}_{\phi }X)\) of global volume forms. That is, by Proposition 3.12, if \(f\) is smooth then \({\mathcal {L}}_{\phi }f\) is Calabi-Yau; passing through this equivalence, \(\omega ({\mathcal {L}}_{\phi }f^{*})\) is the global sections of the unit of the adjunction \(({\mathcal {L}}_{\phi }f^{*}, {\mathcal {L}}_{\phi }f_{*})\) applied to \(\omega _{{\mathcal {L}}_{\phi }Y}\).
Proposition 3.14
Let \(f: X \rightarrow Y\) be map of QCA stacks with compatible proper self-maps \(\phi _{X}\), \(\phi _{Y}\).
-
(1)
There are canonical identifications
$$ HH(\operatorname {QC}^{!}(X), \phi _{*}) \simeq \omega ({\mathcal {L}}_{\phi }X). $$ -
(2)
Suppose \(f\) is proper, and consider \(f_{*}: \operatorname {QC}^{!}(X) \rightarrow \operatorname {QC}^{!}(Y)\). Then, the map \(HH(f_{*}, \phi _{*})\) is canonically identified with the map on global volume forms \(\omega ({\mathcal {L}}_{\phi }f_{*})\).
-
(3)
Suppose that \(f\) is smooth, and consider \(f^{*}: \operatorname {QC}^{!}(Y) \rightarrow \operatorname {QC}^{!}(X)\). Then, the map \(HH(f^{*}, \phi _{*})\) is canonically identified with the map on volume forms \(\omega ({\mathcal {L}}_{\phi }f^{*})\).
3.3 Convolution patterns in Hochschild homology
Convolution patterns in Borel-Moore homology and algebraic \(K\)-theory play a central role in the results of [34]. We now describe a similar pattern which appears in Hochschild homology.
Definition 3.15
We will work with the following general setup (see Sect. 1.5 of [12]).
-
\(f:X\to Y\) is a proper morphism of smooth, QCA stacks over \(k\), and \(Z=X\times _{Y} X\).
-
\(\phi _{X}: X \rightarrow X\) and \(\phi _{Y}: Y \rightarrow Y\) are (representable) proper self-maps commuting with \(f\), inducing a proper self-map \(\phi : Z \rightarrow Z\).
We refer to any \(Z\) arising from the set-up above a convolution space, and call the category \(\operatorname {QC}^{!}(Z)\) a convolution category.
In this setup the category \(\operatorname {QC}^{!}(Z)\) carries a monoidal structure under convolution,Footnote 23 and \(\phi _{*}\) is a monoidal endofunctor. The convolution monoidal structure restricts to the compact objects \({\operatorname {Coh}}(Z)\) thanks to the smoothness of \(X\) (hence finite Tor-dimension of the diagonal of \(X\)) and the properness of \(f\); furthermore, since \(\phi \) is proper, \(\phi _{*}\) has a colimit-preserving right adjoint, and preserves \({\operatorname {Coh}}(Z)\).
By Theorem 1.1.3 of [11], there is an equivalence of small monoidal categoriesFootnote 24

which takes an integral kernel \({\mathcal {K}}\in {\operatorname {Coh}}(X \times _{Y} X)\) to the functor \({\mathcal {F}}\mapsto R\pi _{2*}(R\pi _{1}^{!}{\mathcal {F}}\otimes ^{L} {\mathcal {K}})\) where \(\pi _{1}, \pi _{2}: X \times _{Y} X \rightarrow X\) are the projections. Moreover, we will argue in Theorem 3.25 that \((\operatorname {QC}^{!}(Z),\ast )\) is rigid monoidal. The monoidal unit is the dualizing sheaf of the relative diagonal \(\omega _{\Delta} := \iota _{*} \omega _{X}\), where \(\iota :X\to X\times _{Y} X\).
Recall (from Sect. 3.2) that the Hochschild homology of \({\operatorname {Coh}}(Z)\) (or equivalently of its large variant \(\operatorname {QC}^{!}(Z)\) by Remark 2.2.11 of [31]) for a stack \(Z\) is given geometrically by volume forms on the loop space, or in the case of the trace of \(\phi _{*}\) the derived fixed points:
Thus the vertical trace of the monoidal category \({\operatorname {Coh}}(Z)\) defines an algebra structure on global distributions \(\Gamma ({\mathcal {L}}_{\phi }Z, \omega _{{\mathcal {L}}_{\phi }Z})\).
We want to relate this convolution structure on sheaves to its decategorified version involving volume forms on the corresponding loop spaces. Thus we consider the loop map \({\mathcal {L}}_{\phi }f:{\mathcal {L}}_{\phi }X\to {\mathcal {L}}_{\phi }Y\) to \(f\), whose self-fiber product is \({\mathcal {L}}_{\phi }Z\simeq {\mathcal {L}}_{\phi }X \times _{{\mathcal {L}}_{\phi }Y} {\mathcal {L}}_{ \phi }X\). Note that \({\mathcal {L}}_{\phi }f\) is a proper map of quasismooth derived stacks. In particular, \(\omega _{{\mathcal {L}}_{\phi }X}\) is coherent (a compact object in \(\operatorname {QC}^{!}({\mathcal {L}}_{\phi }X)\)) and \({\mathcal {L}}_{\phi }f_{*}\) preserves coherence. We thus define our main object of interest.
Definition 3.16
We define the universal trace sheaf
The latter isomorphism follows since the loop space of smooth stacks are naturally Calabi-Yau (see Lemma 3.12).
The endomorphisms of the universal trace sheaf have a close relationship to volume forms on the loop space of the convolution space. Namely, we have a canonical equivalence
Furthermore, these equivalences are functorial at the sheafy level; on the left, this was discussed in Definition 3.13. On the right, the functoriality arises via the following functoriality of the universal trace sheaf.
Definition 3.17
Let \((X, Y, f, \phi )\) and \((X', Y', f', \phi ')\) as in Definition 3.15 (with convolution spaces \(Z\), \(Z'\)), and write \({\mathcal {S}}:= {\mathcal {S}}_{X/Y,\phi}\) and \({\mathcal {S}}' := {\mathcal {S}}_{X'/Y',\phi '}\). Suppose we have maps \(\alpha _{X}: X \rightarrow X'\) and \(\alpha _{Y}: Y \rightarrow Y'\) commuting with \(f\), \(f'\), inducing \(\alpha _{Z}: Z \rightarrow Z'\). Then, we have the following due to base change.
-
(1)
Suppose that \(X = X'\) and that \(\alpha _{Y}\) is proper. Then, there is a canonical equivalence \({\mathcal {L}}\alpha _{Y*} {\mathcal {S}}\simeq {\mathcal {S}}'\), and the functor \(\alpha _{Z*}: {\operatorname {Coh}}(Z) \rightarrow {\operatorname {Coh}}(Z')\) is monoidal.
-
(2)
Suppose that \(\alpha _{Y}\) is smooth and \(f\) is base-changed from \(f'\), i.e. \(X = X' \times _{Y'} Y\). Then there is a canonical equivalence \({\mathcal {L}}\alpha _{Y}^{!} {\mathcal {S}}' \simeq {\mathcal {S}}\), and the functor \(\alpha _{Z}^{!}: {\operatorname {Coh}}(Z') \rightarrow {\operatorname {Coh}}(Z)\) is monoidal.
The functorialities on the two sides of the equivalence are compatible.
Proposition 3.18
We let \(p: Z \rightarrow Y\) denote the structure map. In the set-up of Definition 3.15, we have a canonical equivalence
with \(\zeta '\) defined analogously, such that if \(\alpha : Y \rightarrow Y'\) is proper and \(X = X'\), we have commuting squares

while if \(\alpha : Y \rightarrow Y'\) is smooth and \(X = X' \times _{Y'} Y\), we have commuting squares

Proof
Application of Proposition A.1, noting that if \(f\) is smooth then \({\mathcal {L}}_{\phi }f\) is Calabi-Yau by Proposition 3.12. □
Remark 3.19
Convolution of volume forms and endomorphisms of \({\mathcal {S}}_{X/Y}\)
Applying the above proposition to \({\mathcal {L}}_{\phi }f: {\mathcal {L}}_{\phi }X \rightarrow {\mathcal {L}}_{\phi }Y\), i.e. if we sheafify over \({\mathcal {L}}_{\phi }Y\), we can identify this algebra structure more concretely as convolution of volume forms on \({\mathcal {L}}_{\phi }Z\). That is, \({\mathcal {L}}_{\phi }Z={\mathcal {L}}_{\phi }X\times _{{\mathcal {L}}_{\phi }Y} {\mathcal {L}}_{\phi }X\) has the structure of proper monoid in stacks over \({\mathcal {L}}_{\phi }Y\), from which one deduces the structure of algebra object in \((\operatorname {QC}^{!}({\mathcal {L}}_{\phi }Y),\otimes ^{!})\) on the pushforward of \(\omega _{{\mathcal {L}}_{\phi }Z}\). One can also use proper descent for \({\mathcal {L}}_{\phi }f:{\mathcal {L}}_{\phi }X\to {\mathcal {L}}_{\phi }Y\) to identify this sheaf of algebras with the internal endomorphism sheaf of \({\mathcal {S}}_{X/Y}\) – an analog, in the setting of derived categories of coherent sheaves on derived stacks, of the standard proof (see e.g. [34]) that self-Ext of the Springer sheaf is identified with Borel-Moore homology of \(Z\). It would be interesting to see how these arguments globalize over \({\mathcal {L}}_{\phi }Y\) to give the isomorphism \(\Gamma ({\mathcal {L}}_{\phi }Z, \omega _{{\mathcal {L}}_{\phi }Z})\simeq \operatorname {End}_{ \operatorname {QC}^{!}({\mathcal {L}}_{\phi }Y)}({\mathcal {S}}_{X/Y})\) of Theorem 3.25.
3.3.1 Horizontal trace of convolution categories
Recall that Theorem 3.4 identifies the vertical trace \(HH(\operatorname {QC}^{!}(Z),\ast )\) as the endomorphism algebra of the distinguished object in the horizontal trace \({\mathbf {Tr}}(\operatorname {QC}^{!}(Z),\ast )\), under the assumption that this distinguished object is compact (and a rigidity condition to be addressed in Theorem 3.25). In this section we discuss this horizontal trace in the context of convolution spaces following [12], slightly generalizing the main theorem of op. cit.
For this we require a discussion of singular supports; we summarize the main points and refer the reader to [12, 37] for details. Note that singular supports do not appear in our main application Theorem 4.12, since the singular support condition there is actually a classical support condition (see Remark 4.14).
Definition 3.20
Let \(f: X \rightarrow Y\) be a representable map of quasi-smooth stacks.
-
(1)
We define the scheme of singularities or (classical) odd cotangent bundle to be
$$ \mathbb{T}^{*[-1]}_{X} := \operatorname {Spec}_{X} \operatorname {Sym}^{\bullet }_{X} H^{1}({\mathcal {T}}_{X}) = \operatorname {Spec}_{X} \operatorname {Sym}^{\bullet }_{X} H^{0}({\mathcal {T}}_{X}[1]) $$where \({\mathcal {T}}_{X}\) denotes the tangent complex of \(X\), i.e. the \({\mathcal {O}}_{X}\)-linear dual of the cotangent complex.
-
(2)
Any ind-coherent sheaf \({\mathcal {F}}\in \operatorname {QC}^{!}(X)\) has a closed conical singular support \(\mathrm{SS}({\mathcal {F}}) \subset \mathbb{T}^{*[-1]}_{X}\). To any subset \(\Lambda \subset \mathbb{T}^{*[-1]}_{X}\) we can associate the full category \(\operatorname {QC}^{!}_{\Lambda}(X) \subset \operatorname {QC}^{!}(X)\) consisting of sheaves with the specified singular support.
-
(3)
Let \(\Lambda _{X} \subset \mathbb{T}^{*[-1]}_{X}\) and \(\Lambda _{Y} \subset \mathbb{T}^{*[-1]}_{Y}\), and consider the correspondence
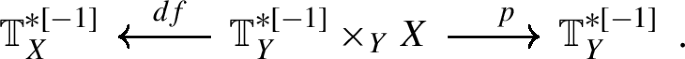
One can push forward and pull back singular support conditions
$$ f_{*}\Lambda _{X} = \overline{p(df^{-1}(\Lambda _{X}))}, \;\;\;\;\;\; \; f^{!}\Lambda _{Y} = \overline{df(p^{-1}(\Lambda _{Y}))} $$such that the pushforward and pullback functors preserve singular supports, i.e.
$$ f_{*}: \operatorname {QC}^{!}_{\Lambda _{X}}(X) \rightarrow \operatorname {QC}^{!}_{f_{*}\Lambda _{X}}(Y), \;\;\;\;\;\;\; f^{!}: \operatorname {QC}^{!}_{\Lambda _{Y}}(Y) \rightarrow \operatorname {QC}^{!}_{f^{!} \Lambda _{Y}}(X). $$
Example 3.21
If \(X\) is smooth, then \(\mathbb{T}^{*[-1]}_{X} = X\), i.e. there are no possible singular codirections to consider. In particular, the nontrivial fibers of the map \(\mathbb{T}^{*[-1]}_{X} \rightarrow X\) live over the singular locus of \(X\).
When \(\Lambda = \mathbb{T}^{*[-1]}_{X}\), we have \(\operatorname {QC}^{!}_{\Lambda}(X) = \operatorname {QC}^{!}(X)\). At the opposite extreme, when \(\Lambda = \{0\}_{X}\) is the zero section, we have \(\operatorname {QC}^{!}_{\Lambda}(X) = \operatorname {QC}(X)\). If \(Z \subset X\) is a closed subscheme and \(\Lambda = Z \times _{X} \mathbb{T}^{*[-1]}_{X}\), then \(\operatorname {QC}^{!}_{\Lambda}(X) = \operatorname {QC}^{!}_{Z}(X)\), i.e. the full subcategory of ind-coherent sheaves with classical support at \(Z \subset X\). If instead we take \(\Lambda = Z \times \{0\}_{X}\), then \(\operatorname {QC}^{!}_{\Lambda}(X) = \operatorname {QC}_{Z}(X)\).
The following singular support condition appears when taking traces of convolution categories.
Definition 3.22
Recall the notation from Definition 3.5 and Definition 3.9. We have the following trace correspondence:

We define a singular support condition \(\Lambda _{X/Y,\phi} := \pi _{*}\delta ^{!}\mathbb{T}^{*[-1]}_{Z}\).
We now give a description of the horizontal trace. The following statement is more general than the statement of Theorem 3.3.1 in [12], but follows from the same argument in the proof with the definitions given above; the proof is in Appendix A.2.
Theorem 3.23
There is a canonical identification of the horizontal trace (i.e. the monoidal Hochschild homology)
with the universal trace given byFootnote 25
Next we identify the universal trace sheaf (i.e. coherent Springer sheaf) as the trace of the monoidal unit (which is a compact object of the trace category) or regular representation.
Lemma 3.24
There is a natural equivalence \({\mathcal {S}}_{X/Y,\phi} \simeq [\omega _{\Delta}] = \pi ^{*} \delta ^{!} \omega _{\Delta}\) in \({\operatorname {Coh}}({\mathcal {L}}_{\phi }Y)\).
Proof
The calculation of \(\delta ^{!} \omega _{\Delta} = \delta ^{!} \Delta _{*} \omega _{X}\) arises via base change along the diagram

and the statement follows. □
3.3.2 Trace delooping in convolution categories
We now deduce the main structural relation between universal trace sheaves (see Definition 3.16) and iterated categorical traces of convolution categories.
Theorem 3.25
Let \(f: X \rightarrow Y\) be as in Definition 3.15. Then, the convolution category \(\operatorname {QC}^{!}(X \times _{Y} X)\) is rigid. In particular, the statements of Theorem 3.4apply: the vertical trace of the convolution category \((\operatorname {QC}^{!}(Z),\ast )\) is identified as an algebra with the endomorphisms of the universal trace sheaf
Proof
We need to verify that \(\operatorname {QC}^{!}(Z)\) is rigid monoidal. Standard arguments show that integral transforms arising via coherent sheaves preserve compact objects; this statement is also contained within Theorem 1.1.3 in [11]; one further immediately observes that the monoidal unit \(\Delta _{*} \omega _{X}\) is a compact object, i.e. coherent, since the diagonal is a closed embedding. It remains to verify the existence of right and left duals of coherent sheaves \({\mathcal {K}}\in \operatorname {QC}^{!}(Z)\). Using loc. cit., it suffices to show that the right and left adjoints of the corresponding integral transform \(F_{{\mathcal {K}}}: \operatorname {QC}(X) \rightarrow \operatorname {QC}(X)\) preserve compact objects, thus are realized by integral transforms with coherent kernels. We note that since the projection maps \(p: Z \rightarrow X\) are quasi-smooth, the functors \(p^{!}\) and \(p^{*}\) differ by a shifted line bundle. By Lemma 3.0.8 in op. cit. we can consider equivalently either the ∗ or !-transforms up to twisting by Grothendieck duality. For convenience we will consider the ∗-transform.
To see the claim, note that we can write the ∗-integral transform \(F_{{\mathcal {K}}}\) as a composition:

We claim that the right adjoint preserves compact objects. The claim for the left adjoint follows similarly by replacing \(p^{*}\) with a twist of \(p^{!}\) by a shifted line bundle. The right adjoints define a sequence of functors

The functor \(\mathcal {H}om_{\operatorname {QC}^{!}(Z)}({\mathcal {K}}, -): \operatorname {QC}^{!}(Z) \rightarrow \operatorname {QC}(Z)\) is defined as follows. Given \({\mathcal {G}}\in \operatorname {QC}^{!}(Z)\), we may write \({\mathcal {G}}= \operatorname*{colim}_{i} {\mathcal {G}}_{i}\) with \({\mathcal {G}}_{i} \in {\operatorname {Coh}}(Z)\). Since \({\mathcal {K}}\) is compact, we may define:
where the internal Hom on the right is taken inside \({\operatorname {Coh}}(Z) \subset \operatorname {QC}(Z)\) as usual. Let us justify the claim that this functor is a right adjoint to tensoring with \({\mathcal {K}}\). Let \({\mathcal {F}}\in \operatorname {QC}(Z)\), and write \({\mathcal {F}}= \operatorname*{colim}_{j} {\mathcal {F}}_{j}\) with \({\mathcal {F}}_{j} \in \operatorname {Perf}(Z)\). Then, by the usual adjunction in \(\operatorname {QC}(Z)\), and using the facts that the \({\mathcal {F}}_{j}\) are compact in \(\operatorname {QC}(Z)\) and that \({\mathcal {F}}_{j} \otimes {\mathcal {K}}\in {\operatorname {Coh}}(Z)\) are compact in \(\operatorname {QC}^{!}(Z)\) since \({\mathcal {F}}_{j}\) are perfect, we have:
Finally, we claim that \(\mathcal {H}om_{\operatorname {QC}^{!}(Z)}({\mathcal {K}}, -)\) sends \(\operatorname {Perf}(Z)\) to \({\operatorname {Coh}}(Z)\). Assuming this claim, then the composite of the sequence of right adjoints above preserves compact objects, which finishes the proof: since \(X\) is smooth, the image of \({\operatorname {Coh}}(X) = \operatorname {Perf}(X)\) under \(p^{!} = p^{*} \otimes {\mathcal {L}}\) takes values in \(\operatorname {Perf}(Z)\), and since \(p\) is proper (and again since \(X\) is smooth) the image of \({\operatorname {Coh}}(Z)\) under \(p_{*}\) takes values in \({\operatorname {Coh}}(X) = \operatorname {Perf}(X)\). To prove the claim, note that the Grothendieck dual \(\mathbb{D}({\mathcal {K}}) = \mathcal {H}om_{Z}({\mathcal {K}}, \omega _{Z})\) is coherent, and since \(Z\) is quasi-smooth, \(\omega _{Z}\) is a line bundle, so we have for \({\mathcal {E}}\in \operatorname {Perf}(Z)\):
which is coherent. □
3.4 Trace of the standard categorical representation
In Lemma 3.24, we have computed the trace of the regular representation \(\operatorname {QC}^{!}(Z)\) of \(\operatorname {QC}^{!}(Z)\) to be the universal trace sheaf, i.e. \([\operatorname {QC}^{!}(Z), \phi _{*}] \simeq {\mathcal {S}}_{X/Y, \phi} := {\mathcal {L}}_{\phi }f_{*} {\mathcal {O}}_{{\mathcal {L}}_{\phi }X}\). Our convolution set-up comes equipped with another natural module category: the standard representation, i.e. the module category \(\operatorname {QC}^{!}(X)\). In this section we compute the trace of this categorical representation, and relate it to the trace of the regular representation in a special case. We first note a degenerate example.
Example 3.26
Consider the case when \(X = Y = Z\) is smooth. In this case, \(\operatorname {QC}^{!}(Y) = \operatorname {QC}(Y)\), and the trace correspondence of Definition 3.22 is simply given by pullback along the evaluation \(\mathrm{ev}: {\mathcal {L}}_{\phi }Y \rightarrow Y\):

and the corresponding singular support condition \(\Lambda _{Y/Y,\phi} = \{0\}_{{\mathcal {L}}_{\phi }Y}\) is the zero section, i.e. we have \({\mathbf {Tr}}(\operatorname {QC}^{!}(Y),\phi _{*}) = \operatorname {QC}({\mathcal {L}}_{\phi }Y)\) (see Corollary 5.2 of [9]). The standard representation is the regular representation, and by Theorem 3.3.1 of [12] (and Proposition 3.12), the trace of the regular representation is the structure sheaf
We recall a few notions from Sect. 2.3 of [12]. The following functors allow us to pass between categories with different singular supports.
Definition 3.27
For a pair \((X, \Lambda _{X})\), there is an adjoint pair of functors (see Definition 2.3.2 of [12]):

where \(\iota _{\Lambda}\) is the natural inclusion, and \(\Gamma _{\Lambda}\) is the corresponding colocalization.Footnote 26
We need an identification of the relative tensor product of convolution categories, with specified support. We work in the set-up of Definition 3.15: let \(X_{i}\) be smooth QCA stacks over \(k\), proper over \(Y\), and let \(Z_{ij} = X_{i} \times _{Y} X_{j}\).
Definition 3.28
Let \(\Lambda _{12} \subset \mathbb{T}^{*[-1]}_{Z_{12}}\) and \(\Lambda _{23} \subset \mathbb{T}^{*[-1]}_{Z_{23}}\). Consider the diagram

We define the convolution of singular supports
We say that \(\Lambda _{ij}\) is \(Z_{ii}\)-stable if \(\mathbb{T}^{*[-1]}_{Z_{ii}} \ast \Lambda _{ij} \subset \Lambda _{ij}\).
Remark 3.29
The trace singular support condition \(\Lambda _{X/Y}\) of Definition 3.22 can be viewed as the convolution of \(\mathbb{T}^{*[-1]}_{Z}\) with itself “in a circle.”
We immediately observe that the convolution action restricts to an action of \(\operatorname {QC}^{!}_{\Lambda _{ii}}(Z_{ii})\) on \(\operatorname {QC}^{!}_{\Lambda _{ij}}(Z_{ij})\) if and only if \(\Lambda _{ij}\) is \(\Lambda _{ii}\)-stable. In particular, we have the following identification, which we prove in Appendix A.2; a proof will also appear in [33].
Proposition 3.30
In the set-up above, let \(\Lambda _{12} \subset \mathbb{T}^{*[-1]}_{Z_{12}}\) and \(\Lambda _{23} \subset \mathbb{T}^{*[-1]}_{Z_{23}}\) be \(Z_{22}\)-stable. Define \(\Lambda _{13} := \Lambda _{12} \ast \Lambda _{23}\). Then convolution defines an equivalence of categories:

Furthermore, we have the following functoriality of supports: let \(\Lambda _{i,i+1} \subset \Lambda _{i,i+1}'\) be another singular support condition on \(Z_{i,i+1}\) (for \(i=1,2\)) with \(\Lambda _{13}' := \Lambda _{12}' \ast \Lambda _{23}'\). Then, \(\Lambda _{13} \subset \Lambda _{13}'\), and the following squares commute:

These actions are canonically \(\phi _{*}\)-semilinear. We now compute the trace of the categorical representation, which arises via functoriality of horizontal traces (see Sect. 3.5 of [8] for details). Namely, consider the functor
Note that the \(\operatorname {QC}(Y)\)-action on \(\operatorname {QC}(X) = \operatorname {QC}^{!}(X)\) via pullback commutes with the \(\operatorname {QC}^{!}(Z)\)-action by convolution. This functor defines a functor on horizontal traces:Footnote 27
By definition,
Remark 3.31
A variant of the functor \(T\) for quasi-coherent sheaves, and in the setting where \(f: X \rightarrow Y\) is surjective, was studied in [10]. Note that unlike in their setting, this functor \(T\) is not an equivalence since we are considering ind-coherent sheaves \(\operatorname {QC}^{!}(Z)\) rather than quasi-coherent sheaves \(\operatorname {QC}(Z)\). Furthermore, the failure of \(f\) to be surjective in our setting requires the application of local cohomology in the calculation of its trace.
We now identify the trace of the standard representation.
Proposition 3.32
Define the singular support condition \(\{0\}_{f(X)} := \{0\}_{{\mathcal {L}}_{\phi }Y} \cap \Lambda _{X/Y, \phi}\). There is a canonical identification of functors
Furthermore, letting \(\mathrm{ev}^{-1} f(X) \subset {\mathcal {L}}_{\phi }Y\) corresponding to \(\{0\}_{f(X)}\), we have
Proof
We claim that the right dual to \(T\) is
where \(\operatorname {QC}^{!}(X)\) here is considered as a right \(\operatorname {QC}^{!}(Z)\)-module, so that we have
The convolution \(\operatorname {QC}(Y)\)-action can be re-interpreted as the usual pullback and tensor product, while the \(\operatorname {QC}^{!}(Z)\)-action is by convolution. The first isomorphism is due to Proposition 3.30, whereby
i.e. the full subcategory of \(\operatorname {QC}^{!}(Y) = \operatorname {QC}(Y)\) with classical support on the closed subset \(f(X)\) (since \(Y\) is smooth there are no possible singular codirections). The second isomorphism is due to Theorem 4.7 of [9], i.e. we have \(\operatorname {QC}^{!}(X) \otimes _{\operatorname {QC}^{!}(Y)} \operatorname {QC}^{!}(X) = \operatorname {QC}(Z) = \operatorname {QC}^{!}_{\{0\}_{Z}}(Z)\).
To establish duality, we need to write down unit and counit maps
satisfying the usual “Zorro’s identities”. We define \(\eta := \Gamma _{f(X)}\) to be the local cohomology functor, and \(\epsilon = \iota _{\{0\}_{Z}}\) to be the fully faithful inclusion. The verification of Zorro’s identities is immediate from the observation that tensoring \(\eta \) or \(\epsilon \) with \(\mathrm{id}_{\operatorname {QC}^{!}(X)}\) (on either side) gives rise to the identity functor, i.e. that the following diagrams commute:

This follows by Proposition 3.30 and the singular support calculations (note that \(X\) is smooth and thus \(\mathbb{T}^{*[-1]}_{X}\) has no singular codirections):
This establishes the duality of \((T, T^{R})\).
Now, we compute the map on traces, using the functoriality described in Sect. 3.5 of [8]. There is a canonical commuting structure \(\psi : T \circ \phi _{Y*} \rightarrow \phi _{Z*} \circ T\), which for us is an equivalence (thus induces an equivalence on traces). We let \(f(X) \subset \mathbb{T}^{*[-1]}_{Y} = Y\) denote the (necessarily, since \(Y\) is smooth) classical support condition, and define \(\Lambda := \mathrm{ev}^{!}(f(X))\), i.e. the loops with base points classically supported over \(f(X) \subset Y\) and no singular codirections. We have \(\{0\}_{{\mathcal {L}}Y} \supset \Lambda \subset \Lambda _{X/Y}\).

The top and bottom isomorphisms are given by Theorem 3.3.1 in [12]. We argue the middle isomorphisms. A combination of the arguments of Propositions 3.23 and 3.30 gives rise to identifications
where \(\delta _{*}\pi ^{!}\{0\}_{Z}\) is the pull-push of \(\{0\}_{Z}\) along the correspondence in Theorem 3.23. We note that \(\delta _{*}\pi ^{!}\{0\}_{Z} = \delta _{*} \{0\}_{{\mathcal {L}}_{\phi }Y_{X}} = \mathrm{ev}^{!}f(X) = \{0\}_{f(X)}\). The identification of the vertical functors follows via the functoriality of supports in Proposition 3.30 applied to the setting of Proposition 3.23, and the observation that \(\{0\}_{{\mathcal {L}}_{\phi }Y} \supset \Lambda \subset \Lambda _{X/Y,\phi}\). This establishes the first statement of the theorem.
For the second statement, note that \(\omega _{{\mathcal {L}}_{\phi }Y}\) is perfect (since \({\mathcal {L}}Y\) is quasi-smooth), i.e. has no singular codirections. In general, for singular support conditions \(\Lambda _{1}, \Lambda _{2} \subset \mathbb{T}^{*[-1]}_{X}\), we have \(\Gamma _{\Lambda _{2}} \circ \iota _{\Lambda _{1}} \circ \Gamma _{ \Lambda _{1}} = \Gamma _{\Lambda _{1} \cap \Lambda _{2}}\). Now, take \(\Lambda _{1} = \{0\}_{{\mathcal {L}}Y}\) (i.e. no singular codirections with unrestricted classical support) and \(\Lambda _{2} = \mathrm{ev}^{-1}f(X) \times _{{\mathcal {L}}_{\phi }Y} \mathbb{T}^{*[-1]}_{ {\mathcal {L}}_{\phi }Y}\) (i.e. all singular codirections with restricted classical support). The second statement follows, since \(\Gamma _{\Lambda _{1}}(\omega _{{\mathcal {L}}_{\phi }Y}) = \omega _{{\mathcal {L}}_{ \phi }Y}\) and \(\Gamma _{\Lambda _{2}}\) is the classical local cohomology functor with support \(\mathrm{ev}^{-1} f(X)\). □
Corollary 3.33
The functor
takes \(\Gamma _{\mathrm{ev}^{-1}f(X)}({\mathcal {O}}_{{\mathcal {L}}_{\phi }Y})\) to the \(HH(\operatorname {QC}^{!}(Z), \phi _{*})\)-module \(HH(\operatorname {QC}^{!}(X), \phi _{*})\).
Proof
By Theorem 3.4, it suffices to identify the trace of the \(\operatorname {QC}^{!}(Z)\)-module category \(\operatorname {QC}^{!}(X)\). By the above theorem, \([\operatorname {QC}^{!}(X), \phi _{*}] \simeq \Gamma _{\mathrm{ev}^{-1}f(X)}( \omega _{{\mathcal {L}}_{\phi }Y}) \simeq \Gamma _{\mathrm{ev}^{-1}f(X)}({\mathcal {O}}_{ {\mathcal {L}}_{\phi }Y})\) (the latter isomorphism by Proposition 3.12). □
Remark 3.34
Note that it is immediate via adjunctions that
By working at the level of categorical traces, we automatically deduce that this is an identification as \(HH(\operatorname {QC}^{!}(Z), \phi _{*})\)-modules.
3.4.1 Splitting the universal trace sheaf
The coherent Springer sheaf \({\mathcal {S}}_{X/Y, \phi}\) may be realized as the character of the regular \(\operatorname {QC}^{!}(Z)\)-representation \([\operatorname {QC}^{!}(Z), \phi _{*}]\), but also as the character of the \(\operatorname {QC}(Y)\)-representation \([\operatorname {QC}(X), \phi _{*}]\). In this section, we will take the latter point of view. This allows us to do something sneaky in the proof of Theorem 4.12: we swap out \(X = \widetilde {{\mathcal {N}}}/G\) with \(\widetilde {\mathfrak {g}}/G\), and use the observation that their \(q\)-fixed points are canonical equivalent for \(q\) not a root of unity. There is a canonical map
arising via the pushforward of volume forms. In this section we investigate when this map splits, realizing the trace of the standard representation as a summand of the trace of the regular representation. To do so we require a discussion of enhanced vertical traces, i.e. the realization of vertical traces of module categories for a monoidal category as characters in the horizontal trace of the monoidal category.
Definition 3.35
Let us fix a monoidal dg category \(\mathbf {A}\), and a monoidal endofunctor \(F\). For any \(\mathbf {A}\)-module category \(\mathbf {C}\) equipped with a commuting structure \(F_{\mathbf {M}}\) for \(F\) (see Definitions 2.7 and 3.2), we define the enhanced Hochschild homology to be
By Theorem 3.4, the usual Hochschild homology can be recovered by applying the functor \(\operatorname{Hom}_{{\mathbf {Tr}}(\mathbf {A}, F)}([\mathbf {A}, F], -)\).
Remark 3.36
We have seen examples of this enhanced Hochschild homology in Sect. 3.2, namely that in geometric settings Hochschild homology and maps induced by functoriality often sheafify, i.e. arise as global objects via local ones by taking global sections. The category \(\operatorname {QC}(Y)\) is monoidal, and for any module category \(\mathbf {C}\) the Hochschild homology \(HH(\mathbf {C}) := [\mathbf {C}] \in \mathbf {Vect}_{k}\) has an enhancement \(\underline{HH}(\mathbf {C}) \in {\mathbf {Tr}}(\operatorname {QC}(Y)) = \operatorname {QC}({\mathcal {L}}Y)\). Though we do not need or prove it, the enhanced Block-Getzler complex in Definition 2.12 is also an example of this phenomenon, where we view the Hochschild homology of a \(\operatorname {Rep}(G)\)-module category as an object of \({\mathbf {Tr}}(\operatorname {Rep}(G)) = \operatorname {QC}(G/G)\).
We now compute the enhanced trace in an example of interest; see Appendix A.2 for a proof.
Proposition 3.37
Let \(f: X \rightarrow Y\) be a map of QCA (or more generally, perfect) stacks, and \(\phi _{X}\), \(\phi _{Y}\) compatible self-maps such that \(\phi _{Y*}: \operatorname {QC}(Y) \rightarrow \operatorname {QC}(Y)\) is monoidal and \(\phi _{X*}: \operatorname {QC}(X) \rightarrow \operatorname {QC}(X)\) is \(\phi _{Y*}\)-semilinear. Consider \(\operatorname {QC}(X)\) as a \(\operatorname {QC}(Y)\)-module category. Then, we have
We now establish the desired splitting. We note that in the below, we take the category \(\operatorname {QC}\) of quasi-coherent sheaves rather than ind-coherent sheaves.
Proposition 3.38
Let \(f: X \rightarrow Y\) be a proper morphism of smooth QCA stacks, with compatible self-maps \(\phi _{X}\), \(\phi _{Y}\), such that \(\phi _{Y*}\) is a monoidal endofunctor of \(\operatorname {QC}(Y)\) and \(\phi _{X*}\) is a \(\phi _{Y*}\)-semilinear endofunctor of \(\operatorname {QC}(X)\). Furthermore, assume that \(f_{*}{\mathcal {O}}_{X} \simeq {\mathcal {O}}_{Y} \otimes _{k} V\) for a \(\phi _{*}\)-equivariant vector space \(V\) such that \(\mathrm{tr}(\phi _{*}, V) \ne 0\). Then, \([\operatorname {QC}(X), \phi _{X*}] \simeq {\mathcal {L}}_{\phi }f_{*} {\mathcal {O}}_{{\mathcal {L}}_{\phi }X}\) contains \([\operatorname {QC}(Y), \phi _{Y*}] \simeq {\mathcal {O}}_{{\mathcal {L}}_{\phi }Y}\) as a summand in \({\mathbf {Tr}}(\operatorname {QC}(Y), \phi _{Y*}) = \operatorname {QC}({\mathcal {L}}_{\phi }Y)\).
Proof of Proposition 3.38
To prove the claim, we need to produce a splitting. Since the character of the monoidal unit in \(\operatorname {QC}(Y)\) is the monoidal unit in \(\underline{HH}(\operatorname {QC}(Y), \phi _{*})\), applying Proposition 3.37 we obtain a diagram (where ∋ means an element of global sections, i.e. non-enhanced Hochschild homology):

Note that \(f^{*}\) always preserves perfect objects, and \(f_{*}\) preserves perfect objects since \(f\) is proper and \(X\) and \(Y\) are smooth, giving us the functoriality on the left following Proposition 3.37. To see that the composition is an isomorphism, note that a map \({\mathcal {O}}_{{\mathcal {L}}_{\phi }Y} \rightarrow {\mathcal {O}}_{{\mathcal {L}}_{\phi }Y}\) is determined by where the constant function maps; by the above, it maps to \([f_{*}, {\mathcal {O}}_{X}, \phi _{*}] \in HH(\operatorname {QC}(Y), \phi _{*})\). We will show this is a unit, thus the composition of the arrows on the left is an isomorphism.
To this end, let \(p: Y \rightarrow \operatorname {Spec}k\) be the (\(\phi \)-equivariant) projection to a point where \(\phi \) acts trivially on \(\operatorname {Spec}k\), and note that \(f_{*} {\mathcal {O}}_{X} \simeq p^{*} E\). In particular, \([p^{*} V, \phi _{*}]\) is the image of \([V, \phi _{*}] = \mathrm{tr}(V, \phi _{*})\) under the pullback map \({\mathcal {O}}({\mathcal {L}}_{\phi }p^{*}): k \rightarrow {\mathcal {O}}({\mathcal {L}}_{\phi }Y)\), which is a non-zero multiple of the identity by assumption, thus a unit as required. □
4 The affine Hecke algebra and the coherent Springer sheaf
We now specialize the discussion of Sect. 3 to our Springer theory setting. In this section, we will take \(k = \overline {\mathbb{Q}}_{\ell}\) or ℂ. We are interested in the following special cases.
Definition 4.1
Coherent Springer sheaves
Recall that \(G_{\mathrm {gr}}= G \times {\mathbb{G}}_{m}\), and the set-up in Definition 3.15 and the universal trace sheaf of Definition 3.16.
-
(1)
We take
$$ f = \mu : X = \widetilde {{\mathcal {N}}}/G_{\mathrm {gr}}\longrightarrow \widehat {{\mathcal {N}}}/G_{\mathrm {gr}}\hookrightarrow Y = \mathfrak {g}/G_{\mathrm {gr}}$$to be the scaling-equivariant Springer resolution (with codomain in the Lie algebra rather than the nilpotent cone). We call the resulting sheaf \({\mathcal {S}}\) on \({\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})\) (or equivalently, on \({\mathcal {L}}(\mathfrak {g}/G_{\mathrm {gr}})\) supported over \({\mathcal {N}}\)) the coherent Springer sheaf.
-
(2)
We take
$$ f = \mu : X = \widetilde {{\mathcal {N}}}/G \longrightarrow \widehat {{\mathcal {N}}}/G \hookrightarrow Y = \mathfrak {g}/G $$to be the above Springer resolution without \({\mathbb{G}}_{m}\)-equivariance, and \(\phi := q\) to be multiplication by \(q \in {\mathbb{G}}_{m}(k)\). Then we have the derived \(q\)-fixed points:
$$ {\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G) \simeq {\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}}) \times _{{\mathcal {L}}(B{\mathbb{G}}_{m})} \{q\}. $$This is the stack \(\mathbb{L}^{u}_{q,G}\) from the introduction. We call the sheaf \({\mathcal {S}}_{q}\) on \({\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)\) the coherent \(q\)-Springer sheaf.
We note the following convenient presentation of the stacks \({\mathcal {L}}(\widetilde {\mathcal {N}}/G_{\mathrm {gr}})\) and \({\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})\).
Remark 4.2
We realize \({\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})\) as the formal completion of \({\mathcal {L}}(\mathfrak {g}/G_{\mathrm {gr}}) \rightarrow \mathfrak {g}/G_{\mathrm {gr}}\) over the nilpotent cone. By Proposition 2.1.8 of [31], we can write \({\mathcal {L}}(\mathfrak {g}/G_{\mathrm {gr}})\) as the pullback

where the bottom right map is given by subtraction in \(\mathfrak {g}\), \(a\) is the action map, \(p\) the projection, and \(\Delta \) the diagonal. Explicitly, the map \(\mathfrak {g} \times G_{\mathrm {gr}}\rightarrow \mathfrak {g}\) is given by \((x, g, q) \mapsto q^{-1} \mathrm{Ad}_{g}(x) - x\). We also have a version for fixed \(q\):

where \(a_{q}\) is the \(q\)-twisted action map. There is a similar description for \({\mathcal {L}}(\widetilde {\mathcal {N}}/G_{\mathrm {gr}}) = {\mathcal {L}}(\mathfrak {n}/\widetilde {B})\):

We record the following mild generalization and direct consequence of Proposition 4.2 in [51] and Proposition 2.1 in [50] (also proven for \(q\) a prime power in Proposition 3.1.5 of [86]). In particular, when \(q\) is not a root of unity (e.g. for arithmetic applications), we may replace \(\widehat {{\mathcal {N}}}\) or \(\mathfrak {g}\) with \({\mathcal {N}}\) in the \(q\)-twisted loop spaces.
Proposition 4.3
If \(q\) is not a root of unity, then \({\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)\) is a classical stack, i.e. has trivial derived structure and is supported at the nilpotent cone. The maps
are isomorphisms of classical (but a priori derived) stacks.
Proof
We first argue that \({\mathcal {L}}_{q}(\mathfrak {g}/G)\) is supported over the nilpotent cone, thus \({\mathcal {L}}_{q}(\mathfrak {g}/G) = {\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)\). The formation of (twisted) loop spaces commutes with products; note the Cartesian square

The morphisms are \({\mathbb{G}}_{m}\)-equivariant, where \({\mathbb{G}}_{m}\) acts on \(\mathfrak {h}\) by weight 1, and on \(\mathfrak {h}//W\) by weights \(\geq 1\). Thus if \(q\) is not a root of unity, then the (derived and classical) \(q\)-fixed points of \(\mathfrak {h}//W\) is precisely \(\{0\}\). Thus the map on the bottom is an equivalence, and the claim follows. The vanishing of derived structure follows by Proposition 4.2 in [51] and in view of Remark 2.2(b) of [50]. □
Remark 4.4
It is necessary to exclude roots of unity; when \(G = \operatorname {SL}_{2}\), the weight of \(\mathfrak {h}//W\) is 2, so the argument fails for \(q = \pm 1\). When \(G = \operatorname {SL}_{3}\), the weights of \(\mathfrak {h}//W\) are 2 and 3, so the argument fails for \(q = \pm 1\) and any cubic root of unity. A sharper statement is possible: for a fixed group \(G\), the proposition is true if we avoid roots of unity with order dividing any fundamental invariant of \(\mathfrak {g}\). The statements also hold for \(G\) a parabolic subgroup, except that \({\mathcal {L}}_{q}({\mathcal {N}}_{P}/P)\) may fail to be a classical stack (i.e. may have derived structure).
We now give an alternative characterization of the coherent Springer sheaf (and likewise for the \(q\)-version) via coherent parabolic induction.
Definition 4.5
Consider the parabolic induction correspondence

We define the coherent Springer sheaf by applying the loop space of the above correspondence to the reduced structure sheaf of \({\mathcal {L}}(\{0\}/{H_{\mathrm {gr}}})\):
We define the coherent \(q\)-Springer sheaf analogously, or equivalently we can take \({\mathcal {S}}_{q} := \iota _{q}^{*} {\mathcal {S}}\), where \(\iota _{q}: {\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G) \rightarrow {\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})\).
Remark 4.6
Note that a priori, one could define \({\mathcal {S}}_{q}\) via either the ∗ or !-pullback. However, the map \(\iota _{q}\) is base-changed from the map \(i_{q}: \{q\} \rightarrow {\mathbb{G}}_{m}/{\mathbb{G}}_{m}\). Since \(\{q\} \subset {\mathbb{G}}_{m}\) has trivial normal bundle and \(i_{q}\) has relative dimension zero, we have a canonical equivalence \(\iota _{q}^{!} \simeq \iota _{q}^{*}\), i.e. it did not matter which definition we took. Likewise, since derived loop spaces of smooth stacks (or smooth morphisms) are Calabi Yau by Proposition 3.12, we have an equivalence \({\mathcal {L}}\nu ^{*} \simeq {\mathcal {L}}\nu ^{!}\) and can use either.
For number theory applications, we will be interested in specializing at \(q\) a prime power. These are the algebraic specializations of the affine Hecke algebra, which have no derived structure since ℋ is flat over \(k[z,z^{-1}]\).
Definition 4.7
We define the Iwahori-Hecke algebra by
A potentially different algebra arises when specializing geometrically, i.e. taking endomorphisms of a \(q\)-specialized Springer sheaf. We introduce the following unmixed version of the affine Hecke algebra, which is obtained by taking \(G\)-equivariant endomorphisms of the Springer sheaf without taking \({\mathbb{G}}_{m}\)-invariants, i.e. by passing to the base changed stack \({\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}}) \times _{B{\mathbb{G}}_{m}} \operatorname {pt}\).
Definition 4.8
Let \({\mathcal {L}}^{un}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}}) := {\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}}) \times _{B{\mathbb{G}}_{m}} \operatorname {pt}\). We define the unmixed affine Hecke algebra and its specialization by
The algebra \(\mathcal {H}^{{un}}\) has the additional structure of a \({\mathbb{G}}_{m}\)-representation, i.e. a weight grading.
The unmixed affine Hecke algebra arises naturally when considering the trace by pullback by various \(q \in {\mathbb{G}}_{m}\) acting on the affine Hecke category \(\mathbf {H}= {\operatorname {Coh}}({\mathcal {Z}}/G)\) (as opposed to the mixed affine Hecke category \(\mathbf {H}^{{\mathrm {m}}}= {\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}})\)).
Proposition 4.9
There is a natural equivalence of algebras
That is,
Proof
We adopt the shorthand notation \({\mathcal {S}}^{{un}}\) for the corresponding coherent Springer sheaf on \({\mathcal {L}}^{un}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})\). Let \(\iota _{q}: {\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G) \hookrightarrow {\mathcal {L}}^{{un}}(\widehat {{\mathcal {N}}}/ G_{\mathrm {gr}})\) be the base change along the closed immersion \(\{q\} \hookrightarrow {\mathbb{G}}_{m}\). Consider the forgetful functor for the natural map of algebras
obtained via functoriality (Proposition 2.13). Using the \((\iota _{q}^{*}, \iota _{q,*})\) adjunction, we have \(\iota _{q,*} \iota _{q}^{*} {\mathcal {F}}= \operatorname {cone}(q: \mathcal{F} \rightarrow \mathcal{F})\), and an equivalence of complexes

The equivalence is an equivalence of dg algebras, so \(HH(\mathbf {H}, q_{*}) \simeq {\mathcal {H}}^{un}_{q}\). Finally, we have \(HH(\mathbf {H}, q_{*}) \simeq {\mathcal {H}}_{q}\) by Corollary 2.32 (and the identification for \(q=1\) by Corollary 2.30), proving the claim. □
Remark 4.10
The algebra \({\mathcal {H}}^{un}\) can be recovered as the \({\mathbb{G}}_{m}\)-enhanced Hochschild homology of \(\mathbf {H}^{{\mathrm {m}}}\) discussed in [46] and Sect. 3.4.1. In particular, take coordinates \({\mathcal {O}}({\mathbb{G}}_{m}) = k[z,z^{-1}]\), let \(\mathfrak {h}[-n]\) denote the shifted Cartan algebra in cohomological-weight bidegree \((n, 1)\), and define the graded \(k[z,z^{-1}]\) algebra
One can compute (in a similar manner as Corollaries 2.30 and 2.32) that
recovering the above proposition on specialization at various \(z = q\). One can do the same for the variants in Remark 2.34, i.e.
Note that Theorem 4.4.4 in op. cit. establishes a relationship similar to this one.
Remark 4.11
One can similarly argue that \({\mathcal {H}}_{q}\) can be realized as the endomorphisms of the restriction of \({\mathcal {S}}\) along the base change of the inclusion \(\{q\}/{\mathbb{G}}_{m} \hookrightarrow {\mathcal {L}}(B{\mathbb{G}}_{m})\), i.e. where we retain \({\mathbb{G}}_{m}\)-equivariance.
Our main result is the following theorem (see Proposition 4.3).
Theorem 4.12
Assume that \(q \ne 1\).
-
(1)
The dg algebra of endomorphisms of the coherent Springer sheaf is concentrated in degree zero and is identified with the affine Hecke algebra,
$$ \operatorname {End}_{{\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})}({\mathcal {S}}) \simeq \mathcal {H}, \;\;\;\;\;\;\;\;\;\; \;\;\;\; \operatorname {End}_{{\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)}({\mathcal {S}}_{q}) \simeq \mathcal {H}_{q}. $$In particular, \({\mathcal {S}}\) generates full embeddings, the Deligne-Langlands functors:
$$ \mathrm{DL}: \mathcal {H}{\operatorname {-mod}}\hookrightarrow \operatorname {QC}^{!}({\mathcal {L}}(\widehat {{\mathcal {N}}}/ G_{\mathrm {gr}})),\;\;\;\;\;\;\; \mathrm{DL}_{q}: \mathcal {H}_{q}{\operatorname {-mod}}\hookrightarrow \operatorname {QC}^{!}({\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)). $$ -
(2)
On the anti-spherical modules \(M^{\mathrm{asp}} := \operatorname{Ind}_{{\mathcal {H}}^{f}}^{{\mathcal {H}}} (\mathrm{sgn})\) and \(M^{\mathrm{asp}}_{q} := \operatorname{Ind}_{{\mathcal {H}}^{f}_{q}}^{{\mathcal {H}}_{q}}(\mathrm{sgn})\), these functors take values
$$ \mathrm{DL}(M^{\mathrm{asp}}) \simeq \mathrm{pr}_{{\mathcal {S}}}(\omega _{{\mathcal {L}}( \widehat {{\mathcal {N}}}/G_{\mathrm {gr}})}), \;\;\;\;\;\;\; \mathrm{DL}_{q}(M^{\mathrm{asp}}_{q}) \simeq \mathrm{pr}_{{\mathcal {S}}_{q}}(\omega _{{\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)}), $$where \(\mathrm{pr}_{{\mathcal {S}}} = \mathrm{DL} \circ \mathrm{DL}^{R}\) (resp. \(\mathrm{pr}_{{\mathcal {S}}_{q}} = \mathrm{DL}_{q} \circ \mathrm{DL}_{q}^{R}\)), i.e. the composition of the Deligne-Langlands functor with its right adjoint. Furthermore, when \(q\) is not a root of unity,
$$ \mathrm{DL}_{q}(M^{\mathrm{asp}}_{q}) \simeq \mathrm{pr}_{{\mathcal {S}}_{q}}( \omega _{{\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)}) = \omega _{{\mathcal {L}}_{q}({\mathcal {N}}/G)} \simeq {\mathcal {O}}_{{\mathcal {L}}_{q}({\mathcal {N}}/G)} $$and \({\mathcal {O}}_{{\mathcal {L}}_{q}({\mathcal {N}}/G)}\) is a summand of \({\mathcal {S}}_{q}\).
-
(3)
These embeddings are compatible with parabolic induction, i.e. for a parabolic \(P \supset B\) with quotient Levi \(M\), we have commuting diagrams
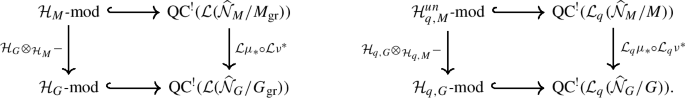
That is, the parabolic induction functor is the pull-push along the correspondence obtained by applying ℒ or \({\mathcal {L}}_{q}\) to the usual correspondence
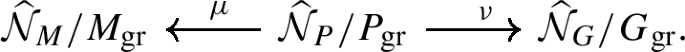
Proof
The first claim of the theorem is a combination of Theorems 2.29 and Theorem 3.25, Corollaries 2.32 and 2.30, and Proposition 4.9, for both general \(q\) and specific \(q\). It remains to prove the claims regarding the anti-spherical module and compatibility with parabolic induction.
We first address the claim regarding anti-spherical modules. By Corollary 3.33, we have an equivalence as \(\operatorname {End}({\mathcal {S}}) \simeq HH({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}}))\)-modules
Thus, it follows that \(\mathrm{pr}_{{\mathcal {S}}}(\omega _{{\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})}) \simeq HH({\operatorname {Coh}}( \widetilde {{\mathcal {N}}}/G_{\mathrm {gr}}))\) as \(HH({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}}))\)-modules (and similarly for special \(q\)). Thus, we need to compute the module \(HH({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}}))\) (and likewise for special \(q\)), and we need to identify the projection for \(q\) not a root of unity.
We first produce an isomorphism \(HH({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}})) \simeq M^{\mathrm{asp}}\) as \(HH({\operatorname {Coh}}({\mathcal {Z}}/ G_{\mathrm {gr}}))\)-modules, and isomorphisms \(HH({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/G), q_{*}) \simeq M^{\mathrm{asp}}_{q}\) as \(HH({\operatorname {Coh}}({\mathcal {Z}}/ G), q_{*})\)-modules. The first isomorphism follows via the identification of \(K_{0}({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/ G_{\mathrm {gr}}))\) as the anti-spherical module for \(K_{0}({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}}))\) in Sect. 7.6 of [34]Footnote 28 once we establish an equivalence \(K_{0}({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/ G_{\mathrm {gr}})) \simeq HH({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/ G_{\mathrm {gr}}))\) as \(K_{0}({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/ G_{\mathrm {gr}})) \simeq HH({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/ G_{\mathrm {gr}}))\)-modules, and the second would follow from an equivalence \(HH({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/G, q_{*})) \simeq HH({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}})) \otimes _{k[ {\mathbb{G}}_{m}]} k_{q}\) (similar to the identification in Proposition 4.9).
To see this, note that \({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}})\) has a semiorthogonal decomposition indexed by \(\lambda \in X^{\bullet}(H)\) characters of the quotient torus \(H = B/[B,B]\), where each subcategory \({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}})_{\lambda}\) is generated over \(\operatorname {Rep}({\mathbb{G}}_{m})\) by the line bundle \({\mathcal {O}}_{\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}}}(\lambda )\). Computing via the Block-Getzler complex of Definition 2.12 (see also Corollary 2.24), and noting that \(\operatorname {End}_{\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}}}({\mathcal {O}}_{\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}}}(\lambda )) = k\) we have that the specialization at \(q\) map is:

The equivalence on the left induces an equivalence \(K_{0}({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}}))_{\lambda} \simeq HH({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/ G_{\mathrm {gr}}))_{\lambda}\). Summing over each subcategory in the semiorthogonal deomposition, this establishes both claims.
It remains to compute the projection \(\mathrm{pr}_{{\mathcal {S}}_{q}}(\omega _{{\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)})\) for \(q\) not a root of unity. By Proposition 4.3, \({\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G) \simeq {\mathcal {L}}_{q}({\mathcal {N}}/G)\); it suffices to show that \(\omega _{{\mathcal {L}}_{q}({\mathcal {N}}/G)} \simeq {\mathcal {O}}_{{\mathcal {L}}_{q}({\mathcal {N}}/G)}\) is a summand of \({\mathcal {S}}_{q}\). Since derived fixed points commutes with fiber products, the diagrams

are Cartesian. When \(q\) is not a root of unity, we have \({\mathcal {L}}_{q}(\{0\}) = {\mathcal {L}}_{q}(\mathfrak {h}//W) = {\mathcal {L}}_{q}(\mathfrak {h})\), so that \({\mathcal {L}}_{q}({\mathcal {N}}/G) = {\mathcal {L}}_{q}(\mathfrak {g}/G)\) and \({\mathcal {L}}_{q}(\widetilde {{\mathcal {N}}}/G) = {\mathcal {L}}_{q}(\widetilde {\mathfrak {g}}/G)\). We then apply Proposition 3.38 to the Grothendieck-Springer resolution \(\mu ': \widetilde {\mathfrak {g}}/G \rightarrow \mathfrak {g}/G\) and \(\phi = q_{*}\) to obtain the splitting, observing that \(\mu '_{*}{\mathcal {O}}_{\widetilde {\mathfrak {g}}} \simeq {\mathcal {O}}_{\mathfrak {g}} \otimes _{{\mathcal {O}}( \mathfrak {h})^{W}} {\mathcal {O}}(\mathfrak {h})\), and that by the main theorem of [36] \({\mathcal {O}}(\mathfrak {h})\) is a free graded \({\mathcal {O}}(\mathfrak {h})^{W}\)-module of rank \(|W|\) with homogeneous basis of degrees \(-\ell (w)\) for \(w \in W\) (in our sign convention), so we may further write
where \(V \in \operatorname {Rep}(\mathbb{G}_{m})\) is the \(k\)-linear span of these \(\mathbb{G}_{m}\)-eigenvector basis elements. In particular the trace of the action of \(q_{*}\) on the free \({\mathcal {O}}(\mathfrak {h})^{W}\)-module \({\mathcal {O}}(\mathfrak {h})\) is the Poincaré polynomial of \(W\) evaluated at \(q\), which is non-zero when \(q\) is not a root of unity [73, Cor. 2.5].
We now address compatibility with parabolic induction. First, note that by Proposition 3.12 we have \({\mathcal {L}}\nu ^{*} = {\mathcal {L}}\nu ^{*}\), since \(\nu \) is smooth. Let \(H = B/U\), fix a parabolic \(P \supset B\) with quotient Levi \(M\), and let \(B_{M} \subset B\) denote the Borel subgroup defined to be the image of \(B \subset P\) under the quotient. Consider the correspondence

Note that the correspondence satisfies the conditions of Proposition 3.17, i.e. since \(\mathfrak {n}/B = \mathfrak {b}/B \times _{\mathfrak {h}/H} \{0\}/H\) (and similarly for \(B_{M}\)), and the formation of loop spaces commutes with fiber products, we have via base change that \({\mathcal {S}}_{G} = {\mathcal {L}}\mu _{*} {\mathcal {O}}_{{\mathcal {L}}(\mathfrak {n}/B)} \simeq {\mathcal {L}}\mu _{*} {\mathcal {L}}\nu ^{*} {\mathcal {O}}_{{\mathcal {L}}(\{0\}/H)}\), and similar formulas hold for \({\mathcal {S}}_{M}\). That is, the coherent Springer sheaf is the parabolic induction of the structure sheaf of \({\mathcal {L}}(\{0\}/H)\). Thus, we have a Cartesian diagram

thus \({\mathcal {L}}\mu _{*} {\mathcal {L}}\nu ^{*} {\mathcal {S}}_{M} \simeq {\mathcal {S}}_{G}\) by base change. By the commuting diagram

it remains to check that the map \(HH({\operatorname {Coh}}({\mathcal {Z}}_{M}/M_{{\mathrm {gr}}})) \rightarrow HH({\operatorname {Coh}}({\mathcal {Z}}_{G}/G_{\mathrm {gr}}))\) induces the parabolic induction map on affine Hecke algebras. By Corollary 2.26 we can argue for \(K_{0}\) instead, i.e. we show that the map
agrees with the natural parabolic induction map of affine Hecke algebras \({\mathcal {H}}_{M} \rightarrow {\mathcal {H}}_{G}\) which takes \(T_{M,w} \mapsto T_{G,w}\) where \(w \in W_{a,M}\) (in the notation of Sect. 7.1 of [34]). We will assume \(G\) has simply connected derived subgroup, but the general case follows by passing to invariants of finite central subgroups (i.e. as in Sect. 2.4.2). It suffices to show that they agree for finite simple reflections and on the lattice. Via the proof of Theorem 7.2.5 in [34], it is clear that the map is as claimed on the lattice; we argue that parabolic induction on \(K_{0}\) sends \([\mathcal{Q}_{M,s}] \mapsto [\mathcal{Q}_{G,s}]\) where \(s\) is a finite simple reflection of \(M\).
Let us recall the definition of \({\mathcal {Q}}_{M, s}\). The underlying closed, reduced scheme of \({\mathcal {Z}}_{M}\) is a disjoint union of conormal bundles to closures of \(M\)-orbits \(\overline{Y}_{M,s} \subset M/B_{M} \times M/B_{M}\); we denote these subschemes and the projection by \(\pi _{M,s}: {\mathcal {Z}}_{M,s} \rightarrow \overline{Y}_{M,s}\) and the inclusion \(\iota _{M,s}: {\mathcal {Z}}_{M,s} \hookrightarrow {\mathcal {Z}}_{M}\). We define \({\mathcal {Q}}_{M,s} := \iota _{M,s,*} \pi ^{*}_{M,s} \Omega ^{1}_{ \overline{Y}_{M,s}/(M/B_{M})^{2}}\).
We have a similar description of \({\mathcal {Z}}_{P,s} \subset {\mathcal {Z}}_{P}\). The map \(p: {\mathcal {Z}}_{P} \rightarrow {\mathcal {Z}}_{M}\) is a \(\mathfrak {u}/U\)-fibration, base changed from the quotient the quotient map \(\mathfrak {p}/P \rightarrow \mathfrak {m}/M\). In particular, \({\mathcal {Z}}_{P,s}\) and \({\mathcal {Z}}_{M,s} \times _{{\mathcal {Z}}_{M}} {\mathcal {Z}}_{P}\) are closed reduced underived subschemes of \({\mathcal {Z}}_{P}\) with the same points, and thus agree. On the other hand, we have \(\overline{Y}_{P, s} = (B \backslash P / B) \times _{\overline{Y}_{M,s}} (B_{M} \backslash M/B_{M})\), so that denoting the projection \(p: \overline{Y}_{P,s} \rightarrow \overline{Y}_{M,s}\) we have \(\Omega ^{1}_{\overline{Y}_{P,s}/(P/B)^{2}} \simeq p^{*}\Omega ^{1}_{ \overline{Y}_{M,s}/(M/B_{M})^{2}}\) and thus \(p^{*} {\mathcal {Q}}_{M,s} \simeq {\mathcal {Q}}_{P,s}\) by base change. We have \({\mathcal {Q}}_{G,s} = i_{*} {\mathcal {Q}}_{P,s}\) by definition, and the claim follows. Finally, the statements for specialized \(q\) follow by Proposition 4.10, completing the proof. □
Remark 4.13
A few remarks on the theorem.
-
(1)
Analogous statements hold when \(q=1\), where Hochschild homology of the Steinberg stack does not agree with the Grothendieck group, i.e. we have
$$ HH({\operatorname {Coh}}({\mathcal {Z}}/G)) \simeq \operatorname {End}_{{\mathcal {L}}({\mathcal {N}}/G)}({\mathcal {S}}_{1}) \simeq kW^{a} \otimes \operatorname {Sym}(\mathfrak {h}^{*}[-1] \oplus \mathfrak {h}^{*}[-2]) \simeq {\mathcal {H}}_{1}^{un} $$while \(K_{0}({\operatorname {Coh}}({\mathcal {Z}}/G))_{k} \simeq kW^{a} \simeq {\mathcal {H}}_{1}\). However, the anti-spherical module arising via Hochschild homology agrees with \(K_{0}\), i.e.
$$ HH({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/G)) \simeq K_{0}({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/G))_{k} \simeq k W^{a} \otimes _{k W^{f}} k_{\mathrm{sgn}}, $$where \(\mathfrak {h}^{*}[-1] \oplus \mathfrak {h}^{*}[-2] \subset {\mathcal {H}}_{1}^{un}\) acts by zero.
-
(2)
Compatibility with parabolic induction implies that the action of the lattice subalgebra \(k[X^{\bullet}(H)] \subset {\mathcal {H}}\) on the coherent Springer sheaf comes from the \({\mathcal {O}}({\mathcal {L}}(\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}}))\)-action on \({\mathcal {S}}= {\mathcal {L}}\mu _{*} {\mathcal {O}}_{{\mathcal {L}}(\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}})}\) via the natural \({\mathcal {O}}({\mathcal {L}}(\{0\}/H)) = {\mathcal {O}}(H)\)-algebra structure on \({\mathcal {O}}({\mathcal {L}}(\widetilde {\mathcal {N}}/G_{\mathrm {gr}}))\).
-
(3)
If \(G = T\) is a torus, then \({\mathcal {L}}({\mathcal {N}}_{T}/T) \simeq \widehat {\{e\}} \times T \times BT\) and \({\mathcal {S}}= {\mathcal {O}}_{\{e\} \times T \times BT}\), and we see immediately that \(\operatorname {End}({\mathcal {S}}) \simeq k[T] = k[X^{\bullet}(T)]\).
-
(4)
Let \(\widetilde {\mathfrak {g}}_{P} = G \times ^{P} \mathfrak {p}\); applying our methods in Sects. 3.4 and 3.4.1 to the \(\operatorname {QC}(\mathfrak {g}/G)\)-module category \(\operatorname {QC}(\widetilde {\mathfrak {g}}_{P}/G)\), one can show that for \(q\) not a root of unity, the coherent “partial Whittaker” sheaves, obtained by applying the parabolic induction correspondence
$$ \mathbb{L}^{u}_{q,M} = {\mathcal {L}}_{q}({\mathcal {N}}_{M}/M) \longleftarrow \mathbb{L}^{u}_{q,P} = {\mathcal {L}}_{q}({\mathcal {N}}_{P}/P) \longrightarrow \mathbb{L}^{u}_{q,G} = {\mathcal {L}}_{q}({\mathcal {N}}_{G}/G) $$to the structure sheaf \({\mathcal {O}}_{\mathbb{L}^{u}_{q,M}}\) are also summands of the coherent Springer sheaf. For example, at the extremes taking \(P = G\) we obtain the statement for the anti-spherical sheaf, and taking \(P = B\) we obtain the coherent Springer sheaf itself.
Remark 4.14
We explain the absence of a singular support condition. There are two Koszul dual versions of the Steinberg variety leading to two versions of the unipotent affine Hecke algebra: the “Springer” version \({\mathcal {Z}}= \widetilde {{\mathcal {N}}} \times _{\mathfrak {g}} \widetilde {{\mathcal {N}}}\) we consider and a “Grothendieck-Springer” version \({\mathcal {Z}}_{\mathfrak {g}} := \widetilde {\mathfrak {g}} \times _{\mathfrak {g}} \widetilde {\mathfrak {g}}\). Theorem 4.4.1 of [12] shows the singular support condition appearing for trace sheaves in \({\mathbf {Tr}}({\operatorname {Coh}}({\mathcal {Z}}_{\mathfrak {g}}/G_{\mathrm {gr}}))\) in the “Grothendieck-Springer” version can be characterized by a nilpotence condition.
We now argue that the singular support condition for the “Springer” version \({\mathbf {Tr}}({\operatorname {Coh}}({\mathcal {Z}}/G_{\mathrm {gr}}))\) is vacuous, i.e. that the singular support locus \(\Lambda _{\widetilde {{\mathcal {N}}}/\mathfrak {g}}\) is the entire scheme of singularities \(\operatorname {Sing}({\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}}))\). The singular locus of \({\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})\) at a \(k\)-point \(\eta = (n, z = (g, q))\) where \(gng^{-1} = qn\) is the set (after identifying \(\mathfrak {g} \simeq \mathfrak {g}^{*}\) via a non-degenerate form \(\langle -,-\rangle \)):
A calculationFootnote 29 shows that the singular support locus is given by:
Note that \(n\), \(v\) generate a two-dimensional solvable Lie algebra, thus are contained in a Borel, so \(\operatorname {Sing}({\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}}))_{\eta }= \Lambda _{\widetilde {{\mathcal {N}}}/\mathfrak {g}}\). In particular, the singular codirection \(v\) need not be nilpotent.
The analogous claim at specific \(q \in {\mathbb{G}}_{m}\) follows by a similar argument and a calculation of the singular support locus at a point \(\eta \in \{(n, g) \in {\mathcal {N}}\times G \mid gng^{-1} = qn\}\) as
In the case of \(q\) not a root of unity, the argument in Proposition 4.3 shows that the singular codirection \(v\) must be nilpotent, i.e. \(\operatorname {Sing}({\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G))\) can only contain nilpotent singular codirections. This condition is not imposed by the singular support condition itself, i.e. in this case all singular codirections are nilpotent to begin with.
It is natural to conjecture that the coherent Springer sheaf is in fact a sheaf – i.e., lives in the heart of the dg category \({\operatorname {Coh}}({\mathcal {L}}(\mathfrak {g}/G_{\mathrm {gr}}))\). We prove this in the case \(G = \operatorname {GL}_{2}, \operatorname {SL}_{2}\) in Proposition 4.19.
Conjecture 4.15
The Springer sheaf \({\mathcal {S}}\) lives in the abelian category \({\operatorname {Coh}}({\mathcal {L}}(\widehat {{\mathcal {N}}}/ G_{\mathrm {gr}}))^{\heartsuit}\).
Remark 4.16
One consequence of the conjecture would be an explicit description of the endomorphisms of the cohrent Springer sheaf. Namely, it is easy to see that the underived parabolic induction from \({\mathcal {L}}(\{0\}/H)\) is generated as a module by the lattice \(X^{\bullet}(H)\), and via the identification with \(K\)-theory and Theorem 7.2.16 of [34] we would obtain a description of the action of finite simple reflections in terms of Demazure operators.
Remark 4.17
A variant of Conjecture 4.15 was answered in the affirmative in Corollary 4.4.6 of [49]. Namely, in loc. cit. it is proven that the Lie algebra version of our coherent Springer sheaf at \(q=1\) has vanishing higher cohomology.
Remark 4.18
When \(G_{\mathrm {gr}}\) acts on \(\widetilde {\mathcal {N}}\) by finitely many orbits, then \({\mathcal {L}}(\widetilde {\mathcal {N}}/G_{\mathrm {gr}})\) has trivial derived structure, and the conjecture is implied by the vanishing of higher cohomology of a classical scheme \(H^{i}({\mathcal {L}}(\widetilde {\mathcal {N}}/G_{\mathrm {gr}}) \times _{BG_{\mathrm {gr}}} \operatorname {pt}, \pi _{0}({\mathcal {O}}_{{\mathcal {L}}(\widetilde {\mathcal {N}}/ G_{\mathrm {gr}}) \times _{BG_{\mathrm {gr}}} \operatorname {pt}}))\) for \(i > 0\). The \(G\)-orbits in the Springer resolution are known to be finite exactly in types \(A_{1}\), \(A_{2}\), \(A_{3}\), \(A_{4}\), \(B_{2}\) by [56].
4.1 Conjectures and examples for \(G = \operatorname {SL}_{2}, \operatorname {GL}_{2}, {\operatorname {PGL}}_{2}\)
In this case, \(G_{\mathrm {gr}}\) acts on both \(\widehat {{\mathcal {N}}}\) and \(\widetilde {\mathcal {N}}\) by finitely many orbits, the derived loop spaces \({\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})\) and \({\mathcal {L}}(\widetilde {\mathcal {N}}/G_{\mathrm {gr}})\) are classical stacks. Recall that \(\widehat {{\mathcal {N}}}\) is a formal completion; if the reader would rather do so, they may replace \(\widehat {{\mathcal {N}}}\) with \(\mathfrak {g}\), which is also acted on by finitely many orbits. We prove Conjecture 4.15 in these cases.
Proposition 4.19
Conjecture 4.15holds for \(G = \operatorname {SL}_{2}, \operatorname {GL}_{2}, {\operatorname {PGL}}_{2}\).
Proof
We give a proof for \(G = \operatorname {SL}_{2}\); the case of \(G = \operatorname {GL}_{2}\) is the same. In view of Remark 4.18, it suffices to forget equivariance and show vanishing of higher cohomology. Since \(X := {\mathcal {L}}(\widetilde {\mathcal {N}}/G_{\mathrm {gr}}) \times _{BG_{\mathrm {gr}}} \operatorname {pt}\) is a closed subscheme of \(\mathfrak {g} \times G/B \times G\), and \(\dim (G/B) = 1\), we know that \(R\Gamma ^{i}(X, -) = 0\) for \(i > 1\). To verify vanishing for \(i=1\), let \(i: X \hookrightarrow \widetilde {\mathcal {N}}\times G_{\mathrm {gr}}\) be the closed immersion. We have a short exact sequence of sheaves:
leading to a long exact sequence with vanishing \(H^{2}\) terms (for the above reason). Thus, it suffices to show that \(H^{1}(\widetilde {\mathcal {N}}\times G_{\mathrm {gr}}, {\mathcal {O}}_{\widetilde {\mathcal {N}}\times G_{\mathrm {gr}}})\). By the projection formula, we have \(H^{1}(\widetilde {\mathcal {N}}\times G_{\mathrm {gr}}, {\mathcal {O}}_{\widetilde {\mathcal {N}}\times G_{\mathrm {gr}}}) \simeq H^{1}(\widetilde {\mathcal {N}}, {\mathcal {O}}_{\widetilde {\mathcal {N}}}) \otimes _{k} {\mathcal {O}}(G_{\mathrm {gr}})\), but it is well-known that \(H^{i}(\widetilde {\mathcal {N}}, {\mathcal {O}}_{\widetilde {\mathcal {N}}}) = 0\) for \(i > 0\). □
Example 4.20
Geometry of the loop space of the Springer resolution
We describe the geometry of the looped Springer resolution \({\mathcal {L}}(\widetilde {\mathcal {N}}/G_{\mathrm {gr}}) \rightarrow {\mathcal {L}}(\widehat {{\mathcal {N}}}/G_{\mathrm {gr}})\) for \(G = \operatorname {SL}_{2}\). Though this example is well-known, we reproduce it for the reader’s convenience. Let \(A(s, n)\) denote the component group of the double stabilizer group, i.e. the component group of \(\{g \in G \mid gng^{-1} = n, gs = sg\}\). Let \(\mathbb{A}^{1}_{\mathrm{node}} = \operatorname {Spec}k[x,y]/xy\) denote the affine nodal curve, and \((-)^{\nu}\) the normalization. The fibers are described in Table 1.
Example 4.21
Generators and relations
For \(G = \operatorname {SL}_{2}\), with some work, one can write down generators and relations for the (underived) scheme \({\mathcal {L}}(\mathfrak {g}/G_{\mathrm {gr}})\) and the coherent Springer sheaf \({\mathcal {S}}\). Let us fix coordinates
We implicitly impose the equations \(ad-bc=1\) and \(x^{2}+yz=0\), and by convention we take the commuting relation \(gxg^{-1} = qx\); note that this is the relation that arises when \({\mathbb{G}}_{m}\) acts on fibers by weight −1 (i.e. inversely). Then, we have that \({\mathcal {S}}\) is the module with generators \(\lambda ^{n}\) for \(n \in \mathbb{Z}\):
In particular, multiplication by \(\lambda ^{n}\) defines the action of the lattice, and one can verify that the Demazure operator for the anti-spherical module (see Theorem 7.2.16 of [34]) defines the endomorphism
corresponding to the finite reflection. In particular, it preserves the relations in the module, and the endomorphism satisfies \((T -q)(T+1)=0\). For fixed \(q\), and letting \(k_{\mathrm{sgn}}\) denote the character of \({\mathcal {H}}^{f}\) with \(T \mapsto -1\), one can verify that \({\mathcal {S}}\otimes _{{\mathcal {H}}^{f}} k_{\mathrm{sgn}} \simeq {\mathcal {O}}_{{\mathcal {L}}_{q}( \widehat {{\mathcal {N}}}/G)}\), i.e. amounts to imposing the relation \(\lambda ^{2} = q\), thus identifying the structure sheaf with the anti-spherical module.
5 Moduli of Langlands parameters for \(\operatorname {GL}_{n}\)
We now turn to arithmetic applications of our results, in particular the study of moduli spaces of Langlands parameters for \(G = \operatorname {GL}_{n}\). Let \(F\) be a non-archimedian local field with residue field \({\mathbb{F}}_{q}\), and let \(G^{\vee}\) denote a connected, split, reductive group over \(F\) (i.e. on the automorphic side of Langlands).
The derived category \(D(G^{\vee})\) of smooth complex representations of \(G^{\vee}\) admits a decomposition into blocks, and the so-called principal block of \(D(G^{\vee})\) (that is, the block containing the trivial representation) is naturally equivalent to the category of \({\mathcal {H}}_{q}\)-modules, where \({\mathcal {H}}_{q}\) now denotes the affine Hecke algebra associated to \(G\) with parameter \(q\). Theorem 4.12 then gives a fully faithful embedding from this principal block into \(\operatorname {QC}^{!}({\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G))\).
The space \({\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)\) has a natural interpretation in terms of Langlands (or Weil-Deligne) parameters for \(G^{\vee}(F)\). Recall that a Langlands parameter for \(G^{\vee}\) is a pair \((\rho ,N)\), where \(\rho : W_{F} \rightarrow G({\mathbb{C}})\) is a homomorphism with open kernel, and \(N\) is a nilpotent element of \(\operatorname {Lie}G\) such that, for all \(\sigma \) in the inertia group \(I_{F}\) of \(W_{F}\), one has \(\operatorname{Ad}(\rho (\operatorname {Fr}^{n} \sigma ))(N) = q^{n} N\), where \(\operatorname {Fr}\) denotes a Frobenius element of \(W_{F}\).
On the other hand, the underlying stack of \({\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)\) can be regarded as the moduli stack of pairs \((s,N)\), where \(s \in G({\mathbb{C}})\), \(N \in \operatorname {Lie}G\), and \(\operatorname{Ad}(s) (N) = qN\), up to \(G\)-conjugacy (i.e. the map \(\rho \) above vanishes on inertia). To such a pair we can attach the Langlands parameter \((\rho ,N)\), where \(\rho \) is the unramified representation of \(W_{F}\) taking \(\operatorname {Fr}\) to \(s\). Such a Langlands parameter is called unipotent, and this construction identifies \({\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)\) with the moduli stack of unipotent Langlands parameters, modulo \(G\)-conjugacy.Footnote 30 We thus obtain a fully faithful embedding from the principal block of \(D(G^{\vee})\) into the category of ind-coherent sheaves on the moduli stack of unipotent Langlands parameters.
It is natural to ask if this extends to an embedding of all of \(D(G^{\vee})\) into a category of sheaves on the moduli stack of all Langlands parameters. We will show that, at least when \(G = \operatorname {GL}_{n}\) over \(F\), this is indeed the case. For the remainder of the section, we will take \(G = G^{\vee }= \operatorname {GL}_{n}\).
5.1 Blocks, semisimple types, and affine Hecke algebras
Our argument proceeds by reducing to the principal block. On the representation theory side, this reduction is a consequence of the Bushnell-Kutzko theory of types and covers [26, 27], which we now recall. For this subsection only, we will reverse our conventions to avoid cumbersome notation; that is, we let \(G\) be a connected reductive split group over \(F\) on the automorphic side of Langlands duality.
5.1.1 Supercuspidal support
Let \(P \subset G\) be a parabolic subgroup with Levi \(M\) and unipotent radical \(U\), and let \(\pi \) be a smooth complex representation of \(M\). Recall that the parabolic induction \(i_{P}^{G}(\pi )\) is obtained by inflating \(\pi \) to a representation of \(P\), twisting by the square root of the modulus character of \(P\), and inducing to \(G\). The parabolic induction functor \(i_{P}^{G}\) has a natural left adjoint, the parabolic restriction \(r_{G}^{P}\) (restriction to \(P\), untwist, and \(U\)-coinvariants).
Definition 5.1
A complex representation \(\pi \) of \(G\) is supercuspidal if, for all proper parabolic subgroups \(P\) of \(G\), the parabolic restriction \(r_{G}^{P}(\pi )\) vanishes. Let \(\pi \) be an irreducible supercuspidal representation of \(M\); an irreducible complex representation \(\Pi \) has supercuspidal support \((M,\pi )\) if \(\Pi \) is isomorphic to a subquotient of \(i_{P}^{G}(\pi )\) (this is well-defined up to conjugacy).
A character \(\chi \) of \(M\) is unramified if it is trivial on every compact open subgroup of \(M\), and the Levi-supercuspidal pairs \((M,\pi )\) and \((L,\pi ')\) are inertially equivalent if there exists an unramified character \(\chi \) of \(L\) such that \((M, \pi )\) and \((L, \pi ' \otimes \chi )\) are \(G\)-conjugate.
For such a pair \((M, \pi )\) up to inertial equivalence, following Bernstein-Deligne [14], we define \(D(G)_{[M,\pi ]} \subset D(G)\) to be the full subcategory of objects such that every subquotient of \(\Pi \) has supercuspidal support inertially equivalent to \((M,\pi )\). Then Bernstein-Deligne show:
Theorem 5.2
The full subcategory \(D(G)_{[M,\pi ]}\) is a block of \(D(G)\), i.e. summing over supercuspidals up to inertial equivalence,
5.1.2 Types and Hecke algebras
We recall the notion of a type.
Definition 5.3
A type for \(G\) is a pair \((K,\tau )\), where \(K \subset G\) is a compact open subgroup and \(\tau \) is an irreducible complex representation of \(K\), such thatFootnote 31 the full subcategory \(\operatorname {Rep}(G,K, \tau )^{\heartsuit }\subset \operatorname {Rep}(G)^{\heartsuit}\) of representations \(V\) which are generated by the image of the evaluation \(\operatorname{Hom}_{K}(\tau , V) \otimes \tau \rightarrow V\) is closed under taking subquotients. Attached to a type we have its Hecke algebra
and an equivalence of abelian categories \(\operatorname {Rep}(G, K, \tau )^{\heartsuit }\simeq D({\mathcal {H}}(G, K, \tau ))^{ \heartsuit}\).
The main result of [27] describes an arbitrary block of \(D(G)\) as a category of modules for a certain tensor product of Hecke algebras, via the theory of \(G\)-covers, providing a connection between parabolic induction methods (which involve subgroups which are not compact open) and Hecke algebra methods (which only make sense for compact open subgroups).
We first consider the block \(D(L)_{[L, \pi ]}\), where \(L \) be a Levi subgroup of \(G\) and \(\pi \) a supercuspidal representation of \(L\). We denote by \(L_{0} \subset L\) the smallest subgroup containing every compact open; then \(L/L_{0}\) is free abelian of rank equal to \(\dim (Z(L))\). Furthermore, the unramified characters of \(L\) are in bijection with the characters of \(L/L_{0}\). There is a bijection
where we denote \(X^{\bullet}(L/L_{0}) = \operatorname{Hom}(L/L_{0}, {\mathbb{C}}^{\times})\) and \(H \subset X^{\bullet}(L/L_{0})\) is the subgroup of unramified characters \(\chi \) such that \(\pi \otimes \chi \simeq \pi \). Moreover, there is an equivalence of categories:
We may rephrase this equivalence in terms of types and Hecke algebras as follows: first, we may (by Sect. 1.2 in [27]) choose a maximal simple cuspidal type \((K_{L },\tau _{L })\) occurring in \(\pi \). One then has a natural support-preserving isomorphism of \({\mathcal {H}}(L ,K_{L },\tau _{L }) \simeq {\mathbb{C}}[X^{\bullet}(L/L_{0})]^{H}\), and thus an (inverse) equivalence
We are interested in understanding the induction of \((L, \pi )\) to \(G\). This is achieved by the following composite of results of [27]; we refer the reader to op. cit. for the definitions of simple type and \(G\)-cover.
Theorem 5.4
[27]
Let \([L,\pi ]\) and the cuspidal type \((K_{L },\tau _{L })\) be as above, and let \(P \subset G \) be a parabolic subgroup with Levi factor \(L \). There exists an intermediateFootnote 32Levi subgroup \(L \subset L^{\dagger} \subset G \), and types \((K^{\dagger},\tau ^{\dagger})\) of \({L^{\dagger}}\) and \((K,\tau )\) of \(G \) with the following properties:
-
(1)
The type \((K^{\dagger},\tau ^{\dagger})\) is a simple type of \(L^{\dagger}\).
-
(2)
\((K,\tau )\) is a \(G \)-cover of \((K^{\dagger},\tau ^{\dagger})\), and \((K^{\dagger},\tau ^{\dagger})\) is an \(L^{\dagger}\)-cover of \((K_{L },\tau _{L })\). In particular we have natural injections:
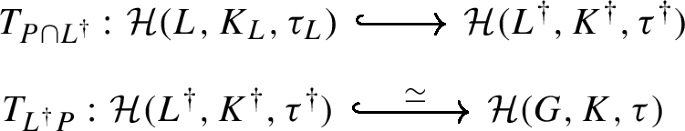
with \(T_{L^{\dagger} P }\) an isomorphism.
-
(3)
The functors
are equivalences of categories. Moreover, for any representation \(V\) in \(D(L )\), one has an isomorphism of \({\mathcal {H}}(G ,K,\tau )\)-modules:
$$ \operatorname{Hom}_{K}(\tau , i_{P'}^{G } V) \cong \operatorname{Hom}_{K_{L }}(\tau _{L }, V) \otimes _{{\mathcal {H}}(L ,K_{L },\tau _{L })} {\mathcal {H}}(G ,K,\tau ), $$where \(P'\) denotes the opposite parabolic to \(P \), and where \({\mathcal {H}}(G ,K,\tau )\) is regarded as an \({\mathcal {H}}(L ,K_{L },\tau _{L })\)-module via the map \(T_{P } := T_{L^{\dagger} P } \circ T_{P \cap L^{\dagger}}\).
-
(4)
Suppose \(L^{\dagger }\simeq \prod _{i} L^{\dagger}_{i}\), with each \(L^{\dagger}_{i} \simeq \operatorname {GL}_{n_{i}}\) for some \(n_{i}\). Let \(L_{i}\) be the projection of \(L\) to \(L^{\dagger}_{i}\), and let \(\pi _{i}\) be the projection of \(\pi \) to \(L _{i}\). Let \(H_{i}\) denote the group of unramified characters \(\chi \) of \(L^{\dagger}_{i}\) such that \(\pi \otimes \chi \simeq \pi \), and let \(r_{i}\) denote the order of \(H_{i}\). Then \(n_{i} = r_{i}m_{i}\) for some positive integer \(m_{i}\), and there is a natural isomorphism (depending on \(\pi \)):
$$ {\mathcal {H}}(L^{\dagger},K^{\dagger},\tau ^{\dagger}) \cong \bigotimes _{i} \mathcal {H}_{q^{r_{i}}}(m_{i}), $$where \(\mathcal {H}_{q^{r_{i}}}(m_{i})\) denotes the affine Hecke algebra associated to \(\operatorname {GL}_{m_{i}}\) with parameter \(q^{r_{i}}\).
These constructions are naturally compatible with parabolic induction, in the following sense: let \(M\) be a Levi with \(L \subset M \subset G\), and with parabolic \(Q = M P \). Then Theorem 5.4 gives us an \(M \)-cover \((K_{M },\tau _{M })\) of \((K_{L },\tau _{L })\) and a \(G \)-cover \((K,\tau )\) of \((K_{L },\tau _{L })\), as well as maps:
We then have:
Theorem 5.5
[27]
There exists a unique map:
such that \(T_{P } = T_{Q } \circ T_{P \cap M }\). Moreover, for any \(V \in D(M )\), we have an isomorphism of \({\mathcal {H}}(G ,K,\tau )\)-modules:
Example 5.6
The fundamental (and motivating) example for this is when \(L=T\) is the standard maximal torus with parabolic \(P=B\) the standard Borel, and \(\tau = 1\) is the trivial character of \(T \). In this setting \(K_{L }\) is the maximal compact subgroup \(T _{0} = T(O) \subset T \), and \(\tau _{L }\) is the trivial character. Moreover \(L^{\dagger }= G \), the subgroup \(K = I \subset G\) is the Iwahori subgroup, and \(\tau \) is the trivial representation of \(I\). We then have natural identifications of the Hecke algebra:
and a commutative diagram:

More generally, if \(M \subset G\) is a Levi subgroup and \(Q\) is its standard parabolic, then \(K_{M}\) is the Iwahori subgroup \(I \cap M\) of \(M\), and the map
is uniquely determined by the following properties:
-
(1)
\(T_{Q} \circ T_{B \cap M} = T_{B}\),
-
(2)
If \(w \in W(M)\) is an element of the Iwahori-Weyl group of \(M\), then \(T_{Q}(I_{M} w I_{M}) = I w I\).
This picture is compatible with the general situation in the following sense. Suppose for simplicity that \(L^{\dagger }= G \). Then \(L \) is a product of \(m\) copies of \(\operatorname {GL}_{\frac{n}{m}}\) for some divisor \(m\) of \(n\), and (after an unramified twist) we may assume that \(\pi \) has the form \(\pi _{0}^{\otimes m}\). There is an extension \(E/F\) of degree \(\frac{n}{m}\) and ramification index \(r\), and an embedding \(\operatorname {GL}_{m}(E) \subset G = \operatorname {GL}_{n}(F)\), such that the intersection \(L \cap GL_{m}(E)\) is the standard maximal torus of \(GL_{m}(E)\).
We denote the subgroup \(GL_{m}(E)\) by \(G_{E}\), its standard maximal torus by \(T_{E}\) and its standard Iwahori by \(I_{E}\). Let \(M\) be a Levi such that \(L \subset M \subset G\), define \(M_{E} = M \cap G_{E}\) and take \((K_{M}, \tau _{M})\) to be a cover of \((K_{L}, \tau _{L})\) via Theorem 5.4. The choice of \(\pi \) then gives rise to an isomorphism \({\mathbb{C}}[X_{\bullet}(T)] \simeq {\mathcal {H}}(L ,K_{L },\tau _{L })\), such that for each coharacter \(\lambda \in X_{\bullet}(T)\) the image of \(\lambda \) is supported on the double coset \(K_{L } \lambda (\varpi _{E}) K_{L }\), and such that the induced action of \(X_{\bullet}(T)\) on the Hecke module attached to \(\pi \) is trivial. We then have:
Theorem 5.7
Theorem 6.4 [25]
Assume that \(L^{\dagger}=G\). There is an isomorphism \(\mathcal {H}_{q^{r}}(m) \simeq {\mathcal {H}}(G ,K,\tau )\) fitting into a commutative diagram:
Thus when \([L,\pi ]\) is “simple” (that is, when \(L^{\dagger }= G\)), we have a natural reduction of \(D(G )_{[L,\pi ]}\) to the principal block of \(D(G_{E} )\), in a manner compatible with parabolic induction. In general we obtain a reduction of \(D(G )_{[L,\pi ]}\) to a tensor product of such principal blocks.
5.2 The moduli spaces \(X_{F,G}^{\nu}\)
We now turn to our study of moduli stacks of Langlands parameters for \(G = \operatorname {GL}_{n}\). Henceforth we revert to our default notation, where \(G\) denotes a group on the spectral side of Langlands duality.
Moduli stacks of Langlands parameters for \(\operatorname {GL}_{n}\) have been studied extensively in mixed characteristic, for instance in [51] in the case of \(\operatorname {GL}_{n}\), or more recently in [4, 24], and [35] for more general groups. Since in our present context we work over ℂ, the results we need are in general simpler than the results of the above papers, and have not appeared explicitly in the literature in the form we need.
We first consider these moduli spaces as underived stacks; it will follow by Proposition 4.3 that they have trivial derived structure. As in the previous section, we take \(G = \operatorname {GL}_{n}\), considered as the Langlands dual of \(G^{\vee} = \operatorname {GL}_{n}(F)\). We use \(X_{F,G}\) to denote the moduli scheme whose quotient stack is the moduli stack \(\mathbb{L}_{F, G}\) in the introduction.
Definition 5.8
Let \(I\) be an open normal subgroup of the inertia subgroup \(I_{F} \subset W_{F}\). Then there is a scheme \(X_{F,G}^{I}\) parameterizing pairs \((\rho ,N)\), where \(\rho : W_{F}/I \rightarrow \operatorname {GL}_{n}\) is a homomorphism, and \(N\) is a nilpotent \(n\) by \(n\) matrix such that for all \(\sigma \in I_{F}\), \(\operatorname{Ad} \rho (\operatorname {Fr}^{n} \sigma ) (N) = q^{n} N\). For any \(\nu : I_{F}/I \rightarrow \operatorname {GL}_{n}({\mathbb{C}})\), we may consider the subscheme \(X_{F,G}^{\nu} \subset X_{F,G}^{I}\) corresponding to pairs \((\rho ,N)\) such that the restriction of \(\rho \) to \(I_{F}\) is conjugate to \(\nu \); it is easy to see that \(X_{F,G}^{\nu}\) is both open and closed in \(X_{F,G}^{I}\). We will say that a Langlands parameter is of “type \(\nu \)” if it lies in \(X_{F,G}^{\nu}\).
Example 5.9
When \(\nu = 1\) is the trivial representation, the quotient stack \(X_{F,G}^{1}/G\) is isomorphic to the underlying underived stack of \({\mathcal {L}}_{q}(\widehat {{\mathcal {N}}}/G)\), as we remarked in the previous section.
We will show that in fact, for \(\nu \) arbitrary, the stack \(X_{F,G}^{\nu}/G\) is isomorphic to a product of stacks of the form \({\mathcal {L}}_{q^{r_{i}}}(\widehat {{\mathcal {N}}}_{i}/G_{i})\), in a manner that exactly parallels the type-theoretic reductions of the previous section. This will allow us to transfer the structures we have built up on \({\mathcal {L}}_{q^{r_{i}}}(\widehat {{\mathcal {N}}}_{i}/G_{i})\) to stacks of the form \(X_{F,G}^{\nu}/G\) for arbitrary \(\nu \). Our approach very closely parallels the construction of Sects. 7 and 8 of [51] with the exception that we are able to work with the full inertia group \(I_{F}\), whereas the integral \(\ell \)-adic setting of [51] requires one to work with the prime-to-\(\ell \) inertia instead.
Our strategy will be to rigidify the moduli space \(X_{F.G}^{\nu}\). For any ℂ-algebra \(R\), let us fix a representative \(\rho : W_{F}/I \rightarrow \operatorname {GL}_{n}(R)\) of type \(\nu \), i.e. of the conjugacy class.
For any irreducible complex representation \(\eta \) of \(I_{F}\), let \(W_{\eta}\) be the finite index subgroup of \(W_{F}\) consisting of all \(w \in W_{F}\) such that \(\eta ^{w}\) is isomorphic to \(\eta \). Then \(\eta \) extends to a representation of \(W_{\eta}\), although not uniquely; let \(\tilde{\eta}\) be a choice of such an extension. This choice defines a natural \(W_{\eta}/I_{F}\)-action on the space \(\operatorname{Hom}_{I_{F}}(\eta ,\rho )\), and an injection of \(W_{\eta}\)-representations
Frobenius reciprocity then gives an injection:
The image of this injection is the sum of the \(I_{F}\)-subrepresentations of \(\rho \) isomorphic to a \(W_{F}\)-conjugate of \(\eta \). We thus have a direct sum decomposition of \(W_{F}\)-representations:
where \(\eta \) runs over a set of representatives for the \(W_{F}\)-orbits of irreducible representations of \(I_{F}/I\). Moreover, the mapFootnote 33\(N\) is \(I_{F}\)-equivariant, and thus induces, for each \(\eta \), a nilpotent endomorphism \(N_{\eta}\) of \(\operatorname{Hom}_{I_{F}}(\eta ,\rho )\). If \(\operatorname {Fr}_{\eta}\) is a Frobenius element of \(W_{\eta}\), we have \(\operatorname {Fr}_{\eta} N_{\eta} \operatorname {Fr}_{\eta}^{-1} = q^{r_{\eta}} N_{\eta}\).
Let \(n_{\eta}(\rho )\) be the dimension of the space \(\operatorname{Hom}_{I_{F}}(\eta ,\rho )\); since \(n_{\eta}(\rho )\) only depends on the type \(\nu \) of \(\rho \), we may also write this as \(n_{\eta}(\nu )\). A choice of \(R\)-basis for \(\operatorname{Hom}_{I_{F}}(\eta ,\rho )\) then gives a homomorphism:
and realizes \(N_{\eta}\) as a nilpotent element of \(M_{n_{i}}(R)\) such that \((\rho _{\eta},N_{\eta})\) is an \(R\)-point of \(X^{1}_{E_{\eta}, \operatorname {GL}_{n_{\eta}(\rho )}}\). We thus define:
Definition 5.10
A pseudo-framing of a Langlands parameter \((\rho ,N)\) over \(R\) is a choice, for all \(\eta \) such that \(n_{\eta}(\rho )\) is nonzero, of an \(R\)-basis for \(\operatorname{Hom}_{I_{F}}(\eta ,\rho )\). Let \({\widetilde{X}}_{F,G}^{\nu}\) be the moduli scheme parameterizing parameters \((\rho ,N)\) of type \(\nu \) together with a pseudo-framing, and define
The scheme \(\widetilde {X}_{F,G}^{\nu}\) is equipped with a \(G \times G_{\nu}\)-action.
We denote by \(E_{\eta}\) the fixed field of \(W_{\eta}\), by \(r_{\eta}\) the degree of \(E_{\eta}\) over \(F\), and by \(d_{\eta}\) the dimension of \(\eta \). We see that \(G_{\nu}\) acts on \({\widetilde{X}}_{F,G}^{\nu}\) via “change of pseudo-framing”, and this action makes \({\widetilde{X}}_{F,G}^{\nu}\) into a \(G_{\nu}\)-torsor over \(X^{\nu}_{F,G}\). On the other hand, given an \(R\)-point \((\rho ,N)\) of \({\widetilde{X}}_{F,G}^{\nu}\), the pseudo-framing gives, for each \(\eta \), an \(R\)-point \((\rho _{\eta},N_{\eta})\) of \(X^{1}_{E_{\eta}, \operatorname {GL}_{n_{\eta}(\nu )}}\). We thus obtain a natural map:
which is a torsor for the conjugation action of \(G\) on \(\widetilde {X}_{F,G}^{\nu}\). We thus obtain natural isomorphisms of quotient stacks:
Note that the composite isomorphism depends on the choice, for each \(\eta \), of an extension \({\tilde{\eta}}\) of \(\eta \) to \(W_{F}\).
5.3 The \(\nu \)-Springer sheaves
We define a Springer sheaf by transporting across the above isomorphism.
Definition 5.11
We define the \(\nu \)-Springer sheaf \(S_{\nu }\in {\operatorname {Coh}}(X^{\nu}_{F,G}/G)\) to be the product, over \(\eta \), of the sheaves \({\mathcal {S}}_{q^{r_{\eta}}}\) on the moduli stack \(X^{1}_{E_{\eta}, \operatorname {GL}_{n_{\eta}(\nu )}}/\operatorname {GL}_{n_{\eta}(\nu )}\).
By Theorem 4.12, the endomorphisms of the \(\nu \)-Springer sheaf are a tensor product of affine Hecke algebras, and we introduce the notation
We thus obtain a fully faithful embedding \(D(\mathcal {H}_{\nu}) \hookrightarrow \operatorname {QC}^{!}(X_{F,G}^{\nu}/G)\). However, since our identifications depend, ultimately, on our choices of \(\tilde{\eta}\), this embedding will also depend on these choices. (By contrast, the sheaf \({\mathcal {S}}_{\nu}\) itself is, at least up to isomorphism, independent of the choices of \(\tilde{\eta}\).) We can remove this dependence by rephrasing this embedding in terms of smooth representations of \(G^{\vee}\), via the type theory of the previous section.
Proposition 5.12
There is a \(G\)-type \((K_{\nu}, \tau _{\nu})\) such that \({\mathcal {H}}(G^{\vee}, K_{\nu}, \tau _{\nu}) \simeq \mathcal {H}_{\nu}\) (depending on choices), and an identification of dg algebras
which is independent of the choices of \({\tilde{\eta}}\).
Proof
Let \(L_{\nu}^{\vee}\) be the standard Levi of \(G^{\vee}\) corresponding to block diagonal matrices whose blocks consist, for each \(\eta \), of \(n_{\eta}(\nu )\) blocks of size \(r_{\eta} d_{\eta}\). Let \(\pi ^{0}_{\eta}\) be the cuspidal representation of \(\operatorname {GL}_{r_{\eta} d_{\eta}}\) corresponding to \(\operatorname{Ind}_{W_{\eta}}^{W_{F}} \tilde{\eta}\) under the local Langlands correspondence, and let \(\pi _{\nu}\) be the cuspidal representation:
of \(L_{\nu}^{\vee}\). Then representations in the block \(D(G^{\vee})_{[L^{\vee}_{\nu},\pi _{\nu}]}\) correspond, via local Langlands, to Langlands parameters for \(G\) of type \(\nu \).
For each \(\eta \), we can find a cuspidal type \((K_{\eta},\tau _{\eta})\) in \(\operatorname {GL}_{r_{\eta}d_{\eta}}\) for \(\pi ^{0}_{\eta}\). From this we can form the type \((K_{L_{\nu}},\tau _{L_{\nu}})\) in \(L_{\nu}^{\vee}\), by setting \(K_{L_{\nu}} = \prod _{\eta} K_{\eta}^{n_{\eta}(\nu )}\) and \(\tau _{L_{\nu}} = \bigotimes _{\eta} \tau _{\eta}^{\otimes n_{\eta}( \nu )}\). This type is associated to the block \([L^{\vee}_{\nu},\pi _{\nu}]\) in \(D(L_{\nu}^{\vee})\). Let \(P^{\vee}\) be the standard parabolic of \(G^{\vee}\) with Levi \(L^{\vee}\), and let \((P')^{\vee}\) denote the opposite parabolic. The theory of Sect. 5.1 then gives us a Levi subgroup \((L^{\dagger})^{\vee}\) of \(G^{\vee}\) containing \(L^{\vee}_{\nu}\), an \((L^{\dagger})^{\vee}\)-cover \((K^{\dagger}_{\nu},\tau ^{\dagger}_{\nu})\) of \((K_{L_{\nu}},\tau _{L_{\nu}})\), and a \(G^{\vee}\)-cover \((K_{\nu},\tau _{\nu})\) of \((K^{\dagger}_{\nu},\tau ^{\dagger}_{\nu})\). These covers depend on a choice of parabolic with Levi \(L^{\vee}\); we choose our covers to be the ones associated to the opposite parabolic \((P')^{\vee}\). In particular we obtain a map
that is compatible with the parabolic induction functor \(i_{P^{\vee}}^{G^{\vee}}\) on \(D(L_{\nu}^{\vee})\) in the sense of Theorem 5.4.
One verifies, by compatibility of local Langlands with unramified twists, that for each \(\eta \) the group of unramified characters \(\chi \) of \(\operatorname {GL}_{r_{\eta}d_{\eta}}\) such that \(\pi ^{0}_{\eta} \otimes \chi \) is isomorphic to \(\pi ^{0}_{\eta}\) is \(r_{\eta}\). Thus there is an isomorphism of Hecke algebras \({\mathcal {H}}(G^{\vee},K_{\nu},\tau _{\nu}) \simeq \mathcal {H}_{\nu}\). Moreover, the composition:
is independent of the choices of \({\tilde{\eta}}\). This essentially boils down to the compatibility of the local Langlands correspondence with unramified twists and parabolic induction. □
Since \(D(G^{\vee})_{[L_{\nu}^{\vee},\pi _{\nu}]}\) is canonically equivalent to the category of \({\mathcal {H}}(G^{\vee},K_{\nu},\tau _{\nu})\)-modules, and this equivalence associates the representations \(\operatorname {cInd}_{K_{\nu}}^{G^{\vee}} \tau _{\nu}\) to the free \({\mathcal {H}}(G^{\vee},K_{\nu},\tau _{\nu})\)-module of rank one, we have shown:
Theorem 5.13
For each \(\nu \) there is a natural fully faithful functor:
that takes the generator \(\operatorname {cInd}_{K_{\nu}}^{G^{\vee}} \tau _{\nu}\) to \({\mathcal {S}}_{\nu}\).
Remark 5.14
We will say that an inertial type \(\nu \) is cuspidal if the representations of \(W_{F}\) corresponding to points of \(X^{\nu}_{F,G}\) are irreducible. For \(G = \operatorname {GL}_{n}\) this happens precisely when \(n_{\eta} = 1\) for a single \(\eta \) and is zero for all other \(\eta \). In such cases \(X^{\nu}_{F,G}\) is simply a copy of \({\mathbb{G}}_{m}\), the sheaf \({\mathcal {S}}_{\nu}\) is the structure sheaf, and the corresponding affine Hecke algebra is simply \({\mathbb{C}}[T,T^{-1}]\), which our choices above identify with the global functions on \(X^{\nu}_{F,G} \cong {\mathbb{G}}_{m}\). In particular for such \(\nu \) the functor \(\operatorname{LL}_{G,\nu}\) is an abelian equivalence, that takes an irreducible \({\mathbb{C}}[T,T^{-1}]\)-module to a skyscraper sheaf on the corresponding point of \(X^{\nu}_{F,G}\).
By taking products of the above picture we see that a similar statement holds for Levi subgroups \(M\) of \(G\) (with a suitable torus in place of \({\mathbb{G}}_{m}\).)
5.3.1 A direct construction of \({\mathcal {S}}_{\nu}\)
In this section we give a more intrinsic construction of \({\mathcal {S}}_{\nu}\). Fix a particular \(\nu \), and let \(L_{\nu}\) denote the Langlands dual of \(L_{\nu}^{\vee}\); we identify \(L_{\nu}\) with the standard block diagonal Levi of \(G\) containing \(n_{\eta}(\nu )\) blocks of size \(r_{\eta} d_{\eta}\). Let \(\nu ': I_{F} \rightarrow L_{\nu}\) be the representation of \(I_{F}\) on \(L\) whose projection to each block of \(L_{\nu}\) of type \(\eta \) is the sum of the \(W_{F}\)-conjugates of \(\eta \). We then have a moduli space \(X_{F,L_{\nu}}^{\nu '}\) parameterizing Langlands parameters for \(L_{\nu}\) that are of type \(\nu '\).
Let \(P\) be the standard (block upper triangular) parabolic of \(G\) containing \(L_{\nu}\). We then also have a moduli space \(X_{F,P}^{\nu '}\) parameterizing Langlands parameters for \(G\) that factor through \(P\), and whose projection to \(L_{\nu}\) is of type \(\nu '\). The inclusion of \(P \hookrightarrow G\), and the projection of \(P \twoheadrightarrow L\) induce parabolic induction maps

We then have:
Theorem 5.15
There are natural isomorphisms:
where \({\mathcal {O}}_{F,P}^{\nu '}\) and \({\mathcal {O}}_{F,L_{\nu}}^{\nu '}\) denote the structure sheaves on \(X_{F,P}^{\nu '}/P\) and \(X_{F,L_{\nu}}^{\nu '}/L_{\nu}\), respectively.
Proof
Let \(L^{\dagger}\) be the standard Levi of \(G\) that is block diagonal of block sizes \(n_{\eta}(\nu ) r_{\eta} d_{\eta}\). Let \(Q\) be the standard block upper triangular parabolic of \(G\) with Levi \(L^{\dagger}\), and let \(\nu ''\) be the composition of \(\nu '\) with the inclusion of \(L_{\nu}\) in \(L^{\dagger}\). We then have spaces \(X_{F,L^{\dagger}}^{\nu ''}\) and \(X_{F,Q}^{\nu ''}\), where the former parameterizes pairs \((\rho ,N)\) for \(L^{\dagger}\) that are of type \(\nu ''\), and the latter parameterizes pairs \((\rho ,N)\) for \(G\) that factor through \(Q\) and whose projection to \(L^{\dagger}\) is of type \(\nu ''\). We may also consider the space \(X_{F,P \cap L^{\dagger}}^{\nu '}\), which parameterizes pairs \((\rho ,N)\) for \(L^{\dagger}\) that factor through \(P \cap L^{\dagger}\) and whose projection to \(L\) is of type \(\nu '\). We then have a natural Cartesian diagram:

from which we conclude that \((\iota _{P})_{*} \pi _{P}^{*} {\mathcal {O}}_{F,L_{\nu}}^{\nu '}\) is isomorphic to \((\pi _{Q})_{*} \iota _{Q}^{*} (\iota _{P \cap L^{\dagger}})_{*} \pi _{P \cap L^{\dagger}}^{*} {\mathcal {O}}_{F,L_{\nu}}^{\nu '}\), where \(\pi _{Q}: X_{F,Q}^{\nu ''}/Q \rightarrow X_{F,G}^{\nu}/G\), and \(\pi _{P \cap L^{\dagger}}: X_{F, P \cap L^{\dagger}}^{\nu '}/ (P \cap L^{\dagger}) \rightarrow X_{F,L_{\nu}}^{\nu '}/L_{\nu}\).
On the other hand, let \(B_{\eta}\) and \(T_{\eta}\) denote the standard Borel subgroup and maximal torus of \(\operatorname {GL}_{n_{\eta}(\nu )}\), for each \(\eta \). We then have a commutative diagram (note that we transport derived structures across the isomorphisms by definition):
where the bottom two vertical maps on the left are the identity. It follows that the iterated pull-push \((\iota _{Q})_{*} \pi _{Q}^{*} (\iota _{P \cap L^{\dagger}})_{*} \pi _{P \cap L^{\dagger}}^{*} {\mathcal {O}}_{F,L_{\nu}}^{\nu '}\) corresponds, under the bottom isomorphism, to \({\mathcal {S}}_{\nu}\), as the latter is simply the pushforward to \(\prod _{\eta} {\mathcal {L}}_{q^{r_{\eta}}}(\widehat {{\mathcal {N}}}_{n_{\eta}(\nu )}/{ G_{n_{ \eta}(\nu )}})\) of the structure sheaf on \(\prod _{\eta} {\mathcal {L}}_{q^{r_{\eta}}}(\widehat {{\mathcal {N}}}_{B_{\eta}}/{B})\). □
5.3.2 Compatibility with parabolic induction
As in the previous subsection, we fix a particular \(\nu \) and let \(L_{\nu}^{\vee}\), \(L_{\nu}\) and \(P\) be as above. Let \(Q\) be a standard Levi subgroup of \(G\) whose standard Levi subgroup \(M\) contains \(L_{\nu}\), and let \(M^{\vee}\) and \(Q^{\vee}\) be the corresponding dual subgroups of \(G^{\vee}\). Let \(\nu '\) be the inertial type \(I_{F} \rightarrow L_{\nu}\) constructed in the previous subsection, and let \(\nu ''\) be the composition of \(\nu '\) with the inclusion of \(L_{\nu}\) in \(M\). We have a diagram with the square Cartesian:

Theorem 5.15 shows that \({\mathcal {S}}_{\nu}\) is isomorphic to the pushforward to \(X_{F,G}^{\nu}/G\) of the structure sheaf on \(X_{F,P}^{\nu '} / P\), and the corresponding sheaf \({\mathcal {S}}_{\nu ,M}\) on \(X_{F,M}^{\nu ''}\) is the pushforward to \(X_{F,M}^{\nu ''} / M\) of the structure sheaf on \(X_{F,P \cap M}^{\nu '}/ (P \cap M)\). The above diagram then gives us a natural isomorphism:
Via functoriality and this isomorphism one obtains an embedding of \(\operatorname {End}({\mathcal {S}}_{\nu ,M})\) in \(\operatorname {End}({\mathcal {S}}_{\nu})\).
Recall that we have identified these endomorphism rings with certain Hecke algebras via type theory. In particular, we have the type \((K_{L_{\nu}},\tau _{L_{\nu}})\) of \(L_{\nu}^{\vee}\), an \(M^{\vee}\)-cover \((K_{M^{\vee}},\tau _{M^{\vee}})\) coming from the parabolic \((P')^{\vee} \cap M^{\vee}\) opposite \(P^{\vee} \cap M^{\vee}\), and a \(G^{\vee}\)-cover \((K,\tau )\) coming from the parabolic \((P')^{\vee}\) opposite \(P^{\vee}\). Theorem 5.5 then gives us a map:
Lemma 5.16
We have a commutative diagram:

where the right hand map is induced by the isomorphism of \({\mathcal {S}}_{\nu} \simeq (\iota _{Q})_{*} \pi _{Q}^{*} {\mathcal {S}}_{\nu ,M}\).
Proof
The machinery of the previous subsection, together with the compatibility of the general case with the Iwahori case in Sect. 5.1 allow us to reduce to the case where \(\nu = 1\). In this case the claim reduces to the compatibility of the Ginsburg-Kazhdan-Lusztig interpretation of the affine Hecke algebra as \(K_{0}\) of the Steinberg variety with parabolic induction, checked in the proof of Theorem 4.12. □
As a consequence, we deduce:
Theorem 5.17
We have a commutative diagram of functors:

Proof
We have isomorphisms:
from which the result follows. □
Notes
Note that the finite Hecke algebra and hence the category of unipotent principal series representations is insensitive to Langlands duality. From our perspective it is in fact more natural to consider here representations of the Langlands dual Chevalley group \(G^{\vee}(\mathbb{F}_{q})\).
Further if one had an \((s,q)\)-version of Rider’s formality theorem, one could deduce a full embedding of the corresponding module categories into equivariant derived categories of constructible sheaves on \({\mathcal {N}}^{(s,q)}\). See Theorem 3.1 of [57] for an accounting.
Note that for any formal completion \(\widehat {Z}\) along a closed substack \(Z \subset X\), following [45] we define the category \({\operatorname {Coh}}(\widehat {Z})\) so that it is canonically equivalent to the category \({\operatorname {Coh}}_{Z}(X)\) of coherent sheaves on the ambient stack set-theoretically supported at \(Z\). Thus the reader unfamiliar with formal completions may replace \(\widehat {{\mathcal {N}}}\) with \(\mathfrak {g}\), and impose nilpotent support conditions on all categories of sheaves.
I.e. the corresponding modules for Hecke algebras are finitely generated.
The horizontal trace is also the natural receptacle for characters of \(\mathbf {C}\)-module categories, and \([{\mathbf {C}}]\) appears as the character of the regular left \(\mathbf {C}\)-module, see Definition 3.2.
The notion of a QCA stack in [38] is slightly more general; only automorphism groups at geometric points are required to be affine, and they are not required to be of finite presentation.
Letting \(q\) denote the action by \(q\) in the above convention (i.e. multiplication by \(q^{-1}\)), we have \(q_{*} = \mathbf{q}^{*}\), where \(\mathbf{q}^{*}\) is the functor in Sect. 11.1 of [18]. Thus, given an identification \({\mathcal {H}}\simeq \mathrm{tr}(\mathbf {H}^{{\mathrm {m}}}, \mathrm{id}_{\mathbf {H}^{{\mathrm {m}}}})\) as in Theorem 2.29, this implies an identification \({\mathcal {H}}_{q} \simeq \mathrm{tr}(\mathbf {H}, q_{*}) \simeq \mathrm{tr}(\mathbf {H}, \mathrm{Fr}^{*})\). This convention is compatible with [2, 18, 34, 58].
This may also sometimes be referred to as a trace, but we call it a character to avoid overloading the term.
Note that for consistency we label using cohomological grading, and that we are defining the complex of Hochschild chains and not the complex of Hochschild cochains.
Note that if \(F\) is the identity functor, then the Block-Getzler simplicial chain complex is a cyclic object, and thus the associated chain complex has the natural structure of a mixed complex. However, the enhanced Block-Getzler complex is not cyclic, since the “rotation” twists by the coaction \(\gamma \) which can be nontrivial on nontrivial \(G\)-isotypic components. One can view this object as an \(S^{1}\)-equivariant object in \(\operatorname {QC}(G/G)\).
We use this terminology to avoid overloading the word “trace.”
This definition is independent of the choice of presentation, since by [16] Theorem 3.4.1(ii) if \(G_{i} \rightarrow G_{j}\) is a surjection with unipotent kernel, then \(\operatorname {Sh}^{G_{j}}(Y) \rightarrow \operatorname {Sh}^{G_{i}}(Y)\) is an equivalence for any \(Y\) on which \(G_{j}\) acts. See also Section A.4 of [42].
Note that our \(q_{*}\) corresponds to \(\mathbf{q}^{*}\) in [2].
The category \(\mathbf {A}^{rv}\) is obtained by reversing the monoidal product, not taking opposite morphisms.
More generally, the horizontal trace may take as an input an \(\mathbf {A}\)-bimodule category \(\mathbf {Q}\); we will not need this.
The arguments in [46] do not require the use of non-invertible 3-morphisms in \(\mathbf {Mor}_{k}\).
Roughly, this is the data of \(F_{\mathbf {M}} \in \mathbf {End}(\mathbf {M})\) with natural compatibility isomorphisms \(F_{\mathbf {M}}(A \ast M) \simeq F(A) \ast F_{\mathbf {M}}(M)\) for \(A \in \mathbf {A}\), \(M \in \mathbf {M}\), i.e. for a functor to be \(\mathbf {A}\)-linear is a structure, not merely a property.
The monoidal structure on \(F\) gives rise to an \(F\)-equivariant structure on \(1_{\mathbf {A}}\).
The opposite algebra appears because we took left modules in Definition 3.2.
By this we mean such that the relative cotangent complex is perfect of Tor amplitude \([0, 1]\), i.e. the fibers are allowed to be stacky, and in particular, this map does not need to be representable by schemes.
The definition of Hochschild homology implicitly requires us to choose an orientation on the circle \(S^{1}\). We make one such choice, once and for all, which forces a particular choice here (i.e. a choice of sign).
As explained in Remark 3.0.7 and Lemma 3.0.8 of [11], on the compact objects \({\operatorname {Coh}}(Z)\) there are two monoidal products, given by ∗- or !-convolution, intertwined by Grothendieck duality. We will default to the !-version, which is amenable to the ind-completed category \(\operatorname {QC}^{!}(Z)\).
Via the discussion in Sect. 4.7 of [65], endofunctor categories naturally possess the structure of an associative monoidal \(\infty \)-category. Theorem 1.1.3 in [11] identifies the underlying categories, with convolution corresponding to composition object-by-object. Thus we can simply define the monoidal structure (with all its higher coherence compatibilities) on the left by transporting it from the right.
Note that our trace functor is given by \(\delta ^{!}\) rather than the \(\delta ^{*}\) in [12], since we employ the !-transform rather than the ∗-transform.
I.e. a “projection” functor to the subcategory \(\operatorname {QC}^{!}_{\Lambda}(X)\), which we view as a singular support analogue of local cohomology. Note the abusive notation, i.e. the local cohomology functor usually refers to the functor \(\iota _{\Lambda }\circ \Gamma _{\Lambda}\).
Note that, as discussed in Example 3.21, \(\operatorname {QC}^{!}_{\{0\}_{{\mathcal {L}}_{\phi }Y}}({\mathcal {L}}_{\phi }Y) = \operatorname {QC}({\mathcal {L}}_{\phi }Y)\).
In our convention, we identify \(K_{0}({\operatorname {Coh}}(\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}}))\) with the anti-spherical module, and \(K_{0}({\operatorname {Coh}}_{{\mathcal {B}}/G_{\mathrm {gr}}}(\widetilde {{\mathcal {N}}}/G_{\mathrm {gr}}))\) with the spherical module.
In contrast to the singular support calculation for \({\operatorname {Coh}}({\mathcal {Z}}_{\mathfrak {g}}/G_{\mathrm {gr}})\), it is the Lie algebra of the Borel \(\mathfrak {b}\) that appears in the above condition rather than its nilradical \(\mathfrak {n}\) since
$$ \operatorname {Sing}(\widetilde {{\mathcal {N}}} \times _{\mathfrak {g}} \widetilde {{\mathcal {N}}})_{(n, B, B')} \subset \mathfrak {b} \cap \mathfrak {b}', \;\;\;\;\;\;\; \operatorname {Sing}(\widetilde {\mathfrak {g}} \times _{G} \widetilde {\mathfrak {g}})_{(x, B, B')} \subset \mathfrak {n} \cap \mathfrak {n}'. $$Strictly speaking, a Langlands parameter is a pair \((\rho ,N)\) as above in which \(\rho \) is semisimple. When building a moduli space of Langlands parameters we must drop this condition, however, as the space of semisimple parameters is not a well-behaved geometric object. In particular the locus in \({\mathcal {L}}_{q}\) consisting of pairs \((s,N)\) in which \(s\) is semisimple is neither closed nor open in \({\mathcal {L}}_{q}\).
See pp. 594 of [26] for why this is necessary.
Defined to be the smallest Levi containing the \(G\)-normalizer of the type \((K_{L}, \tau _{L})\).
I.e. viewed as a map \(N: I_{F} \twoheadrightarrow I_{F}/P_{F} \simeq \prod _{\ell '} \overline{\mathbb{Q}}_{\ell '} \twoheadrightarrow \overline {\mathbb{Q}}_{\ell}\simeq {\mathbb{C}}\rightarrow \operatorname {GL}_{n}(R)\).
References
Arinkin, D., Gaitsgory, D., Kazhdan, D., Raskin, S., Rozenblyum, N., Varshavsky, Y.: The stack of local systems with restricted variation and geometric Langlands theory with nilpotent singular support. Preprint (2020). arXiv:2010.01906v1
Arkhipov, S., Bezrukavnikov, R.: Perverse sheaves on affine flags and Langlands dual group. With an appendix by Bezrukavnikov and Ivan Mirković. Isr. J. Math. 170, 135–183 (2009)
Aubert, A.-M., Baum, P., Plymen, R., Solleveld, M.: Conjectures About \(p\)-Adic Groups and Their Noncommutative Geometry. Around Langlands Correspondences. Am. Math. Soc., Providence (2017)
Bellovin, R., Gee, T.: \(G\)-Valued local deformation rings and global lifts. Algebra Number Theory 13(2), 333–378 (2019)
Ben-Zvi, D., Nadler, D.: Loop spaces and connections. J. Topol. 5(2), 377–430 (2012)
Ben-Zvi, D., Nadler, D.: Loop spaces and representations. Duke Math. J. 162(9), 1587–1619 (2013)
Ben-Zvi, D., Nadler, D.: The character theory of a complex group. Preprint (2015). arXiv:0904.1247v3
Ben-Zvi, D., Nadler, D.: Nonlinear Traces. Derived Algebraic Geometry. Panor. Synth., vol. 55, pp. 39–84. Société Mathématique de France (SMF), Paris (2021)
Ben-Zvi, D., Francis, J., Nadler, D.: Integral transforms and Drinfeld centers in derived algebraic geometry. J. Am. Math. Soc. 23, 909–966 (2010)
Ben-Zvi, D., Francis, J., Nadler, D.: Morita equivalence for convolution categories. Appendix to [9] (2012)
Ben-Zvi, D., Nadler, D., Preygel, A.: Integral transforms for coherent sheaves. J. Eur. Math. Soc. 19(12), 3763–3812 (2017)
Ben-Zvi, D., Nadler, D., Preygel, A.: A spectral incarnation of affine character sheaves. Compos. Math. 153(9), 1908–1944 (2017)
Ben-Zvi, D., Chen, H., Helm, D., Nadler, D.: Between coherent and constructible local Langlands correspondences. Proc. Symp. Pure Math. (2023, to appear)
Bernstein, J.: Le “centre” de Bernstein. In: Deligne, P. (ed.) Representations des groups redutifs sur un corps local, Traveaux en cours, pp. 1–32. Hermann, Paris (1984)
Bernstein, J.: Hidden sign in Langlands’ correspondence. Preprint (2020). arXiv:2004.10487v2
Bernstein, J., Lunts, V.: Equivariant Sheaves and Functors. Lecture Notes in Mathematics, vol. 1578. Springer, Berlin (1994)
Bezrukavnikov, R.: Noncommutative counterparts of the Springer resolution. In: International Congress of Mathematicians. Vol. II, pp. 1119–1144. Eur. Math. Soc., Zürich (2006)
Bezrukavnikov, R.: On two geometric realizations of an affine Hecke category. Publ. Math. Inst. Hautes Études Sci. 123, 1–67 (2016)
Bezrukavnikov, R., Yun, Z.: On Koszul duality for Kac-Moody groups. Represent. Theory 17, 1–98 (2013)
Bezrukavnikov, R., Finkelberg, M., Ostrik, V.: Character \({\mathcal {D}}\)-modules via Drinfeld center of Harsih-Chandra bimodules. Invent. Math. 188(3), 589–620 (2012)
Block, J., Getzler, E.: Equivariant cyclic homology and equivariant differential forms’. Ann. Sci. Éc. Norm. Supér. (4) 27(4), 493–527 (1994)
Blumberg, A.J., Gepner, D., Tabuada, G.: A universal characterization of higher algebraic \(K\)-theory. Geom. Topol. 17(2), 733–838 (2013)
Blumberg, A.J., Gepner, D., Tabuada, G.: Uniqueness of the multiplicative cyclotomic trace. Adv. Math. 260, 191–232 (2014)
Booher, J., Patrikis, S.: \(G\)-Valued Galois deformation rings when \(\ell \neq p\). Math. Res. Lett. 26(4), 973–990 (2019)
Bushnell, C., Kutzko, P.: The Admissible Dual of \(GL(N)\) via Compact Open Subgroups. Annals of Mathematics Studies, vol. 129. Princeton University Press, Princeton (1993)
Bushnell, C., Kutzko, P.: Smooth representations of reductive \(p\)-adic groups: structure theory via types. Proc. Lond. Math. Soc. (3) 77(3), 582–634 (1998)
Bushnell, C., Kutzko, P.: Semisimple types in \(GL_{n}\). Compos. Math. 119, 53–97 (1999)
Buzzard, K., Gee, T.: The Conjectural Connections between Automorphic Representations and Galois Representation, Automorphic Forms and Galois Representations. Vol. 1. London Math. Soc. Lecture Note Ser., vol. 414, pp. 135–187. Cambridge University Press, Cambridge (2014)
Căldăraru, A.: The Mukai pairing. II: the Hochschild-Kostant-Rosenberg isomorphism. Adv. Math. 194(1) (2005)
Campbell, J.A., Ponto, K.: Iterated traces in 2-categories and Lefschetz theorems. Algebraic Geom. Topol. 22(2), 815–879 (2022)
Chen, H.: Equivariant localization and completion in cyclic homology and derived loop spaces. Adv. Math. 364, 107005 (2020)
Chen, H.: Categorical cyclic homology and filtered \({\mathcal {D}}\)-modules on stacks: Koszul duality. Preprint (2023). arXiv:2301.06949
Chen, H., Dhillon, G.: Langlands dual realizations of partial affine Hecke categories. Preprint (2023). arXiv:2310.10539
Chriss, N., Ginzburg, V.: Representation Theory and Complex Geometry. Birkhäuser Boston, Boston (1997)
Dat, J.-F., Helm, D., Kurinczuk, R., Moss, G.: Moduli of Langlands parameters. Preprint (2020). arXiv:2009.06708
Demazure, M.: Invariants symétriques entiers des groupes de Weyl et torsion. Invent. Math. 21, 287–301 (1973)
Dima, A., Gaitsgory, D.: Singular support of coherent sheaves and the geometric Langlands conjecture. Sel. Math. New Ser. 21(1), 1–199 (2015)
Drinfeld, V., Gaitsgory, D.: On some finiteness questions for algebraic stacks. Geom. Funct. Anal. 23(1), 149–294 (2013)
Emerton, M., Helm, D.: The local Langlands correspondence for \(GL_{n}\) in families. Ann. Sci. Éc. Norm. Supér. (4) 47(4), 655–722 (2014)
Fargues, L.: Geometrization of the local Langlands correspondence: an overview. Preprint (2016). arXiv:1602.00999
Fargues, L., Scholze, P.: Geometrization of the local Langlands correspondence. Preprint (2021). arXiv:2102.13459
Gaitsgory, D.: Construction of central elements in the affine Hecke algebra via nearby cycles. Invent. Math. 144(2), 253–280 (2001)
Gaitsgory, D.: Ind-coherent sheaves. Mosc. Math. J. 13(3), 399–528, 553 (2013)
Gaitsgory, D.: From geometric to function-theoretic Langlands (or how to invent shtukas). Preprint (2016). arXiv:1606.09608v1
Gaitsgory, D., Rozenblyum, N.: A Study in Derived Algebraic Geometry. Mathematical Surveys and Monographs, vol. 221. Am. Math. Soc., Providence (2017)
Gaitsgory, D., Kazhdan, D., Rozenblyum, N., Varshavsky, Y.: A toy model for the Drinfeld-Lafforgue Shtuka construction. Indag. Math. 33(1), 39–189 (2022)
Genestier, A., Lafforgue, V.: Chtoucas restreints pour les groupes réductifs et paramétrisation de Langlands locale. Preprint (2018). arXiv:1709.00978v2
Ginzburg, V.: Geometric methods in the representation theory of Hecke algebras and quantum groups. Notes by Vladimir Baranovsky. In: Representation Theories and Algebraic Geometry, Montreal, PQ, 1997. NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., vol. 514, pp. 127–183. Kluwer Academic, Dordrecht (1998)
Ginzburg, V.: Isospectral commuting variety, the Harish-Chandra D-module, and principal nilpotent pairs. Duke Math. J. 161(11), 2023–2111 (2012)
Hellmann, E.: On the derived category of the Iwahori-Hecke algebra. Compos. Math. 159(5), 1042–1110 (2023)
Helm, D.: Curtis homomorphisms and the integral Bernstein center for \(GL_{n}\). Algebra Number Theory 14(10), 2607–2645 (2020)
Helm, D., Moss, G.: Converse theorems and the local Langlands correspondence in families. Invent. Math. 214(2), 999–1022 (2018)
Hemo, T., Zhu, X.: In preparation
Ho, Q.P., Li, P.: Revisiting mixed geometry. Preprint (2021). arXiv:2202.04833v1
Hoyois, M., Scherotzke, S., Sibilla, N.: Higher traces, noncommutative motives, and the categorified Chern character. Adv. Math. 309, 97–154 (2017)
Kashin, V.V.: Orbits of an adjoint and co-adjoint action of Borel subgroups of a semisimple algebraic group. In: Problems in Group Theory and Homological Algebra, pp. 141–158. Matematika, Yaroslav. Gos. Univ., Yaroslavl (1990) (Russian)
Kato, S.: A homological study of Green polynomials. Ann. Sci. Éc. Norm. Supér. (4) 48(5), 1035–1074 (2015)
Kazhdan, D., Lusztig, G.: Proof of the Deligne-Langlands conjecture for Hecke algebras. Invent. Math. 87(1), 153–215 (1987)
Keller, B.: On differential graded categories. In: International Congress of Mathematicians. Vol. II, pp. 151–190. Eur. Math. Soc., Zürich (2006)
Lafforgue, V.: Chtoucas pour les groupes réductifs et paramétrisation de Langlands globale. J. Am. Math. Soc. 31(3), 719–891 (2018)
Lafforgue, V.: Shtukas for reductive groups and Langlands correspondence for function fields. In: Proceedings, 2018 International Congress of Mathematicians (2018)
Lafforgue, V., Zhu, X.: Décomposition au-dessus des paramètres de Langlands elliptiques (2019). Preprint. arXiv:1811.07976v2
Laszlo, Y., Olsson, M.: The six operations for sheaves on Artin stacks. II. Adic coefficients. Publ. Math. Inst. Hautes Études Sci. 107, 169–210 (2008)
Loday, J.-L.: Cyclic Homology. Grundlehren der Mathematischen Wissenschaften, vol. 301. Springer, Berlin (1992). Appendix E by Marìa O. Ronco.
Lurie, J.: Higher Algebra (2017). http://www.math.harvard.edu/~lurie/
Lusztig, G.: Some examples of square integrable representations of semisimple p-adic groups. Trans. Am. Math. Soc. 277(2), 623–653 (1983)
Lusztig, G.: Intersection cohomology complexes on a reductive group. Invent. Math. 75, 205–272 (1984)
Lusztig, G.: Cuspidal local systems and graded Hecke algebras. I. Inst. Hautes Études Sci. Publ. Math. 67 (1988)
Lusztig, G.: Affine Hecke algebras and their graded version. J. Am. Math. Soc. 2(3), 599–635 (1989)
Lusztig, G.: Cuspidal local systems and graded Hecke algebras. II. In: CMS Conf. Proc., 16, Representations of Groups (Banff, AB, 1994). Am. Math. Soc., Providence (1995)
Lusztig, G.: Classification of unipotent representations of simple p-adic groups. Int. Math. Res. Not. 11, 517–589 (1995)
Lusztig, G.: Bases in equivariant K-theory I. Represent. Theory 2, 298–369 (1998)
Macdonald, I.G.: The Poincaré series of a Coxeter group. Math. Ann. 199, 161–174 (1972)
Nadler, D., Yun, Z.: Geometric Langlands correspondence for SL(2), PGL(2) over the pair of pants. Compos. Math. 155(2), 324–371 (2019)
Opdam, E., Solleveld, M.: Homological algebra for affine Hecke algebras. Adv. Math. 220(5), 1549–1601 (2009)
Reeder, M.: Isogenies of Hecke algebras and a Langlands correspondence for ramified principal series representations. Represent. Theory 6, 101–126 (2002)
Rider, L.: Formality for the nilpotent cone and a derived Springer correspondence. Adv. Math. 235, 208–236 (2013)
Sakellaridis, Y., Venkatesh, A.: Periods and harmonic analysis on spherical varieties. Astérisque 396 (2017)
Toën, B., Vezzosi, G.: Caractères de Chern, traces équivariantes et géométrie algébrique dérivée. Sel. Math. New Ser. 21(2), 449–554 (2015)
Virk, R.: Tate classes, equivariant geometry and purity. Preprint (2015). arXiv:1507.07279v2
Virk, R.: Motivic splitting principle. Preprint (2016). arXiv:1609.00721v1
Vogan, D.: The local Langlands conjecture. In: Representation Theory of Groups and Algebras. Contemp. Math., vol. 145, pp. 305–379. Am. Math. Soc., Providence (1993)
Zelevinsky, A.: The p-adic analogue of the Kazhdan-Lusztig conjecture. Funkc. Anal. Prilozh. 15(2), 9–21, 96 (1981)
Zhu, X.: An introduction to affine Grassmannians and the geometric Satake equivalence. In: Geometry of Moduli Spaces and Representation Theory. IAS/Park City Math. Ser., vol. 24. Am. Math. Soc., Providence (2017)
Zhu, X.: Geometric Satake, categorical traces, and arithmetic of Shimura varieties. In: Current Developments in Mathematics 2016, pp. 145–206. Int. Press, Somerville (2018)
Zhu, X.: Coherent sheaves on the stack of Langlands parameters. Preprint (2020). arXiv:2008.02998
Acknowledgements
We would like to thank Xinwen Zhu for very enlightening conversations on the topic of categorical traces, the Drinfeld-Lafforgue sheaf and its relation to the coherent Springer sheaf and for sharing with us an early draft of his paper [86], Pramod Achar for discussions of purity and Tate-ness properties in Springer theory, and Sam Raskin for suggestions related to renormalized categories of sheaves on formal odd tangent bundles. We would also like to thank Matthew Emerton for comments regarding Whittaker normalizations, Xuhua He for pointing out the reference [76], Maarten Solleveld for discussion surrounding results in [75] and Gurbir Dhillon for numerous helpful discussions. Finally, we would like to thank the anonymous referee for their thoughtful and detailed suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proofs
Appendix: Proofs
This appendix contains proofs of technical results used in the body of the paper.
1.1 A.1 Functoriality of Hochschild homology in geometric settings
Proof of Proposition 3.14
The first and second statements are Theorem 2.21 (or Proposition 5.5) in [8]. We give a direct argument for the third statement (which can also be adapted toward the second). We let \(Z := X \times _{Y} X\), and denote the diagonals by \(\Delta _{X}: X \hookrightarrow X \times X\) (and likewise for \(Y\)), the relative diagonal by \(\Delta : X \hookrightarrow Z = X \times _{Y} X\), and its inclusion by \(i: Z = X \times _{Y} X \hookrightarrow X \times X\).
Note that we use !-integral transforms in our convention; thus to describe the integral transforms it is convenient to pass between ∗-pullbacks and !-pullbacks. For any quasi-smooth map \(g: E \rightarrow B\) we denote by \(\beta _{g}^{*}: f^{*}(-) \simeq f^{!}(-) \otimes _{{\mathcal {O}}_{X}} \omega _{E/B}^{-1}\) and \(\beta _{g}^{!}: f^{!}(-) \simeq f^{*}(-) \otimes _{{\mathcal {O}}_{X}} \omega _{E/B}\) the canonical equivalences.
The integral transform corresponding to \(f_{*} f^{*}: {\operatorname {Coh}}(Y) \rightarrow {\operatorname {Coh}}(Y)\) is given by the kernel
Letting \(\eta _{f}\) denote the unit for the adjunction \((f^{*}, f_{*})\), the unit \(\eta \in \operatorname{Hom}_{Y \times Y}(\Delta _{Y*} \omega _{Y}, {\mathcal {K}}_{f_{*}f^{*}})\) is defined:
The integral transform corresponding to \(f^{*} f_{*}: {\operatorname {Coh}}(X) \rightarrow {\operatorname {Coh}}(X)\) is given by the kernel:
Letting \(\eta _{\Delta}\) denote the unit for the adjunction \((\Delta ^{*}, \Delta _{*})\), the counit \(\epsilon \in \operatorname{Hom}_{X \times X}({\mathcal {K}}_{f^{*}f_{*}}, \Delta _{X*} \omega _{X})\) is defined:
where we implicitly use the canonical identification \(\Delta ^{*} \omega _{Z/X}^{-1} \simeq \omega _{X/Z}\) (i.e. since \(\omega _{X/X}\) is canonically trivial). We leave verification of the adjunction identites to the reader.
The functoriality \(\omega ({\mathcal {L}}_{\phi }Y) \rightarrow \omega ({\mathcal {L}}_{\phi }X)\) is given by composing the unit and counit after applying \(\Gamma \circ \Gamma _{\phi _{Y}}^{!}\) and \(\Gamma \circ \Gamma _{\phi _{X}}^{!}\) (where, somewhat confusingly, \(\Gamma \) denotes the global sections functor, and \(\Gamma _{\phi}\) denotes the graph). Recall the factorization and notation of Lemma 3.10, let \(p_{X}: {\mathcal {L}}_{\phi }Y_{X} \rightarrow X\) and \(p_{Y}: {\mathcal {L}}_{\phi }Y_{X} \rightarrow Y\) denote the natural maps, and \(\mathrm{ev}_{X}: {\mathcal {L}}_{\phi }X \rightarrow X\) the evaluation (and likewise for \(Y\)). For the unit map \(\eta \), we have
We perform a base change along the diagram:

to find
and an identification of \(\eta \) with the unit \(\eta _{\pi}\) for the adjunction \((\pi ^{*}, \pi _{*})\):
For the counit map \(\epsilon \), we have
We perform a base change along the diagram:

to find that
Due to the canonical Calabi-Yau equivalence \(\omega _{{\mathcal {L}}_{\phi }X/{\mathcal {L}}_{\phi }Y} \simeq {\mathcal {O}}_{{\mathcal {L}}_{\phi }X}\) of Proposition 3.12, we have a canonical equivalence \(\omega _{{\mathcal {L}}_{\phi }X/ {\mathcal {L}}_{\phi }Y_{X}} \simeq \delta ^{*}\omega _{ {\mathcal {L}}_{\phi }Y_{X}/{\mathcal {L}}_{\phi }Y}^{-1}\). Passing through this equivalence, we have
Thus, \(\epsilon \) is identified with the unit \(\eta _{\delta}\) for the adjunction \((\delta ^{*}, \delta _{*})\):
Taking global sections and composing, we see that the map
is induced by the unit of the adjunction \(({\mathcal {L}}_{\phi }f^{*}, {\mathcal {L}}_{\phi }f_{*})\), twisted by the Calabi-Yau equivalence. □
The following is a generalization of Proposition 3.18. While Proposition 3.18 is stated in the setting of derived loop spaces, the arguments hold in the following more general setting.
Proposition A.1
Let \(f: X \rightarrow Y\) be a proper map of derived stacks, and let \(Z = X \times _{Y} X\) with projections \(p_{1}, p_{2}: Z \rightarrow X\) and \(p: Z \rightarrow Y\). There is a canonical equivalence:
In particular, if \(X\) is Calabi-Yau, then we have a natural equivalence \(\omega (Z) \simeq \operatorname {End}_{Y}(f_{*}\omega _{X})\). This equivalence is functorial in the following sense. Let \(f': X' \rightarrow Y'\) (and \(p': Z' \rightarrow Y'\)) be as above.
-
Suppose that \(\alpha _{Y}: Y \rightarrow Y'\) is proper, and that \(X = X'\). We let \(f: X \rightarrow Y\) be as above, \(f' = \alpha _{Y} \circ f: X \rightarrow Y \rightarrow Y'\). We have commuting squares
-
Suppose that \(\alpha _{Y}: Y \rightarrow Y'\) is Calabi-Yau, and that \(X = X' \times _{Y'} Y\) (so \(\alpha _{X}\) is also Calabi-Yau). Then we have commuting squares
Proof
The first statement is a formal consequence of adjunctions and base change:
Functoriality for proper morphisms follows by a diagram chase on:

where we use the identification in the middle left terms \(\alpha _{Y*} f_{*} \simeq f'_{*}\alpha _{X*} \simeq f'_{*}\) (i.e. since \(X=X'\) and \(\alpha _{X} = \mathrm{id}_{X}\)), and the middle horizontal maps are given by functoriality of pushforwards of dualizing sheaves. In the Calabi-Yau case, we pass to left adjoints, apply the base change \(\alpha ^{*}f'_{*} \simeq f_{*}\alpha ^{*}\) and chase the diagram:

where the middle arrows arise by functoriality of Calabi-Yau pullback (as in Definition 3.13) after passing to left adjoints. □
1.2 A.2 Horizontal trace of convolution categories
Proof of Theorem 3.23
We will employ the notation in Theorem 3.3.1 of [12] to point out how its argument can be modified to acommodate this more general setting. First, note that the surjectivity condition is not needed nor used in the proof of the theorem; it is subsumed by the singular support condition, so we omit it from the statement. The quasi-smoothness of \(q_{n}\) follows by quasi-smoothness of the graph \(\Gamma _{\phi}\). We replace, in the definition of \({\mathcal {C}}_{\bullet}\), the diagonal module \(\operatorname {Perf}(X)\) with the module defined by the graph \(\Gamma _{\phi}\). In the definition of \(Z_{\bullet}\), this amounts to replacing \({\mathcal {L}}Y\) with \(Y^{\phi}\) (informally, introducing a twist by \(\phi \) as we “come around the circle,” i.e. in Lemma 3.3.2 the automorphism \(\ell \) lives in \(\operatorname {Map}_{Y(k)}(y, \phi (y))\)). In the definition of \(W_{\bullet}\), this amounts to replacing the last factor of \(X \times _{Y} X = X \times _{f,Y,f} X\) representing the “segment containing the twist by \(\phi \)” with \(X \times _{f,Y,\phi _{X} \circ f} X\) (i.e. in Lemma 3.3.3, the final point \(x_{n}\) should lie in the fiber \(f^{-1}(\phi (y))\) rather than \(f^{-1}(y)\)). The rest of the proof goes through without modification as the formulas still hold with the \(\phi \)-twist. □
Proof of Proposition 3.30
The argument in Theorem 3.3.1 of [12] may be adapted in the following way. Let \(\mathbf {M} = \operatorname {QC}^{!}(Z_{12})\) and \(\mathbf {N} = \operatorname {QC}^{!}(Z_{23})\), and following the notation of loc. cit. we let \(\mathbf {A} = \operatorname {QC}^{!}(Z_{22})\) and \(\mathbf {B} = \operatorname {QC}^{!}(X_{2})\). Then, writing \(\mathbf {M} \otimes _{\mathbf {A}} \mathbf {N} = \mathbf {M} \otimes _{\mathbf {A}} \mathbf {A} \otimes _{\mathbf {A}} \mathbf {N}\), and (following the argument of loc. cit.) resolving \(\mathbf {A}\) as a \(\mathbf {A} \otimes _{\mathbf {B}} \mathbf {A}^{rv}\)-module via the relative bar complex for \(\mathbf {A}\) over \(\mathbf {B}\), we find that \(\mathbf {M} \otimes _{\mathbf {A}} \mathbf {N}\) can be realized as the geometric realization of the cosimplicial object:
where we define
Explicitly, for \(\eta = (x_{1}, x_{2}^{(0)}, \ldots , x_{2}^{(n)}, x_{3}) \in Z_{n}(k)\) with each coordinate living in the fiber over \(y \in Y(k)\), we have
Here, we note that the fiber of the singular support condition \(\Lambda _{ij}\) at the point \((x_{i}, x_{j}) \in Z_{ij}(k)\) in the fiber over \(y\) is naturally a subset \(\Lambda _{ij, (x_{i}, x_{j})} \subset \mathbb{T}^{*}_{Y,y}\). The singular support stability condition implies that the face maps \((Z_{m}, \Lambda _{m}) \rightarrow (Z_{n}, \Lambda _{n})\) are maps of pairs. Pullback along the augmentation is conservative by definition of \(\Lambda _{13}\). Analogous formulas in Lemma 3.3.9 of op. cit. hold in this situation (without the need to “loop around”), and the strictness condition follows by an argument analogous to Proposition 3.3.8 of op. cit. Thus, we have an equivalence
For functoriality, we note that the resulting maps \((Z_{n}, \Lambda _{n}) \rightarrow (Z_{n}, \Lambda '_{n})\) are maps of pairs by our description above for \(n \geq 0\), and the case \(n=-1\) is a straightforward verification. The claim then follows by functoriality of the descent with support discussed in Sect. 2.4 of [12]. We adopt the notation of loc. cit.: let \((X_{\bullet}, \Lambda _{\bullet}) \rightarrow (X_{-1}, \Lambda _{-1})\) and \((Y_{\bullet}, \Theta _{\bullet}) \rightarrow (Y_{-1}, \Theta _{-1})\) be augmented simplicial diagrams of maps of pairs satisfying the descent conditions of Theorem 2.4.1 and Corollary 2.4.2 of [12], and let \(g_{\bullet}: (X_{\bullet}, \Lambda _{\bullet}) \rightarrow (Y_{ \bullet}, \Theta _{\bullet})\) be a level-wise proper map of augmented simplicial diagrams of pairs. We claim that we have a limit \(\operatorname {Tot}(\mathfrak {g}_{\bullet}^{!}) \simeq \mathfrak{g}_{-1}^{!}\) and a colimit \(\mathrm{Real}(\mathfrak {g}_{\bullet *}) \simeq \mathfrak{g}_{-1*}\), which proves the functoriality claims (i.e. since the maps \(\mathfrak {g}_{\bullet}\) are the identity, the functors \(\mathfrak {g}_{\bullet *}\) are the inclusion functors and \(\mathfrak {g}_{\bullet}^{!}\) are the local cohomology functors). The first statement follows by commutativity of !-pullbacks with supports (see Remark 2.3.3 of [12]) and by universal property of the limit. The second statement follows by passing to left adjoints (as in Corollary 2.4.2 of op. cit.). □
Proof of Proposition 3.37
Consider the functors
We claim that \((T, T^{R})\) are adjoint. Let \(\Delta _{X}: X \rightarrow X \times X\) denote the diagonal, \(p: X \rightarrow \operatorname {pt}\) denote the structure map, and \(\Delta _{X/Y}: X \rightarrow X \times _{Y} X\) the relative diagonal. We define the unit \(\eta : \mathrm{id}_{\mathbf {dgCat}_{k}} \rightarrow T^{R} \circ T\) via the functor \(\Delta _{X/Y*}p^{*}: \operatorname {QC}(\operatorname {pt}) \rightarrow \operatorname {QC}(X \times _{Y} X)\) and the counit \(\epsilon : T \circ T^{R} \rightarrow \mathrm{id}_{\operatorname {QC}(Y)\text{-}\mathbf {mod}}\) by the functor \(f_{*}\Delta _{X}^{*}: \operatorname {QC}(X \times X) \rightarrow \operatorname {QC}(Y)\). Verification of the adjunction axioms is a straightforward application of base change and Theorem 4.7 of [9]. To compute the trace, we apply base change and find that \([\operatorname {QC}(X), \phi _{X*}]\) is the pull-push of \(k \in \operatorname {QC}(\operatorname {pt})\) along the diagram (where \(\Delta _{Y}: Y \rightarrow Y \times Y\) is the diagonal):

i.e. \([\operatorname {QC}(X), \phi _{X*}] \simeq {\mathcal {L}}_{\phi }f_{*} {\mathcal {O}}_{{\mathcal {L}}_{\phi }X}\). □
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ben-Zvi, D., Chen, H., Helm, D. et al. Coherent Springer theory and the categorical Deligne-Langlands correspondence. Invent. math. 235, 255–344 (2024). https://doi.org/10.1007/s00222-023-01224-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-023-01224-2




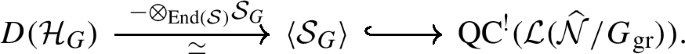
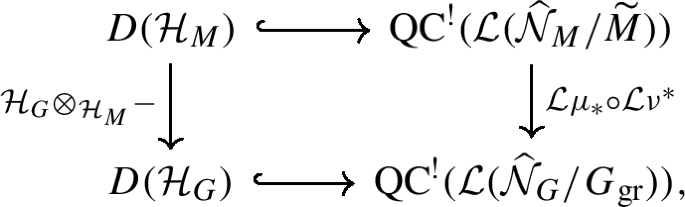
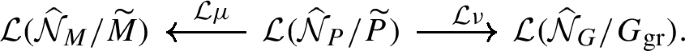


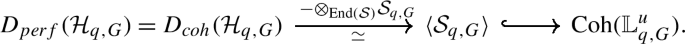
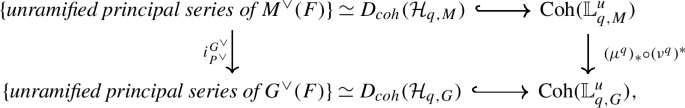
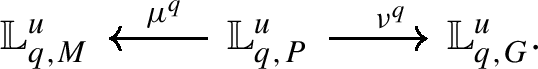
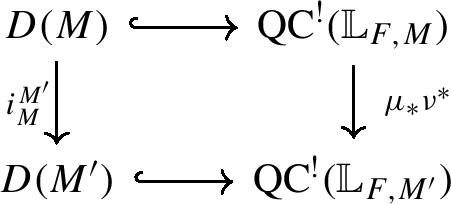
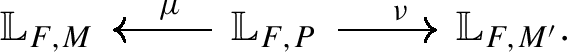
 (resp.
(resp.  ) with the action of
) with the action of  is defined to be the tilting extension of the constant sheaf
is defined to be the tilting extension of the constant sheaf  .
.