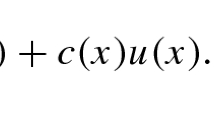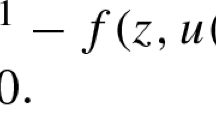On approximation of the Dirichlet problem for divergence form operators by Robin problems

Abstract

We show that, under natural assumptions, solutions of Dirichlet problems for uniformly elliptic divergence form operators can be approximated pointwise by solutions of some versions of Robin problems. The proof is based on the stochastic representation of solutions and properties of reflected diffusions corresponding to divergence form operators.

1 Introduction

Let D be a bounded Lipschitz domain in ${{\mathbb {R}}}^d$, $d\ge 3$, and

$$\begin{aligned} L=\sum ^d_{i,j=1}\partial _{x_i}(a_{ij}(x)\partial _{x_j}) \end{aligned}$$

be the operator with measurable coefficients $a_{ij}:D\rightarrow {{\mathbb {R}}}$ such that

$$\begin{aligned} a_{ij}=a_{ji},\qquad \Lambda ^{-1}|\xi |^2\le \sum ^{d}_{i,j=1}a_{ij}(x)\xi _i\xi _j\le \Lambda |\xi |^2,\quad x\in D,\,\,\xi \in {{\mathbb {R}}}^d, \end{aligned}$$

(1.1)

for some $\Lambda \ge 1$. For $\lambda >0$, $f:D\rightarrow {{\mathbb {R}}}$, $g:\partial D\rightarrow {{\mathbb {R}}}$, and $n\ge 1$, we consider the following boundary-value problem

$$\begin{aligned} -Lu_n+\lambda u_n=f\quad \text{ in } D,\qquad -(a\nabla u_n)\cdot {\textbf{n}} +nu_n=ng\quad \text{ on } \partial D, \end{aligned}$$

(1.2)

where $a=\{a_{ij}\}_{1\le i,j\le d}$ and ${\textbf{n}}(x)$ is the inward unit normal at $x\in \partial D$. Note that (1.2) is a particular version of the Robin problem (also known as Fourier problem or the third boundary-value problem). It is known (see, e.g., [7, Appendix I, Section 4.4]) that if $f\in L^2(D)$, $g\in H^1(D)$, and in the boundary condition in (1.2) the trace of g is used, then for each $n\ge 1$, there exists a unique weak solution of (1.2) and $u_n\rightarrow u$ in $H^1(D)$ as $n\rightarrow \infty$, where u is the unique weak solution of the Dirichlet problem

$$\begin{aligned} -Lu+\lambda u=f\quad \text{ in } D,\qquad u=g\quad \text{ on } \partial D. \end{aligned}$$

(1.3)

If $f\in L^p(D)$ with $p>d$ and $g\in H^1(D)\cap C(\partial D)$, then $u_n,u$ have continuous versions and one may ask whether $u_n\rightarrow u$ for every $x\in {{\bar{D}}}$. In this note, we give a positive answer to this question. Our proof is quite simple and is based on the stochastic representation of solutions of (1.2), (1.3). But let us stress that in the proof of our convergence results, we use deep results from [5, 6] (see also [2] for the case $L=(1/2)\Delta$) saying that one can construct a reflected diffusion ${{\mathbb {M}}}$ on ${{\bar{D}}}$ associated with L having a strong Feller resolvent.

2 Preliminaries

In this paper, $D\subset {{\mathbb {R}}}^d$, $d\ge 3$, is a bounded Lipschitz domain (for a definition, see, e.g., [4, Exercise 5.2.2]), ${{\bar{D}}}=D\cup \partial D$. We denote by m or simply by dx the d-dimensional Lebesgue measure, and by $\sigma$ the surface measure on $\partial D$. ${{\mathcal {B}}}({{\bar{D}}})$ is the set of Borel subsets of ${{\bar{D}}}$, ${{\mathcal {B}}}_b({{\bar{D}}})$ (resp. $C({{\bar{D}}})$) is the set of bounded Borel (resp. continuous) functions on ${{\bar{D}}}$. To shorten notation, we write $L^2(D)$ instead of $L^2(D;m)$ and $L^2(\partial D)$ instead of $L^2(\partial D;\sigma )$.

We assume that the matrix a satisfies (1.1) and consider the Dirichlet form $({{\mathcal {E}}},D({{\mathcal {E}}}))$ on $L^2(D)$ defined by

$$\begin{aligned} {{\mathcal {E}}}(u,v)=\sum ^d_{i,j=1}\mathop {\int }\limits _Da_{ij}(x)\partial _{x_i}u(x)\partial _{x_j}v(x)\,dx,\quad u,v\in D({{\mathcal {E}}}):=H^1(D), \end{aligned}$$

(2.1)

where $H^1(D)$ is the usual Sobolev space of order 1, and for $\lambda >0$, set ${{\mathcal {E}}}_{\lambda }(u,v)={{\mathcal {E}}}(u,v)+\lambda (u,v)$, where $(\cdot ,\cdot )$ is the usual inner product in $L^2(D;m)$. We denote by $(T_t)_{t>0}$ the strongly continuous semigroup of Markovian symmetric operators on $L^2(D)$ associated with ${{\mathcal {E}}}$ (see [4, Section 1.3]).

In the paper, we define quasi-notions (exceptional sets, quasi-continuity) with respect to $({{\mathcal {E}}},H^1(D))$. We will say that a property of points in ${{\bar{D}}}$ holds quasi everywhere (q.e. in abbreviation) if it holds outside some exceptional set. It is known (see [4, Lemma 2.1.4, Theorem 2.1.3]) that each element of $H^1(D)$ admits a quasi-continuous m-version, which we denote by ${\tilde{u}}$, and ${\tilde{u}}$ is q.e. unique for every $u\in H^1(D)$.

In [6, Theorems 2.1 and 2.2] (see also [5]), it is proved that there exists a conservative diffusion process ${{\mathbb {M}}}=\{(X,P_x),x\in {{\bar{D}}}\}$ on ${{\bar{D}}}$ associated with the Dirichlet form (2.1) in the sense that the transition density of ${{\mathbb {M}}}$ defined as $p_t(x,B)=P_x(X_t\in B)$, $t>0,x\in {{\bar{D}}}$, $B\in {{\mathcal {B}}}({{\bar{D}}})$, has the property that $P_tf$ is an m-version of $T_tf$ for every $f\in {{\mathcal {B}}}_b({{\bar{D}}})$, where $P_tf(x)=\mathop {\int }\nolimits _Df(y)p_t(x,dy)=E_xf(X_t)$. Moreover, $(P_t)_{t>0}$ is strongly Feller in the sense that $P_t({{\mathcal {B}}}_b({{\bar{D}}}))\subset C({{\bar{D}}})$ and $\lim _{t\downarrow 0}P_tf(x)=f(x)$ for $x\in {{\bar{D}}}$, $f\in C({{\bar{D}}})$. In particular (see [4, Exercise 4.2.1]), the transition density satisfies the following absolute continuity condition: $p_t(x,\cdot )\ll m$ for any $t>0$, $x\in {{\bar{D}}}$. In fact, in [5, 6], the strong Feller property is proved for less regular and possibly unbounded domains.

We denote by $(R_{\alpha })_{\alpha >0}$ the resolvent associated with ${{\mathbb {M}}}$ (or with $(P_t)_{t>0})$, that is,

$$\begin{aligned} R_{\alpha }f(x)=E_x\mathop {\int }\limits ^{\infty }_0e^{-\alpha t}f(X_t)\,dt, \quad f\in {{\mathcal {B}}}_b({{\bar{D}}}). \end{aligned}$$

Of course

$$\begin{aligned} R_{\alpha }f(x)=\mathop {\int }\limits _{{{\bar{D}}}}r_{\alpha }(x,y)f(y)\,dy,\quad \text{ where }\quad r_{\alpha }(x,y)=\mathop {\int }\limits ^{\infty }_0e^{-\alpha t}p_t(x,y)\,dt. \end{aligned}$$

For a Borel measure $\mu$ on ${{\bar{D}}}$, we also set

$$\begin{aligned} R_{\alpha }\mu (x)=\mathop {\int }\limits _{{{\bar{D}}}}r_{\alpha }(x,y)\,\mu (dy),\quad x\in {{\bar{D}}},\quad \alpha >0, \end{aligned}$$

whenever the integral makes sense.

By [6, Lemma 5.1, Theorem 5.1], the surface measure $\sigma$ belongs to the space of smooth measures in the strict sense, and hence, by [4, Theorem 5.1.7], there is a unique positive continuous additive functional of ${{\mathbb {M}}}$ in the strict sense with Revuz measure $\sigma$. In what follows, we denote it by A. For $g\in {{\mathcal {B}}}_b({{\bar{D}}})$, let $g\cdot \sigma$ be the measure on ${{\bar{D}}}$ defined by $g\cdot \sigma (B)=\mathop {\int }\nolimits _Bg(x)\,\sigma (dx)$, $B\in {{\mathcal {B}}}({{\bar{D}}})$. Note that for any $g\in {{\mathcal {B}}}_b({{\bar{D}}})$, we have

$$\begin{aligned} R_{\alpha }(g\cdot \sigma )(x)=E_x\mathop {\int }\limits ^{\infty }_0e^{-\alpha t}g(X_s)\,dA_s,\quad x\in {{\bar{D}}}. \end{aligned}$$

Indeed, by [4, Theorem 5.1.3], the above equality holds for m-a.e. $x\in {{\bar{D}}}$, and hence, by [3, Theorem A.2.17], for every $x\in {{\bar{D}}}$ because $p_t$ satisfies the absolute continuity condition and for any nonnegative $g\in {{\mathcal {B}}}_b({{\bar{D}}})$, both sides of the above equality are $\alpha$-excessive functions. Also note that the support of A is contained in $\partial D$. Hence

$$\begin{aligned} \mathop {\int }\limits ^t_0g(X_s)\,dA_s=\mathop {\int }\limits ^t_0{{\textbf{1}}}_{\partial D}(X_s)g(X_s)\,dA_s,\quad P_x\text{-a.s. },\quad x\in {{\bar{D}}} \end{aligned}$$

(2.2)

(for more details, see the beginning of the proof of Lemma 4.1). It follows that in fact the right-hand side of (2.2) is well defined for $g\in {{\mathcal {B}}}_b(\partial D)$.

Remark 2.1

If, in addition, $\partial _{x_i}a_{ij}\in L^{\infty }(D)$, $i,j=1,\dots ,d$, then $X=(X^1, \dots ,X^d)$ has the following Skorohod representation: for $i=1,\dots ,d$ and every $x\in {{\bar{D}}}$,

$$\begin{aligned} X^i_t=X_0^i+M^i_t+N^i_t,\quad t\ge 0,\quad P_x\text{-a.s. }, \end{aligned}$$

(2.3)

where $M^i$ are martingale additive functionals in the strict sense with covariations $\langle M^i,M^j\rangle _t=2\mathop {\int }\nolimits ^t_0a_{ij}(X_s)\,ds$, $t\ge 0$, $P_x$-a.s., and

$$\begin{aligned} N^i_t=\sum ^d_{j=1}\mathop {\int }\limits ^t_0\partial _{x_j} a_{ij}(X_s)\,ds +\sum ^d_{j=1}\mathop {\int }\limits ^t_0a_{ij}(X_s){{\textbf{n}}}_j(X_s)\,dA_s,\quad t\ge 0,\quad P_x\text{-a.s. } \end{aligned}$$

In case of the classical Dirichlet form defined by

$$\begin{aligned} {{\mathbb {D}}}(u,v)=\frac{1}{2}\sum _{i=1}\mathop {\int }\limits _D\partial _{x_i}u(x) \partial _{x_j}v(x)\,dx,\quad u,v\in H^1(D), \end{aligned}$$

i.e., if $a=\frac{1}{2} I$, the process ${{\mathbb {M}}}$ is called a reflecting Brownian motion. By Lévy’s characterization of Brownian motion, the representation (2.3) reads

$$\begin{aligned} X^i_t-X_0^i=B^i_t+\frac{1}{2}\mathop {\int }\limits ^t_0{\textbf{n}}_i(X_s)\,dA_s,\quad t\ge 0,\quad P_x\text{-a.s. }, \end{aligned}$$

(2.4)

where $B=(B^1,\dots ,B^d)$ is a standard Brownian motion. For the proof of (2.4), see [4, Example 5.2.2] and for the general case (2.3), see [6, Theorem 2.3]. In case a is a general function satisfying (1.2), some representation of X (Lyon–Zheng–Skorohod decomposition) is given in [14] (for bounded $C^2$ domain D and $x\in D$).

Let

$$\begin{aligned} \tau _D=\inf \{t>0:X_t\notin D\},\quad X^D_t= X_t\quad \text{ if } t<\tau _D,\quad X^D_t=\partial \quad \text{ if } t\ge \tau _D, \end{aligned}$$

where $\partial$ is a point adjoined to D as an isolated point (cemetery state). We adopt the convention that every function f on D is extended to $D\cup \partial$ by setting $f(\partial )=0$. We denote by ${{\mathbb {M}}}^{\lambda }$ the canonical subprocess of ${{\mathbb {M}}}$ with respect to the multiplicative functional $e^{-\lambda t}$. For its detailed construction, we refer to [4, Section A.2]. Here let us only note that we may assume that ${{\mathbb {M}}}^{\lambda }=(X^{\lambda },P_x)$ is defined on the same probability space on which ${{\mathbb {M}}}$ is defined and

$$\begin{aligned} X^{\lambda }_t= X_t\quad \text{ if } t<Z/\lambda ,\quad X^{\lambda }_t=\partial \quad \text{ if } t\ge Z/\lambda , \end{aligned}$$

where Z is a nonnegative random variable independent of $(X_t)_{t\ge 0}$ having exponential distribution with mean 1.

3 Weak and probabilistic solutions

For the convenience of the reader, below we recall the variational formulation of problems (1.2), (1.3). For more details, we refer to [7, Appendix I].

Definition 3.1

(i) Let $f\in L^2(D)$, $g\in L^2(\partial D)$. A function $u_n\in H^1(D)$ is called a weak solution of (1.2) if for every $v\in H^1(D)$,

$$\begin{aligned} {{\mathcal {E}}}_{\lambda }(u_n,v)=\mathop {\int }\limits _Dfv\,dx+n\mathop {\int }\limits _{\partial D}(g-u_n)v\,d\sigma . \end{aligned}$$

(3.1)

(ii) Let $f\in L^2(D)$, $g\in H^1(D)$. A function $u\in H^1(D)$ is called a weak solution of (1.3) if $u-g\in H^1_0(D)$ and ${{\mathcal {E}}}_{\lambda }(u,v)= \mathop {\int }\nolimits _Dfv\,dx$ for every $v\in H^1_0(D)$.

The existence and uniqueness of weak solutions of (1.2), (1.3) are well known. For proofs by classical variational methods, we refer for instance to [7, Appendix I]. In Proposition 3.2 below, we give proofs by using the probabilistic potential theory. The advantage of using these less classical methods lies in the fact that they provide probabilistic representations of quasi-continuous versions of weak solutions. We would like to stress that the proof of Proposition 3.2 is simply a compilation of known facts. We provide it for completeness and later use.

Proposition 3.2

• (i) Let $f\in L^2(D)$, $g\in L^2(\partial D)$. Then there exists a unique weak solution $u_n$ of (1.2) and ${\tilde{u}}_n$ defined q.e. on D by

  $$\begin{aligned} {\tilde{u}}_n(x)=E_x\mathop {\int }\limits ^{\infty }_0e^{-\lambda t-nA_t} (f(X_t)\,dt+ng(X_t)\,dA_t) \end{aligned}$$

  (3.2)

  is a quasi-continuous m-version of $u_n$.

• (ii) Let $f\in L^2(D)$, $g\in H^1(D)$. Then there exists a unique weak solution u of (1.3) and ${\tilde{u}}$ defined q.e. on D by

  $$\begin{aligned} {\tilde{u}}(x)=E_x\Big (e^{-\lambda \tau _D}g(X_{\tau _D})+\mathop {\int }\limits ^{\tau _D}_0e^{-\lambda t} f(X_t)\,dt\Big ) \end{aligned}$$

  (3.3)

  is a quasi-continuous m-version of u.

Proof

(i) Let $({{\mathcal {E}}}^{n\sigma },D({{\mathcal {E}}}^{n\sigma }))$ denote the form ${{\mathcal {E}}}$ perturbed by the measure $n{{\textbf{1}}}_{\partial D}\cdot \sigma$, that is,

$$\begin{aligned} {{\mathcal {E}}}^{n\sigma }_{\lambda }(u,v)={{\mathcal {E}}}_{\lambda }(u,v)+n\mathop {\int }\limits _{\partial D}uv\,d\sigma ,\quad u,v\in D({{\mathcal {E}}}^{n\sigma }):=H^1(D)\cap L^2({{\bar{D}}};{{\textbf{1}}}_{\partial D}\cdot \sigma ). \end{aligned}$$

By the classical trace theorem, $D({{\mathcal {E}}}^{n\sigma })=H^1(D)$, so $u_n$ is a weak solution of (3.1) if and only if $u_n\in D({{\mathcal {E}}}^{n\sigma })$ and

$$\begin{aligned} {{\mathcal {E}}}^{n\sigma }_{\lambda }(u_n,v)=\mathop {\int }\limits _Dfv\,dx+n\mathop {\int }\limits _{\partial D}gv\,d\sigma ,\quad v\in D({{\mathcal {E}}}^{n\sigma }). \end{aligned}$$

(3.4)

Therefore we have to show that there is a unique $u_n\in H^1(D)$ satisfying (3.4). Suppose that $u^1_n,u^2_n\in H^1(D)$ satisfy (3.4) and let $u=u^1_n-u^2_n$. Then from (3.4) with test function $v=u$, we get ${{\mathcal {E}}}^{n\sigma }_{\lambda }(u,u)=0$, hence that ${{\mathcal {E}}}_{\lambda }(u,u)=0$. Clearly, this implies that $u=0$ m-a.e. To prove the existence and its representation, it suffices to note that ${\tilde{u}}_n$ can be written in the form ${\tilde{u}}_n=R^{nA}_{\lambda }f+nU^{\lambda }_{n,A}g$, where $R^{nA}_{\lambda }f(x)=E_x\mathop {\int }\nolimits ^{\infty }_0e^{-\lambda t-nA_t}f(X_t)\,dt$ and $U^{\lambda }_{n,A}g(x)=E_x\mathop {\int }\nolimits ^{\infty }_0e^{-\lambda t-nA_t}g(X_t)\,dA_t$ and then use [4, (6.1.5), (6.1.12)]. Furthermore, ${\tilde{u}}_n$ is quasi-continuous because $R^{nA}_{\lambda }f$ is quasi-continuous by [4, Lemma 5.1.5] and $U^{\lambda }_{n,A}g$ is quasi-continuous by [4, Lemma 6.1.3].

(ii) With our convention, ${\tilde{u}}$ can be written in the form ${\tilde{u}}=H^{\lambda }_{\partial D}{\tilde{g}}+R^D_{\lambda }f,$ where $H^{\lambda }_{\partial D}{\tilde{g}}(x)=E_xe^{-\lambda \tau _D}{\tilde{g}}(X_{\tau _D})$ and $R^D_{\lambda }f(x)=\mathop {\int }\nolimits ^{\infty }_0e^{-\lambda t}f(X^D_t)\,dt.$ Let $H^1_D=\{u\in H^1(D):{\tilde{u}}=0 \text{ q.e. } \text{ on } \partial D\}$. It is known (see [4, Exercise 2.3.1]) that $H^1_D=H^1_0(D)$. Furthermore, by [4, Theorem 4.3.1], $H^{\lambda }_{\partial D}{\tilde{g}}$ is an m-version of the orthogonal projection of g on the orthogonal complement of the space $H^1_D$ in the Hilbert space $(H^1(D),{{\mathcal {E}}}_{\lambda })$. Hence, for every $v\in H^1_0(D)$, ${{\mathcal {E}}}_{\lambda }(H^{\lambda }_{\partial D}{\tilde{g}},v)=0$. Therefore, if ${\tilde{u}}$ is defined by (3.3), then for every $v\in H^1_0(D)$, we have

$$\begin{aligned} {{\mathcal {E}}}_{\lambda }({\tilde{u}},v)={{\mathcal {E}}}_{\lambda }(R^D_{\lambda }f,v)=\mathop {\int }\limits _Dfv\,dx, \end{aligned}$$

the second equality being a consequence of [4, Theorem 4.4.1]. Furthermore, ${\tilde{u}}-g={\tilde{u}}-(H^{\lambda }_{\partial D}{\tilde{g}}+g-H^{\lambda }_{\partial D}{\tilde{g}}) =R^D_{\lambda }f-(g-H^{\lambda }_{\partial D}{\tilde{g}})\in H^1_0(D)$ since $g-H^{\lambda }_{\partial D}{\tilde{g}}\in H^1_0(D)$ and $R^D_{\lambda }f\in H^1_0(D)$ by [4, Theorem 4.4.1] again. Therefore ${\tilde{u}}$ is a weak solution of (1.3). Note that ${\tilde{u}}$ is quasi-continuous because $H^{\lambda }_{\partial D}{\tilde{g}}$ is quasi-continuous by [4, Theorem 4.3.1] and $R^D_{\lambda }f$ is quasi-continuous by [4, Theorem 4.4.1]. $\square$

Note that since D is Lipschitz, there is the trace operator $\gamma :H^1(D)\rightarrow L^2(\partial D)$. Therefore in Definition 3.1(i) and Proposition 3.2(ii), one can assume that $g\in H^1(D)$ and then replace g by $\gamma (g)$ in (3.1), (3.2).

If $f\in L^p(D)$ with $p>d$, then $R_{\lambda }|f|\in C({{\bar{D}}})$ by [6, Theorem 2.1], and if $g\in {{\mathcal {B}}}_b(\partial D)$, then $nE_x\mathop {\int }\nolimits ^{\infty }_0e^{-n A_t}g(X_t)\,dA_t\le \Vert g\Vert _{\infty }E_x(1-e^{-nA_{\infty }})$, $x\in {{\bar{D}}}$. Therefore, under these assumptions on f and g, the integrals on the right-hand side of (3.2) are well defined for every $x\in {{\bar{D}}}$. Similarly, the right-hand side of (3.3) is well defined for every $x\in {{\bar{D}}}$.

The above remarks and Proposition 3.2 justify the following definition of probabilistic solutions of (1.2), (1.3).

Definition 3.3

Let $f\in L^p(D)$ with $p>d$ and $g\in {{\mathcal {B}}}_b(\partial D)$. The function $v_n:{{\bar{D}}}\rightarrow {{\mathbb {R}}}$ defined by the right-hand side of (3.2) is called the probabilistic solution of (1.2). The function $v:{{\bar{D}}}\rightarrow {{\mathbb {R}}}$ defined by the right-hand side of (3.3) is called the probabilistic solution of (1.3).

An equivalent definition of a probabilistic solution of (1.2), resembling (3.1), will be given in Proposition 3.4 below.

For a deep study of connections between probabilistic solutions, weak solutions as well of other kind of solutions to the Dirichlet problem with possibly irregular domain, we refer the reader to [9]. Here let us only note that if D is bounded and Lipschitz (as in the present paper), then it satisfies Poincare’s cone condition. Therefore modifying slightly the proof of [1, Proposition II.1.13] (we use Aronson’s estimates for the transition densities of ${{\mathbb {M}}}$), one can show that each point $x\in \partial D$ is regular for $D^c$, i.e.,

$$\begin{aligned} P_{x}(\tau _D=0)=1, \quad x\in \partial D. \end{aligned}$$

(3.5)

Using this, similarly to the proof of [1, Proposition II.1.11], one can show that $H^{\lambda }_{\partial D}g\in C({{\bar{D}}})$ if $g\in C(\partial D)$. For an analytical proof of this well known fact, see, e.g., [13]. Furthermore, it is known (see [15, Section 9] or [12]) that if $f\in L^p(D)$ with $p>d$, then $R^D_{\lambda }f\in C({{\bar{D}}})$. Thus $v\in C({{\bar{D}}})$ when $f\in L^p(D)$ with $p>d$ and $g\in C(\partial D)$.

Proposition 3.4

Let $f\in L^p(D)$ with $p>d$ and $g\in {{\mathcal {B}}}_b(\partial D)$. Then the probabilistic solution $v_n$ of (1.2) is continuous. Moreover, $v_n\in C({{\bar{D}}})$ is the probabilistic solution if and only if it satisfies the equation

$$\begin{aligned} v_n(x)= & {} R_{\lambda }(f\cdot m+n(g-v_n)\cdot \sigma )(x)\nonumber \\= & {} E_x\mathop {\int }\limits ^{\infty }_0e^{-\lambda t}(f(X_t)\,dt+n(g-v_n)(X_t)\,dA_t),\quad x\in {{\bar{D}}}. \end{aligned}$$

(3.6)

Proof

Define $u_n,{\tilde{u}}_n$ as in Proposition 3.2 and for $x\in {{\bar{D}}}$, set

$$\begin{aligned} w_n(x)= & {} R_{\lambda }(f\cdot m+n(g-{\tilde{u}}_n)\cdot \sigma )(x)\nonumber \\= & {} \mathop {\int }\limits _{D}r_{\lambda }(x,y)f(y)\,dy +n\mathop {\int }\limits _{\partial D}r_{\lambda }(x,y)(g-{\tilde{u}}_n)(y)\,\sigma (dy). \end{aligned}$$

(3.7)

By the remarks following the proof of Proposition 3.2, $w_n(x)$ is well defined and finite for each $x\in {{\bar{D}}}$. Moreover, there is $C>0$ such that $|{\tilde{u}}_n|\le C$ q.e. Since $\sigma$ is smooth, $|{\tilde{u}}_n|\le C$ $\sigma$-a.e. on $\partial D$. From this and [6, Theorem 2.1], it follows that in fact $w_n\in C({{\bar{D}}})$. For every $v\in H^1(D)$, we have

$$\begin{aligned} {{\mathcal {E}}}_{\lambda }(w_n,v)=(f,v)+n\mathop {\int }\limits _{\partial D}(g-{\tilde{u}}_n)v\,d\sigma =(f,v)+n\mathop {\int }\limits _{\partial D}(g-u_n)v\,d\sigma . \end{aligned}$$

By this and (3.1), ${{\mathcal {E}}}_{\lambda }(w_n,v)={{\mathcal {E}}}_{\lambda }(u_n,v)$, $v\in H^1(D)$, which implies that $w_n=u_n$ m-a.e., and hence $w_n={\tilde{u}}_n$ q.e. on ${{\bar{D}}}$. From this and (3.7), it follows that $w_n$ is a continuous solution of (3.6). It is the probabilistic solution of (1.2). To see this, we first note that (3.6), with $v_n$ replaced by $w_n$, can be equivalently written as

$$\begin{aligned} w_n(x)=E_x\mathop {\int }\limits ^{\infty }_0(f(X^{\lambda }_t)\,dt+n(g-w_n)(X^{\lambda }_t)\,dA_t), \quad x\in {{\bar{D}}}. \end{aligned}$$

(3.8)

Since the integrals $E_x\mathop {\int }\nolimits ^{\infty }_0|f(X^{\lambda }_t)|\,dt$, $E_x\mathop {\int }\nolimits ^{\infty }_0|g-w_n|(X^{\lambda }_t)\,dA_t$ exist and are finite for each $x\in {{\bar{D}}}$, in much the same way as in [10, Remark 3.3(ii)], we show that there is a martingale additive functional M such that for each $x\in {{\bar{D}}}$, the pair $(Y^n,M)$, where $Y^n_t=w_n(X^{\lambda }_t)$, $t\ge 0$, is a solution of the backward stochastic differential equation

$$\begin{aligned} Y^n_t=\mathop {\int }\limits ^{\infty }_tf(X^{\lambda }_s)\,ds +n\mathop {\int }\limits ^{\infty }_t(g(X^{\lambda }_s)-Y^n_s)\,dA_s -\mathop {\int }\limits ^{\infty }_tdM_s, \quad t\ge 0. \end{aligned}$$

(3.9)

Integrating by parts, we get

$$\begin{aligned} e^{-n A_T}Y^n_T-Y^n_0=-n\mathop {\int }\limits ^T_0e^{-n A_t}Y^n_t\,dA_t +\mathop {\int }\limits ^T_0e^{-n A_t}\,dY^n_t,\quad T>0. \end{aligned}$$

Hence

$$\begin{aligned} E_xY^n_0=E_xe^{-nA_T}Y^n_T+\mathop {\int }\limits ^T_0e^{-nA_t}(f(X^{\lambda }_t)\,dt +ng(X^{\lambda }_t)\,dA_t). \end{aligned}$$

Letting $T\rightarrow \infty$ gives

$$\begin{aligned} w_n(x)=E_xY^n_0&=E_x\mathop {\int }\limits ^{\infty }_0e^{-nA_t}(f(X^{\lambda }_t)\,dt +ng(X^{\lambda }_t)\,dA_t)\\&=E_x\mathop {\int }\limits ^{\infty }_0e^{-\lambda t-nA_t}(f(X_t)\,dt+n g(X_t)\,dA_t)=v_n(x) \end{aligned}$$

for every $x\in {{\bar{D}}}$. This shows that $v_n$ is continuous and satisfies (3.6), and moreover, any continuous solution of (3.8) coincides with $v_n$. $\square$

Note that (3.6) is a very special case of an equation with smooth measure data and (3.9) is the corresponding backward stochastic differential equation (BSDE). More general, semilinear equations of the form (3.6), (3.9) are considered in [11]. Note also that one can prove the existence of a quasi-continuous $v_n$ satisfying (3.6) for q.e. $x\in {{\bar{D}}}$ by solving the corresponding BSDE, i.e., by probabilistic methods (we do not need to know in advance that there is a weak solution $u_n$). For a general result of this kind, see [11, Theorem 4.3].

4 A convergence result

Recall that A is an additive functional (AF in abbreviation) of ${{\mathbb {M}}}$ in the strict sense with Revuz measure $\sigma$. We denote by $F_A$ the support of A, i.e., $F_A=\{x\in {{\bar{D}}}:P_x(A_t>0 \text{ for } \text{ all } t>0)=1\}.$

Lemma 4.1

$P_x(A_{t\wedge \tau _D}=0 \text{ for } \text{ all } t\ge 0)=1$ and $P_x(A_{t+\tau _D}>0 \text{ for } \text{ all } t>0)=1$ for every $x\in {{\bar{D}}}$.

Proof

In view of (3.5), the first part of the lemma is trivial for $x\in \partial D$. To show it for $x\in D$, we denote by F the quasi-support of $\sigma$. We may and will assume that $F\subset \partial D$ (see [4, p. 190]). Since A is an AF in the strict sense, by [4, Lemma 5.1.11], we have $P_x(A_t=({{\textbf{1}}}_{F_A}\cdot A)_t,t>0)=1$ for every $x\in {{\bar{D}}}$, where $({{\textbf{1}}}_{F_A}\cdot A)_t=\mathop {\int }\nolimits ^t_0{{\textbf{1}}}_{F_A}(X_s)\,dA_s$, $t\ge 0$. By [4, Theorem 5.1.5], $F_A=F$, so $P_x(A_t=({{\textbf{1}}}_{F}\cdot A)_t,t>0)=1$ for every $x\in {{\bar{D}}}$. Since $F\subset \partial D$, it follows that for $x\in D$, $A_t=0$ $P_x$-a.s. on $[0,\tau _D)$. Since A is continuous, in fact $A_t=0$ $P_x$-a.s. on $[0,\tau _D]$ for $x\in D$, which proves the first part of the lemma. Let B be a standard Brownian motion appearing in (2.4). We have $P_{y}({\bar{\tau }}_D=0)=1$ for $y\in \partial D$, where ${\bar{\tau }}_D=\inf \{t>0:B_t\notin D\}$. From this, (2.4), and the fact that the reflecting Brownian motion is a diffusion with sample paths in ${{\bar{D}}}$, it follows that the support of the additive functional appearing in (2.4), which we denote for the moment by ${{\bar{A}}}$, equals $\partial D$. Let $\text{ Cap}_L$ denote the capacity associated with ${{\mathcal {E}}}$ and Cap the capacity associated with ${{\mathbb {D}}}$ (see [4, Section 2.1] for the definitions). Assumption (1.1) implies that $2\lambda ^{-1}\text{ Cap }\le \text{ Cap}_L\le 2\lambda \text{ Cap }$. Therefore F is a quasi-support of $\sigma$ considered as a smooth measure with respect to $\text{ Cap}_L$ if and only if it is a quasi-support of $\sigma$ considered as a smooth measure with respect to Cap. By what has already been proved and [4, Theorem 5.1.5], $F=F_{{{\bar{A}}}}=\partial D$, so by [4, Theorem 5.1.5] again, $F_A=\partial D$. From this and the definition of $F_A$, we get the second part of the lemma. $\square$

Theorem 4.2

Assume that $f\in L^p(D)$ with $p>d$ and $g\in C(\partial D)$. Then $v_n(x)\rightarrow v(x)$ for every $x\in {{\bar{D}}}$.

Proof

Recall that $v_n$ is defined by the right-hand side of (3.2). First assume that $x\in D$. By Lemma 4.1 and the dominated convergence theorem, for $x\in D$, we have

$$\begin{aligned} E_x\mathop {\int }\limits ^{\infty }_0\!e^{-\lambda t-nA_t}f(X_t)\,dt= & {} E_x\mathop {\int }\limits ^{\tau _D}_0\!e^{-\lambda t}f(X_t)\,dt +E_x\mathop {\int }\limits ^{\infty }_{\tau _D}e^{-\lambda t-nA_t}f(X_t)\,dt\nonumber \\\rightarrow & {} E_x\mathop {\int }\limits ^{\tau _D}_0e^{-\lambda t}f(X_t)\,dt=R^D_{\lambda }f(x) \end{aligned}$$

(4.1)

as $n\rightarrow \infty$. We are going to show that for every $x\in D$,

$$\begin{aligned} nE_x\mathop {\int }\limits ^{\infty }_0e^{-\lambda t-nA_t}g(X_t)\,dA_t= & {} nE_x\mathop {\int }\limits ^{\infty }_{\tau _D}e^{-\lambda t-nA_t}g(X_t)\,dA_t\nonumber \\\rightarrow & {} E_xe^{-\lambda \tau _D}\!g(X_{\tau _D})=H^{\lambda }_{\partial D}g(x) \end{aligned}$$

(4.2)

as $n\rightarrow \infty$. We know that $(P_t)_{t>0}$ is a strongly Feller semigroup on $C({{\bar{D}}})$. Let $({{\hat{L}}},D({{\hat{L}}}))$ denote its generator. Since $D({{\hat{L}}})$ is dense in $C({{\bar{D}}})$, one can choose a sequence $\{g_k\}\subset D({{\hat{L}}})$ such that $\sup _{x\in {{\bar{D}}}}|g_k-g|\le k^{-1}$. By [8, Theorem 3.6.5], $g_k(X)$ is a semimartingale under $P_x$ for $x\in {{\bar{D}}}$. In fact,

$$\begin{aligned} M^{g_k}_t:=g_k(X_t)-g_k(X_0)-\mathop {\int }\limits ^t_0({{\hat{L}}}g_k)(X_s)\,ds,\quad t\ge 0, \end{aligned}$$

is a martingale under $P_x$ for $x\in {{\bar{D}}}$. Integrating by parts, for all $k\ge 1$ and $t\ge 0$, we obtain

$$\begin{aligned}&e^{-\lambda ( t+\tau _D)-nA_{t+\tau _D}}g_k(X_t) -e^{-\lambda \tau _D-nA_{\tau _D}}g_k(X_{\tau _D})\\&\quad =-\mathop {\int }\limits ^{t+\tau _D}_{\tau _D}e^{-\lambda s-nA_s}g_k(X_s)\,d(\lambda s+nA_s) +\mathop {\int }\limits ^{t+\tau _D}_{\tau _D}e^{-\lambda s-nA_s}\,dg_k(X_s) \\&\qquad +\mathop {\int }\limits ^{t+\tau _D}_{\tau _D}e^{-\lambda s-nA_s}\,dM^{g_k}_s. \end{aligned}$$

Since $e^{-\lambda t-nA_t}\rightarrow 0$ as $t\rightarrow \infty$ and $A_{\tau _D}=0$ $P_x$-a.s., we get

$$\begin{aligned}&nE_x\mathop {\int }\limits ^{\infty }_{\tau _D}e^{-\lambda s-nA_s}g_k(X_s)\,dA_s =E_xe^{-\lambda \tau _D}g_k(X_{\tau _D})\\&\quad -\lambda E_x\mathop {\int }\limits ^{\infty }_{\tau _D}e^{-\lambda s-nA_s}g_k(X_s)\,ds +E_x\mathop {\int }\limits ^{\infty } _{\tau _D}e^{-\lambda s-nA_s} ({{\hat{L}}}g_k)(X_s)\,ds. \end{aligned}$$

Since $g_k,{{\hat{L}}}g_k\in C({{\bar{D}}})$, applying Lemma 4.1 and the dominated convergence theorem shows that the second and third term on the right-hand side of the above equality converge to zero as $n\rightarrow \infty$. This proves that

$$\begin{aligned} n E_x\mathop {\int }\limits ^{\infty }_0e^{-\lambda s-nA_s}g_k(X_s)\,dA_s \rightarrow E_xe^{-\lambda \tau _D}g_k(X_{\tau _D}). \end{aligned}$$

(4.3)

Furthermore,

$$\begin{aligned} n\mathop {\int }\limits ^{\infty }_{\tau _D}e^{-\lambda s-nA_s}\,dA_s \le ne^{-\lambda \tau _D}\mathop {\int }\limits ^{\infty }_0e^{-n A_s}\,dA_s = e^{-\lambda \tau _D}(1-e^{-nA_{\infty }}), \end{aligned}$$

so

$$\begin{aligned} n E_x\mathop {\int }\limits ^{\infty }_{\tau _D}e^{-\lambda s-nA_s}|g_k-g|(X_s)\,dA_s \le k^{-1}E_xe^{-\lambda \tau _D}. \end{aligned}$$

(4.4)

We also have $E_xe^{-\lambda \tau _D}|g_k-g|(X_{\tau _D})\le k^{-1}$. From this and (4.3), (4.4), we get (4.2), which together with (4.1) shows the desired convergence for $x\in D$. Since $P_x(\tau _D=0)=1$ for $x\in \partial D$, the above arguments also show that $v_n(x)\rightarrow E_xg(X_0)=g(x)=v(x)$ for $x\in \partial D$, which completes the proof. $\square$

Remark 4.3

Let $f\in L^2(D)$, $g\in C(\partial D)$, and ${\tilde{u}}_n,{\tilde{u}}$ be defined as in Proposition 3.2. Then ${\tilde{u}}_n\rightarrow u$ q.e. because the proof of Theorem 4.2 shows that then (4.1) holds for q.e. $x\in D$ and (4.2) holds for every $x\in D$. In particular, if $f\in L^2(D)$ and $g\in H^1(D)\cap C(\partial D)$, then $\{u_n\}$ converges q.e. to the weak solution u of (1.3). If $f\in L^2(D),g\in H^1(D)$, then the convergence holds in $H^1(D)$ and hence a.e. For an analytical proof of this fact, we refer the reader to [7, Appendix I, Section 4.4].