Characterization of tropical plane curves up to genus six

Abstract

We provide a new forbidden criterion for the realizability of smooth tropical plane curves. This in turn provides us a complete classification of smooth tropical plane curves up to genus six.

1 Introduction

Tropical plane curves exhibit duality with respect to regular subdivisions of a certain lattice polygon. Smooth tropical plane curves are those that are dual to unimodular triangulations. The tropical plane curves also come with a metric with which they can be considered as metric graphs, where each edge length can be understood as a metric. The skeleton is a trivalent, planar metric graph which allows a deformation retract from the tropical plane curve to itself. It can be obtained via a graph theoretic operation from the tropical curve. An important invariant under this duality is the genus of the tropical curve which is equal to the number of independent cycles in the skeleton and which is also equal to the number of interior lattice points of the corresponding lattice polygon. A central problem concerning skeleta of smooth tropical plane curves has been to categorize which trivalent, planar graphs can occur as skeleta of smooth tropical plane curves.

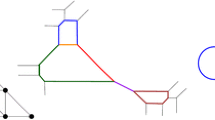
The graphs which do occur as skeleta of tropical curves are referred as troplanar or tropically planar [3]. Starting from the work in [1], there has been immense interest to find forbidden criteria to rule out classes of graphs which can not be realizable. We illustrate the duality between the unimodular triangulations, tropical plane curves, and skeletons by Fig. 1, where we notice that the skeleton as a trivalent graph is obtained from the dual tropical curve by deletion of degree one unbounded edges and smoothening the degree two edges, which are obtained after the said deletion and continuing this process till we obtain a trivalent graph. We refer the reader to [1, 3, 4] for further details about the duality and the graph theoretic operation to obtain the skeleton. In [1], computational techniques were employed to classify all troplanar graphs for lower genera $g=3,4,$ and $g=5$. Their study provided a computational classification up to genus 5, and a theory-based classification up to genus four. In [3], this computational study is pushed to the case of genus seven and many new criteria are also established. However the classification still remained incomplete for genus five and six. Some of the previously known forbidden patterns are sprawling [1], crowded [6], and TIE-fighter [3]. In [4], for the first time a complete classification of all troplanar graphs up to genus five was achieved which is independent of computational enumeration. Along with completing the case for genus five, [4] provided the classification for all graphs of genus six besides the eight graphs appearing in Fig. 2.

Fig. 1

A unimodular triangulation of a genus 6 polytope (left), its dual graph (center), and the corresponding skeleton which has a double heavy cycle with two loops (right)

In this article, we provide the first complete classification of all troplanar graphs up to genus six in the form of Theorem 4.1, i.e., we describe a finite set of obstructions which if present in a graph of genus up to six prevents the graph from being troplanar. We provide a new criterion stated as heavy cycle with one loop, which extends the arguments of the criterion heavy cycle with two loops discussed in [4]. We also define a new graph structure called double heavy cycle and provide a structural result for a graph with double heavy cycle to be troplanar, which helps us in completely classifying all genus six graphs. Also, we believe that with the updated list of criteria the classification of skeleta for higher genus can also be considerably reduced.

Fig. 2

The eight trivalent planar graphs of genus six, which are not realizable [3], and remained unclassified up till now

2 Heavy cycle with one loop

Let P be a lattice polygon and $\partial P$ represent the boundary of P. A lattice polygon with all interior lattice points in a line is called a hyperelliptic polygon. We refer to the convex hull of the interior lattice points of a lattice polygon P as $\text {int}(P)$. A split is a subdivision with exactly two maximal cells. The hyperplane along a split is referred to as the split hyperplane. If one of the two maximal cells with respect to a split does not contain any interior lattice point, we call it a trivial split. We recall the following lemma from [4].

Lemma 2.1

Let P contain a unimodular triangle face with vertices a, b, z such that neither a nor b is a vertex of P, and z is an interior lattice point. If a and b lie on $\partial P$, then either a and b lie on a common edge of P or the lattice point $a+b-z$ is contained in P.

We state the following definitions of a heavy cycle and a heavy cycle with two loops from [4].

Definition 2.2

We say that a cycle C in a planar graph G is heavy if

• 1. it has two nodes $v_1$ and $v_2$ such that $v_i$ is incident with a cut edge $e_i$ connecting $v_i$ with a subgraph $G_i$ of positive genus;

• 2. and there is a third subgraph $G_3$, also of positive genus, which shares at least one node with the cycle C; cf. Fig. 3.

We recall some basic notations from [4] concerning heavy cycle. From [4, Lemma 1], we know that there are split lines $S_1$ and $S_2$ dual to the edges $e_1$ and $e_2$ of G. Also by [4, Lemma 4], P is decomposed into a union of three lattice polygons $P_1$, $P_2$, and $P_{3}$ such that $\Delta$ induces triangulations of all three. We obtain triangulations $\Delta _1$, $\Delta _2$, and $\Delta _{3}$ such that the component $G_i$ is the skeleton of $\Delta _i$ for $i=1,2,$ and $G_{3} \cup C$ is realized by $\Delta _{3}$. $T_{1}$ and $T_{2}$ represent the triangular faces in $\Delta$ dual to $v_{1}$ and $v_{2}$ respectively. The polygon $P_{3}$ is referred to as the heavy component of P, and $\Delta _{3}$ is referred as the heavy component of $\Delta$.

In [4], a structural result concerning heavy cycles is proved specifying the conditions under which a graph with a heavy cycle is realizable as the skeleton of a smooth plane tropical curve.

Lemma 2.3

Suppose that G has a heavy cycle with cut edges $e_1$ and $e_2$ as in Fig. 3. Then the triangles $T_1$ and $T_2$ in $\Delta$ share an edge [z, w], where z is the interior lattice point dual to C, and the split lines $S_1$ and $S_2$ intersect in w, which is a vertex of $P_{3}$, and which lies in the boundary of P.

Definition 2.4

We say that a connected trivalent planar graph G has a heavy cycle with two loops if it has the form as described in Fig. 4, where $G_{3}$ represents a subgraph of positive genus.

Fig. 3

Graph with the heavy cycle C

Fig. 4

Heavy cycle with two loops

Using [3, Lemma 2.3], the following forbidden criterion is established.

Theorem 2.5

Suppose G is a graph with a heavy cycle C and two loops with cut edges $e_{1}$ and $e_{2}$ as in Fig. 4. Then the heavy component $P_{3}$ can have at most three interior lattice points, and these lie on the line spanned by the edge $[z,w] \in \Delta$, where z is the interior lattice point dual to C, and w is the intersection point of the split edges $s_{1}$ and $s_{2}$. In particular, $P_{3}$ is hyperelliptic and $g\le 5$.

Inspired from these definitions, we define a graph with a heavy cycle with one loop.

Definition 2.6

We say that a planar, trivalent graph G has a heavy cycle with one loop if it is of the form shown in Fig. 5, where $G_{2}$ and $G_{3}$ represent subgraphs of positive genus.

Fig. 5

Heavy cycle with one loop

Similar to Theorem 2.5, we prove the first new forbidden criterion in this article, along with additional conditions in the specific case of $g = 6$.

Theorem 2.7

Suppose G is a tropically planar graph with a heavy cycle with one loop as shown in Fig. 5. Then the heavy component $P_{3}$ is hyperelliptic and can have at most three interior lattice points. Also, $P_{2}$ can have at most three interior lattice points. In the case when genus $g = 6$ and $g(P_{2}) = 2$, $P_{2}$ is hyperelliptic and the triangulation restricted to $P_{2}$, i.e, $\Delta _{2}$ cannot have a nontrivial split. In particular, the genus of G can be at most seven.

Fig. 6

This illustrates Theorem 2.7: general sketch (left) and the case when $g(P') \ge 4$ (right), which is impossible

Proof

We utilize the convention used in [4, Theorem 2] and let $T_{1} = {{\,\textrm{conv}\,}}\{ (0,0), (1,0),(0,1)\}$ and $T_{2}= {{\,\textrm{conv}\,}}\{(0,0),(-1,-k), (0,1)\}$ be the triangles dual to $v_{1}$ and $v_{2}$ respectively in $\Delta$ with the edges $s_{1}$ (between the points (1, 0) and (0, 1)) and $s_{2}$ (between the points (0, 1) and $(-1,-k)$, depicted in Figure  6) being the split edges corresponding to the cut edges $e_{1}$ and $e_{2}$ in Fig. 5.

We let $z=(0,0)$ be the point corresponding to the heavy cycle C and by Lemma 2.3, we know that $T_{1}$ and $T_{2}$ share an edge and the split edges intersect at a point, in this case that point is $w = (0,1)$. This is illustrated in Fig. 6.

Invoking Lemma 2.1 for $T_{1}$, we realize that the point $r = (1,1)$ is in P. If we consider the case that r is in $\partial P$, that implies that the subpolygon of P realizing the loop lies in between the parallel lines $y=0$ and $y=1$, which gives a contradiction as this does not contain any interior lattice point. Hence, r lies in the interior of P. Similarly, for $T_{2}= {{\,\textrm{conv}\,}}\{(0,0),(-1,-k),(0,1)\}$, we obtain that the point $r' = (-1,-k+1)$ lies in the interior of P. Similar to the arguments used in the case of heavy cycle with two loops, we realize that when we invoke convexity of P along with the condition that r and $r'$ are interior points of P, then we obtain that the subpolygon realizing the subgraph $G_{2}$ lies between the lines $x=1$ and $x=-1$ illustrated in Fig. 6, which implies that $P_{3}$ is hyperelliptic.

We now move on to show that $g(P_{3}) \le 3$. We proceed by contradiction and assume $g(P')\ge 4$. By our assumption, $(0,-3)$ is an interior lattice point of $P_{3}$. We notice that the point $p_1 = (1,0)$, which is a boundary point, and $r = (1,1)$, which is an interior lattice point, both lie on the line $x=1$. We now consider the possibilities for the point (1, 2); either $(1,2)\in P_1$, in which case $(1,2)\in \partial P_1$ or the boundary edge at w passes through a point in the open interval ((1, 2), (1, 1)). Also, no point in $\partial P_{1}$ can be present on the line $y=3x-3$ because $(0,-3)$ is an interior lattice point. Hence, we conclude that $P_{1}$ is contained in the triangle ${{\,\textrm{conv}\,}}\{p_1,w,(1,3)\}$. However, this triangle is not valid because (1, 3) has been excluded; see Fig. 6. This provides the desired contradiction, and thus $g(P') \le 3$.

Now we show that $g(P) \le 7$. We know that the points $r = (1,1)$ and $(0,-2)$ are interior points of P. Hence, no point in $\partial P_{1}$ can be present on the line $y=2x-2$ because $(0,-2)$ is an interior lattice point. Again, (1, 2) is either in $\partial P$ or the boundary edge at w passes through a point in the open interval ((1, 2), (1, 1)). Therefore, we conclude that $P_{1}$ =${{\,\textrm{conv}\,}}\{p_{1},w, (2,3)\}$. Now, we try to find the maximal subpolygon $P_{2}$ (in terms of area) that we can obtain given the above constraints. We realize that the maximal polygon in this case ${P_{2}}^{max} = {{\,\textrm{conv}\,}}\{(0,1),(-1,-3),(-4,-3)\}$, which is shown as the triangle wCR in Fig. 7. Thus $g(P) \le 7$.

With the general statement proven, we now consider the specific case of genus $g = 6$. In the case that $g(P_{2}) = 2$, $P_{2}$ is hyperelliptic since all lattice polygons with $g \le 2$ are hyperelliptic [1]. We again proceed by constructing the maximal polygon P in this case. Since $g(P_{2}) = 2$ and $P_{2}$ is hyperelliptic, we realize that the point $(-1,-1)$ is an interior point of P because if it is not in P or is in $\partial P$, then it contradicts $g(P_{2}) = 2$. This implies that for a point $p=(x,y) \in P$, $x \ge -2$. This implies that the maximal polygon $P_{2}$ in this case is ${P_{2}}^{\text {max}} = {{\,\textrm{conv}\,}}\{w,(-2,-1),(-2,-3),(-1,-3)\}$, which is depicted in Fig. 7 as the quadrilateral wPQR. We realize that for $P_{2}$ and all its subpolygons, none of the corresponding triangulations $\Delta _{2}$ can posses a nontrivial split edge such that it divides $P_{2}$ into two subpolygons each of which has a positive genus. Hence, we get the claimed result. $\square$

Fig. 7

This illustrates the case when $g=6$ and $g(P_{2}) = 2$

We state the forbidden criterion we obtain as a result of Theorem 2.7.

Corollary 2.8

Let G be a planar trivalent graph of genus $g \ge 8$ such that G has a heavy cycle with one loop. Then G cannot be tropically planar.

Remark 2.9

Figure 8 shows the unimodular triangulation which realizes a graph with a heavy cycle and one loop. Notice that $G_{2}$ has no cut edges and hence $P_{2}$ has no nontrivial split.

Fig. 8

A unimodular triangulation of genus six with $g(P_{2}) = 2$ (left), corresponding skeleton with a heavy cycle with one loop with $G_{2}$ that does not have a cut edge (right)

3 Double heavy cycle

We now define a double heavy cycle.

Definition 3.1

We say that cycles $C_{1},C_{2}$ in a planar graph G are double heavy if

• 1. it has two nodes $v_1$ and $v_2$ such that $v_i$ is incident with a cut edge $e_i$ connecting $v_i$ with a subgraph $G_i$ of positive genus;

• 2. and there is a third subgraph $G_3$, also of positive genus, which shares at least one node with the cycles $C_{1}$ and $C_{2}$; cf. Fig. 9.

Fig. 9

Graph with double heavy cycles $C_{1}$ and $C_{2}$

We fix some additional notation concerning double heavy cycles. Let $T,T_{1}$, and $T_{2}$ denote the triangles in $\Delta$ dual to $v,v_{1}$, and $v_{2}$ in G respectively. Let $z_{1}$ and $z_{2}$ represent the interior lattice points dual to $C_{1}$ and $C_{2}$. We also recall that the unimodular triangles in $\Delta$ can be categorized into degree one, two, and three depending on the number of triangles adjacent to them in $\Delta$. Similar to Lemma 2.3, we now prove a structural result concerning double heavy cycles.

Lemma 3.2

Suppose that G has double heavy cycles $C_{1}$ and $C_{2}$ with cut edges $e_1$ and $e_2$ as in Fig. 3. Then the triangles T and $T_1$ in $\Delta$ share an edge $[z_{1},w]$, the triangles T and $T_2$ in $\Delta$ share an edge $[z_{2},w]$ where $z_{1}$ is the interior lattice point dual to $C_{1}$ and $z_{2}$ is the interior lattice point dual to $C_{2}$. The the split lines $S_1$ and $S_2$ intersect in w, which is a shared vertex between $T_{1}$ and $T_{2}$.

Proof

Similar to the earlier proofs, we fix a unimodular triangle $T_{1} ={{\,\textrm{conv}\,}}\{(0,0),(0,1),(1,0)\}$, where $z_{1} = (0,0)$, with the split edge $s_{1}$ being between the points (0, 1) and (1, 0). Since the cycles $C_{1}$ and $C_{2}$ are adjacent in G, the interior lattice points dual to them would be hyperelliptic, i.e., they would lie on a line. Hence, $z_{2}$ would lie on the line $x=-1$. Also, by using Lemma 2.1 on $T_{1}$, we infer that the point (1, 1) is an interior lattice point of P.

We now show that T and $T_{1}$ share an edge. We assume to the contrary that there exists at least one face $T'$ inbetween T and $T_{1}$ which is either a degree two triangular face or a degree three triangular face adjacent to a degree one face. In both these cases, after deletion of degree one faces, $T'$ is a degree two triangular face. We consider the polygon $P'$ obtained from P by recursive deletion of degree one faces. If G is a graph realizable by P, then it is also realizable by $P'$. Henceforth, we consider the triangulation in $P'$. Given the structure of G and our choice of $T_{1}$, we realize that the common edge between $T_{1}$ and $T'$ would be [(0, 0), (0, 1)]. Using the unimodularity of $T'$, we realize that the third vertex of $T'$ lies on the line $x=-1$. Invoking convexity, presence of $T_{1}$ in $P'$, and the point (1, 1) being an interior lattice point, we observe that any point $(-1,q)$ with $q=1$ cannot be a vertex of $T'$. Therefore we consider the third vertex of $T'$ to be $(-1,q), q \le 0$. Since $T'$ is a degree two triangular face, this would imply that one of its edges is along $\partial P'$, which gives us a contradiction because then it can only be adjacent to T and $T_{1}$ and not to any other triangle, but it has to be adjacent to at least one other triangle from the heavy component which realizes $G_{3}$. Hence, we conclude that T and $T_{1}$ share an edge in this case. Since v is symmetric with respect to $v_{1}$ and $v_{2}$ in G, we have that T is symmetric with respect to $T_{1}$ and $T_{2}$. Hence, we also conclude that T and $T_{2}$ share an edge, illustrated in Fig. 10.

We now are left to show that $T_{1}$ and $T_{2}$ share a vertex. We realize that given $T_{1} = {{\,\textrm{conv}\,}}\{(0,0),(1,0),(0,1)\}$ and $T = \{(0,0), (0,1), (-1,q)\}, \> q \le 0$, the edge that is shared by T and $T_{2}$ is the edge between the points $(-1,q)$ and (0, 1). When we consider all possible candidates for the third vertex $(\alpha ,\beta )$ of $T_{2}$, we realize that $\alpha < 0$. Also, if $\beta > 1$, then this contradicts convexity of P, at the point (0, 1). Hence, $\beta \le 1$. If $\beta = 1$, this would imply that $P_{1}$ is squeezed between the line $y = 0$ and $y =1$, which has no interior lattice points. Therefore, $\beta \le 0$. We obtain that for all such values of $\alpha$ and $\beta$ the split edge $s_{2}$ is of the form $[(\alpha ,\beta ),(0,1)]$. This implies that $T_{1}$ and $T_{2}$ share the vertex $w = (0,1)$, illustrated in Fig. 10. Hence, the proof is complete. $\square$

Fig. 10

Possibilities for the face T (left) and an example with the faces $T_{2}$, T, and $T_{1}$ in $\Delta$ for $q=0$ (right)

We now define a graph having a double heavy cycle with two loops.

Definition 3.3

We say that a connected trivalent planar graph G has a double heavy cycle with two loops if it has the form as described in Fig. 11, where the shaded region $G_{3}$ is a subgraph of positive genus.

Fig. 11

Double heavy cycle with two loops

We now establish a structural result concerning double heavy cycles with two loops.

Theorem 3.4

Suppose G is a tropically planar graph with double heavy cycles $C_{1}$ and $C_{2}$ with two loops with cut edges $e_{1}$ and $e_{2}$ as in Fig. 11. If $g(P)= 6$, then the interior lattice polygon of the heavy component, i.e., $\text {int}(P_{3})$, is a unit parallelogram.

Proof

We fix the triangle $T_{1} = {{\,\textrm{conv}\,}}\{(0,0),(0,1),(1,0)\}$, where $z_{1} = (0,0)$. We know by Lemma 3.2 that $T= {{\,\textrm{conv}\,}}\{(0,0), (0,1), (-1,q)\}, q \le 0$, and the triangles $T,T_{1}$, and $T_{2}$ each share an edge amongst themselves. By applying Lemma 2.1 on $T_{1}$, we obtain that (1, 1) is the unique interior lattice point of $P_{1}$. We see that in this case the interior lattice points of the heavy component are squeezed between the lines $y = (1-q)x+1$ and $y=3x-3$. Also, using convexity of P at the point (1, 0), we conclude that $(-1,q-1)$ is an interior point of $P_{3}$ if $(0,-1) \in \text {int}(P_{3})$. We realize that for the case when $g(P_{3}) =4$, the point $(0,-1) \in \text {int}(P_{3})$ and we need to show that both the lines $x=0$ and $x=-1$ each have one interior lattice point other than the points (0, 0) and $(-1,q)$. We assume the contrary, i.e., the line $x=0$ has two interior lattice points. If $-1 \le q \le 0$, then this contradicts the convexity of P at the point $(-1,q)$. If $q \le -1$, then we obtain more interior lattice points in $P_{3}$ which contradicts the fact that $g(P_{3}) = 4$. Hence, we conclude that for $g=6$, the interior lattice polygon of the heavy component, i.e., $\text {int}(P_{3})$, is a unit parallelogram. $\square$

Fig. 12

The triangular faces $T,T_{1}$, and $T_{2}$ in a triangulation dual to a graph with double heavy cycle with two loops

4 Conclusions

We now furnish conclusions to what our results entail with respect to classification of skeletons of genus six. Firstly, we call the graph ‘g’ in Fig. 2 an enve-loop graph (envelope + loop). We also recognize that the graphs ‘a’, ‘b’, ‘c’, and ‘d’ all have a heavy cycle with one loop. Out of these, the heavy component in the graph ‘a’ cannot arise from a hyperelliptic polygon of genus 3, hence it can be ruled out by Theorem 2.7. Also, graph ‘b’ does have a heavy component which can arise from a hyperelliptic polygon of genus 3, although the orientation of the hyperelliptic points is not permissible according to Theorem 2.7, hence it can be ruled out as well. Graphs ‘c’ and ‘d’ both have permissible hyperelliptic heavy components, but both of them have a genus two component which has a cut edge, which would correspond to a nontrivial split in $P_{2}$ which is not possible by Theorem 2.7, hence these two graphs are also ruled out.

Subsequently, we realize that graphs ‘e’, ‘f’, and ‘h’ all have double heavy cycle with two loops. By Theorem 3.4, we know that the convex hull of the interior lattice points of the heavy component $P_{3}$ is a unit parallelogram for a lattice polygon P realizing a double heavy cycle with two loops. Hence, graph ‘f’ is eliminated as the heavy component cannot be a parallelogram in this case. Let $C_{1},C_{2},C_{3}$, and $C_{4}$ be the four cycles in the subgraph dual to the heavy component $P_{3}$, within a realizable graph of $g=6$ with double heavy cycle with two loops. Given that the graph is trivalent, we realize that the subgraph cannot have two connected components each of genus two. Only connected components of genus three and genus one are possible. Since the interior points dual to the $C_{i}'$s form a unit parallelogram, this implies that either the cycles $C_{1},C_{2}$, and $C_{3}$ share a vertex or the the cycles $C_{1},C_{2}$, and $C_{4}$ share a vertex. Hence, we conclude that for a realizable graph G of genus six with a double heavy cycle with two loops, in the subgraph realizing the heavy component, at least three cycles should share a vertex. Therefore, with this characterization we can rule out the graphs ‘e’ and ‘h’. Now we are ready to state the full characterization of all tropical plane curves up to genus six, which can be seen as a generalization of [3, Theorem 3].

Theorem 4.1

A trivalent planar graph G other than the enve-loop graph, of genus $g \le 6$, is tropically planar if and only if none of the following obstructions occur

• 1. it contains a sprawling node, or

• 2. it contains a sprawling triangle and $g \ge 5$, or

• 3. it is crowded, or

• 4. it is a TIE-fighter, or

• 5. it has a heavy cycle with two loops such that the interior lattice points of the heavy component do not align with the intersection of the two split lines, or

• 6. for a cut edge e in G, the connected components of $G {\setminus } \{e\}$, after smoothing out 2-valent vertices, are not tropically planar, or

• 7. it has a heavy cycle with one loop such that either the interior lattice points of the heavy component do not align with the intersection of the two split lines or the connected component with genus greater than one has a cut edge, or

• 8. it has a double heavy cycle with two loops such that either the interior lattice points of the heavy component do not form a unit parallelogram or no three cycles in the heavy component share a vertex.

We know that as the genus increases almost all graphs are not troplanar [3, Theorem 4.2]. Additionally, the class of troplanar graphs is not minor-closed [3, Figure 6]. Hence, such classifications become increasingly difficult as the genus increases. One area of future exploration could be to finish the classification for the case of genus seven, however no list of unclassified graphs is available for it. Also, there has been recent progress in finding criteria which do not include a cut edge namely the criteria of big face graphs defined in [5], the techniques of which can be used to define new criteria for higher genus. Additionally, there has been recent progress in the form of [2] where the authors are interested in understanding the locus of tropical plane curves in the moduli space of metric graphs $\mathbb {M}_{g}$ for lower genera and in such a study the classiffication of graphs in terms of forbidden criteria shows promise for a better understanding.