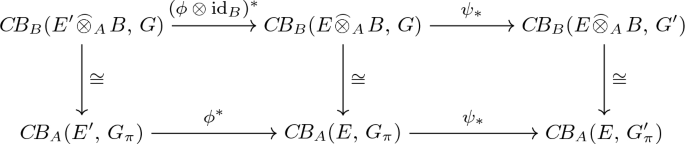Abstract
We prove a change of base theorem for operator space modules over C*-algebras, analogous to the change of rings for algebraic modules. We demonstrate how this can be used to show that the category of (right) matrix normed modules and completely bounded module maps has enough injectives.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let A be a Banach algebra. A right A-module E is called a right Banach A-module if it is a Banach space and, for each \(x\in E\), \(a\in A\), we have \(\Vert x\cdot {a}\Vert \le \Vert x\Vert \Vert a\Vert \). The book of Helemskii [10], e.g., deals with homological algebra in this setting. For C*-algebras, there are good reasons to employ modules which also carry an operator space structure; the most common ones are the h-modules and the matrix normed modules. In [14], Paulsen introduced the notions of relative injectivity and relative projectivity for h-modules, and various pieces of homological algebra, including results on homological dimension, have been obtained in this setting; see, e.g., [11, Section 7] and [17].
The categories that appear in functional analysis, such as  and
and  whose objects are the (complex) Banach spaces and the operator spaces with bounded and with completely bounded linear mappings, respectively, as morphisms, are not abelian. Thus the standard homological algebra does not apply. The more general setting of exact categories in the sense of Quillen, see [5], has been successfully applied to
whose objects are the (complex) Banach spaces and the operator spaces with bounded and with completely bounded linear mappings, respectively, as morphisms, are not abelian. Thus the standard homological algebra does not apply. The more general setting of exact categories in the sense of Quillen, see [5], has been successfully applied to  in [6], and exploited in [15] to define a cohomological dimension for C*-algebras, and in [1] to develop a sheaf cohomology theory; cf. also [13]. In particular in the latter setting, there are too few projective objects; this is why we focus on injectives. The Arveson–Wittstock Hahn–Banach theorem states that B(H), the space of bounded operators on a Hilbert space H, is injective even in
in [6], and exploited in [15] to define a cohomological dimension for C*-algebras, and in [1] to develop a sheaf cohomology theory; cf. also [13]. In particular in the latter setting, there are too few projective objects; this is why we focus on injectives. The Arveson–Wittstock Hahn–Banach theorem states that B(H), the space of bounded operators on a Hilbert space H, is injective even in  (which has the same objects as
(which has the same objects as  but the morphisms are the complete contractions), and injectivity in an additive category of h-modules has been investigated by Frank and Paulsen [9]. Injective matrix normed modules (see Definition 3.1 below) seem to be less well understood; we will discuss this in Sections 3 and 4 and prove that every injective operator space provides us with an injective matrix normed module in a canonical way (Corollary 4.11).
but the morphisms are the complete contractions), and injectivity in an additive category of h-modules has been investigated by Frank and Paulsen [9]. Injective matrix normed modules (see Definition 3.1 below) seem to be less well understood; we will discuss this in Sections 3 and 4 and prove that every injective operator space provides us with an injective matrix normed module in a canonical way (Corollary 4.11).
The main topic of this paper is a change of base procedure for matrix normed modules over unital C*-algebras. Change of base, also called ‘change of rings’ in algebraic module theory, is an adjunction of module categories and as such more general than equivalence. Hence, it extends Morita equivalence of rings. The ‘extension of scalars’ (Definition 4.5) makes use of the module operator space projective tensor product, which we therefore recall in Section 3. The paper’s main theorem is Theorem 4.9; as a consequence of it, we find that every matrix normed module can be completely isometrically embedded into an injective one (Proposition 4.13). Change of base is a fundamental tool in algebraic geometry for sheaves of modules over ringed spaces and, in a similar vein, for operator module sheaves over C*-ringed spaces in [1].
2 Terminology, notations, and conventions
Our standard references are [2] and [8]; in particular, we will always assume that operator spaces are complete. The category  consists of objects: the operator spaces, and morphisms: completely bounded linear maps. The subcategory
consists of objects: the operator spaces, and morphisms: completely bounded linear maps. The subcategory  consist of the same objects, but the morphisms are the complete contractions. When \(m,n\in \mathbb {N}\) and E is a vector space, if we want to emphasise indexing, we will sometimes identify elements in the vector space \(M_{nm}(E)\) of (\(nm\times {}nm\))-matrices as \([[x_{ij}^{k l}]_{(i,j)}]_{(k,l)}\in M_m(M_n(E))\) where \(i,j\in \{1,\ldots , n\}\) and \(k,l\in \{1,\ldots , m\}\). If E, F are operator spaces, we will denote the operator space consisting of all completely bounded linear maps from E to F by \(C\!B({E},\,{F})\). We write the completely bounded norm of an element \(\phi \in C\!B({E},\,{F})\) as \(\Vert \phi \Vert _{cb }\). If moreover, E and F are right Banach A-modules for a C*-algebra A, then the space \(C\!B_{A}({E},\,{F})\), of all completely bounded A-module maps, is a closed subspace of \(C\!B({E},\,{F})\).
consist of the same objects, but the morphisms are the complete contractions. When \(m,n\in \mathbb {N}\) and E is a vector space, if we want to emphasise indexing, we will sometimes identify elements in the vector space \(M_{nm}(E)\) of (\(nm\times {}nm\))-matrices as \([[x_{ij}^{k l}]_{(i,j)}]_{(k,l)}\in M_m(M_n(E))\) where \(i,j\in \{1,\ldots , n\}\) and \(k,l\in \{1,\ldots , m\}\). If E, F are operator spaces, we will denote the operator space consisting of all completely bounded linear maps from E to F by \(C\!B({E},\,{F})\). We write the completely bounded norm of an element \(\phi \in C\!B({E},\,{F})\) as \(\Vert \phi \Vert _{cb }\). If moreover, E and F are right Banach A-modules for a C*-algebra A, then the space \(C\!B_{A}({E},\,{F})\), of all completely bounded A-module maps, is a closed subspace of \(C\!B({E},\,{F})\).
We equip each matrix algebra \(M_n(A)\) with the unique C*-algebra norm with respect to the involution \([a_{ij}]\mapsto [a^*_{ji}]\). This yields the canonical operator space structure on A. We will only consider the case where A is unital (with multiplicative identity \(1_A\)).
Let \(\mathscr {A}\) be a category. To indicate that E belongs to the class of objects in \(\mathscr {A},\) we write \(E\in \mathscr {A}\). The set of morphisms from \(E\in \mathscr {A}\) to \(F\in \mathscr {A}\) is denoted \(Mor _{\mathscr {A}}{({E},{F})}.\) If \(\mathscr {M}\) is a class of morphisms in \(\mathscr {A}\), we denote the subset of \(Mor _{\mathscr {A}}{({E},{F})}\) that consists only of the morphisms in \(\mathscr {M}\) by \({\mathscr {M}}{({E},\,{F})}\). Suppose \(E, F, G\in \mathscr {A}\) and \(f\in Mor _{\mathscr {A}}{({F},{G})}\), we write \({{f}^*_{E}}\) for the function \(Mor _{\mathscr {A}}{({G},{E})}\rightarrow Mor _{\mathscr {A}}{({F},{E})}\), \(g\mapsto {gf}\), and \({f}_*^{E}\) for the function \(Mor _{\mathscr {A}}{({E},{F})}\rightarrow Mor _{\mathscr {A}}{({E},{G})}\), \(g\mapsto {fg}\). We often drop the subscript or superscript E when there is no danger of confusion.
Let \(\mathscr {A}\) and \(\mathscr {B}\) be categories. An adjoint pair \((\mathrm {L},\mathrm {R})\) is a pair of functors \({\mathrm {L}}:{\mathscr {A}}\rightarrow {\mathscr {B}}\) and \({\mathrm {R}}:{\mathscr {B}}\rightarrow {\mathscr {A}}\) such that, if \(E\in \mathscr {A}, F\in \mathscr {B},\) there exists a natural bijection \({\sigma _{E,F}}:{Mor _{\mathscr {B}}{({{\mathrm {L}}(E)},{F})}}\rightarrow {Mor _{\mathscr {A}}{({E},{{\mathrm {R}}(F)})}}.\) Natural here means that, if \(E\xrightarrow {f}E'\) is a morphism in \(\mathscr {A}\) and \(F\xrightarrow {g}F'\) is a morphism in \(\mathscr {B},\) there exists a commutative diagram of sets and maps

where each vertical arrow is a bijection. If the morphism sets for both \(\mathscr {A}\) and \(\mathscr {B}\) are objects in a third category \(\mathscr {C}\), the adjoint pairs considered are those such that the associated commutative diagram is of morphisms in \(\mathscr {C}\). For more information on adjoint pairs, see, e.g., [12, Chapter IV].
3 Injective operator space modules
In this section, we fix a unital C*-algebra A, and all modules will henceforth be assumed to be unital. We will discuss two types of modules over A, the h-modules and the matrix normed modules. Both are related to different notions of multilinear mappings on operator spaces and appeared in independent papers by Blecher–Paulsen [3] and Effros–Ruan [7].
Definition 3.1
Let E, F, G be operator spaces and \({\phi }:{E\times {F}}\rightarrow {G}\) be a bilinear map. The map \(\phi \) is multiplicatively completely bounded if there exists \(K>0\) such that, for each \(n\in \mathbb {N}\), and \([x_{ij}]\in {M_n(E)}, [y_{ij}]\in {M_n(F)},\)

We say \(\phi \) is jointly completely bounded if there exists \(K>0\) such that, for each \(n, m\in \mathbb {N}\), and \([x_{ij}]\in M_n(E), [z_{kl}]\in M_m(F),\)
We denote the infimum of all K in equation (3.1) (respectively, in equation (3.2)) by \(\Vert \phi \Vert _{mcb }\) (resp., \(\Vert \phi \Vert _{jcb }\)). If \(\Vert \phi \Vert _{mcb }\le 1\) (resp., \(\Vert \phi \Vert _{jcb }\le 1\)), then \(\phi \) is multiplicatively (resp., jointly) completely contractive. Suppose E is a right A-module that is also an operator space. If the module action \(E\times {A}\rightarrow {}E,\) \((x,a)\mapsto {x\cdot {a}}\), is multiplicatively (resp., jointly) completely contractive, then E is a right h-module over A (resp., a right matrix normed A-module). There are similar definitions for left modules and bimodules.
For our modules, we have used the naming conventions of [2]; we will however avoid the term “operator module” as it has been used for matrix normed modules elsewhere in the past. We use “operator space module” as the over-arching terminology. It is not difficult to show that any multiplicatively completely contractive map is also jointly completely contractive so any right h-module over A is also a right matrix normed A-module. We also note that the operator spaces are precisely the right h-modules over \(\mathbb {C}\) which agree with the right matrix normed \(\mathbb {C}\)-modules. It has become customary to drop the adverb ‘multiplicatively’ whereas ‘jointly completely bounded’ was called ‘matricially bounded’ at a time [7].
For operator spaces E, F, G, the space \(M\!C\!B({E\times {F}},\,{G})\) of all multiplicatively completely bounded bilinear maps (resp., \(J\!C\!B({E\times {F}},\,{G})\) of all jointly completely bounded bilinear maps) becomes a Banach space with norm \(\Vert \cdot \Vert _{mcb }\) (resp., \(\Vert \cdot \Vert _{jcb }\)). Definition 3.1 can be reformulated in terms of the following operator space tensor products.
Definition 3.2
Let E and F be operator spaces. The operator space projective tensor product (resp., Haagerup tensor product), denoted  (resp., \({{E}}\otimes _{{h}}{{F}}\)), is the unique (up to completely isometric isomorphism) operator space such that there is a jointly (resp., multiplicatively) completely contractive map
(resp., \({{E}}\otimes _{{h}}{{F}}\)), is the unique (up to completely isometric isomorphism) operator space such that there is a jointly (resp., multiplicatively) completely contractive map  (resp., \({\theta '}:{{E}\times {F}}\rightarrow {{{E}}\otimes _{{h}}{{F}}}\) ) such that, for each operator space G, the map
(resp., \({\theta '}:{{E}\times {F}}\rightarrow {{{E}}\otimes _{{h}}{{F}}}\) ) such that, for each operator space G, the map  (resp.,
(resp.,  ), is a surjective isometry.
), is a surjective isometry.
For the existence of each of these tensor products, see [8, Chapters 7 and 9]. They involve the completion of the algebraic tensor product \(E\otimes {}F\) with respect to particular matrix norms. We denote an elementary tensor in \(E\otimes {}F\) by \(x\otimes {}y\), where \(x\in E, y \in F.\) A right module E that is also an operator space is a right h-module (resp., matrix normed module) over A precisely when the module action induces a complete contraction \({{E}}\otimes _{{h}}{{A}}\xrightarrow {}E\) (resp.,  ). A benefit of working with the operator space projective tensor product is its relationship to spaces of completely bounded linear mappings.
). A benefit of working with the operator space projective tensor product is its relationship to spaces of completely bounded linear mappings.
Proposition 3.3
([8, Proposition 7.1.2]). Let E, F, and G be operator spaces. Then there exists a completely isometric isomorphism

such that each  is associated with a mapping \(\psi \in C\!B({E},\,{C\!B({F},\,{G})}),\) where for each \(x\in E, y\in F,\) \(\psi (x)(y)=\phi (x\otimes y).\)
is associated with a mapping \(\psi \in C\!B({E},\,{C\!B({F},\,{G})}),\) where for each \(x\in E, y\in F,\) \(\psi (x)(y)=\phi (x\otimes y).\)
Using the language of Section 2, this states that the tensor product functor  and the hom-functor \({C\!B({F},\,{-})}\) form an adjoint pair on the category
and the hom-functor \({C\!B({F},\,{-})}\) form an adjoint pair on the category  as
as  . There is no such relation for the Haagerup tensor product; on the other hand, h-modules are characterised by the CES-theorem ([2, Theorem 3.3.1]) which allows for a common completely isometric representation of the C*-algebra and the module on one Hilbert space.
. There is no such relation for the Haagerup tensor product; on the other hand, h-modules are characterised by the CES-theorem ([2, Theorem 3.3.1]) which allows for a common completely isometric representation of the C*-algebra and the module on one Hilbert space.
Turning towards injectivity, we note that the usual reference to all monomorphisms as the ‘embeddings of a subobject’ often is not the right choice and it is therefore desirable to specify a particular class of morphisms as in the following definition.
Definition 3.4
Let \(\mathscr {M}\) be a class of monomorphisms in a category \(\mathscr {A}\) (which is typically assumed to be closed under composition and contains all isomorphisms). An object \(I\in {\mathscr {A}}\) is \(\mathscr {M}\)-injective if, for all \(E,F\in {\mathscr {A}}\) and morphisms \(\mu \in {\mathscr {M}}{({E},\,{F})}\) and any morphism \(f\in Mor {({E},{I})},\) there exists a morphism \(\widetilde{f}\in Mor {({F},{I})}\) such that \(f=\widetilde{f}\mu .\) That is, there exists a filler arrow making the following diagram commutative.

A category \(\mathscr {A}\) is said to have enough \(\mathscr {M}\)-injectives if for every object \(E\in {\mathscr {A}}\), there exists a morphism \(\mu \in {\mathscr {M}}{({E},\,{I})}\) for some \(\mathscr {M}\)-injective I.
The Arveson–Wittstock Hahn–Banach theorem [8, Theorem 4.1.5] is equivalent to saying that B(H), for any Hilbert space H, is \(\mathscr {M}^1\)-injective in  , where \(\mathscr {M}^1\) is the class of complete isometries. Blecher and Paulsen have shown [4, Theorem 2.6] that a right h-module over A is \(\mathscr {M}^1\)-injective in
, where \(\mathscr {M}^1\) is the class of complete isometries. Blecher and Paulsen have shown [4, Theorem 2.6] that a right h-module over A is \(\mathscr {M}^1\)-injective in  if and only if it is \(\mathscr {M}^1_{A}\)-injective in
if and only if it is \(\mathscr {M}^1_{A}\)-injective in  , where
, where  is the category whose objects are the right h-modules over A, whose morphisms are the completely contractive A-module mappings, and \(\mathscr {M}^1_{A}\) is the class of completely isometric A-module maps. This relies on Wittstock’s result [16, Theorem 4.1] stating that, if A is a C*-subalgebra of B(H), then B(H) is \(\mathscr {M}^1_{A}\)-injective in
is the category whose objects are the right h-modules over A, whose morphisms are the completely contractive A-module mappings, and \(\mathscr {M}^1_{A}\) is the class of completely isometric A-module maps. This relies on Wittstock’s result [16, Theorem 4.1] stating that, if A is a C*-subalgebra of B(H), then B(H) is \(\mathscr {M}^1_{A}\)-injective in  .
.
In the additive category  , of h-modules over A with completely bounded A-module maps, the class \({\mathscr {M}}^\infty _A\) of embeddings to consider are the completely bounded injective module maps with closed range and completely bounded inverse from the range. The corresponding \({\mathscr {M}}^\infty _A\)-injectives are less studied; however, there are some nice results of Frank and Paulsen on when A is \({\mathscr {M}}^\infty _A\)-injective as an h-module over itself [9].
, of h-modules over A with completely bounded A-module maps, the class \({\mathscr {M}}^\infty _A\) of embeddings to consider are the completely bounded injective module maps with closed range and completely bounded inverse from the range. The corresponding \({\mathscr {M}}^\infty _A\)-injectives are less studied; however, there are some nice results of Frank and Paulsen on when A is \({\mathscr {M}}^\infty _A\)-injective as an h-module over itself [9].
It is clear that every \(\mathscr {M}_A^1\)-injective object in  is also \(\mathscr {M}_A^\infty \)-injective. Thus the afore-mentioned CES-theorem yields the following.
is also \(\mathscr {M}_A^\infty \)-injective. Thus the afore-mentioned CES-theorem yields the following.
Proposition 3.5
Let A be a unital C*-algebra. The additive category  has enough \(\mathscr {M}_A^\infty \)-injectives.
has enough \(\mathscr {M}_A^\infty \)-injectives.
Proof
Let  . By a version of the Christensen–Effros–Sinclair representation theorem (see [2, Theorem 3.3.1, Lemma 3.3.5]), there exist a Hilbert space H, an injective unital *-homomorphism \({\pi }:{A}\rightarrow {B(H)}\), and a complete isometry \({\phi }:{E}\rightarrow {B(H)}\) such that \(\phi (x\cdot {a})=\phi (x)\pi (a)\) for all \(x\in E\), \(a\in A\). That is, \(\phi \) is a morphism in \(\mathscr {M_A^\infty }\) into the \(\mathscr {M_A^\infty }\)-injective object B(H). \(\square \)
. By a version of the Christensen–Effros–Sinclair representation theorem (see [2, Theorem 3.3.1, Lemma 3.3.5]), there exist a Hilbert space H, an injective unital *-homomorphism \({\pi }:{A}\rightarrow {B(H)}\), and a complete isometry \({\phi }:{E}\rightarrow {B(H)}\) such that \(\phi (x\cdot {a})=\phi (x)\pi (a)\) for all \(x\in E\), \(a\in A\). That is, \(\phi \) is a morphism in \(\mathscr {M_A^\infty }\) into the \(\mathscr {M_A^\infty }\)-injective object B(H). \(\square \)
Matrix normed modules are not necessarily representable; therefore we need a different device to ensure that there are enough injectives among them. This will be done in the next section.
4 Change of base
Restriction and extension of scalars for matrix normed modules turn out to form a pair of adjoint functors in the sense of diagram (2.1). We will use this to establish the existence of enough injectives in the appropriate module category.
In this section, we fix a unital *-homomorphism \({\pi }:{A}\rightarrow {B}\) between unital C*-algebras A and B. The category whose objects are the right matrix normed A-modules and whose morphisms are the completely bounded A-module maps will be denoted  There is also the similarly defined category of left matrix normed A-modules
There is also the similarly defined category of left matrix normed A-modules  . If
. If  , we denote the set of morphisms from E to F by \(C\!B_{A}({E},\,{F}),\) it is clear that this forms a closed subspace of \(C\!B({E},\,{F})\). For left matrix normed A-modules, we use the notation \({}_{A}C\!B({E},\,{F}).\) A matrix normed A-B-bimodule is an operator space that is both an object in
, we denote the set of morphisms from E to F by \(C\!B_{A}({E},\,{F}),\) it is clear that this forms a closed subspace of \(C\!B({E},\,{F})\). For left matrix normed A-modules, we use the notation \({}_{A}C\!B({E},\,{F}).\) A matrix normed A-B-bimodule is an operator space that is both an object in  and
and  with the associativity condition \(({a}\cdot {x})\cdot {b}=a\cdot (x\cdot {b}).\) The corresponding category is denoted by
with the associativity condition \(({a}\cdot {x})\cdot {b}=a\cdot (x\cdot {b}).\) The corresponding category is denoted by  and here the morphism sets are denoted by \({}_{A}{C\!B_{B}({E},\,{F})}.\) Thus
and here the morphism sets are denoted by \({}_{A}{C\!B_{B}({E},\,{F})}.\) Thus  via the left action of A given by \(a\cdot b=\pi (a)b\), \(a\in A\), \(b\in B\), and the canonical right action of B on itself.
via the left action of A given by \(a\cdot b=\pi (a)b\), \(a\in A\), \(b\in B\), and the canonical right action of B on itself.
Like in the theory of modules over rings, we make use of module tensor products. Our source for operator space module tensor products is [2, Section 3.4].
Definition 4.1
Let E and F be right and left A-modules, respectively. Suppose \({\phi }:{E\times {F}}\rightarrow {G}\) is a bilinear map, where G is a vector space. Then \(\phi \) is A-balanced if for \(x\in E, y\in F, a\in A,\) we have \(\phi (x\cdot {a},y)=\phi (x,{a}\cdot {y})\). Suppose  and
and  . The module operator space projective tensor product is the quotient of
. The module operator space projective tensor product is the quotient of  by the closure of the subspace spanned by \(\left\{ {(x\cdot {a})\otimes {y}-x\otimes (a\cdot {y})}\,|\,{x\in E, y\in F, a\in A} \right\} \). This is denoted by
by the closure of the subspace spanned by \(\left\{ {(x\cdot {a})\otimes {y}-x\otimes (a\cdot {y})}\,|\,{x\in E, y\in F, a\in A} \right\} \). This is denoted by  . We still use the notation \(x\otimes {y}\), now for the coset in
. We still use the notation \(x\otimes {y}\), now for the coset in  of the elementary tensor \(x\otimes {y}\).
of the elementary tensor \(x\otimes {y}\).
It is not difficult to show, via the universal property of the operator space projective tensor product described in Definition 3.2, that the above tensor product ‘linearises jointly completely bounded balanced bilinear maps’. That is, we have the following:
Proposition 4.2
Suppose  and
and  . Let
. Let  be the canonical jointly completely contractive bilinear mapping. Given an operator space G and a jointly completely contractive A-balanced bilinear map \({\phi }:{E\times {}F}\rightarrow {G},\) there exists a unique completely contractive linear map
be the canonical jointly completely contractive bilinear mapping. Given an operator space G and a jointly completely contractive A-balanced bilinear map \({\phi }:{E\times {}F}\rightarrow {G},\) there exists a unique completely contractive linear map  such that \(u=\psi \phi \).
such that \(u=\psi \phi \).
Suppose  and
and  . Then
. Then  via the module action \((x\otimes {y})\cdot {}b=x\otimes (y\cdot {b})\), and the closed subspace spanned by
via the module action \((x\otimes {y})\cdot {}b=x\otimes (y\cdot {b})\), and the closed subspace spanned by
is a submodule. Thus the quotient module  is a right matrix normed B-module (for details, see [2, paragraph 3.4.9]). In order to define the extension of scalars, we need the following property for the module operator space projective tensor product.
is a right matrix normed B-module (for details, see [2, paragraph 3.4.9]). In order to define the extension of scalars, we need the following property for the module operator space projective tensor product.
Lemma 4.3
([2, Lemma 3.4.5]). Let  and
and  . Suppose \(\phi \in C\!B_{A}({E_1},\,{E_2})\), \(\psi \in {}_{A}{C\!B_{B}({F_{1}},\,{F_2})}.\) Then \({\phi \otimes \psi }:{{E_1}\otimes _{{}}{F_1}}\rightarrow {{E_2}\otimes _{{}}{F_2}}\) extends uniquely to a completely bounded B-module map
. Suppose \(\phi \in C\!B_{A}({E_1},\,{E_2})\), \(\psi \in {}_{A}{C\!B_{B}({F_{1}},\,{F_2})}.\) Then \({\phi \otimes \psi }:{{E_1}\otimes _{{}}{F_1}}\rightarrow {{E_2}\otimes _{{}}{F_2}}\) extends uniquely to a completely bounded B-module map  , with \(\Vert \phi \otimes {\psi }\Vert _{cb }\le \Vert \phi \Vert _{cb }\Vert \psi \Vert _{cb }\).
, with \(\Vert \phi \otimes {\psi }\Vert _{cb }\le \Vert \phi \Vert _{cb }\Vert \psi \Vert _{cb }\).
Proposition 4.4
([2, Lemma 3.4.6]). Let A be a C*-algebra. Suppose  . Then there exists a completely isometric isomorphism
. Then there exists a completely isometric isomorphism  .
.
We shall now introduce the main concepts of this paper.
Definition 4.5
The extension of scalars from A to B is the covariant functor

where  is the extension as in Lemma 4.3 of the map \({\phi \otimes {id _{B}}}:{E\otimes {B}}\rightarrow {F\otimes {B}}\).
is the extension as in Lemma 4.3 of the map \({\phi \otimes {id _{B}}}:{E\otimes {B}}\rightarrow {F\otimes {B}}\).
Let  ; then we can consider E as a right matrix normed A-module when we define the module action \(x\cdot {a}=x\cdot \pi (a)\). We will write E with this module action as \(E_\pi .\) Note then that the module action \(E\times {B}\rightarrow E\) is a jointly completely contractive A-balanced map and so by Proposition 4.2, we have a canonical completely contractive map
; then we can consider E as a right matrix normed A-module when we define the module action \(x\cdot {a}=x\cdot \pi (a)\). We will write E with this module action as \(E_\pi .\) Note then that the module action \(E\times {B}\rightarrow E\) is a jointly completely contractive A-balanced map and so by Proposition 4.2, we have a canonical completely contractive map  .
.
Definition 4.6
The covariant functor

is called the restriction of scalars from B to A.
That the extension and restriction of scalars are, in fact, functors is routinely checked. We aim to make use of a matrix normed module version of Proposition 3.3 involving the module operator space projective tensor product and use that for the change of base.
Proposition 4.7
Let A and B be unital C*-algebras. Suppose that  and
and  . Then
. Then  .
.
Proof
The canonical identifications \(M_n(C\!B_{B}({E},\,{F}))\cong C\!B_{B}({E},\,{M_n(F)})\) yield the operator space structure. For each \(a\in A,\) \(f\in C\!B_{B}({E},\,{F})\), define \((f\cdot {a})(x)=f(a\cdot {x})\). When \(n\in \mathbb {N}\) and \(x\in M_n(E)\), we have \(\Vert (f\cdot {a})_{n}(x)\Vert =\Vert f_n(a[x_{i j}])\Vert \le \Vert f\Vert _{cb }\Vert a\Vert \Vert x\Vert \). So \(f\cdot {a}\) is completely bounded. Also it is clear that when \(b\in B,\) \((f\cdot {a})(x\cdot {b})=f(a\cdot (x\cdot {b}))=f(a\cdot {x})\cdot {b}\), so \(f\cdot {a}\) is a B-module map. We have shown that \(C\!B_{B}({E},\,{F})\) is a Banach right A-module.
Suppose \(f=[f_{i j}]\in M_n(C\!B_{B}({E},\,{F}))\) and \(a=[a_{k l}]\in M_m(A)\) for some \(n,m\in \mathbb {N}\). We are done if we show \(\Vert ([f_{i j}\cdot {a_{k l}}])_{t}\Vert \le \Vert f\Vert \Vert a\Vert \) for all \(t\in \mathbb {N}.\) Let \(x=[x_{p q}]\in M_{t}\), then
Before we arrive at our main result, we record the following.
Lemma 4.8
Suppose  . There exists a completely isometric A-module isomorphism \({\omega }:{F_\pi }\rightarrow {C\!B_{B}({B},\,{F})}\).
. There exists a completely isometric A-module isomorphism \({\omega }:{F_\pi }\rightarrow {C\!B_{B}({B},\,{F})}\).
Proof
Considering the C*-algebra B as a matrix normed A-B-bimodule as above, by Proposition 4.7,  . For each \(y\in F\), define \(\omega (y)(b)\) to be \(y\cdot {b}\) for all \(b\in B\). Then \({\omega }:{F}\rightarrow {C\!B_{B}({B},\,{F})}\) is a completely isometric surjective linear map ([2, Lemma 3.5.4]) and an A-module map. Indeed, if \(a\in A, y\in F\), we have that, for each \(b\in B\),
. For each \(y\in F\), define \(\omega (y)(b)\) to be \(y\cdot {b}\) for all \(b\in B\). Then \({\omega }:{F}\rightarrow {C\!B_{B}({B},\,{F})}\) is a completely isometric surjective linear map ([2, Lemma 3.5.4]) and an A-module map. Indeed, if \(a\in A, y\in F\), we have that, for each \(b\in B\),
That is, \(\omega (y\cdot {a})=\omega (y)\cdot {a}\). \(\square \)
The following theorem, the first part of which appears in [2, Proposition 3.5.9], is the main result of this paper. We will use the notation introduced in Section 2.
Theorem 4.9
Let A and B be unital C*-algebras.
-
(i)
For each
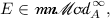
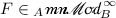 , and
, and 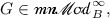 there is a completely isometric isomorphism
there is a completely isometric isomorphism 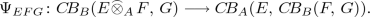
-
(ii)
Moreover, if
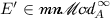 and
and 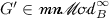 with \(\phi \in C\!B_{A}({E},\,{E'})\) and \(\psi \in C\!B_{B}({G},\,{G'})\), we have the following commutative diagram of operator spaces and completely bounded linear maps.
with \(\phi \in C\!B_{A}({E},\,{E'})\) and \(\psi \in C\!B_{B}({G},\,{G'})\), we have the following commutative diagram of operator spaces and completely bounded linear maps. 
-
(iii)
Suppose \(\pi :A\rightarrow B\) is a unital *-homomorphism. Let
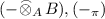 be the extension of scalars from A to B and \((-_{\pi })\) be the restriction of scalars from B to A. Then
be the extension of scalars from A to B and \((-_{\pi })\) be the restriction of scalars from B to A. Then 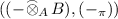 is an adjoint pair.
is an adjoint pair.
Proof
-
(i)
: Let q denote the canonical complete quotient map
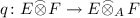 . Then we have the following complete isometry
. Then we have the following complete isometry 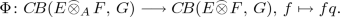
Moreover, by Proposition 3.3, there exists a completely isometric isomorphism

Let \(\Psi \) denote \(\Theta \Phi .\) Let \(\Psi _{EFG}\) be \(\Psi \) restricted to
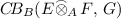 . We show that \(\Psi _{EFG}\) is the desired isometric isomorphism. If
. We show that \(\Psi _{EFG}\) is the desired isometric isomorphism. If 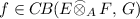 , we have $$\begin{aligned} (\Psi ({f})(x))(y)={f}(x\otimes y) \end{aligned}$$
, we have $$\begin{aligned} (\Psi ({f})(x))(y)={f}(x\otimes y) \end{aligned}$$for each \(x\in ~\!E, y\in ~\!F.\) Hence, if f is a B-module map, then \(\Psi ({f})(x)\) is a B-module map and so \(\Psi ({f})\in C\!B_{A}({E},\,{C\!B_{B}({F},\,{G})})\). So \(\Psi _{EFG}\) is a complete isometry
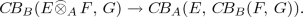
To prove the first statement of the theorem, all that remains is to show that \(\Psi _{EFG}\) is surjective. Suppose \(\kappa \in C\!B_{A}({E},\,{C\!B_{B}({F},\,{G})})\). Then \(\kappa \in C\!B({E},\,{C\!B({F},\,{G})})\) and so there exists, by Proposition 3.3, a map
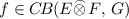 such that \({f}(x\otimes y)=\kappa (x)(y)\) for each \(x\in E, y\in F.\) Then, for each \(a\in A,\) we also have $$\begin{aligned} {f}(x\cdot {a}\otimes {y})=\kappa (x\cdot {}a)(y)=(\kappa (x)\cdot {}{a})(y) =\kappa (x)(a\cdot {}y)={f}(x\otimes {a}\cdot {}{y}). \end{aligned}$$
such that \({f}(x\otimes y)=\kappa (x)(y)\) for each \(x\in E, y\in F.\) Then, for each \(a\in A,\) we also have $$\begin{aligned} {f}(x\cdot {a}\otimes {y})=\kappa (x\cdot {}a)(y)=(\kappa (x)\cdot {}{a})(y) =\kappa (x)(a\cdot {}y)={f}(x\otimes {a}\cdot {}{y}). \end{aligned}$$Therefore, by the universal property of the module operator space projective tensor product, there exists
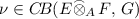 such that \(\nu {q}={f}\). Then \(\Psi (\nu )=\kappa \) and it is easy to check that \(\nu \) is a B-module map as required.
such that \(\nu {q}={f}\). Then \(\Psi (\nu )=\kappa \) and it is easy to check that \(\nu \) is a B-module map as required. -
(ii)
: We now show commutativity of the diagram. Let
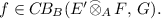 For each \(x\in E, y\in F\), we have $$\begin{aligned} \begin{aligned} \phi ^*(\Psi _{E'FG}(f))(x)(y)&= \Psi _{E'FG}(f)(\phi (x))(y) =f(\phi (x)\otimes {y}) \\&=f(\phi \otimes id _{F}(x\otimes {y})) = (\phi \otimes {id _{F}})^*(f)(x\otimes {y}) \\&=\Psi _{EFG}((\phi \otimes {id _{F}})^*(f))(x)(y). \end{aligned} \end{aligned}$$
For each \(x\in E, y\in F\), we have $$\begin{aligned} \begin{aligned} \phi ^*(\Psi _{E'FG}(f))(x)(y)&= \Psi _{E'FG}(f)(\phi (x))(y) =f(\phi (x)\otimes {y}) \\&=f(\phi \otimes id _{F}(x\otimes {y})) = (\phi \otimes {id _{F}})^*(f)(x\otimes {y}) \\&=\Psi _{EFG}((\phi \otimes {id _{F}})^*(f))(x)(y). \end{aligned} \end{aligned}$$Let
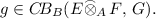 For each \(x\in E, y\in F\), we have $$\begin{aligned} \begin{aligned} \psi _*(\Psi _{EFG}(g))(x)(y)&=\psi {g}(x\otimes {y})=\psi {g}(x\otimes {y}) \\&=\Psi _{EFG'}(\psi {g})(x)(y)=\Psi _{EFG'}(\psi _*(g))(x)(y). \end{aligned} \end{aligned}$$
For each \(x\in E, y\in F\), we have $$\begin{aligned} \begin{aligned} \psi _*(\Psi _{EFG}(g))(x)(y)&=\psi {g}(x\otimes {y})=\psi {g}(x\otimes {y}) \\&=\Psi _{EFG'}(\psi {g})(x)(y)=\Psi _{EFG'}(\psi _*(g))(x)(y). \end{aligned} \end{aligned}$$ -
(iii)
: Statements (i) and (ii) show that the tensor product functor
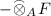 and the hom-functor \({C\!B_{B}({{F}},\,{-})}\) form an adjoint pair between the categories
and the hom-functor \({C\!B_{B}({{F}},\,{-})}\) form an adjoint pair between the categories 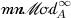 and
and 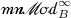 . Specialising to \(F=B\) and applying Lemma 4.8, we thus obtain, for each
. Specialising to \(F=B\) and applying Lemma 4.8, we thus obtain, for each 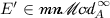 and
and 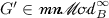 with \(\phi \in C\!B_{A}({E},\,{E'})\) and \(\psi \in C\!B_{B}({G},\,{G'})\), the following commutative diagram of operator spaces and bounded linear maps
with \(\phi \in C\!B_{A}({E},\,{E'})\) and \(\psi \in C\!B_{B}({G},\,{G'})\), the following commutative diagram of operator spaces and bounded linear maps 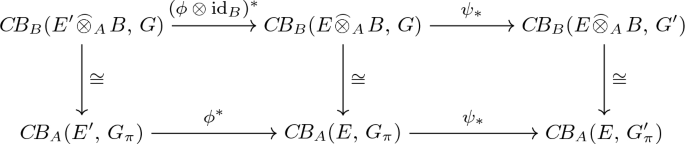
as required. \(\square \)
Remark 4.10
The only connection between the C*-algebras A and B that we require in parts (i) and (ii) is that there exists some  .
.
When we specialise the above to the canonical embedding \({\mathbb {C}}\hookrightarrow B\), where B is a unital C*-algebra, the restriction of scalars becomes the forgetful functor  and the extension of scalars the functor
and the extension of scalars the functor  .
.
On the other hand, noting that  and
and  are isomorphic categories, we can take \(F=A\) in Theorem 4.9, part (i), and \(B={\mathbb {C}}\). Combining this with Propositions 4.4 and 4.7, we obtain, for every
are isomorphic categories, we can take \(F=A\) in Theorem 4.9, part (i), and \(B={\mathbb {C}}\). Combining this with Propositions 4.4 and 4.7, we obtain, for every  and every operator space G, the following chain of isometric isomorphisms
and every operator space G, the following chain of isometric isomorphisms

We apply this to prove the existence of enough injectives in the category of matrix normed modules. Recall, from Section 3, that \({\mathscr {M}}^\infty \) denotes the class of all (not necessarily surjective) completely bounded isomorphisms and \({\mathscr {M}}^\infty _A\) the subclass of those which are A-module maps.
Corollary 4.11
Let A be a unital C*-algebra and I be an \({\mathscr {M}}^\infty \)-injective object in  . Then \(C\!B({A},\,{I})\) with matrix normed right A-module structure as in Proposition 4.7 is an \({\mathscr {M}}^\infty _A\)-injective object in
. Then \(C\!B({A},\,{I})\) with matrix normed right A-module structure as in Proposition 4.7 is an \({\mathscr {M}}^\infty _A\)-injective object in  .
.
Proof
Let \(\mu \in {\mathscr {M}}^\infty _A(E,F)\) be an embedding of  into
into  . Suppose \(f\in C\!B_{A}({E},\,{C\!B({A},\,{I})})\). By (4.2) above, f corresponds to a unique \(g\in C\!B({E},\,{I})\) with \(\Vert f\Vert _{cb }=\Vert g\Vert _{cb }\) such that \(f(x)(a)=g(x\cdot a)\) for \(x\in E\), \(a\in A\). As I is injective and \(\mu \in {\mathscr {M}}^\infty (E,F)\), there exists \(\tilde{g}\in C\!B({F},\,{I})\) such that \(g=\tilde{g}\,\mu \). Setting \(\tilde{f}(y)(a)=\tilde{g}(y\cdot a)\), \(y\in F\), \(a\in A\), we get the extension as an A-module map from F into \(C\!B({A},\,{I})\) of f as desired. \(\square \)
. Suppose \(f\in C\!B_{A}({E},\,{C\!B({A},\,{I})})\). By (4.2) above, f corresponds to a unique \(g\in C\!B({E},\,{I})\) with \(\Vert f\Vert _{cb }=\Vert g\Vert _{cb }\) such that \(f(x)(a)=g(x\cdot a)\) for \(x\in E\), \(a\in A\). As I is injective and \(\mu \in {\mathscr {M}}^\infty (E,F)\), there exists \(\tilde{g}\in C\!B({F},\,{I})\) such that \(g=\tilde{g}\,\mu \). Setting \(\tilde{f}(y)(a)=\tilde{g}(y\cdot a)\), \(y\in F\), \(a\in A\), we get the extension as an A-module map from F into \(C\!B({A},\,{I})\) of f as desired. \(\square \)
Remark 4.12
Suppose I is an \({\mathscr {M}}^1\)-injective object in  (what is usually called an ‘injective operator space’). Then an extension of \(g\in C\!B({E},\,{I})\) can be found such that the cb-norm of g is preserved, provided \(\mu \) is completely isometric. In this case, \(\Vert \tilde{f}\Vert _{cb }=\Vert \tilde{g}\Vert _{cb }=\Vert g\Vert _{cb }=\Vert f\Vert _{cb }\) so that \(C\!B({A},\,{I})\) is \({\mathscr {M}}^1\)-injective in
(what is usually called an ‘injective operator space’). Then an extension of \(g\in C\!B({E},\,{I})\) can be found such that the cb-norm of g is preserved, provided \(\mu \) is completely isometric. In this case, \(\Vert \tilde{f}\Vert _{cb }=\Vert \tilde{g}\Vert _{cb }=\Vert g\Vert _{cb }=\Vert f\Vert _{cb }\) so that \(C\!B({A},\,{I})\) is \({\mathscr {M}}^1\)-injective in  .
.
Proposition 4.13
Let A be a unital C*-algebra. Then every matrix normed right A-module can be completely isometrically embedded into an injective one. In particular,  has enough injectives.
has enough injectives.
Proof
Let  . There exists a Hilbert space H such that E inherits its operator space structure as a closed subspace of B(H). As B(H) is injective in
. There exists a Hilbert space H such that E inherits its operator space structure as a closed subspace of B(H). As B(H) is injective in  , \(C\!B({A},\,{B(H)})\) is injective in
, \(C\!B({A},\,{B(H)})\) is injective in  by Corollary 4.11. By Lemma 4.8 (with \(B=A\)), we have the following
by Corollary 4.11. By Lemma 4.8 (with \(B=A\)), we have the following
where the isomorphism is in  and the inclusions are completely isometric embeddings in
and the inclusions are completely isometric embeddings in  . \(\square \)
. \(\square \)
References
Ara, P., Mathieu. M.: Sheaf cohomology for \({C}^{*}\)-algebras. In preparation
Blecher, D.P., Le Merdy, C.: Operator Algebras and Their Modules: An Operator Space Approach. London Mathematical Society Monographs, vol. 30. New Series. The Clarendon Press, Oxford University Press, Oxford (2004)
Blecher, D.P., Paulsen, V.: Tensor products of operator spaces. J. Funct. Anal. 99(2), 262–292 (1991)
Blecher, D.P., Paulsen, V.: Multipliers of operator spaces, and the injective envelope. Pac. J. Math. 200(1), 1–17 (2001)
Bühler, T.: Exact categories. Expo. Math. 28(1), 1–69 (2010)
Bühler, T.: On the algebraic foundations of bounded cohomology. Mem. Amer. Math. Soc., 214(1006), xxii+97 pp. (2011)
Effros, E.G., Ruan, Z.-J.: A new approach to operator spaces. Canad. Math. Bull. 34(3), 329–337 (1991)
Effros, E.G., Ruan, Z.-J.: Operator Spaces. London Mathematical Society Monographs, vol. 23. New Series. The Clarendon Press, Oxford University Press, New York (2000)
Frank, M., Paulsen, V.: Injective envelopes of C*-algebras as operator modules. Pac. J. Math. 212(1), 57–69 (2003)
Helemskii, A.Y.: The Homology of Banach and Topological Algebras. Translated from the Russian by Alan West. Mathematics and its Applications (Soviet Series), vol. 41. Kluwer Academic Publishers Group, Dordrecht (1989)
Helemskii, A.Y.: Projective modules in classical and quantum functional analysis. J. Math. Sci. 159(5), 600–652 (2009)
Mac Lane, S.: Categories for the Working Mathematician. Graduate Texts in Mathematics, vol. 5, 2nd edn. Springer, New York (1998)
Mathieu, M.: Towards a sheaf cohomology theory for C*-algebras. In: Banach algebras and their applications: Proceedings of the International Conference held at the University of Oulu, July 3–11: De Gruyter Proceedings in Mathematics, p. 2019. De Gruyter, Berlin (2017)
Paulsen, V.I.: Relative Yoneda cohomology for operator spaces. J. Funct. Anal. 157(2), 358–393 (1998)
Rosbotham, M.: Cohomological dimensions for \(C^{*}\)-algebras. PhD thesis, Queen’s University Belfast, Belfast (2020)
Wittstock, G.: Extension of completely bounded \(C^{*}\)-module homomorphisms. In: Operator Algebras and Group Representations, vol. II, (Neptun, 1980), pp. 238–250, Monogr. Stud. Math., vol. 18. Pitman, Boston, MA (1984)
Wood, P.: Homological algebra in operator spaces with applications to harmonic analysis. PhD thesis, University of Waterloo (Canada) (1999)
Acknowledgements
The work presented here forms part of the author’s PhD project under the supervision of Dr. Martin Mathieu.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rosbotham, M. Change of base for operator space modules. Arch. Math. 116, 67–78 (2021). https://doi.org/10.1007/s00013-020-01525-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00013-020-01525-5
Keywords
- Operator space modules
- C*-algebras
- Restriction of scalars
- Extension of scalars
- Change of base
- Enough injectives



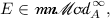
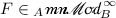 , and
, and 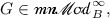 there is a completely isometric isomorphism
there is a completely isometric isomorphism 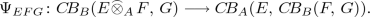
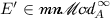 and
and 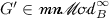 with
with 
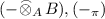 be the extension of scalars from A to B and
be the extension of scalars from A to B and 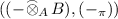 is an adjoint pair.
is an adjoint pair.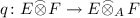 . Then we have the following complete isometry
. Then we have the following complete isometry 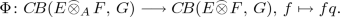

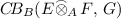 . We show that
. We show that 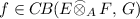 , we have
, we have 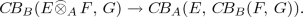
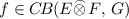 such that
such that 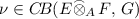 such that
such that 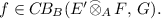 For each
For each 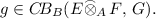 For each
For each 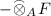 and the hom-functor
and the hom-functor 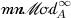 and
and 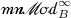 . Specialising to
. Specialising to 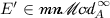 and
and 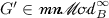 with
with