Abstract
We consider S-operations \(f :A^{n} \rightarrow A\) in which each argument is assigned a signum \(s \in S\) representing a “property” such as being order-preserving or order-reversing with respect to a fixed partial order on A. The set S of such properties is assumed to have a monoid structure reflecting the behaviour of these properties under the composition of S-operations (e.g., order-reversing composed with order-reversing is order-preserving). The collection of all S-operations with prescribed properties for their signed arguments is not a clone (since it is not closed under arbitrary identification of arguments), but it is a preclone with special properties, which leads to the notion of S-preclone. We introduce S-relations \(\varrho = (\varrho _{s})_{s \in S}\), S-relational clones, and a preservation property ( ), and we consider the induced Galois connection \({}^{S}{}\textrm{Pol}\)–\({}^{S}{}\textrm{Inv}\). The S-preclones and S-relational clones turn out to be exactly the closed sets of this Galois connection. We also establish some basic facts about the structure of the lattice of all S-preclones on A.
), and we consider the induced Galois connection \({}^{S}{}\textrm{Pol}\)–\({}^{S}{}\textrm{Inv}\). The S-preclones and S-relational clones turn out to be exactly the closed sets of this Galois connection. We also establish some basic facts about the structure of the lattice of all S-preclones on A.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Clones of operations have been studied since the seminal publication by Emil Post [16] (announced in [15], in full detail in [17]) and are fundamental algebraic objects in universal algebra. They have been generalized to Lawvere theories and preclones (i.e., operads), and investigations into the lattice of clones on a finite set have been greatly illuminated by the Pol–Inv Galois connection between clones and relational clones. The collection of all order-preserving operations on a poset form a clone, and theories of ordered algebras are classified by subclones of this type. In algebraic logic, formulas (i.e., elements of the algebras) are ordered by a consequence relation, and logical operations such as negation and implication are not order-preserving in all arguments. They are however order-preserving or order-reversing in each argument. The collection of all such operations on a nontrivial poset (our “motivating example” presented in more detail as Example 2.5) is not a clone since it is not closed under arbitrary identification of arguments, but it is a preclone.
In this paper we study a generalization of such preclones, so-called S-preclones. On one hand they provide a classification of the generating sets of operations for partially ordered algebras. But on the other hand these new algebraic structures of S-preclones are applicable to situations where the arguments of an operation should have different “properties” \(s\in S\) “expressible” by relations (like order-preserving and order-reversing via partial order relations). The set S of “properties” (called signa) itself has an algebraic structure which reflects composition of operations, i.e., we need S to be a monoid (e.g. order-reversing composed with order-reversing gives order-preserving, thus S is a two-element group for our motivating example, see Example 2.5). A universal algebraic perspective on partially ordered algebras can be found in [11].
Our results in the current paper (Part I) are about preclones of S-operations on a finite base set A. In a subsequent paper (Part II) we consider in detail the case of Boolean S-preclones, where A is a 2-element set.
In Section 2 we introduce the basic notions of an S-operation, S-preclone, S-relation and S-relational clone which generalize the classical notions in a natural way. In Section 3 the Galois connection \({}^{S}{}\textrm{Pol}\)–\({}^{S}{}\textrm{Inv}\) induced by the crucial property “S-operation S-preserves S-relation”,  , is defined. It is shown that the Galois closed sets of S-operations form an S-preclone and likewise the Galois closed sets of S-relations form an S-relational clone.
, is defined. It is shown that the Galois closed sets of S-operations form an S-preclone and likewise the Galois closed sets of S-relations form an S-relational clone.
Section 4 contains the central result that for a finite set A and a set F of S-operations on A, the set \({}^{S}{}\textrm{Pol}\,{}^{S}{}\textrm{Inv}\,F\) is the smallest S-preclone containing F, hence all S-preclones are Galois closed (Theorem 4.1). On the relational side the corresponding result holds (Theorem 4.6): for a set Q of S-relations, \({}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Pol}\,Q\) is the smallest S-relational clone containing Q, i.e., the Galois closures are exactly the S-relational clones.
Section 5 contains results about the lattice of all S-preclones on a fixed (finite) set A. It is shown that this lattice is atomic and coatomic, with finitely many atoms and coatoms. Several symmetries of the lattice, including some that are determined by automorphisms of the monoid S, are established, and it is proved that the clone lattice on A is embeddable in the lattice of S-preclones in several ways. We conclude in Section 6 with some open problems and a brief preview of the results that are contained in Part II.
2 \(\varvec{S}\)-preclones and \(\varvec{S}\)-relational clones for a monoid \(\varvec{S}\)
Definition 2.1
(Operations). Recall that an operation on a set A is a mapping \(f :A^n \rightarrow A\) for some \(n \in \mathbb {N}_{+}:=\{1,2,\dots \}\). The number n (notation \({{\,\textrm{ar}\,}}(f)\)) is called the arity of f. Denote by \({{\,\textrm{Op}\,}}^{(n)}(A)\) the set of all n-ary operations on A, and let \({{\,\textrm{Op}\,}}(A):= \bigcup _{n \in \mathbb {N}_{+}} {{\,\textrm{Op}\,}}^{(n)}(A)\).
The i-th n-ary projection is the operation \(p_i^{(n)} \in {{\,\textrm{Op}\,}}^{(n)}(A)\) given by the rule \(p_i^{(n)}(a_1, \dots , a_n):= a_i\) for all \((a_1, \dots , a_n) \in A^n\).
Definition 2.2
(S-operations). Assume that S is a fixed monoid with unit element e. Denote by \({}^{S}{}\textrm{Op}^{(n)}(A)\) the set of all n-ary operations \(f :A^n \rightarrow A\) where each argument has a label \(s \in S\). Such operations are called S-signed operations, or S-operations for short. Let \({}^{S}{}\textrm{Op}(A):= \bigcup _{n \in \mathbb {N}_{+}} {}^{S}{}\textrm{Op}^{(n)}(A)\).
The labels are given by the signum \({{\,\textrm{sgn}\,}}(f)\) which is an n-tuple \(\lambda = (s_{1}, \dots , s_{n}) \in S^{n}\) assigning \(s_{i} \in S\) to the i-th argument of f (\(i \in \{1, \dots , n\}\)). We also say, that \(s_{i}\) is the signum of the i -th argument of f. For \({{\,\textrm{sgn}\,}}(f) = (s_{1}, \dots , s_{n})\), let \({{\,\textrm{Sgn}\,}}(f):= \{s_{1}, \dots , s_{n}\}\) be the set of components of \({{\,\textrm{sgn}\,}}(f)\).
We write \(f^{\lambda }\) if we want to indicate that \(f \in {}^{S}{}\textrm{Op}(A)\) has signum \(\lambda \); furthermore, for \(f \in {{\,\textrm{Op}\,}}^{(n)}(A)\) and \(\lambda = (s_{1}, \dots , s_{n})\) we denote by \(f^{\lambda }\) the same function in \({}^{S}{}\textrm{Op}(A)\) equipped with signum \(\lambda \). For unary functions \(f \in {}^{S}{}\textrm{Op}^{(1)}(A)\) with \({{\,\textrm{sgn}\,}}(f) = (s)\) we also write \(f^{s}\) (instead of \(f^{(s)}\)). Sometimes it is useful to have an explicit notation for the underlying function of some \(f = f^{\lambda }\in {}^{S}{}\textrm{Op}(A)\) that is obtained by just ignoring the signum \(\lambda ={{\,\textrm{sgn}\,}}(f)\). Then we shall write \(\mathring{f}\) (or \(f\,\mathring{}\,\)); thus, \(f = (\mathring{f})^{\lambda }\) for \(f \in {}^{S}{}\textrm{Op}(A)\) and \((f^{\lambda })\,\mathring{} = f\) for \(f \in {{\,\textrm{Op}\,}}(A)\).
Definition 2.3
(S-preclones). A set \(F \subseteq {}^{S}{}\textrm{Op}(A)\) is called an S -preclone if it contains \(\textsf{id}_{A}\) and is closed under the operations \(\zeta \), \(\tau \), \(\nabla ^s\), \(\Delta \), \(\circ \) that are defined as follows. Let \(f, g \in {}^{S}{}\textrm{Op}(A)\) with \({{\,\textrm{sgn}\,}}(f) = (s_1, \dots , s_n) \in S^n\) and \({{\,\textrm{sgn}\,}}(g) = (s'_1, \dots , s'_m)\), and let \(s \in S\). Then
-
(1)
\({{\,\textrm{sgn}\,}}(\textsf{id}_A) = (e)\) (e is the neutral element of S) and
$$\begin{aligned} \textsf{id}_A(x):=x\quad \text {(}identity\, operation \text {);} \end{aligned}$$ -
(2)
if \(n \ge 2\) then \({{\,\textrm{sgn}\,}}(\zeta f) = (s_n, s_1, \dots , s_{n-1})\) and
$$ (\zeta f)(x_{1}, x_{2}, \dots , x_{n}):= f(x_{2}, \dots , x_{n}, x_{1}) \quad \text {(}cyclic\, shift \text {);} $$if \(n = 1\) then \(\zeta f:= f\),
-
(3)
if \(n \ge 2\) then \({{\,\textrm{sgn}\,}}(\tau f) = (s_2, s_1, s_3, \dots , s_n)\) and
$$\begin{aligned}&(\tau f)(x_{1}, x_{2}, x_{3}, \dots , x_{n}) := f(x_{2}, x_{1}, x_{3}, \dots , x_{n}) \\&\text {(}permuting\, the\, first\, two\, arguments \text {);} \end{aligned}$$if \(n = 1\) then \(\tau f:= f\),
-
(4)
for \(s \in S\), \({{\,\textrm{sgn}\,}}(\nabla ^s f) = (s, s_1, \dots , s_n)\) and
$$\begin{aligned}&(\nabla ^s f)(x_{1}, x_{2}, \dots , x_{n+1}) := f(x_{2}, \dots , x_{n+1}) \\&\text {(}adding\, a\, fictitious\, argument\, with\, signum \,s\text { at the first place),} \end{aligned}$$ -
(5)
if \(n \ge 2\) and \(s_{1} = s_{2} = s\), then \({{\,\textrm{sgn}\,}}(\Delta f) = (s, s_3, \dots , s_n)\) and
$$ (\Delta f)(x_{1}, x_{2}, \dots , x_{n-1}):= f(x_{1}, x_{1}, x_{2}, \dots , x_{n-1}), $$(identification of the first two arguments, if these have the same signum s); otherwise \(\Delta f:= f\),
-
(6)
\({{\,\textrm{sgn}\,}}(f \circ g)=(s'_1 s_1, \dots , s'_m s_1, s_2, \dots , s_n)\) and
$$\begin{aligned} (f \circ g)&(x_{1},\dots , x_{m},x_{m+1}, \dots , x_{m+n-1}) \\&:= f(g(x_{1}, \dots , x_{m}), x_{m+1}, \dots , x_{m+n-1}) \qquad \text {(}composition \text {).} \end{aligned}$$
For \(F \subseteq {}^{S}{}\textrm{Op}(A)\) the S-preclone generated by F (i.e., the least S-preclone containing F) is denoted by \({}^{S}{}\!\langle F \rangle _{}\) or \({}^{S}{}\!\langle F \rangle _{A}\).
Remark 2.4
(A) With iterated applications of the basic operations of Definition 2.3, we can obtain further operations on S-operations, such as arbitrary permutations of arguments and respective signa, adding a fictitious argument of signum s at an arbitrary position, identification of arguments at positions i and j if they have the same signum, or composing f with g in the i-th position. We can also get arbitrary compositions of the form
where f is n-ary and \(g_i\) is \(m_i\)-ary for \(i \in \{1, \dots , n\}\), and the signum of the composition is determined analogously to Definition 2.3(6).
(B) By adding fictitious arguments and permuting arguments, we obtain from \(\textsf{id}_{A}\) every S-operation of the form \((p_i^{(n)})^\lambda \), where \(\lambda = (s_1, \dots , s_n) \in S^n\) with \(s_i = e\). We call such S-operations trivial S -operations or (trivial) projections. All other S-operations are nontrivial (in particular, there also exist nontrivial projections where the essential argument has signum \(s_{i}\ne e\), e.g., the operations \(\textsf{id}^{s}:=\textsf{id}_{A}^{s}:=\textsf{id}_{A}^{\lambda }\) with \(\lambda =(s)\), \(s\in S{\setminus }\{e\}\)). The trivial S-operations form an S-preclone, denoted by \({}^{S}{}\!\!J_{A}\), which is the least S-preclone and is contained in every S-preclone.
(C) In the special case when S is the trivial monoid \(\{e\}\), the labels of arguments play no essential role, and hence this case clearly corresponds to usual unsigned operations. In this case, the notion of S-preclone essentially agrees with the notion of clone. For \(F \subseteq {{\,\textrm{Op}\,}}(A)\), we denote by \(\langle F \rangle _{}\) or \(\langle F \rangle _{A}\) the clone generated by F, i.e., the smallest clone containing F.
(D) S-preclones are special preclones, also known as operads, which can be thought of as “clones where identification of arguments is not allowed” (more precisely, they contain \(\textsf{id}_{A}\) and are closed under \(\zeta \), \(\tau \), and \(\circ \) (see Definition 2.3(2), (3) and 6), ignoring all signa). The term preclone was introduced by Ésik and Weil [4] in a study of the syntactic properties of recognizable sets of trees. A general characterization of preclones as Galois closures via so-called matrix collections can be found in [6]. The notion of operad originates from the work in algebraic topology by May [10] and Boardman and Vogt [1]. For general background and basic properties of operads, we refer the reader to the survey article by Markl [9].
Example 2.5
(“motivating example”). Let \((A,\le )\) be a poset. We consider operations \(f\in {{\,\textrm{Op}\,}}^{(n)}(A)\) (\(n\in \mathbb {N}_{+}\)) such that f in each argument is either order-preserving (then the argument gets signum \(+\)) or order-reversing (signum −), respectively, i.e., for constants \(c_{j}\) (\(j\in \{1,\dots ,n\}{\setminus }\{i\}\)) and \(x_{i},y_{i}\in A\) (\(i\in \{1,\dots ,n\}\)) we have \(f(c_{1},\dots ,x_{i},\dots ,c_{n})\le f(c_{1},\dots ,y_{i},\dots ,c_{n})\) whenever \(x_{i}\le y_{i}\) or \(x_{i}\ge y_{i}\), respectively. All these operations can be seen as S-operations and form an S-preclone F where \(S:= \{\mathord {+}, \mathord {-}\}\) is understood as a (multiplicative) group (isomorphic to the 2-element group \(\{+1,-1\}\)) with unit element \(+\). E.g., if \({{\,\textrm{sgn}\,}}(f)=(\mathord {-},\mathord {+})\) and \({{\,\textrm{sgn}\,}}(g)=(\mathord {+},\mathord {-})\), then \((f \circ g)(x_{1},x_{2},x_{3})=f(g(x_{1},x_{2}),x_{3})\) has signum \((\mathord {+} \cdot \mathord {-}, \mathord {-} \cdot \mathord {-}, \mathord {+}) = (\mathord {-}, \mathord {+}, \mathord {+})\) according to 2.3(6), which coincides with the intuition for composition.
We give two further examples in a more formalized form.
Example 2.6
Let \(S':=\{\mathord {+}, o\}\) be the 2-element monoid with zero o and let \(\widehat{S} = \{\mathord {+}, \mathord {-}, o\}\) be the monoid obtained from the group S from Example 2.5 by adding a zero, i.e., we have the multiplication tables
Let \(\le \) be a partial order on A. Let \(F'\subseteq {}^{{S^\prime }}{}\textrm{Op}(A)\) and \(\widehat{F}\subseteq {}^{\widehat{S}}{}\textrm{Op}(A)\) be the set of all \(S'\)- or \(\widehat{S}\)-operations, respectively, such that each argument with signum \(s\in \{\mathord {+}, \mathord {-}, o\}\) has the property as given in the following table:

(the property for o is equivalent to order-preserving and order-reversing). Then \(F'\) as well as \(\widehat{F}\) are S-preclones for \(S=S'\) and \(S=\widehat{S}\), respectively.
Here, for a property P for unary functions \(g\in A^{A}\), we define that an n-ary operation \(f(x_{1},\dots ,x_{n})\) has property P in an argument, say in \(x_{i}\) (\(i\in \{1,\dots ,n\}\)), if each translation \(x_{i}\mapsto f(c_{1},\dots ,x_{i},\dots ,c_{n})\) (\(x_{i}\) on the i-th place) has this property P (with \(c_{1},\dots ,c_{i-1},c_{i+1},\dots ,c_{n}\in A\)).
Note that also Example 2.5 fits into this scheme: the arguments of the S-operations in the S-preclone F (cf. Example 2.5) have the property order-preserving if they have signum \(+\), otherwise (signum −) they have the property order-reversing.
Definition 2.7
(Relations). Let \(m\in \mathbb {N}_{+}\). Recall that subsets of \(A^m\) are called m-ary relations on A. Since \(\emptyset \subseteq A^{m}\), the empty set can be considered as m-ary for arbitrary m. Sometimes it is convenient to write formally \(\emptyset ^{(m)}\) if \(\emptyset \) is considered as an m-ary relation. Denote by \({{\,\textrm{Rel}\,}}^{(m)}(A)\) the set of all m-ary relations on A, and let \({{\,\textrm{Rel}\,}}(A):= \bigcup _{m \in \mathbb {N}_{+}} {{\,\textrm{Rel}\,}}^{(m)}(A)\).
It is often useful to think of an m-ary relation \(\varrho \) as an \(m \times |\varrho |\) matrix whose columns are the tuples belonging to \(\varrho \). Keeping this point of view in mind, we will often regard a tuple belonging to a relation as a column, and we will refer to its components as rows. We are shortly going to consider certain operations on relations, and it will be helpful to (informally) describe them in terms of simple manipulations of rows of matrices.
We briefly recall the “elementary operations” \(\zeta \), \(\tau \), \({{\,\textrm{pr}\,}}\), \(\times \) and \(\wedge \) on relations (see, e.g., Lau [5, Section II.2.3]). Let \(\sigma \) and \(\sigma '\) be m-ary and \(m'\)-ary relations on a set A, respectively. Then \(\zeta \sigma := \sigma \), \(\tau \sigma := \sigma \) and \({{\,\textrm{pr}\,}}\sigma := \sigma \) for \(m = 1\), and

The operation \(\zeta \) is called cyclic shift of rows, \(\tau \) is called transposition of the first two rows, \({{\,\textrm{pr}\,}}\) is called deletion of the first row, \(\times \) is called Cartesian product, and \(\wedge \) is called intersection.
For \(m \in \mathbb {N}_{+}\) and an equivalence relation \(\varepsilon \) on \(\{1, \dots , m\}\), let
Formally we also allow \(\varepsilon =\top \) (where \(\top \) is considered as an extra top element in the lattice of all equivalence relations, i.e., \(\varepsilon \subsetneq \top \) for all equivalence relations \(\varepsilon \)) and define
Relations of the form \(\delta ^m_{\varepsilon ,A}\) for some m and \(\varepsilon \) are called diagonal relations on A. The set of all diagonal relations on A is denoted by \(D_{A}\). Examples of diagonal relations are the full m-ary relation \(A^m\), in particular \(\nabla :=\nabla _{A}:=A^{2}\) (formally this is \(\delta ^{2}_{\{(1,1),(2,2)\},A}\)), and the binary equality relation \(\Delta :=\Delta _{A}:= \{ \, (x,x) \mid x \in A \, \}\) (formally this is \(\delta ^{2}_{\{1,2\}^{2},A}\)).
A set Q of relations on A is called a relational clone if it is closed under the “elementary operations” \(\zeta \), \(\tau \), \({{\,\textrm{pr}\,}}\), \(\times \) and \(\wedge \) and contains the diagonal relations. For \(Q \subseteq {{\,\textrm{Rel}\,}}(A)\), we denote by \([Q]_{}\) or \([Q]_{A}\) the relational clone generated by Q, i.e., the smallest relational clone containing Q.
Definition 2.8
(S-relations). Let \({}^{S}{}\textrm{Rel}^{(m)}(A)\) be the set of all families \(\varrho = (\varrho _{s})_{s \in S}\) of m-ary relations \(\varrho _{s} \subseteq A^{m}\), and \({}^{S}{}\textrm{Rel}(A):= \bigcup _{m \in \mathbb {N}_{+}} {}^{S}{}\textrm{Rel}^{(m)}(A)\), the elements of which are called (finitary) S -relations.
Sometimes, instead of \(\varrho =(\varrho _{s})_{s\in S}\) we use the notation \(\varrho =(r_{1},\dots ,r_{n})\) where \(r_{1},\dots ,r_{n}\) is a list of all elements of all \(\varrho _{s}\), i.e., \(n=\sum _{s\in S}|\varrho _{s}|\), together with the corresponding signum \(\varvec{\lambda }_{\varrho }:=(s_{1},\dots ,s_{n})\) specifying which element belongs to which part \(\varrho _{s}\), i.e., if \(r_{i}\) was chosen from \(\varrho _{s}\) then we put \(s_{i}=s\), such that \(\varrho _s = \{ \, r \mid \exists i \in \{1, \dots , n\}: s_i = s\text { and }r_i = r \, \} \). Note that in \(\varvec{\lambda }_{\varrho }\) each \(s\in S\) appears exactly \(|\varrho _{s}|\) times.
Remark: The signum \(\varvec{\lambda }_{\varrho }\) is characteristic for \(\varrho \) and unique up to permutation of the \(s_{i}\)’s. One might order the entries such that all signa \(s_{i}\) with \(s_{i}=s\) appear consecutively, but we keep more flexibility and allow each signum (as above) for \(\varvec{\lambda }_{\varrho }\) with the property that each \(s\in S\) appears exactly \(|\varrho _{s}|\) times.
It is straightforward to define operations on \({}^{S}{}\textrm{Rel}(A)\) analogously to the above-defined operations for usual relations, just by applying them componentwise to S-relations. This will lead to the notion of S-relational clones. We mainly adopt the approach known from multi-sorted algebras as developed in [7, Section 4, pages 13–14]. However, we still have to introduce special, in some sense “trivial” S-relations, called S-diagonals, which generalize the usual diagonal relations. The motivation will become clear later in Proposition 3.8.
Definition 2.9
(S-diagonals). An S-relation \((\varrho _{s})_{s\in S}\), say m-ary, is called an S -diagonal (or an S -diagonal S -relation) if \(\varrho _{s}\) is a diagonal relation \(\delta ^{m}_{\varepsilon _{s}}\in D_{A}\) for each \(s\in S\) and the following condition is satisfied for all \(s,t\in S\):
Here St denotes the left ideal \(\{ \, st \mid s \in S \, \}\) generated by t. Note that \(Ss \subseteq St \iff s \in St\) and \(\delta ^{m}_{\varepsilon _{s}}\subseteq \delta ^{m}_{\varepsilon _{t}}\iff \varepsilon _{t}\subseteq \varepsilon _{s}\) (the case \(\varepsilon _{s}=\top \), i.e., \(\delta ^{m}_{\varepsilon _{s}}=\emptyset \), is allowed).
The set of all S-diagonals is denoted by \({}^{S}{}\!D_{A}\).
Remark 2.10
Let \(I(S):= \{ \, s \in S \mid \exists \bar{s} \in S :\bar{s}s = e \, \}\) be the set of all elements for which a left inverse exists. Then (for finite monoids S) any left inverse \(\bar{s}\) is also a right inverse (thus \(\bar{s}=s^{-1}\)) and I(S) is a group (with unit e), the largest subgroup of S. We have \(t\in I(S)\iff St=S\) (otherwise \(St\subsetneq S\)). If S is a group, then an S-diagonal \((\delta _{\varepsilon _{s}})_{s\in S}\) must be of the form \((\delta ^{m}_{\varepsilon })_{s\in S}\) (\(\varepsilon _{t}=\varepsilon _{s}\) for all \(s,t\in S\) since \(Ss=St=S\)).
Definition 2.11
(S-relational clones). A set of S-relations is called an S -relational clone if it contains \(\delta ^{S}\) (see below) and is closed under the operations \(\zeta \), \(\tau \), \({{\,\textrm{pr}\,}}\), \(\times \), and \(\wedge \) as well as under the operations \(\mu _{v}\) and \(\sqcap ^{v}\), which we will refer to as index translation by v and v -self-intersection for \(v\in S\). These operations are defined as follows. For \(\varrho = (\varrho _s)_{s \in S}\) and \(\varrho ' = (\varrho '_s)_{s \in S}\) in \({}^{S}{}\textrm{Rel}(A)\), and \(v\in S\), we let
-
(1)
\(\delta ^{S}:= (\Delta _{A})_{s \in S}\), i.e., \(\delta ^{S}_{s} = \Delta _{A}\) for all \(s \in S\),
-
(2)
\(\zeta (\varrho ) = \zeta ((\varrho _s)_{s \in S}):= (\zeta \varrho _s)_{s \in S}\) (cyclic shift),
-
(3)
\(\tau (\varrho ) = \tau ((\varrho _s)_{s \in S}):= (\tau \varrho _s)_{s \in S}\) (transposition of the first two rows),
-
(4)
\({{\,\textrm{pr}\,}}(\varrho ) = {{\,\textrm{pr}\,}}((\varrho _s)_{s \in S}):= ({{\,\textrm{pr}\,}}\varrho _s)_{s \in S}\) (deletion of the first row),
-
(5)
\(\varrho \times \varrho ' = (\varrho _s)_{s \in S} \times (\varrho '_s)_{s \in S}:= (\varrho _s \times \varrho '_s)_{s \in S}\) (Cartesian product),
-
(6)
\(\varrho \wedge \varrho ' = (\varrho _s)_{s \in S} \wedge (\varrho '_s)_{s \in S}:= (\varrho _s \wedge \varrho '_s)_{s \in S}\) (intersection),
-
(7)
\(\mu _v(\varrho ) = \mu _v((\varrho _{s})_{s \in S}):= (\varrho _{sv})_{s \in S}\) (index translation by v),
-
(8)
\(\sqcap ^{v}\varrho =((\sqcap ^{v}\varrho )_{s})_{s\in S}:=(\bigcap \{\varrho _{s'}\mid s'v=s\})_{s\in S}\) (v -self-intersection) (i.e., via the (right) multiplicative action of an element \(v\in S\)),
in particular, \((\sqcap ^{v}\varrho )_{s}=\bigcap \emptyset =A^{m}\) if \(s\in S \,{\setminus } Sv\) and \({{\,\textrm{ar}\,}}(\varrho )=m\).
For \(Q \subseteq {}^{S}{}\textrm{Rel}(A)\) the S -relational clone generated by Q, i.e., the least S-relational clone containing Q, is denoted by \({}^{S}{}\![Q]_{}\) or \({}^{S}{}\![Q]_{A}\).
The operations (7) and (8) are special cases of a more general operation called \(\mathcal {M}\)-self-intersection:
Definition 2.12
Let \(\mathcal {M}=(M_{s})_{s\in S}\) be a family of subsets of S satisfying the following condition
where \(s'M_{s}:=\{s'm\mid m\in M_{s}\}\). Then we define
-
(9)
\(\sqcap _{\mathcal {M}}\varrho =((\sqcap _{\mathcal {M}}\varrho )_{s})_{s\in S}:= (\bigcap \{ \, \varrho _{s'} \mid s' \in M_{s} \, \})_{s\in S}\) \(\text {(}\mathcal {M}-self -intersection \text {),}\)
in particular, \((\sqcap _{\mathcal {M}}\varrho )_{s}:=A^{m}\) if \(M_{s}=\emptyset \) and \({{\,\textrm{ar}\,}}(\varrho )=m\).
Note that \((\sqcap _{\mathcal {M}}\varrho )_{s}\subseteq \varrho _{s'}\) for all \(s'\in M_{s}\).
Remark 2.13
For \(v\in S\), consider the special families \(\mathcal {T}^{v}:=(\{sv\})_{s\in S}\) and \(\mathcal {M}^{v}=(M^{v}_{s})_{s\in S}\) with \(M^{v}_{s}:= \{ x \in S \mid xv = s \}\) (which easily can be seen to satisfy condition (*) of Definition 2.12). Then we have \(\mu _{v}(\varrho )=\sqcap _{\mathcal {T}^{v}}(\varrho )\) (cf. Definition 2.11(7)) and \(\sqcap ^{v}\varrho =\sqcap _{\mathcal {M}^{v}}\varrho \) (cf. Definition 2.11(8)).
For \(v \in S\) let \(\alpha _{v}:S \rightarrow S\), \(x \mapsto xv\) be the right multiplication with v. Then \(M^{v}_{s}=\alpha _{v}^{-1}(s)\) for \(s\in S\). For later use we mention the following properties of \(\mathcal {M}^{v}=(M^{v}_{s})_{s\in S}\):
-
(a)
\(e\in M^{v}_{v}\),
-
(b)
\(M^{v}_{s}\cap M^{v}_{t}=\emptyset \) for \(s,t\in S\), \(s\ne t\),
-
(c)
\(\forall s,t\in S: s\in M^{v}_{t}\implies sv=t\).
These properties can be checked easily (e.g., (b) follows from the fact that the \(M^{v}_{s}\) (\(s\in S\)) are the equivalence classes of the kernel of \(\alpha _{v}\)).
Remark 2.14
(A) If \(v\in S\) is an invertible element of the monoid S, then \(M^{v}_{s}=\{sv^{-1}\}\) for \(s\in S\), thus \(\mathcal {M}^{v}=\mathcal {T}^{v^{-1}}\), in particular the operation \(\sqcap ^{v}\) equals \(\mu _{v^{-1}}\) (cf. Remark 2.13 and Definition 2.11(7),(8)). Consequently, if S is a group and therefore each element is invertible, S-relational clones are characterized by the closure under the operations (1)–(7) of Definition 2.11.
(B) Analogously to the case of usual relational clones (cf. [5, Part II, 2.5] or [14, 1.1.9]), with the operations (1)–(8) it is possible to construct many other operations under which an S-relational clone is closed. We mention here some: all S-diagonal S-relations (see Lemma 2.15), arbitrary permutation of rows, deletion of arbitrary rows, identification of rows, doubling of rows, relational product, and so on. In particular, we will need in the proofs of later theorems the following operations that are derivable from the “elementary operations”. For an m-ary relation \(\varrho \) and any \(z_1, \dots , z_t \in \{1, \dots , m\}\) (not necessarily distinct elements), the projection of \(\varrho \) to rows \(z_1, \dots , z_t\) is the t-ary relation
This naturally extends to S-relations by componentwise application: for \(\varrho = (\varrho _s)_{s \in S} \in {}^{S}{}\textrm{Rel}^{(m)}(A)\), \({{\,\textrm{pr}\,}}_{z_1, \dots , z_t}(\varrho ):= ({{\,\textrm{pr}\,}}_{z_1, \dots , z_t}(\varrho _s))_{s \in S}\). Clearly, \({{\,\textrm{pr}\,}}(\varrho )={{\,\textrm{pr}\,}}_{2,\dots ,m}(\varrho )\) for an m-ary \(\varrho \) (cf. Definition 2.11(4)).
Note also that the empty S -relation \((\emptyset )_{s \in S}\) (that can be considered as \((\emptyset ^{(m)})_{s\in S}\) for an arbitrary \(m\in \mathbb {N}_{+}\)) belongs to every S-relational clone; it is obtained by taking the intersection of two S-relations of distinct arities.
(C) It is well known (see, e.g., [14, 2.1.3(i)]) that in the classical case of usual (unsigned) relational clones, the relational clone \([Q]_{}\) generated by a set Q of relations (using the “elementary operations” \(\delta ,\zeta ,\tau ,{{\,\textrm{pr}\,}},\times ,\wedge \)) equals the set of relations that are primitively positively first-order definable (pp-definable) from the relations in Q. More explicitly (cf. [13, 1.6]): Each primitive positive first-order formula \(\varphi =\varphi (\bar{\sigma }_{1},\dots ,\bar{\sigma }_{q};x_{1},\dots ,x_{m})\), (i.e., \(\varphi \) contains only \(\exists , \wedge , =\), and relation symbols, say \(m_{i}\)-ary \(\bar{\sigma }_{i}\), \(i\in \{1,\dots ,q\}\), and free variable symbols, say \(x_{1},\dots ,x_{m}\)) defines a so-called logical operation \(t_{\varphi }\) which can be applied to \(m_{i}\)-ary relations \(\sigma _{i}\subseteq A^{m_{i}}\) and gives the m-ary relation
Then the closure \([Q]_{}\) is the closure under all pp-definitions, which means explicitly the closure under all logical operations \(t_{\varphi }\).
As for S-relational clones, it follows from Definition 2.11 that a set of S-relations is an S-relational clone if and only if it is closed under pp-definitions (now we apply the same pp-formula to each component of S-relations), index translations and self-intersections. Moreover, S-relational clones are closed also under \(\mathcal {M}\)-self-intersections for arbitrary families \(\mathcal {M}\) satisfying condition (*) of Definition 2.12. In order to see this, in the proof of Lemma 3.9 we shall explicitly show that each set of the form \({}^{S}{}\textrm{Inv}\,F\) – and therefore, due to Theorem 4.6, also each S-relational clone – is closed under \(\mathcal {M}\)-self-intersections.
Lemma 2.15
\({}^{S}{}\!D_{A}={}^{S}{}\![\emptyset ]_{A}={}^{S}{}\![\delta ^{S}]_{A}\) is the least S-relational clone contained in every S-relational clone.
Proof
We show that each S-diagonal S-relation can be generated from \(\delta ^{S}\). It is well known that \(D_{A}=[\Delta ]_{A}\) (cf., e.g., [14, 1.1.9(R1)], the diagonal relation \(\delta _{3}^{\{1;2,3\}}(A)\) used there, can be derived from \(\Delta \) with the “elementary operations” from Definition 2.7 as follows: \(\delta _{3}^{\{1;2,3\}}(A)={{\,\textrm{pr}\,}}(\Delta )\times \Delta \)). Thus all \((\delta ^{m}_{\varepsilon })_{s\in S}\) can be constructed from \(\delta ^{S}=(\Delta )_{s\in S}\). We show that all further S-diagonals can be derived from these.
Let \(\varrho =(\delta ^{m}_{\varepsilon _{s}})_{s\in S}\in {}^{S}{}\!D_{A}\) (for notation, see Definition 2.9) and \(\delta ^{S}_{\varepsilon }:=(\delta ^{m}_{\varepsilon })_{s\in S}\). According to Definition 2.11(8), for \(v\in S\), \((\sqcap ^{v}\delta ^{S}_{\varepsilon })_{s}\) equals \(\delta ^{m}_{\varepsilon }\) if \(s\in Sv\) and it equals \(A^{m}\) if \(s\in S\,{\setminus } Sv\). Consequently, the conditions in Definition 2.9 for the S-diagonal \(\varrho \) imply \(\varrho =\bigwedge \{ \, \sqcap ^{v}\delta ^{S}_{\varepsilon _{v}} \mid v \in S \, \} \in {}^{S}{}\![\delta ^{S}]_{}\).
It remains to mention that \({}^{S}{}\!D_{A}\) really is an S-relational clone. Namely, the closure under each of the operations (1)–(8) of Definition 2.11 can be directly checked (however, it also follows immediately from Proposition 3.8 and Lemma 3.9). \(\square \)
3 Invariant \(\varvec{S}\)-relations and \(\varvec{S}\)-polymorphisms and the Galois connection \(\varvec{{}^{S}{}\textrm{Pol}}\)–\(\varvec{{}^{S}{}\textrm{Inv}}\)
In this section we introduce the Galois connection \({}^{S}{}\textrm{Pol}\)–\({}^{S}{}\textrm{Inv}\) induced by the S-preservation relation  and give some preliminary results. This parallels the classical Galois connection \({{\,\textrm{Pol}\,}}\)–\({{\,\textrm{Inv}\,}}\) induced by the preservation relation on usual (unsigned) operations and relations, which we will first briefly recall.
and give some preliminary results. This parallels the classical Galois connection \({{\,\textrm{Pol}\,}}\)–\({{\,\textrm{Inv}\,}}\) induced by the preservation relation on usual (unsigned) operations and relations, which we will first briefly recall.
Notation 3.1
Let \(f \in {{\,\textrm{Op}\,}}^{(n)}(A)\), and let \(r_i = (r_i^{(1)}, \dots , r_i^{(m)}) \in A^m\) (\(i \in \{1, \dots , n\}\)) We write
(componentwise application of f to m-tuples). Furthermore, if \(\varrho _i \subseteq A^m\) (\(i \in \{1, \dots , n\}\)), then we let
Definition 3.2
(Preservation). Let \(f \in {{\,\textrm{Op}\,}}^{(n)}(A)\) and \(\varrho \in {{\,\textrm{Rel}\,}}^{(m)}(A)\). We say that f preserves \(\varrho \) (or f is a polymorphism of \(\varrho \), or \(\varrho \) is an invariant of f), and we write \(f \mathrel {\triangleright }\varrho \), if \(f(\varrho , \dots , \varrho ) \subseteq \varrho \).
The relation \(\mathrel {\triangleright }\) induces a Galois connection between operations and relations. The corresponding operators are denoted as follows.
Definition 3.3
Let \(F \subseteq {{\,\textrm{Op}\,}}(A)\) and \(Q \subseteq {{\,\textrm{Rel}\,}}(A)\). Then we define
It is well known that \({{\,\textrm{Pol}\,}}Q\) is a clone for any \(Q \subseteq {{\,\textrm{Rel}\,}}(A)\) and \({{\,\textrm{Inv}\,}}F\) is a relational clone for any \(F \subseteq {{\,\textrm{Op}\,}}(A)\). Moreover, if A is finite, then it holds that \(\langle F \rangle _{} = {{\,\textrm{Pol}\,}}{{\,\textrm{Inv}\,}}F\) and \([Q]_{} = {{\,\textrm{Inv}\,}}{{\,\textrm{Pol}\,}}Q\) ([2], cf. [14, Folgerung 1.2.4]).
Definition 3.4
(S-preservation). Let \(f \in {}^{S}{}\textrm{Op}(A)\) with \({{\,\textrm{sgn}\,}}(f) = (s_{1}, \dots , s_{n})\) and \(\varrho = (\varrho _{s})_{s \in S} \in {}^{S}{}\textrm{Rel}^{(m)}(A)\). The preservation property  is defined by
is defined by

If  , then we say that f S-preserves \(\varrho \), or f is an S-polymorphism of \(\varrho \), or \(\varrho \) is invariant for f. Note that in particular we have \(f(\varrho _{s_{1}}, \dots , \varrho _{s_{n}}) \subseteq \varrho _{e}\) (e is the neutral element of S). If it is clear from the context that we deal with S-operations and S-relations, then, for
, then we say that f S-preserves \(\varrho \), or f is an S-polymorphism of \(\varrho \), or \(\varrho \) is invariant for f. Note that in particular we have \(f(\varrho _{s_{1}}, \dots , \varrho _{s_{n}}) \subseteq \varrho _{e}\) (e is the neutral element of S). If it is clear from the context that we deal with S-operations and S-relations, then, for  , we also say f preserves \(\varrho \) or f is a polymorphism of \(\varrho \).
, we also say f preserves \(\varrho \) or f is a polymorphism of \(\varrho \).
For S-relations or S-operations of a special form, the S-preservation property can be expressed by the usual preservation property:
Lemma 3.5
-
(i)
For \(f \in {}^{S}{}\textrm{Op}(A)\) and \(\sigma \in {{\,\textrm{Rel}\,}}(A)\) we have
Here \((\sigma )_{s \in S}\) is the S-relation \((\varrho _{s})_{s \in S}\) with \(\varrho _{s} = \sigma \) for all \(s \in S\).
-
(ii)
If \({{\,\textrm{sgn}\,}}(f) = (e, \dots , e)\) and \(\varrho = (\varrho _{s})_{s \in S}\), then

Proof
This follows immediately from the definition of S-preservation (for (ii) see also Proposition 4.7). \(\square \)
The S-preservation relation  induces a Galois connection between S-operations \({}^{S}{}\textrm{Op}(A)\) and S-relations \({}^{S}{}\textrm{Rel}(A)\). The corresponding operators are denoted as follows.
induces a Galois connection between S-operations \({}^{S}{}\textrm{Op}(A)\) and S-relations \({}^{S}{}\textrm{Rel}(A)\). The corresponding operators are denoted as follows.
Definition 3.6
Let \(F \subseteq {}^{S}{}\textrm{Op}(A)\) and \(Q \subseteq {}^{S}{}\textrm{Rel}(A)\). Then we define

Example 3.7
Let \((A,\le )\) be a poset and \(S = \{\mathord {+}, \mathord {-}\}\). Then the S-preclone F considered in Example 2.5 can be characterized as
Moreover, let \(\sigma :=(B_{1}\times B_{1})\cup \cdots \cup (B_{m}\times B_{m})\) where \(B_{1},\dots ,B_{m}\) are the connected components of the partial order \(\le \). Then the \(S'\)-preclone \(F'\) and the \(\widehat{S}\)-preclone \(\widehat{F}\) considered in Example 2.6 can be characterized by \(S'\)- and \(\widehat{S}\)-relations, resp., as follows:
Trivial projections and S-diagonals play a special role: they can be considered as trivial with respect to S-preservation (in particular, this motivates why S-diagonals should belong to each S-relational clone, cf. Definition 2.11(1) and Lemma 2.15):
Proposition 3.8
We have \({}^{S}{}\!\!J_{A}={}^{S}{}\textrm{Pol}\,{}^{S}{}\textrm{Rel}(A)\) and \({}^{S}{}\!D_{A}={}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Op}(A)\), i.e., (trivial) projections are those S-operations which S-preserve every S-relation, and S-diagonals are those S-relations which are invariant for every S-operation.
Proof
First we prove \({}^{S}{}\!\!J_{A}={}^{S}{}\textrm{Pol}\,{}^{S}{}\textrm{Rel}(A)\). It is easy to check that any (trivial) projection (see Remark 2.4(B)) preserves every relation, i.e., \({}^{S}{}\!\!J_{A}\subseteq {}^{S}{}\textrm{Pol}{}^{S}{}\textrm{Rel}(A)\). Conversely, let \(f\in {}^{S}{}\textrm{Pol}\,{}^{S}{}\textrm{Rel}(A)\) with \({{\,\textrm{sgn}\,}}(f)=(s_{1},\dots ,s_{n})\). From Lemma 3.5(i) we conclude that \(\mathring{f}\mathrel {\triangleright }\sigma \) for each \(\sigma \in {{\,\textrm{Rel}\,}}(A)\). Because \({{\,\textrm{Pol}\,}}{{\,\textrm{Rel}\,}}(A)=J_{A}\) (this follows from well-known results about clones: since \({{\,\textrm{Inv}\,}}J_{A}={{\,\textrm{Rel}\,}}(A)\), see [14, 1.1.15], one can conclude \(J_{A}={{\,\textrm{Pol}\,}}{{\,\textrm{Inv}\,}}J_{A}={{\,\textrm{Pol}\,}}{{\,\textrm{Rel}\,}}(A)\)) we get \(\mathring{f}\in J_{A}\) is a projection, i.e., \(f(x_{1},\dots ,x_{n})=x_{i}\). If \(s_{i}\ne e\) then f does not preserve \(\varrho :=(\Delta ,\dots ,\Delta ,\nabla ,\Delta ,\dots ,\Delta )\) (with \(\nabla \) at the i-th place), a contradiction to the choice of f. Thus \(s_{i}=e\) and \(f\in {}^{S}{}\!\!J_{A}\); consequently \({}^{S}{}\textrm{Pol}\,{{\,\textrm{Rel}\,}}(A)\subseteq {}^{S}{}\!\!J_{A}\).
Now we show \({}^{S}{}\!D_{A}={}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Op}(A)\). Let \(f\in {}^{S}{}\textrm{Op}(A)\) with \({{\,\textrm{sgn}\,}}(f)=(s_{1},\dots ,s_{n})\) and \(\varrho =(\varrho _{s})_{s\in S}=(\delta ^{m}_{\varepsilon _{s}})_{s\in S}\in {}^{S}{}\!D_{A}\), in particular we have \(\varrho _{s_{i}t}\subseteq \varrho _{t}\) for all \(t \in S\) since \(s_{i}t\in St\) (cf. Definition 2.9) for \(i\in \{1,\dots ,n\}\). Thus \(f(\varrho _{s_{1}t},\dots ,\varrho _{s_{n}t})\subseteq f(\varrho _{t},\dots ,\varrho _{t})\subseteq \varrho _{t}\) (note for the last inclusion that the diagonal \(\varrho _{t}\in D_{A}\) is preserved by every function, thus also by \(\mathring{f}\)), which shows that  . Thus \({}^{S}{}\!D_{A}\subseteq {}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Op}(A)\).
. Thus \({}^{S}{}\!D_{A}\subseteq {}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Op}(A)\).
Conversely, let \(\varrho \in {}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Op}(A)\). Note that \(\{ \, \mathring{f} \mid f \in {}^{S}{}\textrm{Op}(A), \; {{\,\textrm{Sgn}\,}}(f) = \{e\} \, \} = {{\,\textrm{Op}\,}}(A)\). From Lemma 3.5(ii) we conclude that \(\mathring{f} \mathrel {\triangleright }\{ \, \varrho _{s} \mid s \in S \, \}\) for every \(\mathring{f} \in {{\,\textrm{Op}\,}}(A)\). Thus \(\{ \, \varrho _{s} \mid s \in S \, \} \subseteq {{\,\textrm{Inv}\,}}{{\,\textrm{Op}\,}}(A) = D_{A}\) (the latter equality is well known, see e.g., [14, 1.1.15]). Furthermore, let \(Ss\subseteq St\), i.e., there exists \(s_{1}\in S\) such that \(s=s_{1}t\). Consequently, from  we get \(\varrho _{s}=\textsf{id}^{s_{1}}(\varrho _{s})=\textsf{id}^{s_{1}}(\varrho _{s_{1}t})\subseteq \varrho _{t}\), which proves \(\varrho \in {}^{S}{}\!D_{A}\) (because the compatibility condition in Definition 2.9 is fulfilled). Thus we also have \({}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Op}(A)\subseteq {}^{S}{}\!D_{A}\). \(\square \)
we get \(\varrho _{s}=\textsf{id}^{s_{1}}(\varrho _{s})=\textsf{id}^{s_{1}}(\varrho _{s_{1}t})\subseteq \varrho _{t}\), which proves \(\varrho \in {}^{S}{}\!D_{A}\) (because the compatibility condition in Definition 2.9 is fulfilled). Thus we also have \({}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Op}(A)\subseteq {}^{S}{}\!D_{A}\). \(\square \)
The operators \({}^{S}{}\textrm{Pol}\) and \({}^{S}{}\textrm{Inv}\) of the Galois connection produce S-preclones and S-relational clones, as shown by the following lemma. The main question, if every S-preclone and S-relational clone can be “produced” in this way, shall be answered in the next section (Theorems 4.1, 4.6).
Lemma 3.9
Let \(F \subseteq {}^{S}{}\textrm{Op}(A)\) and \(Q \subseteq {}^{S}{}\textrm{Rel}(A)\). Then \({}^{S}{}\textrm{Pol}\,Q\) is an S-preclone and \({}^{S}{}\textrm{Inv}\,F\) is an S-relational clone. Moreover, \({}^{S}{}\textrm{Pol}\,Q = {}^{S}{}\textrm{Pol}\,{}^{S}{}\![Q]_{}\) and \({}^{S}{}\textrm{Inv}\,F = {}^{S}{}\textrm{Inv}\,{}^{S}{}\!\langle F \rangle _{}\).
Proof
We show first that \({}^{S}{}\textrm{Pol}\,Q\) is an S-preclone. Let \(\varrho = (\varrho _s)_{s \in S}\) be an S-relation in Q. For all \(s \in S\), \(\textsf{id}_{A}(\varrho _{es}) = \varrho _{es} = \varrho _s\); hence \(\textsf{id}_{A} \in {}^{S}{}\textrm{Pol}\,Q\). Let \(f, g \in {}^{S}{}\textrm{Pol}\,Q\) with \({{\,\textrm{sgn}\,}}(f) = (s_1, \dots , s_n) \in S^n\) and \({{\,\textrm{sgn}\,}}(g) = (s'_1, \dots , s'_m) \in S^m\), and let \(s \in S\). If \(n = 1\), then we have \(\zeta f = \tau f = f \in {}^{S}{}\textrm{Pol}\,Q\); otherwise
For each \(t \in S\),
and if \(s_1 = s_2 = t\) then
otherwise \(\Delta f = f \in {}^{S}{}\textrm{Pol}\,Q\). Finally,
This shows that \({}^{S}{}\textrm{Pol}\,Q\) is an S-preclone.
Now we show that \({}^{S}{}\textrm{Inv}\,F\) is an S-relational clone. By Proposition 3.8 we have \(\delta ^{S}\in {}^{S}{}\!D_{A}\subseteq {}^{S}{}\textrm{Inv}F\), thus condition (1) of Definition 2.11 is satisfied. Let \(\varrho , \varrho ' \in {}^{S}{}\textrm{Inv}\,F\), say \(\varrho \) is m-ary and \(\varrho '\) is \(m'\)-ary. If \(m = 1\), then \(\zeta \varrho = \tau \varrho = {{\,\textrm{pr}\,}}\varrho = \varrho \in {}^{S}{}\textrm{Inv}\,F\). If \(m \ne m'\), then \(\varrho \wedge \varrho ' = (\emptyset ^{(m)})_{s \in S} \in {}^{S}{}\textrm{Inv}\,F\). In all other cases, it is straightforward to verify that for \(f\in F\) with \({{\,\textrm{sgn}\,}}(f)=(s_{1},\dots ,s_{n})\) and \(\pi \in \{\zeta ,\tau , {{\,\textrm{pr}\,}}\}\) we have
so  ,
,  and
and  .
.
For the remaining two operations (i.e., index translation and self-intersection, see Definition 2.11(7),(8)) we use the more general operation \(\mathcal {M}\)-self-intersection (see Definition 2.12(9)). Because of Remark 2.13 this will prove the result for the operations (7) and (8), too.
Thus let \(f\in F\) with \({{\,\textrm{sgn}\,}}(f)=(s_{1},\dots ,s_{n})\) and \(\varrho \in {}^{S}{}\textrm{Inv}\,F\), i.e.,  . Furthermore, let \(\mathcal {M}=(M_{s})_{s\in S}\) satisfy the condition (*) in Definition 2.12. For shorter notation put \(\varrho ':=\sqcap _{\mathcal {M}}\varrho \). We have to show \( f(\varrho '_{s_{1}s},\dots ,\varrho '_{s_{n}s})\subseteq \varrho '_{s}\) for every \(s\in S\). Since \(s_{i}s'\in s_{i}M_{s}\subseteq M_{s_{i}s}\) for each \(s'\in M_{s}\), by the definition of \(\varrho '_{s_{i}s}\) we have \(\varrho '_{s_{i}s}\subseteq \varrho _{s_{i}s'}\) for all \(s'\in M_{s}\) (\(i\in \{1,\dots ,n\}\)). Consequently,
. Furthermore, let \(\mathcal {M}=(M_{s})_{s\in S}\) satisfy the condition (*) in Definition 2.12. For shorter notation put \(\varrho ':=\sqcap _{\mathcal {M}}\varrho \). We have to show \( f(\varrho '_{s_{1}s},\dots ,\varrho '_{s_{n}s})\subseteq \varrho '_{s}\) for every \(s\in S\). Since \(s_{i}s'\in s_{i}M_{s}\subseteq M_{s_{i}s}\) for each \(s'\in M_{s}\), by the definition of \(\varrho '_{s_{i}s}\) we have \(\varrho '_{s_{i}s}\subseteq \varrho _{s_{i}s'}\) for all \(s'\in M_{s}\) (\(i\in \{1,\dots ,n\}\)). Consequently,
for each \(s'\in M_{s}\), thus \( f(\varrho '_{s_{1}s},\dots ,\varrho '_{s_{n}s})\) is contained in \(\varrho '_{s}\) being the intersection of all such \(\varrho _{s'}\). Consequently,  .
.
This shows that \({}^{S}{}\textrm{Inv}\,F\) is an S-relational clone.
Finally, the last statement of the Lemma follows from the above. Indeed, we clearly have \({}^{S}{}\textrm{Pol}\,{}^{S}{}\![Q]_{} \subseteq {}^{S}{}\textrm{Pol}\,Q\) and \(Q \subseteq {}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Pol}\,Q\) (by the general properties of a Galois connection, here \({}^{S}{}\textrm{Pol}\)–\({}^{S}{}\textrm{Inv}\)). The latter implies \({}^{S}{}\![Q]_{} \subseteq {}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Pol}\,Q\) since \({}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Pol}\,Q\) is an S-relational clone (by what we have shown above); consequently \({}^{S}{}\textrm{Pol}\,Q = {}^{S}{}\textrm{Pol}\,{}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Pol}\,Q \subseteq {}^{S}{}\textrm{Pol}\,{}^{S}{}\![Q]_{}\), which proves the equality \({}^{S}{}\textrm{Pol}\,Q = {}^{S}{}\textrm{Pol}\,{}^{S}{}\![Q]_{}\). The equality \({}^{S}{}\textrm{Inv}\,F = {}^{S}{}\textrm{Inv}\,{}^{S}{}\!\langle F \rangle _{}\) follows analogously from the fact that \({}^{S}{}\textrm{Pol}\,{}^{S}{}\textrm{Inv}\,F\) is an S-preclone. \(\square \)
A characterization of the (usual) clones generated by S-operations, in particular by S-preclones F, is also possible.
Proposition 3.10
Let \(F \subseteq {}^{S}{}\textrm{Op}(A)\). Then the clone \(\langle \mathring{F} \rangle _{} \subseteq {{\,\textrm{Op}\,}}(A)\) generated by \(\mathring{F}\) (i.e., all functions of F ignoring the signum of the operations) can be characterized as follows:
Proof
It is well known that \(\langle \mathring{F} \rangle _{} = {{\,\textrm{Pol}\,}}{{\,\textrm{Inv}\,}}\mathring{F}\) ([2], cf. [14, Folgerung 1.2.4]). By Lemma 3.5(i) we have \(\sigma \in {{\,\textrm{Inv}\,}}\mathring{F} \iff (\sigma )_{s \in S} \in {}^{S}{}\textrm{Inv}\,F\), which finishes the proof. \(\square \)
Definition 3.11
Let \(F \subseteq {}^{S}{}\textrm{Op}(A)\) and \(\varrho \in {}^{S}{}\textrm{Rel}^{(m)}(A)\). Let
where \(\varrho \subseteq \sigma \) means \(\varrho _{s} \subseteq \sigma _{s}\) for each \(s \in S\). Thus \(\Gamma _{F}(\varrho )\) is the least S-relation which contains \(\varrho \) and is invariant for F (note that \({}^{S}{}\textrm{Inv}\,F\) is closed under intersections, cf. Definition 2.11(6)). Moreover, we have \(\Gamma _{F}(\varrho ) = \Gamma _{{}^{S}{}\!\langle F \rangle _{}}(\varrho )\) (by definition, since \({}^{S}{}\textrm{Inv}\,F = {}^{S}{}\textrm{Inv}\,{}^{S}{}\!\langle F \rangle _{}\); see Lemma 3.9).
Lemma 3.12
(cf. [14, 1.1.20]). For any \(F\subseteq {}^{S}{}\textrm{Op}(A)\) and \(\varrho \in {}^{S}{}\textrm{Rel}(A)\),
Proof
The claims about \(\zeta \) and \(\tau \) are easy to verify. For the claim about \({{\,\textrm{pr}\,}}_{z_1, \dots , z_m}\), observe that \({{\,\textrm{pr}\,}}_{z_1, \dots , z_m}(\varrho ) \subseteq {{\,\textrm{pr}\,}}_{z_1, \dots , z_m}(\Gamma _F(\varrho )) \in {}^{S}{}\textrm{Inv}\,F\) and that every S-relation \(\sigma \in {}^{S}{}\textrm{Inv}\,F\) that contains \({{\,\textrm{pr}\,}}_{z_1, \dots , z_m}(\varrho )\) can be turned into a relation \(\sigma ' \in {}^{S}{}\textrm{Inv}\,F\) with \(\varrho \subseteq \sigma '\) by introduction of fictitious rows and identification of equal rows. \(\square \)
Proposition 3.13
(Characterization of \({\Gamma _F(\varrho )}\)).
-
(i)
Let \(F\subseteq {}^{S}{}\textrm{Op}(A)\) and \(\varrho \in {}^{S}{}\textrm{Rel}(A)\). For \(i\in \mathbb {N}\) we define
$$\begin{aligned} \varrho ^{(0)}&:=\varrho \\ \varrho ^{(i+1)}&:=(\varrho ^{(i+1)}_{s})_{s\in S}, \text { where}\\ \varrho ^{(i+1)}_{s}&:=\varrho ^{(i)}_{s}\cup \{ \, f(r_{1},\dots ,r_{n}) \mid \begin{array}{@{}l@{}} f \in F^{(n)}, \, n \in \mathbb {N}_{+}, \\ r_{1}\in \varrho ^{(i)}_{s_{1}s}, \dots , r_{n}\in \varrho ^{(i)}_{s_{n}s}, \\ {\text {where }}(s_{1},\dots ,s_{n}) := {{\,\textrm{sgn}\,}}(f) \, \}. \end{array} \end{aligned}$$Then we have \(\Gamma _{F}(\varrho )=\bigcup _{i=0}^{\infty }\varrho ^{(i)}\).
-
(ii)
Let \(r\in \Gamma _{F}(\varrho )_{s}\) for some \(s\in S\). Then there exist an S-operation \(f\in {}^{S}{}\!\langle F \rangle _{}\) with \({{\,\textrm{sgn}\,}}(f)=(s_{1},\dots ,s_{q})\) (for some \(q\in \mathbb {N}_{+}\) and \(s_{1},\dots ,s_{q}\in S\)) and \(r_{j}\in \varrho _{s_{j}s}\) (\(j\in \{1,\dots ,q\}\)) such that \(r=f(r_{1},\dots ,r_{q})\).
-
(iii)
Let \(\varrho \in {}^{S}{}\textrm{Rel}(A)\) and \(\varvec{\lambda }_{\varrho }=(s_{1},\dots ,s_{n})\), \(\varrho =(r_{1},\dots ,r_{n})\) (cf. Definition 2.8). Then
$$ (\Gamma _{F}(\varrho ))_{e} = \{ \, f(r_{1},\dots ,r_{n}) \mid f \in {}^{S}{}\!\langle F \rangle _{}, {{\,\textrm{sgn}\,}}(f) = \varvec{\lambda }_{\varrho } \, \}. $$
Remark: Note that the union in Proposition 3.13(i) is in fact a finite union because the increasing sequence \(\varrho ^{(0)}\subseteq \varrho ^{(1)}\subseteq \dots \subseteq \varrho ^{(i)} \subseteq \dots \subseteq (A^{m})_{s\in S}\) (\(m={{\,\textrm{ar}\,}}(\varrho )\)) must stabilize after a finite number of steps (since A and S are finite).
Proof
(i): Let \(\gamma :=\bigcup _{i=0}^{\infty }\varrho ^{(i)}\). At first we show \(\gamma \in {}^{S}{}\textrm{Inv}\,F\) (this will imply \(\Gamma _{F}(\varrho )\subseteq \gamma \) by definition of \(\Gamma _{F}(\varrho )\) since \(\varrho \subseteq \gamma \)).
Indeed, let \(f\in F\), \({{\,\textrm{sgn}\,}}(f)=(s_{1},\dots ,s_{n})\) and \(r_{j}\in \gamma _{s_{j}s}\) for some \(s\in S\), \(j\in \{1,\dots ,n\}\). We have to show \(f(r_{1},\dots ,r_{n})\in \gamma _{s}\). Since \(\gamma \) is the union of the increasing sequence \((\varrho ^{(i)})_{i\in \mathbb {N}}\), there must exist \(i\in \mathbb {N}\) such that \(r_{j}\in \varrho ^{(i)}_{s_{j}s}\) for all \(j\in \{1,\dots ,n\}\). Consequently, we have \(f(r_{1},\dots ,r_{n})\in \varrho ^{(i+1)}_{s}\subseteq \gamma _{s}\) by definition of \(\varrho ^{(i+1)}_{s}\).
It remains to show \(\gamma \subseteq \Gamma _{F}(\varrho )\). We show \(\varrho ^{(i)}\subseteq \Gamma _{F}(\varrho )\) for all \(i\in \mathbb {N}\) by induction on i. For \(i=0\), \(\varrho ^{(0)}=\varrho \subseteq \Gamma _{F}(\varrho )\) is clear. Assume \(\varrho ^{(i)}\subseteq \Gamma _{F}(\varrho )\) for some \(i\in \mathbb {N}\). Then, for \(f\in F^{(n)}\) with \({{\,\textrm{sgn}\,}}(f)=(s_{1},\dots ,s_{n})\), \(s\in S\), \(r_{1}\in \varrho ^{(i)}_{s_{1}s}\subseteq \Gamma _{F}(\varrho )_{s_{1}s},\dots , r_{n}\in \varrho ^{(i)}_{s_{n}s}\subseteq \Gamma _{F}(\varrho )_{s_{n}s}\), we get \(f(r_{1},\dots ,r_{n})\in \Gamma _{F}(\varrho )_{s}\) (because \(\Gamma _{F}(\varrho )\) is invariant), which implies \(\varrho ^{(i+1)}_{s}\subseteq \Gamma _{F}(\varrho )_{s}\) according to the definition of \(\varrho ^{(i+1)}_{s}\). Thus we also have \(\gamma \subseteq \Gamma _{F}(\varrho )\) and therefore, as shown above, equality.
(ii): According to (i) it is enough to show the claim for \(r\in \varrho ^{(i)}_{s}\) for each \(i\in \mathbb {N}\). This we shall do by induction on i. For \(i=0\) and \(r\in \varrho ^{(0)}_{s}=\varrho _{s}\) we obviously have \(\textsf{id}(r)=r\), i.e., we can take \(q=1\), \(f=\textsf{id}\in {}^{S}{}\!\langle F \rangle _{}\), \(r_{1}=r\), \(s_{1}=e\).
Assume that the claim holds for all elements in \(\varrho ^{(i)}_{s}\) and all \(s\in S\). Let \(r\in \varrho ^{(i+1)}_{s}\). Then (according to the definition of \(\varrho ^{(i+1)}\)) there exist \(f\in F^{(n)}\) with \({{\,\textrm{sgn}\,}}(f)=(s_{1},\dots ,s_{n})\) (\(n\in \mathbb {N}_{+}\)) and \(b_{1}\in \varrho ^{(i)}_{s_{1}s},\dots , b_{n}\in \varrho ^{(i)}_{s_{n}s}\) such that \(r=f(b_{1},\dots ,b_{n})\). By induction hypothesis each \(b_{j}\in \varrho ^{(i)}_{s_{j}s}\) can be represented as \(b_{j}=f_{j}(r_{j1},\dots ,r_{jq_{j}})\) with \({{\,\textrm{sgn}\,}}(f_{j})=(s_{j1},\dots ,s_{jq_{j}})\) (\(j\in \{1,\dots ,n\}\)) for suitable \(r_{jk}\in \varrho _{s_{jk}s_{j}s}\) (\(k\in \{1,\dots ,q_{j}\}\)). Consequently, for
we have
which shows the claim for \(\varrho ^{(i+1)}_{s}\). By induction, (ii) is proved.
(iii): Let \(r\in \Gamma _{F}(\varrho )_{e}\). According to (ii) (for \(s=e\)) there exist \(f\in {}^{S}{}\!\langle F \rangle _{}\) with \({{\,\textrm{sgn}\,}}(f)=(t_{1},\dots ,t_{q})\) and \(r_{k_{i}}\in \varrho _{t_{i}}\), \(k_{i}\in \{1,\dots ,n\}\), \(i\in \{1,\dots ,q\}\) such that \(r=f(r_{k_{1}},\dots ,r_{k_{q}})\). We can assume that all the \(r_{k_{i}}\)’s on arguments with the same signum are different (otherwise the corresponding arguments can be identified according to Definition 2.3(5)). Since \(r_{i}\in \varrho _{s_{i}}\) (by definition), we have \(r_{k_{i}}\in \varrho _{s_{k_{i}}}\) with \(s_{k_{i}}=t_{i}\) and therefore \({{\,\textrm{sgn}\,}}(f)=(t_{1},\dots ,t_{q})=(s_{k_{1}},\dots ,s_{k_{q}})\).
For each \(r_{j}\) which does not appear among the \(r_{k_{i}}\)’s, more precisely, for each \(r_{j} \in \varrho _{s_{j}} \,{\setminus }\, \{ \, r_{k_{i}} \mid s_{k_{i}} = s_{j},\, i \in \{1,\dots ,q\} \, \}\) (\(j\in \{1,\dots ,n\}\)) we add a fictitious argument with signum \(s_{j}\) to f (according to Definition 2.3(4)). Thus we obtain an S-operation \(f'\in {}^{S}{}\!\langle F \rangle _{}\), the signum of which contains exactly all \(s_{1},\dots ,s_{n}\). With a suitable permutation of the arguments of \(f'\) (according to Definition 2.3(2), (3), cf. Remark 2.4(A)) we finally get an S-operation with \({{\,\textrm{sgn}\,}}(f'')=(s_{1},\dots ,s_{n})=\varvec{\lambda }_{\varrho }\) such that \(f''(r_{1}, \dots , r_{n})=f(r_{k_{1}},\dots ,r_{k_{q}})=r\). \(\square \)
Proposition 3.15 below shows that the S-operations in an S-preclone generated by F can be characterized by the preservation of special S-relations \(\Gamma _{F}(\chi ^{\lambda })\) where the \(\chi ^{\lambda }\) are defined as follows.
Definition 3.14
For a signum \(\lambda = (s_{1}, \dots , s_{n}) \in S^{n}\), let \(\chi ^{\lambda } \in {}^{S}{}\textrm{Rel}^{(k^{n})}(A)\) be defined by
In the above, for \(k:= |A |\) and fixed \(n\in \mathbb {N}_{+}\), the tuples \(\varkappa _{i}\) are defined as in the “classical” case ([14, 1.1.16]): \((\varkappa _{1}, \dots , \varkappa _{n})\) is the \((k^{n}\times n)\)-matrix with columns \(\varkappa _{1}, \dots , \varkappa _{n}\) such that the rows are all n-tuples from \(A^{n}\) (may be ordered lexicographically). Thus we have \(\varkappa _{i}\in \chi ^{\lambda }_{s_{i}}\). With the notation introduced in Definition 2.8 we have \(\lambda =\varvec{\lambda }_{\chi ^{\lambda }}\).
Proposition 3.15
Let \(F \subseteq {}^{S}{}\textrm{Op}(A)\), let \(\lambda = (s_{1}, \dots , s_{n}) \in S^{n}\) be a signum and let \(g \in {}^{S}{}\textrm{Op}^{(n)}(A)\) with \({{\,\textrm{sgn}\,}}(g) = \lambda \). Then we have

Proof
The implication “\(\Longrightarrow \)” is clear since \(\Gamma _{F}(\chi ^{\lambda })\) is invariant (by definition) for every S-operation in \({}^{S}{}\!\langle F \rangle _{}\) (cf. Lemma 3.9).
“\(\Longleftarrow \)”:  implies that \(g(\Gamma _{F}(\chi ^{\lambda })_{s_{1}},\dots ,\Gamma _{F}(\chi ^{\lambda })_{s_{n}})\subseteq \Gamma _{F}(\chi ^{\lambda })_{e}\) (cf. 3.4(1)), in particular \(g(\varkappa _{1},\dots ,\varkappa _{n})\in \Gamma _{F}(\chi ^{\lambda })_{e}\). According to Proposition 3.13(iii) (for \(u=e\)) we have
implies that \(g(\Gamma _{F}(\chi ^{\lambda })_{s_{1}},\dots ,\Gamma _{F}(\chi ^{\lambda })_{s_{n}})\subseteq \Gamma _{F}(\chi ^{\lambda })_{e}\) (cf. 3.4(1)), in particular \(g(\varkappa _{1},\dots ,\varkappa _{n})\in \Gamma _{F}(\chi ^{\lambda })_{e}\). According to Proposition 3.13(iii) (for \(u=e\)) we have
Hence there exists some \(f\in {}^{S}{}\!\langle F \rangle _{}^{(\lambda )}\) such that \(g(\varkappa _{1},\dots ,\varkappa _{n})=f(\varkappa _{1},\dots ,\varkappa _{n})\). Therefore g and f agree on each element of \(A^{n}\) (the rows of \(\chi ^{\lambda }\)), i.e., \(g=f\in {}^{S}{}\!\langle F \rangle _{}\). \(\square \)
4 The Galois closures for the Galois connection \(\varvec{{}^{S}{}\textrm{Pol}}\)–\(\varvec{{}^{S}{}\textrm{Inv}}\)
Now we are able to characterize the Galois closures of the Galois connection \({}^{S}{}\textrm{Pol}\)–\({}^{S}{}\textrm{Inv}\). Recall that throughout the paper we assume that A and S are finite.
Theorem 4.1
Let S be an arbitrary monoid. Then, for \(F\subseteq {}^{S}{}\textrm{Op}(A)\), we have
i.e., the Galois closure is the S-preclone generated by F.
Proof
Since \({}^{S}{}\textrm{Pol}\,{}^{S}{}\textrm{Inv}\) is a closure operator, we have the inclusion \({}^{S}{}\!\langle F \rangle _{}\subseteq {}^{S}{}\textrm{Pol}\,{}^{S}{}\textrm{Inv}\,{}^{S}{}\!\langle F \rangle _{}={}^{S}{}\textrm{Pol}\,{}^{S}{}\textrm{Inv}\,F\) (the last equality follows from Lemma 3.9). For the converse inclusion let \(g\in {}^{S}{}\textrm{Pol}\,{}^{S}{}\textrm{Inv}\,F\) with \({{\,\textrm{sgn}\,}}(g)=\lambda \). Then \(g\in {}^{S}{}\textrm{Pol}\,\Gamma _{F}(\chi ^{\lambda })\) (since \(\Gamma _{F}(\chi ^{\lambda })\) is invariant by Definition 3.11) and we get \(g\in {}^{S}{}\!\langle F \rangle _{}\) by Proposition 3.15. \(\square \)
In Theorem 4.6 we shall characterize the Galois closed S-relational clones. In preparation of the proof we need several lemmata.
Lemma 4.2
(cf. [14, Lemma 1.2.2]). Let \(F \subseteq {}^{S}{}\textrm{Op}(A)\). Then each invariant \(\varrho \in {}^{S}{}\textrm{Inv}^{(m)} F\) (\(m\in \mathbb {N}_{+}\)) can be obtained from \(\Gamma _{F}(\chi ^{\varvec{\lambda }_{\varrho }})\) by projections. Consequently, \({}^{S}{}\textrm{Inv}\,F = {}^{S}{}\![\{ \, \Gamma _F(\chi ^{\varvec{\lambda }_\varrho }) \mid \varrho \in {}^{S}{}\textrm{Rel}(A) \, \}]_{}\).
Proof
According to Definition 2.8, for \(\varvec{\lambda }_{\varrho }=(s_{1},\dots ,s_{n})\), we have \(\varrho _{s} = \{ \, r_{i} \mid s_{i} = s \, \}\). Thinking of \(\varrho \) as the \(m \times n\) matrix \(M=(r_{1}, \dots , r_{n})\) (\(r_{i}\in A^{m}\)), we see that each row of M appears as a row of the \(|A|^n\times n\) matrix \(\chi ^{\varvec{\lambda }_\varrho }=(\varkappa _1, \dots , \varkappa _n)\) say, the j-th row of \(\varrho \) is the \(z_j\)-th row of \(\chi ^{\varvec{\lambda }_\varrho }\) (\(j \in \{1, \dots , m\}\)). Then \(\varrho = {{\,\textrm{pr}\,}}_{z_1, \dots , z_m}(\chi ^{\varvec{\lambda }_\varrho })\). By Lemma 3.12, we have \(\Gamma _F(\varrho ) = {{\,\textrm{pr}\,}}_{z_1, \dots , z_m}(\Gamma _{F}(\chi ^{\varvec{\lambda }_\varrho }))\). Since \(\varrho \in {}^{S}{}\textrm{Inv}\,F\), we get \(\varrho = \Gamma _F(\varrho ) = {{\,\textrm{pr}\,}}_{z_1, \dots , z_m}(\Gamma _F(\chi ^{\varvec{\lambda }_\varrho }))\). Therefore, \({}^{S}{}\textrm{Inv}\,F \subseteq {}^{S}{}\![\{ \, \Gamma _F(\chi ^{\varvec{\lambda }_\varrho }) \mid \varrho \in {}^{S}{}\textrm{Rel}(A) \, \}]_{}\) by Remark 2.14(B). The inclusion \({}^{S}{}\![\{ \, \Gamma _F(\chi ^{\varvec{\lambda }_\varrho }) \mid \varrho \in {}^{S}{}\textrm{Rel}(A) \, \}]_{} \subseteq {}^{S}{}\textrm{Inv}\,F\) holds, because \(\{ \, \Gamma _F(\chi ^{\varvec{\lambda }_\varrho }) \mid \varrho \in {}^{S}{}\textrm{Rel}(A) \, \} \subseteq {}^{S}{}\textrm{Inv}\,F\) and \({}^{S}{}\textrm{Inv}\,F\) is an S-relational clone by Lemma 3.9. \(\square \)
Notation 4.3
For given \(Q\subseteq {}^{S}{}\textrm{Rel}(A)\) and \(\varrho \in {}^{S}{}\textrm{Rel}(A)\) let
be the smallest S-relation in \({}^{S}{}\![Q]_{}\) that has the same arity as \(\varrho \) and contains \(\varrho \) (the index Q for \(\gamma _{Q}\) is omitted if the \(Q\subseteq {}^{S}{}\textrm{Rel}(A)\) under consideration is fixed). Note that \(\gamma (\varrho )\in {}^{S}{}\![Q]_{}\) because \({}^{S}{}\![Q]_{}\) is an S-relational clone and therefore closed under intersections (cf. Definition 2.11(6)).
Lemma 4.4
Let \(Q\subseteq {}^{S}{}\textrm{Rel}(A)\) and \(F:={}^{S}{}\textrm{Pol}\,Q\). If \(\Gamma _{F}(\chi ^{\lambda })=\gamma (\chi ^{\lambda })\) for each signum \(\lambda =(s_{1},\dots ,s_{n})\) (\(s_{1},\dots ,s_{n}\in S\), \(n\in \mathbb {N}_{+}\)), then \({}^{S}{}\![Q]_{} = {}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Pol}\,Q\).
Proof
By Lemma 3.9 and the general properties of Galois connections, we have \({}^{S}{}\![Q]_{}\,\subseteq {}^{S}{}\textrm{Inv}\,{}^{S}{}\textrm{Pol}\,{}^{S}{}\![Q]_{} = {}^{S}{}\textrm{Inv}\,F\). In order to prove the converse inclusion, it suffices to show that \(\Gamma _F(\chi ^\lambda ) \in {}^{S}{}\![Q]_{}\) for all signa \(\lambda \), because this implies, by Lemma 4.2, that
where \(S^{*}\) denotes the set of all signa (finite words over S). Furthermore, \(\gamma (\chi ^{\lambda })\in {}^{S}{}\![Q]_{}\) by Definition 4.3. Thus the assumption \(\Gamma _{F}(\chi ^{\lambda })=\gamma (\chi ^{\lambda })\) implies \(\Gamma _{F}(\chi ^{\lambda })\in {}^{S}{}\![Q]_{}\) and we are done. \(\square \)
For the next lemmata we always assume that \(Q\subseteq {}^{S}{}\textrm{Rel}(A)\) is arbitrarily chosen but fixed and that \(F:={}^{S}{}\textrm{Pol}\,Q\).
Lemma 4.5
We have \(\Gamma _{F}(\chi ^{\lambda })_{e}=\gamma (\chi ^{\lambda })_{e}\) for all signa \(\lambda =(s_{1},\dots ,s_{n})\) (\(s_{1},\dots , s_{n}\in S\), \(n\in \mathbb {N}_{+}\)).
Proof
Recall that \(\chi ^\lambda _s = \{ \, \varkappa _i \mid s_i = s,\, i \in \{1, \dots , n\} \, \}\) for \(s\in S\) and \(\lambda =(s_{1},\dots ,s_{n})\), where \((\varkappa _1, \dots , \varkappa _n)\) is an \(|A |^n\times n\) matrix with columns \(\varkappa _1, \dots , \varkappa _n\) such that the rows are all n-tuples from \(A^n\).
Let \(\gamma :=\gamma (\chi ^{\lambda })\) and assume that there exists \(\textbf{r}\in \gamma _e\, {\setminus }\,\Gamma _F(\chi ^\lambda )_e\) (and we are going to show that this leads to a contradiction). By Proposition 3.13(iii) (take \((r_{1},\dots ,r_{n})=(\varkappa _{1},\dots ,\varkappa _{n})\) and note \(e\in I(S)\)), the function \(f_{\textbf{r}}\) of signum \(\lambda \) that is defined by \(f_{\textbf{r}}(\varkappa _1, \dots , \varkappa _n) = \textbf{r}\) does not belong to \(F = {}^{S}{}\textrm{Pol}\,Q\). Therefore there exists an S-relation \(\theta \in Q\), say m-ary, that is not S-preserved by \(f_{\textbf{r}}\), i.e., there exist a \(v \in S\) and tuples \(\textbf{r}_i \in \theta _{s_i v}\) (\(i \in \{1, \dots , n\}\)) such that \(\textbf{a}:= f_{\textbf{r}}(\textbf{r}_1, \dots , \textbf{r}_n) \notin \theta _v\). By index translation by v, we obtain the S-relation \(\theta ^*:= \mu _{v}(\theta ) \in {}^{S}{}\![Q]_{}\) with \(\theta ^*_s = \theta _{sv}\) (\(s \in S\)) that is not S-preserved by \(f_{\textbf{r}}\) either, because \(\textbf{r}_i \in \theta _{s_i v} = \theta ^*_{s_i}\) (\(i \in \{1, \dots , n\}\)) and \(\textbf{a} \notin \theta _v = \theta ^*_e\).
Consider the matrix \(M = (\textbf{r}_1, \dots , \textbf{r}_n)\). The rows of M occur as rows of \((\varkappa _1, \dots , \varkappa _n)\); say the j-th row of M equals the \(h_j\)-th row of \(\chi ^\lambda \). Let \((\delta _{\tau }^{q+m})_{s\in S}\) be the diagonal relation with \(\tau = \{ \, (h_j, q + j) \mid j \in \{1, \dots , m\} \, \}\), and let \(\theta ':= (\gamma \times \theta ^{*}) \wedge \delta _{\tau }^{q+m}\). In other words, \(\theta '_s\) comprises those tuples from \((\gamma \times \theta ^{*})_s\) whose \(h_j\)-th and \((q + j)\)-th components are equal, for \(j \in \{1, \dots , m\}\). By removing the last m rows, we obtain the S-relation \(\theta '':= {{\,\textrm{pr}\,}}_{1, \dots , q}(\theta ')\). Since the tuple \(\varkappa _i \times \textbf{r}_i\) belongs to \((\gamma \times \theta ^{*})_{s_i}\) and hence also to \(\theta '_{s_i}\), for all \(i \in \{1, \dots , n\}\), we have \(\varkappa _i \in \theta ''_{s_i}\) for all \(i \in \{1, \dots , n\}\), i.e., \(\chi ^\lambda \subseteq \theta ''\). Moreover, \(\theta '' \subseteq \gamma \) holds by construction. The S-relation \(\theta ''\) was built from relations in Q by using operations described in Definition 2.11 and Remark 2.14; therefore \(\theta '' \in {}^{S}{}\![Q]_{}\).
We show that \(\textbf{r}\notin \theta ''_{e}\). Indeed, if \(\textbf{r}\in \theta ''_{e}\) then there would exist a \(\textbf{b}\in \theta ^{*}_{e}\) such that \(\textbf{r}\times \textbf{b}\in \delta _{\tau }^{q+m}\) (recall the definitions of \(\theta '\) and \(\theta ''\), and that \(\textbf{r}= f_{\textbf{r}}(\varkappa _1, \dots , \varkappa _n) \in \gamma _e\) thus \(\textbf{r}\times \textbf{b}\in \gamma _{e}\times \theta ^{*}_e\)), consequently
a contradiction.
Thus \(\theta ''_e \subsetneqq \gamma _e\) and so \(\theta '' \subsetneqq \gamma \). We conclude that \(\gamma \) is not the smallest S-relation in \({}^{S}{}\![Q]_{}\) containing \(\chi ^\lambda \). We have reached the desired contradiction. \(\square \)
The following theorem generalizes the characterization of (usual) relational clones (cf. [14, Satz 1.2.3]) to S-relational clones.
Theorem 4.6
Let S be an arbitrary monoid. Then, for \(Q\subseteq {}^{S}{}\textrm{Rel}(A)\), we have
i.e., the Galois closure is the S-relational clone generated by Q.
Proof
Again we use the notation \(F:={}^{S}{}\textrm{Pol}\,Q\) and \(\gamma \) as in the lemmata before. Because of Lemma 4.4 it is enough to show \(\Gamma _{F}(\chi ^{\lambda })_{v}=\gamma (\chi ^{\lambda })_{v}\) for each \(v\in S\) and arbitrary signa \(\lambda \).
By Lemma 4.5 this is true for \(v=e\). Thus let \(v\in S\,{\setminus }\,\{e\}\) and let \(\lambda =(t'_{1},\dots ,t'_{p})\). We have to show \(\Gamma _{F}(\chi ^{\lambda })_{v}=\gamma (\chi ^{\lambda })_{v}\). Note that the entries of \(\lambda \) could be permuted arbitrarily without changing this equality (this follows from the fact that S-preclones are closed under permutation of arguments, cf. Remark 2.4).
Let \(\Lambda =\{t_{1},\dots ,t_{n}\}\) be the set of all different entries in the signum \(\lambda \), i.e., \(\Lambda =\{t'_{1},\dots ,t'_{p}\}\). Ordering the entries of \(\lambda \) correspondingly we can assume that
where \(t_{i}\) appears \(\ell _{i}\) times (\(i\in \{1,\dots ,n\}\)), thus \(p=t_{1}+ \cdots + t_{n}\). The corresponding elements (columns) of \(\chi ^{\lambda }\) are denoted as follows
Let \(\mathcal {M}^{v}=(M_{s})_{s\in S}\) with \(M_{s} = \{ \, x \in S \mid xv = s \, \}\) be the family as defined in Remark 2.13 (for simplicity we write \(M_{s}\) instead of \(M^{v}_{s}\)). Now we consider the signum
where each \(s_{i}\in M_{t_{i}}\) appears exactly \(\ell _{i}\) times (\(i\in \{1,\dots ,n\}\)). Because of Remark 2.13(b) no \(s\in S\) can appear in different \(M_{t_{i}}\).
At first consider the case \(\widehat{\lambda }=\emptyset \), i.e., \(M_{t_{1}}=\cdots =M_{t_{n}}=\emptyset \), consequently (by the definition of \(M_{t}\)) we have \(\{t_{1},\dots ,t_{n}\}\cap Sv=\emptyset \). Let \(m:=|A^{p}|\) be the arity of \(\chi ^{\lambda }\), and let \(d\in {}^{S}{}\!D_{A}\) denote the m-ary diagonal relation (cf. Definition 2.9) with \(d_{s}=\emptyset \) for \(s\in Sv\) and \(d_{s}= A^{m}\) otherwise. We get
Then \(\chi ^{\lambda }\subseteq \varrho :=\gamma (\chi ^{\lambda })\wedge d\in {}^{S}{}\![Q]_{}\), consequently \(\gamma (\chi ^{\lambda })\subseteq \varrho \), in particular we have \(\gamma (\chi ^{\lambda })_{v}\subseteq \varrho _{v}=\emptyset \). Therefore \(\Gamma _{F}(\chi ^{\lambda })_{v}=\gamma (\chi ^{\lambda })_{v}=\emptyset \), and we are done.
Thus, from now on, we can assume that \(M_{t}\ne \emptyset \) for at least one \(t\in \{t_{1},\dots ,t_{n}\}\). The S-relation \(\chi ^{\widehat{\lambda }}\) consists of \(\widehat{n}:=\ell _{1}\cdot |M_{t_{1}}|+\cdots +\ell _{n}\cdot |M_{t_{n}}|\ge 1\) columns which are denoted by
i.e., \(\chi ^{\widehat{\lambda }}_{s}=\{\widehat{\varkappa }_{s,1},\dots ,\widehat{\varkappa }_{s,\ell _{i}}\}\) for \(s\in M_{t_{i}}\), \(i\in \{1,\dots ,n\}\).
Let \(\widehat{m}:=|A|^{\widehat{n}}\). Note that the colums of \(\chi ^{\lambda }\) and \(\chi ^{\widehat{\lambda }}\) are elements of \(A^{m}\) and \(A^{\widehat{m}}\), respectively.
Choose the rows of \(\chi ^{\widehat{\lambda }}\) with indices \(z_{1},\dots ,z_{m}\) such that (for notation, see Remark 2.14(B))
i.e., \({{\,\textrm{pr}\,}}_{z_{1},\dots ,z_{m}}(\widehat{\varkappa }_{s,j})=\varkappa _{t_{i},j}\) for \(s\in M_{t_{i}}\), \(j\in \{1,\dots ,\ell _{i}\}\), therefore

for \(s\in M_{t_{i}}\), \(i\in \{1,\dots ,n\}\). Note that the rows \(z_{1},\dots ,z_{m}\) must exist because the rows of \(\chi ^{\widehat{\lambda }}\) are exactly all tuples in \(A^{\widehat{m}}\) (cf. Definition 3.14). The structure of \(\widehat{\lambda }\) and \(\chi ^{\widehat{\lambda }}\) and the introduced notation can be seen schematically in Figure 1.
We define \(\varrho :={{\,\textrm{pr}\,}}_{z_{1},\dots ,z_{m}}(\gamma (\chi ^{\widehat{\lambda }}))\) and \(\overline{\varrho }:=\sqcap _{\mathcal {M}^{v}}\varrho =\sqcap ^{v}\varrho \) (the last equation follows from Remark 2.13). Since \(\gamma (\chi ^{\widehat{\lambda }})\in {}^{S}{}\![Q]_{}\), also \(\overline{\varrho }\) belongs to \({}^{S}{}\![Q]_{}\), moreover we have \(\overline{\varrho }_{v}\subseteq \varrho _{e}\) because of property Remark 2.13(a) (cf. Definition 2.11(8) or 2.12(9)).
In particular, \(\chi ^{\lambda }\subseteq \overline{\varrho }\) because (with the above-mentioned equality (\(^\circ \))) we have \(\chi ^{\lambda }_{t}=({{\,\textrm{pr}\,}}_{{z_{1},\dots ,z_{m}}}(\chi ^{\widehat{\lambda }}))_{s} \subseteq ({{\,\textrm{pr}\,}}_{{z_{1},\dots ,z_{m}}}(\gamma (\chi ^{\widehat{\lambda }}))_{s} \) for all \(s\in M_{t}\), \(t\in \Lambda \) (note that \(\overline{\varrho }_{t} = \bigcap \{ \, \varrho _{s} \mid s \in M_{t} \, \}\)). Consequently, \(\gamma (\chi ^{\lambda })\subseteq \overline{\varrho }\) since \(\gamma (\chi ^{\lambda })\) is the least S-relation in \({}^{S}{}\![Q]_{}\) which contains \(\chi ^{\lambda }\).
Now, for \(\Gamma :=\Gamma _{F}(\chi ^{\lambda })\) we can prove \(\Gamma _{v}=\gamma (\chi ^{\lambda })_{v}\). We have to show only \(\gamma (\chi ^{\lambda })_{v}\subseteq \Gamma _{v}\) (the other inclusion is always fulfilled).
Let \(\textbf{r}\in \gamma (\chi ^{\lambda })_{v}\). Then \(\textbf{r}\in \varrho _{e}\) since \(\gamma (\chi ^{\lambda })_{v}\subseteq \overline{\varrho }_{v}\subseteq \varrho _{e}\). By the definition of \(\varrho \) there must exist \(\mathbf {\widehat{r}}\in \gamma (\chi ^{\widehat{\lambda }})_{e}\) such that \({{\,\textrm{pr}\,}}_{{z_{1},\dots ,z_{m}}}(\mathbf {\widehat{r}})=\textbf{r}\). By Lemma 4.5, \(\Gamma _{e}=\gamma (\chi ^{\lambda })_{e}\), thus \(\mathbf {\widehat{r}}\in \Gamma _{e}\). According to Proposition 3.13(iii) (with \(\varrho =\chi ^{\widehat{\lambda }}\), \(r=\mathbf {\widehat{r}}\)) there exist \(f\in F\) with \({{\,\textrm{sgn}\,}}(f)=\widehat{\lambda }=(v_{1},\dots ,v_{\widehat{n}})\) and \(\widehat{\textbf{r}}_{j}\in \chi ^{\widehat{\lambda }}_{v_{j}}\) (\(j\in \{1,\dots ,\widehat{n}\}\)) such that \(\widehat{\textbf{r}} =f(\widehat{\textbf{r}}_{1},\dots ,\widehat{\textbf{r}}_{\widehat{n}})\).
By the definition of \(\widehat{\lambda }\), each \(v_{j}\) belongs to \(M_{t}\) for some \(t\in \Lambda \), consequently \({{\,\textrm{pr}\,}}_{{z_{1},\dots ,z_{m}}}(\chi ^{\widehat{\lambda }}_{v_{j}})=\chi ^{\lambda }_{t}=\chi ^{\lambda }_{v_{j}v}\), the last equality follows from condition 2.13(c).
Applying \({{\,\textrm{pr}\,}}_{{z_{1},\dots ,z_{m}}}\) to \(\widehat{\textbf{r}} =f(\widehat{\textbf{r}}_{1},\dots ,\widehat{\textbf{r}}_{\widehat{n}})\), we get \(\textbf{r}=f(\textbf{r}_{1},\dots ,\textbf{r}_{\widehat{n}})\) where \(\textbf{r}_{j}={{\,\textrm{pr}\,}}_{{z_{1},\dots ,z_{m}}}(\widehat{\textbf{r}}_{j})\) (\(j\in \{1,\dots ,\widehat{n}\}\)) is an element of \({{\,\textrm{pr}\,}}_{{z_{1},\dots ,z_{m}}}(\chi ^{\widehat{\lambda }}_{v_{j}}) =\chi ^{\lambda }_{v_{j}v}\). Thus \(\textbf{r}\in f(\chi ^{\lambda }_{v_{1}v},\dots ,\chi ^{\lambda }_{v_{\widehat{n}}v})\subseteq f(\Gamma _{v_{1}v},\dots ,\Gamma _{v_{\widehat{n}}v})\subseteq \Gamma _{v}=\Gamma _{F}(\chi ^{\lambda })_{v}\) (the last inclusion follows from  , cf. 3.4(1), because \(f\in F\)). Since \(\textbf{r}\) was chosen arbitrarily, \(\gamma (\chi ^{\lambda })_{v}\subseteq \Gamma _{F}(\chi ^{\lambda })_{v}\) and we are done. \(\square \)
, cf. 3.4(1), because \(f\in F\)). Since \(\textbf{r}\) was chosen arbitrarily, \(\gamma (\chi ^{\lambda })_{v}\subseteq \Gamma _{F}(\chi ^{\lambda })_{v}\) and we are done. \(\square \)
As a final remark to conclude this section, we would like to present a connection between S-preclones and minions (and between the corresponding Galois connections).
Let \(f :A^n \rightarrow B\) and \(g :A^m \rightarrow B\). We say that f is a minor of g, and we write \(f \le g\), if there exists a map \(\sigma :\{1, \dots , m\} \rightarrow \{1, \dots , n\}\) such that \(f(a_1, \dots , a_n) = g(a_{\sigma (1)}, \dots , a_{\sigma (m)})\) for all \(a_1, \dots , a_n \in A\). The minor relation \(\le \) is a quasiorder (a reflexive and transitive relation) on the set \({{\,\textrm{Fun}\,}}(A,B):= \bigcup _{m\in \mathbb {N}_{+}}B^{A^{m}}\). Downwards closed subsets of \(({{\,\textrm{Fun}\,}}(A,B), \mathord {\le })\) are called minor-closed classes or minions.
Minor-closed classes can be characterized with a Galois connection analogous to \({{\,\textrm{Pol}\,}}\)–\({{\,\textrm{Inv}\,}}\) (see Definition 3.3). Instead of relations, the dual objects are now relation pairs, i.e., pairs \((\varrho ,\varrho ')\), where \(\varrho \in {{\,\textrm{Rel}\,}}^{(m)}(A)\) and \(\varrho ' \in {{\,\textrm{Rel}\,}}^{(m)}(B)\) for some \(m \in \mathbb {N}\). Denote by \({{\,\textrm{RelP}\,}}(A,B)\) the set of all such relation pairs. Let \(f \in {{\,\textrm{Fun}\,}}(A,B)\) and \((\varrho ,\varrho ') \in {{\,\textrm{RelP}\,}}(A,B)\). We say that f preserves \((\varrho ,\varrho ')\), and we write \(f \mathrel {\triangleright }(\varrho ,\varrho ')\), if \(f(\varrho , \dots , \varrho ) \subseteq \varrho '\). For \(F \subseteq {{\,\textrm{Fun}\,}}(A,B)\) and \(Q \subseteq {{\,\textrm{RelP}\,}}(A,B)\), we define
It was shown by Pippenger [12, Theorem 2.1] that if A and B are finite, then a set \(F \subseteq {{\,\textrm{Fun}\,}}(A,B)\) is a minion if and only if \(F = {{\,\textrm{PolP}\,}}Q\) for some \(Q \subseteq {{\,\textrm{RelP}\,}}(A,B)\). This was later generalized by Couceiro and Foldes [3, Theorem 2.1] for functions defined and valued on arbitrary sets; in this case, the Galois closed sets of functions are the locally closed minions.
For \(s \in S\), let \(F^{[s]}:= \{ \, f \in {}^{S}{}\textrm{Op}(A) \mid {{\,\textrm{Sgn}\,}}(f) = \{s\} \, \}\) be the S-signed part of F, i.e., all S-operations in F where each argument has signum s.
Proposition 4.7
If F is an S-preclone on A, then for each \(s \in S\), \(F^{[s]}\) is a minion; in particular, for the neutral element e of S, \(F^{[e]}\) is a clone. Moreover if \(F = {}^{S}{}\textrm{Pol}\,Q\) for some set \(Q \subseteq {}^{S}{}\textrm{Rel}(A)\), then \(F^{[s]} = {{\,\textrm{Pol}\,}}\{ \, (\varrho _{st}, \varrho _t) \mid \varrho \in Q, \, t \in S \, \}\); in particular, \(F^{[e]} = {{\,\textrm{Pol}\,}}\{ \, \varrho _t \mid \varrho \in Q, t \in S \, \}\).
Proof
It is clear from the definition that \(F^{[s]}\) is minor-closed; in particular, it is closed under arbitrary identification of arguments. For the neutral element e, we furthermore have that \(F^{[e]}\) is closed under composition; hence \(F^{[e]}\) is a clone (this also follows from Lemma 3.5(ii)). Moreover, an S-operation f with \({{\,\textrm{sgn}\,}}(f) = (s, \dots , s)\) S-preserves \(\varrho = (\varrho _s)_{s \in S}\) if and only if \(f(\varrho _{st}, \dots , \varrho _{st}) \subseteq \varrho _t\) for all \(t \in S\). The latter is equivalent to the condition that the operation f (ignoring signum) preserves the relation pair \((\varrho _{st}, \varrho _t)\) for all \(t \in S\). Therefore, if \(F = {}^{S}{}\textrm{Pol}\,Q\), then (ignoring signa)

For the neutral element e of S, we get furthermore (see also Lemma 3.5(ii)) that
\(\square \)
5 The lattice \({}^{S}{}\!\mathcal {L}_{A}\) of \(\varvec{S}\)-preclones
The S-preclones on a set A form a lattice \({}^{S}{}\!\mathcal {L}_{A}\) (with respect to inclusion). The least element is \({}^{S}{}\!\!J_{A}\) (cf. Remark 2.4) and the largest element is \({}^{S}{}\textrm{Op}(A)\). In this section we deal with atoms and coatoms of \({}^{S}{}\!\mathcal {L}_{A}\), with embeddings of the lattice \(\mathcal {L}_{A}\) of (usual) clones on A into \({}^{S}{}\!\mathcal {L}_{A}\), and with some inner symmetries of \({}^{S}{}\!\mathcal {L}_{A}\). But at first we shall look for generating systems of the S-preclone \({}^{S}{}\textrm{Op}(A)\) and the S-relational clone \({}^{S}{}\textrm{Rel}(A)\).
Proposition 5.1
-
(1)
The S-preclone \({}^{S}{}\textrm{Op}(A)\) is finitely generated.
For instance, for \(A=\{0,1,\dots ,k-1\}\) we have
$$ {}^{S}{}\!\langle \{m^{(e,e)}\} \cup \{ \, \textsf{id}^{s} \mid s \in S \, \} \rangle _{} = {}^{S}{}\textrm{Op}(A)\,, $$where \(m^{(e,e)}\) is the binary S-operation defined by \(m(x,y):=\max (x,y)\oplus 1\) (\(\oplus \) denotes addition modulo k) with \({{\,\textrm{sgn}\,}}(m)=(e,e)\).
-
(2)
The S-relational clone \({}^{S}{}\textrm{Rel}(A)\) is finitely generated.
For instance, for \(A=\{0,1,\dots ,k-1\}\) and \(k\ge 3\), we have
$$\begin{aligned} {}^{S}{}\![(\Delta ,\nabla ,\dots ,\nabla ), (\mathord {\le }, \mathord {\le }, \dots , \mathord {\le }), (\mathord {\ne }, \mathord {\ne }, \dots , \mathord {\ne })]_{} = {}^{S}{}\textrm{Rel}(A). \end{aligned}$$Here \((\sigma ,\sigma ',\dots ,\sigma ')\) denotes the relation \(\varrho \in {}^{S}{}\textrm{Rel}(A)\) with \(\varrho _{e}=\sigma \) and \(\varrho _{s}=\sigma '\) for \(s\in S{\setminus }\{e\}\).
-
(3)
The lattice \({}^{S}{}\!\mathcal {L}_{A}\) is atomic and coatomic, i.e., each nontrivial S-preclone contains a minimal one, and is contained in a maximal one.
Proof
(1): It is known (cf., e.g., [14, 5.1.4]), that m is a so-called Sheffer function, i.e., the clone generated by m is the full clone of all operations. Thus \({}^{S}{}\!\langle m \rangle _{}\) contains all functions \(f\in {}^{S}{}\textrm{Op}(A)\) with \({{\,\textrm{Sgn}\,}}(f)=\{e\}\). Let \(g\in {}^{S}{}\textrm{Op}(A)\) with \({{\,\textrm{sgn}\,}}(g)=(s_{1},\dots ,s_{n})\) and let \(f\in {}^{S}{}\textrm{Op}(A)\) be given by \(f(x_{1},\dots ,x_{n}):=g(x_{1},\dots ,x_{n})\) (i.e., \(\mathring{f}=\mathring{g}\)) and \({{\,\textrm{sgn}\,}}(f)=(e,\dots ,e)\). Then \(g^{\lambda }(x_{1},\dots ,x_{n})=f(\textsf{id}^{s_{1}}(x_{1}),\dots ,\textsf{id}^{s_{n}}(x_{n}))\) (cf. Definition 2.3(6)), thus \(g \in {}^{S}{}\!\langle \{f\} \cup \{\textsf{id}^{s_{1}},\dots ,\textsf{id}^{s_{n}}\} \rangle _{} \subseteq {}^{S}{}\!\langle \{m\} \cup \{ \, \textsf{id}^{s} \mid s \in S \, \} \rangle _{}\). Since g was chosen arbitrarily, we are done.
(2): It is known (cf., e.g., [14, 1.1.22]), that for \(k\ge 3\), \(\mathring{f}\in {{\,\textrm{Pol}\,}}\{\le ,\ne \}\) implies that \(\mathring{f}\) is a projection (because \([\le ,\ne ]_{A}={{\,\textrm{Rel}\,}}(A)\)). In case \(k=2\) one must take a ternary relation \(\sigma \) (see [14, 5.4.5]). Thus, because of Lemma 3.5(i), \(f\in {}^{S}{}\textrm{Pol}\{(\le ,\le ,\dots ,\le ),(\ne ,\ne ,\dots ,\ne )\}\) (or \(f\in {}^{S}{}\textrm{Pol}(\sigma ,\sigma ,\dots ,\sigma )\) for \(k=2\)) implies that \(\mathring{f}\) is a projection. From  we can conclude that all arguments with signum \(s\ne e\) must be fictitious, i.e., f is a trivial projection (\(\in {}^{S}{}\!\!J_{A}\)). Consequently, by Theorem 4.6, the S-relational clone generated by the above relations equals
we can conclude that all arguments with signum \(s\ne e\) must be fictitious, i.e., f is a trivial projection (\(\in {}^{S}{}\!\!J_{A}\)). Consequently, by Theorem 4.6, the S-relational clone generated by the above relations equals  .
.
(3): It is well known from universal algebra that the subalgebra lattice of a finitely generated algebra is coatomic (cf. [14, proof of 3.1.5]). Thus it follows from (1) that \({}^{S}{}\!\mathcal {L}_{A}\) (as lattice of sub-S-preclones of \({}^{S}{}\textrm{Op}(A)\)) is coatomic. Analogously, by (2), the lattice of all S-relational clones is coatomic. However, due to the Galois connection \({}^{S}{}\textrm{Pol}\)–\({}^{S}{}\textrm{Inv}\) and Theorems 4.1 and 4.6, the latter lattice is dual to \({}^{S}{}\!\mathcal {L}_{A}\), consequently \({}^{S}{}\!\mathcal {L}_{A}\) is atomic. \(\square \)
Proposition 5.2
There are finitely many maximal and finitely many minimal S-preclones in \({}^{S}{}\!\mathcal {L}_{A}\).
Proof
(a) Let \(F\subsetneq {}^{S}{}\textrm{Op}(A)\) be a maximal S-preclone (coatom). We consider the following S-relations \(\varrho ^{(s)}\), \(s\in S\): \(\varrho ^{(e)}:=\Gamma _{F}(\chi ^{(e,e)})\) and \(\varrho ^{(s)}:=\Gamma _{F}(\chi ^{(s)})\) for \(s\in S\,{\setminus }\,\{e\}\). If all these \(\varrho ^{(s)}\) were S-diagonals, then the functions \(m^{(e,e)}\) and \(\textsf{id}^{s}\) (see Proposition 5.1(1)) would belong to F by Proposition 3.15, i.e., F would contain a generating system for \({}^{S}{}\textrm{Op}(A)\), which contradicts the assumption \(F\subsetneq {}^{S}{}\textrm{Op}(A)\). Thus at least one of the \(\varrho ^{(s)}\), say \(\varrho ^{(s_{i})}\), is nontrivial and we have \(F\subseteq {}^{S}{}\textrm{Pol}\,{}^{S}{}\textrm{Inv}\,F\subseteq {}^{S}{}\textrm{Pol}\,\varrho ^{(s_{i})}\subsetneq {}^{S}{}\textrm{Op}(A)\). By the maximality of F we get \(F={}^{S}{}\textrm{Pol}\,\varrho ^{(s_{i})}\). This means that each maximal S-preclone is determined by an S-relation of bounded arity (more precisely, it is the arity of \(\chi ^{(e,e)}\) or \(\chi ^{(s)}\), i.e., \(|A|^{2}\) or |A|). But there exist only finitely many S-relations of fixed arity. Consequently there are only finitely many maximal S-preclones.
(b) Let F be a minimal S-preclone. Then F is generated by each nontrivial S-operation \(f\in F\,{\setminus } \,{}^{S}{}\!\!J_{A}\). We are going to show that there is always a nontrivial function \(f'\) in F with arity at most \(m:=|A^{2}|\cdot |S|\). Since there are only finitely many functions \(f'\) of fixed bounded arity, there are also only finitely many minimal S-preclones (because they are of the form \(F={}^{S}{}\!\langle f' \rangle _{}\)), and we are done.
Let \(f\in F\,{\setminus }\, {}^{S}{}\!\!J_{A}\), \({{\,\textrm{sgn}\,}}(f)=(s_{1},\dots ,s_{n})\). Then f does not preserve at least one of the three binary relations (denoted by \(\varrho \) here) in Proposition 5.1(2) generating \({}^{S}{}\textrm{Rel}(A)\) (otherwise  is trivial). The condition \(f\mathrel {\not \triangleright }\varrho \) means that there must exist \(s\in S\) and \(r_{1}\in \varrho _{s_{1}s},\dots ,r_{n}\in \varrho _{s_{n}s}\) such that \(f(r_{1},\dots ,r_{n})\notin \varrho _{s}\). Because \(\varrho \) is binary, \(|\varrho _{t}|\le |A^{2}|\) for all \(t\in S\), i.e., there exist at most \(|A^{2}|\cdot |S|\) different elements for \(r_{1},\dots ,r_{n}\) (\(|A^{2}|\) for each signum \(t\in S\)). Thus, if \(n> m\), one can identify arguments in \(f(x_{1},\dots ,x_{n})\) (namely \(x_{i}\) with \(x_{j}\) if \(r_{i}=r_{j}\) and \(s_{i}=s_{j}\)) and gets a function \(f'\in {}^{S}{}\!\langle f \rangle _{}=F\) of arity at most m which still does not preserve \(\varrho \), i.e., \(f'\notin {}^{S}{}\!\!J_{A}\) is nontrivial, which was to be shown. \(\square \)
is trivial). The condition \(f\mathrel {\not \triangleright }\varrho \) means that there must exist \(s\in S\) and \(r_{1}\in \varrho _{s_{1}s},\dots ,r_{n}\in \varrho _{s_{n}s}\) such that \(f(r_{1},\dots ,r_{n})\notin \varrho _{s}\). Because \(\varrho \) is binary, \(|\varrho _{t}|\le |A^{2}|\) for all \(t\in S\), i.e., there exist at most \(|A^{2}|\cdot |S|\) different elements for \(r_{1},\dots ,r_{n}\) (\(|A^{2}|\) for each signum \(t\in S\)). Thus, if \(n> m\), one can identify arguments in \(f(x_{1},\dots ,x_{n})\) (namely \(x_{i}\) with \(x_{j}\) if \(r_{i}=r_{j}\) and \(s_{i}=s_{j}\)) and gets a function \(f'\in {}^{S}{}\!\langle f \rangle _{}=F\) of arity at most m which still does not preserve \(\varrho \), i.e., \(f'\notin {}^{S}{}\!\!J_{A}\) is nontrivial, which was to be shown. \(\square \)
Concerning maximal S-preclones in \({}^{S}{}\!\mathcal {L}_{A}\) we have the following characterization.
Proposition 5.3
Each maximal S-preclone \(F\le {}^{S}{}\textrm{Op}(A)\) can be characterized as \(F={}^{S}{}\textrm{Pol}\,\varrho \) for some \(\varrho \in {}^{S}{}\textrm{Rel}(A)\) such that we have \((^{*})_{s}\) for each \(s\in S\), where

Proof
Let \(F\in {}^{S}{}\!\mathcal {L}_{A}\) be a maximal S-preclone and let \(\varrho \in {}^{S}{}\textrm{Inv}\,F\,{\setminus }\,{}^{S}{}\!D_{A}\). Then \(F\subseteq {}^{S}{}\textrm{Pol}\,{}^{S}{}\textrm{Inv}\,F\subseteq {}^{S}{}\textrm{Pol}\,\varrho \subsetneq {}^{S}{}\textrm{Op}(A)\), thus, by the maximality of F, \(F={}^{S}{}\textrm{Pol}\,\varrho \) for each nontrivial S-relation \(\varrho \) in \({}^{S}{}\textrm{Inv}\,F\).
Let \(F={}^{S}{}\textrm{Pol}\,\varrho \) be maximal and assume \(\varrho _{s}\notin D_{A}\) (not diagonal, not empty) for some \(s\in S\). If \((^{*})_{s}\) is not satisfied, then (since \(\varrho _{s}\) is nontrivial) there exists a minimal relational clone \([\sigma _{s}]\subseteq [\varrho _{s}]\) where we choose \(\sigma _{s}\) such that \({{\,\textrm{ar}\,}}(\sigma _{s})\) is minimal. Thus there exists a “construction” \(t_{\varphi }\) (logical operation with pp-formula \(\varphi \)) such that \(\sigma _{s}=t_{\varphi }(\varrho _{s})\). Thus \(\varrho ':=t_{\varphi }(\varrho )\) is a nontrivial S-relation with \(\varrho '_{s}=\sigma _{s}\). Moreover we have \(\varrho '\in {}^{S}{}\textrm{Inv}\,F\) (by Lemma 3.9), consequently \(F={}^{S}{}\textrm{Pol}\,\varrho '\) as well. By construction, \(\varrho '_{s}\) satisfies \((^{*})_{s}\). Clearly \({{\,\textrm{ar}\,}}(\varrho ')\le {{\,\textrm{ar}\,}}(\varrho )\).
If \(\varrho '\) does not satisfy \((^{*})_{s}\) for all \(s\in S\), one chooses the next \(s'\in S\) with nontrivial \(\varrho '_{s'}\) and repeats the above procedure getting \(\varrho ''=t_{\varphi '}(\varrho ')\) with some \(t_{\varphi '}\) such that \(t_{\varphi '}(\varrho '_{s'})=\sigma '_{s'}\) with minimal relational clone \([\sigma '_{s'}]\) (and minimal arity \({{\,\textrm{ar}\,}}(\sigma '_{s'})={{\,\textrm{ar}\,}}(\varrho '')\le {{\,\textrm{ar}\,}}(\varrho ')\)). Note that \(\sigma '_{s}:=t_{\varphi '}(\varrho '_{s})\in [\varrho '_{s}]=[\sigma _{s}]\) and therefore either \(\sigma '_{s}\in D_{A}\) (this, in particular, is the case if \({{\,\textrm{ar}\,}}(\varrho '')<{{\,\textrm{ar}\,}}(\sigma _{s})={{\,\textrm{ar}\,}}(\varrho ')\)) or \([\sigma '_{s}]=[\sigma _{s}]\) is minimal (by minimality of \([\sigma _{s}]\)). Consequently \(\varrho '':=t_{\varphi '}(\varrho ')\) satisfies both \((^{*})_{s}\) and \((^{*})_{s'}\).
One can continue this until one gets an S-relation \(\omega \) with \(F={}^{S}{}\textrm{Pol}\omega \) satisfying \((^{*})_{s}\) for each \(s\in S\) (i.e., that each \(\omega _{s}\) is trivial or \({{\,\textrm{Pol}\,}}\omega _{s}\) is a maximal clone and \({{\,\textrm{ar}\,}}(\omega )\) is the minimal arity of a nontrivial relation in \([\omega _{s}]_{}\)). \(\square \)
Remark 5.4
The maximal clones that appear in the conditions \((^{*})_{s}\) are known from the classical result of Rosenberg [18]. Therefore Proposition 5.3 provides useful candidates for determining all maximal S-preclones. It “only” remains the task to exclude those \(\varrho \) which do not give a maximal S-preclone \(F={}^{S}{}\textrm{Pol}\,\varrho \) (such as, trivially, all diagonal S-relations). This we shall do in Part II for Boolean S-preclones (there exist 9 maximal Boolean S-preclones for the two-element group S).
At the end of this section we shall deal with the complexity of \({}^{S}{}\!\mathcal {L}_{A}\) versus \(\mathcal {L}_{A}\) and present two (nearly trivial) embeddings of the clone lattice \(\mathcal {L}_{A}\) into the S-preclone lattice \({}^{S}{}\!\mathcal {L}_{A}\). Moreover we generalize symmetries of \(\mathcal {L}_{A}\) (inner automorphisms) to \({}^{S}{}\!\mathcal {L}_{A}\).
Proposition 5.5
We define the mappings \(\Psi ,\Phi :\mathcal {L}_{A}\rightarrow {}^{S}{}\!\mathcal {L}_{A}\) as follows (for \(F\in \mathcal {L}_{A}\)):
Then \(\Psi \) is a lattice embedding into the interval \([{}^{S}{}\!\!J_{A},\Psi ({{\,\textrm{Op}\,}}(A))]_{{}^{S}{}\!\mathcal {L}_{A}}\) in \({}^{S}{}\!\mathcal {L}_{A}\), i.e., into the principal ideal generated by \(\Psi ({{\,\textrm{Op}\,}}(A))\) in \({}^{S}{}\!\mathcal {L}_{A}\), and \(\Phi \) is a lattice embedding into the interval \([\Phi (J_{A}),{}^{S}{}\textrm{Op}(A)]_{{}^{S}{}\!\mathcal {L}_{A}}\), i.e., into the principal filter generated by \(\Phi (J_{A})\) in \({}^{S}{}\!\mathcal {L}_{A}\) (where \(\Phi (J_{A}) = {}^{S}{}\!\langle \{ \, \textsf{id}^{s} \mid s \in S \,\} \rangle _{}\)). If S is a group then \(\Phi \) is an embedding onto the principal filter generated by \({}^{S}{}\!\langle \{ \, \textsf{id}^{s} \mid s \in S \, \} \rangle _{}\) in \({}^{S}{}\!\mathcal {L}_{A}\).
Proof
For a clone \(F \in \mathcal {L}_{A}\), \(\Psi (F)\) is obtained by taking the functions in F, giving all arguments the signum e, and then adding an arbitrary number of fictitious arguments of arbitrary signum in all possible ways. Thus each S-operation in \(\Psi (F)\) has essential arguments only for signum e, in particular we have \((\Psi (F)^{[e]})\,\mathring{}=F\) (note that the e-part of each S-preclone is a clone by Proposition 4.7). Thus \(\Psi \) is injective; moreover \(\Psi (J_{A})={}^{S}{}\!\!J_{A}\).
Clearly, \(\Phi (F)\) is an S-preclone. For a clone \(F \in \mathcal {L}_{A}\), \(\Phi (F)\) contains, for each operation \(f \in F\), every S-operation g with \(\mathring{g}=f\) and arbitrary signum. Thus \(\Phi ({{\,\textrm{Op}\,}}(A))={}^{S}{}\textrm{Op}(A)\) and \(\Phi (J_{A}) = {}^{S}{}\!\langle \{ \, \textsf{id}^{s} \mid s \in S \, \} \rangle _{}\). Note also that \((\Phi (F))\,\mathring{}=F\).
From the definitions it easily follows that \(\Psi \) and \(\Phi \) are lattice embeddings (the image of joins (or meets) are joins (or meets) of the images).
If S is a group, then \(\{ \, \textsf{id}^{s} \mid s \in S \, \}\subseteq H\) (for some \(H\in {}^{S}{}\!\mathcal {L}_{A}\)) implies the following property for H: If \(f^{\lambda }\in H\) then \(f^{\lambda '}\in H\) for arbitrary signa \(\lambda =(s_{1},\dots ,s_{n})\), \(\lambda '=(s'_{1},\dots ,s'_{n})\). This proves \(H=\Phi (F)\) with \(F = \{ \, \mathring{f} \mid f \in H \, \} \in \mathcal {L}_{A}\) and we are done. In fact, for \(s_{i}, s_{i}'\) there exists \(u_{i}\in S\) such that \(s_{i}'=s_{i}u_{i}\) (\(i\in \{1,\dots ,n\}\)). Then \(f^{\lambda '}(x_{1},\dots ,x_{n})=f(\textsf{id}^{u_{1}}(x_{1}),\dots ,\textsf{id}^{u_{n}}(x_{n}))\) is a composition of f and the \(\textsf{id}^{s}\) (cf. Definition 2.3(6)) and therefore belongs to H by the assumption on H. \(\square \)
The preceding result contains two embeddings of the lattice of clones into the lattice of S-preclones. It is worth noting that Proposition 3.10 defines an inverse of the map \(\Phi \) by mapping each S-preclone to the clone generated by all operations in the S-preclone, ignoring the signa of these operations.
Definition 5.6
Let \(\pi :A\rightarrow A\) be a permutation on A. Then, for \(f\in {}^{S}{}\textrm{Op}(A)\), \(\varrho =(\varrho _{s})_{s\in S}\in {}^{S}{}\textrm{Rel}^{(m)}(A)\), \(F\subseteq {}^{S}{}\textrm{Op}(A)\) and \(Q\subseteq {}^{S}{}\textrm{Rel}(A)\) we define the \(\pi \)-dual \(f^{\pi }\), \(\varrho ^{\pi }=(\varrho ^{\pi }_{s})_{s\in S}\), \(F^{\pi }\) and \(Q^{\pi }\) as follows:
An S-operation f with \(f^{\pi }=f\) and an S-preclone F with \(F^{\pi }=F\) are called \(\pi \)-selfdual. (\(\pi \)-selfdual S-relations and S-relational clones are defined analogously.)
Remark 5.7
The mapping \((-)^{\pi }:{}^{S}{}\textrm{Op}(A)\rightarrow {}^{S}{}\textrm{Op}(A): f\mapsto f^{\pi }\) is an automorphism, called an inner automorphism, of the full S-preclone \({}^{S}{}\textrm{Op}(A)\) considered as an algebra equipped with the operations \(\textsf{id}_{A},\zeta ,\tau ,\nabla ^{s},\Delta ,\circ \) (cf., e.g., [8, 14, 3.4.1]).
For the classical clone \({{\,\textrm{Op}\,}}(A)\), there are only inner automorphisms ([8, Theorem 2]). However, for S-preclones there are further automorphisms, which are induced by the automorphisms of the monoid S.
Definition 5.8
Let \(h:S\rightarrow S\) be an automorphism of the monoid S. For \(f\in {}^{S}{}\textrm{Op}(A)\), with \({{\,\textrm{sgn}\,}}(f)=(s_{1},\dots ,s_{n})\) and \(\varrho \in {}^{S}{}\textrm{Rel}(A)\) we define \(f^{h}\) and \(\varrho ^{h}\) as follows:
Note that \(\varrho ^{h}\) is well defined because h is bijective.
Remark 5.9
The mapping \((-)^{h}:{}^{S}{}\textrm{Op}(A)\rightarrow {}^{S}{}\textrm{Op}(A): f\mapsto f^{h}\) changes only the signum of f and not the underlying function \(\mathring{f}\). It is also an automorphism of the full S-preclone \(\langle {}^{S}{}\textrm{Op}(A);\textsf{id}_{A},\zeta ,\tau ,\nabla ^{s},\Delta ,\circ \rangle \) (considered as an algebra). This can be checked easily. We show only for \(\circ \) that indeed \((f\circ g)^{h}=f^{h}\circ g^{h}\) (we have to check the signa only; for the notation, see Definition 2.3(6)):
The automorphisms also provide inner symmetries of the lattice \({}^{S}{}\!\mathcal {L}_{A}\).
Proposition 5.10
The mappings \((-)^{\pi }:{}^{S}{}\!\mathcal {L}_{A}\rightarrow {}^{S}{}\!\mathcal {L}_{A}: F\mapsto F^{\pi }\) and \((-)^{h}:{}^{S}{}\!\mathcal {L}_{A}\rightarrow {}^{S}{}\!\mathcal {L}_{A}: F\mapsto F^{h}\) are lattice automorphisms.
Proof
It is easy to check that \((F_{1}\wedge F_{2})^{\pi }=(F_{1}\cap F_{2})^{\pi }= F_{1}^{\pi }\cap F_{2}^{\pi }=F_{1}^{\pi }\wedge F_{2}^{\pi }\) and \((F_{1}\vee F_{2})^{\pi }= ({}^{S}{}\!\langle F_{1}\cup F_{2} \rangle _{})^{\pi }={}^{S}{}\!\langle (F_{1}\cup F_{2})^{\pi } \rangle _{}= {}^{S}{}\!\langle F_{1}^{\pi }\cup F_{2}^{\pi } \rangle _{}=F_{1}^{\pi }\vee F_{2}^{\pi }\), analogously for h instead of \(\pi \). \(\square \)
Finally, we show the interplay of the “duality” operator \((-)^{\pi }\) and the “signum permuting” operator \((-)^{h}\) with the Galois connection \({}^{S}{}\textrm{Pol}\)–\({}^{S}{}\textrm{Inv}\):
Proposition 5.11
Let \(\pi \) be a permutation on A, let h be an automorphism of S and \(f\in {}^{S}{}\textrm{Op}(A)\), \(\varrho \in {}^{S}{}\textrm{Rel}(A)\), \(F\subseteq {}^{S}{}\textrm{Op}(A)\), \(Q\subseteq {}^{S}{}\textrm{Rel}(A)\). Then we have
-
(i)
 ,
,  ,
, -
(ii)
\({}^{S}{}\textrm{Inv}\,F^{\pi }=({}^{S}{}\textrm{Inv}\,F)^{\pi }\), \({}^{S}{}\textrm{Inv}\,F^{h}=({}^{S}{}\textrm{Inv}\,F)^{h}\),
-
(iii)
\({}^{S}{}\textrm{Pol}\,Q^{\pi }=({}^{S}{}\textrm{Pol}\,Q)^{\pi }\), \({}^{S}{}\textrm{Pol}\,Q^{h}=({}^{S}{}\textrm{Pol}\,Q)^{h}\).
Proof
(i): Let \({{\,\textrm{sgn}\,}}(f)=(s_{1},\dots ,s_{n})\) and \(s\in S\). Then
According to 3.4(1) we get the first part of (i).
Furthermore, with \((t_{1},\dots ,t_{n}):=(h(s_{1}),\dots ,h(s_{n}))={{\,\textrm{sgn}\,}}(f^{h})\) and \(t:=h(s)\) we have (according to the definitions):
According to 3.4(1) we get the second part of (i) (note that if s runs through all elements of S then also \(t=h(s)\) does so, because h is bijective).
(ii) and (iii) follow directly from (i). \(\square \)
6 Concluding remarks
In Sect. 2 we defined the Galois connection \({}^{S}{}\textrm{Pol}\)–\({}^{S}{}\textrm{Inv}\) for S-preclones and S-relational clones, and Theorems 4.1, 4.6 show that on a finite set, S-preclones correspond exactly to Galois closed sets of S-operations and S-relational clones are captured precisely by Galois closed sets of S-relations. Since the correspondence of clones with relational clones is a fundamental result that has many applications, one can now ask whether similar applications hold for S-preclones and S-relational clones. For example:
Problem
Classify the maximal S-preclones for a finite monoid S and finite set A (analogously to Rosenberg’s classification of maximal clones [18]).
The motivating example for S-preclones is based on the 2-element group \(S = \{\mathord {+}, \mathord {-}\}\) and the S-relation \((\mathord {\le },\mathord {\ge })\) for a poset \((A,\mathord {\le })\) (cf. Examples 2.5 and 3.7). S-preclones for this group are referred to as ±-preclones, and the problem above may be more approachable if it is first restricted to ±-preclones.
Likewise, for any result about clones, one might investigate whether a similar result holds about S-preclones.
Proposition 5.2 shows that for a finite set A there are only finitely many maximal and finitely many minimal S-preclones. In Part II we take a detailed look at the lattice of ±-preclones over a 2-element set and find a complete list of atoms and coatoms of this lattice. In particular, it is shown that \({}^{S}{}\textrm{Pol}\{(\mathord {\le },\mathord {\ge })\}\) (see Example 3.7) is a maximal ±-preclone.
Moreover, there appears the question if the notions of S-preclone and S-relational clone can be extended to the setting where the monoid S of signa is only assumed to be a semigroup.
Finally it is an interesting problem to develop the theory of S-algebras \((A,(f_{i})_{i\in I})\) with fundamental operations \(f_{i}\in {}^{S}{}\textrm{Op}(A)\) for a fixed finite monoid S.
Data availability
Data sharing is not applicable to this article as datasets were neither generated nor analysed.
References
Boardman, J.M., Vogt, R.M.: Homotopy Invariant Algebraic Structures on Topological Spaces. Lecture Notes in Mathematics, vol. 347. Springer, Berlin (1973)
Bodnarčuk, V.G., Kalužnin, L.A., Kotov, N.N., Romov, B.A.: Galois theory for Post algebras I. Kibernetika (Kiev) 3, 1–10 (1969). (Russian)
Couceiro, M., Foldes, S.: On closed sets of relational constraints and classes of functions closed under variable substitutions. Algebra Universalis 54, 149–165 (2005)
Ésik, Z., Weil, P.: Algebraic recognizability of regular tree languages. Theor. Comput. Sci. 340(2), 291–321 (2005)
Lau, D.: Function Algebras on Finite Sets. Springer Monographs in Mathematics. Springer, Berlin (2006)
Lehtonen, E.: Characterization of preclones by matrix collections. Asian-Eur. J. Math. 3(3), 457–473 (2010)
Lehtonen, E., Pöschel, R., Waldhauser, T.: Reflections on and of minor-closed classes of multisorted operations. Algebra Universalis 79(3), 71 (2018)
Mal’cev, A.I.: Iterative algebras and Post manifolds. Algebra i Logika Sem. 5(2), 5–24 (1966). (Russian)
Markl, M.: Operads and PROPs. In: Hazewinkel,M.(ed.), Handbook of Algebra, vol. 5, pp. 87–140. Elsevier/North-Holland, Amsterdam (2008)
May, J.P.: The Geometry of Iterated Loop Spaces. Lecture Notes in Mathematics, vol. 271. Springer, Berlin (1972)
Pigozzi, D.: Partially ordered varieties and quasivarieties. http://www.researchgate.net/publication/250226836_PARTIALLY_ORDERED_VARIETIES_AND_QUASIVARIETIES (2004)
Pippenger, N.: Galois theory for minors of finite functions. Discrete Math. 254(1–3), 405–419 (2002)
Pöschel, R.: Galois connections for operations and relations. In: Denecke, K., Erné, M., Wismath, S.L. (eds.) Galois Connections and Applications. Mathematics and Its Applications, vol. 565, pp. 231–258. Kluwer Academic Publishers, Dordrecht (2004)
Pöschel, R., Kalužnin, L.A.: Funktionen- und Relationenalgebren. Deutscher Verlag der Wissenschaften, Berlin (1979). Math. Reihe Bd. 67. Birkhäuser Verlag, Basel (1979)
Post, E.L.: Determination of all closed systems of truth tables. Bull. Am. Math. Soc. 26, 437 (1920)
Post, E.L.: Introduction to a general theory of elementary propositions. Am. J. Math. 43, 163–185 (1921)
Post, E.L.: The Two-valued Iterative Systems of Mathematical Logic. Annals of Mathematics Studies, vol. 5. Princeton University Press, Princeton (1941)
Rosenberg, I.G.: Über die funktionale Vollständigkeit in den mehrwertigen Logiken. Rozpr. ČSAV Řada Mat. Přir. Věd. Praha 80(4), 3–93 (1970)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no Conflict of interest.
Additional information
Communicated by Presented by P. Mayr.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jipsen, P., Lehtonen, E. & Pöschel, R. \(\varvec{S}\)-preclones and the Galois connection \(\varvec{{}^{S}{}\textrm{Pol}}\)–\(\varvec{{}^{S}{}\textrm{Inv}}\), Part I. Algebra Univers. 85, 34 (2024). https://doi.org/10.1007/s00012-024-00863-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00012-024-00863-7


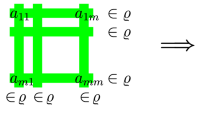



 ,
,  ,
,