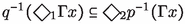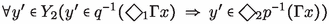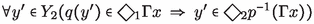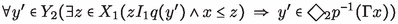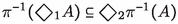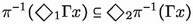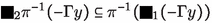Abstract
We revisit the problem of Stone duality for lattices with quasioperators, presenting a fresh duality result. The new result is an improvement over that of our previous work in two important respects. First, the axiomatization of frames is now simplified, partly by incorporating Gehrke’s proposal of section stability for relations. Second, morphisms are redefined so as to preserve Galois stable (and co-stable) sets and we rely for this, partly again, on Goldblatt’s recently proposed definition of bounded morphisms for polarities. In studying the dual algebraic structures associated to polarities with relations we demonstrate that stable/co-stable set operators result as the Galois closure of the restriction of classical (though sorted) image operators generated by the frame relations to Galois stable/co-stable sets. This provides a proof, at the representation level, that non-distributive logics can be regarded as fragments of sorted residuated (poly)modal logics, a research direction recently initiated by this author.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this article we address and resolve the problem of Stone duality for the category of lattices with quasioperators. The work presented here is a significant improvement over our own [21] (with Dunn) and [15]. The axiomatization of frames and frame relations in [15] was rather cumbersome and it is now simplified, partly by incorporating Gehrke’s proposal [9] of section stability for relations. Morphisms in the category of frames (polarities with relations) dual to lattices with quasioperators are defined so that not only clopens in the dual complex algebra of the frame be preserved (as in [15, 21]) but so that the inverses of frame morphisms are morphisms of the complete lattices of stable sets dual to frames (their full complex algebras), preserving arbitrary joins and meets. Polarity morphisms, as we define them, are the same as Goldblatt’s bounded morphisms for polarities [11], but we diverge from [11] in the extension to morphisms for polarities with relations. We also diverge from [9, 11] in the definition of canonical relations and in the way operators are defined from frame relations. We do this with the express objective of demonstrating that quasioperators in the complex algebra of stable sets of a frame can be obtained as the Galois closure of the restriction to Galois sets of the classical though sorted image operators generated from the relations, in the Jónsson–Tarski style [24]. The logical significance of this is that it demonstrates at the representation level that non-distributive logics are fragments of sorted residuated polymodal logics (their modal companions).
The structure of this article is as follows. Section 2 is an introductory section, defining the category NLE\(_\tau \) of normal lattice expansions of some similarity type \(\tau \) (a sequence of distribution types of lattice operators).
In Section 3 we present basic definitions and results for polarities (equivalently, sorted residuated frames). In Remark 3.2 we carefully list all our notational conventions, to ensure the reader has an effortless and seamless understanding of our notation.
With Section 3.1 we address the first issue of significance for our purposes, which is to define operators from relations, properly axiomatized, so as to ensure complete distribution properties of the defined operators. In the same section we list the first four axioms for the objects of the category SRF\(_\tau \) of sorted residuated frames (polarities) with relations.
Section 3.2 turns to studying morphisms, first for frames in the absence of additional relations (Section 3.2.1) and then for frames with additional relations of sort types in some similarity type \(\tau \) (Section 3.2.2). Further axioms for frame morphisms are stated and the category SRF\(_\tau \) defined (Definition 3.26).
Section 4 defines a contravariant functor from the category NLE\(_\tau \) to the category SRF\(_\tau \). For the lattice representation, we rely on [21] and for the representation of normal lattice operators we draw on [14] and [15] and we review the canonical frame construction in Section 4.1. Sections 4.2 and 4.3 are devoted to proving that the frame axioms hold for the dual frame of a normal lattice expansion and for the duals of normal lattice expansion homomorphisms.
Stone duality is addressed in Section 5. To ensure a Stone duality theorem can be proven we extend the axiomatization for frames (defining a smaller category \(\mathbf{SRF}^*_\tau \) and topologizing the frames), drawing on [15, 21], we verify that all additional axioms hold for the canonical frame construction and we conclude with a Stone duality theorem (Theorem 5.8).
In the Conclusions in Section 6 we summarize the results obtained and sketch a potential area for further research.
2 Normal Lattice Expansions (NLEs)
Let \(\{1,\partial \}\) be a 2-element set, \({\mathcal {L}}^1={\mathcal {L}}\) and \({\mathcal {L}}^\partial ={\mathcal {L}}^{op}\) (the opposite lattice). Extending established terminology [24], a function \(f:{\mathcal {L}}_1\times \dots \times {\mathcal {L}}_n\longrightarrow {\mathcal {L}}_{n+1}\) will be called additive and normal, or a normal operator, if it distributes over finite joins of the lattice \({\mathcal {L}}_i\), for each \(i=1,\ldots n\), delivering a join in \({\mathcal {L}}_{n+1}\).
Definition 2.1
An n-ary operation f on a bounded lattice \({\mathcal {L}}\) is a normal lattice operator of distribution type \(\delta (f)=(i_1,\ldots ,i_n;i_{n+1})\in \{1,\partial \}^{n+1}\) if it is a normal additive function \(f:{\mathcal L}^{i_1}\times \dots \times {{\mathcal {L}}}^{i_n}\longrightarrow {\mathcal {L}}^{i_{n+1}}\) (distributing over finite joins in each argument place), where each \(i_j\), for \(j=1,\ldots ,n+1\), is in the set \(\{1,\partial \}\), hence \({{\mathcal {L}}}^{i_j}\) is either \({\mathcal {L}}\), or \({{\mathcal {L}}}^\partial \).
If \(\tau \) is a tuple (sequence) of distribution types, a normal lattice expansion of (similarity) type \(\tau \) is a lattice with a normal lattice operator of distribution type \(\delta \) for each \(\delta \) in \(\tau \).
Normal lattice operators in the above sense are sometimes referred to in the literature as quasioperators, see for example Moshier and Jipsen [27, 28]. Remarks 4.2 and 4.8 provide some clarifications on the connections between [27, 28] and related work by this author [14, 15, 21], including the present article.
Definition 2.2
The category NLE\(_\tau \), for a fixed similarity type \(\tau \), has normal lattice expansions of type \(\tau \) as objects. Its morphisms are the usual algebraic homomorphisms.
Example 2.3
A modal normal diamond operator \(\Diamond \) is a normal lattice operator of distribution type \(\delta (\Diamond )=(1;1)\), i.e., \(\Diamond :{\mathcal {L}}\longrightarrow {\mathcal {L}}\), distributing over finite joins of \({\mathcal {L}}\). A normal box operator \(\Box \) is also a normal lattice operator in the sense of Definition 2.1, of distribution type \(\delta (\Box )=(\partial ;\partial )\), i.e., \(\Box :{\mathcal {L}}^\partial \longrightarrow {\mathcal {L}}^\partial \) distributes over finite joins of \({\mathcal {L}}^\partial \), which are then just meets of \({\mathcal {L}}\).
An FL\(_{\mathrm {ew}}\)-algebra (also referred to as a full BCK-algebra, or a commutative integral residuated lattice) \({\mathcal {A}}=(L,\wedge ,\vee ,0,1,\circ ,\rightarrow )\) is a normal lattice expansion, where \(\delta (\circ )=(1,1;1)\), \(\delta (\rightarrow )=(1,\partial ;\partial )\), i.e., \(\circ :{\mathcal {L}}\times {\mathcal {L}}\longrightarrow {\mathcal {L}}\) and \(\rightarrow \;:{\mathcal {L}}\times {\mathcal {L}}^\partial \longrightarrow {\mathcal {L}}^\partial \) are both normal lattice operators with the familiar distribution properties.
The Grishin operators [13] \(\leftharpoondown ,\star ,\rightharpoondown \), satisfying the familiar co-residuation conditions \(a\ge c\leftharpoondown b\) iff \(a\star b\ge c\) iff \(b\ge a\rightharpoondown c\) have the respective distribution properties, which are exactly captured by assigning to them the distribution types \(\delta (\star )=(\partial ,\partial ;\partial )\) (\(\star \) behaves like a binary box operator), \(\delta (\leftharpoondown )=(1,\partial ;1)\) and \(\delta (\rightharpoondown )=(\partial ,1;1)\).
Distributive normal lattice expansions are the special case where the underlying lattice is distributive. BAOs (Boolean algebras with operators) [24, 25] are the special case where the underlying lattice is a Boolean algebra and all normal operators distribute over finite joins of the Boolean algebra, i.e., they are all of distribution types of the form \((1,\ldots ,1;1)\). For BAOs, operators of other distribution types can be obtained by composition of operators with Boolean complementation. For example, in studying residuated Boolean algebras [26], Jónsson and Tsinakis make use of a notion of conjugate operators, introduced in [24, 25], and they show that intensional implications (division operations) \(\backslash ,/\) (the residuals of the product operator \(\circ \)) are interdefinable with the conjugates (at each argument place) \(\lhd ,\rhd \) of \(\circ \), i.e., \(a\backslash b=(a\rhd b^-)^-\) and \(a\rhd b=(a\backslash b^-)^-\) (and similarly for / and \(\lhd \), see [26] for details). Note that \(\backslash , /\) are not operators, whereas \(\lhd ,\rhd \) are.
The relational representation of BAOs in [24], extending Stone’s representation [35] of Boolean algebras using the space of ultrafilters of the algebra, forms the technical basis of the subsequently introduced by Kripke possible worlds semantics, which has had a well-known impact on the development of normal modal logics. This has been extended to the case of the logics of distributive lattices with various quasioperators, see [7] and [32, 33], for example, now based on the Priestley representation [31] of distributive lattices in ordered Stone spaces (simplifying Stone’s original representation [34] of distributive lattices), using the space of prime filters.
For non-distributive lattices, a number of different representation results have been published [1, 14, 21, 23, 30, 37]. Following the definition of canonical extensions for general lattices [10], interest in the subject was renewed [3,4,5,6], see also [12, 27, 28]. A brief review of the area was given in [16], slightly expanded in [22], to which we refer the reader for more details. As noted in [22], there appear to be two settings in which both a canonical extension construction and a full categorical duality can be carried through for bounded lattices. The first is obtained by combining as in [3, 4, 6] results from Urquhart’s representation [37] and its variants [30] (Ploščica) and [1] (Allwein and Hartonas). The second is based on the Hartonas and Dunn representation and duality [21], or on the Moshier and Jipsen [27] simplification of the representation and duality of [14], combining with the proofs in [10, 27] that [21, 27] deliver a canonical lattice extension. In [5], Craig and Haviar have in fact established a connection between the first and the second approach.
A Stone type duality for normal lattice expansions however has only first been presented in [15], extending [21]. Part of the difficulty was in defining an appropriate notion of morphism and Goldblatt [11, page 1021] reviews the related attempts to this issue. In [15] this problem was somewhat side-stepped, by restricting the definition of frame morphisms to such that their inverses are homomorphisms of the sublattices of clopen elements of the full complex algebras of the frames, as in the lattice duality of [21]. Another source of difficulty has been to define operators from suitably axiomatized relations on frames, so that the framework can serve the semantics of logics without distribution as Jónsson and Tarski’s BAOs [24] have served the semantics of modal logics. In [15] we proposed an axiomatization of frames and relations, though the axiomatization appears to be somewhat forced and we provide a significant improvement in the present article.
3 Sorted Residuated Frames (SRFs)
Regard \(\{1,\partial \}\) as a set of sorts and let \(Z=(Z_1,Z_\partial )\) be a sorted set. Sorted residuated frames \({\mathfrak {F}}=(Z_1,I,Z_\partial )\) are triples consisting of nonempty sets \(Z_1=X,Z_\partial =Y\) and a binary relation \(I\subseteq X\times Y\). The relation I generates residuated operators  (
( iff
iff  ), defined by
), defined by

The dual sorted residuated modal algebra of the (sorted residuated) frame (X, I, Y) is the algebra  . By residuation, the compositions
. By residuation, the compositions  and
and  are closure operators on
are closure operators on  and
and  , respectively.
, respectively.
For a sorted frame (X, I, Y), the complement of the frame relation I will be consistently designated by  and referred to as the Galois relation of the frame. It generates a Galois connection
and referred to as the Galois relation of the frame. It generates a Galois connection  (
( iff
iff  )
)

Triples \((X,R,Y), R\subseteq X\times Y\), where R is treated as the Galois relation of the frame, are variously referred to in the literature as polarities, after Birkhoff [2], as formal contexts, in the Formal Concept Analysis (FCA) tradition [8], or as object-attribute (categorization, classification, or information) systems [29, 38], or as generalized Kripke frames [9], or as polarity frames in the bi-approximation semantics of [36].
Note that the residuated and Galois connected operators generate the same closure operators, on  ,
,  and on
and on  ,
,  . This follows from the fact that
. This follows from the fact that  and
and  .
.
Proposition 3.1
The discrete categories of polarities and sorted residuated frames are equivalent. \(\square \)
The equivalence allows us to move in our arguments and definitions back-and-forth between sorted residuated frames and polarities. Indeed, for our purposes, both the residuated pairs  and
and  , as well as the Galois connection will be involved in definitions and arguments and we do not differentiate between polarities
, as well as the Galois connection will be involved in definitions and arguments and we do not differentiate between polarities  and their associated sorted residuated frames (X, I, Y), with I being the complement of
and their associated sorted residuated frames (X, I, Y), with I being the complement of  .
.
A subset \(A\subseteq X\) will be called stable if  . Similarly, a subset \(B\subseteq Y\) will be called co-stable if
. Similarly, a subset \(B\subseteq Y\) will be called co-stable if  . Stable and co-stable sets will be referred to as Galois sets, disambiguating to Galois stable or Galois co-stable when needed and as appropriate.
. Stable and co-stable sets will be referred to as Galois sets, disambiguating to Galois stable or Galois co-stable when needed and as appropriate.
By \({{\mathcal {G}}}(X),{{\mathcal {G}}}(Y)\) we designate the complete lattices of stable and co-stable sets, respectively. Note that the Galois connection restricts to a dual isomorphism  .
.
Preorder relations are induced on each of the sorts, by setting for \(x,z\in X\), \(x\preceq z\) iff  and, similarly, for \(y,v\in Y\), \(y\preceq v\) iff
and, similarly, for \(y,v\in Y\), \(y\preceq v\) iff  . A (sorted) frame is called separated if the preorders \(\preceq \) (on X and on Y) are in fact partial orders \(\le \).
. A (sorted) frame is called separated if the preorders \(\preceq \) (on X and on Y) are in fact partial orders \(\le \).
Remark 3.2
(Notational conventions). For a sorted relation \(R\subseteq \prod _{j=1}^{j=n+1}Z_{i_j}\), where \(i_j\in \{1,\partial \}\) for each j (and thus \(Z_{i_j}=X\) if \(i_j=1\) and \(Z_{i_j}=Y\) when \(i_j=\partial \)), we make the convention to regard it as a relation \(R\subseteq Z_{i_{n+1}}\times \prod _{j=1}^{j=n}Z_{i_j}\), we agree to write its sort type as \(\sigma (R)=(i_{n+1};i_1\dots i_n)\) and for a tuple of points of suitable sort we write \(uRu_1\dots u_n\) for \((u,u_1,\ldots ,u_n)\in R\). We often display the sort type as a superscript, as in \(R^\sigma \). Thus, for example, \(R^{\partial 1\partial }\) is a subset of \(Y\times (X\times Y)\). In writing then \(yR^{\partial 1 \partial }xv\) it is understood that \(x\in X=Z_1\) and \(y,v\in Y=Z_\partial \). The sort superscript is understood as part of the name designation of the relation, so that, for example, \(R^{111}, R^{\partial \partial 1}\) name two different relations.
We use \(\Gamma \) to designate upper closure \(\Gamma U=\{z\in X\vert \exists x\in U\;x\preceq z\}\), for \(U\subseteq X\), and similarly for \(U\subseteq Y\). The set U is increasing (an upset) iff \(U=\Gamma U\). For a singleton set \(\{x\}\subseteq X\) we write \(\Gamma x\), rather than \(\Gamma (\{x\})\) and similarly for \(\{y\}\subseteq Y\).
We typically use the standard FCA [8] priming notation for each of the two Galois maps  . This allows for stating and proving results for each of \({{\mathcal {G}}}(X),{{\mathcal {G}}}(Y)\) without either repeating definitions and proofs, or making constant appeals to duality. Thus for a Galois set \(G, \), if \(G\in {{\mathcal {G}}}(X)\) (G is a Galois stable set), and otherwise
. This allows for stating and proving results for each of \({{\mathcal {G}}}(X),{{\mathcal {G}}}(Y)\) without either repeating definitions and proofs, or making constant appeals to duality. Thus for a Galois set \(G, \), if \(G\in {{\mathcal {G}}}(X)\) (G is a Galois stable set), and otherwise  , if \(G\in {{\mathcal {G}}}(Y)\) (G is a Galois co-stable set).
, if \(G\in {{\mathcal {G}}}(Y)\) (G is a Galois co-stable set).
For an element u in either X or Y and a subset W, respectively of Y or X, we write u|W, under a well-sorting assumption, to stand for either  (which stands for
(which stands for  , for all \(w\in W\)), or
, for all \(w\in W\)), or  (which stands for
(which stands for  , for all \(w\in W\)), where well-sorting means that either \(u\in X, W\subseteq Y\), or \(W\subseteq X\) and \(u\in Y\), respectively. Similarly for the notation u|v, where u, v are elements of different sort.
, for all \(w\in W\)), where well-sorting means that either \(u\in X, W\subseteq Y\), or \(W\subseteq X\) and \(u\in Y\), respectively. Similarly for the notation u|v, where u, v are elements of different sort.
We designate n-tuples (of sets, or elements) using a vectorial notation, setting \((G_1,\ldots ,G_n)=\mathbf {G}\in \prod _{j=1}^{j=n}{\mathcal {G}}(Z_{i_j})\),  , \(\mathbf {u}\in \prod _{j=1}^{j=n}Z_{i_j}\) (where \(i_j\in \{1,\partial \}\)). Most of the time we are interested in some particular argument place \(1\le k\le n\) and we write \(\mathbf {G}[F]_k\) for the tuple \(\mathbf {G}\) where \(G_k=F\) (or \(G_k\) is replaced by F). Similarly \(\mathbf {u}[x]_k\) is \((u_1,\ldots ,u_{k-1},x,u_{k+1},\ldots ,u_n)\).
, \(\mathbf {u}\in \prod _{j=1}^{j=n}Z_{i_j}\) (where \(i_j\in \{1,\partial \}\)). Most of the time we are interested in some particular argument place \(1\le k\le n\) and we write \(\mathbf {G}[F]_k\) for the tuple \(\mathbf {G}\) where \(G_k=F\) (or \(G_k\) is replaced by F). Similarly \(\mathbf {u}[x]_k\) is \((u_1,\ldots ,u_{k-1},x,u_{k+1},\ldots ,u_n)\).
For brevity, we write \(\mathbf {u}\preceq \mathbf {v}\) for the pointwise ordering statements \(u_1\preceq v_1,\ldots ,u_n\preceq v_n\). We also let \(\mathbf {u}\in \mathbf {W}\) stand for the conjunction of componentwise membership \(u_j\in W_j\), for all \(j=1,\ldots ,n\).
To simplify notation, we write \(\Gamma \mathbf {u}\) for the n-tuple \((\Gamma u_1,\ldots ,\Gamma u_n)\). For a unary map f and a tuple \(\mathbf {u}\) we write \(f[\mathbf {u}]\) for the tuple \((f(u_1),\ldots ,f(u_n))\). Note that the same notation is used for the image \(f[S]=\{f(x)\vert x\in S\}\) of a set under a function f, but context will make it clear what the intended meaning is. The convention can be nested, so that if S is a set (or sequence) of tuples \(\mathbf {u}_i\), then f[S] is the set (or sequence) consisting of the elements \(f[\mathbf {u}_i]\).
To refer to sections of relations (the sets obtained by leaving one argument place unfilled) we make use of the notation \(\mathbf {u}[\_]_k\) which stands for the \((n-1)\)-tuple \((u_1,\ldots ,u_{k-1},[\_]\;,u_{k+1},\ldots ,u_n)\) and similarly for tuples of sets, extending the membership convention for tuples to cases such as \(\mathbf {u}[\_]_k\in \mathbf {F}[\_]_k\) and similarly for ordering relations \(\mathbf {u}[\_]_k\preceq \mathbf {v}[\_]_k\). We also quantify over tuples (with, or without a hole in them), instead of resorting to an iterated quantification over the elements of the tuple, as for example in \(\exists \mathbf {u}[\_]_k\in \mathbf {F}[\_]_k\exists v,w\in G\;wR\mathbf {u}[v]_k\).
We extend the vectorial notation to distribution types, summarily writing \(\delta =(\mathbf {i_j};i_{n+1})\) for \((i_1,\ldots ,i_n;i_{n+1})\). Then, for example, \(\mathbf {i_j}[\partial ]_k\) is the tuple with \(i_k=\partial \). Furthermore, we let \(\overline{i_j}=\partial \), if \(i_j=1\) and \(\overline{i_j}=1\), when \(i_j=\partial \).
Lemma 3.3
Let  be a polarity and \(u\in Z=X\cup Y\).
be a polarity and \(u\in Z=X\cup Y\).
-
(1)
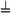 is increasing in each argument place (and thereby its complement I is decreasing in each argument place).
is increasing in each argument place (and thereby its complement I is decreasing in each argument place). -
(2)
\((\Gamma u)'=\{u\}'\) and \(\Gamma u=\{u\}^{\prime \prime }\) is a Galois set.
-
(3)
Galois sets are increasing, i.e., \(u\in G\) implies \(\Gamma u\subseteq G\).
-
(4)
For a Galois set G, \(G=\bigcup _{u\in G}\Gamma u\).
-
(5)
For a Galois set G, \(G=\bigvee _{u\in G}\Gamma u=\bigcap _{v|G}\{v\}'\).
-
(6)
For a Galois set G and any set W, \(W^{\prime \prime }\subseteq G\) iff \(W\subseteq G\).
Proof
By simple calculation. Proof details are included in [15, Lemma 2.2]. For claim 4, \(\bigcup _{u\in G}\Gamma u\subseteq G\) by claim 3 (Galois sets are upsets). In claim 5, given our notational conventions, the claim is that if \(G\in {{\mathcal {G}}}(X)\), then  and if \(G\in {{\mathcal {G}}}(Y)\), then
and if \(G\in {{\mathcal {G}}}(Y)\), then  . \(\square \)
. \(\square \)
Definition 3.4
(Closed and open elements). The principal upper sets of the form \(\Gamma x\), with \(x\in X\), will be called closed, or filter elements of \({{\mathcal {G}}}(X)\), while sets of the form  , with \(y\in Y\), will be referred to as open, or ideal elements of \({{\mathcal {G}}}(X)\). Similarly for \({{\mathcal {G}}}(Y)\). A closed element \(\Gamma u\) is clopen iff there exists an element v, with u|v, such that \(\Gamma u=\{v\}'\).
, with \(y\in Y\), will be referred to as open, or ideal elements of \({{\mathcal {G}}}(X)\). Similarly for \({{\mathcal {G}}}(Y)\). A closed element \(\Gamma u\) is clopen iff there exists an element v, with u|v, such that \(\Gamma u=\{v\}'\).
By Lemma 3.3, the closed elements of \({{\mathcal {G}}}(X)\) join-generate \({{\mathcal {G}}}(X)\), while the open elements meet-generate \({{\mathcal {G}}}(X)\) (similarly for \({{\mathcal {G}}}(Y)\)).
Definition 3.5
(Galois dual relation). For a relation R, of sort type \(\sigma \), its Galois dual relation \(R'\) is the relation defined by \(uR'\mathbf {v}\) iff \(\forall w\;(wR\mathbf {v}\longrightarrow w|u)\). In other words, \(R'\mathbf {v}=(R\mathbf {v})'\).
For example, given a relation \(R^{111}\) its Galois dual is the relation \(R^{\partial 11}\) where for any \(x,z\in X\),  and, similarly, for a relation \(S^{\partial 1\partial }\) its Galois dual is the relation \(S^{11\partial }\) where for any \(z\in X, v\in Y\) we have
and, similarly, for a relation \(S^{\partial 1\partial }\) its Galois dual is the relation \(S^{11\partial }\) where for any \(z\in X, v\in Y\) we have  , i.e., \(xS^{11\partial }zv\) holds iff for all \(y\in Y\), if \(yS^{\partial 1\partial }zv\), then
, i.e., \(xS^{11\partial }zv\) holds iff for all \(y\in Y\), if \(yS^{\partial 1\partial }zv\), then  .
.
Definition 3.6
(Sections of relations). For an \((n+1)\)-ary relation \(R^\sigma \) and an n-tuple \(\mathbf {u}\), \(R^\sigma \mathbf {u}=\{w\vert wR^\sigma \mathbf {u}\}\) is the section of \(R^\sigma \) determined by \(\mathbf {u}\). To designate a section of the relation at the k-th argument place we let \(\mathbf {u}[\_]_k\) be the tuple with a hole at the k-th argument place. Then \(wR^\sigma \mathbf {u}[\_]_k=\{v\vert wR^\sigma \mathbf {u}[v]_k\}\subseteq Z_{i_k}\) is the k-th section of \(R^\sigma \).
We defer the definition of the category SRF\(_\tau \) of sorted residuated frames of type \(\tau \) for later (see Definition 3.26), after establishing the necessary facts.
3.1 Frame relations and operators
If \(R^\sigma \) is a relation on a sorted residuated frame \({\mathfrak {F}}=(X,I,Y)\), of some sort type \(\sigma =(i_{n+1};i_1\dots i_n)\), then as in the unsorted case, \(R^\sigma \) (but we shall drop the displayed sort type when clear from context) generates a (sorted) image operator \(\alpha _R\), defined by (3.1), of sort \(\sigma (\alpha _R)=(i_1,\ldots ,i_n;i_{n+1})\), defined by the obvious generalization of the Jónsson–Tarski image operators [24],
where for each j, \(W_j\subseteq Z_{i_j}\) (and recall that \(Z_{i_j}=X\) when \(i_j=1\) and \(Z_{i_j}=Y\), if \(i_j=\partial \)).
Thus  is a sorted normal and completely additive function in each argument place, therefore it is residuated, i.e., for each k there is a set-operator \(\beta _R^k\) satisfying the condition
is a sorted normal and completely additive function in each argument place, therefore it is residuated, i.e., for each k there is a set-operator \(\beta _R^k\) satisfying the condition
Hence \(\beta _R^k(\mathbf {W}[U]_k)\) is the largest set V s.t. \(\alpha _R(\mathbf {W}[V]_k)\subseteq U\) and it is thereby definable by
Definition 3.7
\({\overline{\alpha }}_R\) is the closure of the restriction of \(\alpha _R\) to Galois sets \(\mathbf {F}\),
where \(F_j\in {\mathcal {G}}(Z_{i_j})\), for each \(j\in \{1,\ldots ,n\}\).
In Theorem 3.12 we establish conditions under which the sorted operation \({\overline{\alpha }}_R\) on Galois sets is completely distributive, in each argument place.
The operator \({\overline{\alpha }}_R\) is sorted and its sorting is inherited from the sort type of R. For example, if \(\sigma (R)=(\partial ;11)\),  , hence \({\overline{\alpha }}_R:{{\mathcal {G}}}(X)\times {{\mathcal {G}}}(X)\longrightarrow {{\mathcal {G}}}(Y)\). Single-sorted operations
, hence \({\overline{\alpha }}_R:{{\mathcal {G}}}(X)\times {{\mathcal {G}}}(X)\longrightarrow {{\mathcal {G}}}(Y)\). Single-sorted operations
can be then extracted by composing appropriately with the Galois connection: \({\overline{\alpha }}^1_R(A,C)=({\overline{\alpha }}_R(A,C))'\) (where \(A,C\in {{\mathcal {G}}}(X)\)) and, similarly, \({\overline{\alpha }}^\partial _R(B,D)\) \(={\overline{\alpha }}_R(B',D')\) (where \(B,D\in {{\mathcal {G}}}(Y)\)). Similarly for the n-ary case and for an arbitrary distribution type.
Definition 3.8
(Full complex algebra). Let  be a polarity with a relation R of some sort \(\sigma (R)=(i_{n+1};i_1\dots i_n)\). The full complex algebra of \({\mathfrak {F}}\) is the structure \({\mathfrak {F}}^+=({{\mathcal {G}}}(X),{\overline{\alpha }}^1_R)\) and its dual full complex algebra is the structure \({\mathfrak {F}}^\partial =({{\mathcal {G}}}(Y),{\overline{\alpha }}^\partial _R)\). Subalgebras of full complex algebras will be referred to as complex algebras of a frame.
be a polarity with a relation R of some sort \(\sigma (R)=(i_{n+1};i_1\dots i_n)\). The full complex algebra of \({\mathfrak {F}}\) is the structure \({\mathfrak {F}}^+=({{\mathcal {G}}}(X),{\overline{\alpha }}^1_R)\) and its dual full complex algebra is the structure \({\mathfrak {F}}^\partial =({{\mathcal {G}}}(Y),{\overline{\alpha }}^\partial _R)\). Subalgebras of full complex algebras will be referred to as complex algebras of a frame.
Most of the time we work with the dual sorted algebra of Galois sets

as it allows for considering sorted operations that distribute over joins in each argument place (which are either joins of \({{\mathcal {G}}}(X)\), or of \({{\mathcal {G}}}(Y)\), depending on the sort type of the operation). Single-sorted normal operators are then extracted in the complex algebra by composition with the Galois maps, as indicated above.
Definition 3.9
(Conjugates). Let \(\alpha \) be an image operator (generated by some relation R) of sort type \(\sigma (\alpha )=(\mathbf {i_j};i_{n+1})\) and \({\overline{\alpha }}\) the closure of its restriction to Galois sets in each argument place, as defined above. A function \({\overline{\gamma }}^k\) on Galois sets, of sort type \(\sigma ({\overline{\gamma }}^k)=(\mathbf {i_j}[\overline{i_{n+1}}]_k;\overline{i_k})= (i_1,\ldots ,i_{k-1},\overline{i_{n+1}},i_{k+1},\ldots ,i_n;\overline{i_k})\) (where \(\overline{i_j}=\partial \) if \(i_j=1\) and \(\overline{i_j}=1\) when \(i_j=\partial \)) is a conjugate of \({\overline{\alpha }}\) at the k-th argument place (or a k-conjugate) iff the following condition
holds for all Galois sets \(F_j\in {\mathcal {G}}(Z_{i_j})\) and \(G\in {\mathcal {G}}(Z_{i_{n+1}})\).
It follows from the definition of a conjugate function that \({\overline{\gamma }}\) is a k-conjugate of \({\overline{\alpha }}\) iff \({\overline{\alpha }}\) is one of \({\overline{\gamma }}\) and we thus call \({\overline{\alpha }},{\overline{\gamma }}\) k-conjugates. Note that the priming notation for both maps of the duality  packs together, in one form, four distinct (due to sorting) cases of conjugacy.
packs together, in one form, four distinct (due to sorting) cases of conjugacy.
Example 3.10
In the case of a ternary relation \(R^{111}\) of the indicated sort type, an image operator  is generated. Designate the closure of its restriction to Galois stable sets by
is generated. Designate the closure of its restriction to Galois stable sets by  . Then
. Then  is of sort type
is of sort type  . If \({\overline{\gamma }}^2_R=\triangleright :{{\mathcal {G}}}(X)\times {{\mathcal {G}}}(Y)\longrightarrow {{\mathcal {G}}}(Y)\), with \(\sigma (\triangleright )=(1,\partial ;\partial )\), then
. If \({\overline{\gamma }}^2_R=\triangleright :{{\mathcal {G}}}(X)\times {{\mathcal {G}}}(Y)\longrightarrow {{\mathcal {G}}}(Y)\), with \(\sigma (\triangleright )=(1,\partial ;\partial )\), then  , \(\triangleright \) are conjugates iff for any Galois stable sets \(A,F,C\in {{\mathcal {G}}}(X)\) it holds that
, \(\triangleright \) are conjugates iff for any Galois stable sets \(A,F,C\in {{\mathcal {G}}}(X)\) it holds that  iff \(A\triangleright C'\subseteq F'\).
iff \(A\triangleright C'\subseteq F'\).
Note that, given an operator \(\triangleright :{{\mathcal {G}}}(X)\times {{\mathcal {G}}}(Y)\longrightarrow {{\mathcal {G}}}(Y)\), if we now define \(\Rightarrow \;:{{\mathcal {G}}}(X)\times {{\mathcal {G}}}(X)\longrightarrow {{\mathcal {G}}}(X)\) by  , it is immediate that
, it is immediate that  are conjugates iff
are conjugates iff  are residuated. In other words
are residuated. In other words

Lemma 3.11
The following are equivalent.
-
(1)
\({\overline{\alpha }}_R\) distributes over any joins of Galois sets at the k-th argument place
-
(2)
\({\overline{\alpha }}_R\) has a k-conjugate \({\overline{\gamma }}_R^k\) defined on Galois sets by
$$\begin{aligned} {\overline{\gamma }}_R^k(\mathbf {F})=\bigcap \{G\vert {\overline{\alpha }}_R(\mathbf {F}[G']_k)\subseteq F'_k\} \end{aligned}$$ -
(3)
\({\overline{\alpha }}_R\) has a k-residual \({\overline{\beta }}_R^k\) defined on Galois sets by
$$\begin{aligned} {\overline{\beta }}_R^k(\mathbf {F}[G]_k)= ({\overline{\gamma }}_R^k(\mathbf {F}[G']_k))'=\bigvee \{G^\prime \vert {\overline{\alpha }}_R(\mathbf {F}[G']_k)\subseteq F'_k\}. \end{aligned}$$
Proof
Existence of a k-residual is equivalent to distribution over arbitrary joins and the residual is defined by
We show that the distributivity assumption 1) implies that 2) and 3) are equivalent, i.e., that
We illustrate the proof for the unary case only, as the other parameters remain idle in the argument.
Assume \({\overline{\alpha }}_R(G)\subseteq H\) and let \({\overline{\gamma }}_R(H^\prime )=\bigcap \{E\vert {\overline{\alpha }}_R(E')\subseteq H\}\), a Galois set by definition, given that G, H, E are assumed to be Galois sets. Then \(G^\prime \) is in the set whose intersection is taken. Hence \({\overline{\gamma }}_R(H^\prime )\subseteq G^\prime \) follows from the definition of \({\overline{\gamma }}_R\). It also follows by definition that \(G\subseteq {\overline{\beta }}_R(H)=({\overline{\gamma }}_R(H^\prime ))^\prime \).
Assuming \(G\subseteq {\overline{\beta }}_R(H)\) we obtain by definition that \(G\subseteq ({\overline{\gamma }}_R(H^\prime ))^\prime \), hence \(G\subseteq \bigvee \{E^\prime \vert {\overline{\alpha }}_R(E^\prime )\subseteq H\}\), using the definition of \({\overline{\gamma }}_R\) and duality. Hence by the distributivity assumption \({\overline{\alpha }}_R(G)\subseteq \bigvee \{{\overline{\alpha }}_R(E^\prime )\vert {\overline{\alpha }}_R(E^\prime )\subseteq H\}\subseteq H\). This establishes that \({\overline{\alpha }}_R(G)\subseteq H\) iff \({\overline{\gamma }}_R(H^\prime )\subseteq G^\prime \) iff \(G\subseteq {\overline{\beta }}_R(H)\). \(\square \)
Theorem 3.12
Let  be a frame with an \((n+1)\)-ary sorted relation, of some sort \(\sigma (R)=(i_{n+1};\mathbf {i_j})\) and assume that for any \(w\in Z_{\overline{i_{n+1}}}\) and any \((n-1)\)-tuple \(\mathbf {p}[\_]_k\) with \(p_j\in Z_{i_j}\), for each \(j\in \{1,\ldots ,n\}\setminus \{k\}\), the sections \(wR'\mathbf {p}[\_]_k\) of the Galois dual relation \(R'\) of R are Galois sets. Then \({\overline{\alpha }}_R\) distributes at the k-th argument place over arbitrary joins in \({\mathcal {G}}(Z_{i_k})\).
be a frame with an \((n+1)\)-ary sorted relation, of some sort \(\sigma (R)=(i_{n+1};\mathbf {i_j})\) and assume that for any \(w\in Z_{\overline{i_{n+1}}}\) and any \((n-1)\)-tuple \(\mathbf {p}[\_]_k\) with \(p_j\in Z_{i_j}\), for each \(j\in \{1,\ldots ,n\}\setminus \{k\}\), the sections \(wR'\mathbf {p}[\_]_k\) of the Galois dual relation \(R'\) of R are Galois sets. Then \({\overline{\alpha }}_R\) distributes at the k-th argument place over arbitrary joins in \({\mathcal {G}}(Z_{i_k})\).
Proof
Define the relation T from R by setting,
then use equation (3.6) below, to define a relation S
Note that the sort type of S, as defined, is \(\sigma (S)=(\overline{i_k};\mathbf {i_j}[\overline{i_{n+1}}]_k)\) . Let \({\overline{\eta }}_S\) be the closure of the restriction of the image operator \(\eta _S\) to Galois sets, according to the sort type of S. We show that \({\overline{\alpha }}_R\) and \({\overline{\eta }}_S\) are k-conjugates. To establish the conjugacy condition \({\overline{\alpha }}_R(\mathbf {F})\subseteq G\) iff \({\overline{\eta }}_S(\mathbf {F}[G']_k)\subseteq F'_k\) it suffices by Lemma 3.3 to verify that \(\alpha _R(\mathbf {F})\subseteq G\) iff \(\eta _S(\mathbf {F}[G']_k)\subseteq F'_k\). We have
-
\(\alpha _R(\mathbf {F})\subseteq G\) iff \(\bigcup _{\mathbf {p}\in \mathbf {F}}{R\mathbf {p}}\subseteq G\) iff \(\forall \mathbf {p}(\mathbf {p}\in \mathbf {F}\longrightarrow (R\mathbf {p}\subseteq G))\)
-
iff \(\forall \mathbf {p}(\mathbf {p}\in \mathbf {F}\longrightarrow (G'\subseteq R'\mathbf {p}))\)
-
iff \(\forall \mathbf {p}(\mathbf {p}\in \mathbf {F}\longrightarrow \forall v\in Z_{\overline{i_{n+1}}}(G|v\longrightarrow vR'\mathbf {p}))\)
-
iff \(\forall \mathbf {p}\forall v\in Z_{\overline{i_{n+1}}}(\mathbf {p}[\_]_k\in \mathbf {F}[\_]_k\wedge p_k\in F_k\wedge G|v\longrightarrow vR'\mathbf {p}[p_k]_k)\)
-
iff \(\forall \mathbf {p}\forall v\in Z_{\overline{i_{n+1}}}(\mathbf {p}[\_]_k\in \mathbf {F}[\_]_k \wedge G|v\longrightarrow (p_k\in F_k\longrightarrow vR'\mathbf {p}[p_k]_k))\)
-
iff \(\forall \mathbf {p}[\_]_k\forall v\in Z_{\overline{i_{n+1}}}(\mathbf {p}[\_]_k\in \mathbf {F}[\_]_k \wedge G|v\longrightarrow (F_k\subseteq vR'\mathbf {p}[\_]_k))\)
-
(using the hypothesis that the k-th sections of \(R'\) are Galois sets)
-
iff \(\forall \mathbf {p}[\_]_k\forall v\in Z_{\overline{i_{n+1}}}(\mathbf {p}[\_]_k\in \mathbf {F}[\_]_k \wedge G|v\longrightarrow ((vR'\mathbf {p}[\_]_k)'\subseteq F^\prime _k))\)
-
(using the definition of T)
-
iff \(\forall \mathbf {p}[\_]_k\forall v\in Z_{\overline{i_{n+1}}}\left( \mathbf {p}[\_]_k\in \mathbf {F}[\_]_k \wedge G|v\longrightarrow \forall w\in Z_{\overline{i_k}} (vT\mathbf {p}[w]_k\longrightarrow F_k|w)\right) \)
-
iff \(\forall \mathbf {p}[\_]_k\forall v\in Z_{\overline{i_{n+1}}}\forall w\in Z_{\overline{i_k}} \left( vT\mathbf {p}[w]_k \wedge \mathbf {p}[\_]_k\in \mathbf {F}[\_]_k \wedge G|v\longrightarrow F_k|w\right) \)
-
(using the definition of S)
-
iff \(\forall \mathbf {p}[\_]_k\forall v\in Z_{\overline{i_{n+1}}}\forall w\in Z_{\overline{i_k}} \left( wS\mathbf {p}[v]_k \wedge \mathbf {p}[\_]_k\in \mathbf {F}[\_]_k \wedge G|v\longrightarrow F_k|w\right) \)
-
iff \(\bigcup _{\mathbf {p}[v]_k\in \mathbf {F}[G']_k} S\mathbf {p}[v]_k\subseteq F^\prime _k\)
-
iff \(\eta _S(\mathbf {F}[G']_k)\subseteq F^\prime _k\).
Hence \({\overline{\alpha }}_R\) and \({\overline{\eta }}_S\) are k-conjugates. Consequently, by Lemma 3.11, \({\overline{\alpha }}_R\) distributes at the k-th argument place over arbitrary joins in \({\mathcal {G}}(Z_{i_k})\). \(\square \)
Definition 3.13
We let \(\beta ^k_{R/}\) be the restriction of \(\beta ^k_R\) of equation (3.3) to Galois sets, according to its sort type, explicitly defined by (3.7)
Theorem 3.14
If \({\overline{\alpha }}_R\) is residuated in the k-th argument place, then \(\beta ^k_{R/}\) is its residual and \( \beta ^k_{R/}(\mathbf {E}[G]_k)\) is a Galois set, i.e., the union in equation (3.7) is actually a join in \({\mathcal {G}}(Z_{i_k})\).
Proof
We illustrate the proof for the unary case only, since the other parameters that may exist remain idle in the argument. In the unary case, \(\beta _{R/}(G)=\bigcup \{F\vert \alpha _R(F)\subseteq G\}\), for Galois sets F, G.
Note first that \({\overline{\alpha }}_R(F)\subseteq G\) iff \(F\subseteq \beta _{R/}(G)\). Left-to-right is obvious by definition and by the fact that for a Galois set G and any set U, \(U^{\prime \prime }\subseteq G\) iff \(U\subseteq G\). If \(F\subseteq \beta _{R/}(G)\subseteq \beta _R(G)\), then by residuation \(\alpha _R(F)\subseteq G\). Given that G is a Galois set, it follows \({\overline{\alpha }}_R(F)\subseteq G\).
If indeed \({\overline{\alpha }}_R\) is residuated on Galois sets with a map \({\overline{\beta }}_R\), then the residual is defined by \({\overline{\beta }}_R(G)=\bigvee \{F\vert {\overline{\alpha }}_R(F)\subseteq G\}=\bigvee \{F\vert \alpha _R(F)\subseteq G\}\) and this is precisely the closure of \(\beta _{R/}(G)=\bigcup \{F\vert \alpha _R(F)\subseteq G\}\). But in that case we obtain \(F\subseteq {\overline{\beta }}_R(G)\) iff \({\overline{\alpha }}_R(F)\subseteq G\) iff \(\alpha _R(F)\subseteq G\) iff \(F\subseteq \beta _{R/}(G)\) and setting \(F={\overline{\beta }}_R(G)\) it follows that \({\overline{\beta }}_R(G)\subseteq \beta _{R/}(G)\subseteq {\overline{\beta }}_R(G)\). \(\square \)
Lemma 3.15
\(\beta ^k_{R/}\) is equivalently defined by (3.8) and by (3.9)
Proof
\(\beta ^k_{R/}\) is defined by equation (3.7), so if \(u\in \beta ^k_{R/}(\mathbf {E}[G]_k)\), let \(F\in {\mathcal {G}}(Z_{i_k})\) be such that \(u\in F\) and \(\alpha _R(\mathbf {E}[F]_k)\subseteq G\). Then \(\Gamma u\subseteq F\) and by monotonicity of \(\alpha _R\) we have \( \alpha _R(\mathbf {E}[\Gamma u]_k)\subseteq \alpha _R(\mathbf {E}[F]_k)\subseteq G \) and this establishes the left-to-right inclusion for the first identity of the lemma. The converse inclusion is obvious since \(\Gamma u\) is a Galois set.
For the second identity, the inclusion right-to-left is obvious. Now if u is such that \(\alpha _R(\mathbf {E}[\Gamma u]_k)\subseteq G\) and \(u\preceq w\), then \(\Gamma w\subseteq \Gamma u\) and then by monotonicity of \(\alpha _R\) it follows that \(\alpha _R(\mathbf {E}[\Gamma w]_k)\subseteq \alpha _R(\mathbf {E}[\Gamma u]_k)\subseteq G\).
This shows that \(\bigcup \{\Gamma u\in {\mathcal {G}}(Z_{i_k})\vert \alpha _R(\mathbf {E}[\Gamma u]_k)\subseteq G\}\) is contained in the set \(\{ u\in Z_{i_k}\vert \alpha _R(\mathbf {E}[\Gamma u]_k)\subseteq G\}\), and given the first part of the lemma, the second identity holds as well. \(\square \)
We summarize our results obtained thus far with the following observations.
Let \({\mathbb {C}}_\tau \) be the class of sorted residuated frames (equivalently, polarities) with relations \(R_\sigma \) of sort type \(\sigma \), for each \(\sigma =(i_{n+1};\mathbf {i_j})\in \{1,\partial \}^{n+1}\) in the similarity type \(\tau \). Assume the stability axiom below (F4 in Table 1) for \({\mathbb {C}}_\tau \).
-
For each relation R of type \(\sigma =(i_{n+1};\mathbf {i_j})\) and each \(w\in Z_{\overline{i_{n+1}}}\) and \(\mathbf {u}[\_]_k\) with \(u_j\in Z_{i_j}\) for each \(j\in \{1,\ldots ,n\}\setminus \{k\}\), the k-th section \(wR^\prime \mathbf {u}[\_]_k\) of the Galois dual relation \(R'\) of R is a Galois set, for each \(k=1,\ldots ,n\).
Let \(\alpha _R\) be the classical sorted image operator generated by R, as in equation (3.1), and \(\beta ^k_R\) its k-residual for any \(k=1,\ldots ,n\), defined as usual by equation (3.3). Then
-
(1)
the closure \({\overline{\alpha }}_R\) (Definition 3.7) of the restriction of \(\alpha _R\) to Galois sets is residuated at the k-th argument place with the restriction \(\beta ^k_{R/}\) (Definition 3.13) of \(\beta ^k_R\) to Galois sets (Lemma 3.11, Theorem 3.12, Theorem 3.14)
-
(2)
a completely normal operator \({\overline{\alpha }}^1_R:{{\mathcal {G}}}(X)^n\longrightarrow {{\mathcal {G}}}(X)\) of distribution type \(\delta =(\mathbf {i_j};i_{n+1})\) is obtained by composition with the Galois connection
$$\begin{aligned} {\overline{\alpha }}^1_R(A_1,\ldots ,A_n)=\left\{ \begin{array}{cl} {\overline{\alpha }}_R\left( \ldots ,\underbrace{A_j}_{i_j=1},\ldots , \underbrace{A'_r}_{i_r=\partial },\ldots \right) &{} \text{ if } i_{n+1}=1\\ \left( {\overline{\alpha }}_R\left( \ldots ,\underbrace{A_j}_{i_j=1},\ldots , \underbrace{A'_r}_{i_r=\partial },\ldots \right) \right) ^\prime &{} \text{ if } i_{n+1}=\partial \end{array} \right. \end{aligned}$$ -
(3)
similarly for its dual operator \({\overline{\alpha }}^\partial _R:{{\mathcal {G}}}(Y)^n\longrightarrow {{\mathcal {G}}}(Y)\).
We list in Table 1 the frame axioms we shall assume in the sequel, for a sorted residuated frame with relations \({\mathfrak {F}}=(X,I, Y, (R_\sigma )_{\sigma \in \tau })\).
Note that axioms F1 and F2 imply that there is a (sorted) function \({\widehat{f}}_R\) on the points of the frame such that \({\widehat{f}}_R(\mathbf {u})=w\) iff \(R\mathbf {u}=\Gamma w\). The following immediate observation will be useful in the sequel.
Lemma 3.16
Let \({\mathfrak {F}}\) be a frame of similarity type \(\tau \) and assume that axioms F1–F3 in Table 1 hold. Then for a frame relation R of type \(\sigma \) in \(\tau \), \({\overline{\alpha }}_R(\Gamma \mathbf {u})=R\mathbf {u}=\alpha _R(\Gamma \mathbf {u})=\Gamma ({\widehat{f}}_R(\mathbf {u}))\).
Proof
By definition (3.1), \(\alpha _R(\Gamma \mathbf {u})=\bigcup _{\mathbf {u}\le \mathbf {w}}R\mathbf {w}\). By axiom F3, \(\bigcup _{\mathbf {u}\le \mathbf {w}}R\mathbf {w}=R\mathbf {u}\), which is a closed element by axiom F2, generated by a unique point \(w={\widehat{f}}_R(\mathbf {u})\), by axiom F1, so that \(\alpha _R(\Gamma \mathbf {u})=R\mathbf {u}=\Gamma w=(\alpha _R(\Gamma \mathbf {u}))^{\prime \prime }={\overline{\alpha }}_R(\Gamma \mathbf {u})\), where \(\Gamma w=\Gamma ({\widehat{f}}_R(\mathbf {u}))\). \(\square \)
The axiomatization will be strengthened in Section 5, imposing among others a topology on each of X and Y, in order to be able to carry out a Stone duality proof.
3.2 Weak bounded morphisms
Recall that a bounded morphism \(p:(W_1,R_1)\longrightarrow (W_2,R_2)\), for classical Kripke frames, is defined as a map that preserves the frame relation, i.e., \(uR_1v\) implies that \(p(u)R_2p(v)\) and so that its inverse \(p^{-1}\) is a homomorphism of the dual modal algebras  , i.e., such that
, i.e., such that  . This can be re-written as the familiar first-order condition typically used to define bounded morphisms.
. This can be re-written as the familiar first-order condition typically used to define bounded morphisms.
For sorted frames, when their dual sorted residuated modal algebras are of interest, morphisms of sorted frames can be taken to be the natural generalization of bounded morphisms to the sorted case, to wit a pair of maps \((p,q):(X_2,I_2,Y_2)\longrightarrow (X_1,I_1,Y_1)\), such that their inverses commute with the residuated set-operators  and
and  (equivalently, with the Galois connections). One direction of the required inclusions is ensured by requiring preservation of the frame relation, as in the unsorted case. Since inverse maps preserve unions and every set can be written as the union of the singletons of its elements, the reverse inclusion
(equivalently, with the Galois connections). One direction of the required inclusions is ensured by requiring preservation of the frame relation, as in the unsorted case. Since inverse maps preserve unions and every set can be written as the union of the singletons of its elements, the reverse inclusion  will hold iff it holds for singletons
will hold iff it holds for singletons  . Rephrasing and expressing it as a first-order condition we obtain condition (3.10). Similarly for the other reverse inclusion, after replacing boxes with diamonds, working with co-atoms \(-\{x\}\) and contraposing a number of times we obtain the equivalent first-order condition (3.11).
. Rephrasing and expressing it as a first-order condition we obtain condition (3.10). Similarly for the other reverse inclusion, after replacing boxes with diamonds, working with co-atoms \(-\{x\}\) and contraposing a number of times we obtain the equivalent first-order condition (3.11).
We then arrive at the natural generalization and a sorted bounded morphism \((p,q):(X_2,I_2,Y_2)\longrightarrow (X_1,I_1,Y_1)\) is defined as a pair of maps \(p:X_2\longrightarrow X_1\), \(q:Y_2\longrightarrow Y_1\) such that the relation preservation condition (3.12) below,
as well as conditions (3.10) and (3.11) hold. Note that sorted bounded morphisms preserve the closure operators

therefore they preserve arbitrary joins, since these are closures of unions and as inverse maps preserve both unions and intersections, sorted bounded morphisms are homomorphisms of the complete lattices of Galois stable and co-stable sets.
3.2.1 Morphisms for sorted residuated frames
Singletons are atoms of the powerset Boolean algebras, they join-generate any subset, i.e., \(U=\bigcup _{u\in U}\{u\}\), and this was used in computing the first-order conditions (3.10), (3.11) for sorted bounded morphisms. For stable and co-stable sets, join generators are the closed elements \(\Gamma x\;(x\in X)\) and \(\Gamma y\; (y\in Y)\) so that we have, respectively, \(A=\bigvee _{x\in A}\Gamma x=\bigcup _{x\in A}\Gamma x\), using Lemma 3.3. We have, for any \(x\in X\),
-
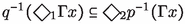
-
iff
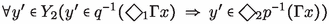
-
iff
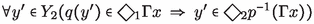
-
iff
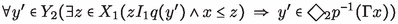
-
iff

-
iff \(\forall y'\in Y_2(xI_1q(y')\;\Rightarrow \;\exists x'\in X_2(x\le p(x')\wedge x' I_2 y'))\)
and this is the weakened version of (3.10) we shall need. We point out that the proof used the fact that the frame relation I is decreasing in both argument places (Lemma 3.3), hence \(\exists z\in X_1(zI_1q(y')\wedge x\le z)\) iff \(xI_1q(y')\).
Definition 3.17
If \((p,q):(X_2,I_2,Y_2)\rightarrow (X_1,I_1,Y_1)\), with \(p:X_2\rightarrow X_1\) and \(q:Y_2\rightarrow Y_1\), then we let \(\pi =(p,q)\) and we define \(\pi ^{-1}\) by setting

Similarly, we let
Lemma 3.18
If \(\pi =(p,q):(X_2,I_2,Y_2)\longrightarrow (X_1,I_1,Y_1)\) is a pair of maps \(p:X_2\longrightarrow X_1\), \(q:Y_2\longrightarrow Y_1\), then the following are equivalent:
-
(1)
for any increasing subset \(A\subseteq X_1\),
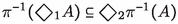
-
(2)
for any \(x\in X_1\),
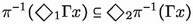
-
(3)
\(\forall x\in X_1\forall y'\in Y_2(xI_1 \pi (y')\longrightarrow \exists x'\in X_2(x\le \pi (x')\wedge x'I_2y') ))\).
Proof
(1)\(\Rightarrow \)(2) Immediate, since \(\Gamma x=\{z\in X_1\vert x\le z\}\subseteq X_1\) is increasing. (2)\(\Leftrightarrow \)(3) This was shown above. (3)\(\Rightarrow \)(1) Let  , i.e.,
, i.e.,  and let then \(x\in X_1\) be such that \(xI_1q(y')\) and \(x\in A\). From \(xI_1q(y')\) and condition (3) we obtain that there exists \(x'\in X_2\) such that \(x'I_2y'\) and \(x\le p(x')\). Given the assumption that A is an increasing subset and since \(x\in A\) it follows that \(p(x')\in A\), as well. This shows that
and let then \(x\in X_1\) be such that \(xI_1q(y')\) and \(x\in A\). From \(xI_1q(y')\) and condition (3) we obtain that there exists \(x'\in X_2\) such that \(x'I_2y'\) and \(x\le p(x')\). Given the assumption that A is an increasing subset and since \(x\in A\) it follows that \(p(x')\in A\), as well. This shows that  .
.
Therefore, (1)\(\Leftrightarrow \)(2)\(\Leftrightarrow \)(3). \(\square \)
Similarly, we obtain the following lemma.
Lemma 3.19
If \(\pi =(p,q):(X_2,I_2,Y_2)\longrightarrow (X_1,I_1,Y_1)\) is a pair of maps \(p:X_2\longrightarrow X_1\), \(q:Y_2\longrightarrow Y_1\), then the following are equivalent:
-
(1)
for any decreasing subset \(B\subseteq Y_1\),

-
(2)
for any \(y\in Y_1\),
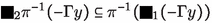
-
(3)
\(\forall x'\in X_2\forall y\in Y_1(\pi (x')I_1y\longrightarrow \exists y'\in Y_2(y\le \pi (y')\wedge x'I_2y'))\).
Note that case (3) of Lemma 3.19 is a weakened analogue of (3.11).
Definition 3.20
If \(\pi =(p,q):(X_2,I_2,Y_2)\longrightarrow (X_1,I_1,Y_1)\) is a pair of maps \(p:X_2\longrightarrow X_1\), \(q:Y_2\longrightarrow Y_1\), then \(\pi \) will be called a (sorted) weak bounded morphism iff
-
(1)
\(\forall x'\in X_2\forall y'\in Y_2\;(x'I_2y'\longrightarrow \pi (x')I_1\pi (y'))\)
-
(2)
\(\forall x\in X_1\forall y'\in Y_2(xI_1 \pi (y')\longrightarrow \exists x'\in X_2(x\le \pi (x')\wedge x'I_2y') )\)
-
(3)
\(\forall x'\in X_2\forall y\in Y_1(\pi (x')I_1y\longrightarrow \exists y'\in Y_2(y\le \pi (y')\wedge x'I_2y') )\).
Corollary 3.21
The inverse \(\pi ^{-1}=(p,q)^{-1}\) of a weak bounded morphism is a complete lattice homomorphism of the lattices of Galois stable sets of sorted residuated frames.
Proof
The proof is an immediate consequence of Lemmas 3.18 and 3.19. \(\square \)
Summarizing, we have shown that all squares in the diagrams in the middle and right below commute

where  ,
,  denote, respectively, the set of increasing and decreasing subsets.
denote, respectively, the set of increasing and decreasing subsets.
Remark 3.22
Goldblatt [11] was first to propose bounded morphisms for polarities and our definition is equivalent to his. For morphisms of frames with relations (restricted in [11] to relations of sort type that generate either join-preserving or meet-preserving operators only) we will diverge from his definition, as the relations Goldblatt considers on frames, expanding on Gehrke’s [9], do not coincide with ours and they can be in fact construed as the Galois duals of the frame relations we consider. In [19] we discussed the connections between our approach and Gehrke’s generalized Kripke frames approach.
For later use, we make an observation in the next lemma.
Lemma 3.23
If \(\pi ^{-1}\) preserves closed elements, then it preserves clopen elements, as well.
Proof
Letting \(\pi ^{-1}(\Gamma u)=\Gamma w_u\) and \(\pi ^{-1}(\Gamma v)=\Gamma w_v\), we have \((\pi ^{-1}(\Gamma v))'=(\Gamma w_v)'=\{w_v\}'\) and \(\Gamma w_u=\pi ^{-1}(\Gamma u)=\pi ^{-1}(\{v\}')\) = \(\pi ^{-1}((\Gamma v)')\) \(=(\pi ^{-1}(\Gamma v))'=\{w_v\}'\), assuming \(\Gamma u=\{v\}'\) is clopen, using Lemma 3.3 and using also the fact that weak bounded morphisms commute with the Galois connection (by the results of Section 3.2.1, specifically, Corollary 3.21). \(\square \)
3.2.2 Morphisms for frames with relations
Let \(\pi \) be a weak bounded morphism, \(\pi =(p,q):(X_2,I_2,Y_2,(S_\sigma )_{\sigma \in \tau })\longrightarrow (X_1,I_1,Y_1,(R_\sigma )_{\sigma \in \tau })\), and let \(R_\sigma ,S_\sigma \) be corresponding relations in the two frames, of the same sort type. For simplicity, we omit the subscript \(\sigma \) in the sequel.
Proposition 3.24
If for any \(\mathbf {u}\) it holds that \(\pi ^{-1}{\overline{\alpha }}_R(\Gamma \mathbf {u})={\overline{\alpha }}_S(\pi ^{-1}[\Gamma \mathbf {u}])\), then for any tuple \(\mathbf {F}\) of Galois sets of the required sort \(\pi ^{-1}{\overline{\alpha }}_R(\mathbf {F})={\overline{\alpha }}_S(\pi ^{-1}[\mathbf {F}])\).
Proof
We have
For the last line, note that if \(\mathbf {u}\in \mathbf {F}\) and \(\mathbf {u}\le \pi [\mathbf {w}]\), then \(\pi [\mathbf {w}]\in \mathbf {F}\), since Galois sets are increasing. Hence \(\bigvee _{\mathbf {u}\le \pi [\mathbf {w}]}^{\mathbf {u}\in \mathbf {F}}{\overline{\alpha }}_S(\Gamma \mathbf {w})\subseteq \bigvee _{\mathbf {w}\in \pi ^{-1}[\mathbf {F}]}{\overline{\alpha }}_S(\Gamma \mathbf {w})\). Conversely, if \(\mathbf {w}\in \pi ^{-1}[\mathbf {F}]\), let \(\mathbf {u}=\pi [\mathbf {w}]\), so that \(\mathbf {u}\in \mathbf {F}\) and \(\mathbf {u}\le \pi [\mathbf {w}]\), which shows that the converse inclusion also holds. \(\square \)
Lemma 3.25
Assuming the frame axioms of Table 1, the condition in the statement of Proposition 3.24 can be replaced by the requirement in equation (3.14), which is equivalent to condition (3.13)
Proof
By Lemma 3.16 for any relation R in the frame it holds that \({\overline{\alpha }}_R(\Gamma \mathbf {u})=R\mathbf {u}=\alpha _R(\Gamma \mathbf {u})\). It follows that if equation (3.14) holds, then \(\alpha _S(\pi ^{-1}[\Gamma \mathbf {u}])\) is a Galois set, hence \(\alpha _S(\pi ^{-1}[\Gamma \mathbf {u}])={\overline{\alpha }}_S(\pi ^{-1}[\Gamma \mathbf {u}])\). Hence the identity in (3.14) implies the hypothesis in the statement of Proposition 3.24. Since
and \(v\in \pi ^{-1}\alpha _R(\Gamma \mathbf {u})\) iff \(\pi (v)R\mathbf {u}\) it follows that the two conditions in (3.14) and (3.13) are equivalent. \(\square \)
We conclude with the definition of the category of \(\tau \)-frames, for a similarity type (sequence of distribution types) \(\tau \).
Definition 3.26
The objects \({\mathfrak {F}}=(X,I,Y,(R_\sigma )_{\sigma \in \tau })\) of the category SRF\(_\tau \) of \(\tau \)-frames are sorted residuated frames (equivalently, polarities) with a relation of sort type \(\sigma \), for each \(\sigma \) in \(\tau \), subject to axioms F1–F4 of Table 1. Its morphisms \(\pi =(p,q):(X_2,I_2,Y_2,(S_\sigma )_{\sigma \in \tau })\longrightarrow (X_1,I_1,Y_1,(R_\sigma )_{\sigma \in \tau })\) are the weak bounded morphisms specified in Definition 3.20 that, in addition, satisfy condition (3.13) (axiom M4). Table 2 collects together all axioms.
Hereafter, by a weak bounded morphism we shall always mean that condition (3.13) (axiom M4) is also satisfied. Note that axiom M4 assumes proper sorting of \(\mathbf {u}, v\) and \(\mathbf {w}\) as necessitated by the sorting of the relations. We also point out that the axiomatization of the category SRF\(_\tau \) will be strengthened in Section 5, including an axiom that both X, Y are carriers of a Stone topology, for the purpose of deriving a Stone duality result.
4 Dual sorted residuated frames of NLEs
A bounded lattice expansion is a structure \({\mathcal {L}}=(L,\le ,\wedge ,\vee ,0,1,{\mathcal {F}}_1,{\mathcal {F}}_\partial )\), where \({\mathcal {F}}_1\) consists of normal lattice operators f of distribution type \(\delta (f)=(\mathbf {i_j};1)\) (i.e., of output type 1), while \({\mathcal {F}}_\partial \) consists of normal lattice operators h of distribution type \(\delta (h)=(\mathbf {t_j};\partial )\) (i.e., of output type \(\partial \)). For representation purposes, nothing depends on the size of the operator families \({\mathcal {F}}_1\) and \({\mathcal {F}}_\partial \) and we may as well assume that they contain a single member, say \({\mathcal {F}}_1=\{f\}\) and \({\mathcal {F}}_\partial =\{h\}\). In addition, nothing depends on the arity of the operators, so we may assume they are both n-ary.
4.1 Canonical lattice frame construction
The canonical frame is constructed as follows, based on [14, 15, 20, 21].
First, the base polarity  consists of the sets \(X=\mathrm{Filt}({\mathcal {L}})\) of filters and \(Y=\mathrm{Idl}({\mathcal {L}})\) of ideals of the lattice and the relation
consists of the sets \(X=\mathrm{Filt}({\mathcal {L}})\) of filters and \(Y=\mathrm{Idl}({\mathcal {L}})\) of ideals of the lattice and the relation  is defined by
is defined by  iff \(x\cap y\ne \emptyset \), while the representation map \(\zeta _1\) sends a lattice element \(a\in L\) to the set of filters that contain it, \(\zeta _1(a)=\{x\in X\vert a\in x\}=\{x\in X\vert x_a\subseteq x\}=\Gamma x_a\). Similarly, a co-represenation map \(\zeta _\partial \) is defined by \(\zeta _\partial (a)=\{y\in Y\vert a\in y\}=\{y\in Y\vert y_a\subseteq y\}=\Gamma y_a\). It is easily seen that \((\zeta _1(a))'=\zeta _\partial (a)\) and, similarly, \((\zeta _\partial (a))'=\zeta _1(a)\). The images of \(\zeta _1,\zeta _\partial \) are precisely the families (sublattices of \({{\mathcal {G}}}(X),{{\mathcal {G}}}(Y)\), respectively) of clopen elements of \({{\mathcal {G}}}(X),{{\mathcal {G}}}(Y)\), since clearly
iff \(x\cap y\ne \emptyset \), while the representation map \(\zeta _1\) sends a lattice element \(a\in L\) to the set of filters that contain it, \(\zeta _1(a)=\{x\in X\vert a\in x\}=\{x\in X\vert x_a\subseteq x\}=\Gamma x_a\). Similarly, a co-represenation map \(\zeta _\partial \) is defined by \(\zeta _\partial (a)=\{y\in Y\vert a\in y\}=\{y\in Y\vert y_a\subseteq y\}=\Gamma y_a\). It is easily seen that \((\zeta _1(a))'=\zeta _\partial (a)\) and, similarly, \((\zeta _\partial (a))'=\zeta _1(a)\). The images of \(\zeta _1,\zeta _\partial \) are precisely the families (sublattices of \({{\mathcal {G}}}(X),{{\mathcal {G}}}(Y)\), respectively) of clopen elements of \({{\mathcal {G}}}(X),{{\mathcal {G}}}(Y)\), since clearly  and
and  .
.
Second, for each normal lattice operator a relation is defined, such that if \(\delta =(i_1,\ldots ,i_n;i_{n+1})\) is the distribution type of the operator, then \(\sigma =(i_{n+1};i_1\dots i_n)\) is the sort type of the relation. Without loss of generality, we have restricted to the families of operators \({\mathcal {F}}_1=\{f\}\) and \({\mathcal {F}}_\partial =\{h\}\), so that we shall define two corresponding relations R, S of respective sort types \(\sigma (R)=(1;i_1\dots i_n)\) and \(\sigma (S)=(\partial ;t_1\dots t_n)\), where for each j, \(i_j\) and \(t_j\) are in \(\{1,\partial \}\). In other words \(R\subseteq X\times \prod _{j=1}^{j=n}Z_{i_j}\) and \(S\subseteq Y\times \prod _{j=1}^{j=n}Z_{t_j}\). To define the relations, we use the point operators introduced in [14] (see also [15]). In the generic case we examine, we need to define two sorted operators
Assuming for the moment that the point operators have been defined, the canonical relations R, S are defined by
Returning to the point operators and letting \(x_e,y_e\) be the principal filter and principal ideal, respectively, generated by a lattice element e, these are uniformly defined as follows, for \(\mathbf {u}\in \prod _{j=1}^{j=n}Z_{i_j}\) and \(\mathbf {v}\in \prod _{j=1}^{j=n}Z_{t_j}\)
In other words, \({\widehat{f}}(\mathbf {u})\) is the filter generated by the set \(\{f(\mathbf {a})\vert \mathbf {a}\in \mathbf {u}\}\). Similarly \({\widehat{h}}(\mathbf {v})\) is the ideal generated by the set \(\{h(\mathbf {a})\vert \mathbf {a}\in \mathbf {v}\}\).
Example 4.1
(FL\(_{\mathrm {ew}}\)) We consider as an example the case of associative, commutative, integral residuated lattices \({\mathcal {L}}=(L,\le ,\wedge ,\vee ,0,1,\circ ,\rightarrow )\), the algebraic models of FL\(_{\mathrm {ew}}\) (the associative full Lambek calculus with exchange and weakening), also referred to in the literature as full BCK. By residuation of \(\circ ,\rightarrow \), the distribution types of the operators are \(\delta (\circ )=(1,1;1)\) and \(\delta (\rightarrow )=(1,\partial ;\partial )\). Let  be the canonical frame of the bounded lattice \((L,\le ,\wedge ,\vee ,0,1)\). Designate the corresponding canonical point operators by
be the canonical frame of the bounded lattice \((L,\le ,\wedge ,\vee ,0,1)\). Designate the corresponding canonical point operators by  and \(\leadsto \), respectively. They are defined by (4.2)
and \(\leadsto \), respectively. They are defined by (4.2)

where recall that we write \(x_e,y_e\) for the principal filter and ideal, respectively, generated by the lattice element e, so that  , while \((x\leadsto v)\in \mathrm{Idl}({\mathcal {L}})\).
, while \((x\leadsto v)\in \mathrm{Idl}({\mathcal {L}})\).
The relations \(R^{111},S^{\partial 1\partial }\) are then defined by

of sort types \(\sigma (R)=(1;11)\) and \(\sigma (S)=(\partial ;1\partial )\). The canonical FL\(_{\mathrm {ew}}\)-frame is therefore the structure  .
.
Remark 4.2
In [27] a lattice duality is presented, \(\mathrm{Filt}:\mathbf{Lat}\leftrightarrows \mathbf{BL}^\partial :\mathtt{KOF}\), where for a given lattice \({\mathcal {L}}\) we have \({\mathcal {L}}{\mathop {\backsimeq }\limits ^{}}\mathtt{KOF}(\mathrm{Filt}({\mathcal {L}}))\subseteq \mathtt{FSat}(\mathrm{Filt}({\mathcal {L}}))\) where the latter is shown in [27] to be a concrete realization of a canonical extension of \({\mathcal {L}}\). In their sequel article [28], Moshier and Jipsen extend their work to lattice expansions (L, j), proving that normal lattice operators j (which they refer to as quasioperators) are in bijective correspondence with functions \(f_j\) on points of the corresponding product of their dual BL-spaces that are succintly characterized as (1) strongly continuous in the product topology and (2) preserving finite meets in each argument place. It follows by simple calculation that the definition of the point operators \(f_j\) given by Moshier and Jipsen in [28] is a rephrasing of the definition of the point operators introduced in [14] (and thereafter used in [15], as well as in the current article). Indeed, examining for simplicity only the case of a quasioperator that is additive (join-preserving), \(j:L_1\times \dots \times L_n\longrightarrow L_{n+1}\), Moshier and Jipsen define \(f_j:\mathrm{Filt}(L_1)\times \dots \times \mathrm{Filt}(L_n)\longrightarrow \mathrm{Filt}(L_{n+1})\) by setting
Designate by \(x_e\) the principal filter generated by a lattice element e. Letting
be the point operator introduced in [14, page 420], also used above in equation (4.2), it is readily seen that
i.e., the function \(f_j\) defined by Moshier and Jipsen in [28] coincides with the function \({\hat{j}}\) of [14], since \(u_1\times \dots \times u_n\subseteq j^{-1}(x)\) iff \(\bigwedge _{k=1}^{k=n}(a_k\in u_k)\;\Longrightarrow \;j(a_1,\ldots ,a_n)\in x\) iff \(\bigvee \{x_{j(a_1,\ldots ,a_n)}\vert \bigwedge _{k=1}^{k=n}(a_k\in u_k)\}\subseteq x\) iff \({\hat{j}}(u_1,\ldots ,u_n)\subseteq x\). In [14, Lemma 6.8] the distribution properties of the point operators were established, but no topological characterization as given in [28] was sought for in [14].
4.2 Properties of the canonical frame
We first verify that axioms F1–F3 of Table 2 hold for the canonical sorted residuated frame (polarity).
Lemma 4.3
The following hold for the canonical frame.
-
(1)
The frame is separated.
-
(2)
For \(\mathbf {u}\in \prod _{j=1}^{j=n}Z_{i_j}\) and \(\mathbf {v}\in \prod _{j=1}^{j=n}Z_{t_j}\) the sections \(R\mathbf {u}\) and \(S\mathbf {v}\) are closed elements of \({{\mathcal {G}}}(X)\) and \({{\mathcal {G}}}(Y)\), respectively.
-
(3)
For \(x\in X, y\in Y\), the n-ary relations xR, yS are decreasing in every argument place.
Proof
For (1), just note that the ordering \(\preceq \) is set-theoretic inclusion (of filters, and of ideals, respectively), hence separation of the frame is immediate.
For (2), by the definition of the relations, \(R\mathbf {u}=\{x\vert {\widehat{f}}(\mathbf {u})\subseteq x\}=\Gamma ({\widehat{f}}(\mathbf {u}))\) is a closed element of \({{\mathcal {G}}}(X)\) and similarly for \(S\mathbf {v}\).
For (3), if \(w\subseteq u_k\), then \(\{x_{f(a_1,\ldots ,a_n)}\vert a_k\in w\wedge \bigwedge _{j\ne k}(a_j\in u_j)\}\) is a subset of the set \(\{x_{f(a_1,\ldots ,a_n)}\vert \bigwedge _{j}(a_j\in u_j)\}\), hence taking joins it follows that \({\widehat{f}}(\mathbf {u}[w]_k)\subseteq {\widehat{f}}(\mathbf {u})\). By definition, if \(xR\mathbf {u}\) holds, then we obtain \({\widehat{f}}(\mathbf {u}[w]_k)\subseteq {\widehat{f}}(\mathbf {u})\subseteq x\), hence \(xR\mathbf {u}[w]_k\) holds as well. Similarly for the relation S. \(\square \)
Lemma 4.4
In the canonical frame, \(xR\mathbf {u}\) holds iff \(\forall \mathbf {a}\in L^n\;(\mathbf {a}\in \mathbf {u}\longrightarrow f(\mathbf {a})\in x)\). Similarly, \(yS\mathbf {v}\) holds iff \(\forall \mathbf {a}\in L^n\;(\mathbf {a}\in \mathbf {v}\longrightarrow h(\mathbf {a})\in y)\).
Proof
By definition \(xR\mathbf {u}\) holds iff \({\widehat{f}}(\mathbf {u})\subseteq x\), where \({\widehat{f}}(\mathbf {u})\), by its definition (4.2) is the filter generated by the elements \(f(\mathbf {a})\), for \(\mathbf {a}\in \mathbf {u}\), hence clearly \(\mathbf {a}\in \mathbf {u}\) implies \(f(\mathbf {a})\in x\). Similarly for the relation S. \(\square \)
Lemma 4.5
Where \(R',S'\) are the Galois dual relations of the canonical relations R, S, \(yR'\mathbf {u}\) holds iff  iff \(\exists \mathbf {b}(\mathbf {b}\in \mathbf {u}\wedge f(\mathbf {b})\in y)\). Similarly, \(xS'\mathbf {v}\) holds iff
iff \(\exists \mathbf {b}(\mathbf {b}\in \mathbf {u}\wedge f(\mathbf {b})\in y)\). Similarly, \(xS'\mathbf {v}\) holds iff  iff \(\exists \mathbf {e}(\mathbf {e}\in \mathbf {v}\wedge h(\mathbf {e})\in x)\).
iff \(\exists \mathbf {e}(\mathbf {e}\in \mathbf {v}\wedge h(\mathbf {e})\in x)\).
Proof
The proof is given in [19, Lemma 24], to which we refer the reader. \(\square \)
We can now prove that the frame axiom F4 of Table 2 also holds in the canonical frame.
Lemma 4.6
In the canonical frame, all sections of the Galois dual relations \(R', S'\) of the canonical relations R, S are Galois sets.
Proof
There are two cases to handle, one for each of the relations \(R',S'\), with two subcases for each one, depending on whether \(i_k\) is 1, or \(\partial \). The cases of the two relations are similar, we have presented the proof for the relation \(R'\) in [19, Lemma 25] and we only detail here the other case.
Case of the relation \(S'\):
The section \(S'\mathbf {v}=(S\mathbf {v})^\prime \) is a Galois (stable) set, by its definition. Recall that the sort type of S is \(\sigma (S)=(\partial ;t_1\dots t_n)\), where \(t_k\in \{1,\partial \}\) for each \(1\le k\le n\), and that S was defined given the lattice normal operator h, of distribution type \(\delta (h)=(t_1,\ldots ,t_n;\partial )\).
Let now \(x\in X\) and consider any section \(xS'\mathbf {v}[\_]_k\). We distinguish the subcases \(i_k=1\), or \(i_k=\partial \). When \(i_k=\partial \) (same as the output type of h), then h is monotone at the k-th argument place and it distributes over finite lattice meets, whereas when \(i_k=1\), then h is antitone at the k-th argument place and it co-distributes over finite lattice joins, turning them to meets. Furtheremore, by Lemma 4.5, \(xS'\mathbf {y}\) holds iff  iff \(\exists \mathbf {e}(\mathbf {e}\in \mathbf {y}\wedge h(\mathbf {e})\in x)\).
iff \(\exists \mathbf {e}(\mathbf {e}\in \mathbf {y}\wedge h(\mathbf {e})\in x)\).
Subcase \(i_k=\partial \):
Then \(xS'\mathbf {y}[\_]_k\subseteq Y=\mathrm{Idl}({\mathcal {L}})\) and note that the output type of h is also \(t_{n+1}=\partial \).
Let \(W=\{b\in L\vert \exists \mathbf {e}[\_]_k\in \mathbf {y}[\_]_k\;\;h(\mathbf {e}[b]_k)\in x\}\) and w be the filter generated by W. If v is an ideal such that \(xS'\mathbf {y}[v]_k\) holds, then by Lemma 4.5 , equivalently, for some tuple of lattice elements \(\mathbf {e}[b]_k\in \mathbf {y}[v]_k\) we have \(h(\mathbf {e}[b]_k)\in x\). Then \(b\in w\cap v\), i.e.,
, equivalently, for some tuple of lattice elements \(\mathbf {e}[b]_k\in \mathbf {y}[v]_k\) we have \(h(\mathbf {e}[b]_k)\in x\). Then \(b\in w\cap v\), i.e.,  and then
and then  .
.
Let now q be an ideal \(q\in (xS'\mathbf {y}[\_]_k)^{\prime \prime }\). We show that \(xS'\mathbf {y}[q]_k\) holds.
By the assumption on q and the fact that  we obtain
we obtain  , i.e., there is some element \(b\in w\cap q\ne \emptyset \). By definition of w, there exist lattice elements \(b_1,\ldots ,b_s\in W\), for some positive integer s, such that \(b_1\wedge \dots \wedge b_s\le b\). Since \(b_r\in W\), for \(1\le r\le s\), there exist tuples of lattice elements \(\mathbf {c}^r[\_]_k=(c^r_1,\ldots ,c^r_{k-1},\_\;,c^r_{k+1},\ldots ,c^r_n)\), for \(1\le r\le s\), such that \(h(\mathbf {c}^r[b_r]_k)\in x\). Define
, i.e., there is some element \(b\in w\cap q\ne \emptyset \). By definition of w, there exist lattice elements \(b_1,\ldots ,b_s\in W\), for some positive integer s, such that \(b_1\wedge \dots \wedge b_s\le b\). Since \(b_r\in W\), for \(1\le r\le s\), there exist tuples of lattice elements \(\mathbf {c}^r[\_]_k=(c^r_1,\ldots ,c^r_{k-1},\_\;,c^r_{k+1},\ldots ,c^r_n)\), for \(1\le r\le s\), such that \(h(\mathbf {c}^r[b_r]_k)\in x\). Define
Considering the monotonicity properties of h, observe that for each \(1\le r\le s\) we have
and so \(\bigwedge _{r=1}^{r=s}h(\mathbf {e}[b_r]_k)\in x\). In (4.5), \(\mathbf {c}^r[b_r]_k[e_j]_j^{t_j=\partial }[e_{j'}]_{j'}^{t_{j'}=1}\) designates the result of replacing \(c^r_j\) by \(e_j\) in \(\mathbf {c}^r[b_r]_k\), for every \(j\ne k\) from 1 to n such that \(t_j=\partial \) in the distribution type of h, and also replacing \(c^r_{j'}\) by \(e_{j'}\), for every \(j'\ne k\) from 1 to n such that \(t_{j'}=1\).
By the case assumption, h is monotone and it distributes over finite meets at the k-th argument place, hence we obtain
By Lemma 4.5, given \(\mathbf {e}[b]_k\in \mathbf {v}[q]_k\) and \(h(\mathbf {e}[b]_k)\in x\) we conclude that \(xS'\mathbf {v}[q]_k\) holds and this proves that the section \(xS'\mathbf {v}[\_]_k\) is a Galois (co-stable) set.
Subcase \(i_k=1\):
Then \(xS'\mathbf {y}[\_]_k\subseteq X=\mathrm{Filt}({\mathcal {L}})\).
Let \(W=\{b\in L\vert \exists \mathbf {e}[\_]_k\in \mathbf {y}[\_]_k\;\;h(\mathbf {e}[b]_k)\in x\}\) and v be the ideal generated by W. If z is any filter such that \(xS'\mathbf {y}[z]_k\), then by Lemma 4.5 there is a tuple of lattice elements \(\mathbf {e}[b]_k\in \mathbf {y}[z]_k\) such that \(h(\mathbf {e}[b]_k)\in x\). Thus \(b\in z\cap v\) and this shows that  .
.
We now assume that \(z\in (xS'\mathbf {y}[\_]_k)^{\prime \prime }\) and show that \(xS'\mathbf {y}[z]_k\) holds.
By \(z\in (xS'\mathbf {y}[\_]_k)^{\prime \prime }\) and  it follows that
it follows that  , so for some lattice element b we have \(b\in z\cap v\ne \emptyset \).
, so for some lattice element b we have \(b\in z\cap v\ne \emptyset \).
By definition of the ideal v, there exist elements \(b_1,\ldots ,b_s\in W\), for some positive integer s, such that \(b\le b_1\vee \dots \vee b_s\). By definition of W there exist tuples of lattice elements \(\mathbf {c}^r[\_]_k\), with \(1\le r\le s\), such that \(h(\mathbf {c}^r[b_r]_k)\in x\) for each \(1\le r\le s\). Define
Considering the monotonicity properties of h and using the notation introduced in the previous case, observe that, for each \(1\le r\le s\) we have
and so \(\bigwedge _{r=1}^{r=s}h(\mathbf {e}[b_r]_k)\in x\). By the case assumption, h is antitone and it co-distributes over finite joins at the k-th argument place, turning them to meets, hence we obtain that
By Lemma 4.5, given \(\mathbf {e}[b]_k\in \mathbf {y}[z]_k\) and \(h(\mathbf {e}[b]_k)\in x\), we conclude that \(xS'\mathbf {y}[z]_k\) holds and this shows that the section \(xS'\mathbf {y}[\_]_k\) is a Galois (stable) set. \(\square \)
The canonical frame for a lattice expansion \({\mathcal {L}}=(L,\le ,\wedge ,\vee ,0,1,f,h)\), where \(\delta (f)=(i_1,\ldots ,i_n;1)\) and \(\delta (h)=(t_1,\ldots ,t_n;\partial )\) (\(i_j,t_j\in \{1,\partial \}\)) is the structure  . By Lemma 4.6, the canonical relations R, S are compatible with the Galois connection generated by
. By Lemma 4.6, the canonical relations R, S are compatible with the Galois connection generated by  , in the sense that all sections of their Galois dual relations are Galois sets. Set operators \(\alpha _R, \eta _S\) are defined as in Section 3 and we let \({\overline{\alpha }}_R,{\overline{\eta }}_S\) be the closures of their restrictions to Galois sets (according to their distribution types). Note that \({\overline{\alpha }}_R(\mathbf {F})\in {{\mathcal {G}}}(X)\), while \({\overline{\eta }}_S(\mathbf {G})\in {{\mathcal {G}}}(Y)\), given the output types of f, h (alternatively, given the sort types of R, S).
, in the sense that all sections of their Galois dual relations are Galois sets. Set operators \(\alpha _R, \eta _S\) are defined as in Section 3 and we let \({\overline{\alpha }}_R,{\overline{\eta }}_S\) be the closures of their restrictions to Galois sets (according to their distribution types). Note that \({\overline{\alpha }}_R(\mathbf {F})\in {{\mathcal {G}}}(X)\), while \({\overline{\eta }}_S(\mathbf {G})\in {{\mathcal {G}}}(Y)\), given the output types of f, h (alternatively, given the sort types of R, S).
It follows from Theorem 3.12 and Lemma 4.6, that the sorted operators \({\overline{\alpha }}_R,{\overline{\eta }}_S\) on Galois sets distribute over arbitrary joins of Galois sets (stable or co-stable, according to the sort types of R, S) in each argument place.
Note that \({\overline{\alpha }}_R,{\overline{\eta }}_S\) are sorted maps, taking their values in \({{\mathcal {G}}}(X)\) and \({{\mathcal {G}}}(Y)\), respectively. We define single-sorted maps on \({{\mathcal {G}}}(X)\) (analogously for \({{\mathcal {G}}}(Y)\)) by composition with the Galois connection
Given that the Galois connection is a duality of Galois stable and Galois co-stable sets, it follows that the distribution type of \({\overline{\alpha }}_f\) is that of f and that \({\overline{\alpha }}_f\) distributes, or co-distributes, over arbitrary joins and meets in each argument place, according to its distribution type, returning joins in \({{\mathcal {G}}}(X)\). Similarly, for \({\overline{\eta }}_h\).
Definition 4.7
The lattice representation maps \(\zeta _1:(L,\le ,\wedge ,\vee ,0,1)\longrightarrow {{\mathcal {G}}}(X)\) and \(\zeta _\partial :(L,\le ,\wedge ,\vee ,0,1)\longrightarrow {{\mathcal {G}}}(Y)\) are extended to maps \(\zeta _1:{\mathcal {L}}\longrightarrow {{\mathcal {G}}}(X)\) and \(\zeta _\partial :{\mathcal {L}}\longrightarrow {{\mathcal {G}}}(Y)\) by setting
Remark 4.8
Recall from Remark 4.2 that Moshier and Jipsen [28] show that normal lattice operators j are in bijective correspondence with meet-preserving strongly continuous maps \({\hat{j}}\) on the dual lattice spaces (BL-spaces, in the terminology of [27, 28]) and that these maps, as defined in [28], coincide with the maps introduced in [14] and subsequently used in [15, 16, 19, 22] and in this article, defined by equation (4.2). Furthermore, given a meet-preserving strongly continuous n-ary map f on BL-spaces \({\mathcal {X}}_i\), a join-preserving map \(j_f\) is defined in [28] on \(\prod _{i}^{}{{\,\mathrm{FSat}\,}}(X_i)\) with values in \({{\,\mathrm{FSat}\,}}(X_n)\) by
and this provides for a representation of a normal lattice operator as a map on the canonical extension of the lattice, but the issue is not discussed in any detail in [28]. There is however a clear similarity with the approach we have taken, as witnessed by Lemma 3.16 and its preceding remark.
In [10], Gehrke and Harding introduced the so-called \(\sigma \) and \(\pi \)-extensions of lattice maps. The reader may recall from [10] that if \((\alpha ,C)\) is a canonical extension of a bounded lattice L, and \(\mathtt{K,O}\) are its sets of closed and open elements, the \(\sigma \) and \(\pi \)-extensions \(f_\sigma ,f_\pi :{{\mathcal {L}}}_\sigma \longrightarrow {{\mathcal {L}}}_\sigma \) (where, following the notation of [10], \({{\mathcal {L}}}_\sigma \) designates the canonical extension of \({\mathcal {L}}\)) of a unary monotone map \(f:L\longrightarrow L\) are defined in [10], taking also into consideration [10, Lemma 4.3], by setting, for \(k\in \mathtt{K}\), \(o\in \mathtt{O}\) and \(u\in C\)
where in these definitions \({\mathcal {L}}\) is identified with its isomorphic image in C and \(a\in {{\mathcal {L}}}\) is then identified with its representation image. This easily extends to n-ary maps, as detailed in [10, 15]. We have explained in [16] and in [19, Section 3.3] that the representation of a normal lattice operator f, as we define it in this article and in our previous work, for example [16, 19, 22], is the \(\sigma \)-extension of f, if f is of output type 1 (it returns joins), and it is its \(\pi \)-extension otherwise.
Both in the current article and in recent work by the author, a relational representation of operators is sought for and this is also the case in the generalized Kripke frames approach [9]. In [19, Remark 29] we have detailed the similarities and differences in the approach taken by Gerhke and by this author. It suffices to point out here that the relations used in the generalized Kripke frames approach are typically the Galois dual relations of the relations that we define.
4.3 Duals of lattice expansion homomorphisms
With the next proposition, we verify that the frame axioms M1–M4 also hold in the canonical frame construction.
Proposition 4.9
Let \(h:{\mathcal {L}}\longrightarrow {\mathcal {L}}^*\) be a homomorphism of normal lattice expansions of similarity type \(\tau \), with corresponding normal operators \(f_\sigma , f^*_\sigma \), for each \(\sigma \in \tau \), and \({\mathfrak {F}}=(X,I,Y,(R_\sigma )_{\sigma \in \tau })\), \({\mathfrak {F}}^*=(X^*,I^*,Y^*,(S_\sigma )_{\sigma \in \tau })\) their canonical dual frames, as defined in Section 4.1. For \(x^*\in X^*\) and \(y^*\in Y^*\) define \(p(x^*)=h^{-1}[x^*]=\{a\in {\mathcal {L}}\vert h(a)\in x^*\}\), \(q(y^*)=h^{-1}[y^*]=\{a\in {\mathcal {L}}\vert h(a)\in y^*\}\). Then \(\pi =(p,q):(X^*,I^*,Y^*,(S_\sigma )_{\sigma \in \tau }) \longrightarrow (X,I,Y,(R_\sigma )_{\sigma \in \tau })\) is a weak bounded morphism of their dual sorted residuated frames.
Proof
For the first condition (relation preservation, axiom M1 of Table 2), assume \(x^*I^*y^*\), i.e., \(x^*\cap y^*=\emptyset \). If \(p(x^*)\cap q(y^*)\ne \emptyset \) and \(a\in h^{-1}[x^*]\cap h^{-1}[y^*]\), then \(h(a)\in x^*\cap y^*\ne \emptyset \), contradicting the hypothesis.
For the second condition (axiom M2 of Table 2), let \(x\in X, y^*\in Y^*\) be arbitrary and assume \(xI q(y^*)\), which means \(x\cap h^{-1}[y^*]=\emptyset \), i.e., \(\forall a\in {\mathcal {L}}(a\in x\longrightarrow h(a)\not \in y^*)\). Let \(x^*\) be the filter generated by the set \(\{h(a)\vert a\in x\}=h[x]\). Then \(x\subseteq h^{-1}[x^*]=p(x^*)\). Suppose now that \(e\in x^*\cap y^*\). Let \(a_1,\ldots ,a_n\in x\) such that \(h(a_1)\wedge \dots \wedge h(a_n)\le e\). Since h is a lattice homomorphism and x is a filter, if \(a=a_1\wedge \dots \wedge a_n\), then \(a\in x\) and \(h(a_1)\wedge \dots \wedge h(a_n)=h(a)\le e\in y^*\), but \(y^*\) is an ideal, hence \(h(a)\in y^*\), contradiction. Hence it also holds for this \(x^*\) that \(x^*I^*y^*\).
The proof of the third condition (axiom M3 of Table 2) is similar, but we detail it anyway. So let \(x^*\in X^*, y\in Y\), arbitrary, and assume that \(p(x^*)I y\), i.e., \(h^{-1}[x^*]\cap y=\emptyset \). In other words, \(\forall a\in {\mathcal {L}}(a\in y\longrightarrow h(a)\not \in x^*)\). Let \(y^*\) be the ideal generated by the set \(h[y]=\{h(e)\vert e\in y\}\). Then \(y\subseteq h^{-1}[y^*]=q(y^*)\). If \(e\in x^*\cap y^*\), let \(a_1,\ldots , a_n\in y\) such that \(e\le h(a_1)\vee \dots \vee h(a_n)=h(a_1\vee \dots \vee a_n)\), since h is a homomorphism. Put \(a=a_1\vee \dots \vee a_n\in y\). Then \(e\in x^*\), a filter, hence \(h(a)\in x^*\), while \(a\in y\), contradiction. Hence we obtain \(x^*I^*y^*\) for the ideal \(y^*\) defined above.
Let \(R_\sigma , S_\sigma \) be the canonical relations in the two frames, of the same sort type \(\sigma =(i_{n+1};\mathbf {i_j})\), corresponding to the normal lattice operators \(f_\sigma \) and \(f^*_\sigma \). Let \(\alpha _R,\alpha _S\) (we drop the subscript \(\sigma \), for simplicity) be the induced image operators.
We show that \(\pi ^{-1}\) is a homomorphism, i.e., that axiom M4 of Table 2 holds, or, equivalently by Lemma 3.25, that \(\pi ^{-1}\alpha _R(\Gamma \mathbf {u})=\alpha _S(\pi ^{-1}[\Gamma \mathbf {u}])\).
We calculate that
-
\(v\in \pi ^{-1}\alpha _R(\Gamma \mathbf {u})\) iff \(\pi (v)\in \alpha _R(\Gamma \mathbf {u})\)
-
iff \(h^{-1}[v]\in \alpha _R(\Gamma \mathbf {u})\) definition of \(\pi \) (v a filter, or an ideal)
-
iff \(h^{-1}[v]\in R\mathbf {u}\) Lemma 3.16
-
iff \(h^{-1}[v]\in \Gamma ({\widehat{f}}\mathbf {u})\) definition of the canonical relation
-
iff \({\widehat{f}}\mathbf {u}\le h^{-1}[v]\) the order is inclusion
-
iff \({\widehat{f}}\mathbf {u}\subseteq h^{-1}[v]\) in the canonical frame
-
iff \(\forall \mathbf {a}(\mathbf {a}\in \mathbf {u}\longrightarrow f(\mathbf {a})\in h^{-1}[v])\) definition of \({\widehat{f}}\)
-
iff \(\forall \mathbf {a}(\mathbf {a}\in \mathbf {u}\longrightarrow h(f(\mathbf {a}))\in v)\)
-
iff \(\forall \mathbf {a}(\mathbf {a}\in \mathbf {u}\longrightarrow f^*(h[\mathbf {a}])\in v)\) h is a homomorphism.
Note that \(\mathbf {w}\in \pi ^{-1}[\Gamma \mathbf {u}]\) iff \(\mathbf {u}\subseteq \pi [\mathbf {w}]\) and since \(\pi ^{-1}[\Gamma \mathbf {u}]\) is a Galois set, by Lemma 3.3 we obtain \(\pi ^{-1}[\Gamma \mathbf {u}]=\bigcup _{\mathbf {u}\subseteq \pi [\mathbf {w}]}\Gamma \mathbf {w}\), hence we compute
We first prove that \(\bigcup _{h[\mathbf {u}]\subseteq \mathbf {w}}\Gamma (\widehat{f^*}\mathbf {w})\subseteq \pi ^{-1}\alpha _R(\Gamma \mathbf {u})\). To clarify notation, \(h[\mathbf {u}]\) is the tuple \((h[u_1],\ldots ,h[u_n])\), where \(h[u_j]=\{h(e)\vert e\in u_j\}\). Then by \(h[\mathbf {u}]\subseteq \mathbf {w}\) we mean the (conjunction of the) pointwise inclusions \(h[u_j]\subseteq w_j\).
Let then \(\mathbf {w}\) be such that \(h[\mathbf {u}]\subseteq \mathbf {w}\) and assume that \(\widehat{f^*}\mathbf {w}\subseteq v\). To show that \(v\in \pi ^{-1}\alpha _R(\Gamma \mathbf {u})\) we assume that \(\mathbf {a}\in \mathbf {u}\) and prove that \(f^*(h[\mathbf {a}])\in v\).
By \(\mathbf {a}\in \mathbf {u}\) and \(h[\mathbf {u}]\subseteq \mathbf {w}\) we obtain \(h[\mathbf {a}]\in \mathbf {w}\) (i.e., \(h(a_j)\in w_j\), for all \(j=1,\ldots ,n\)). By definition in the canonical frame \(\widehat{f^*}\mathbf {w}\) is (the filter, or ideal, depending on the distribution type \(\sigma \)) generated by the set \(\{f^*(\mathbf {e})\vert \mathbf {e}\in \mathbf {w}\}\). By the hypothesis that \(\widehat{f^*}\mathbf {w}\subseteq v\) we obtain that \(\{f^*(\mathbf {e})\vert \mathbf {e}\in \mathbf {w}\}\subseteq v\). Since \(h[\mathbf {a}]\in \mathbf {w}\), we have in particular that \(f^*(h[\mathbf {a}])\in v\).
Conversely, we show that \(\pi ^{-1}\alpha _R(\Gamma \mathbf {u})\subseteq \bigcup _{h[\mathbf {u}] \subseteq \mathbf {w}}\Gamma (\widehat{f^*}\mathbf {w})\).
Let \(v\in \pi ^{-1}\alpha _R(\Gamma \mathbf {u})\) which means, by the calculation above, that \(\pi (v)R\mathbf {u}\), equivalently in the canonical frame it means that \(\{f^*(h[\mathbf {a}])\vert \mathbf {a}\in \mathbf {u}\}\subseteq v\). The claim is that there is a tuple \(\mathbf {w}=(w_1,\ldots ,w_n)\), where \(w_j\) is a filter if \(i_j=1\) in the distribution type of \(f,f^*\) and \(w_j\) is an ideal when \(i_j=\partial \), such that \(h[\mathbf {u}]\subseteq \mathbf {w}\) and \(\widehat{f^*}\mathbf {w}\subseteq v\).
Define \(w_j=\langle h[u_j]\rangle \) to be the filter of \({\mathcal {L}}^*\) generated by the set \(h[u_j]\), if \(i_j=1\) and otherwise let it be the ideal generated by the same set. Thus trivially \(h[\mathbf {u}]\subseteq \mathbf {w}\) holds. By definition of \(\widehat{f^*}\), it suffices to get its set of generators \(\{f^*(\mathbf {e})\vert \mathbf {e}\in \mathbf {w}\}\) to be contained in v.
Let \(\mathbf {e}\in \mathbf {w}\) so that for \(1\le j\le n\), \(e_j\in w_j\).
If \(i_j=1\), then \(w_j\) is the filter generated by the set \(h[u_j]\) (where \(u_j\) is also a filter) and there are elements \(a^j_1,\dots ,a^j_s\in u_j\) such that \(h(a^j_1)\wedge \dots \wedge h(a^j_s)\le e_j\). Since h is a homomorphism and \(u_j\) is a filter, letting \(a^j=a^j_1\wedge \dots \wedge a^j_s\in u_j\) we obtain \(h(a^j)\le e_j\).
If \(i_j=\partial \), then \(w_j\) is the ideal generated by the set \(h[u_j]\) (where \(u_j\) is also an ideal) and there are elements \(a^j_1,\dots ,a^j_t\in u_j\) such that \(e_j\le h(a^j_1)\vee \dots \vee h(a^j_t)\). Letting \(a^j\) be the disjunction \(a^j=a^j_1\vee \dots \vee a^j_t\) we similarly obtain \(e_j\le h(a^j)\).
If the output type \(i_{n+1}=1\), then v is a filter, \(f,f^*\) are monotone at the j-th position, whenever \(i_j=1\) and they are antitone at any position \(i_{j'}\) with \(i_{j'}=\partial \). Therefore, \(f^*(h(a^1),\ldots ,h(a^n))\le f^*(e_1,\ldots ,e_n)\), which we may compactly write as \(f^*(h[\mathbf {a}])\le f^*(\mathbf {e})\). From the hypothesis on v we have that \(f^*(h[\mathbf {a}])\in v\), which is a filter when \(i_{n+1}=1\), hence also \(f^*(\mathbf {e})\in v\).
If the output type \(i_{n+1}=\partial \), then v is an ideal, \(f,f^*\) are monotone at the j-th position, whenever \(i_j=\partial \) and they are antitone at any position \(i_{j'}\) with \(i_{j'}=1\). Thereby, \(f^*(e_1,\ldots ,e_n)\le f^*(h(a^1),\ldots ,h(a^n))\), i.e., \(f^*(\mathbf {e})\le f^*(h[\mathbf {a}])\in v\), now an ideal, hence again \(f^*(\mathbf {e})\in v\). \(\square \)
5 Stone duality
The results we have presented can be extended to a Stone duality, by combining them with our results in [15, 21]. The functor \(\mathtt{F}:\mathbf{NLE}_\tau \longrightarrow \mathbf{SRF}_\tau ^{op}\) sends a normal lattice expansion \({\mathfrak {L}}\) in NLE\(_\tau \) to its dual frame \({\mathcal {L}}_+={\mathfrak {F}}\) in SRF\(_\tau \) (detailed in Section 4.1) and a lattice expansion homomorphism h to a weak bounded morphism \(\pi \) (detailed in Section 4.3). Conversely, we have constructed a functor \(\mathtt{L}:\mathbf{SRF}_\tau ^{op}\longrightarrow \mathbf{NLE}_\tau \), sending a frame \({\mathfrak {F}}\) in SRF\(_\tau \) to its full complex algebra \({\mathfrak {F}}^+\) (Definition 3.8), which is a complete normal lattice expansion, and a weak bounded morphism \(\pi \) to a complete normal lattice expansion homomorphism \(\pi ^{-1}\) (detailed in Section 3.2.2).
For a full Stone duality, a subcategory SRF\(^*_\tau \) will be identified, by strengthening the axiomatization of sorted residuated frames with relations, imposing in particular that the sort sets of a sorted frame are carriers of a Stone topology. In addition, we replace axiom F2 with a stronger version, we add axioms F5–F7 from [15, 21] as well as axioms M5, M6. The full axiomatization of the category SRF\(^*_\tau \) is presented in Table 3. Call a point \(u\in X\cup Y\) clopen if \(\Gamma u\) is clopen, i.e., if there exists a point v of the dual sort such that \(\Gamma u=\{v\}'\).
Remark 5.1
Axioms F1 and F5–F7 are an equivalent axiomatization of the L-frames of [21]. Lattice expansions were studied in [15] and axioms R7–R10 were postulated in order to derive that the defined operators from relations have the complete distribution properties corresponding to the distribution type of the operator represented. We have followed in this article an alternative approach, presenting a simpler axiomatization of frames, relying only on axiom F4 in order to obtain proof of the required distribution properties. Though differences in the presentation exist, the representation of normal lattice operators is the same in this article and in [15], see in particular [15, Remark 3.2]. Frame morphisms in this article are the weak bounded morphisms axiomatized by M1–M6, whereas in [15] a weaker notion of morphism was employed, requiring essentially only preservation of clopen sets.
For a frame \({\mathfrak {F}}\) of SRF\(^*_\tau \), the following result ensures that its lattice of clopen elements is an object of NLE\(_\tau \).
Proposition 5.2
Let \({\mathfrak {F}}=(X,I,Y,(R_\sigma )_{\sigma \in \tau })\) be a sorted residuated frame in the category SRF\(^*_\tau \), with a relation \(R_\sigma \) of sort \(\sigma =(i_{n+1};\mathbf {i_j})\) for each \(\sigma \) in \(\tau \). Then the clopen elements in \({{\mathcal {G}}}(X)\) form a lattice and \({\overline{\alpha }}^1_{R_\sigma }\) restricts to a normal operator of distribution type \(\delta =(\mathbf {i_j};i_{n+1})\) on the lattice of clopens.
Proof
By the fact that the Galois connection restricts to a duality on clopens, the clopen elements of \({{\mathcal {G}}}(X)\) and \({{\mathcal {G}}}(Y)\) are lattices, given axiom F5. By definition and axiom F2 (Table 3), \({\overline{\alpha }}_{R_\sigma }(\mathbf {F})=\bigvee _{\mathbf {u}\in \mathbf {F}}(R_\sigma \mathbf {u})^{\prime \prime }=\bigvee _{\mathbf {u}\in \mathbf {F}}R_\sigma \mathbf {u}= \bigvee _{\mathbf {u}\in \mathbf {F}}\Gamma w\), for some w depending on \(\mathbf {u}\) (which is unique, by the separation axiom F1). In particular, \({\overline{\alpha }}_{R_\sigma }(\Gamma w_1,\ldots ,\Gamma w_n)=\bigvee _{\mathbf {w}\le \mathbf {u}}R_\sigma \mathbf {u}\). By axiom F3, if \(\mathbf {w}\le \mathbf {u}\), then \(R_\sigma \mathbf {u}\subseteq R_\sigma \mathbf {w}\), hence \({\overline{\alpha }}_{R_\sigma }(\Gamma w_1,\ldots ,\Gamma w_n)=R_\sigma \mathbf {w}\), a closed element, by axiom F2. Again by axiom F2 (Table 3), if all sets \(\Gamma w_j\) are clopen elements, then also \(R_\sigma \mathbf {w}\) is a clopen element. Hence \({\overline{\alpha }}_{R_\sigma }\) restricts to an operator on clopen elements. By Theorem 3.12, using axiom F4, \({\overline{\alpha }}_{R_\sigma }\) (which is a sorted operator, of sort \((\mathbf {i_j};i_{n+1})\)), distributes over arbitrary joins in each argument place. It follows that the single-sorted operator \({\overline{\alpha }}^1_{R_\sigma }\) obtained by appropriate composition with the Galois connection is a normal operator of distribution type \(\delta =(\mathbf {i_j};i_{n+1})\) on the lattice of clopen elements in \({{\mathcal {G}}}(X)\). \(\square \)
Propositions 5.2 and the next proposition verify that \(\mathtt{L}^*\) is a well defined functor, \(\mathtt{L}^*:\mathbf{SRF}^*_\tau \longrightarrow \mathbf{NLE}_\tau \).
Proposition 5.3
Let \(\mathtt{L}^*\) be defined so that for a sorted residuated frame \({\mathfrak {F}}\) with relations in SRF\(^*_\tau \), \(\mathtt{L}^*({\mathfrak {F}})\) is the normal lattice expansion of its stable clopen elements (the clopens of \({{\mathcal {G}}}(X)\)). If \(\pi =(p,q):{\mathfrak {F}}_2\longrightarrow {\mathfrak {F}}_1\) is a morphism in SRF\(^*_\tau \), then \(\mathtt{L}^*(\pi )=\pi ^{-1}\) is a homomorphism of normal lattice expansions from clopens in \({\mathcal {G}}(X_1)\) to clopens of \({\mathcal {G}}(X_2)\).
Proof
Axiom M5 and Lemma 3.23 ensure that \(\mathtt{L}^*(\pi )=\pi ^{-1}\) maps clopens to clopens, hence it restricts to a homomorphism of the normal lattice expansions of clopens. \(\square \)
We next verify that the functor \(\mathtt{F}:\mathbf{NLE}_\tau \longrightarrow \mathbf{SRF}_\tau \) is in fact a functor \(\mathtt{F}:\mathbf{NLE}_\tau \longrightarrow \mathbf{SRF}^*_\tau \).
Proposition 5.4
The canonical frame of a normal lattice expansion is a sorted residuated frame in the category \(\mathbf{SRF}^*_\tau \).
Proof
Axioms F1–F3 were verified in Lemma 4.3. For the strengthened axiom F2 (Table 3), the proof follows from the fact, proven in [14, Lemma 6.7], that the point operators \({\widehat{f}}\) map principal filters (ideals) to principal filters (ideals). Lemma 4.6 verified axiom F4. Clopens in the canonical frame are the sets \(\Gamma x_a\), for a principal filter \(x_a\) (similarly for ideals) and \(\Gamma x_a\cap \Gamma x_b=\Gamma x_{a\vee b}\), so axiom F5 holds. By join-density of principal filters (similarly for ideals) \(x=\bigvee _{a\in x}x_a\) and then \(\Gamma x=\Gamma (\bigvee _{a\in x}x_a)=\bigcap _{a\in x}\Gamma x_a\), hence axiom F6 is true in the canonical frame. Clopen sets \(\Gamma x_a\) are precisely the sets in the image of the representation map \(\zeta _1(a)=\{x\in \mathrm{Filt}({\mathcal {L}})\vert a\in x\}\) and it is by a standard argument in Stone duality that the topology generated by the subbasis \({\mathcal {S}}=\{\zeta _1(a)\vert a\in {\mathcal {L}}\}\cup \{-\zeta _1(a)\vert a\in {\mathcal {L}}\}\) is compact and totally separated and the compact-open sets (clopen, since the space is totally separated, hence Hausdorff) are precisely the sets \(\zeta _1(a)\), for a lattice element a. Proof details can be found in [21, Lemma 2.5], and thereby axiom F7 holds for the canonical frame as well, which is then an object of the category SRF\(^*_\tau \), as claimed. \(\square \)
Theorem 5.5
The representation map \(\zeta _1\) (Definition 4.7 ) is a homomorphism of normal lattice expansions, indeed an isomorphism of the normal lattice expansion \({\mathfrak {L}}\) and its second dual \(({\mathcal {L}}_+)^+\), i.e., the normal lattice expansion of the clopen sets of filters. Similarly, \(\zeta _\partial \) is a dual isomorphism of \({\mathcal {L}}\) and the normal lattice expansion of clopen sets of ideals.
Proof
The fact that \(\zeta _1\) is a lattice isomorphism was shown in [21, Theorem 2.4]. By the axiomatization of the category SRF\(^*_\tau \) and Proposition 5.4, the operations \({\overline{\alpha }}_R\), for a frame relation R, restrict to additive operators on clopen sets (in \({{\mathcal {G}}}(X)\), or in \({{\mathcal {G}}}(Y)\), in accordance to the sort of the relation R), hence the operators derived by composition with the Galois connection as in Definition 4.7 are normal lattice operators of the same distribution type as that of the lattice operator they represent. The representation of normal lattice operators in this article is no different from that of [15] (see, in particular, [15, Remark 3.2]), the difference of approach between this article and [15] having to do only with the axiomatization of frame relations. Hence we may appeal to the results of [15], in particular, [15, Theorem 4.5], concluding the proof of the present theorem. \(\square \)
Proposition 5.6
Let \(h:{\mathcal {L}}\longrightarrow {\mathcal {L}}^*\) be a morphism in the category NLE\(_\tau \) and \(\pi =(p,q):{\mathcal {L}}^*_+\longrightarrow {\mathcal {L}}_+\) be the canonical \(\mathbf{SRF}_\tau \) morphism, \(p=h^{-1}:X^*\longrightarrow X\) and \(q=h^{-1}:Y^*\longrightarrow Y\). Then for a filter \(u\in X\), \(\pi ^{-1}(\Gamma u)\) is a closed element in \({\mathcal {G}}(X^*)\). Similarly for ideals.
Proof
Let \(w_u\) be the filter generated by the set \(h[u]=\{h(a)\vert a\in u\}\). By calculating \(\pi ^{-1}(\Gamma u)\), it is easily seen that \(\pi ^{-1}(\Gamma u)=\Gamma w_u\). Similarly for ideals. \(\square \)
Proposition 5.7
The canonical map \(\pi =(p,q):{\mathcal {L}}^*_+\longrightarrow {\mathcal {L}}_+\) is continuous, in the topological sense.
Proof
The proof is part of the argument in the proof of [21, Lemma 2.5]. \(\square \)
By the above arguments, \(\mathtt{L}^*\) and \(\mathtt{F}\) are contravariant functors on our categories of interest \(\mathtt{F}:\mathbf{NLE}_\tau \leftrightarrows (\mathbf{SRF}^*_\tau )^{op}:\mathtt{L}^*\).
Theorem 5.8
(Stone duality) For any objects \({\mathcal {L}}, {\mathfrak {F}}\) of the categories \(\mathbf {NLE}_\tau \) and \(\mathbf {SRF}^*_\tau \), respectively, \({\mathcal {L}}\backsimeq \mathtt{L}^*\mathtt{F}({\mathcal {L}})\) and \({\mathfrak {F}}\backsimeq \mathtt{F}\mathtt{L}^*({\mathfrak {F}})\).
Proof
The isomorphism \({\mathcal {L}}\backsimeq \mathtt{L}^*\mathtt{F}({\mathcal {L}})\) was handled in Theorem 5.5, referring for proof details to [21, Theorem 2.4], for the lattice isomorphism, and to [15, Theorem 4.5], for the case of lattice expansions of similarity type \(\tau \).
For the second isomorphism, \({\mathfrak {F}}\backsimeq \mathtt{F}\mathtt{L}^*({\mathfrak {F}})\), we may base the argument either on [21], or on [16]. In [21], we argued that any sorted frame \({\mathfrak {F}}\) (L-frame in [21]) subject to the axioms F1, F5–F7 is the frame dual to a lattice. More specifically, if \({\mathcal {S}}=(C_s)_{s\in L}\) is the family of compact-open subsets of X (\({\mathcal {S}}\) is in fact a normal lattice expansion of similarity type \(\tau \), by the frame axioms and by Proposition 5.2), indexed in some set L, then L inherits the structure of the family \({\mathcal {S}}\). Hence, it is a normal lattice expansion \({\mathcal {L}}\) of type \(\tau \) isomorphic to \({\mathcal {S}}\) and \({\mathfrak {F}}\) is, up to isomorphism, its dual frame. In other words, \(\mathtt{L}^*({\mathfrak {F}})={\mathcal {S}}\backsimeq {\mathcal {L}}\) and \({\mathfrak {F}}\backsimeq \mathtt{F}({\mathcal {L}})\). Therefore, we have \(\mathtt{F}\mathtt{L}^*({\mathfrak {F}})\backsimeq \mathtt{F}\mathtt{L}^*\mathtt{F}({\mathcal {L}})\backsimeq \mathtt{F}({\mathcal {L}})\backsimeq {\mathfrak {F}}\). \(\square \)
6 Concluding remarks and further research
We revisited in this article the question of Stone duality for lattices with quasioperators (normal lattice expansions, in our terminology), first addressed in [15]. We improved on the results of [15] in the following sense.
First, the category of frames is specified with a simpler axiomatization on relations, to ensure that the induced operators are completely normal lattice operators. Gehrke’s notion of stability of sections [9] was used and, by introducing a notion of sorted conjugate operators we argued that the induced sorted operators, for any sort type \(\sigma =(i_{n+1};\mathbf {i_j})\) of the relations, distribute over arbitrary joins of Galois sets (stable, or co-stable, according to the sort type of the relation). By composition with the Galois connection, completely normal single-sorted operators of distribution type \(\delta =(\mathbf {i_j};i_{n+1})\) are obtained. The section stability requirement implies complete distribution, but as far as we can see the two are not equivalent.
Second, frame morphisms in [15] were tailored to the need to prove a Stone duality and were thus keyed only to the requirement that their inverses preserve clopens. Based on Goldblatt’s recent notion of bounded morphisms for polarities [11] we defined weak bounded morphisms for polarities (equivalently, sorted residuated frames) and extended to the case of frames with relations. The extended definition for morphisms is different and simpler than Goldblatt’s. The extended notion of a frame morphism was shown to satisfy the requirement that its inverse is a homomorphism of the full complex algebras of the frames. To ensure that a Stone duality result is provable, we strengthened the axiomatization of frame relations and morphisms in Section 5.
Third, we expanded on our results in [18] by showing that completely normal operators on the lattice of stable sets of a frame are obtained by taking the closure of the restriction of classical sorted image operators to Galois sets. This provides a proof, at the representation level, that the logics of normal lattice expansions are fragments of corresponding sorted residuated polymodal logics (their modal companions).
This latter development opens up some new problems to investigate, given the results established in this article. Essentially, the research direction opened is one of reducing problems on non-distributive logics (via translation to their modal companions) to problems on sorted residuated polymodal logics. We leave these issues for further research (initiated in [17, 18]).
References
Allwein, G., Hartonas, C.: Duality for bounded lattices. Tech. Rep. IULG-93-25, Indiana University Logic Group (1993)
Birkhoff, G.: Lattice theory, third edn. American Mathematical Society Colloquium Publications 25, American Mathematical Society, Providence, Rhode Island (1979)
Craig, A.: Canonical extensions of bounded lattices and natural duality for default bilattices. Ph.D. thesis, University of Oxford (2012)
Craig, A., Gouveia, M.J., Haviar, M.: TiRS graphs and TiRS frames: a new setting for duals of canonical extensions. Algebra Universalis 74, 123–138 (2015)
Craig, A., Haviar, M.: Reconciliation of approaches to the construction of canonical extensions of bounded lattices. Math. Slovaca 64, 1335–1356 (2014)
Craig, A., Haviar, M., Priestley, H.: A fresh perspective on canonical extensions for bounded lattices. Appl. Categ. Structures 21, 725–749 (2013)
Dunn, J..M.: Gaggle theory: An abstraction of Galois connections and residuation with applications to negations and various logical operations. In: Logics in AI, Proceedings of European Workshop JELIA 1990, LNCS 478, 31–51 (1990)
Ganter, B., Wille, R.: Formal Concept Analysis: Mathematical Foundations. Springer (1999)
Gehrke, M.: Generalized Kripke frames. Studia Logica 84, 241–275 (2006)
Gehrke, M., Harding, J.: Bounded lattice expansions. J. Algebra 238, 345–371 (2001)
Goldblatt, R.: Morphisms and duality for polarities and lattices with operators. FLAP 7, 1017–1070 (2020)
Gouveia, M.J., Priestley, H.A.: Canonical extensions and profinite completions of semilattices and lattices. Order 31, 189–216 (2014)
Grishin, V.: On a generalization of the Ajdukiewicz–Lambek system. In: A. Mikhailov (ed.) Studies in Nonclassical Logics and Formal Systems, 315–334. Nauka (1983)
Hartonas, C.: Duality for lattice-ordered algebras and for normal algebraizable logics. Studia Logica 58, 403–450 (1997)
Hartonas, C.: Stone Duality for Lattice Expansions. Log. J. IGPL 26, 475–504 (2018)
Hartonas, C.: Discrete duality for lattices with modal operators. J. Log. Comput. 29, 71–89 (2019)
Hartonas, C.: Lattice logic as a fragment of (2-sorted) residuated modal logic. J. Appl. Non-Class. Log. 29, 152–170 (2019)
Hartonas, C.: Modal translation of substructural logics. J. Appl. Non-Class. Log. 30, 16–49 (2020)
Hartonas, C.: Reconciliation of approaches to the semantics of logics without distribution. In: Bimbo K. (ed) Relevance Logics and other Tools for Reasoning. Essays in Honor of J. Michael Dunn. College Publications, Tributes 46, 215–236 (2022). (London,UK)
Hartonas, C., Dunn, J.M.: Duality theorems for partial orders, semilattices, Galois connections and lattices. Tech. Rep. IULG-93-26, Indiana University Logic Group (1993)
Hartonas, C., Dunn, J.M.: Stone duality for lattices. Algebra Universalis 37, 391–401 (1997)
Hartonas, C., Orłowska, E.: Representation of lattices with modal operators in two-sorted frames. Fundam. Inform. 166, 29–56 (2019)
Hartung, G.: A topological representation for lattices. Algebra Universalis 29, 273–299 (1992)
Jónsson, B., Tarski, A.: Boolean algebras with operators I. Amer. J. Math. 73, 891–939 (1951)
Jónsson, B., Tarski, A.: Boolean algebras with operators II. Amer. J. Math. 74, 127–162 (1952)
Jónsson, B., Tsinakis, C.: Relation algebras as residuated Boolean algebras. Algebra Universalis 30, 469–478 (1993)
Moshier, M.A., Jipsen, P.: Topological duality and lattice expansions, I: A topological construction of canonical extensions. Algebra Universalis 71, 109–126 (2014)
Moshier, M.A., Jipsen, P.: Topological duality and lattice expansions, II: Lattice expansions with quasioperators. Algebra Universalis 71, 221–234 (2014)
Orłowska, E.: Modal logics in the theory of information systems. Mathematical Logic Quarterly 30, 213–222 (1984)
Ploščica, M.: A natural representation of bounded lattices. Tatra Mountains Math. Publ. 5, 75–88 (1995)
Priestley, H.: Representation of distributive lattices by means of ordered Stone spaces. Bull. Lond. Math. Soc. 2, 186–190 (1970)
Sofronie-Stokkermans, V.: Duality and canonical extensions of bounded distributive lattices with operators, and applications to the semantics of non-classical logics I. Studia Logica 64, 93–132 (2000)
Sofronie-Stokkermans, V.: Duality and canonical extensions of bounded distributive lattices with operators, and applications to the semantics of non-classical logics II. Studia Logica 64, 151–172 (2000)
Stone, M.H.: Topological representation of distributive lattices and Brouwerian logics. Časopsis pro Pěsiování Matematiky a Fysiky 67, 1–25 (1937)
Stone, M.H.: The representation of Boolean algebras. Bull. Amer. Math. Soc. 44, 807–816 (1938)
Suzuki, T.: On polarity frames: Applications to substructural and lattice-based logics. In: R. Goré, B. Kooi, A. Kurucz (eds.) Advances in Modal Logic 10, 533–552 (2014). (CSLI Publications)
Urquhart, A.: A topological representation of lattices. Algebra Universalis 8, 45–58 (1978)
Vakarelov, D.: Information Systems, Similarity Relations and Modal Logics, chap. 16, 492–550. Studies in Fuzziness and Soft Computing. Heidelberg: Physica-Verlag (1998)
Funding
Open access funding provided by HEAL-Link Greece.
Author information
Authors and Affiliations
Corresponding author
Additional information
Presented by M. Haviar.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hartonas, C. Duality for normal lattice expansions and sorted residuated frames with relations. Algebra Univers. 84, 5 (2023). https://doi.org/10.1007/s00012-023-00802-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00012-023-00802-y
Keywords
- Stone duality
- Lattices with quasioperators
- Normal lattice expansions
- Polarities with relations
- Non-distributive logics




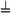 is increasing in each argument place (and thereby its complement I is decreasing in each argument place).
is increasing in each argument place (and thereby its complement I is decreasing in each argument place).