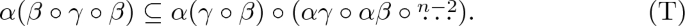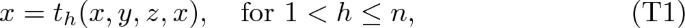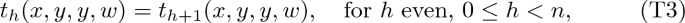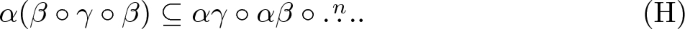Abstract
We show that, under the assumption of congruence distributivity, a condition by S. Tschantz characterizing congruence modularity is equivalent to a variant of the classical Jónsson condition. Here equivalence is intended in a strong sense, to the effect that the corresponding sequences of terms have exactly the same length.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Characterizations of congruence modularity
Alan Day [2] showed, in equivalent form, that a variety \({\mathcal {V}}\) is congruence modular if and only if there is some natural number n such that \({\mathcal {V}}\) satisfies the congruence inclusion

In the above formula juxtaposition denotes intersection and \(\alpha \gamma \circ \alpha \beta \circ {{\mathop {\dots }\limits ^{n}}}\) is a shorthand for \(\alpha \gamma \circ \alpha \beta \circ \alpha \gamma \circ \alpha \beta \dots \) with \(n-1\) occurrences of \( \circ \). As usual, we say that a variety \({\mathcal {V}}\) satisfies some congruence inclusion if the inclusion is satisfied in every algebra in \({\mathcal {V}}\).
Later H.-P. Gumm [5] found another characterization. A congruence identity equivalent to Gumm condition asserts that a variety \({\mathcal {V}}\) is congruence modular if and only if there is some natural number \(p \ge 2\) such that \({\mathcal {V}}\) satisfies the congruence inclusion

While identities (D\(^r\)) and (G) are formally incomparable, usually the latter is considered to be stronger and anyway it has found many applications that seem out of reach using (D\(^r\)) alone. S. Tschantz [11] has found a common generalization. It will be convenient for our purposes to recall the two equivalent forms of Tschantz condition.
Theorem 1.1
[11, Lemma 4 and Theorem 5] A variety \({\mathcal {V}}\) is congruence modular if and only if there is some natural number \(n \ge 2\) such that \({\mathcal {V}}\) satisfies one of the following equivalent conditions.
-
(1)
The following congruence inclusion holds in \({\mathcal {V}}\):
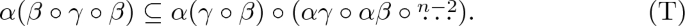
-
(2)
\({\mathcal {V}}\) has a sequence \(t_0, \dots , t_n\) of Tschantz terms, that is, 4-ary terms such that the following equations are satisfied in all algebras in \({\mathcal {V}}\):
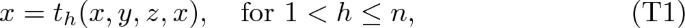

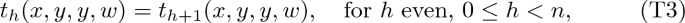


Obviously, (T) implies (G) with \(p=n\), since \(\alpha ( \beta \circ \gamma ) \subseteq \alpha ( \beta \circ \gamma \circ \beta )\). Moreover, (T) implies (D\(^r\)), by taking \( \alpha \gamma \) in place of \(\gamma \) in (T) and since \(\alpha ( \alpha \gamma \circ \beta ) = \alpha \gamma \circ \alpha \beta \). In order to give a meaning to the above identities for all values of the parameters, it is convenient to set \(\alpha \gamma \circ \alpha \beta \circ {{\mathop {\dots }\limits ^{1}}} = \alpha \gamma \) and \(\alpha \gamma \circ \alpha \beta \circ {{\mathop {\dots }\limits ^{0}}}=0\), the minimal congruence on the algebra under consideration.
Within a variety, identities (D\(^r\)) and (G), too, can be equivalently expressed by means of the existence of certain terms, in a way similar to Theorem 1.1. We shall briefly recall the condition equivalent to (D\(^r\)) below, but we shall not need it here.
1.2 Connections with congruence distributivity
Obviously, a congruence distributive variety is congruence modular. As already pointed out by Day [2], it is interesting to see how this implication works at the level of terms, equivalently, at the level of congruence identities. B. Jónsson [6] showed that a variety is congruence distributive if and only if there is some p such that

This is a slightly different formulation, equivalent to a condition appeared in [10]. It has been called the alvin condition in [4]. (The expression ALVIN, possibly an acronym, has been informally used to refer to the book [10] since at least 2007.) See [8] for a full discussion and further references.
Comparing (G) and (A), we immediately see that congruence distributivity implies congruence modularity also from this point of view. In this way we can also appreciate the strength of Gumm’s condition: congruence modularity falls short of being equivalent to congruence distributivity just for a factor of the form \(\alpha ( \gamma \circ \beta )\) which cannot be factored out as \(\alpha \gamma \circ \alpha \beta \). As a side remark, for the reader who knows the characterizations by means of terms, we mention that the terms arising from Gumm condition can be seen in two ways. First, as the combination of a term witnessing congruence permutability with a sequence of Jónsson terms. Second, as a “defective” version of (a longer sequence of) alvin terms. In the latter sense, the fact that \(\alpha ( \beta \circ \gamma )\) cannot be turned into \(\alpha \beta \circ \alpha \gamma \) corresponds to one missing equation. See [8], in particular, the comments at the beginning of Section 7 and references there for more details.
In [9] we proved the quite unexpected result that if some congruence distributive variety \({\mathcal {V}}\) satisfies (G), for some given p, then \({\mathcal {V}}\) satisfies (A) for the very same p. In more detail, we proved the following theorem.
Theorem 1.2
If \({\mathcal {V}}\) is a nontrivial congruence distributive variety, then the minimal p such that \({\mathcal {V}}\) satisfies (G) is equal to the minimal p such that \({\mathcal {V}}\) satisfies (A).
Of course, the assumption that \({\mathcal {V}}\) is congruence distributive is necessary in Theorem 1.2, since there is a congruence modular variety \({\mathcal {W}}\) which is not congruence distributive. In particular, such a \({\mathcal {W}}\) satisfies (G), for some p, but \({\mathcal {W}}\) fails to satisfy (A), no matter the value of p. However, it follows from [9] that if \({\mathcal {V}}\) has terms witnessing (G), for some given p, and \({\mathcal {V}}\) is congruence distributive, hence \({\mathcal {V}}\) has a (possibly much longer than p) sequence of terms witnessing (A), then all the above terms can be combined in order to obtain a sequence witnessing (A) for the given p. From the point of view of congruence identities, under the assumption of congruence distributivity, we can factor out \(\alpha ( \gamma \circ \beta )\) in (G) to \(\alpha \gamma \circ \alpha \beta \). Obviously, congruence distributivity implies that \(\alpha ( \gamma \circ \beta ) \subseteq \alpha \gamma \circ \alpha \beta \circ \alpha \gamma \dots \) The point is that, under the above assumptions, we need not enlarge the number of factors on the right-hand side of (A). More suggestively, we can partially work as if we were in an arithmetical variety.
1.3 A “higher” alvin condition
In this note we prove a result parallel to Theorem 1.2, but dealing with the identity (T). In order to state the result, we need to mention a condition equivalent to congruence distributivity and which is stronger than (T). Of course, every congruence distributive variety satisfies

since \(\alpha ( \beta \circ \gamma \circ \beta ) \subseteq \alpha ( \beta + \gamma )\). It is standard to see that if some variety \({\mathcal {V}}\) satisfies (1), then there is some n depending on \({\mathcal {V}}\) such that \({\mathcal {V}}\) satisfies

On the other hand, if \({\mathcal {V}}\) satisfies (H), then \({\mathcal {V}}\) satisfies (A) with \(p=n\), hence \({\mathcal {V}}\) is congruence distributive, by Jónsson’s Theorem. Classical arguments then give a proof of the following proposition. See, e. g., [7] for full details and for more general notions and arguments.
Proposition 1.3
A variety \({\mathcal {V}}\) is congruence distributive if and only if there is some natural number \(n \ge 2\) such that \({\mathcal {V}}\) satisfies one of the following equivalent conditions.
-
(1)
The following congruence inclusion holds in \({\mathcal {V}}\):
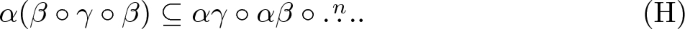
-
(2)
\({\mathcal {V}}\) has a sequence \(t_0, \dots , t_n\) of higher alvin terms, that is, 4-ary terms satisfying conditions (T2)–(T5) from Theorem 1.1(2), as well as

(the difference in comparison with (T1) is that in (H1) we ask for the equation to be valid also in the case \(h=1\).)
The smallest n given by Proposition 1.3 for a congruence distributive variety \({\mathcal {V}}\) is \( J _{ {\mathcal {V}}} ^\smallsmile (2) + 1\) in the notation from [7].
1.4 Statement of the main result
Recall the definition of Tschantz terms from clause (2) in the statement of Theorem 1.1. The definition of higher alvin terms appears in clause (2) in the above Proposition 1.3.
We can now state our main result.
Theorem 1.4
Suppose that \({\mathcal {V}}\) is a congruence distributive variety. Then, for every natural number \(n \ge 2\), \({\mathcal {V}}\) has a sequence \(t_0, \dots , t_n\) of Tschantz terms if and only if \({\mathcal {V}}\) has a sequence \(t'_0, \dots , t'_n\) of higher alvin terms.
In order to prove Theorem 1.4 we need some auxiliary results of independent interest. For the most part, the results do not need the assumption of congruence distributivity, the existence of Tschantz terms, namely, congruence modularity, is enough.
1.5 Day terms
Day terms correspond to identity (D\(^r\)) when \(\beta \) and \(\gamma \) are exchanged on the right. Reversed Day terms, as we call them, correspond to (D\(^r\)) as it stands. We shall not use Day terms in this note; however, Lemmata 2.1 and 2.3 below hold for Day terms, too, and this fact might be of interest and find subsequent applications. In detail, reversed Day terms are terms satisfying equations (T2)–(T5) from Theorem 1.1, as well as

In comparison with (T1) the equations (D1) depend only on two variables. Day terms are defined in a similar way, except that even and odd are exchanged in (T3) and (T4). See [8] for further details.
2 Proofs
Lemma 2.1
Suppose that \(t_0, \dots , t_n\) is a sequence of Tschantz (higher alvin, Day, reversed Day) terms. For \(h=0, \dots , n\), define

Then \(t^*_0, \dots , t^*_n\) is a sequence of Tschantz (higher alvin, Day, reversed Day) terms.
Proof
The terms \(t^*_0\) and \(t^*_n\) satisfy (T2) and (T5) since \(t_0\) and \(t_n\) satisfy these equations. Then compute:

where superscripts indicate the equations we have used and (I) indicates that we have used idempotence. The above computations take care of both Tschantz and higher alvin terms.
To deal with the case of Day and reversed Day terms, exchange even and odd above when appropriate and perform the following additional computation:
\(\square \)
In passing, for possible further applications, we notice that Lemma 2.1 holds in a much more general context, namely, for identities involving “modular quadruplets”. In [8] we defined a modular quadruplet as one of the following quadruplets of variables
Compare also [3, Corollary 3.5]. By slightly modifying the position (*), we do not even need idempotence. The next proposition shall not be used in what follows.
Proposition 2.2
Suppose that \({\mathcal {V}}\) is a variety and s, t are 4-ary terms. Suppose that \((x_1,x_2,x_3,x_4)\), \((y_1,y_2,y_3,y_4)\) are (possibly distinct) modular quadruplets and the equation

holds in \({\mathcal {V}}\). Define

and define \(t^*\) correspondingly. Then
holds in \({\mathcal {V}}\), as well.
Proof
For example, if (Q) is \(s(x,x,w,w) = t(x,x,x,w)\), then
The other cases are treated in a similar way. See also Lemma 2.1. \(\square \)
Once we have given the definition (*), the remaining parts of this section follow [9] very closely. For a binary relation \(\Theta \), we let \(\Theta ^m = \Theta \circ \Theta \circ {{\mathop {\dots }\limits ^{m}}} \)
Lemma 2.3
Suppose that \(n \ge 2\). If \({\mathcal {V}}\) is a variety with a sequence \(t_0, \dots , t_n\) of Tschantz (higher alvin, reversed Day) terms, then, for every \(m \ge 1\), \({\mathcal {V}}\) has a sequence \(s_0, \dots , s_n\) of Tschantz (higher alvin, reversed Day) terms such that \(s_1\) satisfies the following additional property.
- (U\(_m\)):
-
For every \({\mathbf {A}} \in {\mathcal {V}}\) and every tolerance \(\Theta \) on \({\mathbf {A}}\), if \(a,d \in A\) and \( a \mathrel { \Theta ^m} d\), then \( a \mathrel { \Theta } s_1 (a,a,d,d) \).
Proof
The property (U\(_1\)) is satisfied by the term \(t_1\) of the original sequence. Indeed, if \( a \mathrel { \Theta } d\), then \( a = t_1 (a,a,a,a) \mathrel { \Theta } t_1 (a,a,d,d) \), since \(\Theta \) is reflexive and compatible.
Suppose that \(m \ge 1\) and \({\mathcal {V}}\) has a sequence \(s_0, \dots , s_n\) of Tschantz (higher alvin, reversed Day) terms such that \(s_1\) satisfies (U\(_m\)). Define \(s^*_0, \dots , s^*_n\) according to equations (*) (with the \(s_h\)’s in place of the \(t_h\)’s). We are going to show that \(s^*_1\) satisfies (U\(_{m+1}\)), thus the lemma follows by induction on m, by Lemma 2.1.
Assume that \({\mathbf {A}} \) belongs to \( {\mathcal {V}}\), \(\Theta \) is a tolerance on \({\mathbf {A}}\), \(a,d \in A\) and \( a \mathrel { \Theta ^{m+1}} d\), thus there is \(b \in A\) such that \( a \mathrel { \Theta ^{m}} b \mathrel \Theta d\). Then
where underlined elements are those moved by \(\Theta \). In the above formula we have used (T2)–(T3), the assumption that \(\Theta \) is reflexive and compatible and the inductive hypothesis, to the effect that \(a \mathrel \Theta s_1(a,a,b,b)\), by (U\(_m\)), hence \( s_1(a,a,b,b) \mathrel \Theta a\), since \(\Theta \) is symmetric. \(\square \)
2.1 Some auxiliary results
Proposition 2.4
Suppose that \(n \ge 2\), \(\ell \ge 3\), \(\ell \) is odd, \(k = (n-2)\frac{\ell -1}{2} \) and \(q = (n-2)\frac{\ell +1}{2} \). Suppose further that \({\mathbf {A}}\) is an algebra belonging to a variety with Tschantz terms \(t_0, \dots , t_n\). If \(\alpha \), \(\beta \), \(\gamma \) are congruences and \(\Theta \), \(\Psi \) are tolerances on \({\mathbf {A}}\), then the following inclusions hold.
-
(1)
\(( \beta \circ \gamma \circ \beta )(\alpha \beta + \alpha \gamma ) \subseteq \alpha \gamma \circ \alpha \beta \circ {{\mathop {\dots }\limits ^{n}}}\),
-
(2)
\( \alpha ( \beta \circ \gamma \circ {{\mathop {\dots }\limits ^{\ell }}} ) \subseteq \alpha ( \gamma \circ \beta ) \circ (\alpha \gamma \circ \alpha \beta \circ {{\mathop {\dots }\limits ^{k}}}),\)
-
(3)
\(( \beta \circ \gamma \circ {{\mathop {\dots }\limits ^{\ell }}}) (\alpha \beta + \alpha \gamma ) \subseteq \alpha \gamma \circ \alpha \beta \circ {{\mathop {\dots }\limits ^{2+k}}}, \)
-
(4)
\(\Psi \Theta ^ \ell \subseteq (\Psi \Theta )^{1+q} \).
Proof
The proof is very similar to the proof of [9, Corollary 6]. We present explicit details for (1) and only sketch the proofs of (2)–(4). In any case, (2)–(4) shall not be used in what follows.
As in [9], let \(\Theta \) be the tolerance \( (\alpha \beta \circ \alpha \gamma ) (\alpha \gamma \circ \alpha \beta )\). Notice that \(\Theta \) contains both \(\alpha \beta \) and \(\alpha \gamma \). Suppose that \( (a,d) \in ( \beta \circ \gamma \circ \beta )(\alpha \beta + \alpha \gamma )\). From \((a,d)\in \alpha \beta + \alpha \gamma \) we get that there is some m (depending on a and d, in general) such that \((a,d)\in \alpha \beta \circ \alpha \gamma \circ {{\mathop {\dots }\limits ^{m}}} \subseteq \Theta ^m \). By Lemma 2.3, we have Tschantz terms \(s_0, \dots , s_n\) such that \(s_1\) satisfies (U\(_{m}\)), hence \((a, s_1(a,a,d,d)) \in \Theta \subseteq \alpha \gamma \circ \alpha \beta \). If \(n=2\), then \(s_1(a,a,d,d) = d\) and (1) follows. If \(n >2\), we employ the standard argument proving the equivalence of (1) and (2) in Theorem 1.1. Since \( (a,d) \in \beta \circ \gamma \circ \beta \), there are \(b,c \in A\) such that \( a \mathrel { \beta } b \mathrel { \gamma } c \mathrel { \beta } d \), thus \(s_2(a,a,d,d) \mathrel { \beta } s_2(a,b,c,d)\). Moreover, since \( (a,d) \in \alpha \beta + \alpha \gamma \), in particular \( a \mathrel { \alpha } d \), we get
by (T1). Hence \(s_2(a,a,d,d) \mathrel { \alpha \beta } s_2(a,b,c,d)\). From \((a, s_1(a,a,d,d)) \in \alpha \gamma \circ \alpha \beta \), \(s_1(a,a,d,d) = s_2(a,a,d,d)\) and \(s_2(a,a,d,d) \mathrel { \alpha \beta } s_2(a,b,c,d)\), we get \((a, s_2(a,b,c,d)) \in \alpha \gamma \circ \alpha \beta \), since \(\alpha \beta \) is a transitive relation.
The argument showing that
is entirely standard, thus we get \((s_2(a,b,c,d), d) \in \alpha \gamma \circ \alpha \beta \circ {{\mathop {\dots }\limits ^{n-2}}}\), since \(s_n(a,b, c,d)=d\). From \((a, s_2(a,b,c,d)) \in \alpha \gamma \circ \alpha \beta \) we finally obtain \((a, d) \in \alpha \gamma \circ \alpha \beta \circ {{\mathop {\dots }\limits ^{n}}}\).
(2) As in [9], let \(\Psi \) be the tolerance \( ( \beta \circ \gamma ) (\gamma \circ \beta )\). Notice that \(\Psi \) contains both \( \beta \) and \( \gamma \). If \( (a,d) \in \alpha ( \beta \circ \gamma \circ {{\mathop {\dots }\limits ^{\ell }}} ) \), then \( (a,d) \in \Psi ^ \ell \), thus \((a, s_1(a,a,d,d)) \in \Psi \subseteq \gamma \circ \beta \), for the term given by Lemma 2.3. Now we get \(s_1(a,a,d,d) = s_2(a,a,d,d) \in \alpha \beta \circ \alpha \gamma \circ \alpha \beta \circ {{\mathop {\dots }\limits ^{1+k}}} \) arguing as in the proof of [7, Theorem 2.1]. Here we exemplify the argument in the case \(\ell = 5\). We have elements \(b_1, b_2, b_3, b_4\) such that \(a \mathrel { \beta } b_1 \mathrel { \gamma } b_2 \mathrel { \beta } b_3 \mathrel { \gamma } b_4 \mathrel { \beta } d \), hence
All the elements in the above chain are \(\alpha \)-related, by (T1) and arguing as in (1). The last element in the above chain is either \(s_n(a,a,d,d)\) or \(s_n(a,b_2,b_2,d)\), according to the parity of n; in any case it is equal to d, by (T5). Finally, notice that \(\alpha ( \gamma \circ \beta ) \circ \alpha \beta = \alpha ( \gamma \circ \beta ) \), hence we can save one occurrence of \(\alpha \beta \).
Clause (3) combines the arguments in (1) and (2). The proof of (4) is similar, except that we are not allowed to use transitivity in order to get a smaller number of factors. We can allow \(\Psi \) to be a tolerance by an argument from [1]. Compare also the second displayed formula on [7, p. 6]. \(\square \)
2.2 Proof of Theorem 1.4
A sequence of higher alvin terms is a sequence of Tschantz terms, hence one implication is obvious.
On the other hand, suppose that \({\mathcal {V}}\) is congruence distributive and has a sequence \(t_0, \dots , t_n\) of Tschantz terms. We shall show that \({\mathcal {V}}\) satisfies identity (H), thus \({\mathcal {V}}\) has higher alvin terms \(t'_0, \dots , t'_n\), by Proposition 1.3.
Suppose that \((a,d) \in \alpha ( \beta \circ \gamma \circ \beta )\), for certain elements and congruences of some algebra in \({\mathcal {V}}\). Since \({\mathcal {V}}\) is congruence distributive,
Then we get \((a,d) \in \alpha \beta \circ \alpha \gamma \circ {{\mathop {\dots }\limits ^{n}}} \) by Proposition 2.4(1). We have proved that (H) holds, thus Proposition 1.3 implies that \({\mathcal {V}}\) has higher alvin terms \(t'_0, \dots , t'_n\). \(\square \)
3 Generalizations and problems
In this section we prove some generalizations of Theorem 1.4; in particular, we deal with conditions weaker than Tschantz’. For simplicity, we generally state the results in the form of a congruence identity. As in Theorem 1.1 and Proposition 1.3, the results admit reformulations by means of sequences of terms. Proofs, too, use terms.
Proposition 3.1
A variety \({\mathcal {V}}\) is congruence modular if and only if there is some natural number \(\ell \ge 1\) such that \({\mathcal {V}}\) satisfies the following congruence inclusion:
If \({\mathcal {V}}\) is congruence distributive and \({\mathcal {V}}\) satisfies (Tvar), then \({\mathcal {V}}\) satisfies

for the same \(\ell \).
Proof
If \({\mathcal {V}}\) is congruence modular, then, by Theorem 1.1, \({\mathcal {V}}\) satisfies (T), for some n, hence \({\mathcal {V}}\) satisfies the weaker identity (Tvar), taking \(\ell \ge \frac{n}{2} \). Conversely, if \({\mathcal {V}}\) satisfies (Tvar), then, by taking \(\alpha \gamma \) in place of \(\gamma \), we get the identity (D\(^r\)) mentioned at the beginning of the introduction, with \(n = 2 \ell \). Hence \({\mathcal {V}}\) is congruence modular by [2].
In order to prove the second statement, let \(n= 2\ell \). The Maltsev condition associated to (Tvar) involves a sequence \(t_0, \dots , t_n\) of 4-ary terms satisfying equations (T2)–(T5), as well as \(x=t_h(x,y,z,x)\), for h even, \( h \le n\). Arguing as in Lemma 2.1, the above equations are preserved under the position (*). Then the proof of Lemma 2.3 provides a sequence of terms \(s_0, \dots , s_n\) satisfying the same equations and such that \(s_1\) enjoys the property (U\(_m\)). Finally, using congruence distributivity, the arguments in the proof of Proposition 2.4(1) give \((a, s_2(a,b,c,d)) \in \alpha \gamma \circ \alpha \beta \), since the equations involving \(s_3, s_4, \dots \) are not used to prove this relation. Using such additional equations, it is standard to see that \((s_2(a,b,c,d),d) \in \alpha (\gamma \circ \beta ) ^{\ell -1} \). Hence (Hvar) holds. \(\square \)
Notice a difference between Proposition 3.1 and Theorem 1.4 (through the corresponding identities given by Theorem 1.1 and Proposition 1.3). The existence of some n for which (H) holds is equivalent to congruence distributivity. On the other hand, the existence of some \(\ell \) for which (Hvar) holds is equivalent to congruence modularity. The latter assertion is proved using the same arguments we have used for (Tvar).
There is a common generalization of Theorem 1.4 and Proposition 3.1. In both cases we have started with an identity whose right-hand side begins with a block of the form \(\alpha (\gamma \circ \beta )\), followed by blocks either of the same form, or of the forms \( \alpha \gamma \) or \(\alpha \beta \). In both cases we have proved that, within congruence distributive varieties, the first block can be factored out as \(\alpha \gamma \circ \alpha \beta \). We now show that the sequence of the “blocks” after the first one can be taken to be somewhat arbitrary. We also get a “bilateral” version.
Theorem 3.2
Suppose that \(r \ge 1\) and, for each i with \( 1 < i \le r\), \(A_i \) has one of the following forms:
If \({\mathcal {V}}\) is a congruence distributive variety and \({\mathcal {V}}\) satisfies
then \({\mathcal {V}}\) satisfies
If in addition \(r \ge 2\) and \(A_r= \alpha ( \beta \circ \gamma )\), then \({\mathcal {V}}\) satisfies

Proof
In order to prove (Hgen), apply the arguments in the second part of the proof of Proposition 3.1. Simply adjust the set of those indices h such that the equation \(x=t_h(x,y,z,x)\) is required, according to the specific forms of the \(A_i\)’s. Possibly, adjust also the indices for which (T3) and (T4) are assumed, though it seems that the most interesting cases are those in which the two equations alternate as in clause (2) in Theorem 1.1. Notice that, due to the form of (Tgen), the equation \(x=t_2(x,y,z,x)\) always holds, hence \(x=s_2(x,y,z,x)\), a fact which is needed in the proof of Proposition 2.4.
Now we get (Hgen\(^+\)) by applying the symmetrical arguments to (Hgen), or just observing that if \(A_r= \alpha ( \beta \circ \gamma )\), then, taking converses, (Hgen) is equivalent to \(\alpha ( \beta \circ \gamma \circ \beta ) \subseteq \alpha (\gamma \circ \beta ) \circ A _{ r -1} ^\smallsmile \circ A _{ r -2} ^\smallsmile \circ \dots \circ A _{ 3} ^\smallsmile \circ A _{ 2} ^\smallsmile \circ \alpha \beta \circ \alpha \gamma \), where \( ^\smallsmile \) denotes converse. Then apply the first statement of the theorem and take converses again. \(\square \)
In particular, a congruence distributive variety satisfying
satisfies also
Theorems 1.2, 1.4, 3.2 and Proposition 3.1 imply that in a congruence distributive variety the first occurrence of \(\alpha (\gamma \circ \beta )\) in certain identities can be substituted for \(\alpha \gamma \circ \alpha \beta \), and possibly symmetrical facts hold. Can we substitute more occurrences?
Problem 3.3
-
(a)
Is the following true? If \({\mathcal {V}}\) is a congruence distributive variety and (Tvar) \(\alpha ( \beta \circ \gamma \circ \beta ) \subseteq (\alpha (\gamma \circ \beta )) ^\ell \) holds in \({\mathcal {V}}\) for \(\ell \), then (H) \(\alpha ( \beta \circ \gamma \circ \beta ) \subseteq \alpha \gamma \circ \alpha \beta \circ {{\mathop {\dots }\limits ^{n}}}\) holds in \({\mathcal {V}}\) for \(n=2\ell \).
-
(b)
Is the following true? If \({\mathcal {V}}\) is a congruence distributive variety and
$$\begin{aligned} \alpha ( \beta \circ \gamma ) \subseteq (\alpha (\gamma \circ \beta )) ^\ell \end{aligned}$$(Gvar)holds in \({\mathcal {V}}\) for \(\ell \), then (A) \(\alpha ( \beta \circ \gamma ) \subseteq \alpha \gamma \circ \alpha \beta \circ {{\mathop {\dots }\limits ^{p}}}\) holds in \({\mathcal {V}}\) for \(p=2\ell \).
Of course, (a) and (b) admit a reformulation dealing with sequences of terms, as in Theorem 1.1 and Proposition 1.3. Stating problems and results in the form of congruence identities appears simpler and intuitively clearer.
In passing, we mention that if \(\ell \ge 3\), then identity (Gvar) does not imply congruence modularity. See [8, Remark 10.11(a)].
The above problems might be difficult. Our present methods work only for the terms \(t_1\) and \(t_{n-1}\), the terms lying at the “edges” of the sequence. On one hand, if the answer to the above problems is positive, one needs some significant improvements on the available methods in order to prove it. On the other hand, the work [8] presents many examples of congruence distributive varieties, but none of them is a counterexample to (b). This suggests that if counterexamples do indeed exist, it might be not obvious to find them.
-
(c)
We do not know whether, for \(n \ge 6\), the congruence identity
$$\begin{aligned} \alpha ( \beta \circ \gamma \circ \beta ) \subseteq \alpha (\gamma \circ \beta ) \circ ( \alpha \gamma \circ \beta \circ {{\mathop {\dots }\limits ^{n-2}}}) \end{aligned}$$(TvarB)implies congruence modularity within a variety. We do not claim that the above problem is difficult.
Notice that, on the other hand, the existence of some \(n \ge 2\) such that
$$\begin{aligned} \alpha ( \beta \circ \gamma \circ \beta ) \subseteq \alpha (\gamma \circ \beta ) \circ ( \gamma \circ \alpha \beta \circ {{\mathop {\dots }\limits ^{n-2}}}), \end{aligned}$$(TvarC)is equivalent to congruence modularity. One direction is immediate from Theorem 1.1. In order to get congruence modularity from (TvarC), just take \(\alpha \gamma \) in place of \(\gamma \).
-
(d)
Is it true that in a congruence distributive variety each of the identities (TvarB) and (TvarC) is equivalent to the corresponding identity in which \(\alpha (\gamma \circ \beta ) \) is factored out as \(\alpha \gamma \circ \alpha \beta \)?
In this respect, the methods in the present note fail to work, since the Maltsev conditions associated to (TvarB) and (TvarC) involve also equations of the form \(t_h(x,y,z,x) = t_{h+1}(x,y,z,x)\), for the appropriate indices. However, it seems that Lemma 2.1 does not apply to such equations.
-
(e)
If in the inclusions (G) and (Gvar) we exchange \(\beta \) and \(\gamma \) on the right-hand side, we get trivial inclusions. In particular, the variant of Theorem 1.2 badly fails, if such an exchange is made.
However, it is an open problem whether a version of Theorem 1.4 still holds when we exchange even and odd in the definitions of Tschantz and alvin higher terms, for \(n \ge 4\). This corresponds to exchanging \(\beta \) and \(\gamma \) on the right-hand side in the inclusions (T) and (H). A similar problem can be asked for the second statement in Proposition 3.1 if \(\ell \ge 2\), as well as for Theorem 3.2. The above problems in (a) and (d), too, can be modified in this way.
-
(f)
Can we generalize the results of the present note to terms of larger arity? In other words, which are the consequences of identities of the form
$$\begin{aligned} \alpha ( \beta \circ \gamma \circ {{\mathop {\dots }\limits ^{q}}} ) \subseteq \alpha (\gamma \circ \beta \circ {{\mathop {\dots }\limits ^{k}}}) \circ \dots \ ? \end{aligned}$$Definition (*) can be extended as
$$\begin{aligned} t^*_h(x,y,z,u,v, \dots , w)= t_h(x, t_h(x,y,y,y,y, \dots , y), \\ t_h(x,y,z,z,z, \dots , z), t_h(x,y,z,u,u, \dots , u), \dots , t_h(x,y,z,u,v, \dots , w)) \end{aligned}$$and a result analogue to Lemma 2.1 holds. However, it is not clear how to generalize Property (U\(_{m}\)) in Lemma 2.3.
References
Czédli, G., Horváth, E.K.: Congruence distributivity and modularity permit tolerances. Acta Univ. Palack. Olomuc. Fac. Rerum Nat. Math. 41, 39–42 (2002)
Day, A.: A characterization of modularity for congruence lattices of algebras. Can. Math. Bull. 12, 167–173 (1969)
Dent, T., Kearnes, K.A., Szendrei, Á.: An easy test for congruence modularity. Algebra Univers. 67, 375–392 (2012)
Freese, R., Valeriote, M.A.: On the complexity of some Maltsev conditions. Int. J. Algebra Comput. 19, 41–77 (2009)
Gumm, H.-P.: Congruence modularity is permutability composed with distributivity. Arch. Math. (Basel) 36, 569–576 (1981)
Jónsson, B.: Algebras whose congruence lattices are distributive. Math. Scand. 21, 110–121 (1967)
Lipparini, P.: The Jónsson distributivity spectrum. Algebra Univers. 79(2), 1–16 (2018). (Art. 23)
Lipparini, P.: Day’s Theorem is sharp for \(n\) even, pp. 1–57 (2020). arXiv:1902.05995v3
Lipparini, P.: The Gumm level equals the alvin level in congruence distributive varieties. Arch. Math. (Basel) 115, 391–400 (2020)
McKenzie, R.N., McNulty G.F., Taylor, W.F.: Algebras, Lattices, Varieties. Vol. I. Wadsworth & Brooks/Cole Advanced Books & Software, Monterey (1987). Corrected reprint with additional bibliography. AMS Chelsea Publishing/American Mathematical Society, Providence (2018)
Tschantz, S.T.: More conditions equivalent to congruence modularity. In: Comer, S.D. (ed) Universal Algebra and Lattice Theory (Charleston, S.C., 1984), Lecture Notes in Math., vol. 1149, pp. 270–282. Springer, Berlin (1985)
Acknowledgements
We thank an anonymous referee for a stimulating comment which has led to Problem 3.3(e) above.
Funding
Open access funding provided by Università degli Studi di Roma Tor Vergata within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Presented by: K.A. Kearnes.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Work performed under the auspices of G.N.S.A.G.A. Work partially supported by PRIN 2012 “Logica, Modelli e Insiemi”. The author acknowledges the MIUR Department Project awarded to the Department of Mathematics, University of Rome Tor Vergata, CUP E83C18000100006.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lipparini, P. The Tschantz and the alvin higher conditions are equivalent in congruence distributive varieties. Algebra Univers. 82, 4 (2021). https://doi.org/10.1007/s00012-020-00697-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00012-020-00697-z
Keywords
- Tschantz terms
- Higher alvin terms
- Congruence distributive variety
- Congruence modular variety
- Congruence identity