Abstract
It is well known that a square complex matrix is called EP if it commutes with its Moore–Penrose inverse. In this paper, new classes of matrices which extend this concept are characterized. For that, we consider commutative equalities given by matrices of arbitrary index and generalized inverses recently investigated in the literature. More specifically, these classes are characterized by expressions of type \(A^mX=XA^m\), where X is an outer inverse of a given complex square matrix A and m is an arbitrary positive integer. The relationships between the different classes of matrices are also analyzed. Finally, a picture presents an overview of the overall studied classes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and notations
A square complex matrix A is said to be EP (or range-Hermitian) if its range space is equal to the range space of its conjugate transpose \(A^*\) or, equivalently, if the orthogonal projector onto its range coincides with the orthogonal projector onto the range of \(A^*\). EP matrices were defined in 1950 by H. Schwerdtfeger [22] and since then, this class of matrices has attracted the attention of several authors [4, 5, 17,18,19,20, 23]. The EP matrix class includes as special cases the wide classes of matrices such as hermitian matrices, skew-hermitian matrices, unitary matrices, normal matrices, orthogonal projectors and, of course, nonsingular matrices.
EP matrices have been generalized in many ways. The first two generalizations, known as bi-dagger and bi-EP matrices, were given by Hartwig et al. in [10]. Several generalizations include them, such as conjugate EP matrices [14], K-EP matrices [15], weighted EP matrices [23], relative EP matrices [9], etc. All these classes of matrices can be expressed in terms of the Moore–Penrose inverse. Others generalized inverses, such as DMP [12] inverses, core EP inverses [13], CMP inverses [16] and WG inverses [25], were introduced and thoroughly studied in the last years.
By using these inverses in equalities of type \(A^kX=XA^k\), where k is the index of A, in [8], generalizations of EP matrices gave rise to new classes of matrices, such as k-index EP (originally called index-EP in [26]), k-EP matrices [11], k-CMP matrices, k-DMP matrices, dual k-DMP matrices, and k-core EP matrices.
In [19], Pearl proved that a square complex matrix is EP if and only if it commutes with its Moore–Penrose inverse. Recently, related to this result, in [26] the authors presented the weak group matrix as a square complex matrix A that commute with its WG inverse as we will recall later. This new class of matrices is wider than that of the well-known group matrices, given by those matrices of index at most one, to which EP matrices belong.
Motivated by these papers, our purpose is to give new characterizations of the aforementioned classes of matrices in terms of only equalities of type \(AX=XA\), for X being an outer generalized inverse. Consequently, we will provide an easier condition for that to be checked. Since the power of A will turn out not to be relevant, the main advantage is now that shall be not necessary to compute explicitly the index.
The symbol \({{\mathbb {C}}^{m\times n}}\) stands for the set of all \(m\times n\) complex matrices. For any matrix \(A\in {{\mathbb {C}}^{m\times n}}\), we denote its conjugate transpose, inverse (whenever it exists), rank, null space, and range space of A by \(A^{*},\) \(A^{-1}\), \(\textrm{rk}(A)\), \({\mathcal {N}}(A)\), and \({\mathcal {R}}(A)\), respectively. Moreover, \(I_n\) will refer to the \(n \times n\) identity matrix. The index of \(A\in {{\mathbb {C}}^{n\times n}}\), denoted by \(\textrm{Ind}(A)\), is the smallest nonnegative integer k such that \(\textrm{rk}(A^k) = \textrm{rk}(A^{k+1})\). Throughout this paper, we will assume that \(\textrm{Ind}(A)=k\ge 1\).
We start recalling the definitions of some generalized inverses. For \(A\in {{\mathbb {C}}^{m\times n}}\), the Moore–Penrose inverse \(A^\dag \) of A is the unique matrix \(X \in {{\mathbb {C}}^{n\times m}}\) satisfying the following four equations: \(AXA=A\), \(XAX=X\), \((AX)^*=AX\), and \((XA)^*=XA\). The Moore–Penrose inverse can be used to represent the orthogonal projectors \(P_A:=AA^{\dag }\) and \(Q_A:=A^{\dag }A\) onto \({\mathcal {R}}(A)\) and \({\mathcal {R}}(A^*)\), respectively. A matrix \(X\in {{\mathbb {C}}^{n\times m}}\) satisfying \(AXA=A\) is called an inner inverse of A, while a matrix \(X\in {{\mathbb {C}}^{n\times m}}\) satisfying \(XAX=X\) is called an outer inverse of A.
For \(A\in {{\mathbb {C}}^{n\times n}}\), the Drazin inverse \(A^d\) of A is the unique matrix \(X\in {{\mathbb {C}}^{n\times n}}\) satisfying \(X A X=X\), \(AX=XA\), and \(XA^{k+1}=A^k\). If \(\textrm{Ind}(A)\le 1\), then the Drazin inverse is called the group inverse of A and denoted by \(A^\#\). It is known that \(A^\#\) exists if and only if \(\textrm{rk}(A)=\textrm{rk}(A^2)\), in which case A is called a group matrix.
The symbols \({\mathbb {C}}_n^{\textrm{GM}}\) and \({\mathbb {C}}_n^{\textrm{EP}}\) will denote the subsets of \({{\mathbb {C}}^{n\times n}}\) consisting of group matrices and EP matrices, respectively. It is well known that \({\mathbb {C}}_n^{\textrm{EP}}\subseteq {\mathbb {C}}_n^{\textrm{GM}}\) [2].
In 1972, Rao et al. [21] introduced the (uniquely determined) generalized inverse \(A^-_{\rho ^*,\chi }=A^\#P_A\) of \(A \in {{\mathbb {C}}^{n\times n}}\). In 2010, Baksalary et al. [1] rediscovered it and denote it by \(A^{\textcircled {\#}}\).
By exploiting this same idea of generating a generalized inverse, new generalized inverses of a matrix/operator/element in a ring were recently defined by using known generalized inverses and projectors (idempotent elements). In Table 1, a glossary with the main definitions and notations related to these inverses is added, where \(A \in {{\mathbb {C}}^{n\times n}}\) with \(\textrm{Ind}(A)=k\).
The matrix classes corresponding to some of aforementioned generalized inverses are listed in Table 2.
In order to recall some relationships between these sets, we refer the reader to [8, Theorem 3.20] and [26, Remark 2.1 and Theorem 4.6].
Moreover, in the same paper, it was proved the following interesting characterization for k-index EP matrices

Motivated by (1) and the sets \({\mathbb {C}}_{n}^{k,\textrm{WG}}\) and  , our purpose is to give new characterizations of the classes of matrices given in Table 2 in terms of commutative type equalities \(AX=XA\) (where only the first power of A is involved), or even \(A^mX=XA^m\) for any positive integer m, for X being an outer inverse.
, our purpose is to give new characterizations of the classes of matrices given in Table 2 in terms of commutative type equalities \(AX=XA\) (where only the first power of A is involved), or even \(A^mX=XA^m\) for any positive integer m, for X being an outer inverse.
We will also consider the new classes of matrices introduced in Table 3.
We would like to highlight that the powerful of the results obtained in this paper is that we do not need to check \(A^kX=XA^k\) for k being the index of A (for the different generalized inverses), but only \(A^mX=XA^m\) for any positive integer m or even \(AX=XA\), which offers much more flexibility in computational aspects.
The remainder of this paper is structured into five sections. In Sect. 2, some preliminaries are given. In Sect. 3, we study new classes of matrices by expressions of type \(A^mX=XA^m\), where X is an outer inverse of a given complex square matrix A and m is an arbitrary positive integer. In particular, a new characterization of the Drazin inverse is obtained. In Sect. 4, we obtain new characterizations of matrix classes defined in Table 2 as well as we characterize the matrix classes given in Table 3 by using the core EP decomposition. The equivalence between classes k-index EP, k-core EP, \(\{m,k\}\)-core EP, and k-MPCEP are provided in Sect. 5. Finally, in order to illustrate the whole situation, a picture presents an overview of the overall studied classes.
2 Preliminaries
As stated in [24], every matrix \(A\in {{\mathbb {C}}^{n\times n}}\) can be written in its Core EP decomposition
where \(U\in {{\mathbb {C}}^{n\times n}}\) is unitary, \(T\in {\mathbb {C}}^{t\times t}\) is nonsingular, \(t:=\text {rk}(T)=\text {rk}(A^k)\), and \(N\in {\mathbb {C}}^{(n-t)\times (n-t)}\) is nilpotent of index k.
Throughout, we consider the notations
and
From (3) and applying induction on m, it is easy to see the following property:
Moreover, if \(m \ge k\), then
and so
The generalized inverses previously introduced can be represented by using the core EP decomposition [3, 6, 8, 25]. We summarize them in Table 4. Here, unitary similarity will be denoted by \({\mathop {\approx }\limits ^{*}}\). Suppose \(A\in {{\mathbb {C}}^{n\times n}}\) is of the form (2) with \(\text {Ind}(A)=k\). Then:
From (2) and Table 4 we derive the following expressions for the orthogonal projectors
3 Generalized inverses commuting with \(A^m\)
In this section, we study classes of matrices by means of equalities of the form \(A^mX=XA^m\), where X is a \(\{2\}\)-inverse of A, and m is an arbitrary positive integer. We investigate characterizations of this new type of matrices by applying the core-EP decomposition. In particular, we derive a new characterization of the Drazin inverse.
We start with an auxiliary lemma.
Lemma 3.1
Let \(A\in {{\mathbb {C}}^{n\times n}}\) be written as in (2) with \(\text {Ind}(A)=k\). Then \(Z\in A\{2\}\) and \({\mathcal {R}}(Z)={\mathcal {R}}(A^k)\) if and only if
where \(Z_2\) is an arbitrary matrix of adequate size.
Proof
It is clear that
where \(\tilde{T}_k\) is the expression (3). Assuming that \( Z= U\left[ \begin{array}{cc} Z_1 &{} Z_2 \\ Z_3 &{} Z_4 \end{array}\right] U^* \) is partitioned according to the blocks of (2), by [8, Lemma 4.2] we know that \(Z\in A\{2\}\) and \({\mathcal {R}}(Z)={\mathcal {R}}(A^k)\) is equivalent to \(Z A^{k+1}=A^k\) and \({\mathcal {R}}(Z)\subseteq {\mathcal {R}}(A^k)\). From (7), it clear that \(Z A^{k+1}=A^k\) implies \(Z_1=T^{-1}\) and \(Z_3=0\). Moreover, by [7, Lemma 2.5], we have
Thus, as \({\mathcal {R}}(Z)\subseteq {\mathcal {R}}(A^k)\) is equivalent to \(P_{A^k}Z=Z\), from (8), we obtain \(Z_4=0\).
Since the converse is evident, the proof is complete. \(\square \)
Proposition 3.2
Let \(A\in {{\mathbb {C}}^{n\times n}}\) with \(\text {Ind}(A)=k\). Let \(X=Q_AZ\), where \(Z\in A\{2\}\) and \({\mathcal {R}}(Z)={\mathcal {R}}(A^k)\). The following conditions are equivalent:
-
(a)
\(X=A^d\);
-
(b)
\(A^m X= X A^m\), for all \(m \in {\mathbb {N}}\);
-
(c)
\(A^m X= X A^m\), for some \(m \in {\mathbb {N}}\).
Proof
\((a) \Rightarrow (b) \Rightarrow (c)\) are trivial.
\((c) \Rightarrow (a)\) Let \(s\in \mathbb {N}\) be such that \(sm\ge k\). Premultiplying by \(A^{m}\) both sides of the equality \(A^m X= X A^m\) we have
Following in this way, we arrive at \(A^{sm}X=XA^{sm}\).
Since \(X=Q_AZ\), \(Z\in A\{2\}\), and \({\mathcal {R}}(Z)={\mathcal {R}}(A^k)\), from (6) and Lemma 3.1 we have
It is clear that
where \(\tilde{T}_m\) has been defined in (3).
By using (9) and (10), it is easy to see that \(A^{sm} X= X A^{sm}\) if and only if the following conditions simultaneously hold:
(i) \(T^{sm} X_1+\tilde{T}_{sm} X_3=X_1T^{sm}\),
(ii) \(T^{sm} X_2+\tilde{T}_{sm} X_4=X_1 \tilde{T}_{sm}\),
(iii) \(0=X_3T^{sm}\),
(iv) \(0=X_3\tilde{T}_{sm}\).
From (iii) and nonsingularity of T we deduce that \(X_3=0\). Thus, (9) implies \((I_{n-t}-Q_N)S^* \Delta =0\), and therefore \(\Delta ^{-1}=TT^*\), \(X_1=T^{-1}\) and \(X_4=0\). So, from (ii)
where \( X_2=T^{-(sm+1)} \tilde{T}_{sm}\). According to (5) we have
Hence, \(X=A^d\) by using Table 4. \(\square \)
Similarly, one can prove the following result.
Proposition 3.3
Let \(A\in {{\mathbb {C}}^{n\times n}}\) with \(\text {Ind}(A)=k\). Let \(X\in A\{2\}\) be such that \({\mathcal {R}}(X)= {\mathcal {R}}(A^k)\). The following conditions are equivalent:
-
(a)
\(X=A^d\);
-
(b)
\(A^m X= X A^m\), for all \(m \in {\mathbb {N}}\);
-
(c)
\(A^m X= X A^m\), for some \(m \in {\mathbb {N}}\).
Proof
\((a) \Rightarrow (b) \Rightarrow (c)\) are trivial.
\((c) \Rightarrow (a)\) Let \(s\in \mathbb {N}\) be such that \(sm\ge k\). As in the proof of Proposition 3.2 we have \(A^{sm}X=XA^{sm}\). According to Lemma 3.1 we obtain
where \(X_2\) is an arbitrary matrix of adequate size. By using (10), it is easy to see that \(A^{sm} X= X A^{sm}\) if and only if \( X_2=T^{-(sm+1)}\tilde{T}_{sm}\). Therefore, (5) and Table 4 complete the proof. \(\square \)
Proposition 3.4
Let \(A\in {{\mathbb {C}}^{n\times n}}\) with \(\text {Ind}(A)=k\). Let \(X=ZP_A\), where \(Z\in A\{2\}\) and \({\mathcal {R}}(Z)={\mathcal {R}}(A^k)\). The following conditions are equivalent:
-
(a)
\(X=A^d\);
-
(b)
\(A^m X= X A^m\), for all \(m \in {\mathbb {N}}\);
-
(c)
\(A^m X= X A^m\), for some \(m \in {\mathbb {N}}\).
Proof
Let \(X=ZP_A\). Note that \(ZAZ=Z\) implies \(XAX=X\). In consequence, as \({\mathcal {R}}(Z)={\mathcal {R}}(A^k)\) we obtain
Now, the result follows from Proposition 3.3. \(\square \)
Theorem 3.5
Let \(A\in {{\mathbb {C}}^{n\times n}}\) with \(\text {Ind}(A)=k\). For each generalized inverse

the following conditions are equivalent:
-
(a)
\(X=A^d\);
-
(b)
\(A^m X= X A^m\), for all \(m \in {\mathbb {N}}\);
-
(c)
\(A^m X= X A^m\), for some \(m \in {\mathbb {N}}\).
Proof
If  , it is well known that X is an outer inverse of A and its range space is \({\mathcal {R}}(A^k)\) [13]. So, by Proposition 3.3, we have the required equivalence.
, it is well known that X is an outer inverse of A and its range space is \({\mathcal {R}}(A^k)\) [13]. So, by Proposition 3.3, we have the required equivalence.
If \(X=A^{d,\dag }\), by using Table 1 we have \(X=Z P_A\) with \(Z=A^d\). Clearly, \(A^d\in A\{2\}\) and \({\mathcal {R}}(A^d)={\mathcal {R}}(A^k)\). So, the result follows from Proposition 3.4.
If \(X=A^{\textcircled {w}}\), by [25, Remark 3.5] we know that \(A^{\textcircled {w}}AA^{\textcircled {w}}=A^{\textcircled {w}}\) and \({\mathcal {R}}(A^{\textcircled {w}})={\mathcal {R}}(A^k)\). Thus, Proposition 3.3 implies the equivalence of conditions (a)–(c).
If \(X=A^{\textcircled {w}, \dag }\), from Table 1 we have \(X=Z P_A\) with \(Z=A^{\textcircled {w}}\). As mentioned above, \(A^{\textcircled {w}}\in A\{2\}\) and \({\mathcal {R}}(A^{\textcircled {w}})={\mathcal {R}}(A^k)\). Thus, Proposition 3.4 gives the result.
Similarly, for  , from Table 1 and Proposition 3.2 we can obtain the required equivalences. \(\square \)
, from Table 1 and Proposition 3.2 we can obtain the required equivalences. \(\square \)
Other important consequence from Proposition 3.3 is a new characterization of the Drazin inverse (and the particular case for the group inverse), which closes this section.
Theorem 3.6
Let \(A\in {{\mathbb {C}}^{n\times n}}\) with \(\text {Ind}(A)=k\). The following conditions are equivalent:
-
(a)
\(X=A^d\);
-
(b)
\(AX^2=X\), \(A^kX=XA^k\), \({\mathcal {R}}(A^k) \subseteq {\mathcal {R}}(X)\).
Proof
\((a) \Rightarrow (b)\) is obvious.
\((b) \Rightarrow (a)\) Suppose that
We claim that \(XAX=X\).
Indeed, if \(k=1\), it is obvious. We assume \(k>1\). Post-multiplying (11) by X we have \( A^k X^2=X A^k X\). Since \(AX^2=X\) we get
Again, post-multiplying this last equality by X, we get \(XA^kX^2=A^{k-1}X^2\), and we deduce that \(XA^kX^2=A^{k-2}AX^2= A^{k-2}X\). On the other hand, we also have \(XA^kX^2=X A^{k-1}A X^2=XA^{k-1}X\). Then,
Following this way, we derive \(XA^2X=AX\). Post-multiplying by X once again, we deduce that \(XA^2X^2=AX^2= X\). Thus,
As \({\mathcal {R}}(A^k) \subseteq {\mathcal {R}}(X)\), from [8, Lemma 4.1] we deduce that
Finally (1)–(13) and Proposition 3.3 imply \(X=A^d\). \(\square \)
Corollary 3.7
Let \(A\in {{\mathbb {C}}^{n\times n}}\). Then \(X=A^\#\) if and only if \(AX^2=X\), \(AX=XA\), \({\mathcal {R}}(A) \subseteq {\mathcal {R}}(X)\).
4 New characterizations of recent classes of matrices
In this section, we obtain new characterizations of k-EP matrices (or equivalently k-CMP matrices), k-DMP matrices, and dual k-DMP matrices, as well as we investigate the sets of k-WC and dual k-WC matrices.
The set of k-DMP matrices was characterized in [8] as follows:
provided that A is written as in (2). Next, we give some more characterizations of k-DMP matrices.
Theorem 4.1
Let \(A\in {{\mathbb {C}}^{n\times n}}\) be written as in (2) with \(\text {Ind}(A)=k\). The following conditions are equivalent:
-
(a)
\(A\in {\mathbb {C}}_{n}^{k,d \dagger }\);
-
(b)
\(A^m A^{d,\dagger }=A^{d,\dagger }A^m\), for all \(m\in {\mathbb {N}}\);
-
(c)
\(A^m A^{d,\dagger }=A^{d,\dagger }A^m\), for some \(m\in {\mathbb {N}}\);
-
(d)
\(A^{d,\dagger }=A^d\);
-
(e)
\(A^{k+1} A^\dag = A^k\).
Proof
\((b) \Leftrightarrow (c)\Leftrightarrow (d)\) It directly follows from Theorem 3.5 with \(X=A^{d,\dag }\).
\((a)\Rightarrow (c)\) and \((d)\Rightarrow (a)\) are clear. \((a)\Rightarrow (e)\) Assume \(A^{k} A^{d,\dag }=A^{d,\dag } A^k\). From definitions of Moore–Penrose and Drazin inverses, and by using Table 1 we have
Now, multiplying on the left the above equation by A and by using the properties \(A^d A=AA^d\) and \(A^d A^{k+1}=A^k\), item (e) follows. \((e)\Rightarrow (a)\) If \(A^{k+1} A^{\dag } = A^{k}\), in the same manner as above, we get
\(\square \)
The set of dual k-DMP matrices was characterized in [8] as follows:
provided A is written as in (2). Next, we present new characterizations for dual k-DMP matrices.
Theorem 4.2
Let \(A\in {{\mathbb {C}}^{n\times n}}\) be written as in (2) with \(\text {Ind}(A)=k\). The following conditions are equivalent:
-
(a)
\(A\in {\mathbb {C}}_{n}^{k,\dagger d}\);
-
(b)
\(A^m A^{\dagger ,d}=A^{\dagger ,d} A^m\), for all \(m\in {\mathbb {N}}\);
-
(c)
\(A^m A^{\dagger ,d}=A^{\dagger ,d} A^m\), for some \(m\in {\mathbb {N}}\);
-
(d)
\(A^{\dagger ,d}=A^d\);
-
(e)
\(A^\dag A^{k+1} = A^k\).
Proof
\((b) \Leftrightarrow (c) \Leftrightarrow (d)\) follow directly from Theorem 3.5 with \(X=A^{\dag ,d}\).
\((a)\Rightarrow (c)\) and \((d)\Rightarrow (a)\) are clear. \((a)\Leftrightarrow (e)\) can be shown analogously to the proof of Theorem 4.1. \(\square \)
By [8], Theorems 4.1 and 4.2, we can to obtain easily the following characterizations for k-EP matrices.
Theorem 4.3
Let \(A\in {{\mathbb {C}}^{n\times n}}\) be written as in (2) with \(\text {Ind}(A)=k\). The following conditions are equivalent:
-
(a)
\(A \in {\mathbb {C}}_n^{k,\dag }\);
-
(b)
\(A^m X = X A^m\), for all \(m\in {\mathbb {N}}\), where \(X\in \{A^{d,\dagger },A^{\dagger ,d}\}\);
-
(c)
\(A^m X = X A^m\), for some \(m\in {\mathbb {N}}\), where \(X\in \{A^{d,\dagger },A^{\dagger ,d}\}\);
-
(d)
\(X=A^d\), where \(X \in \{A^{d,\dagger },A^{\dagger ,d}\}\);
-
(e)
\(A^{k+1} A^\dag = A^\dag A^{k+1} =A^k\).
In [26], the following equivalences were proved:
provided that A is written as in (2).
Recently, in [28], some more characterizations of WG matrices were obtained by using the core-EP decomposition. More precisely, the authors proved the following equivalences:
Now, another characterizations of WG matrices are analysed.
Theorem 4.4
Let \(A\in {{\mathbb {C}}^{n\times n}}\) be written as in (2) with \(\text {Ind}(A)=k\). The following conditions are equivalent:
-
(a)
\(A\in {\mathbb {C}}_{n}^{k, \textrm{WG}} \);
-
(b)
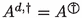 ;
; -
(c)
 ;
; -
(d)
 ;
; -
(e)
\({\mathcal {R}}(N) \subseteq {\mathcal {N}}(\tilde{T}_k)\).
Proof
\((a)\Leftrightarrow (d)\) In [26, Theorem 4.4], it was proved that A is a WG matrix if and only if  commute with
commute with  . Now, the result follows by using that
. Now, the result follows by using that  is an outer inverse of A.
is an outer inverse of A.
\((b)\Leftrightarrow (c) \Leftrightarrow (e)\) By using Table 4, we have that  is equivalent to \(T^{-(k+1)} \tilde{T}_k NN^\dag =0\) which in turn is equivalent to \(\tilde{T}_k N=0\) because T is nonsingular and \(N^\dag \) is an inner inverse of N. Clearly, \(\tilde{T}_k N=0\) if and only if \({\mathcal {R}}(N) \subseteq {\mathcal {N}}(\tilde{T}_k)\). According to Table 4 we have that the equality
is equivalent to \(T^{-(k+1)} \tilde{T}_k NN^\dag =0\) which in turn is equivalent to \(\tilde{T}_k N=0\) because T is nonsingular and \(N^\dag \) is an inner inverse of N. Clearly, \(\tilde{T}_k N=0\) if and only if \({\mathcal {R}}(N) \subseteq {\mathcal {N}}(\tilde{T}_k)\). According to Table 4 we have that the equality  is equivalent to \(\tilde{T}_k N=0\).
is equivalent to \(\tilde{T}_k N=0\).
\((a)\Leftrightarrow (e)\) follows directly from (16) for \(m=k\). \(\square \)
The case for k-WC matrices is studied in the following result.
Theorem 4.5
Let \(A\in {{\mathbb {C}}^{n\times n}}\) be written as in (2) with \(\text {Ind}(A)=k\). The following conditions are equivalent:
-
(a)
\(A \in {\mathbb {C}}_{n}^{k,\textcircled {w}\dag }\);
-
(b)
\(A^m A^{\textcircled {w},\dagger }=A^{\textcircled {w},\dagger }A^m\), for all \(m\in {\mathbb {N}}\);
-
(c)
\(A^m A^{\textcircled {w},\dagger }=A^{\textcircled {w},\dagger }A^m\), for some \(m\in {\mathbb {N}}\);
-
(d)
\(A^{\textcircled {w},\dagger }=A^d\);
-
(e)
\(A \in {\mathbb {C}}_{n}^{{\textrm{WC}}} \cap {\mathbb {C}}_{n}^{k,d \dagger }\);
-
(f)
\({\mathcal {R}}(N^2)\subseteq {\mathcal {N}}(S)\) and \({\mathcal {N}}(N^*) \subseteq {\mathcal {N}}(\tilde{T}_k)\);
-
(g)
\(SN+TS(I_{n-t}-P_N)=0\).
Proof
\((b) \Leftrightarrow (c) \Leftrightarrow (d)\) It follows from Theorem 3.5 with \(X=A^{\textcircled {w}, \dag }\).
\((a)\Rightarrow (c)\) and \((d)\Rightarrow (a)\) are clear.
\((e)\Leftrightarrow (f)\) By [6, Theorem 5.5] and [8, Theorem 3.13].
\((f)\Rightarrow (g)\) Clearly \({\mathcal {R}}(N^2)\subseteq {\mathcal {N}}(S)\) and \({\mathcal {N}}(N^*) \subseteq {\mathcal {N}}(\tilde{T}_k)\) are equivalent to \(SN^2=0\) and \(\tilde{T}_k(I_{n-t}-P_N)=0\), respectively. So, from (3) we obtain
whence \(SN+TS(I_{n-t}-P_N)=0\) because T es nonsingular.
\((g)\Rightarrow (f)\) Postmultiplying \(SN+TS(I_{n-t}-P_N)=0\) by N we immediately get \(SN^2=0\), hence \({\mathcal {R}}(N^2)\subseteq {\mathcal {N}}(S)\). By using this fact, the equality \(\tilde{T}_k(I_{n-t} -P_N)=0\) can be obtained as before.
\((d) \Leftrightarrow (f)\) By [6, Theorem 6.1 (b)]. \(\square \)
Remark 4.6
Note that if \(k\le 2\) then \({\mathbb {C}}_{n}^{k,d \dag }={\mathbb {C}}_{n}^{k,\textcircled {w}\dag }\). In fact, if \(A\in {{\mathbb {C}}^{n\times n}}\) is written as in (2), it is clear that \(SN^2=0\) (or equivalently \({\mathcal {R}}(N^2)\subseteq {\mathcal {N}}(S)\)) always is true. Now, the assertion holds by (14) and Theorem 4.5 (f). Moreover, in this case, \(A^{d,\dag }=A^{\textcircled {w},\dag }=A^d\) and \(A^{c,\dag }=A^{\dag , d} \).
Finally, next result provides characterizations for dual k-WC matrices.
Theorem 4.7
Let \(A\in {{\mathbb {C}}^{n\times n}}\) be written as in (2) with \(\text {Ind}(A)=k\). The following conditions are equivalent:
-
(a)
\(A \in {\mathbb {C}}_{n}^{k,\dag \textcircled {w}}\);
-
(b)
\(A^m A^{\dagger ,\textcircled {w}}=A^{\dagger , \textcircled {w}}A^m\), for all \(m\in {\mathbb {N}}\);
-
(c)
\(A^m A^{\dagger , \textcircled {w}}=A^{\dagger , \textcircled {w}}A^m\), for some \(m\in {\mathbb {N}}\);
-
(d)
\(A^{\dagger , \textcircled {w}}=A^d\);
-
(e)
\(A \in {\mathbb {C}}_{n}^{k, \textrm{WG}} \cap {\mathbb {C}}_{n}^{k, \dagger d}\);
-
(f)
\({\mathcal {R}}(N)\subseteq {\mathcal {N}}(S)\) and \({\mathcal {N}}(N) \subseteq {\mathcal {N}}(S)\);
-
(g)
\(SN +TS(I_{n-t}-Q_N)=0\).
Proof
\((b) \Leftrightarrow (c) \Leftrightarrow (d)\) follows from Theorem 3.5 with \(X=A^{\dag ,\textcircled {w}}\).
\((a)\Rightarrow (c)\) and \((d)\Rightarrow (a)\) are clear.
\((e)\Leftrightarrow (f)\) is a consequence of (16) and [8, Theorem 3.16].
\((b)\Leftrightarrow (f)\) Firstly, by using Table 1 note that \(A A^{\dag , \textcircled {w}}=AA^{\textcircled {w}}\) holds. Thus, from Table 4 we have that \(A A^{\dag , \textcircled {w}} = A^{\dag , \textcircled {w}} A\) is equivalent to
which in turn is equivalent to \((I_{n-t}-Q_N)S^*=0\) and \(SN=0\), because T and \(\Delta \) are nonsingular. Clearly, \((I_{n-t}-Q_N)S^*=0\) and \(SN=0\) are equivalent to \({\mathcal {N}}(N) \subseteq {\mathcal {N}}(S)\) and \({\mathcal {R}}(N)\subseteq {\mathcal {N}}(S)\), respectively. Now, from \((b)\Leftrightarrow (c)\) we obtain the desired equivalence.
\((f)\Rightarrow (g)\) As before, (f) is equivalent to \(SN=0\) and \(S(I_{n-t}-Q_N)=0\), respectively. So, \(SN +TS(I_{n-t}-Q_N)=0\).
\((g)\Rightarrow (f)\) Assume \(SN +TS(I_{n-t}-Q_N)=0\). Post-multiplying by \(Q_N\) we have \(SN=0\), and consequently \(S(I_{n-t}-Q_N)=0\) because T is nonsingular. Thus, (f) holds. \(\square \)
5 k-index EP, k-core EP, {m,k}-core EP, and k-MPCEP matrices
In 2018, Ferreyra et al. [8] showed that A is k-core EP if and only if the core EP inverse and Drazin inverse coincide. More precisely, they gave the following characterization by using the core-EP decomposition of A given in (2):

In [26], the authors proved that if A is written as (2), then

Also recall that the set of \(\{m,k\}\)-core EP matrices given in Table 2 was introduced in order to extend the set of k-core EP matrices. In [28], the authors derived the following characterization by using core-EP decomposition:

where \(\widetilde{T}_m\) is as in (3). Note that if \(m=k\), the concepts of \(\{m,k\}\)-core EP matrix and k-core EP matrix coincide. Next, we will show that both notions are always equivalent even for \(m\ne k\). In particular, we derive that the classes given above are equivalent to the class of k-MPCEP matrices given in Table 3.
Theorem 5.1
Let \(A\in {{\mathbb {C}}^{n\times n}}\) be written as in (2) with \(\text {Ind}(A)=k\). The following conditions are equivalent:
-
(a)
 ;
; -
(b)
\(A\in {\mathbb {C}}_{n}^{k,iEP}\);
-
(c)
 , where m is an arbitrary positive integer;
, where m is an arbitrary positive integer; -
(d)
 ;
; -
(e)
\(A\in {\mathbb {C}}_n^{k,\textcircled {w}\dag }\cap {\mathbb {C}}_n^{k, \dag \textcircled {w}}\);
-
(f)
 , for all \(m\in {\mathbb {N}}\);
, for all \(m\in {\mathbb {N}}\); -
(g)
 , for some \(m\in {\mathbb {N}}\);
, for some \(m\in {\mathbb {N}}\); -
(h)
 ;
; -
(i)
 , for all \(m\in {\mathbb {N}}\);
, for all \(m\in {\mathbb {N}}\); -
(j)
 , for some \(m\in {\mathbb {N}}\);
, for some \(m\in {\mathbb {N}}\); -
(k)
 ;
; -
(l)
\(S=0\);
-
(m)
\(\tilde{T}_k=0\);
-
(n)
\(\tilde{T}_m=0\), where m is an arbitrary positive integer;
-
(o)
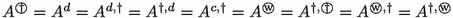 .
.
Proof
\((a)\Leftrightarrow (b) \Leftrightarrow (h)\Leftrightarrow (l) \Leftrightarrow (m)\) follows from (17) and (18).
\((a)\Leftrightarrow (c) \Leftrightarrow (f)\Leftrightarrow (g) \Leftrightarrow (n)\) is a consequence from (19) and Theorem 3.5 with  .
.
\((i) \Leftrightarrow (j) \Leftrightarrow (k)\) follows from Theorem 3.5 with  .
.
\((d)\Rightarrow (j)\) and \((k)\Rightarrow (d)\) are clear.
\((e) \Leftrightarrow (l)\) is a consequence of items (a) and (g) in Theorem 4.5 and items (a), (f) and (g) in Theorem 4.7.
\((i) \Rightarrow (l)\) Let \(m=1\). From Table 4, it is easy to see that  implies \(T^* \Delta S=0\), which is equivalent to \(S=0\) because T and \(\Delta \) are nonsingular.
implies \(T^* \Delta S=0\), which is equivalent to \(S=0\) because T and \(\Delta \) are nonsingular.
\((l)\Rightarrow (k)\) If \(S=0\), from Table 4 we have  .
.
\((k)\Rightarrow (o)\) Since (k) is equivalent to (l) we have \(S=0\). Now, the assertion follows from (2) and Table 4.
\((o)\Rightarrow (k)\) Trivial. \(\square \)
Note that if \(A\in {{\mathbb {C}}^{n\times n}}\) is written as in (2), it is easy to see that \(A\in {\mathbb {C}}_n^{\textrm{EP}}\) if and only if \(S=0\) and \(N=0\). Now, from (2), Table 4, and Theorem 5.1 we have the following corollary.
Corollary 5.2
Let \(A\in {{\mathbb {C}}^{n\times n}}\). If \( A\in {\mathbb {C}}_n^{\textrm{EP}}\) then

Conversely, if \(X=A^\dag \) for some  then \(A\in {\mathbb {C}}_n^{\textrm{EP}}\).
then \(A\in {\mathbb {C}}_n^{\textrm{EP}}\).
The following examples show that the class \({\mathbb {C}}_{n}^{k, iEP}\) is strictly included in \({\mathbb {C}}_n^{k,\textcircled {w}\dag }\) and \({\mathbb {C}}_n^{k,\dag \textcircled {w}}\), which in turn are included in \({\mathbb {C}}_n^{k,d \dag }\) and \({\mathbb {C}}_n^{k,\dag d}\), respectively.
Example 5.3
Consider the matrix
Clearly, \(\textrm{Ind}(A)=3\). Denoting \(T=1\), \(S=\left[ \begin{array}{rrr} 0&-1&1 \end{array}\right] \) and \(N= \left[ \begin{array}{rrr} 0 &{}\quad -1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0\\ \end{array}\right] \), we have \(SN =\left[ \begin{array}{rrr} 0&0&-1 \end{array}\right] \) and \(P_N=NN^\dag = \left[ \begin{array}{rrr} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0\\ \end{array}\right] \). Therefore,
and consequently \(A\in {\mathbb {C}}_n^{k,\textcircled {w}\dag }\) by Theorem 4.5. However, since \(S\ne 0\), according to Theorem 5.1 we have \(A\notin {\mathbb {C}}_{n}^{k, iEP}\).
Example 5.4
Let
It is easy to see that \(\textrm{Ind}(A)=2\). Since \(T=1\), \(S=\left[ \begin{array}{rrr} 0&0&1 \end{array}\right] \) and \(N = \left[ \begin{array}{rrr} 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0\\ \end{array}\right] \), we have \(SN =\left[ \begin{array}{rrr} 0&0&0 \end{array}\right] \) and \(Q_N=N^\dag N= \left[ \begin{array}{rrr} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1\\ \end{array}\right] \). Thus,
and so \(A\in {\mathbb {C}}_n^{k,\dag \textcircled {w}}\) by Theorem 4.7. However, from Theorem 5.1 we get \(A\notin {\mathbb {C}}_{n}^{k, iEP}\).
Example 5.5
The class \({\mathbb {C}}_n^{k,\textcircled {w}\dag }\) is a proper subset of \({\mathbb {C}}_n^{k, d \dagger }\). In fact, we consider the matrix
It is easy to see that \(\textrm{Ind}(A)=3\). Moreover, we have
Therefore, since \(A^{d,\dag }=A^d\), from Theorem 4.1 we have \(A\in {\mathbb {C}}_{n}^{k,d \dagger }\). However, as \(A^{\textcircled {w},\dag }\ne A^d\), from Theorem 4.5 it is clear that \(A\notin {\mathbb {C}}_n^{k,\textcircled {w}\dag }\).
Example 5.6
The class \({\mathbb {C}}_n^{k,\dag \textcircled {w}}\) is a proper subset of \({\mathbb {C}}_n^{k, \dagger d}\). In fact, we consider the matrix
It is easy to see that \(\textrm{Ind}(A)=3\). Moreover, we have
Therefore, since \(A^{\dag , d}=A^d\), from Theorem 4.2 we have \(A\in {\mathbb {C}}_{n}^{k,\dagger d}\). However, as \(A^{\dag , \textcircled {w}}\ne A^d\), from Theorem 4.7 it is clear that \(A\notin {\mathbb {C}}_n^{k,\dag \textcircled {w}}\).
The other inclusions reflected in Fig. 1 are also strict and examples of them can be found at [6, 8, 26].
6 Conclusions
It is well known that a square complex matrix is called EP if it commutes with its Moore–Penrose inverse. In [8], by using generalized inverses in expressions of type \(A^kX=XA^k\), where k is the index of A, generalizations of EP matrices was studied, which led to the emergence of new matrix classes, such as k-index EP, k-CMP matrices, k-DMP matrices, dual k-DMP matrices, and k-core EP matrices, investigated in detail by several authors. This paper presents characterizations of these matrix classes in terms of only commutative equalities of type \(AX=XA\), for X being an outer generalized inverse, improving the known results in the literature. We extend widely the results by considering expressions of the form \(A^mX=XA^m\), where m is an arbitrary positive integer. The Core-EP decomposition is efficient for investigating the relationships between the different matrix classes induced by generalized inverses. Following the current trend in the research of generalized inverses and its applications, we believe that investigation related to matrix classes involving recent generalized inverses will attract attention, and we describe perspectives for further research: 1. Extending the matrix classes to Hilbert space operators. 2. Considering matrix classes induced by weighted generalized inverse such that weighted core-EP inverse, weighted weak group inverse, weighted BT inverse, etc.
Data availability
Not applicable
References
Baksalary, O.M., Trenkler, G.: Core inverse of matrices. Linear Multilinear Algebr. 58(6), 681–697 (2010)
Ben-Israel, A., Greville, T.N.E.: Generalized Inverses: Theory and Applications. Springer-Verlag, New York (2003)
Chen, J.L., Mosić, D., Xu, S.Z.: On a new generalized inverse for Hilbert sapce operators. Quaest. Math. 43(9), 1331–1348 (2020)
Cheng, S., Tian, Y.: Two sets of new characterizations for normal and EP matrices. Linear Algebr. Appl. 375, 181–195 (2003)
Djordjević, D.S.: Characterizations of normal, hyponormal and EP operators. J. Math. Anal. Appl. 329(2), 1181–1190 (2007)
Ferreyra, D.E., Levis, F.E., Priori, A.N., Thome, N.: The weak core inverse. Aequat. Math. 95, 351–373 (2021)
Ferreyra, D.E., Levis, F.E., Thome, N.: Revisiting of the core EP inverse and its extension to rectangular matrices. Quaest. Math. 41(2), 265–281 (2018)
Ferreyra, D.E., Levis, F.E., Thome, N.: Characterizations of \(k\)-commutative equalities for some outer generalized inverses. Linear Multilinear Algebr. 68(1), 177–192 (2020)
Ferreyra, D.E., Malik, S.B.: Relative EP matrices. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas 116, 69 (2022)
Hartwig, R.E., Spindelböck, K.: Matrices for which \(A^*\) and \(A^{\dagger }\) conmmute. Linear Multilinear Algebr. 14(3), 241–256 (1984)
Malik, S.B., Rueda, L., Thome, N.: The class of m-EP and m-normal matrices. Linear Multilinear Algebr. 64(11), 2119–2132 (2016)
Malik, S.B., Thome, N.: On a new generalized inverse for matrices of an arbitrary index. Appl. Math. Comput. 226, 575–580 (2014)
Manjunatha Prasad, K., Mohana, K.S.: Core EP inverse. Linear Multilinear Algebr. 62(6), 792–802 (2014)
Meenakshi, A.R., Indira, R.: On conjugate EP matrices. Kyungpook Math. J. 37(1), 67–72 (1997)
Meenakshi, A.R., Krishnamoorthy, S.: On \(k\)-EP matrices. Linear Algebr. Appl. 269(1–3), 219–232 (1998)
Mehdipour, M., Salemi, A.: On a new generalized inverse of matrices. Linear Multilinear Algebr. 66(5), 1046–1053 (2018)
Mitra, S.K., Bhimasankaram, P., Malik, S.B.: Matrix Partial Orders, Shorted Operators and Applications. World Scientific Publishing Company, Singapore (2010)
Mosić, D., Djordjević, D.S., Koliha, J.J.: EP elements in rings. Linear Algebr. Appl. 431(5–7), 527–535 (2009)
Pearl, M.H.: On normal and \(EP_r\) matrices. Mich. Math. J. 6(1), 1–5 (1959)
Rao, C.R., Mitra, S.K.: Generalized Inverse of Matrices and its Applications. John Wiley and Sons, New York (1971)
Rao, C.R., Mitra, S.K.: Generalized inverse of a matrix and its application. In: Le Cam, L.M., Neyman, J., Scott, E.L., (eds). Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability. University of California Press, Berkeley. pp. 601–620 (1972)
Schwerdtfeger, H.: Introduction to Linear Algebra and the Theory of Matrices. In: P. Noordhoff, Groningen (1950)
Tian, Y., Wang, H.: Characterizations of EP matrices and weighted-EP matrices. Linear Algebr. Appl. 434(5), 1295–1318 (2011)
Wang, H.: Core-EP decomposition and its applications. Linear Algebr. Appl. 508, 289–300 (2016)
Wang, H., Chen, J.L.: Weak group inverse. Open Math. 16(1), 1218–1232 (2018)
Wang, H., Liu, X.: The weak group matrix. Aequat. Math. 93, 1261–1273 (2019)
Zhou, M., Chen, J.L.: Integral representations of two generalized core inverses. Appl. Math. Comput. 333, 187–193 (2018)
Zhou, M., Chen, J.L., Thome, N.: New characterizations of weak group matrices, Filomat, to appear
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature. This work was supported by the Universidad Nacional de Río Cuarto (UNRC) under Grant 18/C614-2; Universidad Nacional de La Pampa (UNLPam), Facultad de Ingeniería under Grant Resol. Nro. 135/19; Universidad Nacional de Río Cuarto, Grant PPI 18/C634; Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) under Grant PIP PIBAA 28720210100658CO; and Ministerio de Ciencia, Innovación y Universidades of Spain (MICINN) under Grant RED2022-134176-T.
Author information
Authors and Affiliations
Contributions
The whole research was developed by the four authors in close cooperation. Results were obtained by the four authors and improved by themselves in different iterations. N. Thome wrote the Introduction. D.E. Ferreyra and F. Levis wrote Sections 2 and 3. A. Priori and N. Thome wrote Sections 4 and 5. D. Ferreyra wrote Conclusions. F. Levis and A. Priori made Fig. 1.
Corresponding author
Ethics declarations
Ethical approval
Not applicable.
Conflict of interest
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ferreyra, D.E., Levis, F.E., Priori, A.N. et al. Extending EP matrices by means of recent generalized inverses. Aequat. Math. (2024). https://doi.org/10.1007/s00010-024-01091-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00010-024-01091-z



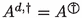 ;
; ;
; ;
; ;
; , where m is an arbitrary positive integer;
, where m is an arbitrary positive integer; ;
; , for all
, for all  , for some
, for some  ;
; , for all
, for all  , for some
, for some  ;
;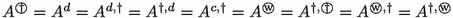 .
.