On the functional equation $\hbox {f}(\hbox {x}+\hbox {y})=\hbox {g}(\hbox {xy})$

Abstract

The functional equation $f(x+y)=g(xy)$ is investigated with unknown functions $f:A+A\rightarrow Y$, $g:A\cdot A\rightarrow Y$ in the following cases: $A:=\left]\alpha ,\beta \right[\subseteq \mathbb {F}_{+}$ where $\mathbb {F}$ is an Archimedean ordered field; A is the set of all positive integers; A is the set of all positive dyadic rational numbers. The set Y is an arbitrarily fixed (infinite) set. The main result of the paper shows that there exists a set $A\subseteq \mathbb {R}_{+}$ that is closed under addition and multiplication and there exist functions f, $g:A\rightarrow Y$ which satisfy the equation $f(x+y)=g(xy)$ for all $x,y\in A$ such that the range of the function f is infinite. Finally, some application of the above results is also given.

1 Introduction

The main purpose of this paper is to give the general solution of the functional equation

$$\begin{aligned} f(x+y)=g(xy) \end{aligned}$$

(1)

for all x, $y\in A$ with unknown functions $f:A+A:=\left\{ a+b\mid a,b\in A\right\} \rightarrow Y$, $g:A\cdot A:=\left\{ ab\mid a,b\in A\right\} \rightarrow Y$ in the following cases:

• the set A is a nonempty open interval of the set of all positive elements of an Archimedean ordered field $\mathbb {F}$;

• the set A is the set of all positive integers;

• the set A is the set of all positive dyadic rational numbers.

In all of the above cases Y is an arbitrary infinite set.

In [13] the second author of this paper together with Lajkó showed that if $\mathbb {F}(+,\cdot ,\le )$ is an ordered field, Y is an arbitrary nonempty set, then the functional Eq. (1) has only constant function solutions on $\mathbb {F}_{+}$. In [13] Eq. (1) is necessary to show that a Pexider type functional equation has only quasi logarithmic function solutions.

In the paper of Rimán [18] an extension of the Pexider equation is given. Chudziak and Sobek [2, 3] considered the problem of existence and uniqueness of extensions for the generalized Pexider equation on an open domain. Sobek [16] investigated the Pexider equation on a restricted domain.

In [7] there is a functional equation that can be brought back to the so-called generalized Davidson functional equation [5,6,7] by functional Eq. (1).

In [4, Problem B. 4456] the investigated functional equation is

$$\begin{aligned} f\left( \frac{x+y}{2}\right) =f(\sqrt{xy})\quad (x,y\in \mathbb {R}_{+}) \end{aligned}$$

with unknown functions f, $g:\mathbb {R}_{+}\rightarrow \mathbb {R}$.

In the problem book [19, 1.13 Problem 2, p. 26] the investigated functional equation is

$$\begin{aligned} f(x+y)=f(xy)\quad (x,y\in \mathbb {R}_{+}) \end{aligned}$$

with unknown function $f:\mathbb {R}_{+}\rightarrow \mathbb {R}$. Both of the above two functional equations are similar to functional Eq. (1).

In this paper a construction is given to show that if the set Y is an arbitrarily fixed countable set, then there exists a set $A\subseteq \mathbb {R}_{+}$ that is closed under addition and multiplication and there exist functions f, $g:A\rightarrow Y$ that satisfy the functional Eq. (1) for all $x,y\in A$ and the range of the function f is the set Y.

Finally, it will be shown that some restricted Pexider type functional equation system has only constant function solutions.

In the sequel, we will use the following concepts and statements.

An ordered group $\mathbb {G}(+,\le )$ is said to be dense (in itself), if for all x, $y\in \mathbb {G}$ with $x<y$ there exists an element $z\in \mathbb {G}$ such that $x<z<y$.

If $\mathbb {G}(+,\le )$ is an ordered dense group, $\left]\underline{a},\overline{a}\right[$, $\left]\underline{b},\overline{b}\right[\subseteq \mathbb {G}$, then

$$\begin{aligned} \left]\underline{a},\overline{a}\right[+\left]\underline{b},\overline{b}\right[= \left]\underline{a}+\underline{b},\overline{a}+ \overline{b}\right[; \end{aligned}$$

If $\mathbb {F}(+,\cdot \le )$ is an ordered field, $\left]\underline{a},\overline{a}\right[$, $\left]\underline{b},\overline{b}\right[\subseteq \mathbb {F}_{+}$, then

$$\begin{aligned} \left]\underline{a},\overline{a}\right[\cdot \left]\underline{b}, \overline{b}\right[=\left]\underline{a}\underline{b},\overline{a} \overline{b}\right[ \end{aligned}$$

[11], see also [12].

2 The case when the set A is an open interval of an Archimedean ordered field

An (linearly) ordered field $\mathbb {F}(+,\cdot ,\le )$ is said to be Archimedean ordered if for all $x,y\in \mathbb {F}_{+}:=\left\{ x\in \mathbb {F}\mid x>0\right\}$ there exists a positive integer n such that $nx:=x+\cdots +x>y$.

If $\mathbb {F}(+,\cdot ,\le )$ is an ordered field, $\alpha$, $\beta \in \mathbb {F}$ with $\alpha <\beta$, then we can define the open interval with endpoints $\alpha$ and $\beta$ by

$$\begin{aligned} \left]\alpha ,\beta \right[:=\left\{ x\in \mathbb {F}\mid \alpha<x<\beta \right\} . \end{aligned}$$

Let $(a_{n})$ be a monotone sequence in $\mathbb {F}$ such that $\lim _{n\rightarrow \infty }a_{n}=a\in \mathbb {F}$. (The topology on $\mathbb {F}$ is generated by the family of all open intervals.) We shall use the notation $a_{n}\uparrow a$, if the sequence $(a_{n})$ is increasing and similarly $a_{n}\downarrow a$, if $(a_{n})$ is decreasing.

Theorem 2.1

If $\mathbb {F}(+,\cdot ,\le )$ is an Archimedean ordered field, $\alpha$, $\beta \in \mathbb {F}$ with $0\le \alpha <\beta$, Y is an arbitrarily fixed countable infinite set and the functions $f:\left]2\alpha ,2\beta \right[\rightarrow Y$ and $g\left]\alpha ^{2},\beta ^{2}\right[\rightarrow Y$ satisfy Eq. (1) for all $x,y\in \left]\alpha ,\beta \right[$, then these functions are constant functions.

Proof

Let x, $y\in A+A=\left]2\alpha ,2\beta \right[$ such that $x<y$. Then there exists $\varepsilon \in \mathbb {F}_{+}$ such that $2\alpha <x-\varepsilon$ and $y+\varepsilon <2\beta$. Define the sequences $(\delta _{n})$ and $(\lambda _{n})$ by

$$\begin{aligned} \delta _{n}:=\dfrac{y-x}{n},\quad \lambda _{n}:=\dfrac{\delta _{n}+\varepsilon }{\delta _{n}+2\varepsilon }\quad ( n\in \mathbb {Z}_{+}:=\{1,2,3,\ldots \}). \end{aligned}$$

Since $\lambda _{n}> \frac{1}{2}$, we have

$$\begin{aligned} 1-\lambda _{n} <\lambda _{n}. \end{aligned}$$

(2)

Find the number $N\in \mathbb {Z}_{+}$ such that

$$\begin{aligned} \alpha<(1-\lambda _{N})(x-\varepsilon )\quad \text {and}\quad \lambda _{N}(y+\varepsilon )<\beta . \end{aligned}$$

(3)

Since

$$\begin{aligned} \frac{\alpha }{x-\varepsilon }<\frac{1}{2}\quad \text {and}\quad \frac{\varepsilon }{\delta _{n}+2\varepsilon }\uparrow \frac{1}{2} \end{aligned}$$

there exists $n_{0}\in \mathbb {Z}_{+}$ such that

$$\begin{aligned} \frac{ \alpha }{x-\varepsilon }<\frac{\varepsilon }{\delta _{n}+2\varepsilon }=1-\lambda _{n} \end{aligned}$$

for all $n>n_{0}$, that is,

$$\begin{aligned} \alpha <(1-\lambda _{n})(x-\varepsilon )\quad (n>n_{0}). \end{aligned}$$

(4)

On the other hand, since

$$\begin{aligned} \frac{1}{2}<\frac{\beta }{y+\varepsilon }\quad \text {and}\quad 1-\frac{\varepsilon }{\delta _{n}+2\varepsilon }\downarrow \frac{1}{2} \end{aligned}$$

there exists $n_{1}\in \mathbb {Z}_{+}$ such that

$$\begin{aligned} \lambda _{n}=1-\frac{\varepsilon }{\delta _{n}+2\varepsilon }<\frac{\beta }{y+\varepsilon } \end{aligned}$$

for all $n>n_{1}$, that is,

$$\begin{aligned} \lambda _{n}(y+\varepsilon )<\beta \quad (n>n_{1}). \end{aligned}$$

(5)

Let $N>\max (n_{0},n_{1})$ be an arbitrarily fixed integer. By (4) and (5) inequality (3) is fulfilled. Let $\lambda :=\lambda _{N}$, $\delta :=\delta _{N}$ and define the sequence $(x_{k})$ by

$$\begin{aligned} x_{k}:= x+k\delta \quad (k=0,1,\ldots ,N). \end{aligned}$$

Let the number $k\in \{0,1,\ldots ,N-1\}$ be arbitrarily fixed. By (2) and (3) we have that

$$\begin{aligned} \alpha&<(1-\lambda )(x-\varepsilon )<(1-\lambda )(x_{k}-\varepsilon )\\&< \lambda (x_{k}-\varepsilon )<\lambda (x_{k+1}+\varepsilon ) \le \lambda (y+\varepsilon )<\beta , \end{aligned}$$

and

$$\begin{aligned} \alpha&<(1-\lambda )(x-\varepsilon )<(1-\lambda )(x_{k+1}+\varepsilon )\\&< \lambda (x_{k+1}+\varepsilon ) \le \lambda (y+\varepsilon )<\beta , \end{aligned}$$

whence we obtain that

$$\begin{aligned} \lambda (x_{k}-\varepsilon ),\quad (1-\lambda )(x_{k+1}+\varepsilon ),\quad (1-\lambda )(x_{k}-\varepsilon ),\quad \lambda (x_{k+1}+\varepsilon )\in \left]\alpha ,\beta \right[. \nonumber \\ \end{aligned}$$

(6)

A simple calculation shows that

$$\begin{aligned}&\lambda (x_{k}-\varepsilon ) +(1-\lambda )(x_{k+1}+\varepsilon ) \nonumber \\&\quad = \dfrac{\delta +\varepsilon }{\delta +2\varepsilon }(x_{k}-\varepsilon ) + \dfrac{\varepsilon }{\delta +2\varepsilon }(x_{k}+\delta +\varepsilon )=x_{k}, \nonumber \\&(1-\lambda )(x_{k}-\varepsilon ) +\lambda (x_{k+1}+\varepsilon )\nonumber \\&\quad =\dfrac{\varepsilon }{\delta +2\varepsilon }(x_{k+1}-\delta -\varepsilon )+ \dfrac{\delta +\varepsilon }{\delta +2\varepsilon }(x_{k+1}+\varepsilon )=x_{k+1}. \end{aligned}$$

(7)

By (6) and (7) we obtain that

$$\begin{aligned} f(x_{k})&=f(\lambda (x_{k}-\varepsilon )+(1-\lambda )(x_{k+1}+\varepsilon ))\\&= g(\lambda (x_{k}-\varepsilon )(1-\lambda )(x_{k+1}+\varepsilon ))\\&= g((1-\lambda )(x_{k}-\varepsilon )\lambda (x_{k+1}+\varepsilon ))\\&= f((1-\lambda )(x_{k}-\varepsilon )+\lambda (x_{k+1}+\varepsilon ))=f(x_{k+1}). \end{aligned}$$

Thus we have that $f(x)=f(x_{0})=f(x_{1})$, $f(x_{1})=f(x_{2})$, $\ldots$, $f(x_{N-1})=f(x_{N})=f(y)$, that is, the function f is constant. $\square$

Let $\mathbb {F}=\mathbb {F}(+,\le )$ be an Archimedean ordered field, $X=\mathbb {F}$, or $X=\mathbb {F}^{2}:=\mathbb {F}\times \mathbb {F}$ and $D\subseteq X$, in addition, let $x\in \mathbb {F}$ or $x:=(x_{1},x_{2})\in \mathbb {F}^{2}$ and $\varepsilon >0$. We can define

$$\begin{aligned} B(x,\varepsilon ):= \left\{ \begin{array}{ll} \left]x-\varepsilon ,x+\varepsilon \right[, &{}\quad \hbox {if}\quad x\in \mathbb {F}; \\ \\ \left]x_{1}-\varepsilon ,x_{1}+\varepsilon \right[\times \left]x_{2}-\varepsilon ,x_{2}+\varepsilon \right[,&{}\quad \text {if}\quad x\in \mathbb {F}^{2}. \end{array} \right. \end{aligned}$$

The set D is said to be open if for every point x in D there exists $\varepsilon \in \mathbb {F}_{+}$ such that $B(x,\varepsilon )\subseteq D$.

A subset $D\subseteq X$ is said to be well-chained if for all $x,y\in D$ there exists a finite sequence $B_{i}:=B(x_{i},\varepsilon _{i})$ $(i=0,1,\ldots ,n)$ such that $B_{i}\subseteq D$ for all $i=0,1,\ldots ,n$, $x\in B_{0}$, $y\in B_{n}$ and $B_{i-1}\cap B_{i}\ne \emptyset$ for all $i=1$, $\ldots$, n.

Corollary 2.1

Let $\mathbb {F}(+,\cdot ,\le )$ be an Archimedean ordered field, I be a nonempty well-chained open subset of $\mathbb {F}_{+}$. If the functions $f:I+I\rightarrow \mathbb {F}$, $g:I\cdot I\rightarrow \mathbb {F}$ satisfy the functional Eq. (1) for all $x,y\in I$, then these functions are constant functions.

Problem 2.1

Let $\mathbb {F}(+,\cdot ,\le )$ be an Archimedean ordered field, $\alpha$, $\gamma$, $h\in \mathbb {F}$ with $0\le \alpha <\gamma$ and $h>0$. In addition, let $f:\left]\alpha +\gamma ,\alpha +\gamma +2h\right[\rightarrow Y$, $g:\left]\alpha \gamma ,(\alpha +h)(\gamma +h)\right[\rightarrow Y$ be functions satisfying Eq. (1) for all $x\in \left]\alpha ,\alpha +h\right[$, $y\in \left]\gamma ,\gamma +h\right[$. Prove that the function f is a constant function.

3 The case when the set A is the set of all positive integers

Proposition 3.1

If $f:\left\{ 2,3,4,\ldots \right\} \rightarrow Y$, $g:\left\{ 1,2,3,\ldots \right\} \rightarrow Y$ are functions satisfying Eq. (1) for all x, $y\in \mathbb {Z}_{+}$ and the function $T:\{4,5,6,\ldots \}\rightarrow \mathbb {Z}_{+}$ is defined by

$$\begin{aligned} T(x):=\left\{ \begin{array}{ll} \dfrac{x}{2}+3,&{} \quad \text {if}\quad x~ \text {is even};\\ \\ \dfrac{x-1}{2}+2,&{}\quad \text {if}\quad x~\text {is odd}, \end{array} \right. \end{aligned}$$

then T has the following properties:

• 1. $f(x)=f(T(x))$ for all $x\ge 4$;

• 2. $T(x)<x$ for all $x\ge 8$;

• 3. If $x\equiv i\pmod {3}$, then $T(x)\equiv 3-i\pmod {3}$ for all $i=0,1,2$.

Proof

If the number n is even, then

$$\begin{aligned} f(n)&=f(2k)=f(2(k-1)+2)=g(4(k-1))=f(k+3)\\&=f\left( \dfrac{2k}{2}+3\right) =f\left( \dfrac{n}{2}+3\right) =f(T(n)). \end{aligned}$$

If the number n is odd, then

$$\begin{aligned} f(n)&=f(2k+1)=g(2k)=f(k+2)\\&=f\left( \dfrac{(2k+1)-1}{2}+2\right) =f\left( \dfrac{n-1}{2}+2\right) =f(T(n)), \end{aligned}$$

thus property 1. is proven. Properties 2. and 3. can also be proven easily by simple calculations. $\square$

Proposition 3.2

Preserve the notations of Proposition 3.1 and define the sequence $(x_{n})$ by

$$\begin{aligned} x_{1}:= a,\quad x_{n+1}:= T(x_{n})\quad (n\in \mathbb {Z}_{+}), \end{aligned}$$

where $a\in \{3,4,5,\ldots \}$. The sequence $(x_{n})$ has the following properties:

• 1. $f(x_{m})=f(x_{n})$ for all m, $n\in \mathbb {Z}_{+}$;

• 2. If $x_{n}\ge 8$, then $x_{n+1}<x_{n}$;

• 3. If $a>12$, then $8<T(x_{n})=x_{n+1}$;

• 4. If a can be divided by 3, then the tail of the sequence $(x_{n})$ is 6, 6, 6, 6, $\ldots$ and if a can not be divided by 3, then the tail of the sequence $(x_{n})$ is 4, 5, 4, 5, $\ldots$.

Proof

By Proposition 3.1 one can easily derive the above properties of the sequence $(x_{n})$. $\square$

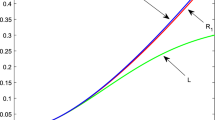
The following figure shows the sequences $(x_{n})$ if $4\le a\le 12$.

Theorem 3.1

If $A:=\mathbb {Z}_{+}$ and the functions f and g satisfy functional Eq. (1) for all x, $y\in \mathbb {Z}_{+}$, then these functions are of the form

$$\begin{aligned} \begin{aligned} f(x)=\left\{ \begin{array}{ll}y_{1},&{}\quad \text{ if }\quad x=2; \\ y_{2},&{}\quad \text{ if }\quad x=3; \\ y_{3},&{}\quad \text{ if }\quad x\ge 4; \end{array} \right. \end{aligned} \quad \begin{aligned} g(x)=\left\{ \begin{array}{ll}y_{1},&{}\quad \text{ if }\quad x=1; \\ y_{2},&{}\quad \text{ if }\quad x=2; \\ y_{3},&{}\quad \text{ if }\quad x\ge 3. \end{array} \right. \end{aligned} \end{aligned}$$

(8)

where $y_{1}$, $y_{2}$, $y_{3}\in Y$ are constants.

Proof

Let us assume that the functions f and g satisfy Eq. (1) for all x, $y\in \mathbb {Z}_{+}$. Since $f(n+1)=g(n)$ for all $n\in \mathbb {Z}_{+}$, it is enough to show that $f(x)=f(4)$ whenever $x\ge 4$. By Proposition 3.2. we have that $f(x)\in \{f(5),f(6)\}$ whenever $x\ge 4$. Since

$$\begin{aligned} f(6)=f(3+3)=g(9)=g(1\cdot 9)=f(10)=f(8)=f(7)=f(5), \end{aligned}$$

the function f is constant on the set $[4,+\infty [\cap \mathbb {Z}_{+}$.

Conversely, assume that the functions f and g are of the form in (8). Define the sets $\textrm{C}_{i}$ $i=1$, 2, 3 by

$$\begin{aligned} \textrm{C}_{1}&:=\left\{ (1,1)\right\} ;\\ \textrm{C}_{2}&:=\left\{ (1,2),(2,1)\right\} ;\\ \textrm{C}_{3}&:=\left\{ (u,v)\in \mathbb {Z}_{+}^{2}\mid (u,v)=(2,2)\vee u\ge 3\vee v\ge 3 \right\} . \end{aligned}$$

It is easy to see that

$$\begin{aligned} \textrm{C}_{1}&=\left\{ (u,v)\in \mathbb {Z}_{+}^{2}\mid u+v=2\right\} =\left\{ (u,v)\in \mathbb {Z}_{+}^{2}\mid u\cdot v=1\right\} ;\\ \textrm{C}_{2}&=\left\{ (u,v)\in \mathbb {Z}_{+}^{2}\mid u+v=3\right\} =\left\{ (u,v)\in \mathbb {Z}_{+}^{2}\mid u\cdot v=2\right\} ;\\ \textrm{C}_{3}&=\left\{ (u,v)\in \mathbb {Z}_{+}^{2}\mid u+v\ge 4\right\} =\left\{ (u,v)\in \mathbb {Z}_{+}^{2}\mid u\cdot v\ge 3\right\} , \end{aligned}$$

moreover, $\mathbb {Z}_{+}^{2}=C_{1}\cup C_{2}\cup C_{3}$ and $C_{i}\cap C_{j}=\emptyset$ whenever $i\ne j$. Thus we obtain that if $(u,v)\in \textrm{C}_{i}$, then $f(u+v)=y_{i}$ $g(uv)=y_{i}$ for all $i=1$, 2, 3, that is, the functions f and g satisfy Eq. (1). $\square$

Problem 3.1

Define $X:=\left\{ (a,b)\in \mathbb {Z}_{+}^{2}\ \mid \ a<b\right\}$ and

$$\begin{aligned} I_{ab}:=\left\{ a,a+1,\ldots ,b\right\} \quad \text {and}\quad I_{a}:=\left\{ a,a+1,\ldots \right\} . \end{aligned}$$

Let ${\mathcal {F}}_{ab}$ be the set of all pairs of functions (f, g) such that $f:I_{ab}+I_{ab}\rightarrow Y$, $g:I_{ab}\cdot I_{ab}\rightarrow Y$ with $f(x+y)=g(xy)$ for all $(x,y)\in I_{ab}$.

Similarly, let ${\mathcal {F}}_{a}$ the set of all pairs of functions (f, g) with $f:I_{a}+I_{a}\rightarrow Y$, $g:I_{a}\cdot I_{a}\rightarrow Y$ and $f(x+y)=g(xy)$ for all $x,y\in I_{a}$.

Finally, define the functions $\Phi :X\rightarrow Y$, $\Psi :\mathbb {Z}_{+}\rightarrow Y$ by

$$\begin{aligned} \Phi (a,b)&:=\max \left\{ \textrm{card}\ {\mathcal {R}}_{f}\ \mid \ \exists g:(f,g)\in {\mathcal {F}}_{ab}\right\} \\ \Psi (a)&:=\max \left\{ \textrm{card}\ {\mathcal {R}}_{f}\ \mid \ \exists g:(f,g)\in {\mathcal {F}}_{a}\right\} . \end{aligned}$$

Find the values of the functions $\Phi$ and $\Psi$. For example, by Theorem 3.1 we have that $\Psi (1)=3$.

4 The case when the set A is the set of all positive dyadic rational numbers

Denote by ${\mathcal {R}}_{\{2\}}$ the set of all positive dyadic rational numbers, that is,

$$\begin{aligned} {\mathcal {R}}_{\{2\}}:=\left\{ \left. \frac{k}{2^{n}}\right| k=1,2,3,\ldots ;n=0,1,2,\ldots \right\} . \end{aligned}$$

Theorem 4.1

If the functions f, $g: {\mathcal {R}}_{\{2\}}\rightarrow Y$ satisfy functional Eq. (1) for all x, $y\in {\mathcal {R}}_{\{2\}}$, then these functions are constant functions.

Proof

Let x, $y\in {\mathcal {R}}_{\{2\}}$ such that $x<y$. Then there exist positive integers k, $l\ge 4$ and an element $z\in {\mathcal {R}}_{\{2\}}$ such that $x=kz$ and $y=lz$. Define the functions $F:\{2,3,\ldots \}\rightarrow Y$, $G:\{1,2,3,\ldots \}\rightarrow Y$ by

$$\begin{aligned} \begin{aligned} F(u)&:= f(uz)\\ G(v)&:= g(vz^{2})\\ \end{aligned} \quad \begin{aligned} u&\in \{2,3,4,\ldots \},\\ v&\in \{1,2,3,\ldots \}. \end{aligned} \end{aligned}$$

The functions F and G satisfy the functional equation

$$\begin{aligned} F(u+v)=G(uv)\quad (u,v\in \mathbb {Z}_{+}), \end{aligned}$$

whence by Theorem 3.1 we have that the function F is a constant function. Thus $f(x)=f(kz)=F(k)=F(l)=f(lz)=f(y)$ thus the function f is a constant function. $\square$

Remark 4.1

Let $R(+,\cdot ,\le )$ be an ordered ring such that for all a, $b\in R_{+}$ there exist an element $c\in R$ and integers $m\ge 4$, $n\ge 4$ such that $a=mc$, $b=nc$ and, in addition, $lc\in R_{+}$ for all $l\in \mathbb {Z}_{+}$. If the functions f, $g:R_{+}\rightarrow Y$ satisfy functional Eq. (1) for all x, $y\in R_{+}$, then these functions are constant functions.

Example 4.1

Let ${\mathcal {P}}$ be the set of all positive prime numbers and P be an arbitrarily fixed nonempty subset of ${\mathcal {P}}$. Let ${\mathcal {R}}_{P}$ be the set of all rational numbers which can be represented in the form a/b where $a\in \mathbb {Z}$, $b\in \mathbb {Z}_{+}$ such that $a=0$ or a and b are relative primes and all the prime divisors of the integer b are in P. The ring ${\mathcal {R}}_{P}$ has the property described in Remark 4.1. For example, if $P=\{2\}$, then ${\mathcal {R}}_{P}$ is the set of all positive dyadic rational numbers.

By this example it is also easy to see that the cardinality of the set

$$\begin{aligned} \left\{ R\mid \mathbb {Z}\subseteq R\subseteq \mathbb {R}\text { and } R \text { is a ring}\right\} \end{aligned}$$

is equal to the cardinality of the continuum.

5 A function solutions of Eq. (1) which has infinite range

In this section we prove the following Theorem:

Theorem 5.1

There exists a set $A\subseteq \mathbb {R}_{+}$ with the following properties:

• 1. $A+A\subseteq A$; $A\cdot A\subseteq A$;

• 2. For every sets $Y=\left\{ y_{1},y_{2},y_{3},\ldots \right\}$ there exist functions f, $g:A\rightarrow Y$ satisfying Eq. (1) for all x, $y\in A$ such that ${\mathcal {R}}_{f}=Y$.

Although the proof of the above statement is simple, we will briefly describe it for the sake of the readers.

The set of all square-free positive integers is denoted by ${\mathcal {F}}_{2}$, that is,

$$\begin{aligned} {\mathcal {F}}_{2}=\{1,2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17,\ldots \}. \end{aligned}$$

Let $(p_{n})$ be the strictly increasing sequence of all positive prime numbers. Thus ${\mathcal {P}}=\left\{ p_{n}|n\in \mathbb {Z}_{+}\right\}$ and we can define the sets ${\mathcal {P}}_{n}$ by

$$\begin{aligned} {\mathcal {P}}_{n}:=\left\{ p_{i}\in {\mathcal {P}}\mid i\le n\right\} \end{aligned}$$

for all $n\in \mathbb {Z}_{+}$.

Define the sets $X_{n}\subseteq {\mathcal {F}}_{\{2\}}$ by

$$\begin{aligned} X_{n}:=\{x\in {\mathcal {F}}_{\{2\}}{\setminus }\{1\}\mid \text { if }p|x,\text { then } p\in {\mathcal {P}}_{k}\}:=\{x_{2},x_{3},\ldots ,x_{2^{n}}\} \end{aligned}$$

for all $n\in \mathbb {Z}_{+}$ where p|x denotes that x can be divided by p.

If $K\subseteq \mathbb {R}$ is a field and $a_{1}$, $\ldots$, $a_{n}\in \mathbb {R}$, then we can define the field $K(a_{1},\ldots ,a_{n})$ by

$$\begin{aligned} K(a_{1},\ldots ,a_{n}):=\bigcap \{L\subseteq \mathbb {R}\mid L\text { is a field such that }K\cup \{a_{1},\ldots ,a_{n}\}\subseteq L\}. \end{aligned}$$

It is easy to see that $K(a_{1},\ldots ,a_{n})=K(a_{1},\ldots ,a_{n-1})(a_{n})$.

We shall use the abbreviations

$$\begin{aligned} \mathbb {Q}_{n}&:=\mathbb {Q}(\sqrt{p_{1}},\ldots ,\sqrt{p_{n}}),\\ K_{n}&:=\left\{ \left. \lambda _{1}+\sum _{i=1}^{2^{n}}\lambda _{i}\sqrt{x_{i}}\ \right| \ \lambda _{i}\in \mathbb {Q};\quad x_{i}\in X_{n}\quad (i=1,2,\ldots ,n)\right\} . \nonumber \end{aligned}$$

(9)

One can easily prove the following Proposition.

Proposition 5.1

If L is a subfield of the field $\mathbb {R}$ and $a\in L$, then

$$\begin{aligned} L(\sqrt{a})=\{u+v\sqrt{a}\mid u,v\in L\}. \end{aligned}$$

(10)

Theorem 5.2

$K_{n}=\mathbb {Q}_{n}$ for all $n\in \mathbb {Z}_{+}$.

Proof

We prove the Theorem by mathematical induction. The base case $(k=1)$ is Proposition 5.1. For the induction step let us assume that $K_{k}=\mathbb {Q}_{k}$ and let $x\in K_{k+1}$. Since $\mathbb {Q}_{k+1}=\mathbb {Q}_{k}(\sqrt{p_{k+1}})$, by Proposition 5.1, there exist elements $u,v\in K_{k}$ such that $x=u+v\sqrt{p_{k+1}}$ whence by the inductive hypothesis we obtain that $K_{k+1}=\mathbb {Q}_{k+1}$. $\square$

One can easily prove the following Proposition.

Proposition 5.2

If L is a subfield of the field $\mathbb {R}$ and $a\in L$ but $\sqrt{a}\notin L$, then for all $x\in L(\sqrt{a})$ there uniquely exist u, $v\in L$, such that $x=u+v\sqrt{a}$.

Proposition 5.3

If L is a subfield of the field $\mathbb {R}$, $a,b\in L$ such that $\sqrt{a}\in L(\sqrt{b})$, then either $\sqrt{a}\in L$, or $\sqrt{ab}\in L$.

Proof

If $\sqrt{a}\notin L$, then by $\sqrt{a}\in L(\sqrt{b})$ and by Proposition 5.1. there exist $u,v\in L$, $v\ne 0$ such that $\sqrt{a}=u+v\sqrt{b}$. Thus we obtain, that $\sqrt{a}-v\sqrt{b}=u$, whence we have that

$$\begin{aligned} \sqrt{ab}=\dfrac{a+v^{2}b-u^{2}}{2v}\in L. \end{aligned}$$

$\square$

Proposition 5.4

If $x\in {\mathcal {F}}_{2}$, such that $\sqrt{x}\in \mathbb {Q}_{k}$, then all the prime divisors p of x are in ${\mathcal {P}}_{k}$ for all $k\in \mathbb {Z}_{+}$. Thus $\sqrt{p_{k+1}}\notin \mathbb {Q}_{k}$ for all $k\in \mathbb {Z}_{+}$.

Proof

We prove the statement by mathematical induction. For the case $k=1$ assume that $x\in {\mathcal {F}}_{2}$ and $\sqrt{x}\in \mathbb {Q}(\sqrt{p_{1}})$. Thus, by Proposition 5.3., we obtain that either $\sqrt{x}\in \mathbb {Q}$ or $\sqrt{xp_{i}}\in \mathbb {Q}$. If $\sqrt{x}\in \mathbb {Q}$, then $x=1$ thus the statement holds. If $\sqrt{xp_{1}}\in \mathbb {Q}$, then $x=p_{1}$, thus the statement holds too.

For the induction step assume that $x\in {\mathcal {F}}_{2}$ and $\sqrt{x}\in \mathbb {Q}_{k+1}=\mathbb {Q}_{k}(\sqrt{p_{k+1}})$. By Proposition 5.3. we obtain, that either $\sqrt{x}\in \mathbb {Q}_{k}$ or $\sqrt{xp_{k+1}}\in \mathbb {Q}_{k}$. By the inductive hypothesis we obtain, that if $p\in {\mathcal {P}}$ such that p|x and $p\ne p_{k+1}$, then $p\in {\mathcal {P}}_{k}$ which completes the proof. $\square$

Theorem 5.3

The form of $x\in K_{n}$ in (9) is unique for all $n\in \mathbb {Z}_{+}$.

Proof

We prove the Theorem by mathematical induction. By Theorem 5.2. we have that $K_{n}=\mathbb {Q}_{n}$ for all $n\in \mathbb {Z}_{+}$.

The base case ($k=1$) follows from Proposition 5.2.

For the induction step assume, that $\sqrt{x}\in \mathbb {Q}_{k+1}=\mathbb {Q}_{k}(\sqrt{p_{k+1}})$. By Proposition 5.4 we have that $\sqrt{p_{k+1}}\notin \mathbb {Q}_{k}$ thus by Proposition 5.2 we obtain that there uniquely exist u, $v\in \mathbb {Q}_{k}$ such that $x=u+v\sqrt{p_{k+1}}$ whence, by the induction hypothesis the statement is proven. $\square$

By Theorem 5.3, one can easily prove Theorem 5.1.

Proof

Let ${\mathcal {Q}}$ be the set of all elements of the real line which can be represented in the form

$$\begin{aligned} x=\lambda _{0}+\sum _{i=1}^{n}\lambda _{i}\sqrt{x_{i}} \end{aligned}$$

(11)

where $n\in \mathbb {Z}_{+}$, $\lambda _{0}$, $\lambda _{i}\in \mathbb {Q}_{+}$ and $x_{i}\in {\mathcal {F}}_{2}{\setminus }\{1\}$ for all $i=1$, 2, $\ldots$, n, moreover, $x_{j}\ne x_{k}$ whenever $j\ne k$.

By Theorems 5.2 and 5.3. the form of $x\in {\mathcal {Q}}$ in (11) is unique. Let $A:={\mathcal {Q}}$.

Define the function $\varphi :{\mathcal {Q}}\rightarrow \mathbb {Z}_{+}$ by

$$\begin{aligned} \varphi \left( \lambda _{0}+\sum _{k=1}^{n}\lambda _{k}\sqrt{x_{k}}\right) :=\max \{k\in \mathbb {Z}_{+}\mid \exists i\in \{1,\ldots ,n\}\exists p_{k}\in {\mathcal {P}}:p_{k}|x_{i}\}. \end{aligned}$$

It can be easily seen, that

$$\begin{aligned} \varphi (x+y)=\varphi (xy)\quad (x,y\in {\mathcal {Q}}). \end{aligned}$$

Define the functions $f:{\mathcal {Q}}+{\mathcal {Q}}\rightarrow Y$ and $g:{\mathcal {Q}}\cdot {\mathcal {Q}}\rightarrow Y$ by

$$\begin{aligned} f(u+v):= y_{\varphi (u+v)},\quad g(uv):= y_{\varphi (uv)}\quad (u,v\in {\mathcal {Q}}). \end{aligned}$$

Then the functions f and g satisfy functional Eq. (1) for all $x,y\in {\mathcal {Q}}$ and ${\mathcal {R}}_{f}=Y$. $\square$

Problem 5.1

Find a subset $A\subseteq \mathbb {R}_{+}$ with the properties:

• 1. $A+A\subseteq A$; $A\cdot A\subseteq A$;

• 2. there exist functions $f:A+A\rightarrow Y$, $g:A\cdot A\rightarrow Y$ such that these functions satisfy the functional Eq. (1) for all x, $y\in A$ and the ranges of these functions are uncountable.

6 Applications

Let $\mathbb {F}(+,\cdot ,\le )$ be an ordered field, and $D\subseteq \mathbb {F}^{2}$. Define the sets $D_{x}$, $D_{y}$, $D_{x+y}$, and $D_{xy}\subseteq \mathbb {F}$ by

$$\begin{aligned} D_{x}&:=\left\{ u\in \mathbb {F}~|~\exists v\in \mathbb {F}:(u,v)\in D\right\} ,\\ D_{y}&:=\left\{ v\in \mathbb {F}~|~\exists v\in \mathbb {F}:(u,v)\in D\right\} ,\\ D_{x+y}&:=\left\{ z\in \mathbb {F}~|~\exists (u,v)\in D:z=u+v\right\} ,\\ D_{xy}&:=\left\{ z\in \mathbb {F}~|~\exists (u,v)\in D:z=uv\right\} . \end{aligned}$$

A function $a:X(+)\rightarrow Y(+)$ is said to be additive if

$$\begin{aligned} a(x+y)=a(x)+a(y)\quad (x,y\in X){.} \end{aligned}$$

A function $l:X(\cdot )\rightarrow Y(+)$ is said to be logarithmic if

$$\begin{aligned} l(xy)=l(x)+l(y)\quad (x,y\in X){.} \end{aligned}$$

There are many results concerning the additive and logarithmic functions, see for example [1, 14].

In the sequel we will use the following three theorems from [8, 10]:

Let $\mathbb {G}(+,\le )$ be an Archimedean ordered dense Abelian group, $\mathbb {F}(+,\cdot ,\le )$ be an Archimedean ordered field and $Y(+)$ be a group.

Theorem 6.1

(Extension Theorem for the restricted Pexider additive functional equation) If $D\subseteq \mathbb {G}^{2}$ is a nonempty, well-chained open set, $Y(+)$ is a group, and $f:D_{x+y}\rightarrow Y$, $g:D_{x}\rightarrow Y$, $h:D_{y}\rightarrow Y$ are functions such that

$$\begin{aligned} f(x+y)=g(x)+h(y)\quad ((x,y)\in D), \end{aligned}$$

then there exist an additive function $a:\mathbb {G}\rightarrow Y$ and constants c, $d\in Y$ such that

$$\begin{aligned} \begin{aligned} f(u)&=a(u)+c+d\\ g(v)&=a(v)+c\\ h(z)&=a(z)+d \end{aligned} \quad \begin{aligned} (u&\in D_{x+y}),\\ (v&\in D_{x}),\\ (z&\in D_{y}). \end{aligned} \end{aligned}$$

Theorem 6.2

(Extension Theorem for the restricted Pexider logarithmic functional equation) If $D\subseteq \mathbb {F}_{+}^{2}$ is a nonempty, well-chained, open set, $Y(+)$ is a group, and $f:D_{x\cdot y}\rightarrow Y$, $g:D_{x}\rightarrow Y$, $h:D_{y}\rightarrow Y$ are functions such that

$$\begin{aligned} f(xy)=g(x)+h(y)\quad ((x,y)\in D), \end{aligned}$$

then there exist a logarithmic function $l:\mathbb {F}_{+}\rightarrow Y$ and constants c, $d\in Y$ such that

$$\begin{aligned} \begin{aligned} f(u)&=l(u)+c+d\\ g(v)&=l(v)+c\\ h(z)&=l(z)+d \end{aligned} \quad \begin{aligned} (u&\in D_{x+y}),\\ (v&\in D_{x}),\\ (z&\in D_{y}). \end{aligned} \end{aligned}$$

Theorem 6.3

(Uniqueness Theorem for additive functions) If $a_{1}$, $a_{2}:\mathbb {G}\rightarrow Y$ are additive functions and there exist a nonempty open interval $\left]\alpha ,\beta \right[\subseteq \mathbb {G}$ and a constant $c\in Y$ such that

$$\begin{aligned} a_{1}(x)=a_{2}(x)+c\quad (x\in \left]\alpha ,\beta \right[), \end{aligned}$$

then $a_{1}(x)=a_{2}(x)=0$ for all $x\in \mathbb {G}$.

Now we give a simple application of Theorem 2.1.

Theorem 6.4

Let $\mathbb {F}(+,\cdot ,\le )$ be an Archimedean ordered field, $Y=Y(+)$ be a group, $D\subseteq \mathbb {F}^{2}$, $E\subseteq \mathbb {F}_{+}^{2}$ be nonempty, well-chained open sets. Define the sets $I_{i}\subseteq \mathbb {F}$, $J_{i}\subseteq \mathbb {F}_{+}$ ($i=1,2,3$) by

$$\begin{aligned} \begin{aligned} I_{1}&:=D_{x+y},\\ J_{1}&:=E_{xy}. \end{aligned} \quad \begin{aligned} I_{2}&:=D_{x},\\ J_{2}&:=E_{x}. \end{aligned} \quad \begin{aligned} I_{3}&:=D_{y},\\ J_{3}&:=E_{y}. \end{aligned} \end{aligned}$$

If $F_{i}:I_{i}\rightarrow Y$, $G_{i}:J_{i}\rightarrow Y$ $(i=1,2,3)$ are functions such that

$$\begin{aligned} \begin{aligned} F_{1}(x+y)&=F_{2}(x)+F_{3}(y)\\ G_{1}(xy)&=G_{2}(x)+G_{3}(y) \end{aligned} \quad \begin{aligned} ((x,y)&\in D),\\ ((x,y)&\in E) \end{aligned} \end{aligned}$$

(12)

and there exist $i,j\in \{1,2,3\}$ such that $I:=I_{i}\cap J_{j}\ne \emptyset$ and $F_{i}(x)=G_{j}(x)$ for all $x\in I$, then the functions $F_{i}$ and $G_{i}$ are constant functions for all $i=1,2,3$.

Proof

It is sufficient to investigate the case when $I:=I_{1}\cap J_{1}\ne \emptyset$ and

$$\begin{aligned} F_{1}(x)=G_{1}(x)\quad (x\in I), \end{aligned}$$

(13)

since the other cases are similar. From the Eq. (12), by the above Extension Theorems, there exist an additive function $a:\mathbb {F}\rightarrow Y$, a logarithmic function $l:\mathbb {F}_{+}\rightarrow Y$ and constants c, $d\in Y$ such that

$$\begin{aligned} F_{1}(x)&= a(x)+c\quad (x\in I_{1}), \nonumber \\ G_{1}(x)&= l(x)+d\quad (x\in J_{1}), \end{aligned}$$

(14)

whence we have that

$$\begin{aligned} F_{1}(x)+F_{1}(y)&=a(x)+a(y)+2c=a(x+y)+2c\quad (x,y \in I),\\ G_{1}(x)+G_{1}(y)&=l(x)+l(y)+2d=l(xy)+2d\quad (x,y \in I). \end{aligned}$$

By (13) and by Corollary 2.1, we obtain that there exists a constant $C\in Y$ such that

$$\begin{aligned} a(x)+2c=C\quad (x\in I+I). \end{aligned}$$

Since $I+I$ is a nonempty, well-chained open set, by the above Uniqueness Theorem for additive functions we obtain that $F_{1}(x)=c$ for all $x\in I_{1}$ and $G_{1}(x)=d$ for all $x\in J_{1}$ which completes the proof. $\square$

Adding the two equations of (12) we obtain the Maksa equation [15]. The local version of the Maksa equation is included in the following Problem.

Problem 6.1

Let $\mathbb {F}(+,\cdot ,\le )$ be an Archimedean ordered field, $Y(+)$ be a group, $D\subseteq \mathbb {F}_{+}^{2}$ be a well-chained, nonempty, open set. Let $f:D_{x+y}\rightarrow Y$, $g:D_{xy}\rightarrow Y$, $h:D_{x}\rightarrow Y$, $k:D_{y}\rightarrow Y$ such that

$$\begin{aligned} f(x+y)+g(xy)=h(x)+k(y) \quad ((x,y)\in D). \end{aligned}$$

(15)

Find the general solution of Eq. (15).