1 Introduction

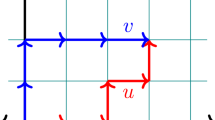
By definition, a bargraph is a non-intersecting lattice path in \(\mathbb {N}_0^2\) with three allowable steps: up (0, 1), down \((0,-1)\) and horizontal (1, 0). An up step may not immediately follow a down step nor vice versa. A bargraph starts at the origin with an up step and terminates immediately upon return to the x-axis. We consider bargraphs defined by semi-perimeter. The well-known generating function B(x, y) for these is given by

$$\begin{aligned} B(x,y)=\frac{1-x-y-xy-\sqrt{(1-x-y-xy)^2-4x^2y}}{2x}, \end{aligned}$$
(1)

where y tracks the number of up steps and x tracks the number of horizontal steps. See for example [2, 4]. Replacing both x and y by z in this generating function results in z then tracking the semi-perimeter. The focus, however, of this paper is to provide generating functions for the prefixes of such bargraphs and their various extensions. A bargraph prefix follows all rules for bargraphs except that it is allowed to terminate at any height before the path reaches height 0. Prefix generating functions for various types of lattice paths have been recently studied in various papers by Prodinger and other authors, for example, see [1, 9,10,11,12,13]. As originally defined, bargraphs only end on a first return (with a down step) to the x-axis. Prefixes, however may end at any height and with any of the possible steps. So our first bargraph extension is Sect. 2, which studies prefixes that end in any of the three allowed steps according to semi-perimeter as defined for the original bargraphs. We refine this in Sect. 4 where we track all the up, down and horizontal steps separately in the generating functions. In the original bargraph definition the number of up steps is the same as the number of down steps but this is no longer true for prefixes. The final natural extension is studied in Sect. 5, where the bargraph definition is extended to allow bargraphs to go into negative territory. Asymptotics (as the lengths of the paths tend to infinity), for the number of paths as well as the average end height are studied in Sects. 3, 4.1 and 5.1.

2 Bargraph prefixes that end in each of the three allowed steps

Let the generating function for bargraph prefixes that end at height i and where the last step is respectively an up, horizontal or down step be given respectively by \(f_i\), \(h_i\) and \(g_i\). Each of these generating functions track the number of up and horizontal steps in the prefix by z. In line with the definition of semi-perimeter, the number of down steps is not tracked in this section. To begin we write down a system of equations that expresses each of \(f_i\), \(h_i\) and \(g_i\) in terms of these same functions but where the latter are expressed in terms of the second last step. According to the definition of a bargraph an up step followed by a down step or vice-versa is disallowed. Therefore our equations for \(f_i\) and \(g_i\) do not depend in the last step on a different level version of each other. Hence we obtain for \(i\ge 1\):

$$\begin{aligned} f_0(z)=1; \ f_i(z)=zf_{i-1}(z)+zh_{i-1}(z). \end{aligned}$$
(2)

And for \(i\ge 1\)

$$\begin{aligned} h_0(z)=0;\ h_i(z)=zf_i(z)+zh_i(z)+zg_i(z). \end{aligned}$$
(3)

And for \(i\ge 0\)

$$\begin{aligned} g_i(z)=h_{i+1}(z)+g_{i+1}(z). \end{aligned}$$
(4)

Note that \(h_0(z)=0\), since horizontal steps on the x-axis are forbidden.

Next, we define bivariate generating functions:

$$\begin{aligned} F(z,u):=\sum _{i\ge 0} f_i(z)u^i, \ G(z,u):=\sum _{i\ge 0} g_i(z)u^i, \ H(z,u):=\sum _{i\ge 0} h_i(z)u^i, \end{aligned}$$

in which u tracks the height of the endpoint of the final step.

Summing the recursions for \(i\ge 0\), we obtain

$$\begin{aligned} F(z,u)=1+\sum _{i\ge 1} (zf_{i-1}(z)+zh_{i-1}(z))u^i; \\ G(z,u)=\sum _{i\ge 0}(h_{i+1}(z)+g_{i+1}(z))u^i; \\ H(z,u)=\sum _{i\ge 1}( zf_i(z)+zh_i(z)+zg_i(z))u^i. \end{aligned}$$

So

$$\begin{aligned} F(z,u)=1+zu F(z,u)+zu H(z,u), \\ G(z,u)=\frac{1}{u}(H(z,u)+G(z,u)-g_0(z)) \end{aligned}$$

and

$$\begin{aligned} H( z,u)=z(F(z,u)-1+H(z,u)+G(z,u)-g_0(z)). \end{aligned}$$

Solving these equations simultaneously, we obtain the following solutions:

$$\begin{aligned} F(z,u)= & {} -\frac{-1+u-u z+u z^2-u^2 z^2-u^2 z^2 G(z,0)}{1-u+u^2 z-u z^2}, \end{aligned}$$
(5)
$$\begin{aligned} G(z,u)= & {} -\frac{u z^2-G(z,0)+u z G(z,0)+u z^2 G(z,0)}{1-u+u^2 z-u z^2} \end{aligned}$$
(6)

and

$$\begin{aligned} H(z,u)=-\frac{u z (-z+u z-G(z,0)+u z G(z,0))}{1-u+u^2 z-u z^2}. \end{aligned}$$
(7)

Factorizing these denominators we obtain

$$\begin{aligned} 1-u+u^2 z-u z^2=z(u-u_0)(u-u_1) \end{aligned}$$
(8)

where

$$\begin{aligned} u_0=\frac{1+z^2-\sqrt{1-4 z+2 z^2+z^4}}{2 z}; \ u_1=\frac{1+z^2+\sqrt{1-4 z+2 z^2+z^4}}{2 z}. \end{aligned}$$

Cross multiplying Eq. (6) by the denominator on the right hand side and then setting \(u=u_0\), we can then solve for G(z, 0) to obtain

$$\begin{aligned} G(z,0)=\frac{1-2 z-z^2-\sqrt{1-4 z+2 z^2+z^4}}{2 z}. \end{aligned}$$
(9)

This is the generating function for bargraphs of semi perimeter n since a path ends with a down step at height zero only at the end of a complete bargraph path.

Next, we eliminate G(z, 0) from Eqs. (5), (6) and (7) by substituting Eq. (9) into these. Putting \(X=1-4 z+2 z^2+z^4\) we obtain:

$$\begin{aligned}{} & {} F(z,u)=\frac{2-u^2 z \left( -1+\sqrt{X}+z^2\right) -2 u\left( 1-z+z^2\right) }{2(1-u+u^2 z-u z^2)} \end{aligned}$$
(10)
$$\begin{aligned}{} & {} G(z,u)=\nonumber \\{} & {} \frac{1-\sqrt{X}+\left( -2+u \left( -1+\sqrt{X}\right) \right) z+\left( -1+u+u \sqrt{X}\right) z^2+u z^3+u z^4}{2 z \left( 1-u+u^2 z-u z^2\right) } \nonumber \\ \end{aligned}$$
(11)
$$\begin{aligned}{} & {} H(z,u)=\frac{u \left( 1-\sqrt{X}+\left( -2+u \left( -1+\sqrt{X}\right) \right) z+z^2+u z^3\right) }{2(1-u+u^2 z-u z^2)}. \end{aligned}$$
(12)

Following the kernel method as explained by Prodinger in [8], we see that the “bad” factor \((u-u_0)\rightarrow 0\) in the denominator as \(z, u\rightarrow 0\). But the full expansions in Eqs. (10), (11) and (12) must converge and have a series expansion around \((z,u)=(0,0)\). This is the essence of the kernel method and implies that the bad factor is an exact factor of the numerator (i.e., divides into the numerator without remainder). So, we divide the bad factor from the numerator to obtain

$$\begin{aligned} F(z,u)= & {} -\frac{1+\sqrt{X}+z^2+u z \left( -1+\sqrt{X}+z^2\right) }{2z (u-u_1)}, \end{aligned}$$
(13)
$$\begin{aligned} G(z,u)= & {} \frac{\left( -1+\sqrt{X}\right) z+\left( 1+\sqrt{X}\right) z^2+z^3+z^4}{2 z^2 (u-u_1)} \end{aligned}$$
(14)

and

$$\begin{aligned} H(z,u)= \frac{u \left( -1+z^2+\sqrt{X}\right) }{2 (u-u_1)}. \end{aligned}$$
(15)

Now adding together Eqs. (13), (14) and (15) we obtain the prefix generating function \(S(z,u):=F(z,u)+G(z,u)+H(z,u)\) given by

$$\begin{aligned} S(z,u)= \frac{-2+z+\sqrt{X} z+z^3}{2 (u-u_1) z}= -\frac{-2+z+\sqrt{X} z+z^3}{1+\sqrt{X}-2 u z+z^2}. \end{aligned}$$
(16)

We can also extract the coefficient of \(u^j\) in S(z, u)

$$\begin{aligned} s_j:=[u^j] \frac{2-z-\sqrt{X} z-z^3}{2 u_1\left( 1- (u/u_1)\right) z}=\frac{2-z-\sqrt{X} z-z^3}{2 u_1^{j+1} z} \end{aligned}$$
(17)

which gives the number of bargraph prefixes ending at height j. From this we find, for example, that

$$\begin{aligned}{} & {} s_0(z)=1+g_0(z)=\frac{1-z^2-\sqrt{1-4 z+2 z^2+z^4}}{2 z}, \\{} & {} s_1(z)=\frac{1-2 z+z^2-\sqrt{1-4 z+2 z^2+z^4}}{2 z},\\{} & {} s_2(z)=-\frac{-1+3 z-2 z^2+z^3-z^4+\left( 1-z+z^2\right) \sqrt{1-4 z+2 z^2+z^4}}{2 z} \end{aligned}$$

and

$$\begin{aligned}{} & {} s_3(z)=\frac{1-4 z+5 z^2-5 z^3+3 z^4-z^5+z^6+\left( -1+2 z-2 z^2+z^3-z^4\right) \sqrt{X}}{2 z}, \end{aligned}$$

where X is as before.

If we do not specify the end of the paths, in other words we sum over all \(j\ge 0\), then at the level of generating functions this is very easy, since we only have to set \(u:= 1\) in S(u). We find

$$\begin{aligned} S(1)=\frac{2-z-\sqrt{X} z-z^3}{\sqrt{X}+(1-z)^2}=\frac{1-z-z^2-z^3-(1+z) \sqrt{1-4 z+2 z^2+z^4}}{2 z^2}. \end{aligned}$$

This has the series expansion

$$\begin{aligned}{} & {} 1+z+3 z^2+\mathbf{7 z^3}+18 z^4+48 z^5+132 z^6+372 z^7+1069 z^8+3121 z^9\\{} & {} \quad +9232 z^{10}+27610 z^{11}+O\left( z^{12}\right) . \end{aligned}$$

For example, the bold term represents the seven possible paths, each with a total of 3 up or horizontal steps:

$$\begin{aligned} \text {uuu, uuh, uuhd, uuhdd, uhu, uhh, uhhd} \end{aligned}$$

where \(\text {u}\), \(\text {h}\) and \(\text {d}\) respectively represent up, horizontal and down steps. As stated at the outset of this section, the length of the path is the number of up and horizontal steps only. The above series is not in OEIS, [14].

3 Asymptotics for average end height of bargraph prefixes

From Eq. (1), the generating function that counts all bargraphs is given by

$$\begin{aligned} B(z,z)=\frac{1-2z-z^2-\sqrt{1-4z+2z^2+z^4}}{2z}, \end{aligned}$$
(18)

where z counts the number of up and horizontal steps, i.e., the semi-perimeter, (see, for example, [6, 7]).

The asymptotics of the coefficient of \(z^n\) in B(z, z) was considered in [3], and in order to compute it, the dominant singularity \(\rho \) is the positive root of \(1-4z+2z^2+z^4=0\). By singularity analysis (for example, see Chapter 6 in [5]), we have

$$\begin{aligned}{}[z^n]B(z,z)\sim \frac{1}{2}\sqrt{\frac{1-\rho -\rho ^3}{\pi \rho n^3}}\rho ^{-n} \end{aligned}$$
(19)

with

$$\begin{aligned} \rho =\frac{1}{3}\left( -1-\frac{2^{8/3}}{(13+3\sqrt{3})^{1/3}}+2^{1/3}(13+3\sqrt{33})^{1/3}\right) \approx 0.295598\cdots . \end{aligned}$$
(20)

Similarly, we have

$$\begin{aligned}{}[z^n]S(1)\sim \frac{1+\rho }{2\rho }\sqrt{\frac{1-\rho -\rho ^3}{\pi \rho n^3}}\rho ^{-n}. \end{aligned}$$
(21)

Next, we do the asymptotics for the sum of the end heights of bargraph prefixes. This is given by

$$\begin{aligned} \frac{\partial }{\partial u}S(z,u)\Big |_{u=1}= \frac{1-3 z+z^3+z^4-\left( 1-z-z^2\right) \sqrt{1-4 z+2 z^2+z^4}}{2 (1-z) z^3}.\qquad \end{aligned}$$
(22)

Now

$$\begin{aligned}{}[z^n]\frac{\partial }{\partial u}S(z,u)\Big |_{u=1}\sim \frac{1-\rho -\rho ^2}{2\rho ^2(1-\rho )}\sqrt{\frac{1-\rho -\rho ^3}{\pi \rho n^3}}\rho ^{-n}. \end{aligned}$$
(23)

Dividing Eqs. (23) by (21) we obtain

Theorem 1

The average end height of a bargraph prefix tends to

$$\begin{aligned} \frac{1-\rho -\rho ^2}{\rho \left( 1-\rho ^2\right) }=2.28723\cdots \end{aligned}$$

as \(n \rightarrow \infty \).

4 Tracking horizontal and down steps in bargraph prefixes

Unlike bargraphs, which must end on the x-axis, prefixes may end at any positive height and this implies that the numbers of up and down steps are not equal. Hence we want to track these variables separately. We use an approach similar to that in Sect. 2 where now variable y tracks the number of up steps, v tracks the number of horizontal steps and w tracks the number of down steps. Later we will set \(y=v=w=z\) and thus measure prefixes by the total length, unlike in Sect. 2.

As before we let \(f_i:=f_i(y,v,w)\), \(h_i:=h_i(y,v,w)\) and \(g_i:=g_i(y,v,w)\) be the generating functions for prefixes ending at height i with the last step being respectively an up, horizontal or down step. Also, as before the bargraph definition requires that it begins at the origin with an up step. We obtain the following generating functions: For \(i\ge 1\)

$$\begin{aligned} f_0=1; \ f_i=yf_{i-1}+yh_{i-1}. \end{aligned}$$
(24)

And for \(i\ge 1\)

$$\begin{aligned} h_0=0;\ h_i=vf_i+vh_i+vg_i. \end{aligned}$$
(25)

And for \(i\ge 0\)

$$\begin{aligned} g_i=wh_{i+1}+wg_{i+1}. \end{aligned}$$
(26)

Next, we define multivariate generating functions:

$$\begin{aligned} F(u):=\sum _{i\ge 0} f_i(y,v,w)u^i, \ G(u):=\sum _{i\ge 0} g_i(y,v,w)u^i, \ H(u):=\sum _{i\ge 0} h_i(y,v,w)u^i, \end{aligned}$$

in which u tracks the height of the endpoint of the final step. Note that for brevity we have suppressed the variables y, v, w when we use any of F(u), G(u) and H(u).

Summing the recursions for \(i\ge 0\), we obtain

$$\begin{aligned} F(u)=1+\sum _{i\ge 1} (yf_{i-1}+yh_{i-1})u^i; \\ G(u)=\sum _{i\ge 0}(wh_{i+1}+wg_{i+1})u^i;\\ H(u)=\sum _{i\ge 1}( vf_i+vh_i+vg_i)u^i. \end{aligned}$$

So

$$\begin{aligned} F(u)=1+yu F(u)+yu H(u), \\ G(u)=\frac{w}{u}(H(u)+G(u)-g_0) \end{aligned}$$

and

$$\begin{aligned} H(u)=v(F(u)-1+H(u)+G(u)-g_0). \end{aligned}$$

Solving these equations simultaneously, we obtain the following solutions:

$$\begin{aligned} F(u)= & {} -\frac{u-u v-w-u^2 v y+u v w y-u^2 v y G(0)}{-u+u v+w+u^2 y-u w y-u v w y}, \end{aligned}$$
(27)
$$\begin{aligned} G(u)= & {} -\frac{u v w y-w G(0)+u w y G(0)+u v w y G(0)}{-u+u v+w+u^2 y-u w y-u v w y} \end{aligned}$$
(28)

and

$$\begin{aligned} H(u)=-\frac{u (u v y-v w y-v G(0)+u v y G(0))}{-u+u v+w+u^2 y-u w y-u v w y}. \end{aligned}$$
(29)

Factorizing these denominators we obtain

$$\begin{aligned} -u+u v+w+u^2 y-u w y-u v w y=y(u-u_0)(u-u_1) \end{aligned}$$
(30)

where

$$\begin{aligned} u_0=\frac{1-v+w y+v w y-\sqrt{-4 w y+(-1+v-w y-v w y)^2}}{2y};\\ u_1=\frac{1-v+w y+v w y+\sqrt{-4 w y+(-1+v-w y-v w y)^2}}{2y}. \end{aligned}$$

Cross multiplying Eq. (28) by the denominator on the right hand side and then setting \(u=u_0\), we can then solve for G(0) to obtain

$$\begin{aligned} G(0)=\frac{1-v-w y-v w y-\sqrt{-4 w y+(1+w y+v (-1+w y))^2}}{2 v}. \end{aligned}$$
(31)

Putting \(w=1\) and \(v=y=z\) we obtain the semi-perimeter generating function in Eq. (18) as expected.

Next, we eliminate G(0) from Eqs. (27), (28) and (29) by substituting Eq. (31) into these. Putting \(X=-4 w y+(1+w y+v (-1+w y))^2\) we obtain:

$$\begin{aligned}{} & {} F(u)=-\frac{-2 w-u^2 y+u^2 \sqrt{X} y+u^2 w y^2+u^2 v y (-1+w y)+2 u (1+v (-1+w y))}{2 \left( -u+u v+w+u^2 y-u w y-u v w y\right) }, \nonumber \\ \end{aligned}$$
(32)
$$\begin{aligned}&G(u)= -\frac{w \left( v-u v \sqrt{X} y+u v^2 y (1-w y)-(-1+u y) \left( -1+\sqrt{X}+w y\right) +v w \left( y-2 u y^2\right) \right) }{2 v \left( -u+u v+w+u^2 y-u w y-u v w y\right) } \nonumber \\ \end{aligned}$$
(33)

and

$$\begin{aligned}{} & {} H(u)=-\frac{-u \sqrt{X} (-1+u y)-u (1-u y+w y (-1+u y)+v (1+u y) (-1+w y))}{2 \left( -u+u v+w+u^2 y-u w y-u v w y\right) }. \end{aligned}$$
(34)

We define \(S(u):=F(u)+G(u)+H(u)\) and obtain

$$\begin{aligned} S(u)&=\frac{w \left( -1+\sqrt{X}+w y+v (-1+w y)\right) }{2 v \left( u-w-u^2 y+u w y+u v (-1+w y)\right) }\nonumber \\&-\frac{u \left( v^2 (-1+w y)^2+w y \left( -1+\sqrt{X}+w y\right) +v (-1+w y) \left( 1+\sqrt{X}+2 w y\right) \right) }{2 v \left( u-w-u^2 y+u w y+u v (-1+w y)\right) } . \end{aligned}$$
(35)

Using the kernel method on S(u), the “bad factor” \(u-u_0\) in the denominator divides exactly into the numerator (i.e., without remainder) to give:

$$\begin{aligned}{} & {} S(u)=\frac{v^2 (-1+w y)^2+w y \left( -1+\sqrt{X}+w y\right) +v (-1+w y) \left( 1+\sqrt{X}+2 w y\right) }{2 v y \left( u-u_1\right) }.\qquad \end{aligned}$$
(36)

We now extract the coefficient \(s_j:=[u^j]S(u)\):

$$\begin{aligned}{} & {} s_j=-\frac{v^2 (-1+w y)^2+w y \left( -1+\sqrt{X}+w y\right) +v (-1+w y) \left( 1+\sqrt{X}+2 w y\right) }{2 v y u_0^{j+1}}, \qquad \end{aligned}$$
(37)

which gives the number of bargraph prefixes ending at height j. From this we find, for example, that

$$\begin{aligned}{} & {} s_0=-\frac{v^2 (-1+w y)^2+w y \left( -1+\sqrt{X}+w y\right) +v (-1+w y) \left( 1+\sqrt{X}+2 w y\right) }{v \left( 1-v+\sqrt{X}+w y+v w y\right) }, \\{} & {} s_1=-\frac{2 y \left( v^2 (-1+w y)^2+w y \left( -1+\sqrt{X}+w y\right) +v (-1+w y) \left( 1+\sqrt{X}+2 w y\right) \right) }{v \left( 1-v+\sqrt{X}+w y+v w y\right) ^2} \end{aligned}$$

and

$$\begin{aligned}{} & {} s_2 =-\frac{4 y^2 \left( v^2 (-1+w y)^2+w y \left( -1+\sqrt{X}+w y\right) +v (-1+w y) \left( 1+\sqrt{X}+2 w y\right) \right) }{v \left( 1-v+\sqrt{X}+w y+v w y\right) ^3} \end{aligned}$$

where \(X=-4 w y+(1+w y+v (-1+w y))^2\) as before.

Next, we set y, w and v equal to z and thus obtain the generating function for bargraph prefixes ending at heights 0, 1 and 2 where we track the total length by z:

$$\begin{aligned} s_0=\frac{1+z-z^2-z^3-\sqrt{1-2 z-z^2-z^4+2 z^5+z^6}}{2 z}, \end{aligned}$$
(38)

with series beginning

$$\begin{aligned}{} & {} 1+z^3+z^4+2 z^5+4 z^6+8 z^7+16 z^8+33 z^9+69 z^{10}+146 z^{11}+312 z^{12}\\{} & {} \quad +O\left( z^{13}\right) \end{aligned}$$

which is sequence A004149 in [14]. Also by removing the last down step in the path which ends at height 0, we see that \(s_0=1-z^2+z s_1\) and therefore

$$\begin{aligned} s_1=z+\frac{s_0-1}{z}. \end{aligned}$$

Next,

$$\begin{aligned} s_2=\frac{1-2 z+z^3-2 z^4+z^5+z^6+\left( -1+z-z^3\right) \sqrt{1-2 z-z^2-z^4+2 z^5+z^6}}{2 z^3}. \end{aligned}$$

The coefficient sequence for \(s_2\) is not in OEIS [14].

If we do not specify the end of the paths, in other words we sum over all \(j\ge 0\), then at the level of generating functions, we only have to set \(u:= 1\) in Eq. (36), (as well as \(y=w=v=z\)). We find

$$\begin{aligned} S(1)=-\frac{1}{2}z(1+z)-\frac{(2+z) \sqrt{1-2 z-z^2-z^4+2 z^5+z^6}}{2 \left( -1+2 z+z^2\right) }. \end{aligned}$$
(39)

This has the series expansion

$$\begin{aligned}{} & {} 1+z+2 z^2+5 z^3+\mathbf{10 z^4}+22 z^5+49 z^6+110 z^7+249 z^8+568 z^9+1303 z^{10}\\{} & {} \quad +3003 z^{11}+6948 z^{12}+O\left( z^{13}\right) . \end{aligned}$$

For example, the bold term represents the ten possible paths, each with a total of 4 allowed steps of types up, horizontal and down:

$$\begin{aligned} \text {{uuuu},{uuhu},{uhuu},{uhhu},{uuuh},{uuhh},{uhuh}, {uhhh},{uuhd},{uhhd}}. \end{aligned}$$

The sequence is not in OEIS [14].

4.1 Asymptotics for \(s_0\) and S(1)

We note that \(-1+\sqrt{2}\) is the dominant singularity in Eqs. (38) and (39). From the generating function for \(s_0\) given in (38), we find using singularity analysis (see [5]) that

$$\begin{aligned}{}[z^n]s_0\sim \frac{\sqrt{3-2 \sqrt{2}}}{\sqrt{\pi n^3}}\left( 1+\sqrt{2}\right) ^{n+\frac{1}{2}} \end{aligned}$$

and from the generating function for S(1) in Eq. (39), we find that

$$\begin{aligned}{}[z^n]S(1)=\frac{\sqrt{3-2 \sqrt{2}}}{\sqrt{2 \pi n}}\left( 1+\sqrt{2}\right) ^{n+\frac{3}{2}}, \end{aligned}$$
(40)

as \(n\rightarrow \infty .\)

Next, we repeat the asymptotics for the sum of the end heights of bargraph prefixes, this time counting down steps as part of the path length. This is given by the derivative of Eq. (36) evaluated at \(u=1\):

$$\begin{aligned} \frac{\partial }{\partial u}S(z,u)\Big |_{u=1}= \frac{1+z-z^2-z^3-\sqrt{1-2 z-z^2-z^4+2 z^5+z^6}}{2 \left( 1-3 z+z^2+z^3\right) }. \end{aligned}$$
(41)

Now

$$\begin{aligned}{}[z^n]\frac{\partial }{\partial u}S(z,u)\Big |_{u=1}\sim \frac{\left( 1+\sqrt{2}\right) ^{n+1}}{2 \sqrt{2}}. \end{aligned}$$
(42)

Dividing Eqs. (42) by (40) we obtain

Theorem 2

The average end height of a bargraph prefix (measured by total length) is asymptotic to

$$\begin{aligned} \frac{1}{2} \sqrt{\big (1+\sqrt{2}\big ) \pi n }\approx 1.376996\sqrt{n} \end{aligned}$$

as \(n \rightarrow \infty \).

5 Bargraphs that can go into negative territory

These are non-intersecting lattice paths which consist of up (0, 1), down \((0,-1)\) or horizontal (1, 0) steps which end on the x-axis with any of these steps and which may begin at the origin with any of these steps. Let the generating function for such bargraph prefixes that end at height i and where the last step is respectively an up, horizontal or down step be given respectively by \(f_i\), \(h_i\) and \(g_i\). Each of these generating functions track the number of up, horizontal and down steps in the prefix by z. From these definitions we deduce the following equations:

For all integers i

$$\begin{aligned} f_i(z)= & {} [[i=0]]+zf_{i-1}(z)+zh_{i-1}(z), \end{aligned}$$
(43)
$$\begin{aligned} h_i(z)= & {} -z[[i=0]]+zf_i(z)+zh_i(z)+zg_i(z) \end{aligned}$$
(44)

and

$$\begin{aligned} g_i(z)=[[i=0]]+z h_{i+1}(z)+z g_{i+1}(z), \end{aligned}$$
(45)

where the Iverson brackets above represent the required initial conditions ensuring that the prefixes can start at the origin with any of the three allowed steps.

Note that by symmetry if \(i\ge 0\),

$$\begin{aligned} f_i(z)=g_{-i}(z), \ g_i(z)=f_{-i}(z), \ h_i(z)=h_{-i}(z). \end{aligned}$$

For this reason, we only consider the bivariate generating functions defined below for non-negative ending heights i.

$$\begin{aligned} F(z,u):=\sum _{i\ge 0} f_i(z)u^i, \ G(z,u):=\sum _{i\ge 0} g_i(z)u^i, \ H(z,u):=\sum _{i\ge 0} h_i(z)u^i. \end{aligned}$$

Multiplying the f, g, h equations by \(u^i\) and summing for \(i\ge 0\), we obtain

$$\begin{aligned} F(z,u)-f_0(z)= & {} zuF(z,u)+zuH(z,u), \end{aligned}$$
(46)
$$\begin{aligned} H(z,u)= & {} -z+zF(u,z)+zH(z,u)+zG(z,u) \end{aligned}$$
(47)

and

$$\begin{aligned} G(z,u)=1+\frac{z}{u} (H(z,u)-h_0(z))+\frac{z}{u} (G(z,u)-g_0(z)). \end{aligned}$$
(48)

By symmetry, \(f_0(z)=g_0(z)\). Also note that \(F(z,0)=f_0(z); \ G(z,0)=g_0(z); \ H(z,0)=h_0(z). \) Henceforth, we will use the following abbreviations \(F(0)=F(z,0); \ G(0)=G(z,0); \ H(0)=H(z,0). \)

Simultaneously solving Eqs. (46), (47) and (48), we obtain

$$\begin{aligned}{} & {} F(z,u)=\frac{u z^3+u F(0)-z F(0)-u z F(0)-u z^3 F(0)-u z^3 H(0)}{u-z-u z-u^2 z-u z^2+u z^3}, \end{aligned}$$
(49)
$$\begin{aligned}{} & {} G(z,u)=\frac{u-u z-u^2 z-z^2+u z^3-\left( z-2 z^2-u z^2\right) F(0)-\left( z-z^2-u z^2\right) H(0)}{u-z-u z-u^2 z-u z^2+u z^3} \nonumber \\ \end{aligned}$$
(50)

and

$$\begin{aligned} H(z,u)= \frac{z \left( z-u z^2+u F(0)-2 z F(0)+u z^2 F(0)-z H(0)+u z^2 H(0)\right) }{u-z-u z-u^2 z-u z^2+u z^3}.\nonumber \\ \end{aligned}$$
(51)

The kernel or denominator of these equations factorises as

$$\begin{aligned} u-z-u z-u^2 z-u z^2+u z^3=-z(u-r_1)(u-r_2), \end{aligned}$$
(52)

where

$$\begin{aligned} r_1=\frac{1-z+z^2+z^3-\sqrt{1-2 z-z^2-z^4+2 z^5+z^6}}{2 z} \end{aligned}$$
(53)

and

$$\begin{aligned} r_2=\frac{1-z+z^2+z^3+\sqrt{1-2 z-z^2-z^4+2 z^5+z^6}}{2 z}. \end{aligned}$$
(54)

Using the kernel method, the “bad factor” \(u-r_1\) in the denominator divides exactly into the numerator (i.e., without remainder) to give:

$$\begin{aligned} F(z,u)= & {} \frac{-z^3-F(0)+z F(0)+z^3 F(0)+z^3 H(0)}{z \left( u-r_2\right) }, \end{aligned}$$
(55)
$$\begin{aligned} G(z,u)= & {} \frac{z u+\left( -1+z+r_1 z-z^3-z^2 F(0)-z^2 H(0)\right) }{z \left( u-r_2\right) } \end{aligned}$$
(56)

and

$$\begin{aligned} H(z,u)=-\frac{-z^2+F(0)+z^2 F(0)+z^2 H(0)}{u-r_2}. \end{aligned}$$
(57)

Now we may substitute \(u=0\) into Eqs. (55) and (57) to obtain

$$\begin{aligned} F(0)=-\frac{z^3 (-1+H(0))}{-1+z+r_2 z+z^3} \end{aligned}$$
(58)

and

$$\begin{aligned} H(0)=\frac{-z^2+F(0)+z^2 F(0)}{r_2-z^2}. \end{aligned}$$
(59)

Solving these simultaneously gives

$$\begin{aligned} F(0)= \frac{1}{2} \left( 1+\frac{(1-z) \sqrt{1-2 z-z^2-z^4+2 z^5+z^6}}{1-2 z-2 z^3-z^4}\right) \end{aligned}$$
(60)

and

$$\begin{aligned} H(0)=\frac{z \sqrt{1-2 z-z^2-z^4+2 z^5+z^6}}{1-2 z-2 z^3-z^4}. \end{aligned}$$
(61)

Note that by definition H(0) is the generating function for the lattice paths under consideration which end on the x-axis with a horizontal step. Removing this end step means that we have a generating function for such lattice paths that end on the x-axis with any of the allowed steps, i.e., the generating function \(F(0)+ G(0)+H(0)-1\). The term \(-1\) arises here, because the initial conditions reflected by the Iverson brackets in Eqs. (43) and (45) enables us to start with either an up or a down step but we don’t wish this to be duplicated in the combined generating function. Thus we have

$$\begin{aligned} F(0)+G(0)+H(0)-1=\frac{H(0)}{z}=\frac{\sqrt{1-2 z-z^2-z^4+2 z^5+z^6}}{1-2 z-2 z^3-z^4}. \end{aligned}$$
(62)

The series obtained from this is A136029 in OEIS [14] and is described equivalently as the number of one-sided n-step prudent walks, starting from (0,0) and ending on the y-axis, with east, west and north steps.

Next we obtain the generating functions F(z, u), G(z, u) and H(z, u) for all such lattice paths that may end at any positive height, tracked by the variable u. We do this by substituting Eqs. (58) and (61) into Eqs. (55), (56) and (57). We obtain

$$\begin{aligned}{} & {} F(z,u) \nonumber \\{} & {} =\frac{\left( 1-2 z+z^2-z^3-z^4\right) \sqrt{Y}+1-3 z+2 z^2-z^3-z^4+z^5-2 z^6-z^7}{2 \left( -1+2 z+2 z^3+z^4\right) z (u-{r_2})}, \nonumber \\ \end{aligned}$$
(63)

where

$$\begin{aligned} Y=1-2 z-z^2-z^4+2 z^5+z^6. \end{aligned}$$

For the rest of this section, Y will be used as this abbreviation. Also

$$\begin{aligned} G(z,u){=} \frac{1}{2 z (u-{r_2})}\left( {-}1{+}z{+}2 u z{-}z^3{-}\frac{\left( -1+2 z-z^2+z^3+z^4\right) \sqrt{Y}}{-1+2 z{+}2 z^3+z^4}\right) \nonumber \\ \end{aligned}$$
(64)

and

$$\begin{aligned} H(z,u)= \frac{\left( 1-z+z^2+z^3\right) \sqrt{Y}+1-2 z-z^2-z^4+2 z^5+z^6}{2 \left( -1+2 z+2 z^3+z^4\right) (u-{r_2})}. \end{aligned}$$
(65)

Eventually, from \(S(z,u):=F(z,u)+G(z,u)+H(z,u)-1\) we obtain the bivariate prefix generating function for all such lattice paths ending at non-negative height tracked by u. This is

$$\begin{aligned} S(z,u)=\frac{\sqrt{Y} \left( -2+3 z-z^2+z^3+z^4\right) +\left( 2-(1+2 u) z+z^3\right) \left( -1+2 z+2 z^3+z^4\right) }{2 (u-r_2) z \left( 1-2 z-2 z^3-z^4\right) }. \nonumber \\ \end{aligned}$$
(66)

Now setting \(u=1\), we obtain the univariate prefix generating function abbreviated as \(S(1):=S(z,1)\) for all such lattice paths ending at non-negative height. We call these paths generalised bargraph prefixes. The generating function for these is:

$$\begin{aligned} S(1)=\frac{1+ z+z^2+ z^3+\sqrt{1-2 z-z^2-z^4+2 z^5+z^6}}{2-4 z-4 z^3-2 z^4}. \end{aligned}$$
(67)

The series expansion for this begins as

$$\begin{aligned} S(1)= & {} 1+2 z+4 z^2+10 z^3+24 z^4+57 z^5+136 z^6+326 z^7 \nonumber \\{} & {} +782 z^8+1877 z^9+4509 z^{10}. \end{aligned}$$
(68)

By symmetry the generating function for paths ending at any positive or negative height is \(2S(1)-S(0)\). This gives the generating function

$$\begin{aligned} G(z):=\frac{1+z}{1-2z-z^2} \end{aligned}$$
(69)

which is A001333 in [14] and has an equivalent description as the number of n step non-self-intersecting paths starting at (0, 0) with steps of types (1, 0), \((-1, 0)\) or (0, 1).

We can also extract the coefficient of \(u^j\) for \(j\ge 1\) in S(z, u):

$$\begin{aligned} s_j:=[u^j] S(z,u)=\frac{1}{2} \left( -2+\frac{2-z+z^3}{z r_2}+\frac{\sqrt{Y} \left( -2+3 z-z^2+z^3+z^4\right) }{z \left( -1+2 z+2 z^3+z^4\right) r_2}\right) r_2^{-j} \nonumber \\ \end{aligned}$$
(70)

which gives the number of such lattice path prefixes ending at height j. From this we find, for example, that

$$\begin{aligned} s_1=\frac{-1+2 z+z^2+z^4-2 z^5-z^6+\left( 1-z+z^2+z^3\right) \sqrt{1-2 z-z^2-z^4+2 z^5+z^6}}{2 z \left( 1-2 z-2 z^3-z^4\right) } \nonumber \\ \end{aligned}$$
(71)

which has a series which begins as

$$\begin{aligned} s_1= & {} z+2 z^2+3 z^3+6 z^4+14 z^5+32 z^6+72 z^7+164 z^8+377 z^9\\{} & {} +870 z^{10}+2014 z^{11}. \end{aligned}$$

Also

$$\begin{aligned} s_2=\frac{2-6 z+4 z^2-8 z^4+4 z^5-4 z^6+6 z^8+2 z^9-2 \sqrt{Y} \left( 1-2 z+z^2-z^4+2 z^5+z^6\right) }{4 z^2 \left( -1+2 z+2 z^3+z^4\right) } \nonumber \\ \end{aligned}$$
(72)

which has a series which begins as

$$\begin{aligned} s_2=z^2+3 z^3+6 z^4+12 z^5+27 z^6+63 z^7+146 z^8+338 z^9+786 z^{10}+1834 z^{11}. \end{aligned}$$

The series expansions of Eqs. (67), (71) and (72) which are explicitly given above are not currently found in [14].

5.1 Asymptotics for S(0), S(1) and G(z)

Once again \(-1+\sqrt{2}\) is the dominant singularity from Eqs. (62), (67) and (69). By singularity analysis, from the generating function for \(S(0)-1\) given in (62), we find that as \(n \rightarrow \infty \),

$$\begin{aligned}{}[z^n]S(0) \sim \frac{\sqrt{3-2 \sqrt{2}}}{2 \sqrt{\pi n}}\left( 1+\sqrt{2}\right) ^{n+\frac{3}{2}}. \end{aligned}$$
(73)

Similarly from Eqs. (67) and (69), we obtain

$$\begin{aligned}{}[z^n]2S[1]\sim [z^n]G(z)\sim \frac{1}{2} \left( 1+\sqrt{2}\right) ^{n+1}, \end{aligned}$$
(74)

as \(n \rightarrow \infty \).

By symmetry, the expected end height for paths counted by G(z) is zero. It remains to determine the average end height of non-negative paths as counted by S(1) in Eq. (67).

For the total end height we require the derivative of Eq. (66) evaluated at \(u=1\):

$$\begin{aligned} \frac{\partial }{\partial u}S(z,u)\Big |_{u=1}= \frac{z \sqrt{1-2 z-z^2-z^4+2 z^5+z^6}}{(1-z) \left( 1+z^2\right) \left( 1-2 z-z^2\right) ^2}. \end{aligned}$$
(75)

Again by singularity analysis,

$$\begin{aligned}{}[z^n]\frac{\partial }{\partial u}S(z,u)\Big |_{u=1}\sim 2 \sqrt{\frac{-8+6 \sqrt{2}}{\pi }} \left( 1+\sqrt{2}\right) ^{n-\frac{1}{2}}\sqrt{n}. \end{aligned}$$
(76)

Dividing Eq. (76) by half of the right hand side of Eq. (74) we obtain

Theorem 3

The average end height of generalised bargraph prefixes (measured by total length) is asymptotic to

$$\begin{aligned} 8 \sqrt{20-14 \sqrt{2}} \left( \sqrt{2}-1\right) \sqrt{\frac{n}{\pi }}\approx 0.838201\sqrt{n} \end{aligned}$$

as \(n \rightarrow \infty \).