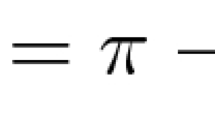When is a spherical body of constant diameter of constant width?

Abstract

We prove that a smooth convex body of diameter $\delta < \frac{\pi }{2}$ on the d-dimensional unit sphere $S^d$ is of constant diameter $\delta$ if and only if it is of constant width $\delta$. We also show this equivalence for all convex bodies on $S^2$. Since, as shown earlier, the equivalence on $S^d$ is true for every $\delta \ge \frac{\pi }{2}$, the question whether spherical bodies of constant diameter and constant width on $S^d$ coincide remains open for non-smooth bodies on $S^d$, where $d\ge 3$.

1 Introduction

The subject of this paper belongs to spherical geometry. For a larger context see the monographs [2, 9] and [10].

In the next section we recall the notions of a spherical convex body and of a spherical convex body of constant width. Shortly speaking, by a body of constant width on the d-dimensional unit sphere $S^d$ we mean a spherical convex body all of whose widths are equal (see [5] and [7]). Here by the width ofC determined by a supporting hemisphere K of C we understand the thickness of any narrowest lune $K \cap K^*$, where $K^*$ is a different hemisphere, containing C. In [8] the notion of the spherical body of constant width is considered in the larger context of bodies of constant width in other spaces.

Let $C \subset S^d$ be a convex body of diameter $\delta$. If the spherical distance |pq| of points $p, q \in C$ is $\delta$, we call pq a diametral chord of C and we say that p, q are diametrically opposed points ofC. Clearly, $p, q \in \mathrm{bd}(C)$.

After Part 4 of [7] we say that a convex body $D \subset S^d$ of diameter $\delta$ is of constant diameter$\delta$ provided for every point $p \in \mathrm{bd}(D)$ there exists at least one point $p' \in \mathrm{bd}(D)$ such that $|pp'| = \delta$ (in other words, that $pp'$ is a diametral chord of D). For the analogous notion of a body of constant diameter in $E^d$ see [1].

In this paper, in order to point out that a body is of constant diameter we denote it by D, and not by C, which is used for arbitrary convex bodies on $S^d$.

Recall that in Theorem 5 of [7] it is proved that an arbitrary convex body on $S^d$ of diameter $\delta \ge \frac{\pi }{2}$ is of constant diameter if and only if it is a body of constant width $\delta$. Moreover, it is shown that the “if” part holds also for $\delta < \frac{\pi }{2}$. At the end of [7] the problem is put whether every spherical body of constant diameter $\delta < \frac{\pi }{2}$ on $S^d$ is also a body of constant width $\delta$?

In Sect. 4 we prove that a smooth convex body of diameter $\delta < \frac{\pi }{2}$ on $S^d$ is of constant diameter $\delta$ if and only if it is of constant width $\delta$. Also that this equivalence holds true for all convex bodies on $S^2$. As a consequence of these facts and those from the preceding paragraph, the above problem remains open only for non-smooth bodies of diameter below $\frac{\pi }{2}$ on $S^d$ with $d \ge 3$.

By the way, in [3, 4] and [6] spherical bodies of constant width and constant diameter $\frac{\pi }{2}$ are applied for the relevant task of recognizing if a Wulff shape is self-dual.

2 On spherical geometry

By $S^d$ denote the unit sphere in the $(d+1)$-dimensional Euclidean space $E^{d+1}$, where $d\ge 2$. The intersection of $S^d$ with any $(k+1)$-dimensional Euclidean space, where $0 \le k \le d-1$, is called a k-dimensional subsphere of$S^d$. For $k=1$ we call it a great circle, and for $k=0$ a pair of antipodes. If different points $a, b \in S^d$ are not antipodes, by the arcab connecting them we mean that part of the great circle containing a and b, which does not contain any pair of antipodes. By the spherical distance |ab|, or shortly distance, of these points we understand the length of the arc connecting them.

By a d-dimensional spherical ball of radius$\rho \in (0, {\frac{\pi }{2}}]$, or shorter a ball, we mean the set of points of $S^d$ which are at a distance at most $\rho$ from a fixed point, called the center of this ball. For $d=2$ it is called a disk, and its boundary is called a circle of radius$\delta$. Spherical balls of radius $\frac{\pi }{2}$ are called hemispheres. In other words, by a hemisphere of $S^d$ we mean the common part of $S^d$ with any closed half-space of $E^{d+1}$. We denote by H(c) the hemisphere whose center is c. Two hemispheres whose centers are antipodes are called opposite hemispheres.

By a spherical $(d-1)$-dimensional ball of radius$\rho \in (0, {\frac{\pi }{2}}]$ we mean the set of points of a $(d-1)$-dimensional great sphere of $S^d$ at a distance at most $\rho$ from a point, called the center of this ball. The $(d-1)$-dimensional balls of radius $\frac{\pi }{2}$ are called $(d-1)$-dimensional hemispheres.

Let a set $C \subset S^d$ not contain any pair of antipodes. We say that C is convex if together with every two of its points, C contains the whole arc connecting them. If the interior of a closed convex set C is non-empty, we call C a convex body. Its boundary is denoted by $\mathrm{bd}(C)$.

If a hemisphere H contains a convex body C and if $p \in \mathrm{bd}(H) \cap C$, we say that HsupportsCat p or that H is a supporting hemisphere of C at p. If exactly one hemisphere supports a convex body C at its boundary point p, we say that p is a smooth point of$\mathrm{bd}(C)$, and in the opposite case we say that p is an acute point of$\mathrm{bd}(C)$. If every boundary point of $C \subset S^d$ is smooth, then C is called smooth. We call Cstrictly convex if $\mathrm{bd}(C)$ does not contain any arc.

If hemispheres G and H of $S^d$ are different and not opposite, then $L = G \cap H$ is called a lune of $S^d$. This notion is considered in many books and papers. The parts of $\mathrm{bd}(G)$ and $\mathrm{bd}(H)$ contained in $G\cap H$ are denoted by G/H and H/G, respectively. By the thickness $\Delta (L)$of the lune$L = G \cap H \subset S^d$ we mean the spherical distance of the centers of the $(d-1)$-dimensional hemispheres G/H and H/G.

For any convex body $C \subset S^d$ and any hemisphere K supporting C we define the width $\mathrm{width}_K (C)$of Cdetermined byK as the thickness of any narrowest lune $K \cap K^*$ containing C (so that no lune of the form $K \cap K'$ with a smaller thickness contains C). By the thickness$\Delta (C)$ of C we mean the minimum of $\mathrm{width}_K (C)$ over all hemispheres K supporting C. Clearly, $\Delta (C)$ is nothing else but the thickness of a “narrowest” lune containing C. We say that C is of constant widthw if all its widths $\mathrm{width}_K (C)$ are equal to w.

The above notions are given and a few properties of lunes and convex bodies in $S^d$ are presented in [5] and [7].

Lemma

Let K be a hemisphere of $S^d$ and let $p \in \mathrm{bd}(K)$. Moreover, let $pq \subset K$ be an arc orthogonal to $\mathrm{bd}(K)$ with q in the interior of K and $|pq| < \frac{\pi }{2}$. Then amongst all the lunes of the form $K \cap M$, with q in the boundary of the hemisphere M, only the lune $K \cap K_\dashv$ such that pq is orthogonal to $\mathrm{bd}(K_\dashv )$ at q has the smallest thickness.

Proof

Denote by m the center of M/K. Observe that $m \in K \setminus M$. Consequently, $|pm| \ge |pq|$ with equality only when m coincides with q. Since $\Delta (K\cap M) = |pm|$ and $\Delta (K\cap K_\dashv ) = |pq|$, we conclude that only the lune $K \cap K_\dashv$ is of the smallest thickness amongst all our lunes $K \cap M$. $\square$

3 Spherical bodies of constant diameter

The notion of a spherical body of constant diameter is recalled in the Introduction. In this section we present a few propositions on bodies of constant diameter.

Proposition 1

Every convex body $D \subset S^d$ of constant diameter $\delta < \frac{\pi }{2}$ is strictly convex.

Proof

Assume the opposite that D is not strictly convex. Then $\mathrm{bd}(D)$ contains an arc xz. Denote its midpoint by y. Clearly, $y \in \mathrm{bd}(D)$. Since D is of constant diameter $\delta$, there is a point $y' \in \mathrm{bd}(D)$ such that $|yy'| = \delta$. This, $y \in xz$ and $\delta < \frac{\pi }{2}$ imply that $|y'x| > \delta$ or $|y'z| > \delta$. Thus $\mathrm{diam}(D) > \delta$ in contradiction to the fact that D is of constant diameter $\delta$. Consequently, D is strictly convex.

$\square$

Proposition 2

Let $D \subset S^2$ be a body of constant diameter. Then every two diametral chords of D intersect.

Proof

Denote the diameter of D by $\delta$. Suppose that some diametral chords ab and cd of D do not intersect (let for instance a, b, d, c be in this order on $\mathrm{bd}(D)$). Then abdc is a convex spherical non-degenerate quadrangle. Hence ad and bc intersect at exactly one point. Denote it by x. Since $|ab|= \delta$ and $|cd|= \delta$, by the triangle inequality we get $|ax| + |xb| \ge \delta$ and $|cx| + |xd| \ge \delta$. What is more, since $x \not \in ab$ and $x \not \in cd$, we get $|ax| + |xb| > \delta$ and $|cx| + |xd| > \delta$. This leads to $|ax| + |xb| + |cx| + |xd| > 2\delta$. So $|ax| + |xd| > \delta$ or $|cx| + |xb| > \delta$. In other words, $|ad| > \delta$ or $|bc| > \delta$ in contradiction to $\mathrm{diam}(D) = \delta$. Consequently, every two diametral chords of D intersect. $\square$

Proposition 3

If a hemisphere K supports a convex body $D \subset S^d$ of constant diameter $\delta < \frac{\pi }{2}$ at a smooth point of its boundary, then $\mathrm{width}_K (D) = \delta$.

Proof

Let p be a smooth point of $\mathrm{bd}(D)$ (see Fig. 1). Since D is of constant diameter, there exists a diametrally opposed point $p' \in \mathrm{bd}(D)$. Hence the ball B of radius $\delta$ and center $p'$ contains D. Clearly, $p \in \mathrm{bd}(B)$.

Since p is a smooth point of $\mathrm{bd}(D)$, we see that K is the only supporting hemisphere of D at p. Consequently, the hemisphere K supports the ball B at p.

From $\mathrm{diam}(D) = \delta$ and $p' \in \mathrm{bd}(D)$ we see that the spherical ball $B'$ of radius $\delta$ centered at p contains D and supports it at $p'$.

Denote by $K'$ the hemisphere supporting $B'$ at $p'$. Clearly, we have $D \subset B \cap B' \subset K \cap K'$.

Since our chord $pp'$ of length $\delta$ is orthogonal to $\mathrm{bd}(K)$ at p and to $\mathrm{bd}(K')$ at $p'$, by the definition of the thickness of a lune we see that the lune $K \cap K'$ has thickness $|pp'|= \delta$. Consequently, by $D \subset K \cap K'$ we conclude that $\mathrm{width}_K (D) \le \delta$.

By the Lemma the lune $K \cap K'$ is the narrowest lune from the family ${\mathcal L}_1$ of lunes of the form $K \cap M$ with $p' \in \mathrm{bd}(M)$ containing $pp'$. From $pp' \subset D \subset K \cap K'$ we conclude that $K \cap K'$ is also the narrowest lune from the family ${\mathcal L}_2$ of all lunes of the form $K \cap M$ containing D. Since every lune from ${\mathcal L}_2$ contains a lune from ${\mathcal L}_1$, every lune from ${\mathcal L}_2$ is of thickness at least $\delta$. Consequently, $\mathrm{width}_K (D) \ge \delta$.

From the above two paragraphs we conclude that $\mathrm{width}_K (D) = \delta$. $\square$

Fig. 1

Illustration to the Proof of Proposition 3

4 Two cases in which spherical convex bodies of constant diameter are of constant width

Since the question is answered for $\delta \ge \frac{\pi }{2}$ and since, as mentioned in the Introduction, every spherical body of constant width is of constant diameter, now we concentrate on checking when a spherical body of constant diameter $\delta < \frac{\pi }{2}$ is of constant width. The following theorem gives a partial answer. It results immediately from Proposition 3 and from the fact that every body of constant width $\delta$ is of constant diameter $\delta$.

Theorem 1

Let $0< \delta < \frac{\pi }{2}$. A spherical smooth convex body on $S^d$ is of constant diameter $\delta$ if and only if it is of constant width $\delta$.

Below is our main theorem. Since in its proof we apply polar sets, let us recall this notion. For a convex body $C \subset S^d$ by its polar we mean the set $C^\circ = \{r: \ C \subset H(r)\}$. It is known that $C^\circ$ is a convex body. Recall that $\mathrm{bd}(C^\circ )$ is the set of points r such that H(r) is a supporting hemisphere of C.

Theorem 2

Let $0< \delta < \frac{\pi }{2}$. A convex body on the two-dimensional sphere is of constant diameter $\delta$ if and only it is of constant width $\delta$.

Proof

In the first part of Theorem 5 of [7] it is shown that every body of constant width on $S^d$ is a body of constant diameter.

It remains to show that every body $D \subset S^2$ of constant diameter $\delta < \frac{\pi }{2}$ is of constant width $\delta$, i.e., that $\mathrm{width}_K (D) = \delta$ for every supporting hemisphere K of D.

By Proposition 1 there is exactly one point p of support of D by K.

When p is a smooth point of $\mathrm{bd}(D)$, then we apply Proposition 3.

Consider the case when p is an acute point of $\mathrm{bd}(D)$. Denote by $H_1=H(r_1)$ the first supporting hemisphere and by $H_2 = H(r_2)$ the last supporting hemisphere of D at p, as we go counterclockwise with the center r of H(r) on $\mathrm{bd}(D^\circ )$, see Fig. 2.

For $i=1,2$ provide the arc $pp_i \subset H_i$ of length $\delta$ orthogonal to $\mathrm{bd}(H_i)$ at p. So $p_i \in pr_i$ for $i=1,2$. By $B_i$ denote the disc of radius $\delta$ centered at $p_i$, where $i=1,2$.

Of course, $D \subset B_1 \cap B_2 \subset H_1 \cap H_2$.

Consider the piece P of the circle with center p and radius $\delta$ when we go counterclockwise from $p_1$ to $p_2$. Denote by $s_i$ the point of $\mathrm{bd}(D)$ in the arc $pp_i$, where $i=1,2$, and by S the piece of $\mathrm{bd}(D)$, when going counterclockwise from $s_1$ to $s_2$. Take any $s \in S$. There exists a diametrally opposed point $s'$ of D in $\mathrm{bd}(D)$. By Proposition 2 the diametral chord $ss'$ intersects the diametral chords $pp_1$ and $pp_2$. Consequently, $s'$ must be at p. This and $|ss'| = \delta$ imply that $s \in P$, which means that the whole P is in the boundary of D.

Fig. 2

Illustration to the proof of Theorem 2

Consequently, for every hemisphere H supporting D at p the chord of D orthogonal to H at p is a diametral chord of D. Thus by the Lemma we get $\mathrm{width}_H (D) = \delta$ also if p is an acute point of $\mathrm{bd}(D)$.

We see that $\mathrm{width}_K (D) = \delta$ both when K supports D at a smooth and acute boundary point of $\mathrm{bd}(D)$, as required. $\square$

By the proof of Theorem 2 and also Proposition 3 any supporting hemisphere $H = H(r)$ of D determines a unique diametral chord $pp'$ of D; it is orthogonal to the great circle bounding H. Moreover, the center r of H belongs to $\mathrm{bd}(D^\circ )$. On the other hand, take any $r \in \mathrm{bd}(D^\circ )$. Then H(r) supports D at exactly one point p. Clearly, $D \subset H(r)$. Consequently, for any body $D \subset S^2$ we have a one-to-one correspondence between the following objects:

• the supporting hemispheres of D,

• the points of $\mathrm{bd}(D^\circ )$,

• the diametral chords of D.

Every position of a diametral chord is determined by a supporting hemisphere of D. It is also determined by a point of $\mathrm{bd}(D^\circ )$; still such a point r determines exactly one point p, and the considered diametral chord is in the arc $pp'$.

A forthcoming paper is devoted to showing analogous facts as in Propositions 1–3 and Theorems 1 and 2 for any diameter $\delta >0$ in the Euclidean space (we conjecture that they are also true in the hyperbolic space). The proofs of these analogous statements apply parallelism, which does not make sense here on the sphere.