Exceptional Dehn Surgeries on Some Infinite Series of Hyperbolic Knots and Links

Abstract

We study closed connected orientable 3-manifolds obtained by Dehn surgery along the oriented components of a link, introduced and considered by Motegi and Song (2005) and Ichihara et al. (2008). For such manifolds, we find a finite balanced group presentation of the fundamental group and describe exceptional surgeries. This allows us to construct an infinite family of tunnel number one strongly invertible hyperbolic knots with three parameters, which admit toroidal surgeries and Seifert fibered surgeries. Among the obtained results, we mention that for every integer $n >5$ there are infinitely many hyperbolic knots in the 3–sphere, whose $(n-2)$ and $(n+1)$-surgeries are toroidal, and $(n-1)$ and n-surgeries are Seifert fibered.

1 Introduction

Dehn surgery on links with rational coefficients is a basic method for constructing closed connected orientable 3-manifolds. In the early 1960’, Lickorish [17] proved that all such manifolds can be obtained by Dehn surgeries on links in the oriented 3-sphere. Kirby [16] and Rolfsen [33] found an equivalence relation on the class of all links with rational coefficients with the property that two such links are equivalent if and only if they represent the same surgery manifold. If the link is hyperbolic, then the Thurston–Jorgensen theory [38] of hyperbolic surgery implies that the resulting manifolds are hyperbolic for almost all surgery coefficients. Non-hyperbolic surgeries are called exceptional, as they can produce reducible manifolds, Seifert manifolds, lens spaces (possibly, including the 3-sphere), or closed 3-manifolds which contain incompressible tori (that is, toroidal manifolds).

A Dehn surgery is called a Seifert fibering surgery if it yields a Seifert fibered manifold. See [29] for a basic reference on Seifert manifolds. It has been conjectured that nontrivial Seifert fibering surgeries on knots in the oriented 3-sphere are integral surgeries unless the knot is a trivial knot, or a torus knot, or a cable of a torus knot. This conjecture has been proved for 2-bridge knots by Brittenham and Wu [6], for satellite knots by Miyazaki and Motegi [20,21,22] and Boyer and Zhang [5], and for hyperbolic alternating knots by Ichihara [13]. Motegi and Song [27] proved that for each integer n, there exists a tunnel number one hyperbolic knot $K_n$ in the oriented 3-sphere such that the n-surgery on $K_n$ produces a small Seifert fibered space (with at most three exceptional fibers). Miyazaki and Motegi [23] showed that if a periodic knot K in the 3-sphere yields a Seifert fibered space by Dehn surgery, then the quotient of K by the group action generated by any periodic map of K is a torus knot (except for a special case).

A knot in the oriented 3-sphere is called an L-space knot if it admits a nontrivial Dehn surgery yielding a lens space (possibly, including the standard 3-sphere). Concrete examples of infinitely many hyperbolic L-space knots have been described by several authors. See, for example, [7, 11, 26], and [28].

A further conjecture states that a hyperbolic knot admits at most three Dehn surgeries which yield closed toroidal 3-manifolds. Teragaito [35, 36] proved that there exist infinitely many hyperbolic knots which attain the conjectural maximum number. Interestingly, those toroidal surgeries correspond to consecutive integers. Successively, Teragaito [37] proved that for any positive even integer m, there exists a hyperbolic knot such that its longitudinal Dehn surgery yields a closed toroidal 3-manifold containing a unique separating incompressible torus, which meets the core of the attached solid torus in m points minimally. Ichihara et al. [14] provided a complete description of the exceptional surgeries on pretzel knots of type $(-2, p, p)$ with $p \ge 5$. Such a knot admits a unique surgery yielding a toroidal 3-manifold with a unique incompressible torus. On the other hand, all such pretzel knots have not Seifert fibered surgeries.

Infinite family of hyperbolic (1, 1)-knots having exceptional Dehn surgeries has been described in [10]. Miyazaki and Motegi [27] showed that an arbitrary knot can be deformed into a hyperbolic knot with no exceptional surgeries by a single crossing change. Applications of Dehn surgery theory to codimension two PL embeddings of spheres and peripheral acyclicity in 3-manifolds can be found in Cencelj et al. [12] and Repovš [31], respectively.

In this paper we study the closed orientable manifolds obtained by Dehn surgeries on the components of a link, first considered by Motegi and Song in [27] (see also [15]). Then we derive some applications on the exceptional surgeries on a 3-parametrized family of hyperbolic knots. The obtained results extend and complete those given in the quoted papers. Among them, we show that for every integer $n >5$ there are infinitely many tunnel number one hyperbolic knots in the oriented 3-sphere whose $(n-1)$- and n-surgeries are small Seifert fibered spaces and $(n-2)$- and $(n + 1)$-surgeries are toroidal graph manifolds. Furthermore, we also construct infinitely many tunnel number one strongly invertible hyperbolic knots in the oriented 3-sphere whose $-1$ and 1-surgeries give toroidal graph manifolds, and 0-surgery gives a Seifert fiber space over ${\mathbb {S}}^2$ with exactly three exceptional fibers. The proofs are based on the combinatorial representations of closed manifolds by spines and surgery on framed links. Spines and surgery descriptions of graph manifolds are discussed in a recent paper of the authors [8], which is most valuable to derive the results presented here.

2 Dehn surgeries on the Motegi-Song link

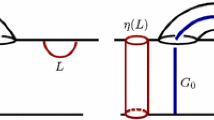
In this section, we consider the closed connected orientable 3–manifolds $M=L(r/s; 1/k; 1/h; q/p)$ obtained by doing Dehn surgeries on the oriented components of the link $L={{\textbf{k}}} \cup t_1 \cup t_2 \cup {{\textbf{c}}}$ illustrated in Fig. 1.

Fig. 1

Dehn surgery description of the manifolds $M=L(r/s; 1/k; 1/h; q/p)$

This link was first considered by Motegi and Song in [27] and Ichihara et al. in [15]; each component of L is a trivial knot in the standard 3–sphere. Of course, we assume that the surgery along each component of L is not trivial $(\ne \infty )$, and that (r, s) and (q, p) are pairs of coprime integers.

Now we determine a finite balanced presentation for the fundamental group of M. A Wirtinger presentation of the link group $\pi (L) \cong \pi _1({\mathbb {S}}^3 {\setminus } L)$ has generators x, y, z, w and relations $x^{-1}wx=zxz^{-1}x^{-1}w$, $yw=x^{-1}wxy$ and $yz=zwyw^{-1}$. The meridians ${\textbf{m}}_i$ and the longitudes ${\varvec{\ell }}_i$ of the oriented components of L are:

$$\begin{aligned} \begin{aligned} {\textbf{c}}: \quad {\textbf{m}}_0=x \qquad \qquad \qquad {\varvec{\ell }}_0&=x^{-1}w^{-1} x z \\ {\textbf{k}}: \quad {\textbf{m}}_1=y \qquad \qquad \qquad {\varvec{\ell }}_1&=w^{-1} z^{-1} \\ t_1: \quad {\textbf{m}}_2=z \qquad \qquad \qquad {\varvec{\ell }}_2&=y^{-1}x^{-1} w x w^{-1} x = w y^{-1}w^{-1} x \\ t_2: \quad {\textbf{m}}_3=w \qquad \qquad \qquad {\varvec{\ell }}_3&=y^{-1}x^{-1} \end{aligned} \end{aligned}$$

where $[{\textbf{m}}_i,{\varvec{\ell }}_i]=1$, for every $i=0,1,2,3$.

A finite presentation for the fundamental group $\pi _1(M)$ of the surgery manifold $M=L(r/s; 1/k; 1/h; q/p)$ is obtained from that of $\pi (L)$ by adding the relations

$$\begin{aligned} {\textbf{m}}_0^q {\varvec{\ell }}_0^p=1 \qquad {\textbf{m}}_1^r {\varvec{\ell }}_1^s=1 \qquad {\textbf{m}}_2 {\varvec{\ell }}_2^k=1 \qquad {\textbf{m}}_3 {\varvec{\ell }}_3^h=1. \end{aligned}$$

Now we improve the presentation of $\pi _1(M)$. Since the integers of the pairs (q, p) and (r, s) are coprime, there are integer pairs $(\alpha , \beta )$ and $(\gamma , \delta )$ such that $p \alpha -\beta q=1$ and $s \gamma -r \delta =1$.

Let us define

$$\begin{aligned} \begin{aligned} a:= {\textbf{m}}_0^{\alpha } {\varvec{\ell }}_0^{\beta } \qquad \qquad&c:= {\textbf{m}}_2 {\varvec{\ell }}_2^{\xi } \\ b:= {\textbf{m}}_1^{\gamma } {\varvec{\ell }}_1^{\delta } \qquad \qquad&d:={\textbf{m}}_3 {\varvec{\ell }}_3^{\eta } \end{aligned} \end{aligned}$$

where $\xi =k-1$ and $\eta =h-1$.

Then we have

$$\begin{aligned} \begin{aligned} a^p&= ( {\textbf{m}}_0^{\alpha } {\varvec{\ell }}_0^{\beta })^p= {\textbf{m}}_0 {\textbf{m}}_0^{\beta q} {\varvec{\ell }}_0^{\beta p}= {\textbf{m}}_0 ( {\textbf{m}}_0^{q} {\varvec{\ell }}_0^{p})^{\beta }={\textbf{m}}_0=x \\ b^s&= ( {\textbf{m}}_1^{\gamma } {\varvec{\ell }}_1^{\delta })^s={\textbf{m}}_1 {\textbf{m}}_1^{\delta r} {\varvec{\ell }}_1^{\delta s}= {\textbf{m}}_1 ( {\textbf{m}}_1^{r} {\varvec{\ell }}_1^{s})^{\delta }={\textbf{m}}_1=y \\ c^k&= ( {\textbf{m}}_2 {\varvec{\ell }}_2^{\xi })^k= {\textbf{m}}_2 {\textbf{m}}_2^{\xi } {\varvec{\ell }}_2^{\xi k}= {\textbf{m}}_2 ( {\textbf{m}}_2 {\varvec{\ell }}_2^{k})^{\xi }={\textbf{m}}_2=z \\ d^h&= ( {\textbf{m}}_3 {\varvec{\ell }}_3^{\eta })^h= {\textbf{m}}_3 {\textbf{m}}_3^{\eta } {\varvec{\ell }}_3^{\eta h}= {\textbf{m}}_3 ( {\textbf{m}}_3 {\varvec{\ell }}_3^{h})^{\eta }={\textbf{m}}_3=w \\ a^{- q}&= ( {\textbf{m}}_0^{\alpha } {\varvec{\ell }}_0^{\beta })^{-q}= {\textbf{m}}_0^{-\alpha q} {\varvec{\ell }}_0^{-\alpha p} {\varvec{\ell }}_0= ( {\textbf{m}}_0^{q} {\varvec{\ell }}_0^{p})^{-\alpha } {\varvec{\ell }}_0= {\varvec{\ell }}_0 \\ b^{-r}&= ( {\textbf{m}}_1^{\gamma } {\varvec{\ell }}_1^{\delta })^{-r}= {\textbf{m}}_1^{-\gamma r} {\varvec{\ell }}_1^{-\gamma s} {\varvec{\ell }}_1= ( {\textbf{m}}_1^{r} {\varvec{\ell }}_1^{s})^{-\gamma } {\varvec{\ell }}_1= {\varvec{\ell }}_1 \\ c^{-1}&= ( {\textbf{m}}_2 {\varvec{\ell }}_2^{\xi })^{-1}= {\textbf{m}}_2^{-1} {\varvec{\ell }}_2^{-k} {\varvec{\ell }}_2= ( {\textbf{m}}_2 {\varvec{\ell }}_2^{k})^{-1} {\varvec{\ell }}_2= {\varvec{\ell }}_2 \\ d^{-1}&= ( {\textbf{m}}_3 {\varvec{\ell }}_3^{\eta })^{-1}= {\textbf{m}}_3^{-1} {\varvec{\ell }}_3^{-h} {\varvec{\ell }}_3= ( {\textbf{m}}_3 {\varvec{\ell }}_3^{h})^{-1} {\varvec{\ell }}_3= {\varvec{\ell }}_3. \end{aligned} \end{aligned}$$

Substituting these relations into those of $\pi (L)$ and using the corresponding formulas for the longitudes ${\varvec{\ell }}_i$, $i=0,1,2,3$, we get a finite group presentation for $\pi _1(M)$ with generators a, b, c, d and relations $a^{q-p}d^{-h}a^p c^k=1$, $b^rd^{-h}c^{-k} =1$, $c^{-1}=b^{-s}a^{-p}d^h a^pd^{-h}a^p$ and $d^{-1}=b^{-s} a^{-p}$. Eliminating the generators c and d by using the last two relations yields a 2-generator group presentation for $\pi _1(M)$.

Theorem 2.1

With the above notations, the fundamental group of the surgery manifold $M=L(r/s; 1/k; 1/h; q/p)$ admits the finite balanced group presentation

$$\begin{aligned} \begin{aligned} \pi _1(M)&\cong \langle a,b :\, a^q (a^{-p}b^{-s})^h b^r (b^{-s}a^{-p})^h=1, \\&\quad b^r (b^{-s}a^{-p})^h [b^{-s} (b^s a^p)^h (b^{-s}a^{-p})^h a^p]^k=1 \rangle . \end{aligned} \end{aligned}$$

.

We determine conditions on the parameters for which the surgery manifolds are Seifert fibered or toroidal. We say that a Seifert fiber space is of type ${\mathbb {S}}^2 ((\alpha _1, \beta _1)\, (\alpha _2, \beta _2) \, (\alpha _3, \beta _3))$ if it has a Seifert fibration over the 2–sphere ${\mathbb {S}}^2$ with $\le 3$ exceptional fibers of indices $(\alpha _i, \beta _i)$, for $i=1,2,3$. This representation also includes lens spaces as a particular subclass. A compact orientable 3-manifold is called a graph manifold if it can be obtained by gluing several copies of the manifolds $D \times {\mathbb {S}}^1$ and $N \times {\mathbb {S}}^1$ together by homeomorphisms of some components of their boundaries. Here D is the 2-disk and N denotes the 2-disk with two holes. A closed connected 3-manifold is said to be toroidal if it contains an incompressible torus.

The following result from [8, 9] and [30] will be useful to classify the homeomorphism type of exceptional surgeries.

Theorem 2.2

Let M be a closed connected prime 3–manifold whose fundamental group is presented by

$$\begin{aligned} \langle x,y :\, (x^p y^q)^{t+1} y^{nu}=1, \quad (y^n x^m)^{r+1}x^{ps} =1 \rangle \end{aligned}$$

where $|p|, |n| >1$, $r,t \ge 0$, and the pairs (p, m), (n, q), $(r+1,s)$ and $(t+1,u)$ are formed by coprime integers. Then we have

• i) If $r,t >0$, then M is homeomorphic to the toroidal graph manifold defined by the invariants

  $$\begin{aligned} (D \, (p,m) \, (r+1,s)) \cup _{\begin{pmatrix} 0 &{} \quad 1 \\ 1 &{} \quad 0 \end{pmatrix}} (D\, (n,q) \, (t+1,u)). \end{aligned}$$

• ii) If $t=u=0$, then M is the Seifert fibered space of type

  $$\begin{aligned} {\mathbb {S}}^2((-r-1,s) \, (-p,m) \, (q,n)). \end{aligned}$$

Now we present the main results of the section.

Theorems 2.3, 2.4 and 2.5 provide a description of many exceptional surgeries giving Seifert fibered manifolds (including lens spaces).

Theorem 2.3

Let $M=L(r/s; 1/k; 1/h; q/p)$ be the surgery manifold obtained from the framed link L in Fig. 1. Then we have

• i) If $r=s=1$, then M is the Seifert fiber space of type

  $$\begin{aligned} {\mathbb {S}}^2((-2k+1,-k)\, (-2h+1,h-1) \, (q-p,-p)). \end{aligned}$$

• ii) If $r=0$ and $h=-1$, then M is the Seifert fiber space of type

  $$\begin{aligned} {\mathbb {S}}^2((2,1) \, (-3k+1,2k-1) \, (q-2p,-p)). \end{aligned}$$

• iii) If $r=0$ and $k=-1$, then M is the Seifert fiber space of type

  $$\begin{aligned} {\mathbb {S}}^2((2,-1) \, (3h-1,h) \, (q-2p,-p)). \end{aligned}$$

Remark

• (1) For particular values of parameters, some manifolds, listed in Theorem 2.3, may become lens spaces. For example, if $q=p+1$ and $k=1-h$ in Theorem 2.3 (i), then M is the lens space $L(\xi , \eta )$, where $\xi = |p| (2\,h-1)^2$ and $\eta =2p(2\,h-1)-1$. Again, if $p=-1$ and $q=-3$ in Theorem 2.3 (iii), then M is the lens space $L(|7h-3|,7)$.

• (2) Theorem 2.3 (i) with $p=4-n$, $q=3n-11$, $k=-2$ and $h=-1$ gives an alternative proof of Lemma 2.1 [27], that is, the resulting surgery manifold is the Seifert fiber space of type ${\mathbb {S}}^2((5,2)\, (3,-2) \, (4n-15, n-4))$. This result serves in [27] to show that for every n there is a hyperbolic knot whose n–surgery is a small Seifert manifold.

• (3) Theorem 2.3 (i) with $p=2n+2$, $q=1-(2n+1)(2n+2)$, $k=-n-1$ and $h=-n$ gives an alternative proof of Lemma 2.5 from [15], that is, the resulting surgery manifold is homeomorphic to the Seifert fiber space of type ${\mathbb {S}}^2((2n+3, n+1) \, (2n+1, -n-1) \, ((2n+1)(2n+3), 2n+2))$. This result serves in [15] to prove the existence of an infinite family of hyperbolic fibered knots in ${\mathbb {S}}^3$, each of which admits a longitudinal Seifert fibered surgery.

Proof of Theorem 2.3

i) By Theorem 1.1, $\pi _1(M)$ has a balanced group presentation with generators a, b and relations

$$\begin{aligned} a^q (a^{-p}b^{-1})^h b (b^{-1} a^{-p})^h=1 \end{aligned}$$

and

$$\begin{aligned} b(b^{-1}a^{-p})^h [b^{-1}(ba^p)^h (b^{-1}a^{-p})^h a^p]^k=1. \end{aligned}$$

Setting $x=ba^p$ and $y=a$ (with inverse relation $b=xy^{-p}$), the first relation becomes

$$\begin{aligned} y^qx^{-h}x y^{-p} (y^p x^{-1} y^{-p})^h=1, \end{aligned}$$

hence

$$\begin{aligned} y^q x^{-h} x x^{-h} y^{-p}=1 \end{aligned}$$

or, equivalently,

$$\begin{aligned} x^{2h-1}y^{p-q}=1. \end{aligned}$$

This expression coincides with the relation $(x^\textbf{p} y^\textbf{q})^{t+1} y^{nu} =1$ in Theorem 2.2 with $\textbf{p} =2\,h-1$, $\textbf{q}=p-q$ and $t=u=0$.

The second relation becomes

$$\begin{aligned} xy^{-p}(y^p x^{-1} y^{-p})^h [y^p x^{-1} x^h (y^p x^{-1} y^{-p})^hy^p]^k=1, \end{aligned}$$

hence

$$\begin{aligned} x x^{-h}y^{-p}[y^p x^{h-1}y^p x^{-h}]^k=1 \end{aligned}$$

or, equivalently,

$$\begin{aligned} x^{1-h} y^{-p}[y^p x^{h-1} y^p x^{-2h+1}x^{h-1}]^k=1. \end{aligned}$$

From the first relation $x^{-2h+1}$ commutes with x and y. Using this fact, the second relation reduces to $x^{1-h} y^{-p}(y^p x^{h-1})^{2k} x^{k(-2\,h+1)}=1$, hence

$$\begin{aligned} (y^p x^{h-1})^{2k-1} x^{k(-2h+1)} =1. \end{aligned}$$

This expression coincides with the relation $(y^nx^m)^{r+1} x^{\textbf{p}s}=1$ in Theorem 2.2 with $n=p$, $m=h-1$, $r=2k-2$, $\textbf{p}= 2\,h-1$ (see above) and $s=-k$. Now the result follows from Theorem  2.2 (ii). An alternative proof can also be obtained by drawing extended Heegaard diagrams of genus 2 which induce the group presentation with generators x, y and relations $x^{2\,h-1} y^{p-q}=1$ and $x^{k(-2\,h+1)} (y^p x^{h-1})^{2k-1}=1$. All such diagrams are 2-symmetric, that is, they admit an involution with six fixed points. Then by [4, 19, 34] the represented manifolds are 2–fold branched coverings of ${\mathbb {S}}^3$. The singular links of these branched coverings are equivalent to the Montesinos links $\textbf{m}\left( \dfrac{k}{2k-1}; \dfrac{h-1}{-2\,h+1}; \dfrac{p}{p-q}\right)$. So the result follows from [25].

ii) By Theorem 1.1, $\pi _1(M)$ has a balanced group presentation with generators a, b and relations

$$\begin{aligned} a^qb a^{2p}b=1 \end{aligned}$$

and

$$\begin{aligned} a^pb[b^{-1}a^{-p}b^{-1} a^p b a^p]^k=1. \end{aligned}$$

Setting $x=a^pba^p$ and $y=a$ (with inverse relation $b=y^{-p}x y^{-p}$), the first relation becomes

$$\begin{aligned} y^qy^{-p}x y^{-p} y^{2p} y^{-p} x y^{-p}=1, \end{aligned}$$

hence

$$\begin{aligned} x^2y^{q-2p}=1. \end{aligned}$$

This expression coincides with the relation $(x^\textbf{p} y^\textbf{q})^{t+1} y^{nu} =1$ in Theorem 2.2 with $\textbf{p} =2$, $\textbf{q}=q-2p$ and $t=u=0$.

The second relation becomes

$$\begin{aligned} y^py^{-p}x y^{-p} [y^p x^{-1} y^p y^{-p} y^p x^{-1}y^p x]^k=1, \end{aligned}$$

hence

$$\begin{aligned} x y^{-p}[y^p x^{-2}x y^p x^{-2} x y^p x]^k=1. \end{aligned}$$

From the first relation $x^{-2}$ commutes with y and x. So the second relation becomes $y^{-p}(y^p x)^{3k} x^{-4k+1}=1$, hence $(xy^p)^{3k}y^{-p} x^{-4k+1}=1$ or, equivalently, $(y^{-p} x^{-1})^{-3k+1} x^{-4k+2}=1$. This expression coincides with the relation $(y^nx^m)^{r+1} x^{\textbf{p}s}=1$ in Theorem 2.2 with $n=-p$, $m=-1$, $r=-3k$, $\textbf{p}= 2$ (see above) and $s=-2k+1$.Then the result follows from Theorem 2.2 (ii).

iii) By Theorem 1.1, $\pi _1(M)$ has a balanced group presentation with generators a, b and relations

$$\begin{aligned} a^q(a^{-p}b^{-1})^h (b^{-1} a^{-p})^h=1 \end{aligned}$$

and

$$\begin{aligned} (b^{-1}a^{-p})^h a^{-p} (a^p b)^h ( a^{-p} b^{-1})^h b=1. \end{aligned}$$

Setting $x=a$ and $y=a^pb$ (with inverse relation $b=x^{-p}y$) yields a balanced group presentation for $\pi _1(M)$ with generators x, y and relations $x^{q-2p}y^{-3h+1}=1$ and $(y^{-h}x^p)^2 x^{q-2p}=1$. The first relation coincides with $(x^\textbf{p} y^\textbf{q})^{t+1} y^{nu} =1$ in Theorem 2.2 with $\textbf{p} =q-2p$, $\textbf{q}=-3\,h+1$ and $t=u=0$. The second relation coincides with $(y^nx^m)^{r+1} x^{\textbf{p}s}=1$ in Theorem 2.2 with $n=-h$, $m=p$, $r=1$, $\textbf{p}=q- 2p$ (see above) and $s=1$. Then the result follows from Theorem 2.2 (ii). $\square$

The next two results can be proved in the same way as done for Theorem 2.3 above.

Theorem 2.4

Let us consider the surgery manifold $M=L(r/s; 1/k; 1/h; q/p)$ for $p=-1$ and $q=1$. Then we have

• i) If $r=2$ and $s=1$, then M is the Seifert fiber space (SFS) of type

  $$\begin{aligned} {\mathbb {S}}^2 ((3,-1) \, (1-h, -1) \, (k-1, k-2)). \end{aligned}$$

  If, in addition, $h=2$, then M is the lens space $L(|7k-4|, 2k-1)$.

• ii) If $r=3$ and $s=1$, then M is homeomorphic to the lens space $L(\xi , \eta )$, where $\xi =|-4kh+2(h+k)+3|$ and $\eta =2kh -k-2$.

Theorem 2.5

Let us consider the surgery manifold $M=L(r/s; 1/k; 1/h; q/p)$ for $p=-1$ and $h=2$. Then we have

• i) If $r=2$ and $s=1$, then M is the SFS of type

  $$\begin{aligned} {\mathbb {S}}^2 ((2,-1) \, (q, -1) \, (-3k+2,-k+1)). \end{aligned}$$

  If, in addition, $q=1$, then M is the lens space $L(|7k-4|, 2k-1)$.

• ii) If $r=3$ and $s=1$, then M is the SFS of type

  $$\begin{aligned} {\mathbb {S}}^2 ((2,-1) \, (3,1) \, (q(k-1)-k, 1-k)). \end{aligned}$$

  If, in addition, $q=1$, then M is the lens space $L(|6k-7|, 3k-2)$.

The next result provides a description of many exceptional surgeries along the components of the framed link L, which give toroidal graph manifolds

Theorem 2.6

Let $M=L(r/s; 1/k; 1/h; q/p)$ be the surgery manifold obtained from the framed link L in Fig. 1. Then we have

• i) If $r=0$ and $h,k, q-2p \ne \pm 1$, then M is the toroidal graph manifold defined by the invariants

  $$\begin{aligned} (D \, (k,-1) \, (-h,-2h+1)) \cup _{\begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}} (D \, (2,1) \, (q-2p,p)). \end{aligned}$$

• ii) If $r=2$, $s=1$, $h, k \ne 0,2$ and $q \ne \pm 1$, then M is the toroidal graph manifold

  $$\begin{aligned} (D\, (k-1,1) \, (1-h,1-2h)) \cup _{\begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}} (D\, (2,1) \, (q,-p)). \end{aligned}$$

• iii) If $r=-s=h=-1$ and $k,p \ne \pm 1$, then M is the toroidal graph manifold

  $$\begin{aligned} (D \, (2,-1) \, (3,1)) \cup _{\begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}} (D\, (k,1) \, (p,q-3p)). \end{aligned}$$

Proof

i) By Theorem 1.1, $\pi _1(M)$ has a balanced group presentation with generators a, b and relations

$$\begin{aligned} a^q (a^{-p}b^{-1})^h (b^{-1}a^{-p})^h=1 \\ \end{aligned}$$

and

$$\begin{aligned} (b^{-1}a^{-p})^h [b^{-1} (b a^p)^h (b^{-1}a^{-p})^h a^p]^k=1. \end{aligned}$$

Setting $x=ba^p$ and $y=a$ (with inverse relation $b=xy^{-p}$), the first relation becomes $y^q x^{-h} (y^p x^{-1} y^{-p})^h=1$, hence $y^q x^{-h} y^p x^{-h} y^{-p}=1$ or, equivalently, $(x^{-h} y^p)^2 y^{q-2p}=1$. This expression coincides with the relation $(x^{{{\textbf {p}}}} y^{{{\textbf {q}}}} )^{t+1} y^{nu}=1$ in Theorem 2.2 with ${{\textbf {p}}}=-h$, ${{\textbf {q}}}=p$, $t=1$ and $nu=q-2p$.

The second relation becomes

$$\begin{aligned} (y^px^{-1}y^{-p})^h [y^px^{-1}x^h (y^p x^{-1}y^{-p})^h y^p]^k=1, \end{aligned}$$

hence

$$\begin{aligned} y^p x^{-h} y^{-p}[y^px^{h-1} y^p x^{-h}]^k=1, \end{aligned}$$

or equivalently,

$$\begin{aligned} x^{-h}[x^{h-1} y^p x^{-h} y^p]^k=1. \end{aligned}$$

From the first relation, we have $y^px^{-h}= x^h y^{p-q}$. Substituting this expression into the second relation yields $x^{-h}(x^{2h-1} y^{2p-q})^k=1$. Taking the inverse relation gives $(y^{q-2p} x^{1-2h})^k x^h=1$. This expression coincides with the relation $(y^nx^m)^{r+1} x^{{{\textbf {p}}} s}=1$ in Theorem 2.2 with $n=q-2p$ (hence $u=1$ as $nu=q-2p$), $m=1-2\,h$, $r=k-1$ and ${{\textbf {p}}} s=h$. Since ${{\textbf {p}}}=-h$ (see above), the last relation implies $s=-1$. Now the result follows from Theorem 2.2 (i).

ii) By Theorem 1.1, $\pi _1(M)$ has a balanced group presentation with generators a, b and relations

$$\begin{aligned} a^q (a^{-p}b^{-1})^h b^2 (b^{-1}a^{-p})^h=1 \\ \end{aligned}$$

and

$$\begin{aligned} b^2(b^{-1}a^{-p})^h [b^{-1} (b a^p)^h (b^{-1}a^{-p})^h a^p]^k=1. \end{aligned}$$

Setting $x=ba^p$ and $y=a$ (with inverse relation $b=xy^{-p}$), the first relation becomes $y^q x^{-h} (xy^{-p} x y^{-p}) (y^{p} x^{-1} y^{-p})^h=1$, hence

$$\begin{aligned} y^q x^{-h+1} y^{-p} x^{-h+1} y^{-p}=1, \end{aligned}$$

or, equivalently,

$$\begin{aligned} (x^{-h+1} y^{-p})^2 y^{q}=1. \end{aligned}$$

This expression coincides with the relation $(x^{{{\textbf {p}}}} y^{{{\textbf {q}}}} )^{t+1} y^{nu}=1$ in Theorem 2.2 with ${{\textbf {p}}}=-h+1$, ${{\textbf {q}}}=-p$, $t=1$ and $nu=q$.

The second relation becomes

$$\begin{aligned} (xy^{-p})^2 (y^px^{-1}y^{-p})^h [y^px^{-1}x^h (y^p x^{-1}y^{-p})^h y^p]^k=1, \end{aligned}$$

hence

$$\begin{aligned} x y^{-p} x^{1-h} y^{-p}[y^px^{h-1} y^p x^{-h}]^k=1. \end{aligned}$$

From the first relation, we have $y^px^{h-1}= x^{1-h} y^{q-p}$. Substituting this expression into the second relation gives

$$\begin{aligned} xy^{-p} x^{1-h}y^{-p}[x^{1-h} y^{q} x^{-h} x^{1-h} x^{h-1}]^{k}=1, \end{aligned}$$

hence

$$\begin{aligned} x y^{-p}x^{1-h}y^{-p} x^{1-h} (y^q x^{1-2h})^k x^{h-1}=1, \end{aligned}$$

or, equivalently,

$$\begin{aligned} x^h y^{-p}x^{1-h}y^{-p} x^{1-h} (y^q x^{1-2h})^k =1. \end{aligned}$$

From the first relation, we have $y^{-p}x^{1-h}y^{-p}= x^{h-1} y^{-q}$. Substituting this expression into the second relation yields $x^{2h-1} y ^{-q}x^{1-h} (y^q x^{1-2h})^k=1$, hence

$$\begin{aligned} (y^q x^{1-2h})^{k-1} x^{1-h}=1. \end{aligned}$$

This expression coincides with the relation $(y^nx^m)^{r+1} x^{{{\textbf {p}}} s}=1$ in Theorem 2.2 with $n=q$ (hence $u=1$ as $nu=q$ from above), $m=1-2\,h$, $r=k-2$ and ${{\textbf {p}}} s=1-h$. Since ${{\textbf {p}}}=-h+1$ (see above), the last relation implies $s=1$. Now the result follows from Theorem 2.2 (i).

iii) By Theorem 1.1, $\pi _1(M)$ has a balanced group presentation with generators a, b and relations

$$\begin{aligned} a^q b a^p b^{-1}a^{p} b=1 \end{aligned}$$

and

$$\begin{aligned} b^{-1}a^{p} b [b^{-1} a^{-p} b^{-1 }a^{p} b a^p]^k=1. \end{aligned}$$

Setting $x=a^{-q}b^{-1}$ and $y=a$ (with inverse relation $b=x^{-1}y^{-q}$), we get a finite group presentation for $\pi _1(M)$ with generators x, y and relations $(y^px)^2 x^{-3}=1$ and $(x^3 y^{q-3p})^k y^p=1$. The first relation coincides with $(y^nx^m)^{r+1} x^{{{\textbf {p}}} s}=1$ in Theorem 2.2 with $n=p$, $m=r=1$ and ${{\textbf {p}}} s=-3$. The second relation coincides with $(x^{{{\textbf {p}}}} y^{{{\textbf {q}}}} )^{t+1} y^{nu}=1$ in Theorem 2.2 with ${{\textbf {p}}}=3$, ${{\textbf {q}}}=q-3p$, $t=k-1$ and $nu=p$. Since ${{\textbf {p}}}=3$ and $n=p$, the equations ${{\textbf {p}}} s=-3$ and $nu=p$ imply $s=-1$ and $u=1$, respectively. Then the result follows from Theorem 2.2 (i). $\square$

Fig. 2

The hyperbolic knots $K_{h,k,p}$ with $h,k <0$ and $|p| >1$ and the surgery manifolds $K_{h,k,p} (\gamma )$

3 Exceptional surgeries on hyperbolic knots

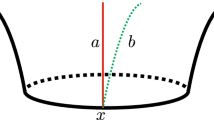
Let ${{\textbf {k}}} \cup {{\textbf {c}}}$ be the 2–bridge link given in Fig. 2, and let $K_{h,k,p}$ denote the knot obtained from ${{\textbf {k}}}$ by 1/p surgery $(p \ne 0)$ along ${{\textbf {c}}}$, that is, doing a $(-p)$-twist along ${{\textbf {c}}}$. For $h=-1$, $k=-2$ and $p=-n+4$, $K_{h,k,p}$ coincides with the knot $K_n$ considered by Motegi and Song in [27] (see also [15]), for every natural number n. Let $K_{h,k,p} (\gamma )$ be the 3-manifold obtained from ${\mathbb {S}}^3$ by $\gamma$-surgery on $K_{h,k,p}$, for every $\gamma \in {\mathbb {Q}}$, $\gamma \ne \infty$.

Lemma 3.1

With the above notations, the surgery manifold $K_{h,k,p} (\gamma )$ is homeomorphic to the manifold $M=L(r/s; 1/k; 1/h; q/p)$ from Sect. 2, where $q=1+p(h+k)$ and $r/s= \gamma +p[h-k]^2 +h+k.$

Proof

We use Kirby–Rolfsen calculus on links with rational coefficients (see [16, 32], and [33]) to give equivalent surgery descriptions of the closed connected orientable 3-manifold $K_{h,k,p} (\gamma )$. Since the linking number of ${{\textbf {c}}}$ and ${{\textbf {k}}}$ (with the orientations chosen in Fig. 2) is exactly $lk({{\textbf {c}}}, {{\textbf {k}}})=h-k$, the manifold $K_{h,k,p} (\gamma )$ has a surgery description as in Fig. 2. In fact, twist p times about the component ${{\textbf {c}}}$ gives the surgery coefficient $\gamma +p[lk ({{\textbf {c}}}, {{\textbf {k}}})]^2= \gamma +p[h-k]^2$ for the component (again denoted by ${{\textbf {k}}}$) arising from ${{\textbf {k}}}$. Furthermore, equivalent surgery descriptions of the manifold $K_{h,k,p} (\gamma )$ are given in Figs. 3 (a) and 3 (b), where $r/s= \gamma +p[h-k]^2+h+k$. Thus $K_{h,k,p} (\gamma )$ is homeomorphic to the surgery manifold $M=L(r/s; 1/k; 1/h; q/p)$, where $q=1+p(h+k)$ and $r/s= \gamma +p[h-k]^2+h+k$. Of course, if $\gamma \in {\mathbb {Z}}$, we can take the integers $r=\gamma +p[h-k]^2+h+k$ and $s=1$. $\square$

Fig. 3

Equivalent surgery descriptions of $K_{h,k,p}(\gamma )$

Lemma 3.2

• i) For any $h,k <0$ and $|p| >1$, the knots $K_{h,k,p}$ are hyperbolic;

• ii) For any $h,k <0$ and $p \ne 0$, the knots $K_{h,k,p}$ have tunnel number one. In particular, they are strongly invertible.

Proof

• i) We extend the proof of Lemma 2.2 in [27], where the case $h=-1$, $k=-2$ and $p=-n+4$ has been considered. The knot $K_{h,k,p}$ is obtained from the component ${{\textbf {k}}}$ of the 2-bridge link ${{\textbf {k}}} \cup {{\textbf {c}}}= {{\textbf {b}}}(\alpha , \beta )$ where $\alpha /\beta =[2\,h-1, -2k+1]=2\,h-1+1/(2k-1)$, by twisting along the other component ${{\textbf {c}}}$. Since the above 2-bridge link is not a (2, m)-torus link, it is a hyperbolic link by [19]. By the hypothesis $|p|>1$, it follows from [1, Theorem 1.1] (see also [3, Theorem 1.2] or [2, Theorem 2]) that $K_{h,k,p}$ is a hyperbolic knot.

• ii) We can use the same argument of Lemma 2.3 in [27] (case $h=-1$, $k=-2$ and $p=-n+4$). In fact, ${{\textbf {k}}} \cup {{\textbf {c}}}$ is a 2-bridge link, hence it has tunnel number one. Since ${{\textbf {c}}}$ is unknotted, Claim 2.4 of [27] states that every knot obtained from ${{\textbf {k}}}$ by twisting along ${{\textbf {c}}}$ has tunnel number at most one. Since $K_{h,k,p}$, for any $h,k<0$ and $p \ne 0$, is knotted in ${\mathbb {S}}^3$, the tunnel number of $K_{h,k,p}$ is one. So $K_{h,k,p}$ is embedded in a genus 2 Heegaard surface of ${\mathbb {S}}^3$ so that it does not separate the Heegaard surface. (In fact, if $K_{h,k,p}$ is separating in the Heegaard surface, it has a cyclic period 2 rather than the strong inversion.) This implies that $K_{h,k,p}$ is strongly invertible.

$\square$

The following result generalizes Lemma 2.1 of [27] ($h=-1, k=-2, p=-n+4$, hence $\gamma =n$) and Lemmas 2.4 and 2.5 of [15] ($h=-n, k=-n-1, p=2n+2$, hence $\gamma =0$). From Theorem 2.3 of Sect. 2, we obtain the following consequences

Theorem 3.3

Let $K_{h,k,p}(\gamma )$ be the surgery manifold obtained by $\gamma$-surgery along the knot $K_{h,k,p}$ in Fig. 2. Then we have

• i) If $\gamma =-p[h-k]^2-h-k+1$, then $K_{h,k,p}(\gamma )$ is the Seifert fiber space of type

  $$\begin{aligned} {\mathbb {S}}^2 ((-2k+1, -k) \, (-2h+1, h-1) \, (1+(h+k-1)p, -p)). \end{aligned}$$

• ii) If $h=-1$ and $\gamma =-p[k+1]^2-k+1$, then $K_{h,k,p}(\gamma )$ is the Seifert fiber space of type

  $$\begin{aligned} {\mathbb {S}}^2 ((2,1) \, (-3k+1, 2k-1) \, (1+(k-3)p, -p)). \end{aligned}$$

• iii) If $k=-1$ and $\gamma =-p[h+1]^2-h+1$, then $K_{h,k,p}(\gamma )$ is the Seifert fiber space of type

  $$\begin{aligned} {\mathbb {S}}^2 ((2,-1) \, (3h-1,h) \, (1+(h-3)p, -p)). \end{aligned}$$

  .

From Theorem 2.6 of Sect. 2 we get the following consequences

Theorem 3.4

Let $K_{h,k,p}(\gamma )$ be the surgery manifold obtained by $\gamma$-surgery along the knot $K_{h,k,p}$ in Fig. 2. Then we have

• i) If $h,k \ne \pm 1$, $1+p(h+k-2) \ne \pm 1$ and $\gamma =-p[h-k]^2-h-k$, then $K_{h,k,p}(\gamma )$ is the toroidal graph manifold

  $$\begin{aligned} (D \, (k,-1) \, (-h,-2h+1)) \cup _{\begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}} (D \, (2,1) \, (1+p(h+k-2),p)). \end{aligned}$$

• ii) If $h,k \ne 0,2$, $1+p(h+k) \ne \pm 1$ and $\gamma =2-p[h-k]^2-h-k$, then $K_{h,k,p}(\gamma )$ is the toroidal graph manifold

  $$\begin{aligned} (D \, (k-1,1) \, (1-h,1-2h)) \cup _{\begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}} (D \, (2,1) \, (1+p(h+k),-p)). \end{aligned}$$

• iii) If $h =-1$, $k,p \ne \pm 1$, and $\gamma =-p[k+1]^2-k$, then $K_{h,k,p}(\gamma )$ is the toroidal graph manifold

  $$\begin{aligned} (D \, (2,-1) \, (3,1)) \cup _{\begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}} (D \, (k,1) \, (p,1+p(k-4))). \end{aligned}$$

Let us consider the hyperbolic knots $K_n$ in [27], that is, $K_n=K_{h,k,p}$ for $h=-1$, $k=-2$ and $p=-n+4$, $n \ne 3,4,5$. The following theorem completes the result given in [27]:

Theorem 3.5

Let $K_{n}(\gamma )$ be the surgery manifold obtained by $\gamma$-surgery $\gamma \ne \infty$, $\gamma \in {\mathbb {Q}}$ along the hyperbolic knot $K_{n}$ $n \ne 3,4,5$. Then we have

• i) If $\gamma =n-2$, then $K_{n}(\gamma )$ is homeomorphic to the toroidal graph manifold

  $$\begin{aligned} (D \, (2,-1) \, (3,1)) \cup _{\begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}} (D \, (-2,1) \, (n-4,-1)). \end{aligned}$$

• ii) If $\gamma =n-1$, then $K_{n}(\gamma )$ is the SFS of type

  $$\begin{aligned} {\mathbb {S}}^2 ((2,1) \, (7,-5) \, (5n-19, n-4)). \end{aligned}$$

• iii) If $\gamma =n$, then $K_{n}(\gamma )$ is the SFS of type

  $$\begin{aligned} {\mathbb {S}}^2 ((5,2) \, (3,-2) \, (4n-15, n-4)). \end{aligned}$$

• iv) If $\gamma =n+1$, then $K_{n}(\gamma )$ is homeomorphic to the toroidal graph manifold

  $$\begin{aligned} (D \, (-3,1) \, (2,3)) \cup _{\begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}} (D \, (2,1) \, (3n-11, n-4)). \end{aligned}$$

The knots $K_n$, $n \ne 3,4,5$, in Theorem 3.5 are hyperbolic, strongly invertible and have tunnel number one. By the Wirtinger algorithm applied to a planar projection of $K_n$, we get

Theorem 3.6

The knot $K_{n}$ has the 2–generator presentation

$$\begin{aligned} \pi (K_n)\cong \langle a,b :a^{3n-11}(b^{-2} a b^3a b^{-2})^{4-n}=1 \rangle \end{aligned}$$

where the path ${{\textbf {m}}} =a b^{-1}$ is a meridian of the knot.

If, for example, $n=6$ in Theorem 3.5, then $K_n(\gamma )$ is toroidal (TOR) for $\gamma =4$ and 7, and it is SFS for $\gamma =5$ and 6. Furthermore, $K_n(\gamma )$ is hyperbolic for $\gamma =3$ and 8 by SnapPea program.

From Theorem 3.5 we have proved the following result:

Theorem 3.7

For every integer $n>5$, there are infinitely many tunnel number one strongly invertible hyperbolic knots in the 3-sphere whose $(n-2)$- and $(n+1)$-surgeries give toroidal graph manifolds, and $(n-1)$- and n-surgeries give Seifert fiber spaces over ${\mathbb {S}}^2$ with exactly three exceptional fibers.

Theorem 3.7 relates with Theorem 0.1 in [18] and the results given in [15, 27] and [35].

Theorem 3.8

Let us consider the tunnel number one strongly invertible hyperbolic knots $K_{h,k,p}$ for $h, k \le -2$ and $|p|>1$, and set $q=1+p(h+k)$. Then we have

• i) If $\gamma =-p[h-k]^2-h-k$, then $K_{h,k,p}(\gamma )$ is homeomorphic to the toroidal graph manifold

  $$\begin{aligned} (D \, (k,-1) \, (-h,-2h+1)) \cup _{\begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}} (D \, (2,1) \, (q-2p,p)). \end{aligned}$$

• ii) If $\gamma =-p[h-k]^2-h-k+1$, then $K_{h,k,p}(\gamma )$ is the SFS defined by the invariants

  $$\begin{aligned} {\mathbb {S}}^2( (-2k+1,-k) \, (-2h+1, h-1) \, (q-p,-p)). \end{aligned}$$

• iii) If $\gamma =-p[h-k]^2-h-k+2$, then $K_{h,k,p}(\gamma )$ is homeomorphic to the toroidal graph manifold

  $$\begin{aligned} (D \, (k-1,1) \, (1-h, 1-2h)) \cup _{\begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}} (D \, (2,1) \, (q,-p)). \end{aligned}$$

Remark

• 1) If, for example, $p=-3$, $k=-3$, $h=-5$, hence $q=1+p(h+k)=25$, then $K_{h,k,p}(\gamma )$ in Theorem 3.8 is TOR graph manifold for $\gamma =20$ and 22, and it is SFS for $\gamma =21$. Furthermore, $K_{h,k,p}(\gamma )$ is hyperbolic for $\gamma =19$ and 23 from SnapPea program.

• 2) If $h=k \le -2$, then $\gamma =-2h, -2h+1$, and $-2h+2$ in i), ii), and iii) of Theorem 3.8, respectively. So we get infinitely many distinct hyperbolic knots $K_{h,k,p}(\gamma )$ for $|p|>1$, which have three exceptional surgeries for the same values of slopes.

Let us consider the hyperbolic knots ${{\overline{K}}}_n=K_{h,k,p}$ from Theorem 3.8, where $h=-n$, $k=-n-1$ and $p=2n+2$ for every $n \ge 2$. Set $q=1-(2n+1)(2n+2)$. This class of hyperbolic knots was considered in [15], where it was proved that the 0-surgery on ${{\overline{K}}}_n$ gives a small Seifert fiber space (see [15], Lemma 2.5). The following result completes that given in [15]:

Theorem 3.9

With the above notations, we have

• i) If $\gamma =-1$, then ${{\overline{K}}}_n (\gamma )$ is homeomorphic to the toroidal graph manifold

  $$\begin{aligned} (D \, (-n-1,-1) \, (n,2n+1)) \cup _{\begin{pmatrix} 0 &{} \quad 1 \\ 1 &{} \quad 0 \end{pmatrix}} (D \, (2,1) \, (1-(2n+2)(2n-1),2n+2)). \end{aligned}$$

• ii) If $\gamma =0$, then ${{\overline{K}}}_n(\gamma )$ is the Seifert fiber space of type

  $$\begin{aligned} {\mathbb {S}}^2 ((2n+3,n+1) \, (2n+1,-n-1) \, (-(2n+1)(2n+3), -(2n+2)). \end{aligned}$$

• iii) If $\gamma =1$, then ${{\overline{K}}}_n (\gamma )$ is homeomorphic to the toroidal graph manifold

  $$\begin{aligned} (D (-n\!-\!2,1) (n\!+\!1, 2n\!+\!1)) \cup _{\begin{pmatrix} 0 &{} \quad 1 \\ 1 &{} \quad 0 \end{pmatrix}} (D (2,1) (1\!-\!(2n\!+\!1)(2n\!+\!2), -2n\!-\!2)). \end{aligned}$$

If $n=3$ in Theorem 3.9, hence $h=-3$, $k=-4$, $p=8$ and $q=-55$, then ${{\overline{K}}}_n(-2)$ and ${{\overline{K}}}_n(2)$ are hyperbolic manifolds from SnapPea program.

From Theorem 3.9 we have proved the following result:

Theorem 3.10

For every integer $n\ge 2$, there are infinitely many tunnel number one strongly invertible hyperbolic knots ${{\overline{K}}}_n$ in the 3-sphere whose $-1$ and 1-surgeries give toroidal graph manifolds, and 0-surgery gives a Seifert fiber space over ${\mathbb {S}}^2$ with exactly three exceptional fibers.