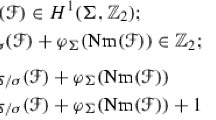On a Conjecture About Higgs Bundles and Some Inequalities

Abstract

We briefly review an open conjecture about Higgs bundles that are semistable after pulling back to any curve, and prove it in the rank 2 case. We also prove some results in higher rank under suitable additional assumptions. Moreover, we establish a set of inequalities holding for H-nef Higgs bundles that generalize some of the Fulton–Lazarsfeld inequalities for numerically effective vector bundles.

1 Introduction

The progenitor of the results discussed in this paper may be traced back to a theorem by Miyaoka [20], which characterizes the semistability of a vector bundle E on a smooth projective curve X in terms of the nefness of a numerical class in the projectivized bundle ${{\mathbb {P}}}E$: if

$$\begin{aligned} \lambda (E) = c_1({{\mathcal {O}}}_{{{\mathbb {P}}}E}(1)) - \tfrac{1}{r}\pi _1^*(c_1(E)) \in N^1({{\mathbb {P}}}E) \otimes {{\mathbb {Q}}}, \end{aligned}$$

(1)

where $\pi _1:{{\mathbb {P}}}E \rightarrow X$ is the projection, and $r= {\text {rk}}E$, then E is semistable if and only if $\lambda (E)$ is nef (note that $r\lambda (E)$ is the relative anticanonical class of ${{\mathbb {P}}}E$ over X).

1.1 Curve Semistable (Higgs) Bundles

The following theorem was proved in [21] and rediscovered in [6] in a slightly different and seemingly stronger, albeit equivalent form. It may be regarded as a higher dimensional generalization of Miyaoka’s theorem. Let X be an n-dimensional smooth connected complex projective variety. For any coherent ${{\mathcal {O}}}_X$-module F of positive rank define its discriminant as

$$\begin{aligned} \Delta (F) = c_2(F) - \tfrac{{\text {rk}}F-1}{2{\text {rk}}F} \, c_1(F)^2 \in H^4(X,{{\mathbb {Q}}}). \end{aligned}$$

Moreover, if E is a vector bundle on X, the class $\lambda (E)$ is defined as in Eq. (1).

Theorem 1.1

Let E be a vector bundle on X. The following conditions are equivalent:

• (i) E is semistable with respect to some polarization H, and $\Delta (E)=0$;

• (ii) for any morphism $f:C\rightarrow X$, where C is a smooth projective curve, the vector bundle $f^* E$ is semistable;

• (iii) the class $\lambda (E)$ is nef.

(In Nakayama the condition on the discriminant was $\Delta (E)\cdot H^{n-2} = 0$, but via Theorem 2 in [24] this is readily shown to be equivalent to $\Delta (E)=0$ whenever E is semistable with respect to H.) We shall call curve semistable the vector bundles satisfying condition (ii). It may be natural to wonder if Theorem 1.1 also holds true for Higgs bundles. We recall that a Higgs sheaf is a pair ${\mathfrak {F}}=(F,\phi )$, where F is a coherent ${{\mathcal {O}}}_X$-module, and $\phi :F \rightarrow F\otimes \Omega ^1_X$ is an ${{\mathcal {O}}}_X$-linear morphism such that the composition

$$\begin{aligned} \phi \wedge \phi :F \xrightarrow {\phi } F\otimes \Omega ^1_X \xrightarrow {\phi \times \textrm{id}} F\otimes \Omega ^1_X\otimes \Omega ^1_X \rightarrow F\otimes \Omega ^2_X \end{aligned}$$

is zero. A Higgs bundle is a Higgs sheaf with F locally free. Semistability and stability are defined as for vector bundles but only with reference to $\phi$-invariant subsheaves. Curve semistability is defined as for vector bundles. So the Higgs bundle version of Theorem 1.1 is the following conjecture:

Conjecture 1.2

Let ${\mathfrak {E}}=(E,\phi )$ be a Higgs bundle on X. The following conditions are equivalent:

• (i) ${\mathfrak {E}}$ is semistable with respect to some polarization H, and $\Delta (E)=0$;

• (ii) for any morphism $f:C\rightarrow X$, where C is a smooth projective curve, the Higgs bundle $f^* {\mathfrak {E}}$ is semistable.

(We shall state the condition generalizing the nefness of the class $\lambda (E)$ later on.) The fact that condition (i) implies condition (ii) was proved in [6]. A motivation for expecting that the opposite implication may hold true is Bogomolov inequality [14]: if E is a vector bundle on an n-dimensional smooth projective variety, semistable with respect to a polarization H, then $\Delta (E)\cdot H^{n-2} \ge 0$. The underlying vector bundle E of a semistable Higgs bundle ${\mathfrak {E}}=(E,\phi )$ satisfies the same inequality, even when E itself is not semistable [23]; i.e., semistability is a sufficient but non-necessary condition for the non-negativity of the quantity $\Delta (E)\cdot H^{n-2}$, and one can imagine the same happens for the vanishing of $\Delta (E)$ for curve semistable bundles.

We conjecture that the reverse implication holds true for any smooth projective variety. In this paper we prove this when ${\mathfrak {E}}$ has rank two; actually, we prove the implication in any rank when the Grassmannian of Higgs quotients of some rank (to be defined later) has a component that is a divisor in the full Grassmannian and surjects onto X. Then we prove that such a component always exists in rank two.

1.2 Higgs Varieties

One easily shows that a curve semistable Higgs bundle is semistable with respect to any polarization. So the nontrivial content of the conjecture is the following statement:

A curve semistable Higgs bundle has vanishing discriminant.

Here curve semistability for Higgs bundles is defined as in condition (ii) of Conjecture 1.2. Waiting for the conjecture to be eventually settled in the positive or negative, it makes sense to prove it for specific classes of varieties. The authors of [8] defined a Higgs variety X as one on which the conjecture holds. The easiest case is that of varieties with slope-semistable cotangent bundle of nonnegative degree, simply because in this situation the underlying vector bundle E of a curve semistable Higgs bundle is itself curve semistable. Starting from this one can identify other Higgs varieties, such as:

• Rationally connected varieties;

• Abelian varieties;

• Fibrations over a Higgs variety whose fibers are rationally connected;

• Bases of finite étale covers whose total space is a Higgs variety;

• Varieties of dimension $\ge 3$ containing an effective ample divisor which is a Higgs variety;

• Varieties with nef tangent bundle (in dimension 2 and 3 these were classified in [10]);

• Varieties birational to a Higgs variety.

Moreover, in [7] it was shown that algebraic K3 surfaces are Higgs varieties, and this was extended, using different techniques, to simply connected Calabi–Yau varieties in [3]. Some results in the case of elliptic surfaces are proved in [9]. A review of this problem updated to 2017 can be found in [18].

1.3 Contents

The main tool we use in this paper is the Higgs Grassmannian of a Higgs bundle ${\mathfrak {E}}=(E, \phi )$, a notion that some of us introduced in [6]. This object is defined in Sect.  2, where some of its basic properties are studied. It seems quite difficult to find general results about the Higgs Grassmannian, but its structure is quite clear in the case ${\text {rk}}E=2$, and this is indeed the key to the proof of the conjecture in the rank 2 case that we give in Sect. 4.2. Actually in Sect. 3 we prove the conjecture assuming that the rank d Higgs Grassmannian ${\text {Gr}}_{d}({\mathfrak {E}})$ has a component that is a divisor in the full Grassmann bundle ${\text {Gr}}_d(E)$ which surjects onto X. Such a divisor always exists in the rank 2 case, due to the fact that the Higgs Grassmiannian of a rank 2 Higgs bundle over a curve is never empty, thus providing a full proof of the conjecture in the rank 2 case.

The Higgs Grassmannian allows one to introduce a notion of numerical effectiveness for Higgs bundles, a notion that “feels” the Higgs field. This was studied in [4, 5]. In the final Sect. 5 of this paper we show that Higgs bundles that are numerically effective in this sense satisfy some inequalities which generalize some of the Fulton–Lazarsfeld inequalities for numerically effective vector bundles ( [13], see also [10]).

Notation and conventions. All varieties and schemes are over the complex numbers, and, unless otherwise stated, all varieties are supposed to be connected. A “sheaf” on a scheme X will be a coherent ${{\mathcal {O}}}_X$-module.

2 The Higgs Grassmannian

The Higgs Grassmannian is an object that parameterizes locally free Higgs quotients of a Higgs bundle

exactly as the usual Grassmann bundle parameterizes locally free quotients of a vector bundle. This was introduced in [6]. We recall here its definition and some of its properties.

2.1 Definition of the Higgs Grassmannian

Let X be a smooth variety over ${{\mathbb {C}}}$. For a given rank r vector bundle E on X, and for every d in the range $0< d < r$, we denote the Grassmann bundle of rank d locally free quotients of E as ${\text {Gr}}_{d}(E)$. Since ${\text {Gr}}_{1}(E)={{\mathbb {P}}}E$ we shall use the latter notation. One has the universal exact sequence

$$\begin{aligned} 0 \rightarrow S_d \rightarrow \pi _d^*E \rightarrow Q_d \rightarrow 0 \end{aligned}$$

of vector bundles on ${\text {Gr}}_{d}(E)$, where $Q_d$ is the rank d universal quotient bundle, $S_d$ is the corresponding kernel, and $\pi _d:{\text {Gr}}_{d}(E) \rightarrow X$ is the projection. If ${\mathfrak {E}}=(E,\phi )$ is a Higgs bundle, we form the diagram

(2)

The d-th Higgs Grassmannian of ${\mathfrak {E}}$, denoted ${\text {Gr}}_{d}({\mathfrak {E}})$, is the subscheme of ${\text {Gr}}_{d}(E)$ defined by the zero locus of the composition ${b}_d\circ \pi _d^*\phi \circ {a}_d$. By construction, the restrictions of the bundles $S_d$ and $Q_d$ to ${\text {Gr}}_{d}({\mathfrak {E}})$ carry Higgs fields induced by $\pi _d^*\phi$, so that we have an exact sequence of Higgs bundles on ${\text {Gr}}_{d}({\mathfrak {E}})$

$$\begin{aligned} 0 \rightarrow {\mathfrak {S}}_d \rightarrow \rho _d^*{\mathfrak {E}}\rightarrow {\mathfrak {Q}}_d \rightarrow 0 . \end{aligned}$$

The scheme ${\text {Gr}}_{d}({\mathfrak {E}})$ may be singular, reducible, nonreduced, non-equidimensional. On the positive side, it enjoys the analogous universal property of the usual Grassmann bundles: if $f:Y \rightarrow X$ is a scheme morphism, and ${\mathfrak {G}}$ is a rank d locally free Higgs quotient of $f^*{\mathfrak {E}}$, there is a morphism $g:Y \rightarrow {\text {Gr}}_{d}({\mathfrak {E}})$ such that ${\mathfrak {G}}=g^*{\mathfrak {Q}}_d$, and the diagram

commutes.

Now assume that X is projective. Given a rank r Higgs bundle ${\mathfrak {E}}=(E,\phi )$ on X, for every $0< d < r$ we define the following classes in $N^1({\text {Gr}}_{d}({\mathfrak {E}}))\otimes {{\mathbb {Q}}}$

$$\begin{aligned} \theta _d({\mathfrak {E}}) = c_1(Q_d) - \tfrac{d}{r} \rho _d^*(c_1(E)). \end{aligned}$$

(3)

It was proved in [6] (see also [5]) that ${\mathfrak {E}}$ is curve semistable if and only if all classes $\theta _d({\mathfrak {E}})$ are nef. Note that $\theta _1({\mathfrak {E}})$ is the restriction of the class $\lambda (E) \in N^1({{\mathbb {P}}}E)\otimes {{\mathbb {Q}}}$ to ${\text {Gr}}_{1}({\mathfrak {E}})$. Here one can note a different behavior of Higgs bundles as opposed to vector bundles: while in the latter case the condition that the class $\lambda (E)$ is nef is equivalent to curve semistability, in the Higgs case one needs the nefness of all classes $\theta _d({\mathfrak {E}})$; see [6] for an example of a rank 3 Higgs bundle on a curve with $\theta _1({\mathfrak {E}})$ nef, $\theta _2({\mathfrak {E}})$ not nef, which is not semistable.

2.2 Higgs Numerical Effectiveness

In [5] by means of the Higgs Grassmannians a notion of numerical effectiveness for Higgs bundles was introduced. It is a definition based on recursion on the rank of the successive universal quotient bundles. Since we are going to use this definition later on, we recall it here.

Definition 2.1

A Higgs bundle ${\mathfrak {E}}=(E, \phi )$ of rank one on a smooth projective variety is said to be Higgs-numerically effective (for short, H-nef) if the underlying vector bundle E is numerically effective in the usual sense. If ${\text {rk}}E \ge 2$ we require that:

• (i) All bundles ${\mathfrak {Q}}_{k}$ are Higgs numerically effective;

• (ii) The line bundle $\det (E)$ is nef.

If both ${\mathfrak {E}}$ and ${\mathfrak {E}}^*$ are Higgs-numerically effective, ${\mathfrak {E}}$ is said to be Higgs-numerically flat (H-nflat).

3 The Conjecture in any Rank

3.1 A Push-Forward Formula

We recall from [16] a push-forward formula for the Segre classes of the universal quotient bundle over Grassmann bundles $\pi _d:{\text {Gr}}_d(E)\rightarrow X$. Here X will be a smooth projective variety of dimension n and E a rank $r>1$ vector bundle.

Greek letters such as $\lambda$, $\mu$ will denote a partition, i.e., a finite nonincreasing sequence of natural numbers. We let

$$\begin{aligned} \vert \lambda \vert = \sum _{i=1}^q \lambda _i , \end{aligned}$$

where $\lambda = (\lambda _1, \dots ,\lambda _q)$, while $\pi _*$ will denote the push-forward of Chow groups

$$\begin{aligned} \pi _*:A^k({\text {Gr}}_d(E)) \rightarrow A^{k - d(r-d)}(X). \end{aligned}$$

Moreover, we define the Segre classes of the vector bundle F on a variety X by the formula

$$\begin{aligned} s(F)= \sum _{i=0}^{\dim X} (-1)^i s_i(F) = \frac{1}{c(F)} \end{aligned}$$

where c(F) is the total Chern class of F (we follow the normalization of [12], hence the minus signs).

Lemma 3.1

[15, 16] Let Q be the rank d universal quotient bundle of a rank r vector bundle E over X. The following push-forward formula holds:

$$\begin{aligned} \pi _*\Delta _\mu (s(Q))=\Delta _{\mu -\varepsilon }(s(E)). \end{aligned}$$

Here

• (i) $\varepsilon$ is the partition of length d whose elements are all $r-d$;

• (ii) for every $c\in A^\bullet (X)$, $\Delta _\lambda (c)$ is the Schur polynomial associated with $\lambda$ computed on the components of c in $A^\bullet (X)$, that is,

  $$\begin{aligned} \Delta _\lambda (c) = \det [ c_{\lambda _i+j-i}]_{1\le i,j \le n}. \end{aligned}$$

Corollary 3.2

Let $\chi = c_1(Q)$. For N in the range $d(r-d) \le N \le d(r-d)+ n$ one has

$$\begin{aligned} \pi _*\chi ^N = \sum _{\vert \lambda \vert = N - d(r-d)} f^{\lambda +\varepsilon }\, \Delta _\lambda (s(E)) \end{aligned}$$

where $f^\lambda$ is the number of standard Young tableaux of shape $\lambda$. ¹

Some notation and facts:

• A natural number k is regarded as a partition of length 1. For every k, $\Delta _k(c) = c_k$, i.e., the degree k term of c. In particular,

  $$\begin{aligned} \Delta _k(c(E))=c_k(E), \qquad \Delta _k(s(E))=s_k(E). \end{aligned}$$

• Conjugate partitions: given a partition $\lambda$, let ${{\bar{\lambda }}}$ be the conjugate partition, i.e., the partition which describes the conjugate Young tableau of $\lambda$ (the one obtained by flipping it with respect to its diagonal.) Then

  $$\begin{aligned} \Delta _{{{\bar{\lambda }}}}(c(E)) = \Delta _\lambda (s(E)). \end{aligned}$$

• We shall denote by p(k) the partition made up by k 1’s. Then k and p(k) are conjugate partitions, so that

  $$\begin{aligned} \Delta _{p(k)}(s(E)) = c_k(E). \end{aligned}$$

• An explicit formula for $f^\lambda$ is the following [11, 19]. Let $\lambda$ be a partition of length $q>1$. Then

  $$\begin{aligned} f^\lambda = \frac{\vert \lambda \vert !}{\prod _{i=1}^q\ell _i!} \prod _{1 \le i < j \le q} (\ell _i-\ell _j),\qquad \ell _i = \lambda _i + q - i \end{aligned}$$

We note that

$$\begin{aligned} f^{\varepsilon +1} = \frac{md}{r} f^\varepsilon , \qquad f^{\varepsilon +p(2)} = \frac{m(m+1)d(d-1)}{2r(r-1)}) f^\varepsilon \\ f^{\varepsilon +2} = \frac{m(m+1)d(d+1)}{2r(r+1)} f^\varepsilon \end{aligned}$$

where $m=d(r-d)+1$. So, setting $n=2$, Corollary 3.2 yields

$$\begin{aligned} \pi _*\chi ^{m-1}= & {} f^\varepsilon , \qquad \pi _*\chi ^m= \frac{md}{r} f^\varepsilon c_1(E) \end{aligned}$$

(4)

$$\begin{aligned} \pi _*\chi ^{m+1}= & {} \frac{m(m+1)d(d+1)}{2r(r+1)} f^\varepsilon (c_1(E)^2-c_2(E)) \nonumber \\{} & {} + \frac{m(m+1)d(d-1)}{2r(r-1)}) f^\varepsilon c_2(E). \end{aligned}$$

(5)

3.2 The result

In this Section we prove the main result of this paper.

Theorem 3.3

Given a curve semistable Higgs bundle ${\mathfrak {E}}=(E, \phi )$ on a surface X, if, for some d in the range $0< d < r={\text {rk}}E$, the Higgs Grassmannian ${\text {Gr}}_{d}({\mathfrak {E}})$ has an irreducible component Z which is a divisor in ${\text {Gr}}_d(E)$ and surjects onto X, then $\Delta (E)=0$.

Proof

Using the Leray-Hirsch Theorem we define the classes $\beta _i \in A^i(X)$ by

$$\begin{aligned}{}[Z ] = \chi \, \pi ^*\beta _0 + \pi ^*\beta _1 \in A^1({\text {Gr}}_d(E)), \end{aligned}$$

where [Z] is the class of Z in $A^1(Gr_d(E))$ (for a version of the Leray–Hirsch Theorem for Chow groups which applies to the present case see [17]). Recalling equation (3),

a rather lengthy computation yields²

$$\begin{aligned} \begin{aligned} \int _Z \theta _d({\mathfrak {E}})^ m&= \int _{{\text {Gr}}_d(E)}\theta _d({\mathfrak {E}})^ m \smile \, [Z] = \int _{{\text {Gr}}_d(E)} [\chi - \tfrac{d}{r}\pi ^*c_1(E)]^m (\chi \, \pi ^*\beta _0 + \pi ^*\beta _1) \\&= \int _{{\text {Gr}}_d(E)} \left[ \beta _0\chi ^{m+1} + \left( \beta _1-\beta _0 \frac{md}{r }c_1(E)\right) \chi ^{m} \right. \\&\quad +\left. \left( -\frac{md}{r}\beta _1\,c_1(E)+ \frac{m(m-1)d^2}{2r^2}\beta _0\,c_1(E)^2\right) \chi ^{m-1} \right] \\&= - \frac{m(m+1)d(r-d)}{r(r+1)(r-1)} f^\varepsilon \,\beta _ 0 \, \Delta (E) = - \frac{m(m+1)(m-1)}{r(r+1)(r-1)} f^\varepsilon \,\beta _ 0 \, \Delta (E) . \end{aligned} \end{aligned}$$

In the last line, by integrating over X, we think of $\beta _0$ and $\Delta (E)$ as integers. $\beta _0$ is positive by the following argument. Denote by $\pi _Z$ the restriction of $\pi _d$ to Z, and by $Z_x$ its fiber at a point $x \in X$. We also denote $F_x = \pi _d^{-1}(x)$. We assume that $\pi _Z$ is surjective so that by [1, Lemma 29.28.2] every irreducible component of its fibers has either dimension $d(r-d)$ or $d(r-d)-1$ (to apply that result we need Z to be integral but we can achieve that by replacing it with its reduced subscheme if needed). On the other hand, since $\pi _Z$ is proper, by the semicontinuity of the fiber dimension (see e.g. [1, Lemma 37.29.5]) the locus in X where the fiber $Z_x$ has dimension $d(r-d)-1$ is open. It is nonempty because if all fibers $Z_x$ have dimension $d(r-d)$ then ${\text {Gr}}_{d}({\mathfrak {E}})$ would coincide with ${\text {Gr}}_d(E)$, a situation which we may exclude. So the generic fiber of $\pi _Z$ has dimension $d(r-d)-1$, the “expected dimension”. Hence for generic x, $Z_x$ determines a class in $A^1(F_x)$. Since the restriction $\chi _x$ of $\chi$ to $F_x$ is ample,

$$\begin{aligned} 0 < [Z_x] \cdot \chi _x^{m-2} = \beta _0\, \chi _x^{m-1}, \end{aligned}$$

so that $\beta _0 > 0$. So we get

$$\begin{aligned} \Delta (E) \le 0 \, . \end{aligned}$$

Now by the Bogomolov inequality $\Delta (E) \ge 0$ we obtain $\Delta (E) =0$. $\square$

Note the “miraculous disappearance” of $\beta _1$!

4 The Conjecture in Rank Two

4.1 A Non Emptiness Result

The following result is a key to our proof of the Conjecture in rank two.

Theorem 4.1

Let X be a smooth curve, which may be projective or affine, and let ${\mathfrak {E}}=(E, \phi )$ be a rank 2 Higgs bundle on X. The Higgs Grassmannian ${\text {Gr}}_{1}({\mathfrak {E}})$ of rank one Higgs quotients of ${\mathfrak {E}}$ is not empty.

Lemma 4.2

Let X be a smooth curve (projective or affine), and let ${\mathfrak {E}}=(E, \phi )$ be a rank 2 Higgs bundle on X. Assume that the Higgs Grassmannian ${\text {Gr}}_{1}({\mathfrak {E}})$ of rank one Higgs quotients of ${\mathfrak {E}}$ is empty. Then the Higgs field $\phi$ induces a splitting of the exact sequence

$$\begin{aligned} 0 \rightarrow \pi ^*_1 \Omega ^1_X \rightarrow \Omega ^1_{{{\mathbb {P}}}E}\rightarrow \Omega ^1_{{{\mathbb {P}}}E/X}\rightarrow 0. \end{aligned}$$

(6)

Note that since ${\text {Gr}}_{1}({\mathfrak {E}})$ is assumed to be empty, the Higgs field $\phi$ is necessarily nonzero.

Proof

We refer to diagram (2). Note that $Q^\vee _1 \otimes S_1 \simeq \Omega ^1_{{{\mathbb {P}}}E/X}$. Define a map $s:\Omega ^1_{{{\mathbb {P}}}E/X} \rightarrow \Omega ^1_{{{\mathbb {P}}}E}$ by letting

$$\begin{aligned} s = ({b}_1 \circ \pi ^*_1 \phi \circ {a}_1 ) \otimes {\text {id}}_{Q_1 ^\vee }. \end{aligned}$$

Since $\Omega ^1_{{{\mathbb {P}}}E/X}$ is a line bundle, and $\Omega ^1_{{{\mathbb {P}}}E}$ is locally free, the morphism s is either zero or is injective; but if it were zero, since the Higgs Grassmannian ${\text {Gr}}_{1}({\mathfrak {E}})$ is the zero locus of the composition

$$\begin{aligned} {b}_1 \circ \pi ^*_1 \phi \circ {a}_1 =s \otimes {\text {id}}_{Q_1 }, \end{aligned}$$

the Higgs Grassmannian ${\text {Gr}}_{1}({\mathfrak {E}})$ would be the entire ${{\mathbb {P}}}E$, and therefore would not be empty. So we have an exact sequence

$$\begin{aligned} 0 \rightarrow \Omega ^1_{{{\mathbb {P}}}E/X} \xrightarrow { s} \Omega ^1_{{{\mathbb {P}}}E} \rightarrow R \rightarrow 0 \end{aligned}$$

where R is by definition the quotient, which has rank one.

As the Higgs Grassmannian is empty, s has no zeroes, so that R is locally free. We form the diagram

(7)

We show that the morphism $g = r\circ i :\pi ^*_1 \Omega ^1_X \rightarrow R$ cannot be zero. Indeed if it were zero we would have a morphism $h :\pi ^*_1 \Omega ^1_X \rightarrow \Omega ^1_{{{\mathbb {P}}}E/X}$ which is not zero as $i = s\circ h$. However since the fiber degree of $\Omega ^1_{{{\mathbb {P}}}E/X}$ is $-2$, the restriction of h to each fiber of $\pi$ is zero, i.e., $h=0$, which is a contradiction.

Thus, g is nonzero, hence is injective. We prove it is an isomorphism. We have an exact sequence

$$\begin{aligned} 0 \rightarrow \pi ^*_1 \Omega ^1_X \xrightarrow {g} R \rightarrow N \rightarrow 0 \end{aligned}$$

where N has rank zero. For any fiber F of $\pi _1$, by a standard argument, we have an exact sequence

$$\begin{aligned} 0 \rightarrow {{\mathcal {O}}}_F \rightarrow R_{\vert F} \rightarrow N_{\vert F} \rightarrow 0. \end{aligned}$$

Since R has fiber degree 0, $R_{\vert F}$ is isomorphic to ${{\mathcal {O}}}_F$, so that $N_{\vert F} =0$. As this holds for every fiber, $N=0$, hence g is an isomorphism.

Now we have a diagram

which shows that the sequence (6) splits. $\square$

Proof of Theorem 4.1.

Note that the first line in diagram (7) splits as $i\circ g^{-1}$ is a section of r. Let $t'$ be a retraction of the morphism s. Then $t= t'\otimes {\text {id}}_Q$ is a morphism $Q_1 \otimes \Omega ^1_{{{\mathbb {P}}}E/X} \rightarrow S_1$. Define $\zeta :\pi ^*_1 E \rightarrow S_1$ as

$$\begin{aligned} \zeta = t \circ {b}_1 \circ \pi ^*_1 \phi . \end{aligned}$$

Then

$$\begin{aligned} \zeta \circ {a}_1 = t \circ {b}_1 \circ \pi ^*_1 \phi \circ {a}_1 = (t'\otimes {\text {id}}_{Q _1} )\circ ( s \otimes {\text {id}}_{Q^\vee _1} )= {\text {id}}_{S_1 } \end{aligned}$$

so that the first line in diagram (2) splits. But this is impossible as on each fiber of $\pi _1$ that sequence reduces to the Euler exact sequence. $\square$

Corollary 4.3

Let ${\mathfrak {E}}=(E, \phi )$ be a rank two Higgs bundle on a smooth n-dimensional projective variety X. The Higgs Grassmannian ${\text {Gr}}_{1}({\mathfrak {E}})$ has a component of dimension at least n which surjects onto X.

Proof

If ${\text {Gr}}_{1}({\mathfrak {E}})$ does not have such a component, let Y be its image in X (actually taking its reduced subscheme if it happens to be nonreduced), let C be a curve in X not contained in Y, and let $C'$ be C minus its intersection points with Y, and minus its possible singular points. Then ${\mathfrak {E}}_{|C'}$ has an empty Higgs Grassmannian, a contradiction to Corollary 4.1. $\square$

Remark 5.2

The splitting of the exact sequence (6) means that E is projectively flat, i.e., ${{\mathbb {P}}}E$ comes from a projective representation $\pi _1(X) \rightarrow {\text {PGL}}_2({{\mathbb {C}}})$ of the fundamental group of X. This agrees with the result in [22], whose authors, as a particular case of their equivalence of categories, prove that semistable Higgs bundles on a curve are projectively flat. Note indeed that if the Higgs Grassmannian is empty, the Higgs bundle is stable.

4.2 The proof

We start with the case $\dim X = 2$, i.e., X is smooth projective surface. From Corollary  4.3 we get that ${\text {Gr}}_{1}({\mathfrak {E}})$ has a component Z of dimension 2, and we are in the hypotheses of Sect. 3.2, so that $\Delta (E)=0$.

This can be extended to the higher dimensional case $\dim X=n$. Let H be the class of an ample line bundle $L={{\mathcal {O}}}_X(D)$ and let Y be the intersection of $n-2$ generic divisors in the linear system $\vert m D \vert$ for $m\gg 0$. The result for dimension 2 implies that

$$\begin{aligned} \Delta (E)\cdot H^{n-2}=\tfrac{1}{m^{n-2}}\Delta (E_{|Y})=0. \end{aligned}$$

So we have proved:

Theorem 4.5

Let ${\mathfrak {E}}=(E, \phi )$ be a rank two Higgs bundle on an n-dimensional smooth projective variety. Then the following conditions are equivalent:

• (i) ${\mathfrak {E}}$ is curve semistable;

• (ii) ${\mathfrak {E}}$ is semistable with respect to some polarization and the class $\theta _1({\mathfrak {E}})$ is nef;

• (iii) ${\mathfrak {E}}$ is semistable with respect to a polarization H, and

  $$\begin{aligned} \Delta (E)\cdot H^{n-2}=0. \end{aligned}$$

Proof

We know from [6] that (i) and (ii) are equivalent. The implication (ii) $\Rightarrow$ (iii) was just proved. To prove (iii) $\Rightarrow$ (ii) one can easily adapt the proof of one of the directions of Theorem 1.3 in [6]. $\square$

Actually condition (iii) can be strengthened to $\Delta (E)=0$. To see that we need some preliminary results. In particular, we shall prove that rank 2 H-nflat Higgs bundles have vanishing Chern classes (H-nflat Higgs bundles were defined in Definition 2.1).

Lemma 4.6

If ${\mathfrak {E}}=(E, \phi )$ is an H-nflat Higgs bundle of any rank over a smooth n-dimensional projective variety X and $\Delta (E) \cdot H^{n-2}=0$, then all Chern classes of E vanish.

Proof

One has $c_1(E)=0$ as $\det (E)$ is numerically flat and then the condition on the discriminant implies ${\text {ch}}_2(E) \cdot H^{n-2}=0$. By Theorem 2 in [24] ${\mathfrak {E}}$ has a filtration in (stable) Higgs bundles with zero Chern classes, whence the claim follows (note that H-nflat Higgs bundles are semistable with respect to any polarization, see [5]). $\square$

Theorem 4.7

If ${\mathfrak {E}}=(E, \phi )$ is a rank two H-nflat Higgs bundle over a smooth projective surface X then all Chern classes of E vanish.

Proof

Since H-nflat bundles are curve semistable by Theorem 4.5, if H is an ample class in X, we have $\Delta (E) \cdot H^{n-2}=0$. Then Lemma 4.6 implies the claim. $\square$

We can now strengthen Theorem 4.5 in the following form.

Theorem 4.8

Let ${\mathfrak {E}}=(E, \phi )$ be a rank two Higgs bundle on an n-dimensional smooth projective variety. Then the following conditions are equivalent:

• (i) ${\mathfrak {E}}$ is curve semistable;

• (ii) ${\mathfrak {E}}$ is semistable with respect to some polarization and the class $\theta _1({\mathfrak {E}})$ is nef;

• (iii) ${\mathfrak {E}}$ is semistable with respect to some polarization and $\Delta (E)=0$.

Proof

We only need to show that if (ii) holds then $\Delta (E)=0$. If H is an ample class in X, from Theorem 4.5 we have $\Delta (E) \cdot H^{n-2}=0$, which is equivalent to $\Delta ({ End}\,(E)) \cdot H^{n-2}=0$. So the Higgs bundle ${ End}\,({\mathfrak {E}})$ is curve semistable, and since $c_1({ End}\,(E))=0$, the Higgs bundle ${ End}\,({\mathfrak {E}})$ is H-nflat [5]. By Lemma 4.6$\Delta ({ End}\,(E))=0$, that is, $\Delta (E)=0$. $\square$

Actually we have a stronger result.

Theorem 4.9

Let ${\mathfrak {E}}=(E, \phi )$ be a Higgs bundle on an n-dimensional smooth projective variety, such that the Higgs Grassmannian ${\text {Gr}}_{d}({\mathfrak {E}})$ has an irreducible component Z which is a divisor in ${\text {Gr}}_d(E)$ that surjects onto X. Then the following conditions are equivalent:

• (i) ${\mathfrak {E}}$ is curve semistable;

• (ii) ${\mathfrak {E}}$ is semistable with respect to some polarization and the class $\theta _d({\mathfrak {E}})$ is nef;

• (iii) ${\mathfrak {E}}$ is semistable with respect to some polarization and $\Delta (E)=0$.

Note that, contrary to the general situation, and due to the assumption that ${\text {Gr}}_{d}({\mathfrak {E}})$ has a divisorial component that surjects onto X, the nefness of the class $\theta _d({\mathfrak {E}})$ is enough to have curve semistability (but assuming a priori that ${\mathfrak {E}}$ is semistable).

5 Inequalities for H-nef Higgs Bundles

We know from [10, 13] that a nef vector bundle E on an n-dimensional smooth projective variety satisfies, for every ample class H and for every $1 \le k \le n$, the inequalities

$$\begin{aligned} s_k(E) \cdot H^{n-k} \ge 0, \end{aligned}$$

where $s_k(E)$ are the Segre classes of E. In this Section, we prove a version of these inequalities for H-nef Higgs bundles.

Theorem 5.1

Let ${\mathfrak {E}}=(E, \phi )$ be a rank r H-nef Higgs bundle over an n-dimensional smooth projective variety. Assume that Z is an irreducible component of the Higgs Grassmannian ${\text {Gr}}_{1}({\mathfrak {E}})$, and write its class in $A^{N}({{\mathbb {P}}}E)$, where N is the codimension of Z in ${{\mathbb {P}}}E$, as

$$\begin{aligned}{}[Z] = \sum _{i=0}^N \pi _1^*\beta _i \cdot \xi ^{N-i}, \end{aligned}$$

where $\beta _i \in A^{i}(X)$. Then for every $1 \le k \le n$ we have the inequality

$$\begin{aligned} \sum _{i=0}^{r-1} \beta _i \cdot s_{k-i}(E) \cdot H^{n-k}\ge 0 \end{aligned}$$

for any ample class H in X.

Proof

We first prove the inequality for $k=n$. Since ${\mathfrak {E}}$ is H-nef, the hyperplane class $\xi$ of ${{\mathbb {P}}}E$ is nef on Z. We shall use the identity [12, Sect. 3.1]

$$\begin{aligned} \pi _{1*}\xi ^{r+i-1}=s_i(E) \end{aligned}$$

for $0 \le i \le n= \dim X$. Now we have

$$\begin{aligned} 0 \le \xi ^{r+n-1-N} \frown [Z]= & {} \int _{{{\mathbb {P}}}E}\xi ^{r+n-1-N}\smile \sum _{i=0}^N \pi _1^*\beta _i \cdot \xi ^{N-i}\\= & {} \sum _{i=0}^N \int _{{{\mathbb {P}}}E} \xi ^{r+n-i-1}\smile \pi _1^*\beta _i =\sum _{i=0}^{r-1}\beta _i \cdot s_{n-i}(E) \end{aligned}$$

For $k<n$ we have

$$\begin{aligned} 0 \le (\pi _1^*H^{n-k} \smile \xi ^{r+k-1-N}) \frown [Z]= & {} \sum _{i=0}^{r-1}\beta _i \cdot s_{k-i}(E) \cdot H^{n-k} . \end{aligned}$$

$\square$

Since $1\le N \le r-1$, the last summation in both equations may contain terms with $i>N$ but these are zero as $\beta _i=0$ in that range.

Remark 1.17 In the non-Higgs case we have $\beta _0=1$, $\beta _i=0$ for $i>0$ and we recover the identities of [10, 13] when the Schur polynomial is a Segre class.