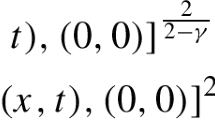Abstract
Let X be a real Banach space and \(T: X\rightarrow X\) be a \(\beta \)-expansive and continuous operator. When X is a real Hilbert space, Nirenberg proposed a problem as to whether or not T is surjective provided that R(T) (range of T) has a nonempty interior. Recently, Asfaw gave a positive solution for this problem provided that \(\overset{\circ }{R(T)}\) is unbounded. In this paper, a new surjectivity result for T is proved provided that X is a real Banach space and the condition on \(\overset{\circ }{R(T)}\) is replaced by the condition that there exists a suitable nonnegative constant \(\alpha \) satisfying \(\langle Tx-Ty, j(x-y)\rangle \ge -\alpha \Vert x-y\Vert ^2\) for all \((x, y)\in X^{2}\) and some \(j(x-y)\in J(x-y)\), where J is the duality mapping on X. Existence theorems are derived for compact perturbations of T. The results are applied to establish existence of solution (weak) in \(W^{1,p}_{0}(\Omega )\) (with \(p\ge 2\)) for the nonlinear equation given by
where \(\Omega \) is a nonempty, bounded and open subset of \({\textbf{R}}^{N}\) (for \(N\ge 1\)) with smooth boundary, the convection term F is Lipschitz continuous (not necessarily monotone), \(a:{\textbf{R}}\rightarrow {\textbf{R}}\) satisfies suitable conditions and \(\varepsilon >0\) is sufficiently small.
Similar content being viewed by others
Data Availability
No data were used to complete the research.
References
Asfaw, T.M.: A positive answer on Nirenberg’s problem on expansive mappings in Hilbert spaces. Abstr. Appl. Anal. 5, 2 (2022)
Barbu, V.: Nonlinear Differential Equations of Monotone Types in Banach Spaces. Springer Monographs in Mathematics, New York (2010)
Barbu, V.: Continuous perturbations of nonlinear m-accretive operators in Banach spaces. Boll. Un. Mat. Ital. 6, 270–278 (1972)
Chang, K., Shujie, L.: A remark on expanding maps. Proc. Am. Math. Soc. 85, 583–586 (1982)
Coclite, M.M., Palmieri, G.: On a singular nonlinear Dirichlet problem. Commun. Partial Differ. Equ. 14(10), 1315–1327 (1989)
Cioranescu, I.: Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems. Kluwer Acad. Publ, Boston (1990)
Faraci, F., Puglisi, D.: A singular semilinear problem with dependence on the gradient. J. Differ. Equ. 260, 3327–3349 (2016)
Garcia-Falset, J., Morales, C.H.: Existence theorems for \(m\)-accretive operators in Banach spaces. J. Math. Anal. Appl. 309, 453–461 (2005)
Kartsatos, A.G.: On the connection between the existence of zeros and the asymptotic behaviour of resolvents of maximal monotone operators in reflexive Banach spaces. Tran. Am. Math. Soc. 350, 3967–3987 (1998)
Liu, Z., Motreanu, D., Zeng, S.: Positive solutions for nonlinear singular elliptic equations of \(p\)-Laplacian type with dependence on the gradient. Calc. Var. 58, 22 (2019)
Motreanu, D., Motreanu, V., Papageorgiou, N.: Topological and Variational Methods with Applications to Nonlinear Boundary value Problems. Springer-Verlag, New York (2014)
Nagumo, M.: Degree of mapping in convex linear topological spaces. Am. J. Math. 73, 497–511 (1951)
Nirenberg, L.: Topics in nonlinear functional analysis. Lecture notes, Courant Institute of Mathematical Sciences, New York University, New York (1974)
Morel, J.M., Steinlein, H.: On a problem of Nirenberg concerning exapading maps. J. Funct. Anal. 59, 145–150 (1984)
Simon, J.: Regularit‘e de la solution d’une equation non lineaire dans. IRN Lectures Notes in Math. No. 665 P. Benilan editors. Springer Verlag (1978)
Peral, I.: Multiplicity of Solutions for the p-Laplacian, Second School of Nonlinear Functional Analysis and Applications to Differential Equations. ICTP, Trieste (1997)
Pascali, D., Sburlan, S.: Nonlinear Mappings of Monotone Type. Sijthoff and Noordhoff, Bucharest (1978)
O’Regan, D., Cho, Y.-J., Chen, Y.-Q.: Topological Degree Theory and Applications, Series in Mathematical Analysis and Applications, 10. Chapman and Hall/CRC, Boca Raton (2006)
Showalter, R.: Monotone operators in Banach space and nonlinear partial differential equations. Proc. Am. Math. Soc. (1997)
Szczepański, J.: A new result on the Nirenberg problem for expanding maps. Nonlinear. Anal. 43, 91–99 (2001)
Szczepański, J.: On a problem of Nirenberg concerning expanding maps in Hilbert space. Proc. Am. Math. Soc. 116, 1041–1044 (1992)
Vrabie, I.: Compactness Methods for Nonlinear Evolutions, 2nd edn. LONGMAN, John Wiley and Sons Inc., New York (1998)
Xiang, T.: Notes on expansive mappings and a partial answer to Nirenberg’s problem. Electron. J. Differ. Equ. No. 02, 1–16 (2013)
Zeidler, E.: Nonlinear Functional Analysis and Its Applications, vol. II/B. Springer-Verlag, New York (1990)
Acknowledgements
I wish to thank the editor and the anonymous knowledgeable reviewer for reviewing the manuscript very carefully and forwarding important comments and suggestions.
Funding
No funding is received to complete the research.
Author information
Authors and Affiliations
Contributions
I (Teffera M. Asfaw) am the only author of the complete research paper.
Corresponding author
Ethics declarations
Conflict of interests
The authors declare no competing interests.
Ethical Approval
Not applicable
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Asfaw, T.M. On Nirenberg’s Problem for Compact Perturbations of Expansive Operator and an Application to p-Laplacian Type Equation with Nonmonotone Convection Function. Mediterr. J. Math. 20, 209 (2023). https://doi.org/10.1007/s00009-023-02406-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00009-023-02406-1
Keywords
- \(\beta \)-expansive mapping
- Nirenberg’s problem
- compact perturbations
- nonlinear p-Laplacian equation
- nonmonotone convection function