Probability of Occurrence of Some Planar Random Quasi-homogeneous Vector Fields

Abstract

The objective of this work is the study of the probability of occurrence of phase portraits in a family of planar quasi-homogeneous vector fields of quasi degree q,  that is a natural extension of planar linear vector fields, which correspond to $q=1.$ We obtain the exact values of the corresponding probabilities in terms of a simple one-variable definite integral that only depends on q. This integral is explicitly computable in the linear case, recovering known results, and it can be expressed in terms of either complete elliptic integrals or of generalized hypergeometric functions in the non-linear one. Moreover, it appears a remarkable phenomenon when q is even: the probability to have a center is positive, in contrast with what happens in the linear case, or also when q is odd, where this probability is zero.

1 Introduction and Main Results

In this work, a random planar vector field will be a polynomial vector field whose coefficients are normally distributed independent random variables with zero mean and standard deviation one. This is the natural distribution when one is worried about the probability of appearance of some phase portrait for given family of planar vector fields, see for instance [15, 16] or [4, Thm 2.1] to have more details. Some related papers that use a similar approach and also study planar random systems are [2, 3, 17]. In [2] the quadratic systems are considered, in [3] the authors study the homogeneous systems of degree 1,2 and 3 and in [17] the linear systems.

Since we will deal with a class of quasi-homogeneous planar polynomial vector fields, in next section we will recall some usual notations and definitions and some of their properties. One of the most important to our interests is that their local phase portraits at the origin determine their global phase portraits.

It is also worth to comment that here are many mathematical models involving differential equations where coefficients and parameters come from sources with uncertainty. For instance, this is the case of some epidemiological or viral expansion models. This variability may be due to errors in measurements, virus replication and mutation, and many others. A way to tackle this uncertainty, i.e. a way to establish with accuracy the parameters, is by assuming them to be random variables. As we have already said, under this assumption, it is commonly supposed that parameters follow a Gaussian distribution. In this way, diverse phenomena can be approached by using different mathematical approaches. See [5,6,7], for instance.

A similar analysis can be performed in the case of linear systems of differential and difference equations of arbitrary dimension and not necessary Gaussian random variables. See [4, 8, 9], for instance.

In this paper we consider the family of random quasi-homogeneous vector fields

$$\begin{aligned} {\dot{x}}=Ax^q + B y, \quad \dot{y}=Cx^{2q-1}+D x^{q-1}y, \end{aligned}$$

(1)

where q is an integer positive number, and A, B, C and D independent and identically distributed (iid) random variables with normal distribution N(0, 1),  and we study the probability of appearance of each of its phase portraits. When we consider a realization of system (1), we obtain a deterministic equation given by

$$\begin{aligned} {\dot{x}}=ax^q + b y, \quad {\dot{y}}=c x^{2q-1}+d x^{q-1}y, \end{aligned}$$

(2)

where $a, b, c, d \in {\mathbb {R}}$. Notice that phase portraits of deterministic systems, characterized by equalities among the parameters a, b, c and d,  will have probability zero when they are regarded in the probabilistic setting due to the fact that A, B, C, D are iid random variables with a continuous distribution. For this reason these situations will be disregarded in our study.

As we will prove, the only phase portraits of system (1) with positive probability, depend on the parity of q and correspond to the following cases: saddle, elliptic$+$hyperbolic, node, center and focus. Moreover, all these phase portraits will be not only local, but global, due the the quasi homogeneity property.

Observe that the saddle has index $-1$ while all the above other type of critical points have index $+1.$ Recall that a critical point is said to be monodromic if given a transversal section through it, the flow defines a return map on this section. In particular, the only monodromic points in the above list are the center and the focus. By way of notation, the subscripts m and nm in our main result stand for “monodromic” and “non-monodromic” critical points of index $+1.$

Theorem 1.1

Consider the quasi-homogeneous random vector field (1), which has weight exponents $s_1=1$ and $s_2=q$ and weight degree q. Their global phase portraits with positive probability are:

• Saddle, node or focus, when q is odd.

• Saddle, elliptic$+$hyperbolic or center, when q is even.

Moreover, if $P_s=P(\texttt {saddle}),$

$$\begin{aligned} P_{nm}&=P_{nm}(q)={\left\{ \begin{array}{ll}P(\texttt {node})\quad &{}\hbox {when}\quad q \quad \hbox {is}\quad odd,\\ P(\texttt {elliptic}+\texttt {hyperbolic})\quad &{}\hbox {when}\quad q \quad \hbox {is}\quad even, \end{array}\right. }\\ P_{m}&=P_m(q)={\left\{ \begin{array}{ll}P(\texttt {focus})\quad &{}\hbox {when}\quad q \quad \hbox {is}\quad odd,\\ P(\texttt {center})\quad &{}\hbox {when}\quad q \quad \hbox {is}\quad even, \end{array}\right. } \end{aligned}$$

it holds that $P_s=1/2,$ $P_{nm}(q)=1/2-P_m(q),$ and

$$\begin{aligned} P_m(q)=\frac{1}{\pi }\int _{0}^{\pi /2} \sqrt{\frac{\sin (x)}{\sin (x) + Q}}\, \mathrm{d} x, \quad \hbox {where}\quad Q=\frac{1+q^2}{2q}. \end{aligned}$$

(3)

It is a remarkable and somehow surprising fact that when q is even the probability to have a center is positive, in contrast with what happens in the linear case, or also when q is odd, where this probability is zero.

As a corollary of our result we recover a well-known result for the linear case $q=1:$

$$\begin{aligned} P(\texttt {saddle})=\frac{1}{2},\quad P(\texttt {node})=\frac{\sqrt{2}-1}{2},\quad P(\texttt {focus})=1- \frac{\sqrt{2}}{2}. \end{aligned}$$

See [3, Thm. 1], for instance. We remark that only for $q=1$ the value $P_m(q)$ can be obtained explicitly, giving that $P_m(1)=P(\texttt {focus})=1-\sqrt{2}/2,$ see the beginning of Sect. 4 for a proof. For $q>1,$ in that section we express $P_m(q)$ in terms of complete elliptic integrals or of generalized hypergeometric functions. We also develop some tools to approach this value. With this objective in mind we study properties of the function $q\rightarrow P_m(q).$ For instance we prove that it is a decreasing convex function or that $P_m(q)\sim M/\sqrt{q},$ at $q=\infty ,$ for a given explicit M. For completeness we also approximate $P_m(q),$ for some values of q,  by using Monte Carlo method.

The study of the deterministic system (2) is done in Sect. 2. Section 3 is devoted to study the random system (1) and to prove Theorem 1.1. In this Theorem one of the relevant results is the computation of the probability $P_m(q).$ This value is obtained in two different ways, firstly simply by reducing a 3-dimensional integral to a 1-variable definite integral, and secondly by relating it with the number of expected real roots of a random polynomial that controls the number of quasi-homogeneous invariant curves of (1). This expected value is then computed by using the nice Edelman-Kostlan formula ( [12, 13]).

2 Results for the Deterministic Case

In this section we recall some general properties of planar quasi-homogeneous vector fields and we study the global phase portraits of the deterministic differential system (2).

A polynomial vector field $X=(P,Q)$ is $(s_1,s_2)$ quasi-homogeneous, where $(s_1,s_2)\in {\mathbb {N}}^2,$ if

$$\begin{aligned} P(\lambda ^{s_1}x,\lambda ^{s_2}y)=\lambda ^{s_1+r-1}P(x,y),\,\, Q(\lambda ^{s_1}x,\lambda ^{s_2}y)=\lambda ^{s_2+r-1}Q(x,y), \end{aligned}$$

(4)

for all $\lambda \in {\mathbb {R}}^+=\{a\in {\mathbb {R}}\,:\,a>0\}$ and some non negative integer r. We call $s_1$ and $s_2$ the weight exponents of the vector field X and r the weight degree (or quasi-degree) with respect to the weight exponents $s_1$ and $s_2$. A well-known nice dynamical feature of such systems is that the local behaviour near the origin gives also its global behaviour. For completeness we state and this fact in next proposition.

Proposition 2.1

Consider the differential system

$$\begin{aligned} \dot{x}= P(x,y),\quad \dot{y}=Q(x,y), \end{aligned}$$

with (P, Q) is a quasi-homogeneous polynomial vector field satisfying (4). If (x(t), y(t)) is one of its solutions, then for all $\lambda \in {\mathbb {R}}^+,$

$$\begin{aligned} ({\bar{x}}(t),{\bar{y}}(t))=\big (\lambda ^{s_1} x(\lambda ^{r-1}t),\lambda ^{s_2} y(\lambda ^{r-1}t)\big ) \end{aligned}$$

is another solution. As a consequence, the behaviour of all its solutions is controlled by the behaviour of its solutions in any neighbourhood of the origin. Moreover it has no limit cycles.

Proof

The proof of the stated property can be done by simple computations. For instance,

$$\begin{aligned} \dot{\bar{x}}(t)&= \lambda ^{s_1+r-1}\dot{x} (\lambda ^{r-1}t)=\lambda ^{s_1+r-1}P\big (x(\lambda ^{r-1}t),y(\lambda ^{r-1}t)\big )\\ {}&=\lambda ^{s_1+r-1} P\left( \frac{{\bar{x}}(t)}{\lambda ^{s_1}} ,\frac{\bar{y}(t)}{\lambda ^{s_2}}\right) =P({\bar{x}}(t),{\bar{y}}(t)). \end{aligned}$$

Then the first result follows because, for a suitable $\lambda$, the weighted homothety $(x,y)\rightarrow (\lambda ^{s_1}x,\lambda ^{s_2} y)$ transforms any small neighbourhood of the origin to any arbitrarily large neighbourhood of the origin.

The non existence of limit cycles is also a consequence of the same property because if the system has a periodic solution then all solutions must be periodic as well and it has a global center. $\square$

Next result gives, in the generic cases, the global phase portrait of a realization of system (1). Its proof is based on the classical work of A.F. Andreev about the study of nilpotent critical points, see [1], and on Proposition 2.1, that allows to transform local results into global ones.

Proposition 2.2

Consider the quasi-homogeneous vector field

$$\begin{aligned} \dot{x}=ax^q + b y, \quad \dot{y}=c x^{2q-1}+d x^{q-1}y, \end{aligned}$$

where $a, b, c, d \in {\mathbb {R}}$ and define

$$\begin{aligned} \phi =ad - bc \,\,\, \hbox {and}\, \,\,\delta =(q a - d)^2+ 4 q bc=(q a + d)^2- 4 q \phi . \end{aligned}$$

(5)

Assume that $b\phi \ne 0.$ Then the origin is its unique singularity and it is a global saddle when $\phi < 0$ (index -1) and a point of index $+1$ when $\phi >0.$ Moreover, in this latter case,

• (i) If $\delta \ge 0$, the the origin is a global non-monodromic point and:

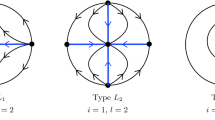
  • (i.1) if q is even then the phase portrait is globally formed by the union of a hyperbolic and an elliptic sector,

  • (i.2) if q is odd then the origin is a global node, stable if $qa+d <0$ and unstable if $qa+d >0$.

• (ii) If $\delta < 0$ then the origin is a global monodromic point and:

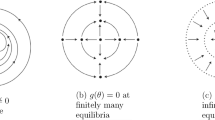
  • (ii.1) if q is odd then it is a global focus, stable if $qa+d <0$ and unstable if $qa+d >0;$ and a global center if $qa+d=0$,

  • (ii.2) if q is even then it is a global center.

Proof

The case $q=1$ corresponds to the linear case and the stated results are well-known. From now one, we will concentrate on the case $q>1.$

Recall that (2) is a quasi-homogeneous vector field with weight exponents $s_1=1$ and $s_2=q$ and weight degree q. By Proposition 2.1 to get its global phase portrait it suffices to study its local behaviour at the origin.

In [1] there is an explicit result that allows to know the local behaviour of any planar isolated nilpotent singularity for any analytic vector field, modulus the so called center-focus problem (that is the distinction in the monodromic case between center and focus). Andreev’s result is usually stated for systems in the normal form

$$\begin{aligned} \dot{x}=y+ X(x,y), \quad \dot{y}=Y(x,y), \end{aligned}$$

where X and Y have expansions at the origin that begin at least with second order terms in x and y. Then the type of critical points (modulus the center-focus problem) depends on some properties of the two functions

$$\begin{aligned} Y(x,h(x))&= u x^\alpha (1+O(x)),\\ \Psi (x)&=\left( \frac{\partial X}{\partial x}+\frac{\partial Y}{\partial y}\right) (x,h(x))=v x^\beta (1+O(x)), \end{aligned}$$

where $y=h(x)$ is the analytic function satisfying $h(0)=0$ and such that $h(x)+X(x,h(x))=0$ and $u\ne 0,$ $2\le \alpha \in {\mathbb {N}}$ and $1\le \beta \in {\mathbb {N}}$ and $v\ne 0$ are well defined, unless $\Psi =0.$. This behaviour only depends on $\alpha ,\beta ,u,v$ when $\Psi \ne 0$ and on $\alpha$ and u when $\Psi =0.$ See [1, 11] for more details.

For simplicity, before applying the above result, we start writing (2) in a more suitable form. Straightforward computations give that it is equivalent to the Liénard equation $\ddot{x}+ f(x) \dot{x} + g(x)=0$, where $f(x)=-(qa+d)x^{q-1}$ and $g(x)=\phi x^{2q-1}$. When $b\ne 0,$ this equation leads us to the generalized Liénard system

$$\begin{aligned} \dot{x}=z,\quad \dot{z}=-g(x) - f(x) z=-\phi x^{2q-1}+(qa+d)x^{q-1}z , \end{aligned}$$

(6)

that is already in Andreev’s form. Then, under condition $b\delta \ne 0,$ the origin is an isolated singularity for (6). Moreover $h=0$ and

$$\begin{aligned} Y(x,h(x))&=Y(x,0)=-g(x)=-\phi x^{2q-1},\\ \Psi (x)&=-f(x)=(qa+d)x^{q-1}. \end{aligned}$$

Hence $u=-\phi ,$ $\alpha =2q-1$ and either $\Psi =0,$ or $v=qa+d$ and $\beta =q-1.$ In short, either $\Psi =0$ or $\alpha =2\beta +1,$ and we can apply Andreev’s approach (we skip the details). We obtain the list of cases given in the statement, where in item (iii) his result only ensures that the origin is a monodromic critical point and we yet have the center-focus disjunctive. To resolve it we study separately the cases q odd and q even.

In the first case, q odd, the divergence of the vector field X associated to (6) is ${\text {div}}(X)=-f(x)=(qa+d)x^{q-1}.$ Hence, when $qa+d\ne 0$ it does not change sign (only vanishes on the straight line $x=0$). Hence, by the divergence theorem, the system has not periodic orbits and as a consequence the origin is a global focus. Clearly, its stability is given the the sign of $qa+d.$ When $qa+d=0,$ then $f=0$ and system (6) is easily integrable and its solutions are contained in the closed curves $qz^2+\delta x^{2q}=k,$ for $0<k\in {\mathbb {R}}.$ Hence a global center arises.

When q is even, system (6) is invariant by the change of variables and time $(x,z,t)\longrightarrow (-x,z,-t).$ Moreover, by Andreev’s approach we know that it is monodromic. Therefore, the Poincaré reversibility criterion implies that the origin is a global center. $\square$

Remark 2.3

(i) In the case $q=1$, we get back to the linear case and this classification coincides with the non-degenerate linear one, where $\phi$ is the determinant of the matrix and $\delta$ is the discriminant of the characteristic polynomial.

(ii) When for system (2), $b\phi =0,$ the origin is no more an isolated critical point. The phase portraits for these cases are much easier to be obtained. We will not describe them because in the probabilistic case they will have probability zero.

(iii) In this work we are not interested on the behaviour of the orbits of system (2) on the Poincaré disk. In any case, it is worth to know that near infinity on the Poincaré-Lyapunov disk, the behaviour of the equivalent Liénard system (6) can be easily obtained using the classification given in the work of F. Dumortier and C. Herssens [10].

Trying to understand why in the non-linear case the determinant $\phi =ad-bc$ plays a role similar to its role in the linear situation we have obtained an alternative way for proving Proposition 2.1. The point is that system (2) in the new variables

$$\begin{aligned} X=x^q,\quad Y=y\quad \hbox {and}\quad \frac{\mathrm{d} s}{\mathrm{d} t }= x^{q-1} \end{aligned}$$

(7)

writes as

$$\begin{aligned} X'=qaX + qb Y, \quad Y'=c X+d Y. \end{aligned}$$

(8)

Therefore, when q is odd, (7) is an actual change of variables, the new jacobian is simply $q(ad-bc),$ with the same sign that $ad-bc,$ and the new trace is $qa+d.$ Hence the same type of critical points that when $q=1$ appear.

On the other hand, when q is even, (7) is no more a change of variables, but a folding. Then the phase portrait of (8) on the plane $X>0$ appears diffeomorphically in the phase portrait of (2) on $x>0$ and as its specular image through a mirror located in $x=0$ when $x<0.$ In short, focus and nodes for system (8) go to centers, saddles go to saddles and nodes are transformed into points with one elliptic and one hyperbolic sector.

3 The Probabilistic Case: Proof of Theorem 1.1

In this section, we prove Theorem 1.1 that gives the probability of the different phase portraits described in Proposition 2.2. Inspired by the results of that proposition we define the new random variables $\Phi$ and $\Delta$,

$$\begin{aligned} \Phi =AD - BC \quad \hbox {and} \quad \Delta =(qA-D)^2 + 4qBC= (qA+D)^2-4q\Phi . \end{aligned}$$

Hence the desired probabilities can be computed as follows

$$\begin{aligned} P_s&=P\{\omega \, |\, \Phi (\omega )<0\},\\ P_{nm}&=P\{\omega \, |\, \Phi (\omega )>0,\, \Delta (\omega )> 0\},\\ P_{m}&=P\{\omega \, |\, \Phi (\omega ) >0,\, \Delta (\omega )< 0\}=P\{\omega \, |\, \Delta (\omega ) < 0\}, \end{aligned}$$

where notice that last equality holds because if $\Delta < 0$ then $\Phi >0$ due to the equality $\Delta = (qA+D)^2 -4q \Phi .$

Let us prove first that $P_s=P(\Phi <0)=1/2$. From the fact that the variables A, B, C and D are continuous, independent and identically distributed, the variables $\Phi =AD-BC$ and $\Psi =-AD+BC$ are continuous and identically distributed. As a consequence, $P(\Phi>0)=P(\Psi >0)=P(\Phi <0)$. Since $P(\Phi =0)=0$ it follows that $P(\Phi >0)=P(\Phi <0)=P_s=1/2$. Note also that

$$\begin{aligned} \frac{1}{2} = P(\Phi>0)= P(\Phi>0, \, \Delta>0)+P(\Phi >0, \, \Delta <0) \\ =P_{nm} + P_{m}. \end{aligned}$$

The final step is to compute $P_m=P(\Phi >0, \, \Delta < 0).$ If we denote by $Z=q A - D$, then Z is a normal random variable with zero mean and standard deviation $\sqrt{1+q^2}$. We consider the random vector $(X,Y,Z)=(B, C, qA-D)$, where X, Y, Z are independent normal variables with zero mean, $\sigma _X=\sigma _Y=1$ and $\sigma _Z=\sqrt{1+q^2}$. Thus the joint density function is

$$\begin{aligned} \Psi (x,y,z)=\frac{1}{(2\pi )^{3/2}\sqrt{1+q^2}}\,\exp \left( -\frac{(x^2+y^2)(1+q^2) + z^2}{2(1+q^2)}\right) . \end{aligned}$$

Hence

$$\begin{aligned} P_m=P(\Delta< 0)=P(Z^2+4qXY<0)=\int _K \Psi (x,y,z)\, \mathrm{d} x \, \mathrm{d} y \, \mathrm{d} z,\end{aligned}$$

where $K=\{ (x,y,z)\in {\mathbb {R}}^3\, :\, z^2+4qxy < 0\}$. To compute this integral, following the same ideas that in [3], we perform the change of variables

$$\begin{aligned} x=r\sin (t)\, \cos (s),\, y=r\sin (t)\, \sin (s),\, z=\sqrt{1+q^2}\, r \cos (t), \end{aligned}$$

where $t\in (-\frac{\pi }{2},\frac{\pi }{2})$, $s\in (0,2\pi )$ and $r>0$. Since the determinant of the Jacobian of the change is $\sqrt{1+q^2} \sin (t) r^2$, we have

$$\begin{aligned} P(\Delta < 0)=\frac{1}{(2\pi )^{3/2}}\int _{{\tilde{K}}}\int _0^{+\infty }|\sin (t)| r^2 \mathrm{e}^{-\frac{1}{2} r^2} \, \mathrm{d} r \, \mathrm{d} s\, \mathrm{d} t \end{aligned}$$

where ${\tilde{K}}=\{(s,t)\, :\, (1+q^2)\cos ^2( t )+ 2 q \sin ^2 (t) \sin (2s) < 0 \}$. Recall that

$$\begin{aligned} \int _0^{+\infty } r^2 \mathrm{e}^{-\frac{1}{2} r^2} \mathrm{d} r = \sqrt{\frac{\pi }{2}}. \end{aligned}$$

Hence

$$\begin{aligned} P(\Delta < 0)=\frac{1}{4\pi }\int _{{\tilde{K}}}|\sin (t)|\, \mathrm{d} s\, \mathrm{d} t . \end{aligned}$$

We consider the curve $(1+q^2)\cos ^2 (t) + 2 q \sin ^2 (t) \sin (2s) = 0$, that is, $t=\pm \arctan \left( \sqrt{\frac{1+q^2}{2q}}\, \frac{1}{\sqrt{-\sin (2s)}}\right) =:\pm g(s)$. Taking into account the symmetries we obtain that

$$\begin{aligned} \frac{1}{4\pi }\int _{{\tilde{K}}} |\sin (t)|\, \mathrm{d} s\, \mathrm{d} t = \frac{1}{\pi }\int _{\pi /2}^{\pi } \int _{g(s)}^{\pi /2} \sin (t)\, \mathrm{d} t \, \mathrm{d} s. \end{aligned}$$

Using that $\cos (\arctan (\alpha ))=1/\sqrt{\alpha ^2 +1}$, and doing $u=2s$, we get

$$\begin{aligned} \int _{\pi /2}^{\pi } \int _{g(s)}^{\pi /2} \sin (t)\, \mathrm{d} t \, \mathrm{d} s=\frac{1}{2} \int _{\pi }^{2\pi } \sqrt{\frac{\sin (u)}{\sin (u) - Q}}\, \mathrm{d}u, \end{aligned}$$

where $Q=\frac{1+q^2}{2q}$. Note that $Q\ge 1$. Finally, by doing the change of variable $x=u-\pi$ and taking into account the symmetry of $\sin (x),$

$$\begin{aligned} \int _{\pi }^{2\pi } \sqrt{\frac{\sin (u)}{\sin (u) - Q}}\, \mathrm{d}u=\int _{0}^{\pi } \sqrt{\frac{\sin (x)}{\sin (x) + Q}}\, \mathrm{d} x = 2\int _{0}^{\pi /2} \sqrt{\frac{\sin (x)}{\sin (x) + Q}}\, \mathrm{d} x \end{aligned}$$

At this point, from all previous calculations we get

$$\begin{aligned} P_m=P_m(q)=P(\Delta < 0)=\frac{1}{\pi }\int _{0}^{\pi /2} \sqrt{\frac{\sin (x)}{\sin (x) + Q}}\, \mathrm{d} x, \end{aligned}$$

as we wanted to prove.

There is a alternative way for obtaining $P_m(q)$ which uses a beautiful result od Edelman and Kostlan for computing the expected number of real zeros of a family of polynomials whose coefficients are Gaussian random variables, see [12, 13]

Proof

(Alternative way for obtaining $P_m(q)$) This different approach has two steps: First, we relate $P_m$ with the expected number of invariant curves of the form $\alpha y+ \beta x^q=0$ by the flow of the random system (1). Secondly, we compute this expected number.

For linear vector fields the existence of invariant lines $\alpha x+\beta y=0$ and the flow over them allows to determine the type of phase portrait. For instance, when a linear planar systems has not invariant straight lines then the origin is monodromic and it is either a focus or a center. In the same way, the existence of invariant curves of the form $\alpha x^q+\beta y=0$ and the flow over them plays a similar role to know the global phase portrait of a quasi-homogeneous system (2). Since the line $x=0$ is invariant only when $b=0$ we can skip this case (this is so, because it corresponds to the event $B=0$ for the random vector field (1) and therefore it has probability of appearance 0). Hence, we restrict our attention to find conditions for (2) to have an invariant curve of the form $y=\lambda x^q,$ where $\lambda =-\alpha /\beta .$ To get these conditions on $\lambda$ notice that

$$\begin{aligned} 0&=\frac{\mathrm{d}}{\mathrm{d} t} \left. \left( y-\lambda x^{q}\right) \right| _{y=\lambda x}=\left. \left( \dot{y}-\lambda q x^{q-1}{\dot{x}}\right) \right| _{y=\lambda x}\\ {}&=\left. \left( (c x^{2q-1}+d x^{q-1}y)-\lambda q x^{q-1}(ax^q + b y)\right) \right| _{y=\lambda x} \\ {}&=\left( c+(d-qa)\lambda -qb\lambda ^2 \right) x^{2q-1}. \end{aligned}$$

Hence the conditions on $\lambda$ for the random system (1) to have an invariant curve $y=\lambda x^q$ is that

$$\begin{aligned} T(\lambda )=C_2 \lambda ^2 +C_1\lambda + C_0=0, \end{aligned}$$

where T is a random polynomial and $C_2=-qB$, $C_1=D-qA$ and $C_0=C$. Moreover, since A, B, C, D have N(0, 1) distribution and are independent, that implies $C_0$ is N(0, 1), $C_1$ is $N(0,1+q^2)$ and $C_2$ is $N(0,q^2)$ and they are also independent. In a while we will compute the number of expected roots E(q) of this random polynomial. Let as see, firstly how this value is related with $P_m(q).$

The point is that the following results hold:

• If a realization of the polynomial T has two real roots then the corresponding of system (1) has either a saddle or a non-monodromic critical point of index $+1.$

• If a realization of the polynomial T has not real roots then the corresponding of system (1) has a monodromic critical point.

• That a realization of the polynomial T has exactly one real root happens with probability zero.

As a consequence, the expectation number of real roots of T is

$$\begin{aligned} E(q)=&2\cdot P(T\,\hbox { has 2 real roots})+1\cdot P(T\, \hbox { has 1 real root})\\ {}&+0\cdot P(T\, \hbox { has 0 real roots})=2\cdot (P_s+P_{nm})+1\cdot 0+0\cdot P_m. \end{aligned}$$

Using that $P_s=1/2$ and that $P_{nm}=1/2-P_m$ we obtain that

$$\begin{aligned} P_m(q)=1-\frac{E(q)}{2}, \end{aligned}$$

(9)

which is the desired relation.

To end the proof, let us compute E(q). The coefficients of $T(\lambda ),$ $C_i$, $i=1,2,3$, are independent normal random variables with zero mean and covariance matrix M where

$$\begin{aligned} M^{1/2}= \begin{pmatrix} 1 &{} 0 &{} 0 \\ 0 &{} \sqrt{1+q^2} &{} 0 \\ 0 &{} 0 &{} q \end{pmatrix}. \end{aligned}$$

Following [12, Thm 3.1], if we define $w( t )=M^{1/2}\cdot (1, t , t ^2)^T$ and ${{{\textbf {w}}}}( t )=w( t )/||\omega ( t )||$, then the expected number of real zeros of T is given by the Edelman-Kostlan formula:

$$\begin{aligned} E(q) = \frac{1}{\pi }\int _{-\infty }^{\infty }||{{{\textbf {w}}}}'( t )||\, d t . \end{aligned}$$

By straightforward computations, we obtain

$$\begin{aligned} {{{\textbf {w}}}}( t )=\frac{1}{\sqrt{q^2 t ^4+(q^2+1) t^2+1}}\big (1,\sqrt{q^2+1}\, t , q t ^2\big ) \end{aligned}$$

and as a consequence

$$\begin{aligned} E(q)&=\frac{1}{\pi }\int _{-\infty }^{\infty } \frac{\sqrt{(q^4+q^2) t ^4+4q^2 t ^2+q^2+1}}{( t ^2+1)(q^2 t ^2+1)}\, \mathrm{d} t \end{aligned}$$

(10)

$$\begin{aligned}&=\frac{1}{\pi }\int _{0}^{\infty } \frac{\sqrt{(q^4+q^2)s^2+4q^2s+q^2+1}}{(s+1)(q^2s+1)\sqrt{s}}\, \mathrm{d} s. \end{aligned}$$

(11)

where this last equality follows by taking $s= t ^2.$ Finally, by using (9) we obtain a new expression of $P_m(q).$ $\square$

4 Equivalent Expressions and Properties of $P_m$

We start giving a different expression of the integral given in (3) that is suitable for obtaining $P_m(1).$ Similarly, (11) could be used. In this integral we do the change of variables $y=1/\sin (x).$ We obtain that

$$\begin{aligned} P_m(q)= \frac{1}{\pi }\int _1^\infty \frac{1}{y\sqrt{(Qy+1)(y^2-1)}}\,\mathrm{d}y. \end{aligned}$$

(12)

If we substitute when $q=1,$ then $Q=1,$ and by introducing $w=\sqrt{y-1}$ we obtain that

$$\begin{aligned} P_m(1)&=\frac{1}{\pi }\int _1^\infty \frac{1}{y(y+1)\sqrt{y-1}}\,\mathrm{d}y=\frac{1}{\pi }\int _0^\infty \frac{2}{(1+w^2)(2+w^2)}\,\mathrm{d}w\\ {}&=\frac{1}{\pi }\int _0^\infty \left( \frac{2}{1+w^2}-\frac{2}{2+w^2}\right) \,\mathrm{d}w\\ {}&=\left. \frac{2}{\pi }\arctan (w)\right| _{0}^{\infty }-\left. \frac{\sqrt{2}}{\pi }\arctan \left( \frac{w}{\sqrt{2}}\right) \right| _{0}^{\infty }=1-\frac{\sqrt{2}}{2}. \end{aligned}$$

Another similar expression for $P_m(q)$ follows, again starting from expression (3), using the related change $\sin (x) = y.$ We arrive to

$$\begin{aligned} P_m(q)=\frac{1}{\pi }\int _0^1 \sqrt{\frac{y}{(y+Q)(1-y^2)}}\, \mathrm{d} y. \end{aligned}$$

(13)

Next we present two expressions of $P_m(q)$ in terms of some classical transcendental function obtained using Maple and Mathematica.

First expression, starting from (3):

$$\begin{aligned} P_m(q)= & {} \frac{1}{12\pi \sqrt{2\pi }Q^{3/2}}\left( 24Q\,\Gamma ^2\left( \frac{3}{4}\right) {_3}{\text {F}}_2\left( \frac{1}{4},\frac{3}{4},\frac{3}{4};\frac{1}{2},\frac{5}{4};\frac{1}{Q^2}\right) \right. \\&-\left. \Gamma ^2\left( \frac{1}{4}\right) {_3}{\text {F}}_2\left( \frac{3}{4},\frac{5}{4},\frac{5}{4};\frac{3}{2},\frac{7}{4};\frac{1}{Q^2}\right) \right) \end{aligned}$$

where $\Gamma$ is the gamma function and ${_3}{\text {F}}_2$ is the generalized hypergeometric function.

Second expression, starting from (12):

$$\begin{aligned} P_m(q)=\frac{\sqrt{2}}{\pi \,\sqrt{Q}} \left( \left( 1+Q \right) {\Pi } \left( -\frac{1}{Q},\sqrt{\frac{Q-1}{2Q}} \right) -Q{\text {K}}\left( \sqrt{\frac{Q-1}{2Q}} \right) \right) \end{aligned}$$

where ${\text {K}}(\,\cdot \,)$, the EllipticK function, is the complete elliptic integral of the first kind while ${\Pi }(\,\cdot \,,\,\cdot \,)$, the EllipticPi function, is the complete elliptic integral of the third kind.

4.1 Some Properties of $P_m(q)$

Recall that from (3) it holds that

$$\begin{aligned} P_m(q)= H\left( \frac{1+q^2}{2q}\right) ,\hbox { where } H(Q)=\frac{1}{\pi }\int _{0}^{\pi /2} \sqrt{\frac{\sin (x)}{\sin (x) + Q}}\, \mathrm{d} x. \end{aligned}$$

(14)

Next result collect several properties of H that can be used to approach $P_m(q).$

Proposition 4.1

Let $H:(0,\infty )\rightarrow {\mathbb {R}}$ be the function defined in (14). The following holds:

• (i) It is completely monotone, that is, $(-1)^n H^{(n)}(Q)>0,$ for all $n\ge 0.$

• (ii) For all $n\ge 0,$ it holds that

  $$\begin{aligned} H^{(n)}(1)=\frac{(-1)^n(2n-1)!!}{2^{n-1}\pi }\int _0^\infty \frac{(1+w^2)^{n-1}}{(2+w^2)^{n+1}}\,\mathrm{d}w \end{aligned}$$

  and all these values can be computed explicitly in terms of elementary functions.

• (iii) Let $T_m(Q)$ denote the Taylor polynomial of degree m at $Q=1,$ that is, $T_m(Q)=\sum _{n=0}^m \frac{H^{(n)}(1)}{n!}(Q-1)^n.$ Then, for all $j,k\ge 1,$ and all $Q>1,$

  $$\begin{aligned} T_{2j-1}(Q)< H(Q)< T_{2k}(Q). \end{aligned}$$

  (15)

• (iv) For all $Q>0,$

  $$\begin{aligned} \frac{L}{\sqrt{Q+1}}\le H(Q) \le \frac{L}{\sqrt{Q}}, \end{aligned}$$

  (16)

  where

  $$\begin{aligned} L=\frac{\Gamma \left( 3/4\right) }{2 \sqrt{\pi }\,\Gamma \left( 5/4\right) } \approx 0.38138. \end{aligned}$$

  and hence, $H(Q)\sim L/\sqrt{Q}$ at $Q=\infty .$

• (v) For $Q>1$ it holds that

  $$\begin{aligned} H(Q)= \sum _{n=0}^\infty { {-1/2}\atopwithdelims ()n } \frac{\Gamma \left( 3/4+n/2 \right) }{2 \sqrt{\pi }\,\Gamma \left( 5/4+n/2 \right) }\frac{1}{Q^n\sqrt{Q}}. \end{aligned}$$

Proof

(i) Notice first that for $Q>0$ the function $\sqrt{\frac{\sin (x)}{\sin (x) + Q}}$ and all its derivatives with respect to Q are integrable in $[0,\pi /2].$ Therefore, for all $n\ge 0,$

$$\begin{aligned} H^{(n)}(Q)&= \frac{1}{\pi }\frac{\mathrm{d}^{n}}{\mathrm{d} Q^n} \int _{0}^{\pi /2}\!\! \sqrt{\frac{\sin (x)}{\sin (x) + Q}}\, \mathrm{d} x= \frac{1}{\pi }\int _{0}^{\pi /2}\!\!\frac{\partial ^{n}}{\partial Q^n} \sqrt{\frac{\sin (x)}{\sin (x) + Q}}\, \mathrm{d} x\\&=\frac{(-1)^n(2n-1)!!}{2^{n}\pi }\int _{0}^{\pi /2}\frac{1}{(\sin (x)+Q)^n}\sqrt{\frac{\sin (x)}{\sin (x) + Q}}\, \mathrm{d} x. \end{aligned}$$

Then, clearly $(-1)^nH^{(n)}(Q)>0,$ as we wanted to show. We remark that complete monotone function are a subject of interest by themselves, see for instance [18].

(ii) By replacing $Q=1$ above and introducing the new variable $y=1/\sin (x),$ and then $w^2=y-1,$ as in the beginning of this section to obtain $P_m(1),$ we get that

$$\begin{aligned} H^{(n)}(1)&=\frac{(-1)^n(2n-1)!!}{2^{n}\pi }\int _{1}^\infty \frac{y^{n-1}}{(1+y)^{n+1}} \frac{\mathrm{d} y}{\sqrt{y-1}}\\&=\frac{(-1)^n(2n-1)!!}{2^{n-1}\pi }\int _0^\infty \frac{(1+w^2)^{n-1}}{(2+w^2)^{n+1}}\,\mathrm{d}w, \end{aligned}$$

as desired. For each given n the above functions have a primitive in terms of elementary functions and the values $H^{(n)}(1)$ can be explicitly obtained. For instance,

$$\begin{aligned} H'(1)=-\frac{\sqrt{2}}{16},\quad H''(1)=\frac{15\sqrt{2}}{256},\quad H'''(1)=-\frac{195\sqrt{2}}{2048}. \end{aligned}$$

(iii) Both inequalities are consequence of Taylor’s formula and the results of item (i).

(iv) Clearly, for all $0\le x\le \pi /2$, $Q\le \sin (x)+Q\le 1+ Q.$ Hence

$$\begin{aligned} \frac{\sqrt{\sin (x)}}{\pi \sqrt{1+Q}}\le \frac{1}{\pi }\sqrt{\frac{\sin (x)}{\sin (x) + Q}}\le \frac{\sqrt{\sin (x)}}{\pi \sqrt{Q}}. \end{aligned}$$

By integrating the above inequalities between 0 and $\pi /2$ we get that $L/\sqrt{1+Q}\le P_m(q)\le L/\sqrt{Q},$ where

$$\begin{aligned} L=\frac{1}{\pi }\int _0^{\pi /2} \sqrt{\sin (x)\,}\,\mathrm{d}x=\frac{\Gamma \left( 3/4\right) }{2 \sqrt{\pi }\,\Gamma \left( 5/4\right) }. \end{aligned}$$

We have used the equality

$$\begin{aligned} \int _0^{\pi /2} \sin ^\alpha (x)\,\mathrm{d}x= \frac{\Gamma \left( 1/2+\alpha /2 \right) }{\Gamma \left( 1+\alpha /2 \right) }\frac{\sqrt{\pi }}{2}, \end{aligned}$$

(17)

valid for all $\alpha >-1,$ when $\alpha =1/2.$

(v) If we introduce the new variable $U=1/\sqrt{Q}>0$ we have that $H(Q)=G(U),$ where G is the smooth function at $U=0,$

$$\begin{aligned} G(U)=&\frac{1}{\pi }\int _0^{\pi /2} \sqrt{\frac{U^2\sin (x)}{U^2\sin (x)+1}}\,\mathrm{d}x=\frac{U}{\pi }\int _0^{\pi /2}\!\!\! \sqrt{\frac{\sin (x)}{U^2\sin (x)+1}}\,\mathrm{d}x\nonumber \\ =&\frac{U}{\pi }\int _0^{\pi /2} \sum _{n=0}^\infty \sqrt{\sin (x)} { {-1/2}\atopwithdelims ()n } U^{2n}\sin ^n(x)\,\mathrm{d}x\nonumber \\ =&\frac{U}{\pi }\sum _{n=0}^\infty { {-1/2}\atopwithdelims ()n } \left( \int _0^{\pi /2} \sin ^{n+1/2}(x) \,\mathrm{d}x \right) U^{2n}, \end{aligned}$$

(18)

where we have used the uniform convergence of the series to interchange it with the integral. Using again (17), with $\alpha =n+1/2,$ the final expression of G follows. By replacing U by $1/\sqrt{Q}$ we get the desired result.

$\square$

From results (ii) and (iii) of the above proposition we can obtain good approximations of $P_m(q)$ for q not big. This is so just by recalling that, for big values of q, the remainder term of the Taylor’s formula can give a big error. On the contrary, since the boundedness given by expression (16) is better the higher the q value is taken, the results of item (iv) are suitable for big q. Finally, although the results of item (v) apply for all $q>1$, its convergence is faster when 1/Q is not big, hence we can apply it for medium and large values of q. Let us see some examples where we approach $P_m(2),$ $P_m(10)$ and $P_m(100).$

An approximation of $P_m(2).$ If $q=2,$ then $Q=5/4.$ By item (iii) we know for instance that

$$\begin{aligned} T_3\left( \frac{5}{4}\right)<H\left( \frac{5}{4}\right) =P_m(2)<T_2\left( \frac{5}{4}\right) . \end{aligned}$$

Some computations give that

$$\begin{aligned} 0.273035\approx 1-{\frac{134753\,\sqrt{2}}{262144}}<P_m(2)<1-{\frac{4209\,\sqrt{2}}{8192}}\approx 0.273386. \end{aligned}$$

Similarly, using $T_8$ and $T_9$ we get that

$$\begin{aligned} 0.273079881<P_m(2)<0.273079890 \end{aligned}$$

The integral (3) computed numerically gives the value $P_m(2)\approx 0.2730798826.$

An approximation of $P_m(100).$ As a consequence of (16) it easily follows that

$$\begin{aligned} P_m(q)\sim \frac{M}{\sqrt{q}}\quad \hbox {at}\quad q=\infty , \hbox { where } M=\sqrt{2\,} L \end{aligned}$$

(19)

For instance, it holds that $M/\sqrt{100}\approx 0.053935$ is a good approximation of $P_m(100).$ This is so because using the inequalities (16) we know that $0.0534<P_m(100)<0.0539.$ By evaluating numerically the definite integral given in (3) we get that $P_m(100)\approx 0.053544,$ see Table 1.

An approximation of $P_m(10).$ When $q=10,$ $Q=101/20.$ By item (v) we know that for $Q>1,$ $H(Q)=\lim _{k\rightarrow \infty } H_k(Q),$ where

$$\begin{aligned} H_k(Q)= \sum _{n=0}^k{ {-1/2}\atopwithdelims ()n } \frac{\Gamma \left( 3/4+n/2 \right) }{2 \sqrt{\pi }\,\Gamma \left( 5/4+n/2 \right) }\frac{1}{Q^n\sqrt{Q}}. \end{aligned}$$

Hence $P_m(10)=\lim _{k\rightarrow \infty } H_k(101/20).$ If we compute $H_k(101/20)$ for $k=2,3,4,5,6$ we get

$$\begin{aligned} 0.15895\ldots , 0.158736\ldots , 0.1587702\ldots , 0.1587648\ldots , 0.1587657\ldots \end{aligned}$$

providing good approximations of $P_m(10)\approx 0.158766,$ see again Table 1. For bigger values of Q the convergence is faster. For instance, taking $q=100,$ $Q=10001/200$ and

$$\begin{aligned} P_m(100)\approx H_3(10001/200)=0.053543958\ldots \end{aligned}$$

4.2 Some Numerical Simulations

Although we have a closed form in terms of a defined integral for $P_m(q)$ that allows to compute it simply by computing numerically this integral, in this section we show how to approximate $P_m(q)$ for some values of q,  using the celebrated Monte Carlo method.

In our setting we simply will take $N=10^6$ samples of the random vector (A, B, C, D) where the four variables are iid, with distribution N(0, 1),  and check how many of them, say J,  satisfy $\Delta =(qA-D)^2+4qBC<0.$ Then simply $P_m(q)\approx J/N.$ Due to the law of large numbers and the law of iterated logarithm it is known that this approach gives an absolute error of order $O(((\log \log N)/N)^{1/2}),$ which in practice behaves as $O(N^{-1/2}),$ see [14, 16]. Hence, since $N=10^6$ this absolute error is expected to be of order $O(10^{-3})$ and in Table 1 we only show 4 digits of the Monte Carlo results. Notice that comparing these values with the ones obtained by approximating the 1-variable definite integral, given in the second row of that table, the actual differences are the expected ones. To see more details about the probability that $|P_m(q)-J/N|$ is big see the discussion in [4, Sec. 3.2].

Table 1 Some approximated values of $P_m(q)$ obtained computing numerically the expression (3) and with Monte Carlo method taking $10^6$ random systems