From the Strong Differential to Italian Domination in Graphs

Abstract

Given a graph G and a subset of vertices $D\subseteq V(G)$, the external neighbourhood of D is defined as $N_e(D)=\{u\in V(G){\setminus } D:\, N(u)\cap D\ne \varnothing \}$, where N(u) denotes the open neighbourhood of u. Now, given a subset $D\subseteq V(G)$ and a vertex $v\in D$, the external private neighbourhood of v with respect to D is defined to be $\mathrm{epn}(v,D)=\{u\in V(G){\setminus } D: \, N(u)\cap D=\{v\}\}.$ The strong differential of a set $D\subseteq V(G)$ is defined as $\partial _s(D)=|N_e(D)|-|D_w|,$ where $D_w=\{v\in D:\, \mathrm{epn}(v,D)\ne \varnothing \}$. In this paper, we focus on the study of the strong differential of a graph, which is defined as

$$\begin{aligned} \partial _s(G)=\max \{\partial _s(D):\, D\subseteq V(G)\}. \end{aligned}$$

Among other results, we obtain general bounds on $\partial _s(G)$ and we prove a Gallai-type theorem, which states that $\partial _s(G)+\gamma _{_I}(G)=\mathrm{n}(G)$, where $\gamma _{_I}G)$ denotes the Italian domination number of G. Therefore, we can see the theory of strong differential in graphs as a new approach to the theory of Italian domination. One of the advantages of this approach is that it allows us to study the Italian domination number without the use of functions. As we can expect, we derive new results on the Italian domination number of a graph.

1 Introduction

Given a graph $G=(V(G), E(G))$ and a vertex $v\in V(G)$, the open neighbourhood of v is defined to be $N(v)=\{u\in V(G) :\, uv\in E(G)\}$. The open neighbourhood of a set $S\subseteq V(G)$ is defined as $N(S)=\cup _{v\in S}N(v)$, while the external neighbourhood of S, or boundary of S, is defined as $N_e(S)=N(S){\setminus } S$. The differential of a set $S\subseteq V(G)$ is defined as $\partial (S)=|N_e(S)|-|S|$, while the differential of a graph G is defined to be

$$\begin{aligned} \partial (G)=\max \{\partial (S):\, S\subseteq V(G)\}. \end{aligned}$$

As described in [19], the definition of $\partial (G)$ was given by Hedetniemi about 25 years ago in an unpublished paper, and was also considered by Goddard and Henning [9]. After that, the differential of a graph has been studied by several authors, including [1,2,3, 5, 19, 20].

Lewis et al. [19] motivated the definition of differential from the following game, what we call graph differential game. “You are allowed to buy as many tokens as you like, say k tokens, at a cost of one dollar each. You then place the tokens on some subset D of k vertices of a graph G. For each vertex of G which has no token on it, but is adjacent to a vertex with a token on it, you receive one dollar. Your objective is to maximize your profit, that is, the total value received minus the cost of the tokens bought”. Obviously, $\partial (D)=|N_e(D)|-|D|$ is the profit obtained with the placement D, while the maximum profit equals $\partial (G)$.

Given a set $D\subseteq V(G)$ and a vertex $v\in D$, the external private neighbourhood of v with respect to D is defined to be

$$\begin{aligned} \mathrm{epn}(v,D)=\{u\in V(G){\setminus } D: \, N(u)\cap D=\{v\}\}. \end{aligned}$$

We define the sets $D_w=\{v\in D:\, \mathrm{epn}(v,D)\ne \varnothing \}$ and $D_s=D{\setminus } D_w$.

We consider a version of the graph differential game in which you will get a refund of one dollar for each token placed in a vertex with no external private neighbour with respect to D, i.e., we will get a refund of one dollar for a token placed in a vertex v if either every neighbour of v has a token on it or every neighbour of v which has no token on it is also adjacent to a vertex different from v with a token on it. This version of the game can be called graph differential game with refund. Thus, we define the strong differential of D, denoted by $\partial _s(D)$, as the profit obtained with the placement D in the graph differential game with refund, which is $\partial _s(D)=|N_e(D)|-|D_w|$. Notice that

$$\begin{aligned} \partial _s(D)=|N_e(D)|-|D_w|=|N_e(D)|-|D|+|D_s|=\partial (D)+|D_s|. \end{aligned}$$

In the graph differential game with refund, the maximum profit equals the strong differential of G, which is defined as

$$\begin{aligned} \partial _s(G)=\max \{\partial _s(D):\, D\subseteq V(G)\}. \end{aligned}$$

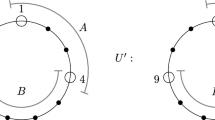
For instance, consider the graph G shown in Fig. 1. If D is the set of (gray and black) coloured vertices, and we place a token in each vertex belonging to D, then in the graph differential game with refund we get a refund of four dollars, as the black-coloured vertices do not have external private neighbours with respect to D. Although the gray-coloured vertex has four neighbours not belonging to D, it only contributes in three dollars to the profit, as it does not produce any refund. Hence, the total profit obtained with the placement D equals $\partial _s(D)=|N_e(D)|-|D_w|=9-1=8$. Notice that for this graph, the maximum profit equals $\partial _s(G)=\partial _s(D)=8$.

Fig. 1

A graph G with $\partial _s(G)=8$

Suppose that one “entity” is stationed at some of the vertices of a graph G and that an entity at a vertex can deal with a problem at any vertex in its neighbourhood. In general, an entity could consist of a robot, an observer, a legion, a guard, and so on. In this sense, given a set $D\subseteq V(G)$, we say that all vertices in N(D) are defended by the vertices in D. The whole graph is deemed protected under D if every vertex not in D has a neighbour in D, and in such a case we say that D is a protector of G. A vertex $u\in N_e(D)$ is strongly defended under D if $|N(u)\cap D|\ge 2$, otherwise u is weakly defended under D. Now, a vertex $v\in D$ is a weak defender with respect to D if $\mathrm{epn}(v,D)\ne \varnothing$, as there are vertices which are only defended by v, and so v does not have any help to defend its private neighbours. The set of weak defenders with respect to D is $D_w$, while any $v\in D_s=D{\setminus } D_w$ will be a strong defender with respect to D. In this sense, we can see the strong differential $\partial _s(D)=|N_e(D)|-|D_w|$ as a manner of quantify the quality of the protection of G with the placement D of entities. In this case, we have a penalty of one unit per each weak defender in D. With this approach, the strong differential allows us to compare two protectors, i.e., the larger $\partial _s(D)$ is, the better protector the set D is. In Sect. 3 we will show that for any graph, there exists a protector (dominating set) D with $\partial _s(D)=\partial _s(G)$. Thus, $\partial _s(G)$ quantifies the maximum quality among the protectors of G. In the same section we will see that the concept of strong differential is closely related to the theory of Italian domination, which is one of the approaches to protection of graphs. In that section, the role of weak and strong defenders will be clearly shown.

The remainder of the paper is organized as follows. In Sect. 2 we introduce some notation and tools needed to develop the remaining sections. In Sect. 3 we prove a Gallai-type theorem which states that $\partial _s(G)+\gamma _{_I}(G)=\mathrm{n}(G)$, where $\gamma _{_I}(G)$ denotes the Italian domination number of G. We conclude the section showing that the problem of finding $\partial _s(G)$ is NP-hard. Section  4 is devoted to provide general results on the strong differential. We obtain tight bounds, we show some classes of graphs for which the bounds are achieved and, in some cases, we characterize the graphs achieving the bounds. Some of these results are derived from known results on the Italian domination number, while from others we can infer new results on this invariant. The paper ends with a brief concluding remark section (Sect. 5) where we summarize some of these results.

2 Notation, Terminology and Basic Tools

Throughout the paper, we will use the notation $G \cong H$ if G and H are isomorphic graphs. The closed neighbourhood of a vertex v is defined as $N[v]=N(v) \cup \{v\}$. Given a set $S\subseteq V(G)$, $N[S]=N(S)\cup S$ and the subgraph of G induced by S will be denoted by G[S]. We denote by $\deg (v)=|N(v)|$ the degree of vertex v, as well as $\delta (G)=\min _{v \in V(G)}\{\deg (v)\}$ the minimum degree of G, $\Delta (G)=\max _{v \in V(G)}\{\deg (v)\}$ the maximum degree of G and $\mathrm{n}(G)=|V(G)|$ the order of G.

A leaf of G is a vertex of degree one. A support vertex of G is a vertex which is adjacent to a leaf. The set of leaves and support vertices of G will be denoted by ${\mathcal {L}}(G)$ and ${\mathcal {S}}(G)$, respectively.

A set $S\subseteq V(G)$ of vertices is a dominating set if $N(v)\cap S\ne \varnothing$ for every vertex $v\in V(G){\setminus } S$. Let ${\mathcal {D}}(G)$ be the set of dominating sets of G. The domination number of G is defined to be,

$$\begin{aligned} \gamma (G)=\min \{|S|:\, S\in {\mathcal {D}}(G)\}. \end{aligned}$$

The domination number has been extensively studied. For instance, we cite the following books, [11, 12].

We define a $\gamma (G)$-set as a set $S\in {\mathcal {D}}(G)$ with $|S|=\gamma (G)$. The same agreement will be assumed for optimal parameters associated to other characteristic sets defined in the paper. For instance, a $\partial _s(G)$-set will be a set $D\subseteq V(G)$ such that $\partial _s(D)=\partial _s(G)$.

A set S of vertices of G is a vertex cover if every edge of G is incident with at least one vertex in S. The vertex cover number of G, denoted by $\beta (G)$, is the minimum cardinality among all vertex covers of G. Recall that the largest cardinality of a set of vertices of G, no two of which are adjacent, is called the independence number of G and it is denoted by $\alpha (G)$. The following well-known result, due to Gallai, states the relationship between the independence number and the vertex cover number of a graph.

Theorem 1

(Gallai’s theorem, [8]) For any graph G,

$$\begin{aligned} \alpha (G)+\beta (G) = \mathrm{n}(G). \end{aligned}$$

Let $f: V(G)\longrightarrow \{0,1,2\}$ be a function and $V_i=\{v\in V(G):\; f(v)=i\}$ for $i\in \{0,1,2\}$. We will identify f with these subsets of V(G) induced by f, and write $f(V_0,V_1, V_2).$ The weight of f is defined to be

$$\begin{aligned} \omega (f)=f(V(G))=\sum _{v\in V(G)}f(v)=\sum _ii|V_i|. \end{aligned}$$

Cockayne et al. [7] defined a Roman dominating function, abbreviated RDF, on a graph G to be a function $f(V_0,V_1, V_2)$ satisfying the condition that every vertex $u\in V_0$ is adjacent to at least one vertex $v\in V_2$. The Roman domination number, denoted by $\gamma _{_R}(G)$, is the minimum weight among all RDFs on G, i.e.,

$$\begin{aligned} \gamma _{_R}(G)=\min \{\omega (f):\, f \text { is a RDF on } G\}. \end{aligned}$$

A generalization of Roman domination, called Italian domination, was introduced by Chellali et al. [6], where it was called Roman $\{2\}$-domination. The concept was studied further in [16, 18]. An Italian dominating function, abbreviated IDF, on a graph G is a function $f(V_0,V_1,V_2)$ satisfying that $f(N(v))=\sum _{u\in N(v)}f(u)\ge 2$ for every $v\in V_0$, i.e., $f(V_0,V_1,V_2)$ is an IDF if $N(v)\cap V_2\ne \varnothing$ or $|N(v)\cap V_1|\ge 2$ for every $v\in V_0$.

The Italian domination number, denoted by $\gamma _{_I}(G)$, is the minimum weight among all IDFs on G, i.e.,

$$\begin{aligned} \gamma _{_I}(G)=\min \{\omega (f):\, f \text { is an IDF on } G\}. \end{aligned}$$

Given a function f on G and a vertex $v\in V(G)$, we can assume that f(v) is the number of entities placed in v. In the theory of Italian domination, a graph G is deemed protected under f if every vertex of weight zero is protected by at least two entities, i.e., if f is an IDF. An IDF of weight $\omega (f)=\gamma _{_I}(G)$ is called a $\gamma _{_I}(G)$-function. In Sect. 3 we will see that for any $\gamma _{_I}(G)$-function $f(V_0,V_1,V_2)$ on G, the set $D=V_1\cup V_2$ is a protector of G of maximum quality, as $\partial _s(D)=\partial _s(G)$. Furthermore, $D_w=V_2$ and $D_s=V_1$. Therefore, in the theory of Italian domination, any $\gamma _{_I}(G)$-function provides the minimum number of entities needed to protect the graph and also provides a protector of maximum quality, according to the approach described in the previous section.

We assume that the reader is familiar with the basic concepts, notation and terminology of domination in graph. If this is not the case, we suggest the textbooks [11, 12]. For the remainder of the paper, definitions will be introduced whenever a concept is needed. In particular, this is the case for concepts, notation and terminology to be used only once.

3 A Gallai-Type Theorem

To deduce our results, we need to state the following basic lemma.

Lemma 1

For any graph G, there exists a $\partial _s(G)$-set which is a dominating set of G.

Proof

Let D be a $\partial _s(G)$-set such that |D| is maximum among all $\partial _s(G)$-sets. If $D \in {\mathcal {D}}(G)$, then we are done. Suppose that $D\not \in {\mathcal {D}}(G)$. Let $v\in V(G){\setminus } D$ such that $N(v)\cap D=\varnothing$ and let $D'=D\cup \{v\}$. We differentiate two cases.

Case 1. $epn(v,D')\ne \varnothing$. In this case, $D'_w\subseteq D_w\cup \{v\}$ and $|N(v){\setminus } N[D]|\ge 1$, which implies that $\partial _s(D')\ge |N_e(D)|+|N(v){\setminus } N[D]|-(|D_w|+1)\ge |N_e(D)|-|D_w|=\partial _s(D)=\partial _s(G).$ Therefore, $D'$ is a $\partial _s(G)$-set with $|D'|>|D|$, which is a contradiction.

Case 2. $epn(v,D')= \varnothing$. In this case, $D'_w\subseteq D_w$ and $N_e(D')=N_e(D)$, which implies that $\partial _s(D')\ge |N_e(D)|-|D_w|=\partial _s(D)=\partial _s(G).$ As above, $D'$ is a $\partial _s(G)$-set with $|D'|>|D|$, which is a contradiction.

According to the two cases above, D is a dominating set. Therefore, the result follows. $\square$

The following straightforward remark will be one of our tools.

Remark 1

If $D\in {\mathcal {D}}(G)$ is a $\partial _s(G)$-set, then

$$\begin{aligned} \partial _s(G)=\mathrm{n}(G)-|D|-|D_w|=\mathrm{n}(G)-|D_s|-2|D_w|. \end{aligned}$$

A Gallai-type theorem has the form $a(G)+ b(G)=\mathrm{n}(G)$, where a(G) and b(G) are parameters defined on G. This terminology comes from Theorem 1, which was stated in 1959 by the prolific Hungarian mathematician Tibor Gallai.

Theorem 2

(Gallai-type theorem for the differential and the Roman domination number, [2]) For any graph G,

$$\begin{aligned} \gamma _{_R}(G)+\partial (G)=\mathrm{n}(G). \end{aligned}$$

Inspired by the previous result, it is natural to ask if we are able to establish a Gallai-type theorem involving the strong differential. Precisely, the next result states the relationship between the strong differential and the Italian domination number.

Theorem 3

(Gallai-type theorem for the strong differential and the Italian domination number) For any graph G,

$$\begin{aligned} \gamma _{_I}(G)+\partial _s(G)=\mathrm{n}(G). \end{aligned}$$

Proof

By Lemma 1, there exists a $\partial _s(G)$-set D which is a dominating set of G. Hence, the function $g(W_0,W_1,W_2)$, defined from $W_1=D_s$ and $W_2=D_w$, is an IDF on G, which implies that $\gamma _{_I}(G)\le \omega (g)= 2|D_w|+|D_s|$. Therefore, Remark 1 leads to $\gamma _{_I}(G)\le \mathrm{n}(G)-\partial _s(G).$

We proceed to show that $\gamma _{_I}(G)\ge \mathrm{n}(G)-\partial _s(G).$ Let $f(V_0,V_1,V_2)$ be a $\gamma _{_I}(G)$-function. It is readily seen that for $D'=V_1\cup V_2$ we have that $D'_s=V_1$ and $D'_w=V_2$. Thus,

$$\begin{aligned} \partial _s(G)&\ge \partial _s(D')\\&=|N_e(D')|-|D'_w|\\&=|V(G){\setminus } (V_1\cup V_2)|-|V_2|\\&=\mathrm{n}(G)-2|V_2|-|V_1|\\&=\mathrm{n}(G)-\gamma _{_I}(G). \end{aligned}$$

Therefore, the result follows. $\square$

Theorem 3 allows us to derive results on the Italian domination number from results on the strong differential and vice versa. In the next sections, we present some of these results.

Now we analyse the case of the computational complexity. Given a positive integer k and a graph G, the problem of deciding if G has an Italian dominating function f of weight $\omega (f)\le k$ is NP-complete [6]. Hence, the problem of computing the Italian domination number of a graph is NP-hard. Therefore, by Theorem 3 we immediately obtain the analogous result for the strong differential.

Theorem 4

The problem of computing the strong differential of a graph is NP-hard.

4 General Bounds

We next present tight bounds on the strong differential of a graph. In some cases, we provide classes of graphs achieving the bounds, while in other cases, we characterize the graphs reaching the equalities.

4.1 Bounds in Terms of the Order

In this subsection, we show some interesting results on the strong differential in terms of the order of G. These results are directly derived from known results on the Italian domination number.

Theorem 5

[18]. If G is a connected graph with $\mathrm{n}(G)\ge 3$, then

$$\begin{aligned} \gamma _{_I}(G)\le \frac{3}{4}\mathrm{n}(G). \end{aligned}$$

Furthermore, if G is a connected graph with $\delta (G)\ge 2$, then

$$\begin{aligned} \gamma _{_I}(G)\le \frac{2}{3}\mathrm{n}(G), \end{aligned}$$

while if $\delta (G)\ge 3$, then

$$\begin{aligned} \gamma _{_I}(G)\le \frac{1}{2}\mathrm{n}(G). \end{aligned}$$

Therefore, from Theorems  3 and 5 we derive the following result on the strong differential.

Theorem 6

If G is a connected graph with $\mathrm{n}(G)\ge 3$, then

$$\begin{aligned} \partial _s(G)\ge \frac{1}{4}\mathrm{n}(G). \end{aligned}$$

Furthermore, if G is a connected graph with $\delta (G)\ge 2$, then

$$\begin{aligned} \partial _s(G)\ge \frac{1}{3}\mathrm{n}(G), \end{aligned}$$

while if $\delta (G)\ge 3$, then

$$\begin{aligned} \partial _s(G)\ge \frac{1}{2}\mathrm{n}(G). \end{aligned}$$

The reader is referred to [13] for a characterization of all graphs achieving the equalities in the bounds above.

4.2 Bounds in Terms of Order, Domination Number, 2-Domination Number and Number of Support Vertices

The following results show some basic property of the Italian domination number. Recall that a nontrivial tree is a tree of order at least 2.

Theorem 7

• [18] If T is a nontrivial tree, then $\gamma _{_I}(T) \ge \gamma (T)+1.$

• [6] For every graph G, $\gamma _{_I}(G) \le \gamma _{_R}(G) \le 2\gamma (G).$

• [6] For every graph G, $\gamma _{_I}(G) \le \gamma _{_2}(G).$

The trees satisfying $\gamma _{_I}(T)= \gamma (T)+1$, and the trees satisfying $\gamma _{_I}(T)= 2\gamma (T)$, were characterized in [16].

From Theorems 3 and 7 we conclude that if T is a nontrivial tree, then $\partial _s(T) \le n(T)- \gamma (T)-1$. As the next result shows, we can state a more general bound, which improves the previous one for some classes of trees. Here $\sigma (G)$ denotes the number of support vertices of G which are adjacent to more than one leaf.

Theorem 8

For any graph G,

$$\begin{aligned} \mathrm{n}(G)-\min \{2\gamma (G), \gamma _{_2}(G) \} \le \partial _s(G)\le \mathrm{n}(G)-\gamma (G)-\sigma (G). \end{aligned}$$

Proof

By Lemma 1, there exists $D\in {\mathcal {D}}(G)$ which is a $\partial _s(G)$-set. For every $x\in {\mathcal {S}}(G)$ we define ${\mathcal {L}}(x)=N(x)\cap {\mathcal {L}}(G)$ and ${\mathcal {L}}[x]=\{x\}\cup {\mathcal {L}}(x)$. Let ${\mathcal {S}}'(G)=\{x\in {\mathcal {S}}(G): \, |{\mathcal {L}}(x)|\ge 2\}$ and $D'={\mathcal {S}}'(G)\cup D{\setminus }(\cup _{x\in {\mathcal {S}}'(G)}{\mathcal {L}}(x))$. Notice that $D'$ is a dominating set of G and for any $x\in {\mathcal {S}}'(G)$, either $|D\cap {\mathcal {L}}[x]|=1$ and $x\in D_w$ or $|D\cap {\mathcal {L}}[x]|\ge 2$, while $|D'\cap {\mathcal {L}}[x]|=1$ and $x\in D'_w$. Hence, $\gamma (G)\le |D'|\le |D|$, $\sigma (G)\le |D'_w|$ and $|D'|+|D'_w|\le |D|+|D_w|$. Therefore, by Remark 1,

$$\begin{aligned} \partial _s(G)= \mathrm{n}(G)-|D|-|D_w|\le \mathrm{n}(G)-|D'|-|D'_w|\le \mathrm{n}(G)-\gamma (G)-\sigma (G). \end{aligned}$$

Finally, the lower bounds are derived from Theorems 3 and 7. $\square$

We next present some classes of graphs for which the bounds above are achieved. To begin with, we consider the following result, which is an immediate consequence of Theorem 8.

Corollary 1

Let G be a graph. If $\gamma _{_2}(G)=\gamma (G)$, then $\partial _s(G)=\mathrm{n}(G)-\gamma _{_2}(G)$.

Fig. 2

The set of (gray and black) coloured vertices forms a $\partial _s(G)$-set and a $\gamma _{_2}(G)$-set, while the set of black-coloured vertices forms a $\gamma (G)$-set

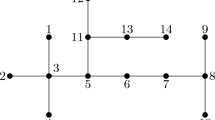
The converse of Corollary 1 does not hold. For instance, for the graph G shown in Fig. 2 we have that $\partial _s(G)=4=\mathrm{n}(G)-\gamma _{_2}(G)$, while $\gamma _{_2}(G)=4>2=\gamma (G)$.

Now, if ${\mathcal {G}}$ is the family of graphs of order at least three, where $\{{\mathcal {L}}(G),{\mathcal {S}}(G)\}$ is a partition of V(G) and every support vertex is adjacent to at least two leaves, then for every $G\in {\mathcal {G}}$ we have that $\gamma (G)=|{\mathcal {S}}(G)|=\sigma (G)$. In such a case, the only $\gamma (G)$-set is ${\mathcal {S}}(G)$, and we have that $\partial _s(G)\ge \partial _s(S)= |{\mathcal {L}}(G)|-|{\mathcal {S}}(G)|=\mathrm{n}(G)-2\gamma (G)$. Therefore, Theorem 8 leads to the following remark.

Remark 2

If $G\in {\mathcal {G}}$, then $\partial _s(G)=\partial (G)=\mathrm{n}(G)-2\gamma (G)=\mathrm{n}(G)-\gamma (G)-\sigma (G)$.

Next we proceed to discuss the case of graphs with $\partial _s(G)=\mathrm{n}(G)-\gamma (G)$.

Proposition 1

Given a graph G, the following statements are equivalent.

• (i) $\partial _s(G)=\mathrm{n}(G)-\gamma (G)$.

• (ii) $\gamma _{_2}(G)=\gamma (G)$.

Proof

First, assume $\partial _s(G)=\mathrm{n}(G)-\gamma (G)$. By Lemma 1, there exists $D\in {\mathcal {D}}(G)$ which is a $\partial _s(G)$-set. Since $\gamma (G)\le |D|$, Remark 1 leads to $\partial _s(G)=\mathrm{n}(G)-|D|-|D_w|\le \mathrm{n}(G)-\gamma (G).$ Hence, $|D|=\gamma (G)$ and $|D_w|=0$, which implies that $D=D_s$ and so D is also a 2-dominating set of G. Therefore, $\gamma _{_2}(G)\le |D|=\gamma (G)\le \gamma _{_2}(G)$, which leads to $\gamma _{_2}(G)=\gamma (G)$.

Conversely, if $\gamma _{_2}(G)=\gamma (G)$, then Theorem 8 leads to $\partial _s(G)=\mathrm{n}(G)-\gamma (G)$, which completes the proof. $\square$

Our next result describes the structure of some particular $\partial _s(G)$-sets for graphs with $\partial _s(G)=\mathrm{n}(G)-\gamma _{_2}(G)$.

Proposition 2

Given a graph G, the following statements are equivalent.

• (i) $\partial _s(G)=\mathrm{n}(G)-\gamma _{_2}(G)$.

• (ii) There exists a $\partial _s(G)$-set D which is a dominating set and $D_w=\varnothing$.

Proof

If there exists a $\partial _s(G)$-set D which is a dominating set with $D_w=\varnothing$, then D is a 2-dominating set. Hence, $\partial _s(G)=\partial _s(D)=|N_e(D)|=\mathrm{n}(G)-|D|\le \mathrm{n}(G)-\gamma _{_2}(G)$. By Theorem 8 we deduce that $\partial _s(G)=\mathrm{n}(G)-\gamma _{_2}(G)$.

Conversely, assume $\partial _s(G)=\mathrm{n}(G)-\gamma _{_2}(G)$. For any $\gamma _{_2}(G)$-set X we have that $X_w=\varnothing$, and so $\partial _s(G)=\mathrm{n}(G)-\gamma _{_2}(G)=|N_e(X)|=|N_e(X)|-|X_w|=\partial _s(X)$. This implies that X is a $\partial _s(G)$-set satisfying the required conditions, which completes the proof. $\square$

Next we consider the case of graphs with $\partial _s(G)=\mathrm{n}(G)-\gamma _{_2}(G)$.

Proposition 3

Given a graph G, the following statements are equivalent.

• (i) $\partial _s(G)=\mathrm{n}(G)-2\gamma (G)$.

• (ii) Every $\gamma (G)$-set D is a $\partial _s(G)$-set with $D_s=\varnothing$.

Proof

First, assume $\partial _s(G)=\mathrm{n}(G)-2\gamma (G)$, and let D be a $\gamma (G)$-set. Since $|N_e(D)|=\mathrm{n}(G)-\gamma (G)$, we have that $\mathrm{n}(G)-2\gamma (G)+|D_s|=|N_e(D)|-|D|+|D_s|=\partial _s(D) \le \partial _s(G)=\mathrm{n}(G)-2\gamma (G),$ which implies that $D_s=\varnothing$ and $\partial _s(D) = \partial _s(G)$.

Conversely, if very $\gamma (G)$-set D is a $\partial _s(G)$-set and $D_s=\varnothing$, then $\partial _s(G) = \partial _s(D)=|N_e(D)|-|D|=\mathrm{n}(G)-2\gamma (G)$. $\square$

By Theorem 8 and Proposition 3 we deduce the following result.

Proposition 4

If there exists a $\gamma (G)$-set D such that $D_s\ne \varnothing$, then

$$\begin{aligned} \partial _s(G)\ge \mathrm{n}(G)-2\gamma (G)+1. \end{aligned}$$

The bound above is tight. For instance, it is achieved by any graph G of order $r+2$ obtained from a star $K_{1,r}$ by subdividing one edge. In such a case, $\partial _s(G)=r-1= \mathrm{n}(G)-2\gamma (G)+1.$

Theorem 9

Let G be a graph. If $\delta (G)\ge 2$, then

$$\begin{aligned} \partial _s(G)\ge \frac{1}{2}\left( \mathrm{n}(G)-\gamma (G)\right) . \end{aligned}$$

Proof

Let S be a $\gamma (G)$-set and $C\subseteq V(G){\setminus } S$ the set of isolated vertices of the graph $G[V(G){\setminus } S]$. Assume $\delta (G)\ge 2$. If $V(G)=S\cup C$, then $S_w=\varnothing$ and so

$$\begin{aligned} \partial _s(G)\ge \partial _s(S)=|N_e(S)|=\mathrm{n}(G)-\gamma (G)\ge \frac{1}{2}(\mathrm{n}(G)-\gamma (G)). \end{aligned}$$

Now, assume $V(G){\setminus } (S\cup C)\ne \varnothing$. Let $S'$ be a $\gamma (G[V(G){\setminus } (S\cup C)])$-set. Since $G[V(G){\setminus } (S\cup C)]$ does not have isolated vertices, $|S'|\le \frac{1}{2}(\mathrm{n}(G)-(|S|+|C|))\le \frac{1}{2}(\mathrm{n}(G)-\gamma (G))$. Let $D=S\cup S'$. Notice that D is a dominating set of G and $D_w=\varnothing$. Hence,

$$\begin{aligned} \partial _s(G)&\ge \partial _s(D)\\&=|N_e(D)|\\&=\mathrm{n}(G)-|D|\\&\ge \mathrm{n}(G)-\left( \gamma (G)+\frac{1}{2}(\mathrm{n}(G)-\gamma (G))\right) \\&=\frac{1}{2}(\mathrm{n}(G)-\gamma (G)). \end{aligned}$$

Therefore, the result follows. $\square$

To show a class of graphs with $\partial _s(G)=\frac{1}{2}(\mathrm{n}(G)-\gamma (G))$, we consider the case of corona graphs. Given two graphs $G_1$ and $G_2$, the corona product graph $G_1\odot G_2$ is the graph obtained from $G_1$ and $G_2$, by taking one copy of $G_1$ and $\mathrm{n}(G_1)$ copies of $G_2$ and joining by an edge every vertex from the $i^{th}$-copy of $G_2$ with the $i^{th}$-vertex of $G_1$. For every $x\in V(G_1)$, the copy of $G_2$ in $G_1\odot G_2$ associated to x will be denoted by $G_{2,x}$. The following result was presented without proof in [4]. The reader is referred to [5] for a detailed proof.

Proposition 5

[4] For any graph $G_1$ and any nontrivial graph $G_2$,

$$\begin{aligned} \partial (G_1\odot G_2)=\mathrm{n}(G_1)(\mathrm{n}(G_2)-1). \end{aligned}$$

From the previous result, we can easily deduce the following proposition.

Proposition 6

For any graph $G_1$ and any nontrivial graph $G_2$,

$$\begin{aligned} \partial _s(G_1\odot G_2)=\mathrm{n}(G_1)(\mathrm{n}(G_2)-1). \end{aligned}$$

Proof

By Theorem 10 and Proposition  5 we deduce that

$$\begin{aligned} \partial _s(G_1\odot G_2)\ge \mathrm{n}(G_1)(\mathrm{n}(G_2)-1). \end{aligned}$$

Now, let S be a $\partial _s(G_1\odot G_2)$-set and $S'=\{x\in V(G_1) : \, S\cap (\{x\}\cup V(G_{2,x}))\ne \varnothing \}$. Thus,

$$\begin{aligned} \partial _s(G_1\odot G_2)= & {} |N_e(S)|-|S_w|\le (\mathrm{n}(G_1)-|S'|)+\sum _{x\in S'} (\mathrm{n}(G_2)-1)\\\le & {} \mathrm{n}(G_1)(\mathrm{n}(G_2)-1). \end{aligned}$$

Therefore, the result follows. $\square$

The bound given in Theorem 9 is achieved by any corona graph of the form $G\cong G_1\odot K_2$, where $G_1$ is an arbitrary graph. In this case, $\gamma (G)=\mathrm{n}(G_1)$, so that $\partial _s(G)=\mathrm{n}(G_1)=\frac{1}{2}(\mathrm{n}(G)-\gamma (G)).$

4.3 Bounds in Terms of Domination Number and Differential

Theorem 10

For any graph G,

$$\begin{aligned} \partial (G) \le \partial _s(G)\le \partial (G)+\gamma (G)-1. \end{aligned}$$

Proof

It is well known that for every graph G,

$$\begin{aligned} \partial (G)\ge \mathrm{n}(G)-2\gamma (G). \end{aligned}$$

(1)

From Theorem 8 and Eq. (1) we have that $\partial _s(G)\le \mathrm{n}(G)-\gamma (G)\le \partial (G)+\gamma (G)$. Now, if $\partial _s(G)= \partial (G)+\gamma (G)$, then $\partial (G)=\mathrm{n}(G)-2\gamma (G)$ and $\partial _s(G)= \mathrm{n}(G)-\gamma (G)$. Hence, by Proposition 1, $\gamma _2(G)=\gamma (G)$. Thus, any $\gamma _{_2}(G)$-set S is an independent set, and so for any $v\in S$, we have that $N_e(S{\setminus } \{v\})=V(G){\setminus } S$. This implies that

$$\begin{aligned} \partial (G)\ge \partial (S{\setminus } \{v\})=|N_e(S{\setminus } \{v\})|-|(S{\setminus } \{v\})|= \mathrm{n}(G)-2\gamma (G)+1, \end{aligned}$$

which is a contradiction. Therefore, $\partial _s(G)\le \partial (G)+\gamma (G)-1$.

On the other side, for any $\partial (G)$-set D,

$$\begin{aligned} \partial (G)=\partial (D)= |N_e(D)|-|D|\le |N_e(D)|-|D_w|= \partial _s(D)\le \partial _s(G). \end{aligned}$$

Therefore, the result follows. $\square$

The upper bound $\partial _s(G)\le \partial (G)+\gamma (G)-1$ is tight. For instance, it is achieved by the complete bipartite graph $K_{2, r}$.

Next we proceed to discuss the structure of some particular $\partial _s(G)$-sets for graphs with $\partial _s(G)=\partial (G)$.

Proposition 7

Given a graph G, the following statements are equivalent.

• (i) $\partial _s(G)=\partial (G)$.

• (ii) There exists a $\partial _s(G)$-set D such that $D_s=\varnothing$.

Proof

If there exists a $\partial _s(G)$-set D with $D_w=D$, then

$$\begin{aligned} \partial _s(G)=\partial _s(D)=|N_e(D)|-|D_w|= |N_e(D)|-|D|=\partial (D)\le \partial (G). \end{aligned}$$

Hence, Theorem 10 leads to $\partial _s(G)=\partial (G)$.

Conversely, assume $\partial _s(G)=\partial (G)$. If $D'$ is a $\partial (G)$-set, then

$$\begin{aligned}&|N_e(D')|-|D'_w|= \partial _s(D')\le \partial _s(G)=\partial (G)=|N_e(D')|-|D'|\\&\qquad \qquad \qquad \qquad \qquad \qquad \le |N_e(D')|-|D'_w|, \end{aligned}$$

and since $D'_w\subseteq D'$, we conclude that $D'=D'_w$ and also $D'$ is a $\partial _s(G)$-set, which completes the proof. $\square$

To conclude this subsection we proceed to derive a result for the particular case of trees. To this end, we need to recall the following known result.

Theorem 11

[6]. For any tree T,

$$\begin{aligned} \gamma _{_I}(T)\ge \frac{3}{4}\gamma _{_R}(T). \end{aligned}$$

The following bound is a direct consequence of Theorems 3 and 11.

Theorem 12

For any tree T,

$$\begin{aligned} \partial _s(T)\le \left\lfloor \frac{\mathrm{n}(T)+3\partial (T)}{4} \right\rfloor . \end{aligned}$$

The bound above is tight. For instance, it is achieved by any path of order $6k+3$, as $\partial _s(P_{6k+3})=3k+1$ and $\partial (P_{6k+3})=2k+1$, which implies that $\partial _s(P_{6k+3})=\left\lfloor \frac{6k+3+3\partial (P_{6k+3})}{4} \right\rfloor$.

4.4 Bounds in Terms of Order and Maximum Degree

Next we present another basic result obtained in [6].

Theorem 13

[6]. For any connected graph G, $\gamma _{_I}(G)\ge \frac{2\mathrm{n}(G)}{\Delta (G)+2}$.

It is not difficult to observe that the result above works for non-connected graphs.

Theorem 14

For any graph G,

$$\begin{aligned} \Delta (G)-1 \le \partial _s(G)\le \frac{\mathrm{n}(G)\Delta (G)}{\Delta (G)+2}. \end{aligned}$$

Proof

To prove the lower bound, we only need to observe that for every vertex v of maximum degree, $\partial _s(G)\ge \partial _s(\{v\})=\Delta (G)-1$.

The upper bound is a direct consequence of Theorems 3 and 13. $\square$

It is well known that $\gamma _{_2}(G)\ge \frac{2\mathrm{n}(G)}{\Delta (G)+2}$ for every graph G. The next result shows that the case $\gamma _{_2}(G)=\frac{2\mathrm{n}(G)}{\Delta (G)+2}$ characterises the graphs with $\partial _s(G)= \frac{\mathrm{n}(G)\Delta (G)}{\Delta (G)+2}$. Consequently, these graphs satisfy $\partial _s(G)=\mathrm{n}(G)-\gamma _{_2}(G)$.

Proposition 8

Given a graph G, the following statements are equivalent.

• (i) $\partial _s(G)= \frac{\mathrm{n}(G)\Delta (G)}{\Delta (G)+2}$.

• (ii) $\gamma _{_2}(G)=\frac{2\mathrm{n}(G)}{\Delta (G)+2}$.

Proof

If $\gamma _{_2}(G)=\frac{2\mathrm{n}(G)}{\Delta (G)+2}$, then Theorems 8 and 14 immediately lead to $\partial _s(G)= \frac{\mathrm{n}(G)\Delta (G)}{\Delta (G)+2}$.

To prove the converse, let D be a $\partial _s(G)$-set which satisfies Lemma 1. Let $X=\cup _{v\in D_w}\mathrm{epn}(v,D)$. Notice that $|X|\le \Delta (G)|D_w|$. Moreover, since every vertex $v\in N_e(D){\setminus } X$ satisfies that $|N(v)\cap D_s|\ge 2$, we obtain that $2|N_e(D){\setminus } X|\le \Delta (G)|D_s|$. Hence, since $D\in {\mathcal {D}}(G)$,

$$\begin{aligned} \mathrm{n}(G)&=|D|+|N_e(D)|\\&\le |D_w|+|D_s|+ \Delta (G)|D_w|+\frac{1}{2}\Delta (G)|D_s|\\&\le (\Delta (G)+1)|D_w| + \frac{1}{2}(\Delta (G)+2)|D_s|\\&\le \frac{1}{2}(\Delta (G)+2)(2|D_w|+|D_s|)\\&= \frac{1}{2}(\Delta (G)+2)(\mathrm{n}(G)-\partial _s(G)). \end{aligned}$$

Thus, if $\partial _s(G)= \frac{\mathrm{n}(G)\Delta (G)}{\Delta (G)+2}$, then we have equalities in the previous inequality chain, which implies that $D_w=\varnothing$. Therefore, by Proposition 2, $\frac{\mathrm{n}(G)\Delta (G)}{\Delta (G)+2}=\partial _s(G)=\mathrm{n}(G)-\gamma _{_2}(G)$, which implies that $\gamma _{_2}(G)=\frac{2\mathrm{n}(G)}{\Delta (G)+2}$. $\square$

To conclude this subsection, we characterize the trees for which the bound $\partial _s(G)\ge \Delta (G)-1$ is achieved. To this end, we need to introduce some additional notation.

Given a tree T and $v\in V(T)$, the eccentricity of v is denoted by ecc(v). We also define the following sets associated to v,

$$\begin{aligned} {\mathcal {L}}(v)=N(v)\cap {\mathcal {L}}(T) \quad \text { and }\quad {\mathcal {S}}_2(v)=\{u\in N(v):\, \deg (u)=2\}. \end{aligned}$$

We say that a tree T belongs to the family ${\mathcal {T}}$ if the following conditions hold for every vertex $v\in V(T)$ with $\deg (v)=\Delta (T)$.

A.1::

$v\in {\mathcal {S}}(T)$ and $ecc(v)\le 3$.

A.2::

$\deg (u)\le 3$ and $|{\mathcal {S}}_2(u)|\le 1$ for every $u\in N(v)$.

A.3::

$\deg (u)\le 2$ for every $u\in V(T){\setminus } N[v]$.

A.4::

$|{\mathcal {L}}(v)|\ge 2$ or there exists $u\in N(v)\cap {\mathcal {S}}(T)$ such that $\deg (u)=2$.

Lemma 2

Let $T\in {\mathcal {T}}$ and $v\in V(T)$. If $\deg (v)=\Delta (T)$, then there exists a $\partial _s(T)$-set D such that $v\in D_w$.

Proof

Suppose to the contrary that $v\notin D_w$ for every $\partial _s(T)$-set D. Let us fix a $\partial _s(T)$-set D. Notice that $v\in {\mathcal {S}}(T)$, by A.1. If $|{\mathcal {L}}(v)|\ge 2$, then $\partial _s(\{v\}\cup (D{\setminus } {\mathcal {L}}(v))\ge \partial _s(D)$, which is a contradiction. Now, if $|{\mathcal {L}}(v)|=1$, then by A.4, there exists $u\in N(v)\cap {\mathcal {S}}(T)$ such that $\deg (u)=2$. So, for $X=\{v\}\cup {\mathcal {L}}(u)\cup D{\setminus } ({\mathcal {L}}(v)\cup \{u\})$ we have that $\partial _s(X)\ge \partial _s(D)$, which is again a contradiction, as X is a $\partial _s(T)$-set and $v\in X_w$. Therefore, the result follows. $\square$

Proposition 9

Let T be a tree with $\mathrm{n}(T)\ge 3$. Then $\partial _s(T)=\Delta (T)-1$ if and only if $T\in {\mathcal {T}}$.

Proof

Assume $\partial _s(T)=\Delta (T)-1$ and let $v\in V(T)$ with $\deg (v)=\Delta (T)$. First, we proceed to prove that A.1 holds. If $v\not \in {\mathcal {S}}(T)$, then $\partial _s(T)\ge \partial _s(V(T){\setminus } N(v))= \Delta (T)$, which is a contradiction. Hence, $v\in {\mathcal {S}}(T)$. Now, if $ecc(v)\ge 4$, then there exists a vertex $v'\in V(T)$, which is at distance three from v, such that $\deg (v')\ge 2$. Notice that $\partial _s(\{v,v'\})\ge \Delta (T)$, which is again a contradiction. Hence, $ecc(v)\le 3$, as desired.

Now, we proceed to prove that A.2 holds. Suppose that there exists $u\in N(v)$ such that $\deg (u)\ge 4$. In this case, $\partial _s(\{v,u\})\ge \Delta (T)$, which is a contradiction. Now, if there exists $u\in N(v)$ such that $|{\mathcal {S}}_2(u)|\ge 2$, then $\partial _s(\{v\}\cup N({\mathcal {S}}_2(u)) )\ge \Delta (T)$, which is a contradiction. Therefore, A.2 follows.

From A.1 and A.2, if T is a path, then $T\cong P_3$ or $T\cong P_4$. Hence, from now on we assume that $\Delta (T)\ge 3$.

Now, if there exists $u\in V(T){\setminus } N[v]$ such that $\deg (u)\ge 3$, then $\partial _s(\{v,u\})\ge \Delta (T)$, which is a contradiction. Therefore, A.3 follows.

Finally, we proceed to prove that A.4 holds. Suppose to the contrary that $|{\mathcal {L}}(v)|=1$ and for every $u\in N(v){\setminus } {\mathcal {L}}(v)$ either ${\mathcal {S}}_2(u)\ne \varnothing$ or ${\mathcal {S}}_2(u)=\varnothing$ and $\deg (u)=3$. Let $U'=\{u\in N(v):\, {\mathcal {S}}_2(u)\ne \varnothing \}$ and $U''=N(v){\setminus } (U'\cup {\mathcal {L}}(v))$. Notice that if $u\in U'$, then $|{\mathcal {S}}_2(u)|=1$ and $|{\mathcal {L}}(u)|\le 1$, by A.2. Also, if $u\in U''$, then $|{\mathcal {L}}(u)|=2$. Now, let $X=X'\cup U''$, where

$$\begin{aligned} X'={\mathcal {L}}(v)\cup \left( \bigcup _{u\in U'}(\{u\}\cup {\mathcal {S}}_2(u)\cup {\mathcal {L}}(u))\right) . \end{aligned}$$

Since $X_s=X'$ and $X_w=U''$, we have that $\partial _s(X)=|N_e(X)|-|X_w|=(1+|X'|+2|U''|)-|U''|=1+|X'|+|U''|=\Delta (v)$, which is a contradiction. Therefore, A.4 follows.

Conversely, assume that $T\in {\mathcal {T}}$. By Theorem 14, we only need to prove that $\partial _s(T)\le \Delta (T)-1$. As above, let $v\in V(T)$ with $\deg (v)=\Delta (T)$. By Lemma 2, there exists $\partial _s(T)$-set D such that $v\in D_w$. We take D of minimum cardinality among these sets. Now, if $N(v)\cap D=\varnothing$, then A.1 and A.3 lead to $|N(x)\cap D |\le 1$ for every $x\in V(T){\setminus } N[v]$, which implies that $\partial _s(T)=\partial _s(D)\le \partial _s(\{v\})=\Delta (T)-1$. Now, suppose to the contrary that there exists $v'\in N(v)\cap D$. Let $T_{v'}$ be the sub-tree of T with root $v'$ obtained from T by removing the edge $\{v,v'\}$. By A.2 we have that $\deg (v')\le 3$ and $|{\mathcal {S}}_2(v')|\le 1$. Now, if $\deg (v')\le 2$, then by A.1 either $T_{v'}$ is a trivial tree or $T_{v'}\cong P_2$. Hence, $\partial _s(T)=\partial _s(D)<\partial _s(D{\setminus } (\{v'\}\cup {\mathcal {L}}(v')))$, which is a contradiction. Finally, if $\deg (v')=3$, then either $T_{v'}\cong P_3$ or $T_{v'}\cong P_4$, and so $\partial _s(T)=\partial _s(D)\le \partial _s(D{\setminus } V(T_{v'}))$, which is a contradiction, as $|D|>|D{\setminus } V(T_{v'})|$. Therefore, the result follows. $\square$

4.5 Bounds in Terms of Vertex Cover Number and Independence Number

If G is a graph with $\delta (G)\ge 2$, then any vertex cover S is a 2-dominating set, as $V(G){\setminus } S$ is an independent set. Hence, $\delta (G)\ge 2$ leads to $\mathrm{n}(G)-\gamma _{_2}(G)\ge \mathrm{n}(G)-\beta (G)=\alpha (G)$. Therefore, the following result is a direct consequence of Theorem 8.

Corollary 2

If G is a graph with $\delta (G)\ge 2$, then $\partial _s(G)\ge \alpha (G)$.

The bound above is tight. For instance, the graph G shown in Fig. 1 satisfies $\partial _s(G)=4= \alpha (G)$.

The following result, which states that $\partial _s(G)\ge \frac{1}{2}(\mathrm{n}(G)-\alpha (G))=\frac{1}{2}\beta (G),$ is not restricted to the case of graphs with $\delta (G)\ge 2$.

Theorem 15

Let G be a graph. If every component of G has maximum degree at least two, then

$$\begin{aligned} \partial _s(G)\ge \frac{1}{2}\beta (G). \end{aligned}$$

Proof

Assume that every component of G has maximum degree at least two. Let S be an $\alpha (G)$-set containing all leaves. Let $C\subseteq V(G){\setminus } S$ be the set of isolated vertices of $G[V(G){\setminus } S]$. If $V(G)=S\cup C$, then

$$\begin{aligned} \partial _s(G)\ge \partial _s(S)=|N_e(S)|-|S_w|=\mathrm{n}(G)-\alpha (G)\ge \frac{1}{2}(\mathrm{n}(G) -\alpha (G))=\frac{1}{2}\beta (G). \end{aligned}$$

Assume $V(G){\setminus } (S\cup C)\ne \varnothing$. Let $S'$ be a $\gamma (G[V(G){\setminus } (S\cup C)])$-set. Since the subgraph $G[V(G){\setminus } (S\cup C)]$ does not have isolated vertices,

$$\begin{aligned} |S'|\le \frac{1}{2}(\mathrm{n}(G)-(|S|+|C|))\le \frac{1}{2}(\mathrm{n}(G)-\alpha (G)). \end{aligned}$$

Now, let $D=S\cup S'$. Notice that D is a dominating set of G and $D_w=\varnothing$. Hence,

$$\begin{aligned} \partial _s(G)&\ge \partial _s(D)\\&=|N_e(D)|\\&=\mathrm{n}(G)-|D|\\&\ge \mathrm{n}(G)-\left( \alpha (G)+\frac{1}{2}(\mathrm{n}(G)-\alpha (G))\right) \\&=\frac{1}{2}(\mathrm{n}(G)-\alpha (G))\\&=\frac{1}{2} \beta (G). \end{aligned}$$

Therefore, the result follows. $\square$

The bound given in Theorem 15 is achieved by any corona graph of the form $G\cong G_1\odot K_2$, where $G_1$ is an arbitrary graph. In this case, $\beta (G)=2\mathrm{n}(G_1)$ and $\alpha (G)=\mathrm{n}(G_1)$, so that $\partial _s(G)=\mathrm{n}(G_1)=\frac{1}{2} \beta (G)=\frac{1}{2}(\mathrm{n}(G)-\alpha (G)).$

4.6 Bounds in Terms of Order and Semitotal Domination Number

A semitotal dominating set of a graph G without isolated vertices, is a dominating set D of G such that every vertex in D is within distance two of another vertex of D. The semitotal domination number, denoted by $\gamma _{_{t2}}(G)$, is the minimum cardinality among all semitotal dominating sets of G. This parameter was introduced by Goddard et al. [10], and it was also studied in [14, 15, 17].

Since every semitotal dominating set is also a dominating set, and every 2-dominating set is a semitotal dominating set, the next inequality chain holds.

$$\begin{aligned} \gamma (G)\le \gamma _{_{t2}}(G)\le \gamma _{_2}(G). \end{aligned}$$

(2)

The following result improves the upper bound given in Theorem 8 for graphs without isolated vertices.

Theorem 16

For any graph without isolated vertices,

$$\begin{aligned} \partial _s(G)\le \mathrm{n}(G)-\gamma _{_{t2}}(G). \end{aligned}$$

Proof

By Lemma 1, there exists $D\in {\mathcal {D}}(G)$ which is a $\partial _s(G)$-set. We consider a set $X\subseteq V(G)$ of minimum cardinality among the sets satisfying that $D\subseteq X$ and for any $x\in D_w$, there exists $u\in N(x)\cap X$. Since D is a dominating set of G, it is readily seen that X is a semitotal dominating set and also $|X|\le |D_s|+2|D_w|$. Hence, Remark 1 leads to

$$\begin{aligned} \partial _s(G)=\mathrm{n}(G)-(|D_s|+2|D_w|)\le \mathrm{n}(G)-|X|\le \mathrm{n}(G)-\gamma _{_{t2}}(G). \end{aligned}$$

$\square$

The bound above is achieved by the graph shown in Fig. 1. In this case, $\gamma _{_{t2}}(G)=6$ and $\partial _s(G)=\mathrm{n}(G)-\gamma _{_{t2}}(G)=8$.

The following result is an immediate consequence of Theorems 8 and  16.

Proposition 10

Let G be a graph. If $\gamma _{_{t2}}(G)=\gamma _{_2}(G)$, then $\partial _s(G)=\mathrm{n}(G)-\gamma _{_2}(G)$.

The converse of Proposition 10 does not hold. For instance, for the graph G shown in Fig. 2 we have that $\partial _s(G)=4=\mathrm{n}(G)-\gamma _{_2}(G)$, while $\gamma _{_2}(G)=4>2=\gamma _{_{t2}}(G)$.

4.7 Trivial Bounds and Extreme Cases

In this subsection, we discuss the trivial bounds on $\partial _s(G)$ and we characterize the extreme cases.

Proposition 11

Given a graph G of order $\mathrm{n}(G)\ge 3$, the following statements hold.

• (i) $0\le \partial _s(G)\le \mathrm{n}(G)-2.$

• (ii) $\partial _s(G)=0$ if and only if $\Delta (G)\le 1$.

• (iii) $\partial _s(G)=1$ if and only if either $G\cong G_1$ or $G\cong G_1\cup G_2$, where $G_1\in \{C_3,P_3,P_4\}$ and $\Delta (G_2)\le 1$.

• (iv) $\partial _s(G) = \mathrm{n}(G)-2$ if and only if $\Delta (G)=\mathrm{n}(G)-1$ or $\gamma _{_2}(G)=2$.

• (v) $\partial _s(G) = \mathrm{n}(G)-3$ if and only if $\gamma _{_2}(G)=3$ and $\Delta (G)\le \mathrm{n}(G)-2$ or $\gamma _{_2}(G)>3$ and $\Delta (G)=\mathrm{n}(G)-2$.

Proof

Since $\partial _s(\varnothing )=0$, we have that $\partial _s(G)\ge 0$. To prove the remaining statements, we take a $\partial _s(G)$-set $D\in {\mathcal {D}}(G)$, which exists due to Lemma 1. Now, since $|D|\ge 1$, either $|N_e(D)|\le \mathrm{n}(G)-2$ or $|D_w|\ge 1$, which implies that $\partial _s(G)=\partial _s(D)\le \mathrm{n}(G)-2$.

We proceed to prove (ii). If $\Delta (G)\le 1$, then $|N_e(D)|\le |D_w|$. This implies that $\partial _s(G)=\partial _s(D)=0$. Conversely, if $\partial _s(G)=0$, then $\deg (v)-1=\partial _s(\{v\})\le \partial _s(G)=0$ for every $v\in V(G)$, which implies that $\Delta (G)\le 1$. Therefore, (ii) follows.

We next proceed to prove (iii). If $\partial _s(G)=1$, then (i) and (ii) lead to $\Delta (G)=2$. If G is connected, then it is easy to see that $G\in \{C_3,P_3,P_4\}$. If G is not connected, then by (ii) we deduce that $G\cong G_1\cup G_2$, where $G_1\in \{C_3,P_3,P_4\}$ and $\Delta (G_2)\le 1$. The other implication is straightforward. Thus, (iii) follows.

Now, we proceed to prove (iv). If $\Delta (G)=\mathrm{n}(G)-1$, then (i) leads to $\partial _s(G) = \mathrm{n}(G)-2$. Moreover, if $\gamma _{_2}(G)=2$, then by Theorem 8 and (i) we deduce that $\partial _s(G) = \mathrm{n}(G)-2$. Conversely, assume $\partial _s(G) = \mathrm{n}(G)-2$. In this case, Remark 1 leads to $|D_s|+2|D_w|=2$, which implies that either $|D_w|=1$ and $|D_s|=0$ or $|D_s|=2$ and $|D_w|=0$. Since D is a dominating set of G, we obtain that $\Delta (G)=\mathrm{n}(G)-1$ or $\gamma _{_2}(G)=2$, as desired. Therefore, (iv) follows.

Finally, we proceed to prove (v). If either $\gamma _{_2}(G)=3$ and $\Delta (G)\le \mathrm{n}(G)-2$ or $\gamma _{_2}(G)>3$ and $\Delta (G)=\mathrm{n}(G)-2$, then by Theorem 8, and the statements (i) and (iv) we deduce that $\partial _s(G)=\mathrm{n}(G)-3$. Conversely, assume that $\partial _s(G) =\mathrm{n}(G)-3$. From (i) and (iv) we deduce that $\Delta (G)\le \mathrm{n}(G)-2$ and $\gamma _{_2}(G)\ge 3$. In this case, Remark 1 leads to $|D_s|+2|D_w|=3$, which implies that either $|D_w|=|D_s|=1$ or $|D_s|=3$ and $|D_w|=0$. If $|D_w|=|D_s|=1$, then $\Delta (G)=\mathrm{n}(G)-2$, while if $|D_s|=3$ and $|D_w|=0$, then $\gamma _{_2}(G)=3$, which completes the proof. $\square$

5 Concluding Remarks

In this paper, we have introduced the theory of strong differentials in graphs. This new branch of the domination theory, allows us to develop the theory of Italian domination without the use of functions. This interesting connection is due to Theorem 3, which is a Gallai-type theorem. For this reason, this article presents the challenge of obtaining new results on Italian domination following this novel approach. As an example, the following table summarizes some of those results obtained here. The first column describes the result that combined with Theorem 3 leads to the result on the second column.

From	Result
Theorem 8	$\gamma _{_I}(G)\ge \gamma (G)+\sigma (G)$
Proposition 1	$\gamma _{_I}(G)=\gamma (G)$ $\longleftrightarrow$ $\gamma _{_2}(G)=\gamma (G)$
Theorem 9	$\delta (G)\ge 2$ $\longrightarrow$ $\gamma _{_I}(G)\le \frac{1}{2}\left( \mathrm{n}(G)+\gamma (G)\right)$
Theorem 10	$\gamma _{_I}(G)\ge \gamma _{_R}(G)-\gamma (G)+1$
Proposition 8	$\gamma _{_I}(G)=\frac{2\mathrm{n}(G)}{\Delta (G)+2}$ $\longleftrightarrow$ $\gamma _{_2}(G)=\frac{2\mathrm{n}(G)}{\Delta (G)+2}$
Corollary 2	$\delta (G)\ge 2$ $\longrightarrow$ $\gamma _{_I}(G)\le \alpha (G)$
Theorem 15	G connected and $\mathrm{n}(G)\ge 3$ $\longrightarrow$ $\gamma _{_I}(G)\le \frac{1}{2}\beta (G)$
Theorem 16	$\delta (G)\ge 1$ $\longrightarrow$ $\gamma _{_I}(G)\ge \gamma _{_{t2}}(G)$
Proposition 10	$\gamma _{_{t2}}(G)=\gamma _{_2}(G)$ $\longrightarrow$ $\gamma _{_I}(G)= \gamma _{_{2}}(G)$