Abstract
Because of the isomorphism \(C \ell _{1,3}({\mathbb {C}})\cong C \ell _{2,3}({\mathbb {R}})\), it is possible to complexify the spacetime Clifford algebra \(C \ell _{1,3}({\mathbb {R}})\) by adding one additional timelike dimension to the Minkowski spacetime. In a recent work we showed how this treatment provide a particular interpretation of Dirac particles and antiparticles in terms of the new temporal dimension. In this article we thoroughly study the structure of the real Clifford algebra \(C \ell _{2,3}({\mathbb {R}})\) paying special attention to the isomorphism \(C \ell _{1,3}({\mathbb {C}})\cong C \ell _{2,3}({\mathbb {R}})\) and the embedding \(C \ell _{1,3}({\mathbb {R}})\subseteq C \ell _{2,3}({\mathbb {R}})\). On the first half of this article we analyze the Pin and Spin groups and construct an injective mapping \({\text {Pin}}(1,3)\hookrightarrow {\text {Spin}}(2,3)\), obtaining in particular elements in \({\text {Spin}}(2,3)\) that represent parity and time reversal. On the second half of this paper we study the spinor space of the algebra and prove that the usual structure of complex spinors in \(C \ell _{1,3}({\mathbb {C}})\) is reproduced by the Clifford conjugation inner product for real spinors in \(C \ell _{2,3}({\mathbb {R}})\).



Similar content being viewed by others
Notes
see chapter 6 of [27] for terminology.
The idempotent \(u_{1}\) appearing in [16] can only be constructed in the complex case: in the real spacetime algebra such an element does not exist.
N.B.: Pronounced /gemil/ in international phonetic alphabet, which is close to the English pronunciation of the word “gaemil”. It is a symbol present in the culture of the Mapuche people, which is a native people from the region of Patagonia, in the south of Argentina and Chile. As I searched for a name for this shape this was the one I found more accurate.
This can be seen easily because any element x in the Pin group is the product of a finite number of non-isotropic vectors. For a product of an even number of vectors \(\alpha (x)=x\) and for an odd number of vectors \(\alpha (x)=-x\).
Because S is a minimal left ideal and \(SS=C \ell _{p,q}f{f}C \ell _{p,q}f\) is a left ideal contained in S, then \(SS=S\).
For simple algebras, this is a consequence of the adjoint action of \({C \ell }_{p,q}^{*}\) being transitive on primitive idempotents, together with f and \(f^{\circ }\) being both primitive idempotents. In semisimple algebras the adjoint action has two orbits on primitive idempotents, and f and \(f^{\circ }\) belong to the same one. See Ref. [2] for a deeper analysis of idempotents on Clifford algebras.
See Sect. 6.1 to see in which sense \(A^{i}_{j}\) are the components of A in the basis
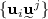 .
.In Appendix A.2 we write a very simple algorithm to find such an element in the Clifford standard basis.
References
Abłamowicz, R., Fauser, B.: Mathematics of Clifford—a Maple package for Clifford and Graßmann algebras. Adv. Appl. Clifford Algebras 15(2), 157–181 (2005). https://doi.org/10.1007/s00006-005-0009-9
Abłamowicz, R., Fauser, B., Podlaski, K., Rembieliński, J.: Idempotents of Clifford algebras. Czech J. Phys. 53(11), 949–954 (2003). https://doi.org/10.1023/B:CJOP.0000010517.40303.67
Abłamowicz, R., Lounesto, P.: On Clifford algebras of a bilinear form with an antisymmetric part. In Clifford Algebras with Numeric and Symbolic Computations, eds. R. Abłamowicz, P. Lounesto, and J. Parra, Birkhäuser, Boston (1996) 167–188. https://doi.org/10.1007/978-1-4615-8157-4_11
Abłamowicz, R., Gonçalves, I., da Rocha, R.: Bilinear covariants and spinor fields duality in quantum Clifford algebras. J. Math. Phys. 55(10), 103501 (2014). https://doi.org/10.1063/1.4896395
Aldrovandi, R., Almeida, J.P.B., Mayor, C.S.O., Pereira, J.G.: de sitter relativity and quantum physics. AIP Conf. Proc. 962(1), 175–184 (2007). https://doi.org/10.1063/1.2827302
Arcodía, M.R.A., Bellini, M.: Particle-antiparticle duality from an extra timelike dimension. Eur. Phys. J. C 79(9), 796 (2019). https://doi.org/10.1140/epjc/s10052-019-7311-5
Bars, I.: Survey of two time physics. Class. Quant. Grav. 18, 3113–3130 (2001). https://doi.org/10.1088/0264-9381/18/16/303
Barut, A., Ziino, G.: On parity conservation and the question of the ’missing’ (right-handed) neutrino. Mod. Phys. Lett. A 8, 1011–1020 (1993). https://doi.org/10.1142/S021773239300249X
Berg, M., DeWitt-Morette, C., Gwo, S., Kramer, E.: The Pin groups in physics: C, P, and T. Rev. Math. Phys. 13, 953–1034 (2001). https://doi.org/10.1142/S0129055X01000922
Crumeyrolle, A. (ed.): The Clifford groups, the twisted clifford groups and their fundamental subgroups. In: Orthogonal and Symplectic Clifford Algebras: Spinor Structures, pp. 58–67. Springer Netherlands, Dordrecht (1990). https://doi.org/10.1007/978-94-015-7877-6_4
Fauser, B.: Clifford geometric parameterization of inequivalent vacua. Math. Methods Appl. Sci. 24(12), 885–912 (2001). https://doi.org/10.1002/mma.247. https://onlinelibrary.wiley.com/doi/abs/10.1002/mma.247
Gallier, J.: Clifford algebras, Clifford groups, and a generalization of the quaternions (2008)
Henneaux, M., Teitelboim, C.: Asymptotically anti-de sitter spaces. Commun. Math. Phys. 98(3), 391–424 (1985). https://doi.org/10.1007/BF01205790
Hestenes, D.: Real spinor fields. J. Math. Phys. 8(4), 798–808 (1967). https://doi.org/10.1063/1.1705279
Hestenes, D.: Local observables in the Dirac theory. J. Math. Phys. 14(7), 893–905 (1973). https://doi.org/10.1063/1.1666413
Hestenes, D.: Observables, operators, and complex numbers in the Dirac theory. J. Math. Phys. 16(3), 556–572 (1975). https://doi.org/10.1063/1.522554
Hull, C., Townsend, P.: Unity of superstring dualities. Nucl. Phys. B 438(1), 109–137 (1995). https://doi.org/10.1016/0550-3213(94)00559-W. http://www.sciencedirect.com/science/article/pii/055032139400559W
Kocinski, J.: A five-dimensional form of the Dirac equation. J. Phys. A Math. Gen. 32(23), 4257–4277 (1999). https://doi.org/10.1088/0305-4470/32/23/306
Linch, W.D., Luty, M.A., Phillips, J.: Five-dimensional supergravity in \(\cal{N}=1\) superspace. Phys. Rev. D 68, 025008 (2003). https://doi.org/10.1103/PhysRevD.68.025008. https://link.aps.org/doi/10.1103/PhysRevD.68.025008
Lounesto, P.: Clifford Algebras and Spinors. 2nd edn., Cambridge University Press, Cambridge (2001). https://doi.org/10.1017/CBO9780511526022
Ma, G.W., Guo, Z.K.: 5d Dirac equation in induced-matter theory. Int. J. Theor. Phys. 41(9), 1733–1743 (2002). https://doi.org/10.1023/A:1021063202077
Monakhov, V.: The five-dimensional Dirac equation in the theory of algebraic spinors. Bull. Russ. Acad. Sci. Phys. 81(10), 1219–1224 (2017). https://doi.org/10.3103/S1062873817100197
Porteous, I.R.: Clifford Algebras and the Classical Groups. Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge (1995). https://doi.org/10.1017/CBO9780511470912
Ramond, P.: Field Theory: A Modern Primer. Frontiers in physics. Addison-Wesley Publishing Company, Advanced Book Program (2007). https://books.google.com.ar/books?id=mgVBjnLXT4cC
da Rocha, R., Vaz Jayme, J.: Conformal structures and twistors in the paravector model of spacetime. Int. J. Geom. Methods Mod. Phys. 4, 547–576 (2008). https://doi.org/10.1142/S0219887807002193
Sánchez, P.A., Anabitarte, M., Bellini, M.: Dirac equation for massive neutrinos in a Schwarzschild–de sitter spacetime from a 5d vacuum. Phys. Lett. B 705(5), 535–538 (2011). https://doi.org/10.1016/j.physletb.2011.10.058. http://www.sciencedirect.com/science/article/pii/S0370269311013128
Vaz, J., da Rocha, R.: An Introduction to Clifford Algebras and Spinors. Oxford University Press (2016). https://books.google.com.ar/books?id=VNMTDAAAQBAJ
Wesson, P.: Space-Time-Matter: Modern Kaluza-Klein Theory. World Scientific (1999). https://books.google.com.ar/books?id=l6xmSWLQJqkC
Wesson, P., Ponce de Leon, J., Liu, H., Mashhoon, B., Kalligas, D., Everitt, C., Billyard, A., Lim, P., Overduin, J.: A theory of space, time and matter. Int. J. Mod. Phys. A 11(18), 3247–3255 (1996). https://doi.org/10.1142/S0217751X96001553
Wesson, P.S.: Five-dimensional relativity and two times. Phys. Lett. B 538(1), 159–163 (2002). https://doi.org/10.1016/S0370-2693(02)01956-1. http://www.sciencedirect.com/science/article/pii/S0370269302019561
Wigner, E.: On unitary representations of the inhomogeneous Lorentz group. Ann. Math. 40(1), 149–204 (1939). http://www.jstor.org/stable/1968551
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Roldão da Rocha
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Code for computations on the \({C \ell }_{2,3}({\mathbb {R}})\) using the Clifford package for Maple
Appendix A. Code for computations on the \({C \ell }_{2,3}({\mathbb {R}})\) using the Clifford package for Maple
In this appendix we use the Clifford package for Maple [1], developed by Abłamowicz and Fauser to perform some calculations. We are going to use the following preamble, which contains information about the Clifford algebra and define the idempotent f, for all the calculations:
1.1 A.1. Computation of the \({\mathbb {K}}\)-basis for S
In order to compute the \({\mathbb {K}}\)-basis for S we use the command spinorKbasis. This command takes four inputs:
-
1.
a real basis for the space S,
-
2.
the idempotent f,
-
3.
a list of elements from the standard basis of \({C \ell }_{p,q}\) that generate \({\mathbb {K}}\) as a real vector space.
-
4.
the string “left” or “right” indicating if S is the left minimal ideal, \({C \ell }_{p,q}{f}\), or the right one, \(f{C \ell }_{p,q}\).
As a matter of fact spinorKbasis returns three elements, the \({\mathbb {K}}\)-basis for S is the first one. Let’s find all this objects needed as inputs using the Clifford package. To generate a real basis of S we are going to use the command minimalideal in the following way:
Lastly, we define the set of generators of \({\mathbb {K}}\), and compute the \({\mathbb {K}}\)-basis for S:
The basis obtained in this way, although rendering \(\gamma _{0}=-ie_{4}e_{0}\) diagonal, it is not the matrix for the Dirac representation. However, by the following reordering:
we obtain the basis in Eq. (58).
1.2 A.2. Finding the element s for the reversion inner product
The following algorithm finds the element s in Eq. (51), as long as it belongs in the standard basis, which is the case for the idempotent f in Eq. (53).
Rights and permissions
About this article
Cite this article
Arcodía, M.R.A. Complexifying the Spacetime Algebra by Means of an Extra Timelike Dimension: Pin, Spin and Algebraic Spinors. Adv. Appl. Clifford Algebras 31, 17 (2021). https://doi.org/10.1007/s00006-020-01109-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00006-020-01109-0




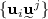 .
.