Abstract
Polar plumes are thin long ray-like structures that project beyond the limb of the Sun polar regions, maintaining their identity over distances of several solar radii. Plumes have been first observed in white-light (WL) images of the Sun, but, with the advent of the space era, they have been identified also in X-ray and UV wavelengths (XUV) and, possibly, even in in situ data. This review traces the history of plumes, from the time they have been first imaged, to the complex means by which nowadays we attempt to reconstruct their 3-D structure. Spectroscopic techniques allowed us also to infer the physical parameters of plumes and estimate their electron and kinetic temperatures and their densities. However, perhaps the most interesting problem we need to solve is the role they cover in the solar wind origin and acceleration: Does the solar wind emanate from plumes or from the ambient coronal hole wherein they are embedded? Do plumes have a role in solar wind acceleration and mass loading? Answers to these questions are still somewhat ambiguous and theoretical modeling does not provide definite answers either. Recent data, with an unprecedented high spatial and temporal resolution, provide new information on the fine structure of plumes, their temporal evolution and relationship with other transient phenomena that may shed further light on these elusive features.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Before space-borne instrumentation became available, the solar corona was observed only at the time of eclipses or with the ground-based coronagraphs introduced by Lyot in the early 1930s (Lyot, 1933). In spite of the paucity of observations, already at the beginning of the last century it was widely recognized that the outer atmosphere of the Sun was not homogeneous: thin bright features projecting beyond the solar limb in polar regions, named “rays” (Schuster, 1912) or “streamers” (Campbell et al., 1923), had been observed and their role investigated. Were they an indication that the Sun is a magnet or the hypothesis that they are “composed of charged particles ejected … from the Sun and moving under the influence of its magnetic field” (Campbell et al., 1923) was not really supported by the available observations? This discussion went on for several years but, by the 1950s, the “brush-like” plumes — as van de Hulst (1950) describes polar rays — were commonly acknowledged to provide information on the general magnetic field of the Sun and their interest for the physics of the Sun was associated with this issue. Hence, it became crucial to define the shape of the rays and identify the regions where they are rooted. It was at about that time, that scientists also started investigating these structures quantitatively, trying to determine their lifetime and sizes (see, e.g., Waldmeier, 1955) and their densities (see, e.g., van de Hulst, 1950; Saito, 1956) and turned their interest towards whether they represented outward flowing material or whether they were indicative of a hydrostatic corona. Van de Hulst (1950), on the ground that the profile of electron densities vs. heliocentric distance has approximately the same shape in rays and inter-rays, favored the hypothesis that both regions were static.
Nowadays, we are able to solve some of the puzzles that scientists had been pondered over during the last century. Undoubtedly, the continuous progress of space instrumentation, coupled with the opportunities offered by XUV spectroscopy, provided us with the means to solve some of those problems. At the same time, freed from waiting for eclipses to get data, the scientific community has been flooded by a wealth of observational material that raised new questions. First among these, plumes observed in EUV lines, such as those detected by the Naval Research Laboratory (NRL) and Harvard experiments on the Skylab mission (see, e.g., Bohlin et al., 1975a) are to be identified with the white-light rays/plumes observed at the time of eclipses or are they different features? How do physical parameters inferred from UV data — like element abundances, otherwise unknown — contribute to our understanding of plumes and of their role in coronal physics?
The reason why plumes are so relevant should be obvious at this stage: on a side they provide information on coronal magnetic fields as far out as they are identifiable, on the other, they may be responsible for solar wind, by supplying (most of) the solar wind mass flux and/or being the site where solar wind is accelerated. By comparing plume properties with those of wind streams observed in situ far away from the Sun, we also have the capability of linking coronal and distant solar wind plasmas. Quite obviously, this might be done also for the ambient coronal plasma, but the enhanced visibility of plumes establishes them as a better laboratory for this type of analysis.
This review illustrates how research on solar plumes developed through the years and starts (Section 2) discussing the plume morphology, from the identification of plumes in different wavelengths to how far they can be traced, and to the implications we draw for the magnetic field expansion. Plumes’ lifetime, size, shape, and source regions are also examined. Section 3 focusses on the physical characteristics of plumes, describing the methods used to derive their densities, temperatures and element abundances and the results obtained over the years. Especially relevant in this context are techniques to infer the presence, if any, of outflows in these structures. Section 4 deals with the search and identification of waves in plumes: the search is motivated by the need to check whether plumes (or their background interplume plasma) act as ducts that transport wave energy to higher layers, possibly feeding the wind. The next Section 5, is an attempt to give an account — we might say “write the biography” — of a plume, through the different stages of its life: Do plumes lead a quiet, uneventful, life, or do they experience dramatic changes? And, how far away from the Sun do they preserve their identity? Whether we are able to detect plumes with in situ experiments in the interplanetary medium is discussed in Section 6: What are the implications of a positive/negative outcome of this search? We proceed then to illustrate empirical and theoretical models of plumes (Section 7), looking for theoretical results that might guide us getting the meaning of what, at times, appear as ambiguous observations. So far, however, there are not so many models and many questions keep being unanswered. The final Section 8 summarizes areas that will likely be the focus of future research.
2 Plume Morphology
In this section, we review the long path taken from early eclipse observations of plumes in WL, to the acquisition of XUV data and to the recent STEREO observations of these features from two vantage points. As can be expected from the Introduction, the plume morphology is relevant not only per se, as a means to get a better knowledge of the shape/size/lifetime of these objects, but it also has a bearing on the shape of the magnetic field in the near and outer corona. We start summarizing the history of the WL imaging of plumes and of their impact on our concept of the magnetic field of the Sun.
2.1 Ground observations of WL plumes
Eclipses, once regarded as an inexplicable event, have been observed since the origin of mankind and, for a long time, only visually. Given the limited duration of an eclipse, not much could be learned, but even these unaided observations provide useful information. Captain Stanmyan, is the very first person credited for having taken notice, during the eclipse of May 12, 1706, of the red flash which is produced by spicules, immediately before and after totality (Lynn, 1885): because spicules require the presence of magnetic fields, Stanmyan report implies that significant magnetic fields were present on the Sun, even at the time of the Maunder minimum (Foukal and Eddy, 2007).
Obviously more significant data have been produced when eclipses have been, in some way, recorded. The first photograph of the solar corona, made with a daguerreotype and correctly exposed, was taken during the totality phase of the July 28, 1851 eclipse, in Königsberg, by a photographer, Berkowski, who had already made test experiments of the technique, taking pictures of the moon (Schielicke and Wittmann, 2005). This may be considered as an historical date: the time when eclipses started to be recorded by objective means. From then on, eclipse photographs of the outer layers of the Sun have been taken by experienced scientists who started organizing expeditions to observe the phenomenon wherever the totality path happened to be. The presence of “rays” or “streamers” was widely acknowledged and, by the end of the 19th century, already were explained in terms of tracers of the “lines of force emanating from the Sun” (Bigelow, 1891). Also, in his textbook, Abetti (1938) describes the different shapes of the corona as a function of the solar cycle.
Early photometric studies of rays (van de Hulst, 1950) lead to the first tentative estimates of the density enhancements of rays with respect to the ambient atmosphere (factor ≈ 5) and also to crude measurements of the ray width (≈ 2 degrees, for the larger structures), of their increase with heliocentric distance (increase of a factor 2, over a distance of 0.3 R⊙ above the limb of the Sun) and of their lifetime (hours/days) and percentage occupation of the polar surface (5%). We will see in the following how these initial estimates compare with more recent and sophisticated evaluations of these parameters, inferred from the analysis of higher quality data.
Going back to the configuration of the magnetic field inferred from eclipse observations of polar plumes, what did it imply for the global magnetic field of the Sun? Although the rays’ shape hints to a dipolar field, rays have an inclination to the radial that increases as the distance from the pole increases (see Figure 1). Hence, they are incompatible with the magnetic field of an infinitesimal dipole located at the Sun center and favor the idea of a magnet, whose poles are separated by about 2/3 of the solar diameter, as suggested in 1923 by Campbell et al. (1923).Footnote 1 Although van de Hulst’s results (van de Hulst, 1950) agreed with those of Campbell et al. (1923), it did not take long to realize that the outcome from this kind of analyses depends on the phase of the solar cycle at the time of the eclipse, thus leading to the suggestion that the Sun was kind of a “magnetically variable star” (Saito, 1956). The change of the magnetic field configuration with the solar cycle was then mimicked by different displacement of the magnetic monopoles from the center of the Sun (Shimooda, 1958) or by changing the length of the magnet (Rušin and Rybansky, 1976). An example of these first attempts to reproduce the plume orientation via simulations of the magnetic field of the Sun is shown in Figure 2.
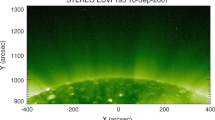
Ground image of the white-light solar corona at the 2010 July 11 eclipse, as seen from Atoll Hao, in the French Polynesia. Plumes, with an higher inclination to the radial as their distance from the Pole increases, are clearly visible in the north and South polar regions. A simultaneous disk image of the Sun, acquired in the 174 Å filter by the ESA/Proba-2 SWAP imager, shows these regions to correspond to coronal holes. Notice that it is hard to say which of the white-light structures seen above the polar holes are rooted inside, or outside, the holes. This ambiguity may account for some of the discrepancies between different studies of WL plumes (see also Section 7.1). Image reproduced with permission, copyright by ESA/Proba-2 consortium/SWAP team/Institut d’Astrophysique de Paris (CNRS & UPMC), S. Koutchmy/J. Mouette.
Simulation of polar magnetic fields, supposedly traced by polar rays, during the eclipses of 30 June 1954 (left) and of 20 June 1955 (right). Different parameters have been used to reproduce the observed rays configuration in the two eclipses. Image reproduced with permission from Shimooda (1958), copyright by ASJ.
It was around the 1960s, when the first computer codes to calculate coronal magnetic fields were developed (Schmidt, 1964) and became widely available: taking advantage of this new facility, Newkirk Jr and Harvey (1968) made a detailed study of plumes and polar fields, to establish a firm association between plumes and surface features lying at the footpoints of fieldlines. A possible association of plumes with polar faculae had been suggested by previous authors and it was on this basis that the lifetime of plumes had been guessed. Alternatively, Harvey (1965) used calcium K3 spectroheliograms as a proxy for the distribution and intensity of polar fields and established a correlation between plumes and K3 emission. Newkirk Jr and Harvey (1968) built on the collected evidence and concluded that most likely plumes form above the magnetic-field knots that show up at the intersection of network boundaries. The authors then assumed an idealized chromospheric network of cells with high field knots along their boundaries and used the potential field extrapolation code to mimic the shape of plumes in the corona and show that the calculated fieldline configuration looked very similar to that of plumes. Obviously, the result holds within the limitation of a potential extrapolation, but, at least in the lower corona, where the plume β is ≪ 1 (β being the ratio of the gas to the magnetic pressure), the current free approximation is perfectly tenable.
These studies have been further pursued in successive years: e.g., Suess (1982) modeled plumes with magnetic flux concentrations and, still in the current free approximation, reproduced the observed divergence of plumes in the lower corona. More sophisticated models (Suess et al., 1998), that adopt the potential field approximation at lower altitudes and global MHD simulation at higher levels, show that, at an heliographic altitude r, the expansion factor f(r) of plumesFootnote 2 is of order 15 within a height comparable to the typical distance between plumes, but it may increase reaching a value as high as 40, within the first 5 R⊙, if we take into account the spreading imposed by the geometry of the CH wherein plumes are embedded.
The outcome from these and previous works led to a picture of the polar magnetic field which diverges superradially, within the first solar radii to eventually become radial. Conversely, standard magnetic field superradially expanding models, such as that of Banaszkiewicz et al. (1998), have been used, with a pre-assumed spatial polar plume distribution, to reproduce typical configuration of polar regions (Raouafi et al., 2006). It is fair to mention that a few scientists do not share the concept of a superradial coronal field and favor a radially expanding geometry, as illustrated in a series of papers mainly focussing on links between coronal and interplanetary solar wind parameters (e.g., Woo and Habbal, 1997; Habbal and Woo, 2001; Woo et al., 2004). However, this suggestion meets with some skepticism within the solar community. The interest in the geometry of the polar magnetic field arises from its relevance to solar wind models, as different geometries imply different solutions of the solar wind equations (e.g., Kopp and Holzer, 1976). Obviously, an observational estimate of f(r) will be extremely valuable for solar wind modelers.
WL eclipse observations may contribute also to our knowledge of the plume dynamics. As seen in one location, eclipses are too short to provide valuable information on the plume dynamics, but coordinated observations along the path of eclipse may result in a long enough data set: Pasachoff et al. (2008) have been able to follow the propagation of a brightening within a plume over 1:09 hour at the 2006 March 29 eclipse. Tracking the positions of the brightest spot within a plume at different times, these authors give a mean outward speed on the order of 59–74 km s−1, over the height interval from the solar limb to ≈ 1.22 R⊙. The nature of the phenomenon they track is not clear: plasma motions or outward propagating waves possibly accounting for the observed behavior. Analogously, Bělík et al. (2013) examined WL images from the 2006 March 1, 2008 August 1, 2009 July 22, and 2010 July 11 eclipses analyzing a total of about 40 plumes. Their results agree with those of Pasachoff et al. (2008): outward propagating brightenings have been detected with speeds in the range 32–146 km s−1, whose nature, however, is not clear.
In conclusion, we realize that ground-based WL observations have allowed us to estimate the plume sizes and densities and have provided extremely relevant clues on their dynamics and on the location of their roots as well as on the configuration of the magnetic field of the Sun. The question of how far out in the corona plumes maintain their identity could be only vaguely answered by ground-based coronagraphs as their data are limited to the inner corona: for instance, plumes observed at the 2009 July 22 total solar eclipse, appear to be on the average only about 290 Mm long (Yang et al., 2011) and could not be identified beyond ≈ 0.5 R⊙. Although other WL eclipse data trace plumes to much larger distances (e.g., Koutchmy and Bocchialini, 1998), no information on the persistence of plumes at heliocentric distances on the order of 10–30 R⊙ could be obtained from ground data. Nor we know their temperatures, outflow speeds (if any) and element composition. Hence, although providing a wealth of information, a real advancement in plume physics was reached only with the advent of the space era, with space-based WL coronagraphs and XUV experiments that yield a completely new view of these features. Also, in situ experiments give us the possibility of checking how far out do plumes maintain their identity: are they still identifiable at interplanetary distances? The next Section 2.2 describes how plumes show up in XUV wavelengths and in WL space-borne coronagraphs.
2.2 XUV, radio and WL observations of plumes from space-borne experiments
Over a few years around the 1970s, the XUV data collected by early rocket flights and by OSO satellites, led to a series of papers that raised a large interest in coronal holes (CHs): as a consequence, CHs became one of the most interesting objectives of the Skylab mission, and, in particular, of its Apollo Telescope Mount (ATM; Tousey, 1977). ATM carried, beside a WL coronagraph and two Hα telescopes, two X-ray telescopes, an EUV spectroheliograph and two UV experiments (a spectroheliometer and a spectrograph), that provided the first images of plumes at XUV wavelengths. XUV plumes turned out to be much shorter than WL plumes: this, because the Thomson scattered WL intensity depends linearly on the electron density ne, while the XUV emission depends on \(n_e^2\). Hence XUV data provide crucial information at the very low coronal levels hardly imaged in WL. The first XUV images of plumes — see, e.g., Bohlin et al. (1975a,b); Ahmad and Withbroe (1977); Ahmad and Webb (1978) — showing analogous size and orientation of these features and WL rays, confirmed they were the same objects. This scenario was not accepted, e.g., by Koutchmy and Bocchialini (1997), who claimed that WL rays do not correspond exactly to UV features; by Li et al. (2000), who associate rays not to CHs but to active regions; and by Sornette et al. (1980), who identified WL rays with the upper section of jets originating at the boundaries of coronal holes. Projections effects, as well as the superradial expansion of the magnetic field within the first solar radii, make it difficult to solve this controversy. Also, recent observations show that polar jets and plumes are closely related (see Section 5.1) and may possibly account for Sornette et al., 1980 results.
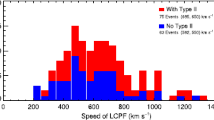
After these first experiments, plumes have been observed by many other space missions, like, e.g., SOHO, TRACE, STEREO, HINODE, SDO. Their data allowed us to follow plumes from the low corona (via, for instance, the SOHO/EIT telescope — see Delaboudinière et al., 1995 — that has a Field of View of approximately 1.5 R⊙) to far out in the corona, via e.g., the SOHO/LASCO C2 and C3 coronagraphs (Brueckner et al., 1995) that acquire WL images of the corona out to 30 R⊙. Studies by DeForest et al. (1997), DeForest et al. (2001b), and Wang et al. (2007a) where the base of plumes is identified via SOHO data, confirmed the continuity of plumes and WL rays. However, analogously using data from SOHO/EIT and LASCO, e.g., Llebaria et al. (1998), conclude that plumes and ray are distinct phenomena. More recently, this kind of analysis has been done by Gabriel, Tison and Llebaria (unpublished talk in Bern, ISSI Institute, at the meeting of the International Team on ‘Structure and dynamic of coronal plumes and interplume regions in solar coronal holes’, 2007–2010), who looked for correlations between the SOHO/EIT intensity of plumes in the 171 A band at 1.1 R⊙ and the intensity of LASCO C2 polarised brightness plumes at 3.1 R⊙. Although a negative correlation was seen only in ≈ 5% of the data, the authors found uncontroversial positive correlation only in ≈ 28% of their dataset and concluded that their study does not lead to a very convincing evidence.
The source of this discrepancy is not clear: however, if we look at Figure 3, we realize that there is an individual factor in interpreting data. Also, because of the weak signal of plumes at large distances, only the brightest structures can be identified out to these high altitudes — and extra care needs to be taken in the observing and processing procedures. The variability of plumes (see Section 5) adds to the uncertainties. Likely, a study where plumes and WL rays are followed in time will shed light on this issue, while missions with a more direct view of polar regions than obtained so far will solve this problem, because data will not be hindered by projection/superposition effects.
Polar plumes, imaged from the lower corona to 30 R⊙ solar radii, by SOHO/EIT (lowest altitudes, plume base, in the 195 Å radiation) and LASCO C2 and C3 (WL images from ≈ 2.5 R⊙ to 30 R⊙). Intermediate levels are covered by data from HAO Mk3 WL coronameter. Image reproduced with permission from DeForest et al. (2001b), copyright by AAS.
So far, we have examined “polar” plumes. However, if these features are rooted in coronal holes, there is no reason why they should not be hosted by non-polar CHs as well, although identifying low-latitude plumes in WL images among the variety of bright structures projected onto the disk or beyond the limb of the Sun from the fore and background may be a very difficult task. Hence, XUV data have been crucial in the identification of non-polar plumes: Wang and Sheeley Jr (1995a) examining Skylab data acquired by the NRL slitless spectrograph (Bohlin et al., 1975a) were able to identify plumes in the Mg ix 368 Å images of low latitude holes at the time they were crossing the limb of the Sun, while Del Zanna and Bromage (1999) were the first to report about SOHO observations of a low-latitude plume, that showed up in the “elephant’s trunk” equatorial coronal hole. As described later in the paper, polar and non-polar plumes share the same characteristics. Non-polar structures allow a better separation of plumes from the ambient corona, whose foreground/background effects can hardly be estimated in polar plumes. On the other hand, in equatorial plumes we only have line-of-sight (LOS) integrated quantities that cover different altitudes along the plume axis.
At about the same time, Woo (1996) and Woo and Habbal (1997) presented further evidence for the presence of low-latitude plumes from Ulysses radio measurements (at 3.6 and 13 cm) in the range 23–42 R⊙, in agreement with DeForest et al. (2001b) identification of plumes, in SOHO/LASCO data, out to more than 30 R⊙ (see also Figure 3). These results are based on a comparison of the profiles of WL measurements in the inner corona and path integrated density profiles from Ulysses data, but have been criticized by Pätzold (see Pätzold and Bird, 1998, 1999, and the answer to the criticisms by Woo and Habbal, 1998). Direct radio observations (see, e.g., Nindos et al., 1999; Pohjolainen et al., 2000; Pohjolainen, 2000; Moran et al., 2001) of coronal holes did not bring any clear evidence for plume emission, when compared with EIT maps. Hence, as of today, there is no definite conclusion on plume observability at radio wavelengths.
We like to close this section, pointing out an unconventional work, based on SOHO/EIT and STEREO/EUVI (Wülser et al., 2004) data, made by de Patoul et al. (2013a), who, starting from the plume orientation and assuming that the magnetic field of the Sun changes slowly with respect to the solar rotation rate, developed a procedure to calculate the temporal evolution of the magnetic poles of the Sun. Because the orientation of the plumes changes when new magnetic flux emerges, in an interesting future application of this research, we might be able to probe indirectly the flux emergence on the far side of the Sun, via observations of the inclination of plumes and of flux emergence in the visible side of the Sun. We notice that the technique of de Patoul et al. (2013a) does not take advantage of the different vantage points of the SOHO and STEREO spacecraft, being independent of the availability of data from multiple vantage points.
2.3 The size, shape and lifetime of plumes
The large quantity and variety of data accumulated by ground and space observations of plumes should have led to a good knowledge of basic parameters of plumes, like their shape, size, percentage occupancy of CH areas and duration. However, this is not completely true, because, as usual, new data bring new questions. For instance, the concept that plumes are, as inferred by traditional WL observations, approximately cylindrical objects, with a base diameter typically on the order of 30 000 km, (e.g., Saito, 1965; Fisher and Guhathakurta, 1995; DeForest et al., 1997) has been questioned by Gabriel et al. (2009), who suggest there are two distinct populations of plumes, the so-called beam plumes (which correspond to the traditional WL plumes) and network plumes. The latter, also dubbed curtain plumes, are envisaged as the outcome of the integrated emission of weak individual fine-scale microplumes (whose size could not be measured) rooted along the edge of supergranular cell boundaries. This LOS effect occurs whenever we look horizontally along one side of the network cell at the time it crosses the solar limb. On the contrary, beam plumes are supposed to overlie bright points (BPs), that is, localized magnetic flux areas emerged within a region of predominant opposite flux.
Non-polar plumes can help us identify the two classes of plumes: LOS integration effects occur along the plume axis, for structures seen at low latitudes, while polar plumes are affected by the horizontal integration over the plume-interplume ambient corona, that may include multiple unobserved structures. As described in Section 2.2, Wang and Sheeley Jr (1995a) identified non polar plumes in a low latitude hole, from Skylab S082 EUV images. Later on, Wang and Muglach (2008), examining SOHO/EIT images of low-latitude holes, as they rotate across the limb, confirmed the occurrence of low-latitude plumes and also report on the occasional occurrence of sheet-like structures associated with chains of decaying BPs, that might justify Gabriel et al. (2009) scenario: whether these chance alignments are to be identified with the network plumes and whether they justify the introduction of a new population of plumes is, however, questionable.
Beam plumes appear to be better identifiable than the ill-defined curtain plumes and indeed there have been recently a few attempts to reproduce their 3D structure, applying the rotational tomography technique to SOHO EIT data or using triangulation techniques on STEREO/SECCHI (Howard et al., 2008) EUVI plume observations. Because the rotational tomography should be applied to stable structures, Barbey et al. (2008) assumed that polar plumes are stationary objects, whose intensity changes homogeneously in time. Recently, Barbey et al. (2013) developed a more sophisticated procedure and tested it on polar plumes. Their results might be consistent with the two classes of plumes described above.
Feng et al. (2009) applied the triangulation techniques to STEREO/EUVI observations of 10 plumes, aiming at reconstructing their 3D geometry: their results support the superradial expansion of plumes and the increasing inclination to the radial that was emphasized by previous scientists (see Section 2.1). de Patoul et al. (2013b) applied both techniques (tomography and stereoscopic triangulation) to STEREO/SECCHI and SOHO/EIT data: the authors conclude that plumes may have all sort of shapes, once more in agreement with the two classes of plumes proposed by Gabriel et al. (2009), but point out that the time variability of plumes and their limited lifetime may affect their calculations. In conclusion, the 3D reconstruction of plumes might provide relevant information on their structure but is based on techniques complicated enough to limit their use to a few dedicated people. Also, possibly, they are still not wholly reliable because of the non stationary nature of plumes. Saez et al. (2007) implemented a method for the 3D reconstruction of large-scale structures, based on a forward modeling technique and extended it also to polar plumes: clearly stable large objects, like streamers, are best suited for their reconstruction process.
If a property of curtain plumes is, by definition, their filamentary structure, beam plumes as well may be composed of microstructures. The interplay between instrument resolution, substructures and inferred macroscopic parameters of plumes, has been discussed by DeForest (2007), who gives examples of the difference in plume parameters derived from data taken by different instruments. Llebaria et al. (2002), from the spectral analysis of the plume pattern in LASCO C2 data claim plumes are fractal structures and, as such, their typical diameter (as well as their lifetime) cannot be established. This implies a fibrous structure of CHs, at least over the spatial scale of WL observations. This would not be surprising, given the possibility for a fractal nature of the magnetic flux tubes and of the solar wind (see, e.g., Milovanov and Zelenyi, 1994) and is a promising future research area. However, so far, these studies have been done by only a very few authors (see also Boursier and Llebaria, 2008) and, from here onwards, we will ignore this possibility and deal with plumes as macroscopic structures.
As far as the lifetime of plumes, there is indeed a variety of different values in the literature, ranging from the “typical” duration of 20 hours of Lamy et al. (1997), to the 2–3 days of Young et al. (1999) and up to the two weeks of Withbroe et al. (1991) and DeForest et al. (2001a). These differences arise from the variability of plumes: plumes show up, decay and re-appear at the same location, and this may lead to different estimates of their lifetime. Also, DeForest et al. (1997) pointed out that the lifetime of a plume may depend on the spatial scale we examine, as plumes appear to be stationary over about 1 day when examining spatial scales greater than 10 arcsec, but to vary over a timescale of a few minutes on smaller spatial scales. We will come back on plume variability in Section 5.
What fraction of a CH area do plumes cover? This is not an otiose question, as it may first appear to be. We know that plumes are seen in CHs and that CHs have been recognized to be the source of the fast wind streams (see, e.g., Krieger et al., 1973). Hence, because plumes are the highest density structures within holes, if their plasma can be shown to be outflowing, their percentage occupancy becomes a key factor to estimate how much they contribute to the solar wind. Although here as well we have some spread among different estimates, plumes do not occupy more than a few percent of the CH area (see, e.g., van de Hulst, 1950; Wilhelm et al., 1998). In Sections 3.2.2 and 3.2.3, we will see whether plumes are static or whether they host outflowing plasma that reaches out to the interplanetary space.
3 The Physical Parameters of Plumes
We described in Section 2 what we know about the morphology of plumes and why we are interested in these objects. Since the time they had been imaged in WL, it was obvious they have a higher density than the ambient corona, being brighter in WL than the interplume plasma. Densities are indeed the only physical parameters that can be inferred from WL data and are higher than the ambient corona (e.g., van de Hulst, 1950; Fisher and Guhathakurta, 1995; DeForest et al., 2001b) even at large distances from the coronal base (a factor ≈ 3 at an altitude of 30 R⊙). Usually, these inferences neglect the brightness variation across plumes: however, Newkirk Jr and Harvey (1968) assumed densities to decline also with distance from the plume axis and built a 2D model of the plume density that accounts for the observed tapered (rather than cylindrical) shape of plumes. Temperatures can be guessed only by interpreting the radial density gradient in terms of a scale height temperature: this assumption leads to peak temperatures of plumes lower by 10–15% than peak temperatures of coronal holes (Fisher and Guhathakurta, 1995). Although relevant, these information are insufficient, if we aim at understanding the process that leads to the formation of plumes and the role of plumes in solar wind. For a more complete knowledge of the plume physical parameters, including their kinetic temperatures, outflow speeds (if any) and elemental abundances, we need to resort to space observations and XUV spectroscopy. Results from the XUV diagnostics of plumes’ plasma are given in Sections 3.1, 3.2 and 3.3.
3.1 Densities and temperatures of plumes from XUV data
Soon after the ATM on Skylab started operating and plumes were identified, first reports on their physical parameters appeared in the literature. Bohlin et al. (1975b), with the NRL S082 slitless spectrograph, observed plumes in 34 lines, over the range 250–610 Å originating from at least four different ions: their presence suggested electron temperatures in the range 0.7 to 1.2 MK. The relative brightness of lines from different ions provided a first clue to the plume temperature.
The first detailed analyses of XUV plumes date back to the works of Ahmad and Withbroe (1977) and Ahmad and Webb (1978). Ahmad and Withbroe (1977) evaluated the electron temperature of three plumes observed (with a spatial resolution of 5 × 5 arcsec) by the Harvard Skylab experiment, from the ratio of the intensities of the Mg x λ 625 Å and O VI λ 1032 Å lines and give a mean electron temperature of 1.1 MK. Their technique is based on the relationship for the radiance Iline (ph cm−2 s−1 sterad−1) of an optically thin line which forms by collisional excitation and radiative decay from level j to a lower level
where const includes the spectroscopic parameters of the line; G(Te), known as the contribution function, depends on the electron temperature via the ionization equilibrium of the ion emitting the line; ne is the electron density and the integral extends over the LOS. The integral of the square of the electron density ne over the LOS has come to be known as the line plasma emission measure (EM). In Eq. (1), we have assumed G(Te) ≈ G(Te, ne) because for most of the lines the contribution function peaks at a temperature Tf, known as the temperature of formation of the line, and depends much more strongly on Te than on density. More precisely, the contribution function of the line originating from the transition from level j to the fundamental level in the spectrum of an ion of charge state q of the element X can be written as:
where \({\textstyle{{{n_j}({X^{+ q}})} \over {n({X^{+ q}})}}}\) is the relative population of level j of the ion with charge state \(+ q,\;{\textstyle{{n({X^{+ q}})} \over {n(X)}}}\) is the relative population of the charge state \(+ q,\;{\textstyle{{n(X)} \over {n(H)}}}\) is the element abundance relative to hydrogen and \({\textstyle{{n(H)} \over {{n_e}}}}\) is the hydrogen abundance relative to that of the electrons. Aj is the radiative transition rate from level j to the fundamental level: here we make the usual assumption that only the two lowest levels of the ion are populated. In order to evaluate G(Te) we need to know the abundance of the element X, its ionization equilibrium and the atomic data of the transition. Equation (1) shows that from the ratio of the intensities of two lines of different elements (or of two lines of different ions of the same element), we get the value of the electron temperature, provided plasma is isothermal, the element abundances are precisely known, the contribution function depends only on temperature and the lines form, in the same volume, exclusively by collisional excitation and radiative de-excitation. The latter assumption does not hold for O VI lines, whose upper level is populated both by collisional and radiative excitation of the chromospheric radiation. Hence, the determination of Ahmad and Withbroe (1977) is rather crude; nevertheless their conclusion that plumes are cooler than the ambient CH is valid to these days.
Ahmad and Withbroe (1977) also inferred plume densities, across and along the plume axis, by assuming a priori the profiles of the density decrease with distance from the axis and from the base of the plume and adjusting the free parameters of their profiles to reproduce the observed line intensities. Densities along the axis of the plumes turned out to be ≈ a factor 3 higher than densities in coronal holes over the observed range of altitudes (≈ 70 000 km) along the plume. However, the density profiles were slightly different than implied by a static atmosphere: hence the authors conclude that the plume plasma is most likely outflowing at a speed of several times 10 km s−1. This might have been predicted by the simple, semi-qualitative argument that plumes are too tall, to be in hydrostatic equilibrium at the consensus temperature (see, e.g., DeForest, 2007) and was supported by a further analysis of Ahmad and Webb (1978), who examined the same plumes, imaged by the Skylab S0-54 X-ray telescope in the 2–32 and 44–54 Å X-ray bands. We postpone dealing with outflows in plumes to Sections 3.2.2 and 3.2.3.
Over the following years, more precise evaluations of temperatures and densities have been done by many authors: the reader may refer to Tables 3 and 4 of Wilhelm et al. (2011) for a summary of the inferred values. Improvements over the first determinations can be attributed both to the better data provided by the post-Skylab space missions and to the adoption of more sophisticated spectroscopic techniques.
A method quite analogous to that used by Ahmad and Withbroe (1977) has been adopted by, e.g., DeForest et al. (1997) and Moses et al. (1997), who, from the ratio of the intensities of plumes imaged by SOHO/EIT in the 171 (Fe ix/x) and 195 (Fe xii) channels, derived temperatures in the range 1–1.5 MK. Figure 4 shows images of plumes acquired by the SOHO/EIT telescope in two wave bands, the 171 Fe ix/x and the Fe xii 195 Å with peak sensitivities, respectively, at ≈ 1 MK and 1.5 MK. Del Zanna et al. (2003) cross-checked DeForest et al. (1997) results via SOHO/CDS data, showing that temperatures from EIT observations tend to be higher than temperatures from other experiments, possibly because of uncertainties in the cross calibration of different experiments. Del Zanna et al. (2003) also compared polar and equatorial plumes and concluded that they share the same characteristics.
Polar plumes, imaged by the SOHO/EIT experiment on May 8, 1996, in the 195 Å and in the 171 Å radiation. Plumes are better visible in the 195 Å channel because of its wide bandpass, that includes contribution from lower temperature lines. As shown by Del Zanna et al. (2003), the 195 Å plume emission originates mainly from the Fe vii and Fe viii ions, while the 171 Å plume emission originates mainly from the Fe ix ion.
Most of the post-Skylab works use SOHO SUMER (Wilhelm et al., 1995) and CDS (Harrison et al., 1995) spectral observations: these experiments provide the profiles of many lines that are especially suited for electron density and temperature diagnostics, because their formation mechanism depends crucially on these parameters. There are couple of lines, mostly from the same ion, whose intensity ratio is density-sensitive (or temperature-sensitive) because the intensities of the two lines depend on ne (or Te) via different functions. As a consequence, their ratio is a function of only this physical parameter. The interested reader can find a thorough description of the line ratio techniques in Mason and Fossi (1994): as the methods described earlier, these techniques are affected by density or temperature inhomogeneities along the LOS. Typically, ratios of the Si viii 1446 and 1440 and Si ix 342 and 345 Å line intensities have been used to evaluate densities, while temperatures have been inferred from the ratios of the O VI 1730 and 1032 and of the Mg ix 706 and 750 Å line intensities (e.g., Wilhelm et al., 1998; Del Zanna and Bromage, 1999; Mohan et al., 2000; Wilhelm, 2006; Banerjee et al., 2009).
A profile of the electron density vs. heliocentric distance of plumes/rays over the first 8 R⊙ has been given by Guhathakurta et al. (1999), using density-sensitive EUV line-ratios from SOHO/CDS in the 1–1.15 R⊙ height interval and WL data, from Mauna Loa, SOHO/LASCO C2 and C3 coronagraphs, at higher altitudes. Densities inferred from spectral and WL data appear to be consistent. Because the authors give only pB images, it is not easy to ascertain whether the EUV plume and the WL ray are the same structure. Also, as the authors themselves point out, there is a data gap between 1.4 R⊙ and 2.2 R⊙ (respectively, the highest/lowest level for reliable Mauna Loa/LASCO coronagraphs data) where densities cannot be directly inferred.
Whenever spectra with a variety of lines were available, emission measure diagnostic methods have been adopted, analogously to what done by Ahmad and Withbroe (1977), still assuming plasma to be isothermal. A more sophisticated technique, that does not require this approximation, is the differential emission measure (DEM) analysis. The DEM Φ(T) function provides an estimate of the amount of plasma between temperature T and T + dT along the LOS: in terms of the DEM Eq. (1) is rewritten as
where \(\Phi ({T_e}) = {\textstyle{{n_e^2\;{\rm{d}}l} \over {{\rm{d}}T}}}\). An example of the DEM distribution of a plume is given in Figure 5, from the work of Del Zanna et al. (2003). The narrowness of the DEM distribution reveals that the plume plasma is approximately isothermal.
The distribution of the DEM of a plume, observed by the SOHO/CDS experiment in the low latitude CH, dubbed the “elephant trunk”, as a function of temperature. Image reproduced with permission from Del Zanna et al. (2003), copyright by ESO.
It should be mentioned that determining the emission measure distribution is challenging (see, e.g., Testa et al., 2011), being the evaluation of the DEM an ill-posed inverse problem. Discussing solutions to this problem is beyond the aim of the present paper; we point out only that knowledge of the element abundances and of the atomic data is crucial as well. The continuing effort to obtain higher quality atomic data leads to an adjournement of the CHIANTI database (e.g., Dere et al., 1997) and is a further source of improvements with respect to previous works.
What are the outputs of these works? Rather than giving values inferred in individual papers, which can be found in the Wilhelm et al. (2011) review already mentioned, we conclude that all authors agree in defining plumes as structures with a higher density and a lower electron temperature than the ambient corona, the latter being usually identified with the weakest emitting region in between plumes. The amount by which these parameters differ may change in different works and at different heliocentric levels. Densities below two solar radii are typically a factor 3 larger in plumes than in the nearby ambient plasma. At higher levels it becomes difficult to give a typical value for the plume density enhancement as values between 2 and 7 have been given depending on the technique being used and on the altitude where the ratio is calculated. The electron temperature of plumes has a typical value of 0.8 MK, with negligible variation with altitude (at least below 1.2 R⊙: we do not have any estimate above this level), with the ambient corona temperature higher by 0.1 (at the base of plumes) − 0.3 MK (at 1.2 R⊙). This value has been raised to ≈ 0.4 MK by Del Zanna et al. (2008), who recalculated the electron-impact excitation of Be-like Mg ions: revisiting these values modified entries in the CHIANTI database and lead to the revision of the value of the temperature ratio. This is a good example of how atomic data may affect the calculation of physical parameters. We conclude pointing out that we have a more or less consistent scenario of plumes densities and temperatures and of their relationship with the parameters of the ambient CH within which they are immersed, but we have comparatively little information about how the physical conditions vary across a plume’s lifetime (see Section 5).
3.2 Element abundances and outflows in plumes
The analysis of the composition of the solar atmosphere reveals systematic differences in the element abundances measured in the photosphere, corona and solar wind. Indeed what justifies dealing, in the same section, with element abundances and outflows, that may at first appear as altogether disparate subjects, is the possibility of establishing a link between plumes and solar wind, via the comparison of the element abundances in plume and in the solar outflowing wind plasma. The next sections deal with the search for abundance anomalies in plumes (Section 3.2.1); the identification of the location, on the Sun, where line shifts, possibly indicative of nascent outflowing wind, occur (Section 3.2.2); and the detection of radial outflows in the intermediate corona in plumes and in the ambient interplume plasma (Section 3.2.3).
3.2.1 FIP effect in plumes?
The difference in the composition of elements throughout the solar atmosphere can be expressed via the first ionization potential (FIP) bias, which is defined as the ratio of the element abundance in the upper atmosphere (be it the corona or the wind plasma) to the abundance measured in the photosphere. Setting the division between low and high FIP ions around 10–11 eV, it has been established that the abundance of low FIP elements is enhanced by a factor 3–4 in the slow wind, while there is hardly any FIP effect in fast wind (see, e.g., Heber et al., 2012). Independent of any measurement of flows, evaluating the FIP bias in plumes and in the ambient medium may provide an indication about the presence and role of plumes in the wind. As plumes occur in CHs, which are the sources of fast streams, we need to compare plume and fast wind abundances. The first estimate of the abundance of elements in plumes has been done by Widing and Feldman (1992) who evaluated the ratio Mg/Ne, where Ne, with an ionization potential of 21.6 and Mg, with an ionization potential of 7.6 are representative, respectively, of the high and low FIP elements. Data had been acquired by the Skylab S082 spectroheliograph and abundances were inferred from Eq. (1), under the hypothesis of hydrostatic equilibrium. This assumption allows Widing and Feldman (1992) to derive a value of temperature, from the observed profile of the line intensities with height, and values of densities from some ad hoc assumptions about their profiles along and across the plume. The outcome of this analysis appeared to rule out plumes as sources of fast wind, because the abundance of Mg, relative to Ne, turned out to be ≈ a factor 10 higher than that measured in the photosphere, because of a strong enhancement of the plume Mg abundance — typically, in the photosphere, Mgab = 3.8 × 10−5 (Anders and Grevesse, 1989), Neab = 1.2 × 10−4 (Grevesse et al., 1992). A few years later, the abundance ratio of Mg to Ne in plume and interplume plasma was re-evaluated by Wilhelm and Bodmer (1998), who examined SOHO/SUMER data acquired in 1997 and used the line-ratio technique to infer temperature and densities of the emitting plasma. These authors support previous results confirming a higher Mg/Ne than found in the photosphere, but give a value of the ratio of ≈ 1.7–3.5, much lower than estimated by Widing and Feldman (1992). This result was supported by the Young et al. (1999) analysis of SOHO/CDS data, who give Mg/Ne ≈ 1.5 and by Del Zanna et al. (2003), who claim Ne to be depleted (with respect to oxygen), but find no evidence for a FIP effect in plumes. The latter authors, who analyzed SOHO/CDS-GIS (grazing incidence spectrometer) spectra, also re-examined the Skylab data of Widing and Feldman (1992) and show that their earlier results can be explained, taking into account the temperature structure of the plume and more recent atomic and ionization equilibrium calculations.
The brief review of the observational results for the abundance of elements in plumes suggests that plume FIP values, given by different authors, have been, over the years, progressively decreasing. This is certainly not a proof that plumes have a role in fast wind, but does not dismiss this hypothesis. On the other hand, there are theoretical arguments that justify a high FIP in plumes: in Section 5.1 we will see that plumes require an heating source at their base that promotes an enhanced evaporation of chromospheric material. Wang (1996) suggests that transient heating processes, and ensuing evaporation flows, excite an upward ambipolar drift that may account for the enrichment of low FIP elements in the corona, while not affecting the abundance of high FIP elements. This effect may be operating in plumes, while in CH regions the absence of an upward ambipolar flow explains the lack, or weak, FIP effect observed in high speed streams.
It becomes crucial to check the behavior of the ambient plasma: has a FIP effect ever been observed in interplumes? Doschek et al. (1998), from SOHO/SUMER data inferred a Si/Ne abundance about twice as large as the photospheric value, but this value is within the uncertainties of their work. A decade later, Curdt et al. (2008) give a nice visual image (Figure 6) of the variation of the Ne viii λ 770 to Mg viii λ 772 Å intensity ratio in a CH area at the South polar regions of the Sun observed by the SOHO/SUMER experiment in April 2007. The spatial changes of the ratio outline the plume pattern and seem to confirm an over abundance of low FIP elements. The problem of the abundance of elements is not settled, yet, especially if we consider that different estimates may be also related to when, over the plume lifetime, observations have been acquired. That the FIP effect may depend on the time elements have been confined within a structure has been suggested by, e.g., Feldman and Widing (2003): this might possibly account for the different values obtained by different authors. A recent paper, Guennou et al. (2015), further supports this hypothesis. These authors give values of relative element abundances in plumes and interplume regions, inferred from HINODE/EIS off-limb observations acquired in March 2007. Unfortunately, the data do not include lines from high-FIP elements and the FIP bias has been evaluated from the ratio of Fe and Si to S abundance, S being a moderate-FIP element (the sulphur FIP being ≈ 10.36 eV). Over 24-hour observations, one of the plume analyzed by Guennou et al. (2015) revealed a decrease of the FIP bias, while other plumes (and interplume regions) have values independent of time. Guennou et al. (2015) suggest this effect is related to the phase of the BP lifetime when plumes form above the associated BP, possibly plumes being representative of the abundances of the bright point. The topic is still open to discussion and can be the subject of future research.
Top panel: the electron density, inferred from the ratio of lines of Si viii, observed by SOHO/SUMER at the South limb of the Sun in April 2007. The limb of the Sun is shown as a dotted line at the top of the figure. Density enhancements reveal the presence of plumes. Bottom panel: the ratio of radiances in the Mg viii and Ne viii lines. The ratio changes as a function of the location, an effect that may be interpreted in terms of FIP effect in plumes/interplume regions. The two panels cover the same area. The solid/dotted lines trace plumes, a superdotted pixel corresponds to eight detector pixels. Image reproduced with permission from Curdt et al. (2008), copyright by ESO.
3.2.2 Plume outflows in the low corona
A more direct information about the role of plumes in solar wind can be obtained by direct observations of outflows. These may be revealed by Doppler line shifts: because Doppler shifts are sensitive only to motions along the LOS, off-limb radial outflows leave the line unaffected. On disk measurements will sample the lower coronal levels, possibly detecting the nascent solar wind with a technique that is independent of the local temperature and densities: however, we need to know (or to hypothesize) the flow geometry to infer, from the LOS component, the outflowing speed value.
Hassler et al. (1999) examined SOHO/SUMER on-disk observations of a polar CH measuring the Doppler shift of the Ne viii 770 Å line: the inferred velocity field appeared to correlate well with the underlying chromospheric magnetic structure detected in the Si ii λ 1533 Å line. The right panel of Figure 7 gives the Ne viii Doppler velocity map of a CH area, with the chromospheric network superposed, to help visualize the close correspondence between network boundaries and blueshifts. The map in the left panel refers to a midlatitude non-CH region. It is obvious from the figure that most of the blueshifts occur in the CH and are concentrated along the boundaries of the network. Assuming blueshifts reveal bulk motions, Figure 7 provides a 2D map of the nascent wind and suggests that the fast CH wind originates in the network boundaries with radial outflows on the order of 5–10 km s−1. Occasional higher speed outflows (10–20 km s−1) in quiet regions occur at the intersection of boundaries. Analogous results were obtained by several authors (e.g., Wilhelm et al., 2000; Stucki et al., 2000; Xia et al., 2003; Popescu et al., 2004): Xia et al. (2003) examined also the magnetogram of the equatorial CH area they were analyzing and concluded that the larger Ne viii blueshifts occurred in dark regions, with strong single polarity magnetic flux. Mixed polarity areas were associated with smaller blueshifts. Tian et al. (2010) examined HINODE/EIS EUV Imaging Spectrometer (Culhane et al., 2007) data, focussing on the Ne viii behavior and complementary SUMER observations, confirming the occurrence of larger blueshifts in CHs, with respect to the quiet Sun, and of blueshifts on a side and redshifts on the other side, in the bright points observed within the analyzed CH (October 10, 2007). However, plumes are not mentioned in the paper.
Right panel: SUMER Ne viii Doppler shifts map measured in a polar CH on September 21, 1996. The chromospheric magnetic network boundaries inferred from Si ii images has been superposed to the Ne viii (temperature of formation log T = 5.8) map, to facilitate the identification of the origin of the highest blueshifts. The zero velocity reference has been identified by using off-limb unbinned data and a moment technique to fit the line profiles. Left panel: same as the right panel in a midlatitude non-CH region. Blueshifts (outflowing plasma) occur both in CH and non-CH regions but occupy most of the CH area while at midlatitude tend to appear sporadically only at the intersection of network boundaries. Image reproduced with permission from Hassler et al. (1999), copyright by AAAS.
These works are potentially very relevant to the plume-solar wind association, once the plume — network relationship is clear. Early observers suggested plumes to be rooted in rosettes, typically found in the network and Newkirk Jr and Harvey (1968), as well as later scientists, claimed the base of plumes corresponds to bright portions of the network (DeForest et al., 1997). Nowadays, we recognize plumes to overlie small bipolar regions within dominant unipolar open field areas (Wang and Sheeley Jr, 1995b; Wang et al., 1997; Wang and Muglach, 2008): indeed the area analyzed by Hassler et al. (1999) hosted a couple of plumes, located above bright points (as seen in the Si ii line) but no relevant Doppler velocity signature was found to be associated with them. Analogously, Wilhelm et al. (2000) found no significant Doppler shift in bright plumes. Altogether, we may say that plumes originate from unbalanced mixed polarity magnetic field areas.
If we consider the network/intranetwork scenario suggested by Tu et al. (2005), we realize that plumes may not fit at all the role of structures contributing to the wind. Tu et al. (2005) made a correlation of the Doppler shift and UV line radiance from SUMER data with magnetic fields extrapolated at several heights from the observed photospheric magnetograms and concluded that wind emerges from areas of nearly vertical fields along the network. These rapidly expanding flux tubes (funnels) are the sources of solar wind: flows are accelerated by waves originated by the reconnection episodes triggered by intranetwork loops being pushed towards the network by supergranular convection. Figure 8 illustrates the funnel scenario.
An illustration of the funnel scenario. Left (A) panel: the dark shaded regions correspond to areas where outflows larger than 8 km s−1 have been detected from the Doppler shifts of Ne viii lines. They all map to open fieldlines. Right (B) panel: the boundary of the funnel, where closed loops are pushed towards the open field giving rise to reconnection episodes. Image reproduced with permission from Tu et al. (2005), copyright by AAAS.
We may conclude that, until a few years ago, all studies converged towards a scenario where plumes have no role as fast wind contributors. However, a recent work challenges this view. Fu et al. (2014) analyzed the same data set, acquired by the HINODE/EIS experiment in a polar CH, in October 2007, used by Tian et al. (2010) and further data acquired in a low latitude hole in January 2011. Fu et al. (2014) focussed on plumes and measured the Doppler shift of several coronal emission lines (e.g., Fe x λ 184.54 Å, Fe xii λ 195.12, Fe xiii λ 202.04 Å, with temperature of formation between 106 and 3.106 K) reaching the conclusion that quasi-steady outflows, increasing with height, are present in plumes and increase from 10 km s−1, at 1.02 R⊙, to about 25 km s−1, at 1.05 R⊙.
Figure 9 shows the profile of outflows in plumes, as inferred by different authors, with different techniques, some of which will be discussed later in this paper. The results of Hassler et al. (1999), Hassler (2000) and Wilhelm et al. (2000) discussed above refer to the lowest coronal level and are not inconsistent with HINODE Fu et al. (2014) results, if the outflowing plasma accelerates upwards. Fu et al. (2014) also show quiet sun and CH Doppler shift as a function of temperature in Fe viii to Fe xii ions, getting higher outflows in plumes than in other regions. These conclusions should be supported by further studies as the authors warn readers about stray light effect possibly affecting their data (they obtain a higher density in CH than in quiet sun, which is obviously unlikely). However, if confirmed, Fu et al. (2014) results imply that the role of plumes in fast wind crucially depends on their excess density, percentage occupation of the CH area at any time and on the acceleration processes in plumes vs. CH plasma. Data at higher altitudes than sampled by SOHO/SUMER may provide novel information about the plume role in solar wind: hence, we turn to observations at higher coronal levels to check what new contributions they yield to the fuzzy scenario described so far.
3.2.3 Plume outflows in the intermediate corona
SOHO/UVCS spectrometer (Kohl et al., 1995) data offered the opportunity of applying the Doppler dimming technique to observations of the H Lyman-α and O VI 1032 and 1037 doublet lines acquired in the intermediate corona, at altitudes reaching about 2.3 R⊙. The Doppler dimming (DD) technique (Noci et al., 1987) takes advantage of the mechanism of formation of these lines, that, unlike most of the coronal lines that are collisionally excited by electron impact, have also a component radiatively excited by photons originating in lower atmospheric levels. This is the case for the H and O VI lines, whose intensities can be written as the sum of a collisional Fcoll and a radiative Frad component. Among other factors, the latter depends on the outflow speed of the coronal plasma, because when the exciting radiation becomes Doppler shifted, the photoexcitation process is less efficient and the radiative component is Doppler dimmed, that is, is weaker. Inferring outflows via the DD technique implies the identification of the radiative component of the line and the evaluation of the decrease brought about by the speed of the outflowing plasma. Without entering into a detailed description of the technique, it is obvious that we are unable to identify observationally, from the measured total line intensity, its radiative component and we can infer outflows only by building a model atmosphere, calculating Fcoll and Frad, and find, by successive approximations, how fast should the plasma move to reproduce observations. Opposite to the Doppler shift technique, DD is not a measurement, but a check of the consistency of a model-predicted vs. the observed line intensity.
The lack of coronal lines in SUMER spectra makes DD very useful to extend results from SUMER (and other low coronal experiments) to higher coronal levels where solar wind is undoubtedly present. Knowing the atomic parameters of the line, the element abundance, the temperature and density of the emitting plasma and the ion speed distribution, the line intensities and their height profile are evaluated and compared with observations. Generally, the plasma speed is altogether unknown, and an iterative process is adopted: starting with a static atmosphere, the value of the plasma speed is increased until simulated intensities converge towards the observed values. Plasma parameters, like densities and temperatures, are either inferred from the same data set or taken from the literature. Any DD analysis results in speed values of the atom/ion emitting the line: the speeds not being necessarily the same for different species (for more information see, e.g., Cranmer et al., 1999).
A preliminary, rather crude, attempt to identify whether plumes or interplume regions were privileged sources of outflowing wind via the DD technique, was made by Corti et al. (1997), who did not reach a clear answer, as both areas, between 1.5 R⊙ and 2.3 R⊙, turned out to host similar outflows. A few years later, Giordano et al. (2000) analyzed UVCS polar CH data acquired at 1.82 R⊙ and claimed the background/interplume oxygen ions to flow at a speed of 105–110 km s−1, faster than the plume ions that were moving at ≈ 65 km s−1. Patsourakos and Vial (2000) supported the results of Giordano et al. (2000) inferring the outflow speed of the wind, by combining Doppler shifts and DD measurements, from SUMER data at 1.05 R⊙: these authors report a speed of about 67 km s−1, in interplume regions.
More complete analyses of UVCS data, aimed at identifying the profile of the wind speed vs. height, have been made by Teriaca et al. (2003), Gabriel et al. (2003) and Gabriel et al. (2005). Results from these works are in a not complete agreement: Teriaca et al. (2003) identified plume and interplume lanes in a composite image of a polar CH observed by EIT, CDS, SUMER and UVCS data (see Figure 10) and applied the DD technique to SUMER O VI data below 1.35 R⊙ and UVCS O VI and Lyman-α data from 1.5 R⊙ to 21 R⊙. Teriaca et al. (2003) conclude that outflowing O VI ions and H I atoms, in interlanes, accelerate, over the examined height interval, although at a different rate, reaching at 2.2 R⊙ speeds of the order of 100 to 300 km s−1 (respectively, for H I and O VI ions). On the opposite, the reconstruction of a static plume, embedded in this outflowing atmosphere, turns out to reproduce nicely its observed line radiance. Hence, plumes turn out to be either static or flowing at a negligible rate.
Map of the 1996 June 3, northern CH in a EIT, CDS, SUMER, UVCS composite image that clearly shows the plume and interplume regions that have been used by Teriaca et al. (2003) for their analyses of flows in the two regions in the first solar radii above the limb of the Sun. Image reproduced with permission from Teriaca et al. (2003), copyright by AAS.
On the other hand, Gabriel et al. (2003) applied the DD technique to SUMER data in the height range of 1.05–1.351 R⊙, obtaining outflow speeds on the order of 60 km s−1, approximately constant over that altitude interval, but persistently higher than the interplume speed. This result led Gabriel et al. (2003) to suggest that plumes and interplume might equally contribute (50% each) to the total fast wind flux. The apparent discrepancy with the outcome from Teriaca et al. (2003) work was solved by a later paper by Gabriel et al. (2005), who extended their previous analysis to higher levels, analyzing UVCS data as well. They concluded that plume plasma is faster than interplume plasma only up to about 1.61 R⊙: higher up, the opposite occurs, with interplume flowing faster than plumes because of their higher acceleration. Results by Teriaca et al. (2003), below 1.51 R⊙, were attributed to the low statistical significance of their SUMER data. A compendium of the outflow speeds derived by different authors, appears in Figure 9.
A different approach to the plume/interplume controversy, has been adopted by Raouafi et al. (2007), who compared the H I Lyman-α and O VI line profiles and intensities observed in plume and interplumes, with model calculations, assuming that the two species have Maxwellian velocity distributions of different widths in the two regions (we will see in the next Section what justifies this assumption), a higher plume density, and other constraints from the literature. Plumes (and interplume regions) are assumed to expand superradially within the global magnetic field configuration of Banaszkiewicz et al. (1998). In reconstructing the observed quantities, the contribution of plumes crossing the LOS has been taken into account and different profiles of the outflow speed with height have been assumed. The best agreement between modeled and observed line intensities and profiles was reached assuming a lower outflow speed in plumes, eventually reaching the interplume speed at about 3–4 R⊙.
Altogether it looks like most of the authors agree on plumes moving at a lower speed than interplumes and on a negligible role of plumes, as fast wind contributors. The recent work by Fu et al. (2014) seems to contradict earlier conclusions and further work is needed to clarify the source of this discrepancy. Also, we postpone discussing transient flows that have been observed in plumes to Sections 5.1 and 5.2 where we will see whether episodic events, rather than the stationary plume upflows examined here, may be a source of mass supply to the wind.
3.3 The plume effective temperature
We examined, so far, line intensities and Doppler shifts and their variation in plume/interplume regions. However, the widths of the lines provide further relevant information, pointing, whenever they exceed their thermal values, to the occurrence of unresolved plasma motions originating from waves or turbulence. We remind the reader that the line width Δλ (assuming the instrumental width is negligible) can be written as
where M, T are the ion mass and temperature, ξ and Teff are, respectively, the non-thermal velocity and the effective temperature of the ion. If we consider that fast wind undoubtedly originates, and is accelerated, in CHs, we conclude there must be a mechanism, operating there, capable of heating and accelerating plasma. Taking into account the higher densities of plumes (with respect to the interplume medium) and their simple magnetic field geometry, we recognize they are regions of lower Alfvén speed that represent natural guides for waves whose presence may be observationally verified and theoretically predicted. In particular, Alfvén waves are known to be incompressible, transverse waves that, propagating along off-limb plumes approximately lying in the plane of the sky, result in velocity oscillations along the LOS, and, hence, in broad line widths. Once/if waves are detected, they become obvious candidates for wind acceleration.
Hassler et al. (1997), using SUMER data, report a broader line width in interplume regions, with respect to plumes. This result has been confirmed by further studies, from either ground-based coronagraph data (Raju et al., 2000), or from data acquired by space-borne experiments like SUMER (see, e.g., Wilhelm et al., 1998; Banerjee et al., 1998, 2000b) and CDS (see, e.g., Banerjee et al., 2000a, 2001; O’Shea et al., 2003). A summary of the plume/interplume line widths can be found in Table 2 of Wilhelm (2012). Figure 11 gives an example from Banerjee et al. (2009) of the increase with altitude above the limb of the line widths, in plume and interplume regions, observed by SUMER in the Si viii 1445.75 Å line and by HINODE EIS in the Fe xii 195 Å line. Although widths are larger in interplumes than in plumes, the difference is minor.
Profile of the non-thermal velocity vs. distance above the limb in plume and interplume plasma, inferred from the width of the Fe xii 195 Å line, from data acquired by HINODE EIS spectrograph. The solid line gives the nonthermal velocity of the Si viii 1445.75 Å line, from data acquired by SUMER. Image reproduced with permission from Banerjee et al. (2009), copyright by ESO.
Generally, the observed behavior is ascribed to Alfvén waves that propagate in the ambient medium without any damping: their energy flux, through a surface area A, assuming a flux-tube geometry, can be written as
where ρ is the mass density, 〈δυ2〉 is the mean square velocity amplitude (with ξ2 ≈ 1/2〈δυ2〉) and B is the magnetic field strength. As waves propagate outwards, conservation of wave energy implies
which, for BA constant with height, yields
If the broadening of a line increases with height according to Eq. (7), we may conclude that the observed behavior is consistent with what expected for Alfvén waves propagating upwards. Figure 11 shows that indeed we have evidence for Alfvén waves, both in plumes and interplumes and that the difference in the width of the lines tends to disappear at about 1.1 R⊙. The large width of the lines points to effective temperatures higher than electron temperatures: in comparison with electron temperatures on the order of 8 × 106 K in plumes and 1–1.5 × 106 K in interplumes, the effective temperatures raises to ≥ 2 × 106 K, with an upper limit, in very dark area, of 20 × 106 K. These values have been inferred from Eq. (4) assuming T is the temperature of formation of the line.
The presence of outwardly propagating Alfvén waves may appear to be well established (but see Section 8.3, Thurgood et al., 2014). However, there are a few alternative suggestions that account for the line width increase, without invoking waves. For instance, at the position of plumes, most of the emission originates from these localized high density structures, while plasma all along the LOS contributes to the interplume emission: in presence of radial or superradial flows, emission along the LOS originates from a multitude of Doppler shifted components, which add up resulting in a broader line profile than in plume regions. Doyle et al. (2005) point out that the broad line widths above the limb may be a byproduct of spicules/macrospicules activity, as lines appear to be broader in regions where spicules are seen, with respect to areas devoid of spicules. Alternatively, Tu et al. (1998) suggest an increase of ion temperatures with increasing heliocentric distance that results as well in broad profiles increasing with height above the limb.
4 Searching for Waves in Plumes
The analysis of the effective temperatures of plumes leads us to a new issue: are plumes (interplumes) hosting waves? In Section 3.3, we have seen that an effective temperature higher than the electron temperature may hint to the presence of Alfvén waves propagating along plumes, but other hypotheses are able to account for observations as well. Are there other phenomena suggesting waves are present in plumes? How can waves be revealed?
The occurrence of waves may be tested also from observations of temporal fluctuations in the line parameters. Alfvén waves are incompressible, but slow mode waves are compressional and, producing a modulation of densities, result in a modulation of UV line intensities, that may be observationally detected. Indeed, the first observations of short period variations in plumes emission have been made by Withbroe (1983), analyzing a 40 min sequence of O vi and Mg x spectroheliograms acquired by the Skylab S082 experiment. The paper does not point to the occurrence of waves, but ascribes the observed Mg x radiance oscillations to temperature perturbations, produced by fluctuations in the heating rate, possibly associated with propagating phenomena moving at a speed higher than 100–200 km s−1. These figures compare well with the acoustic speed cs in an isothermal atmosphere (cs = (γp/ρ)1/2 ≃ 150 km s−1, for a 106 K corona). Nowadays the evidence for compressible MHD waves in coronal holes is indisputable (see, e.g., Gupta et al., 2012) and the literature on the subject is extremely abundant. Hereafter, we only refer to CH studies that specifically address plume (or interplume) regions.
The first detection of MHD waves in plumes dates back to DeForest and Gurman (1998) who analyzed SOHO EIT brightness perturbations in the 171 Å channel. Brightness oscillations on the order of 10–20%, propagating outwards with periods of 10–15 min at a speed of 75–150 km s−1 were interpreted in terms of sound waves, carrying a mechanical energy flux of ≈ 3 × 104 erg cm−2 s−1 — lower than the measured solar wind energy flux (≈ 105 erg cm−2 s−1, Le Chat et al., 2012) by a factor 3. This doesn’t rule out waves as providing for the wind energy flux, as other waves may possibly contribute to the total wave flux. Ofman et al. (1999a) further examined the DeForest and Gurman (1998) dataset and pointed out that the relative wave amplitude that increases with height identified the oscillations with slow magnetosonic waves, in agreement with the authors’ simulation of the propagation of this kind of waves in a gravitationally stratified atmosphere. In a successive study, Ofman et al. (2000a) took into account the previously neglected wave dissipation and found that the non-linear steepening of the waves leads to wave damping with a dissipation length on the order of 0.08 R⊙. Hence, it is unlikely that waves propagate beyond the first solar radius above the surface.
The presence of compressional waves was supported also by studies of Banerjee et al. (2000a) who, on the basis of CDS data, got slightly longer periods (20–30 min). Analogous periodicities were found in interplume regions, still from CDS data, by Banerjee et al. (2001), who report compressional waves with periods of 20–50 min (or longer), close to the limb of the Sun, possibly originating at the network boundaries. Also Popescu et al. (2005) focussed on an interplume region and, via SUMER data, inferred, from fluctuations in lines intensities, periodicities of 10–90 min, but, in addition to these, also a very long periodicity of ≈ 170 min. Because the acoustic cutoff frequency (γg/2cs) is, in an isothermal atmosphere, on the order of 90 min, the authors suggest that the latter may not result from waves but from recurrent reconnection processes.
These observations refer to the low coronal levels that can be sampled by EIT or CDS, i.e., to altitudes below 1.5 R⊙. Ofman et al. (1999b) and Ofman et al. (2000b) in an attempt to check whether waves detected at lower levels reach higher altitudes, made WL polarization brightness (pB) observations at 1.9 R⊙ and 2.1 R⊙ with the UVCS coronagraph: because UV line fluctuations originate from density fluctuations, we expect the WL pB brightness to fluctuate as well (because also the WL pB depends on density — more precisely on density integrated along the LOS). Fluctuations were indeed detected and, from a cross-correlation analysis of the pB values at the two heights, Ofman et al. (2000b) inferred a propagation speed of 160–260 km s−1. Waves are present both in plumes and interplumes; occur in short bursts (duration about 30 min) with periods of 6–10 min and is not clear what differentiates them.
A different technique not yet mentioned in this review, has been adopted by Gupta et al. (2010) to analyze HINODE/EIS and SOHO/SUMER data in plume and interplume regions of a north polar coronal hole acquired during a joint campaign. These authors used the radiance information provided by EIS (in plume and interplumes) and by SUMER (in interplume) to build distance-time x-t radiance maps that reveal the presence of waves with a periodicity of 15–20 min, in both regions. However, the propagation speed is markedly higher in interplumes (where it increases from about 130 km s−1 just above the limb to about 330 ± 140 km s−1, at 160 arcsec above the limb) than in plumes, where, the speed, although having about the same value, at the lower level, only rises to about 165 km s−1. Plume waves also merge with the background at lower altitudes than interplume.
In interplumes, Ne viii Doppler shift and width x-t maps do not show any propagating disturbance. However, a wavelet analysis of an on-disk CH bright area and of its off-limb extension, reveals waves with the same periodicity and in phase with those seen in the radiance. Oscillations in lines forming at different temperatures have the same propagation speed, opposite to what expected for compressional waves. The authors solve this apparent discrepancy suggesting they observe Alfvén waves that propagate in a density stratified atmosphere and, because of non-linear effects, also show some radiance fluctuation. In conclusion, Gupta et al. (2010) propose that interplume regions host Alfvénic or fast magnetoacoustic waves, while waves in plumes likely are of the magnetoacoustic type. Moreover, the observed acceleration of interplume waves makes them good carriers for transporting energy to the outer coronal layers. Tracing back the source region of the interplume waves, it turns out they originate from bright patches of the CH area, in agreement with the suggestion of Tu et al. (2005) (see Section 3.2.2) that wind flows from funnel regions along the network. As to the plume waves they are most probably dissipated shortly above the limb because of shock formation (see, e.g., Cuntz and Suess, 2001).
The unprecendented high spatial (plate scale of 0″.6 per pixel) and temporal resolution (12 s cadence) of the SDO (Solar Dynamic Observatory) AIA experiment (Atmospheric Imaging Assembly, Lemen et al., 2012) provided novel opportunities for high quality observations of waves in plumes/interplumes regions. Krishna Prasad et al. (2011, 2012) analyzed AIA data acquired at plume, interplume and in on-disk plume locations. Results from these works are not in complete agreement with those of Gupta et al. (2010) described above, as the x-t maps shows the ubiquitous presence of quasi-periodic disturbances (periodicities of 10–30 min) that appear to be of slow-magnetoacoustic type, as their propagation speed is a function of the observational passband, i.e., is temperature dependent. The data point to a higher propagation speed in interplumes, but there is hardly any sign of acceleration over the altitude interval (300 arcsec above the limb) covered by the AIA FOV. The reason for this discrepancy may be at least in part ascribed to the way acceleration is calculated. The speeds of the propagating disturbances are evaluated from the inclination of the slanted lines, drawn in a subjective procedure over the x-t maps, in an attempt to follow the oscillations trajectories. As seen in Figure 12, personal judgment enters heavily in the choice of the trajectories. Also, oscillations in plumes persist up to higher altitudes than shown in Gupta et al. (2010). As to the damping of oscillations, Krishna Prasad et al. (2012) claim it is faster in hotter channel, which points to thermal conduction as the damping mechanism, as predicted by, e.g., Ofman and Wang (2002) in their analysis of the slow magnetosonic wave damping in SUMER observations of coronal loops.
Top panels: enhanced x-t map of the Fe xii radiance measured by EIS, over an ≈ 5 hours time interval, on November 13, 2007, in an interplume region of the north polar coronal hole. White solid lines have been superposed onto the bright travelling disturbances to help visualize their trajectories as they propagate upwards: the change in their inclination is evidence of acceleration. Image reproduced with permission from Gupta et al. (2010), copyright by ESO. Bottom panel: Same as above for the interplume region observed by AIA in the southern polar coronal hole on July 20, 2010, in the 193 Å band. Image reproduced with permission from Krishna Prasad et al. (2011), copyright by ESO. There is obviously some ambiguity in the choice of the inclination and position of the lines representing the propagation trajectories.
A recent analysis by Krishna Prasad et al. (2014), building up on their 2012 paper (Krishna Prasad et al., 2012), addressed specifically the frequency dependent damping mechanisms of slow magnetosonic waves in plumes. These authors analyzed AIA observations of about 10 plume/interplume structures, where slow waves were propagating, and measured the damping lengths as a function of the wave frequency. They confirmed their earlier findings that damping occurs because of thermal conduction, but pointed out a different behavior in on-disk vs. off-disc structures, suggesting polar structures require damping mechanisms not well described by linear theories.
We have so far omitted discussing the possibility that the observed propagating disturbances originate from flows, rather than from wave motions. This alternative interpretation may be very relevant, if we aim at identifying the source, or sources, of the wind mass flux. In Sections 3.2.2 and 3.2.3, we illustrated the evidence we have for outflows in plumes: in the next Section 5, we examine the evidence we have for episodic plume outflows. We should not forget, however, that both phenomena, flows and waves, may occur simultaneously and are not mutually exclusive.
5 The Dynamic Life of Plumes
All the physical parameters of plumes that have been described in Section 3 have been considered as typical of plumes. Does this imply that plumes’ properties do not change in time, or did we ignore this issue? We have to recognize that the literature on the time-dependent variability of plumes is rather scanty, although sufficient to let us predict that plumes have a dynamic life (see, e.g., DeForest et al., 1997) and go through drastic changes over their lifetime. In the following we review what we know on this topic: this leads us also to illustrate the interaction of plumes with several associated structures/events.
5.1 The birth of plumes
We mentioned several times in this paper (see, e.g., Section 3.2.2) that plumes are associated with network: can we explain what physical processes occur over there to give birth to a plume? Before describing observations of the birth of a plume, let us examine whether we understand the physics underlying its formation. In the scenario proposed by Wang and Sheeley Jr (1995b), bipoles, emerging within a supergranular cell, migrate by convection towards unipolar flux concentrations at the border of the cell, triggering reconnection episodes. These result in an enhanced heating, which, as pointed out by Wang (1994), is a prerequisite for the maintenance of plumes, in order to sustain their densities, higher than those of the interplume regions. Wang (1998) has given a good description of the processes that generate and maintain plumes. Because the extra heat input cannot be completely dissipated by radiative cooling (as initially densities are low and radiative cooling is inefficient, being a function of \(n_e^2\)), is, at least in part, conducted downwards, promoting the upward evaporation of material. Over a time-scale of the order of a few hours, a plume shows up.
Figure 13 is a cartoon representative of plume formation. We point out that during the processes described above, the base field is being modified and brightenings generated by the formation of closed loops may be observed. Also, the reconnection involving different fieldlines at a time, leads us to envisage a plume as a structure integrated over multiple fine-scale features, possibly reminding us of the suggestion of Llebaria et al. (2002) for a fractal nature of plumes.
A cartoon showing the formation of a plume, when a bipole is dragged towards the preexisting unipolar field and reconnection occurs. As a consequence new closed fieldlines are created while the open dark flow tube representative of the plume forms from the open fieldlines originating from the process. Image reproduced with permission from Wang (1998).
The association between plumes and brightenings at their base, makes us open a short digression on the plume/bright point association. X-ray BPs are easily observed within the dark CH emission: at the time they started being analyzed, XBPs, or BP-like features, were shown to be closely associated with plumes (Ahmad and Webb, 1978) and the BP/plume combination was suggested to be the source of mass injection into the solar wind. This proposal was further supported by Davis (1980), who pointed out that, over several months of observations, the BP number per unit area appeared to be well correlated with the average solar wind density, suggesting that the wind behavior over the solar activity cycle was related to the BP number/areal coverage. This possibility is interesting because, even in absence of a one-to-one association between BPs and plumes, shifts the emphasis to BPs rather than to the less easily detectable plumes.
Years later, Poletto et al. (1994) checked whether the long-term association claimed by Davis (1980) could be confirmed on the basis of YOHKOH/SXT (Tsuneta et al., 1991) data. The analysis, however, was unable to confirm the expectations and Hara and Nakakubo-Morimoto (2004) pointed out the previously neglected effect of the variable background X-ray intensity on the evaluation of the number of BPs, casting doubts on previous estimates of the changes in the BP number along the solar cycle. These negative results affected the interest in the topic that was, thereafter, virtually abandoned. Karachik and Pevtsov (2011) readdressed the subject, assuming BPs are sites of magnetic reconnection and hence checking whether, establishing a correlation between the number of BPs and solar wind speed, they could point to magnetic reconnection as a primary mechanism for solar wind acceleration. The lack of such a correlation lead the authors to dismiss the possibility that BPs might provide the main mechanism for wind acceleration. Although Karachik and Pevtsov (2011) do not explicitly mention plumes, their work casts doubts also on the role of plumes in fast wind.
Going back to the mechanism that gives rise to plumes, at about the same time as Wang (1998) proposed his model, Veselovsky et al. (1998) took a different approach to the problem. These authors suggest that plumes form because plasma drifting in the electric field induced by evolving ephemeral regions interacts with the global magnetic field, leading to compression that may be perceived as structures — the plumes — that trace the global magnetic solar configuration. This process will establish an interesting link between local and global conditions, but, possibly, holds only for a minority of the observed features.
The standard view of plume formation described in Figure 13 was obviously developed on the basis of observational data. Over the about 20 years since the model was proposed, the quality of coronal observations has enormously improved and we may ask what the new data added to our knowledge of plume development. A phenomenon that emerged from HINODE XRT (Kano et al., 2004) observations is an unpredicted high frequency of polar X-ray jets (Cirtain et al., 2007): these phenomena share some properties with plumes, as they are transient, originate because of flux emergence, and are seen at network boundaries. Opposite to the fuzzy appearance of plumes, they look as collimated, sharp edged, plasma beams: however, we do not know whether the plume haziness is real or it is a consequence of an inadequate low spatial resolution and background effects.
In the late 1990s, Moses et al. (1997) described UV jets in polar CHs and shortly afterwards Lites et al. (1999) from WL and EIT data, detected a jet embedded in a polar plume propagating upwards at a speed of ≈ 200 km s−1. About a decade later, Raouafi et al. (2008) addressed the issue of the relationship, if any, between plumes and X-ray jets. From HINODE/XRT and STEREO/SECCHI/EUVI data, Raouafi et al. (2008) and Raouafi (2009) claim jets are precursor of plume formation. Briefly, these authors suggest that jets are created because of catastrophic reconnection triggered by flux emergence, while plumes result from the opening of previously closed loops (possibly triggered by secondary low-rate reconnection episodes). The jet is the manifestation of fast, explosive dissipation of magnetic energy over a short time, while the plume plasma is may be driven by a pressure gradient, thus accounting for the low upflow speed (see Section 3.2.2) inferred for plumes. The authors claim that about 70% of the jets they examined had been followed, within minutes — tens of minutes, by a plume occurrence. Should this be the case, how can be reconciled with the “gentle” plume formation envisaged in the Wang (1998) scenario?
Because plumes and jets appear in the same locations, it is likely that they are somehow connected: in the Raouafi et al. (2008) scenario, the link between the two phenomena is more strict, as the plumes’ birth is sort of a follow up of the jet occurrence. In a successive paper, Raouafi and Stenborg (2014) further examined the link between plumes and nearby phenomena, focussing on the activity occurring near plume footpoints. The data for this analysis have been acquired by SDO/AIA and further processed via a wavelet filtering technique that yields sharper images. Context magnetic fields were provided by SDO/Helioseismic and Magnetic Imager (HMI, Scherrer et al., 2012) line-of-sight magnetograms. Raouafi and Stenborg (2014) analysis lead to the identification of minor events occurring near the plume footpoints, dubbed “jetlets” and “plume transient bright points” (PTBPs): these events appear to support the previous claim that the jet results from catastrophic reconnection and that the leftover weak episodes of low-rate reconnection between residuals fragments of the emerged bipole and the unipolar background field cause a number of weak events responsible for the sparse heat sources that create and maintain the plume.
We point out that this fine-structure scenario seems to imply jets as a necessary step for the birth of plumes, but both jets unaccompanied by plumes, and jets within well developed plumes, have been observed as well. Hence, further work is necessary to define the characteristics of the plume-jet association and establish whether jets should be included as a necessary step in plume formation models. On this issue, the analysis of Pucci et al. (2014), who examined a polar plume and the BP at its base, provides a case where only a weak jet was observed before the birth of a plume. The Pucci et al. (2014) plume was observed (still by SDO/AIA) beyond the limb of the Sun, in a polar region, and was rooted in a BP. About 2 hours before its formation, a weak jet (possibly a blowout, clearly visible in the 304 Å channel, but only weakly emitting in the 171 Å channel), had occurred. Hence, this case is only marginally consistent with the Raouafi et al. (2008); Raouafi and Stenborg (2014) scenario, as it is the BP that apparently plays a key role in the plume occurrence. In the successive phases of their lives, however, the BP/plume link is more subtle, and it is difficult to establish a relationship between the brightness fluctuations of the two phenomena. As of today, the BP vs. plume relationship is not clear at all: Del Zanna et al. (2003) for instance suggested that BPs may be seen at the base of a plume, only in the early stage of the plumes’ lives. In the present case, the BP persisted throughout the plume life span, although there was no plume before the BP emergence.
The variety of observations of BPs, that show the occurrence both of BP-associated plumes and of isolated BPs, show that the emergence of a small bipole within a unipolar CH area, is not sufficient to trigger the plume phenomenon. Most likely, factors like the rate at which flows drag the bipole polarities toward opposite sign fields, the distance between the poles of the bipole (short distances likely resulting in closed loops hardly connecting to external polarities), the location where bipolar flux emerges within a supergranular cell, affect the formation of a plume. Wang and Sheeley Jr (1995b) suggest that old, dispersed bipoles generate stronger plumes than compact bipoles, but these effects have not yet been thoroughly investigated.
5.2 The main phase of the life of a plume
In Section 2.3, we listed values for the plume lifetimes, ranging from hours to days (and, possibly, weeks). What sustains such long lives? Raouafi and Stenborg (2014) point to the flux unbalance that is persistently present in the areas of plume footpoints: this may indeed be a pre-requisite for the long duration of plumes. Low-rate reconnection that keeps going on throughout the plumes’ life span shows up in the small-scale jetlets and PTBPs described in the previous Section (Section 5.1). In the Raouafi and Stenborg (2014) scenario, these become the building blocks of plumes and, playing a key role in their sustainability, account for their long life. On the contrary, jets originate in an impulsive high rate reconnection episode. The diverse outcome of reconnection have been invoked also by Zhang et al. (2012) to account for the different behavior of jets vs. plumes.
An alternative mechanism for the plume heating has been proposed by Wu and Fang (2003), who suggests plume may be maintained via the dissipation of kinetic Alfvén waves. On the basis of a priori defined radial profiles of plume density, Te, radial flow speed and magnetic field, these authors calculate the heating resulting from the dissipation of kinetic Alfvén waves, assuming different ratios for the plume to background densities. They conclude that the dissipation of wave energy may be enough to compensate for the enhanced radiative losses of plumes. The scenario of Wu and Fang (2003) envisages a stable plume (for at least 24 hours) that can be modeled as a radial steady flow with transverse pressure balance: this view is challenged by the recent observations of the unsteady life of plumes, apparently favoring transient heating sources, as illustrated here under.
Over the plume lifetime, the plume goes through brightenings and/or fadings: for instance, over the 2-day life duration analyzed by Pucci et al. (2014), the plume faded a few times by ≈ 30% (in the 171 Å passband). DeForest et al. (2001a) (see Section 2.3) has shown that plumes are both transient and persistent, as they brighten and fade but keep reappearing at the same location: if these recurrent structures are considered to be a unique object, obviously plumes have a long life over which they experience dramatic fluctuations. In Section 4, we noticed how minor brightness fluctuations have been often interpreted as evidence of wave propagation within plumes. Alternative interpretations, however, have been proposed. McIntosh et al. (2010), from data acquired by STEREO/EUVI, analyzed time series of detrended brightness images, along a virtual slit set normal to the limb of the Sun, and suggested that the observed fluctuations signalled the occurrence of repeated high-speed outflow events, where plasma is accelerated upwards at a mean speed of the order of 135 km s−1. The same conclusion was reached by Tian et al. (2011) and by Pucci et al. (2014) who used observation of SDO/AIA to make space-time (s-t) plots of detrended intensities in three AIA passbands (171, 193, 211 Å). The reason why these authors favored an interpretation of the s-t plots in terms of outflows, rather than in terms of waves, lies in the lack of temperature dependent differences between the speeds of events observed in different AIA channels (opposite to what expected for waves propagating at the temperature-dictated sound speed) and in the analogies between the plume behavior and that inferred for upflows associated with other phenomena, like the type II spicules.
Tian et al. (2011) claim that outflows are present also in interplume regions (although not showing any s-t plot in such regions), but are more easily detected in plumes because of their enhanced densities. Pucci et al. (2014) built histograms of the number of events vs. their speed, both in plumes and interplumes, in the 171 and 193 Å channels, concluding that the number of events is lower in interplume regions, but there are otherwise no substantial differences in the two distributions: they peak at the same speed (100 km s−1) in the 193 Å channel and at a slightly lower speed (110 km s−1 vs. 167 km s−1) in interplumes, with respect to the plume value, in the 171 Å channel. Pucci et al. (2014) also studied whether s-t plots might change as a function of the age of the plume: to this end the authors chose different stages in the plume evolution and showed that s-t plots shared the same frequency of occurrence and the same peak outflow speed independent of the stage that was sampled. The typical event rate is on the order of 8.7/hr in the initial stage of the plume life, vs. 8/hr at a time close to the plume disappearance (in the 171 Å channel). The detection of upflowing events in plumes and in the background interplume corona may lead to a revision of our current ideas of the solar wind origin. We discuss this issue in Section 8.3.
In Figure 5, we have given a representative illustration of the DEM distribution in plumes. How does this evolve over the plume lifetime? Pucci et al. (2014) have given plots of the DEM vs. Te, at an early stage, at the time of its peak brightness, and in the final stage of the life of a plume. The authors point out that the electron temperature does not change appreciably over the entire lifespan of the plume. This is not the case for density: its decrease leading to the disappearance of the plume.
5.3 The death of a plume
There are not many observations of the plume disappearance. In the Pucci et al. (2014) plume, the authors observed a decrease of its density with time that amounts to a factor ≈ 60% close to the base, and to about a factor 2 at higher levels. The highest density was found at the plume birth, not at the time of the plume peak brightness: this suggests that the disappearance of a plume depends not only on the energy delivered in reconnection episodes but also on how sparse, in space an time, they become. This substantially agrees with Wang and Muglach (2008) statement that plumes live as long as the injection of the minority-polarity flux continues. Raouafi and Stenborg (2014) invoke, in the plume decay phase, a dispersal of the dominant unipolar magnetic field leading to the formation of delocalized sub-plumes. A still missing detailed observation of the behavior of the magnetic field is required for a precise description of the death of a plume. Even in absence of any reconnection phenomenon, at the end of its life, the finite radiative cooling time implies the plume does not die suddenly but over a few hours.
6 Plumes in the Distant Solar Wind
We have seen in Section 2.1 that plumes, and the polar magnetic field, expand with height: because the plasma pressure decreases with heliocentric distance less rapidly (as r−2.5 − r−3) than the magnetic pressure (that varies as r−4), we expect the magnetic field to spread laterally until the whole corona is filled by an homogeneous field. However, because plasma diffusion across the magnetic field is extremely inefficient, different flow tubes keep their identity, and might be observable in the interplanetary medium by in situ experiments. Identifying the plumes flow tubes in the distant wind will give a definite answer about their contribution to the fast wind mass loss.
There are two structures identified by Ulysses in the distant fast wind, that might possibly be associated with plumes: pressure balanced structures (PBS), defined by an anticorrelation between plasma and magnetic pressure (McComas et al., 1995), and microstreams, characterized by organized velocity variations (amplitudes on the order of ± 25 km s−1, lasting at least 6 hours) and other more subtle properties described by Neugebauer et al. (1995). Both structures have been observed in situ by Ulysses experiments beyond 1 AU. However, even prior to Ulysses, Helios had already identified small structures, at a distance of about 0.3 AU, within which the decrease in gas pressure was compensated by a rise in magnetic pressure that kept constant the total pressure.
Thieme et al. (1989, 1990) analyzing Helios data, presented power spectra of the physical parameters (gas and magnetic pressure, plasma β) of these structures vs. both frequency and the angle traversed by the probe over the appropriate time interval. In high speed streams the power spectra showed “sharp kinks” at 3.5° that the authors interpreted as evidence of solar structures of approximately this size: hence, their results were consistent with the hypothesis of plumes undergoing superradial expansion, while maintaining their identity. Also, by analyzing data acquired when the two Helios experiments had the opportunity of sampling the same plasma parcel, at successive times, they proved that PBS physical properties could not to be ascribed to turbulence, but to stable plasma structures. Hence the identification of PBS with plumes’ remnants appeared to be well grounded. The only problem was the seemingly progressive disappearance of their characteristic properties with heliographic distance.
Indeed, successive analyses, on the basis of Ulysses data, by McComas et al. (1996) and Poletto et al. (1996), although on different basis, cast doubt on this association and suggest there is no solid evidence for the identification of plumes with PBSs at interplanetary distances. A few years later, Reisenfeld et al. (1999) reexamined Ulysses PBSs focussing on their He abundance and pointing out that fluctuations of plasma β within PBSs correlate well (particularly in high β structures) with fluctuations of the He abundance. Figure 14 shows that this only occurs at high latitudes and that the correlation weakens with heliocentric distance. The authors point out that the He abundance is established near the base of the corona and that abundance anomalies have been detected in plumes (see Section 3.2.1: at the time of Reisenfeld et al. (1999) this was a widely shared view): hence it is reasonable to assume that many PBSs are related to solar structures and since plumes are the only structures within CHs most likely many PBSs are related with plumes. Speculating on the reason why He is enriched at the base of plumes, Reisenfeld et al. (1999) suggest a higher Coulomb collision rate promoted by the higher density of plumes with respect to the interplume ambient.
The correlation coefficient of the ratio between the He abundance and the plasma β (He/β) measured within PBS structures observed by Ulysses experiment vs. the distance of the spacecraft from the Sun. Circles (squares) indicate the northern (southern) polar pass; data in the left hand corner have been acquired during the Ulysses rapid latitude scan, at a latitude ≤ 25°. Values of He/β are averaged over 1 month time interval (points within 1.5 AU have been averaged over 2 weeks). Image reproduced with permission from Reisenfeld et al. (1999), copyright by ESO.
Yamauchi et al. (2002) focussed on another characteristics of PBS: their magnetic structure. They found that PBS contain tangential discontinuities, as opposed to non-PBS regions, that contain preferentially rotational discontinuities. The authors suggest that tangential discontinuities trace solar current sheets (CSs), possibly originating from magnetic activity at the plume locations. Somewhat along the same lines, Yamauchi et al. (2004) examined switchbacks in Ulysses data: these are folds in the heliospheric magnetic field, where the magnetic field folds back on itself and, as a consequence, the radial component reverses its direction. The origin of these features is not well known and Yamauchi et al. (2004) suggest they might be driven by the magnetic folds and the shear in the velocity that characterizes plumes. Hence, there are possibly several features that may be remnants of plumes, but, so far, there is no undisputable evidence for their presence in the far wind.
The emerging scenario is one where plumes do indeed preserve their identity in the solar wind, but possibly only within not too large distances. Their disappearance at large distances may be explained in terms of the Kelvin-Helmholtz (KH) instability, that sets in when the shear speed between two contiguous fluids becomes large enough and leads to a mixed two fluid plasma. Suess (1998), recalling that the MHD KH instability occurs for shear speeds larger than the Alfvén speed, made an estimate of the Alfvén speed vs. heliocentric distance in coronal holes and, by comparing the observed upflowing plasma speeds with the computed Alfvén speeds, concluded that the KH instability might be a viable means to account for the disappearance of plumes at about 15 ± 10 R⊙. Parhi et al. (1999) also made a numerical simulation of the onset of the KH instability and ensuing plume disruption. However, these conclusions were challenged by Andries et al. (2000) and Andries and Goossens (2001) who examined the effects of the velocity shear between plume and interplume plasma on the MHD waves trapped within the plume. The authors show that the shear affects the wave spectrum: waves may be subject to resonance absorption and the ensuing resonant flow instability sets in at lower velocity shears than required by the KH instability, analogously disrupting plumes and leading to a mixed plume interplume plasma. Thus there are at least two mechanisms that may account for the plume disappearance at some distance from the coronal base: the poor knowledge of the profile of the velocity vs. heliocentric distance of the plume/interplume plasma does not allow us, at present, to identify which may be actually operating.
Microstreams, on the other hand, were proposed by Neugebauer et al. (1995) to be possibly associated with plumes/jets/supergranulation boundaries: we have seen that network boundaries are related with plumes (see, e.g., Section 3.2.2) and that also jets and plumes might be related (Section 5.1): hence Neugebauer et al.’s claim implies that microstreams are possibly related with solar based features and do not originate in the interplanetary medium. A composition oriented study has been made by von Steiger et al. (1999), who looked for variations in the element abundance in microstreams vs. the ambient fast polar wind that might be associated with analogous variations of the plume vs. ambient corona composition. However, von Steiger et al. (1999) found no significant deviations from the fast polar wind abundances in microstreams and concluded that, if the plume composition is indeed anomalous, their negative results implied that no remnants of plumes survived in the fast wind they analyzing.
More recently, Neugebauer (2012) reinvestigated the microstream-plumes relationship and suggested an association between microstream and jets originating from reconnection episodes of BP loops: being BPs closely related with plumes (see Section 5.1), this implies an indirect association microstreams/plumes, although limited at the times BP plumes host a jet. This suggestion was motivated by a more thorough analysis of microstreams, which Neugebauer (2012) divided into two categories, peaks and dips, according to whether their speed is higher or lower than the average ambient speed over an extended time interval (several hours). Peaks turned out to be likely associated with jets, because of their high temperatures and sharp boundaries, which distinguish them from the background plasma: the same characteristics that show up in jets, but are not observed in plumes. It has to be ascertained, however, whether peaks are related with the WL jets observed by SOHO/LASCO (which are only partially associated with plumes: see, e.g., Wang et al., 1998), or with the X-ray jets observed near the solar surface. Should really peaks be representative of jets, are dips possibly associated with plumes? As of today, this is only a speculative hypothesis. However, we point out that the effort of Neugebauer (2012) to establish an association between short-lived phenomena and in situ structures adds to what described in Section 5.2 shifting our attention to an episodic feeding of the solar wind.
Concluding this section, we can say there is no unambiguous interpretation of structures observed in the interplanetary space in terms of solar features. In the next Section 7, we review what theoretical models suggest about the ability of plumes to maintain their identity in the interplanetary medium: is the plume undetectability/disappearance at large heliocentric distances consistent with model predictions?
7 Empirical and Theoretical Plume Models
The first plume models gave a description of the plume structure in the low corona, on the basis of the few observational data available at the time. As models started becoming more sophisticated, they focussed on predicting whether plume plasma is capable of escaping the solar gravitational attraction to become part of the fast wind streams. As described in the previous Section 6, in situ observations cannot establish exactly what kind of feature might be representative of plumes at interplanetary distances. To know whether theoretical arguments dismiss or predict their persistence at such large distances would help scientists understand what exactly they need to search or whether the so far mainly negative results are justified. The next two Sections 7.1 and 7.2 describe the work done in these areas.
7.1 Empirical models
Electron densities, at different altitudes along plumes, have been inferred since early WL observations of plumes (e.g Saito, 1956). What was not known was the distribution of densities across plumes: this was inferred by Newkirk Jr and Harvey (1968), in the section “A model of plumes” of their paper, assuming
where ρ is the radius of the plume and r is the distance from its axis. Newkirk Jr and Harvey (1968) aimed at reproducing the WL radiance vs. position angle observed in eclipse data, assuming a plume distribution in the corona and a “typical” model of plumes, where n0 and p were free parameters.
Following this first reconstruction of the density distribution, Saito (1965) went a step forward, giving the distribution of temperature along the plume and suggesting the presence of an outflowing plasma that propagates along the plume at a speed, initially very low, that, within 0.31 R⊙, increases by a factor 10. This outflow might possibly be representative of solar wind: “if any exists”, in Saito’s words.
As described in Section 3.1, Ahmad and Withbroe (1977) and Ahmad and Webb (1978) analogously built a model of the density across plumes, assuming a cylindrical structure wherein the electron density decreases exponentially with distance from the axis of the plume. They also inferred the temperature (from the ratio of the intensities of the Mg x and O vi lines) and the density profiles along the plume axis and checked through the momentum and continuity equation whether the hypothesis of hydrostatic equilibrium was tenable. After first maintaining that observations were marginally consistent with hydrostatic equilibrium (Ahmad and Withbroe, 1977), in a more detailed analysis Ahmad and Webb (1978) built the gradient of pressure vs. height in plumes and reached the conclusion that hydrostatic equilibrium does not hold and plumes may well feed the solar wind. Results from these models and those developed by Saito (1965) and Newkirk Jr and Harvey (1968) are not substantially different, but earlier models were based on WL and the latter on XUV observations.
About 15–20 years later, Walker Jr et al. (1993) and Allen et al. (1997) developed models that start from the conservation of mass and momentum, but deal differently with the energy equation. Walker Jr et al. (1993) adopted an isothermal and/or a polytropic model both for the background interplume and the plume ambient (the interplume models being used to derive the background subtracted plume emission), while Allen et al. (1997) put down a complete energy equation, taking into account the conduction flux and the radiative losses and assuming, for the unknown mechanism of mechanical energy input, an arbitrary heating law, exponentially decreasing with altitude.
Figure 15 gives representative solutions for plume models of Walker Jr et al. (1993) and Allen et al. (1997). Both authors predict outflows in plumes; although Allen et al. (1997) warn the reader that most of the plumes they examined do not show conclusive flows, they predict any individual plume contributes about 0.6% of the wind particle flux. Hence, 40 plumes (the number of plumes Saito, 1965, identified at the 1962 New Guinea eclipse) will account for ≈ 25% of the solar wind flux. Walker Jr et al. (1993) do not comment on this issue, but point out that the isothermal flow rate at 1 AU yields a solar speed of the order of 550 km s−1, lower than typical speeds of fast wind. Hence plumes may, in case, be sources of slow, rather than of fast, wind.
Top panel: Representative solutions for the temperature and flow speed of a plume vs. heliocentric distance, obtained by Allen et al. (1997). Bottom panel: Representative solutions for the electron density and flow speed of a plume vs. heliocentric distance, obtained by Walker Jr et al. (1993). Images reproduced with permission, copyright by Kluwer.
The most recent paper where a plume model has been developed along the lines of previously described works, is that by Farid et al. (2008): the authors aim at determining whether plumes show a deviation from hydrostatic equilibrium, via an hydrodynamical model with an a priori assumed exponential heating rate. Farid et al. (2008) research is based on WL data acquired at the time of the 2006 Ghana eclipse and on EUV data from the SOHO/EIT experiment: the authors try to match the observed rate of decay of the intensity vs. distance profiles by choosing free parameters such as the plume base velocity and pressure and the base heating and decay rates. They conclude that plumes cannot be in hydrostatic equilibrium and that, most likely, plasma outflows reach supersonic speeds, although they cannot give any more precise information on the plume vs. distance speed profile.
Before concluding this section, it may be worth mentioning the work of Habbal et al. (1995), who developed a two-fluid model of CHs and dense structures that adopts, as empirical constraints, densities obtained from polarization brightness measurements (made by Fisher and Guhathakurta, 1994, in the low corona, with the HAO Mauna Loa coronagraph and, from 1.5 R⊙ to 5.5 R⊙, with the SPARTAN 201-01 experiment), together with proton mass flux and typical wind speeds measured at 1 AU by in situ experiments. The model predicts CH plasma to reach 764 km s−1 at 1 AU (with the sonic point at 2.3 R⊙), while the dense structure plasma reaches at 1 AU a lower speed of 590 km s−1 (with sonic point at 3.4 R⊙ and a speed lower than the CH plasma speed throughout the corona). This model yields higher proton than electron temperatures in the inner corona, a possibility that has been ignored by previous authors, but it is consistent with spectroscopic measurements that suggest Te is lower than proton temperatures (e.g., Kohl et al., 1996, 1998) in CH plasmas. However, Habbal et al. (1995) results cannot be blindly applied to plumes, because the dense structures imaged by the coronagraphs have not been unambiguously associated with plumes, but, possibly, with CH boundaries. Also, we do not know whether the temperature anisotropy that has been detected in CHs, and that is known to hold in the interplanetary medium, holds in plume plasma as well. More recently, Grappin et al. (2011) built a two-fluid plume (and interplume) model, which shows that, over the first few solar radii, the proton temperature in plumes is higher than the electron temperature, because electrons cool efficiently via heat conduction. However, the higher plume density allows protons to transfer more of their energy through Coulomb collisions, making the difference between the two temperatures lower in plumes than in the ambient interplume plasma. As of today, there is no observational measurement allowing us to check these predictions.
7.2 Theoretical models
As we have seen in the previous Section 7.1, empirical models have been unable to make uncontroversial predictions about outflows from plumes and did not face the problem of the persistence of plumes in the interplanetary medium. Can theoretical models provide better information than available from other sources?
The first theoretical models of plumes date back to only about 20 years ago. In 1994, Velli et al. (1994) and Wang (1994) built models, based on different assumptions. Velli et al. (1994) main interest was in far solar wind, aiming at checking whether the Thieme et al. (1989, 1990) observations (see Section 6) were consistent with theoretical predictions of the persistence of plumes at large heliocentric distances. Taking into account that plumes are immersed in a background medium and that plumes and the ambient corona must be in pressure equilibrium, Velli et al. (1994) assumed an a priori percentage areal occupation of plumes at the coronal base, magnetic flux conservation in the two regions, and solved the isothermal stationary wind equations for the two media. The outcome of their model predicts a plume to background speed that increases with distance and it is larger than observed at 0.3 AU — where Helios took the data analyzed by Thieme et al. (1989, 1990) — implying that further efforts were necessary to reach more realistic results. Wang (1994), on the contrary, focussed on solutions for the CH and plume flows at lower heliocentric distances and neglected the interaction between the plume and ambient medium. Wang (1994) solved the one-fluid mass, momentum and energy conservation equations assuming an exponential heating of the plume with two components, a global and a base heating, with different damping lengths. Alfvén waves, supposed to propagate without dissipation, yield an Alfvén wave flux, that is kept distinct from the global heating rate. The high pressure at the base of plumes can be achieved only via a base heating term, which, as anticipated in Section 5.1, allows high densities to be maintained at the base of plumes. Different choices of the free parameters (that include, among others, plume temperature, base heating, conductive flux and damping lengths) yield different solutions, which we do not individually illustrate here. But is interesting to notice that asymptotic solutions for the plasma temperature and speed predict lower values in plumes than in the background regions.
The models of Velli et al. (1994) and Wang (1994) ignored the magnetic field configuration of plumes, which expand superradially (see Section 2.1), at least close to their base. Del Zanna et al. (1997) and Del Zanna et al. (1998) focussed on this issue and built a 2-D MHD model that, at lower heights, derives the plasma parameters along the fieldlines of a quasi-potential field that mimics the superradial expansion of plumes. At higher altitudes, the authors use a 1-D model where plumes expand quasi-radially and are in pressure equilibrium with the background medium. In the low corona, magnetic forces predominate over all other forces and temperature is constant; in the higher corona, the temperature profile is given a priori.
These models pointed out that temperature plays a crucial role in determining the behavior of density and flow speed: in particular, the ratio between the temperature along the plume axis and the background temperature, heavily affects the position of the sonic point and the difference between plume and background wind. This issue was further explored by Casalbuoni et al. (1999) in an attempt to predict whether PBS or microstreams (see Section 6) might be associated with plumes. Casalbuoni et al. (1999) showed that plumes flow may be faster or slower than interplume flows, depending on the choice of the profiles of temperature in the two media. Also, they show that microstreams characteristic lower or higher local velocities, can be easily reproduced by varying the wave energy flux, at the coronal base, in the two regions: for equal temperature profiles, plumes are slower than interplumes if the wave flux is the same, but are faster if the wave flux is larger than that in the interplume ambient. In conclusion, theoretical models are unable to give clear indications about what can be expected at large heliocentric distances, as a different choice of the parameters may lead to opposite predictions and observational constraints are not stringent enough to provide modelers with unambiguous information on their values.
More recent models have been trying to reproduce the initial and final stages of the life of plumes. This requires a time-dependent simulation: Pinto et al. (2009) adopted a time-dependent 1-D hydrodynamical code to simulate the flow of a radially oriented diverging flux-tube, assuming the magnetic field changes as a function of heliocentric distance as
where Rss, the source surface height, is set at 2.5 R⊙ and ν ≥ 2. The energy equation includes radiative losses, the conductive heating flux and a mechanical heating flux Fh, which is a combination of a term proportional to a power of the magnetic field B and of a term exponentially decreasing with distance. The latter, whose need had been pointed out by Wang (1994), represents the extra heating operating at the base of the plume. Hence, the total heating function of Pinto et al. (2009) takes the form
Figure 16 gives the profiles of temperature and density in the plume at representative times along the plume birth and death cycles. The background interplume solution is obtained setting Fp0 to zero; the plume solution has Fb0 = Fp0 = 4 × 105 erg cm−2 s−1. To simulate, respectively, the birth and death of a plume, Pinto et al. (2009) suddenly increase Fp0 from Fp0 = 0 to Fp0 = 4 × 105 erg cm−2 s−1, and then suddenly switch off the Fp0 term to Fp0 = 0. In all simulations H = 0.05 R⊙.
Left panel: Representative solutions for the temperature and flow speed of a plume vs. heliocentric distance, obtained by Pinto et al. (2009), at the time of the birth of a plume. The initial state for the plume formation is given by the ambient corona solution, where Fp0 and Fb0 are set, respectively, to 0 and 4 × 105 erg cm−2 s−1; ν = 2. Right panel: solutions for the temperature and flow speed of a plume vs. heliocentric distance, at the time of the plume decay. The initial state for the plume decay is given by the plume solution; Fp0 is then suddenly set to zero. In both panels, the profiles are shown at t/τ = 0 (thick line), 1, 2, 3, 4, 5, 7, 10, 15, 25 (dashed lines) and 40 (thin solid line), where τ = R⊙/cs0, and cs0 is the sound speed at 106 K. Image reproduced with permission from Pinto et al. (2009), copyright by ESO.
Pinto et al.’s simulations show interesting features: during the formation of a plume, the outflowing plasma speed initially increases, but, subsequently, decays below its initial value. The opposite behavior occurs at the end of the life of the plume with the ambient coronal speed slowly recovering (both the formation and the decay of the plume occur over a time interval of the order of one day). Going back to Section 3.2.2, where we described empirical determination of outflows in plumes, it looks like Pinto et al.’s results support the conclusions of, e.g., Teriaca et al. (2003) and Raouafi et al. (2007), who claim plumes to move at a lower speed than the background interplume plasma. However, we cannot rule out the possibility that observations taken at specific transient stages of the plume’ life might lead to the opposite conclusions — although, being the time spent by the plume plasma in those stages likely shorter than the plume lifetime, the concept of a slower outflow in plumes than in the ambient medium seems to be favored.
The time intervals spent by plumes in their birth/decay stages, might also account for the plume persistence after their associated BP vanishes. That plumes survive the BP was also predicted by Wang and Muglach (2008), who suggest, from an estimate of the radiative cooling time, that plumes typically linger a few hours, after the BP disappears, before fading away. There are still too few observations of the initial and final stages of the life of a plume and of the BP to check how realistic are these suggestions.
A time-dependent generalization of the work of Casalbuoni et al. (1999) appears in a paper by Velli et al. (2011), that aims both at simulating the expansion of a CH and embedded plumes (interacting with the background hole plasma) and at checking how suddenly turning on (and off) the plume heating terms affects solar wind at different heliocentric distances and times. Velli et al. (2011) solve viscous, resistive, time-dependent MHD equations in spherical geometry (with axial symmetry), and follow the behavior of four plumes, rooted in the unipolar CH field and identified by the position of their footpoints, that overlie multipolar magnetic structures. The profiles of the heating functions of the ambient CH and of the four plumes are given a priori and are analogous to those given by Wang (1994) 1-D models. At 1 AU, it turns out that the CH ambient plasma flows faster than plumes, whose speed is inversely dependent on their temperature: the hottest plumes in the low corona flowing at the slowest rate in the distant wind. Also, the plasma (magnetic) pressure is higher (lower) in plumes than in the interplume plasma and the Kelvin-Helmholtz instability does not set in before 75 R⊙, i.e., (see Section 6) further out than predicted by Suess (1998): unless other instabilities operate, plumes should maintain their identity far out in the solar wind. Hence, the lack of observational evidence of in situ structures clearly associated with plumes keeps being unexplained.
An interesting possibility has been advanced by Landi et al. (2006): should we focus on switchbacks (see Section 6), as remnants of plumes? Landi et al. (2006) suggested that these structures form as a consequence of the interaction of Alfvénic turbulence and differential radial streaming, in a different scenario than proposed by Yamauchi et al. (2004). According to Landi et al. (2005) the formation mechanism of Yamauchi et al. (2004) leads to structures that persist only over short distances. On the other hand, Velli et al. (2011) model could not possibly yield these polarity inversion features, as it does not allow for non-linear interactions of Alfvén waves.
Figure 17 illustrates Ulysses data of two switchbacks (observed at distances, respectively, of 2.9 AU and 2.5 AU) compared with simulations by Landi et al. (2006), that reproduce not only the inversion of the polarity of the radial magnetic field but other observed features, like plasma pressure, as well. However, the sheared magnetic field fluctuations back-reaction on the plume plasma, may eventually lead to the mixing of plume and background plasma and not all plumes will be traceable in the far solar wind. We cite in passing that recently Matteini et al. (2014) proposed an altogether different interpretation of switchbacks that, rather than being isolated structures embedded in the solar wind, might represent a natural evolution of Alfvénic fluctuations, with no relations to solar structures.
Comparison of representative radial inversion features observed by Ulysses in 1994 (left panels) with Landi et al. (2006) simulations: from top to bottom, profiles of, respectively, radial velocity, radial component of the magnetic field, total (solid), thermal (dashed) and magnetic (dotted) pressure, and plasma β. Image reproduced with permission from Landi et al. (2006), copyright by AGU.
The effect of the ignition and termination of plumes on solar wind, as shown by Velli et al. (2011) simulations, obviously depends, at any given distance, on the plume heating terms. Roughly, plumes start being observable at 1 AU a few tens of hours after their heating is switched on and gradually disappear after they are turned off. Also, plumes tend to overexpand in late stages of their lifetime. This behavior obviously does not consider the possibility that plumes become unobservable because of some kind of instability.
An interesting effect that however has not been observed, yet, has been recently predicted by Pinto et al. (2013), in an investigation of the properties of Alfvén wave driven plumes. According to the authors, plumes may be generated by Alfvénic torsional wave motions of the footpoints of bipolar fieldlines within a CH region. Depending on the values of the parameter ε (defined as the ratio of the Alfvén wave speed in the photosphere to the coronal Alfvén wave speed) the flow of the plume has a different behavior and shifts from a smooth to a bursty regime, where a series of blobs propagate outwards and may show up in the data as slow-mode wave fronts. This research needs further work to better define the properties of plumes, but the possibility of bursty plumes, if confirmed, represents a so far unobserved behavior of these objects.
8 Conclusions: Going Further
Occasionally, throughout this review, we have been pointing to issues that need to be further explored. Here, we expand on topics, not adequately illustrated in previous sections, that are likely to be the focus of future studies. In particular, we will deal with the relationship between plumes and large and/or small-scale structures, possibly analogous to plumes or associated with them; on the contribution of plumes (and associated structures) to the solar wind; on the observational campaigns planned in the next future. Plumes’ science has still many fuzzy areas: to dissipate these uncertainties is the exciting goal of research over the next years.
8.1 Plumes and small-scale structures
In Section 5.1, we discussed the association of plumes with BPs and X-ray jets, mentioning how both issues need to be further explored. Here, we expand on relationships that have been even less analyzed between plumes and small-scale features, mostly originating from the magnetic network, whose observations have been recently soaring. Among these, spicules have a primary role.
Usually, we refer to spicules when describing thin, elongated, jet-like structures seen at the solar limb, in Hα and other chromospheric lines, from, e.g., Ca ii. An interaction between spicules and plumes had already been suggested by, e.g., Wilhelm (2000). The recent space missions provided data that increased our knowledge of spicules: De Pontieu et al. (2007), analyzing Ca ii HINODE/SOT (Solar Optical Telescope, Tsuneta et al., 2008) data, revealed the occurrence of (at least) two types of spicules, dubbed type I and type II, with different characteristics. Type II spicules, most frequent in quiet Sun and CHs, have shorter lifetimes and move mainly upwards at a higher speed than type I spicules. Because they fade in the Ca ii H passband, it has been speculated they undergo thermal evolution and may show up at higher transition region (TR) and coronal temperatures. This has been confirmed by data from the IRIS mission (De Pontieu et al., 2014) that revealed spicules can be observed at TR temperatures (Pereira et al., 2014).
Also, the X-ray jets discussed in Section 5.1 have been recognized to belong to two categories with different properties: the standard jets and the blowout jets (Moore et al., 2010), the latter being analogous to the large flares often associated with CMEs (coronal mass ejections). Sterling et al. (2010) by analyzing HINODE/SOT/XRT/EIT and STEREO/EUVI data, have been able to establish that the X-ray blowout jet they examine has, either side of the exploding blowout arch, two bright spicule-like objects, possibly identifiable with type II spicules. Although not all Ca ii type II spicules should necessarily correspond to blowout jets, Sterling et al. (2010) suggest a sub-population of type II spicules to be the manifestation of larger scale erupting jets.
Tian et al. (2014) observed quite numerous small-scale jets in IRIS data, at temperatures as high as 105 K, with upward speeds on the order of 80–250 km s−1 and lifetimes on the order of 50 ± 30 s that originate in the network lanes. These phenomena as well have been suggested to be related to type II spicules, although their speed is about twice higher than that of type II spicules. Some of the jets show evidence of acceleration and, although jets show up both in quiet Sun and in CH areas, a preliminary study (Tate Arbacher et al., 2015) yields a higher recurrence, higher speed and larger lengths for CH jets.
Given the link between plumes and jets, we may ask whether there is analogously a link between plumes and type II spicules. Are plumes typically hosting type II spicules? Are perhaps spicule miniature type II jets? Is there any relation between IRIS network jets and type II spicule/blowout jets? We are in a completely unexplored field where questions are unanswered and originate only from speculations. We come back to this point in Section 8.3.
8.2 Plumes and giant plumes
Obviously, the small size of plumes does not help us observing and/or building models that reproduce their behavior. We may ask whether there are larger scale features, analogous to plumes and more easily accessible to observations, that might help us reach a better understanding of the physics of plumes. Wang et al. (2007b) in a study of the 2006 March 29 eclipse, pointed out that some streamer-like large-scale coronal features could not be identified as helmet streamers, as, unlike the latter, were rooted in CHs of the same polarity, rather than being rooted in different polarity regions. Wang et al. (2007b) dubbed these structures “pseudostreamers” and noticed that the closed loop systems they overlie may reconnect with open fieldlines, in a process analogous to what triggers jets when a bipole emerges within an unipolar CH field. The quasi-steady behavior of pseudostreamers was thus suggested to correspond to the behavior of plumes: above pseudostreamers, outflows have indeed been observed (see Figure 18). These analogies justify the term “giant plumes” occasionally adopted with reference to pseudostreamers.
Top left: Background-subtracted LASCO C2 image of the 2005, April 25 corona, with labels identifying pseudostreamers (PS), plumes (PL), helmet streamers (H) and an helmet streamer blowout (H/CME). The north polar regions host a mixture of plumes and pseudostreamers. Top right: Formation of a jet-like feature (giant plume) in the model of Pinto et al. (2010): the occurrence of higher density blobs is highlighted by the red and yellow colours. Note the analogy between the magnetic configuration shown in this panel and that of Figure 13. Bottom: Height-time map of outflows above a pseudostreamer observed on April 22, 2006, with arrows corresponding to a radial flow speed of 200 km s−1. Images reproduced with permission from [top left, bottom] Wang et al. (2007b), copyright by AAS, and [top right] Pinto et al. (2010) copyright by AIP.
Pinto et al. (2010) built a model of giant plumes supposedly generated above a bipole, embedded in a unipolar field region, by the injection of Alfvén waves. The 2.5D isothermal MHD model predicts the formation of a high density column, representative of the giant plume/pseudostreamer, hosting blobs that propagate along the axis of the structure as slow mode wavefronts. The work of Pinto et al. (2010) focusses on the formation and decay of the structure and on the differences between this and the model of Pinto et al. (2009) where plumes form because of an increase in the base heating rate. As in the previous work, plasma outflows are envisaged, but the models are still too crude to make accurate predictions. The inclusion of dissipative effects is necessary to reach more reliable results. We notice that blobs have been observed in helmet streamers (Wang, 2009), but not in pseudostreamers, and a study of waves in these structures is still missing.
There is a different means to predict the speed of plasma outflows from pseudostreamers. In the Wang et al. (2007b) paper, the authors suggest these structures are sources of fast wind streams, on the basis of the empirical inverse relationship proposed by Wang and Sheeley Jr (1990) between solar wind speed and the flux tube divergence rate. Because flux tubes at the boundary of holes of the same polarity have no chance of rapidly expanding, they are likely sources of fast wind. More recently, Wang et al. (2012) revisited this conclusion, taking into account previously neglected factors, like the separation between the same-polarity holes, that may affect the expansion factor of the structure. Wang et al. (2012) conclude that pseudostreamers are sources of a “hybrid” type wind, of moderate speed. Observationally, several authors (e.g., Crooker et al., 2012; Riley and Luhmann, 2012), tried to identify the wind emanating from pseudostreamers in in situ wind observations, concluding pseudostreamers are sources of slow wind, while Panasenco and Velli (2013) suggest that a 3D expansion factor has to be computed before drawing any conclusion on the wind emanating from these giant plumes. How much of these studies can be applied to plumes is still unclear: possibly the wind originating in plumes may change, both in time and as a function of geometrical factors still not accounted for. We expect that further theoretical and observational studies will help us understand whether the analogies between these structures contribute to a better knowledge of their characteristics.
8.3 Do plumes contribute to solar wind?
There are two means by which plumes may contribute to solar wind mass and energy supply: either being privileged channels by which a high enough wave flux is transported upwards, or by hosting a high enough number of outflowing events, likely generated by reconnection, capable of contributing the right amount of mass and energy.
In Sections 3.3 and 4, we reviewed the evidence we have for Alfvén and other waves in plumes. A recent advancement in this area has been made by Thurgood et al. (2014), who made the first direct measurement of transverse waves in a plume, using SDO/AIA 171 A channel data. Alfvén waves in AIA data have already been observed (McIntosh et al., 2011) and claimed to be energetic enough to accelerate the fast wind. However, these data, although acquired above the limb of the Sun and suggesting waves are ubiquitous, do not differentiate between plume/interplume regions. The work of Thurgood et al. (2014) rejects the hypothesis plumes are a preferential channel for Alfvén wave propagation and claims the measured wave flux is 4–10 times lower than required for solar wind acceleration. Further work in this area is being done by, e.g., Guennou et al. (2014), who are leading an analysis of wave amplitudes in plumes/interplume regions via HINODE/EIS data.
In Section 5.2, we discussed alternatives to the interpretation of plume brightness fluctuations in terms of waves. A few authors (e.g., McIntosh et al., 2010; Tian et al., 2011; Pucci et al., 2014) claim that high speed outflows occur in plumes. Research in this area is still scanty: it is not clear whether upflows occur preferentially in plumes rather than in interplumes (or whether the faint interplume ambient hinders their identification) and it is difficult to guess how large can be their contribution to the wind mass. Pucci et al. (2014) suggest that 60% of the wind mass may originate from plumes, but warn the reader that the figure can be easily off by an order of magnitude, since basic parameters for this estimate are still uncertain. The percentage of the CH areas covered by plumes (10%, Ahmad and Withbroe, 1977) is known only vaguely, we do not know whether upflows occur throughout the whole plume area or only sparsely within some sub-regions and whether the detected upflows reach far out in the corona to become part of the wind. We expect this to be a major research area in the near future.
With respect to older works, such as those of, e.g., Teriaca et al. (2003) and Gabriel et al. (2003), where the authors were looking for steady plume outflows, recentl emphasis has shifted to small-scale episodic outflowing events that occur within plumes. Among those, jets are the first candidates as contributors to solar wind. Given the properties of standard and blowout jets (e.g., Pucci et al., 2013), it suffices to estimate what blowout can contribute to solar wind, being the latter the more energetic events. A crude estimate of the mass and energy fluxes possibly supplied to the wind by blowouts has been done by Poletto et al. (2014) and leads to too low figures to provide for the wind fluxes. These estimates implicitly assume that an unidentified mechanism supplies additional energy to the jets, increasing their speed, generally lower than the escape speed, so that they may become part of the solar wind. In conclusion, it looks unlikely that blowouts can significantly contribute to the wind. Still, this estimate may change, if type II spicules were proved to accompany blowouts: it is well known (see, e.g., McIntosh et al., 2011) that the type II spicular mass flux can easily balance the wind mass loss. Here we are on a still unknown territory.
Analogously, is there any relationship between the IRIS small-scale jets originating in network lanes (Tian et al., 2014) and plumes? Network jets can be the transition region counterparts of type II spicules, and have been shown to be well capable to provide for the solar wind. The interrelationships of these episodic phenomena are still largely unexplored and the issue of their connection with coronal plumes remains to be examined. Connecting these transient events throughout the solar atmosphere and understanding their contribution to solar wind (and coronal heating) may lead to change our ideas on the source of the wind mass and energy and will likely be the focus of many future researches.
8.4 Future eclipse campaigns
The progress done over the years, from the time plumes were observed in WL only at the time of eclipses by ground equipments, is impressive and the advent of space era acted, and still acts, as a trigger for new advances. Does this mean that eclipse ground campaigns have become obsolete and there is no point in pursuing that kind of observations? Certainly this is not the case, for more than one reason.
If we compare ground and space-based coronagraphs, we realize they face different obstacles: briefly, from ground, we need to fight with stray light and sky luminosity and it becomes difficult to make observations at large distances beyond the limb; from space, it is hard to take data close enough to the limb of the Sun. For instance, considering present operational instruments, Mauna Loa coronagraphs take data from ≈ 1.1 R⊙, up to about 1.5–2 R⊙ above the limb; the SOHO C2 coronagraph starts taking data at ≈ 2 R⊙ above the limb. While the Mark IV has a plate scale of 5.97 arcsec per pixel, the SOHO C2 coronagraph has a spatial resolution of 11 arcsec. These characteristics are dictated by the need of creating artificial eclipses, that are reproduced via internal or external occulters. Natural eclipses offer the ideal solution to decrease the sky brightness and to get the highest spatial resolution, on the order of 1 arcsec (see, e.g., Habbal et al. (2011); for a comparison, SOHO/EIT data have a spatial resolution of the order of 5 arcsec).
The problem with eclipses is, obviously, their limited duration. This also can be, at least partially, overcome, with, e.g., the planned Megamovie project, to be enforced at the time of the 2017 August 21 eclipse (Hudson et al., 2011). This eclipse, with a totality phase of 2 min and 40 s, will be visible throughout 14 US states and provides the opportunity of building, through the coordinated effort of numerous, differently located, observers, a movie showing dynamical events in the corona with an unprecedented high temporal resolution and over a large range of altitudes over the limb of the Sun. With favorable weather conditions, the project will monitor changes in the low corona never ever sampled at such high cadence, providing information unavailable from space experiments. Natural eclipses still offer unique advantages over man-made instrumentation: the UV emission observed from space decreases steeply with altitude (because, see Section 2.2, it usually depends on the square of the electron density), while the forbidden lines used in ground-based observations have a radiative component that keeps being visible at much further distances (because the radiative component is a linear function of density) and accounts for the large distances covered by ground data. Hence, even in these days, it looks like coordinated efforts of the WL and XUV communities are the most productive means for advancements in this area.
Notes
Nowadays, this phenomenological result can be interpreted in terms of the poleward migration of the magnetic flux, induced by meridional surface flows, that makes polar fieldlines fan out more rapidly than predicted by a dipolar field (see, e.g., Wang and Sheeley Jr, 1992).
With f(r) being defined by A(r) = (r/r0)2f(r)A0, where A0 is the base area of the plume and f(r) = 1 for a radial expansion.
References
Abetti, G., 1938, The Sun: Its Phenomena and Physical Features, Lockwood, London. (Cited on page 7.)
Ahmad, I. A. and Webb, D. F., 1978, “X-ray analysis of a polar plume”, Solar Phys., 58, 323–336. [DOI], [ADS]. (Cited on pages 11, 16, 17, 34, and 41.)
Ahmad, I. A. and Withbroe, G. L., 1977, “EUV analysis of polar plumes”, Solar Phys., 53, 397–408. [DOI], [ADS]. (Cited on pages 11, 16, 17, 41, and 51.)
Allen, M. J., Oluseyi, H. M., Walker, A. B. C., Hoover, R. B. and Barbee Jr, T. W., 1997, “Chromospheric and Coronal Structure of Polar Plumes. I. Magnetic Structure and Radiative Energy Balance”, Solar Phys., 174, 367–401. [DOI], [ADS]. (Cited on pages 41, 42, and 43.)
Anders, E. and Grevesse, N., 1989, “Abundances of the elements: Meteoritic and solar”, Geochim. Cosmochim. Acta, 53, 197–214. [DOI], [ADS]. (Cited on page 19.)
Andries, J. and Goossens, M., 2001, “Kelvin-Helmholtz instabilities and resonant flow instabilities for a coronal plume model with plasma pressure”, Astron. Astrophys., 368, 1083–1094. [DOI], [ADS]. (Cited on page 39.)
Andries, J., Tirry, W. J. and Goossens, M., 2000, “Modified Kelvin-Helmholtz Instabilities and Resonant Flow Instabilities in a One-dimensional Coronal Plume Model: Results for Plasma β = 0”, Astrophys. J., 531, 561–570. [DOI], [ADS]. (Cited on page 39.)
Banaszkiewicz, M., Axford, W. I. and McKenzie, J. F., 1998, “An analytic solar magnetic field model”, Astron. Astrophys., 337, 940–944. [ADS]. (Cited on pages 10 and 26.)
Banerjee, D., Teriaca, L., Doyle, J. G. and Wilhelm, K., 1998, “Broadening of Si VIII lines observed in the solar polar coronal holes”, Astron. Astrophys., 339, 208–214. [ADS]. (Cited on page 26.)
Banerjee, D., O’Shea, E. and Doyle, J. G., 2000a, “Long-Period Oscillations in Polar Plumes as Observed by CDS on Soho”, Solar Phys., 196, 63–78. [DOI], [ADS]. (Cited on pages 26 and 29.)
Banerjee, D., Teriaca, L., Doyle, J. G. and Lemaire, P., 2000b, “Polar Plumes and Inter-plume regions as observed by SUMER on SOHO”, Solar Phys., 194, 43–58. [ADS]. (Cited on page 26.)
Banerjee, D., O’Shea, E., Doyle, J. G. and Goossens, M., 2001, “Long period oscillations in the inter-plume regions of the Sun”, Astron. Astrophys., 377, 691–700. [DOI], [ADS]. (Cited on pages 26 and 29.)
Banerjee, D., Pérez-Suárez, D. and Doyle, J. G., 2009, “Signatures of Alfvén waves in the polar coronal holes as seen by EIS/Hinode”, Astron. Astrophys., 501, L15–L18. [DOI], [ADS], [arXiv:0906.4600]. (Cited on pages 17, 26, and 27.)
Barbey, N., Auchère, F., Rodet, T. and Vial, J.-C., 2008, “A Time-Evolving 3D Method Dedicated to the Reconstruction of Solar Plumes and Results Using Extreme Ultraviolet Data”, Solar Phys., 248, 409–423. [DOI], [ADS], [arXiv:0802.0113]. (Cited on page 14.)
Barbey, N., Guennou, C. and Auchère, F., 2013, “TomograPy: A Fast, Instrument-Independent, Solar Tomography Software”, Solar Phys., 283, 227–245. [DOI], [ADS], [arXiv:1103.5904 [astro-ph.SR]]. (Cited on page 14.)
Bělík, M., Barczyński, K. and Marková, E., 2013, “Dynamic of Polar Plumes Observed During 2006, 2008, 2009 and 2010 Total Solar Eclipses”, Solar Phys., 284, 439–445. [DOI], [ADS]. (Cited on page 10.)
Bigelow, F. H., 1891, “The extension of the corona, and the details of its structure”, Observatory, 14, 50–52. [ADS]. (Cited on page 7.)
Bohlin, J. D., Purcell, J. D., Sheeley Jr, N. R. and Tousey, R., 1975a, “Polar Plumes in XUV Emission-Line Corona”, Bull. Am. Astron. Soc., 7, 356. [ADS]. (Cited on pages 5 and 11.)
Bohlin, J. D., Sheeley Jr, N. R. and Tousey, R., 1975b, “Structure of the sun’s polar cap at wavelengths 240–600 Å”, in Space Research XV, Proceedings of open meetings of working groups on physical sciences of the seventeenth plenary meeting of COSPAR, São Paulo, Brazil, June 1974, (Ed.) Rycroft, M. J., pp. 651–656, Akademie Verlag, Berlin. [ADS]. (Cited on pages 11 and 16.)
Boursier, Y. and Llebaria, A., 2008, “3D dynamic forward modeling of polar plumes using Hidden Markov Trees”, Stat. Methodol., 5, 328–339. [DOI], [ADS]. (Cited on page 14.)
Brueckner, G. E., Howard, R. A., Koomen, M. J. et al., 1995, “The Large Angle Spectroscopic Coronagraph (LASCO)”, Solar Phys., 162, 357–402. [DOI], [ADS]. (Cited on page 11.)
Campbell, W. W., Moore, J. H. and Baker, R.H., 1923, “The Axis of Symmetry of the Polar Streamers in the Solar Corona”, Publ. Astron. Soc. Pac., 35, 163–166. [DOI], [ADS]. (Cited on pages 5 and 7.)
Casalbuoni, S., Del Zanna, L., Habbal, S. R. and Velli, M., 1999, “Coronal plumes and the expansion of pressure-balanced structures in the fast solar wind”, J. Geophys. Res., 104, 9947–9962. [DOI], [ADS]. (Cited on pages 44 and 46.)
Cirtain, J. W., Golub, L., Lundquist, L. et al., 2007, “Evidence for Alfvén Waves in Solar X-ray Jets”, Science, 318, 1580. [DOI], [ADS]. (Cited on page 34.)
Corti, G., Poletto, G., Romoli, M., Michels, J., Kohl, J. and Noci, G., 1997, “Physical Parameters in Plume and Interplume Regions from UVCS Observations”, in The Corona and Solar Wind Near Minimum Activity, Proceedings of the Fifth SOHO Workshop, held at the University of Oslo, Norway, 17–20 June 1997, (Ed.) Wilson, A., ESA Special Publication, SP-404, p. 289, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 24.)
Cranmer, S. R., Kohl, J. L., Noci, G. et al., 1999, “An Empirical Model of a Polar Coronal Hole at Solar Minimum”, Astrophys. J., 511, 481–501. [DOI], [ADS]. (Cited on page 24.)
Crooker, N. U., Antiochos, S. K., Zhao, X. and Neugebauer, M., 2012, “Global network of slow solar wind”, J. Geophys. Res., 117, A04104. [DOI], [ADS]. (Cited on page 49.)
Culhane, J. L., Harra, L. K., James, A. M. et al., 2007, “The EUV Imaging Spectrometer for Hinode”, Solar Phys., 243, 19–61. [DOI], [ADS]. (Cited on page 21.)
Cuntz, M. and Suess, S. T., 2001, “Shock Formation of Slow Magnetosonic Waves in Coronal Plumes”, Astrophys. J. Lett., 549, L143–L146. [DOI], [ADS]. (Cited on page 30.)
Curdt, W., Wilhelm, K., Feng, L. and Kamio, S., 2008, “Multi-spacecraft observations of polar coronal plumes”, Astron. Astrophys., 481, L61–L64. [DOI], [ADS]. (Cited on pages 20 and 21.)
Davis, J. M., 1980, “Observations Linking X-Ray Bright Points with the Source of the Mass Input to the Solar Wind”, Bull. Am. Astron. Soc., 12, 518. [ADS]. (Cited on page 34.)
de Patoul, J., Inhester, B. and Cameron, R., 2013a, “Polar plumes’ orientation and the Sun’s global magnetic field”, Astron. Astrophys., 558, L4. [DOI], [ADS], [arXiv:1309.5916 [astro-ph.SR]]. (Cited on page 13.)
de Patoul, J., Inhester, B., Feng, L. and Wiegelmann, T., 2013b, “2D and 3D Polar Plume Analysis from the Three Vantage Positions of STEREO/EUVI A, B, and SOHO/EIT”, Solar Phys., 283, 207–225. [DOI], [ADS], [arXiv:1111.4123 [astro-ph.SR]]. (Cited on page 14.)
De Pontieu, B., McIntosh, S., Hansteen, V. H. et al., 2007, “A Tale of Two Spicules: The Impact of Spicules on the Magnetic Chromosphere”, Publ. Astron. Soc. Japan, 59, 655. [DOI], [ADS], [arXiv:0710.2934]. (Cited on page 48.)
De Pontieu, B., Title, A. M., Lemen, J. R. et al., 2014, “The Interface Region Imaging Spectrograph (IRIS)”, Solar Phys., 289, 2733–2779. [DOI], [ADS], [arXiv:1401.2491 [astro-ph.SR]]. (Cited on page 48.)
DeForest, C. E., 2007, “On the Size of Structures in the Solar Corona”, Astrophys. J., 661, 532–542. [DOI], [ADS], [arXiv:astro-ph/0610178]. (Cited on pages 14 and 17.)
DeForest, C. E. and Gurman, J. B., 1998, “Observation of Quasi-periodic Compressive Waves in Solar Polar Plumes”, Astrophys. J. Lett., 501, L217–L220. [DOI], [ADS]. (Cited on page 29.)
DeForest, C. E., Hoeksema, J. T., Gurman, J. B., Thompson, B. J., Plunkett, S. P., Howard, R., Harrison, R. C. and Hassler, D. M., 1997, “Polar Plume Anatomy: Results of a Coordinated Observation”, Solar Phys., 175, 393–410. [DOI], [ADS]. (Cited on pages 11, 13, 14, 17, 22, and 33.)
DeForest, C. E., Lamy, P. L. and Llebaria, A., 2001a, “Solar Polar Plume Lifetime and Coronal Hole Expansion: Determination from Long-Term Observations”, Astrophys. J., 560, 490–498. [DOI], [ADS]. (Cited on pages 14 and 36.)
DeForest, C. E., Plunkett, S. P. and Andrews, M. D., 2001b, “Observation of Polar Plumes at High Solar Altitudes”, Astrophys. J., 546, 569–575. [DOI], [ADS]. (Cited on pages 11, 12, 13, and 15.)
Del Zanna, G. and Bromage, B. J. I., 1999, “The Elephant’s Trunk: Spectroscopic diagnostics applied to SOHO/CDS observations of the August 1996 equatorial coronal hole”, J. Geophys. Res., 104, 9753–9766. [DOI], [ADS]. (Cited on pages 11 and 17.)
Del Zanna, G., Bromage, B. J. I. and Mason, H. E., 2003, “Spectroscopic characteristics of polar plumes”, Astron. Astrophys., 398, 743–761. [DOI], [ADS]. (Cited on pages 15, 17, 18, 19, and 35.)
Del Zanna, G., Rozum, I. and Badnell, N. R., 2008, “Electron-impact excitation of Be-like Mg”, Astron. Astrophys., 487, 1203–1208. [DOI], [ADS]. (Cited on page 18.)
Del Zanna, L., Hood, A. W. and Longbottom, A. W., 1997, “An MHD model for solar coronal plumes”, Astron. Astrophys., 318, 963–969. [ADS]. (Cited on page 44.)
Del Zanna, L., von Steiger, R. and Velli, M., 1998, “The Expansion of Coronal Plumes in the Fast Solar Wind”, Space Sci. Rev., 85, 349–356. [DOI], [ADS]. (Cited on page 44.)
Delaboudinière, J.-P., Artzner, G. E., Brunaud, J. et al., 1995, “EIT: Extreme-Ultraviolet Imaging Telescope for the SOHO Mission”, Solar Phys., 162, 291–312. [DOI], [ADS]. (Cited on page 11.)
Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C. and Young, P. R., 1997, “CHIANTI — an atomic database for emission lines”, Astron. Astrophys. Suppl., 125, 149–173. [DOI], [ADS]. (Cited on page 18.)
Doschek, G. A., Laming, J. M., Feldman, U., Wilhelm, K., Lemaire, P., Schühle, U. and Hassler, D. M., 1998, “The Si/Ne Abundance Ratio in Polar Coronal Hole and Quiet-Sun Coronal Regions”, Astrophys. J., 504, 573–587. [DOI], [ADS]. (Cited on page 21.)
Doyle, J. G., Giannikakis, J., Xia, L. D. and Madjarska, M. S., 2005, “Line broadening of EUV lines across the Solar limb: A spicule contribution?”, Astron. Astrophys., 431, L17–L20. [DOI], [ADS]. (Cited on page 28.)
Farid, S. I., Oluseyi, H. M., Sterling, S., Tan, A., Williamson, J. L. and Winebarger, A. R., 2008, “Observation and Modeling of Polar Plumes Observed during the March 29, 2006 Total Solar Eclipse”, in Proceedings of the National Society of Black Physicists, Boston, Massachusetts, 21–24 February 2007, (Ed.) Oluseyi, H. M., AIP Conf. Proc., 991, pp. 10–26, American Institute of Physics, Melville, NY. [DOI], [ADS]. (Cited on page 43.)
Feldman, U. and Widing, K. G., 2003, “Elemental Abundances in the Solar Upper Atmosphere Derived by Spectroscopic Means”, Space Sci. Rev., 107, 665–720. [DOI], [ADS]. (Cited on page 21.)
Feng, L., Inhester, B., Solanki, S. K. et al., 2009, “Stereoscopic Polar Plume Reconstructions from STEREO/SECCHI Images”, Astrophys. J., 700, 292–301. [DOI], [ADS], [arXiv:0908.2365]. (Cited on page 14.)
Fisher, R. and Guhathakurta, M., 1995, “Physical Properties of Polar Coronal Rays and Holes as Observed with the SPARTAN 201-01 Coronagraph”, Astrophys. J. Lett., 447, L139. [DOI], [ADS]. (Cited on pages 13 and 15.)
Fisher, R. R. and Guhathakurta, M., 1994, “SPARTAN 201 white light coronagraph experiment”, Space Sci. Rev., 70, 267–272. [DOI], [ADS]. (Cited on page 43.)
Foukal, P. and Eddy, J., 2007, “Did the Sun’s Prairie Ever Stop Burning?”, Solar Phys., 245, 247–249. [DOI], [ADS]. (Cited on page 7.)
Fu, H., Xia, L., Li, B., Huang, Z., Jiao, F. and Mou, C., 2014, “Measurements of Outflow Velocities in on-disk Plumes from EIS/Hinode Observations”, Astrophys. J., 794, 109. [DOI], [ADS], [arXiv:1408.5473 [astro-ph.SR]]. (Cited on pages 22, 23, 24, and 26.)
Gabriel, A., Bely-Dubau, F., Tison, E. and Wilhelm, K., 2009, “The Structure and Origin of Solar Plumes: Network Plumes”, Astrophys. J., 700, 551–558. [DOI], [ADS]. (Cited on pages 13 and 14.)
Gabriel, A. H., Bely-Dubau, F. and Lemaire, P., 2003, “The Contribution of Polar Plumes to the Fast Solar Wind”, Astrophys. J., 589, 623–634. [DOI], [ADS]. (Cited on pages 25 and 51.)
Gabriel, A. H., Abbo, L., Bely-Dubau, F., Llebaria, A. and Antonucci, E., 2005, “Solar Wind Outflow in Polar Plumes from 1.05 to 2.4 R⊙”, Astrophys. J. Lett., 635, L185–L188. [DOI], [ADS]. (Cited on page 25.)
Giordano, S., Antonucci, E., Noci, G., Romoli, M. and Kohl, J. L., 2000, “Identification of the Coronal Sources of the Fast Solar Wind”, Astrophys. J. Lett., 531, L79–L82. [DOI], [ADS], [arXiv:astro-ph/0001257]. (Cited on page 24.)
Grappin, R., Wang, Y.-M. and Pantellini, F., 2011, “Two-temperature Models for Polar Plumes: Cooling by Means of Strong Base Heating”, Astrophys. J., 727, 30. [DOI], [ADS]. (Cited on page 43.)
Grevesse, N., Noels, A. and Sauval, A. J., 1992, “Photospheric abundances”, in Coronal Streamers, Coronal Loops, and Coronal and Solar Wind Composition, Proceedings of the First SOHO Workshop, held in Annapolis, MD, 25–28 August 1992, (Ed.) Mattok, C., ESA Conference Proceedings, 348, pp. 305–308, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 19.)
Guennou, C., Savin, D. W. and Hahn, M., 2014, “Hinode/EIS observations signatures of plume and interplume regions.”, Bull. Am. Astron. Soc., 46, 323.53. [ADS]. (Cited on page 51.)
Guennou, C., Hahn, M. and Savin, D. W., 2015, “Relative Abundance Measurements in Plumes and Interplumes”, Astrophys. J., 807, 145. [DOI], [ADS], [arXiv:1503.06044]. (Cited on page 21.)
Guhathakurta, M., Fludra, A., Gibson, S. E., Biesecker, D. and Fisher, R., 1999, “Physical properties of a coronal hole from a coronal diagnostic spectrometer, Mauna Loa Coronagraph, and LASCO observations during the Whole Sun Month”, J. Geophys. Res., 104, 9801–9808. [DOI], [ADS]. (Cited on page 17.)
Gupta, G. R., Banerjee, D., Teriaca, L., Imada, S. and Solanki, S., 2010, “Accelerating Waves in Polar Coronal Holes as Seen by EIS and SUMER”, Astrophys. J., 718, 11–22. [DOI], [ADS], [arXiv:1005.3453[astro-ph.SR]]. (Cited on pages 30 and 31.)
Gupta, G. R., Teriaca, L., Marsch, E., Solanki, S. K. and Banerjee, D., 2012, “Spectroscopic observations of propagating disturbances in a polar coronal hole: evidence of slow magneto-acoustic waves”, Astron. Astrophys., 546, A93. [DOI], [ADS], [arXiv:1209.3524 [astro-ph.SR]]. (Cited on page 29.)
Habbal, S. R. and Woo, R., 2001, “Connecting the Sun and the Solar Wind: Comparison of the Latitudinal Profiles of Coronal and Ulysses Measurements of the Fast Wind”, Astrophys. J. Lett., 549, L253–L256. [DOI], [ADS]. (Cited on page 10.)
Habbal, S. R., Esser, R., Guhathakurta, M. and Fisher, R. R., 1995, “Flow properties of the solar wind derived from a two-fluid model with constraints from white light and in situ interplanetary observations”, Geophys. Res. Lett., 22, 1465–1468. [DOI], [ADS]. (Cited on page 43.)
Habbal, S. R., Druckmüller, M., Morgan, H. et al., 2011, “Thermodynamics of the Solar Corona and Evolution of the Solar Magnetic Field as Inferred from the Total Solar Eclipse Observations of 2010 July 11”, Astrophys. J., 734, 120. [DOI], [ADS]. (Cited on page 52.)
Hara, H. and Nakakubo-Morimoto, K., 2004, “Variation of the X-ray Bright Point Number over the Solar Activity Cycle”, in The Solar-B Mission and the Forefront of Solar Physics, (Eds.) Sakurai, T., Sekii, T., ASP Conference Series, 325, p. 307, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 34.)
Harrison, R. A., Sawyer, E. C., Carter, M. K. et al., 1995, “The Coronal Diagnostic Spectrometer for the Solar and Heliospheric Observatory”, Solar Phys., 162, 233–290. [DOI], [ADS]. (Cited on page 17.)
Harvey, J. W., 1965, “Coronal Polar Rays and Polar Magnetic Fields”, Astrophys. J., 141, 832–833. [DOI], [ADS]. (Cited on page 9.)
Hassler, D. M., 2000, “Spectroscopic Observations of Polar Plumes with SOHO/SUMMER”, in Last Total Solar Eclipse of the Millennium in Turkey, Proceedings of a symposium held in Istanbul, Turkey, 13–15 August 1999, (Eds.) Livingston, W., Özgüç, A., ASP Conference Series, 205, p. 83, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 23.)
Hassler, D. M., Wilhelm, K., Lemaire, P. and Schühle, U., 1997, “Observations of Polar Plumes with the SUMER Instrument on SOHO”, Solar Phys., 175, 375–391. [DOI], [ADS]. (Cited on page 26.)
Hassler, D. M., Dammasch, I. E., Lemaire, P., Brekke, P., Curdt, W., Mason, H. E., Vial, J.-C. and Wilhelm, K., 1999, “Solar Wind Outflow and the Chromospheric Magnetic Network”, Science, 283, 810–813. [DOI], [ADS]. (Cited on pages 21, 22, and 23.)
Heber, V. S., Baur, H., Bochsler, P., McKeegan, K. D., Neugebauer, M., Reisenfeld, D. B., Wieler, R. and Wiens, R. C., 2012, “Isotopic Mass Fractionation of Solar Wind: Evidence from Fast and Slow Solar Wind Collected by the Genesis mission”, Astrophys. J., 759, 121. [DOI], [ADS]. (Cited on page 19.)
Howard, R. A., Moses, J. D., Vourlidas, A. et al., 2008, “Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI)”, Space Sci. Rev., 136, 67–115. [DOI], [ADS]. (Cited on page 14.)
Hudson, H. S., McIntosh, S. W., Habbal, S. R., Pasachoff, J. M. and Peticolas, L., 2011, “The U.S. Eclipse Megamovie in 2017: a white paper on a unique outreach event”, arXiv, e-print. [ADS], [arXiv:1108.3486 [astro-ph.SR]]. (Cited on page 52.)
Kano, R., Hara, H., Shimojo, M. et al., 2004, “SolarB X-Ray Telescope (XRT)”, in The Solar-B Mission and the Forefront of Solar Physics, (Eds.) Sakurai, T., Sekii, T., ASP Conference Series, 325, p. 15, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 34.)
Karachik, N. V. and Pevtsov, A. A., 2011, “Solar wind and coronal bright points inside coronal holes”, Astrophys. J., 735, 47. [DOI], [ADS]. (Cited on page 34.)
Kohl, J. L., Esser, R., Gardner, L. D. et al., 1995, “The Ultraviolet Coronagraph Spectrometer for the Solar and Heliospheric Observatory”, Solar Phys., 162, 313–356. [DOI], [ADS]. (Cited on page 23.)
Kohl, J. L., Strachan, L. and Gardner, L. D., 1996, “Measurement of Hydrogen Velocity Distributions in the Extended Solar Corona”, Astrophys. J. Lett., 465, L141. [DOI], [ADS]. (Cited on page 43.)
Kohl, J. L., Noci, G., Antonucci, E. et al., 1998, “UVCS/SOHO Empirical Determinations of Anisotropic Velocity Distributions in the Solar Corona”, Astrophys. J. Lett., 501, L127–L131. [DOI], [ADS]. (Cited on page 43.)
Kopp, R. A. and Holzer, T. E., 1976, “Dynamics of coronal hole regions. I. Steady polytropic flows with multiple critical points”, Solar Phys., 49, 43–56. [DOI], [ADS]. (Cited on page 10.)
Koutchmy, S. and Bocchialini, K., 1997, “Eclipse WL polar plumes: what is the connection with the disk activity?”, in Robotic Exploration Close to the Sun: Scientific Basis, Marlboro, MA, 1996, (Ed.) Habbal, S. R., AIP Conf. Proc., 385, pp. 137–144, American Institute of Physics, Woodbury, NY. [DOI], [ADS]. (Cited on page 11.)
Koutchmy, S. and Bocchialini, K., 1998, “White-light polar plumes from solar eclipses”, in Solar Jets and Coronal Plumes, 23–26 Feb 1998, Guadeloupe, France, (Ed.) Guyenne, T.-D., ESA Special Publication, SP-421, pp. 51–62, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 10.)
Krieger, A. S., Timothy, A. F. and Roelof, E. C., 1973, “A Coronal Hole and Its Identification as the Source of a High Velocity Solar Wind Stream”, Solar Phys., 29, 505–525. [DOI], [ADS]. (Cited on page 14.)
Krishna Prasad, S., Banerjee, D. and Gupta, G. R., 2011, “Propagating intensity disturbances in polar corona as seen from AIA/SDO”, Astron. Astrophys., 528, L4. [DOI], [ADS], [arXiv:1102.2979 [astro-ph.SR]]. (Cited on pages 30 and 31.)
Krishna Prasad, S., Banerjee, D., Van Doorsselaere, T. and Singh, J., 2012, “Omnipresent long-period intensity oscillations in open coronal structures”, Astron. Astrophys., 546, A50. [DOI], [ADS], [arXiv:1209.2536 [astro-ph.SR]]. (Cited on page 30.)
Krishna Prasad, S., Banerjee, D. and Van Doorsselaere, T., 2014, “Frequency-dependent Damping in Propagating Slow Magneto-acoustic Waves”, Astrophys. J., 789, 118. [DOI], [ADS], [arXiv:1406.3565 [astro-ph.SR]]. (Cited on page 30.)
Lamy, P., Liebaria, A., Koutchmy, S., Reynet, P., Molodensky, M., Howard, R., Schwenn, R. and Simnett, G., 1997, “Characterisation of Polar Plumes from LASCO-C2 Images in Early 1996”, in The Corona and Solar Wind Near Minimum Activity, Proceedings of the Fifth SOHO Workshop, held at the University of Oslo, Norway, 17–20 June 1997, (Ed.) Wilson, A., ESA Special Publication, SP-404, p. 487, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 14.)
Landi, S., Hellinger, P. and Velli, M., 2005, “On the Origin of the Heliospheric Magnetic Field Polarity Inversion at High Latitudes”, in Connecting Sun and Heliosphere, Proceedings of Solar Wind 11 / SOHO 16, 12–17 June 2005, Whistler, Canada, (Eds.) Fleck, B., Zurbuchen, T. H., Lacoste, H., ESA Conference Proceedings, SP-592, p. 785, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 46.)
Landi, S., Hellinger, P. and Velli, M., 2006, “Heliospheric magnetic field polarity inversions driven by radial velocity field structures”, Geophys. Res. Lett., 33, 14101. [DOI], [ADS]. (Cited on pages 46 and 47.)
Le Chat, G., Issautier, K. and Meyer-Vernet, N., 2012, “The Solar Wind Energy Flux”, Solar Phys., 279, 197–205. [DOI], [ADS], [arXiv:1203.1316 [astro-ph.SR]]. (Cited on page 29.)
Lemen, J. R., Title, A. M., Akin, D. J. et al., 2012, “The Atmospheric Imaging Assembly (AIA) on the Solar Dynamics Observatory (SDO)”, Solar Phys., 275, 17–40. [DOI], [ADS]. (Cited on page 30.)
Li, J., Kuhn, J., LaBonte, B., Raymond, J. C. and Acton, L. W., 2000, “Global Solar Corona Revealed by Time Series Observations”, Astrophys. J., 538, 415–423. [DOI], [ADS]. (Cited on page 11.)
Lites, B. W., Card, G., Elmore, D. F., Holzer, T., Lecinski, A., Streander, K. V., Tomczyk, S. and Gurman, J. B., 1999, “Dynamics of polar plumes observed at the 1998 February 26 eclipse”, Solar Phys., 190, 185–206. [DOI], [ADS]. (Cited on page 34.)
Llebaria, A., Lamy, P., DeForest, C. and Koutchmy, S., 1998, “Time domain analysis of polar plumes observed with LASCO-C2 and EIT”, in Solar Jets and Coronal Plumes, 23–26 Feb 1998, Guadeloupe, France, (Ed.) Guyenne, T.-D., ESA Special Publication, SP-421, pp. 87–94, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 11.)
Llebaria, A., Saez, F. and Lamy, P., 2002, “The fractal nature of the polar plumes”, in From Solar Minto Max: Half a Solar Cycle with SOHO, Proceedings of the SOHO-11 Symposium, 11–15 March 2002, Davos, Switzerland, (Ed.) Wilson, A., ESA Special Publication, SP-508, pp. 391–394, ESA Publications Division, Noordwijk. [ADS]. (Cited on pages 14 and 34.)
Lynn, W. T., 1885, “The Total Eclipse of May 12th, 1706”, Observatory, 8, 270–271. [ADS]. (Cited on page 7.)
Lyot, B., 1933, “The Study of the Solar Corona without an Eclipse”, J. R. Astron. Soc. Can., 27, 265. [ADS]. (Cited on page 5.)
Mason, H. E. and Fossi, B. C. M., 1994, “Spectroscopic diagnostics in the VUV for solar and stellar plasmas”, Astron. Astrophys. Rev., 6, 123–179. [DOI], [ADS]. (Cited on page 17.)
Matteini, L., Horbury, T. S., Neugebauer, M. and Goldstein, B. E., 2014, “Dependence of solar wind speed on the local magnetic field orientation: Role of Alfvénic fluctuations”, Geophys. Res. Lett., 41, 259–265. [DOI], [ADS]. (Cited on page 47.)
McComas, D. J., Barraclough, B. L., Gosling, J. T., Hammond, C. M., Phillips, J. L., Neugebauer, M., Balogh, A. and Forsyth, R. J., 1995, “Structures in the polar solar wind: Plasma and field observations from Ulysses”, J. Geophys. Res., 100, 19 893–19 902. [DOI], [ADS]. (Cited on page 38.)
McComas, D. J., Hoogeveen, G. W., Gosling, J. T., Phillips, J. L., Neugebauer, M., Balogh, A. and Forsyth, R., 1996, “Ulysses observations of pressure-balance structures in the polar solar wind”, Astron. Astrophys., 316, 368–373. [ADS]. (Cited on page 38.)
McIntosh, S. W., Innes, D. E., De Pontieu, B. and Leamon, R. J., 2010, “STEREO observations of quasi-periodically driven high velocity outflows in polar plumes”, Astron. Astrophys., 510, L2. [DOI], [ADS], [arXiv:1001.3377 [astro-ph.SR]]. (Cited on pages 36 and 51.)
McIntosh, S. W., De Pontieu, B., Carlsson, M., Hansteen, V., Boerner, P. and Goossens, M., 2011, “Alfvénic waves with sufficient energy to power the quiet solar corona and fast solar wind”, Nature, 475, 477–480. [DOI], [ADS]. (Cited on page 51.)
Milovanov, A. V. and Zelenyi, L. M., 1994, “Development of fractal structure in the solar wind and distribution of magnetic field in the photosphere”, in Solar System Plasmas in Space and Time, (Eds.) Burch, J. L., Waite Jr, J. H., Geophysical Monograph Series, 84, pp. 43–52, American Geophysical Union, Washington, DC. [DOI], [ADS]. (Cited on page 14.)
Mohan, A., Dwivedi, B. N. and Landi, E., 2000, “Electron Density and Temperature Measurements, and Abundance Anomalies in the Solar Atmosphere”, J. Astrophys. Astron., 21, 407. [DOI], [ADS]. (Cited on page 17.)
Moore, R. L., Cirtain, J. W., Sterling, A. C. and Falconer, D. A., 2010, “Dichotomy of Solar Coronal Jets: Standard Jets and Blowout Jets”, Astrophys. J., 720, 757–770. [DOI], [ADS]. (Cited on page 48.)
Moran, T., Gopalswamy, N., Dammasch, I. E. and Wilhelm, K., 2001, “A multi-wavelength study of solar coronal-hole regions showing radio enhancements”, Astron. Astrophys., 378, 1037–1045. [DOI], [ADS]. (Cited on page 13.)
Moses, D., Clette, F., Delaboudiniere, J.-P. et al., 1997, “EIT Observations of the Extreme Ultraviolet Sun”, Solar Phys., 175, 571–599. [DOI], [ADS]. (Cited on pages 17 and 34.)
Neugebauer, M., 2012, “Evidence for Polar X-Ray Jets as Sources of Microstream Peaks in the Solar Wind”, Astrophys. J., 750, 50. [DOI], [ADS]. (Cited on page 40.)
Neugebauer, M., Goldstein, B. E., McComas, D. J., Suess, S. T. and Balogh, A., 1995, “Ulysses observations of microstreams in the solar wind from coronal holes”, J. Geophys. Res., 100, 23 389–23 396. [DOI], [ADS]. (Cited on pages 38 and 39.)
Newkirk Jr, G. and Harvey, J., 1968, “Coronal Polar Plumes”, Solar Phys., 3, 321–343. [DOI], [ADS]. (Cited on pages 9, 15, 22, and 41.)
Nindos, A., Kundu, M. R., White, S. M., Gary, D. E., Shibasaki, K. and Dere, K. P., 1999, “Microwave and Extreme Ultraviolet Observations of Solar Polar Regions”, Astrophys. J., 527, 415–425. [DOI], [ADS]. (Cited on page 13.)
Noci, G., Kohl, J. L. and Withbroe, G. L., 1987, “Solar wind diagnostics from Doppler-enhanced scattering”, Astrophys. J., 315, 706–715. [DOI], [ADS]. (Cited on page 23.)
Ofman, L. and Wang, T., 2002, “Hot Coronal Loop Oscillations Observed by SUMER: Slow Magnetosonic Wave Damping by Thermal Conduction”, Astrophys. J. Lett., 580, L85–L88. [DOI], [ADS]. (Cited on page 30.)
Ofman, L., Nakariakov, V. M. and DeForest, C. E., 1999a, “Slow Magnetosonic Waves in Coronal Plumes”, Astrophys. J., 514, 441–447. [DOI], [ADS]. (Cited on page 29.)
Ofman, L., Romoli, M., Noci, G., Poletto, G., Kohl, J. L., Howard, R. A., St Cyr, O. C. and DeForest, C. E., 1999b, “SOHO Observations of Density Fluctuations in Coronal Holes”, Space Sci. Rev., 87, 287–290. [DOI], [ADS]. (Cited on page 29.)
Ofman, L., Nakariakov, V. M. and Sehgal, N., 2000a, “Dissipation of Slow Magnetosonic Waves in Coronal Plumes”, Astrophys. J., 533, 1071–1083. [DOI], [ADS]. (Cited on page 29.)
Ofman, L., Romoli, M., Poletto, G., Noci, G. and Kohl, J. L., 2000b, “UVCS WLC Observations of Compressional Waves in the South Polar Coronal Hole”, Astrophys. J., 529, 592–598. [DOI], [ADS]. (Cited on pages 29 and 30.)
O’Shea, E., Banerjee, D. and Poedts, S., 2003, “Variation of coronal line widths on and off the disk”, Astron. Astrophys., 400, 1065–1070. [DOI], [ADS]. (Cited on page 26.)
Panasenco, O. and Velli, M., 2013, “Coronal pseudostreamers: Source of fast or slow solar wind?”, in Solar Wind 13, 17–22 June 2012, Big Island, Hawaii, (Eds.) Zank, G. P., Borovsky, J., Bruno, R., Cirtain, J., Cranmer, S., Elliott, H., Giacalone, J., Gonzalez, W., Li, G., Marsch, E., Moebius, E., Pogorelov, N., Spann, J., Verkhoglyadova, O., AIP Conf. Proc., 1539, pp. 50–53, American Institute of Physics, Melville, NY. [DOI], [ADS], [arXiv:1211.6171 [astro-ph.SR]]. (Cited on page 49.)
Parhi, S., Suess, S. T. and Sulkanen, M., 1999, “Can Kelvin-Helmholtz instabilities of jet-like structures and plumes cause solar wind fluctuations at 1 AU?”, J. Geophys. Res., 104, 14 781–14 788. [DOI], [ADS]. (Cited on page 39.)
Pasachoff, J. M., Rušin, V., Druckmüller, M. et al., 2008, “Polar Plume Brightening During the 2006 March 29 Total Eclipse”, Astrophys. J., 682, 638–643. [DOI], [ADS]. (Cited on page 10.)
Patsourakos, S. and Vial, J.-C., 2000, “Outflow velocity of interplume regions at the base of Polar Coronal Holes”, Astron. Astrophys., 359, L1–L4. [ADS]. (Cited on page 24.)
Pätzold, M. and Bird, M. K., 1998, “Polar plumes and fine-scale coronal structures — On the interpretation of coronal radio sounding data”, Geophys. Res. Lett., 25, 1845–1848. [DOI], [ADS]. (Cited on page 13.)
Pätzold, M. and Bird, M. K., 1999, “Erratum: ‘Polar plumes and fine-scale coronal structures — On the interpretation of coronal radio sounding data’”, Geophys. Res. Lett., 26, 585–586. [DOI], [ADS]. (Cited on page 13.)
Pereira, T. M. D., De Pontieu, B., Carlsson, M. et al., 2014, “An Interface Region Imaging Spectrograph first view on solar spicules”, Astrophys. J. Lett., 792, L15. [DOI], [ADS], [arXiv:1407.6360 [astro-ph.SR]]. (Cited on page 48.)
Pinto, R., Grappin, R., Wang, Y.-M. and Léeorat, J., 2009, “Time-dependent hydrodynamical simulations of slow solar wind, coronal inflows, and polar plumes”, Astron. Astrophys., 497, 537–543. [DOI], [ADS]. (Cited on pages 44, 45, and 49.)
Pinto, R., Grappin, R. and Léorat, J., 2010, “Coronal Inflows and Giant Polar Plumes”, in Twelfth International Solar Wind Conference, Saint-Malo, France, 21–26 June 2009, (Eds.) Maksimovic, M., Issautier, K., Meyer-Vernet, N., Moncuquet, M., Pantelli, F., AIP Conf. Proc., 1216, pp. 80–83, American Institute of Physics, Melville, NY. [DOI], [ADS], [arXiv:0912.3226 [astro-ph.SR]]. (Cited on pages 49 and 50.)
Pinto, R. F., Grappin, R., Velli, M. and Verdini, A., 2013, “Coupling the solar surface and the corona: Coronal rotation, Alfvén wave-driven polar plumes”, in Solar Wind 13, 17–22 June 2012, Big Island, Hawaii, (Eds.) Zank, G. P., Borovsky, J., Bruno, R., Cirtain, J., Cranmer, S., Elliott, H., Giacalone, J., Gonzalez, W., Li, G., Marsch, E., Moebius, E., Pogorelov, N., Spann, J., Verkhoglyadova, O., AIP Conf. Proc., 1539, pp. 58–61, American Institute of Physics, Melville, NY. [DOI], [ADS], [arXiv:1301.0341 [astro-ph.SR]]. (Cited on page 47.)
Pohjolainen, S., 2000, “On the origin of polar radio brightenings at short millimeter wavelengths”, Astron. Astrophys., 361, 349–358. [ADS]. (Cited on page 13.)
Pohjolainen, S., Portier-Fozzani, F. and Ragaigne, D., 2000, “Comparison of 87 GHz solars polar structures with EUV and soft X-ray emission”, Astron. Astrophys. Suppl., 143, 227–263. [DOI], [ADS]. (Cited on page 13.)
Poletto, G., Suess, S. T., Khan, J. I. et al., 1994, “X-ray bright points and high-speed wind streams: a preliminary analysis from Yohkoh and Ulysses data”, in Solar Dynamic Phenomena and Solar Wind Consequences, Proceedings of the Third SOHO Workshop held 26–29 September, 1994 in Estes Park, Colorado, (Ed.) Hunt, J. J., ESA Special Publication, SP-373, p. 143, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 34.)
Poletto, G., Parenti, S., Noci, G., Livi, S., Suess, S. T., Balogh, A. and McComas, D. J., 1996, “Searching for coronal plumes in Ulysses observations of the far solar wind”, Astron. Astrophys., 316, 374–383. [ADS]. (Cited on page 38.)
Poletto, G., Sterling, A. C., Pucci, S. and Romoli, M., 2014, “The contribution of X-ray polar blowout jets to the solar wind mass and energy”, in Nature of Prominences and their Role in Space Weather, Proceedings of IAU Symposium 300, June 2013, (Eds.) Schmieder, B., Malherbe, J.-M., Wu, S. T., IAU Symposium, 300, pp. 239–242, Cambridge University Press, Cambridge; New York. [DOI], [ADS]. (Cited on page 51.)
Popescu, M. D., Doyle, J. G. and Xia, L. D., 2004, “Network boundary origins of fast solar wind seen in the low transition region?”, Astron. Astrophys., 421, 339–348. [DOI], [ADS]. (Cited on page 21.)
Popescu, M. D., Banerjee, D., O’Shea, E., Doyle, J. G. and Xia, L. D., 2005, “Very long period activity at the base of solar wind streams”, Astron. Astrophys., 442, 1087–1090. [DOI], [ADS]. (Cited on page 29.)
Pucci, S., Poletto, G., Sterling, A. C. and Romoli, M., 2013, “Physical Parameters of Standard and Blowout Jets”, Astrophys. J., 776, 16. [DOI], [ADS]. (Cited on page 51.)
Pucci, S., Poletto, G., Sterling, A. C. and Romoli, M., 2014, “Birth, Life, and Death of a Solar Coronal Plume”, Astrophys. J., 793, 86. [DOI], [ADS]. (Cited on pages 35, 36, 37, and 51.)
Raju, K. P., Sakurai, T., Ichimoto, K. and Singh, J., 2000, “The Physical Conditions in a Polar Coronal Hole and Nearby Regions from Norikura and SOHO Observations”, Astrophys. J., 543, 1044–1050. [DOI], [ADS]. (Cited on page 26.)
Raouafi, N.-E., 2009, “On the Relationship between Polar Coronal Jets and Plumes”, in The Second Hinode Science Meeting: Beyond Discovery-Toward Understanding, Proceedings of a meeting at the NCAR, Boulder, CO, USA, held 29 September–3 October, 2008, (Eds.) Lites, B., Cheung, M., Magara, T., Mariska, J., Reeves, K., ASP Conference Series, 415, p. 144, Astronomical Society of the Pacific, San Francisco. [ADS], [arXiv:0902.0591 [astro-ph.SR]]. (Cited on page 34.)
Raouafi, N.-E. and Stenborg, G., 2014, “Role of Transients in the Sustainability of Solar Coronal Plumes”, Astrophys. J., 787, 118. [DOI], [ADS]. (Cited on pages 35, 36, and 37.)
Raouafi, N.-E., Harvey, J. W. and Solanki, S. K., 2006, “Plasma dynamics in the polar coronal plumes”, in Solar Activity and its Magnetic Origin, Proceedings of IAU Symposium 233, held in Cairo, Egypt, March 31–April 4, 2006, (Eds.) Bothmer, V., Hady, A. A., IAU Symposium, 233, pp. 193–194, Cambridge University Press, Cambridge; New York. [DOI], [ADS]. (Cited on page 10.)
Raouafi, N.-E., Harvey, J. W. and Solanki, S. K., 2007, “Properties of Solar Polar Coronal Plumes Constrained by Ultraviolet Coronagraph Spectrometer Data”, Astrophys. J., 658, 643–656. [DOI], [ADS], [arXiv:astro-ph/0703745]. (Cited on pages 25 and 45.)
Raouafi, N.-E., Petrie, G. J. D., Norton, A. A., Henney, C. J. and Solanki, S. K., 2008, “Evidence for Polar Jets as Precursors of Polar Plume Formation”, Astrophys. J. Lett., 682, L137–L140. [DOI], [ADS], [arXiv:0806.3045]. (Cited on pages 34 and 35.)
Reisenfeld, D. B., McComas, D. J. and Steinberg, J. T., 1999, “Evidence of a solar origin for pressure balance structures in the high-latitude solar wind”, Geophys. Res. Lett., 26, 1805–1808. [DOI], [ADS]. (Cited on pages 38 and 39.)
Riley, P. and Luhmann, J. G., 2012, “Interplanetary Signatures of Unipolar Streamers and the Origin of the Slow Solar Wind”, Solar Phys., 277, 355–373. [DOI], [ADS]. (Cited on page 49.)
Rusin, V. and Rybansky, M., 1976, “Polar rays of the solar corona observed during the 1973 June 30 eclipse”, Bull. Astron. Inst. Czech., 27, 279–286. [ADS]. (Cited on page 9.)
Saez, F., Llebaria, A., Lamy, P. and Vibert, D., 2007, “Three-dimensional reconstruction of the streamer belt and other large-scale structures of the solar corona. I. Method”, Astron. Astrophys., 473, 265–277. [DOI], [ADS]. (Cited on page 14.)
Saito, K., 1956, “Photometry of the Solar Corona at the Eclipse on June 20, 1955”, Publ. Astron. Soc. Japan, 8, 126–141. [ADS]. (Cited on pages 5, 9, and 41.)
Saito, K., 1965, “Polar Rays of the Solar Corona. II”, Publ. Astron. Soc. Japan, 17, 1. [ADS]. (Cited on pages 13, 41, and 43.)
Scherrer, P. H., Schou, J., Bush, R. I. et al., 2012, “The Helioseismic and Magnetic Imager (HMI) Investigation for the Solar Dynamics Observatory (SDO)”, Solar Phys., 275, 207–227. [DOI], [ADS]. (Cited on page 35.)
Schielicke, R. E. and Wittmann, A. D., 2005, “On the Berkowski daguerreotype (Königsberg, 1851 July 28): the first correctly-exposed photograph of the solar corona”, in Development of Solar Research / Entwicklung der Sonnenforschung, Proceedings of the Colloquium Freiburg (Breisgau), September 15, 2003, (Eds.) Wittmann, A. D., Wolfschmidt, G., Duerbeck, H. W., Acta Hist. Astron., 25, p. 128, Harri Deutsch, Frankfurt am Main. [ADS]. (Cited on page 7.)
Schmidt, H. U., 1964, “On the Observable Effects of Magnetic Energy Storage and Release Connected With Solar Flares”, in The Physics of Solar Flares, Proceedings of the AAS-NASA Symposium held 28–30 October, 1963 at the Goddard Space Flight Center, Greenbelt, MD, (Ed.) Hess, W. N., NASA Special Publication, SP-50, p. 107, NASA, Washington, DC. [ADS]. (Cited on page 9.)
Schuster, A., 1912, “A Critical Examination of the Possible Causes of Terrestrial Magnetism”, Proc. Phys. Soc. London, 24, 121–137. [DOI]. (Cited on page 5.)
Shimooda, H., 1958, “Solar and Interplanetary Magnetic Field. II. Polar Rays and the General Magnetic Field”, Publ. Astron. Soc. Japan, 10, 107–119. [ADS]. (Cited on page 9.)
Sornette, B., Fort, B., Picat, J. P. and Cailloux, M., 1980, “On the physical significance of white light polar plumes in the solar corona”, Astron. Astrophys., 90, 344–349. [ADS]. (Cited on page 11.)
Sterling, A. C., Harra, L. K. and Moore, R. L., 2010, “Fibrillar Chromospheric Spicule-like Counterparts to an Extreme-ultraviolet and Soft X-ray Blowout Coronal Jet”, Astrophys. J., 722, 1644–1653. [DOI], [ADS]. (Cited on page 48.)
Stucki, K., Solanki, S. K., Schühle, U. and Rüedi, I., 2000, “On the relationship between shift and intensity of ultraviolet lines in coronal holes and the quiet Sun”, Astron. Astrophys., 362, L49–L52. [ADS]. (Cited on page 21.)
Suess, S. T., 1982, “Polar coronal plumes”, Solar Phys., 75, 145–159. [DOI], [ADS]. (Cited on page 9.)
Suess, S. T., 1998, “Models of plumes: Their flow, their geometric spreading and their mixing with interplume flows”, in Solar Jets and Coronal Plumes, 23–26 Feb 1998, Guadeloupe, France, (Ed.) Guyenne, T.-D., ESA Special Publication, SP-421, p. 223, ESA Publications Division, Noordwijk. [ADS]. (Cited on pages 39 and 46.)
Suess, S. T., Poletto, G., Wang, A.-H., Wu, S. T. and Cuseri, I., 1998, “The Geometric Spreading of Coronal Plumes and Coronal Holes”, Solar Phys., 180, 231–246. [DOI], [ADS]. (Cited on page 9.)
Tate Arbacher, R., Tian, H. and Cranmer, S. R., 2015, “Comparing High-speed Transition Region Jets in Coronal Holes and Quiet Sun Regions”, Bull. Am. Astron. Soc., 47, 137.05. [ADS]. (Cited on page 48.)
Teriaca, L., Poletto, G., Romoli, M. and Biesecker, D.A., 2003, “The nascent solar wind: Origin and acceleration”, Astrophys. J., 588, 566–577. [DOI], [ADS]. (Cited on pages 25, 45, and 51.)
Testa, P., Reale, F., Landi, E., DeLuca, E. E. and Kashyap, V., 2011, “Temperature Distribution of a Non-flaring Active Region from Simultaneous Hinode XRT and EIS Observations”, Astrophys. J., 728, 30. [DOI], [ADS], [arXiv:1012.0346 [astro-ph.SR]]. (Cited on page 18.)
Thieme, K. M., Schwenn, R. and Marsch, E., 1989, “Are structures in high-speed streams signatures of coronal fine structures?”, Adv. Space Res., 9, 127–130. [DOI], [ADS]. (Cited on pages 38, 43, and 44.)
Thieme, K. M., Marsch, E. and Schwenn, R., 1990, “Spatial structures in high-speed streams as signatures of fine structures in coronal holes”, Ann. Geophys., 8, 713–723. [ADS]. (Cited on pages 38, 43, and 44.)
Thurgood, J. O., Morton, R. J. and McLaughlin, J. A., 2014, “First Direct Measurements of Transverse Waves in Solar Polar Plumes Using SDO/AIA”, Astrophys. J. Lett., 790, L2. [DOI], [ADS], [arXiv:1406.5348 [astro-ph.SR]]. (Cited on pages 27 and 51.)
Tian, H., Tu, C., Marsch, E., He, J. and Kamio, S., 2010, “The Nascent Fast Solar Wind Observed by the EUV Imaging Spectrometer on Board Hinode”, Astrophys. J. Lett., 709, L88–L93. [DOI], [ADS], [arXiv:0912.4316 [astro-ph.SR]]. (Cited on pages 21 and 22.)
Tian, H., McIntosh, S. W., Habbal, S. R. and He, J., 2011, “Observation of High-speed Outflow on Plume-like Structures of the Quiet Sun and Coronal Holes with Solar Dynamics Observatory/Atmospheric Imaging Assembly”, Astrophys. J., 736, 130. [DOI], [ADS], [arXiv:1105.3119 [astro-ph.SR]]. (Cited on pages 36 and 51.)
Tian, H., DeLuca, E. E., Cranmer, S. R. et al., 2014, “Prevalence of small-scale jets from the networks of the solar transition region and chromosphere”, Science, 346(27), 1255711. [DOI], [ADS], [arXiv:1410.6143 [astro-ph.SR]]. (Cited on pages 48 and 51.)
Tousey, R., 1977, “Apollo Telescope Mount of Skylab: an overview”, Appl. Opt., 16, 825–836. [DOI], [ADS]. (Cited on page 10.)
Tsuneta, S., Acton, L., Bruner, M. et al., 1991, “The Soft X-ray Telescope for the SOLAR-A Mission”, Solar Phys., 136, 37–67. [DOI], [ADS]. (Cited on page 34.)
Tsuneta, S., Ichimoto, K., Katsukawa, Y. et al., 2008, “The Solar Optical Telescope for the Hinode Mission: An Overview”, Solar Phys., 249, 167–196. [DOI], [ADS], [arXiv:0711.1715]. (Cited on page 48.)
Tu, C.-Y., Marsch, E., Wilhelm, K. and Curdt, W., 1998, “Ion Temperatures in a Solar Polar Coronal Hole Observed by SUMER on SOHO”, Astrophys. J., 503, 475–482. [DOI], [ADS]. (Cited on page 28.)
Tu, C.-Y., Zhou, C., Marsch, E., Xia, L.-D., Zhao, L., Wang, J.-X. and Wilhelm, K., 2005, “Solar Wind Origin in Coronal Funnels”, Science, 308, 519–523. [DOI], [ADS]. (Cited on pages 22, 23, and 30.)
van de Hulst, H. C., 1950, “On the polar rays of the corona”, Bull. Astron. Inst. Neth., 11, 150. [ADS]. (Cited on pages 5, 7, 14, and 15.)
Velli, M., Habbal, S. R. and Esser, R., 1994, “Coronal plumes and final scale structure in high speed solar wind streams”, Space Sci. Rev., 70, 391–396. [DOI], [ADS]. (Cited on pages 43 and 44.)
Velli, M., Lionello, R., Linker, J. A. and Mikić, Z., 2011, “Coronal Plumes in the Fast Solar Wind”, Astrophys. J., 736, 32. [DOI], [ADS]. (Cited on pages 46 and 47.)
Veselovsky, I. S., Panassenko, O. A. and Koutchmy, S., 1998, “Solar plume formation in the solar corona”, in Solar Jets and Coronal Plumes, 23–26 Feb 1998, Guadeloupe, France, (Ed.) Guyenne, T.-D., ESA Special Publication, SP-421, p. 345, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 34.)
von Steiger, R., Fisk, L. A., Gloeckler, G., Schwadron, N. A. and Zurbuchen, T. H., 1999, “Composition variations in fast solar wind streams”, in Solar Wind Nine, Proceedings of the Ninth International Solar Wind Conference, Nantucket, MA, 5–9 October 1998, (Eds.) Habbal, S. R., Hollweg, J. V., Isenberg, P. A., AIP Conf. Proc., 471, pp. 143–146, American Institute of Physics, Woodbury, NY. [DOI], [ADS]. (Cited on page 40.)
Waldmeier, M., 1955, “Die Minimumsstruktur der Sonnenkorona”, Z. Astrophys., 37, 233. [ADS]. (Cited on page 5.)
Walker Jr, A. B. C., DeForest, C. E., Hoover, R. B. and Barbee Jr, T. W., 1993, “Thermal and Density Structure of Polar Plumes”, Solar Phys., 148, 239–252. [DOI], [ADS]. (Cited on pages 41, 42, and 43.)
Wang, Y.-M., 1994, “Polar plumes and the solar wind”, Astrophys. J. Lett., 435, L153–L156. [DOI], [ADS]. (Cited on pages 33, 43, 44, 45, and 46.)
Wang, Y.-M., 1996, “Element Separation by Upward Proton Drag in the Chromosphere”, Astrophys. J. Lett., 464, L91–L94. [DOI], [ADS]. (Cited on page 20.)
Wang, Y.-M., 1998, “Network Activity and the Evaporative Formation of Polar Plumes”, Astrophys. J. Lett., 501, L145–L150. [DOI], [ADS]. (Cited on pages 33, 34, and 35.)
Wang, Y.-M., 2009, “Coronal Holes and Open Magnetic Flux”, Space Sci. Rev., 144, 383–399. [DOI], [ADS]. (Cited on page 49.)
Wang, Y.-M. and Muglach, K., 2008, “Observations of Low-Latitude Coronal Plumes”, Solar Phys., 249, 17–35. [DOI], [ADS]. (Cited on pages 13, 22, 37, and 46.)
Wang, Y.-M. and Sheeley Jr, N. R., 1990, “Solar wind speed and coronal flux-tube expansion”, Astrophys. J., 355, 726–732. [DOI], [ADS]. (Cited on page 49.)
Wang, Y.-M. and Sheeley Jr, N. R., 1992, “On potential field models of the solar corona”, Astrophys. J., 392, 310–319. [DOI], [ADS]. (Cited on page 7.)
Wang, Y.-M. and Sheeley Jr, N. R., 1995a, “Identification of Low-Latitude Coronal Plumes in Extreme-Ultraviolet Spectroheliograms”, Astrophys. J. Lett., 446, L51–L53. [DOI], [ADS]. (Cited on pages 11 and 13.)
Wang, Y.-M. and Sheeley Jr, N. R., 1995b, “Coronal Plumes and Their Relationship to Network Activity”, Astrophys. J., 452, 457–461. [DOI], [ADS]. (Cited on pages 22, 33, and 35.)
Wang, Y.-M., Sheeley Jr, N. R., Dere, K. P. et al., 1997, “Association of Extreme-Ultraviolet Imaging Telescope (EIT) Polar Plumes with Mixed-Polarity Magnetic Network”, Astrophys. J. Lett., 484, L75–L78. [DOI], [ADS]. (Cited on page 22.)
Wang, Y.-M., Sheeley Jr, N. R., Socker, D. G. et al., 1998, “Observations of Correlated White-Light and Extreme-Ultraviolet Jets from Polar Coronal Holes”, Astrophys. J., 508, 899–907. [DOI], [ADS]. (Cited on page 40.)
Wang, Y.-M., Biersteker, J. B., Sheeley Jr, N. R., Koutchmy, S., Mouette, J. and Druckmüller, M., 2007a, “The Solar Eclipse of 2006 and the Origin of Raylike Features in the White-Light Corona”, Astrophys. J., 660, 882–892. [DOI], [ADS]. (Cited on page 11.)
Wang, Y.-M., Sheeley Jr, N. R. and Rich, N. B., 2007b, “Coronal Pseudostreamers”, Astrophys. J., 658, 1340–1348. [DOI], [ADS]. (Cited on pages 49 and 50.)
Wang, Y.-M., Grappin, R., Robbrecht, E. and Sheeley Jr, N. R., 2012, “On the Nature of the Solar Wind from Coronal Pseudostreamers”, Astrophys. J., 749, 182. [DOI], [ADS]. (Cited on page 49.)
Widing, K. G. and Feldman, U., 1992, “Element abundances and plasma properties in a coronal polar plume”, Astrophys. J., 392, 715–721. [DOI], [ADS]. (Cited on pages 19 and 20.)
Wilhelm, K., 2000, “Solar spicules and macrospicules observed by SUMER”, Astron. Astrophys., 360, 351–362. [ADS]. (Cited on page 48.)
Wilhelm, K., 2006, “Solar coronal-hole plasma densities and temperatures”, Astron. Astrophys., 455, 697–708. [DOI], [ADS]. (Cited on page 17.)
Wilhelm, K., 2012, “SUMER Observations of Coronal-Hole Temperatures”, Space Sci. Rev., 172, 57–68. [DOI], [ADS]. (Cited on page 26.)
Wilhelm, K. and Bodmer, R., 1998, “Solar EUV and UV Emission Line Observations Above a Polar Coronal Hole”, Space Sci. Rev., 85, 371–378. [DOI], [ADS]. (Cited on page 19.)
Wilhelm, K., Curdt, W., Marsch, E. et al., 1995, “SUMER — Solar Ultraviolet Measurements of Emitted Radiation”, Solar Phys., 162, 189–231. [DOI], [ADS]. (Cited on page 17.)
Wilhelm, K., Marsch, E., Dwivedi, B. N., Hassler, D. M., Lemaire, P., Gabriel, A. H. and Huber, M. C. E., 1998, “The Solar Corona above Polar Coronal Holes as Seen by SUMER on SOHO”, Astrophys. J., 500, 1023. [DOI], [ADS]. (Cited on pages 14, 17, and 26.)
Wilhelm, K., Dammasch, I. E., Marsch, E. and Hassler, D. M., 2000, “On the source regions of the fast solar wind in polar coronal holes”, Astron. Astrophys., 353, 749–756. [ADS]. (Cited on pages 21, 22, and 23.)
Wilhelm, K., Abbo, L., Auchère, F. et al., 2011, “Morphology, dynamics and plasma parameters of plumes and inter-plume regions in solar coronal holes”, Astron. Astrophys. Rev., 19, 35. [DOI], [ADS], [arXiv:1103.4481]. (Cited on pages 17 and 18.)
Withbroe, G. L., 1983, “Evidence for temporal variations in polar plumes”, Solar Phys., 89, 77–88. [DOI], [ADS]. (Cited on page 29.)
Withbroe, G. L., Feldman, W. C. and Ahluwalia, H. S., 1991, “The solar wind and its coronal origins”, in Solar Interior and Atmosphere, (Eds.) Cox, A. N., Livingston, W. C., Matthews, M. S., pp. 1087–1106, University of Arizona Press, Tucson, AZ. [ADS]. (Cited on page 14.)
Woo, R., 1996, “Detection of Low-Latitude Plumes in the Outer Corona by ULYSSES Radio Ranging Measurements”, Astrophys. J. Lett., 464, L95–L98. [DOI], [ADS]. (Cited on page 13.)
Woo, R. and Habbal, S. R., 1997, “Extension of coronal structure into interplanetary space”, Geophys. Res. Lett., 24, 1159–1162. [DOI], [ADS]. (Cited on pages 10 and 13.)
Woo, R. and Habbal, S. R., 1998, “Comment on: ‘Polar plumes and fine-scale coronal structures-On the interpretation of coronal radio sounding data’ by Pätzold and Bird”, Geophys. Res. Lett., 25, 1849–1850. [DOI], [ADS]. (Cited on page 13.)
Woo, R., Habbal, S. R. and Feldman, U., 2004, “Role of Closed Magnetic Fields in Solar Wind Flow”, Astrophys. J., 612, 1171–1174. [DOI], [ADS]. (Cited on page 10.)
Wu, D. J. and Fang, C., 2003, “Coronal Plume Heating and Kinetic Dissipation of Kinetic Alfvén Waves”, Astrophys. J., 596, 656–662. [DOI], [ADS]. (Cited on page 36.)
Wülser, J.-P., Lemen, J. R., Tarbell, T. D. et al., 2004, “EUVI: the STEREO-SECCHI Extreme Ultraviolet Imager”, in Telescopes and Instrumentation for Solar Astrophysics, San Diego, California, USA, August 3, 2003, (Eds.) Fineschi, S., Gummin, M. A., Proc. SPIE, 5171, pp. 111–122, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on page 13.)
Xia, L. D., Marsch, E. and Curdt, W., 2003, “On the outflow in an equatorial coronal hole”, Astron. Astrophys., 399, L5–L9. [DOI], [ADS]. (Cited on page 21.)
Yamauchi, Y., Suess, S. T. and Sakurai, T., 2002, “Relation between Pressure Balance Structures and polar plumes from Ulysses high latitude observations”, Geophys. Res. Lett., 29(10), 1383. [DOI], [ADS]. (Cited on page 38.)
Yamauchi, Y., Suess, S. T., Steinberg, J. T. and Sakurai, T., 2004, “Differential velocity between solar wind protons and alpha particles in pressure balance structures”, J. Geophys. Res., 109(A18), 3104. [DOI], [ADS]. (Cited on pages 38 and 46.)
Yang, S., Zhang, J., Zhang, Z. et al., 2011, “Polar plumes observed at the total solar eclipse in 2009”, Sci. China Phys. Mech. Astron., 54, 1906–1910. [DOI], [ADS]. (Cited on page 10.)
Young, P. R., Klimchuk, J. A. and Mason, H. E., 1999, “Temperature and density in a polar plume — measurements from CDS/SOHO”, Astron. Astrophys., 350, 286–301. [ADS]. (Cited on pages 14 and 19.)
Zhang, Q. M., Chen, P. F., Guo, Y., Fang, C. and Ding, M. D., 2012, “Two Types of Magnetic Reconnection in Coronal Bright Points and the Corresponding Magnetic Configuration”, Astrophys. J., 746, 19. [DOI], [ADS]. (Cited on page 36.)
Acknowledgements
It is a pleasure to thank the Editorial Board of Living Reviews in Solar Physics for inviting me to write this review. Comments by C. DeForest and a second unknown referee helped me improving the paper. Conversations with Y.-M. Wang and G. Del Zanna are also gratefully acknowledged. I also like to thank F. Schulz for his precious work on my manuscript, which he turned into a better and easier readable paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Poletto, G. Solar Coronal Plumes. Living Rev. Sol. Phys. 12, 7 (2015). https://doi.org/10.1007/lrsp-2015-7
Published:
DOI: https://doi.org/10.1007/lrsp-2015-7