Abstract
This review describes observations of the polar magnetic fields, models for the cyclical formation and decay of these fields, and evidence of their great influence in the solar atmosphere. The polar field distribution dominates the global structure of the corona over most of the solar cycle, supplies the bulk of the interplanetary magnetic field via the polar coronal holes, and is believed to provide the seed for the creation of the activity cycle that follows. A broad observational knowledge and theoretical understanding of the polar fields is therefore an essential step towards a global view of solar and heliospheric magnetic fields. Analyses of both high-resolution and long-term synoptic observations of the polar fields are summarized. Models of global flux transport are reviewed, from the initial phenomenological and kinematic models of Babcock and Leighton to present-day attempts to produce time-dependent maps of the surface magnetic field and to explain polar field variations, including the weakness of the cycle 23 polar fields. The relevance of the polar fields to solar physics extends far beyond the surface layers from which the magnetic field measurements usually derive. As well as discussing the polar fields’ role in the interior as seed fields for new solar cycles, the review follows their influence outward to the corona and heliosphere. The global coronal magnetic structure is determined by the surface magnetic flux distribution, and is dominated on large scales by the polar fields. We discuss the observed effects of the polar fields on the coronal hole structure, and the solar wind and ejections that travel through the atmosphere. The review concludes by identifying gaps in our knowledge, and by pointing out possible future sources of improved observational information and theoretical understanding of these fields.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The magnetic field located at the heliographic poles of the Sun has a large-scale (±60–90° latitude) unipolar distribution. These distributions have opposite polarity at the two poles, except during times of polarity reversal. Although the polar field is highly structured, with small-scale features of facular (kG) strength, the average flux density of the polar fields is only about 5 G. The polar fields are therefore much weaker than active region fields, and they contain less magnetic flux than a major active region. Nevertheless, they have far-reaching importance because of their unipolarity over large spatial scales, and because of their role in the solar activity cycle.
Most polar magnetic flux does not connect back to the Sun, unlike active region flux which is generally closed. This means that the polar fields supply most of the interplanetary mean field and channel most of the fast solar wind. The open polar flux takes the form of polar coronal holes, which dominate the large-scale structure of the corona over most of the cycle. The exception is when the polar fields are reversing polarity, which occurs approximately every 11 years during solar activity maximum. This observed interrelationship between polar field reversal and the solar activity cycle is believed to be just the surface manifestation of a unified cycle linking the active regions and polar fields. This review will summarize in some detail the basic observed properties of the polar fields, their role in the solar cycle according to observations and models, and their influence over coronal and heliospheric phenomena.
The importance of the polar fields to the global magnetic field of the Sun therefore lies both in their central role in the solar cycle and in their dominant influence over the heliosphere. Frustratingly, the polar fields are the most difficult of the Sun’s surface fields to measure. The polar fields are intrinsically weak compared to the active region fields located at low latitudes, and there is a large projection angle when the polar latitudes are observed from Earth. For these reasons, measurement of the polar fields is challenging, particularly with the spatial resolution of present-day full-disk magnetographs.
Routine and continuous full-disk line-of-sight magnetogram observations began at Mt. Wilson Observatory (MWO) in the 1960s (Howard, 1989), and have been taken at the National Solar Observatory (NSO) and the U. Stanford’s Wilcox Solar Observatory (WSO) since the 1970s (Livingston et al., 1976; Svalgaard et al., 1978). Regrettably, the MWO observations stopped in 2012, but the data series from NSO and WSO continue to the present day. Only since the launch of the Hinode spacecraft in late 2006 have detailed vector maps of the polar magnetic field distribution been possible (Tsuneta et al., 2008), under optimal observing conditions, viz. when the pole is tilted a little (about 7.25°) towards us. In this review we will describe the Hinode results in some detail, before relating them to the more long-term results based on synoptic observations of the line-of-sight field component. These observations revealed a unipolar but highly complex and non-uniform flux distribution, containing ubiquitous fields of greater strength (> 1 kG) than many had previously expected, though bundles of kilogauss field had previously been observed at high latitudes (Homann et al., 1997; Okunev and Kneer, 2004; Blanco Rodríguez et al., 2007) as well as in the low-latitude quiet-Sun photosphere (Orozco Suárez et al., 2007).
From full-disk measurements of the line-of-sight field, butterfly diagrams (latitude-time plots of the inferred radial field distribution) can be constructed. These plots are very useful because they reveal the interactions between strong, low-latitude fields and weak, high-latitude fields including the polar fields, that occur over long timescales. Babcock (1959) observed the asymmetric pattern of the cycle 19 polar reversal, the first observations of reversing polar fields, and reported that the south polar reversal preceded the north by nearly 18 months. Guided by some earlier pioneering work in solar dynamo theory, Babcock (1961) presented his phenomenological model for the solar cycle, based on his full-disk magnetogram observations. This model was supported by a comparison of polar facular counts and sunspot numbers by Sheeley Jr (1964), and a numerical kinematic flux transport model by Leighton (1969). This cyclical interaction between the active regions and polar fields has been a central focus of observational and theoretical study for solar physicists since these initial studies. We will discuss the observed relationship in some detail before reviewing numerical kinematic flux transport models for the cycle, beginning with Leighton (1964, 1969) and continuing to the present.
Of course, kinematic models for the transport of photospheric flux are unable to describe the physics of the polar fields in their full complexity, but they have given us critical insight into the causes of polar field phenomena. The effectiveness of these models has improved. Under the guidance of ever more refined observations of the photosphere and the interior, the models have become steadily more flexible, stable and accurate. It is now possible to produce full-surface snapshots of the photospheric field using these models, and these “synchronic” synoptic magnetograms (sometimes referred to synoptic charts or maps) are an essential raw material for models of the solar atmosphere.
Whereas the dynamics of the interior and photosphere are dominated by the fluid flow, the much less dense plasma in the corona (up to about a solar radius) is dominated by the magnetic field, whose distribution and structure are determined by the surface magnetic flux distribution. Models of the atmospheric field show the dominant influence of the polar fields via the axial dipole component, and observations of coronal holes, solar wind distributions, and prominence eruptions and coronal mass ejections, the solar phenomena that most directly impact us here on Earth, all bear the mark of the waxing and waning influence of the polar fields over the cycle.
Observations of polar faculae and filaments have been taken over many decades, starting much earlier than full-disk magnetograph measurements, and they enable statistical comparisons of cycle-by-cycle polar fields and sunspot numbers (Sheeley Jr, 1964; Muñoz-Jaramillo et al., 2013). Filaments mark neutral lines between predominantly unipolar bodies of weak, opposite-polarity flux at high latitudes, and they enable us to follow the progress of the poleward-transported flux that forms the polar fields. Their eruptions at high latitudes, and the removal of the helicity that they have carried there from lower latitudes, are an essential part of the polar field reversal. We will summarize observational and modeling results concerning the role of filaments and eruptions in polar magnetism.
Petrie et al. (2014) recently reviewed observations and models of the interactions between active regions and the polar field, focusing in particular on the interrelated phenomena that are observed to migrate in both directions across the high-latitude corridor between the active and polar latitudes, and Petrie and Ettinger (2015) reviewed in detail the interaction of decayed active-region flux with polar fields via poleward surges at the photospheric level. While there is overlap between that review and this one, here we focus much more closely on observations and flux transport modeling of the polar fields, before reviewing atmospheric phenomena that clearly exhibit signs of the polar fields’ global influence.
The review is structured in three broadly-themed sections, designed to convey the basic observed facts and theoretical understanding of the polar fields, before discussing their far-reaching influence and importance throughout the solar atmosphere. Section 2 presents observational analyses of direct polar field observations, beginning with the high-resolution photospheric vector measurements of Hinode, relating them to the more traditional line-of-sight photospheric measurements, and introducing new types of synoptic data products, before summarizing the patterns of flux transport in the 40 years of magnetogram observations from NSO. Section 3 continues the theme of flux transport and focuses on it in the context of modeling, beginning with the initial phenomenological and kinematic models of Babcock (1961) and Leighton (1964, 1969), and continuing with recent efforts to explain the unusual behavior of the polar fields during the cycle 23 minimum. Section 4 explores the global influence of the polar fields over the heliospheric structure, and the solar wind and ejections that travel through it. We will conclude in Section 5.
2 Observations of the Polar Magnetic Field
2.1 High-resolution observations of polar fields
While the polar regions are very important to several of the major branches of global solar physics, from the solar dynamo to the acceleration of the fast solar wind, the magnetic behavior of the polar fields is not comprehensively understood. Polar field measurements are very challenging. The tilt angle between the solar rotation axis and our viewpoint on the Earth’s ecliptic plane, usually referred to as the B0 tilt angle, is approximately 7.25°, meaning that the viewing angle of the poles is never less than about 83°. Optimal polar viewing angles only occur annually, on 6 March for the south pole and 8 September for the north pole. Over the first/second half of each year the north/south pole is unobservable from the direction of Earth. When a pole is observable, strong intensity gradients and foreshortening at the limb, and variable seeing conditions in the case of ground-based observations, all pose difficulties.
Full Stokes polarimetry for the polar regions has been performed only rarely and, until the Hinode satellite was launched in late 2006, such efforts were generally confined to ground-based observations under variable seeing conditions. Also, polar vector field observations have often been restricted to limited fields of view and therefore haven’t provided a picture of the global distribution of the polar field.
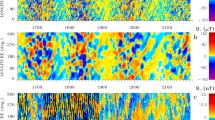
Using the Hinode Solar Optical Telescope (SOT) Spectro-polarimeter (SP), Tsuneta et al. (2008) observed the south polar field on 2007 March 16 when the B0 tilt angle was around −7° and the south pole was visible on the solar disk from the ecliptic plane. Figure 1 shows a spatial map of the measured magnetic field strength. A highly structured, non-uniform distribution of intense, unipolar magnetic features is strikingly evident in the map, with numerous sizable concentrations of kilogauss flux quite evenly distributed across it. Structure of this kind is usually not resolved in the standard full-surface synoptic maps of the photospheric field that we will discuss in later sections.
South polar view of the magnetic field strength taken at 12:02:19–14:55:48 UT on 2007 March 16 by the Hinode Solar Optical Telescope (SOT) Spectro-polarimeter (SP). The original observing field of view is 327.52″ (east-west) by 163.84″ (north-south) and was converted to a map seen from above the south pole. East is to the left, west is to the right, and the observation was carried out from the top down. Spatial resolution is lost near the extreme limb (i.e., near the bottom of the figure). The field of view is 327.52″ (east-west) by 472.96″ (north-south along the line of sight). The field of view for the line-of-sight direction (163.84″) expands to 472.96″ as a result of correction for foreshortening. The pixel size is 0.16″. Latitudinal lines for 85°, 80°, 75°, and 70° are shown as large circles, while the plus sign marks the south pole. Image reproduced with permission from Tsuneta et al. (2008), copyright by AAS.
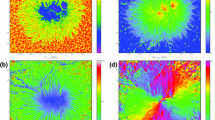
Measurements of the solar magnetic vector field using the Zeeman effect have an inherent 180° ambiguity in the determination of the azimuth angle of the transverse field component. However, because the distribution of the inclination (zenith) angle of the magnetic vector with respect to the local normal has two peaks, one at the local vertical direction and the other at the local horizontal direction (Orozco Suárez et al., 2007), it is possible to determine the inclination angle close to the solar limb without the usual 180° azimuth ambiguity (Ito et al., 2010). Figure 2 shows a map of the continuum brightness distribution over the domain corresponding to the portion of Figure 1 poleward of 80°. The red and blue contours indicate approximately vertical (< 25°) and approximately horizontal (> 65°) magnetic fields. The stronger flux concentrations in the figure correspond to enhanced continuum brightness and tend to have approximately vertical magnetic field. These features are also coherently unipolar. In the measurements all large patches had fields vertical to the solar surface to within 25° while the smaller patches tended to be nearly horizontal (> 65°). Most patches had inclination angle either < 25° or > 65° and the two classes appeared not to be spatially correlated. The larger patches coincided with polar faculae seen in continuum intensity images. The horizontal fields were symmetrically distributed about the average continuum intensity, whereas the vertical fields tended to correspond to higher-than-average continuum intensities. The vertical kilogauss patches evolved on timescales around 5–10 hr compared to < 30 min for the horizontal fields, consistent with observations of seething horizontal photospheric fields by Harvey et al. (2007).
Polar view in the continuum for latitudes above 80°, corresponding to the plot in Figure 1. Colored contours indicate locations with average field strength of 200 G. (The region inside the contour has average field strength larger than 200 G.) Red indicates regions where the local inclination angle < 25° (vertical), while blue shows regions with local inclination angle > 65° (horizontal). East is to the left, and west is to the right. Latitudinal lines for 85° and 80° are shown, with the plus sign indicating the south pole. Near the extreme limb (to the bottom), spatial resolution is lost. Image reproduced with permission from Tsuneta et al. (2008), copyright by AAS.
The estimated total polar flux according to these measurements (above 70°) was 5.6 × 1021 Mx with the nominal filling factor applied and 2.5 × 1022 Mx with filling factor set to 1. Thus the total polar magnetic flux was less than that of a major active region. If the polar fields were evenly distributed, they would have average strength 3.1 G with the nominal filling factor applied, 13.9 G with filling factor set to 1, and 10.0 G with 50% of stray light taken into account (Tsuneta et al., 2008). This estimate of average field strength is roughly consistent with the values derived from lower-resolution synoptic line-of-sight measurements that we will discuss in Section 2.7.
Shiota et al. (2012) collected annual polar vector field measurements from Hinode SOT/SP. Each year since 2007 the south pole was observed in March and the north pole in September. They found a diverse population of flux patches ranging from 1015–1020 Mx. Figure 3 shows a plot of the flux patches’ number densities and average flux densities binned according to magnetic flux, based on polar field observations taken on 2007 March 16 and 2007 September 25. These observations were compared to low-latitude quiet Sun observations taken during the same year. At each pole the positive and negative fluxes were approximately balanced in the population of patches with < 1017 Mx but the larger patches had significant polarity biases. In contrast, the low-latitude quiet Sun patches have approximately balanced flux in all size bins. It would be interesting also to compare the polar field measurements to observations of a low-latitude unipolar region or coronal hole.
Plots of magnetic flux per patch in terms of number density (top panels) and average flux density (bottom panels) for north pole (left), south pole (center), and a quiet-Sun region at the east limb (right). The magnetic flux concentrations here refer to the concentrations of the vertical magnetic vectors. The average flux density is defined as the total flux (contributed by the magnetic concentrations in each bin of the horizontal axis) divided by the SOT observation area. Black dashed and red bold lines represent the negative and positive concentrations, respectively. The data for the north and the south polar regions and the quiet region were obtained during 00:10–07:26 UT on 2007 September 25 (panels (a) and (d)), 12:02–14:56 UT on 2007 March 16 (panels (b) and (e)), and 18:36–20:52 UT on 2007 November 28 (panels (c) and (f)), respectively. The exposure times for the north polar region and the quiet Sun are the same (12.8 s). The exposure time for the south polar region is shorter (4.8 s); thus, the south pole plot cannot be directly compared with those for the north pole and the quiet Sun because the signal/noise level is different. Image adapted from Shiota et al. (2012); courtesy of D. Shiota.
The patches at the higher end of this range were an order of magnitude larger than those found in the quiet Sun, and were nearly as large as pores. The number densities of flux concentrations as functions of total magnetic flux were found to decrease over the four orders of magnitude studied. The polar regions had comparable number densities of both polarities in the flux range 1015—1017 Mx but significant flux imbalances in the patches larger than 1017 Mx. In contrast the quiet Sun’s flux concentrations were flux-balanced over their entire flux range.
As in the study by Tsuneta et al. (2008), two distinct populations were found in the polar regions, large concentrations that varied with the solar cycle and determined the overall polarities of the polar fields, and smaller concentrations of mixed polarity that appeared to be cycle-invariant. Almost all large patches (> 1017 Mx) had the same polarity at each pole while the population of smaller patches had approximately balanced flux. The polarities of the polar caps were therefore determined by the large patches.
The year-by-year evolution of the average field intensity at the north and south poles between 2008 and 2012 is plotted in Figure 4, separately for vertical and horizontal field components, and separating vertical fields in large (> 1018 Mx) and small (< 1018 Mx) patches. This analysis shows that there is generally stronger horizontal field than vertical field in the polar regions on average. The net flux of the polar regions decreased significantly during the rise of solar cycle 24, more quickly in the north than in the south. The decrease in net flux was caused by a decrease in both the number and size of large patches and also by the appearance of opposite-polarity patches from lower latitudes. The distribution of small flux patches and horizontal fields did not appear to change over this period.
Yearly variation in the average flux density of the vertical and horizontal magnetic vectors in the north and south polar regions from 2008 to 2012. The upper panels (a) and (b) show the average flux density of the vertical magnetic concentrations with total magnetic flux (per patch) larger than 1018 Mx. Black ‘x’ and red ‘+’ symbols represent positive and negative polarities, respectively. Absolute values are shown in the panels. The middle panels (c) and (d) show the average flux density of the vertical magnetic concentrations with total magnetic flux (per patch) smaller than 1018 Mx. The bottom panels (e) and (f) show the average flux density of the horizontal magnetic vectors. Image adapted from Shiota et al. (2012); courtesy of D. Shiota.
Comparing Figures 2 and 4, we see that the largest and strongest flux concentrations generally have approximately vertically-directed field, but that horizontal field intensity is significantly greater than the vertical field intensity on average. Also, the vertical field in large concentrations has more long-term variability than the other fields, consistent with the idea that it is the vertical field that determines the overall polarity of the polar caps and that plays a role in the global behavior of the solar field and the solar cycle. The horizontal fields, despite their larger average strength, appear to have much more limited influence, connecting small, adjacent magnetic features that do not contribute significantly to the large-scale polar flux and do not play a major role in the global cycle.
2.2 Are the polar fields radial, and do they have a topknot distribution?
Synoptic observations of the polar fields do not capture in detail the structure of the polar fields that high-resolution magnetograph like Hinode SOT can resolve. At present full-disk vector magnetographs lack the spatial resolution and sensitivity of the Hinode instruments. NSO Synoptic Optical Long-term Investigations of the Sun (SOLIS) and Hinode polar images for the longitudinal (i.e., line-of-sight) magnetic field component are compared in Figure 5. Both photospheric and chromospheric images from each telescope are compared. The two telescopes both detect the general distribution of the field, but the intense flux elements that were discussed in the previous section are much better resolved by Hinode than by SOLIS. This is partly due to the superior spatial resolution of the Hinode magnetograph and partly due to effects of atmospheric seeing on the SOLIS images
Nearly simultaneous south pole line-of-sight field observations with the pole tipped toward Earth by 7°. 04. Left: Hinode observations. Right: VSM observations. The top row shows photospheric (630.2 nm) observations and the bottom row shows low and mid chromosphere observations. White represents the fields directed toward the observer and black away. The dominant polarity in this polar region is positive (light). VSM and SP observations saturate at ± 30 G, and Hinode filtergtaph (FG) observation saturates at ±0.006 IC in circular polarization. Image reproduced with permission from Jin et al. (2013), copyright by AAS.
Moreover, longitudinal observations, though they can have sub-gauss instrumental noise levels, suffer from the foreshortening problem associated with our large viewing angle from the ecliptic plane, and the fact that any radially-directed field at polar latitudes, such as those identified in the largest concentrations of flux at the poles by Hinode, have only a small component directed along our line of sight. In spite of these problems, it is possible to extract much information about the solar surface fields’ tilt angles from long time series of longitudinal field measurements by using changes in the viewing angle caused by solar rotation and the tilt of the rotation axis with respect to the ecliptic plane.
In an influential calculation by Svalgaard et al. (1978), low-latitude field measurements from the Wilcox Solar Observatory (WSO) were binned according to heliocentric angle ρ (the angle between the local radial vector and the line of sight) and plotted against cos ρ, separately for east and west hemispheres, and also separating the fields by their sign during their passage across central meridian. The result was a rhombus-shaped plot, shown in Figure 6, representing a linear decrease of average field strength for decreasing cos ρ, consistent with the line-of-sight projection of a radially-directed field. Then, exploiting the observation that the line-of-sight polar field strength varied in the observations by a factor of around two over the year, in a sinusoidal manner consistent with B0-angle variation, they fitted a radial field of the form Bp cosn θ, where θ is the colatitude, together with a parametrized meridional field component, to over a year of WSO polar line-of-sight data. The best-fitting solution was a radial field with n = 8, from which they concluded that the average flux density poleward of 55° is about 6 G, peaking at more than 10 G at the pole itself. The WSO spatial resolution is particularly low, with pixel size 3′, with the last aperture centered about 15° from the limb, producing different sensitivity compared to higher-resolution instruments. Using potential coronal field models based on Wilcox and Mt. Wilson data, Wang and Sheeley Jr (1988) found a similar cosine-colatitude distribution with n = 7.75 and strength 5.7 G.
Top: Observed center-to-limb variation of measured line-of-sight magnetic field component Bl for weak average fields (less than 150 µT at central meridian) from the Wilcox Solar Observatory. Only data within 16° of the equator are used. Open symbols represent positive fields and closed symbols negative fields. Each point is an average of more than 500 measurements. Bottom: Same as above, but for strong fields only (greater than or equal to 150 µT at central meridian passage). The number of cases is much lower than for the weak field regions and the scatter is correspondingly larger. In addition, the assumption of constant intrinsic field strength for the two-week disk passage is more likely to be invalid for these strong fields. Image reproduced with permission from Svalgaard et al. (1978), copyright by D. Reidel.
The conclusion of Svalgaard et al. (1978) that much of the photospheric field is approximately radially directed has had a major influence on solar global atmospheric modeling, as we shall see in Section 2.5, but it has not escaped criticism. Rudenko (2004) argued that a similar linear decrease could be produced by a change of sign of line-of-sight flux near the limb for a non-radial field vector, and therefore concluded that this type of calculation could not determine whether or not the photospheric field is radial.
Petrie and Patrikeeva (2009) repeated the experiment using photospheric and chromospheric magnetogram images from the SOLIS/VSM, first by binning the data using as the selection criterion the sign of the line-of-sight field component at central meridian as did Svalgaard et al. (1978), and second by binning positive and negative line-of-sight fields separately at every position on the disk. The latter experiment had the unsettling property that different measurements of the field at the same location on the photosphere appeared in different sides of the rhombus-like plot, but this exercise did enable the authors to demonstrate the problem flagged by Rudenko (2004). Whereas the calculation performed using the method of Svalgaard et al. (1978) yielded rhombus-like plots for both photospheric and chromospheric fields, the second experiment resulted in contrasting plots for the two sets of observations: the photospheric plot was an almost unchanged rhombus-shaped graph while the chromospheric plot had much-altered, nearly constant graphs. This plot (not shown) contrasted the photospheric and chromospheric fields, suggesting that the former are nearly radial and the latter are not.
One criticism of the rhombus-shaped graph of Svalgaard et al. (1978), that the variance of each data bin is very large, is difficult to circumvent because these bins do not contain repeated measurements of a single bundle of fields, but an average of many diverse fields. Petrie and Patrikeeva (2009) instead studied the evolution of bundles of line-of-sight flux using time series of SOLIS magnetograms. For the flux bundle observed at disk-center in a given magnetogram, they used the solar rotation rate to identify the location of this bundle in earlier and later magnetograms, and plotted the line-of-sight flux at this location as a function of cos ρ. They then derived a forward model of this flux bundle by finding the linear combination of projected radial and azimuthal vector components that best fitted the observed variation of line-of-sight flux against cos ρ. They found that a vast majority of fields of significant strength exhibited a ρ-dependence consistent with a vector rotating with the Sun. The distribution of vector tilt angles, shown in Figure 7, confirmed that the photospheric and chromospheric fields behave very differently even though the corresponding magnetogram images from the two atmospheric layers look superficially very similar as in Figure 5. The histograms of the tilt angles indicate that most of the photospheric fields are within about 12° of the vertical direction whereas the chromospheric fields tend to expand in all directions to a significant degree. This result was in agreement with past evidence that chromospheric fields are often much more tilted than photospheric fields (e.g., Jones, 1985).
Histograms of photospheric (left) and chromospheric (right) east-west tilt angles and best Gaussian fits, based on SOLIS/VSM line-of-sight data. According to the Gaussian fits, the photospheric fields have tilt angle 1.8 ± 10.8° and the chromospheric fields 5.5 ± 35°. These histograms are consistent with a field structure that is nearly radial in the photosphere that expands in a greater variety of directions at chromospheric heights. Image reproduced with permission from Petrie and Patrikeeva (2009), copyright by AAS.
Petrie and Patrikeeva (2009) analyzed the polar fields by exploiting the B0 tilt angle of the solar rotation axis. Observations of line-of-sight flux were collected from fixed locations on the solar disk at central meridian, while the heliographic latitudes at these locations varied as known functions of B0. The photospheric line-of-sight fields were well-defined functions of latitude at both poles, increasing in strength monotonically between ±46° and ±80° with approximately linear trends. Petrie and Patrikeeva (2009) solved the linear system of equations,
to estimate the magnetic vector (Br, Bθ) at latitude L. This calculation yielded well-defined results between ±60° and ±75°, and indicated that the fields at both poles were approximately radial. Figure 8 displays the resulting average net, positive and negative radial and poloidal field strengths as functions of latitude. The fields become increasingly unipolar and radially directed closer to the poles, particularly poleward of ±65°. Applying this result, the radial polar fields were then estimated by directly dividing the line-of-sight measurements by the heliospheric angle cosine. Following Svalgaard et al. (1978) and Wang and Sheeley Jr (1988), the results were found to have distribution of the form Bp cosn θ, with Bp = −5.3 and n = 8.8 at the north pole, and Bp = 5.8 and n = 9.7 at the south pole. Figure 9 shows the average net, positive and negative radial field strengths as functions of latitude. The straight lines of symbols in the figure represent the local linear trends of the line-of-sight field component as a function of latitude at various chosen fixed positions on the disk along central meridian. These trends are found by collecting measurements from each fixed central-meridian position on the disk while the annual B0 tilt angle variation brings a fixed range of latitudes to this fixed position on the disk each year. For a steady polar field distribution, the field intensity values produce a linear distribution when plotted against latitude. In a well-defined set of measurements of a steady radial field distribution, distinct measurements deriving from the same heliographic latitude but at different times of year (i.e., different positions on the disk) should be almost equal, and hence the set straight lines should approximate a continuous curve. Figure 9 shows that this calculation produced well-defined results up to about ±80° and clearly describe a well-defined top-knot flux distribution at both poles. A well-defined average field distribution could be derived from 5 years of data because of the stability of the polar fields over this 5-year period.
Estimated radial and poloidal photospheric field components as functions of latitude during 2003–2008 for the north pole (left) and the south pole (right), based on SOLIS/VSM photospheric line-of-sight data. Note the domination of the radial component at both poles beyond 60°. Image reproduced with permission from Petrie and Patrikeeva (2009), copyright by AAS.
Polar photospheric field distributions derived assuming that the field is approximately radial. Shown are the distributions of positive (diamonds), negative (squares) and net (‘+’ symbols). The net field data are fitted with a function of the form Bpole cosn θ. For the north pole, the best-fitting parameter values are Bpole = −5.3 and n = 8.8, and for the south pole, Bpole = 5.8 and n = 9.7. Each straight line of symbols represents the change of field strength and latitude at a fixed central-meridian position on the solar disk as the B0 angle varies. In a well-defined set of measurements of a steady radial field distribution, those measurements deriving from the same heliographic latitude but at different times of year (i.e., different positions on the disk) should be almost equal, and hence the straight lines should approximate a continuous curve. It is evident from the figure that this is the case over most of the latitude range plotted. Image reproduced with permission from Petrie and Patrikeeva (2009), copyright by AAS.
When Petrie and Patrikeeva (2009) applied this method to SOLIS Ca ii 6542 A chromospheric field measurements, these fields had evolved too much to produce well-defined line-of-sight flux functions of latitude, except during 2008 when the north polar field was approximately radial and the south polar field was expanding towards the observer, i.e., super-radially (see also Jin et al., 2013).
In an earlier study by Raouafi et al. (2007) of polar field measurements in the same series of SOLIS Ca ii 6542 Å chromospheric magnetograms, the analysis focused on small-scale features in the polar field structure. They found that the number density and line-of-sight magnetic flux of identified magnetic elements decreased poleward as functions of latitude. The superficial disagreement between this result and the results of Petrie and Patrikeeva (2009) may be due to the effects of foreshortening on the visibility of field structure: the effective spatial resolution in heliographic coordinates decreases sharply close to the limb, and consequently less surface structure, such as the magnetic elements studied by Raouafi et al. (2007), can be identified as one observes closer to the limb.
2.3 Vector photospheric synoptic maps
The polar magnetic flux can be estimated using line-of-sight field measurements using the radial field assumption discussed in the previous section, and this is how polar fluxes are generally estimated at present. Reliable and continuous measurements of the polar vector field would provide more reliable information. We will see in Sections 2.5 and 2.6 the importance to global atmospheric modeling of estimating the strength of the polar fields accurately. A useful boundary data set for such observational and modeling projects would consist of full-surface vector synoptic magnetograms. Section 2.1 showed that it is possible to measure the polar photospheric vector field in impressive detail under optimal conditions. But can this be achieved on a routine basis? We currently have two synoptic vector magnetographs collecting full-disk vector images of the photospheric field, NSO’s SOLIS/VSM and NASA’s Solar Dynamics Observatory (SDO) satellite’s Helioseismic and Magnetic Imager (HMI). Gosain et al. (2013) recently produced vector synoptic maps from SOLIS data. An example vector field map is shown in Figure 10. The two boxes indicate a typical bipolar active region (Box 1) and a diffuse bipolar region (Box 2). The Bϕ component between the two polarities in Box 1 is consistent with the field trajectories connecting them, and Bθ is consistent with Joy’s law. In Box 2, both foot points of the field show negative Bϕ, which means that the field lines are connected such that the foot points make an obtuse angle with the solar surface, measured from the neutral line. Furthermore, in the diffuse bipolar region in Box 2, the Bθ distribution is positive/negative where Br is positive/negative, consistent with a loop structure tilted toward the equator. This tilt of this structure matches the direction of expansion of the northern polar coronal hole, which in April 2011 was still present, though the influence of the coronal field on the photospheric field is expected to be small.
Synoptic Carrington map of the vector magnetic field components synthesized using full-disk SOLIS/VSM vector magnetograms is shown for Carrington Rotation 2109. The panels from top to bottom show the distribution of the Br, Bθ, and Bϕ components, respectively. The Br map is scaled between ± 100 G, and the Bθ and Bϕ maps are scaled to ± 20 G. The positive values of Br, Bθ, and Bϕ point, respectively, upward, southward, and to the right (westward). Image reproduced with permission from Gosain et al. (2013), copyright by AAS.
Conspicuously absent from this vector map are measurements from the polar latitudes. This is because the high-latitude fields are too weak to be reliably inverted from Stokes data with the 1″ pixel size of the SOLIS/VSM images. The effective spatial resolution at the poles is also compromised by foreshortening effects and atmospheric by seeing. This exercise demonstrates the challenging nature of routine synoptic vector field measurements at high latitudes, where the field is weak. The Hinode SOT has demonstrated that vector field at the poles can be measured in great detail under optimal conditions, but it remains true that routine synoptic measurements of the polar magnetic vector have not yet been achieved. SOLIS and HMI lack the resolution or sensitivity to provide detailed maps of the polar vector field. Synoptic line-of-sight magnetograms from, e.g., SOLIS, HMI, NSO’s Global Oscillations Network Group (GONG) and WSO include measurements of weak fields down to 1 G or weaker, much less than the average flux density of the polar field measured by Hinode as described in Section 2.1, but enough to catch the approximately 5 G large-scale high-latitude field distribution. For this reason, the weak line-of-sight field can be diagnosed at high latitudes with low-resolution instruments.
More recently, SOLIS has performed long-exposure observations of polar latitudes with more limited fields of view. Also it is planned to combine vector field measurements of strong fields and line-of-sight measurements of weak fields in a single map. As Section 2.1 indicates, full-Stokes measurements will play a central role in characterizing the polar fields in the future, and over time the contribution of routine synoptic measurements to this process will increase.
2.4 Polar field interpolation for missing data
As we have seen, the photospheric magnetic field at high latitudes, in particular at the poles, is difficult to observe from Earth because the angle between the solar rotation axis and the ecliptic plane is small, 7.25°. So far all of our solar magnetographs have been confined to the ecliptic plane. The Ulysses spacecraft traveled in a poloidal orbit around the Sun but it did not carry a magnetograph. From Earth or locations nearby, the south pole is visible early in the year and the north pole late in the year, with optimal viewing angles on 6 March and 8 September, respectively. For most of the year, one or the other pole is not observable. At all times the large projection angle makes it difficult to resolve magnetic features at the poles using a present-day full-disk synoptic magnetograph. An observation of the polar field by such a magnetograph, such as SOLIS or HMI, generally shows a less structured, almost unipolar flux distribution covering the polar cap, whose average field strength peaks somewhere in the range 5–10 G at solar minimum. Measurements of even a weak line-of-sight field component are often reliable to high latitudes but, as described in Section 2.2, the properties of the measured fields are not well defined all the way to the limb, reflecting the fact that the measurements are not reliable there. Pixels at the edges of full-disk magnetograms tend to be noisier than those near disk-center and, because the large-scale fields are generally approximately radially directed, the line-of-sight component of the field near the limb tend to be weaker than those near disk-center. The limb field data are therefore more prone to being unreliable. The limb data corresponding to low-latitude locations can be compared to observations taken at other times when these locations are facing the Earth, but this solution is not available for high-latitude fields.
In tension with this unfortunate fact, there are several important branches of solar physics that rely on accurate descriptions of the polar field distribution. For example, the large-scale distribution of the polar field has a dominant influence on the structure of global coronal models, as well as the models for the solar wind based on them (Section 4.3). Furthermore, modelers of the global solar dynamo (Section 3) rely on measured polar field strengths to build and test their models.
In the absence of optimal conditions for measuring the polar fields, field data for these latitudes must be derived either by flux-transport modeling, where the polar field is built from well-measured active-region fields that are transported to the poles as we will discuss in Section 3, or by interpolating or extrapolating from better-quality measurements of lower-latitude fields. For many years solar observatories have used simple interpolation or extrapolation techniques to fill missing pixels in their synoptic maps.
One way to mitigate the problem is to exploit high-latitude observations taken with optimal B0 tilt angles. The large-scale distribution of the polar fields evolves gradually enough that it is possible to derive a reasonable field-strength estimate by interpolating between annual measurements taken when the pole in question was tilted towards the Earth. Even with this information some spatial interpolation is always necessary. Spatial interpolation across the pole based on lower-latitude measurements can be performed in one dimension by fitting curves in meridional slices, or in two dimensions by fitting surfaces.
A successful pole-fitting method must give a reasonable estimate for the polar fields by using good-quality observations to the fullest possible extent. There is no obviously optimal solution to this problem but some comparative studies of various methods have been made. Liu et al. (2007) compared the results of seven different pole-filling techniques. These included one-dimensional cubic spline interpolation with and without smoothing, two-dimensional low-degree polynomial surface fitting with or without temporal interpolation, a “topknot” model based on fitting a surface of the form Bp cosn θ (Svalgaard et al., 1978, see Section 2.2), and the flux transport method described by Schrijver (2001) (see Section 3.5). Liu et al. (2007) concluded that the best technique for filling missing polar data was one combining two-dimensional low-degree polynomial surface fitting and temporal interpolation.
Sun et al. (2011) developed a new method based on this technique. They derived estimates of high-latitude field distributions based on the best available data, i.e., those taken with the most advantageous B0 angles from 8 September and 6 March for the north and south poles, respectively. They built an annual time series in this way corresponding to each Carrington coordinate and interpolated in time between the annual measurements using a low-order polynomial. These synthetic data were then merged with the original observations via weighted averages. In near-real-time it is not possible to interpolate between two annual measurements at high latitudes because data from the following March or September are not yet available. In this case it is necessary to extrapolate forward in time, a less reliable method that can lead to temporal discontinuities when the high-latitude measurements eventually become available. To illustrate this, Figure 11 shows a comparison between averages of annual field measurements poleward of ±75° and the results of four extrapolation methods for estimating the polar field strengths in advance. The four extrapolation methods are based on lower-latitude data (±62°–±75°), and linear, quadratic and cubic spline function fits to high-latitude data. In all four cases the extrapolation depends heavily on the data most closely preceding the target time of the estimate but the most successful estimate is in most cases the one based on the lower-latitude data. This result seems to reflect the importance of comparatively high-quality measurements that are possible only at lower latitudes, and also the value of flux transport modeling in understanding polar field changes.
Comparison of four extrapolation methods for estimating the polar field strength of the next year from existing measurements: average from low latitudes, and cubic spline, quadratic, and linear fits of existing polar data. The results of these methods are represented by the symbols indicated on the plot. Open squares (diamonds) indicate smoothed and averaged polar field flux density above 75° latitude in the north (south) during September (March) measured by MDI. Each extrapolated point is based only on the data points before it. The low-latitude data are the average of the flux density between 62° and 75° multiplied by 1.1, from the previous year. The dashed curve shows the average field strength difference between two poles after smoothing and averaging, which represents the residual imbalanced flux of the polar field based on the smoothed and averaged positive and negative polar flux densities (the open squares and diamonds). Image reproduced with permission from Sun et al. (2011), copyright by Springer.
The Wang-Sheeley-Arge model (Wang and Sheeley Jr, 1990; Arge and Pizzo, 2000, see Section 4.3) for the solar wind was used to test the pole-fitting methods, and the new method of Sun et al. (2011) resulted in better model predictions of solar wind speed and interplanetary mean field (IMF) polarity than a one-dimensional method, according to comparisons with Advanced Composition Explorer (ACE) solar wind data. Figure 12 shows a comparison between the new method of Sun et al. (2011) and a one-dimensional interpolation method. The top plots show the simulated polar field distribution, and in the bottom plots the solar wind source distributions are over-plotted, with estimated solar wind speeds represented by color. The plots for the one-dimensional interpolation illustrate that even when a pole is well observed, noisy data that include spurious opposite-polarity flux contributions can lead to sizable unphysical closed structure at the pole. Temporal interpolation and merging with selected high-quality data helps to avoid such artifacts, which are absent from the plots for the new method.
Comparison of derived open field line footpoints as the source location for high-latitude fast solar wind during solar minimum (CR 1920), computed with the preferred polar field correction of Sun et al. (2011) and with a simpler 1D spatial interpolation method. For latitudes poleward of ±65°, (a) shows the north-pole view, and (b) shows the south pole. In each panel, the top row shows the magnetic data after correction. The bottom shows the wind source over-plotted on synoptic map, with colors indicating corresponding solar wind speed. Image reproduced with permission from Sun et al. (2011), copyright by Springer.
2.5 The radial photospheric field and potential coronal field models
One major application of full-surface solar magnetic field measurements is as boundary data for models of the solar atmosphere. These models are of practical as well as scientific importance because they help us to locate sources of the solar wind. Global models for the solar atmosphere place a heavy burden on the polar field measurements because, while the polar fields are difficult to measure, they play a leading role in structuring these global models. In this section and in Section 2.6 we discuss efforts to apply line-of-sight observations from the photosphere and chromosphere as boundary data for global models.
A sensitive issue with the use of photospheric data as boundary data in atmospheric modeling in general is the great physical mismatch between the highly forced, plasma-dominated photospheric layers where the measurements originate, and the atmospheric models which either are force-free or, in the MHD case, do not resolve the extremely complex lower atmospheric layers between the photosphere and the corona. In this sense, the boundary data supplied by the photospheric field measurements are physically inconsistent with the models.
The photospheric field is non-potential, being in a fluid-dominated medium, and is typically nearly radial at the height of the measurements, as Section 2.2 showed. Matching the line-of-sight component of a potential field model for the corona to line-of-sight measurements of the photospheric field is strictly not a physically consistent approach because the field is not likely to be approximately current-free at the height of the observations. Wang and Sheeley Jr (1992) argued that a procedure more consistent with nearly-radial, non-potential photospheric fields is to convert the line-of-sight field measurements to radial fields by dividing by cos ρ, where ρ is the heliocentric angle between the line-of-sight vector and the local vertical. This method generally implies a discontinuity between the vanishing horizontal field component in the photosphere and the finite horizontal field component of the model immediately above the photosphere. Wang and Sheeley Jr (1992) interpreted this discontinuity as a mathematical idealization of a very thin but finite boundary layer between the non-potential and approximately radial photospheric field and the approximately potential and non-radial coronal field. On global coronal scales this model estimates the radial magnetic flux into the corona as well as can be done based on line-of-sight observations. It clearly enhances the strength and influence of fields observed near the limb, most notably the polar fields.
Wang and Sheeley Jr (1992) compared PFSS models calculated using the direct line-of-sight approach to equivalent models derived using the radial field correction. Figure 13 shows modeled open-field footpoint distributions for CR 1776, representing coronal holes, from the two approaches. Also shown for comparison is the NSO Kitt Peak He i 10830 Å synoptic map for CR 1776, in which bright regions represent coronal holes. Coronal holes are low-density regions in the corona that are identified with regions of open field in coronal models. We will discuss coronal holes more fully in Section 4.2. The model derived by the radial field method has significantly larger polar coronal holes than the line-of-sight model, which includes low-latitude coronal holes that are absent from the radial-field model. The radial-field model gives better overall agreement with the He i map which also has large polar coronal holes and only weak and noisy features at low latitudes.
Distributions of open field regions over the solar surface during Carrington rotation 1776 (sunspot minimum), according to PFSS models calculated using (a) radial and (b) line-of-sight photospheric boundary data. The source surface is at 2.35 solar radii. Gray stippling indicates the footpoint areas of positive-polarity open field lines. For comparison, (c) displays the corresponding NSO/Kitt Peak synoptic map taken in the He i 10830 absorption line, where the lightest areas represent coronal holes. The model based on radial boundary data reproduces the polar coronal hole distributions in the He i 10830 map more accurately. Image reproduced with permission from Wang and Sheeley Jr (1992), copyright by AAS.
Wang and Sheeley Jr (1992) also modeled the K-coronal intensity using an idealized plasma density model assuming that the plasma emission is concentrated at the PFSS model’s source-surface neutral line. Figure 14 shows their results for CR 1762. The top row of the figure shows the source-surface neutral line derived using the radial (left) and line-of-sight (right) models, the middle row shows the simulated intensity maps, and the bottom row shows the observed distribution of tangentially polarized white-light intensity at 3.5 solar radii based on east-limb data from the SOLWIND coronagraph. The model derived using the radial-field method clearly results in a much flatter neutral line than the line-of-sight approach. This difference is due to the much stronger polar fields in the radial field model. Again the radial-field model gives much better agreement with the observations than the line-of-sight model. Wang and Sheeley Jr (1992) demonstrated this with examples both from solar minimum and maximum.
K-coronal structures for Carrington rotation 1762 (1985 May). The top panels show the shape of the source-surface neutral line (black), as derived by extrapolating WSO magnetograph measurements using the radial (left) and line-of-sight (right) methods for applying lower-boundary data to the model. The middle panels show the corresponding simulated patterns of scattered light intensity, with black indicating the brightest structures and white representing the regions of lowest intensity. For comparison, the bottom panels (which are identical to each other) display the SOLWIND coronal intensity patterns at r = 3.5 solar radii during rotation 1762. Here an arbitrary background intensity has been subtracted from the data and the brightest structures are again denoted by black. Image reproduced with permission from Wang and Sheeley Jr (1992), copyright by AAS.
The radial-field approach generally produces open-field and source-surface neutral line distributions that match observed coronal holes and streamer structures better than does the line-of-sight approach. Wang and Sheeley Jr (1992) argued that the radial field approximation makes the best possible use of the available magnetogram data, consistent with the conclusion of Section 2.2 that the photospheric field is typically nearly radial at the height of the measurements.
2.6 Chromospheric synoptic maps and potential-field extrapolations
Most global coronal modeling relies on photospheric radial field maps based on line-of-sight measurements, implicitly applying the physical assumptions discussed by Wang and Sheeley Jr (1992) described in the last section. This is partly due to the much wider availability of photospheric line-of-sight field measurements than measurements from higher in the solar atmosphere, though routine chromospheric full-disk measurements and synoptic maps are available from the SOLIS/VSM. In this section we describe a recent effort to apply chromospheric field observations as lower-boundary data for coronal PFSS models.
Chromospheric fields differ significantly from the underlying photospheric fields. Whereas photospheric fields are directed approximately radially over most of the solar surface, the chromospheric fields often form canopy structures so that the fields spread horizontally (Jones, 1985), as discussed in Section 2.2. A powerful motivation for using chromospheric field observations in coronal modeling is that the chromosphere is not separated from the corona by a complex transition region like the photosphere is, and the chromosphere is much more similar to the corona physically, generally being magnetically dominated and approximately force-free. The main challenge in using chromospheric data is that, since the field expands in all directions the radial magnetic flux into the atmosphere cannot be easily estimated from line-of-sight chromospheric data — there is no analog of the radial field assumption for the chromosphere, as also discussed in Section 2.2. Of course one could apply chromospheric line-of-sight data directly as boundary data to the PFSS model, relying on the model to determine the radial flux, but this turns out to be an unreliable method. A major difficulty is that the global radial flux generally does not balance because the high-latitude radial flux is not estimated accurately by a potential field model constrained by line-of-sight observations. PFSS models are constructed neglecting the monopole component of the surface magnetogram. A large monopole component in the surface data, when subtracted for modeling purposes, is often indicated by a spurious net displacement of the neutral line at the source surface (outer boundary) from the equator. Such artifacts are characteristic of models whose high-latitude radial fluxes are not accurately represented. If the potential field model does not reproduce the real tilt of the chromospheric polar fields then the polar flux is doomed to be poorly estimated.
It is much more practical to work with boundary data for the radial field component. Jin et al. (2013) took such an approach. They developed a method for producing synoptic maps for the chromospheric radial field component based on full-disk chromospheric Ca ii line-of-sight magnetograms taken by the SOLIS/VSM between April 2006 and November 2009. They used the annual change in our viewing angle from Earth of the polar regions to estimate the radial and meridional components of the chromospheric polar fields. Significant radial and meridional components were detected at both poles, and the south polar field was tilted more strongly away from the pole (see also Section 2.2, Petrie and Patrikeeva, 2009).
Because of loss of resolution due to foreshortening and the nearly radial orientation of the vector field, line-of-sight field components observed near the limb appear weaker in general than line-of-sight fields observed near the center of the disk. For nearly unipolar fields, such as the polar fields, the loss of resolution is not necessarily a problem because not much flux is likely to be lost. The center-to-limb variation of polar field measurements cannot be investigated directly because we can only observe the polar fields from the ecliptic plane with large viewing angles. Instead, Jin et al. (2013) investigated the center-to-limb variation of nearly unipolar low-latitude regions, which are believed to be similar to polar fields. They tracked 20 unipolar regions, of unsigned flux density > 8 G and ratio of major-polarity flux to minor-polarity flux > 3. They arrived at a correction function increasing from 1 at central meridian to about 2.25 at the limb. They corrected their full-disk measurements using this function.
The changing viewing angle resulting from solar rotation can be used to resolve a series of line-of-sight field observations into radial, meridional and zonal field components for nearly static fields, at least in principle. In practice, Jin et al. (2013) were able to derive useful estimates of the meridional and zonal components. They then derived estimates for the radial component by exploiting the fact that the meridional field component is dominated by the radial component at low latitudes whereas at polar latitudes the north-south component is significant. By subtracting longitudinal averages of the meridional field at each latitude, and by adding at all latitudes the running annual average of the radial flux density mentioned above, derived using changes in the B0 angle, they produced hybrid maps for the chromospheric radial field. The process is illustrated in Figure 15. The resulting chromospheric radial field maps are, for modeling purposes, functionally very similar to standard photospheric radial field maps. The physical relationship between the map and the model is very different, however. In Section 2.2 we discussed how radial photospheric boundary data in a coronal PFSS model implies a discontinuity between a vanishing photospheric tangential field component and the finite tangential component of the coronal field, and how this current layer idealizes the transition region. With chromospheric data this discontinuity is assumed to be absent since there is no physical transition region between the level of the boundary-data measurements and the model. The physical consistency and success of the model relies on a smooth transition between the chromosphere and the corona.
Three synoptic maps of Carrington rotation 2062 showing chromospheric magnetic flux density from −13 to 13 G. Abscissa is the Carrington longitude from 0 to 360 deg. Ordinates are sine latitude from −1 to 1. The upper panel is the meridional plane component. Note the strong signal near the south pole. The middle panel is the same minus the average of each latitude row. The lower panel is the middle map plus the average radial component at each latitude based on a 365-day data set. Note the nearly equally strong poles. See the text for details. Image reproduced with permission from Jin et al. (2013), copyright by AAS.
Jin et al. (2013) extrapolated potential-field models from the chromospheric synoptic magnetograms, and these were found to be slightly superior to the PFSS models routinely generated from standard GONG photospheric synoptic maps. Models for selected rotations are shown in Figure 16. However, both sets of models showed evidence of overestimated polar field strengths and a known zero-point issue in the case of the GONG models. The PFSS extrapolations from the chromospheric radial data appear to have generally similar properties to PFSS models extrapolated from standard photospheric synoptic maps, and are free from the north-south asymmetries that often result from applying line-of-sight chromospheric field measurements directly as boundary data.
Five pairs of maps for selected Carrington rotations. The left column includes simulated coronal hole locations (green and red colored areas) and a neutral line at 2.5 solar radii (smooth line near the equator) based on PFSS extrapolations of chromospheric measurements. The right column is the same but for extrapolated photospheric (GONG) measurements. The gray-scale image is streamer locations from STEREO/SECCHI observations at 2.2 solar radii. The irregular line indicates coronal hole boundaries estimated from STEREO/SECCHI observations using 171 and 304 A wavelengths. Image reproduced with permission from Jin et al. (2013), copyright by AAS.
Thus, it is possible to estimate the polar flux from chromospheric measurements after some work, but the photospheric radial field approximation provides a simpler and approximately equally accurate estimate. For this reason, PFSS and MHD models extrapolated from boundary data based on photospheric line-of-sight measurements and the radial field assumption remain competitive (Section 2.5).
2.7 Cycle relationship between polar and active fields: the magnetic butterfly diagram
Figure 17 shows a butterfly diagram (latitude-time plot) of the radial field component, based on full-disk longitudinal photospheric magnetograms from the NSO’s three Kitt Peak magnetographs, the SOLIS/VSM, the spectro-magnetograph and the 512-channel magnetograph instruments, covering the nearly 4 solar cycles from the beginning of cycle 21 to the declining phase of cycle 24. Here it was assumed that the photospheric field is approximately radial (Svalgaard et al., 1978; Wang and Sheeley Jr, 1992; Petrie and Patrikeeva, 2009, see Section 2.2), and the line-of-sight observations were divided by the cosine of the heliocentric angle ρ. Images with geometry problems or missing pixels were excluded from this plot and the subsequent analysis.
Butterfly diagram (latitude-time plot) based on Kitt Peak magnetogram data, summarizing the photospheric radial field distributions derived from the longitudinal photospheric field measurements. Each pixel is colored to represent the average radial magnetic flux density at each time and latitude. Red/blue represents positive/negative flux, with the color scale saturated at 15 G. Image updated from Petrie (2012, 2013).
An important advantage of studying approximately radial fields is that the full magnetic flux through the photosphere can be estimated reasonably accurately over most of the solar disk. However, because the solar rotation axis is tilted at an angle of 7.25° with respect to the ecliptic plane, the fields near the solar poles are either observed with very large viewing angles or, for six months at a time, not observed at all. Also the noise level is inflated near the poles by the radial field correction discussed above. For these reasons we have had to fill the locations in the butterfly diagram nearest the poles using estimated values for these fields. This is a well-known problem in the construction of synoptic magnetograms (e.g., Sun et al., 2011, see Section 2.4). The polar flux is generally found to become stronger as one observes further poleward (Svalgaard et al., 1978; Wang and Sheeley Jr, 1988; Petrie and Patrikeeva, 2009, see Section 2.2), and the polar field distribution in Figure 17 reflects this. The fields at the highest latitudes in Figure 17 were calculated from measurements taken with advantageous solar axis tilt (B0) angles (B0 > 5° for northern and B0 < −5° for southern high-latitude fields). The resulting fields are well defined and regular functions of time for all but the two most poleward sin(latitude) bins at each pole (there are 180 uniformly-spaced sin(latitude) bins in the butterfly diagram overall). For these two most poleward bins, simulated data were used based on a polynomial fit for each image. The simulated data were then blended with the measurements in a B0-dependent fashion.
Figure 17 covers cycles 21–23 in their entirety, as well as the end of cycle 20 and the ascent and maximum of cycle 24. The diagram shows several distinctive patterns in the long-term behavior of the fields at active and polar latitudes, and at latitudes in between. The active fields begin each cycle emerging at latitudes around ±30° and subsequently emerge at progressively lower latitudes on average, a phenomenon referred to as Spörer’s law, creating the distinctive wings of the butterfly patterns first reported by Maunder (1913). The diagram also shows the change of polarity of the polar fields once each cycle, coinciding with activity maximum but not occurring simultaneously at the two poles. Between the active and polar latitudes, around ±50°, there is clear evidence of poleward flux transport of both polarities in each hemisphere during each cycle, which appears most intense during the most active phases of the cycle. Most of the flux that emerges in active regions cancels with flux of opposite polarity, but a critical proportion survives as weak flux that is carried poleward by the a poleward surface meridional flow and by the diffusion-like effect of the photospheric convection (see Section 3). This poleward drift of the weak, decayed magnetic flux appears in Figure 17 as plumes of one dominant polarity, the trailing sunspot polarity, at high latitudes between about 40° and 65°, sometimes referred to as a “rush to the poles”. Such patterns were first reported by Bumba and Howard (1969) who named them unipolar magnetic regions. The dominant polarity of the poleward plumes is of opposite sign in each hemisphere, and it alternates from cycle to cycle. Howe et al. (2013) compared the poleward migration rate estimated from the high-latitude surges in a Kitt Peak magnetic butterfly diagram to the subsurface meridional flow rates measured in helioseismic data from the GONG network since 2001, and found the two rates to be in reasonable agreement. Note that there is no evidence of equatorward high-latitude counter-cell meridional flow in Figure 17. The high-latitude flux transport appears to be exclusively poleward.
The alternating pattern of poleward surges is related to well-known patterns of the bipolar active regions that emerge at low latitudes. The latitude centroids of the positive and negative magnetic fluxes of the active regions in each hemisphere were found by Petrie (2012) to swap positions each cycle, with the positive centroids north/south of the negative centroids in each hemisphere over even-numbered/odd-numbered cycles. These patterns are shown in Figure 18. The active region flux centroid calculations are based on imdividual sky images and include only strong fields, and so they reflect the Joy’s law tilt of the regions and not the transport of the weak, decayed flux. Active regions are usually bipolar in structure, and the alternating latitude centroid patterns reflect the well-known facts that bipolar regions are typically asymmetric and tilted so that the leading polarity is stronger, more compact and slightly closer to the equator than the following polarity (Hale et al., 1919, referred to as “Joy’s law tilt”), and the vast majority of bipoles in each hemisphere have the same leading polarity, the leading polarities are opposite in the two hemispheres during any given cycle, and all polarity patterns reverse each cycle (Hale and Nicholson, 1925, referred to as “Hale’s polarity rule”). The Joy’s law tilt plays a central role in the phenomenological model for the solar activity cycle of Babcock (1961), where decaying flux from the following, generally more dispersed and more poleward polarity of the bipole contributes more to the polar fields than the leading, generally more compact and more equatorward polarity. These ideas were used to develop a kinematic model for photospheric flux transport and the solar cycle by Leighton (1964, 1969), initiating a class of models known as “Babcock-Leighton” models (see Sections 3.1 and 3.2). Durrant et al. (2004) found evidence of a net transport of leading-polarity flux across the equator, corresponding to a poleward flow of net following-polarity flux across latitudes ±60°, consistent with the above picture.
The latitudinal centroids of the active region fields as functions of time for positive (red) and negative (blue) polarities in the northern (solid lines) and southern (dotted lines) hemispheres for the Kitt Peak data summarized in Figure 17. The error bars indicate the standard deviations of the annual means. The displacements between the positive and negative centroids are a consequence of and consistent with Joy’s law. Image updated from Petrie (2012).
In these “Babcock-Leighton” models, the cycle-dependent polarity patterns and the Joy’s law tilt preference are assumed to be responsible for creating the polar field cycle from the activity cycle. The contribution to the polar field in a given hemisphere from decayed active region flux seems to be proportional to the total active region flux in that hemisphere and to the latitude displacement between the positive and negative active-region flux centroids in that hemisphere. Petrie (2012) found a correlation between the annual-averaged high-latitude (approx. ±50°) poleward stream fluxes and the product of the annual-averaged latitude flux centroid displacements and total active-region fluxes. A correlation was also found between the annual-averaged high-latitude poleward stream fluxes and the annual-average polar (±63–70°) field changes. These correlations were found in both hemispheres with both NSO Kitt Peak data and Mt. Wilson Observatory (MWO) 150-foot tower data.
The Joy’s law tilt and polarity biases are not strict. Even in averaged form, the poleward flux surges appear to be approximately periodic in time (Ulrich and Tran, 2013) with frequent changes in sign. The widths of the surges are approximately equal to the meridional flow travel time between the active latitudes and the poles, between 1 and 1.5 yr, also approximately equal to the equatorial dipole decay time (Wang et al., 2009). The streams originate from sizable densely packed groups of sunspots that survive for many months and are almost continuously refreshed during their lifetimes by the emergence of new bipoles (Gaizauskas et al., 1983; Schrijver and Zwaan, 2000). The interaction of multiple tilted bipoles may produce large poleward surges of flux and large polar field changes in a relatively short time.
Figure 19 shows estimates of the average field strengths at polar latitudes based on measurements from NSO Kitt Peak and Wilcox Solar Observatory (WSO). At WSO the north and south polar line-of-sight field strengths are measured daily in the 3′ apertures nearest the poles, north and south. The NSO/KP estimates are derived from the butterfly map shown in Figure 17 and represent the radial field component. This is part of the reason why the NSO polar data are so much stronger than the WSO measurements. There are also well documented calibration issues with the WSO data (Svalgaard et al., 1978) causing the fields to be underestimated by a factor of 1.8. Nevertheless, the time series shown in the two panels of Figure 19 are clearly well correlated with each other, evidence that they represent real patterns in the polar field evolution. They agree, for example, on the widely-reported fact that the polar fields, both north and south, have been only about 60% as strong since the cycle 23 polarity reversal compared to before (e.g., Hoeksema, 2010; de Toma, 2011). Around the time of this reversal of polarity, 2002–2003, the positive and negative flux latitude centroids began to converge in each hemisphere (Petrie, 2012, see Figure 18). This forced the latitude displacement, and therefore the net flux contribution from the decaying active regions to the polar fields, to become significantly smaller than previously. It appears that the polar fields were starved of unipolar decayed active-region flux between the cycle 23 polar reversal and the end of cycle 23. The high-latitude surges carried weaker flux of more mixed polarity during cycle 23 maximum than during the maxima of cycles 21 and 22, as we saw in Figure 17. Therefore the polar fields did not strengthen as much as during these previous polarity reversals. This had many consequences that we will describe in Section 4, including record-low interplanetary magnetic field measurements (Smith and Balogh, 2008).
10-day averages of the north (red solid lines) and south (blue dotted lines) polar fields measured at Kitt Peak (top) and Wilcox (bottom) are plotted against time. The Kitt Peak data are for the radial field component and derive from heliographic latitudes between about latitudes ranging from about ±63° to about ±70°. The Wilcox measurements are for the line-of-sight field component and come from the 3′ apertures nearest the poles, which cover between about ±55° and the poles. Changes tend to occur earlier in the Wilcox curves than in the Kitt Peak curves because the Wilcox data derive from lower latitudes on average. Updated from Petrie (2013).
Figure 18 shows that, during the decline of cycle 23, the centroids converged in both hemispheres around 2003, and stayed together until the end of the cycle — see also Section 3.6. In the south this convergence occurred earlier, around 2001. Correspondingly, according to Figure 19, the south polar field became stable after 2001 and the south polar field around 2003. There is evidence in Figure 18 that this was not the first time the positive and negative latitude centroids converged, During cycle 22 the centroid separation and the activity amplitude (measured in terms of active region flux) peaked together in the north, compatible with the abrupt polar field reversal, followed by convergence of the latitude centroids and stability in the polar fields, shown in Figure 19. In the south the centroid separation was small during the ascent of cycle 22, but increased as the decline of the cycle got under way. Meanwhile, the south polar field began to reverse in the south more slowly than in the north, but sped up and reversed as the centroid separation increased.
When cycle 24 began in 2010, the northern hemisphere developed ahead of the south. Figure 17 shows that positive field-carrying surges traveled poleward as shown by the red streaks, causing the north polar field to reverse first as shown in Figures 17 and 19. This is consistent with the Hinode results of Shiota et al. (2012) shown in Figure 4, in which the polar flux density decreased in the north than in the south. Svalgaard and Kamide (2013) and Mordvinov and Yazev (2014) emphasized the link of this asymmetry to an asymmetry in the decayed active region fields that are transported poleward. This asymmetry is a major reason for the asynchronous north and south polar reversals seen in Figure 19. During 2013, however, a surge of negative flux moved poleward, threatening to cancel the progress of the north polar field. In the south the opposite happened: the activity started late and initially sent mixed polarity-flux poleward, and the south polar field was slow to reverse. But the south polar field has been fed a steady diet of negative flux in the past few years, represented by the blue streaks in the bottom right of Figure 17. In response the south polar field has reversed and has been strengthening ever since. The most recent active regions appear to be sending more negative flux towards the south pole, followed by a more weakly net-positive surge beginning early this year (2015) but a long-duration positive surge towards the north pole. The fate of the north polar field reversal is therefore becoming clearer after its interrupted reversal. Although at the time of writing the north polar field has turned positive again and is strengthening, we still have highly asymmetric polar fields.
3 Polar-Field Reconstruction in Kinematic Flux-Transport Models for the Solar Cycle
In the previous section, we summarized observations of high-latitude magnetic fields, special observations at high resolution and long-term synoptic observations. The synoptic observations revealed a coherent pattern of high-latitude flux transport, a “march to the poles” of surface magnetic flux. In this section, we will begin in Section 3.1 by discussing the phenomenological model of Babcock (1961), the first attempt to unite the diverse cyclical patterns of bipolar active regions and polar fields into a coherent picture of the solar cycle. We will then describe in the following subsections the subsequent numerical kinematic modeling of the cycle, an effort that continues to this day.
Models of the solar magnetic cycle kinematically have focused on the role of global plasma flows in producing the organized behavior of the fields. Kinematic flux transport models for the solar cycle are governed by the induction equation relating the fluid flow and the magnetic flux transport. In the axisymmetric case, the induction equation breaks down into two simple coupled equations, one for the vector potential of the poloidal field and the other for the toroidal field component — see, e.g., Charbonneau (2010), Eqs. (11, 12). In the equation for the toroidal field, the conversion of poloidal field to toroidal field is clearly represented by a source term describing the shearing effect of interior differential rotation. However, the equation for the poloidal field has only an advection term that can neither create nor destroy magnetic flux, and a diffusion term that can only destroy magnetic flux. Thus whatever an axisymmetric flow field does, the poloidal field must ultimately decay away, and the toroidal field must also decay as a consequence (Cowling, 1933).
Therefore, a non-axisymmetric process is needed to provide a poloidal field source. Parker (1955) introduced a poloidal field source term representing the effect of helical turbulent flows on buoyantly rising loops that twist in response to the Coriolis force, creating poloidal field components in previously toroidal loops. Such a process, commonly called the “alpha effect”, and its associated poloidal field source term, enables dynamo models to produce cyclical behavior. In the “Babcock-Leighton” mechanism (Babcock, 1961; Leighton, 1969) the alpha effect is contained in the Joy’s law tilt of the active regions, whose flux is converted into polar flux by surface and near-surface transport.
Flux transport dynamo models have been the main theoretical tool for understanding the origins of the solar cycle and solar activity, and have produced a complex theoretical picture of how the solar dynamo may operate and how the solar convection zone and tachocline may behave. For simplicity, we will focus here on Babcock-Leighton-type models, both data-driven and self-excited, where near-surface flows produce the alpha effect. The interested reader is referred to Charbonneau (2010) for a much more general discussion of solar dynamo models.
In both, surface flux transport models and self-excited flux transport dynamo models, the polar fields form from the decay of tilted bipolar active regions. Flux transport dynamo models are self-excited in that they produce new activity cycles from old cycles by transporting decayed photospheric active region flux poleward and then transporting the same flux equatorward beneath the surface, amplifying it at active latitudes by differential rotation (in the Babcock-Leighton models), whereupon some of this flux emerges to create the new cycle. Surface flux transport models, by contrast, use sunspot number or magnetogram data as input for the new cycle. The photospheric fluid motions that break the active regions down and transport the flux poleward — diffusion, differential rotation and meridional flow — are essentially the same in both types of model. But flux transport dynamo models are generally (though not in all cases) axisymmetric, and they have depth-dependence in modeling both the latitudinal and radial components of the meridional flow as well as having a radially-varying turbulent diffusivity. Surface flux transport models more often include longitude-dependence, and describe the response of the radial field component to a latitude-dependent surface meridional flow and a constant surface diffusivity. We will discuss examples of both types of model in the following. But before discussing the kinematic models, we will begin with the initial phenomenological model of Babcock (1961).
3.1 Babcock’s phenomenological model for the solar cycle
Babcock (1961) developed a phenomenological model for the solar cycle that accounted for the reversal of the polar fields, the equatorward migration of sunspot emergence (Spörer’s law), Hale’s and Joy’s laws governing the polarities and tilts of sunspots (extended to bipolar active regions in general), and the fact that bipolar active regions appear to decay away. In this model, the interior differential rotation provides the energy that amplifies the interior field and produces the new activity cycle. While this model has been much modified by subsequent observational and modeling work, most of the basic picture has survived to this day.
Figure 20 shows the different stages of the solar cycle according to the model. The first stage (a) begins at cycle minimum with a dipole field formed by the polar fields. The differential rotation then amplifies the internal field strength and gives the interior field a dominant toroidal component (b), forming a flux rope, until a critical field strength is reached where buoyant rise and emergence (c) is inevitable. These fields then emerge as bipolar active regions. This bipole emergence takes place at progressively lower latitudes as the cycle proceeds because the structure of the differential rotation produces toroidal fields of critical strength at lower and lower latitudes. Babcock (1961) expected the emergence to terminate at a given latitude because of the eventual fragmentation of the flux rope there, caused by the emergence of many active regions. This assumption proved to be controversial as we shall see, but it was clear that the differential rotation shear flow plays a role in expanding the regions in the east-west direction, weakening their field, and giving them the long, slanted appearance often found in high-latitude flux distributions (see Figures 21 and 48 for examples from flux-transport modeling and from magnetogram observations). On the other hand, the causes of the observed latitudinal expansion (f) remained obscure at that time. Babcock (1961) did mention the possibility of poleward meridional surface flow (g, h), that would in later decades become central to flux transport modeling, but at the time evidence for such flows was lacking. The expansion of bipoles and the poleward transport of trailing-polarity flux was taken as well established by observations, though the physical causes remained obscure. Responding to the expansion and dispersal of the photospheric fields, the coronal flux loops expand under their thermal and magnetic pressure (f), whereupon, the leading-polarity flux in each hemisphere come into contact and reconnect to form trans-equatorial loops, while the following-polarity flux expands poleward, ultimately forming new polar fields (i) of reversed polarity compared to (a).
Schematic diagram of the major global photospheric flux-transport dynamo processes. The red inner sphere represents the Sun’s radiative core and the blue mesh the solar surface. In between is the solar convection zone. (a) Shearing of poloidal field by the Sun’s differential rotation near the bottom of the convection zone. (b) The toroidal field resulting from this shearing by differential rotation. (c) When the toroidal field is strong enough, buoyant loops rise to the surface, twisting as they rise due to the Coriolis force. Tilted bipoles are formed from these loops. (d–f) Additional flux emerges (d, e) and spreads (f) in latitude and longitude from decaying spots. (g) Meridional flow (yellow circulation with arrows) carries surface magnetic flux poleward, causing the polar fields to reverse. (h) Some of this flux is transported downward to the bottom and towards the equator. These poloidal fields have sign opposite to those at the beginning of the sequence, in (a). (i) This reversed poloidal flux is sheared by the differential rotation to produce the new toroidal field opposite in sign to that shown in (b). Babcock (1961) did not explicitly include meridional circulation in his model, though he speculated about its existence. Image reproduced with permission from Dikpati and Gilman (2007), copyright by IOP and DPG.
The development of a bipolar active region subject to diffusion and differential rotation in a kinematic flux-transport model. Note the characteristic elongation and tilt of the region, and the poleward shift of the less intense trailing polarity. Image reproduced with permission from Leighton (1964), copyright by AAS.
Since, at the beginning of a cycle, the following-polarity flux in each hemisphere is preferentially of opposite polarity to the polar field in that hemisphere, and the trailing-polarity flux emerges poleward of the leading-polarity flux on average, this ongoing process weakens the polar fields and reverses them. The process continues until the end of the cycle, as the poleward expansion of following-polarity flux forms a new polar cap in each hemisphere, of opposite polarity to the one at the beginning of the cycle. The vast majority of the flux not involved in reversing and forming the polar fields is eliminated by the merging of expanded field from the active regions accompanied by reconnection in the atmosphere.
Babcock (1961) noted the lack of stability inherent in the model. The amplitude of a cycle is strongly dependent on the details of active region emergence — high-amplitude cycles would not necessarily be followed by high-amplitude cycles, and a strong polar field is not guaranteed to be reversed by a weak activity cycle, with consequences for the following cycle. But his model represented a major advance in our understanding of how the cyclical relationship between the active regions and the polar fields proceeds, and it also stimulated the first efforts to model the solar cycle kinematically.
3.2 Leighton’s numerical kinematic model for the solar cycle
The phenomenological solar cycle model of Babcock (1961) was based on an observed interrelationship between the active regions and the polar fields. His picture of the deformation and amplification of the Sun’s interior field by differential rotation, the emergence and decay of this field, and the cycle-dependent latitude separation of leading- and following-polarity flux that creates the polarity bias of the flux that expands to the poles, provided the first theoretical link between the activity and polar cycles, and still forms the basis of global dynamo modeling today. Two important gaps in the model were its lack of explanation for the latitudinal dispersal of surface active region flux (differential rotation can only expand the flux longitudinally), and a quantitative description of how the cycle may proceed. Both problems were addressed by Leighton (1964, 1969).
Leighton (1964) proposed a specific physical mechanism for the expansion and transport of decayed active region flux. Such a mechanism is essential for the preferentially following-polarity flux to reach the poles and change the field there, and also helped to explain the observed relative longevity of leading-polarity flux compared to following-polarity flux.
The supergranular convection flow field (Leighton et al., 1962) concentrates the decaying, large-scale field of an active region into narrow lanes at the boundaries of convective cells (Parker, 1963). Because these lanes are non-stationary (Leighton et al., 1962), they move an element of plasma around on the photosphere in a manner similar to a random walk. The solar plasma is highly conducting so that fields penetrating the photosphere must be dragged on this random walk. This process accounts for the relatively short lifetimes of individual flux elements in bipolar or unipolar flux patterns whose total fluxes are approximately conserved over much longer timescales. Treating magnetic concentrations as atom-like particles, Leighton (1964) assumed that adjacent positive and negative fluxes do not attract or repel each other but instead move independently of each other, dependent only on the fluid motions. Based on this random-walk process, Leighton (1964) developed a diffusion model for the breakdown and expansion of photospheric fields.
Leighton (1964) presented a formal solution of this diffusion model in spherical harmonics showing that diffusion time scales decrease with increasing multipole order. The smaller-scale structures tend to diffuse away, leaving the lowest-order structure, a dipole, which has a 5-yr decay timescale, approximately half a solar cycle. Leighton (1964) also presented numerical kinematic flux transport models for the decay by differential rotation and diffusion of active regions, featuring Joy’s law tilt and stronger leading- than following-polarity flux. The combination of differential rotation and diffusion resulted in poleward expansion in the form of two tilted, longitudinally stretched bands, one of each polarity, shown in Figure 21. The following-polarity band of flux expanded more and dominated the polar latitudes, consistent with the model of Babcock (1961). This diffusion model applied to multiple bipolar active regions leads to a dipolar field with sign reflecting the Joy’s law tilt bias of the bipoles. The model also reproduces the 90° phase lag between the polar-field and activity cycles first reported by Sheeley Jr (1964, see Section 4.4).
The sporadic character of sunspot formation and the resulting complex magnetic distributions indicate that there are significant irregularities in the subsurface fields. On the other hand, the long-term regularity of the solar cycle suggests that there is an underlying regularity in the field distribution that drives the cycle. Leighton (1969) focused on the regular component of the solar field by imposing constant or uniformly-varying models for the physical quantities within a relatively thin shear layer close to the solar surface. The resulting kinematic model reproduced the equatorward migration of active region flux emergence seen in magnetic butterfly diagrams, as well as the poleward migration of the zero contour of radial field, modeling the poleward march of the polar filaments that occurs before each polar field reversal (see Section 4.5).
Leighton (1964) imposed a critical field strength corresponding to that of the weakest sunspot fields then observed, a few hundred gauss. In his model, the emergence of azimuthal field decreases the strength of the remaining azimuthal field, an assumption consistent with the idea of Babcock (1961) that flux emergence would terminate at a given latitude when the interior toroidal flux rope became too fragmented. This idea was later challenged by Parker (1984), who argued that a net toroidal flux decrease would require a chain of active regions to erupt simultaneously over 360° of longitude. Whereas in Babcock’s model the equatorward migration of the flux emergence is a direct consequence of the differential rotation geometry alone, in Leighton’s model the emergence of flux at a given latitude strengthens the radial and meridional field components at adjacent lower latitudes and weakens them at higher latitudes, preferentially enhancing the toroidal field growth rate at lower latitudes. These assumptions would be challenged by subsequent modeling and observational work, but many of the critical components of Leighton’s model are still in use.
3.3 The influence of meridional flows on the Babcock—Leighton model
Kinematic flux-transport modeling took major steps forward in the 1980s, stimulated by new observational evidence of meridional circulation flows in Doppler measurements by Duvall Jr (1979) and Labonte and Howard (1982), along with evidence of subsurface equatorward return flow in torsional oscillation patterns found by Howard and Labonte (1980). These observations were followed by photospheric feature-tracking (Komm et al., 1993), Doppler (Ulrich, 1993) and helioseismic observations (Hathaway et al., 1996) of poleward surface meridional flows of 20 ms−1. The observations provided critical guidance for modelers of the solar cycle.
Sheeley Jr et al. (1985) extended the photospheric flux transport work of Leighton (1969) by adding a background meridional flow explicitly to the model, and by modeling the flux transport in the two surface spatial dimensions over an entire solar cycle and comparing the results with observations of photospheric and interplanetary mean field strengths and coronal hole distributions. They found reasonable agreement between the model results and the observations. The main effect of the meridional flow was to weaken the mean photospheric field by disrupting long-lived patterns of strong photospheric flux, and by removing active region flux from active to polar latitudes.
Wang et al. (1989) presented an azimuthally and radially averaged kinematic flux transport model similar to the one developed by Leighton (1969), but with the Sheeley Jr et al. (1985) meridional flow model included. They applied this model to study the combined effects of super-granular diffusion and meridional flow on the development of polar fields. They found that the meridional flow plays an important role in carrying the trailing-polarity flux poleward, and concentrating the polar fields at the poles against the spreading effect of diffusion. Whereas diffusion alone would tend to produce a dipole-like distribution (see Leighton, 1964, and Section 3.2), the observed distribution is much more concentrated (see Section 2.2), of the form cosn θ, where n is in the range 8–11, and polar fields with this degree of spatial concentration can only be achieved by including significant poleward surface meridional flow. They also found that, to reproduce the very intense poleward surges of decayed active region flux and major polar field changes observed during 1980–1982, they needed both accelerated meridional flow and enhanced bipole emergence rates.
Wang et al. (1989) studied the effects of changing the meridional flow speeds and diffusion rates. Enhanced diffusion causes more leading-polarity flux to merge across the equator with leading-polarity flux in the opposite hemisphere, and therefore frees more trailing-polarity flux to be transported poleward and to change the polar field. Figure 22 shows three butterfly diagrams (latitude-time plots) for example models of a full solar cycle: one without meridional flow, one with moderate meridional flow and one with fast meridional flow. Compared to examples without meridional flow, which produce butterfly diagrams in which distinct poleward surges are absent, examples with moderate meridional flow (10 m s−1) produce the streaks of alternating polarity that are a distinctive feature of butterfly diagrams of observed fields. But the major surges that are large enough to reverse a polar field quickly and decisively are absent from models with flows of this amplitude. Enhanced meridional flow speeds and emergence rates are needed to produce such surges.
Gray-scale maps showing the latitudinal field distributions as a function of time, representing the simulated evolution of photospheric fields in the presence of diffusion at a rate n = 600 km2 s−1 and meridional flows of different speeds as follows. Top: υ = 0 m s−1. Middle: υ = 10 m s−1. Bottom: υ = 20 m s−1. These plots show that the poleward transport of flux by diffusion alone does not produce the observed surges, and yields a polar field that is too weak and too broadly spread over latitude. Poleward flow and equatorward diffusion combine to establish strong, concentrated fields, as observed; however, the simulation with υ = 10 m s−1 does not reproduce the observed giant surges and the accompanying fluctuations of the polar field strengths during 1980–1982. The simulation with υ = 20 m s−1 reproduces better the giant surges observed near sunspot maximum and the corresponding fluctuations in the polar field strength. Image reproduced with permission from Wang et al. (1989), copyright by AAS.
It is not known whether the meridional flows really accelerated to higher speeds during 1980–1982 to produce the large polar field changes observed during this time. The fact that Wang et al. (1989) had to multiply the observed flux emergence rate by 1.6 to reproduce the observed polar reversal suggests that other factors were involved in producing these surges, such as changes in the bipoles’ size or Joy’s law tilt distribution. In the model of Wang et al. (1989) the latitude separation between the positive and negative polarities in each hemisphere was kept constant, but this parameter may vary over time and might produce large effects on the poleward surges of flux and the polar fields themselves.
Wang and Sheeley Jr (1991) studied the emergence and subsequent evolution of bipoles in some detail. They suggested that Coriolis forces acting on a rising, expanding flux loop can account for the observed magnitude and latitudinal variation of bipole tilt angles. They then investigated the effects of the large-scale photospheric flows on the emerged bipoles. Differential rotation has no effect on the axisymmetric component of the field, including the axial dipole moment. The discrepancy between the dipole moments that the bipoles emerge with and the subsequent dipole moment of the photospheric field is therefore due to diffusion and meridional flow.
Leighton (1964) — see Section 3.2 — showed that in the presence of diffusion alone the magnetic multipoles would decay such that the low-order multipoles decay slowest and the lowest-order multipole, the dipole, would decay on a timescale comparable to a solar cycle. On the other hand, as Wang and Sheeley Jr (1991) agued, for a poleward meridional flow in the absence of diffusion, a bipole not straddling the equator would be transported to the nearest pole, and its two polarities would merge there or in transit. Thus, either diffusion or meridional flow acting alone would reduce the dipole moment of an emerged bipole.
Wang and Sheeley Jr (1991) studied the behavior of bipoles situated at a variety of latitudes and subjected to diffusion and meridional flows of different speeds, and Figure 23 summarizes the results. At most latitudes meridional flow and diffusion acting together on a bipole will decrease its dipole moment or the reasons given above, except in some cases of bipoles at low latitudes. The dipole moment can increase if some of the bipole’s flux manages to diffuse across the equator and a significant flux imbalance is created in each hemisphere. If this happens the meridional flows can carry these unbalanced fluxes to the two poles and concentrate them there, producing an enhanced dipole moment. However, this happens to a small minority of active regions on the real Sun, in which case the effect on the hemispherec net flux balance can be significant (Cameron et al., 2013). The general effect of diffusion and meridional flow on most bipoles is to decrease a bipole’s dipole moment.
The effect of bipole location and meridional flow speed on the axial dipole contribution of a decaying bipole. Shown is the evolution of the axial dipole strength of a single large bipolar active region deposited at latitudes: 7° north (top left), middle 15° north (top right), 23° north (bottom). The bipolar region has its leading flux of 2.0 × 1022 Mx located 3° equatorward of its trailing flux of −2.0 × 1022 Mx. The diffusion rate κ was fixed at 600 km2 s−1. The four curves shown in each plot represent four meridional flow amplitudes: υ = 0 m s−1 (short dashed lines), υ = 5 m s−1 (thin solid lines), υ = 10 m s−1 (thick solid lines), υ = 20 ms−1, (long dashed lines). Image reproduced with permission from Wang and Sheeley Jr (1991), copyright by AAS.
Because of this effect, diffusion and meridional flow can cause the axial dipole moment of a bipole to increase or decrease after emergence, depending on the bipole’s latitude, but in general the effect of the flows is to decrease a bipole’s dipole moment. Over most of the active latitude range and with solar-like diffusion rates and meridional flow speeds (10–20 m s−1), the diffusion and meridional flow can be relied upon to reduce the dipole moment of a bipole. The conversion from toroidal to poloidal flux in the Babcock-Leighton model is therefore due to the tilt angles with which the bipoles emerge and not to the subsequent flux transport. The flux transport only serves to redistribute the poloidal bipole flux component poleward and concentrate the polar fields.
Wang et al. (1991) presented a development of the flux transport model including not only surface flux transport by super granular diffusion and poleward meridional flow but also the effects of subsurface turbulent diffusion and equatorward return flow. As in Babcock’s and Leighton’s models, differential rotation shears subsurface poloidal fields to produce strong toroidal fields. Unlike Babcock and Leighton, Wang et al. (1991) did not assume that toroidal flux emergence decreases the toroidal flux beneath the surface. Instead, the subsurface toroidal field is destroyed by unwinding the toroidal field during the declining phase of each cycle due to the poloidal field having switched polarity, and by subsurface diffusion as the toroidal flux is transported equatorward by the subsurface meridional flow and merged with oppositely-directed toroidal flux in the opposite hemisphere.
Meridional circulation also allows the equatorward migration of flux emergence to occur without requiring a radial gradient in the interior differential rotation profile. Helioseismic results from Thompson et al. (1996) and Schou et al. (1998) showed that radial gradients in subsurface angular velocity are small in the convection zone down to around 0.7 solar radii, and that the large radial shears that occur around 0.7 solar radii are such that the rotation rate decreases with depth at low latitudes, contrary to the assumption of Leighton (1969). Unlike the model of Leighton (1969), the Wang et al. (1991) model behaved in a stable, oscillatory manner without a radial gradient in the interior angular velocity.
In this model, as in the radially and azimuthally averaged model of Wang et al. (1989), the polar fields underwent less sudden reversals than the solar polar fields are observed to do. The authors attributed this difference to the fact that the meridional flow speed in the model was independent of time, whereas the solar meridional flow speeds may vary significantly. This topic has become particularly important recently in the context of efforts to explain the weak polar fields of cycle 23 — see Section 3.6.
3.4 The evolving, “synchronic” synoptic map
We now discuss a very useful application of photospheric flux transport modeling: the creation of time-dependent, full-surface synoptic photospheric magnetograms. Since the 1960s and 1970s (Howard, 1967; Schatten et al., 1969; Harvey et al., 1980), synoptic maps for the photospheric magnetic field have been constructed using a fixed coordinate system defined by Carrington, where the vertical axis represents heliographic latitude or sine(latitude) and the horizontal axis represents both longitude and time, a full rotation corresponding to both 360° and 27.27 days, based on the rotation rate of latitudes ±26°, representative typical latitudes of sunspots, as observed from Earth. Each full-disk magnetogram is remapped from sky-image coordinates to heliographic coordinates. The remapped images are then positioned in the Carrington coordinate grid and either pasted together or averaged together in some fashion, often giving more weight in the averaging to measurements near central meridian than to measurements near the east and west limbs. In these maps the magnetic field at any given location on the photosphere remains unchanged as long as that location is not observed. Because of this, different longitudes are represented by observations taken at different times, up to 27.27 days apart. In this way such a map is “diachronic”. This is how the synoptic maps discussed in Section 2 were created. Maps of this kind have proved to be very useful in the past. The slowness of the dispersal and transport of active region flux, and the slow evolution of the polar fields allow even such infrequently updated maps to represent the full-surface field reasonably well most of the time. On the other hand, the development of a time-dependent, “synchronic” map, a map of the full surface as if it were observed all at a single time, is clearly a necessary step towards more accurate synoptic maps and extrapolated models for atmospheric magnetic fields.
As the basic concepts of photospheric flux transport have become more established, increasingly realistic models for the photospheric magnetic field distribution have been developed in the form of synoptic, full-surface maps of the photospheric field. Unlike the “diachronic” synoptic maps described above and featuring elsewhere in this review, (e.g., in Sections 2.6 and 4.5), these “synchronic” maps are designed to provide a snapshot of the full-surface photospheric field distribution at any time. Since these maps necessarily include longitudes that have not been observed for two weeks, and polar latitudes that remain unobserved for months at a time, a model for the photospheric flux transport seems to be a necessary condition for an accurate full-surface snapshot.
Worden and Harvey (2000) developed a model for two-dimensional photospheric flux transport, with physical ingredients similar to those of Leighton (1969) and Sheeley Jr et al. (1985), and that could be used to derive an instantaneous snapshot of the global photospheric field at any given moment. In this model, however, new observations are added to the portion of the map representing the front side of the Sun, while unobserved fields are evolved according to the flux-transport model.
In the transformation of the full-disk images from sky-image coordinates to heliographic coordinates, the number of sky image pixels per heliographic remap pixel is not constant. This ratio, an information density, is maximum at disk-center and decreases towards the limb. This information density distribution is taken into account when new observations are added to the map. When different observations of a single solar location are averaged together, the average is weighted by the information density, so that data observed close to central meridian contribute most to the map. In most implementations a further weighting is applied favoring central meridian data to account for the superior sensitivity of the measurements near disk-center. In this calculation, the polar latitudes have relativity low information density and sensitivity, but central-meridian polar data still have highest weighting at these latitudes.
Worden and Harvey (2000) did not include sky image pixels beyond a certain distance from disk-center. This means that observations for the field at each pole are only included in the model over about four months per year. The polar regions are filled with fields transported poleward by the flux-transport model over the remainder of the year. The modeled polar fields were found to be most sensitive to the meridional flow speed, consistent with the flux transport modeling discussed in Section 3.3.
The model includes the Snodgrass (1983) differential rotation law and a meridional flow profile similar to that of Sheeley Jr et al. (1985). It departs from the standard flux-transport model of Sheeley Jr et al. (1985) in two important ways. A random Gaussian distribution of magnetic flux with mean field strength 1.8 G is continuously added to the model to sustain the quiet-Sun magnetic fields, and so that their dispersal can be reproduced throughout the photosphere. Without this ingredient the photospheric network field would disappear through flux cancellation in 2–3 days (Schrijver et al., 1997).
Also random attractors are used to model the dispersal of the fields instead of the diffusion model based on random walks introduced by Leighton (1964). Supergranular convective cells are observed to be randomly distributed across the solar surface. The cell flows clearly transport magnetic flux not in a diffusion-like manner in all directions but preferentially towards the cell boundaries and their junctions. Worden and Harvey (2000) therefore modeled these processes using random attractors. Unlike the random-walk diffusion model of Leighton and Wang and Sheeley, a random attractor model clumps magnetic flux together in many small concentrations as seen in observations. Worden and Harvey (2000) created an attractor matrix of (360 × 180 pixels, the same size as the map itself, and assigned each attractor a random number such that the mean attractor number per unit solar area was conserved. For each pixel in the map a search space was defined as all neighboring pixels within a supergranular scale (≈ 13 500 km). The distance, direction and strength of the largest attractor in the search space determined the displacement vector of the pixel’s flux due to the convection. This vector was combined with those associated with the differential rotation and meridional flow to compute the displacement of the pixel’s flux over each time step.
Schrijver (1989) showed that active-region flux is more resistant to dispersal than the weaker surrounding flux. This apparent magnetoconvective coupling between the fields and flows stimulated a new effort to simulate photospheric flux evolution and polar field development with greater realism (Schrijver and Title, 2001, see Section 3.5). Worden and Harvey (2000) applied simulated supergranular motion only to flux weaker than 25 G. The optimal effective diffusion coefficient in their model was 520 km s−1.
Figure 24 (top) shows a “diachronic” synoptic map for CR 1928 in longitude-latitude coordinates. In this map the values for the unobserved polar fields have been interpolated from lower-latitude data using a two-dimensional low-order polynomial surface (see Section 2.4). The middle plot shows the equivalent synoptic map for CR 1929. The bottom plot shows the effects of modeled differential rotation on the CR 1928 field over a full rotation. The middle and bottom plots can therefore be compared to judge how much of the real evolution is due to differential rotation alone. Indeed, the large magnetic field patterns in the boxes labelled 1 and 2 have been longitudinally elongated by the differential rotation model and resemble the real fields in CR 1929, implying that differential rotation is mainly responsible for their evolution. But the region in Box 3 was not removed by differential rotation even though it did disappear in reality. Furthermore, there is fine magnetic structure in both the CR 1928 and CR 1929 maps although the bottom plot shows that such structure did not survive the effects of differential rotation. Meridional flow would not be expected to have a major effect over a single rotation, but Figure 24 demonstrates that other processes besides differential rotation must play important roles in the flux transport over this timescale.
This figure and Figure 25 show the effects of flux-transport processes in a kinematic model. Top: observed magnetic flux synoptic map for Carrington rotation 1928 in latitude-longitude format. Unobserved polar fields are interpolated across the poles from lower latitudes. The boxes labeled 1, 2, and 3 identify flux systems that can be compared from map to map in this figure and Figure 25. Middle: observed magnetic flux synoptic map for Carrington rotation 1929. Bottom: result of evolving the synoptic map for rotation 1928 (top) over one Carrington rotation using the model of Worden and Harvey (2000), and using only differential rotation to transport the flux. Image reproduced with permission from Worden and Harvey (2000), copyright by Springer.
Figure 25 (top) shows the result of evolving the CR 1928 map over a single rotation using the differential rotation, meridional flow and random attractor models, but without updating the map with new observations. The middle plot shows the result of the same experiment but with a small-scale background flux with mean field strength 1.8 G is continuously added to the model. The bottom plot shows the map resulting from evolving the CR 1928 map over a rotation incorporating all flux transport processes and background small-scale flux, and updating the map using daily magnetogram observations.
Top: The result of evolving the synoptic map for rotation 1928 over one Carrington rotation using differential rotation, meridional flow, and supergranular diffusion as the transport processes. No new observations were used to update the map. Middle: The result of evolving the synoptic map for rotation 1928 over one Carrington rotation using differential rotation, meridional flow, and supergranular diffusion as the transport processes and adding a small-scale, background magnetic flux with a mean absolute value of 1.8 G. No new observations were used to update the map. Bottom: The result of evolving the corrected synoptic map for Carrington rotation 1928 if all the different transport processes are applied, a small-scale background magnetic flux is added, and daily magnetogram observations are included. This map is the best estimate for the distribution of magnetic flux at the end of Carrington rotation 1929. The newest observations are near the left edge. Image reproduced with permission from Worden and Harvey (2000), copyright by Springer.
Adding the small-scale background flux maintains the small-scale features of the field at low latitudes against diffusion, but does not alter the dispersal of large-scale features (see also Wang and Sheeley Jr, 1991). Compared to Figure 24 (bottom), the active regions in Figure 25 have dispersed more quickly because of the flux dispersal model, and the flux has a network-like appearance because of the random-attractor form of the flux dispersal. The modeled polar fields are also much more textured than those in the Kitt Peak synoptic maps in Figure 24, more reminiscent of the high-resolution Hinode observations shown in Section 2.1. The polar fields of an evolved synoptic map are unipolar, unlike the Hinode observations described in Section 2.1. The small-scale polar features in Figure 25 can be identified with the large, cycle-dependent class of patches discussed in Section 2.1 that are generally of the same polarity and define the polarity of the polar cap.
The addition of new observations significantly improves the resemblance of the model to the observed field for CR 1929 (Figure 24, middle). The flux transport alone cannot reproduce the disappearance of the small active region in box 3, or the emergence of new active regions. But updates from daily observations successfully catches the disappearance of flux in box 3, and some of the flux emergence elsewhere. Clearly, the model cannot be updated at all longitudes at all times, but the regular additions of new magnetograms keep the model as up-to-date as possible.
Synoptic map construction, whether of traditional Carrington maps or of maps derived from flux-transport models described above, usually assimilate new magnetograms by direct insertion into the model in a weighted average or by blending observations with model data. Such methods do not quantitatively take into account the relative accuracy of the new observation compared to the observations already present or the model.
Using the Los Alamos National Laboratory data assimilation framework, Arge et al. (2011) have developed a version of the model of Worden and Harvey (2000) model, named Air Force Data Assimilative Photospheric Flux Transport (ADAPT), that includes statistical filtering of new data. The filtering methods include ensemble least squares and Kalman filtering. Arge et al. (2011) ran their model over half a solar cycle (2003–2009) using ensemble least squares filtering, and found encouraging agreement between the modeled polar field strengths and MWO polar field measurements taken with optimal B0 angle. They have also developed forecasts of the solar radio flux at 10.7 cm, known as the F10.7 flux, using absolute field strengths from their flux-transport modeling, and improved reconstructions of coronal hole boundaries from potential-field source-surface models. In a case study, Arge et al. (2013) included helioseismic data for active region emergence and development on the far side of the Sun and they reported further improvement in the performance of their model in this case.
3.5 Modifications to random walks due to magnetoconvective coupling
Additional observed properties of the photospheric field were incorporated into the flux transport model of Schrijver (2001). In this work the flux was modeled by an ensemble of concentrations represented by discrete point sources undergoing collisions and fragmentation. Large active regions and small ephemeral regions were included. A flux-dependent field dispersal was applied to recreate the initial decay of active regions, including a reduced rate of this decay seen in observations for strong magnetic fields, believed to be caused by magnetoconvective coupling (Schrijver, 1989).
In mature active regions, the average observed flux density remains around 100–150 G, independent of the region’s age or size (Schrijver and Harvey, 1994). This property is clearly inconsistent with the standard linear random-walk diffusion model of Leighton (1969) and subsequent authors (Sections 3.2–3.3). Whereas the random walk model is remarkably successful at redistributing the large-scale photospheric field in agreement with observations, the necessary diffusion rate of 600 ± 200 km2 s−1 (e.g., Wang et al., 1989; Durrant and Wilson, 2003) is significantly higher than the rate indicated by flux concentration tracking observations.
In his flux transport model, Schrijver (2001) combined the models for collision, fragmentation and magnetoconvective coupling with differential rotation and meridional flow profiles empirically derived by Komm et al. (1993) from NSO/KP magnetograms. Schrijver and Title (2001) proceeded to use this model to study the evolution of polar fields of the Sun during solar cycle 21, and also in non-solar stars including the case of a star 30 times more active than the Sun.
The solar magnetic field near the poles is determined by a balance between random-walk diffusion, which tends to spread the field, and meridional flow which tends to concentrate the field (Wang et al., 1989, see Section 3.3). Because the fields at high solar latitudes tend to be weak, the effects of magnetoconvective coupling are not great there. For stars with flux emergence rates much higher than the Sun’s, Schrijver and Title (2001) found that a tightly nested polarity pattern developed around each polar cap. This pattern is evident in the right column of Figure 26. In the standard model with linear diffusion the poleward migration of trailing-polarity flux and the diffusion of this flux onto the pole results in the polar cap being destroyed quite quickly, in a fraction of a solar cycle. On a much more active star the average flux concentration contains more flux because collisions are more frequent. The modeled random walk at the poles is therefore much slower than in the solar case, and the trailing flux takes a longer time to diffuse to the pole and cancel the trailing flux there. For the same reason the polar flux does not diffuse towards the approaching trailing-polarity flux so quickly. The nonlinearity of the model also produces a narrower transition between the opposite-polarity fluxes, and this layer is closer to the poles. In the solar case the time for flux to diffuse from ±70° to the poles is about 1.4 yr, significantly less than a cycle. For this reason, solar polar reversals take only a fraction of a cycle and a single polarity dominates the polar latitudes in each hemisphere over the vast majority of the cycle, as illustrated by the left column of Figure 26. The efficiency of the diffusion in the solar case therefore appears to be due to the moderate rate of flux emergence and the consequent weakness of the decayed active-region fields. This efficiency is the reason for the responsiveness of the polar fields to the decayed active-region flux and the 90° phase lag between the activity and polar-field cycles. This result suggests that the linear diffusion models may reproduce the formation and reversal of the polar fields quite faithfully, but that they do not accurately model the source of this flux: the initial decay of the active regions.
Simulations of stellar magnetic fields for a star like the Sun (left) and a star with an active region emergence rate 30 times higher (right). The panels show the surface magnetic field, viewed from a position over a latitude of 40°. The gray scale for the Sun-like star saturates at 70 Mx cm−2 and for the active star at 700 Mx cm−2, using a resolution of 1°2. The flux density has been multiplied with a projection factor of cos(μ), with μ the angular distance to the center of the disk, to simulate the weakening of the signal toward the limb for a field that is assumed to be normal to the surface. Image reproduced with permission from Schrijver and Title (2001), copyright by AAS.
3.6 Unusual cycle 23 minimum
Since the beginning of the space age over 40 years ago, when detailed observations of the solar magnetic field began, only four full solar cycles have occurred, cycles 20–23, and a fifth, cycle 24, is in progress. During the minimum of cycle 23 it became apparent that the Sun was behaving like it had not been observed to behave previously. While the photospheric flux transport between the active and polar latitudes is complicated by the interaction of multiple processes, the strength of the polar fields that develop during a cycle is generally expected to be related to the amplitude of the activity during the cycle, measured by, e.g., the sunspot number. According to the sunspot number or the equatorial dipole or other non-axisymmetric multipole components, cycle 23 was about 30% weaker than the two previous cycles (the smoothed maxima were 164.5, 158.5, 120.8 for cycles 21–23, respectively, making cycle 23 27% weaker than cycle 21 and 24% weaker than cycle 22) but the polar fields were about 40% weaker than they had been during the previous 3 minima (Svalgaard and Cliver, 2007). The cycle 23 minimum was also unusually quiet: there were 265 and 261 spotless days in 2008 and 2009, respectively, beaten only by 1878, 1901 and 1913 since 1849 (Jiang et al., 2013). We will discuss some consequences of this unusual behavior in Section 4.
Various explanations for the weakness of the cycle 23 polar fields have been suggested. The polar field strength at the end of a given sunspot cycle depends on several things: the polar field strength at the beginning of the cycle, the total amount of active region flux that emerges during the cycle, the axial tilts and latitudes of the active regions, the supergranular diffusion rate, and the meridional flow speed profile in time and latitude. The two surface flux-transport parameters with arguably the greatest influence over the polar fields are the Joy’s law tilt and the meridional flow speed, which between them mostly determine the polarity bias of the decayed active region flux sent poleward.
Dikpati (2011) used simple numerical estimates and detailed kinematic dynamo modeling to show that even a quite modest decrease in active region field from one cycle to the next, such as between cycles 22 and 23, could produce a large decrease of polar field strength. The amplitude of the polar fields is very sensitive to the details of the strength and decay of the active regions. To see this, suppose that at the end of a given cycle the polar fields have strength one unit. Then it would take a change of minus two units to reverse the polar fields to the same strength. But if the active regions contribute just 20% less flux than is necessary to do this in each hemisphere, then they will still reverse the polar fields but with a 40% drop in the polar field strength compared to the initial strength, a decrease twice as large as the decrease in decayed active region flux (Dikpati, 2011). Indeed, generally speaking, the presence of active region fields is correlated with changes in the polar fields as can be seen by comparing Figures 17 and 19. However, there are intervals of time when significant quantities of active region field are present in the photosphere but the polar fields do not change significantly. In particular, between 2002 and 2006 there were significant active region fields in the photosphere while the polar fields remained remarkably constant. Because there are periods of time when there are active region fields on the Sun that produce no detectable effect on the polar fields, Dikpati’s analysis does not fully explain the weakness of the polar fields.
In Babcock-Leighton flux transport, there are two possible explanations for unchanging polar fields in the presence of active regions. According to both explanations, decaying active fields still reach polar latitudes during these time intervals but these decayed active region fields are of such mixed polarity that their net effect on the polar fields is approximately zero. Figure 17 shows that the plumes of decayed active-region flux moving poleward have been of more mixed polarity since the cycle 23 polar reversal than before. One explanation is that the meridional flows are so fast that the leading polarities in the two hemispheres do not have time to interconnect and interact with each other before being swept poleward (e.g., Schrijver and Liu, 2008; Wang et al., 2009; Nandy et al., 2011; Jiang et al., 2013). An alternative explanation is that the active region Joy’s law tilts changed their hemispheric bias during cycle 23 (e.g., Jiang et al., 2013; Petrie, 2012). In this scenario approximately equal quantities of each polarity would be sent poleward with approximately zero net effect on the polar fields even for slow meridional flow speeds.
Several important ingredients of flux transport models are not well constrained by observations. Unfortunately, these include the meridional flow and the Joy’s law tilt. The meridional flow results often depend on the method used to derive them, e.g., Doppler measurements, magnetic feature tracking and helioseismic inversions of different kinds (global modes, ring diagrams). Surface Doppler (Ulrich, 2010) and helioseismic (Basu and Antia, 2010) meridional flow measurements generally agree with each other, having peak speeds at low latitudes around 25° on average, whereas magnetic feature tracking meridional flow measurements (Hathaway and Rightmire, 2010) have much lower values peaking at higher latitudes, around 50°. Magnetic feature tracking methods give a peak at higher latitudes because they do not separate the bulk fluid flow from the effect of supergranular diffusion. Poleward of active latitudes the diffusion generally acts in the same direction (i.e., poleward) as the meridional flow (Wang et al., 2009; Dikpati et al., 2010). Also, the Joy’s law tilts of sunspot pairs and bipolar active regions are difficult to measure in a comprehensive and objective way, and the results vary (e.g., see the discussion in McClintock and Norton, 2013). Definitions of sunspot pairs often exclude important strong field structures that can contribute to the Babcock-Leighton mechanism, and the details of the tilt calculation vary from study to study.
Meridional flow perturbations local to the activity bands may also play a role in modifying the flux transport. Sun et al. (2015) found an anti-correlation between active region field strength and the mid-latitude poleward flow speed of the associated decayed field, consistent with a field-dependent converging flow towards active regions (Zhao and Kosovichev, 2004). Using a flux-transport model, Jiang et al. (2010) studied the effect of meridional flow perturbations caused by near-surface inflows towards the active region band in each hemisphere, and found that large perturbations reduce the tilt angles of bipoles, thus reducing their contribution to the polar field changes. The amplitude of the meridional flow perturbations are larger for stronger solar cycles, consistent with the anti-correlation between Joy’s law tilt and cycle amplitude reported by Dasi-Espuig et al. (2010).Footnote 1 Such inflows can strongly affect the behavior of flux-transport models (Cameron and Schüssler, 2012).
Guided by results such as those summarized in Section 3.3, modelers have focused most on the effects of changes in the meridional flow speed. Following the long-term flux-transport simulations of Schrijver et al. (2002) whose polar fields did not reverse during every cycle, Wang et al. (2002) demonstrated that polar field reversals could be maintained if the surface meridional flow speeds were systematically higher during large-amplitude cycles than during small-amplitude cycles. Schrijver and Liu (2008) studied the evolution of the axial dipole moment of the global photospheric field from 1997 to 2008. They used three distinct methods to reconstruct the axial dipole: they recorded the axial dipole moments of the standard MDI synoptic maps, they built maps based on the flux transport model described in Section 3.5 and recorded the axial dipole moments of the resulting model fields, and they calculated a pure flux-transport simulation, based on the model of Schrijver et al. (2002), with parameters chosen such that the model photospheric field matched the observations. They adopted a standard meridional flow profile from Schrijver (2001) and varied the gradient of the flow near the equator, effectively controlling the communication between the two hemispheres. They found that the resulting axial dipole was strongly dependent on the low-latitude meridional flow gradient, as shown in Figure 27. In these models the strongest low-latitude gradients of poleward meridional flow produced the weakest polar fields. A strong low-latitude gradient was consistent with some (but not all) observations at the time, and the authors cautioned that the enhanced gradient could only apply post-1997 because the much stronger cycle 22 axial dipole is not consistent with such a flow profile.
Left: Comparison of axial dipole moments for flux equatorward of 75° in latitude for flux-transport models with a range of different low-latitude meridional flow gradients (diamonds). In this plot, a is a parameter that controls the low-latitude meridional flow. The value a = 0.6 represents no flow near the equator, a < 0.6 poleward flow near the equator with a = −1.0 representing the case with strongest flow gradient near the equator, and a > 0.6 flow reversal near the equator. The observed values from the flux-transport model with continuous updates from observed MDI magnetograms, and from the MDI synoptic maps for the end of 2007 are shown by solid and dotted lines, respectively (overlapping in this panel). Right: As on the left, but for flux poleward of 60°. Image reproduced with permission from Schrijver and Liu (2008), copyright by Springer.
Using the flux transport model of Sheeley Jr et al. (1985), Wang et al. (2009) studied the effects of varying meridional flow speeds from cycle to cycle over the previous four cycles (20–23). They compared their model results to synoptic data from MWO (1967–2009) and WSO (1976–2009), taking arithmetic means of the data where they overlapped. They chose a fixed meridional flow profile, adopted from their earlier work, and allowed no changes in the amplitude of this profile during any of the cycles, but changed the meridional flow speed between cycles. They represented active regions as large bipoles of fixed flux content, applied Joy’s law tilts to the regions with a fixed dependence on latitude, and introduced the bipoles at a rate proportional to the sunspot number. The bipoles were introduced randomly in latitude about a prescribed equatorward migration profile, and randomly in longitude and hemisphere. The results are summarized in Figure 28. Approximate agreement was found between the modeled and observed polar fields for peak meridional flow values of 15.5 m s−1 during cycle 20, 15.5 m s−1 during cycle 21, 14.5 m s−1 during cycle 22, and 17.0 m s−1 during cycle 23. According to both the observational data and the models, very large poleward surges of flux were seen during cycles 21 and 22, compared to the narrower and weaker surges seen during cycles 20 and 23. The polar reversals of cycles 20 and 23 were therefore less abrupt than those of cycles 21 and 22. A butterfly diagram of the model fields is shown in Figure 29, with meridional flow stream lines over-plotted. The slopes of the poleward surges were significantly steeper than the streamlines, particularly at high latitudes where the meridional flow speeds decreased. This is consistent with the supergranular convection dominating the flux transport at high latitudes, where the latitudinal field gradients are large.
Simulated evolution of the large-scale magnetic field during solar cycles 20 to 23. The magnetic bipoles sources are all assigned the same strength and deposited at random longitudes at a rate proportional to the observed annual sunspot numbers. The poleward flow amplitude is adjusted from cycle to cycle, so as to approximately match the measured polar field strengths during 1976, 1986, 1996, and 2009. (a) Simulated variation of the Sun’s axial and equatorial dipole components (G). (b) Simulated variation of the north and south polar fields (G), averaged over 30° polar caps. (c) Simulated variation of the near-Earth radial IMF strength (nT) and of the total photospheric flux (expressed as a surface-averaged field strength in units of 4 G). Image reproduced with permission from Wang et al. (2009), copyright by AAS.
Latitude-time plot of the simulated photospheric field. Each column of pixels represents a 27.3-day Carrington map of the photospheric field averaged over longitude. The gray scale ranges from −4 G (black) to +4 G (white). Overlaid color curves indicate the trajectories that flux elements would follow if their poleward transport were determined solely by the underlying meridional flow field υ(L) = ±υm sin 0.1∣L∣ cos1.8L (red: υm = 17 m s−1; green: υm = 15.5 m s−1; blue: υm = 14.5 m s−1). These values for υm are optimized for each solar cycle, so as to approximately match the measured polar field strengths during 1976, 1986, 1996, and 2009. Also over-plotted (yellow curves) are the trajectories corresponding to a latitude-independent poleward flow υ(L) = ±20 m s−1. The slopes of the poleward surges are closer to those of the constant flows because of the contribution of supergranular diffusion to the flux transport. Image reproduced with permission from Wang et al. (2009), copyright by AAS.
Jiang et al. (2013) performed a study that investigated the free parameters of the flux transport model. In this model the bipolar active region emergence was proportional to the monthly sunspot number, with the position, area and tilt angle of each bipole prescribed by an empirical model with random scatter. A model for preferred longitudes, as exhibited by activity complexes (see Section 4.5), was also included. They also imposed cycle-average bipole tilt angles that were inversely proportional to cycle amplitudes, consistent with the results of Dasi-Espuig et al. (2010). They applied the differential rotation profile from Snodgrass (1983) and a meridional flow profile from van Ballegooijen et al. (1998) designed to vanish poleward of ±75° (to preserve filament channels — see Section 4.5). They compared their modeled polar fields to measurements from WSO, and the model agreed well for the cycle 21 and 22 polar fields but was a factor of about 2 too strong compared to the measured polar fields of cycle 23.
Thereupon Jiang et al. (2013) explored the possible causes of the discrepancy by examining the effects of varying each free parameter in the model. Since the diffusivity models the effect of supergranular motion and is not expected to change significantly from cycle to cycle, Jiang et al. (2013) focused on changing the bipole emergence rate, the meridional flow and the bipole tilt. They found that a 40% reduction in the emergence rate, a 28% decrease in the average tilt angle and a 55% increase in the meridional flow speed for cycle 23 resulted in agreement between the modeled and observed polar field strengths for cycle 23. However, the reduction in the emergence rate also resulted in a major reduction in the open flux for cycle 23 (derived from PFSS modeling), and the reduction in the mean bipole tilt produced a 1.5-yr delay in the polar field reversal, whereas the increased meridional flow produced better agreement with the observed open flux and polar reversal time. Therefore, three independent studies, Schrijver and Liu (2008), Wang et al. (2009) and Jiang et al. (2013) all point to the same conclusion: that the likeliest cause of the weak polar fields of cycle 23 was an increase in the meridional flow speed for cycle 23.
The fact that Jiang et al. (2013) required a very large 55% increase in the meridional flow speed, compared to the much more modest 10–15% reguired by Wang et al. (2009), is due to the much smaller low-latitude gradient in the flow profile used by Jiang et al. (2013). Schrijver and Liu (2008) were able to control their polar fields by varying the low-latitude flow gradient alone. Indeed, the very large gradient of the profile used by Wang et al. (2009) may have played an exaggerated role in their results.
Indeed, not only the low-latitude gradients but the overall shapes of the meridional flow profiles are also crucial in determining the duration and timing of solar cycles, including the reversal of the polar fields. Dikpati (2011) studied how the location of the peak flow speed influences the effect of meridional flow speed changes on the polar fields. She argued that when the meridional flow speed peaks at low latitudes, an increase in the overall speed produces a faster poleward transport of the leading polarity compared to the trailing polarity, enhancing the cancellation between them, resulting in weaker polar fields. This is matches the surface flux-transport results of Schrijver and Liu (2008), Wang et al. (2009) and Jiang et al. (2013). If, on the other hand, the flow speed peaks at higher latitudes, then an increase in the flow speed causes the trailing polarity to speed up relative to the leading polarity, inhibiting cancellation. This can result in stronger polar fields if enough trans-equatorial diffusion is allowed to occur (see Section 3.3).
To verify this argument, Dikpati (2011) performed flux transport dynamo simulations, making a sudden change in the meridional flow speed from an initial peak speed of 18 m s−1 to a range of speeds between 6 and 32 m s−1. She used two meridional flow profiles, one peaked at 25° latitude and the other at 50°. The results are shown in Figure 30. The polar field amplitude change is small in all cases, no more than 10%. Dikpati (2011) therefore concluded that the 40% reduction in polar field strength observed during cycle 23, shown in Figure 19, could not have been caused only by changes in meridional flow speed. For the flow profile with high-latitude peak, faster/slower flows produce stronger/weaker polar fields. The situation with the low-latitude flow peak is more complex: the polar fields weaken for flows both faster and slower than the initial value. All of these results are consistent with the simple discussion above, except that the polar field weakens when the high-latitude-peak flow profile becomes slower. Dikpati (2011) explained this exception in terms of the cycle becoming so long that the enough cancellation takes place before the flux reaches the poles, resulting in weaker polar fields.
(a) Typical profiles of the poleward surface flow in meridional circulation used in a set of self-excited flux-transport dynamo simulations: blue curve with a peak near 25° and red curve with a peak near 50°. (b) Polar field amplitudes in the polar cap (latitudes from 55° to 90°) from model simulations, for the cycle immediately following a sudden change in the meridional flow speed from 18 m s−1 to the value shown on the horizontal axis. The red curve has had 9 G added so it can be compared to the blue curve on the same scale. The much lower actual polar fields in the red curve are probably caused by the longer transport time from the source in active latitudes to the poles, since the meridional flow peaks at a much higher latitude in this case. Image reproduced with permission from Dikpati (2011), copyright by AAS.
To affect the polar fields significantly, the meridional flows changes must occur at or equator-ward of active latitudes, as Dikpati (2011) emphasized. The meridional flow speed measurements of Ulrich (2010), Basu and Antia (2010) and Hathaway and Rightmire (2011) do not show evidence of significantly faster flows at active latitudes during cycle 23 than during previous cycles. Moreover, Basu and Antia (2010) concluded that the flow speed variation reported by Hathaway and Rightmire (2010) was associated with a flow pattern that migrated equatorward with the magnetic activity belts. When this pattern was removed from their data, the speed variations vanished. This evidence argues against the flow-related explanations offered by Schrijver and Liu (2008), Wang et al. (2009) and Jiang et al. (2013). The weak polar fields may instead have something to do with a change in the flux emergence patterns, in particular the patterns of bipole tilt angles.
Direct attempts to find changes in average bipole tilt angles have not produced an explanation for the weak polar fields. Schrijver and Liu (2008) selected bipolar active regions observed between 1997 and 2008 by MDI for at least 7 days on the solar disk, and that were at least 30° away from any other region throughout this time. They arrived at a set of 136 regions that met these criteria. They calculated the centers of gravity of the positive and negative fluxes of each region and thereby estimated the Joy’s law tilt angles of the regions, taking geometrical and projection effects into account. They found no systematic change in the tilt angle over a period of up to 8 days on the disk. They did not report a change of mean tilt angle over the cycle. Stenflo and Kosovichev (2012) have analyzed the Joy’s law tilt angle of selected magnetic bipoles over time and found no statistical change in average Joy’s law tilts, and Li and Ulrich (2012) found from a long-term study that tilt angles of spots appear largely invariant with respect to time at a given latitude, but they decrease slowly during each cycle following the butterfly diagram (see McClintock and Norton, 2013, on the difficulty and complexity of sunspot tilt measurements).
Recall that in the flux transport simulations of Jiang et al. (2013), the weak cycle 23 polar fields could also be reproduced by a 28% decrease in the average tilt angle of sunspots, but this would also lead to a 1.5-year delay of the cycle 23 polar field reversal that was not observed. As we will see in Section 4.4, Muñoz-Jaramillo et al. (2013) also stressed the importance of accounting for varying tilt angles in such calculations. Petrie (2012) found that the latitude centroids of the positive and negative active region fields converged in each hemisphere around 2003, implying a much-diminished active-region poloidal field around this time — see Figure 18. In this calculation, the active regions’ contributions to the polar field are found to have a good proxy in the product of the latitude displacement of the positive and negative active region flux centroids and the total active region flux. This quantity was found to track the high-latitude poleward flux surges, which in turn tracked the polar field changes. Thus, the convergence of the positive and negative active region flux centroids in each hemisphere around 2003 could be linked to the lack of major polar field change between this time and the beginning of cycle 24. At the same time as the positive and negative active region flux centroids began to converge in each hemisphere, the high-latitude poleward surges of field were observed to lose their polarity bias in each hemisphere and the polar fields stopped strengthening, as seen in Figure 19. These two related patterns are consistent with the Babcock-Leighton model. Recently, Jiang et al. (2015) found a similar result from surface flux-transport simulations. These results suggest that changes in the meridional flow speed or shape, though potentially influential, may not be necessary to explain the weakness of the polar fields during cycle 23, and that a change in the latitudinal distribution of the active region flux may have been responsible.
Another notable development during cycle 23 was the increased asymmetry between the north and south hemispheres. While time-dependent asymmetry between the two hemispheres is generally not uncommon, the asymmetry that developed during cycle 23 was stronger than previously found since routine magnetogram observations began in the 1960s and 1970s. Figure 17 shows that, whereas the two hemispheres had approximately equal levels of activity throughout cycles 21 and 22, during the decline of cycle 23 the southern hemisphere became much more active than the northern hemisphere, and the north became more active than the south when cycle 24 began, since when the south has again become more active than the north. The physical relationship between the two hemispheres remains mysterious, but idealized models for the solar dynamo can be used to explore this question.
Global photospheric field observations exhibit both antisymmetric modes like the axial dipole and octupole and, to a lesser extent, symmetric modes like the equatorial dipole and the axial quadrupole. Focusing on the axisymmetric multipole components only, DeRosa et al. (2012) showed that the antisymmetric modes tend to be in phase with each other, following the polar fields, and the symmetric modes also tend to be in phase with each other, following the sunspot cycle. The patterns are shown in Figure 31, and they suggest that modes with the same symmetry properties tend to be excited together. The symmetric flow profiles and anti-symmetric α-effect usually imposed on Babcock-Leighton dynamo models produce a bias in the models towards north-south antisymmetric field configurations through the choice of symmetric bipole emergence distributions and meridional flow profiles. The induction equation in the standard Babcock-Leighton dynamo model is linear so that, even if symmetric and antisymmetric modes are both present in the model, they remain uncoupled. DeRosa et al. (2012) illustrated this by running an axisymmetric dynamo model, initialized with an axial dipole field, and analyzing the results in terms of their harmonic order l. As expected, the odd-l modes dominated the even-l modes, which were not excited. But when a small asymmetry was introduced into either the Babcock-Leighton source term, representing the latitude distribution of active region emergence, or the meridional flow profile, then the model, initialized with an axial dipole, quickly produced symmetric modes comparable in size (35%) to the antisymmetric modes. The results of this latter model are shown in Figure 32. These results indicate that even a weak asymmetry in the Sun’s flux emergence or meridional flow could produced the observed magnetic asymmetries seen in, e.g., Figure 17. It is also striking that the asymmetric fields in Figure 32 repeat their pattern from cycle to cycle, whereas the real solar fields show great variety in their behavior over the few cycles shown in Figure 17. But this idealized model helps to clarify how north-south asymmetry can appear and persist in the solar field. Flux transport models cannot reproduce the complex behavior of the photospheric field in its entirety, but they provide valuable insight into the essential processes that govern these fields.
Amplitudes of the first 3 odd (l = {1, 3, 5}; dark red, red, light red lines, respectively) and even (l = {2, 4, 6}; dark blue, blue, light blue, respectively) axisymmetric multipoles, as calculated from WSO synoptic maps. The smoothed sunspot number is plotted below for comparison. The difference between the responses of the odd and even axisymmetric multipoles to the activity cycle is clear. Image reproduced with permission from DeRosa et al. (2012), copyright by AAS.
The time evolution of the coefficients of the lowest-order harmonic functions of the surface magnetic field, grouped by north-south anti-symmetric (“primary family”) and symmetric (“secondary family”) families of solutions, from a Babcock-Leighton dynamo model. In panel (a) are shown the evolution of the first several odd-order multipole amplitudes with l = 1, 3, 5, and 7 in black, blue, green, and red, respectively. In panel (b) are shown the evolution of the even-order multipole amplitudes with l = 2, 4, 6, and 8, respectively, in black, blue, green, and red. Panels (c) and (d) show zoomed-in sections of panels (a) and (b). Image reproduced with permission from DeRosa et al. (2012), copyright by AAS.
PFSS models representing the beginnings of years 1996 (top left), 2000 (top right) and 2009 (bottom). The photospheric radial field strength is represented by the greyscale, saturated at 100 G with white/black indicating positive/negative polarity. Green/red field lines represent open fields of positive/negative polarity and blue lines represent closed fields. Since the solar field cannot have a monopole component, the positive and negative open magnetic flux must balance at all times. In the example from 2000, representing solar maximum, the dipole axis is close to the equatorial plane, and almost all of the positive open flux (green lines) is hidden at the far side of the Sun, and almost all of the visible open lines have negative polarity (red). In 1996 and 2009 the dipole axis was closely aligned with the rotation axis, which is typical of solar minimum (see Figure 35).
4 Polar Fields and the Solar Atmosphere
4.1 The effects of the polar fields on global coronal magnetic structure
The Sun’s polar fields have long been known to have a profound influence on the global structure of the solar atmosphere. There is a close relationship between the polar fields and the axial dipole component such that the polar fields dominate the global coronal structure over much of the cycle. Hoeksema (1984) used WSO synoptic magnetograms and PFSS models to demonstrate that, during most of the solar cycle, the quadrupole and occasionally octupole moments of the field are important for the large-scale structure of the coronal field, including the structure in the ecliptic plane, producing tilts and warps in the streamer belt and equatorial current sheet and creating low-latitude coronal holes. He concluded from a study of the total strengths of the various multipolar orders that the complex field evolution near maximum does not correspond to a dipole rotating from north to south as the polar fields reverse polarity, as had been previously suggested. The rotating dipole interpretation does not fit well with the picture of a rather complex and inefficient process presented in previous sections, of the polar fields being built gradually from the accumulation of small parcels of decayed active region flux with a polarity bias, before being nibbled away again by further parcels of decayed active region flux with opposite polarity bias.
Figure 33 shows three “hairy-ball” plots of the coronal magnetic field from the years 1996, 2000 and 2009. The plots therefore represent the cycle 22 minimum, and cycle 23 maximum and minimum, respectively. The differences between the minimum plots and the maximum plot clearly emphasize the much simpler, nearly axisymmetric axial dipole structure associated with dominant polar fields during solar minimum, and the complex three-dimensional structure that is produced by multiple active regions in the absence of strong polar fields.
Using Kitt Peak and WSO synoptic magnetograms, Petrie (2013) investigated the evolution of the observed photospheric magnetic field and the modeled global coronal magnetic field during the past 3 1/2 solar activity cycles observed since the mid-1970s. Polar field changes were found to be well correlated with the presence of active region fields over most of the period studied, except between 2003 and 2006 when the active fields did not produce significant polar field changes. It was also found that the combined strength of the non-axisymmetric multipoles correlates very well with the sunspot number (cc = 0.97) and the axisymmetric fields correlate almost equally well with the polar field strength, the combined strengths of the north and south polar fields (cc = 0.97 also). However, if the sets of axisymmetric and non-axisymmetric multipoles are subdivided further by primary order l, then a slightly more complex picture emerges. Figure 34 shows that the high-order odd- or even-l non-axisymmetric multipoles are generally correlated with the sunspot number for orders higher than hexadecapole (l = 4) and that the low-order even-l multipoles also correlate well with the sunspot number. But the low-order odd multipoles, the dipole (l = 1) and the octupole (l = 3) follow the polar fields. The low even-order axisymmetric multipoles follow neither the activity cycle nor the polar fields. They do not show cyclical behavior but they are significantly weaker than the other low-order multipoles, and can be ignored for our purposes. The high even axisymmetric orders show some correlation with the sunspot cycle, possibly perturbed by the Joy’s law tilt of active regions, but these components are dominated by their non-axisymmetric counterparts. The excellent overall correlation between the total axisymmetric field strength and the polar field is due to the axial dipole and octupole fields. The axisymmetric dipole is associated with the trans-equatorial streamer and loop structures and the axisymmetric octupole with large arcade structures confined to each hemisphere. Because of the large strength and spatial scale of these components, they have a leading influence on the global structure of the corona over the cycle, except when the polar fields reverse.
For Wilcox data, the first several even- and odd-order multipole components are plotted separately, including all, axisymmetric or non-axisymmetric fields as indicated. For odd orders, red, amber, green, cyan and blue represent fields with l = 1, 3, 5, 7, 9, respectively. For even orders, red, amber, green and cyan represent fields with l = 2, 4, 6, 8, respectively. The same data are presented in the two columns of plots, on a linear scale in the left column and a logarithmic scale in the right column. Image adapted from Petrie (2013).
During the long cycle 23/24 minimum the axisymmetric dipole and octupole components were about 40% weaker than during the previous cycle minimum, whereas the non-axisymmetric multipoles did not become so comparatively weak until 2009. This also resulted in a more complex coronal structure with more low-latitude coronal holes during the cycle 23/24 minimum than during the previous minimum (de Toma, 2011). We will discuss this topic further in Section 4.2.
The relationship between the axial and equatorial dipole strengths and the global structure of the corona is illustrated in Figure 35. These results are based on PFSS models extrapolated from MWO and WSO synoptic magnetograms. In this figure the dipole tilt angle is defined as the ratio of the equatorial to the axial dipole strength, which is small when the axial dipole is dominant, and large when the equatorial dipole is dominant. The dipole tilt is highly correlated with the heliospheric current sheet excursion, defined as the maximum displacement of the potential-field source-surface neutral line from the equator. Both quantities follow the sunspot cycle, but during the cycle 23 minimum they did not decrease to values characteristic of previous minima until the sunspot number and the non-axisymmetric multipoles became unusually low in 2009.
Variation of the maximum latitudinal excursion of the heliospheric current sheet during 1967–2009, based on PFSS model source-surface neutral lines. The highest latitude reached by the source-surface neutral line is averaged between the northern and southern hemispheres. Also plotted are the dipole tilt angle and the sunspot number. Results for MWO and WSO have been averaged, and 3-month running means have been taken. Image reproduced with permission from Wang et al. (2009), copyright by AAS.
4.2 Coronal holes
That low-density regions are present in the solar atmosphere, and are particularly prominent at the Sun’s poles over most of the cycle, has been known for many decades (Waldmeier, 1957), and it has become increasingly clear that these “coronal holes” are associated with open magnetic flux (see the review by Harvey, 2013), represented by the green and red lines in Figure 33. Polar coronal holes have been studied using limb observations of the Fe xiv 5303 A coronal green line (Waldmeier, 1957), K-coronagraph observations (Bravo and Stewart, 1994), X-ray and EUV observations (Broussard et al., 1978), He i 10830 Å spectroheliograms (Harvey et al., 1975) and PFSS (Schatten et al., 1969; Altschuler and Newkirk, 1969), magnetohydrodynamic (e.g., Linker et al., 2011) and magnetofrictional (Mackay and Yeates, 2012) models.
Coronal holes appear in several forms and for a variety of different reasons. Using NSO Kitt Peak He i 10830 A spectroheliograms and longitudinal photospheric magnetograms, Harvey and Recely (2002) identified three classes of coronal hole: polar coronal holes confined to high latitudes (> 60° and < −60°), isolated coronal holes at active latitudes associated with the remnants of decaying active regions, and transient coronal holes that briefly form after coronal mass ejections. The accumulation of nearly unipolar flux from the decay and poleward transport of tilted active regions is clearly the cause of the polar coronal holes. The competition between meridional flow and diffusion at high latitudes strongly influences the extent of the polar coronal holes. In the absence of meridional flow the polar field would have a dipolar distribution, and the polar coronal holes would extend to around ±40° instead of around ±60° for the much more concentrated cosn θ with n = 8–11 as observed (Sheeley Jr et al., 1989).
Harvey and Sheeley Jr (1979) found that, early in the cycle, the decaying leading polarities of active regions can create locally unbalanced flux patterns, which tend to form coronal holes ahead of active regions, while the following flux travels poleward to cancel with the polar field. During the declining phase it is the following flux that tends to open. Petrie and Haislmaier (2013) showed that coronal holes generally open without changing the global coronal topology, at least in the presence of significant polar fields: in the 14 examples that they studied, the hole always formed with polarity matching the polar hole on the side of the streamer belt where the region decayed, demonstrating the dominance of the polar fields over the coronal structure.
Over most of the solar cycle the largest coronal holes are located at the poles, as in the top left and bottom plots in Figure 33. While not as active as and much weaker than the active region fields, the polar fields have great influence in the heliosphere via the polar coronal holes. The large spatial scale and unipolarity of the polar fields prevent these fields from connecting back to the surface before they reach great heights, where the field is too weak to close against the pressure of the expanding solar wind. Because the solar wind is accelerated to super-Alfvénic speeds low in the atmosphere, and the coronal plasma is highly conducting, at a height of around a solar radius the field becomes too weak to pull the magnetic field lines closed, and the solar wind drags the field outward and opens it to the heliosphere (Parker, 1958). During times of maximum activity, and particularly when the polar fields are reversing, the coronal holes are approximately equally spread over all latitudes, with no dominant polar holes, as in the top right plot in Figure 33.
During the cycle 22/23 minimum in 1996 the two polar coronal holes were large and dominant. Using SoHO/EIT Fe xii 195 Å EUV synoptic maps, de Toma (2011) estimated that the polar holes covered about 7.9–8.1% of the solar surface in the north and about 6.9–7.1% in the south, in good agreement with estimates by Harvey and Recely (2002) from He i 10830 Å data from Kitt Peak (see also Kirk et al., 2009). Isolated low-latitude coronal holes were mostly absent, covering less than 0.5% of the solar surface except during mid-1996 when a large extension from the northern polar hole developed, shaped like an elephant’s trunk, and eventually detached itself from the polar hole (Zhao et al., 1999). Even over this period the low-latitude coronal area never exceeded 2% of the solar surface. The cycle 23/24 minimum was quite different (Wang et al., 2009), characterized by smaller polar coronal holes and more low-latitude structure. From STEREO/SECCHI/EUVI Fe xii 195 Å EUV synoptic maps, de Toma (2011) estimated that the maximum areas of the polar coronal holes between 2006 and 2009 were 4.4–4.7% of the solar surface in the north and 5.3–6.0% in the south. Compared to the cycle 22/23 minimum this represents a 40–45% decrease in the north and a 15–25% decrease in the south. Meanwhile, the low-latitude holes covered 2–3% of the Sun’s surface during 2007 and 2008 and dropped to less than 1.5% in 2009. Example coronal hole distributions, derived from SOHO/Extreme-ultraviolet Imaging Telescope (EIT) EUV images and representing the minima of cycles 22 and 23 are shown in Figure 36. The much smaller polar coronal holes and much more numerous low-latitude coronal holes in the plots from cycle 23 are clearly visible.
Top: EUV synoptic maps in the Fe xii 19.5 nm line for CR 1907 (March–April 1996) and CR 1911 (July 1996) during the minimum between cycles 22 and 23 (upper plots) and corresponding coronal-hole maps (lower plots). The mean sunspot number for the two Carrington rotations was 9.5 and 7.6, respectively. The maps are in sin(latitude) and the dashed lines in the coronal hole maps correspond to 60° and 50° latitude. Bottom: Same as top but for CR 2078 (December 2008–January 2009) and CR 2085 (June–July 2009) during the minimum between cycles 23 and 24. The mean sunspot number for the two Carrington rotations was 1.5 and 3.6, respectively. Image reproduced with permission from de Toma (2011), copyright by Springer.
Figure 37 shows estimates of coronal hole areas over the past four cycles, based on PFSS models for the coronal magnetic field extrapolated from MWO and WSO photospheric synoptic maps. The low- and high-latitude coronal hole areas are plotted separately. Here the differences between the cycle 22 and 23 minima are put in context. The cycle 23 minimum polar (high-latitude) coronal holes covered significantly less surface area than the polar holes during the previous three minima, according to these models. The low-latitude coronal hole coverage was higher during the cycle 23 minimum than during the cycle 21 and 22 minima, but it does not appear to have been significantly higher than during the cycle 20 minimum. This latter result may be due to the poorer quality of the earlier magnetograms. The low- and high-latitude open magnetic fluxes are also shown in Figure 37, again estimated using the PFSS models. The high-latitude open flux follows the pattern of the polar fields, being about 50% as large during the cycle 23 minimum as during the previous three minima. The low-latitude open flux follows the sunspot cycle, though its slow descent to unusually low values during the cycle 23 minimum is as much due to the weak polar fields as to the slow descent to unusually low sunspot numbers during this period.
(a) Percentage of the solar surface occupied by high-latitude (poleward of latitudes ±45°) and low-latitude (equatorward of latitudes ±45°) open flux during 1967–2009. (b) Open flux originating from high latitudes (poleward of latitudes ±45°) and low latitudes (equatorward of latitudes ±45°) during 1967–2009, expressed as field strengths (nT) at 1 AU. A PFSS extrapolation was applied to an average of the MWO and WSO photospheric field measurements, and 3-month running means are plotted. Image reproduced with permission from Wang et al. (2009), copyright by AAS.
The polar coronal holes also provide us with another opportunity to study the polar field strengths. While magnetogram measurements of the polar fields suffer from large projection effects, microwave imaging observations at frequencies above 15 GHz provide an alternative means of studying polar regions because coronal holes appear bright at these frequencies, including polar holes. The Nobeyama radioheliograph has been producing daily full-disk brightness temperature maps at 17 GHz since 1992, covering cycles 22–24, with spatial resolution around 10″. Gopalswamy et al. (2012) used butterfly diagrams of microwave brightness temperature and magnetic field strength to show that the polar coronal hole field strength and polar microwave brightness temperature are well correlated, sharing the same north-south hemispheric asymmetry and the same diminution during the cycle 23/24 minimum relative to the cycle 22/23 minimum. This extended an earlier result, where Gopalswamy et al. (2000) found good correlation between the peak microwave brightness temperature and peak field strength of 71 equatorial coronal holes. Figure 38 shows low-latitude brightness features corresponding to active regions, and polar enhancements resembling polar field strengths. The microwave measurements appear more sensitive to the polar coronal holes than to the active regions. The fact that these measurements show good qualitative agreement with the polar field measurements helps to validate these challenging measurements.
Top: the magnetic butterfly diagram from 1992 to the present constructed from NSO Kitt Peak Vacuum Telescope and SOLIS/VSM line-of-sight magnetograms with SOHO/MDI data filling several data gaps. Blue and yellow shading denote positive and negative polarities, respectively. The magnetic field strength ranges from −10 G to +10 G. An annual periodicity is visible in the polar regions, due to solar B0-angle variation. Bottom: a microwave butterfly diagram constructed from the Nobeyama radioheliograph images at 17 GHz. A 13-rotation smoothing was applied along the time axis to eliminate the periodic variation due to solar B0-angle variation in the radio data. The contour levels are at 10 000, 10 300, 10 609, 10 927, 11 255, 11,592, and 11940 K. The vertical dashed lines mark the ends of cycles 22 and 23 around 1996 March and 2008 July, respectively, determined from the low-latitude activity in microwaves. Image reproduced with permission from Gopalswamy et al. (2012), copyright by AAS.
4.3 Relationship between coronal hole structure and solar wind speed
It was discovered during the 1970s from Skylab data that high-speed solar wind streams originate from large coronal holes (Krieger et al., 1973; Nolte et al., 1976; Zirker, 1977). Wang and Sheeley Jr (1990) investigated the empirical relationship between solar wind speed patterns and the magnetic field structure at the solar wind source location. Using solar wind data from a series of spacecraft, they showed that the bulk solar wind speeds tend to be significantly lower during solar maxima than during solar minima. Polar passes of the Ulysses spacecraft have since shown the fundamental differences between the solar wind distributions during solar minimum and maximum conditions.
Wang and Sheeley Jr (1990) showed that the unsigned interplanetary field and the solar wind speed are not highly correlated but that the fraction of solar surface area covered by open magnetic flux, estimated using PFSS models, is better correlated with the wind speed. As the low-latitude coronal hole areas become small and the polar holes become dominant during solar minimum, the solar wind speeds become high. Crucially, a strong correlation was found between the average unsigned photospheric field strength in open-field regions and the solar wind speed at 1 AU.
Nolte et al. (1976) had demonstrated that the areas of large equatorial coronal holes are correlated with the maximum speeds of the associated solar wind streams, a pattern that Levine et al. (1977) interpreted in terms of expanding flux tubes: high-speed winds originate from the centers of large holes because flux tube expansion is minimal there. This suggested that the solar wind flow could be treated in a manner similar to de Laval nozzle theory, in which conservation of mass can be used to relate flux tube cross-sectional expansion to changes in speed. Wang and Sheeley Jr (1990) used this idea to show that the long-term patterns of solar wind speeds could be successfully simulated using magnetogram data and PFSS models. The areal expansion factor of the Earth-directed flux tube between the photosphere and the source surface is fs = (R0/Rs)2[Bp(R0)/Bp(Rs)], where Bp(Rs) is the field strength at the sub-Earth point P on the source surface and Bp(R0) is the field strength at the photospheric footpoint of this flux tube passing through P. Wang and Sheeley Jr (1990) converted flux tube expansion factors into solar wind speeds using a look-up table, their Table 1. The modeled solar wind speeds successfully matched the measurements on a monthly-averaged basis, as Figure 39 shows.
Three-month running averages of the simulated wind speed at 1 AU during 1967–1988 (thick line), based on PFSS models. For comparison, the observed values are indicated by the dotted line. The averages are plotted at monthly intervals. Image reproduced with permission from Wang and Sheeley Jr (1990), copyright by AAS.
The results suggested that the high-speed streams are indeed associated with low areal expansion rates in the corona. The high-speed streams originated mainly from the boundaries of the polar coronal holes, often from extensions that form when decayed active region flux of the same sign as the local polar field is transported poleward, particularly during the declining phase of the cycle. The fast streams can also come from small, detached coronal holes. If a small hole is close to a large hole of like polarity then the small hole can be prevented from expanding by the volume-filling nature of the large hole, in which case the small hole can produce a high-speed stream. In contrast, solar maximum brings a lull in the solar wind speed. During solar maximum the wind comes from small, low-latitude coronal holes. Because the total photospheric area of open flux is small, these small coronal holes generally expand rapidly between the photosphere and the source surface, resulting in low solar wind speeds.
Arge and Pizzo (2000) extended this model by deriving a continuous empirical function relating two parameters, the magnetic expansion factor, fs, and the angular separation between the open field footpoint and the boundary of the nearest coronal hole, to the solar wind speed at the source surface. They also added a simple kinetic model for solar wind propagation between the source surface and Earth, and improved the application of boundary data to the model. This model, now called the Wang-Sheeley-Arge model, is still used in routine solar wind prediction.
The contrast between solar wind structure during solar minimum and maximum has been emphasized by in situ measurements from outside the confines of the ecliptic plane by the Ulysses spacecraft. Ulysses observations of the solar wind from both polar coronal holes have shown clear long-term variations in the solar wind parameters (McComas et al., 2008) and in the interplanetary magnetic field (Smith and Balogh, 2008). Ulysses completed orbits over both poles roughly every six years between 1992 and 2008, nearly three full orbits. Figure 40 summarizes the solar wind structure during the three orbits. The first orbit revealed a simple bimodal structure in the solar wind around the solar minimum of cycle 22, with two distinct kinds of wind: (1) a fast, tenuous and relatively homogeneous wind at high latitudes originating from the polar coronal holes, and (2) slower, denser and highly variable wind at lower latitudes. Around solar minimum the band of solar wind variability was narrow, confined to a few tens of degrees around the equator, consistent with a small dipole tilt angle.
(a–c) Polar plots of the solar wind speed, colored by IMF polarity for Ulysses’ three polar orbits colored to indicate measured magnetic polarity. In each, the earliest times are on the left (nine o’clock position) and progress around counterclockwise. (d) Contemporaneous values for the smoothed sunspot number (black) and heliospheric current sheet tilt (red), lined up to match Figures 1a–1c. In Figures 1a–1c, the solar wind speed is plotted over characteristic solar images for solar minimum for cycle 22 (8/17/96), solar maximum for cycle 23 (12/07/00), and solar minimum for cycle 23 (03/28/06). From the center out, we blend images from the Solar and Heliospheric Observatory (SOHO) Extreme ultraviolet Imaging Telescope (Fe xii at 1950 nm), the Mauna Loa K coronagraph (700–950 nm), and the SOHO C2 white-light coronagraph. Image reproduced with permission from McComas et al. (2008), copyright by AGU.
The second orbit caught the rise and maximum of cycle 23 and showed a complex solar wind structure at all latitudes, including streamers, coronal mass ejections, and small coronal holes. Covering the decline and minimum of cycle 23, the end of Ulysses’ second orbit and the third orbit found the heliosphere in a simpler state but with significantly more complex structure than observed during the first orbit. There was a more complicated current sheet structure with both greater tilt with respect to the equator and a less planar belt of low-speed flow. This result is consistent with the heliospheric current sheet tilt patterns in Figure 35, where the cycle 22 minimum current sheet structure was flatter than the cycle 23 minimum structure. The tilt of the heliospheric current sheet was significantly higher during the cycle 23 minimum than the cycle 22 minimum, at east until the sunspot number became unusually low in 2009 after the end of the Ulysses mission. The band of solar wind variability detected by Ulysses also extended to higher latitudes during cycle 23 minimum than during cycle 22 minimum. The simple bimodal solar wind structure of the left and right plots in Figure 40 corresponds to the simple dipolar structure in the top left and bottom plots in Figure 33, and the more complex middle plot of Figure 40 to the top right plot of Figure 33.
Smith and Balogh (2008) reported that the radial magnetic field strength at high latitudes was about a third weaker during the third Ulysses orbit compared to the first orbit. The open magnetic flux, the strength of the radial field component Br multiplied by the square of the radial distance r of the spacecraft from the Sun, is independent of latitude at both solar minimum and maximum (Balogh et al., 1995; Smith et al., 2001; Smith and Balogh, 2008), so that in situ measurements from different phases of the Ulysses mission can be compared directly. The measurements for the polar scans are summarized in Figure 41, and they show that the average strength of r2Br has decreased from 3.6 nT (AU)2 from 1993.5–1995.0 to 2.3 nT (AU)2 from 2006.0–2007.4, 0.64% of the value from the first scan. The two Ulysses polar scans did not coincide exactly with the cycle 22 and 23 solar minima. However, the measurements of Br from the ecliptic plane by the ACE satellite are highly correlated with the Ulysses measurements at all latitudes. Both sets of measurements are compared in Figure 41 for the two minima. The averages of Br around the two solar minima are 3.3 and 2.4 nT.
Ulysses data for the radial field strength (scaled by spherical area) r2BR, and National Space Science Data Center’s OMNI data for the radial field strength BR are compared. The comparison is at high latitudes and in the ecliptic simultaneously and near two solar minima. The two plots contain 27-day averages of r2BR at Ulysses (red) and BR in the ecliptic plane (black) for the two intervals when Ulysses was in the fast solar wind at high latitudes. Top: Data obtained in 2006.0–2007.4 during the cycle 23/24 solar minimum while Ulysses traveled from −40°, under the south pole and back to −50° (latitude appears along the top scale). The means and standard deviations show that there was no statistically significant difference in the high and low latitude measurements and no evidence of a latitude gradient. Bottom: Same format but r2BR is plotted in blue and the interval covered is 1993.5 to 1995 during the cycle 22/23 solar minimum. Again, there is no evidence of a latitude gradient in r2BR, but the means show a decrease in cycle 23/24 (top) compared to cycle 22/23 (bottom). Image reproduced with permission from Smith and Balogh (2008), copyright by AGU.
Estimates by Wang et al. (2009) for the total open flux and the interplanetary mean field (IMF) strength, based on PFSS models extrapolated from MWO and WSO synoptic magnetograms, are plotted in Figure 42. This plot shows a decline in the IMF during the cycle 23 minimum to values significantly lower than during past minima, which mirrors the decline of the photospheric polar field in Figure 19 and agrees with the results of Smith and Balogh (2008).
Evolution of the total photospheric flux, total open flux, and radial IMF strength at Earth (National Space Science Data Center OMNI 2 data) during 1967–2009. Three-Carrington-month running means are plotted. The total photospheric flux is expressed as an average of ∣Br∣ over the solar surface. The total open flux is obtained by integrating ∣Br∣ over the source surface and dividing by \(4\pi r_{E}^{2}\) to convert it into an equivalent field strength at rE = 1 AU. In both cases, the arithmetic mean of MWO and WSO photospheric field measurements has been taken, after correcting for line profile saturation by multiplying by (4.5–2.5 sin 2L), where L is the latitude. Image reproduced with permission from Wang et al. (2009), copyright by AAS.
The solar wind parameters also showed different behavior during the third orbit compared to the first (McComas et al., 2008). The fast solar wind was about 3% slower, about 17% less dense, about 14% cooler and had about 20% less mass flux. The dynamical and thermal pressures were also significantly smaller (by 22% and 25%, respectively), prompting the authors to speculate that the heliosphere may have shrunk between the two orbits.
Measurements of the solar wind parameters in the ecliptic plane from the ACE spacecraft over the same period quantitatively matched the Ulysses observations and showed identical trends, indicating significant long-term variation at all latitudes. The implied reduction of energy and mass flux below the solar wind sonic point is consistent with a reduction of the open solar magnetic flux over this time interval.
Sections 4–4.3 have shown that the global structure of the solar atmosphere has changed between the cycle 22 and 23 minima, corresponding to decreases in the polar field strength and changes in activity patterns discussed in Sections 2–3. We will next discuss the properties of smaller magnetic features whose behavior is intimately related to the polar fields.
4.4 Polar faculae
The previous subsections discussed the global influence of the polar fields over the solar corona and heliosphere. These observations and models emphasize the importance of the polar fields and how urgently we need to understand them. Alternative ways to study the polar fields are based on smaller-scale solar structures whose connections to the polar fields help us to understand these fields’ behavior and influence. We will discuss such phenomena in the next few subsections.
In Section 4.2, we discussed the correlation between microwave brightness temperature in the polar coronal holes and the polar magnetic field strength. This correlation allows us to infer connections between the surface polar flux and conditions in the atmosphere, and it also allows us to validate or supplement a difficult magnetic field observation using an independent data source. Other sources of information on the polar fields come from smaller-scale structures in the atmosphere that trace the progress of the polar fields, in particular polar faculae, seen in white-light photospheric images, and chromospheric filaments seen in, e.g., Hα or He i 10830 Å images. Observations of faculae and filaments also extend significantly further back in time than systematic magnetograph measurements. We will discuss faculae in this section and filaments in the following section.
We have continuous high-quality full-disk observations of the photospheric line-of-sight magnetic field from the mid-1970s to the present. These 40 years or so represent only a few solar cycles, not enough data points to study the polar fields’ role in the solar cycle for a statistical sample of cycles. Polar faculae data are a possible substitute for times when real polar field measurements are unavailable. Faculae are bright features on the surface of the Sun (Hale, 1922), associated with intergranular accumulations of magnetic flux. The association of polar facular counts with polar field concentrations is clear from Figure 2. It is believed that the strong magnetic field causes depressions to form in the visible surface of the Sun so that relatively hot granular plasmas become visible as bright features at large projection angles. Faculae can therefore be used to estimate surface magnetic flux at the poles. For example, polar magnetic reversal times were estimated by Makarov and Makarova (1996) from observations of faculae back to 1870 (cycle 11). A continuous data set from 1906 to the present is available from MWO. Sheeley Jr (1964) found a clear relationship between the polar faculae numbers and the sunspot numbers such that the polar faculae lag the sunspot number with a 90° phase shift, consistent with the models of Babcock (1961) and Leighton (1969) where the active regions act as the source of the polar field. This pattern is shown in Figure 43. Strong correlations between MWO polar facular and WSO polar field strength measurements were found by Sheeley Jr (1991, 2008). Muñoz-Jaramillo et al. (2012) validated these data using automatically counted facular statistics from MDI intensity images, and calibrated them using polar field measurements from WSO and MDI. The calibrated data are plotted in Figure 44. The MWO facular data can now provide proxy polar field data for over a century of time.
The numbers of north (top) and south (bottom) polar faculae versus time, plotted with positive and negative polarity to represent the polarity of the corresponding polar magnetic field. The signed numbers of polar faculae were recorded at their times of greatest visibility (fall or spring). The annual average sunspot number for the whole disk, multiplied by 0.3 and assigned the polarity of the trailing-polarity sunspots in each hemisphere are over-plotted in dashed lines. The counts of polar faculae for later campaigns of 1974–1975 and 1985–2007 have been multiplied by a calibration factor 1.38. Successive temporal strings of data are indicated by diamonds, asterisks, triangles, crosses, and squares. For some years repeated measurements were made, represented by more than one point for a given year. The polar facular count lags the sunspot number with a 90° phase shift in both hemispheres, consistent with Babcock-Leighton models where the active regions act as the source of the polar field. Image reproduced with permission from Sheeley Jr (2008), copyright by AAS.
Calibrated MWO facular measurements. Each campaign is marked with a different color and marker: green asterisk (1st campaign), red circle (2nd campaign), blue triangle (3rd campaign), and orange star (4th campaign). Measurements for the north (south) pole are shown using a dark dashed (light solid) line. All campaigns are calibrated to the 3rd campaign. Image reproduced with permission from Muñoz-Jaramillo et al. (2012), copyright by AAS.
Muñoz-Jaramillo et al. (2013) have built on the result of Sheeley Jr (1964) by using these facular-based polar-field proxy data to study the cyclical interrelationship between the polar fields and the active fields, represented by the sunspot area, between 1906 and the present time. They used the Joy’s law tilt statistics derived by Dasi-Espuig et al. (2010, see the footnote in Section 3.6). They found that the sunspot area is uncorrelated with the average estimated polar field during the cycle minimum, unless the sunspot area is multiplied by area-weighted average Joy’s law bipole tilt (see Section 2.7). This result, shown in Figure 45, suggests that the average bipole tilt angle varies significantly over time, and this temporal variation plays an important role in determining the polar field strengths (though this experiment should perhaps be repeated using the corrected MWO Joy’s law tilt data of Dasi-Espuig et al., 2013). Therefore, not only sunspot areas but also tilt angles are necessary for successful cycle prediction, consistent with the Babcock-Leighton mechanism for polar field generation (Petrie, 2012, drew a similar conclusion in terms of products of active region flux and latitude displacements of positive and negative active region flux centroids — see Section 2.7.). Muñoz-Jaramillo et al. (2013) also found a reasonable (correlation coefficient = 0.6) correlation between the estimated polar field amplitude and the amplitude of the following cycle, supporting the Babcock-Leighton model for the generation of new cycles from old polar flux. However, this solar cycle “memory” did not extend beyond a single cycle.
Scatter plots of proxy polar magnetic flux (based on polar facular counts) against maximum (left plots) and average (right plots) sunspot area (top plots) and sunspot area multiplied by average Joy’s law tilt (bottom plots). No correlation is found between the maximum (a), or total (b), sunspot area of a cycle and polar flux during the subsequent minimum. However, both maximum (c) and total (d) sunspot area become correlated with polar flux if multiplied by the area-weighted average tilt normalized by latitude of emergence (AWNL). Square (circular) markers represent data for the northern (southern) hemispheres. Markers are numbered using cycle number as reference. The dashed line corresponds to a linear fit using the least absolute residuals method. The text inside the figure panels indicates the Pearson’s correlation coefficients and their statistical significance. Image reproduced with permission from Muñoz-Jaramillo et al. (2013), copyright by AAS.
4.5 High-latitude flux transport and polar filaments
Solar filaments (called prominences when observed at the limb) are long-lived, relatively cool and dense structures suspended by the magnetic field at heights of order 50 Mm above the solar surface (e.g., Mackay et al., 2010). Observations of filaments at high latitudes are, along with polar faculae, the longest available data set providing information on solar magnetism at high latitudes. Filaments and filament channels delineate neutral lines, so the overall structure of the magnetic field can be reconstructed from such data (McIntosh, 1972; Durrant and Wilson, 2003).
Obridko and Shelting (2008) exploited the fact that filaments delineate neutral lines to infer estimates for the polar field strength from 1915. The global configuration of filaments provides information on the polar field evolution without telling us the polar field strength, or its variation from cycle to cycle. However, using Ha synoptic maps Obridko and Shelting (2008) represented only the sign of the magnetic field, deriving field maps with nominal field strength values ± 1 G where positive and negative fields were separated by boundaries indicated by the observed filaments. They then used a potential-field source-surface model to derive the polar field distribution. The resulting polar field strength estimates compared reasonably well to polar field measurements from NSO Kitt Peak, MWO and WSO. The Hα-based surface estimates featured much more abrupt polar field changes than observed by the magnetographs because the gradual evolution of weak magnetic flux is not accounted for, only the structure of the neutral lines as represented by the filaments. Filaments can disappear quickly compared to polar evolution timescales, producing abrupt changes in the Hα-based estimates. On the other hand, the polar field strengths of the potential-field source-surface models based on the Ha are remarkably well correlated at the source surface (outer boundary, at 2.5 solar radii) with the models based on the magnetograph data, as Figure 46 shows. This is because the low-order multipoles that dominate the models at large scales are relatively insensitive to the details of the photospheric or chromospheric fields but are more sensitive to their large-scale distribution. The success of the estimates indicates that the large-scale distribution of the polar fields is reasonably well captured by the filament structure. Obridko and Shelting (2008) also found, like Muñoz-Jaramillo et al. (2013), that the polar field strength at solar minimum and the amplitude of the succeeding cycle are highly correlated, supporting the Babcock-Leighton picture of the cycle.
Polar magnetic field estimates calculated from Hα data for the north pole covering the period 1915–1990 (thin curve) and compared to rescaled direct Stanford WSO observations for 1976–2006 (thick curve). Image reproduced with permission from Obridko and Shelting (2008), copyright by Springer.
McIntosh (2003) presented synoptic charts of the major large-scale magnetic features of the low solar atmosphere, showing the relationship between neutral lines, filaments and coronal holes. Filaments lie along the main neutral lines, and the filaments form a chain-like pattern at high latitudes in each hemisphere, called the polar crown. Gaps in the polar crown are often associated with coronal holes, either extensions of the polar coronal hole or separate high-latitude coronal holes. Filaments and coronal holes are always spatially separated because filaments lie along neutral lines whereas coronal holes are confined to unipolar regions. A secondary crown of filaments sometimes forms at lower latitudes, separating the leading-polartiy active region flux from the trailing-polarity flux, just as the primary polar crown separates the trailing-polarity flux from the polar flux.
McIntosh (2003) recorded the poleward drift of filaments by measuring in each synoptic chart the maximum latitude of the polar crown and plotting the maximum latitude against time. The results are shown in Figure 47. Both the primary and secondary polar crowns are observed to migrate poleward at approximately the same rate during the march to the poles (see also Hyder, 1965). The secondary crown of a given cycle branches off to form the primary crown following the polar field reversal. The disappearance of the primary crown occurs as part of the process of polar field reversal.
The maximum latitude of polar crown filaments plotted against time for solar cycles 22 and 23. Data from the northern and southern hemispheres are superposed. Organized poleward transport of two distinct polar crowns of filaments is evident in the plot. Image reproduced with permission from McIntosh (2003), copyright by ESA.
Gaizauskas et al. (1983) studied the formation of high-latitude filaments from the poleward transport of decayed active region flux of mixed polarity. They plotted the large-scale patterns in the spatio-temporal distribution of large active regions over 27 rotations (1977–1979) using NSO Kitt Peak synoptic magnetograms. The regions tended to be grouped in “complexes of activity”, groups of active regions close in space and time, continuously refreshed by new emerging regions for 3–6 rotations. The authors displayed the data in a useful stack plot format, focusing on the active latitudes 10°–40° in each hemisphere. Gaizauskas et al. (2001) took this approach a step further by plotting a pair of such stack plots, one focusing on the active latitudes 0°–26°, where a pair of adjacent activity complexes was evolving and decaying, and the other on the high latitudes 27°–90°, where the decayed flux was being transported. This double stack plot is shown in Figure 48. In this figure the relationship between the intense active region fields at low latitudes and the associated weak, poleward-transport decayed fields can be clearly seen. Using this figure, Gaizauskas et al. (2001) followed the spatio-temporal evolution of the activity complexes and identified the poleward-transported decayed magnetic flux from the complexes. Since synoptic maps are formed by remapping full-disk images to heliographic coordinates and averaging them together in the Carrington coordinate frame giving highest weighting to central-meridian data, these stack plots of central meridian slices of the maps reveal not only the temporal changes within these complexes but their slanting patterns reveal changes in their rotation rates as well. Comparison with stack plot summaries of other latitude ranges shows patterns of dispersal of weak fields from the activity complexes into quieter latitudes. According to the stack plots the activity complexes generally develop in about a month and, when emergence ceases, the remnant flux disperses within a rotation and principally in situ. The remnant flux rotates more slowly than the complex previously does, as Figure 48 clearly shows.
The left stack-plot shows low-latitude (from the equator to N26°) strips from NSO Kitt Peak synoptic maps of Carrington rotations 1715–1735. The gray scale is adjusted to show no flux densities weaker than 10 G. The right stack-plot in the right shows the corresponding high-latitude strips (N27° to the pole) strips for the same Carrington rotations. The gray scale is adjusted to show flux densities as weak as 1 G. The evolution of the activity complexes in the left stack-plot can be related to the appearance of decayed poleward-transported flux in the right stack-plot. Image reproduced with permission from Gaizauskas et al. (2001), copyright by AAS.
Gaizauskas et al. (2001) used a similar approach to study the relationship between this particular pair of adjacent activity complexes and its poleward surge of magnetic flux, and the formation and evolution of several filament channels and filaments forming within the vicinity of and poleward of the activity complexes. In Figure 49 stacked latitude slices of NSO Kitt Peak He i 10830 Å spectroheliogram synoptic maps are shown, corresponding to a subset of the rotations featuring in the magnetogram stack plots of Figure 48. Comparison of the two figures enabled Gaizauskas et al. (2001) to relate the spatio-temporal evolution of the activity complexes and the poleward-transported decayed magnetic flux to the development (and disappearance) of the filaments. The combined data set covered the formation and removal of neutral lines within and poleward of the activity complexes, and the filaments that form and are destroyed at these neutral lines.
Stack-plot of NSO He i 1083 nm synoptic maps for the northern hemisphere (0° to the north pole), covering Carrington rotations 1722–1732. The evolution of the filament on the return arm of the switchback neutral line continues long after the source region (inside white box) disappears. The eastward-advancing apex of the switchback is marked by black V-shaped wedges from Carrington rotation 1726 onward. The ordinate for each map is in sine latitude. Image reproduced with permission from Gaizauskas et al. (2001), copyright by AAS.
The example studied dates from 1982, towards the end of the cycle 21 maximum and just after the polar field had reversed. The main filament had length approximately a solar radius and it lasted about a year. The main activity complex, indicated by the boxes in Figures 48 and 49, lasted about 20 rotations, and the poleward surge of magnetic flux is visible in the magnetic butterfly diagram as a major positive streak meeting the negative polar cap. This surge of flux weakened as it traveled poleward, and it does not appear to have significantly changed the polar field strength. Some reasons for this can be suggested. Although a large quantity of flux was involved (the supercluster of two complexes contained about 1023 Mx at its height), the complexes were arranged in a complicated quadrupolar configuration with many internal neutral lines. As individual bipoles within and between the complexes expanded, fragmented and cancelled, it was mainly the flux at the outer edges of the cluster that survived to be transported poleward. Thus the various filament channels that quickly formed along neutral lines within the cluster did not survive longer than two rotations. After three rotations the flux streaming poleward from the supercluster was arranged in a simple bipolar pattern that exhibited longitudinal stretching due to differential rotation, clearly evident in Figure 48. A lengthy and long-lasting filament channel formed along the neutral line separating the two opposite-polarity bands of flux in the shape of a “switchback”, marked by V-shaped wedges in Figure 49, with the upper arm forming along the neutral line between the positive-polarity flux and the negative polar cap.
Besides delineating frontiers between bodies of opposite-polarity magnetic flux, filaments also mark where twist is trapped in the magnetic field low in the solar atmosphere. This twist can be characterized in terms of the handedness, or chirality, of the field. Filaments are characterized as having dextral or sinistral chirality (handedness) according to the direction of the filament’s axial field relative to the underlying photospheric polarity distribution. A significant preference for dextral prominences to form in the northern hemisphere and sinistral in the south has been observed at both active and high latitudes (Leroy et al., 1983; Martin et al., 1994). In active regions, the main polarity inversion lines (PILs) have chirality consistent with the overall helicity of the active region (Rust and Martin, 1994), where dextral/sinistral chirality corresponds to negative/positive helicity, but the chirality outside active regions is determined by the complex interactions between active regions. Differential rotation tends to add chirality of the “wrong” sign to neutral lines (Leroy, 1978), and small-scale flux emergence and motions are not expected to add significant net chirality of either sign. If a neutral line is oriented north-south then rotational shearing can create chirality of the “correct” sign (DeVore, 2000), but most neutral lines created by decayed active region flux is highly slanted as in, e.g., Figure 48, making the creation of the observed high-latitude chirality patterns by high-latitude rotational shearing unlikely. Therefore, it appears that chirality of the correct sign must be transported from active to high latitudes. The hemispheric rule is evidently caused by the emergence of active regions whose helicity sign satisfies the rule, not the poleward transport of the active region flux, which merely redistributes the helicity within the same hemisphere (Wang et al., 2013).
The NSO He i 10830 A spectrohelio grams and Ottawa River Solar Observatory Hα images analyzed by Gaizauskas et al. (2001) indicated that significant quantities of negative magnetic helicity accumulated where the active regions in the main complex emerged, and this helicity was still present in the poleward-migrating flux after the complexes had disappeared. Since emergence of opposite-polarity fluxes with negative helicity leads naturally to dextral filaments in the northern hemisphere, consistent with the hemispheric chirality rule described by Martin et al. (1994), 10 filament channels associated with the initial flux emergence and dispersal and its subsequent poleward transport all shared dominant dextral chirality. The physical cause of the hemispheric filament chirality rule may be related to the poleward flux transport of the decayed, helicity-carrying active region fields that form the filaments. The magnetic helicity is introduced into the atmosphere when the active regions emerge, and is carried to high latitudes in the decayed active region flux. The relative helicity of the highly conducting magnetic fields of the solar atmosphere is approximately conserved on the time scales of interest (Berger, 1984), and so when active region flux decays, is transported poleward, and meets flux of opposite polarity, it is expected that the helicity will accumulate along the neutral line.
Using kinematic flux transport models for the photospheric field based on NSO Kitt Peak photospheric longitudinal magnetograms, and magnetofrictionally relaxed non-potential equilibrium models for the coronal field, Yeates and Mackay (2012) modeled 15 years (1996–2011) of coronal field evolution. This simulation enabled the authors to study the formation of high-latitude filaments over an entire solar cycle. The results are shown in Figure 50. The figure shows that the expected dominant chirality in each hemisphere according to the hemispheric rule (dextral in the north and sinistral in the south) was indeed dominant at active latitudes but that the chirality profile at high latitudes changed significantly with time. The expected dominant polarity was dominant at high latitudes during the ascent and the maximum of the activity cycle, including the “rush to the poles” and polar field reversal. Then, during the declining phase, the opposite chirality became dominant at high latitudes. Finally, late in the declining phase and throughout solar minimum the expected dominant polarity again became dominant at high latitudes. Yeates and Mackay (2012) explained this pattern in terms of a competition between flux transport from active latitudes, which tends to add chirality of the expected dominant sign, and differential rotation, which tends to add chirality of opposite sign. According to these results, poleward flux transport is influential in creating non-potential fields at high latitudes, and dominates the high-latitude chirality during the ascent and the maximum of the activity cycle. The poleward flux transport is too weak to overcome differential rotation as the cycle declines, and the average high-latitude chirality changes sign. Late in the cycle, the highest-latitude neutral lines are closer to the equator, so that dominant chirality transported there from active latitudes can more easily dominate.
Butterfly diagrams (time-latitude plots) showing the longitude-averages of (a) the skew sin γ and (b) the current helicity density α0, of a non-potential magnetofrictional simulation of the coronal magnetic field evolution during cycle 23 and early cycle 24. Both the skew and the current helicity density are measured at height 1.033 solar radii. Image reproduced with permission from Yeates and Mackay (2012), copyright by AAS.
4.6 Prominence eruptions and coronal mass ejections
We next discuss the fate of the filaments when they reach high latitudes at times of polar field reversal. Figures 47 and 50 indicate that these high-latitude crowns of filaments disappear during the period of polar reversal. Signatures of polar field reversal include the disappearance and reforming of polar coronal holes as well as the disappearance of polar filaments following their rush to the poles. These two processes are related by the effect of open flux being replaced at the poles with flux of opposite polarity. Before open flux of one polarity is replaced by open flux of opposite polarity, the intervening neutral lines must be removed, a process signaled by the eruption of the filaments that lie along them. Low (2001) has argued that since relative magnetic helicity is approximately conserved in solar atmospheric fields (Berger, 1984), the high-latitude filaments can only be removed by ejection of the twisted field. The filaments’ disappearance is therefore a necessary consequence of the polar reversal.
The high-latitude prominence eruptions and coronal mass ejections (CMEs) provide a natural mechanism for removing relative magnetic helicity and for the disappearance of polar crown filaments that participate in the rush to the poles. Because eruptive prominences are almost always accompanied by CMEs (Munro et al., 1979), prominence eruptions and CMEs can often be identified with each other (Gopalswamy et al., 2003b). We will explore the solar cycle patterns of prominence eruptions and coronal mass ejections (CMEs) in this section.
Gopalswamy et al. (2012) showed that microwave images can be used to study the solar cycle-dependence of prominence eruptions. The long-term latitude distribution of prominence eruptions can help us to characterize the important properties of the solar cycle where prominences play a role, including the rush to the poles and the polar field reversal. Gopalswamy et al. (2012) plotted the locations of prominence eruptions, as observed in Nobeyama radioheliograph full-disk microwave brightness observations at 17 GHz, over the microwave brightness temperature butterfly diagram plotted in Figure 38. The results are shown in Figure 51. Over most of the solar cycle, eruptions are confined to latitudes between ±60°. They occur at higher latitudes only during activity maximum, beginning when the polar fields begin to reverse and ending when the polar reversal is complete. The resemblance between the latitude distributions in Figures 50 and 51 is striking: the pronounced signature of surges to the poles at solar maxima in Figure 50 corresponds to the high-latitude prominence eruptions during solar maximum in Figure 51.
Top: superposition of observed prominence eruption latitudes (open circles) on a butterfly diagram of Nobeyama Radioheliograph microwave brightness. Bottom: the prominence eruption-CME latitude offset plotted as a function of time. The intervals in which the offset is exclusively positive are bracketed by the vertical dashed lines. The CME latitudes were obtained from SOHO’s Large Angle and Spectrometric Coronagraph (LASCO) images. Prominence eruptions occurring in the northern and southern hemispheres are distinguished by different colors. Note that this interval is rather extended during the 23/24 minimum, reflecting the extended nature of the microwave polar brightening. The vertical shaded rectangle marks the interval when active regions from cycles 23 and 24 were present, indicating the overlap between the two cycles. Image reproduced with permission from Gopalswamy et al. (2012), copyright by AAS.
Gopalswamy et al. (2003b) studied the statistics of the association rate, relative timing and spatial relationships between prominence eruptions and CMEs. Among their statistical sample, 72% (134) of the prominence eruptions were associated with CMEs. While the prominence eruptions and CMEs began around the same time, with no cycle-dependence in their temporal relationship (Gopalswamy et al., 2003b), the position angle offset between associated prominence eruptions (observed off-limb near the solar surface) and CMEs (observed in the LASCO field of view) shows a clear cycle-dependence when plotted on a butterfly diagram as in Figure 51 (bottom, Gopalswamy et al., 2012). During cycle minimum the prominence eruptions occur at systematically higher latitudes than the locations where the CMEs appear. Figure 51 indicates a significant average positive offset (prominence eruptions were more poleward than coronal mass ejections) when the polar coronal holes were most prominent, i.e., during solar minimum. This position angle offset is believed to be due to strong polar fields. The intervals of exclusively positive offsets span the solar minima, from the beginning of the SoHO/LASCO data series in 1996 until early 1998, and from early 2007 until late 2010. This average positive offset disappeared whenever significant activity appeared, when the influence of the polar coronal holes on the eruptions appears to have been reduced. Although the polar field strength was comparatively weak during the cycle 23/24 minimum the average offset angle, 19°, was about the same as that during the cycle 22/23 minimum, 22°. Few events were recorded during each minimum.
Furthermore, the rush to the poles of the prominence eruptions begins earlier than the rush of the CMEs, as Figure 52 shows (Gopalswamy et al., 2003b). The rapid spread of the prominence eruption and CME source latitudes during the rush to the poles has been associated with the approach to the maximum tilt angle of the heliospheric current sheet (e.g., Cliver and Ling, 2001). This result matches the pattern seen in Section 4.3 relating the flatness of the current sheet structure to the latitude range of solar wind variability. Both prominence eruptions and CMEs originate from all latitudes over the cycle, but their latitude distributions are quite different (Gopalswamy et al., 2003b). The latitude distribution of the prominence eruptions had two peaks, one in each hemisphere, corresponding to the active belts. In contrast the CME latitude distribution did not have a double peak, only a single broad peak centered at the equator. The influence of the polar fields on CME position angles during solar minimum is indicated by the non-radial trajectories of erupting prominences. The prominences typically originate from the active belt during this time, but the overlying fields that become the frontal structures of the associated CMEs, span the equator and therefore tend to have smaller position angles.
Top: Latitude distribution of all the prominence eruptions detected by the Nobeyama radioheliograph as a function of time from 1996 to 2002 (the Carrington rotation numbers are marked at the top). The 60° latitude is shown as a solid line to indicate the high-latitude eruptions. The solid curves in the northern and southern hemispheres represent the maximum excursions of the heliospheric current sheet, a good indicator of the presence of neutral lines at high latitudes. The vertical lines (solid: north; dashed: south) show the epochs of cessation of high-latitude activity. The overall ratio of high-latitude and low-latitude CMEs is 16%. Bottom: Same as above, but for the associated CMEs. Image reproduced with permission from Gopalswamy et al. (2003a), copyright by AAS.
Focusing on the cycle 23 polar reversal, Gopalswamy et al. (2003a) found a close relationship at both poles between the polar fields’ polarity reversal and the cessation of high-latitude CMEs. The timings of these phenomena are compared in Figure 53. During this reversal, the field strength at both poles declined and reversed over the period 2000–2002, with the north pole leading the south. There was a rapid increase in high-latitude CMEs during 1999, especially in the northern hemisphere. At the time of the polar reversal, marked as October 2000 in the figure, the high-latitude CME rate sharply decreased. The high-latitude eruptions ceased in the northern and southern hemispheres in November 2000 and May 2001, respectively, roughly coinciding with the polarity reversals of the north and south polar fields. These results support the hypothesis that CMEs are the means by which old helicity-carrying magnetic field is removed from the solar atmosphere, to be replaced by decayed active region field associated with the new cycle.
Top: Polar field strength averaged over regions poleward of 70° from NSO/Kitt Peak magnetograms. Times of polarity reversal are marked by the vertical lines (solid: north; dashed: south). CME rates from high (middle) and low latitudes (bottom) distinguished by hemisphere (solid: north; dotted: south). Times when the polar crown filament branch disappeared are marked by small and medium arrows. Large arrows mark the times of cessation of high-latitude prominence eruptions. The direction of the arrows indicates the hemisphere (up: north; down: south). The horizontal lines in the middle and bottom panels show the 3σ levels of the CME rates (solid: north; dotted: south). The standard deviation (σ) of the rates in the north and south are marked in the respective panels. Image reproduced with permission from Gopalswamy et al. (2003a), copyright by AAS.
Luhmann et al. (2011) suggested that the observed enhanced CME rate of cycle 24 may be connected to the weak polar fields allowing more ejections to escape into the heliosphere. Petrie (2013) analyzed the CME rates recorded in the Computer Aided CME Tracking (CACTus Robbrecht et al., 2009) and Solar Eruptive Event Detection System (SEEDS Olmedo et al., 2008) catalogs, both based on SOHO/LASCO coronagraph data, and found evidence that the CME rate itself may be dependent on the polar field strength. Whereas the CME rate as measured from coronagraph data collected by numerous satellites flown during cycle 21 and the rise of cycle 22 (1975–1989) was very well correlated with the sunspot number (Webb and Howard, 1994), the CACTUS and SEEDS CME rates were much less well correlated with the sunspot number over cycle 23 and the rise of cycle 24 (1997–2012). In particular, the ratio of CME rate per sunspot number was systematically higher after the cycle 23 polar reversal than before. Wang and Colaninno (2014) countered that the change of cadence of the LASCO images in 2010 may have been responsible for the increase in CME detection. Normalizing the CME rate using the assumption that the CME detection rate is proportional to the image rate, they found a much higher correlation between the normalized CME rate and the sunspot number and concluded that the polar field strength could have no more than a second-order effect on the CME rate. Petrie (2015) found that the Coordinated Data Analysis Workshops (CDAW) and CACTus LASCO CME rates for CMEs of angular width > 30°, both based on LASCO/C2 and C3 images, matched each other closely, and sharply increased (per sunspot number) on completion of the cycle 23 polar field reversal, around 2004. The SEEDS CME rate, based on C2 images alone, differed from the CDAW and CACTus rates in increasing (per sunspot number) only on the onset of cycle 24, in 2010. It remains to be seen which conclusion is more accurate. It is very difficult to reproduce both the initiation of a CME and its progress through a realistic coronal medium, and so a comprehensive study of the relationship between the polar fields and eruptions has not yet been carried out.
Recently, Gopalswamy et al. (2015) reported that the halo CME rate has been higher during cycle 24 than during cycle 23 (Gopalswamy et al., 2015), and that the distribution of CME sources in apparent longitude has also been much flatter, with proportionally twice as many halo CMEs originating from central meridian distances ≥ 60°. Their explanation is based on the decrease in total (magnetic + plasma) pressure in the corona and heliosphere allowing enhanced CME expansion. Gopalswamy et al. (2014) found evidence for this in a study of CME widths and velocities, whose constant of proportionality has changed by 50% for early cycle 24 compared to early cycle 23. This conclusion, if confirmed, would link the enhanced cycle 24 CME rate to the weakened polar fields via the reduced radial IMF (see Section 4.3).
5 Conclusion
An impressive and coherent body of knowledge of the polar fields has accumulated from several decades of observational and theoretical work. It has become increasingly evident that the polar fields play a central role in the solar cycle, in the solar interior and atmosphere. The pioneering observations from the Hinode spacecraft have changed our observational view of these fields, from a diffuse collection of weak, nearly unipolar magnetic features, closer to our view of diffuse low-latitude quiet-Sun or coronal-hole fields: of a highly complex and non-uniform mixture of intense, nearly vertical fields and smaller patches of nearly horizontal field. It is the vertical patches that represent the polar fields’ pivotal role in the solar cycle and their global influence, even though the patches of nearly horizontal field are much more numerous. This influence of the vertical fields is seen in the cycle-dependent distribution of the coronal holes, solar wind and ejecta.
Since these fields were first observed in the 1950s, we have learnt that they form from a variety of processes that act in concert in a complex and beautiful way, and that they may form the seed field of the solar cycle that follows, though a final dynamo theory of this phenomenon has not yet been established. The properties of the fields depend not only on the combined behavior of these flows but on systematic biases and asymmetries in the bipolar active regions. These properties have so far been only partially explained by the theory of the bipoles’ buoyant emergence from the interior (Fan, 2009). Even the formation of the polar fields from the active regions’ decay, the part of the cycle that occurs in plain sight, is only imperfectly understood by us, as our recent efforts to explain the weak polar fields of cycle 23 have shown. Many ingredients of the kinematic flux transport models are not well determined by observations. The meridional flow profile measurements tend to differ according to whether magnetic feature tracking, Doppler or helioseismic measurements are used, and the model results are highly sensitive to the details. Likewise, analyses of bipole tilt angles provide essential initial conditions for flux transport calculations, but the results are still noisy and inconclusive. Latitude centroid calculations for active region fields seem to produce more stable results that correlate well with observed polar field changes.
Future knowledge of the polar fields will come from a variety of different sources from many areas of solar physics. Continuous high-resolution vector images of the polar fields, such as the unprecedented high-resolution, multi-level observations from the ground-based Daniel K. Inouye Solar Telescope (DKIST), will reveal the detailed behavior of the fields over the cycle. The physical nature of the flux-cancellation processes behind active region decay and polar field reversal can only be revealed by such observations. They will also give us an improved estimate of the polar magnetic flux into the atmosphere and its changes over time, crucial information for the study of the polar fields’ great influence in the heliosphere. At the most basic level, observations of the polar fields are hampered by the large viewing angle from our observing position in the ecliptic plane. It would take an out-of-ecliptic satellite, carrying a good magnetograph, to overcome this limitation. The proposed Polarimetric and Helioseismic Imager (PHI) on ESA’s Solar Orbiter may address this problem. More realistically, vector synoptic magnetograms covering the full solar surface are a highly desirable data product, one that would have application in global modeling of the solar interior and atmospheric magnetic fields. Several obstacles lie in our path. Besides the regions of the solar surface that cannot be observed from Earth for significant periods of time, it is difficult to obtain reliable Stokes parameters from the weak fields that dominate polar latitudes for, although there are kilogauss fields at the poles, they are difficult to resolve on a routine basis because of their small size and the large viewing angle from the ecliptic plane.
The magnetic conditions in the chromosphere much more closely match the conditions in the corona, and so a further desirable data product is a map of the chromospheric field. The SO-LIS/VSM already provides line-of-sight full-disk magnetograms and synoptic magnetograms for the chromospheric field, and a chromospheric vector magnetograph is under development. Because the chromospheric field is, unlike the photospheric field, not approximately radial, a vector measurement is necessary to estimate the chromospheric flux in the atmosphere without relying on annual averages based on viewing angle changes associated with the B0-angle. But, again, it remains to be seen how far poleward reliable chromospheric vector field measurements can be made on a routine basis. A practical compromise is to combine the easier-to-obtain line-of-sight measurements for weak fields, including high latitudes, with full-Stokes vector data for the active regions.
Surface flux transport modeling with magnetogram data assimilation is becoming an essential part of the effort to construct the most accurate possible snapshot of the global photospheric flux distribution at any time. The flux transport model parameters, in particular the meridional flow profile amplitude and shape and the diffusion/dispersal rate, are not tightly constrained by observations. The meridional flow may change significantly in time and may have different effects on fields of different strength, as may also the magnetoconvective coupling. Further detailed observational information is needed to constrain the models and control their behavior. The global atmospheric models extrapolated from improved magnetograms, derived from an optimal combination of observations and modeling, will give us improved estimates of coronal hole locations and structure and solar wind speed distributions, which will enable better forecasts of space weather events, including CME propagation.
Kinematic flux transport and dynamo models have played an essential role in helping us to understand the cyclical behavior of the polar fields, but at present they are only kinematic. Increasingly sophisticated numerical models, and guidance from helioseismology, have advanced the modeling of dynamical processes in the interior, including the interior flows that connect the active regions and the polar fields (Miesch, 2005). Helioseismic measurements of interior flows are telling us more and more about the large-scale flow patterns inside the Sun that, according to the models, must transport old polar flux to lower latitudes and amplify its strength. It is still not known how and at what depth the dynamo process(es) shear the fields and strengthen them, whether near the surface, at the tachocline or somewhere else.
The solar field is behaving in ways unfamiliar to us from previous cycles. The ongoing polar reversal will doubtless prompt new studies on this topic, just as the recent weakness of the cycle 23 polar fields did. The activity level is significantly lower, the polar fields much weaker and north-south asymmetry in the active regions and polar fields has become more common. The consequences of these patterns for the future of both the polar and active region fields give us an excellent opportunity to learn much about the physics of these fields.
Complementing the latest high-resolution observations and detailed physical models, continuous, long-term full-disk magnetogram time series, such as those from NSO and WSO, are essential resources for the long-term study of the polar fields, since only they capture their global behavior on their time-scales of evolution, which are measured in years and cycles. One major message of this review is that, alongside new and exciting high-resolution telescopes, the long-running synoptic projects must be scrupulously maintained if we are to continue to develop our knowledge of the global solar field, including the polar fields.
Notes
An error in the tilt angle analysis of Dasi-Espuig et al. (2010) was pointed out by Ivanov (2012), and corrected by Dasi-Espuig et al. (2013), where an anti-correlation remained in the normalized Kodaikanal sunspot tilt angles for cycles 15–21 that they analyzed, and in weakened form in the MWO data. McClintock and Norton (2013) confirmed the existence of this correlation in the MWO data overall, but found that there was no correlation in the northern hemisphere, only in the southern hemisphere.
References
Altschuler, M. D. and Newkirk, G., 1969, “Magnetic Fields and the Structure of the Solar Corona. I: Methods of Calculating Coronal Fields”, Solar Phys., 9, 131–149. [DOI], [ADS]. (Cited on page 63.)
Arge, C., Henney, C. J., Shurkin, K., Toussaint, W., Koller, J. and Harvey, J. W., 2011, “Comparing ADAPT-WSA Model Predictions With EUV And Solar Wind Observations”, Bull. Am. Astron. Soc., 43, P24.03. [ADS]. (Cited on page 48.)
Arge, C. N. and Pizzo, V. J., 2000, “Improvement in the prediction of solar wind conditions using near-real time solar magnetic field updates”, J. Geophys. Res., 105, 10465–10480. [DOI], [ADS]. (Cited on pages 21 and 69.)
Arge, C. N., Henney, C. J., Hernandez, I. G., Toussaint, W. A., Koller, J. and Godinez, H. C., 2013, “Modeling the corona and solar wind using ADAPT maps that include far-side observations”, in Solar Wind 13, 17–22 June 2012, Big Island, Hawaii, (Eds.) Zank, G. P., Borovsky, J., Bruno, R., Cirtain, J., Cranmer, S., Elliott, H., Giacalone, J., Gonzalez, W., Li, G., Marsch, E., Moebius, E., Pogorelov, N., Spann, J., Verkhoglyadova, O., AIP Conf. Proc., 1539, pp. 11–14, American Institute of Physics, Melville, NY. [DOI], [ADS]. (Cited on page 48.)
Babcock, H. D., 1959, “The Sun’s Polar Magnetic Field”, Astrophys. J., 130, 364–365. [DOI], [ADS]. (Cited on page 5.)
Babcock, H. W., 1961, “The Topology of the Sun’s Magnetic Field and the 22-Year Cycle”, Astrophys. J., 133, 572–587. [DOI], [ADS]. (Cited on pages 5, 6, 31, 35, 36, 37, 38, and 74.)
Balogh, A., Smith, E. J., Tsurutani, B. T., Southwood, D. J., Forsyth, R. J. and Horbury, T. S., 1995, “The Heliospheric Magnetic Field Over the South Polar Region of the Sun”, Science, 268, 1007–1010. [DOI], [ADS]. (Cited on page 71.)
Basu, S. and Antia, H. M., 2010, “Characteristics of Solar Meridional Flows during Solar Cycle 23”, Astrophys. J., 717, 488–495. [DOI], [ADS], [arXiv:1005.3031 [astro-ph.SR]]. (Cited on pages 51 and 56.)
Berger, M. A., 1984, “Rigorous new limits on magnetic helicity dissipation in the solar corona”, Geophys. Astrophys. Fluid Dyn., 30, 79–104. [DOI], [ADS]. (Cited on pages 83 and 84.)
Blanco Rodríguez, J., Okunev, O. V., Puschmann, K. G., Kneer, F. and Sánchez-Andrade Nuño, B., 2007, “On the properties of faculae at the poles of the Sun”, Astron. Astrophys., 474, 251–259. [DOI], [ADS]. (Cited on page 5.)
Bravo, S. and Stewart, G., 1994, “Evolution of polar coronal holes and sunspots during cycles 21 and 22”, Solar Phys., 154, 377–384. [DOI], [ADS]. (Cited on page 63.)
Broussard, R. M., Tousey, R., Underwood, J. H. and Sheeley Jr, N. R., 1978, “A survey of coronal holes and their solar wind associations throughout sunspot cycle 20”, Solar Phys., 56, 161–183. [DOI], [ADS]. (Cited on page 63.)
Bumba, V. and Howard, R., 1969, “Solar Activity and Recurrences in Magnetic-Field Distribution”, Solar Phys., 7, 28–38. [DOI], [ADS]. (Cited on page 30.)
Cameron, R. H. and Schüssler, M., 2012, “Are the strengths of solar cycles determined by converging flows towards the activity belts?”, Astron. Astrophys., 548, A57. [DOI], [ADS], [arXiv:1210.7644 [astro-ph.SR]]. (Cited on page 52.)
Cameron, R. H., Dasi-Espuig, M., Jiang, J., Işık, E., Schmitt, D. and Schüssler, M., 2013, “Limits to solar cycle predictability: Cross-equatorial flux plumes”, Astron. Astrophys., 557, A141. [DOI], [ADS], [arXiv:1308.2827 [astro-ph.SR]]. (Cited on page 42.)
Charbonneau, P., 2010, “Dynamo Models of the Solar Cycle”, Living Rev. Solar Phys., 7, lrsp-2010-3. [DOI], [ADS]. URL (accessed 7 August 2014): http://www.livingreviews.org/lrsp-2010-3. (Cited on page 35.)
Cliver, E. W. and Ling, A. G., 2001, “22 Year Patterns in the Relationship of Sunspot Number and Tilt Angle to Cosmic-Ray Intensity”, Astrophys. J. Lett., 551, L189–L192. [DOI], [ADS]. (Cited on page 86.)
Cowling, T. G., 1933, “The magnetic field of sunspots”, Mon. Not. R. Astron. Soc., 94, 39–48. [ADS]. (Cited on page 35.)
Dasi-Espuig, M., Solanki, S. K., Krivova, N. A., Cameron, R. and Peñuela, T., 2010, “Sunspot group tilt angles and the strength of the solar cycle”, Astron. Astrophys., 518, A7. [DOI], [ADS], [arXiv:1005.1774 [astro-ph.SR]]. (Cited on pages 51, 52, 53, and 74.)
Dasi-Espuig, M., Solanki, S. K., Krivova, N. A., Cameron, R. and Peñuela, T., 2013, “Sunspot group tilt angles and the strength of the solar cycle (Corrigendum)”, Astron. Astrophys., 556, C3. [DOI], [ADS]. (Cited on pages 52 and 74.)
de Toma, G., 2011, “Evolution of Coronal Holes and Implications for High-Speed Solar Wind During the Minimum Between Cycles 23 and 24”, Solar Phys., 274, 195–217. [DOI], [ADS]. (Cited on pages 32, 63, 64, and 65.)
DeRosa, M. L., Brun, A. S. and Hoeksema, J. T., 2012, “Solar Magnetic Field Reversals and the Role of Dynamo Families”, Astrophys. J., 757, 96. [DOI], [ADS], [arXiv:1208.1768 [astro-ph.SR]]. (Cited on pages 57, 58, and 59.)
DeVore, C. R., 2000, “Magnetic Helicity Generation by Solar Differential Rotation”, Astrophys. J., 539, 944–953. [DOI], [ADS]. (Cited on page 83.)
Dikpati, M., 2011, “Polar Field Puzzle: Solutions from Flux-transport Dynamo and Surface-transport Models”, Astrophys. J., 733, 90. [DOI], [ADS], [arXiv:1104.0269 [astro-ph.SR]]. (Cited on pages 50, 51, 55, and 56.)
Dikpati, M. and Gilman, P. A., 2007, “Global solar dynamo models: simulations and predictions of cyclic photospheric fields and long-term non-reversing interior fields”, New J. Phys., 9, 297. [DOI], [ADS]. (Cited on page 37.)
Dikpati, M., Gilman, P. A. and Ulrich, R. K., 2010, “Physical Origin of Differences Among Various Measures of Solar Meridional Circulation”, Astrophys. J., 722, 774–778. [DOI], [ADS], [arXiv:1008.2772 [astro-ph.SR]]. (Cited on page 51.)
Durrant, C. J. and Wilson, P. R., 2003, “Observations and Simulations of the Polar Field Reversals in Cycle 23”, Solar Phys., 214, 23–39. [DOI], [ADS]. (Cited on pages 48 and 78.)
Durrant, C. J., Turner, J. P. R. and Wilson, P. R., 2004, “The Mechanism involved in the Reversals of the Sun’s Polar Magnetic Fields”, Solar Phys., 222, 345–362. [DOI], [ADS]. (Cited on page 32.)
Duvall Jr, T. L., 1979, “Large-scale solar velocity fields”, Solar Phys., 63, 3–15. [DOI], [ADS]. (Cited on page 39.)
Fan, Y., 2009, “Magnetic Fields in the Solar Convection Zone”, Living Rev. Solar Phys., 6, lrsp-2009-4. [DOI], [ADS]. URL (accessed 7 August 2014): http://www.livingreviews.org/lrsp-2009-4. (Cited on page 90.)
Gaizauskas, V., Harvey, K. L., Harvey, J. W. and Zwaan, C., 1983, “Large-scale patterns formed by solar active regions during the ascending phase of cycle 21”, Astrophys. J., 265, 1056–1065. [DOI], [ADS]. (Cited on pages 32 and 78.)
Gaizauskas, V., Mackay, D. H. and Harvey, K. L., 2001, “Evolution of Solar Filament Channels Observed during a Major Poleward Surge of Photospheric Magnetic Flux”, Astrophys. J., 558, 888–902. [DOI], [ADS]. (Cited on pages 80, 81, 82, and 83.)
Gopalswamy, N., Shibasaki, K. and Salem, M., 2000, “Microwave Enhancement in Coronal Holes: Statistical Propeties”, J. Astrophys. Astron., 21, 413. [DOI], [ADS]. (Cited on page 66.)
Gopalswamy, N., Lara, A., Yashiro, S. and Howard, R. A., 2003a, “Coronal Mass Ejections and Solar Polarity Reversal”, Astrophys. J. Lett., 598, L63–L66. [DOI], [ADS]. (Cited on pages 86, 87, and 89.)
Gopalswamy, N., Shimojo, M., Lu, W., Yashiro, S., Shibasaki, K. and Howard, R. A., 2003b, “Prominence Eruptions and Coronal Mass Ejection: A Statistical Study Using Microwave Observations”, Astrophys. J., 586, 562–578. [DOI], [ADS]. (Cited on page 86.)
Gopalswamy, N., Yashiro, S., Mäkelä, P., Michalek, G., Shibasaki, K. and Hathaway, D. H., 2012, “Behavior of Solar Cycles 23 and 24 Revealed by Microwave Observations”, Astrophys. J. Lett., 750, L42. [DOI], [ADS], [arXiv:1204.2816 [astro-ph.SR]]. (Cited on pages 66, 68, 85, and 86.)
Gopalswamy, N., Akiyama, S., Yashiro, S., Xie, H., Mäkelä, P. and Michalek, G., 2014, “Anomalous expansion of coronal mass ejections during solar cycle 24 and its space weather implications”, Geophys. Res. Lett., 41, 2673–2680. [DOI], [ADS]. (Cited on page 88.)
Gopalswamy, N., Xie, H., Akiyama, S., Mäkelä, P., Yashiro, S. and Michalek, G., 2015, “The Peculiar Behavior of Halo Coronal Mass Ejections in Solar Cycle 24”, Astrophys. J. Lett., 804, L23. [DOI], [ADS]. (Cited on page 88.)
Gosain, S., Pevtsov, A. A., Rudenko, G. V. and Anfinogentov, S. A., 2013, “First Synoptic Maps of Photospheric Vector Magnetic Field from SOLIS/VSM: Non-radial Magnetic Fields and Hemispheric Pattern of Helicity”, Astrophys. J., 772, 52. [DOI], [ADS], [arXiv:1305.3294 [astro-ph.SR]]. (Cited on pages 18 and 19.)
Hale, G. E., 1922, “Invisible sun-spots”, Mon. Not. R. Astron. Soc., 82, 168. [ADS]. (Cited on page 74.)
Hale, G. E. and Nicholson, S. B., 1925, “The Law of Sun-Spot Polarity”, Astrophys. J., 62, 270–300. [DOI], [ADS]. (Cited on page 31.)
Hale, G. E., Ellerman, F., Nicholson, S. B. and Joy, A. H., 1919, “The Magnetic Polarity of Sun-Spots”, Astrophys. J., 49, 153–178. [DOI], [ADS]. (Cited on page 31.)
Harvey, J., Gillespie, B., Miedaner, P. and Slaughter, C., 1980, Synoptic solar magnetic field maps for the interval including Carrington Rotation 1601–1680, May 5, 1973–April 26, 1979, NASA STI/Recon Technical Report N, UAG-77, NOAA, Boulder, CO. [ADS]. (Cited on page 42.)
Harvey, J. W., 2013, “The Sun in Time”, Space Sci. Rev., 176, 47–58. [DOI], [ADS]. (Cited on page 63.)
Harvey, J. W. and Sheeley Jr, N. R., 1979, “Coronal holes and solar magnetic fields”, Space Sci. Rev., 23, 139–158. [DOI], [ADS]. (Cited on page 64.)
Harvey, J. W., Krieger, A. S., Davis, J. M., Timothy, A. F. and Vaiana, G. S., 1975, “Comparison of Skylab X-Ray and Ground-Based Helium Observations”, Bull. Am. Astron. Soc., 7, 358. [ADS]. (Cited on page 63.)
Harvey, J. W., Branston, D., Henney, C. J. and Keller, C. U. [SOLIS and GONG Teams], 2007, “Seething Horizontal Magnetic Fields in the Quiet Solar Photosphere”, Astrophys. J. Lett., 659, L177–L180. [DOI], [ADS], [astro-ph/0702415]. (Cited on page 7.)
Harvey, K. L. and Recely, F., 2002, “Polar Coronal Holes During Cycles 22 and 23”, Solar Phys., 211, 31–52. [DOI], [ADS]. (Cited on page 64.)
Hathaway, D. H. and Rightmire, L., 2010, “Variations in the Sun’s Meridional Flow over a Solar Cycle”, Science, 327, 1350–1352. [DOI], [ADS]. (Cited on pages 51 and 56.)
Hathaway, D. H. and Rightmire, L., 2011, “Variations in the Axisymmetric Transport of Magnetic Elements on the Sun: 1996–2010”, Astrophys. J., 729, 80. [DOI], [ADS], [arXiv:1010.1242 [astro-ph.SR]]. (Cited on page 56.)
Hathaway, D. H., Gilman, P. A., Harvey, J. W. et al., 1996, “GONG Observations of Solar Surface Flows”, Science, 272, 1306–1309. [DOI], [ADS]. (Cited on page 39.)
Hoeksema, J. T., 1984, Structure and evolution of the large scale solar and heliospheric magnetic fields, Ph.D. thesis, Stanford University, Stanford, CA. [ADS]. (Cited on page 60.)
Hoeksema, J. T., 2010, “Evolution of the large-scale magnetic field over three solar cycles”, in Solar and Stellar Variability: Impact on Earth and Planets, Brazil, 3–7 August 2009, (Eds.) Kosovichev, A. G., Andrei, A. H., Rozelot, J.-P., IAU Symposium, 264, pp. 222–228, Cambridge University Press, Cambridge; New York. [DOI], [ADS]. (Cited on page 32.)
Homann, T., Kneer, F. and Makarov, V. I., 1997, “Spectro-Polarimetry of Polar Faculae”, Solar Phys., 175, 81–92. [DOI], [ADS]. (Cited on page 5.)
Howard, R., 1967, “Magnetic Field of the Sun (Observational)”, Annu. Rev. Astron. Astrophys., 5, 1–24. [DOI], [ADS]. (Cited on page 42.)
Howard, R. and Labonte, B. J., 1980, “A search for large-scale convection cells in the solar atmosphere”, Astrophys. J., 239, 738–745. [DOI], [ADS]. (Cited on page 39.)
Howard, R. F., 1989, “The magnetic fields of active regions. I. Data and first results”, Solar Phys., 123, 271–284. [DOI], [ADS]. (Cited on page 5.)
Howe, R., Baker, D., Harra, L., van Driel-Gesztelyi, L., Komm, R., Hill, F. and González Hernández, I., 2013, “Magnetic Polarity Streams and Subsurface Flows”, in Fifty Years of Seismology of the Sun and Stars, Proceedings of a Workshop held at The Westin La Paloma, Tucson, Arizona, USA, 6–10 May 2013, (Eds.) Jain, K., Tripathy, S. C., Hill, F., Leibacher, J. W., Pevtsov, A. A., ASP Conference Series, 478, p. 291, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 31.)
Hyder, C. L., 1965, “The ‘Polar Crown’ of Filaments and the Sun’s Polar Magnetic Fields”, Astrophys. J., 141, 272. [DOI], [ADS]. (Cited on page 78.)
Ito, H., Tsuneta, S., Shiota, D., Tokumaru, M. and Fujiki, K., 2010, “Is the Polar Region Different from the Quiet Region of the Sun?”, Astrophys. J., 719, 131–142. [DOI], [ADS], [arXiv:1005.3667 [astro-ph.SR]]. (Cited on page 7.)
Ivanov, V. G., 2012, “Joy’s law and its features according to the data of three sunspot catalogs”, Geomagn. Aeron., 52, 999–1004. [DOI], [ADS]. (Cited on page 52.)
Jiang, J., Işık, E., Cameron, R. H., Schmitt, D. and Schüssler, M., 2010, “The Effect of Activity-related Meridional Flow Modulation on the Strength of the Solar Polar Magnetic Field”, Astrophys. J., 717, 597–602. [DOI], [ADS], [arXiv:1005.5317 [astro-ph.SR]]. (Cited on page 51.)
Jiang, J., Cameron, R. H., Schmitt, D. and Schuüssler, M., 2013, “Can Surface Flux Transport Account for the Weak Polar Field in Cycle 23?”, Space Sci. Rev., 176, 289–298. [DOI], [ADS], [arXiv:1104.4183[astro-ph.SR]]. (Cited on pages 50, 51, 52, 53, 55, and 56.)
Jiang, J., Cameron, R. H. and Schuüssler, M., 2015, “The Cause of the Weak Solar Cycle 24”, Astrophys. J. Lett., 808, L28. [DOI], [ADS], [arXiv:1507.01764 [astro-ph.SR]]. (Cited on page 57.)
Jin, C. L., Harvey, J. W. and Pietarila, A., 2013, “Synoptic Mapping of Chromospheric Magnetic Flux”, Astrophys. J., 765, 79. [DOI], [ADS]. (Cited on pages 13, 18, 26, 27, 28, and 29.)
Jones, H. P., 1985, “Recent studies of magnetic canopies”, Aust. J. Phys., 38, 919–928. [ADS]. (Cited on pages 14 and 26.)
Kirk, M. S., Pesnell, W. D., Young, C. A. and Hess Webber, S. A., 2009, “Automated detection of EUV Polar Coronal Holes during Solar Cycle 23”, Solar Phys., 257, 99–112. [DOI], [ADS], [arXiv:0901.1158[astro-ph.SR]]. (Cited on page 64.)
Komm, R. W., Howard, R. F. and Harvey, J. W., 1993, “Meridional Flow of Small Photospheric Magnetic Features”, Solar Phys., 147, 207–223. [DOI], [ADS]. (Cited on pages 39 and 48.)
Krieger, A. S., Timothy, A. F. and Roelof, E. C., 1973, “A Coronal Hole and Its Identification as the Source of a High Velocity Solar Wind Stream”, Solar Phys., 29, 505–525. [DOI], [ADS]. (Cited on page 66.)
Labonte, B. J. and Howard, R., 1982, “Solar rotation measurements at Mount Wilson. III. Meridional flow and limbshift”, Solar Phys., 80, 361–372. [DOI], [ADS]. (Cited on page 39.)
Leighton, R. B., 1964, “Transport of Magnetic Fields on the Sun”, Astrophys. J., 140, 1547–1562. [DOI], [ADS]. (Cited on pages 6, 32, 38, 39, 40, and 45.)
Leighton, R. B., 1969, “A Magneto-Kinematic Model of the Solar Cycle”, Astrophys. J., 156, 1–26. [DOI], [ADS]. (Cited on pages 5, 6, 32, 35, 38, 39, 40, 42, 44, 48, and 74.)
Leighton, R. B., Noyes, R. W. and Simon, G. W., 1962, “Velocity Fields in the Solar Atmosphere. I. Preliminary Report”, Astrophys. J., 135, 474. [DOI], [ADS]. (Cited on page 38.)
Leroy, J. L., 1978, “On the orientation of magnetic fields in quiescent prominences”, Astron. Astrophys., 64, 247–252. [ADS]. (Cited on page 83.)
Leroy, J. L., Bommier, V. and Sahal-Brechot, S., 1983, “The magnetic field in the prominences of the polar crown”, Solar Phys., 83, 135–142. [DOI], [ADS]. (Cited on page 83.)
Levine, R. H., Altschuler, M. D. and Harvey, J. W., 1977, “Solar sources of the interplanetary magnetic field and solar wind”, J. Geophys. Res., 82, 1061–1065. [DOI], [ADS]. (Cited on page 66.)
Li, J. and Ulrich, R. K., 2012, “Long-term Measurements of Sunspot Magnetic Tilt Angles”, Astrophys. J., 758, 115. [DOI], [ADS], [arXiv:1209.1642 [astro-ph.SR]]. (Cited on page 56.)
Linker, J. A., Lionello, R., Mikić, Z., Titov, V. S. and Antiochos, S. K., 2011, “The Evolution of Open Magnetic Flux Driven by Photospheric Dynamics”, Astrophys. J., 731, 110. [DOI], [ADS]. (Cited on page 63.)
Liu, Y., Hoeksema, J. T., Zhao, X. and Larson, R. M., 2007, “MDI Synoptic Charts of Magnetic Field: Interpolation of Polar Fields”, Bull. Am. Astron. Soc., 39, 129. [ADS]. (Cited on page 21.)
Livingston, W. C., Harvey, J., Pierce, A. K., Schrage, D., Gillespie, B., Simmons, J. and Slaughter, C., 1976, “Kitt Peak 60-cm vacuum telescope”, Appl. Opt., 15, 33–39. [DOI], [ADS]. (Cited on page 5.)
Low, B. C., 2001, “Coronal mass ejections, magnetic flux ropes, and solar magnetism”, J. Geophys. Res., 106, 25141–25164. [DOI], [ADS]. (Cited on page 84.)
Luhmann, J. G., Li, Y., Liu, Y., Jian, L., Russell, C. T., Kilpua, E., Petrie, G. J. D. and Hoeksema, J. T., 2011, “Heliospheric Space Weather at the Start of Cycle 24”, 2011 Fall Meeting, AGU, San Francisco, Calif., 5–9 Dec., conference paper. [ADS]. SH31D-04. (Cited on page 88.)
Mackay, D. H. and Yeates, A. R., 2012, “The Sun’s Global Photospheric and Coronal Magnetic Fields: Observations and Models”, Living Rev. Solar Phys., 9, lrsp-2012-6. [DOI], [ADS], [arXiv:1211.6545[astro-ph.SR]]. URL (accessed 7 August 2014): http://www.livingreviews.org/lrsp-2012-6. (Cited on page 63.)
Mackay, D. H., Karpen, J. T., Ballester, J. L., Schmieder, B. and Aulanier, G., 2010, “Physics of Solar Prominences: II — Magnetic Structure and Dynamics”, Space Sci. Rev., 151, 333–399. [DOI], [ADS], [arXiv:1001.1635 [astro-ph.SR]]. (Cited on page 78.)
Makarov, V. I. and Makarova, V. V., 1996, “Polar Faculae and Sunspot Cycles”, Solar Phys., 163, 267–289. [DOI], [ADS]. (Cited on page 74.)
Martin, S. F., Bilimoria, R. and Tracadas, P. W., 1994, “Magnetic field configurations basic to filament channels and filaments”, in Solar Surface Magnetism, Proceedings of the NATO Advanced Research Workshop, Soesterberg, The Netherlands, November 1–5, 1993, (Eds.) Rutten, R. J., Schrijver, C. J., NATO ASI Series C, 433, pp. 303–338, Kluwer, Dordrecht; Boston. [ADS]. (Cited on page 83.)
Maunder, E. W., 1913, “Sun, Place of the, Distribution of sun-spots in heliographic latitude, 1874–1913”, Mon. Not. R. Astron. Soc., 74, 112. [ADS]. (Cited on page 30.)
McClintock, B. H. and Norton, A. A., 2013, “Recovering Joy’s Law as a Function of Solar Cycle, Hemisphere, and Longitude”, Solar Phys., 287, 215–227. [DOI], [ADS], [arXiv:1305.3205 [astro-ph.SR]]. (Cited on pages 51, 52, and 56.)
McComas, D. J., Ebert, R. W., Elliott, H. A., Goldstein, B. E., Gosling, J. T., Schwadron, N. A. and Skoug, R. M., 2008, “Weaker solar wind from the polar coronal holes and the whole Sun”, Geophys. Res. Lett., 35, L18103. [DOI], [ADS]. (Cited on pages 70 and 71.)
McIntosh, P. S., 1972, “Solar magnetic fields derived from hydrogen alpha filtergrams”, Rev. Geophys. Space Phys., 10, 837–846. [DOI], [ADS]. (Cited on page 78.)
McIntosh, P. S., 2003, “Patterns and dynamics of solar magnetic fields and HeI coronal holes in cycle 23”, in Solar Variability as an Input to the Earth’s Environment, International Solar Cycle Studies (ISCS) Symposium, 23–28 June 2003, Tatranská Lomnica, Slovak Republic, (Ed.) Wilson, A., ESA Special Publication, SP-535, pp. 807–818, ESA Publications Division, Nordwijk. [ADS]. (Cited on pages 78 and 79.)
Miesch, M. S., 2005, “Large-Scale Dynamics of the Convection Zone and Tachocline”, Living Rev. Solar Phys., 2, lrsp-2005-1. [ADS]. URL (accessed 7 August 2014): http://www.livingreviews.org/lrsp-2005-1. (Cited on page 91.)
Mordvinov, A. V. and Yazev, S. A., 2014, “Reversals of the Sun’s Polar Magnetic Fields in Relation to Activity Complexes and Coronal Holes”, Solar Phys., 289, 1971–1981. [DOI], [ADS]. (Cited on page 34.)
Muñoz-Jaramillo, A., Sheeley, N. R., Zhang, J. and DeLuca, E. E., 2012, “Calibrating 100 Years of Polar Faculae Measurements: Implications for the Evolution of the Heliospheric Magnetic Field”, Astrophys. J., 753, 146. [DOI], [ADS], [arXiv:1303.0345 [astro-ph.SR]]. (Cited on pages 74 and 76.)
Muñoz-Jaramillo, A., Dasi-Espuig, M., Balmaceda, L. A. and DeLuca, E. E., 2013, “Solar Cycle Propagation, Memory, and Prediction: Insights from a Century of Magnetic Proxies”, Astrophys. J. Lett., 767, L25. [DOI], [ADS], [arXiv:1304.3151 [astro-ph.SR]]. (Cited on pages 6, 57, 74, 77, and 78.)
Munro, R. H., Gosling, J. T., Hildner, E., MacQueen, R. M., Poland, A. I. and Ross, C. L., 1979, “The association of coronal mass ejection transients with other forms of solar activity”, Solar Phys., 61, 201–215. [DOI], [ADS]. (Cited on page 86.)
Nandy, D., Muñoz-Jaramillo, A. and Martens, P. C. H., 2011, “The unusual minimum of sunspot cycle 23 caused by meridional plasma flow variations”, Nature, 471, 80–82. [DOI], [ADS], [arXiv:1303.0349[astro-ph.SR]]. (Cited on page 51.)
Nolte, J. T., Krieger, A. S., Timothy, A. F. et al., 1976, “Coronal holes as sources of solar wind”, Solar Phys., 46, 303–322. [DOI], [ADS]. (Cited on page 66.)
Obridko, V. N. and Shelting, B. D., 2008, “On Prediction of the Strength of the 11-Year Solar Cycle No. 24”, Solar Phys., 248, 191–202. [DOI], [ADS]. (Cited on pages 78 and 79.)
Okunev, O. V. and Kneer, F., 2004, “On the structure of polar faculae on the Sun”, Astron. Astrophys., 425, 321–331. [DOI], [ADS]. (Cited on page 5.)
Olmedo, O., Zhang, J., Wechsler, H., Poland, A. and Borne, K., 2008, “Automatic Detection and Tracking of Coronal Mass Ejections in Coronagraph Time Series”, Solar Phys., 248, 485–499. [DOI], [ADS]. (Cited on page 88.)
Orozco Suárez, D., Bellot Rubio, L. R., del Toro Iniesta, J. C. et al., 2007, “Quiet-Sun Internetwork Magnetic Fields from the Inversion of Hinode Measurements”, Astrophys. J. Lett., 670, L61–L64. [DOI], [ADS], [arXiv:0710.1405]. (Cited on pages 5 and 7.)
Parker, E. N., 1955, “The Formation of Sunspots from the Solar Toroidal Field”, Astrophys. J., 121, 491–507. [DOI], [ADS]. (Cited on page 35.)
Parker, E. N., 1958, “Dynamics of the Interplanetary Gas and Magnetic Fields”, Astrophys. J., 128, 664–676. [DOI], [ADS]. (Cited on page 64.)
Parker, E. N., 1963, “Kinematical Hydromagnetic Theory and its Application to the Low Solar Photosphere”, Astrophys. J., 138, 552. [DOI], [ADS]. (Cited on page 38.)
Parker, E. N., 1984, “Magnetic buoyancy and the escape of magnetic fields from stars”, Astrophys. J., 281, 839–845. [DOI], [ADS]. (Cited on page 39.)
Petrie, G. J. D., 2012, “Evolution of Active and Polar Photospheric Magnetic Fields During the Rise of Cycle 24 Compared to Previous Cycles”, Solar Phys., 281, 577–598. [DOI], [ADS], [arXiv:1204.1048[astro-ph.SR]]. (Cited on pages 30, 31, 32, 51, 57, and 74.)
Petrie, G. J. D., 2013, “Solar Magnetic Activity Cycles, Coronal Potential Field Models and Eruption Rates”, Astrophys. J., 768, 162. [DOI], [ADS], [arXiv:1303.1218 [astro-ph.SR]]. (Cited on pages 30, 33, 60, 62, and 88.)
Petrie, G. J. D., 2015, “On the Enhanced Coronal Mass Ejection Detection Rate since the Solar Cycle 23 Polar Field Reversal”, Astrophys. J., 812, 74. [DOI], [ADS], [arXiv:1508.06729 [astro-ph.SR]]. (Cited on page 88.)
Petrie, G. J. D. and Ettinger, S., 2015, “Polar Field Reversals and Active Region Decay”, Space Sci. Rev.. [DOI], [ADS]. (Cited on page 6.)
Petrie, G. J. D. and Haislmaier, K. J., 2013, “Low-latitude Coronal Holes, Decaying Active Regions, and Global Coronal Magnetic Structure”, Astrophys. J., 775, 100. [DOI], [ADS], [arXiv:1308.2171 [astro-ph.SR]]. (Cited on page 64.)
Petrie, G. J. D. and Patrikeeva, I., 2009, “A Comparative Study of Magnetic Fields in the Solar Photosphere and Chromosphere at Equatorial and Polar Latitudes”, Astrophys. J., 699, 871–884. [DOI], [ADS], [arXiv:1010.6041 [astro-ph.SR]]. (Cited on pages 14, 16, 17, 18, 26, 27, and 30.)
Petrie, G. J. D., Petrovay, K. and Schatten, K., 2014, “Solar Polar Fields and the 22-Year Activity Cycle: Observations and Models”, Space Sci. Rev., 186, 325–357. [DOI], [ADS]. (Cited on page 6.)
Raouafi, N.-E., Harvey, J. W. and Henney, C. J., 2007, “Latitude Distribution of Polar Magnetic Flux in the Chromosphere Near Solar Minimum”, Astrophys. J., 669, 636–641. [DOI], [ADS]. (Cited on page 18.)
Robbrecht, E., Berghmans, D. and Van der Linden, R. A. M., 2009, “Automated LASCO CME Catalog for Solar Cycle 23: Are CMEs Scale Invariant?”, Astrophys. J., 691, 1222–1234. [DOI], [ADS], [arXiv:0810.1252]. (Cited on page 88.)
Rudenko, G. V., 2004, “On the validity of application of the radial approximation for the photospheric field”, Solar Phys., 220, 1–20. [DOI], [ADS]. (Cited on page 14.)
Rust, D. M. and Martin, S. F., 1994, “A Correlation Between Sunspot Whirls and Filament Type”, in Solar-Active Region Evolution: Comparing Models with Observations, Proceedings of the 14th International Summer Workshop, NSO / Sacramento Peak, Sunspot, New Mexico, USA, 30 August–3 September 1993, (Eds.) Balasubramaniam, K. S., Simon, G. W., ASP Conference Series, 68, p. 337, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 83.)
Schatten, K. H., Wilcox, J. M. and Ness, N. F., 1969, “A model of interplanetary and coronal magnetic fields”, Solar Phys., 6, 442–455. [DOI], [ADS]. (Cited on pages 42 and 63.)
Schou, J., Antia, H. M., Basu, S. et al., 1998, “Helioseismic Studies of Differential Rotation in the Solar Envelope by the Solar Oscillations Investigation Using the Michelson Doppler Imager”, Astrophys. J., 505, 390–417. [DOI], [ADS]. (Cited on page 42.)
Schrijver, C. J., 1989, “The effect of an interaction of magnetic flux and supergranulation on the decay of magnetic plages”, Solar Phys., 122, 193–208. [DOI], [ADS]. (Cited on pages 45 and 48.)
Schrijver, C. J., 2001, “Simulations of the Photospheric Magnetic Activity and Outer Atmospheric Radiative Losses of Cool Stars Based on Characteristics of the Solar Magnetic Field”, Astrophys. J., 547, 475–490. [DOI], [ADS]. (Cited on pages 21, 48, and 52.)
Schrijver, C. J. and Harvey, K. L., 1994, “The photospheric magnetic flux budget”, Solar Phys., 150, 1–18. [DOI], [ADS]. (Cited on page 48.)
Schrijver, C. J. and Liu, Y., 2008, “The Global Solar Magnetic Field Through a Full Sunspot Cycle: Observations and Model Results”, Solar Phys., 252, 19–31. [DOI], [ADS]. (Cited on pages 51, 52, 53, 55, and 56.)
Schrijver, C. J. and Title, A. M., 2001, “On the Formation of Polar Spots in Sun-like Stars”, Astrophys. J., 551, 1099–1106. [DOI], [ADS]. (Cited on pages 45, 48, 49, and 50.)
Schrijver, C. J. and Zwaan, C., 2000, Solar and Stellar Magnetic Activity, Cambridge Astrophysics Series, 34, Cambridge University Press, Cambridge; New York. [ADS], [Google Books]. (Cited on page 32.)
Schrijver, C. J., Hagenaar, H. J. and Title, A. M., 1997, “On the Patterns of the Solar Granulation and Supergranulation”, Astrophys. J., 475, 328. [DOI], [ADS]. (Cited on page 45.)
Schrijver, C. J., De Rosa, M. L. and Title, A. M., 2002, “What Is Missing from Our Understanding of Long-Term Solar and Heliospheric Activity?”, Astrophys. J., 577, 1006–1012. [DOI], [ADS]. (Cited on page 52.)
Sheeley Jr, N. R., 1964, “Polar Faculae during the Sunspot Cycle”, Astrophys. J., 140, 731. [DOI], [ADS]. (Cited on pages 5, 6, 38, and 74.)
Sheeley Jr, N. R., 1991, “Polar faculae: 1906–1990”, Astrophys. J., 374, 386–389. [DOI], [ADS]. (Cited on page 74.)
Sheeley Jr, N. R., 2008, “A Century of Polar Faculae Variations”, Astrophys. J., 680, 1553–1559. [DOI], [ADS]. (Cited on pages 74 and 75.)
Sheeley Jr, N. R., DeVore, C. R. and Boris, J. P., 1985, “Simulations of the mean solar magnetic field during sunspot cycle 21”, Solar Phys., 98, 219–239. [DOI], [ADS]. (Cited on pages 39, 40, 44, and 52.)
Sheeley Jr, N. R., Wang, Y.-M. and DeVore, C. R., 1989, “Implications of a strongly peaked polar magnetic field”, Solar Phys., 124, 1–13. [DOI], [ADS]. (Cited on page 64.)
Shiota, D., Tsuneta, S., Shimojo, M., Sako, N., Orozco Suárez, D. and Ishikawa, R., 2012, “Polar Field Reversal Observations with Hinode”, Astrophys. J., 753, 157. [DOI], [ADS], [arXiv:1205.2154 [astro-ph.SR]]. (Cited on pages 10, 11, 12, and 34.)
Smith, E. J. and Balogh, A., 2008, “Decrease in heliospheric magnetic flux in this solar minimum: Recent Ulysses magnetic field observations”, Geophys. Res. Lett., 35, L22103. [DOI], [ADS]. (Cited on pages 32, 70, 71, and 72.)
Smith, E. J., Balogh, A., Forsyth, R. J. and McComas, D. J., 2001, “Ulysses in the south polar cap at solar maximum: Heliospheric magnetic field”, Geophys. Res. Lett., 28, 4159–4162. [DOI], [ADS]. (Cited on page 71.)
Snodgrass, H. B., 1983, “Magnetic rotation of the solar photosphere”, Astrophys. J., 270, 288–299. [DOI], [ADS]. (Cited on pages 44 and 53.)
Stenflo, J. O. and Kosovichev, A. G., 2012, “Bipolar Magnetic Regions on the Sun: Global Analysis of the SOHO/MDI Data Set”, Astrophys. J., 745, 129. [DOI], [ADS], [arXiv:1112.5226 [astro-ph.SR]]. (Cited on page 56.)
Sun, X., Liu, Y., Hoeksema, J. T., Hayashi, K. and Zhao, X., 2011, “A New Method for Polar Field Interpolation”, Solar Phys., 270, 9–22. [DOI], [ADS]. (Cited on pages 21, 22, and 27.)
Sun, X., Hoeksema, J. T., Liu, Y. and Zhao, J., 2015, “On Polar Magnetic Field Reversal and Surface Flux Transport During Solar Cycle 24”, Astrophys. J., 798, 114. [DOI], [ADS], [arXiv:1410.8867 [astro-ph.SR]]. (Cited on page 51.)
Svalgaard, L. and Cliver, E. W., 2007, “A Floor in the Solar Wind Magnetic Field”, Astrophys. J., 661, L203–L206. [DOI], [ADS], [arXiv:0706.0961]. (Cited on page 50.)
Svalgaard, L. and Kamide, Y., 2013, “Asymmetric Solar Polar Field Reversals”, Astrophys. J., 763, 23. [DOI], [ADS], [arXiv:1207.2077 [astro-ph.SR]]. (Cited on page 34.)
Svalgaard, L., Duvall Jr, T. L. and Scherrer, P. H., 1978, “The strength of the Sun’s polar fields”, Solar Phys., 58, 225–239. [DOI], [ADS]. (Cited on pages 5, 13, 14, 15, 16, 21, 27, 30, and 32.)
Thompson, M. J., Toomre, J., Anderson, E. R. et al., 1996, “Differential Rotation and Dynamics of the Solar Interior”, Science, 272, 1300–1305. [DOI], [ADS]. (Cited on page 42.)
Tsuneta, S., Ichimoto, K., Katsukawa, Y. et al., 2008, “The Magnetic Landscape of the Sun’s Polar Region”, Astrophys. J., 688, 1374–1381. [DOI], [ADS], [arXiv:0807.4631]. (Cited on pages 5, 7, 8, 9, and 10.)
Ulrich, R. K., 1993, “The Controversial Sun”, in Inside the Stars: IAU Colloquium 137, (Eds.) Weiss, W. W., Baglin, A., ASP Conference Series, 40, pp. 25–42, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 39.)
Ulrich, R. K., 2010, “Solar Meridional Circulation from Doppler Shifts of the Fe I Line at 5250 Å as Measured by the 150-foot Solar Tower Telescope at the Mt. Wilson Observatory”, Astrophys. J., 725, 658–669. [DOI], [ADS], [arXiv:1010.0487 [astro-ph.SR]]. (Cited on pages 51 and 56.)
Ulrich, R. K. and Tran, T., 2013, “The Global Solar Magnetic Field — Identification of Traveling, Long-lived Ripples”, Astrophys. J., 768, 189. [DOI], [ADS], [arXiv:1304.1249 [astro-ph.SR]]. (Cited on page 32.)
van Ballegooijen, A. A., Cartledge, N. P. and Priest, E. R., 1998, “Magnetic Flux Transport and the Formation of Filament Channels on the Sun”, Astrophys. J., 501, 866–881. [DOI], [ADS]. (Cited on page 53.)
Waldmeier, M., 1957, Die Sonnenkorona, Bd. II: Struktur und Variationen der Monochromatischen Korona, Birkhüauser, Basel. (Cited on page 63.)
Wang, Y.-M. and Colaninno, R., 2014, “Is Solar Cycle 24 Producing More Coronal Mass Ejections Than Cycle 23?”, Astrophys. J. Lett., 784, L27. [DOI], [ADS]. (Cited on page 88.)
Wang, Y.-M. and Sheeley Jr, N. R., 1988, “The solar origin of long-term variations of the interplanetary magnetic field strength”, J. Geophys. Res., 93, 11227–11236. [DOI], [ADS]. (Cited on pages 14, 16, and 30.)
Wang, Y.-M. and Sheeley Jr, N. R., 1990, “Solar wind speed and coronal flux-tube expansion”, Astrophys. J., 355, 726–732. [DOI], [ADS]. (Cited on pages 21, 66, and 69.)
Wang, Y.-M. and Sheeley Jr, N. R., 1991, “Magnetic flux transport and the Sun’s dipole moment: New twists to the Babcock-Leighton model”, Astrophys. J., 375, 761–770. [DOI], [ADS]. (Cited on pages 40, 43, and 45.)
Wang, Y.-M. and Sheeley Jr, N. R., 1992, “On potential field models of the solar corona”, Astrophys. J., 392, 310–319. [DOI], [ADS]. (Cited on pages 23, 24, 25, 26, and 27.)
Wang, Y.-M., Nash, A. G. and Sheeley Jr, N. R., 1989, “Evolution of the sun’s polar fields during sunspot cycle 21: Poleward surges and long-term behavior”, Astrophys. J., 347, 529–539. [DOI], [ADS]. (Cited on pages 40, 41, 42, 48, and 50.)
Wang, Y.-M., Sheeley Jr, N. R. and Nash, A. G., 1991, “A new solar cycle model including meridional circulation”, Astrophys. J., 383, 431–442. [DOI], [ADS]. (Cited on page 42.)
Wang, Y.-M., Lean, J. and Sheeley Jr, N. R., 2002, “Role of a Variable Meridional Flow in the Secular Evolution of the Sun’s Polar Fields and Open Flux”, Astrophys. J. Lett., 577, L53–L57. [DOI], [ADS]. (Cited on page 52.)
Wang, Y.-M., Robbrecht, E. and Sheeley Jr, N. R., 2009, “On the Weakening of the Polar Magnetic Fields during Solar Cycle 23”, Astrophys. J., 707, 1372–1386. [DOI], [ADS]. (Cited on pages 32, 51, 52, 53, 54, 55, 56, 63, 64, 67, 71, and 73.)
Wang, Y.-M., Sheeley Jr, N. R. and Stenborg, G., 2013, “Fe XII Stalks and the Origin of the Axial Field in Filament Channels”, Astrophys. J., 770, 72. [DOI], [ADS]. (Cited on page 83.)
Webb, D. F. and Howard, R. A., 1994, “The solar cycle variation of coronal mass ejections and the solar wind mass flux”, J. Geophys. Res., 99, 4201–4220. [DOI], [ADS]. (Cited on page 88.)
Worden, J. and Harvey, J., 2000, “An Evolving Synoptic Magnetic Flux map and Implications for the Distribution of Photospheric Magnetic Flux”, Solar Phys., 195, 247–268. [DOI], [ADS]. (Cited on pages 44, 45, 46, 47, and 48.)
Yeates, A. R. and Mackay, D. H., 2012, “Chirality of High-latitude Filaments over Solar Cycle 23”, Astrophys. J. Lett., 753, L34. [DOI], [ADS], [arXiv:1206.2327 [astro-ph.SR]]. (Cited on pages 83 and 84.)
Zhao, J. and Kosovichev, A. G., 2004, “Torsional Oscillation, Meridional Flows, and Vorticity Inferred in the Upper Convection Zone of the Sun by Time-Distance Helioseismology”, Astrophys. J., 603, 776–784. [DOI], [ADS]. (Cited on page 51.)
Zhao, X. P., Hoeksema, J. T. and Scherrer, P. H., 1999, “Changes of the boot-shaped coronal hole boundary during Whole Sun Month near sunspot minimum”, J. Geophys. Res., 104, 9735–9752. [DOI], [ADS]. (Cited on page 64.)
Zirker, J. B., 1977, “Coronal holes and high-speed wind streams”, Rev. Geophys. Space Phys., 15, 257–269. [DOI], [ADS]. (Cited on page 66.)
Acknowledgements
I thank the two referees for their detailed reports, which corrected many errors and made the review more precise in many places. It has been a privilege to review the work of some of the best solar physicists and astronomers. My interest in the Sun’s polar fields developed from some behind-the-scenes programmatic work on the GONG synoptic magnetograms within a team of scientists and programmers, including Jack Harvey, Frank Hill, Richard Clark and Tom Wentzel. I thank these colleagues, and Luca Bertello, Carl Henney, Aimee Norton, Alexei Pevtsov and Valentín Martínez Pillet for various discussions. Many colleagues, notably Janet Luhmann, Giuliana DeToma and Nick Arge, have been very supportive of our work in this field, for which I am very grateful.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Petrie, G.J.D. Solar Magnetism in the Polar Regions. Living Rev. Sol. Phys. 12, 5 (2015). https://doi.org/10.1007/lrsp-2015-5
Published:
DOI: https://doi.org/10.1007/lrsp-2015-5