Abstract
The solar cycle is reviewed. The 11-year cycle of solar activity is characterized by the rise and fall in the numbers and surface area of sunspots. A number of other solar activity indicators also vary in association with the sunspots including; the 10.7 cm radio flux, the total solar irradiance, the magnetic field, flares and coronal mass ejections, geomagnetic activity, galactic cosmic ray fluxes, and radioisotopes in tree rings and ice cores. Individual solar cycles are characterized by their maxima and minima, cycle periods and amplitudes, cycle shape, the equatorward drift of the active latitudes, hemispheric asymmetries, and active longitudes. Cycle-to-cycle variability includes the Maunder Minimum, the Gleissberg Cycle, and the Gnevyshev-Ohl (even-odd) Rule. Short-term variability includes the 154-day periodicity, quasi-biennial variations, and double-peaked maxima. We conclude with an examination of prediction techniques for the solar cycle and a closer look at cycles 23 and 24.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Solar activity rises and falls with an 11-year cycle that affects modern life in many ways. Increased solar activity includes increases in extreme ultraviolet and X-ray emissions from the Sun that produce dramatic effects in Earth’s upper atmosphere. The associated atmospheric heating increases both the temperature and density of the atmosphere at many spacecraft altitudes. The increase in atmospheric drag on satellites in low Earth orbit can dramatically shorten the orbital lifetime of these valuable assets (for a review see Pulkkinen, 2007).
Increases in the number of solar flares and coronal mass ejections (CMEs) raise the likelihood that sensitive instruments in space will be damaged by energetic particles accelerated in these events. These solar energetic particles (SEPs) can also threaten the health of both astronauts in space and airline travelers in high-altitude, polar routes.
Solar activity apparently affects terrestrial climate as well. Although the change in the total solar irradiance seems too small to produce significant climatic effects, there is good evidence that, to some extent, the Earth’s climate heats and cools as solar activity rises and falls (for a review see Haigh, 2007).
There is little doubt that the solar cycle is magnetic in nature and is produced by dynamo processes within the Sun (for a review of the solar dynamo see Charbonneau, 2010). Although the details concerning, how, when, and where the dynamo processes operate are still uncertain, several basic features of the dynamo are fairly well accepted and provide a framework for understanding the solar cycle.
Within the Sun’s interior magnetic fields and the ionized plasma move together. (Any motion of the plasma relative to the magnetic field or vice versa will set up currents that counter those relative displacements.) Furthermore, throughout most of the Sun’s interior the plasma pressure exceeds the magnetic pressure and the plasma kinetic energy exceeds the magnetic energy so that the motion of the plasma controls the magnetic field — the magnetic field is transported and transformed by the plasma flows. (A notable exception is in sunspots where the magnetic field is strong enough to choke off the convective heat flow — leaving sunspots cooler and darker than their surroundings.)
Two basic processes are involved in most dynamo models — shearing motions that strengthen the magnetic field and align it with the flow (the Omega-effect) and helical motions that lift and twist the magnetic field into a different plane (the alpha-effect). Babcock (1961) described a phenomenological dynamo model in which the shearing motions are those of the Sun’s differential rotation (which he assumed was just a latitudinal shear). His model starts with a global dipole field (a poloidal field) closely aligned with the rotation axis at solar cycle minimum. He assumed that this field threaded through a shallow surface layer and connected to the opposite pole along meridional lines. The observed latitudinal differential rotation should take this weak poloidal field and shear it out to produce a much stronger toroidal field wrapped around the Sun nearly parallel to lines of latitude.
Babcock noted that this toroidal field becomes strongest at latitudes near 30° where the shear is strongest (and where sunspots first appear at the start of each cycle). He suggested that sunspot groups form once this toroidal field becomes strong enough to make the magnetized plasma buoyant. As the cycle progresses and the shearing continues, the latitudes at which the toroidal field becomes buoyant should spread to both higher and lower latitudes.
In Babcock’s model the toroidal field is not directed purely east-west along lines of latitude, but retains a small north-south component from the original poloidal field. This gives a slight tilt to the emerging active regions (the alpha-effect) with the following (relative to the direction of rotation) polarity sunspots in a group at slightly higher latitudes.
At the time that Babcock presented his model, little was known about the Sun’s meridional circulation other than the fact that it was much weaker than the differential rotation. There were, however, reports of sunspot groups moving equatorward at low latitudes and poleward at high latitudes (Dyson and Maunder, 1913; Tuominen, 1942). Those observations (possibly coupled with considerations of the effects of the Coriolis force on the differential rotation) led Babcock to suggest the presence of a meridional flow that was equatorward at low latitudes and poleward at high latitudes.
In his model, this meridional flow pattern transports the low latitude (predominantly leading-polarity) magnetic field toward the equator, where it cancels with the opposite polarity fields in the other hemisphere. Meanwhile, the high latitude, following-polarity, magnetic field is transported to the poles. This new cycle flux cancels with the opposite polarity polar field that were there at the start of the cycle and then builds-up new polar fields with reversed polarity — thus completing the magnetic cycle.
While Babcock’s model does help to explain many characteristics of the solar cycle, it fails in other areas. It does not explain why the sunspot zones drift toward the equator. It assumes a highly simplified initial state. It incorporates a meridional flow that does not agree with modern measurements. It neglects the diffusive effects of the convective motions on the magnetic field (convective motions that were unrecognized at the time). Later dynamo models have gone on to include processes that help to explain these other features but, almost without exception, these later models have also faced observations that conflict with the models themselves. The solar cycle remains one of the oldest and biggest unsolved problem in solar physics.
Here, we examine the nature of the solar cycle and the characteristics that must be explained by any viable dynamo model.
2 The Solar Cycle Discovered
Sunspots (dark patches on the Sun where intense magnetic fields loop up through the surface from the deep interior) were almost certainly seen by prehistoric humans viewing the Sun through hazy skies. The earliest actual recordings of sunspot observations were from China over 2000 years ago (Clark and Stephenson, 1978; Wittmann and Xu, 1987). Yet, the existence of spots on the Sun came as a surprise to westerners when telescopes were first used to observe the Sun in the early 17th century. This is usually attributed to western philosophy in which the heavens and the Sun were thought to be perfect and unblemished (see Bray and Loughhead, 1965; Noyes, 1982).
The first mention of possible periodic behavior in sunspots came from Christian Horrebow, who wrote in his 1776 diary:
Even though our observations conclude that changes of sunspots must be periodic, a precise order of regulation and appearance cannot be found in the years in which it was observed. That is because astronomers have not been making the effort to make observations of the subject of sunspots on a regular basis. Without a doubt, they believed that these observations were not of interest for either astronomy or physics. One can only hope that, with frequent observations of periodic motion of space objects, that time will show how to examine in which way astronomical bodies that are driven and lit up by the Sun are influenced by sunspots. (Wolf, 1877a, translation by Elke Willenberg)
2.1 Schwabe’s discovery
Although Christian Horrebow mentions this possible periodic variation in 1776 the solar (sunspot) cycle was not truly discovered until 1844. In that year Heinrich Schwabe reported in Astronomische Nachrichten (Schwabe, 1844) that his observations of the numbers of sunspot groups and spotless days over the previous 18 years indicated the presence of a cycle of activity with a period of about 10 years. Figure 1 shows his data for the number of sunspot groups observed yearly from 1826 to 1843.
Sunspot groups observed each year from 1826 to 1843 by Heinrich Schwabe (1844). These data led Schwabe to his discovery of the sunspot cycle.
2.2 Wolf’s relative sunspot number
Schwabe’s discovery was probably instrumental in initiating the work of Johann Rudolf Wolf (first at the Bern Observatory and later at Zürich) toward acquiring daily observations of the Sun and extending the records to previous years (Wolf, 1861). Wolf recognized that it was far easier to identify sunspot groups than to identify each individual sunspot. His “relative” sunspot number, R, thus emphasized sunspot groups with
where k is a correction factor for the observer, g is the number of identified sunspot groups, and n is the number of individual sunspots. These Wolf, Zürich, or International Sunspot Numbers have been obtained daily since 1849.
Wolf instituted a system based on the use of a primary observer. The sunspot number for the day was that found by the primary observer. If the primary observer was unable to make a count then the count from a designated secondary or tertiary observer was used instead. Wolf himself was the primary observer from 1849 to 1893 and had a personal correction factor, k = 1.0. He was followed by Alfred Wolfer from 1894 to 1926, William Otto Brunner from 1926 to 1944, and Max Waldmeier from 1945 to 1979. Both Wolf and Wolfer observed the Sun in parallel over a 16-year period. Wolfer counted more spots (different instruments were used and Wolf had a more restrictive definition of what constituted a spot). Thus, the k-factor for Wolfer (and subsequent primary observers) was set at k = 0.60 by comparing the sunspot numbers calculated by Wolfer to those calculated by Wolf over the same days.
Beginning in 1981, and continuing through the present, the International Sunspot Number has been provided by the Royal Observatory of Belgium with S. Cortesi as the primary observer. The process was changed from using the numbers from a single primary/secondary/tertiary observer to using a weighted average of many observers but with their k-factors tied to the primary observer.
2.3 Wolf’s reconstruction of earlier data
Wolf himself extended the record back another 100 years using as primary observers Staudacher from 1749 to 1787, Flaugergues from 1788 to 1825, and Schwabe from 1826 to 1847. Although Wolf included many secondary observers, much of that earlier data is incomplete. Wolf often filled in gaps in the sunspot observations using geomagnetic activity measurements as proxies for the sunspot number. The sunspot numbers are quite reliable since Wolf’s time but those earlier numbers are far less reliable. The monthly averages of the daily numbers are shown in Figure 2.
Monthly averages of the daily International Sunspot Number. This illustrates the solar cycle and shows that it varies in amplitude, shape, and length. Months with observations from every day are shown in black. Months with 1–10 days of observation missing are shown in green. Months with 11–20 days of observation missing are shown in yellow. Months with more than 20 days of observation missing are shown in red. [Missing days from 1818 to the present were obtained from the International daily sunspot numbers. Missing days from 1750 to 1818 were obtained from the Group Sunspot Numbers and probably represent an over estimate.]
3 Solar Activity Data
3.1 Sunspot numbers
The International Sunspot Number, RI, is the key indicator of solar activity. This is not because everyone agrees that it is the best indicator but rather because of the length of the available record. Traditionally, sunspot numbers are given as daily numbers, monthly averages, yearly averages, and smoothed numbers. The standard smoothing is a 13-month running mean centered on the month in question and using half-weights for the months at the start and end. Solar cycle maxima and minima are usually given in terms of these smoothed numbers.
Additional sunspot numbers do exist. The Boulder Sunspot Number is derived from the daily Solar Region Summaries (NOAA/SRS) produced by the US Air Force and National Oceanic and Atmospheric Administration (USAF/NOAA) from sunspot drawings obtained from the Solar Optical Observing Network (SOON) sites since 1977. These summaries identify each sunspot group and list the number of spots in each group. The Boulder Sunspot Number is then obtained using Eq. (1) with k = 1.0. This Boulder Sunspot Number is typically about 55% larger than the International Sunspot Number (corresponding to a correction factor k = 0.65) but is available promptly on a daily basis, while the International Sunspot Number is posted monthly. The relationship between the smoothed Boulder and International Sunspot Number is shown in Figure 3.
Boulder Sunspot Number vs. the International Sunspot Number at monthly intervals from 1981 to 2014. The average ratio of the two is 1.55 and is represented by the solid line through the data points. The Boulder Sunspot Numbers can be brought into line with the International Sunspot Numbers by using a correction factor k = 0.65 for Boulder.
A third sunspot number estimate is provided by the American Association of Variable Star Observers (AAVSO) and is usually referred to as the American Sunspot Number. These numbers are available from 1944 to the present. While the American Number occasionally deviates systematically from the International Number for years at a time, it is usually kept closer to the International Number than the Boulder Number through its use of correction factors. (The American Number is typically about 3% lower than the International Number.) The relationship between the American and International Sunspot number is shown in Figure 4.
A fourth sunspot number is the Group Sunspot Number, RG, devised by Hoyt and Schatten (1998). This index counts only the number of sunspot groups, averages together the observations from multiple observers (rather than using the primary/secondary/tertiary observer system), and normalizes the numbers to the International Sunspot Numbers using
where N is the number of observers, ki is the i-th observer’s correction factor, Gi is the number of sunspot groups observed by observer i, and 12.08 normalizes the number to the International Sunspot Number. Hathaway et al. (2002) found that the Group Sunspot Number follows the International Number fairly closely but not to the extent that it should supplant the International Number. In fact, the Group Sunspot Numbers are not readily available after 1995. The primary utility of the Group Sunspot number is in extending the sunspot number observations back to the earliest telescopic observations in 1610. The relationship between the Group and International Sunspot number is shown in Figure 5 for the period 1874 to 1995. For this period the numbers agree quite well, with the Group Number being about 1% higher than the International Number. For earlier dates the Group Number is a significant 24% lower than the International Number.
These sunspot numbers are available from NOAA. The International Number can be obtained monthly directly from SILSO.
3.2 Revised sunspot numbers
As noted earlier, Wolf revised his sunspot numbers based on new information. The previous sections also show that the sunspot number for a given day, month, or year, can vary substantially depending on the source. There is now good evidence that even the modern record (1849 to the present) may need substantial revision. Svalgaard (2013) has noted that when Waldmeier became the primary observer in 1946 he changed the way the sunspot number was calculated (Waldmeier, 1968). Instead of counting each spot within a group once, he gave greater counts (2, 3, or 5) to larger spots. While this change went largely unnoticed by the community, the practice has continued up to the present with the numbers provided by SILSO. By comparing sunspot number counts with and without this weighting, Svalgaard (2013) estimates that the modern sunspot numbers since 1946 have been inflated by about 20%.
The earlier sunspot numbers, of course, have always been considered much less reliable. There are many days (or even months) without any reported observations prior to 1849. Even when observations are reported it can be difficult to determine a sunspot number from the reports. This has led to divergent sunspot numbers for earlier times, as can be seen in Figure 6.
Since the Group Sunspot Number work of Hoyt and Schatten (1998), new observations have come to light. For example, Vaquero et al. (2007a,b) and Arlt (2008) have uncovered previously unknown 18th century observations that indicate possible changes to the Group Sunspot Number in the late 18th century, shortly after the Maunder Minimum. Vaquero et al. (2011) also found observations by G. Marcgraf for the critical years of 1636–1642. These observations suggest that the amplitude of the sunspot cycle just prior to the onset of the Maunder Minimum was much smaller than that given by the Group Sunspot Number (20 vs. 60–70 sunspots at maximum).
New analysis methods (e.g., Pop, 2012; Arlt et al., 2013; Leussu et al., 2013) have also been developed and these continue to reveal errors and inconsistencies in the various sunspot number records. As this is being written, there is a significant effort within the solar physics community to reconcile the differences in the sunspot numbers and to provide a more reliable sunspot record (with error estimates) from 1610 to the present. Any revisions can have far-reaching impact on other areas. Sunspot numbers are used to estimate the Sun’s contribution to climate change (e.g., Lean and Rind, 2008) and to the modulation of galactic cosmic rays and the radioisotopes they produce in Earth’s atmosphere (e.g., Usoskin, 2013).
3.3 Sunspot areas
Sunspot areas are thought to be more physical measures of solar activity. Sunspot areas and positions were diligently recorded by the Royal Observatory, Greenwich (RGO) from May 1874 to the end of 1976 using measurements from photographic plates obtained from RGO itself and its sister observatories in Cape Town, South Africa, Kodaikanal, India, and Mauritius. Both umbral areas and whole spot areas were measured and corrected for foreshortening on the visible disc. Sunspot areas were given in units of millionths of a solar hemisphere (µHem). Comparing the corrected whole spot areas to the International Sunspot Number (Figure 7) shows that the two quantities are indeed highly correlated (r = 0.994, r2 = 0.988). Furthermore, there is no evidence for any lead or lag between the two quantities over each solar cycle. Both measures could almost be used interchangeably except for one aspect — the zero point. Since a single, solitary sunspot gives a sunspot number of 11 (6.6 for a correction factor k = 0.6) the zero point for the sunspot number is shifted slightly from zero. The best fit to the data shown in Figure 7 gives an offset of about 4 and a slope of 16.7.
In 1977, NOAA began reporting much of the same sunspot area and position information in its Solar Region Summary reports. These reports are derived from measurements taken from sunspot drawings done at the USAF SOON sites. The sunspot areas were initially estimated by overlaying a grid and counting the number of cells that a sunspot covered. In late 1981, this procedure was changed to employ an overlay with a number of circles and ellipses with different areas. The sunspot areas reported by USAF/NOAA are significantly smaller than those from RGO (Fligge and Solanki, 1997; Baranyi et al., 2001; Hathaway et al., 2002; Balmaceda et al., 2009). Figure 8 shows the relationship between the USAF/NOAA sunspot areas and the International Sunspot Number. The slope in the straight line fit through the data is 11.22, significantly less than that found for the RGO sunspot areas. This indicates that these later sunspot area measurements should be multiplied by 1.49 to be consistent with the earlier RGO sunspot areas. The combined RGO USAF/NOAA datasets are available online (RGO/USAF).
Smoothed USAF/NOAA Sunspot Area vs. the International Sunspot Number at monthly intervals from January 1977 to August 2014. The two quantities are correlated at the 99.1% level with a proportionality constant of about 11.2. These sunspot areas have to be multiplied by a factor of 1.49 to bring them into line with the RGO sunspot areas. Data obtained prior to cycle 23 are shown with filled dots, while data obtained after 1997 are shown with open circles.
The source of this substantial (40–50%) difference in reported sunspot areas is still uncertain. Sunspot area measurements using the SOHO/MDI intensity images confirm that the error lies with the USAF/NOAA data. While the measurements methods are clearly different (counting squares or pixels vs. selecting the appropriate ellipse) and the images are clearly different (photographic plates or CCD images vs. drawings) it is not clear that this would give an underestimate with the USAF/NOAA method. Foukal (2014) has suggested that the source of the error is in the small spots that appear as single dots with a pencil on the USAF drawings. He argues that these are more accurately recorded by RGO and others using photographs or CCD image and that the large number of such spots can account for the size of the underestimation by USAF/NOAA.
Sunspot areas are also available from a number of other solar observatories, with links to much of that data available at NOAA/NGDC. While individual observatories have data gaps, their data are very useful for helping to maintain consistency over the full interval from 1874 to the present. Many of these observatories (notably Debrecen) provide images in white light, Calcium K, and/or magnetic field as well.
These datasets have additional information that is not reflected in sunspot numbers — positional information — both latitude and longitude. The distribution of sunspot area with latitude (Figure 9) shows that sunspots appear in two bands on either side of the Sun’s equator. At the start of each cycle spots appear at latitudes above about 20–25°. As the cycle progresses the range of latitudes with sunspots broadens and the central latitude slowly drifts toward the equator, but with a zone of avoidance near the equator. This behavior is referred to as “Spörer’s Law of Zones” by Maunder (1903) and was famously illustrated by his “Butterfly Diagram” (Maunder, 1904).
Sunspot area as a function of latitude and time. The average daily sunspot area for each solar rotation since May 1874 is plotted as a function of time in the lower panel. The relative area in equal area latitude strips is illustrated with a color code in the upper panel. Sunspots form in two bands, one in each hemisphere, which start at about 25 from the equator at the start of a cycle and migrate toward the equator as the cycle progresses.
3.4 10.7 cm solar flux
The 10.7 cm Solar Flux is the disc-integrated emission from the Sun at the radio wavelength of 10.7 cm (2800 MHz) (see Tapping and Charrois, 1994). This measure of solar activity has advantages over sunspot numbers and areas in that it is completely objective and can be made under virtually all weather conditions. Measurements of this flux have been taken daily by the Canadian Solar Radio Monitoring Programme since 1946. Several measurements are taken each day and care is taken to avoid reporting values influenced by flaring activity. Observations were made in the Ottawa area from 1946 to 1990. In 1990, a new flux monitor was installed at Penticton, British Columbia and run in parallel with the Ottawa monitor for six months before moving the Ottawa monitor itself to Penticton as a back-up. Measurements are provided daily (Latest Solar Radio Flux Report) and the full dataset is archived (Solar 10.7 cm Flux Data).
The relationship between the 10.7 cm radio flux and the International Sunspot Number is somewhat more complicated than that for sunspot area. First of all, the 10.7 cm radio flux has a base level of about 67 solar flux units. Secondly, the slope of the relationship changes as the sunspot number increases up to about 30. This is captured in a formula given by Holland and Vaughn (1984) as:
In addition to this slightly nonlinear relationship there is evidence that the 10.7 cm radio flux lags behind the sunspot number by about one month (Bachmann and White, 1994).
Figure 10 shows the relationship between the 10.7 cm radio flux and the International Sunspot Number. The two measures are highly correlated (r = 0.995, r2 = 0.990). The Holland and Vaughn formula fits the early data quite well. However, the data after 1997 lies systematically higher than the levels given by the Holland and Vaughn formula. Speculation concerning the cause of this change is discussed in Section 8.
10.7cm radio flux vs. International Sunspot Number for the period of August 1947 to January 2014. Data obtained prior to cycle 23 are shown with filled dots while data obtained after 1997 are shown with open circles. The Holland and Vaughn formula relating the radio flux to the sunspot number is shown with the solid line. These two quantities are correlated at the 99.5% level.
3.5 Total irradiance
The Total Solar Irradiance (TSI) is the radiant energy emitted by the Sun at all wavelengths crossing a square meter each second outside Earth’s atmosphere. Although ground-based measurements of this “solar constant” and its variability were made decades ago (Abbot et al., 1913), accurate measurements of the Sun’s total irradiance have only become available since our access to space. Several satellites have carried instruments designed to make these measurements: Nimbus-7 from November 1978 to December 1993; the Solar Maximum Mission (SMM) ACRIM-I from February 1980 to June 1989; the Earth Radiation Budget Satellite (ERBS) from October 1984 to December 1995; NOAA-9 from January 1985 to December 1989; NOAA-10 from October 1986 to April 1987; Upper Atmosphere Research Satellite (UARS) ACRIM-II from October 1991 to November 2001; ACRIMSAT ACRIM-III from December 1999 to the present; SOHO/VIRGO from January 1996 to the present; and SORCE/TIM from January 2003 to the present.
While each of these instruments is extremely precise in its measurements, their absolute accuracies vary in ways that make some important aspects of the TSI subjects of controversy. Figure 11 shows daily measurements of TSI from some of these instruments. Each instrument measures the drops in TSI due to the formation and disc passages of large sunspot groups as well as the general rise and fall of TSI with the sunspot cycle (Willson and Hudson, 1988). However, there are significant offsets among the absolute measured values. Intercomparisons of the data have lead to different conclusions. Willson (1997) combined the SMM/ACRIM-I data with the later UARS/ACRIM-II data by using intercomparisons with Nimbus-7 and ERBS and concluded that the Sun was brighter by about 0.04% during the cycle 22 minimum than it was during the cycle 21 minimum. Fröhlich and Lean (1998) constructed a composite (the PMOD composite) that includes Nimbus-7, ERBS, SMM/ACRIM-I, UARS/ACRIM-II, and SOHO/VIRGO, which does not show this increase.
This situation has not improved with the addition of data from the decline of cycle 23 and the extraordinary cycle 23/24 minimum. Fröhlich (2013) found that the PMOD composite irradiance dropped well below the lowest values seen at the previous two minima. Scafetta and Willson (2014) found that the ACRIM composite irradiance at cycle 23/24 minimum was intermediate between the values seen at the previous two minima.
Comparing the PMOD composite to the sunspot number (Figure 12) shows a strong correlation between the two quantities but with different behavior during cycle 23 (the VIRGO era). At its peak, cycle 23 had sunspot numbers about 20% smaller than cycle 21 or 22. However, the cycle 23 peak PMOD composite TSI was similar to that of cycles 21 and 22. This behavior is similar to that seen in the 10.7 cm flux in Figure 10, but is complicated by the fact that the cycle 23 PMOD composite falls well below that for cycle 21 and 22 during the decline of cycle 23 toward minimum, while the 10.7 cm flux remained above the corresponding levels for cycles 21 and 22.
Comparing the ACRIM composite to the sunspot number (Figure 13) shows a much weaker correlation between the two quantities. While the tendency for TSI to increase with sunspot number is evident in some intervals (during an individual cycle’s rising and fall phases), any simple proportionality to sunspot number appears less likely. The unresolved differences in the TSI measurements make further conclusions difficult. Both composites indicate that either further adjustments need to be made to the measurements or the Sun’s irradiance is not tied solely to magnetic features.
3.6 Magnetic field
Magnetic fields on the Sun were first measured in sunspots by Hale (1908). The magnetic nature of the solar cycle became apparent once these observations extended over more than a single cycle (Hale et al., 1919). While it is now well recognized that the solar cycle is best represented in terms of the magnetic field itself, systematic daily observations are only available starting in the 1970s and thus only characterize the last three-and-a-half solar cycles. Nonetheless, a number of key characteristics were clear from even the first observations.
Hale et al. (1919) noted “Hale’s Polarity Laws” for sunspots (illustrated in Figure 14):
… the preceding and following spots of binary groups, with few exceptions, are of opposite polarity, and that the corresponding spots of such groups in the Northern and Southern hemispheres are also of opposite sign. Furthermore, the spots of the present cycle are opposite in polarity to those of the last cycle.
Hale’s Polarity Laws. A magnetogram from sunspot cycle 22 (1989 August 2) is shown on the left, with yellow denoting positive polarity and blue denoting negative polarity. A corresponding magnetogram from sunspot cycle 23 (2000 June 26) is shown on the right. Leading spots in one hemisphere have opposite magnetic polarity to those in the other hemisphere and the polarities flip from one cycle to the next.
In addition to Hale’s Polarity Laws for the changing polarity of sunspots, it was found that the Sun’s polar fields changed polarity as well. Babcock and Livingston (1958) noted that the Sun’s south polar field reversed in mid-1957. A year later, Babcock (1959) reported that the north polar field had reversed in late-1958 and suggested that these field reversals occur systematically at about the time of cycle maximum (the maximum for cycle 19 occurred in late-1957). The polar fields are thus out of phase with the sunspot cycle — polar fields are at their peak near sunspot cycle minima.
The polar fields have been measured almost daily from the Wilcox Solar Observatory at Stanford University since the mid 1970s (Scherrer et al., 1977). While the measurements have a very coarse spatial resolution, great care has been taken to account for scattered light and other instrumental effects. Their smoothed polar field strengths are shown in Figure 15, along with the sunspot number for reference. The polar fields reach their peaks late in each cycle at about the time of cycle minimum, and the fields reverse polarity at about the time of cycle maximum. It is also clear that the polar fields vary in strength from cycle to cycle.
The Sun’s polar fields as reported by the Wilcox Solar Observatory. The smoothed field strength in their northernmost pixel is shown with the solid black line. The smoothed field strength in their southernmost pixel is shown with the dashed line. The smoothed sunspot number (scaled to fit on the figure) is shown with the red line.
Systematic, high-resolution, daily observations of the Sun’s magnetic field over the visible solar disc were initiated at the Kitt Peak National Observatory in the early 1970s. Synoptic maps from these measurements are nearly continuous from early-1975 through mid-2003. Shortly thereafter, similar (and even higher resolution) data became available from the National Solar Observatory (NSO) Synoptic Optical Long-term Investigations of the Sun (SOLIS) facility (Keller, 1998). Gaps between these two datasets and within the SOLIS dataset can be filled with data from the Michelson Doppler Imager (MDI) on the Solar and Heliospheric Observatory (SOHO) mission (Scherrer et al., 1995). These synoptic maps are presented in an animation here (Figure 16).
The radial magnetic fields from these synoptic maps are averaged over longitude for each solar rotation to produce a “Magnetic Butterfly Diagram,” as shown in Figure 17. In addition to showing the 11-year cycle, the equatorward drift of the sunspot zones, and the overlapping cycles at minimum, this Magnetic Butterfly Diagram also exhibits Hale’s Polarity Laws, the polar field reversals, and “Joy’s Law” (Hale et al., 1919):
The following spot of the pair tends to appear farther from the equator than the preceding spot, and the higher the latitude, the greater is the inclination of the axis to the equator.
Joy’s Law and Hale’s Polarity Laws are apparent in the “butterfly wings.” The equatorial sides of these wings are dominated by the lower latitude, preceding-spot polarities, while the poleward sides are dominated by the higher latitude, following-spot polarities. These polarities are opposite in opposing hemispheres and from one cycle to the next (Hale’s Law). This figure also shows that the higher latitude fields are transported toward the poles where they eventually reverse the polar field at about the time of sunspot cycle maximum. The number of key characteristics of the solar cycle that are evident within Figure 17 make it a litmus test for dynamo theories.
3.7 Ephemeral regions
Ephemeral regions are small (< 30 Mm across) bipolar magnetic regions that are typically observed for only 1–2 days and usually do not produce sunspots. They appear to extend the spectrum of the bipolar active regions that typically do produce sunspots (see Parnell et al., 2009) to smaller sizes. They were first mentioned by Dodson (1953) in reference to a small, short-lived, high-latitude sunspot.
Harvey and Martin (1973) examined magnetograms and Hα images acquired over three 4-day intervals in 1970 and 1971 (after the peak of cycle 20) and concluded that as many as 100 ephemeral regions may erupt per day with as much total magnetic flux as erupts in the larger active regions. They also noted that the distribution in latitude was broader than that of the active regions and suggested that the occurrence of ephemeral regions did not vary with the sunspot cycle. Later, however, in a larger study extending from 1970 to 1973, Harvey et al. (1975) did find a direct solar cycle dependence. They also found that while the spatial orientation was almost random, there was a small excess of new cycle orientations at the high latitudes in 1973.
A solar cycle dependence for the number of ephemeral regions was also found by Martin and Harvey (1979) but with a slight shift in phase due to the early appearance of new cycle ephemeral regions. Their observations also led to the conclusion that there was more overlap between solar cycles than is seen in sunspots alone (see Section 4.14 on the extended solar cycle).
The small sizes and short lifetimes of ephemeral regions made these early observations with ground-based magnetographs quite difficult. This situation was greatly improved with the advent of space-based magnetographs. Hagenaar (2001) studied the properties of ephemeral regions using the SOHO/MDI instrument and found far more (smaller) ephemeral regions with a rate of emergence sufficient to replace the quiet Sun magnetic field in just 14 hours.
Hagenaar et al. (2003) extended these observations to include the rise from cycle minimum in 1996 to maximum in 2001 and found that the number of the small ephemeral regions varied in anti-phase with the sunspot cycle. Later studies (Abramenko et al., 2006; Hagenaar et al., 2008) found that fewer ephemeral regions emerge in unipolar regions (coronal holes). This might explain some of the cycle dependence since more unipolar regions are found at cycle maximum in the studied area (within 60 of disc center).
3.8 Flares and coronal mass ejections
Carrington (1859) and Hodgson (1859) reported the first observations of a solar flare from white-light observations on September 1, 1859. While observing the Sun projected onto a viewing screen, Carrington noticed a brightening that lasted for about 5 minutes. Hodgson also noted a nearly simultaneous geomagnetic disturbance. Since that time, flares have been observed in H-alpha from many ground-based observatories and characterizations of flares from these observations have been made (e.g., Benz, 2008).
X-rays from the Sun were measured by instruments on early rocket flights and their association with solar flares was recognized immediately. NOAA has flown solar X-ray monitors on its Geostationary Operational Environmental Satellites (GOES) since 1975 as part of its Space Environment Monitor. The solar X-ray flux has been measured in two bandpasses by these instruments: 0.5 to 4.0 Å and 1.0 to 8.0 Å. The X-ray flux is given on a logarithmic scale with A and B levels as typical background levels (depending upon the phase of the cycle), and C, M, and X levels indicating increasing levels of flaring activity. The number of M-class and X-class flares seen in the 1.0–8.0 Å band tends to follow the sunspot number, as shown in Figure 18. The two measures are well correlated (r = 0.95, r2 = 0.90) but there is a tendency to have more flares on the declining phase of a sunspot cycle (the correlation is maximized for a 2-month lag). In spite of this correlation, significant flares can, and have, occurred at all phases of the sunspot cycle. X-class flares have occurred during the few months surrounding the sunspot cycle minima for three of the last four cycles (Figure 19).
Monthly M- and X-class flares vs. International Sunspot Number for the period of March 1976 to December 2013. These two quantities are correlated at the 95% level but show significant scatter when the sunspot number is high (greater than ∼ 100). Data obtained prior to cycle 23 are shown with filled dots, while data obtained after 1997 are shown with open circles.
Coronal mass ejections (CMEs) are often associated with flares but can also occur in the absence of a flare. CMEs were discovered in the early 1970s via spacecraft observations from OSO 7 (Tousey, 1973) and from Skylab (MacQueen et al., 1974). Routine CME observations began with the Solar Maximum Mission and continue with SOHO. The frequency of occurrence of CMEs is also correlated with sunspot number (Webb and Howard, 1994) but with differences depending on the data used, the definition of what constitutes a CME, and the method used for finding them (e.g., Webb and Howard, 2012).
3.9 Geomagnetic activity
Geomagnetic activity also shows a solar cycle dependence but one that is more complex than seen in sunspot area, radio flux, or flares and CMEs. There are a number of indices of geomagnetic activity; most measure rapid (hour-to-hour) changes in the strength and/or direction of Earth’s magnetic field from small networks of ground-based observatories. The ap index is a measure of the range of variability in the geomagnetic field (in 2 nT units), measured in three-hour intervals from a network of about 13 high-latitude stations. The average of the eight daily ap values is given as the equivalent daily amplitude Ap. These indices extend from 1932 to the present. The aa index extends back further (to 1868; see Mayaud, 1972), and is similarly derived from three-hour intervals but from two antipodal stations located at latitudes of about 50°. The locations of these two stations have changed from time to time and there is evidence (Svalgaard et al., 2004) that these changes are reflected in the data itself. Another frequently used index is Dst, disturbance storm time, derived from measurements obtained at four equatorial stations, since 1957.
Figure 20 shows the smoothed monthly geomagnetic index aa as a function of time along with the sunspot number, for comparison. The minima in geomagnetic activity tend to occur just after those for the sunspot number and the geomagnetic activity tends to remain high during the declining phase of each cycle. This late-cycle geomagnetic activity is attributed to the effects of high-speed solar wind streams from low-latitude coronal holes (e.g., Legrand and Simon, 1985). Figure 20 also shows the presence of multi-cycle trends in geomagnetic activity that may be related to changes in the Sun’s magnetic field (Lockwood et al., 1999).
Feynman (1982) decomposed geomagnetic variability into two components — one proportional to and in phase with the sunspot cycle (the R, or Relative sunspot number component) and another out of phase with the sunspot cycle (the I, or Interplanetary component). Figure 21 shows the relationship between geomagnetic activity and sunspot number. As the sunspot number increases there is a baseline level of geomagnetic activity that increases as well. However, uniformly high levels of geomagnetic activity are found even when the sunspot number is quite low.
3.10 Cosmic rays
The flux of galactic cosmic rays at 1 AU is modulated by the solar cycle. Galactic cosmic rays consist of electrons and bare nuclei that are accelerated to GeV energies and higher at shocks produced by supernovae. The positively charged nuclei produce cascading showers of particles in Earth’s upper atmosphere that can be measured by neutron monitors at high-altitude observing sites. The oldest continuously operating neutron monitor is located in Climax, Colorado, USA. Daily observations extend from 1951 to 2006. Monthly averages of the neutron counts are shown as a function of time in Figure 22, along with the sunspot number. As the sunspot numbers rise the neutron counts fall. This anti-correlation is attributed to scattering of the cosmic rays by tangled magnetic field within the heliosphere (Parker, 1965). At times of high solar activity, magnetic structures are carried outward on the solar wind. These structures scatter incoming cosmic rays and reduce their flux in the inner solar system.
Cosmic Ray flux from the Climax Neutron Monitor and rescaled Sunspot Number. The monthly averaged neutron counts from the Climax Neutron Monitor are shown by the solid line. The monthly averaged sunspot numbers (multiplied by five and offset by 4500) are shown by the dotted line. Cosmic ray variations are anti-correlated with solar activity but with differences depending upon the Sun’s global magnetic field polarity (A+ indicates periods with positive polarity north pole, while A− indicates periods with negative polarity).
The reduction in cosmic ray flux tends to lag behind solar activity by 6 to 12 months (Forbush, 1954) but with significant differences between the even numbered and odd numbered cycles. In the even numbered cycles (cycles 20 and 22) the cosmic ray variations seen by neutron monitors lag sunspot number variations by only about 2 months. In the odd numbered cycles (cycles 19, 21, and 23) the lag is from 10 to 14 months. Figure 22 also shows that the shapes of the cosmic ray maxima at sunspot cycle minima are different for the even and odd numbered cycles. The cosmic ray maxima (as measured by the neutron monitors) are sharply peaked at the sunspot cycle minima leading up to even numbered cycles and broadly peaked prior to odd numbered sunspot cycles. This behavior is accounted for in the transport models for galactic cosmic rays in the heliosphere (e.g., Ferreira and Potgieter, 2004). The positively charged cosmic rays drift in from the heliospheric polar regions when the Sun’s north polar field is directed outward (positive). When the Sun’s north polar field is directed inward (negative) the positively charged cosmic rays drift inward along the heliospheric current sheet where they are scattered by corrugations in the current sheet and by magnetic clouds from CMEs. The negatively charged cosmic rays (electrons) drift inward from directions (polar or equatorial) opposite to the positively charged cosmic rays that are detected by neutron monitors.
3.11 Radioisotopes in tree rings and ice cores
The radioisotopes 14C and 10Be are produced in Earth’s stratosphere by the impact of galactic cosmic rays on 14N and 16O. The 14C gets oxidized to form CO2, which is taken up by plants in general and trees in particular, where it becomes fixed in annual growth rings. The 10Be gets oxidized and becomes attached to aerosols that can precipitate in snow, where it then becomes fixed in annual layers of ice. The solar cycle modulation of the cosmic ray flux can then lead to solar cycle related variations in the atmospheric abundances of 14C (Stuiver and Quay, 1980) and 10Be (Beer et al., 1990). While the production rates of these two radioisotopes in the stratosphere should be anti-correlated with the sunspot cycle, the time scales involved in the transport and ultimate deposition in tree rings and ice tends to reduce and delay the solar cycle variations (see Masarik and Beer, 1999). The production rates in the stratospheric are functions of magnetic latitude, which changes as Earth’s magnetic dipole wanders and varies in strength. Furthermore, the latency in the stratosphere/troposphere is a function of the changing reservoirs for these chemical species. This rather complicated production/transport/storage/deposition process makes direct comparisons between Δ14C (the difference between measured 14C abundance and that expected from its 5730-year half-life) and sunspot number difficult. For more details on the influence of solar activity on radioisotopes and on what is learned about solar activity from radioisotopes, see the review by Usoskin (2013).
4 Individual Cycle Characteristics
Each sunspot cycle has its own characteristics. Many of these characteristics are shared by other cycles and these provide important information for models of the solar activity cycle. A paradigm shift in sunspot cycle studies came about when Waldmeier (1935) suggested that each cycle should be treated as an individual outburst with its own characteristics. Prior to that time, the fashion was to consider solar activity as a superposition of Fourier components. This superposition idea probably had its roots in the work of Wolf (1859), who suggested a formula based on the orbits of Venus, Earth, Jupiter, and Saturn to fit Schwabe’s data for the years 1826 to 1848.
Determining characteristics such as period and amplitude would seem simple and straightforward but the published studies show that this is not true. A prime example concerns determinations of the dates (year and month) of cycle minima. A frequently used method is to take monthly averages of the daily International Sunspot Number and to smooth these with the 13-month running mean. Unfortunately, this leaves several uncertain dates. With this method, the minimum that occurred in 1810 prior to cycle 6 could be taken as any month from April to December — all nine months had smoothed sunspot numbers of 0.0!
4.1 Minima and maxima
The dates and values for the cycle minima and maxima are the primary data for many studies of the solar cycle. These data are sensitive to the methods and input data used to find them. Solar activity is inherently noisy and it is evident that there are significant variations in solar activity on time scales shorter than 11 years (see Section 6). Waldmeier (1961) published tables of sunspot numbers along with dates and values of minima and maxima for cycles 1 to 19. McKinnon (1987) extended the data to include cycles 20 and 21. The values they give for sunspot number maxima and minima are those found using the 13-month running mean. However, the dates given for maxima and minima may vary after considering additional indicators. According to McKinnon:
… maximum is based in part on an average of the times extremes are reached in the monthly mean sunspot number, the smoothed monthly mean sunspot number, and in the monthly mean number of spot groups alone.
These dates and the values for sunspot cycle maxima are given in Table 1 (the number of groups is multiplied by 12.08 to produce group sunspot numbers that are comparable to the relative sunspot numbers). It is clear from this table that considerably more weight is given to the date provided by the 13-month running mean. The dates provided by Waldmeier and McKinnon are far closer to those given by the 13-month running mean than they are to the average date of the three indicators. (One exception is the date they give for the maximum of cycle 14, which should be a half-year earlier by almost any averaging scheme.) The monthly numbers of sunspots and spot groups vary widely and, in fact, should be less reliable indicators and given lesser weight in determining maximum.
The minima in these three indicators have been used along with additional sunspot indicators to determine the dates of minima. The number of spotless days in a month tends to maximize at the time of minimum and the number of new cycle sunspot groups begins to exceed the number of old cycle sunspot groups at the time of minimum. Both Waldmeier and McKinnon suggest using these indicators as well when setting the dates for minima. These dates are given in Table 2 where both the spotless days per month and the number of old-cycle and new-cycle groups per month are smoothed with the same 13-month mean filter. The average date given in the last column is the average of: the 13-month mean minimum date; the 13-month mean spotless days per month maximum date; and the date when the 13-month mean of the number of new-cycle groups exceeds the 13-month mean of the number of old-cycle groups. For the early cycles, where spotless days and old-cycle and new-cycle groups are not available, the 13-month mean minimum date is used for those dates in forming the average.
When available, all three indicators tend to give dates that are fairly close to each other and the average of the three is usually close to the dates provided by Waldmeier and McKinnon. There are, however, two notable exceptions. The dates given by Waldmeier for the minima preceding cycles 13 and 14 are both significantly earlier than the dates given by all three indicators. The cycle 13 minimum date of 1889.6 was adopted from Wolf (1892) while the cycle 14 minimum date of 1901.7 was adopted from Wolfer (1903).
Since many researchers simply adopt the date given by the minimum in the 13-month running mean, the date for the minimum preceding cycle 23 is also problematic. The minimum in the smoothed sunspot number came in May of 1996. The maximum in the smoothed number of spotless days per month came in July of 1996. However, the cross-over in the smoothed number of groups from old-cycle groups to new-cycle groups occurred in December of 1996. Harvey and White (1999) provide a good discussion of the problems in determining cycle minimum and have argued that the minimum for cycle 23 should be taken as September 1996 (based on their determination that new-cycle groups exceed old-cycle groups in January of 1997). The average of the three indicators gives August 1996.
Additional problems in assigning dates and values to maxima and minima can be seen when using data other than sunspot numbers. Table 3 lists the dates and values for cycle maxima using the 13-month running mean on sunspot numbers, sunspot areas, and 10.7 cm radio flux. The sunspot areas have been converted to sunspot number equivalents using the relationship shown in Figure 7, and the 10.7 cm radio flux has been converted into sunspot number equivalents using Eq. (3). Very significant differences can be seen in the dates. Over the last five cycles the ranges in dates given by the different indices have been: 4, 27, 25, 1, and 22 months.
These tables illustrate the problems in determining dates and values for cycle minima and maxima. The crux of the problem is in the short-term variability of solar activity. One solution is to use a different smoothing method.
4.2 Smoothing
The monthly averages of the daily International Sunspot Number are noisy and must be smoothed in some manner in order to determine appropriate values for parameters such as minima, maxima, and their dates of occurrence. The daily values themselves are highly variable. They depend upon the number and the quality of observations as well as the time of day when they are taken (the sunspot number changes over the course of the day as spots form and fade away). The monthly averages of these daily values are also problematic. The Sun rotates once in about 27 days but the months vary in length from 28 to 31 days. If the Sun is particularly active at one set of longitudes then some monthly averages will include one appearance of these active longitudes while other months will include two. This aspect is particularly important for investigations of short-term (months) variability (see Section 7). For long-term (years) variability this can be treated as noise and filtered out.
The traditional 13-month running mean (centered on a given month with equal weights for months −5 to +5 and half-weight for months −6 and +6) is both simple and widely used, but does a poor job of filtering out high-frequency variations (although it is better than the simple 12-month average). Gaussian-shaped filters are preferable because they have Gaussian shapes in the frequency domain and effectively remove high-frequency variations (Hathaway et al., 1999). A tapered (to make the filter weights and their first derivatives vanish at the end points) Gaussian filter is given by
with
where t is the time in months and 2a is the Full Width at Half Maximum (FWHM) of the filter (note that this formula is slightly different than that given in Hathaway et al. (1999)). There are significant variations in solar activity on time scales of one to three years (see Section 6). These variations can produce double-peaked maxima that are filtered out by a 24-month Gaussian filter. The frequency responses of these filters are shown in Figure 23.
Signal transmission for filters used to smooth monthly sunspot numbers. The 13-month running mean and the 12-month average pass significant fractions (as much as 20%) of signals with frequencies higher than one cycle per year. The 24-month FWHM Gaussian passes less than 0.3% of those frequencies and passes less than about 1% of the signal with frequencies of a half-cycle per year or higher.
Using the 24-month FWHM Gaussian filter on the data used to create Table 3 gives far more consistent results for both maxima and minima. The results for maxima are shown in Table 4. The ranges of dates for the last five maxima become: 1, 10, 13, 4, and 11 months — roughly half the ranges found using the 13-month running mean.
4.3 Cycle periods
The period of a sunspot cycle is defined as the elapsed time from the minimum preceding its maximum to the minimum following its maximum. This does not, of course, account for the fact that each cycle actually starts well before its preceding minimum and continues long after its following minimum. By this definition, a cycle’s period is dependent upon the behavior of both the preceding and following cycles. The measured period of a cycle is also subject to uncertainties in determining the dates of minimum, as indicated in the previous subsections. Nonetheless, the length of a sunspot cycle is a key characteristic and variations in cycle periods have been well studied. The average cycle period can be fairly accurately determined by simply subtracting the date for the minimum preceding cycle 1 from the date for the minimum preceding cycle 23 and dividing by the 22 cycles those dates encompass. This gives an average period for cycles 1 to 22 of 131.7 months — almost exactly 11 years.
The distribution of cycle periods depends upon the cycles used and the methods used to determine minima. Eddy (1977) noted that the cycle periods did not appear to be distributed normally. Wilson (1987) included cycles 8 to 20 and used the dates for minimum from the 13-month mean of the monthly sunspot numbers. He found that a bimodal distribution best fit the data with short-period (122 month) cycles and long-period (140 month) cycles separated by a gap (the Wilson Gap) surrounding the mean cycle length of 132.7 months. However, Hathaway et al. (2002) used minima dates from the 24-month Gaussian smoothing of the International Sunspot number for cycles 1 to 23 and of the Group Sunspot Numbers for cycles −4 to 23 and found distributions that were consistent with a normal distributions about a mean of 131 months with a standard deviation of 14 months and no evidence of a gap. These cycle periods and their distributions are shown in Figure 24.
The left panel shows cycle periods as functions of Cycle Number. Filled circles give periods determined from minima in the 13-month mean, while open circles give periods determined from the 24-month Gaussian smoothing. Both measurements give a mean period of about 132 months with a standard deviation of about 14 months. The “Wilson Gap” in the periods between 125 and 134 months from the 13-month mean is shown with dashed lines. The right panel shows histograms of cycle periods centered on the mean period with bin widths of one standard deviation. The solid lines show the distribution from the 13-month mean while the dashed lines show the distribution for the 24-month Gaussian. The periods appear normally distributed and the “Wilson Gap” is well populated with the 24-month Gaussian smoothed data.
4.4 Cycle amplitudes
The amplitude of a cycle is another key characteristic. As we have seen in Tables 3 and 4, the actual value for the amplitude of a cycle depends upon the activity index used and the type of smoothing. These uncertainties can even change the relative amplitudes of the cycles. In Table 3, we see that the second largest cycle is cycle 21 according to the 13-month mean of the International Sunspot Numbers. But with the same smoothing, the second largest cycle in sunspot area and 10.7 cm flux is cycle 22. Cycles 15 and 16 were very similar according to sunspot area but cycle 15 is significantly larger than cycle 16 according to the International Sunspot Number. The Group Sunspot Numbers do provide information on earlier cycles but show systematic differences when compared to the International Sunspot Numbers. The maxima determined by the 13-month mean with the International Sunspot Numbers and the Group Sunspot Numbers are given in Table 5.
These cycle maxima and their distributions are shown in Figure 25. The mean amplitude of cycles 1 to 23 from the International Sunspot Numbers is 114 with a standard deviation of 40. The mean amplitude of Cycles −4 to 23 from the Group Sunspot Numbers is 90 with a standard deviation of 41.
The left panel shows cycle amplitudes as functions of cycle number. The filled circles show the 13-month mean maxima with the Group Sunspot Numbers while the open circles show the maxima with the International Sunspot Numbers. The right panel shows the cycle amplitude distributions (solid lines for the Group values, dotted lines for the International values). The Group amplitudes are systematically lower than the International amplitudes for cycles prior to cycle 12 and have a nearly normal distribution. The amplitudes for the International Sunspot Number are skewed toward higher values.
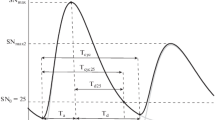
4.5 Cycle shape
Sunspot cycles are asymmetric with respect to their maxima (Waldmeier, 1935). The elapsed time from minimum up to maximum is almost always shorter than the elapsed time from maximum down to minimum. An average cycle can be constructed by stretching and contracting each cycle to the average length, normalizing each to the average amplitude, and then taking the average at each month. This is shown in Figure 26 for cycles 1 to 23. The average cycle takes about 48 months to rise from minimum up to maximum and about 84 months to fall back to minimum again.
Various functions have been used to fit the shape of the cycle and/or its various phases. Stewart and Panofsky (1938) proposed a single function for the full cycle that was the product of a power law for the initial rise and an exponential for the decline. They found the four parameters (starting time, amplitude, exponent for the rise, and time constant for the decline) that give the best fit for each cycle. Nordemann (1992) fit both the rise and the decay with exponentials that each required three parameters — an amplitude, a time constant, and a starting time. Elling and Schwentek (1992) also fit the full cycle but with a modified F-distribution density function which requires five parameters. Hathaway et al. (1994) suggested yet another function — similar to that of Stewart and Panofsky (1938) but with a fixed (cubic) power law and a Gaussian for the decline. This function of time
has four parameters: an amplitude A, a starting time to, a rise time 6, and an asymmetry parameter c. The average cycle is well fit with A = 195, b = 56, c = 0.8, and t0 = −4 months (prior to minimum). This fit to the average cycle is shown in Figure 27. Hathaway et al. (1994) found that good fits to most cycles could be obtained with a fixed value for the parameter c and a parameter 6 that is allowed to vary with the amplitude — leaving a function of just two parameters (amplitude and starting time) that were well determine early in each cycle.
Li (1999) used a similar function to fit quarterly averages of the sunspot area and also found that it could be reduced to a function of the same two parameters that were well determine early in a cycle. Volobuev (2009) introduced yet another (similar) function of four parameters for sunspot numbers that could also be reduced to the same two parameters (note that Volobuev refers to this as a one parameter fit by neglecting the need to fit or determine the starting time). Similar results have also been obtained by Du (2011).
4.6 Double peaks — the Gnevyshev Gap
These simple parametric functions all do a good job of fitting the average cycle shape shown in Figures 26 and 27, but individual cycles often have features that persistently deviate from these smooth profiles. In particular, many cycles are observed to have double peaks. Gnevyshev (1963) noted that cycle 19 had two maxima in solar activity as seen in some activity indices (not so much in sunspot number but quite strong in coronal emission as seen in the coronal green line at 5303 A) with a distinct 1–2-year gap (the Gnevyshev Gap). He later (Gnevyshev, 1967, 1977) suggested that the solar cycle is, in general, characterized by two waves of activity and that these were responsible for the double peaks.
This concept — two separate surges of solar activity — found further support in the study of Feminella and Storini (1997) who noted that it is best seen in the occurrence of large events (big flares but not small flares).
Another suggested source of double-peak behavior is north/south asymmetry in solar activity (see Section 4.11). Activity (e.g., sunspot number or area) can proceed in one hemisphere slightly out of phase with activity in the other hemisphere. This can result in an early peak associated with one hemisphere and a later peak associated with the other hemisphere. Norton and Gallagher (2010) examined this possibility and concluded that the Gnevyshev Gap is a phenomena that occurs in both hemispheres and is not, in general, due to the superposition of two hemispheres out of phase with each other.
4.7 Rise time vs. amplitude — the Waldmeier Effect
A number of relationships have been found between various sunspot cycle characteristics. Among the more significant relationships is the Waldmeier Effect (Waldmeier, 1935, 1939) in which the time it takes for the sunspot number to rise from minimum to maximum is inversely proportional to the cycle amplitude. This is shown in Figure 28 for both the International Sunspot Number and the 10.7 cm radio flux data. Times and values for the maxima are taken from the 24-month Gaussian given in Table 4. Times for the minima are taken from the average dates given in Table 2. Both of these indices exhibit the Waldmeier Effect, but with the 10.7 cm flux maxima delayed by about 6 months. This is larger than, but consistent with the delays seen by Bachmann and White (1994). The best fit through the Sunspot Number data gives
While this effect is widely quoted and accepted it does face a number of problems. Hathaway et al. (2002) found that the effect was greatly diminished when Group Sunspot Numbers were used (the anti-correlation between rise time and amplitude dropped from −0.7 to −0.34). Inspection of Figure 28 clearly shows significant scatter. Dikpati et al. (2008b) noted that the effect is not seen for sunspot area data. This is consistent with the data in Tables 3 and 4, which show that significantly different dates for maxima are found with sunspot area when compared to sunspot number. The dates can differ by more than a year but without any evidence of systematic differences (area sometimes leads number and other time lags).
The Waldmeier Effect. The cycle rise time (from minimum to maximum) plotted versus cycle amplitude for International Sunspot Number data from cycles 1 to 23 (filled dots) and for 10.7 cm radio flux data from cycles 19 to 23 (open circles). This gives an inverse relationship between amplitude and rise time shown by the solid line for the Sunspot Number data and with the dashed line for the radio flux data. The radio flux maxima are systematically later than the Sunspot number data, as also seen in Table 4.
4.8 Period vs. amplitude
Significant relationships are also found between cycle periods and amplitudes. The most significant relationship is between a cycle period and the amplitude of the following cycle (Hathaway et al., 1994; Solanki et al., 2002). This is illustrated in Figure 29. The correlation is fairly strong (r = −0.68, r2 = 0.46) and significant at the 99% level. While there is also a negative correlation between a cycle period and its own amplitude, the correlation is much weaker (r = −0.37, r2 = 0.14).
The Amplitude-Period Effect. The period of a cycle (from minimum to minimum) plotted versus following cycle amplitude for International Sunspot Number data from cycles 1 to 22. This gives an inverse relationship between amplitude and period shown by the solid line with Amplitude(n+1) = 380 − 2 × Period(n).
4.9 Maximum vs. minimum
Although somewhat less significant, a relationship is also found between cycle maxima and the previous minima (Hathaway et al., 1999). This is illustrated in Figure 30. The correlation is fair (r = 0.56, r2 = 0.31) and significant at the 99% level.
4.10 Active latitudes — Sporer’s Law
While Sporer’s name is often attached to the concept of sunspot zones and their drift toward the equator, it appears that Carrington was the first to discover it. Carrington (1858) noted that the sunspots prior to the “minimum of frequency in February 1856” were confined to an equatorial band well below 20 latitude. He went on to note that after that date two new belts of sunspots appeared at latitudes between 20 and 40 latitude in each hemisphere. This equatorward drift of the sunspot zones is a key characteristic of the solar cycle — a characteristic that is often difficult to reproduce in dynamo models with several possible different mechanisms proposed (see Charbonneau, 2010).
Cycle-to-cycle variations in this equatorward drift have been reported and latitudes of the sunspot zones have been related to cycle amplitudes. Vitinskij (1976) used the latitudes of sunspot near minimum as a predictor for the amplitude of cycle 21. Separating the cycles according to size now suggests that this is a poor indicator of cycle amplitude. Regardless of amplitude class, all cycles start with sunspot zones centered at about 25°.
Li et al. (2001) used the RGO/NOAA sunspot area and position data plotted in Figure 9 to quantify the latitudinal drift by fitting the quarterly averaged sunspot group area centroid positions as functions of time, with a quadratic in time relative to the time of minimum for each solar cycle. The individual sunspot cycles can be separated near the time of minimum by the latitudes of the emerging sunspots (and more recently by magnetic polarity data as well). They found that, on average from 1874 to 1999, both hemispheres had the same behavior with faster equatorward drift early in the cycle and slower drift late in the cycle and an average drift rate of ∼ 1.6° yr−1.
Hathaway et al. (2003) used the same data to investigate the variation of the equatorward drift with cycle period and amplitude. They calculated the centroid positions of the sunspot group areas in each hemisphere for each solar rotation in individual solar cycles, and fit those positions to quadratics in time relative to the time of maximum for each cycle. They found that cycles with higher drift rates at maximum tended to have shorter periods and larger amplitudes but with a better correlation between drift rate and the amplitude of the N+2 cycle (Hathaway et al., 2004).
Recently, Hathaway (2011) found that the active latitudes follow a standard path for all cycles (regardless of cycle amplitude) when time is measured relative to the cycle starting times determined from fitting monthly sunspot numbers to the parametric curves given by Eq. (6). The data show far less scatter when plotted relative to this starting time, t0, and are well fit with an exponential function:
where \(\bar \lambda\) is the active latitude and time, t, is measured in months.
These centroid positions are plotted as functions of time relative to t0 in Figure 31. The area weighted averages of these positions in 6-month intervals are shown with the colored lines for different amplitude cycles. At the start of each cycle the centroid position of the sunspot areas is about 28 from the equator. The equatorward drift is more rapid early in the cycle and slows late in the cycle — eventually stopping at about 7 from the equator.
Top: Latitude positions of the sunspot area centroid in each hemisphere for each Carrington Rotation as functions of time from cycle start. Three symbol sizes are used to differentiate data according to the average of the daily total sunspot area for each hemisphere and rotation. Bottom: The centroids of the centroids in 6-month intervals are shown for large amplitude cycles (red line), medium amplitude cycles (green line), and small amplitude cycles (blue line). The exponential fit to the active latitude positions [Eq. (8)] is shown with the black dashed line and 2σ error bars.
The latitudinal width of the sunspot zones also varies over the cycle and as a function of cycle amplitude. This is illustrated in Figure 32, where the latitudinal widths (standard deviation about the mean latitude) of the sunspot zones are plotted for each hemisphere for each Carrington rotation as functions of time since the start of each cycle. The active latitude bands are narrow at minimum, expand to a maximum width at the time of maximum, and then narrow again during the declining phase of the cycle. Larger cycles achieve greater widths than do smaller cycles. Ivanov and Miletsky (2011) found a linear relationship between the width (maximum latitude — minimum latitude, in their study) of the sunspot latitude bands and the number of sunspot groups with no dependence on cycle amplitude. Comparing the RMS width to the sunspot area confirms the lack of any relational dependence on cycle strength but indicates a distinctly nonlinear relationship with an asymptotic limit to the widths as the total sunspot area increases (bottom panel of Figure 32). A satisfactory fit to the data (shown by the black line in the bottom panel of Figure 32) is given by
where σλ is the RMS width of the sunspot zones and A is the total sunspot area in µHem.
Top: Latitudinal widths of the sunspot area centroid in each hemisphere for each Carrington Rotation as functions of time from cycle start. Three symbol sizes are used to differentiate data according to the daily average of the sunspot area for each hemisphere and rotation. The centroids of the centroids in 6-month intervals are shown for large amplitude cycles (red line), medium amplitude cycles (green line), and small amplitude cycles (blue line). Bottom: Latitudinal widths as functions of total sunspot area with color coded symbols for cycle strength. The black dots with 2σ error bars show the data binned in 100 µHem intervals. The black line is given by Eq. 9.
Becker (1954) and Waldmeier (1955) had earlier noted that in large cycles, the latitudes of the sunspot zones are higher at maximum than in small cycles. Li et al. (2003) analyzed the latitudinal distribution of sunspot groups for each cycle and found that the average latitudes were higher in bigger cycles and that there were more sunspot groups at high latitudes (35° and higher) in bigger cycles. This result was supported by the more extensive study of Solanki et al. (2008) who calculated the latitudinal moments of the sunspot group areas. Solanki et al. (2008) used the RGO data from 1874 to 1976, supplemented with Soviet data from 1977 to 1985 and Mount Wilson data from 1986 to 2004 (see Balmaceda et al., 2009). As with the earlier studies, they separated data from each cycle using diagonal lines in the butterfly diagram. They then calculated the latitudinal moments (total area, mean latitude, width, skew, and kurtosis) of the sunspot area integrated over each individual solar cycle for each hemisphere. They found that bigger cycles had higher mean latitudes and greater sunspot zone widths and that the distributions tended to be (weakly) skewed toward the equator but with no systematic kurtosis. (Somewhat surprisingly, they found slightly different behavior in the two hemispheres. The range of variability from cycle to cycle in total area, mean latitude, and width was less in the southern hemisphere and the correlations between total area and mean latitude and total area and width were stronger in the southern hemisphere.)
These results are all consistent with the data shown in Figure 31 and Figure 32. Large amplitude cycles reach their maxima sooner than do medium or small amplitude cycles (the Waldmeier Effect — Section 4.7). Thus, the sunspot zone latitude at the maximum of a large cycle will be higher simply because maximum occurs earlier and sunspot zones are still at higher latitudes. Likewise, the average latitude for a large cycle will be higher for the same reason.
4.11 Active hemispheres
Comparisons of the activity in each solar hemisphere have long shown significant asymmetries. Spoerer (1889) and Maunder (1890, 1904) noted that there were often long periods of time when most of the sunspots were found preferentially in one hemisphere and not the other. Waldmeier (1971) found that this asymmetry extended to other measures of activity including faculae, prominences, and coronal brightness. Roy (1977) reported that major flares and magnetically complex sunspot groups also showed strong north-south asymmetry.
The nature of the asymmetry is often characterized in different ways that can lead to different conclusions. Simply quantifying the asymmetry itself is problematic. Taking the difference between hemispheric measures of activity (absolute asymmetry) produces strong signals around the times of maxima simply because the numbers are large. Taking the ratio of the difference to the sum (relative asymmetry) produces strong signals around the times of minima because the differences are divided by small numbers.
One aspect of asymmetry might make activity in one hemisphere stronger than in the other hemisphere, but without any shift in phase (cycle minima and maxima occurring simultaneously in each hemisphere). Another aspect of asymmetry might be reflected in a change in phase but without a corresponding change in strength — one hemisphere rising to maximum before the other. We find evidence for both of these aspects. However, it is well worth noting that the two hemispheres never get very far out of phase with each other (as seen in Figure 9). This is an indication of a fundamental linkage between the two hemispheres that must be reproduced in dynamo models.
Carbonell et al. (1993) examined the relative asymmetry in sunspot areas with a variety of statistical tools and concluded that the signal is dominated by a random (and intermittent) component, but contains one component that varies over a cycle and a second component that gives long-term trends. The variation in the strength of the asymmetry over the course of an average cycle is strongly dependent upon how the asymmetry is quantified (strong at minimum for relative asymmetry, strong at maximum for absolute asymmetry).
Sunspot numbers (and most other solar activity indicators through their direct association with the emergence of sunspot groups) follow Poisson statistics, which results in variability proportional to the square-root of the number itself. Taking the ratio of the hemispheric differences to the square-root of the sums provides a measure of asymmetry that does not tend to favor either maximum or minimum phases.
Figure 33 shows this “normalized” asymmetry for several key indicators. It is clear from this figure that hemispheric asymmetry is real (it consistently appears in all four indicators) and is often persistent — lasting for many years at a time. Figure 34 uses the RGO/NOAA sunspot group area data to extend the asymmetry record from 1874 to the present. This longer time interval shows that the asymmetry usually switches from north-dominant to south-dominant on time scales shorter than an 11-year sunspot cycle. Note that there are about 30 changes of sign in 130 years which gives a typical time scale of about 4 years — on the order of half a solar cycle.
Systematic variations over the course of a solar cycle or as a function of cycle amplitude have been suggested, but these variations have invariably been found to change from cycle to cycle. For example, Newton and Milsom (1955) showed that the northern hemisphere dominated in the early phases of cycles 12–15 with a switch to dominance in the south later in each cycle while the opposite was true for cycles 17–18. Waldmeier (1957, 1971) noted that a significant part of these variations can be accounted for by the fact that the two hemispheres are not exactly in phase. When the northern hemisphere activity leads that in the southern hemisphere, the north will dominate early in the cycle while the south will dominate in the declining phase.
These changes in phase can be seen more clearly when data for each hemisphere is plotted separately as was done by Temmer et al. (2006) for hemispheric sunspot numbers from 1945 to 2004. Figure 35 uses the RGO/USAF sunspot area data from 1874 to 2014 to illustrate this effect. Zolotova and Ponyavin (2006) employed cross-recurrence plots to explore the phase relationship between northern and southern sunspot areas. They found that the hemispheres drifted slightly out of phase over the course of single or multiple cycles but could suddenly shift to the opposite phase. This is seen in Figure 35, where cycles 17–19 have the south leading the north, but then cycle 20 starts with the north leading the south.
Donner and Thiel (2007) used a wavelet analysis on the sunspot area data and, as might be expected, found near phase coherence only for periods near 11 years. By examining the inter-hemispheric phase difference they found a similar pattern to that found by Zolotova and Ponyavin (2006) and concluded that, at a period of 10.75 years, the two hemispheres never shifted out of phase by more than ± 10 months or, equivalently, 10% of the cycle period. These small phase differences are consistent with the findings of Norton and Gallagher (2010) and support their conclusion the the Gnevyshev gap is not due to the two hemispheres getting out of phase (this would require phase shifts of 24 months or more).
4.12 Active longitudes
Sunspots and solar activity also appear to cluster in “active longitudes.” Maunder (1905) noted that during cycle 13 (1891–1901) sunspots favored three specific longitudes, with one longitude range in particular being more active than the others. Bumba and Howard (1965) and Sawyer (1968) noted that new active regions grow in areas previously occupied by old active regions and referred to these as “complexes of activity” while Castenmiller et al. (1986) referred to similar structures as “sunspot nests.” Bogart (1982) found that this results in a periodic signal that is evident in the sunspot number record.
Figure 36 illustrates the active longitude phenomena. In Figure 36a the sunspot area in 5° longitude bins, averaged over 1805 solar rotations since 1878 and normalized to the average value per bin, is plotted as a function of Carrington longitude. The 2σ uncertainty in these values is represented by the dotted lines. This 2σ limit is reached at several longitudes and significantly exceeded at two (85°–90° and 90°–95°). Figure 36b shows similar data for each individual cycle with the normalized value offset in the vertical by the sunspot cycle number. There are many peaks at twice the normal value and one, in cycle 18 at 85°–90°, at three times the normal value. Some of these peaks persist from one cycle to the next, a result that has been noted by many authors including Balthasar and Schüssler (1983), Bumba and Henja (1991), Miklailutsa and Makarova (1994), and Bai (2003).
Active longitudes in sunspot area. The normalized sunspot area in 5° longitude bins is plotted in the upper panel (a) for the years 1878–2009. The dotted lines represent two standard errors in the normalized values. The sunspot area in several longitude bins meets or exceeds these limits. The individual cycles (12 through 23) are shown in the lower panel (b) with the normalized values offset in the vertical by the cycle number. Some active longitudes appear to persist from cycle to cycle.
Henney and Harvey (2002) noted the persistence of magnetic structures in the northern hemisphere at preferred longitudes (drifting slightly due to the latitude) for two decades but also noted that the sunspot records suggests that two decades is about the limit of such persistence (as seen in Figure 36b). However, Berdyugina and Usoskin (2003) conclude that active longitudes can persist for much longer if changes in rotation rate relative to the Carrington rate are accounted for. They also found that the active longitude in the northern hemisphere tends to be shifted by 180° in longitude from that in the southern hemisphere.
4.13 Active region tilt — Joy’s Law
The tilt of active regions — Joy’s Law — is another important characteristic of the sunspot cycle. First discovered by Joy as reported by Hale et al. (1919), this active region tilt systematically places following-polarity magnetic flux at higher latitudes than the leading-polarity magnetic flux. Since the following-polarity is opposite in sign to the polar fields at the start of each cycle, the poleward transport of this flux by diffusion and the meridional flow leads to the polar field reversals at cycle maximum and the build up of new polar fields during the declining phase of each cycle (see Sheeley Jr, 2005; Charbonneau, 2010).
Wang and Sheeley Jr (1989) studied the tilt of some 2700 bipolar magnetic regions that erupted during cycle 21 (1976–1986 by visually inspecting daily magnetograms from NSO/Kitt Peak. They found that the average tilt angle increased with latitude at the rate of about 4 for each 10 of latitude. They noted that the scatter about this average was quite large with the standard deviations about as large as the average value itself. Furthermore, they noted that this RMS scatter was larger for smaller active regions. They concluded that the latitudinal variation in the tilt did not change systematically from 1977 to 1985 during the course of cycle 21.
Howard (1991a) analyzed daily Mount Wilson magnetograms acquired over two cycles (cycles 20 and 21 from 1967 to 1990). While he noted some differences between his results and those of Wang and Sheeley Jr (1989) (particularly at the highest and lowest latitudes where errors are large), and suggested that these differences can be attributed to differences in data and data analysis, nonetheless, it appears that both studies find a similar dependence of the tilt angles on latitude (about 4 for each 10 of latitude) and no dependence on cycle or cycle phase.
In a companion study, Howard (1991b) analyzed sunspot data derived from daily white-light photographs taken at Mount Wilson from 1917 to 1985. While this data lacks polarity information, the leading and following sunspots are identified by their positions relative to the central meridian distance of the group. He found a different relationship between tilt and latitude using this sunspot data — about 2.5° for each 10 of latitude. This result was also obtained by Sivaraman et al. (1999) using a the same technique on white-light photographs from both Mount Wilson and from Kodaikanal covering the years 1906 to 1987. Sivaraman et al. (1999) also looked at the tilt angle residuals, the deviations of the tilt angles for the sunspot groups from the average at the group’s latitude, and found no significant variation with average cycle phase for cycles 15 through 21.
In a later study, Sivaraman et al. (2007) noted that the sunspot group tilts relax toward the average tilt at their emergent latitude after initial emergence. This behavior, relaxation to the average tilt rather than zero tilt, was also found by Kosovichev and Stenflo (2008) in their study of magnetograms from SOHO/MDI.
The latitudinal variation in the active region tilt from an east-west orientation seems decidedly different depending upon the source of the observations. Measurements made from magnetograms (Wang and Sheeley Jr, 1989; Howard, 1991a; Tlatov et al., 2010; Li and Ulrich, 2012; Stenflo and Kosovichev, 2012) indicate higher values (4–5° for each 10 of latitude) while measurements made from white-light images (Howard, 1991b; Sivaraman et al., 1999) indicate lower values (2.5° for each 10° of latitude). Figure 37 illustrates the scatter in the measurements and shows how the lower values can be obtained with magnetogram measurements when the data is restricted to the sunspot groups themselves.
Active region tilt from SOHO/MDI magnetograms over cycle 23. Each black data point gives the tilt (angle between leading-polarity center of gravity and following-polarity center of gravity measured clockwise from the west to east line) for a NOAA active region on a given day as a function of its latitude. The red dots with 2σ error bars give the averages in 5° latitude bins.
The first investigation of cycle-to-cycle variations in active region tilt was undertaken by Dasi-Espuig et al. (2010). They used the Mount Wilson and Kodaikanal white-light sunspot data and found tilt angles as functions of latitude similar to those found from these data by Howard (1991b) and by Sivaraman et al. (2007). Although they were unable to find the Joy’s Law relation for each cycle, they did calculate a proxy — the average tilt angle divided by the average latitude — and found that it varied inversely with cycle amplitude. Part of this relationship could be due to the fact that the average latitude is bigger in bigger cycles (see Section 4.10: big cycles reach maximum early while the sunspot zones are at higher latitude) but that should be offset by the larger tilt angles at the higher latitudes. This relationship — less active region tilt in large cycles — could provide an important feedback that regulates the amplitudes of the solar cycles (see Cameron et al., 2010).
4.14 The extended solar cycle
The concept of “extended” solar cycles — solar cycles that extend further back in time and to higher latitudes than indicated by the sunspot zones — started with observations of ephemeral regions (Martin and Harvey, 1979) but gained support with observations of the torsional oscillations (Snodgrass, 1987). The torsional oscillations (Howard and Labonte, 1980; Howe, 2009) are weak (∼ 5 m s−1) perturbations to the differential rotation profile in the form of a faster-than-average stream on the equatorward side of a sunspot zone and a slower-than-average stream on the poleward side (giving enhanced latitudinal shear in the sunspot zones themselves). These fast and slow zonal flow features move equatorward along with the sunspot zones themselves over the course of each cycle. However, Snodgrass (1987) noted that these features can be seen starting at even higher latitudes well before the emergence of the first sunspots of a cycle.
Wilson et al. (1988) reported on additional observations that supported the concept of an extended cycle of activity that begins near the poles at about the time of the maximum of the previous cycle and drifts equatorward over the course of 18–22 years. These additional data include observations of coronal emissions and observations of ephemeral active regions (see Section 3.7).
The coronal emission data are derived from scans around the limb obtained from ground-based observatories in the green line of Fe xiv (see Altrock, 1988). One component of this coronal emission emanates from coronal loops overlying active regions. This component follows the sunspot zones along their equatorward track. A second component is associated with prominences in general and polar crown filaments in particular. This component moves poleward with the polar crown filaments as the polar fields reverse at cycle maximum (these filaments lie over the neutral line between the old polar fields and the following-polarity magnetic flux from the new cycle active regions). Shortly after maximum (and the rush to the poles of the polar crown filaments) a third component is seen at high latitudes to slowly move equatorward parallel to the sunspot zones, eventually connecting to the sunspot zones of the next cycle.
This third component may be associated with the ephemeral regions. Ephemeral regions tend to follow Hale’s polarity rules but with an even larger scatter in tilt angles than is seen with active regions. Ephemeral regions can be associated with one cycle or the next by their latitude distributions and their statistically dominant orientation (Martin and Harvey, 1979). Ephemeral regions are found at higher latitudes than sunspots, with distributions that suggest that they represent extensions of the sunspot zones back in time and to higher latitudes — starting at about the time of the previous cycle maximum (Harvey, 1992; Tlatov et al., 2010). However, the interpretation of this coronal signal as an indication of an extended cycle has been questioned by Robbrecht et al. (2010), who have reproduced the signal with magnetic maps produced by the transport of magnetic flux from active regions alone.
5 Long-Term Variability
Systematic variations from cycle to cycle and over many cycles could be significant discriminators in models of the solar cycle and might aid in predicting future cycles. Several key aspects of long-term variability have been noted: a 70-year period of extremely low activity from 1645 to 1715 (the Maunder Minimum); a gradual increase in cycle amplitudes since the Maunder Minimum (a secular trend); an 80–90-year variation in cycle amplitudes (the Gleissberg Cycle); a two-cycle variation with odd-numbered cycles higher than the preceding even-numbered cycles (the Gnevyshev-Ohl Effect); a 210-year cycle in radio isotope proxies (the Suess Cycle); and other long term variations seen in radio isotopes. These aspects of long-term variability are examined in this section.
5.1 The Maunder Minimum
Maunder (1890), reporting on the work of Spörer, noted that for a seventy-year period from 1645–1715 the course of the sunspot cycle was interrupted. Eddy (1976) provided additional references to the lack of activity during this period and referred to it as the Maunder Minimum. He noted that many observers prior to 1890 had noticed this lack of activity and that both he and Maunder were simply pointing out an overlooked aspect of solar activity.
Hoyt and Schatten (1998) compiled observations from numerous sources to provide nearly complete coverage of sunspot observations during the period of the Maunder Minimum. These observations (Figure 38) clearly show the lack of activity and apparent cessation of the sunspot cycle during the Maunder Minimum. Nonetheless, Beer et al. (1998) find evidence for a weak cyclic variation in 10Be during the Maunder Minimum, suggesting that the magnetic cycle was still in progress but too weak to produce the intense magnetic fields in sunspots. In addition, Ribes and Nesme-Ribes (1993) found that the sunspots that were observed in the latter half of the Maunder Minimum were at low latitudes and dominant in the southern hemisphere — another indication of weak/marginal magnetic fields.
5.2 The secular trend
Since the Maunder Minimum there seems to have been a steady increase in sunspot cycle amplitudes (Wilson, 1988). This is readily seen in the yearly Group Sunspot Numbers plotted in Figure 38 and in the cycle amplitudes for Group Sunspot Numbers plotted in Figure 25. Hathaway et al. (2002) found a correlation coefficient of 0.7 between cycle amplitude and cycle number. Radioisotopes also show this recent trend (Solanki et al., 2004) and indicate many upward and downward trends over the last 11 000 years. It is well worth noting, however, that this linear trend is not so apparent in the International Sunspot Numbers plotted in Figure 25. Furthermore, the recent reexaminations of the sunspot number (Svalgaard, 2012), indicate little if any secular increase in cycle amplitudes since the Maunder Minimum.
5.3 The Gleissberg Cycle
Numerous authors have noted multi-cycle periodicities in the sunspot cycle amplitudes. Gleissberg (1939) noted a periodicity of seven or eight cycles in cycle amplitudes from 1750 to 1928. While Garcia and Mouradian (1998) suggest that a third period of this cycle can be found in the sunspot data, others (Hathaway et al., 1999) suggest that the period is changing or (Rozelot, 1994; Ogurtsov et al., 2002) that it consists of two different components (one with a 90–100-year period and a second with a 50–0 year period). A simple sinusoid fit to the residual cycle amplitudes when the secular trend is removed now gives a 9.1-cycle periodicity. This best fit is shown in Figure 39.
In reference to the Gleissberg cycle, Waldmeier (1957) noted that the phase shifts in the north-south asymmetry also seen to have a similar period to that of the cycle amplitudes (Section 4.11).
5.4 Gnevyshev-Ohl Rule (Even-Odd Effect)
Gnevyshev and Ohl (1948) found that if solar cycles are arranged in pairs with an even-numbered cycle and the following odd-numbered cycle then the sum of the sunspot numbers in the odd cycle is higher than in the even cycle. This is referred to as the Gnevyshev-Ohl Rule or Even-Odd Effect. This rule is illustrated in Figure 40. With the exception of the cycle 4/5 pair, this relationship held until cycle 23 showed that the cycle 22/23 pair was also an exception. If cycle amplitudes are compared then the cycle 8/9 pair is also an exception. This rule also holds for other indicators of cycle amplitude such as sunspot area. While much has been said about this rule relative to the 22-year Hale cycle, it is difficult to understand why the order (even-odd vs. odd-even) of the pairing should make a difference. The observed effect does however impact flux transport models for the surface fields (see Sheeley Jr, 2005, for a review). Since the odd cycles all have the same magnetic polarity, stronger odd cycles will tend to build up polar fields of one polarity to the extent that the transport during the even cycles cannot reverse the polar fields without associated changes in transport.
5.5 Long-term variations from radioisotope studies
The solar cycle modulation of cosmic rays (Section 3.10) leaves its imprint in the concentration of the radioisotopes 14C in tree rings and 10Be in ice cores (Section 3.11). The connection between solar activity and radioisotope concentrations is complicated by the transport and storage of these radioisotopes. Nonetheless, estimates of solar activity levels over time scales much longer than the 400-year sunspot record can be obtained (see Usoskin, 2013, for a review).
These reconstructions of solar activity reveal grand minima like the Maunder Minimum as well as grand maxima similar to the last half of the 20th century. The reconstructions suggest that the Sun spends about 1/6th of its current life in a grand minimum phase and about 1/10th in a grand maximum.
5.6 The Suess cycle
One periodicity that arises in many radiocarbon studies of solar activity has a well-defined period of about 210 years. This is often referred to as the Suess or de Vries cycle (Suess, 1980). Although the variations in the calculated production rates of 14C and 10Be are well correlated with each other (Vonmoos et al., 2006) and with the 400-year sunspot record (Berggren et al., 2009), there is little evidence of the Suess cycle in the sunspot record itself (Ma and Vaquero, 2009).
6 Short-Term Variability
There are significant variations in solar activity on time scales shorter than the sunspot cycle. This is evident when the sunspot number record is filtered to remove both solar rotation effects (periods of about 27-days and less) and solar cycle effects. This signal is shown in Figure 41 for the years 1850 to 2013. In this figure the daily sunspot numbers are filtered with a tapered Gaussian-shaped filter, Eq. (4), with a FWHM of 54 days. This reduces all signals with periods shorter than 54-days to less than 2% of their original amplitude. The resulting signal is sampled at 27-day intervals and then filtered again with a similar Gaussian with a FWHM of 24 rotations. The lower panel of Figure 41 shows this final signal for the time period, while the upper panel shows the residual obtained when this smoothed sunspot number signal is subtracted from 54-day filtered data. This residual signal is quite chaotic but shows some interesting behavior and quasi-periodicities.
6.1 154-day periodicity
A 154-day periodic signal was noted in gamma-ray flare activity seen from SMM by Rieger et al. (1984) for the time interval from 1980/02 to 1983/08. This signal was also found by Bai and Cliver (1990) in proton flares for both this interval and an earlier interval from 1958/01 to 1971/12. Ballester et al. (2002) found that this signal was also seen in the Mt. Wilson sunspot index for the 1980–1983 time frame. Lean (1990) analyzed the signal in the sunspot area data and found that it occurs in episodes around the epochs of sunspot cycle maxima and that its frequency drifts as well. A wavelet transform of the bandpass-limited (54 days < period < 2 years) daily sunspot numbers shown in the upper panel of Figure 41 is also shown in Figure 42, with a horizontal red line indicating periods of 154 days. The strong signal in the early 1980s as well as other intermittent intervals is clearly evident in this plot.
Morlet wavelet transform spectrum of the bandpass-limited daily International Sunspot Number. Increasing wavelet power is represented by colors from black through blue, green, yellow, and red. The Cone-Of-Influence (outside of which the data isn’t long enough to give good measurements of wavelet power) is outlined by the white curves. Periods of 154 days are indicated by the horizontal red line.
6.2 Quasi-biennial variations and double-peaked maxima
Another interesting periodicity is one found with a period of about two years (Benevolenskaya, 1995; Mursula et al., 2003). This periodicity is particularly evident at cycle maximum in the form of the double peaks and the Gnevyshev Gap (see Section 4.6). Wang and Sheeley Jr (2003) found that the Sun’s dipole magnetic moment and open magnetic flux exhibits multiple peaks with quasi-periodicities of about 1.3 years, which they attributed to the stochastic processes of active region emergence and a decay time of about 1 year set by the dynamical processes of differential rotation, meridional flow, and supergranule diffusion. These quasi-periodic variations are also evident in the wavelet spectrum shown in Figure 42. Multiple, significant peaks of power are seen intermittently at periods between 1 and 2 years and are most prevalent near the time of cycle maxima (Bazilevskaya et al., 2000).
Similar periods are found in the global magnetic field (Ulrich and Tran, 2013) and in the frequencies of the acoustic oscillations (Broomhall et al., 2012; Simoniello et al., 2012). These quasi-biennial periodicities are probably all linked through the magnetic field and its connection to the frequency changes in the acoustic oscillations.
A signal with a similar period was seen in the tachocline oscillations — periodic variations in the shear at the base of the convection zone (Howe et al., 2000). These tachocline oscillations have also been found to be intermittent (Howe et al., 2007) but do not appear to be directly related to the quasi-biennial variations associated with the surface magnetic field.
7 Solar Cycle Predictions
Predicting the solar cycle is indeed very difficult. A cursory examination of the sunspot record reveals a wide range of cycle amplitudes (Figure 2). Over the last 24 cycles the average amplitude (in terms of the 13-month smoothed monthly averages of the daily sunspot number) was about 114. Over the last 400 years the cycle amplitudes have varied widely — from basically zero through the Maunder Minimum, to the two small cycles of the Dalton Minimum at the start of the 19th century (amplitudes of 49.2 and 48.7), to the recent string of large cycles (amplitudes of 151.8, 201.3, 110.6, 164.5, 158.5, and 120.8). In addition to the changes in the amplitude of the cycle, there are changes in cycle length and cycle shape as discussed in Section 4. A wide variety of methods have been used to predict the solar cycle. For recent reviews see Petrovay (2010) and Pesnell (2012).
7.1 Predicting an ongoing cycle
One popular and often-used method for predicting solar activity was first described by McNish and Lincoln (1949). As a cycle progresses, the smoothed monthly sunspot numbers are compared to the average cycle for the same number of months since minimum. The difference between the two is used to project future differences between predicted and mean cycle. The McNish-Lincoln regression technique originally used yearly values and only projected one year into the future. Later improvements to the technique use monthly values and use an auto-regression to predict the remainder of the cycle.
One problem with the modified McNish-Lincoln technique is that it does not account for systematic changes in the shape of the cycle with cycle amplitude (i.e. the Waldmeier Effect, Section 4.7). Another problem with the McNish-Lincoln method is its sensitivity to choices for the date of cycle minimum. Both the systematic changes in shape and the sensitivity to cycle minimum choice can be accounted for with techniques that fit the monthly data to parametric curves (e.g., Stewart and Panofsky, 1938; Elling and Schwentek, 1992; Hathaway et al., 1994). The two-parameter function of Hathaway et al. (1994) given by Eq. (6) closely mimics the changing shape of the sunspot cycle. Prediction requires fitting the data to the function with a best fit for an initial starting time, to, and amplitude, A.
Both the modified McNish-Lincoln and the curve-fitting techniques work nicely once a sunspot cycle is well under way. The critical point seems to be 2 to 3 years after minimum — near the time of the inflection point on the rise to maximum. Predictions for cycles 22 and 23 using the modified McNish-Lincoln and the Hathaway, Wilson, and Reichmann curve-fitting techniques 24 months after minimum are shown in Figure 43. Since cycle 23 had an amplitude very close to the average of cycles 10–22, both of these predictions are very similar. Distinct differences are seen for larger or smaller cycles and when different dates are taken for minimum with the McNish-Lincoln method.
Predicting the size and timing of a cycle prior to its start (or even during the first year or two of the cycle) requires methods other than auto-regression or curve-fitting. There is a long, and growing, list of measured quantities that can and have been used to predict future cycle amplitudes. Prediction methods range from simple climatological means to physics-based dynamos with assimilated data.
7.2 Predicting future cycle amplitudes based on cycle statistics
The mean amplitude of the last n cycles gives the benchmark for other prediction techniques. The mean of the last 23 cycle amplitudes is 114.1 40.4 where the error is the standard deviation about the mean. This represents a prediction without any skill. If other methods cannot predict with significantly better accuracy, they have little use.
One class of prediction techniques is based on trends and periodicities in the cycle amplitudes. The Group Sunspot Number in particular indicates an upward trend in cycle amplitudes since the Maunder Minimum. Projecting this trend to the next cycle gives a prediction only slightly better than the mean. A number of periodicities have been noted in the cycle amplitude record. Gleissberg (1939) noted a long period variation in cycle amplitudes with a period of seven or eight cycles (Section 5.3 and Figure 39). Gnevyshev and Ohl (1948) noted a two-cycle periodicity with the odd-numbered cycle having larger amplitude than the preceding even-numbered cycle (Section 5.4 and Figure 40). Ahluwalia (1998) noted a three-cycle sawtooth-shaped periodicity in the six-cycle record of the geomagnetic Ap index.
Another class of prediction techniques uses the characteristics of the preceding cycle as indicators of the size of the next cycle. Wilson et al. (1998) found that the length (period) of the preceding cycle is inversely correlated to the amplitude of the following cycle. Another indicator of the size of the next cycle is the level of activity at minimum — the amplitude of the following cycle is correlated with the smoothed sunspot number at the preceding minimum (Brown, 1976). This type of technique has led to searches for activity indicators that are correlated with future cycle amplitude. Javaraiah (2007), for example, has found sunspot areas from intervals of time and latitude that correlate very well with future cycle activity.
In spite of the statistical correlations, these methods based on cycle statistics tend to be only marginally better than using the average cycle (Hathaway et al., 1999).
7.3 Predicting future cycle amplitudes based on geomagnetic precursors
One class of precursors for future cycle amplitudes that has worked well in the past uses geomagnetic activity either during the preceding cycle or near the time of minimum as an indicator of the amplitude for the next cycle. These “geomagnetic precursors” use indices for geomagnetic activity (see Section 3.9) that extend back to 1844. Ohl (1966) found that the minimum level of geomagnetic activity seen in the aa index near the time of sunspot cycle minimum was a good predictor for the amplitude of the next cycle. This is illustrated in Figure 44. The minima in aa are well-defined and are well-correlated with the following sunspot number maxima (r = 0.93). The ratio of max(R) to min(aa) gives
This standard deviation from the relationship is significantly smaller than that associated with the average cycle prediction. The minimum level of the smoothed aa index in 2009 indicated a small cycle 24 − Rmax(24) = 70 ± 18 (open circles in Figure 44). One problem with this method concerns the timing of the aa index minima — they often occur well after sunspot cycle minimum and therefore do not give a much advanced prediction.
Two variations on this method circumvent the timing problem. Feynman (1982) noted that geomagnetic activity has two different sources — one due to solar activity (flares, CMEs, and filament eruptions) that follows the sunspot cycle and another due to recurrent high-speed solar wind streams that peak during the decline of each cycle (see Section 3.9 and Figure 20). She separated the two by finding the sunspot number dependence of the base level of geomagnetic activity and removing it to reveal the “interplanetary” component of geomagnetic activity. The peaks in the interplanetary component prior to sunspot cycle minimum have been very good indicators for the amplitude of the following sunspot cycle, as shown in Figure 45.
Hathaway and Wilson (2006) used a modification of this method to predict cycle 24. At the time of that writing there was a distinct peak in aaI in late 2003 (in hind sight, clearly related to the emergence of the large active regions in October/November of 2003). This large peak led to a prediction of Rmax(24) = 160 ± 25, which is clearly too high. While this method does give predictions prior to sunspot number minimum it is not without its problems. Different smoothing of the data gives very different maxima and different methods are used to extract the sunspot number component for the data shown in Figure 44a. Feynman (1982) and others chose to pass a sloping line through the two lowest points. Hathaway and Wilson (2006) fit a line through the 20 lowest points from 20 bins in sunspot number. These variations add uncertainty in the actual predictions.
Thompson (1993) also noted that some geomagnetic activity during the previous cycle served as a predictor for the amplitude of the following cycle but, instead of trying to separate the two, he simply related the geomagnetic activity (as represented by the number of days with the geomagnetic Ap index ≥ 25) during one cycle to the sum of the amplitudes of that cycle and the following cycle (Figure 46). Predictions for the amplitude of a sunspot cycle are available well before minimum with this method. The number of geomagnetically disturbed days during cycle 23 gives a prediction of Rmax(24) = 131 ± 28, which is also too high. Disadvantages with this method include the fact that two cycle amplitudes are involved, the longer cycle will have more disturbed days simply due to its length. In addition, outbursts like those in the fall of 2003 can also impact this method.
Hathaway et al. (1999) tested these precursor methods by backing up in time to 1950, calibrating each precursor method using only data prior to that time, and then using each method to predict cycles 19–22, updating the data and recalibrating each method for each remaining cycle. The results of this test were examined for both accuracy and stability (i.e., whether the relationships used in the method vary significantly from one cycle to the next). An updated version of their Table 3 (including cycle 23 and corrections to the data) is given here as Table 6. The RMS errors in the predictions show that the geomagnetic precursor methods (Ohl’s method, Feynman’s method, and Thompson’s method) consistently outperform the other tested methods. Furthermore, these geomagnetic precursor methods are also more stable. For example, as time progressed from cycle 19 to cycle 23 the Gleissberg cycle period changed from 7.5-cycles to 8.5-cycles and the mean cycle amplitude changed from 103.9 to 114.1, while the relationships between geomagnetic indicators and sunspot cycle amplitude were relatively unchanged.
The physical mechanisms behind the geomagnetic precursors are uncertain. The geomagnetic disturbances that produce the precursor signal are primarily due to high-speed solar wind streams from low-latitude coronal holes late in a cycle. Schatten and Sofia (1987) suggested that this geomagnetic activity near the time of sunspot cycle minimum is related to the strength of the Sun’s polar magnetic field which is, in turn, related to the strength of the following maximum (see next Section 7.4 on dynamo based predictions). Cameron and Schüssler (2007) suggest that it is simply the overlap of the sunspot cycles and the Waldmeier Effect that leads to these precursor relationships with the next cycle’s amplitude. Wang and Sheeley Jr (2009) argue that Ohl’s method has closer connections to the Sun’s magnetic dipole strength and should therefore provide better predictions.
7.4 Predicting future cycle amplitudes based on polar fields
Dynamo models for the Sun’s magnetic field and its evolution have led to predictions based on aspects of those models. Schatten et al. (1978) suggested using the strength of the Sun’s polar field as a predictor for the amplitude of the following cycle, based on the Babcock (1961) dynamo model. In the Babcock model, the polar field at minimum is representative of the poloidal field that is sheared out by differential rotation to produce the toroidal field that erupts as active regions during the following cycle. Diffusion of the erupting active-region magnetic field and transport by the meridional flow (along with the Joy’s Law tilt of these active regions) then leads to the accumulation of opposite polarity fields at the poles and the ultimate reversal of the polar fields, as seen in Figure 17.
Good measurements of the Sun’s polar field are difficult to obtain. The field is weak and predominantly radially directed, and thus nearly transverse to our line of sight. This makes the Zeeman signature weak and prone to the detrimental effects of scattered light. Nevertheless, systematic measurements of the polar fields have been made at the Wilcox Solar Observatory since 1976 and have been used by Schatten and his colleagues to predict cycles 21–24. These polar field measurements are shown in Figure 15 along with smoothed sunspot numbers.
While the physical basis for these predictions is appealing, the fact that direct measurements were only available for the last three cycles was a distinct problem. The number of polar faculae (available from Mount Wilson photographs since 1906) was recognized as an indicator of polar fields by Sheeley Jr (1966), but an examination (Layden et al., 1991) of the use of the polar faculae counts (Sheeley Jr, 1964, 1976) as a predictor suggested they have little predictive power. Recently, however, Muñoz-Jaramillo et al. (2012) recalibrated these polar faculae counts and found that the revised counts and relationship to polar fields do, in fact, provide very good predictions of cycle amplitudes (Muñoz-Jaramillo et al., 2013b).
It was unclear when these polar field measurements should be taken. Predictions based on the polar fields for previous cycles have given different values at different times. Using the polar faculae measurements, Muñoz-Jaramillo et al. (2013a) found that predictions of cycle amplitudes within 2σ of the observed amplitude were successfully made for more than 80% of the cycles for measurements within 2 years of cycle minimum. The success rate dropped rapidly for predictions made earlier.
The polar fields were obviously much weaker during the cycle 23/24 minimum. This has led to a prediction of Rmax(24) = 75 ± 8 by Svalgaard et al. (2005) — about half the size of the previous three cycles, based on the polar fields being about half as strong. (As of this writing, the maximum of cycle 24 appears to be the peak of 81.9 realized in April 2014.) While in previous minima the strength of the polar fields (as represented by the average of the absolute field strength in the north and in the south) varied as minimum approached, this did not happen on the approach to cycle 24 minimum in late 2008. This suggests that the early prediction made in 2005 was not compromised.
7.5 Predicting future cycle amplitudes based on flux transport dynamos
The use of polar fields at minimum as a predictor for the amplitude of the next cycle is loosely based on dynamo theories like that of Babcock (1961). Predictions have also been made using more fully developed dynamo models along with the assimilation of data from previous years and cycles. Kitiashvili and Kosovichev (2008) used a 1D (time) dynamo model in which the alpha-effect (the lifting and twisting that converts toroidal field into poloidal field) depended non-linearly on the magnetic field itself. After assimilating data from previous cycles, they showed that their model had good predictive powers and predicted a sunspot number maximum of about 80 for cycle 24.
Over the last two decades, 3D (latitude, depth, and time) flux-transport dynamo models have been developed to include the kinematic effects of the Sun’s meridional circulation, finding that it can play a significant role in the magnetic dynamo (Dikpati and Charbonneau, 1999). In these models the speed of the meridional circulation sets the cycle period and influences both the strength of the polar fields and the amplitudes of following cycles. Two predictions were made based on flux transport dynamos with assimilated data, with very different results.
Dikpati et al. (2006) predicted an amplitude for cycle 24 of 150–180 using a flux transport dynamo that included a rotation profile and a near surface meridional flow based on helioseismic observations. They modeled the axisymmetric poloidal and toroidal magnetic field using a meridional flow that returns to the equator at the base of the convection zone and used two source terms for the poloidal field — one at the surface due to the Joy’s Law tilt of the emerging active regions, and one in the tachocline due to hydrodynamic and MHD instabilities. They drive the model with a surface source of poloidal field that depends upon the sunspot areas observed since 1874. Measurements of the meridional flow speed prior to 1996 are highly uncertain (Hathaway, 1996), so they maintained a constant flow speed prior to 1996 and forced each of those earlier cycles to have a constant period as a consequence. The surface poloidal source term drifted linearly from 30 to 5 over each cycle with an amplitude that depended on the observed sunspot areas. The prediction was based on the strength of the toroidal field produced in the tachocline. They found excellent agreement between this toroidal field strength and the amplitude of each of the last eight cycles (the four earlier cycles — during the initialization phase — were also well-fit, but not with the degree of agreement of the later cycles). The correlation they found between the predicted toroidal field and the cycle amplitudes is similar to that found with the geomagnetic precursors and polar field strength indicators. When they kept the meridional flow speed at the same constant level during cycle 23, they found Rmax(24) ∼ 180. When they allowed the meridional flow speed to drop by 40%, as was seen from 1996–2002, they found Rmax(24) ∼ 150, and further predicted that cycle 24 would start late due to the slower meridional flow.
Choudhuri et al. (2007) predicted an amplitude for cycle 24 of 80 using a similar flux-transport dynamo, but using the surface poloidal field at minimum as the assimilated data. They used a similar axisymmetric model for the poloidal and toroidal fields, but with a meridional flow that extends below the base of the convection zone and a diffusivity that remains high throughout the convection zone. In their model, the toroidal field in the tachocline produces flux eruptions when its strength exceeds a given limit. The number of eruptions is proportional to the sunspot number and was used as the predicted quantity. They assimilate data by instantaneously changing the poloidal field at minimum throughout most of the convection zone to make it match the dipole moment obtained from the Wilcox Solar Observatory observations (Figure 15). They found an excellent fit to the last three cycles (the full extent of the data) and found Rmax(24) ∼ 80, in agreement with the polar field prediction of Svalgaard et al. (2005).
Criticism has been leveled against all of these flux-transport-dynamo-based predictions. Dikpati et al. (2006) criticized the use of polar field strengths to predict the sunspot cycle peak (that follows four years later), by questioning how those fields could be carried down to the low-latitude tachocline in such a short time. Cameron and Schüssler (2007) produced a simplified 1D flux transport model and showed that with similar parameters to those used by Dikpati et al. (2006), the flux transport across the equator was an excellent predictor for the amplitude of the next cycle, but the predictive skill was lost when more realistic parameterizations of the active region emergence were used. Yeates et al. (2008) compared an advection-dominated model like that of Dikpati et al. (2006) to a diffusion-dominated models like that of Choudhuri et al. (2007), and concluded that the diffusion-dominated model was better because it gave a better fit to the relationship between meridional flow speed and cycle amplitude. Dikpati et al. (2008a) returned with a study of the use of polar fields and cross equatorial flux as predictors of cycle amplitudes, and concluded that their tachocline toroidal flux was the best indicator. Furthermore, they found that the polar fields followed the current cycle so that the weak polar fields at this minimum were due to the weakened meridional flow.
Another significant problem with these models and their predictions arises from recent measurements of the meridional flow itself. The flux-transport dynamo modelers all assume that the poleward meridional flow observed at the surface sinks inward in the polar regions and returns equatorward at the base of the convection zone, turning equatorward starting at the mid-point depth of 100 Mm. Measurements of this equatorward return flow using both the motions of super-granules (Hathaway, 2012) and acoustic waves (Zhao et al., 2013), indicate that the equatorward return flow starts at a much shallower depth (50–60 Mm). The deeper probing with the acoustic waves indicates that the flow turns poleward again deeper down (below 120 Mm). This double cell structure for the Sun’s meridional flow cannot accommodate any of these flux-transport dynamo models.
An additional problem for these flux transport dynamo models arises from the time dependence of the meridional flow. Nandy et al. (2011) used a flux transport dynamo model to explain both the weak polar fields at the end of cycle 23 and the long period of cycle 23, by assuming that the meridional flow was fast at the beginning of the cycle and slow at the end. In general, the meridional flow is observed to be fast at cycle minima and slow at cycle maxima due to inflows toward the active latitudes (Komm et al., 1993; Gizon, 2004; Zhao and Kosovichev, 2004; González Hernández et al., 2008; Hathaway and Rightmire, 2010). But in particular, the meridional flow was slower at the cycle 22/23 minimum in 1996 and faster at the cycle 23/24 minimum in 2008 (Hathaway and Rightmire, 2010) — exactly the opposite to the variations proposed by Nandy et al. (2011).
Perhaps the strongest criticism of these dynamo-based predictions was given by Tobias et al. (2006) and Bushby and Tobias (2007). They note that even weak stochastic perturbations to the parameters and/or parameterizations in these flux transport models produce substantial changes to the activity cycles. They conclude that the solar dynamo is deterministically chaotic and thus inherently unpredictable.
While we ultimately expect dynamo theory to provide us with a better understanding of the solar cycle and to provide us with better predictions, much progress is still needed.
8 Cycle 23/24 minimum and cycle 24
The long, unexpected delay in the start of cycle 24 left behind a solar cycle minimum unlike any seen in living memory. In December of 2008, the 13-month smoothed sunspot number dropped to 1.7 — its lowest value since July of 1913, and the smoothed number of spotless days in a month reached its highest value since August of 1913. In September of 2009, the geomagnetic aa-index dropped to its lowest value on record (since 1868, see Figure 21), while the galactic cosmic ray flux reached record highs (since 1953).
Since that minimum, we have seen cycle 24 rise slowly through one peak and then another to a maximum smoothed sunspot number of 81.9 in April 2014. While this behavior is exceptional in view of living memory, it is well within the bounds of normal behavior for solar cycles.
We have seen that small cycles start late and thereby leave behind a long cycle (the Amplitude-Period Effect, Section 4.8) and a low minimum (the Maximum-Minimum Effect, Section 4.9). Small cycles also take a longer time to rise to maximum (the Waldmeier Effect, Section 4.7).
Relative to previous cycle behavior, an amplitude of about 82 for cycle 24 suggests (Figure 29) a period of 150 months for cycle 23 (147 months observed); (Figure 30) a minimum of 0.3 for cycle 23/24 minimum (1.7 observed); and (Figure 28) a rise time from minimum to maximum of 56 months (63 observed).
While this behavior is not exceptional in terms of the historical record, it is exceptional when considering that the last time this was seen was 100 years ago. Furthermore, we are blessed with wide-ranging and detailed observations that were not available 100 years ago to help us understand the origin of this behavior. Many papers have been written concerning the chain of events that led to this deep minimum and weak cycle. While some have led us down dead-end paths, others may lead us to a better understanding of how solar cycle amplitudes are modulated and how and why deeper minima, like the Maunder Minimum, occur.
8.1 Deviations from previous behavior in 10.7 cm flux
Tapping and Valdés (2011) noted that the relationship between the 10.7 cm radio flux and the International Sunspot Number changed during cycle 23. This change is evident in Figure 10 where the data for cycles 23 and 24 indicates higher values for the 10.7 cm radio flux relative to the values of the International Sunspot Number, particularly after the first (and higher) peak in sunspot number in early 2000.
8.2 The Livingston-Penn Effect
Penn and Livingston (2006) and Livingston and Penn (2009) reported that their measurements of the magnetic field strength and emergent intensity at the darkest points in sunspot umbrae indicated a linear trend in sunspot properties that would lead to the total loss of sunspots by 2015. Their measurements were made spectroscopically using the highly magnetically sensitive spectral line of neutral iron at 1564.8 nm. Measurements from individual sunspot umbrae were made by moving the entrance aperture of the spectrograph from sunspot to sunspot. Their measurements indicated that, on average, the field strength in sunspot umbrae was getting weaker at the same time that the emergent intensity was getting brighter.
Schad and Penn (2010) examined this effect using the full disc daily line-of-sight magnetograms produced by the NASA/NSO spectromagnetograph at the Kitt Peak Vacuum Telescope between 1993 and 2003. They used an automated algorithm to detect sunspot umbrae and measured the field strength, emergent intensity, and size of nearly 13 000 sunspot umbrae. Their results recover historical relationships between the size of sunspot umbrae and the field strength and emergent intensity, but did not show any systematic secular trend.
Livingston et al. (2012) extended the measurements in the infrared line through cycle 23/24 minimum and into the rise of cycle 24. Although the trends seemed to be leveling off, their data still showed a continued decline in umbral magnetic fields and a rise in umbral intensities. They also noted a minimum of about 1500 G for the field strength in the smallest (and brightest) sunspots. While this relationship may be critical for understanding connections between dynamo theory and the sunspot cycle (the production or non-production of sunspots depends upon a threshold strength of the generated fields), their data showed that few, if any, of these small spots were measured earlier in the program (from 1998 to about 2005). They concluded that this lack of small sunspots was a characteristic of cycle 23 and was related to the changes in the 10.7 cm radio flux.
However, de Toma et al. (2013a), using photometric data from the San Fernando Observatory, found no systematic trends in the emergent intensities from sunspot umbrae over the 27 years from 1986 to 2012.
Finally, Watson et al. (2014) compared sunspot umbral field strengths and emergent intensities measured by Livingston et al. (2012) and compared them with measurements made from space by SOHO/MDI and SDO/HMI using an automated detection algorithm. They noted that the number of umbral measurements per day, obtained with the space-based instruments, was well-correlated with the sunspot number. However, the ground-based measurements obtained at Kitt Peak did not show this correlation until sometime after 2003. One must conclude that large sunspot umbrae were selectively measured prior to 2003 and that measurements representative of the full sunspot distribution were not made until after that time — the Livingston-Penn effect is largely due to selection effects, rather than a systematic trend in sunspot properties.
8.3 Sunspot size distributions
Sunspot umbral areas were found to be distributed log-normally. Bogdan et al. (1988) measured umbral areas on Mount Wilson white-light plates collected from 1917 to 1982 and found that the same log-normal distribution is obtained for all phases of the solar cycle, and for the individual cycles, as well.
However, Kilcik et al. (2011) found a difference in the relative numbers of small and large sunspot groups in cycle 23 when compared to cycle 22, with a deficit of small sunspots in cycle 23. This was based not so much on actual size measurements, but rather on the Zurich sunspot classifications reported by the USAF observers. Lefevre and Clette (2011) performed a detailed analysis of the size distributions of sunspot groups in the USAF database, and of individual sunspots in the Debrecen database, and concluded that cycle 23 did have significantly fewer small (≲ 17 µHem) sunspots and sunspot groups. This is shown by the distributions plotted in Figure 47.
Sunspot group size (area) distributions for cycles 22 and 23. The maximum sizes attained by active regions in the USAF database are used to count each active region in a size bin for its respective cycle. On the left, the bins extend from 10 to 200 µHem in 10 µHem increments. On the right, the bins extend from 100 to 2000 µHem in 100 µHem increments. The deficit of small spots (with areas of 10 and 20 µHem) in cycle 23 appears to be significant. Cycle 23 also appears to have fewer large active regions. While those deviations are well within the 1σ errors, there are consistently fewer numbers in all area bins above ∼ 700 µHem.
However, these small sunspots are difficult to measure. Furthermore, the measurements acquired by the USAF involved several observing sites and dozens of observers, all of which changed over the course of the two cycles. de Toma et al. (2013b) made measurements of sunspot areas from photometric images obtained over cycle 22 and 23 at the San Fernando Observatory, and found that the important difference was in the numbers of large (≲ 700 µHem) sunspots — cycle 23 had fewer of them. This is seen to some extent in the USAF data plotted in Figure 47. The cycle 23 data points fall consistently below the cycle 22 data points for sunspot group areas ≳ 700 µHem.
8.4 Flow variations
The axisymmetric flows — differential rotation and meridional flow — also change with the solar cycle.
If a long-term average rotation profile is subtracted from the instantaneous rotation profile, it reveals the torsional oscillations (Howard and Labonte, 1980) — faster and slower than average zonal flows that drift equatorward with the sunspot zones. The faster zone is found on the equatorward side of the sunspot zones, while the slower zone is found on the poleward side of the sunspot zones — thereby enhancing the latitudinal shear in the rotation rate at the latitudes where sunspots emerge. The instantaneous deviations from the average rotation profile also include changes in the high-latitude (polar) zonal flows, with a speed-up starting at about the time of cycle maximum that is balanced by a slow-down starting at about the time of cycle minimum.
Likewise, if a long-term-average meridional flow profile is subtracted from the instantaneous meridional flow profile it reveals in-flows toward the active latitudes (Gizon, 2004; Zhao and Kosovichev, 2004). These in-flows have the effect of making the meridional flow slower at cycle maxima and faster at cycle minima as was observed earlier by Komm et al. (1993).
Both the torsional oscillations and the in-flows toward the active latitudes were seen in cycle 23 and the rise of cycle 24, but with interesting differences from previous cycles. Howe et al. (2009) noted that the delayed start of cycle 24 could be seen in the slower equatorward progression of the torsional oscillations during the decline of cycle 23. Howe et al. (2013) noted that the high-latitude branch of the torsional oscillations (the polar spin-up) was not yet evident (unless a shorter term average was removed from the data). Hathaway and Rightmire (2010) noted that the meridional flow was slower at cycle 22/23 minimum in 1996 than it was at cycle 23/24 minimum in 2008.
The relationships between these flow variations and solar cycle variability are being explored. Changes in the meridional flow in particular can lead to changes in the polar fields through surface flux transport (Sheeley Jr, 2005). If these changes are directly related to solar activity, then they may help to modulate cycle amplitudes (see Cameron and Schüssler, 2012).
9 Conclusions
Understanding the solar cycle remains one of the biggest problems in solar physics. It is also one of the oldest. Several key features of the solar cycle have been reviewed here and must be explained by any viable dynamo theory or model. They include:
-
The solar cycle has a period of about 11 years but varies in length with a standard deviation of about 14 months.
-
Each cycle appears as an outburst of activity that overlaps with both the preceding and following cycles. This overlap is only about 18 months when measured by the occurrence of sunspots but stretches to years when measured by ephemeral regions, torsional oscillations, and coronal emissions.
-
Solar cycles are asymmetric with respect to their maxima — the rise to maximum is shorter than the decline to minimum, and the rise time is shorter for larger amplitude cycles.
-
Big cycles usually start early and leave behind a short preceding cycle and a high minimum of activity.
-
Sunspots erupt in low-latitude bands on either side of the equator, and these bands drift toward the equator as each cycle progresses with little variation from cycle to cycle.
-
The activity bands widen during the rise to maximum and narrow during the decline to minimum. This width is primarily a direct function of the sunspot number or area with little, if any, further dependence on cycle size or phase.
-
At any time, one hemisphere may dominate over the other, but the northern and southern hemispheres never get out of phase by more than about 10 months.
-
Sunspot groups tend to emerge at longitudes where previous groups had emerged (active longitudes/activity nests).
-
Sunspots erupt in groups extended in longitude but more constrained in latitude, with one magnetic polarity associated with the leading spots (leading in the direction of rotation) and the opposite polarity associated with the following spots.
-
The magnetic polarities of active regions reverse from northern to southern hemispheres and from one cycle to the next, but exceptions occur.
-
The polar fields reverse polarity during each cycle at about the time of cycle maximum.
-
The leading spots in a group are positioned slightly equatorward of the following spots, and this tilt increases with latitude. This tilt may vary inversely with the amplitude of a cycle. There is a wide scatter of tilt angles about the mean, and this scatter is even larger for the smaller and weaker ephemeral regions.
-
Cycle amplitudes exhibit weak quasi-periodicities like the 7 to 8-cycle Gleissberg Cycle (100 years).
-
Cycle amplitudes exhibit extended periods of inactivity, like the Maunder Minimum, where sunspots are not observed but low level magnetic activity continues.
-
Solar activity exhibits quasi-periodicities at time scales shorter than 11 years (quasi-biennial).
-
Predicting the level of solar activity for the remainder of a cycle is reliable 2–3 years after cycle minimum.
-
Predictions for the amplitude of a cycle based on the Sun’s polar field strength or on geomagnetic activity near cycle minimum are significantly better than using the climatological mean.
These characteristics provide strong constraints on dynamo theory. If we consider the Babcock (1961) dynamo as a straw-man for dynamo theory then the toroidal-to-poloidal process is fairly well understood in terms of the surface flux transport of the magnetic field (which emerges in the form of tilted active regions), by the observed meridional flow, differential rotation, and convective motions (Sheeley Jr, 2005). We also understand the poloidal-to-toroidal process, but are faced with three different shear flows (the surface shear layer, the latitudinal shear in the bulk of the convection zone, and the tachocline shear layer) that may each participate in the process.
While the origin of the tilt in active regions is thought to be due to the Coriolis force acting on flux tubes rising from the tachocline (Fan, 2009), those models have difficulty explaining why active regions have such limited longitudinal extent, and why active regions tend to relax to the tilt associated with their latitude of emergence — rather than no tilt at all.
One of the biggest difficulties remains in explaining why the active regions emerge in low-latitude bands that drift equatorward. The earliest dynamo theories explained this in terms of a dynamo wave in the bulk of the convection zone. Observations from helioseismology, and the theory of buoyant flux tubes, pushed the dynamo wave to the tachocline where it then had a problematic poleward branch. Flux-transport dynamos solved this problem by invoking a deep equatorward meridional flow to drive the process, but now, even that seems unlikely.
All of these problems are further compounded by the extensive overlap between cycles. Indeed, to some extent, each of the solar cycle characteristics itemized above need to be better understood with improved dynamo models.
Future observations of sub-surface flows and (perhaps) magnetic fields, observations of activity cycles on other stars, and continued efforts at modeling the solar dynamo will undoubtably lead us closer to better understanding the solar cycle.
References
Abbot, C. G., Fowle, F. E. and Aldrich, L. B., 1913, “The Variation of the Sun”, Astrophys. J., 38, 181–186. [DOI], [ADS]. (Cited on page 18.)
Abramenko, V. I., Fisk, L. A. and Yurchyshyn, V. B., 2006, “The Rate of Emergence of Magnetic Dipoles in Coronal Holes and Adjacent Quiet-Sun Regions”, Astrophys. J. Lett., 641, L65–L68. [DOI], [ADS]. (Cited on page 24.)
Ahluwalia, H. S., 1998, “The predicted size of cycle 23 based on the inferred three-cycle quasi-periodicity of the planetary index Ap”, J. Geophys. Res., 103(A6), 12,103–12,109. [DOI], [ADS]. (Cited on page 61.)
Altrock, R. C., 1988, “Variation of solar coronal Fe xiv 5303 A emission during Solar Cycle 21”, in Solar and Stellar Coronal Structure and Dynamics, Proceedings of the Ninth Sacramento Peak Summer Symposium, Sunspot, NM, August 17–21, 1987, (Ed.) Altrock, R. C., pp. 414–420, National Solar Observatory, Sunspot, NM. [ADS]. (Cited on page 53.)
Arlt, R., 2008, “Digitization of Sunspot Drawings by Staudacher in 1749–1796”, Solar Phys., 247, 399–410. [DOI], [ADS]. (Cited on page 14.)
Arlt, R., Leussu, R., Giese, N., Mursula, K. and Usoskin, I. G., 2013, “Sunspot positions and sizes for 1825–1867 from the observations by Samuel Heinrich Schwabe”, Mon. Not. R. Astron. Soc., 433, 3165–3172. [DOI], [ADS], [arXiv:1305.7400 [astro-ph.SR]]. (Cited on page 14.)
Babcock, H. D., 1959, “The Sun’s Polar Magnetic Field”, Astrophys. J., 130, 364–365. [DOI], [ADS]. (Cited on page 21.)
Babcock, H. D. and Livingston, W. C., 1958, “Changes in the Sun’s Polar Magnetic Field”, Science, 127, 1058. [ADS]. (Cited on page 21.)
Babcock, H. W., 1961, “The topology of the Sun’s magnetic field and the 22-year cycle”, Astrophys. J., 133, 572–587. [DOI], [ADS]. (Cited on pages 7, 65, 66, and 73.)
Bachmann, K. T. and White, O. R., 1994, “Observations of Hysteresis in Solar Cycle Variations Among Seven Solar Activity Indicators”, Solar Phys., 150, 347–357. [DOI], [ADS]. (Cited on pages 18 and 41.)
Bai, T., 2003, “Hot Spots for Solar Flares Persisting for Decades: Longitude Distributions of Flares of Cycles 19–23”, Astrophys. J., 585, 1114–1123. [DOI], [ADS]. (Cited on page 50.)
Bai, T. and Cliver, E. W., 1990, “A 154 Day Periodicity in the Occurrence Rate of Proton Flares”, Astrophys. J., 363, 299–309. [DOI], [ADS]. (Cited on page 58.)
Ballester, J. L., Oliver, R. and Carbonell, M., 2002, “The Near 160 Day Periodicity in the Photospheric Magnetic Flux”, Astrophys. J., 566, 505–511. [DOI], [ADS]. (Cited on page 58.)
Balmaceda, L. A., Solanki, S. K., Krivova, N. A. and Foster, S., 2009, “A homogeneous database of sunspot areas covering more than 130 years”, J. Geophys. Res., 114, A07104. [DOI], [ADS], [arXiv:0906.0942]. (Cited on pages 16 and 47.)
Balthasar, H. and Schüssler, M., 1983, “Preferred longitudes of sunspot groups and high-speed solar wind streams — Evidence for a ‘solar memory’”, Solar Phys., 87, 23–36. [DOI], [ADS]. (Cited on page 50.)
Baranyi, T., Gyõri, L., Ludmány, A. and Coffey, H. E., 2001, “Comparison of sunspot area data bases”, Mon. Not. R. Astron. Soc., 323, 223–230. [DOI], [ADS]. (Cited on page 16.)
Bazilevskaya, G. A., Krainev, M. B., Makhmutov, V. S., Flückiger, E. O., Sladkova, A. I. and Storini, M., 2000, “Structure and Maximum Phase of Solar Cycles 21 and 22”, Solar Phys., 197, 157–174. [DOI], [ADS]. (Cited on page 59.)
Becker, U., 1954, “Die Eigenbewegung der Sonnenflecken in Breite”, Z. Astrophys., 34, 129–136. [ADS]. (Cited on page 44.)
Beer, J., Blinov, A., Bonani, G. et al., 1990, “Use of 10Be in polar ice to trace the 11-year cycle of solar activity”, Nature, 347, 164–166. [DOI], [ADS]. (Cited on page 28.)
Beer, J., Tobias, S. and Weiss, N., 1998, “An active Sun throughout the Maunder Minimum”, Solar Phys., 181, 237–249. [DOI], [ADS]. (Cited on page 55.)
Benevolenskaya, E. E., 1995, “Double Magnetic Cycle of Solar Activity”, Solar Phys., 161, 1–8. [DOI], [ADS]. (Cited on page 59.)
Benz, A. O., 2008, “Flare Observations”, Living Rev. Solar Phys., 5, lrsp-2008-1. [DOI], [ADS]. URL (accessed 3 February 2010): http://www.livingreviews.org/lrsp-2008-1. (Cited on page 25.)
Berdyugina, S. V. and Usoskin, I. G., 2003, “Active longitudes in sunspot activity: Century scale Persistence”, Astron. Astrophys., 405, 1121–1128. [DOI], [ADS]. (Cited on page 50.)
Berggren, A.-M., Beer, J., Possnert, G. et al., 2009, “A 600-year annual 10Be record from the NGRIP ice core, Greenland”, Geophys. Res. Lett., 36, L11801. [DOI], [ADS]. (Cited on page 57.)
Bogart, R. S., 1982, “Recurrence of Solar Activity: Evidence for Active Longitudes”, Solar Phys., 76, 155–165. [DOI], [ADS]. (Cited on page 50.)
Bogdan, T. J., Gilman, P. A., Lerche, I. and Howard, R., 1988, “Distribution of sunspot umbral areas — 1917–1982”, Astrophys. J., 327, 451–456. [DOI], [ADS]. (Cited on page 70.)
Bray, R. J. and Loughhead, R. E., 1965, Sunspots, Wiley, New York. (Cited on page 9.)
Broomhall, A.-M., Chaplin, W. J., Elsworth, Y. and Simoniello, R., 2012, “Quasi-biennial variations in helioseismic frequencies: can the source of the variation be localized?”, Mon. Not. R. Astron. Soc., 420, 1405–1414. [DOI], [ADS], [arXiv:1111.2492 [astro-ph.SR]]. (Cited on page 59.)
Brown, G. M., 1976, “What determines sunspot maximum?”, Mon. Not. R. Astron. Soc., 174, 185–189. [DOI], [ADS]. (Cited on page 61.)
Bumba, V. and Henja, L., 1991, “Low-latitude Active Longitudes on the Sun and in Interplanetary Space”, Bull. Astron. Inst. Czech., 42, 76–84. [ADS]. (Cited on page 50.)
Bumba, V. and Howard, R., 1965, “Large-scale Distribution of Solar Magnetic Fields”, Astrophys. J., 141, 1502–1512. [DOI], [ADS]. (Cited on page 50.)
Bushby, P. J. and Tobias, S. M., 2007, “On Predicting the Solar Cycle Using Mean-Field Models”, Astrophys. J., 661, 1289–1296. [DOI], [ADS], [arXiv:0704.2345 [astro-ph]]. (Cited on page 68.)
Cameron, R. H. and Schüssler, M., 2007, “Solar Cycle Prediction Using Precursors and Flux Transport Models”, Astrophys. J., 659, 801–811. [DOI], [ADS], [arXiv:astro-ph/0612693]. (Cited on pages 65 and 67.)
Cameron, R. H. and Schüssler, M., 2012, “Are the strengths of solar cycles determined by converging flows towards the activity belts?”, Astron. Astrophys., 548, A57. [DOI], [ADS], [arXiv:1210.7644 [astro-ph.SR]]. (Cited on page 71.)
Cameron, R. H., Jiang, J., Schmitt, D. and Schuüssler, M., 2010, “Surface Flux Transport Modeling for Solar Cycles 15–21: Effects of Cycle-Dependent Tilt Angles of Sunspot Groups”, Astrophys. J., 719, 264–270. [DOI], [ADS], [arXiv:1006.3061 [astro-ph.SR]]. (Cited on page 53.)
Carbonell, M., Oliver, R. and Ballester, J. L., 1993, “On the asymmetry of solar activity”, Astron. Astrophys., 274, 497–504. [ADS]. (Cited on page 47.)
Carrington, R. C., 1858, “On the Distribution of the Solar Spots in Latitude Since the Beginning of the Year 1854; with a map”, Mon. Not. R. Astron. Soc., 19, 1–3. [DOI], [ADS]. (Cited on page 42.)
Carrington, R. C., 1859, “Description of a Singular Appearance seen in the Sun on September 1, 1859”, Mon. Not. R. Astron. Soc., 20, 13–15. [DOI], [ADS]. (Cited on page 25.)
Castenmiller, M. J. M., Zwaan, C. and van der Zalm, E. B. J., 1986, “Sunspot nests — Manifestations of sequences in magnetic activity”, Solar Phys., 105, 237–255. [DOI], [ADS]. (Cited on page 50.)
Charbonneau, P., 2010, “Dynamo Models of the Solar Cycle”, Living Rev. Solar Phys., 7, lrsp-2010-3. [DOI], [ADS]. URL (accessed 27 February 2014): http://www.livingreviews.org/lrsp-2010-3. (Cited on pages 7, 44, and 50.)
Choudhuri, A. R., Chatterjee, P. and Jiang, J., 2007, “Predicting Solar Cycle 24 With a Solar Dynamo Model”, Phys. Rev. Lett., 98, 131103. [DOI], [ADS], [arXiv:astro-ph/0701527]. (Cited on page 67.)
Clark, D. H. and Stephenson, F. R., 1978, “An Interpretation of the Pre-Telescopic Sunspot Records from the Orient”, Quart. J. R. Astron. Soc., 19, 387–410. [ADS]. (Cited on page 9.)
Dasi-Espuig, M., Solanki, S. K., Krivova, N. A., Cameron, R. and Penuela, T., 2010, “Sunspot group tilt angles and the strength of the solar cycle”, Astron. Astrophys., 518, A7. [DOI], [ADS], [arXiv:1005.1774 [astro-ph.SR]]. (Cited on page 53.)
de Toma, G., Chapman, G. A., Cookson, A. M. and Preminger, D., 2013a, “Temporal Stability of Sunspot Umbral Intensities: 1986–2012”, Astrophys. J. Lett., 771, L22. [DOI], [ADS]. (Cited on page 70.)
de Toma, G., Chapman, G. A., Preminger, D. G. and Cookson, A. M., 2013b, “Analysis of Sunspot Area over Two Solar Cycles”, Astrophys. J., 770, 89. [DOI], [ADS]. (Cited on page 70.)
Debrecen, “Debrecen Heliophysical Observatory”, project homepage, Debrecen Heliophysical Observatory. URL (accessed 27 February 2014): http://fenyi.solarobs.unideb.hu/DPD/index.html. (Cited on page 16.)
Dikpati, M. and Charbonneau, P., 1999, “A Babcock-Leighton Flux Transport Dynamo with Solar-like Differential Rotation”, Astrophys. J., 518, 508–520. [DOI], [ADS]. (Cited on page 66.)
Dikpati, M., de Toma, G. and Gilman, P. A., 2006, “Predicting the strength of solar cycle 24 using a flux-transport dynamo-based tool”, Geophys. Res. Lett., 33, L05102. [DOI], [ADS]. (Cited on pages 66 and 67.)
Dikpati, M., de Toma, G. and Gilman, P. A., 2008a, “Polar Flux, Cross-equatorial Flux, and Dynamogenerated Tachocline Toroidal Flux as Predictors of Solar Cycles”, Astrophys. J., 675, 920–930. [DOI], [ADS]. (Cited on page 67.)
Dikpati, M., Gilman, P. A. and de Toma, G., 2008b, “The Waldmeier Effect: An Artifact of the Definition of Wolf Sunspot Number?”, Astrophys. J. Lett., 673, L99–L101. [DOI], [ADS]. (Cited on page 42.)
Dodson, H. W., 1953, “High Latitude Sunspot, August 13, 1953”, Publ. Astron. Soc. Pac., 65, 256. [DOI], [ADS]. (Cited on page 24.)
Donner, R. and Thiel, M., 2007, “Scale-resolved phase coherence analysis of hemispheric sunspot activity: a new look at the north-south asymmetry”, Astron. Astrophys., 475, L33–L36. [DOI], [ADS]. (Cited on page 50.)
Du, Z., 2011, “The Shape of Solar Cycle Described by a Modified Gaussian Function”, Solar Phys., 273, 231–253. [DOI], [ADS]. (Cited on page 40.)
Dyson, F. W. and Maunder, E. W., 1913, “The position of the Sun’s Axis as determined from photographs of the Sun from 1874 to 1912, measured at the Royal Observatory, Greenwich (Second Paper)”, Mon. Not. R. Astron. Soc., 73, 673. [DOI], [ADS]. (Cited on page 8.)
Eddy, J. A., 1976, “The Maunder Minimum”, Science, 192, 1189.–1202. [DOI], [ADS]. (Cited on page 55.)
Eddy, J. A., 1977, “Historical evidence for the existence of the solar cycle”, in The Solar Output and Its Variation, Proceedings of a Workshop, held in Boulder, Colorado, April 26–28, 1976, (Ed.) White, O. R., pp. 55–71, Colorado Associated University Press, Boulder, CO. [ADS]. (Cited on page 37.)
Elling, W. and Schwentek, H., 1992, “Fitting the Sunspot Cycles 10–21 by a Modified F-Distribution Density Function”, Solar Phys., 137, 155–165. [DOI], [ADS]. (Cited on pages 40 and 60.)
Fan, Yuhong, 2009, “Magnetic Fields in the Solar Convection Zone”, Living Rev. Solar Phys., 6, lrsp-2009-4. [DOI], [ADS]. URL (accessed 7 Februar 2014): http://www.livingreviews.org/lrsp-2009-4. (Cited on page 73.)
Feminella, F. and Storini, M., 1997, “Large-scale dynamical phenomena during solar activity cycles.”, Astron. Astrophys., 322, 311–319. [ADS]. (Cited on page 41.)
Ferreira, S. E. and Potgieter, M. S., 2004, “Long-Term Cosmic Ray Modulation in the Heliosphere”, Astrophys. J., 603, 744–752. [ADS]. (Cited on page 28.)
Feynman, J., 1982, “Geomagnetic and solar wind cycles, 1900–1975”, J. Geophys. Res., 87(A8), 6153–6162. [DOI], [ADS]. (Cited on pages 27, 62, and 63.)
Fligge, M. and Solanki, S. K., 1997, “Inter-cycle Variations of Solar Irradiance: Sunspot Areas as a Pointer”, Solar Phys., 173, 427–439. [DOI], [ADS]. (Cited on page 16.)
Forbush, S. E., 1954, “World-Wide Cosmic-Ray Variations, 1937–1952”, J. Geophys. Res., 59, 525–542. [DOI], [ADS]. (Cited on page 27.)
Foukal, P., 2014, “An Explanation of the Differences Between the Sunspot Area Scales of the Royal Greenwich and Mt. Wilson Observatories, and the SOON Program”, Solar Phys., 289, 1517–1529. [DOI], [ADS]. (Cited on page 16.)
Fröohlich, C., 2013, “Total Solar Irradiance: What Have We Learned from the Last Three Cycles and the Recent Minimum?”, Space Sci. Rev., 176, 237–252. [DOI], [ADS]. (Cited on page 20.)
Fröhlich, C. and Lean, J., 1998, “The Sun’s total irradiance: Cycles, trends and related climate change uncertainties since 1976”, Geophys. Res. Lett., 25, 4377–4380. [DOI], [ADS]. (Cited on page 20.)
Garcia, A. and Mouradian, Z., 1998, “The Gleissberg Cycle of Minima”, Solar Phys., 180, 495–498. [DOI], [ADS]. (Cited on page 56.)
Gizon, L., 2004, “Helioseismology of Time-Varying Flows Through The Solar Cycle”, Solar Phys., 224, 217–228. [DOI], [ADS]. (Cited on pages 67 and 71.)
Gleissberg, W., 1939, “A long-periodic fluctuation of the sun-spot numbers”, Observatory, 62, 158–159. [ADS]. (Cited on pages 56 and 61.)
Gnevyshev, M. N., 1963, “The corona and the 11-year cycle of solar activity”, Sov. Astron., 7, 311–318. [ADS]. (Cited on page 40.)
Gnevyshev, M. N., 1967, “On the 11-Years Cycle of Solar Activity”, Solar Phys., 1, 107–120. [DOI], [ADS]. (Cited on page 41.)
Gnevyshev, M. N., 1977, “Essential features of the 11-year solar cycle”, Solar Phys., 51, 175–183. [DOI], [ADS]. (Cited on page 41.)
Gnevyshev, M. N. and Ohl, A. I., 1948, “On the 22-year cycle of solar activity”, Astron. Zh., 25, 18–20. (Cited on pages 56 and 61.)
González Hernández, I., Kholikov, S., Hill, F., Howe, R. and Komm, R., 2008, “Subsurface Meridional Circulation in the Active Belts”, Solar Phys., 252, 235–245. [DOI], [ADS], [arXiv:0808.3606]. (Cited on page 67.)
Hagenaar, H. J., 2001, “Ephemeral Regions on a Sequence of Full-Disk Michelson Doppler Imager Magnetograms”, Astrophys. J., 555, 448–461. [DOI], [ADS]. (Cited on page 24.)
Hagenaar, H. J., Schrijver, C. J. and Title, A. M., 2003, “The Properties of Small Magnetic Regions on the Solar Surface and the Implications for the Solar Dynamo(s)”, Astrophys. J., 584, 1107–1119. [DOI], [ADS]. (Cited on page 24.)
Hagenaar, H. J., DeRosa, M. L. and Schrijver, C. J., 2008, “The Dependence of Ephemeral Region Emergence on Local Flux Imbalance”, Astrophys. J., 678, 541–548. [DOI], [ADS]. (Cited on page 24.)
Haigh, J. D., 2007, “The Sun and the Earth’s Climate”, Living Rev. Solar Phys., 4, lrsp-2007-2. [DOI], [ADS]. URL (accessed 3 February 2010): http://www.livingreviews.org/lrsp-2007-2. (Cited on page 7.)
Hale, G. E., 1908, “On the Probable Existence of a Magnetic Field in Sun-Spots”, Astrophys. J., 28, 315–343. [DOI], [ADS]. (Cited on page 21.)
Hale, G. E., Ellerman, F., Nicholson, S. B. and Joy, A. H., 1919, “The Magnetic Polarity of Sun-Spots”, Astrophys. J., 49, 153–178. [DOI], [ADS]. (Cited on pages 21, 22, and 50.)
Harvey, K. L., 1992, “The Cyclic Behavior of Solar Activity”, in The Solar Cycle, (Ed.) Harvey, K. L., ASP Conference Series, 27, p. 335, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 53.)
Harvey, K. L. and Martin, S. F., 1973, “Ephemeral Active Regions”, Solar Phys., 32, 389–402. [DOI], [ADS]. (Cited on page 24.)
Harvey, K. L. and White, O. R., 1999, “What is solar cycle minimum?”, J. Geophys. Res., 104(A9), 19,759–19,764. [DOI], [ADS]. (Cited on page 33.)
Harvey, K. L., Harvey, J. W. and Martin, S. F., 1975, “Ephemeral active regions in 1970 and 1973”, Solar Phys., 40, 87–102. [DOI], [ADS]. (Cited on page 24.)
Hathaway, D. H., 1996, “Doppler measurements of the Sun’s meridional flow”, Astrophys. J., 460, 1027–1033. [DOI], [ADS]. (Cited on page 66.)
Hathaway, D. H., 2011, “A Standard Law for the Equatorward Drift of the Sunspot Zones”, Solar Phys., 273, 221–230. [DOI], [ADS], [arXiv:1108.1722 [astro-ph.SR]]. (Cited on page 44.)
Hathaway, D. H., 2012, “Supergranules as Probes of the Sun’s Meridional Circulation”, Astrophys. J., 760, 84. [DOI], [ADS], [arXiv:1210.3343 [astro-ph.SR]]. (Cited on page 67.)
Hathaway, D. H. and Rightmire, L., 2010, “Variations in the Sun’s Meridional Flow over a Solar Cycle”, Science, 327, 1350–1352. [DOI], [ADS]. (Cited on pages 67 and 71.)
Hathaway, D. H. and Wilson, R. M., 2006, “Geomagnetic activity indicates large amplitude for sunspot cycle 24”, Geophys. Res. Lett., 33, L18101. [DOI], [ADS]. (Cited on page 63.)
Hathaway, D. H., Wilson, R. M. and Reichmann, E. J., 1994, “The Shape of the Sunspot Cycle”, Solar Phys., 151, 177–190. [DOI], [ADS]. (Cited on pages 40, 41, 42, and 60.)
Hathaway, D. H., Wilson, R. M. and Reichmann, E. J., 1999, “A synthesis of solar cycle prediction techniques”, J. Geophys. Res., 104(A10), 22,375–22,388. [DOI], [ADS]. (Cited on pages 35, 42, 56, 61, and 63.)
Hathaway, D. H., Wilson, R. M. and Reichmann, E. J., 2002, “Group Sunspot Numbers: Sunspot Cycle Characteristics”, Solar Phys., 211, 357–370. [ADS]. (Cited on pages 13, 16, 37, 41, and 55.)
Hathaway, D. H., Nandy, D., Wilson, R. M. and Reichmann, E. J., 2003, “Evidence that a Deep Meridional Flow Sets the Sunspot Cycle Period”, Astrophys. J., 589, 665–670. [DOI], [ADS]. (Cited on page 44.)
Hathaway, D. H., Nandy, D., Wilson, R. M. and Reichmann, E. J., 2004, “Erratum: ‘Evidence that a Deep Meridional Flow Sets the Sunspot Cycle Period’ (ApJ, 589, 665 [2003])”, Astrophys. J., 602, 543–543. [DOI], [ADS]. (Cited on page 44.)
Henney, C. J. and Harvey, J. W., 2002, “Phase Coherence of Solar Magnetic Activity”, Solar Phys., 207, 199–218. [DOI], [ADS]. (Cited on page 50.)
Hodgson, R., 1859, “On a Curious Appearance seen in the Sun”, Mon. Not. R. Astron. Soc., 20, 15–16. [DOI], [ADS]. (Cited on page 25.)
Holland, R. L. and Vaughn, W. W., 1984, “Lagrangian Least-Squares Prediction of Solar Flux (F10.7)”, J. Geophys. Res., 89, 11–16. [DOI], [ADS]. (Cited on page 17.)
Howard, R. and Labonte, B. J., 1980, “The sun is observed to be a torsional oscillator with a period of 11 years”, Astrophys. J. Lett., 239, L33–L36. [DOI], [ADS]. (Cited on pages 53 and 70.)
Howard, R. F., 1991a, “The magnetic fields of active regions V. Magnetic axis orientations”, Solar Phys., 132, 49–61. [DOI], [ADS]. (Cited on page 52.)
Howard, R. F., 1991b, “Axial tilt angles of sunspot groups”, Solar Phys., 136, 251–262. [DOI], [ADS]. (Cited on pages 52 and 53.)
Howe, R., 2009, “Solar Interior Rotation and its Variation”, Living Rev. Solar Phys., 6, lrsp-2009-1. [DOI], [ADS], [arXiv:0902.2406 [astro-ph.SR]]. URL (accessed 27 February 2014): http://www.livingreviews.org/lrsp-2009-1. (Cited on page 53.)
Howe, R., Christensen-Dalsgaard, J., Hill, F., Komm, R. W., Larsen, R. M., Schou, J., Thompson, M. J. and Toomre, J., 2000, “Dynamic Variations at the Base of the Solar Convection Zone”, Science, 287, 2456–2460. [DOI], [ADS]. (Cited on page 59.)
Howe, R., Christensen-Dalsgaard, J., Hill, F., Komm, R., Schou, J., Thompson, M. J. and Toomre, J., 2007, “Temporal variations in the solar rotation at the bottom of the convection zone: The current status”, Adv. Space Res., 40, 915–918. [DOI], [ADS]. (Cited on page 59.)
Howe, R., Christensen-Dalsgaard, J., Hill, F., Komm, R., Schou, J. and Thompson, M. J., 2009, “A Note on the Torsional Oscillation at Solar Minimum”, Astrophys. J. Lett., 701, L87–L90. [DOI], [ADS], [arXiv:0907.2965 [astro-ph.SR]]. (Cited on page 71.)
Howe, R., Christensen-Dalsgaard, J., Hill, F., Komm, R., Larson, T. P., Rempel, M., Schou, J. and Thompson, M. J., 2013, “The High-latitude Branch of the Solar Torsional Oscillation in the Rising Phase of Cycle 24”, Astrophys. J. Lett., 767, L20. [DOI], [ADS]. (Cited on page 71.)
Hoyt, D. V. and Schatten, K. H., 1998, “Group Sunspot Numbers: A New Solar Activity Reconstruction”, Solar Phys., 181, 491–512. [DOI], [ADS]. (Cited on pages 13, 14, 15, and 55.)
Ivanov, V. G. and Miletsky, E. V., 2011, “Width of Sunspot Generating Zone and Reconstruction of Butterfly”, Solar Phys., 268, 231–242. [DOI], [ADS], [arXiv:1011.4800 [astro-ph.SR]]. (Cited on page 44.)
Javaraiah, J., 2007, “North-south asymmetry in solar activity: predicting the amplitude of the next solar cycle”, Mon. Not. R. Astron. Soc., 377, L34–L38. [DOI], [ADS], [astro-ph/0701923]. (Cited on page 61.)
Keller, C. U. [NSO Staff], 1998, “SOLIS — A modern Facility for Synoptic Solar Observations”, in Cool Stars, Stellar Systems and the Sun: Tenth Cambridge Workshop, Proceedings of a meeting held at Cambridge, Massachusetts, 15–19 July 1997, (Eds.) Donahue, R. A., Bookbinder, J. A., ASP Conference Series, 154, pp. 636–649, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 22.)
Kilcik, A., Yurchyshyn, V. B., Abramenko, V., Goode, P. R., Ozguc, A., Rozelot, J. P. and Cao, W., 2011, “Time Distributions of Large and Small Sunspot Groups Over Four Solar Cycles”, Astrophys. J., 731, 30. [DOI], [ADS], [arXiv:1111.3999 [astro-ph.SR]]. (Cited on page 70.)
Kitiashvili, I. and Kosovichev, A. G., 2008, “Application of Data Assimilation Method for Predicting Solar Cycles”, Astrophys. J. Lett., 688, L49–L52. [DOI], [ADS], [arXiv:0807.3284]. (Cited on page 66.)
Komm, R. W., Howard, R. F. and Harvey, J. W., 1993, “Meridional Flow of Small Photospheric Magnetic Features”, Solar Phys., 147, 207–223. [DOI], [ADS]. (Cited on pages 67 and 71.)
Kosovichev, A. G. and Stenflo, J. O., 2008, “Tilt of Emerging Bipolar Magnetic Regions on the Sun”, Astrophys. J. Lett., 688, L115–L118. [DOI], [ADS]. (Cited on page 52.)
Latest Solar Radio Flux Report, “Latest Solar Radio Flux Report”, project homepage, Space Weather Canada. URL (accessed 2 September 2015): http://www.spaceweather.ca/solarflux/sx-en.php. (Cited on page 17.)
Layden, A. C., Fox, P. A., Howard, J. M., Sarajedini, A. and Schatten, K. H., 1991, “Dynamo-based scheme for forecasting the magnitude of solar activity cycles”, Solar Phys., 132, 1–40. [DOI], [ADS]. (Cited on page 66.)
Lean, J., 1990, “Evolution of the 155 Day Periodicity in Sunspot Areas During Solar Cycles 12 to 21”, Astrophys. J., 363, 718–727. [DOI], [ADS]. (Cited on page 58.)
Lean, J. L. and Rind, D. H., 2008, “How natural and anthropogenic influences alter global and regional surface temperatures: 1889 to 2006”, Geophys. Res. Lett., 35, L18701. [DOI], [ADS]. (Cited on page 15.)
Lefevre, L. and Clette, F., 2011, “A global small sunspot deficit at the base of the index anomalies of solar cycle 23”, Astron. Astrophys., 536, L11. [DOI], [ADS]. (Cited on page 70.)
Legrand, J.-P. and Simon, P. A., 1985, “Some solar cycle phenomena related to the geomagnetic activity from 1868 to 1980. I. The shock events, or the interplanetary expansion of the toroidal field”, Astron. Astrophys., 152, 199–204. [ADS]. (Cited on page 27.)
Leussu, R., Usoskin, I. G., Arlt, R. and Mursula, K., 2013, “Inconsistency of the Wolf sunspot number series around 1848”, Astron. Astrophys., 559, A28. [DOI], [ADS], [arXiv:1310.8443 [astro-ph.SR]]. (Cited on page 14.)
Li, J. and Ulrich, R. K., 2012, “Long-term Measurements of Sunspot Magnetic Tilt Angles”, Astrophys. J., 758, 115. [DOI], [ADS], [arXiv:1209.1642 [astro-ph.SR]]. (Cited on page 52.)
Li, K., 1999, “The shape of the sunspot cycle described by sunspot areas”, Astron. Astrophys., 345, 1006–1010. [ADS]. (Cited on page 40.)
Li, K. J., Yun, H. S. and Gu, X. M., 2001, “Latitude Migration of Sunspot Groups”, Astron. J., 122, 2115–2117. [DOI], [ADS]. (Cited on page 44.)
Li, K. J., Wang, J. X., Zhan, L. S., Yun, H. S., Liang, H. F., Zhao, H. J. and Gu, X. M., 2003, “On the Latitudinal Distribution of Sunspot Groups over a Solar Cycle”, Solar Phys., 215, 99–109. [DOI], [ADS]. (Cited on page 47.)
Livingston, W. and Penn, M., 2009, “Are Sunspots Different During This Solar Minimum?”, Eos Trans. AGU, 90, 257–258. [DOI], [ADS]. (Cited on page 69.)
Livingston, W., Penn, M. J. and Svalgaard, L., 2012, “Decreasing Sunspot Magnetic Fields Explain Unique 10.7 cm Radio Flux”, Astrophys. J. Lett., 757, L8. [DOI], [ADS]. (Cited on pages 69 and 70.)
Lockwood, M., Stamper, R. and Wild, M. N., 1999, “A doubling of the Sun’s coronal magnetic field during the past 100 years”, Nature, 399, 437–439. [DOI], [ADS]. (Cited on page 27.)
Ma, L. H. and Vaquero, J. M., 2009, “Is the Suess cycle present in historical naked-eye observations of sunspots?”, New Astron., 14, 307–310. [DOI], [ADS]. (Cited on page 57.)
MacQueen, R. M., Eddy, J. A., Gosling, J. T., Hildner, E., Munro, R. H., Newkirk Jr, G., Poland, A. I. and Ross, C. L., 1974, “The Outer Solar Corona as Observed from Skylab: Preliminary Results”, Astrophys. J. Lett., 187, L85–L88. [DOI], [ADS]. (Cited on page 25.)
Martin, S. F. and Harvey, K. H., 1979, “Ephemeral active regions during solar minimum”, Solar Phys., 64, 93–108. [DOI], [ADS]. (Cited on pages 24 and 53.)
Masarik, J. and Beer, J., 1999, “Simulation of particle fluxes and cosmogenic nuclide production in the Earth’s atmosphere”, J. Geophys. Res., 104(D10), 12,099–12,112. [DOI], [ADS]. (Cited on page 30.)
Maunder, E. W., 1890, “Professor Spoerer’s Researches on Sun-spots”, Mon. Not. R. Astron. Soc., 50, 251–252. [ADS]. (Cited on pages 47 and 55.)
Maunder, E. W., 1903, “Spoerer’s Law of Zones”, Observatory, 26, 329–330. [ADS]. (Cited on page 17.)
Maunder, E. W., 1904, “Note on the Distribution of Sun-spots in Heliographic Latitude, 1874 to 1902”, Mon. Not. R. Astron. Soc., 64, 747–761. [DOI], [ADS]. (Cited on pages 17 and 47.)
Maunder, E. W., 1905, “Distribution of sun-spots”, Mon. Not. R. Astron. Soc., 65, 556. [ADS]. (Cited on page 50.)
Mayaud, P.-N., 1972, “The aa indices: A 100-year series characterizing the magnetic activity”, J. Geophys. Res., 77, 6870–6874. [DOI], [ADS]. (Cited on page 25.)
McKinnon, J. A., 1987, Sunspot Numbers: 1610–1985 (based on The Sunspot-Activity in the Years 1610–1960, by Prof. M. Waldmeier, Copyright 1961, Swiss Federal Observatory, Zurich, Switzerland), UAG Reports, UAG-95, National Geophysical Data Center, NOAA, Boulder, CO. (Cited on page 31.)
McNish, A. G. and Lincoln, J. V., 1949, “Prediction of sunspot numbers”, Eos Trans. AGU, 30, 673–685. [DOI]. (Cited on page 60.)
Miklailutsa, V. P. and Makarova, V. V., 1994, “The Sector Structure of the Active Longitudes in Solar Cycles”, Solar Phys., 155, 391–400. [ADS]. (Cited on page 50.)
Muñoz-Jaramillo, A., Sheeley Jr, N. R., Zhang, J. and DeLuca, E. E., 2012, “Calibrating 100 Years of Polar Faculae Measurements: Implications for the Evolution of the Heliospheric Magnetic Field”, Astrophys. J., 753, 146. [DOI], [ADS], [arXiv:1303.0345 [astro-ph.SR]]. (Cited on page 66.)
Muñoz-Jaramillo, A., Balmaceda, L. A. and DeLuca, E. E., 2013a, “Using the Dipolar and Quadrupolar Moments to Improve Solar-Cycle Predictions Based on the Polar Magnetic Fields”, Phys. Rev. Lett., 111(4), 041106. [DOI], [ADS], [arXiv:1308.2038 [astro-ph.SR]]. (Cited on page 66.)
Muñoz-Jaramillo, A., Dasi-Espuig, M., Balmaceda, L. A. and DeLuca, E. E., 2013b, “Solar Cycle Propagation, Memory, and Prediction: Insights from a Century of Magnetic Proxies”, Astrophys. J. Lett., 767, L25. [DOI], [ADS], [arXiv:1304.3151 [astro-ph.SR]]. (Cited on page 66.)
Mursula, K., Zieger, B. and Vilppola, J. H., 2003, “Mid-term Quasi-periodicities in Geomagnetic Activity During the Last 15 Solar Cycles: Connection to Solar Dynamo Strength”, Solar Phys., 212, 201–207. [DOI], [ADS]. (Cited on page 59.)
Nandy, D., Muñoz-Jaramillo, A. and Martens, P. C. H., 2011, “The unusual minimum of sunspot cycle 23 caused by meridional plasma flow variations”, Nature, 471, 80–82. [DOI], [ADS], [arXiv:1303.0349 [astro-ph.SR]]. (Cited on page 67.)
Newton, H. W. and Milsom, A. S., 1955, “Note on the observed differences in spottedness of the Sun’s northern and southern hemispheres”, Mon. Not. R. Astron. Soc., 115, 398–404. [DOI], [ADS]. (Cited on page 48.)
NOAA, “Sunspot Numbers”, project homepage, NOAA National Geophysical Data Center (NGDC). URL (accessed 7 February 2014): http://www.ngdc.noaa.gov/stp/space-weather/solar-data/solar-indices/sunspot-numbers/. (Cited on page 13.)
NOAA/NGDC, “Solar Data”, project homepage, NOAA National Geophysical Data Center (NGDC). URL (accessed 7 February 2014): http://www.ngdc.noaa.gov/ngdcinfo/onlineaccess.html. (Cited on page 16.)
NOAA/SRS, “Solar Region Summaries”, project homepage, NOAA Space Weather Prediction Center (SWPC). URL (accessed 7 February 2014): http://www.swpc.noaa.gov/ftpmenu/forecasts/SRS.html. (Cited on page 12.)
Nordemann, D. J. R., 1992, “Sunspot Number Time Series: Exponential Fitting and Solar Behavior”, Solar Phys., 141, 199–202. [ADS]. (Cited on page 40.)
Norton, A. A. and Gallagher, J. C., 2010, “Solar-Cycle Characteristics Examined in Separate Hemispheres: Phase, Gnevyshev Gap, and Length of Minimum”, Solar Phys., 261, 193–207. [DOI], [ADS], [arXiv:1001.3186 [astro-ph.SR]]. (Cited on pages 41 and 50.)
Noyes, R. W., 1982, The Sun, Our Star, The Harvard Books on Astronomy, Harvard University Press, Cambridge, MA. (Cited on page 9.)
Ogurtsov, M. G., Nagovitsyn, Y. A., Kocharov, G. E. and Jungner, H., 2002, “Long-period cycles of the Sun’s activity recorded in direct solar data and proxies”, Solar Phys., 211, 371–394. [DOI], [ADS]. (Cited on page 56.)
Ohl, A. I., 1966, “Forecast of sunspot maximum number of cycle 20”, Soln. Dannye, (12), 84. (Cited on page 61.)
Parker, E. N., 1965, “The passage of energetic charged particles through interplanetary space”, Planet. Space Sci., 13, 9–49. [DOI], [ADS]. (Cited on page 27.)
Parnell, C. E., DeForest, C. E., Hagenaar, H. J., Johnston, B. A., Lamb, D. A. and Welsch, B. T., 2009, “A Power-Law Distribution of Solar Magnetic Fields Over More Than Five Decades in Flux”, Astrophys. J., 698, 75–82. [DOI], [ADS]. (Cited on page 24.)
Penn, M. J. and Livingston, W., 2006, “Temporal Changes in Sunspot Umbral Magnetic Fields and Temperatures”, Astrophys. J. Lett., 649, L45–L48. [DOI], [ADS]. (Cited on page 69.)
Pesnell, W. D., 2012, “Solar Cycle Predictions (Invited Review)”, Solar Phys., 281, 507–532. [DOI], [ADS]. (Cited on page 60.)
Petrovay, K., 2010, “Solar Cycle Prediction”, Living Rev. Solar Phys., 7, lrsp-2010-6. [DOI], [ADS], [arXiv:1012.5513 [astro-ph.SR]]. URL (accessed 27 February 2014): http://www.livingreviews.org/lrsp-2010-6. (Cited on page 60.)
Pop, M.-I., 2012, “Distribution of the Daily Sunspot Number Variation for the Last 14 Solar Cycles”, Solar Phys., 276, 351–361. [DOI], [ADS], [arXiv:1110.0364 [astro-ph.SR]]. (Cited on page 14.)
Pulkkinen, T., 2007, “Space Weather: Terrestrial Perspective”, Living Rev. Solar Phys., 4, lrsp-2007-1. [DOI], [ADS]. URL (accessed 3 February 2010): http://www.livingreviews.org/lrsp-2007-1. (Cited on page 7.)
RGO/USAF, “Royal Greenwich Observatory — USAF/NOAA Sunspot Data”, project homepage, NASA / Marshall Space Flight Center. URL (accessed 7 February 2014): http://solarscience.msfc.nasa.gov/greenwch.shtml. (Cited on page 16.)
Ribes, J. C. and Nesme-Ribes, E., 1993, “The solar sunspot cycle in the Maunder minimum AD1645 to AD1715”, Astron. Astrophys., 276, 549–563. [ADS]. (Cited on page 55.)
Rieger, E., Share, G. H., Forrest, D. J., Kanbach, G., Reppin, C. and Chupp, E. L., 1984, “A 154-day periodicity in the occurrence of hard solar flares?”, Nature, 312, 623–625. [DOI], [ADS]. (Cited on page 58.)
Robbrecht, E., Wang, Y.-M., Sheeley Jr, N. R. and Rich, N. B., 2010, “On the ‘Extended’ Solar Cycle in Coronal Emission”, Astrophys. J., 716, 693. [DOI], [ADS]. (Cited on page 53.)
Roy, J.-R., 1977, “The North-South Distribution of Major Solar Flare Events, Sunspot Magnetic Classes and Sunspot Areas (1955–1974)”, Solar Phys., 52, 53–61. [DOI], [ADS]. (Cited on page 47.)
Rozelot, J. P., 1994, “On the stability of the 11-year solar cycle period (and a few others)”, Solar Phys., 149, 149–154. [DOI], [ADS]. (Cited on page 56.)
Sawyer, C., 1968, “Statistics of Solar Active Regions”, Annu. Rev. Astron. Astrophys., 6, 115–134. [DOI], [ADS]. (Cited on page 50.)
Scafetta, N. and Willson, R. C., 2014, “ACRIM total solar irradiance satellite composite validation versus TSI proxy models”, Astrophys. Space Sci., 350, 421–442. [DOI], [ADS]. (Cited on page 20.)
Schad, T. A. and Penn, M. J., 2010, “Structural Invariance of Sunspot Umbrae over the Solar Cycle: 1993–2004”, Solar Phys., 262, 19–33. [DOI], [ADS], [arXiv:0912.2370 [astro-ph.SR]]. (Cited on page 69.)
Schatten, K. H. and Sofia, S., 1987, “Forecast of an exceptionally large even-numbered solar cycle”, Geophys. Res. Lett., 14, 632–635. [DOI], [ADS]. (Cited on page 65.)
Schatten, K. H., Scherrer, P. H., Svalgaard, L. and Wilcox, J. M., 1978, “Using dynamo theory to predict the sunspot number during solar cycle 21”, Geophys. Res. Lett., 5, 411–414. [DOI], [ADS]. (Cited on page 65.)
Scherrer, P. H., Wilcox, J. M., Svalgaard, L., Duvall, J., T. L., Dittmer, P. H. and Gustafson, E. K., 1977, “The mean magnetic field of the sun — Observations at Stanford”, Solar Phys., 54, 353–361. [DOI], [ADS]. (Cited on page 21.)
Scherrer, P. H., Bogart, R. S., Bush, R. I. et al., 1995, “The Solar Oscillations Investigation — Michelson Doppler Imager”, Solar Phys., 162, 129–188. [DOI], [ADS]. (Cited on page 22.)
Schwabe, H., 1844, “Sonnen-Beobachtungen im Jahre 1843”, Astron. Nachr., 21(495), 233–236. [DOI], [ADS]. (Cited on page 9.)
Sheeley Jr, N. R., 1964, “Polar Faculae during the Sunspot Cycle”, Astrophys. J., 140, 731. [DOI], [ADS]. (Cited on page 66.)
Sheeley Jr, N. R., 1966, “Measurements of Solar Magnetic Fields”, Astrophys. J., 144, 723–732. [DOI], [ADS]. (Cited on page 66.)
Sheeley Jr, N. R., 1976, “Polar faculae during the interval 1906–1975”, J. Geophys. Res., 81, 3462–3464. [DOI], [ADS]. (Cited on page 66.)
Sheeley Jr, N. R., 2005, “Surface Evolution of the Sun’s Magnetic Field: A Historical Review of the Flux-Transport Mechanism”, Living Rev. Solar Phys., 2, lrsp-2005-5. [DOI], [ADS]. URL (accessed 3 February 2010): http://www.livingreviews.org/lrsp-2005-5. (Cited on pages 50, 56, 71, and 73.)
SILSO, “Sunspot Index and Long-term Solar Observations (SILSO)”, institutional homepage, Royal Observatory of Belgium. URL (accessed February 2014): http://sidc.oma.be/silso/. (Cited on page 13.)
Simoniello, R., Finsterle, W., Salabert, D., Garcia, R. A., Turck-Chieze, S., Jimenez, A. and Roth, M., 2012, “The quasi-biennial periodicity (QBP) in velocity and intensity helioseismic observations. The seismic QBP over solar cycle 23”, Astron. Astrophys., 539, A135. [DOI], [ADS], [arXiv:1201.2773 [astro-ph.SR]]. (Cited on page 59.)
Sivaraman, K. R., Gupta, S. S. and Howard, R. F., 1999, “Measurement of Kodaikanal white-light images. IV. Axial Tilt Angles of Sunspot Groups”, Solar Phys., 189, 69–83. [DOI], [ADS]. (Cited on page 52.)
Sivaraman, K. R., Gokhale, M. H., Sivaraman, H., Gupta, S. S. and Howard, R. F., 2007, “Measurement of Kodaikanal White-Light Images: Relaxation of Tilts of Spot Groups as Indicator of Subsurface Dynamics of Parent Flux Loops”, Astrophys. J., 657, 592–599. [DOI], [ADS]. (Cited on pages 52 and 53.)
Snodgrass, H. B., 1987, “Torsional oscillations and the solar cycle”, Solar Phys., 110, 35–49. [DOI], [ADS]. (Cited on page 53.)
Solanki, S. K., Krivova, N. A., Schuüssler, M. and Fligge, M., 2002, “Search for a relationship between solar cycle amplitude and length”, Astron. Astrophys., 396, 1029–1035. [DOI], [ADS]. (Cited on page 42.)
Solanki, S. K., Usoskin, I. G., Kromer, B., Schuüssler, M. and Beer, J., 2004, “Unusual activity of the Sun during the previous 11,000 years”, Nature, 431, 1084–1087. [DOI], [ADS]. (Cited on page 55.)
Solanki, S. K., Wenzler, T. and Schmitt, D., 2008, “Moments of the latitudinal dependence of the sunspot cycle: a new diagnostic of dynamo models”, Astron. Astrophys., 483, 623–632. [DOI], [ADS]. (Cited on page 47.)
Solar 10.7 cm Flux Data, “Solar 10.7 cm Flux Data”, project homepage, Space Weather Canada. URL (accessed 27 February 2014): ftp://ftp.geolab.nrcan.gc.ca/data/solar_flux/daily_flux_values/. (Cited on page 17.)
Spoerer, M. G., 1889, “Sur les differences que présentent l’hemisphere nord et l’hemisphere sud du soleil”, Bull. Astron. (Paris), 6, 60–63. [ADS]. (Cited on page 47.)
Stenflo, J. O. and Kosovichev, A. G., 2012, “Bipolar Magnetic Regions on the Sun: Global Analysis of the SOHO/MDI Data Set”, Astrophys. J., 745, 129. [DOI], [ADS], [arXiv:1112.5226 [astro-ph.SR]]. (Cited on page 52.)
Stewart, J. Q. and Panofsky, H. A. A., 1938, “The Mathematical Characteristics of Sunspot Variations”, Astrophys. J., 88, 385–407. [DOI], [ADS]. (Cited on pages 38, 40, and 60.)
Stuiver, M. and Quay, P. D., 1980, “Changes in Atmospheric Carbon-14 Attributed to a Variable Sun”, Science, 207, 11–19. [DOI], [ADS]. (Cited on page 28.)
Suess, H. E., 1980, “The radiocarbon record in tree rings of the last 8000 years”, Radiocarbon, 22, 200–209. (Cited on page 57.)
Svalgaard, L., 2012, “How well do we know the sunspot number?”, in Comparative Magnetic Minima: Characterizing Quiet Times in the Sun and Stars, (Eds.) Mandrini, C. H., Webb, D. F., IAU Symposium, 286, pp. 27–33, Cambridge University Press, Cambridge; New York. [DOI], [ADS]. (Cited on page 56.)
Svalgaard, L., 2013, “Solar activity — past, present, future”, J. Space Weather Space Clim., 3, A24. [DOI]. (Cited on page 14.)
Svalgaard, L., Cliver, E. W. and Le Sager, P., 2004, “IHV: a new long-term geomagnetic index”, Adv. Space Res., 34, 436–439. [DOI], [ADS]. (Cited on page 25.)
Svalgaard, L., Cliver, E. W. and Kamide, Y., 2005, “Sunspot cycle 24: Smallest cycle in 100 years?”, Geophys. Res. Lett., 32, L01104. [DOI], [ADS]. (Cited on pages 66 and 67.)
Tapping, K. F. and Charrois, D. P., 1994, “Limits to the Accuracy of the 10.7 cm Flux”, Solar Phys., 150, 305–315. [DOI], [ADS]. (Cited on page 17.)
Tapping, K. F. and Valdés, J. J., 2011, “Did the Sun Change Its Behaviour During the Decline of Cycle 23 and Into Cycle 24?”, Solar Phys., 272, 337–350. [DOI], [ADS]. (Cited on page 69.)
Temmer, M., Rybak, J., Bendik, P., Veronig, A., Vogler, F., Otruba, W., Pützi, W. and Hanslmeier, A., 2006, “Hemispheric sunspot numbers Rn and Rs from 1945–2004: catalogue and N-S asymmetry analysis for solar cycles 18–23”, Astron. Astrophys., 447, 735–743. [DOI], [ADS]. (Cited on page 48.)
Thompson, R. J., 1993, “A Technique for Predicting the Amplitude of the Solar Cycle”, Solar Phys., 148, 383–388. [DOI], [ADS]. (Cited on page 63.)
Tlatov, A. G., Vasil’eva, V. V. and Pevtsov, A. A., 2010, “Distribution of Magnetic Bipoles on the Sun over Three Solar Cycles”, Astrophys. J., 717, 357–362. [DOI], [ADS]. (Cited on pages 52 and 53.)
Tobias, S., Hughes, D. and Weiss, N., 2006, “Unpredictable Sun leaves researchers in the dark”, Nature, 442, 26. [DOI], [ADS]. (Cited on page 68.)
Tousey, R., 1973, “The solar corona”, in Space Research XIII, Proceedings of open meetings of working groups on physical sciences of the 15th plenary meeting of COSPAR, Madrid, Spain, 10–24 May, 1972, (Eds.) Rycroft, M. J., Runcorn, S. K., pp. 713–730, Akademie-Verlag, Berlin. [ADS]. (Cited on page 25.)
Tuominen, J., 1942, “Die systematische Strombewegung der Sonnenflecke in heliographischer Breite. Mit 1 Abbildung”, Z. Astrophys., 21, 96. [ADS]. (Cited on page 8.)
Ulrich, R. K. and Tran, T., 2013, “The Global Solar Magnetic Field — Identification of Traveling, Long-lived Ripples”, Astrophys. J., 768, 189. [DOI], [ADS], [arXiv:1304.1249 [astro-ph.SR]]. (Cited on page 59.)
Usoskin, I. G., 2013, “A History of Solar Activity over Millennia”, Living Rev. Solar Phys., 10, lrsp-2013-1. [DOI], [ADS]. URL (accessed 27 February 2014): http://www.livingreviews.org/lrsp-2013-1. (Cited on pages 15, 30, and 57.)
Vaquero, J. M., Gallego, M. C. and Trigo, R. M., 2007a, “Sunspot numbers during 1736–1739 revisited”, Adv. Space Res., 40, 1895–1903. [DOI], [ADS]. (Cited on page 14.)
Vaquero, J. M., Trigo, R. M., Gallego, M. C. and Moreno-Corral, M. A., 2007b, “Two Early Sunspots Observers: Teodoro de Almeida and Jose Antonio Alzate”, Solar Phys., 240, 165–175. [DOI], [ADS]. (Cited on page 14.)
Vaquero, J. M., Gallego, M. C., Usoskin, I. G. and Kovaltsov, G. A., 2011, “Revisited Sunspot Data: A New Scenario for the Onset of the Maunder Minimum”, Astrophys. J. Lett., 731, L24. [DOI], [ADS], [arXiv:1103.1520 [astro-ph.SR]]. (Cited on page 14.)
Vitinskij, Y. I., 1976, “Forecast of the Height of Solar Cycle 21 Using methods Based on the Latitude Distribution of Sunspots”, Soln. Dannye, 1976(11), 59–63. [ADS]. (Cited on page 44.)
Volobuev, D. M., 2009, “The Shape of The Sunspot Cycle: A One-Parameter Fit”, Solar Phys., 258, 319–330. [DOI], [ADS]. (Cited on page 40.)
Vonmoos, M. V., Beer, J. and Muscheler, R., 2006, “Large variations in Holocene solar activity: Constraints from 10Be in the Greenland Ice Core Project ice core”, J. Geophys. Res., 111(A10), A10105. [DOI], [ADS]. (Cited on page 57.)
Waldmeier, M., 1935, “Neue Eigenschaften der Sonnenfleckenkurve”, Astron. Mitt. Zurich, 14(133), 105–130. [ADS]. (Cited on pages 31, 38, and 41.)
Waldmeier, M., 1939, “Die Zonenwanderung der Sonnenflecken”, Astron. Mitt. Zurich, 14(138), 470–481. [ADS]. (Cited on page 41.)
Waldmeier, M., 1955, Ergebnisse und Probleme der Sonnenforschung, Geest & Portig, Leipzig, 2nd edn. [ADS]. (Cited on page 47.)
Waldmeier, M., 1957, “Der lange Sonnenzyklus”, Z. Astrophys., 43, 149–160. [ADS]. (Cited on pages 48 and 56.)
Waldmeier, M., 1961, The Sunspot-Activity in the Years 1610–1960, Schulthess u. Co. / Swiss Federal Observatory, Zuürich. [ADS]. (Cited on page 31.)
Waldmeier, M., 1968, “Die Beziehung zwischen der Sonnenflecken-relativzahl und der Gruppenzahl”, Astron. Mitt. Zurich, (285), 1. (Cited on page 14.)
Waldmeier, M., 1971, “The Asymmetry of Solar Activity in the Years 1959–1969”, Solar Phys., 20, 332–344. [DOI], [ADS]. (Cited on pages 47 and 48.)
Wang, Y.-M. and Sheeley Jr, N. R., 1989, “Average properties of bipolar magnetic regions during sunspot cycle 21”, Solar Phys., 124, 81–100. [DOI], [ADS]. (Cited on pages 50 and 52.)
Wang, Y.-M. and Sheeley Jr, N. R., 2003, “On the fluctuating component of the Sun’s large-scale magnetic field”, Astrophys. J., 590, 1111–1120. [DOI], [ADS]. (Cited on page 59.)
Wang, Y.-M. and Sheeley Jr, N. R., 2009, “Understanding the Geomagnetic Precursor of the Solar Cycle”, Astrophys. J. Lett., 694, L11–L15. [DOI], [ADS]. (Cited on page 65.)
Watson, F. T., Penn, M. J. and Livingston, W. C., 2014, “A Multi-instrument Analysis of Sunspot Umbrae”, Astrophys. J., 787, 22. [DOI], [ADS]. (Cited on page 70.)
Webb, D. F. and Howard, R. A., 1994, “The solar cycle variation of coronal mass ejections and the solar wind mass flux”, J. Geophys. Res., 99(A3), 4201–4220. [DOI], [ADS]. (Cited on page 25.)
Webb, D. F. and Howard, T. A., 2012, “Coronal Mass Ejections: Observations”, Living Rev. Solar Phys., 9, lrsp-2012-3. [DOI], [ADS]. URL (accessed 27 February 2014): http://www.livingreviews.org/lrsp-2012-3. (Cited on page 25.)
Willson, R. C., 1997, “Total Solar Irradiance Trend During Cycles 21 and 22”, Science, 277, 1963–1965. [DOI], [ADS]. (Cited on page 20.)
Willson, R. C. and Hudson, H. S., 1988, “Solar luminosity variations in solar cycle 21”, Nature, 332, 810–812. [DOI], [ADS]. (Cited on page 20.)
Wilson, P. R., Altrocki, R. C., Harvey, K. L., Martin, S. F. and Snodgrass, H. B., 1988, “The extended solar activity cycle”, Nature, 333, 748–750. [DOI], [ADS]. (Cited on page 53.)
Wilson, R. M., 1987, “On the Distribution of Sunspot Cycle Periods”, J. Geophys. Res., 92(A9), 10,101–10,104. [DOI], [ADS]. (Cited on page 37.)
Wilson, R. M., 1988, “On the Long-term Secular Increase in Sunspot Number”, Solar Phys., 115, 397–408. [DOI], [ADS]. (Cited on page 55.)
Wilson, R. M., Hathaway, D. H. and Reichmann, E. J., 1998, “An estimate for the size of cycle 23 based on near minimum conditions”, J. Geophys. Res., 103(A4), 6595–6603. [DOI], [ADS]. (Cited on page 61.)
Wittmann, A. D. and Xu, Z. T., 1987, “A catalogue of sunspot observations from 165 BC to AD 1684”, Astron. Astrophys. Suppl., 70, 83–94. [ADS]. (Cited on page 9.)
Wolf, R., 1859, “Extract of a Letter from Prof. R. Wolf, of Zurich, to Mr. Carrington, dated Jan. 12, 1859”, Mon. Not. R. Astron. Soc., 19, 85–86. [ADS]. (Cited on page 31.)
Wolf, R., 1861, “Abstract of his latest Results”, Mon. Not. R. Astron. Soc., 21, 77–78. [DOI], [ADS]. (Cited on pages 10 and 15.)
Wolf, R., 1877a, Geschichte der Astronomie, Geschichte der Wissenschaften in Deutschland. Neuere Zeit, 16, Oldenbourg, Muünchen. Online version (accessed 9 February 2010): http://ebooks.ethbib.ethz.ch/fulltext/Rara/1681.pdf. (Cited on page 9.)
Wolf, R., 1877b, “Astronomische Mittheilungen XLII”, Astron. Mitt. Zurich, 42, 29–60. [ADS]. (Cited on page 15.)
Wolf, R., 1892, “Astronomische Mittheilungen, LXXIX”, Astron. Mitt. Zurich, 79, 317–364. [ADS]. (Cited on page 33.)
Wolfer, A., 1903, “Astronomische Mitteilungen, XCIV”, Astron. Mitt. Zurich, 94, 97–150. [ADS]. (Cited on page 33.)
Yeates, A. R., Nandy, D. and Mackay, D. H., 2008, “Exploring the Physical Basis of Solar Cycle Predictions: Flux Transport Dynamics and Persistence of Memory in Advection- versus Diffusion-dominated Solar Convection Zones”, Astrophys. J., 673, 544–556. [DOI], [ADS], [arXiv:0709.1046]. (Cited on page 67.)
Zhao, J. and Kosovichev, A. G., 2004, “Torsional Oscillation, Meridional Flows, and Vorticity Inferred in the Upper Convection Zone of the Sun by Time-Distance Helioseismology”, Astrophys. J., 603, 776–784. [DOI], [ADS]. (Cited on pages 67 and 71.)
Zhao, J., Bogart, R. S., Kosovichev, A. G., Duvall Jr, T. L. and Hartlep, T., 2013, “Detection of Equatorward Meridional Flow and Evidence of Double-cell Meridional Circulation inside the Sun”, Astrophys. J. Lett., 774, L29. [DOI], [ADS], [arXiv:1307.8422 [astro-ph.SR]]. (Cited on page 67.)
Zolotova, N. V. and Ponyavin, D. I., 2006, “Phase asynchrony of the north-south sunspot activity”, Astron. Astrophys., 449, L1–L4. [DOI], [ADS]. (Cited on pages 48 and 50.)
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
41116_2015_9151_MOESM1_ESM.avi
mpg-Movie (26984.0 KB) Still from a movie — A full-disc magnetogram from NSO/Kitt Peak used in constructing magnetic synoptic maps over the last two sunspot cycles. Yellow represents magnetic field directed outward. Blue represents magnetic field directed inward.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hathaway, D.H. The Solar Cycle. Living Rev. Sol. Phys. 12, 4 (2015). https://doi.org/10.1007/lrsp-2015-4
Published:
DOI: https://doi.org/10.1007/lrsp-2015-4
Keywords
Article history
Latest
The Solar Cycle- Published:
- 21 September 2015
DOI: https://doi.org/10.1007/lrsp-2015-4
Original
The Solar Cycle- Published:
- 01 December 2010
DOI: https://doi.org/10.12942/lrsp-2010-1