Abstract
Large-scale, globally propagating wave-like disturbances have been observed in the solar chromosphere and by inference in the corona since the 1960s. However, detailed analysis of these phenomena has only been conducted since the late 1990s. This was prompted by the availability of high-cadence coronal imaging data from numerous spaced-based instruments, which routinely show spectacular globally propagating bright fronts. Coronal waves, as these perturbations are usually referred to, have now been observed in a wide range of spectral channels, yielding a wealth of information. Many findings have supported the “classical” interpretation of the disturbances: fast-mode MHD waves or shocks that are propagating in the solar corona. However, observations that seemed inconsistent with this picture have stimulated the development of alternative models in which “pseudo waves” are generated by magnetic reconfiguration in the framework of an expanding coronal mass ejection. This has resulted in a vigorous debate on the physical nature of these disturbances. This review focuses on demonstrating how the numerous observational findings of the last one and a half decades can be used to constrain our models of large-scale coronal waves, and how a coherent physical understanding of these disturbances is finally emerging.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Overview
The solar corona consists of a magnetized plasma, with typical temperatures of 1–2 MK. Magnetic field strengths range from a few gauss in the quiet corona up to a few kilogauss in active regions (ARs). In the highly non-potential magnetic fields of ARs, a large amount of energy can be stored. This energy can be released impulsively (presumably triggered by magnetic reconnection) in the form of solar eruptive events (SEEs): flares, coronal mass ejections (CMEs), eruptive filaments, and small-scale ejecta. During SEEs, energies of up to 1033 erg are released, plasma is heated to tens of MK, plasma is ejected at speeds beyond 1000 km s−1, and particles are accelerated to relativistic velocities.
It is natural to assume that the effects of such violent processes in ARs will not remain confined there, but will instead influence more remote parts of the corona. In particular, one would expect MHD waves, shocks, or other kinds of disturbances to propagate away from the erupting AR. Indeed, there has been indirect evidence for the existence of such large-scale traveling disturbances for a long time, including the apparent activation of distant filaments by flares (Dodson, 1949; Ramsey and Smith, 1966) and sympathetic flaring, where a flare seems to cause additional flares in a distant AR (Becker, 1958; Biesecker and Thompson, 2000). Less ambiguous evidence has come from type II radio bursts, first reported by Payne-Scott et al. (1947) and Wild and McCready (1950), which were interpreted as signatures of an expanding coronal shock wave (Uchida, 1960). This interpretation is widely accepted.
In the 1960s, the expected disturbances were directly imaged in Ha (Moreton, 1960; Moreton and Ramsey, 1960; Athay and Moreton, 1961), where they are seen as arc-shaped bright fronts. These Moreton waves were interpreted as the chromospheric ground track of an expanding coronal wavefront (Uchida, 1968). These postulated coronal disturbances were finally observed in 1997 with the Extreme Ultraviolet Imaging Telescope (EIT; Delaboudinière et al., 1995) aboard the SOHO spacecraft. They take the form of spectacular wave-like features propagating globally through the corona (Moses et al., 1997; Thompson et al., 1998).
These perturbations have become known under a bewildering multitude of names, including “EIT waves” and the more generic coronal waves (for a discussion of terminology, see Section 1.3). Their initial observation with SOHO/EIT has caused a resurgence of interest in globally propagating coronal waves, and they have since been observed in many additional spectral channels. However, the identification of the coronal wave signatures with the predicted counterpart of More-ton waves has been quickly called into question by the much lower speeds of EIT waves (a few 100 km s−1 compared to typically 1000 km s−1 for Moreton waves; see e.g., Klassen et al., 2000) as well as by the observation of stationary EIT wavefronts (e.g., Delannée and Aulanier, 1999).
These apparent discrepancies have excited a vigorous debate, and despite the much better characterization of coronal waves we now have, no unanimous consensus on the physical nature and of the exciting agent of these perturbations has been reached yet. Several distinct models are being discussed controversially. The main contenders are the MHD wave/shock model (see Sections 2.2 and 6.1) and different magnetic reconfiguration models (Sections 2.3 and 6.2), as well as various combinations of these scenarios (Section 6.3). For more reviews on the topic of large-scale coronal waves, see Warmuth (2007); Wills-Davey and Attrill (2009); Gallagher and Long (2011); Zhukov (2011); Warmuth (2011); Patsourakos and Vourlidas (2012); Liu and Ofman (2014). The recently discovered phenomena of small-scale EUV waves (Innes et al., 2009; Podladchikova et al., 2010) and quasi-periodic fast propagating wave trains (Liu et al., 2010, 2011) are beyond the scope of this review, and the reader is referred to Liu and Ofman (2014) for a discussion.
1.2 Structure of the review
This review will provide a broad overview of the observational and theoretical aspects of large-scale coronal waves, with a focus on demonstrating how the numerous observational findings of the last one and a half decades can be used to constrain our models of large-scale coronal waves. Section 2 introduces the relevant physical concepts on which the various interpretations of coronal waves are based. In Section 3, the various observational signatures of coronal waves (including indirect signatures such as type II radio bursts), their basic characteristics (e.g., morphology) and frequency of occurrence are presented. Section 4 focuses on the physical characteristics of the underlying disturbances that can be deduced from the various observational signatures, and Section 5 deals with the relationship of waves with solar eruptive events, which are the probable wave sources. In Section 6, the different physical interpretations — or models — of coronal waves are discussed, with an emphasis on showing how they are constrained by observations, and how a unified picture of coronal waves is finally emerging. The relevance of coronal waves to other areas of solar physics is reviewed in Section 7. Finally, the conclusions are given in Section 8.
1.3 A note on terminology
The topic covered in this review is to some extent plagued by confusing terminology. The perturbations have become known as “EIT waves”, “coronal EUV waves”, “coronal bright fronts”, and a number of other terms, which either reflect the instrument involved (e.g., EIT wave), the spectral range at which it is observed (e.g., EUV wave), the environment in which the perturbations propagate (e.g., coronal wave), or their physical nature or formation mechanism (e.g., blast wave). In this review, I will adhere to the following convention:
-
Terms like “EUV waves” or “SXR waves” will be used to specifically denote the spectral range of the observations that are referred to. This does not in any way imply disturbances that are physically different from the generic coronal waves.
-
To address coronal waves observed by specific instruments, terms like “EIT waves” or “SXT waves” are used. This terminology is avoided unless the specific instrument is important for the discussion.
-
Chromospheric wave signatures observed in Ha are referred to as Moreton waves.
For further discussions of terminology, see Vršnak (2005) and Zhukov (2011).
2 Physical Concepts
2.1 Linear MHD waves
In the case of a gas or non-magnetized plasma, a linear (i.e., small amplitude) perturbation of the ambient medium will propagate at the sound speed cs, given by
where γad = 5/3 is the adiabatic exponent for fully ionized plasmas, k the Boltzmann constant, T the temperature, \(\bar \mu\) the mean molecular weight (taken as \(\bar \mu = 0.6\) according to Priest, 1982), and mp the proton mass. Sound waves are longitudinal waves and compressive, with the gas pressure gradient acting as restoring force.
The solar corona is characterized by a magnetized plasma, which means that propagating waves have to be treated within the framework of MHD. There are three characteristic (linear) MHD wave modes: Alfvén, fast-mode and slow-mode waves. In the case of Alfvén waves, the magnetic tension acts as the restoring force. The waves are transversal and are incompressible. They propagate along magnetic field lines with the Alfvén speed
where B is the magnetic field strength, ρ the mass density, and n the total particle number density (taken as n = 1.92ne according to Priest, 1982, with ne as the electron density). Coronal waves are clearly compressive (cf. Sections 4.3 and 4.5) and can propagate across magnetic field lines, which rules out Alfvén waves.
For fast- and slow-mode waves, both the magnetic and the gas pressure act as restoring forces. Their speed is
where θB is the inclination between the wave vector and the magnetic field, and cs the sound speed. The plus sign gives the fast-mode speed, υf, while using the minus sign yields the slow-mode speed, υs.
Note that while υf is only weakly dependent on the direction of the magnetic field, υs shows a much stronger dependency, and becomes zero for θB = 90° (i.e., slow-mode waves cannot propagate perpendicularly to the magnetic field). Coronal waves show a quasi-isotropic propagation and travel to large distances in the quiet corona, where the magnetic field is primarily radial (cf. Section 4.1), therefore, they are generally interpreted as fast-mode waves.Footnote 1
For perpendicular propagation, υf reduces to the magnetosonic speed
For an arbitrary inclination towards \(\vec B\), υms gives an upper limit for υf, while υAor cs, whichever is lower, is the lower limit (for θB = 0°). Often υms is used instead of υf because θB is not known. In the particular case of coronal waves, this is reasonable since they propagate along the solar surface, where the magnetic field is predominantly radial.
2.2 Nonlinear fast-mode waves and shocks
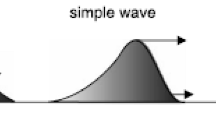
Linear MHD waves are obtained as solutions of the linearized ideal MHD equations (e.g., Priest, 1982), which is a good approximation for small-amplitude perturbations. In the case of large-amplitude perturbations (i.e., large pressure pulses resulting in strong compression of the medium), the fully nonlinear ideal MHD equations have to be treated. This leads to nonlinear MHD waves, as an example so-called simple waves (Landau and Lifshitz, 1959). The nonlinear terms lead to a steepening of the wave profile, as illustrated in Figure 1, since the propagation velocity depends on the amplitude in the case of nonlinear MHD waves in contrast to linear waves (e.g., Mann, 1995). In the case of the fast magnetosonic wave, the crest of the wave propagates at a higher speed than the leading and the trailing edges, which is due to the compression of the density and the magnetic field. This leads to a progressive steepening of the leading edge of the perturbation profile. If the steepening becomes sufficiently strong (this is not necessarily the case, since the amplitude could drop due to geometric expansion), the ideal MHD is not valid any more, since dissipative and dispersive effects become important (for details, see Mann, 1995; Vršnak and Lulć, 2000a,b; Vršnak and Cliver, 2008). These effects prevent a further steepening, and eventually a shock wave may be formed.
Schematics of the nonlinear wave evolution and shock formation process. The x-axis denotes the spatial coordinate x, the y-axis the pressure p. An initial large-amplitude pressure pulse leads to the formation of a nonlinear wave (a so-called simple wave). The wave crest propagates faster than the leading edge, which only moves at the characteristic speed of the medium (υ > υchar), which leads to wave steepening until a discontinuity is established and a shock wave has formed (adapted from Warmuth, 2007).
Basically, a shock wave is defined as a discontinuity with a jump of the entropy, i.e., it is a dissipative structure in contrast to simple waves (Landau and Lifshitz, 1959). At the discontinuity, the conservation laws must be fulfilled, leading to the well-known Rankine-Hugoniot relationships in both hydrodynamics and MHD (cf. Priest, 1982). In reality, the shock waves has a finite width, which is of the order of few ion-inertial lengths (Kennel et al., 1985). In fast-mode shocks, the density downstream is higher than the density upstream (nd > nu), and the downstream magnetic field component parallel to the shock surface increases as compared to the upstream one (Bd > Bu), whereas the component normal to the shock surface does not change. Due to such magnetic field compressions, particles can be accelerated at both simple waves and shock waves (see Section 7.2).
Fast-mode shocks propagate with speeds υshock that are higher than the fast-mode speed of the upstream (undisturbed) plasma υf, u. The shock speed depends on the compression ratio X, which is given by X = nd/nu, where nd and nu are the downstream and upstream plasma densities, respectively. Often, this speed is given in terms of the fast magnetosonic Mach number (i.e., the Mach number of a perpendicular fast-mode shock) Mms = υshock/υms, u. This can be derived from the Rankine-Hugoniot relations according to
with the plasma beta βp and the polytropic index γ, for which usually the adiabatic index γad = 5/3 is substituted.
There are two different processes for shock formation:
-
Piston-driven shocks are generated by the fast and/or impulsive expansion of a driver in all directions, like in an explosion (e.g., Žic et al., 2008; Lulić et al., 2013). The plasma is pushed outwards by the expanding 3D piston and cannot flow behind the piston (the more familiar 1D analog is a piston in a shock tube; see Figure 2). In this geometry, the piston can be slower than the shock (υpiston ≤ υshock), and it even needs not to be supermagnetosonic. However, the piston has to accelerate rapidly: Žic et al. (2008) found that in a low Alfvén velocity environment, a 3D piston can create a shock in the low corona only if it reaches speeds on the order of 1000 km s−1 within a few minutes. During this driving phase, the kinematics of the shock are controlled by the motion of the piston, and the stand-off distance between shock and piston is increasing. Once the piston decelerates, the shock detaches and can continue its propagation, although now without additional energy supply by the piston (such a freely propagating shock is also referred to as a blast wave). Note that the mechanism of nonlinear wave steepening described above is equivalent to the 3D piston scenario once the piston ceases to provide energy input.
-
In contrast, a bow shock is created by a driver that moves through a medium in such a way that the upstream plasma can flow behind it. The best example for this type of shock is the bow shock created by the Earth’s magnetosphere in the solar wind. A bow shock always propagates at the same velocity as the driver and has a fixed stand-off distance (assuming a homogeneous medium). This also means that the formation of a bow shock requires a supermagnetosonic driver.
Schematics of the two types of driven shocks: piston-driven shock (left) and bow shock (right). In a piston-driven shock, the driver can be slower then the shock (υpiston ≤ υshock), while a bow shock always has the same speed as the driver (υpiston = υshock). Adapted from Warmuth (2007).
2.3 Magnetic reconfiguration and pseudo waves
MHD waves (or shocks) are not the only mechanism that can generate large-scale wavelike brightenings in the solar corona. Coronal mass ejections (CMEs) involve the expansion and eruption of large-scale magnetic field structures. Such a restructuring of the coronal magnetic field is associated with several processes that can potentially generate propagating brightenings in the corona, which could be mistaken for true waves.
Three kinds of “pseudo wave” or “magnetic reconfiguration” models that are based on different consequences of magnetic restructuring have been proposed. In the field line stretching model (Section 6.2.1), brightenings are generated by plasma compression at the footpoints of successively stretched or opening magnetic field lines overlying an erupting flux rope. In the current shell model (Section 6.2.2) an electrical current sheet is formed around an erupting flux rope, and the dissipation of the current by Joule heating will generate brightenings. Finally, the reconnection front model (Section 6.2.3) proposes successive reconnection events between a laterally expanding CME and favourably oriented loops in the quiet sun. The reconnection events will cause plasma heating that will be observed as propagating brightenings.
3 Observational Signatures
Large-scale wave-like coronal disturbances have been directly observed in optically thin coronal EUV and SXR emission, as well as in Thompson-scattered white-light radiation (see Section 3.1). Signatures of the perturbations have also been been detected in optically thick chromospheric spectral lines (Section 3.2).Footnote 2 Apart from this direct imaging, waves have been successfully observed via interferometric imaging in the radio domain (see Section 3.3). In addition to these direct observational signatures, coronal waves are closely associated with metric type II radio bursts (Section 3.4.1) and coronal dimmings (Section 3.4.2).
It is worth pointing out that recent studies have shown that many coronal waves show multiple wavefronts. Usually a faster wavelike disturbance is being followed by a slower perturbation that is related to the magnetic reconfiguration of the corona caused by an erupting CME. The vast majority of coronal wave studies has focused on the former, wavelike disturbance, which is usually much easier to identify and track than the more irregular second front. Therefore, unless explicitly stated otherwise, the issues discussed in this review apply to the wavelike component. The multiplicity of wavefronts will be addressed specifically in Section 4.1.4.
Table 1 gives an overview of the instruments that have successfully imaged signatures of coronal waves (or their chromospheric counterparts). For instruments that have flexible operational characteristics, such as variable cadence, the parameters listed are typical ones for studies involving coronal waves. The resolution listed is the actual effective resolution, not the resolution per pixel. Except TRACE, all instruments have full-disk coverage, although Yohkoh/SXT and Hinode/XRT often observed in partial-frame mode. While all space-based instruments are listed separately, this has not been done for the considerable number of Hα and Helium I instruments at ground-based observatories (GBOs). In particular, note the remarkable progress in EUV imaging capabilities in terms of spatial and temporal resolution as well as spectral coverage.
Another important observational asset for the study of coronal waves are coronagraphs, which are essential in establishing the relation between waves and CMEs. For this application, the most important observational capability is a field of view (FOV) that reaches down as low as possible into the corona (i.e., which has a small inner occulter) to get an observational overlap with the EUV and SXR imagers. On SOHO, the C1 instrument (FOV: 1.1–3 RSFootnote 3) of the LASCO coronagraph package (Brueckner et al., 1995) has provided such data only up to 1998. Space-based coronagraphic data from the middle corona have again become available with the COR1 instrument (FOV: 1.4–4 RS) of the SECCHI imaging package (Howard et al., 2008) aboard the two STEREO spacecrafts. Ground-based coronagraphic imaging of the low corona has been provided the MK3 (Fisher et al., 1981) and MK4 K-coronameters at Mauna Loa Solar Observatory (FOV: 1.12–2.44 RS and 1.14–2.86 RS, respectively).
These various imagers are complemented by spectroscopic instruments. Several EUV spectrometers have helped in characterizing the physical parameters of coronal waves and associated phenomena: CDS (Harrison et al., 1995) and UVCS (Kohl et al., 1995) aboard SOHO, and EIS (Culhane et al., 2007) aboard Hinode. In the radio regime, the bulk of the information about wave-associated metric type II bursts comes from various ground-based radiospectrographs and radioheliographs.
3.1 Coronal wavefronts
3.1.1 Extreme Ultraviolet (EUV)
The solar corona emits optically thin EUV radiation which is dominated by emission lines of the various elements at different ionization states, corresponding to different temperatures. EUV spectroscopy has shown that the solar corona is multithermal (e.g., Brosius et al., 1996), which can be quantified by the differential emission measure (DEM). The DEM of the quiet corona typically extends from below 1 MK up to some 2 MK, and peaks near T = 1.5 MK (i.e., the bulk of the plasma has temperatures close to this peak). Since the launch of SOHO in 1995, the corona is observed in this temperature range by EUV imagers of increasing spectral, temporal, and spatial coverage and resolution. The intensities recorded in EUV images result from line-of-sight integration of optically thin radiation, and are therefore proportional to the integral of the electron density squared along the line of sight. Therefore, projection effects may have to be considered (cf. Ma et al., 2009; Hoilijoki et al., 2003; Delannée et al., 2014).
The Extreme-Ultraviolet Imaging Telescope (EIT; Delaboudinière et al., 1995) was the first EUV imager to detect signatures of globally propagating wavelike disturbances in the solar corona.Footnote 4 These disturbances have become known as EIT waves and are primarily observed at 195 Å (which is dominated by line emission of the Fe xii ion, corresponding to a plasma temperature of 1.4 MK). The perturbations take the form of moving fronts of increased EUV emission that propagate quasi-radially away from active regions at speeds of typically a few 100 km s−1 (Moses et al., 1997; Thompson et al., 1998, 1999, see Figure 3 and the animation in Figure 4 for a “textbook example”). The observed pulses are usually quite faint (emission increase below ≈ 25%) and diffuse, can have an angular extent up to 360°, and can propagate over a whole hemisphere (to distances beyond one solar radius). They weaken in the course of their propagation (Klassen et al., 2000).
One of the first large-scale coronal waves observed: the iconic EIT wave of 1997 May 12, studied by Thompson et al. (1998). Running difference images observed at 195 Å are shown. A diffuse bright front is propagating quasi-isotropically through the corona.
Still from a movie — An animation of the EIT wave of 1997 May 12. Shown is a sequence of base difference images obtained at 195 Å. (To watch the movie, please go to the online version of this review article at http://www.livingreviews.org/lrsp-2015-3.)
A small subset (7%) of events, the so called S-waves (Biesecker et al., 2002; Thompson and Myers, 2009) or brow waves (Gopalswamy et al., 2000a) are characterized by arc-like, sharp fronts (see Figure 5b) that later decay to the more usual diffuse fronts (Thompson et al., 2000b; Warmuth et al., 2004b). There are also many propagating disturbances that have been tentatively identified as waves, but which do not propagate to large distances and which show rather irregular fronts (cf. the catalog by Thompson and Myers, 2009, see Figure 5c for an example). In addition to the propagating fronts, stationary brightenings (Section 4.7.4) and extended regions of emission decrease (Section 3.4.2) are often observed in coronal wave events. Signatures corresponding to the EUV wavefronts have also been detected in soft X-rays and white light, as well as in chromospheric absorption lines and in radio (see the following sections).
The diverse morphology of coronal EUV waves. (a): the diffuse globally propagating front of 1997 May 12. (b): the sharp S-wave of 1997 Sep 24. (c): the small-scale irregular wave of 1998 Jun 13. (d): the dome-shaped wave of 2010 Jan 17. All panels show difference images from which a pre-event image has been subtracted. In addition to the bright fronts, note the dark dimming regions close to the erupting active regions.
Understanding the relationship of EIT waves with wave signatures in other spectral channels and with associated flares and CMEs has been hampered by the low image cadence of EIT (typically an image per 12 minutes). This is one of the reasons for the prolonged debate on the physical nature of coronal EUV waves.
While the Transition Region and Coronal Explorer (TRACE; Handy et al., 1999) provided EUV images at sub-minute cadences, its restricted field of view has limited its usefulness for studies of large-scale phenomena, and there is only a single EUV wave event that has been studied extensively using TRACE (Wills-Davey and Thompson, 1999; Wills-Davey, 2006; Wills-Davey et al., 2007). Significant progress has resulted from the high-cadence EUV imaging that has become available with the Extreme Ultraviolet Imager (EUVI; Wülser et al., 2004; Howard et al., 2008) on the two STEREO spacecraft, the Sun Watcher using Active Pixel detectors and Image Processing (SWAP; Halain et al., 2010) aboard PROBA2, and the Atmospheric Imaging Assembly (AIA; Lemen et al., 2012) aboard SDO. These instruments have provided a wealth of observational data, so that the EUV spectral range is now clearly the most important spectral range with respect to coronal waves. This will become clearly evident in Section 4.
In particular, the increased cadence (coupled with the possibility of stereoscopic imaging with STEREO) now allows us to better relate the EUV waves to other wave signatures (Section 4.2) and to features connected with an erupting CME (Section 5.2). The better cadence was also instrumental in showing coronal waves exhibit traits such as refraction, reflection, and transmission, which are strong indications for the true wave nature of the disturbances (Section 4.7). Moreover, the comprehensive spectral coverage of AIA allows a much better characterization of the physical parameters of the observed disturbances, such as density and temperature (Sections 4.3 and 4.5).
High-cadence observations have also confirmed the bimodality of coronal waves originally suggested by Zhukov and Auchère (2004). This means that many EUV wave show a fast bright front that appears to be wavelike in nature, and additionally trailing intensity enhancements that are associated with an erupting CME (Section 4.1.4). Connected to this issue are observations of quasi-circular wave domes (see Figure 5d). In these events, the leading edge is very sharp, and the coronal parts of the dome neatly connect to the on-disk wave signatures. Erupting CME loops are located inside the dome, and the dome shows a much larger lateral expansion than the coronal core dimming (cf. Veronig et al., 2010). All these observations imply that this dome is actually the signature of a coronal wave and not the CME itself (cf. Section 5.2).
3.1.2 Soft X-rays (SXR)
In contrast to EUV, which is dominated by line emission, SXRs from the quiet corona are primarily due to thermal bremsstrahlung continuum. Generally, the temperature response of SXR instruments is broader than for EUV and more weighted towards hotter plasmas (T ≥ 2 MK; see Table 1), so that they observe only the hottest part of the plasma distribution in the quiet corona. Still, coronal disturbances of a compressive nature should be not only observable in EUV, but in SXRs as well, in particular if heating is involved. However, coronal wave signatures in SXRs were first observed (Khan and Aurass, 2002) by the Soft X-ray Telescope (SXT; Tsuneta et al., 1991) aboard the Yohkoh spacecraft five years after EIT waves were discovered. This late detection (and the small number of observed events) was mainly due to instrumental effects (strong contamination by scattered light from the flare) and the observation schemes of SXT, which were mainly tailored for flares (partial-frame images, short exposure times, filters configurations sensitive only to hot plasmas).
As their EUV counterparts, “SXT waves” are observed as fronts of increased coronal emission. Morphologically, they are more homogeneous and have a sharper leading edge as compared to typical EUV waves (see Figure 6 for an example). This may be due to the fact that SXT waves are only observed quite close to the source AR before the waves start to weaken and disintegrate. Moreover, SXT seems to be able to observe only strong disturbances, which are probably sharper defined: all reported SXT waves were associated with metric type II bursts and Hα Moreton waves (Khan and Aurass, 2002; Narukage et al., 2002; Hudson et al., 2003; Warmuth et al., 2004a; Narukage et al., 2004). This is supported by SXT intensity ratios (wavefront vs. background corona) which were consistent with weak to moderate shock waves with fast-mode Mach numbers of 1.1–1.3 (Narukage et al., 2002; Hudson et al., 2003; Narukage et al., 2004). Khan and Aurass (2002) demonstrated that SXT wave, EIT wave, Moreton wave, and type II burst source were actually cospatial, which implies a single underlying physical disturbance.
The coronal wave of 1997 Nov 3 observed in soft X-rays with Yohkoh/SXT. Shown are base images obtained with different filters (with reversed gray scale). The arrows indicate the sharp leading edge of the wave. Bright radial and circular features in the images are due to saturation effects from the flare. Image reproduced with permission from Khan and Aurass (2002), copyright by ESO.
Two interesting SXT limb events have been reported. Hudson et al. (2003) observed an SXT wave that was characterized by an arc-shaped bright front that became increasingly tilted towards the solar surface as it propagated along the solar limb. This can be interpreted in terms of a refracting wave (see Section 6.1). Narukage et al. (2004) reported a limb event, where the SXT wave signatures could be observed to propagate both on the disk (where they were cospatial with an associated Moreton wave) and radially outward above the limb. The 3D structure of the SXT wave can thus be interpreted as a dome that expands in the corona and intersects the chromosphere.
Observing always in full-disk mode, the Solar X-Ray Imager (SXI; see Hill et al., 2005; Pizzo et al., 2005) aboard the GOES-12 satellite has been more successful in recording coronal waves. Thanks to its cadence (2–4 min) SXI has provided a valuable link between the Moreton waves observed close to the AR and the remote EIT fronts. For six events, it could be shown that the wave features seen with SXI are cospatial with and morphologically similar to the EIT fronts (Warmuth et al., 2005; see Figure 7 for an example), as well as being cospatial with the associated chromospheric Moreton and Helium I wavefronts. This is again consistent with a single physical disturbance creating all wave signatures. Note that SXI instruments are also aboard all of the following GOES satellites (up to now, GOES-13, 14, and 15), thus providing routine full-disk SXR imaging capabilities.
The coronal wave of 2003 Nov 3 observed in soft X-rays with GOES/SXI. Shown are running difference images. The wavefront is extended in height and can be observed above the solar limb. In the upper right panel, an EIT 195 Å difference image is shown for comparison. Note the morphological similarities with the X-ray signatures. Image reproduced with permission from Warmuth et al. (2005), copyright by AAS.
Due to observational schedules more focused on flares and telemetry limitations, only a few wave detections have been reported yet from the most recent SXR imager, the X-Ray Telescope (XRT; Golub et al., 2007) aboard the Hinode spacecraft. Asai et al. (2008) observed a faint arc-like ejection with XRT, which was kinematically consistent with an associated EIT wave. Based on XRT intensity ratios, the perturbation was interpreted as a fast-mode shock. Attrill et al. (2009) studied a coronal wave event that was observed with XRT and EUVI. They found that the strongest parts of the perturbation are cospatial in all wavelengths, and that the CME flanks as observed by STEREO/COR1 map back to the wavefronts. Attrill et al. (2009) concluded that the wavefront is actually the expanding CME shell. In a different event, Delannée et al. (2014) observed a coronal wave with EUVI and XRT data. Using a filter ratio method, they deduced a multithermal structure of the wave, with possibly two components around T ≈ 1.5 MK and T ≈ 5 MK.
3.1.3 White light
In white light (WL) coronagraphic observations, some CMEs are associated with smooth emission features that have a sharp leading edge. These features have been identified as density enhancements caused by a CME-driven fast-mode shock (e.g., Vourlidas et al., 2003; Rouillard et al., 2011). This has been verified by UV spectroscopy with SOHO/UVCS (e.g., Raymond et al., 2000; Mancuso et al., 2002; Ciaravella et al., 2005; Bemporad et al., 2014), which also allows to determine the shock parameters. WL shocks have been observed both at the nose and at the flanks of an erupting CME, which poses the question whether these shocks represent the same perturbation that is causing coronal waves (e.g., Tripathi and Raouafi, 2007). To conclusively answer this question, an overlap of the fields of view of the coronagraph and the EUV imager is required. This has first been achieved with COR1 and EUVI aboard the STEREO spacecraft. Recently, Kwon et al. (2013b) identified an laterally propagating wavefront-like feature seen in STEREO/COR1 as the upper coronal counterpart of an EUV coronal wave propagating on the solar disk (see Figure 8). This represents the first unambiguous detection of a coronal wave in the upper corona. Coronal waves may thus really be the counterparts of WL shocks in the low corona.
White-light observations (with STEREO/COR1-B) of the upper coronal counterpart of the coronal EUV wave of 2011 Aug 4. Panel (a) shows a total brightness image, while panels (b)–(d) are running difference images. The cone in panel (b) represents a CME model. An arrow indicates the WL wavefront that is propagating counter-clockwise. Image reproduced with permission from Kwon et al. (2013b), copyright by AAS.
3.2 Chromospheric wavefronts
3.2.1 Hα (Moreton waves)
Historically, large-scale propagating disturbances were first observed in the chromosphere in the optically thick Ha absorption line (6563 Å) using high-cadence filtergrams. These Moreton waves (Moreton, 1960; Moreton and Ramsey, 1960; Athay and Moreton, 1961) appear as arc-shaped fronts propagating away from flaring active regions at speeds of the order of 1000 km s−1 (see Figure 9 and the animation in Figure 10 for an example). The fronts are seen as emission enhancements in the center and in the blue wing of the Hα line (i.e., bright fronts), whereas in the red wing they appear as emission depletions (dark fronts). This was interpreted as a Doppler shift due to a depression of the chromosphere by an invisible agent (Moreton, 1964). The velocity of the downward motion of the chromosphere is of the order of a few tens of km s−1 (e.g., Uchida et al., 1973, and references therein). Often the relaxation of the chromosphere can also be seen, which takes the form of an additional trailing wave (dark in the blue wing and bright in the red wing of Hα). This should no be mistaken for a physically distinct second wave.
The Moreton wave of 1998 May 2 observed in Hα (line center) at Kanzelhöhe Solar Observatory. Shown are difference images from which a pre-event frame has been subtracted. The wave is visible as an arc-shaped front of increased emission that becomes more diffuse as it propagates away from the flaring AR (adapted from Warmuth et al., 2004a).
Still from a movie — An animation of the Moreton wave of 1998 May 2 observed in Ha base difference images at Kanzelhöhe Solar Observatory. (To watch the movie, please go to the online version of this review article at http://www.livingreviews.org/lrsp-2015-3.)
The Doppler shift strongly suggests that the Moreton wave appears only as a reaction to something pressing down from the corona and not due to a wave actually propagating in the chromosphere. This is supported by the observed propagation speeds of the order of 1000 km s−1, which are significantly larger than the sound speed (≈ 10 km s−1) or the Alfvén speed (≈ 100 km s−1) in the chromosphere. Any true chromospheric disturbance would be rapidly dissipated due to the corresponding high Mach numbers. These observations quickly led to the postulation that the chromospheric Moreton wave signature represents the ground track of a coronal wavefront (Uchida, 1968, see also Section 6.1.1).
Morphologically, Moreton waves are characterized by a sharp leading edge. The wavefronts consist of an arc of homogeneously increased emission and a number of small discrete brightenings (Warmuth et al., 2004a). These brightenings can be observed for a few minutes after the wavefront has passed them, and some of them are appearing up to 25 Mm in front of the leading edge of the arc. The excess emission — both homogeneous and discrete — is always arising from an enhancement of pre-existing chromospheric structures, and not from propagating matter such as various form of ejecta. This is consistent with the wavelike nature of Moreton waves that is suggested by the observed downward-upward motion of the chromosphere.
In the course of their propagation Moreton waves become progressively faint, diffuse and irregular, until their propagation can no longer be tracked (cf. Figure 9). This suggests that the coronal influence to which the chromosphere reacts becomes weaker and less coherent. In the course of their propagation, Moreton waves avoid regions of enhanced Alfvén speeds, such as ARs and coronal holes (Warmuth et al., 2004a; Veronig et al., 2006). They also never appear within an AR, but are first observed at an offset distance from the source AR (Warmuth et al., 2004a). There has been one report of an event where three Moreton waves were observed in close succession, apparently launched by the eruption of three filaments (Narukage et al., 2008).
Moreton waves are always associated with cospatial coronal waves (e.g., Thompson et al., 2000b; Warmuth, 2010; Asai et al., 2012, see Section 4.2), and are highly associated with metric type II radio bursts (Section 3.4.1), which both supports Uchida’s model of a coronal wave creating a chromospheric imprint.
3.2.2 Helium I (10 830 Å)
The second channel of information on wave signatures in the chromosphere is the near-infrared Helium I line at 10 830 Å (He I). This line is formed in a complicated manner, because absorption in the line increases with increasing UV and EUV flux from the corona and/or with an increase of collisional processes (due to a rise in temperature or density) in the transition region (e.g., Andretta and Jones, 1997). Thus, He i actually contains influences from the corona, transition region, and chromosphere. While this complicates the interpretation of the data, it provides an interesting link between chromospheric and coronal observations.
Wave signatures in He i were first detected in images recorded by the CHIP instrument (MacQueen et al., 1998) at Mauna Loa Solar Observatory by Vršnak et al. (2002b). They appear as dark fronts, i.e., they are seen in increased absorption, as shown in Figure 11. The fronts are more diffuse and have a broader profile than Moreton waves, and they show a patchy structure that corresponds with the photospheric magnetic field and the chromospheric network.
The He i wave of 1997 Jul 25. Shown are difference images from which a pre-event frame has been subtracted. The He i wave is seen as an expanding diffuse dark front (its leading edge is indicated by black arrows). The bright patches in the upper right corner are due to the associated flare. Image reproduced with permission from Vršnak et al. (2002b), copyright by ESO.
Wavefronts are also seen in He i dopplergrams, which first show a downward swing followed by an upward motion of the chromosphere (Gilbert and Holzer, 2004). This is consistent with the results of Ha line wing observations and supports the notion that both chromospheric wave signatures (He I and Hα) are actually a reaction to a pressure pulse from the corona. This straightforwardly explains the increase of absorption in He i, which can be caused by the increase of UV and EUV flux from the compressed coronal plasma and/or by the increase of collisional processes in the compressed transition region. Both processes could contribute to the observed signatures. The He i wavefronts were found to consist of a weaker frontal segment and a more pronounced main perturbation element. The former could be generated by the higher parts of an inclined coronal wave (see Section 6.1.1), while the latter is generated by the actual impact of the coronal wave on the chromosphere (Vršnak et al., 2002b).
The He i waves observed with CHIP have two attractive properties: the He i fronts can be tracked to larger distances than is possible with Hα, and the temporal cadence (3 min) allows the observation of waves much closer to their origin than is usually possible with EIT. Before the availability of high-cadence EUV imaging, the He i waves have thus acted as a link between Moreton and EIT waves. This has proven that the He i waves are cospatial with the coronal wavefronts (Vršnak et al., 2002b; Gilbert et al., 2004), as well as with the Moreton wavefronts (Vršnak et al., 2002b; Warmuth, 2010).
He I waves seem to be highly associated with Moreton waves: out of the 11 Moreton waves with available He i observations reported by Warmuth (2010), ten also showed He i fronts. Interestingly, several events have been reported that show multiple consecutive wavefronts — in one event, five wavefronts within half an hour (Gilbert and Holzer, 2004; Gilbert et al., 2008). This is normally not observed in Hα, which may imply that the He i line is actually more sensitive to these kinds of disturbances. The multiplicity of wavefronts could reflect several wave generation mechanisms acting in one event, for instance CME- and flare-related mechanisms.
Some regions behind the He i front show a brightening that coincides with the locations of coronal dimming (see Section 3.4.2) in cotemporal EIT images observed behind EIT waves (Vršnak et al., 2002b). This weakening of absorption in He i is probably due to a reduction of EUV irradiation or heat flux from the corona.
3.3 Wavefronts imaged in the radio range
3.3.1 Radio: metric waves
The Nançay radioheliograph (NRH; Kerdraon and Delouis, 1997) provides images at several frequencies in the metric/decimetric regime. Metric signatures of a coronal wave were successfully detected by Vršnak et al. (2005) for the first time (see Figure 12). They observed a broadband radio source (visible at 151, 164, 237, and 327 MHz) that was moving colaterally with a coronal wave seen in Hα, EUV, and SXRs (see also Vršnak et al., 2006). The source was brighter at lower frequencies, and overall it was significantly weaker than the type II and type IV burst sources also present in the event. The emission centroid was located at heights of 0–200 Mm above the solar limb, and while its horizontal extent was comparable to the NRH beam size, its vertical extension was larger than the beam. This is the signature expected for a narrow, vertically extended disturbance, and indeed this is consistent with the coronal wave signatures seen in EUV and SXR (see Figure 7). The source showed a decline in intensity during its propagation, which was interrupted by a brief brightening when the source was crossing an enhanced coronal structure.
The coronal wave of 2003 Nov 3 imaged at metric wavelengths with the Nançay radioheliograph. The wave source (marked W) is propagating northwards along the solar limb towards the pole. The type II and type IV burst sources are also indicated. In each panel, the observing time and frequency is given (adapted from Vršnak et al., 2005).
Based on its spectral characteristics (brighter at lower frequencies), the NRH wave source was interpreted by Vršnak et al. (2005) as being due to optically thin gyrosynchrotron emission (cf. Dulk and Marsh, 1982), which is excited or enhanced by the passage of a coronal shock wave. The shock will temporarily increase the magnetic field strength as well as the energy and density of the electrons, thus resulting in an increase of gyrosynchrotron emissivity. When the source passed an enhanced coronal structure, the radio emission became prolonged, which may indicate the triggering of local energy release by the disturbance.
3.3.2 Radio: microwaves
Radioheliograms in the microwave range (17 and 34 GHz) are routinely provided by the Nobeyama radioheliograph (NoRH; Nakajima et al., 1994). Radio emission at these wavelengths arises from thermal bremsstrahlung as well as non-thermal gyro-resonance and synchrotron radiation. In the quiet sun, the main contribution is thermal bremsstrahlung from the chromosphere (with a brightness temperature of TB ≈ 10 000 K).
The first tentative hint of a wave seen in microwave radioheliograms from NoRH was reported by Aurass et al. (2002) in the form of a bright blob moving with an EIT wave. Warmuth et al. (2004a) observed four actual “NoRH waves” at 17 GHz that were consistent with simultaneously observed Moreton wavefronts in terms of location and morphology. The NoRH waves are more diffuse than the corresponding Moreton waves, but this is probably an effect of the imaging algorithm. The excess brightness temperatures were up to 3500 K. In two limb events, no excess emission was observed above the limb, which would point to chromospheric optically thick bremsstrahlung as the emission mechanism. Compression of these layers (caused by the impact of a coronal wave) would result in enhanced microwave emission.
White and Thompson (2005) have studied one of these waves in more detail (see Figure 13). Based on the radio spectrum, they concluded that the emission is most likely due to coronal optically thin free-free bremsstrahlung. However, the radio spectrum was rather poorly constrained (just the two NoRH frequencies, of which the 34 GHz images were very noisy). Moreover, for the parameters derived from the NoRH wavefronts, the EUV emission of the associated EIT wave could only be reproduced if the emitting plasma was not at the peak formation temperature of the Fe xii line (1.4 MK) or if the abundances were photospheric instead of coronal. In terms of kinematics, White and Thompson (2005) found a high constant speed that was in disagreement with the decelerating Moreton wave reported by Warmuth et al. (2004a).
Top: the wave event of 1997 Sep 24 imaged at 17 GHz with the Nobeyama radioheliograph. Shown is a difference image (with reversed gray table) on which contours of the base image are overplotted. An arc-shaped front of increased brightness temperature is clearly seen to the north of the associated flare. Bottom: the associated sharp EIT wavefront shown in a difference image. Image reproduced with permission from White and Thompson (2005), copyright by AAS.
In summary, there have been only two studies of wave signatures in microwaves, and they come to different conclusions. Further studies of more events will be required to gain more insight into the nature of the microwave signatures. Note that NoRH is the currently the only instrument that provides imaging of waves at extremely high temporal cadences of up to one image per second and is therefore uniquely suited to study details of wave kinematics.
3.4 Indirect signatures
3.4.1 Metric type II radio bursts
Type II radio bursts (Payne-Scott et al., 1947; Wild and McCready, 1950) appear as slowly drifting bands of emission in dynamic radiospectra (see Figure 14a as an example). They are characteristic signatures of shock waves traveling outwards through the corona and IP space. This interpretation, which was originally proposed by Uchida (1960), is supported by a large body of evidence. For an introduction to solar radio bursts, see Warmuth and Mann (2005b), and for a review of type II bursts, see e.g., Nelson and Melrose (1985). Type II radio emission is generated by the conversion of enhanced Langmuir waves to electromagnetic waves, therefore, the radiation is emitted at the fundamental and the first harmonic of the Langmuir frequency, also referred to as electron plasma frequency fpe. The enhanced Langmuir turbulence is thought to be caused by energy input due to electrons that are accelerated by the shock wave (see e.g., Schmidt and Cairns, 2012, and references therein).
(a): metric type II radio burst associated with the coronal wave of 1997 Nov 3 as seen in a dynamic radio spectrum (source: Potsdam-Tremsdorf radiospectrograph). Both fundamental and harmonic emission bands are seen, and each band is split into two emission lanes. (b): Hα difference image (with reversed gray scale; source: Kanzelhöhe Solar Observatory) showing the Moreton wave associated with the same event. The overplotted contours show the type II burst source as imaged by the Nançay radioheliograph. Note that the burst source is cospatial with the Moreton front. Image reproduced with permission from Khan and Aurass (2002), copyright by ESO.
The Langmuir frequency (in CGS units) is given by
where e is the elementary charge, me the electron mass, and ne the electron density. Note that the Langmuir frequency is only dependent on the electron density \(({f_{{\rm{pe}}}} \sim \sqrt {{n_{\rm{e}}}})\). A motion of the source towards larger heights will thus cause a drift of the observed emission towards lower frequencies, since ne(r) decreases with increasing height r in the corona. The relationship between the frequency drift rate Df at the frequency f and the source velocity υsource parallel to the density gradient (which is commonly assumed to be radial) is given by
This shows that a coronal electron density profile is required for deriving source speeds from frequency drift rates.
Metric type II bursts are signatures of shock waves propagating through the low and middle corona (Uchida, 1960) at speeds of the order of 1000 km s−1. While dekametric, hektometric and kilometric type II bursts (which propagate in the outer corona and in interplanetary space) are generally attributed to CME-driven shock waves (e.g., Gopalswamy et al., 2000b), there has been a long discussion about the nature of the shocks generating the metric type II bursts, where both CME-associated shocks and flare-generated blast waves were proposed (cf. Section 2.2). For a review of this discussion, see Vršnak and Cliver (2008). In any case, if coronal waves are signatures of shocks in the low corona, we should expect to find a clear association with metric type II bursts.
Soon after the discovery of EIT waves, Klassen et al. (2000) noted that 90% of metric type II bursts are associated with EIT waves. The converse is not true, since only 21% of EIT waves are accompanied by type II bursts (Biesecker et al., 2002). A recent study by Nitta et al. (2013) found a higher association of AIA waves with type II bursts, namely 54%. This higher percentage could be due to a selection effect, since the AIA wave sample did not include slow and weak disturbances that are part of the EIT wave catalog used by Biesecker et al. (2002). This is consistent with the finding that the median speed of AIA waves without type II bursts was somewhat lower than the speed of the burst-associated waves (550 versus 650 km s−1). However, a recent study of coronal waves observed with EUVI by Muhr et al. (2014) that also omitted weak events found an association rate of 22%, in perfect agreement with the result of Biesecker et al. (2002). At the current point, the reason for the higher association rate of AIA waves with type II bursts thus remains unclear.
Moving onwards to chromospheric wave signatures, a close association between metric type II bursts and Moreton waves has been noted shortly after the discovery of the waves (Moreton, 1964; Smith and Harvey, 1971; Harvey et al., 1974). More recent studies have shown that practically all Moreton events have an associated type II burst (Warmuth et al., 2004b; Warmuth, 2010). Going beyond mere association, there is also a correlation in timing, i.e., type II bursts first appear close to the time where the wave is first observed. Warmuth (2010) found that the radio bursts started within a ± 5 minute interval with respect to the first observed Hα wavefront in 94% of the studied Moreton events, while 52% of the radio bursts started within a 2-minute interval after the first observed Moreton front (see left panel in Figure 15).
Left: Histogram of the time lag between the start of the type II burst and the first observation of a Moreton wavefront (in minutes). Note that in most events, the type II burst and the wave appear close in time to each other. Right: Kinematics of the off-limb expansion of the coronal wave of 2010 Jan 17 and the associated type II burst. The kinematics of the type II burst were obtained by fitting the radiospectrum with a power-law density model. (a) Dynamic radio spectrum of the burst (white line: harmonic emission lane; dashed white line: presumable fundamental emission). (b) Height-time plot of the wavefronts observed with EUVI at 171 Å (blue), 195 Å (red), and COR1 (green). The blue line is a power-law fit to the 171 Å heights, while the black dashed line is a fit of the type II burst frequencies converted into heights. (c) Speed-time plot of the speeds obtained from a power-law fit of the height of coronal wavefronts observed at 171 Å (blue line) and the speeds obtained from the fit of the type II burst frequencies (dashed line). Note the good agreement between the type II burst and the wavefront’s expansion. Images reproduced with permission from [left] Warmuth (2010), copyright by COSPAR, and [right] Grechnev et al. (2011a), copyright by Springer.
Applying a coronal density model to the observed frequency drift rate of the bursts gives the velocity of the source against the density gradient. This has shown that the type II bursts associated with the EIT waves studied by Klassen et al. (2000) have a mean speed of 739 km s−1, which is typical for type II bursts (e.g., 764 km s−1 was found by Robinson, 1985). Moreton-associated type II bursts were found to be significantly faster, with an average speed of 1100 km s−1 (Warmuth et al., 2004b). Moreover, the derived type II burst speeds are actually correlated with the initial Moreton wave velocities: faster waves are associated with faster bursts (Warmuth, 2010). This correlation could not be established for EIT wave speeds (Klassen et al., 2000), most likely due to the severe undersampling of the waves’ kinematics. A kinematical consistency (in terms of distances/heights and speeds) between type II bursts and coronal waves was also found in a large number of case studies (e.g., Vršnak et al., 2006; Pohjolainen et al., 2008; Grechnev et al., 2011b,a; Kozarev et al., 2011; Ma et al., 2011; Kumar et al., 2013; Kumar and Manoharan, 2013). An example is shown in the right panel of Figure 15.
In many type II bursts, the emission lane seen in dynamic radio spectra is split into two bands (cf. Figure 14a). The frequency difference between these bands can be interpreted as being due to emission from ahead and behind the shock, and therefore the amount of band-split is a measure of density compression ratio X of the shock wave (Vršnak et al., 2001a), which is given by the ratio of the downstream to the upstream density. Warmuth et al. (2004b) have derived X = 2.1–2.3 for the Moreton-associated bursts, which is significantly higher than X = 1.3–1.8 for average type II bursts (Vršnak et al., 2002a). From X, the magnetosonic Mach number Mms can be obtained (see Section 2.2). For the Moreton-associated bursts, Mms ≈ 2 is found for a low-beta plasma, while Mms ≈ 1.4 for average type II bursts. This is an independent confirmation of the more energetic nature of the Moreton-associated shocks. Also note that type II bursts are only generated by so-called supercritical shocks, which have an Alfvénic Mach number larger than 1.4 (see Mann et al., 2003, and references therein).
In addition to their larger velocities, Moreton-associated type II bursts start at higher frequencies than average type II bursts (161 versus 81 MHz, according to Warmuth et al., 2004b and Vršnak et al., 2001b), which implies that in the Moreton-associated events the shock wave is formed lower in the corona (≈ 100 Mm versus 200 Mm) and presumably closer to the exciter.
In several wave events, the associated type II burst sources have been imaged with the Nancay radioheliograph (Kerdraon and Delouis, 1997). In three disk events, the burst sources were located cospatially with Hα, EIT and SXR wavefronts (Pohjolainen et al., 2001; Khan and Aurass, 2002; Muhr et al., 2010). Figure 14b illustrates the spatial association of the type II burst source with the Moreton wave in the event reported by Khan and Aurass (2002). In the limb event studied by Vršnak et al. (2005, 2006), a complex type II burst was found to propagate obliquely through the corona, but a broad-band radio source was connecting it with the Hα, EIT, and SXR wavefronts in the low corona (cf. Section 3.3.1). This provides strong evidence for a single physical disturbance creating both the type II burst and the observed coronal wave features. This scenario has been supported by the recent observation of a similar propagating radio source associated with a limb wave seen with AIA (Carley et al., 2013).
Note that speeds derived solely from the frequency drift rates have to be considered with some caution. Firstly, they do not reflect the physical velocity of the wave source (i.e., the coronal shock) but only the velocity component parallel to the density gradient. Secondly, the derived speeds depend on the coronal density profile. Most studies have used density models that reflect some average coronal conditions, which may or may not be a good representation of the actual characteristics of an event. More accurate velocities can be derived when the density model is normalized by either direct density measurements and/or radio imaging observations of the type II burst sources (see e.g., Vršnak et al., 2006; Cho et al., 2007; Mancuso, 2007; Magdalenić et al., 2008).
Recently, a type II-associated limb wave event observed with AIA was studied in detail by several groups. They found that the type II burst kinematics were consistent with the wave and that the wave itself was consistent with a weak shock (Kozarev et al., 2011; Ma et al., 2011). The compression ratios X derived from the band-split of the type II burst and from the EUV imaging data are actually consistent (X ≈ 1.5) and decline during the wave’s propagation (Kouloumvakos et al., 2014). These results point to a freely propagating, shock-like disturbance.
Summing up, there is a now large body of evidence that tightly links metric type II bursts to coronal waves. This is not necessarily true for coronal waves in general, but certainly for the large-amplitude events that are associated with Moreton waves. Most type II bursts are associated with coronal waves, and they show a tight relation with the waves regarding timing, spatial relation, and kinematics (particularly pronounced in wave events with Moreton wave signatures). This all strongly supports a scenario where the coronal (and chromospheric) wave signatures and the type II burst are formed by the same physical disturbance, namely a coronal MHD wavefront that is at least partly shocked.
3.4.2 Coronal dimmings
Coronal waves are often associated with coronal dimmings (also called transient coronal holes), which are localized decreases of coronal emission. Dimmings are most clearly seen in the EUV range (Thompson et al., 1998, 2000a), but have also been reported in SXRs (Sterling and Hudson, 1997). In He i, brightenings that are associated with coronal dimmings can be detected (Vršnak et al., 2002b; Gilbert and Holzer, 2004; de Toma et al., 2005). It is widely accepted that dimmings are primarily due to plasma evacuation (e.g., Hudson et al., 1996; Zarro et al., 1999; Harrison et al., 2003; Harra et al., 2007).
With respect to coronal waves, two different types of dimming are observed (cf. Figure 16). The core dimmings are stationary, long-lived (hours to days), they are located near ARs, and they often appear pairwise. This strongly suggests that they correspond to the footpoints of an erupting flux rope that forms the core of a CME (e.g., Sterling and Hudson, 1997; Webb et al., 2000; Mandrini et al., 2005). In addition to these core dimmings, sometimes more widespread and shallow secondary dimmings are observed to trail behind an expanding EUV wavefront (e.g., Delannée and Aulanier, 1999; Wills-Davey and Thompson, 1999; Thompson et al., 2000b; Attrill et al., 2007; Muhr et al., 2011). The interpretation of these features is less clear-cut as in the case of core dimmings. Secondary dimmings could be due to the same process as core dimmings, namely plasma evacuation behind an erupting flux rope. The fact that they are expanding behind the bright EUV wavefronts would thus be consistent with a magnetic reconfiguration model (see Section 6.2). Alternatively, the secondary dimmings could be the consequence of rarefaction regions in the wake of a compressive wave. This rarefaction is predicted by MHD, and it is consistent with the cooling (see Section 4.5) and upwards flows (see Section 4.6) that are observed behind EUV wavefronts.
3.5 Frequency of occurrence
While there are comprehensive catalogs for flares and CMEs, this is unfortunately still not the case for coronal waves. Therefore, determining their frequency of occurrence is not straightforward, and we are forced to use the few studies that involved a systematic search and encompassed a larger event number. Most of these studies have relied on visual inspection of EUV waves in difference or running difference images and movies, which becomes impractical for large data volumes (e.g., as provided by SDO/AIA). Two automatic wave detection algorithms have been developed: NEMO (Podladchikova and Berghmans, 2005; Podladchikova et al., 2012) is mainly geared towards the detection of dimming associated with EIT waves and eruptions, while CorPITA (Long et al., 2014) uses AIA 193 Å difference images to identify and track coronal waves, including an automatic extraction of information on kinematics and pulse characteristics. There is hope that once these algorithms (after they have been carefully validated) will be able to generate the wave catalogs that are a prerequisite for many statistical studies.
The most comprehensive catalog of coronal wave events was compiled by Thompson and Myers (2009). They searched for waves in the EIT data covering the time from 1997 March to 1998 June (in the ascending phase of solar cycle 23) and found a total of 176 EIT waves. Assuming an instrument duty cycle of 100%, this would result in a maximum EIT wave rate of 141 waves per year. Nitta et al. (2013) found for 171 coronal waves in AIA data from 2010 April to 2013 January (ascending phase and early maximum of solar cycle 24), which gives a wave rate of 60 per year (again assuming a duty cycle of 100%). Muhr et al. (2014) identified more than 1000 EUV transients in EUVI data from 2007 Jan to 2011 Feb, which corresponds to the high rate of 250 transients per year. However, 80% of these events were weak, and many of the transients may not actually have been waves at all.
It is not too surprising that the wave rates derived from these studies are not matching exactly, as they result from different instruments, search strategies, selection criteria, and also reflect different levels of solar activity. We can conclude that there are about 100 coronal waves per year outside solar minima. In the recent deep minimum, the rate fell significantly (34 waves observed with EUVI from 2007 March to 2009 December; see Nitta et al., 2014).
Chromospheric signatures of coronal waves are observed at a significantly lower rate. Smith and Harvey (1971) found 15 Moreton waves in an eight-year interval (1960–1967). Assuming a duty cycle of 27% for a ground-based solar observatory (based on 10 hours of daily observations, with actually useful observations in 65% of this time; cf. Steinegger et al., 2001), this gives a rate of 7 Moreton waves per year. A more recent study (considering the interval from 1997 March to 2001 August) gives rates of 3 and 4 waves per year for the Kanzelhöhe and Big Bear solar observatories, respectively (Warmuth et al., 2004a). Warmuth (2010) found 27 waves from 1997 to 2006 (from several observatories), which gives a rate of 4 waves per year, while Zhang et al. (2011) reported 13 Moreton waves from Hida Observatory in the same time range, yielding a yearly rate of 7 waves. This means that Moreton waves occur at a rate of only ≈ 5% the rate of than coronal EUV waves, which implies that for the formation of a Moreton wave, more stringent conditions have to be met as compared to coronal EUV waves.
For comparison with other energetic solar phenomena, the occurrence rate of CMEs is much higher, ranging from 180 per year in solar minimum up to some 1500 per year during maximum (cf. Yashiro et al., 2004). For flares of GOES class C and larger, the rate is even higher with over 2500 events per year during solar maximum (derived from Ryan et al., 2012). The occurrence rate of metric type II bursts (according to the catalogs compiled by NOAAFootnote 5) ranges from a few events per year during solar minima up to more than 100 bursts during solar maximum. This is comparable to the occurrence rate of coronal waves.
4 Physical Characteristics
4.1 Spatial characteristics
4.1.1 Angular extent, wavefront shape, and radiant point
According with their rather diverse morphology (cf. Figure 5), the shape of coronal EUV wavefronts and their angular extent exhibit considerable variation between events. There are the “textbook” EIT wave events that show nearly circular or slightly elliptical (Attrill et al., 2007) wavefronts extending for 360° (e.g., Thompson et al., 1998) and which are most perfect when there is no other AR on the Sun (see left panel in Figure 17 for an example). In the presence of other ARs, even initially circular wavefronts become distorted due to the fact that the waves avoid ARs and coronal holes (e.g., Thompson et al., 1999). More common are coronal waves that propagate into a limited angular sector from the outset (see the EIT wave catalog by Thompson and Myers, 2009). Still, the shape of the wavefront is quasi-circular in these events. Another category are the sharp S-waves, which are always limited to a certain sector and which always show a circular curvature (e.g., Thompson et al., 2000b). Lastly, there are small wave events that show a very diffuse or irregular front. Often they are too ill-defined to determine a wavefront shape, but they tend to be limited to a rather restricted angular range (e.g., Wills-Davey and Thompson, 1999). In this context, we have to remember that coronal wavefronts are observed as a line-of-sight integration of optically thin emission. Actual observed shapes are thus dependent on both the 3D structure of the feature and the viewing angle (see Section 4.1.3).
Different angular extents and wavefront shapes. Left: The coronal wave of 2009 Feb 13. Shown is a STEREO/EUVI image at 195 Å with overplotted wavefronts derived from 195 Å difference images. Note the nearly isotropic propagation of the wave: its angular extent is 360°, and the wavefronts are well fitted by circles. Right: The large-amplitude wave event of 2011 Aug 9, which was associated with a Moreton wave. Plotted are wavefronts observed at low atmospheric layers (Ha, AIA 1600 and 1700 Å) and in the corona (AIA 211 Å). As is characteristic of Moreton wave events, the angular extent of the wavefronts is confined to a more narrow sector. Images reproduced with permission from [left] Kienreich et al. (2009) and [right] Shen and Liu (2012b), copyright by AAS.
The propagation of Moreton waves is almost always confined to a certain angular extent, on average ≈ 90° (Smith and Harvey, 1971; Warmuth et al., 2004a; Zhang et al., 2011, see right of Figure 17 for an example). Only three events have been reported where Moreton fronts were observed to propagate in a full (or broken) circle like the “textbook” EUV waves (Pick et al., 2005; Liu et al., 2006; Muhr et al., 2010; Balasubramaniam et al., 2010). Interestingly, the associated EUV waves span an angle that is on average twice as larger as for Moreton waves (Zhang et al., 2011). This may indicate that the wave-producing disturbance is stronger at its “nose”, and therefore only its central parts are able to perturb the dense and inert chromosphere. Moreton wavefronts show an excellent agreement with a circular shape, and they retain this shape during propagation (Warmuth et al., 2004a) unless they encounter ARs or coronal holes (e.g., Veronig et al., 2006). Since no line-of-sight integration and projection effects are involved in the case of chromospheric signatures, this proves that the shape of the coronal disturbance impacting on the chromosphere is actually close to circular.
The wavefronts that are close to the wave source tend to show the closest agreement with a circle. These fronts are often used to extrapolate the wave radiant point. This method has been applied to both coronal and chromospheric wavefronts. A number of authors have noted that the extrapolated radiant point of the waves is close to, but slightly offset from the associated flare (e.g., Khan and Aurass, 2002; Hudson et al., 2003; Warmuth et al., 2004b). Moreover, it tends to be located in the periphery of the source AR, with the wave always propagating away from the AR (the wave never appears within or crosses the source AR). In two events, two distinct radiant points located on either side of the source AR have been found (Muhr et al., 2010; Temmer et al., 2011).
4.1.2 Propagation distances
According to their global nature, coronal waves can be tracked over large distances, typically of the order of one solar radius. This is of course not true for all waves: small and weak waves can be traced over shorter distances than large and strong waves. The average propagation distance of the 176 EIT waves measured by Thompson and Myers (2009) was about 500 Mm, but EUV waves have been traced for distances larger than 1000 Mm. The maximum distances are reached when the fronts become too faint or diffuse to be measured, when the wave interacts with coronal structures (see Section 4.7), or when the wave propagates beyond the solar limb.
Moreton waves can be typically tracked out to distances of ≈ 300 Mm (Warmuth et al., 2004a), and up to twice as far in the most extreme events (Muhr et al., 2010). At these distances, the waves become too faint, diffuse, and fragmented to be identified. This means that they cannot be traced as far as EUV waves, which has to be considered when their kinematics are studied (see Section 4.2). Conversely, He i wave signatures are typically observable up to distances of 500 Mm and thus provide an observational link between coronal and chromospheric wave signatures at larger distances.
Accurately measuring minimum distances (i.e., the distance of the earliest observed wavefront from the extrapolated radiant point) requires high-cadence imaging, which is why this was first achieved for Moreton waves. They were found to always appear at a considerable offset distance from the extrapolated radiant points. This distance is typically 100 Mm, and never below 50 Mm (Warmuth et al., 2004a; Narukage et al., 2008). This was also found to be the case for SXR wavefronts (cf. Narukage et al., 2002; Hudson et al., 2003). When high-cadence EUV imaging became available, 100 Mm was confirmed as a typical distance for the appearance of a coronal wave (e.g., Veronig et al., 2008; Warmuth and Mann, 2011; Shen and Liu, 2012b).
The considerable minimum distance can be interpreted in two ways. Either the wave source is compact (such as flaring loops) and the initial disturbance needs time to steepen to a large amplitude that will allow it to become observable. Alternatively, it could imply that the wave source has a considerable extent, such as an erupting flux rope. Naturally a combination of both scenarios is possible, and indeed quite likely according to recent high-cadence observations of the early stages of the waves’ evolution. This will be further discussed in Section 5.2.
4.1.3 Propagation heights and 3D structure
The propagation height of coronal waves (or more accurately height range since the waves are extended structures) is an important parameter. It has an influence on kinematical studies (e.g., Ma et al., 2009; Hoilijoki et al., 2003), and is particularly important when wave signatures in different spectral ranges are compared (i.e., when trying to determine whether signatures are cospatial). Moreover, propagation heights can help to constrain physical models: while wave/shock models tend to predict dome-shaped fronts with a large extent in height, magnetic reconnection models generate signatures preferentially at lower heights (see Section 6). Even within the same theoretical framework, height can make a difference. For example, a wave traveling at a given speed may be shocked if propagating near the coronal base, but could be a linear wave further up in the corona due to the increase of the fast-mode speed with height (cf. Mann et al., 1999a).
The propagation height of coronal waves cannot be straightforwardly determined because the observed fronts are always the result of a line-of-sight integration of optically thin emission. This leads to an ambiguity in determining the exact 3D location of an observed feature, and indeed a structure can appear very different if seen from different viewing angles (cf. Ma et al., 2009; Hoilijoki et al., 2003). Bearing in mind these complications, various attempts have been made to infer the vertical extent of coronal waves.
A straightforward possibility to determine the height range of coronal wavefronts is presented by limb events where the wave propagates along the limb towards one of the poles. This geometry allows a direct measurement of the waves’ height extent above the limb, which represents a lower limit for the true geometric height above the solar surface. Several EIT waves have been reported that showed fronts with a vertical extent from the base of the corona up to 100 Mm and beyond (Warmuth et al., 2004a). The exceptional EIT wave studied by Hudson et al. (2003) could even be traced to a height of 200 Mm. Limb waves have been imaged in SXRs, too. Waves observed in partial-frame images with Yohkoh/SXT show an emission increase from the base of the corona up to heights of ≈ 70 Mm (Hudson et al., 2003). Limb wavefronts observed in SXRs with GOES/SXI were reported to show emission up to a height of 100 Mm above the limb, with the bulk of the emission below 50 Mm (Warmuth et al., 2005).
More recently, stereoscopic observations with STEREO/EUVI were used to deduce heights of coronal waves. Patsourakos et al. (2009) used triangulation techniques to obtain a height of 90 Mm, while Kienreich et al. (2009) used quadrature observations and derived that the EUV wave signature observed on-disk was at a height of 80–100 Mm. Delannée et al. (2014) used three distinct methods to derive heights of 34–154 Mm for an EUVI wave event. They also studied the temporal evolution of the heights and found that the height was initially increasing before decreasing back again to the lower corona.
The different measurements are in quite good agreement: coronal wave signatures have a considerable vertical extent and typically span from the coronal base to about 100 Mm. This corresponds to 1–2 times the coronal scale height for temperatures of 1–2 MK. Optically thin emission is weighted with density squared, so EUV and SXR emission is strongly concentrated towards the low corona, and this is where the strongest signal will be detected. Recently, white-light signatures were detected with STEREO/COR1 that were identified as the continuation of the EUV wavefronts into the higher corona (Kwon et al., 2013b). These observations have extended the maximum height at which signatures of coronal waves were detected to 1400 Mm.
Limb events not only reveal the height range of coronal wavefronts, but also give information on the angle of the wavefronts with respect to the solar surface. Often, these wavefronts are tilted towards the solar surface (i.e., they “lean forwards”) and become progressively tilted during their propagation (cf. Hudson et al., 2003; Patsourakos and Vourlidas, 2009; Kienreich et al., 2009; Liu et al., 2012). An example is shown in Figure 18. The tilting has been interpreted as a consequence of the waves’ refraction due to the increase of fast-mode speed with height in the quite low corona (Mann et al., 1999b, see also Section 4.7.1).
The refracting coronal wave of 1998 May 6. Left: Running difference images in soft X-rays by Yohkoh/SXT showing the propagation of the coronal wave to the north along the solar limb. The black region is an artifact due to overexposure from the flare. Note that the nearly circular wavefronts tilt increasingly forwards toward the solar surface. Right: EIT 195 Å difference image showing a rippled EIT wavefront that shows the same downward tilt as the SXT wave. Images reproduced with permission from Hudson et al. (2003), copyright by Springer.
Some coronal waves do not merely show vertically extended wavefronts at various tilt angles with respect to the solar surface, but a full wave dome that is consistent with a quasi-circular shell (see Figure 19 and the animation in Figure 20). This has been observed both in EUV (Veronig et al., 2010; Grechnev et al., 2011b,a; Li et al., 2012; Cheng et al., 2012) and SXR (Narukage et al., 2004). In these events, the apex of the dome could be traced to heights beyond one solar radius. Such wave domes have been predicted by numerical simulations of fast-mode waves or shocks (e.g., Uchida, 1968; Wang et al., 2009; Afanasyev and Uralov, 2011; Selwa et al., 2012; Downs et al., 2012, see Section 6.1).
Coronal waves showing full quasi-circular wave domes. Left: The limb wave event of 2000 Mar 3 observed by Yohkoh/SXT. A base image with reversed color table is shown. Note that the wave (W) is followed by ejecta (E). (Adapted from Narukage et al., 2004). Right: The coronal wave of 2010 Jan 17 observed with STEREO/EUVI at 195 Å. The difference image shows the wave dome (arrows) and the erupting CME loops (crosses) inside the dome. Image reproduced with permission from Veronig et al. (2010), copyright by AAS.
Still from a movie — An animation of the 2010 Jan 17 full wave dome observed with STEREO/EUVI at 195 Å in running difference images (left) and base images (right). Reproduced with permission from Veronig et al. (2010), copyright by AAS. (To watch the movie, please go to the online version of this review article at http://www.livingreviews.org/lrsp-2015-3.)
4.1.4 Multiple wavefronts
Harra and Sterling (2003) first reported evidence for two distinct wavefronts in an event observed with TRACE. However, other authors (Wills-Davey and Thompson, 1999; Wills-Davey, 2006) interpreted the same event in terms of the single pulse EUV wave that is commonly observed. Based on limb observations of EIT waves, a general bimodality of coronal waves was suggested by Zhukov and Auchère (2004). They noted that some EIT waves actually consist of two distinct parts: a leading front that appears to be wave-like (diffuse, quasi-circular), and a slower trailing front that is followed by coronal dimmings. The leading front was interpreted as a fast-mode wave, while trailing front was attributed to a density compression caused by the magnetic restructuring (e.g., opening of field lines) associated with an erupting CME.
Since these early studies, high-cadence EUV imaging observation with EUVI and AIA have turned up clear evidence for bimodality (see left of Figure 21 for an example) in a substantial fraction of coronal EUV waves (in ≈ 60% of studied AIA waves, according to Liu and Ofman, 2014). In limb events, fast wavelike fronts were clearly observed to decouple from CME-associated fronts which are significantly slower or even come to a halt (e.g., Patsourakos and Vourlidas, 2009; Kienreich et al., 2009; Ma et al., 2011; Chen and Wu, 2011; Dai et al., 2012). This will be discussed in more detail in Section 5.2.
Multiple wavefronts in coronal wave events seen with SDO/AIA. Left: Distance-time intensity stack plot at 193 Å of the coronal wave of 2010 Jul 27. Two fast waves (F1 and F2) and a slower trailing disturbance (S1) can be seen. Right: Difference image at 193 Å showing multiple wavefronts (a fast diffuse pulse and several sharp fronts) in the coronal wave of 2010 Apr 8. Images reproduced with permission from [left] Chen and Wu (2011) and [right] Liu et al. (2010), copyright by AAS.
AIA observations have demonstrated that both the fast wavefront and the slower secondary front can consist of multiple small-scale fronts. Within the fast wave, quasi-periodic structures have been observed (Liu et al., 2012) and have been interpreted as propagating fast-mode wave trains. These quasi-periodic fast propagating wave trains (QFPs) are a strong indication for the true wave nature of the fast primary wave.Footnote 6 Note that a well-defined period was already found for a coronal wave observed with TRACE by Ballai et al. (2005). Sometimes, two fast diffuse fronts can be seen, with the more shallow component leading. This can be interpreted as a line-of-sight integration effect: the leading front represents the leading edge of the 3D wavefront at larger heights where a large column length contributes to emission, while the second front comes from the low parts of the wavefront where emission measure is highest due to the density stratification. This is illustrated in Figure 10 in Grechnev et al. (2011b).
AIA has shown that the secondary “wave” can consist of multiple ripple-like fronts, too (Liu et al., 2010, see right in Figure 21). These fronts propagate behind the fast primary wave at quite low speeds (40–240 km s−1) and can undergo acceleration, which suggests that they are connected with the CME eruption. Possibly the sharp fronts represent compression regions ahead of erupting loops.
Conditions from event to event vary, and it may well be that either of the two fronts is more clearly observable in a particular wave event. The large number of fast, diffuse, wavelike fronts that have been reported in the literature suggests that usually it is the primary front that is dominating in coronal waves. However, in a certain fraction of events the disturbance associated with the CME eruption may be more visible. This might explain why the physical interpretation of coronal waves has remained controversial for so long: studying either the leading fast-mode wave or the trailing brightening associated with a magnetic restructuring will lead to contradicting conclusions.
Sometimes multiple wavefronts are observed in the chromosphere, too, but they were generally interpreted as separate disturbances launched by several individual eruptive events. Narukage et al. (2008) observed three consecutive Moreton waves within a 10-minute time span. These waves were probably independent since each one was associated with a separate filament eruption. In He i, up to five fronts were reported in a single event (Gilbert and Holzer, 2004). They were interpreted as being caused by the CME and the associated flare.
4.2 Kinematics
Kinematics is the most basic characteristic of any moving disturbance, and it is therefore clear that the characterization of the propagation speed of coronal waves forms the backbone of any meaningful study. Speeds are usually derived from the distances of the wavefronts from an extrapolated radiant point. Commonly, the distances refer to the leading edge of the disturbance, which is traced visually using difference or running difference images. Distances on the disk are measured along great circles emanating from the radiant point (cf. Thompson et al., 1999; Warmuth et al., 2001), which accounts for foreshortening, or less frequently via Huygens plotting (cf. Wills-Davey and Thompson, 1999; Hudson et al., 2003), which accounts for changes in propagation direction. An alternative method is to measure intensity profiles and use the detected pulses to derive speeds (cf. Warmuth et al., 2001). The latter method is now being used extensively for wave events observed at high cadences with SDO/AIA (e.g., Long et al., 2014).
4.2.1 Mean velocities of different signatures
Before the SOHO/EIT era, the kinematics of the predicted coronal wavefronts (Uchida, 1968) were inferred from observations of Moreton waves and metric type II bursts. For both types of disturbances, typical speeds on the order of 1000 km s−1 were found, thus giving a coherent picture. Let us consider Moreton wave speeds in more detail. The speeds reported range from a minimum of ≈ 400 km s−1 up to ≈ 1500 km s−1, with average linear speeds of 650 km s−1 (Smith and Harvey, 1971; Warmuth et al., 2004a; Zhang et al., 2011, see Figure 22d). These speeds relate to the leading edge of the disturbance and are measured along great circles on the solar surface, thus accounting for foreshortening effects.
Histograms of the linear speeds of coronal waves obtained from different instruments and wavelengths. The mean of the distributions is given and plotted as a dotted line, and N denotes the number of events. (a): EIT wave speeds from Thompson and Myers (2009). (b): EUVI wave speeds (measured from 195 Å and 171 Å images) from Nitta et al. (2014). (c): AIA wave speeds from Nitta et al. (2013). (d): Moreton wave speeds combined from Smith and Harvey (1971); Warmuth et al. (2004a); Zhang et al. (2011).
When EIT waves were first discovered, their interpretation as the predicted coronal counterpart of Moreton waves was called into question based on their recorded speeds, which were considerably lower than for Moreton waves. Early “textbook” EIT waves had speeds of ≈ 250 km s−1 (Thompson et al., 1998, 1999), while the average EIT wave speed for a sample of 176 events was only 191 km s−1 (Thompson and Myers, 2009, see Figure 22a). Even the waves associated with the fast Moreton waves were comparatively slow at ≈ 300 km s−1 (Thompson et al., 2000b; Warmuth et al., 2004a), which is consistent with the mean speed of 271 km s−1 derived for EIT waves associated with type II bursts (Klassen et al., 2000). Another surprising finding was the large range of speeds, ranging from a few 10 km s−1 up to 700 km s−1 (Thompson and Myers, 2009). This large spread has been interpreted as evidence against the fast-mode wave model (Wills-Davey et al., 2007). It should be noted, however, that the very low speeds are associated with weak and irregular events (cf. Zhukov et al., 2009; Warmuth and Mann, 2011).
The mean speeds of ≈ 300 km s−1 derived for 34 EUVI wave events (Nitta et al., 2014) and the ≈ 250 km s−1 obtained for a sample of 60 EUVI waves (Muhr et al., 2014) are in agreement with the speeds derived from EIT when we disregard the very weak and irregular EIT events (cf. Figure 22b). The EUVI wave speeds of Nitta et al. (2014) were obtained from both the 195 Å and the 171 Å channel at cadences of 10 and 2.5 minutes, respectively. The fact that the speeds measured in the high-cadence 171 Å channel are consistent with those derived from the low-cadence 195 Å observations shows that the low speeds commonly found for coronal waves are not primarily the result of insufficient image cadence. This is supported by Muhr et al. (2014) who did not find a distinct trend for speeds derived from 195 Å observations with a cadence varying from 2.5 to 10 minutes.
4.2.2 Deceleration of a single disturbance
The apparent discrepancy in Moreton and EIT wave velocities has led to models where both phenomena are physically different perturbations propagating independently (i.e., not cospatially) through the corona (Chen et al., 2002, see Section 6.3). However, there is a second possibility to resolve the mismatch in speeds. So far, we have considered mean or linear wave speeds (i.e., obtained from a linear fit of the measured distances). However, Warmuth et al. (2001) found that Moreton waves do not propagate at constant speeds but instead showed pronounced deceleration. Additionally, they could show that Moreton and EIT wavefronts are nearly cospatial and show similarities in morphology, which strongly suggests a single physical disturbance that generates the different signatures.
A decelerating disturbance straightforwardly explains the apparent velocity discrepancy between Moreton and EIT waves, since the low temporal cadence of EIT leads to an undersampling of the early phase of the wave’s propagation where it is still fast, resulting in lower EIT wave speeds. Moreton waves, on the other hand, cannot be tracked to larger distances (see Section 4.1.2), and thus only the fast initial speeds are recorded.
All Moreton waves that have been recorded since are clearly decelerating (cf. Warmuth et al., 2004a; Narukage et al., 2008; Muhr et al., 2010; Balasubramaniam et al., 2010; Warmuth, 2010; Asai et al., 2012; Francile et al., 2013). The initial velocities are in the range of 600–1200 km s−1 and decline to ≈ 500 km s−1 before the Hα wave signatures vanish. A second-degree polynomial fit of the distances gives a mean deceleration on the order of 1 km s−2.
Likewise, all observed Moreton waves are associated with coronal waves observed in EUV and SXRs (e.g., Thompson et al., 2000b; Khan and Aurass, 2002; Warmuth et al., 2004a, 2005; Warmuth, 2010; Asai et al., 2012; Shen and Liu, 2012b), as well as with chromospheric He i signatures (cf. Vršnak et al., 2002b; Warmuth et al., 2004a; Gilbert et al., 2004; Warmuth, 2010; Balasubramaniam et al., 2010). In all of these events, the wavefronts recorded in the different spectral bands are consistent with a decelerating disturbance (see left panel of Figure 23 for an example). This disturbance is observed to start with the Moreton wave speeds (≈ 1000 km s−1) and decelerate to typical EIT wave speeds (≈ 300 km s−1). The amount of deceleration found for the combined wavefronts (typically ≈ −0.2 km s−2) is always lower than for the Hα fronts. This is due to the fact that the rate of deceleration is not constant but decreases with time and distance. Thus a power-law fit in the form of d ∼ tδ (with distance d, time t, and power-law index δ) is actually a better representation of the kinematical curve of coronal waves than a polynomial (Warmuth et al., 2004a; Grechnev et al., 2008; Warmuth and Mann, 2011). This is shown by the power-law indices, which have a typical value of ≈ 0.6 for both Moreton waves and combined fronts (Warmuth et al., 2004a; Warmuth and Mann, 2011). Such power-laws are predicted for the distance-time curves of freely propagating shock waves (Grechnev et al., 2008, 2011b,a) according to the Sedov solution (Sedov, 1959).
Kinematics of decelerating coronal waves. Left: distance-time (top) and velocity-time plot (bottom) of the coronal wave of 2003 Nov 3, derived from a combination of Hα, SOHO/EIT and GOES/SXI wavefronts. The distances are fit with a second-degree polynomial (full line) and with a power-law (dashed line) (adapted from Warmuth et al., 2005). Right: the decelerating coronal wave of 2009 Dec 22 imaged with STEREO/EUVI at 171 and 195 Å. Note that the power-law fits the kinematical curve better than the second-degree polynomial (adapted from Warmuth and Mann, 2011).
Note that Moreton fronts actually tend to lag some ≈ 20–30 Mm behind the coronal EUV and SXR wavefronts (Warmuth, 2010). This could be both due to height effects (coronal waves are extended 3D structures that are seen integrated along the line-of-sight, whereas the Moreton waves are comparatively shallow chromospheric structures) and due to inertia of the dense chromosphere that results in a delayed reaction to the coronal pressure increase. The magnitude of the offset is consistent with simulations (Chen et al., 2005a; Afanasyev and Uralov, 2011).
While multiwavelength observations have been instrumental for the detailed characterization of the waves’ kinematics due to the low cadence of EIT, the conclusions made from them have recently been confirmed by high-cadence coronal EUV imaging data. In particular, clearly decelerating waves have been observed with EUVI (e.g., Veronig et al., 2008; Long et al., 2011b; Warmuth and Mann, 2011, see right panel of Figure 23) and AIA (e.g., Long et al., 2011a; Kozarev et al., 2011; Liu et al., 2012; Cheng et al., 2012; Olmedo et al., 2012). AIA has recorded very fast coronal waves (initial speed > 1000 km s−1) showing strong deceleration (up to −2 km s−1), which is consistent with the kinematics of fast Moreton waves. These observations have also proven that the different wave signatures (both coronal and chromospheric ones) are indeed consistent with a single disturbance (Asai et al., 2012; Shen and Liu, 2012a,b).
4.2.3 Kinematical classification of events
In addition to the clearly decelerating waves, high-cadence EUV observations with EUVI and AIA have also confirmed that there are EUV waves that are propagating at nearly constant speeds in the range of 200–350 km s−1 (e.g., Patsourakos and Vourlidas, 2009; Ma et al., 2009; Veronig et al., 2010; Kienreich et al., 2011; Liu et al., 2011; Warmuth and Mann, 2011, see left panel in Figure 24 for an example). There have also been reports of events with very erratic kinematics: slow disturbances that become even slower (a few tens of km s−1), only to accelerate again (Zhukov et al., 2009, see right panel in Figure 24). It is, therefore, clear that coronal waves can show very different kinematical characteristics.
Left: distance-time plot of the coronal wave of 2010 Jan 17, derived from STEREO/EUVI data. The on-disk wave has a constant speed of 283 km s−1, while the wave dome expands faster in the radial direction (adapted from Veronig et al., 2010). Right: distance-time plot of the coronal wave of 2008 Dec 8, derived from STEREO/EUVI data. The wave shows an erratic propagation: a slow initial speed, and phases of abrupt acceleration and deceleration. Images reproduced with permission from [left] Veronig et al. (2010), copyright by AAS; and from [right] Zhukov et al. (2009), copyright by Springer.
Using the EIT wave catalog of Thompson and Myers (2009), the Moreton-associated waves of Warmuth (2010), and additional STEREO/EUVI observations, Warmuth and Mann (2011) have found kinematic evidence for three different classes of coronal waves (see Figure 25). Class 1 events have large initial speeds (≥ 320 km s−1) and decelerate. Faster waves decelerate more strongly, i.e., while there is a large range of initial speeds, the final speeds are always in the range of 200–300 km s−1. Class 2 waves start with moderate speeds (170–320 km s−1) that remain almost constant during their propagation. Note that there is no clear separation between the classes 1 and 2. While there is no gap between class 1 and 2 events, class 3 events are clearly separated from the other waves and are characterized by low initial speeds and erratic kinematics. Warmuth and Mann (2011) propose that the three different wave classes represent nonlinear fast-mode waves or shocks, linear (or weakly nonlinear) fast-mode waves, and magnetic reconfiguration events, respectively (see Section 6).
Kinematical characteristics of a larger coronal wave sample. Initial wave speed is plotted versus average acceleration (left) and power-law index (right) obtained from EIT and EUVI 195 Å data. Three distinct event classes are indicated. Image reproduced with permission from Warmuth and Mann (2011), copyright by ESO
The anticorrelation between initial speed and acceleration has been confirmed by Muhr et al. (2014) for 60 EUVI wave events. This study shows a smooth transition between class 1 and 2 events. Due to event selection criteria, no class 3 events were present in this sample.
Recently, Nitta et al. (2013) presented the first statistical study involving a large sample of waves observed with SDO/AIA. The speeds of 138 AIA waves observed at 193 Å were measured. With a range 200–1500 km s−1, the distribution of linear speeds is broader than for EIT and EUVI waves, and the mean speed of 644 km s−1 is also significantly higher (see Figure 22c). As in the case of the EUVI waves studied by Nitta et al. (2014), events with speeds below 200 km s−1 are missing due to event selection criteria. Interestingly, the mean of the linear speeds is very close to what was found for Moreton waves.
While a high-cadence instrument will be able to kinematically resolve faster waves, and thus yield a speed distribution that has a high-speed tail as compared to the distributions from EIT and EUVI, the speeds derived are surprisingly high, which suggests that AIA is seeing a class of waves that are not recorded by lower-cadence instruments. Conversely, most case studies of AIA events up to now have found speeds that were consistent with the kinematic scenario described by Warmuth and Mann (2011).
However, distinct kinematical classes could not be reproduced by Nitta et al. (2013), who found a rather smooth distribution of events centered around zero acceleration, and no evident correlation with deceleration for very fast AIA waves, which contrasts with the case studies. Nitta et al. (2013) suggested that the pronounced decelerations found in the class 1 events could be the result of interaction with coronal structures, e.g., an artifact of a wave being deflected at a coronal hole. While this may well be the case for EIT wave events with poor temporal resolution, both multiwavelength and EUVI observations are consistent with a smooth deceleration rate that decreases with time and distance and which is very well reproduced by a power-law (see discussion above). In contrast, a wave interacting with a coronal structure would show a pronounced peak in deceleration rate when encountering the obstacle.
As remarked by Liu and Ofman (2014), the AIA results of Nitta et al. (2013) are not inconsistent with the kinematical classes: there is a weak correlation of speed with deceleration in the 450–800 km s−1 range, and slower waves have constant speeds. Note that Nitta et al. (2013) plot mean speeds versus acceleration, while Warmuth and Mann (2011) and Muhr et al. (2014) use the initial wave speed. This distinction might at least partly explain the differences in the scatter plots. Still, the kinematics of coronal waves as seen by AIA have to be studied in more detail in order to understand the differences as compared to previous observations.
4.2.4 Lateral and radial kinematics
Finally, in the several events that showed full wave domes, we can compare the lateral propagation of the flanks of the dome (i.e., along the solar surface) with the radial propagation of its top. In these events, the radial speed of the top of the dome is consistently higher than the lateral expansion by factors of 1.3–2.3 (cf. Narukage et al., 2004; Veronig et al., 2010; Ma et al., 2011). Note that this is consistent with the finding that metric type II bursts (which often show quasiradial propagation) tend to be faster than the laterally propagating associated waves (Warmuth, 2010; Ma et al., 2011; Grechnev et al., 2011a). The different expansion velocities could either reflect the increase of the fast-mode speed with height in the low corona (a wave or shock would speed up under these circumstances; see e.g., Grechnev et al., 2011a) or a scenario where the upper part of the disturbance is continuously driven by the erupting CME, while its flanks are freely propagation (e.g., Veronig et al., 2010).
4.3 Perturbation profile
Besides kinematics, the perturbation profile of coronal waves can be used to gain insight into the physical nature of the disturbance. The perturbation profile is usually defined as the intensity distribution of a wave as a function of distance, I(r). In practice, intensities on solar images are either measured along individual paths (along great circles when propagating on disk, and along straight lines when off-limb) or averaged laterally over an angular range. The resulting intensity profile I is then normalized by a pre-event profile I0, thus giving the relative intensity change due to the wave, I/I0, or the percentage increase over the pre-event background, (I − I0)/I0. Typically, two parameters are then extracted from the profile: the perturbation amplitude and pulse width. Both parameters are often taken from a Gaussian fit of the profile, with the FWHM of the Gaussian taken as the perturbation width.
Early observations of EIT waves at 195 Å found typical perturbation widths on the order of 100 Mm and amplitudes of less than 25% as compared to the pre-event background (Thompson et al., 1999; Thompson and Myers, 2009), i.e., broad and rather faint wavefronts. A subset (7%) of EIT waves, called S-waves (Biesecker et al., 2002) or brow waves (Gopalswamy et al., 2000a), are characterized by initially sharp wavefronts (≈ 20 Mm width) with a high amplitude (> 100%). These sharp fronts then decay to the broad and faint fronts that are more commonly observed (Thompson et al., 2000b). An increasing width (from about 40 Mm to 150 Mm) and decreasing amplitude (from ≈ 100% to less than 10%) during their propagation was observed for a larger number of Moreton-associated EIT waves (Warmuth et al., 2004b; Warmuth, 2010). Note that the initial amplitudes of Moreton-associated EIT waves is clearly larger than for typical EIT waves (Warmuth, 2010).
Actually, the pulse broadening and amplitude decrease was first measured quantitatively for Hα Moreton wave signatures (Warmuth et al., 2001, 2004a, see Figure 26) and was subsequently found in all Moreton events (Warmuth, 2010). Therefore, the three basic characteristics of the coronal disturbances associated with Moreton waves are deceleration (see Section 4.2), pulse widening, and amplitude decrease. This is consistent with a nonlinear fast-mode wave or shock, as first proposed by Warmuth et al. (2001). Conversely, Wills-Davey (2006) have reported a wave observed with TRACE that retained its coherence (i.e., no pulse broadening). However, this wave was tracked only over a comparatively short distance (200 Mm), which could have been an insufficient distance for the broadening to take effect.
Perturbation profile evolution in the Moreton wave of 1998 May 2 (cf. Figure 9). Left: Hα center line intensity profiles normalized by the pre-event profile. The propagation of the Moreton wave is clearly seen, as is the decrease of its amplitude and the increase of the pulse width. Right: the main panel shows the distance-time diagram of the wave’s leading edge, intensity maximum, and trailing edge, respectively. The evolution of the speeds (depicted at the lower left) clearly shows deceleration. The panel on the lower right shows the decrease of the amplitude (crosses) and the increase of the width (circles) of the wavefronts. Images reproduced with permission from [left] Warmuth et al. (2004b), copyright by ESO, and [right] Warmuth et al. (2001), copyright by AAS.
Recent high-cadence EUV observations have confirmed the early results and consistently find perturbation profile widening and amplitude decrease also in events that are not associated with Moreton waves (cf. Veronig et al., 2010; Long et al., 2011b; Muhr et al., 2011; Kienreich et al., 2011; Muhr et al., 2014). An example is shown in Figure 27. Typically the FWHM widths increase from 20–50 Mm to 70–200 Mm, while the amplitudes drop from 20–60% to 5–20%. In several events, the integral over the wave pules (proportional to amplitude times width) remains constant, which is suggestive of a freely propagating wave (e.g., Veronig et al., 2010; Muhr et al., 2011).
Perturbation profile evolution in the coronal wave of 2010 Jan 17 (cf. Figure 19) derived from STEREO/EUVI data. The profiles are derived from running ratio images at 195 Å. Amplitude decrease and perturbation width increase are clearly seen. Image reproduced with permission from Veronig et al. (2010), copyright by AAS.
If we neglect changes in temperature and line-of-sight integration effects, the observed intensity amplitude can be converted to the density compression factor X according to X = nd/nu ∼ (I/I0)1/2, where nd and nu denote the downstream and upstream densities, respectively. The compression factor of coronal waves with moderate speeds waves is thus X = 1.1 or less, which indicates a small-amplitude disturbance that is consistent with a linear wave, or a slightly nonlinear wave (i.e., a weak shock; cf. Kienreich et al., 2011). On the other hand, fast decelerating waves that are associated with Moreton waves show much larger compression factors early in their propagation (X ≈ 1.5), which is suggestive of large-amplitude nonlinear waves and substantial shocks. Therefore, the perturbation amplitudes support the physical interpretation of the kinematical classes proposed by Warmuth and Mann (2011).
It should be noted that neglecting temperature effects is a rather strong assumption (as will be discussed in Section 4.5), which casts some doubts on the approach described above. Unambiguous values for X can only be obtained from spectroscopic observations of density-sensitive EUV or SXR lines. Unfortunately there has been only one such observations up to now: Veronig et al. (2011) used Hinode/EIS observations of the Fe xiii 202/203 Å line pair to deduce X ≤ 1.1 in one coronal wave event (see also Section 4.6). This was within the noise limit of EIS, so more spectroscopic observations would be highly desirable.
4.4 Mach numbers
The study of Mach numbers requires input from both kinematics and the perturbation profile, which is why the topic is treated here in a separate section. Basically, the measured wave speed is normalized by the characteristic speed (i.e., magnetosonic speed υms) to give the Mach number of the disturbance. For a nonlinear MHD wave or shock, the speed (and therefore the Mach number) is determined by the amplitude of the perturbation (i.e., density compression ratio X). If the Mach numbers derived from the speed and the amplitude of the disturbance match, this can be taken as evidence that the perturbation is indeed an MHD wave or shock.
The magnetosonic Mach number Mms (i.e., the Mach number of a perpendicular fast-mode shock) can be derived from the Rankine-Hugoniot relations and is mainly dependent on the density compression ratio X (see Section 2.2). Taking the compression ratios discussed in Section 4.3, both EUV waves with constant moderate speeds and waves that have decelerated to this speed range (≈ 200–350 km s−1) have Mms ≤ 1.04, and given the uncertainties involved with these estimations, this is consistent with a Mach number of unity and a linear wave (Veronig et al., 2010; Kienreich et al., 2011). Conversely, the amplitudes of the early wavefronts of initially fast waves correspond to Mach numbers of Mms ≥ 1.15, which clearly indicates a nonlinear wave or shock. Very bright EUV waves such as the S-waves observed by EIT are consistent with Mms ≥ 1.3.
Note that the results discussed up to now were all derived from 195 Å observations (corresponding to T ≈ 1.5 MK) and have neglected temperature changes. Observations at other EUV wavelengths that can constrain the thermal evolution will be discussed in Section 4.5.
The amplitudes of coronal waves observed in SXRs tend to be slightly higher than for EUV waves. With Yohkoh/SXT and Hinode/XRT, amplitudes of > 200% were found, corresponding to initial Mach numbers of Mms ≈ 1.3–1.4 (Narukage et al., 2002; Hudson et al., 2003; Narukage et al., 2004; Asai et al., 2008). The higher amplitudes seen in SXRs, which are sensitive to T > 2 MK plasmas, could be either due to the fact that particularly strong events were observed, or there could be an additional effect due to heating (see Section 4.5).
An alternative method to obtain Mach numbers is to compare wave speeds with estimated fast-mode speeds for the quiet corona. In the case of the SXR waves discussed above, this method gives values that are consistent with the ones derived from the intensity amplitudes. Conversely, significantly higher Mach numbers of Mms ≥ 2 are obtained for Moreton waves (Warmuth and Mann, 2005a). It is well possible that the intensity amplitude method underestimates the true Mach numbers because heating and line-of-sight integration effects are neglected. Note that the Mach number of type II bursts can also be derived from density jump inferred from their band split (see Section 3.4.1). In Moreton-associated metric type II bursts, Mach numbers of 1.9–2.2 are found (Warmuth et al., 2004b), which is quite consistent with the Mach numbers derived for the Moreton waves. We, therefore, have two independent lines of evidence that both indicate that Moreton-associated coronal waves are strong fast-mode shocks.
4.5 Thermal characteristics
Direct signatures of coronal waves were first observed in the 195 Å channel (dominated by the Fe xii line) of SOHO/EIT, which has a peak response function at T ≈ 1.4 MK, so the wavefronts have to contain plasma close to this temperature. Since the differential emission measure of the quiet corona also peaks near this value (Brosius et al., 1996), it is clear that the waves are affecting a significant fraction of the coronal plasma.
Subsequently, wavefronts were also detected at 171 Å (Fe ix, T ≈ 0.8 MK; Wills-Davey and Thompson, 1999) and at 284 Å (Fe XV, T ≈ 2 MK; Zhukov and Auchère, 2004) with TRACE and SOHO/EIT. With STEREO/EUVI, wavefronts could be seen for the same event in all three of these channels (Long et al., 2008; Veronig et al., 2008), plus in 304 Å images, where the fronts are comparatively faint and diffuse. These observations have confirmed earlier multiwavelength studies that clearly showed that coronal wave are multithermal phenomena. Still, the waves were best seen in the 195 Å channel.
The seven EUV channels provided by SDO/AIA (see Table 1) now provide a much better thermal characterization of coronal EUV waves. In ascending order of peak temperature response, these channels are 304 Å (He II; T ≈ 0.05 MK), 131 Å (Fe VIII; T ≈ 0.4 MK), 171 Å (Fe ix; T ≈ 0.6 MK), 94 Å (Fe X; T ≈ 1 MK), 193 Å (Fe XII; T ≈ 1.6 MK), 211 Å (Fe XIV; T ≈ 2 MK) and 335 Å (Fe XVI; T ≈ 2.5 MK). Note that the temperature responses are quite broad, and that the peak temperatures listed apply to non-flare plasmas. For details on the AIA temperature responses, see Lemen et al. (2012). With AIA, coronal waves are best seen at 193 and 211 Å, while the intensity enhancements become progressively weaker from 335 to 94, 131, and 304 Å (see Figure 28 for an example).
Multiwavelength view of the coronal EUV wave of 2010 Aug 14 as seen with SDO/AIA and STEREO/EUVI percentage difference images. The observations cover a temperature range from 0.05 to 10 MK. Note that in the non-flaring sun, the 94 Å and 131 Å channels are dominated by emission from lines that are formed at much cooler temperatures (1 and 0.4 MK, respectively) than the ones indicated in the corresponding panels. The wavefront is best seen in the 193/195 and 211 Å channels. Image reproduced with permission from Long et al. (2011a), copyright by AAS.
In the 171 Å channel, wavefronts are either weaker than at 193 Å or are even seen as emission depletions (e.g., Nitta et al., 2013). If the quiet corona (which has a DEM peak near 1.5 MK) is heated by a wave, the DEM distribution will be shifted towards higher temperatures, and spectral channels sensitive to higher temperatures will observe not only the consequences of compression, but an additional increase due to the shift of the DEM. Conversely, channels sensitive to lower temperatures will record an emission increase that is lower than the one expected from the plasma compression, or even an emission depletion.
This anticorrelation between 171 Å and 193/195 Å has been noted by many authors (e.g., Wills-Davey and Thompson, 1999; Dai et al., 2010; Liu et al., 2010; Long et al., 2011a; Schrijver et al., 2011) and implies that plasma heating is taking place between 0.8 and 1.6 MK. Still, 171 Å waves can appear as an emission increase if the ambient corona is quite cool (this may be the reason for the high percentage of bright 171 Å waves found during the recent solar minimum by Nitta et al., 2014), if there is no significant heating, or if the compression is so strong as to overcome the heating-related intensity reduction.
Behind the hot and bright coronal front, AIA has detected a cooling region where the relation between the 171 and 193 Å intensities is reversed (e.g., Downs et al., 2012). This can be understood in terms of adiabatic heating caused by plasma compression, followed by cooling and rarefaction driven by a restoring pressure gradient force. This scenario is supported by EUV spectroscopy, which detects fast plasma downflows in the compression regions followed by slower upflows (see Section 4.6).
The signatures seen at 304 Å have been attributed to coronal emission of the Si XI line (303.32 Å; T ≈ 1.6 MK) rather than to chromospheric emission of the much cooler the He ii line (T ≈ 0.08 MK) that dominates this spectral channel (Long et al., 2008; Patsourakos et al., 2009). This interpretation is based on the morphological similarity of the 304 Å wave with the signatures in the hotter coronal channels (cf. also Veronig et al., 2010), and the observation that the cooler 171 Å channel already shows intensity depletions, which should be even more pronounced for the much cooler He ii line. Note, however, that in one event wavefronts have been detected in the 1600 and 1700 Å UV channels, which show emission from the transition region and upper photosphere (Shen and Liu, 2012b). This event also had a Moreton wave, so clearly the lower atmospheric layers were strongly affected by the wave. In such a case, there may well be a contribution from He ii.
The spectral coverage of AIA has now been exploited to better characterize plasma compression and heating (cf. Section 4.3, where heating was neglected). Assuming adiabatic compression, Schrijver et al. (2011) have derived a density compression of ≈ 10% (X = 1.1) and a temperature increase of ≈ 7% for a large EUV wave. Kozarev et al. (2011) and Ma et al. (2011) analyzed the same event using different techniques. Kozarev et al. (2011) performed a DEM reconstruction and found that compared to the pre-event DEM, which peaks at 1.6 MK, the wave-associated DEM has higher values above this peak temperature (i.e., an enhanced high-temperature tail of the distribution). A lower limit of X = 1.12–1.18 is also found. Ma et al. (2011) have used the compression factor X = 1.56 given by an associated type II burst together with AIA data to deduce plasma heating up to 2.8 MK for this event, which is qualitatively consistent with the results of Kozarev et al. (2011).
With respect to temperatures, the first relevant spectroscopic study has been made by Asai et al. (2008) who observed a strong coronal wave with Hinode/EIS. They detected a strongly blue-shifted feature that was associated with an SXR wave. The wave-associated feature was seen only in the hottest EIS lines (Fe XV and Ca XVII corresponding to temperatures of 2.5 and 6.3 MK, respectively), which implies that the feature was strongly heated to over 2 MK. Asai et al. (2008) conclude that the EUV spectra are consistent with a fast-mode shock.
4.6 Flows
It is well known that flows are present in Moreton waves, in fact, it is the downward-upward motion of the chromospheric plasma that generates the signatures observed in Hα in the first place (see Section 3.2.1). The coronal wave causing this depression should be associated with flows, too, as any propagating fast-mode wave should be. Line-of-sight flow velocities associated with coronal waves can be measured with EUV spectroscopy. There have been only a few wave events that had the benefit of spectroscopic coverage, which is simply due to the fact that the spectrograph slit has to be at the right place at the right time to catch a wave, and that the right observing mode has to be selected (exposure times, selected lines, etc.). Spectroscopic information of coronal waves can thus be obtained either by pure chance, or preferably by dedicated campaigns employing carefully selected observational parameters (e.g., sit-and-stare observations). There are considerably more spectroscopic observations of wave-associated coronal dimmings. The dimmings seen in AR cores and the dimmings expanding behind EUV wavefronts show significant blue shifts (e.g., Harra et al., 2007; Asai et al., 2008; Chen et al., 2010, 2011), which are signatures of the outflows (υ < 50 km s−1) associated with the mass loss causing the dimming.
The first spectroscopic observation of an EUV wave was made by Harra and Sterling (2003) who reported on an EUV wave seen with TRACE that passed through the field of view of SOHO/CDS. In this weak event, little or no line-of-sight motions could be detected in the CDS spectra (υ ≤ 10 km s−1). The first clear detection of flows in an EUV wave were made with Hinode/EIS by Harra et al. (2011) and Veronig et al. (2011). In this event, the usual blueshifts associated with the upflows in dimmings are seen close to the source AR. Additionally, there are redshifted features (υ = 20 km s−1) that move away from the AR and are coincident with the EUV wave (see Figure 29). Actually, the intensity increase lags the redshift peak by one EIS exposure (≈ 50 s), which indicates that the brightening is a reaction to the downward push (and hence compression) of the coronal plasma (Veronig et al., 2011). Behind the redshifted features follow blueshifted ones (υ = −5 km s−1). These observations suggest that the coronal plasma is first being pushed downwards by a coronal wave or shock, after which it relaxes back. This is consistent with the “sweeping skirt” hypothesis of Uchida (1968), which postulates that the chromospheric plasma is being pushed down by a coronal wave (and relaxes back afterwards). This was actually not the case in this event, since there were no mass motions in the chromospheric He ii line, and no large density compression (X ≤ 1.1; see Section 4.3). The low compression factor implies that this coronal disturbance was too weak to perturb the denser atmospheric layers.
Spectroscopic observations of the coronal wave of 2011 Feb 16 with Hinode/EIS. Shown are stack plots of the Doppler velocity (left) and intensity (right) derived from the Fe xiii line (202 Å). Note that the fast redshifted feature starting around 14:25 UT is correlated with a bright feature that corresponds to the coronal wave. Image reproduced with permission from Veronig et al. (2011), copyright by AAS.
4.7 Interaction with coronal structures
The corona is not a homogeneous and isotropic medium. In terms of physical parameters (such as density and magnetic field strength, and consequently wave speed), propagating waves will both encounter large-scale gradients (such as an increase of fast-mode speed with height in the low corona) as well as strong gradients in these parameters when encountering localized structures such as ARs and coronal holes. Coronal waves are known to be affected by these inhomogeneities, and show a range of behaviors that are consistent with true waves. These will be reviewed in the following.
4.7.1 Refraction
Coronal waves and their chromospheric counterparts have been known to avoid ARs and coronal holes (e.g., Thompson et al., 2000b), which is a behavior that is expected for a fast-mode wave. ARs and coronal holes are associated with larger fast-mode speeds (typically 1000 km s−1) than the quiet corona (a few 100 km s−1). When a fast-mode wave encounters such a “hill” of high speeds, it will be refracted away from it. Conversely, the wave will be refracted towards “valleys” of low fast-mode speeds. This behavior was well reproduced by simulations based on geometric acoustics (Uchida, 1968; Uchida et al., 1973; Afanasyev and Uralov, 2011) and 3D MHD simulations (Wang, 2000; Ofman and Thompson, 2002; Terradas and Ofman, 2004). This refracting behavior of coronal waves can now be directly seen with AIA (e.g., Shen et al., 2013).
A second observational evidence for refraction is given by the inclination of coronal wavefronts observed at the limb (see Figure 18 for an example). Often, these wavefronts are tilted towards the solar surface (i.e., they “lean” forwards) and become progressively tilted during their propagation (cf. Hudson et al., 2003; Patsourakos and Vourlidas, 2009; Kienreich et al., 2009; Liu et al., 2012). This is a consequence of the increase of fast-mode speed with height in the low corona (Mann et al., 1999b).
4.7.2 Reflection
The boundary of a coronal hole represents a steep gradient in wave speed at which reflection should take place. This was first observed for a coronal EUV wave by Long et al. (2008) and Veronig et al. (2008), and studied in detail by Gopalswamy et al. (2009). The reflected wave was clearly seen in difference images and in intensity profile stack plots (see Figure 30). Such observations have become possible only since STEREO/EUVI became available. The secondary wave was reflected again from a polar coronal hole. This (multiple) reflection has been interpreted as the first direct evidence for the true wave nature of coronal waves. Reflection at coronal hole boundaries has also been reproduced by 3D MHD modeling (Schmidt and Ofman, 2010).
The first observed reflection of a coronal wave at a coronal hole boundary. Left: STEREO/EUVI image with overplotted wavefronts of the primary wave (red) and the reflected waves (green). Right: Distance-time intensity plot made from stacking EUVI difference images within the rectangular slit shown on the left panel. Note the reflection around 13:00 UT. Image reproduced with permission from Gopalswamy et al. (2009), copyright by AAS.
These findings have been criticized by Attrill (2010), who claimed that optical illusions due to a misinterpretation of running difference images had been mistaken as wavefronts, but it is difficult to see how that could affect the intensity stack plots, which clearly show the reflected wave. Moreover, the improved cadence brought by SDO/AIA has resulted in numerous further cases of wave reflections at coronal holes, ARs, and bright points (e.g., Li et al., 2012; Olmedo et al., 2012; Shen and Liu, 2012a; Shen et al., 2013, see the animation in Figure 31 for an example), and the reality of the phenomenon is now generally accepted. Kienreich et al. (2013) studied three homologous EUV waves using stereoscopic observations from STEREO/EUVI and PROBA2/SWAP, which were all reflected at a coronal hole. The secondary waves were also homologous and followed the Huygens-Fresnel principle (angle of incidence equal to angle of reflection). Interestingly, it could be shown that the reflection did not simply take place in a 2D plane at a fixed height, but that the secondary waves were actually deflected to the higher corona.
Still from a movie — An animation of the 2011 Feb 15 coronal wave and its reflection on a coronal hole as seen on a full sun map combining EUVI-A and EUVI-B (195 Å) with AIA (193 Å) data. Shown is a sequence of running ratio images. The blue lines indicate the predicted wave trajectories and clearly show the reflection at the coronal hole boundary (red line). Reproduced with permission from Olmedo et al. (2012), copyright by AAS. (To watch the movie, please go to the online version of this review article at http://www.livingreviews.org/lrsp-2015-3.)
The reflected waves show the same thermal properties as the incident ones (e.g., heating above the 0.6 MK characteristic of the 171 Å band; see Li et al., 2012), but tend to be slower then the primary waves (100–500 km s−1 versus 300–800 km s−1). There are several possibilities to explain this. The incident disturbance could be a nonlinear wave or shock, which is propagating with a Mach number larger than unity, while the reflected wave is a linear one traveling at the characteristic speed. The reflected wave has to propagate in the rest frame of flow field associated with the primary wave, which will result in an apparently lower speed (Kienreich et al., 2013). Finally, a deflection of the secondary wave into the higher corona could lead to a smaller projected speed (Kienreich et al., 2013).
4.7.3 Transmission
Depending on the magnitude of the wave speed gradient, coronal waves may not only be reflected (or refracted) by coronal structures, but a certain fraction may be able to transmit through the boundary into the structure. EUV waves have been observed to transmit into or through ARs (Shen et al., 2013), coronal cavities (Liu et al., 2012), and coronal holes (Olmedo et al., 2012), and there has been one report of a Moreton wave transmitting into a coronal hole (Veronig et al., 2006). The transmitting waves are generally faster than the incident ones (by typically 10–60%), which is consistent with the higher fast-mode speeds in the structures that are being penetrated. The transmitted wave signatures are also comparatively faint, which explains why transmission of EUV waves has not been observed before AIA became available. Sometimes, the transmitting wave is not seen at all within an AR, but is observed to re-emerge from the far side (e.g., Li et al., 2012). These low observed amplitudes can be understood in terms of the conservation of wave energy flux, which is proportional to the product of amplitude and group velocity. As the wave enters the AR or coronal hole, it will speed up, and consequently the amplitude will decrease.
It should be stressed that the transmissions observed imply that the disturbance is able to cross a topological separatrix. This strongly favors the wave interpretation, since non-wave phenomena are predicted to stop at these surfaces (cf. Chen et al., 2005b).
4.7.4 Stationary brightenings
Small-scale stationary brightenings in EUV (e.g., Warmuth et al., 2004a) and SXR (Attrill et al., 2009) are commonly observed in the wake of a passing coronal wave. Localized brightenings that are associated with small-scale magnetic field concentrations are also seen in Hα and He i (Vršnak et al., 2002b; Warmuth et al., 2004b). On larger scales, stationary bright fronts (persisting for hours) were observed in EUV with SOHO/EIT when a coronal wave reached the boundary of an AR or a coronal hole. Delannée and Aulanier (1999) pointed out that these boundaries were associated with topological separatrices of the coronal magnetic field. A coronal wavefront that actually stops at such a boundary is clearly inconsistent with the wave model. Conversely, stationary fronts at separatrices are predicted by various magnetic reconfiguration models.
However, it has been suggested that an MHD wave can trigger local energy release at such a boundary, which would result in a stationary prolonged emission increase. This was seen at AR boundaries in MHD simulations by Ofman and Thompson (2002), and has been proposed to explain prolonged localized brightenings in Hα and He i (Vršnak et al., 2002b; Warmuth et al., 2004b). The notion of localized energy release triggered by a passing wave was also invoked to explain a temporary emission increase of a broad-band metric radio source associated with a coronal waves (Vršnak et al., 2005).
It is worth pointing out that SDO/AIA has observed refraction, reflection, and transmission of waves at AR and coronal hole boundaries, but no stopping of waves. It is well possible that the cadence of SOHO/EIT was insufficient to detect these phenomena, and therefore a localized brightening triggered by a passing wave could have been mistaken for an actual halting of the propagation. Alternatively, localized brightenings can be generated by all non-wave models, including compression due to field-line opening (Delannée, 2000; Chen et al., 2005b), Joule heating due to current shells (Delannée et al., 2007), and magnetic reconnection (Attrill et al., 2007).
Recently, stationary EUV fronts were found to be located at the footpoints of coronal streamers that were deflected and excited to oscillate when the upper parts of a coronal EUV wave passed through them (Kwon et al., 2013b). The spatial and temporal characteristics of the fronts suggests that they are generated by the bouncing back of the deflected streamer, and not by magnetic reconfiguration associated with the erupting CME. The damping of the streamer oscillations may provide energy input to generate long-lived stationary brightenings, either due to density compression effected by trapped waves, plasma upflows due to an interaction of these waves with magnetic structures, or a combination of these effects.
4.7.5 Excitation of oscillations
Coronal waves can cause the displacement of coronal structures such as coronal loops, filaments, and streamers, which often results in a transverse oscillation of the affected structure.
It has been known for a long time that Moreton waves can cause filament oscillations (Moreton, 1960, 1964; Ramsey and Smith, 1966; Liu et al., 2013), which are usually observed as “winking filaments”. If the line-of sight component of the oscillation exceeds 20 km s−1, the filament vanishes from and subsequently reappears in Hα line center filtergrams (for a review of filament oscillations, see Arregui et al., 2012). Moreton waves were only seen in a quarter of these large-amplitude oscillations, but the speeds derived for the exciter were consistent with Moreton wave speeds (Smith and Harvey, 1971). One could thus assume that filaments are actually a more sensitive tracer of the expanding coronal wavefront proposed by Uchida (1968) than the chromosphere itself (cf. also Balasubramaniam et al., 2007).
With the availability of EUV imaging, it was demonstrated that coronal EUV waves can indeed excite filament oscillations, even without generating Hα wavefronts. Okamoto et al. (2004) found that 11 out of 14 EIT wave events with simultaneous Hα coverage did excite filament oscillations. Recently, Shen et al. (2014) observed a chain of successive winking filaments. The AIA wave that triggered these oscillations was very weak, which confirms the earlier finding that filaments are particularly sensitive tracers of coronal waves.
The association of EUV waves with filament oscillations was called into question in one event where the filament oscillation seemed to start before the wave arrival (Eto et al., 2002). It has been argued that this could be explained in terms of a tilted wavefront (Warmuth et al., 2004b), where higher parts of the front reach the filament earlier than the lower parts that generate stronger signatures.
Filament oscillations have also been detected in He i (Gilbert et al., 2008, see Figure 32) and in EUV, where transverse oscillations are observed (Hershaw et al., 2011; Asai et al., 2012; Gosain and Foullon, 2012). The latter studies showed that the transverse oscillations are caused by the impact of a fast coronal wave.
The Moreton wave of 2006 Dec 6 observed in Hα at Mauna Loa Solar Observatory (top) and the initial stage of the induced filament oscillation in Hα (middle) and He i (bottom). The line-of-sight motion is shifting the filament in and out of the filter passbands. Image reproduced with permission from Gilbert et al. (2008), copyright by AAS.
Transverse oscillations of coronal loops were first observed in EUV with TRACE (e.g., Aschwanden et al., 1999). They typically oscillate at periods of tens to hundreds of seconds and damp after a few cycles. They represent kink mode oscillations in which the loop is bodily displaced while the footpoints remain fixed. Wills-Davey and Thompson (1999) have shown that the impact of a coronal EUV wave can excite these loop oscillations. Note that for a harmonic coronal wave, the dominant period of the resulting loop oscillation will belong to the driver, while a single-pulse disturbance will excite only natural periods of the loop (see Ballai et al., 2008, 2011b).
In most loop oscillation events observed with TRACE, no wave was evident, but they were associated with flares or eruptions, and exciter speed of several hundreds up to 2000 km s−1 could be inferred (Aschwanden et al., 1999; Aschwanden and Schrijver, 2011). Based on the high association of oscillation events with metric type II bursts, Hudson and Warmuth (2004) have argued for a flare-associated blast wave as the probable cause. They also noted that the loops are not disrupted or permanently displaced. Instead, they settle back close to their original position once the oscillation has been damped. This is a strong indication for the wave nature of the disturbance. In contrast, the different versions of magnetic reconfiguration models would lead to permanent changes of the magnetic field structure of the loop and its environment.
Due to its global coverage and high signal-to-noise ratio for short exposure times, SDO/AIA is much better suited to observe both the local oscillations and the fast wavefronts that are triggering them, and indeed loop oscillations are observed in a significant fraction of AIA waves (cf. Liu and Ofman, 2014). There is a sequential triggering of transverse oscillations that follows the propagation of the diffuse EUV wavefront (Liu et al., 2012, see Figure 33). Similar sequential deflection and oscillations have been seen at a lower cadence in an EUVI limb event (Patsourakos and Vourlidas, 2009). This behavior strongly supports the MHD wave model.
Distance-time intensity stack plots along two azimuthal cuts in the coronal wave event of 2010 Sep 8, imaged at 193 Å with SDO/AIA. The plots show a sequence of transverse oscillations that are excited by the arrival of the coronal wave at increasing distances. Image reproduced with permission from Liu et al. (2012), copyright by AAS.
On larger spatial scales, coronal shock waves were reported to cause deflections of coronal streamers (Vršnak et al., 2006; Tripathi and Raouafi, 2007). Recently, Kwon et al. (2013b) showed that coronal streamers were deflected and excited to oscillate after the higher parts of a coronal EUV wave passed through them. The oscillation was identified as a quickly damped kink mode wave (e.g., Liu et al., 2012).
4.7.6 Excitation of eruptions and sympathetic flaring
The first tentative evidence for globally propagating physical disturbance on the Sun was given by flares that were temporally associated with other flares and, thus, seemed to suggest a propagating disturbance emanating from one flare and triggering secondary ones (e.g., Richardson, 1951; Becker, 1958; Valničnek, 1964). The reality of this phenomenon is still not generally accepted. There are studies that find that flares appearing close in time could just be chance events (e.g., Biesecker and Thompson, 2000), while others confirm the existence of sympathetic flaring (e.g., Moon et al., 2002).
Coronal waves are one potential agent that could trigger sympathetic flares (or eruptions in general). Ofman and Thompson (2002) have demonstrated this possibility by numerical simulations that showed that a current-carrying AR can be destabilized by the impact of a coronal wave. However, so far there is no unambiguous observational evidence for such an effect. The global coverage and high temporal resolution and duty cycle of SDO/AIA offers the prospect for observations that should help to answer the question whether coronal waves can trigger remote eruptions. The inherently global nature of some solar eruptive events has already been demonstrated (e.g., Zhukov and Veselovsky, 2007; Schrijver et al., 2013). Such events show a wide variety of coupling processes, of which coronal waves are but one. Given this host of different processes, it will still be a challenge to identify the trigger of sympathetic eruptions.
4.8 Energetics
There have been but a few attempts to estimate the energies associated with coronal waves. Ballai et al. (2005) have calculated the energies involved in coronal loop oscillations that were caused by a coronal wave wave (cf. Section 4.7.5). Assuming that the wave energy is completely transferred into the oscillating loop, this gives a minimum wave energy of
where L is the loop length, R is the loop radius, ρi and ρe are the densities inside and outside the loop, xmax is the maximum deflection of the loop at the time tmax, x1 is an intermediate deflection that occurs at the time t1, and \(\lambda _{\rm{e}}^{{\rm{ - 1}}}\) is the decay length of perturbations outside the cylinder (cf. Ballai et al., 2005). Using the observed properties of a loop oscillation observed with TRACE, Ewave = 3.4 × 1025 erg was deduced.
Applying the same method to a larger event sample, Ballai (2007) derived minimum wave energies in the range of 1023–1026 erg. Along the same lines, but using He i observations, Gilbert et al. (2008) have calculated the energy involved with a wave-filament interaction. The kinetic energy deposited into the filament by the wave was on the order of a few 1027 erg. A minimum wave energy of 1028 erg was derived from an oscillating flux rope cavity by Liu et al. (2012).
It is very likely that these studies severely underestimate the energy content of coronal waves, since probably only a small fraction of the waves’ energy is transferred to loop or filament oscillations. Patsourakos and Vourlidas (2012) have proposed a more comprehensive approach by considering the kinetic energy flux, radiative and conductive losses. The kinetic energy flux is given by
with ρ the mass density, υgr the group speed, and δυ the velocity perturbation. The radiative energy flux is given by
where n is the electron density, Λ(T) the radiative loss function, and L the characteristic length scale associated with the bulk of the emission. Finally, the conductive energy flux is proportional to temperature T and length scale L according to
The total EUV wave energy is then
where the Δ quantities represent the change in the fluxes due to the EUV wave, R and dR are the radius and thickness of the assumed spherical wavefront, and Δt its lifetime. For typical wave parameters, Patsourakos and Vourlidas (2012) deduced an energy of 1029 erg, which is several orders of magnitude higher than the previous estimates.
Here, I propose another estimation that can be made for Moreton waves in terms of the kinetic energy of the flows involved in the compression of the chromosphere. The energy of the coronal wave causing the Moreton wave signatures has to be at least as high as the flow energy in the chromosphere, giving
where A is the area affected by the wave (integrated over the whole propagation), ρcol the column density of the affected chromospheric layer, and υflow the speed of the compressive downward flow. With A corresponding to a 90° circular segment with an outer radius of 300 Mm and an inner radius of 100 M), υflow = 30 km s−1, and ρcol = 1.5 × 10−4 g cm−2 (according to the VAL-C model of Vernazza et al., 1981 when the affected height range is assumed to go down to the level where the Hα line core is formed), an energy of Ewave = 4 × 1029 erg is found. This is consistent with the estimate of Patsourakos and Vourlidas (2012) bearing in mind that Moreton waves are associated with particularly strong events.
These higher estimates of the waves’ energy content is comparable to the energy of a small CME (Vourlidas et al., 2010) and to the thermal and nonthermal energies of a C-class flare as derived from RHESSI (Lin et al., 2002) and GOES data (cf. Saint-Hilaire and Benz, 2005; Mann and Warmuth, 2011; Ryan et al., 2012).Footnote 7 This implies that coronal waves represent a non-negligible fraction of the energy released in a solar eruptive event (at least in smaller events).
5 Relationship with Solar Eruptive Events
Coronal waves are highly associated with solar eruptive events (SEEs), which includes flares, CMEs (and erupting filaments), and other forms of ejections at smaller spatial scales. They are always propagating away from an AR in which some kind of SEE is taking place. In this section, the relation of the waves with these different phenomena is discussed, with the aim of identifying the cause of wave generation. It should be stressed that flares (which are localized, small-scale phenomena involving acceleration of particles and impulsive heating of plasma) and CMEs (which are large-scale eruptions of magnetic field structures) are closely related and represent different signatures of an underlying impulsive restructuring of non-potential magnetic fields in ARs.
On theoretical grounds, the launch of a large-scale (and possibly large-amplitude) MHD wave pulse requires a fast and/or impulsive motion of a source region that generates an initial disturbance that can then propagate as a wave or shock (Section 6.1). If the disturbance is being driven for a substantial part of its propagation, this driver has to propagate over a longer distance, too. This is also required by the magnetic reconfiguration models (cf. Section 6.2).
5.1 Solar flares
Solar flares could launch coronal waves due to an impulsive expansion of magnetic structures such as the flaring loops. In its classic form, commonly referred to as the pressure-pulse mechanism, this scenario assumes that a sudden increase of the flaring volume (which can be considered as a 3D piston) driven by the impulsive increase of flare plasma’s gas pressure leads to the formation of a large-amplitude perturbation of the corona. The gas pressure increase may not be able to cause a sudden source region expansion in regions of strong magnetic fields (i.e., βp ≪ 1, where βp is the plasma beta parameter, which is the ratio of gas pressure to magnetic pressure), such as in ARs. An alternative scenario has been proposed in the form of a “magnetic pressure pulse”. Here, sudden motions of magnetized structures associated with the reconnection process (e.g., the deformation of loops by reconnection outflow jets) generate a large-amplitude perturbation of the ambient medium. For a detailed discussion of these processes, see Vršnak and Cliver (2008).
In both scenarios, the generated large-amplitude disturbance will leave the flaring region in the form of a freely-propagating nonlinear MHD wave, which steepens and may develop into a shock. Such a disturbance is also known as a blast wave (cf. Section 2.2). Note that establishing that a wave is freely propagating is not in itself an argument for a flare-related origin though, since impulsively accelerating CMEs or other ejecta could act as temporary drivers similar to an expanding flaring volume.
Using an EIT wave catalog compiled by Thompson and Myers (2009), Biesecker et al. (2002) made a statistical analysis of the association of EIT waves with flares, CMEs, and type II bursts. 66% of EIT waves were found to be associated with flares. The association increases for waves with higher “quality rating”, which is a measure of the confidence level that the observed event is really an EIT wave. For the highest quality rating, an association of 100% is found. However, there is a significant number of well-defined waves that are not accompanied by a flare. Moreover, Cliver et al. (2005) pointed out that half of the wave-associated flares were very weak (GOES X-ray class B and lower). Only 1% of these weak flares is associated with EIT waves, which raises the question of what makes these events special. Cliver et al. (2005) suggested that CMEs represent this special condition, which distinguishes wave-associated from non-wave-associated flares. Another case against flares was made by Chen (2006) who showed that 14 energetic flares (primarily M class) that were not accompanied by CMEs also did not launch EIT waves.
More recently, Nitta et al. (2013) have found a somewhat stronger association with flares. All of the 138 AIA disk waves studied were associated with flares, and only 15% of these flares were below C class. Most AIA waves were associated with flare classes C and M, with a slight correlation between flare importance and wave speed. Muhr et al. (2014) found that 74% of 60 EUVI wave events were associated with solar flares, and that the initial wave speeds were moderately correlated with GOES flare importance (the correlation with CME speed was much weaker). The stronger association with flares found by these more recent studies is probably caused by different event selection criteria: the catalog of Thompson and Myers (2009) included many weak and irregular events that did not propagate to large distances and may not have been waves at all. This class of events is missing in the samples of Nitta et al. (2013) and Muhr et al. (2014).
Coronal wave events that show Moreton wave signatures (presumably shocks) are always associated with flares (e.g., Smith and Harvey, 1971; Warmuth, 2010). In these cases, the associated flares tend to be strong (M and X-class), but shock events were even found for C-class flares (Warmuth, 2010; Zhang et al., 2011). These flares are comparatively impulsive.
Going beyond association, the relative timing between flare and the probable wave launch time has been studied by several authors. Early studies have found that Moreton waves are launched at the beginning of an explosive phase in the evolution of the associated flare (e.g., Smith and Harvey, 1971). More recently, several authors have found that waves are launched close to the beginning or the peak of the impulsive HXR emission, which is related to the energy input by nonthermal electrons (Gilbert and Holzer, 2004; Warmuth et al., 2005; Vršnak et al., 2006). For example, Warmuth (2010) found that 24 out of 27 coronal waves associated with Moreton waves were launched within a 4 minute interval around the HXR peak (see Figure 34). Such a temporal association is also well established for type II bursts (see the review by Vršnak and Cliver, 2008).
Histogram of the time lag between the first observation of a wavefront and the peak of the associated HXR burst (in minutes). Note that in the majority of events, the wave launch is closely associated with the HXR peak. Image reproduced with permission from Warmuth (2010), copyright by COSPAR.
Timing thus suggests that the wave launch might be connected to the impulsive energy release in the flare. However, it has been shown that the acceleration profile of CMEs tends to peak during this period, too (cf. Zhang et al., 2001; Maričić et al., 2007; Temmer et al., 2008; Berkebile-Stoiser et al., 2012). Since coronal waves are highly associated with CMEs too (Section 5.2), timing alone cannot be used to make a distinction between a flare-related and a CME-related wave launch mechanism.
Extrapolations locate the wave radiant point consistently close to, but slightly offset from the flaring location (see Section 4.1.3). This either implies that the wave is not launched by a symmetric expansion of the flaring volume, or that the wave is somehow “channeled” away from the flare (e.g., by the fast-mode speed profile of the AR) until it spreads out azimuthally. It has also been noted that the wave-associated flares (or at least parts of them) are located at the periphery of their active region, and the waves are always launched into the direction away from the source AR (e.g., Warmuth et al., 2004b). Such a configuration, which gives immediate access to regions of low field strengths (and low Alfen speeds) would be favorable for the formation and the steepening of a pressure pulse.
Using X-ray observations, Hudson et al. (2003) determined the evolution of the gas pressure in flaring loops and found that the timing was inconsistent with the wave launch. They found a better association with the sudden outward motion of a larger-scale loop structure, which in hindsight might well have been the initial expansion of the associated CME (cf. Section 5.2).
Generally, over the recent years a lot of evidence has been presented that favors CMEs over flares as the causes of coronal waves (see the following Section 5.2). Still, the possibility that at least some waves are launched by flare-associated pressure pulses cannot be ruled out. This is particularly suggested by wave events that show several consecutive wavefronts or type II bursts. Gilbert and Holzer (2004) observed an event with five consecutive He i wavefronts, two of which were attributed to the CME, and three to the flare. In the complex limb event studied by Vršnak et al. (2006), a second coronal shock was launched after the main event, as shown by a type II signature, but there was only one CME. Based on timing, this shock could be associated with a second energy release phase in the flare as shown by a late HXR peak. Finally, metric type II bursts without associated CMEs (despite favorable observational configuration) suggest that flares can trigger coronal shocks at least under special conditions (cf. Magdalenić et al., 2008).
5.2 Coronal mass ejections (CMEs)
CMEs are large-scale eruptions of coronal magnetic field structures (for recent reviews, see Chen, 2011; Webb and Howard, 2012). Often, a filament is at the core of the CME, and erupts as a part of the larger-scale structure. It is generally accepted that the radial expansion of CMEs drives coronal shocks in the outer corona and heliosphere (e.g., Sheeley Jr et al., 1985; Cane et al., 1987; Gopalswamy et al., 2000b). Likewise, their azimuthal expansion could generate laterally propagating disturbances that are being continuously driven by the CME flanks. This would be equivalent to a bow shock (see Section 2.2). Alternatively, the early impulsive expansion of the CME-associated magnetic structures could act as a temporary 3D piston, which generates a large-amplitude disturbance that becomes freely propagating once it separates from the expanding piston (similar to the flare-induced pressure pulse; see Section 5.1). In reality, probably both processes are involved, since the early phase of a CME eruption is characterized by both a (quasi-) radial eruption and a lateral over-expansion. Finally, the interaction of the flanks of the expanding CME with the ambient corona could generate pseudo wave signatures in various different ways (see Section 6.2).
CMEs thus provide several potential ways of generating coronal waves, which is why there have been many observational attempts to establish their relationship with the waves. The statistical study by Biesecker et al. (2002) found that 58% of EIT waves were associated with CMEs. More recently, CME association rates of 79% were found for 34 EUVI waves detected during the recent solar minimum (Nitta et al., 2014), 95% for a sample of 60 EUVI waves (Muhr et al., 2014), and 65% for disk AIA waves (Nitta et al., 2013). These association levels seem to be comparable to flares, but they reflect an observational bias: CMEs are best visible when they propagate in the plane of sky (i.e., in limb events), and indeed the association rate becomes significantly larger than for flares when only events within 30° of the limb are considered, or when multi-spacecraft observations are available, as is the case for the more recent studies.Footnote 8 In these categories, all well-defined waves were associated with CMEs. However, CMEs, like flares, are not a sufficient condition for the generation of coronal waves. In the period covered by the EIT wave catalog of Thompson and Myers (2009), only 20% of CMEs were associated with waves. Cliver et al. (2005) showed that wave association increases with CME speed and width. Well-defined coronal waves, in particular shock-associated ones, are always accompanied by fast and wide CMEs.
Timing studies of waves versus CMEs run into the same problem that was already discussed in Section 5.1: the wave launch times are associated with the rise or peak of the CME acceleration profile, but this tends to be synchronized with the impulsive energy release in the flare as observed by HXR emission. Therefore, no distinction can be made whether CMEs or flares are responsible for wave generation.
All theoretical models of wave generation by CMEs require significant motion of the CME and predict a certain spatial and kinematical relationship. MHD waves generated by a CME should be ahead of the CME flanks. Disturbances generated by the 3D piston effect should propagate faster than the lateral expansion speed of the CME, with an increasing stand-off distance, while bow shocks should propagate at the same speed as the driver (in a homogeneous medium). Pseudowaves should be tightly bound to the CME flanks. Therefore, imaging observations that capture positions and kinematics of CME and wave at the same time and in the same region are of highest importance for constraining our models. For the formation of coronal waves, the lateral expansion of the CME flanks is more relevant than the radial propagation. This lateral evolution of CMEs has been studied considerably less extensively than the radial one.
Observationally, this has proven to be a difficult task: CMEs are best observed off-limb with coronagraphs that do not cover the low corona where the waves are observed. Conversely, coronal waves are best observed on-disk, but EUV (and SXR) disk imagers have a limited field-of-view that does not reach into the upper corona, and identifying CME features in EUV images can be ambiguous.Footnote 9 Therefore, establishing a relationship between these different observational regimes is difficult. This may be one of the reasons why studies that did try to relate CME and wave signatures have found four different scenarios:
-
Wave behind CME. In a complex coronal wave event, Vršnak et al. (2006) identified an expanding dome-like feature seen with GOES/SXI as the early signature of the associated CME. The flank of this feature was propagating ≈ 100 Mm ahead of the coronal wave. Vršnak et al. (2006) concluded that the wave was not driven or launched by the CME, but rather by the flare.
-
Wave initially behind CME, then overtaking a stopping CME flank. This was reported by Warmuth (2010) based on coronagraphic observations of the low corona with the MK3 K-coronameter. Just as in the event of Vršnak et al. (2006), the CME flank was observed to propagate ≈ 100 Mm ahead of a Moreton wave. However, the CME flank then decelerated and stopped, while the Moreton wave continued its expansion and propagated well beyond the stationary CME flank.
-
Wave coincident with CME flank. Using high-cadence EUV imaging, several authors have reported events where the coronal waves were cospatial to or remained closely attached to the expanding CME flanks (Chen, 2009; Attrill et al., 2009; Dai et al., 2010).
-
Wave ahead of CME flank. High-cadence EUV imaging with EUVI and AIA has revealed in many events that coronal wavefronts are first detected ahead of (but close to) the legs of rising and expanding loops that presumably represent the early CME (e.g., Long et al., 2008; Veronig et al., 2008; Patsourakos et al., 2009; Patsourakos and Vourlidas, 2009; Kienreich et al., 2009; Veronig et al., 2010). The wavefronts then detach from the loops and propagate freely.
While former two scenarios have been found only in single case studies, the latter two (in particular the last one) have been noted in many studies. The difficulties in relating structures that are seen as line-of-sight integrations of optically thin radiation, at different wavelengths and height ranges, could go a long way in explaining these apparent discrepancies. The recent years have seen significant progress, though. STEREO has contributed high-cadence EUV imaging, a better overlap between EUV and coronagraphic observations, and perhaps most importantly, stereographic observations that allow us to characterize the 3D structure of coronal waves and CMEs. Quadrature observations (in which a wave and an associated CME were seen as limb events by STEREO-A and as disk events by STEREO-B) have allowed the unambiguous identification of the coronal wave being ahead of the CME flank (Patsourakos and Vourlidas, 2009; Kienreich et al., 2009, see Figure 35 and the animation in Figure 36). Initially, the coronal wavefront stays close to the laterally expanding flank and moves at the same speed. Then, the CME flank decelerates, while the coronal wave detaches and continues its propagation. This scenario is consistent with the bimodality observed in coronal EUV waves by Zhukov and Auchère (2004). It is additionally supported by 3D modelling based on tomographic reconstructions, which show that the CME is not cospatial with the coronal wavefront (Patsourakos et al., 2009; Patsourakos and Vourlidas, 2009; Temmer et al., 2011). Given less comprehensive observations, the CME flanks may well have been mistaken for a second wavefront (cf. Section 4.1.4).
STEREO quadrature observations of the 2009 Feb 13 coronal wave. Left: EUVI 171 Å running difference images showing the propagation of the coronal wave in front of the expanding CME flanks. Right: Distance-time plot of the coronal wave (red) and the CME bubble (green). The wave is clearly ahead of the CME flanks and detaches completely when the flanks decelerate. Image reproduced with permission from Patsourakos and Vourlidas (2009), copyright by AAS.
Still from a movie — An animation of the 2009 Feb 13 coronal wave observed in quadrature with STEREO-B (left) and STEREO-A (right). Shown are EUVI 195 Å running difference images. Reproduced with permission from Kienreich et al. (2009), copyright by AAS. (To watch the movie, please go to the online version of this review article at http://www.livingreviews.org/lrsp-2015-3.)
How can we explain the observations that seem to contradict this scenario? Sometimes it is difficult to distinguish the wave from the CME flank because it is very close or very faint, thus the actual wave will be overlooked, and the CME flank will be mis-identified as the wave (cf. Patsourakos and Vourlidas, 2012). On the other hand, the CME that Warmuth (2010) found to lie in front of the Moreton wave could only be measured down to a height of about 100 Mm. It is well possible that due to over-expansion (see discussion below) the CME had a smaller extent at the coronal base, so that its flank would in fact be located behind the wave.
The increased imaging cadence of EUVI and AIA has recently helped to better characterize the very early phase of the CME expansion, which is most relevant for the launch of coronal waves. The typical evolution, based on observations of limb events, is the following: after loops begin to rise and expand in an AR, they form a quasi-circular structure (a “CME bubble”) with low emission in the interior and a bright rim (Patsourakos et al., 2010a,b, see Figure 37). This bubble is interpreted as a signature of the erupting magnetic flux rope and will later form the cavity of the WL CME. Initially, the bubble expands laterally more quickly than radially. During this phase of over-expansion, the coronal wavefronts become observable ahead of the flanks of the bubble (e.g., Patsourakos and Vourlidas, 2009; Patsourakos et al., 2010a, see Figure 37), or around the whole bubble in the form of a wave dome if the expansion is fast enough in all directions (e.g., Veronig et al., 2010; Kozarev et al., 2011; Ma et al., 2011; Cheng et al., 2012; Li et al., 2012, see Figure 38 and the animation in Figure 39 for an example). Note that it is more difficult to form a large-amplitude disturbance in regions of high fast-mode speed, which is expected above an AR. This may explain the fact that most coronal EUV waves do not show full domes but extend only to 1–2 scale heights. An additional effect that will facilitate the generation of a large-amplitude disturbance in the lateral direction is the fact that the lower parts of the expanding bubble are actually moving downwards. Thus, compression near the coronal base will not result just from the lateral motion of the bubble, but additionally from the downward motion of the boundary of the bubble. Note that there is also a strong observational bias against full wave domes, since the bulk of the observable emission comes from the lowest 1–2 scale heights.
The launch of the coronal wave of 2008 Mar 25 by the lateral expansion of a CME cavity, imaged with EUVI/STEREO at 171 Å in base ratio images. It is clearly evident that the EUV wave detaches from the expanding CME flank (from Patsourakos et al., 2010a).
The coronal wave of 2010 Jun 13 observed at ultra-high cadence in EUV with SDO/AIA. Left: 193 Å base image (with reversed color table) showing an expanding CME bubble (CME), which is embedded in a dome-shaped coronal wave (shock). Right: Distance-time intensity stack plot at 193 Å (reversed color table) along the radial direction. The coronal wave is formed closely ahead of the expanding bubble and continuously increases its offset distance. Images reproduced with permission from Ma et al. (2011), copyright by AAS.
Still from a movie — An animation of the coronal wave of 2010 Jun 13 observed at ultrahigh cadence with SDO/AIA. Shown are base images at 193 A. Note the coronal wave forming ahead of the expanding CME bubble. Reproduced with permission from Ma et al. (2011), copyright by AAS. (To watch the movie, please go to the online version of this review article at http://www.livingreviews.org/lrsp-2015-3.)
As the strong lateral expansion of the flux rope comes to an end, the bubble expands self-similarly, and the radial acceleration of the CME reaches its peak. As a consequence, the bubble (or, in other terms, the CME flank) reaches a more or less constant extent in the low corona, whereas the detached coronal wave continues its propagation.
This characteristic evolution strongly suggests that a CME-associated 3D piston is responsible for the generation of coronal waves. The fact that the wave detached from the CME flanks does not support an interpretation in terms of a continuously driven bow shock nor the different magnetic reconfiguration models. Note that the lateral over-expansion of the CME bubble can be very impulsive with accelerations of > 1 km s−2 (Patsourakos et al., 2010a,b; Ma et al., 2011). On theoretical grounds, such an impulsive lateral acceleration of the piston is required in order to form a large-amplitude disturbance that will steepen to a shock (cf. Žic et al., 2008; Lulić et al., 2013, see also Section 2.2), and it has been shown by both analytical (Temmer et al., 2009, 2013) and numerical modeling (e.g., Downs et al., 2012) that coronal waves, which fulfill the observational constraints, can be generated by this mechanism.
The ultimate cause for the rapid expansion of the CME bubble could be the high magnetic pressure inside the flux rope, which would cause an expansion once the flux rope reaches regions of lower field strengths, the decreasing current in the rising flux rope, or reconnection adding new flux (see Patsourakos and Vourlidas, 2012, and references therein).
5.3 Small-scale ejecta
The term small-scale ejecta encompasses eruptive phenomena of a smaller size scale than CMEs or filament eruptions. It includes phenomena seen in Ha, such as flare sprays and surges, and processes visible in the EUV and SXR ranges, like small-scale erupting loops, plasmoids, and jets. The relation of small-scale ejecta to flares and CMEs is not always clear, generally, we may regard them as another signature of the impulsive reconfiguration of non-potential magnetic field structures in ARs. Small-scale ejecta have been proposed as possible causes of coronal waves based on their very impulsive acceleration, high speeds, and high association with coronal waves.
Hα observations of have shown that many Moreton waves are associated with flares that show various signs of fast ejections, such as flare sprays (e.g., Zirin and Russo Lackner, 1969; Švestka, 1976). Flare sprays (see e.g., Warwick, 1957; Vršnak, 2001) accelerate very impulsively (in a few minutes) to speeds larger than the solar escape velocity (670 km s−1).
In the X-ray range, Yohkoh/SXT frequently observed small-scale SXR ejecta, including erupting loops, blobs that were interpreted as plasmoids (with typical speeds of ≈ 500 km s−1; see e.g., Shibata et al., 1995; Ohyama and Shibata, 1998), and jets (e.g., Shibata et al., 1992; Alexander and Fletcher, 1999). There has been evidence for the generation of metric type II bursts by these rapidly expanding loops, plasmoids, and jets (Gopalswamy et al., 1997; Klein et al., 1999; Gopalswamy et al., 2001b; Klassen et al., 2003). This is based on timing (the bursts appear at the time of rapid expansion), location (the bursts are located ahead of the expanding structures), and kinematics (the bursts and ejecta have comparable velocities).
Coronal waves could be generated in the same manner: the small-scale ejection would act as a very impulsive temporary driver and generates an initially driven shock. The shock would then detach from the driver, and continue as a freely propagating blast wave (cf. Section 6.1). This was supported by actual observations of coronal waves in SXR, where corresponding SXR ejecta were identified as likely wave sources (Hudson et al., 2003; Narukage et al., 2004, see Figures 18 and 19, respectively).
Recently, high-cadence EUV observations have associated coronal waves with small-scale ejecta such as plasma blobs (Kumar and Manoharan, 2013, see Figure 40), surges (Zheng et al., 2012a, 2013a), EUV jets (Zheng et al., 2012b), mini-CMEs (Zheng et al., 2011), mini-filament eruptions (Zheng et al., 2012c), and micro-sigmoid eruptions (Zheng et al., 2012d, 2013b). However, even increased observational capabilities are not always sufficient to distinguish between different scenarios. For example, EUV waves associated with an erupting plasmoid observed by AIA have been recently interpreted as being due to a piston-driven shock (Bain et al., 2012; Zimovets et al., 2012) or due to a flare-launched blast wave (Kumar and Innes, 2013).
Eruption of a plasma blob and subsequent formation of an EUV wavefront, observed with STEREO/EUVI at 195 Å. Running difference images are shown (adapted from Kumar and Manoharan, 2013).
Various small-scale ejecta thus remain to be potential wave generation mechanisms, at least in certain events. The distinction between small-scale and large-scale ejections like CMEs may be somewhat arbitrary, though. Small-scale ejecta observed in SXRs, particularly expanding loops, are probably nothing else than early signatures of an expanding CME (cf. Section 5.2). This association represents one step towards a unified picture of wave generation.
6 Physical Interpretation and Models
6.1 MHD wave and shock models
6.1.1 Fast-mode wave/shock model
For typical quiet coronal parameters (ne = 5 × 108 cm−3, T = 1.5 MK, B = 3 G), cs = 185 km s−1, υA = 273 km s−1, and υms = 330 km s−1 (cf. Section 2.1). This means that the typical speeds of coronal waves are consistent with the magnetosonic speed in the quiet corona (see Section 4.2). Conversely, the speeds in the chromosphere are cs ≈ 10 km s−1, and υA ≈ υms ≈ 100 km s−1. If a Moreton wave with a typical speed of 1000 km s−1 would propagate through the chromosphere, this would imply Mach numbers of M ≥ 10. Such a disturbance would be strongly damped and could not reach larger distances. Uchida (1968), therefore, proposed that the Moreton wave is only the chromospheric imprint of a dome-shaped fast-mode wavefront that expands through the corona while its flanks sweep over the chromosphere (“sweeping-skirt hypothesis”).
Uchida (1968) developed a numerical model of the fast-mode wavefront based on linearized MHD equations in a corona with radial magnetic field and exponential density fall-off. The simulations showed a dome-shaped wavefront, with wave packets being refracted away from regions of high Alfvén speed, i.e., towards lower heights (see left panel in Figure 41). Subsequent simulations with more realistic coronal parameters showed good agreement between observed Moreton waves and the intersection of the expanding wave dome with the chromosphere (Uchida, 1970; Uchida et al., 1973). Furthermore, Uchida (1974) considered fast-mode shocks and found that the positions at which type II bursts were appearing were consistent with regions of low Alfvén speed, where linear fast-mode waves could steepen to shocks.
Three generations of numerical MHD wave models. Left: the original coronal fast-mode MHD wave model, a 2D model based on linearized MHD equations. Solid lines represent the dome-shaped coronal wavefronts, dashed lines the paths of wave packets. Middle: 2D, time-dependent, ideal MHD model of an erupting flux rope. The eruption generates a fast-mode shock wave, and in addition, slow-mode shocks, echoes and velocity vortices are formed in the wake of the fast shock. Right: 3D thermodynamic MHD simulation. The panels shows a synthetic 195 Å image generated from the model. Images reproduced with permission from [left] Uchida (1968), copyright by Springer; [middle] Wang et al. (2009) and [right] Downs et al. (2011), copyright by AAS.
This scenario is still the basis of the fast-mode wave/shock model of coronal waves (see e.g., Vršnak and Lulić, 2000a,b; Warmuth et al., 2004b; Vršnak and Cliver, 2008; Grechnev et al., 2011b; Warmuth and Mann, 2011). This model postulates the following:
-
1.
An initial disturbance of the coronal plasma is generated by an eruptive process in an AR (presumably a 3D piston associated with a CME bubble expansion or a flare pressure pulse; see Section 5)
-
2.
A small-amplitude disturbance results from a slow or gradual acceleration of the driver, and/or from a high ambient magnetosonic speed. The perturbation separates from the driver and propagates away from the AR as a single-pulse linear or weakly nonlinear fast-mode wave. Its propagation speed mainly reflects the ambient fast-mode speed, which means that in the comparatively homogeneous quiet corona, it propagates quasi-isotropically at nearly constant velocities on the order of a few 100 km s−1. When encountering variations of the ambient fast-mode speed, the coronal wavefront will show typical wave characteristics such as refraction, reflection, and transmission.
-
3.
Conversely, a large-amplitude disturbance is created by a very fast or rapidly accelerating driver, and/or for a low ambient magnetosonic speed. The large-amplitude disturbance steepens nonlinearly, and after separating from the driver, it propagates away from the AR as a nonlinear simple wave, which may steepen to a shock (Section 2.2). The speed of the wave is faster than the ambient magnetosonic speed (Mms > 1) and dependent on the wave’s amplitude. As the wave propagates, its amplitude decreases due to the geometric expansion of its front and the fact that its leading edge is propagating faster than the trailing edge. The amplitude decrease results in a deceleration of the wave. Once the amplitude becomes small, the nonlinear wave/shock has degenerated to an ordinary linear wave. In this phase of its evolution, the wave shows the same characteristics as the wave discussed above which had been linear (or weakly nonlinear) from the beginning.
A comparison of the predictions of the wave/shock model with the characteristics of coronal waves described in Section 4 shows that most observational constraints of coronal waves are fulfilled by the wave/shock model. In particular, it is consistent both with waves traveling at constant speeds (interpreted as linear or weakly nonlinear waves) and with the large-amplitude, decelerating waves that show amplitude decrease and perturbation broadening (nonlinear waves/shocks). Both measured kinematics (Section 4.2) and wave amplitudes (Section 4.3) are consistent with this unified scenario, which is further supported by the typical wave characteristics exhibited during interaction with coronal structures (Section 4.7).
The kinematical curves of the large-amplitude decelerating waves are consistent with power-laws, which supports their interpretation as freely propagating shocks (cf. Section 4.2.2). In these events, all observational signatures (coronal and chromospheric wavefronts as well as type II radio burst sources) are consistent with a single, tilted wavefront that is at least partly shocked (as evidenced by the associated type II bursts). This is shown schematically in Figure 42. The tilt is established due to the increase of fast-mode speed with height (cf. Mann et al., 1999b; Warmuth and Mann, 2005a), which is observed in limb wave events in EUV (Patsourakos and Vourlidas, 2009; Kienreich et al., 2009; Liu et al., 2012) and SXRs (Hudson et al., 2003), as well as by observations showing an increase of wave propagation speed with height (Cheng et al., 2012). This geometry can explain the observation that Moreton wavefronts often lag behind coronal wavefronts by up to 25 Mm (Warmuth, 2010) and the fact that brightenings can be seen ahead of the leading edge of the wave in Hα and He i (Vršnak et al., 2002b; Warmuth et al., 2004b). These could either be due to thermal conduction from higher parts of the shock, or due to electrons accelerated at the quasi-perpendicular part of the shock. This is also the location where a type II burst will be generated.
Schematic presentation of the passage of a tilted fast-mode MHD shock through the corona (C) and its signatures in the transition region (TR) and chromosphere (Ch). The curves below the main graph show idealized intensity profiles of the waves seen in Hα line center and He i (upper plot), the Doppler velocity profile (middle) and the profiles in the wings of Hα (lowermost plot). The Hα and Doppler signatures, as well as the main He i perturbation are generated by the impact of the coronal shock on the chromosphere. A more shallow signature in He i is generated in front of the main perturbation by increased irradiation, heat flux, and possibly accelerated particles from the higher parts of the inclined shock front. At the quasi-perpendicular part of the shock, a type II burst is generated. Note that the higher parts of the shock will reach a filament (F) before the disturbance in the lower atmosphere. Image reproduced with permission from Warmuth et al. (2004b), copyright by ESO.
Analytical models based on fast-mode shocks have successfully reproduced the kinematics of coronal waves (Grechnev et al., 2008; Temmer et al., 2009; Grechnev et al., 2011b; Afanasyev and Uralov, 2011; Grechnev et al., 2011a; Temmer et al., 2013), while in the framework of numerical MHD simulations, fast-mode waves that were launched by eruptions were found to be consistent with many aspects of coronal EUV waves (e.g., Wang, 2000; Wu et al., 2001, 2005; Pomoell et al., 2008; Wang et al., 2009; Cohen et al., 2009; Patsourakos et al., 2009; Schmidt and Ofman, 2010, see middle panel in Figure 41 for an example). Of course, the results of numerical models must be interpreted with care, since all of them have to make some simplifying assumptions. For example, none of these models incorporates small-scale inhomogeneities of the medium, which are expected in the highly structured the corona. So far, this issue has only been addressed by Murawski et al. (2001) who studied the propagation of a magnetosonic wave in 1D in a medium with randomly structured density inhomogeneities. They found that the wave was attenuated and slower than in the homogeneous case. Unfortunately, this work has not yet been followed up by more realistic simulations.
Currently, the most sophisticated numerical models used are 3D, time-dependent thermodynamic MHD simulations (Downs et al., 2011, 2012). Such models can produce synthesized observables that can be directly compared with actual observations (see right panel in Figure 41). These models have supported the fast-mode wave/shock scenario, but they find additional disturbances in the wake of the wave. This will be discussed further in Section 6.3.
6.1.2 Slow-mode soliton model
Wills-Davey et al. (2007) argued that the fast-mode wave model fails to reproduce several observational constraints, in particular i) the large variation of EIT wave speeds both between different events (cf. Thompson and Myers, 2009) and within one wave event (Wills-Davey and Thompson, 1999), ii) the fact that a significant fraction of these speeds is below the coronal sound speed (i.e., < 185 km s−1 for a coronal temperature of 1.5 MK), and iii) the observation that EIT waves retain their coherence over large distances. They concluded that these characteristics are better reproduced by slow-mode solitons.
Solitons are a particular case of nonlinear waves, where the nonlinear steepening is exactly counterbalanced by dispersive effects. This balance leads to the formation of a localized wave structure: a soliton. Such waves retain their coherence, their speed is dependent on the amplitude (allowing a wide range of speeds), and in the case of slow-mode solitons traveling obliquely to the magnetic field, the propagation speeds can be lower than the sound speed. Thus the observational constraints given above are reproduced by the slow-mode soliton model.
Several arguments have been put forward against the soliton hypothesis. The most basic is the simple fact that slow-mode waves cannot propagate normal to the magnetic field. Therefore, strongly inclined (i.e., at least by 45°) magnetic fields are required across the quiet corona — a configuration for which there is no evidence yet (cf. Zhukov, 2011). Another issue has been raised by Warmuth and Mann (2011) who argue that the soliton interpretation is not likely based on the small spatial scales given by Hall-MHD. In contrast to basic MHD (which is dispersionless), in Hall-MHD there are dispersive effects on the scale of the ion inertial length. Consequently, the spatial scale of the soliton in Hall-MHD is of the order of few ion inertial lengths (see Miteva and Mann, 2008), which only amounts to some 10 m in the corona. Finally, the observational constraint of the retainment of coherence (i.e., no increase in pulse width) is imposed only by a single weak EUV wave observed with TRACE (Wills-Davey and Thompson, 1999; Wills-Davey, 2006). Conversely, most coronal waves do actually show a widening of the perturbation profile, as discussed in Section 4.3. Such a pronounced widening of the pulse is not consistent with a soliton.
6.1.3 Magnetoacoustic surface gravity waves
Ballai et al. (2011a) have considered MHD wave propagation at the spherical density interface between transition region and corona in the presence of a radial magnetic field. The obtained dispersion relation corresponds to magnetoacoustic-gravity waves. The propagation of these waves is guided by the spherical surface associated with the density jump at the coronal base. The model is able to describe the propagation of coronal waves in the low corona, and is also consistent with the downward-upward flow pattern deduced from spectroscopic observations and Moreton waves (see Section 4.6). However, surface gravity waves are not consistent with observations of coronal waves that extend over a considerable height range, and in particular with full wave domes (see Section 4.1.3).
6.2 Magnetic reconfiguration models
Apparent inconsistencies between the wave interpretation and EIT observations were first pointed out by Delannée and Aulanier (1999), who noted stationary bright fronts and dimming regions in EIT wave events (see Sections 4.7.4 and 3.4.2, respectively). Based on these characteristics, it was argued that coronal waves are not real MHD waves, but rather the consequence of the reconfiguration of magnetic field within the framework of an erupting CME (Delannée and Aulanier, 1999; Delannée, 2000). The apparent wave is then nothing else than the disk projection of the expanding CME envelope (or its footpoints), where plasma is compressed and/or heated due to various processes. Depending on the magnetic topology, both propagating and stationary brightenings can be generated.
Along these lines, three different types of models have been developed, which may be summarized under the term magnetic reconfiguration models (also called non-wave or pseudo-wave models). What all these models have in common is that they generate pseudo-wave signatures that are closely tied to the CME boundary. The models cannot account for a decoupling between a wave signature and the CME flanks (see Section 5.2), nor for true wave behavior such as reflection (Section 4.7).
6.2.1 Field line stretching model
In 2D MHD simulations of an erupting flux rope, Chen et al. (2002, 2005b) found evidence for two propagating disturbances: a fast-mode shock followed by a slower density enhancement. Here, the latter perturbation will be discussed, while the two disturbances will be considered together in Section 6.3. The density enhancement is formed at the boundary of the dimming region. It is produced by the successive stretching (and/or opening) of closed field lines overlying the erupting flux rope (see Figure 43 for an illustration). As the rope rises, successively larger-scale field lines are stretched. The deformation starts at the top and is then transferred to the footpoints of the loops, where plasma is compressed. This will be observed as a front of increased emission that is propagating in the quiet corona at ≈ 250 km s−1, which is consistent with typical EIT wave speeds Moreover, the front will stop at separatrix surfaces, which is also observed in some coronal wave events (cf. Section 4.7.4).
The principle of the field line stretching model illustrated as a cartoon. The erupting flux rope deforms progressively higher overlying field lines (A, B), and this perturbation is transferred from the top to the footpoints (C, D) of the loops. This creates a moving density enhancement. Image reproduced with permission from Chen et al. (2005b), copyright by AAS.
The field-line stretching model is not without problems, however: i) being a 2D model, it is not clear how a realistic flux rope in 3D could generate the quasi-circular wavefronts observed, ii) the propagating brightening is closely tied to the expanding dimming region, which is not always observed, iii) the global propagation of coronal waves can only be reproduced for very large initial arcades, iv) the predicted density enhancement is rather weak (a few percent), which is not consistent with the observed intensities, except for very weak events (cf. Section 4.3).
6.2.2 Current shell model
Based on earlier work, Delannée et al. (2008) developed the current shell model. In 3D MHD simulations, they found that an electric current shell is formed around an erupting flux rope by return currents (see Figure 44). The shell rotates with the erupting flux rope, which is consistent with the rotation observed in some coronal EUV waves (Podladchikova and Berghmans, 2005; Attrill et al., 2007). A line-of-sight integration of the current shell results in an elliptical pattern that matches observed EUV wavefronts, and both bright and dark patches in two EIT waves could be reproduced quite well. The observed brightenings are attributed to Joule heating in the current shell. Note that a shell of enhanced density that is co-spatial with the current shell is generated too due to compression (see also Schrijver et al., 2011). However, Joule heating is expected to create stronger wave signatures than the compressive effect.
The current shell model. Depicted is the numerical simulation of an erupting flux rope. The colored surfaces represent the current shell that is induced at the outer edge of the flux rope. Left: projection onto the surface. Right: oblique view. Image reproduced with permission from Delannée et al. (2008), copyright by Springer.
The current will become stronger as the flux rope accelerates, and the model predicts the largest current densities at heights ≈ 300 Mm. This is at odds with the observation that most coronal waves are visible only over the lowest 1–2 scale heights (50–100 Mm; see Section 4.1.3). Even in events where a full wave dome is visible, the excess emission is concentrated towards the lower heights. Delannée et al. (2014) have replied to this critique that the current shell model has to be scaled correctly to the wave-producing AR. They obtained a predicted height of 84 Mm for the EUVI event they were studying, which was found to be consistent with the observed wavefront heights of 34–154 Mm. Another counter-argument is due to kinematics: since the current shell closely maps the boundary of the accelerating flux rope, acceleration should also be evident in the pseudo-wave signature, which is generally not observed (most waves either decelerate or propagate with constant speeds).
6.2.3 Reconnection front model
Attrill et al. (2007) proposed a scenario where a laterally expanding CME flux rope interacts with the ambient corona in a series of sequential reconnections with favourably oriented small-scale magnetic loops in the quiet sun (see Figure 45). These low-energy reconnection events would generate plasma heating that would be perceived as brightenings. Nearly stationary brightenings would be generated near the core dimming region (due to the core magnetic structure that continues to drive reconnections with the low-lying loops there), and diffuse propagating brightenings ahead of a diffuse expanding dimming region. This behavior was supported by observations of a coronal EUV wave and associated CME that were consistent with this scenario (Attrill et al., 2009).
An illustration of the reconnection front model. An expanding CME (dotted line) reconnects (crosses) with favourably oriented small-scale loops (dashed lines) and generates successive brightenings (A, B, C) that are observed as stationary and propagating fronts. Image reproduced with permission from Attrill et al. (2007), copyright by AAS.
The reconnection front model has been criticized based on magnetic field extrapolations that showed that in the event studied by Attrill et al. (2007), reconnection could not have happened with quiet sun fields (Delannée, 2009). Attrill et al. (2009) replied to this critique that large-scale fields would not inhibit reconnection with small-scale quiet sun fields since the latter become open during a CME eruption. However, doubts remain whether a reconnection front can actually propagate globally. Another issue with the model is that reconnection with small scale fields should generate signatures that are concentrated in the very low corona, and there should be a very clear signature of the heating events in the transition region and chromosphere (see discussion in Patsourakos et al., 2009). However, coronal wavefronts are observed typically up to 1–2 scale heights (with the occasional full wave dome that extends to much larger heights), and signatures below the corona are generally weak.
6.3 Hybrid models
Hybrid models incorporate both a wave and a non-wave component. The original hybrid model was developed by Chen et al. (2002, 2005b). In their 2D MHD model of an erupting flux rope, they identified two distinct disturbances (see Figure 46). As the flux rope erupts, a piston-driven shock is established ahead of it. The legs of the shock can extend down to the low corona, where they propagate with a typical speed of ≈ 750 km s−1. These lower parts of the shock are interpreted as the coronal counterpart of a Moreton waves, and where hence termed “coronal Moreton waves”. Trailing behind this shock is a density enhancement that propagates at a third of the shock’s speed. This feature is generated by the successive stretching and opening of overlying magnetic loops by the erupting flux rope (see Section 6.2.1), and was interpreted as the signature of the EIT wave.
The hybrid model of Chen. Top: Evolution of density (colors), magnetic field (lines) and velocity (arrows). A rising flux rope drives a coronal shock wave (red front) whose flanks sweep over the chromosphere and cause the Moreton wave (from Chen et al., 2005b). Bottom: Evolution of the density distribution at the coronal base. Two propagating density enhancements are seen: a fast one due to the shock (coronal Moreton wave), and a slower one due to field line stretching (EIT wave). Image reproduced with permission from Chen et al. (2005b), copyright by AAS.
In the hybrid model of Chen, the Moreton wave and its coronal counterpart are, therefore, a physically different disturbance as opposed to the EIT wave. This scenario was proposed as a solution to the apparent speed discrepancy between Moreton and EIT waves. However, as shown in Section 4.2, numerous studies (using multiwavelength observations or high-cadence EUV imaging) have shown that Moreton and coronal EUV waves are consistent with a single, decelerating physical disturbance.
While the two components of a hybrid model do not provide the explanation for the kinematics of large-amplitude waves and shocks, they do capture the bimodality of coronal waves originally proposed by Zhukov and Auchère (2004). Based on morphology, they argued that there are two fronts present in coronal waves: a leading fast-mode wave and a slower trailing disturbance caused by the magnetic restructuring within the framework of an erupting CME. Recently, this notion has been supported by high-cadence EUV imaging that shows that behind the coronal wave proper there are bright features propagating at lower speeds (see Section 4.1.4).
Since the original models of Chen et al. (2002, 2005b), a fast outer front and a slower inner front have been identified in several different MHD simulations. The models consistently show that the fast outer front is a fast-mode MHD wave (or shock), while there is a larger diversity for the interpretation of the inner front. The latter is variously attributed to plasma compression due to the erupting/expanding CME (Cohen et al., 2009; Downs et al., 2011), a compression front associated with a current shell (Schrijver et al., 2011), a slow-mode wave (Wu et al., 2005), a quite complex combination of slow-mode shocks and velocity vortices (Wang et al., 2009), or due to a wave launched by the collision between the flow behind the flux rope and the flux rope itself (Pomoell et al., 2008).
Hybrid models tend to predict that the fast-mode wave will generate less conspicuous signatures than the slower pseudo-wave, and therefore often associated the observed main wavefronts with the pseudo-wave. Conversely, the latest generation of 3D MHD models has shown that both processes can generate signatures of comparable magnitude (Downs et al., 2012, see Figure 47 and the animation in Figure 48). Moreover, the fast-mode wave is found to be clearly responsible for the main EUV wavefront that has been studied by most authors. It reproduces the nearly isotropic propagation to large distances, the typical wave characteristics exhibited due to fast-mode speed gradients, and the decoupling from the CME flank. Note that no evidence for slow-mode waves were found in the simulation by Downs et al. (2012). The inner front is mainly a consequence of plasma compression due to the expanding CME, with only a small contribution from a current shell and no evidence (and indeed no requirement) for a reconnection front.
Top: tri-color running ratio images of the 2010 Jun 13 coronal wave observed with AIA at 171 (blue), 193 (green), and 211 Å (red). A hot dome-like wavefront is followed by a slower secondary front. Bottom: Synthesized images for the same event obtained from a 3D thermodynamic MHD simulation. Both outer and inner front are reproduced. Image reproduced with permission from Downs et al. (2012), copyright by AAS.
Still from a movie — An animation of the 2010 Jun 13 coronal wave observed in AIA tri-color running ratio images (left) and simulated with a 3D thermodynamic MHD simulation (right). Reproduced with permission from Downs et al. (2012), copyright by AAS. (To watch the movie, please go to the online version of this review article at http://www.livingreviews.org/lrsp-2015-3.)
6.4 A unified scenario for coronal waves
After examining the characteristics of different models and comparing them with observations, we have finally arrived at a unified scenario for coronal waves. As we have seen, there is now compelling evidence that the main perturbation that is observed in large-scale coronal waves is due to a fastmode wave (Section 6.1.1). Depending on the amplitude of the perturbation, this can be a linear wave, or a nonlinear wave or shock (associated type II bursts unambiguously prove the presence of a shock). The original disturbance is generated by a fast and/or impulsive eruption or expansion of a driver associated with eruptive events in ARs. While different eruptive phenomena could launch waves, it has been shown recently that the initial very impulsive expansion of an erupting flux rope (a CME bubble) will generate a single-pulse fast-mode wave. These observations can now be reproduced by numerical simulations.
In addition to the fast-mode wave/shock that is propagating away from the source AR, the associated eruption will create further signatures that are more closely associated with the restructuring of the coronal magnetic field due to the expansion of the driver itself. These will mainly be density enhancements due to compression, but other processes could play a role, too (Section 6.2). These signatures can appear as secondary (inner) wavefronts and are now being detected by high-cadence EUV imaging. Again, numerical simulations support this scenario.
Thus, the bimodal observational characteristics of coronal waves (a fast outer front and a slower inner front, cf. Section 4.1.4) is conveniently explained by a hybrid model that involves a fast-mode wave (or shock) and a non-wave feature associated with the expansion of the driver, which is most likely an erupting CME (Section 6.3). In contrast to the original hybrid model, the outer fast-mode wave can actually reproduce the main characteristics of both coronal EUV waves and Moreton waves (in terms of a large-amplitude decelerating wave or shock), while the inner disturbance has been rarely noted in early observations and has only recently gained more attention.
This unified scenario resolves the long-standing controversy between wave and non-wave interpretation of large-scale coronal waves. In all likelihood, the controversy on the physical interpretation had been caused by the fact that the two physically distinct disturbances are not always easy to identify and/or separate observationally. Dependent on the characteristics of the driver and its interaction with the AR and the surrounding corona, one or the other disturbance could dominate the observational signatures. Thus different event classes would be observed, as suggested by Warmuth and Mann (2011) on kinematical grounds. A very fast or impulsive eruption will generate a large-amplitude fast-mode wave or shock that will be observed as the most prominent disturbance in all spectral channels. Most studies of such an event will focus on this main perturbation, and will tend to disregard secondary brightenings. Conversely, a slow or gradual eruption may not be able to launch a detectable fast-mode wave, and only the non-wave disturbances associated with the expansion of the eruptive structure will be observed. This could be the case in events where weak and irregular wavefronts with erratic propagation have been reported (cf. Section 4.2). The bimodal or hybrid scenario thus provides a unified explanation for seemingly differing classes of coronal waves.
7 The Wider Significance of Coronal Waves for Solar Physics
Coronal waves are not only interesting in themselves as physical phenomena and for the role they play in solar eruptive events. Furthermore, they have significance for other areas of solar physics. In particular, they can be used for coronal diagnostics, and they may play a role in particle acceleration.
7.1 Global coronal seismology
The term coronal seismology refers to the study of the coronal plasma with the use of MHD oscillations and waves. This relatively new area of research has become possible mainly due to the availability of high-cadence coronal imaging data, as first provided by the TRACE mission. In coronal seismology, the observed properties of oscillations and waves provide diagnostics on coronal parameters that cannot be easily measured otherwise, such as the coronal magnetic field strength and its sub-resolution structure, as well as various plasma parameters including density, transport coefficients, and heating functions.
Coronal seismology has mainly been applied to derive physical parameters of localized structures such as individual coronal loops and polar plumes (for a review, see Nakariakov and Verwichte, 2005). Here, both transverse coronal loop oscillations and longitudinal waves in loops and plumes have been utilized. Conversely, global properties of the quiet corona can be derived from global coronal waves. If we assume that coronal waves are fast-mode waves that propagate perpendicular to the mainly radially oriented magnetic field lines, then their measured speed can be equated with the magnetosonic velocity \({v_{{\rm{ms}}}} = \sqrt {v_{\rm{A}}^2 + c_{\rm{s}}^{\rm{2}}}\). Since cs can be readily obtained from the coronal temperature, this yields the Alfvén speed υA. With the coronal density derived from observations or a model, this gives the magnetic field strength in the quiet low corona, Bcor. This important parameter is very difficult to measure directly, and therefore most seismological studies are focused on deriving Bcor.
First applications of this approach have used average EIT wave speeds (Mann et al., 1999b, 2003), a simple magnetic field model, and a combined coronal density model (Newkirk, 1961; Mann et al., 1999a). The focus of these studies has been the characterization of the Alfvén speed distribution in the solar corona in the presence of an AR: above an AR, υA rapidly decreases from thousands of km s−1 to reach a local minimum of several hundred km s−1 at heights of a few 100 Mm, only to rise again to a broad maximum of some 1000 km s−1 that peaks at R = 3.5 RS, beyond which υA decreases steadily. In the quiet corona, the initial decrease with height is absent, and υA steadily rises from about 200 km s−1 to the broad maximum at 3.5 RS. This basic behavior was confirmed by other models (e.g., Gopalswamy et al., 2001a), as well as by observations (Gopalswamy et al., 2012; Kwon et al., 2013a). The predicted rise of fast-mode speed with height in the quiet corona is consistent with the observation of limb events the wavefronts progressively tilt towards the surface (Hudson et al., 2003; Patsourakos and Vourlidas, 2009; Kienreich et al., 2009; Liu et al., 2012).
In a follow-up study using more detailed wave kinematics and photospheric magnetic field data, (Warmuth and Mann, 2005a, see left panel in Figure 49) have derived field strengths of Bcor ≈ 3 G for the quiet low corona. This is in good agreement with the solar mean magnetic field (Chaplin et al., 2003). Using Hinode/EIS to measure coronal densities, West et al. (2011) have found lower values of Bcor ≈ 0.7 G. This probably reflects the conditions of the deep activity minimum between the solar cycles 23 and 24. Using high-resolution TRACE EUV data, Ballai (2007) have derived the spatial distribution of Bcor (right panel in Figure 49). They found field strengths ranging from 0.5 to 5.6 G, thus basically covering the whole range given by Warmuth and Mann (2005a) and West et al. (2011). Recently, Long et al. (2013) have used data from SDO/AIA and Hinode/EIS to derive Bcor = 2–6 G in the low corona, while Kwon et al. (2013b,a) found Bcor = 0.4–2.5 G at larger heights of 1–3 RS using white-light signatures of coronal waves. Global coronal seismology using coronal waves thus gives us a consistent picture, with magnetic field strengths of a few Gauss in the quiet low corona.
Results of coronal seismology. Left: distribution of the magnetosonic velocity based on a coronal density model and an analytic magnetic field model constrained by photospheric magnetograms and observed EIT wave speeds. The distribution is shown for three orientations of the dipole that models an active region. Colors indicate speeds, and arrows show the magnetic field directions. Right: the 2D distribution of the magnetic field strength in the quiet corona derived from observed TRACE wave speeds. Images reproduced with permission from [left] Warmuth and Mann (2005a), copyright by ESO, and [right] Ballai (2007), copyright by Springer.
Note that the approach presented above is only valid if the waves used are actually linear fast-mode waves. In this case, a positive correlation between wave speed and the magnetic field strength should be seen. This was investigated by Yang and Chen (2010), who actually found a negative correlation and thus concluded that coronal waves are not fast-mode waves but are generated by field line stretching (see Section 6.2.1). However, Yang and Chen (2010) focused only on the early propagation of the wave, where it was probably still being driven. Zhao et al. (2011) used the same technique, but traced an AIA wave to larger distances. They found a positive correlation between wave speed and the local υA, and conclude that the wave is consistent with a fast-mode MHD wave.
Coronal seismology can also be applied to derive other physical parameters. For example, Ballai and Erdélyi (2004) have used the velocity attenuation of EIT waves to derive a kinematic viscosity coefficient that turned out to be an order of magnitude higher than the classical Spitzer value. However, this result is of course only valid in case the EIT waves considered are small-amplitude waves. Otherwise, the observed deceleration would be mainly due to the amplitude decrease of a nonlinear wave or shock (cf. Section 4.2), and the viscosity coefficient would in fact be consistent with the classical value.
Going beyond linear fast-mode waves, shocks can also be used for global coronal seismology. Using AIA data, Gopalswamy et al. (2012) derived the Mach number of a coronal shock from its geometry and standoff distance from the erupting CME. Combined with densities derived from the associated type II burst, this yielded Bcor = 1.3–1.5 G at heights of 140–350 Mm, which is again consistent with the results presented above. It should be noted that even in the absence of observable coronal waves, the shock-generated type II radio bursts can be used to derive υA and B in the upper corona and in interplanetary space (see e.g., Vršnak et al., 2002a).
With their unique spatial, temporal, and spectral coverage and resolution, the imaging data provided by AIA have the potential to revolutionize the field of coronal seismology. For a more detailed review of the capabilities and prospects of coronal seismology, the reader is referred to the recent review by Liu and Ofman (2014).
7.2 Acceleration of Solar Energetic Particles (SEPs)
Provided that a coronal wave is really a large-amplitude disturbance, such as a nonlinear simple wave or a shock, it has the ability to accelerate particles to nonthermal energies. We know from the close association of large-amplitude coronal waves with metric type II bursts (see Section 3.4.1) that shocks can be formed immediately after eruption onset in the low corona. Therefore, coronal waves could be another source of solar energetic particles (SEPs), in addition to flares and CME-driven shock waves in the outer corona and interplanetary space (for a recent review of this topic, see Reames, 2013). Coronal waves are globally propagating, hence they offer an attractive explanation for SEP events that show a wide spread of longitude. Such events have been known for a long time in the form of SEP events that were associated with eruptions that took place far from the magnetic field lines in the western solar hemisphere that are well-connected to Earth. Recently, multi-spacecraft observations of SEP events have confirmed that SEPs can indeed be emitted into wide angular sectors, in some cases approaching 360° (e.g., Dresing et al., 2012).
Kocharov et al. (1994) first reported an SEP event that was closely associated with a Moreton wave. They concluded that electrons and protons were promptly accelerated at a Moreton-associated shock. Calculated proton release times were found to be close to the times when EIT waves reached the western limb (Torsti et al., 1998, 1999). Along the same lines, a large sample of impulsive electron events was studied by Krucker et al. (1999). In 75% of the events that were not related to the flare-associated type III bursts, EIT waves were detected. Based on timing and spatial arguments, the authors of this study concluded that at least some of the impulsive electron events were more likely related to the propagating wave than to the flare itself.
Vainio and Khan (2004) have considered particle acceleration at a refracting coronal shock, which refers to a shock front that becomes tilted towards the solar surface due to the increase of the fast-mode speed with height in the low corona (see Section 6.1). In this geometry it is possible that an observer at 1 AU is magnetically connected to the downstream region of the shock (see left panel in Figure 50), which is in contrast to the situation in CME-driven shocks in the outer corona. Diffusive shock acceleration then yields a power-law spectrum of the accelerated ions. This result (which is consistent with observations) is not naturally obtained when the observer is connected to the upstream region of the shock. Moreover, acceleration in such refracting shocks may also provide a pre-acceleration mechanism for subsequent acceleration at CME-driven shocks in large gradual SEP events.
Left: Cartoon illustrating the concept of SEP acceleration at refracting coronal shocks in which the observer is magnetically connected to the downstream side of the shock. Right: SEP onset time plotted against EUV wave arrival time at the connecting magnetic footpoint (both times are given relative to the time of the associated flare). The dashed line is a linear least squares fit to the data, and r is the correlation coefficient. Images reproduced with permission from [left] Vainio and Khan (2004) and [right] from Park et al. (2013), copyright by AAS.
More recently, several studies have exploited multi-spacecraft observations, improved magnetic field modeling, and high-cadence coronal imaging to strengthen the case of an association between coronal waves and SEP injection (Kerdraon et al., 2010; Kozarev et al., 2011; Rouillard et al., 2012). To take an example, Park et al. (2013) have used STEREO and SDO data to find a good correlation between EUV wave arrival times at the connecting magnetic footpoints and the SEP injection times in 12 events (see right panel in Figure 50).
The largest statistical study of wave-associated SEPs was undertaken by Miteva et al. (2014), who analyzed 179 SEP events and found that 87% of them were accompanied by EIT waves. In events with no apparent magnetic connection to Earth, the waves’ arrival time at the footpoint of the Parker spiral showed a significant correlation with the extrapolated injection times of IP protons. However, the near-relativistic electrons are not consistent with this scenario, and show only a weak pitch-angle anisotropy. This leads the authors to conclude that transport processes in IP space, such as cross-field diffusion, plays an important role in distributing SEPs over a wide range of helio-latitudes.
As shown above, many studies do find evidence for a wave-associated acceleration of SEPs. However, these findings have remained ambiguous because coronal waves are only one of many possibilities to explain the wide longitudinal spreading of SEP events — even in the events where an association was found. Other mechanisms include widely extended CME shocks further up in the corona, sympathetic eruptions, non-radial magnetic field configurations in the corona, deviations from the nominal Parker spiral, and cross-field diffusion of SEPs (see e.g., discussion in Wiedenbeck et al., 2013). The unambiguous association of SEPs with acceleration at coronal waves thus remains to be a challenge.
8 Conclusions
With their global propagation, large-scale wavelike disturbances in the solar corona belong to the most striking phenomena of solar activity. The last one and a half decades have seen a vigorous debate on the physical nature of these perturbations, with arguments going back and forth between MHD wave models and various non-wave scenarios. The different models have been constrained by a multitude of space-borne and ground-based observations, as well as by analytical and numerical simulations. No single model can fulfill all observational constraints. Instead, a hybrid picture has emerged as a unified explanation for all observed characteristics of coronal waves.
In this scenario, a solar eruption launches a fast-mode wave (or shock) that is observed as a fast outer wavefront, while magnetic reconfiguration due to the expanding eruptive feature (most likely a coronal mass ejection) creates a slower inner front that is not a real wave in the physical sense. Depending on the characteristics of the eruption and the surrounding corona, either of the two disturbances may be more clearly seen in observations. Usually, it seems to be the outer fastmode wave that is dominating the observations, particularly in the case of large-amplitude waves or shocks that are associated with Moreton wave signatures and metric type II radio bursts.
The scenario described above is increasingly accepted as the standard model of coronal waves. While this represents a significant progress over the situation just a decade ago, there are still unsolved questions that remain to be addressed. Among others, future research should address the following issues:
-
The exceptional observational capabilities in the EUV (high-cadence imaging, stereoscopic observations) have brought the most significant progress in the last few years. Now it is time to integrate these with multiwavelength observations (X-ray, optical, radio). This is particularly important for events associated with shocks that show chromospheric wave signatures and type II radio bursts. This may help to answer the questions of how and under which conditions the disturbances steepen into shock waves, how these shocks evolve, and whether they are efficient accelerators of particles.
-
3D numerical MHD modeling has reached a level of sophistication that allows the direct comparison of synthesized with actual observations. Now, this has to be applied to events with different characteristics in order to understand which observed signatures correspond to which physical disturbances, and which conditions determine whether one signature or the other will be more prominent. Topics that should be addressed by numerical modeling in more detail include large-amplitude waves and shocks (which up to now have been studied mainly analytically) and the interaction of coronal disturbances with the chromosphere (i.e., the generation of Moreton wave signatures).
-
The wave generation mechanism has to be studied in more detail. Simulations have shown how an expanding CME can launch waves, now this detailed modeling has to be applied to alternative scenarios such as flare-associated pressure pulses or smaller-scale ejecta. These phenomena cannot yet be ruled out as additional causes of coronal waves, at least in certain events.
-
One issue that has made the physical interpretation of coronal waves so difficult is that the observational signatures differ between event classes, presumably because either the fast magnetosonic wave or the slower disturbance associated with the CME expansion is more prominently expressed. Case studies of single (or few) events thus often come to mutually contradicting conclusions. Statistical studies of large event samples are, therefore, necessary to derive more representative results, and to find evidence for different event classes in the first place. Comprehensive catalogs of coronal waves (in a manner akin to the existing CME catalogs) would thus be highly desirable. Possibly, automatic wave detection and characterization algorithms could help to populate such catalogs.
-
A thorough understanding of coronal waves has implications beyond the phenomenon itself, particularly with respect to global coronal seismology. This area of research is bound to be intensified during the coming years due to two main reasons: it has now become clear that at least the leading wavefronts are fast-mode MHD waves, and with SDO/AIA, we have an ideal observational asset. A more reliable characterization of coronal parameters (such as quiet-sun magnetic field strengths) is to be expected to result from these coming studies.
Notes
Note, however, that slow-mode waves were invoked to explain very slow (14 km s−1) small-scale coronal waves associated with micro-eruptions (Podladchikova et al., 2010). Gilbert and Holzer (2004) suggested that slow-mode waves propagating downward from the corona into the upper chromosphere will cause the compression and downward motion that is observed in Moreton and He i wavefronts (see Section 3.2).
In addition, there has been a single detection of a wave in the 1600 and 1700 A channels of SDO/AIA (Shen and Liu, 2012b), which reflects increased emission from the upper photosphere, temperature minimum region, and transition region.
RS: solar radius (696 Mm)
Note that a fast traveling EUV disturbance that may well have been a coronal wave was first reported by Neupert (1989).
For more information on QFP wave trains, see the recent review by Liu and Ofman (2014).
Note, however, that the total radiated energy may actually be an order of magnitude higher (cf. Kretzschmar, 2011).
Note that this is consistent with the earlier finding that the CME association rate of type II bursts increases for near-limb events (Cliver et al., 1999).
As a proxy, the relationship between the wave and an eruptive filament (which presumably lies at the center of the erupting flux rope) can be studied. Several studies found that Moreton and EIT waves are formed in front of an erupting filament, consistent with a wave or shock generated by the erupting flux rope (e.g., Foley et al., 2003; Maia et al., 2003; Narukage et al., 2008).
References
Afanasyev, A. N. and Uralov, A. M., 2011, “Coronal Shock Waves, EUV Waves, and Their Relation to CMEs. II. Modeling MHD Shock Wave Propagation Along the Solar Surface, Using Nonlinear Geometrical Acoustics”, Solar Phys., 273, 479–491. [DOI], [ADS], [arXiv:1104.3620 [astro-ph.SR]]. (Cited on pages 33, 38, 47, and 66.)
Alexander, D. and Fletcher, L., 1999, “High-resolution Observations of Plasma Jets in the Solar Corona”, Solar Phys., 190, 167–184. [DOI], [ADS]. (Cited on page 63.)
Andretta, V. and Jones, H. P., 1997, “On the Role of the Solar Corona and Transition Region in the Excitation of the Spectrum of Neutral Helium”, Astrophys. J., 489, 375–394. [DOI], [ADS]. (Cited on page 20.)
Arregui, I., Oliver, R. and Ballester, J. L., 2012, “Prominence Oscillations”, Living Rev. Solar Phys., 9, lrsp-2012-2. [DOI], [ADS]. URL (accessed 20 September 2014): http://www.livingreviews.org/lrsp-2012-2. (Cited on page 50.)
Asai, A., Hara, H., Watanabe, T., Imada, S., Sakao, T., Narukage, N., Culhane, J. L. and Doschek, G. A., 2008, “Strongly Blueshifted Phenomena Observed with Hinode EIS in the 2006 December 13 Solar Flare”, Astrophys. J., 685, 622–628. [DOI], [ADS]. (Cited on pages 17, 43, and 46.)
Asai, A., Ishii, T. T., Isobe, H. et al., 2012, “First Simultaneous Observation of an Hα Moreton Wave, EUV Wave, and Filament/Prominence Oscillations”, Astrophys. J. Lett., 745, L18. [DOI], [ADS]. (Cited on pages 20, 37, 38, 39, and 51.)
Aschwanden, M. J. and Schrijver, C. J., 2011, “Coronal loop oscillations observed with Atmospheric Imaging Assembly — kink mode with cross-sectional and density oscillations”, Astrophys. J., 736, 102. [DOI], [ADS]. (Cited on page 51.)
Aschwanden, M. J., Fletcher, L., Schrijver, C. J. and Alexander, D., 1999, “Coronal Loop Oscillations Observed with the Transition Region and Coronal Explorer”, Astrophys. J., 520, 880–894. [DOI], [ADS]. (Cited on page 51.)
Athay, R. G. and Moreton, G. E., 1961, “Impulsive Phenomena of the Solar Atmosphere. I. Some Optical Events Associated with Flares Showing Explosive Phase.”, Astrophys. J., 133, 935–945. [DOI], [ADS]. (Cited on pages 5 and 18.)
Attrill, G. D. R., 2010, “Dispelling Illusions of Reflection: A New Analysis of the 2007 May 19 Coronal ‘Wave’ Event”, Astrophys. J., 718, 494–501. [DOI], [ADS]. (Cited on page 48.)
Attrill, G. D. R., Harra, L. K., van Driel-Gesztelyi, L. and Démoulin, P., 2007, “Coronal ‘Wave’: Magnetic Footprint of a Coronal Mass Ejection?”, Astrophys. J. Lett., 656, L101–L104. [DOI], [ADS]. (Cited on pages 27, 30, 50, 70, and 71.)
Attrill, G. D. R., Engel, A. J., Wills-Davey, M. J., Grigis, P. and Testa, P., 2009, “Hinode/XRT and STEREO Observations of a Diffuse Coronal ‘Wave’-Coronal Mass Ejection-Dimming Event”, Astrophys. J., 704, 1296–1308. [DOI], [ADS]. (Cited on pages 17, 18, 50, 58, and 71.)
Aurass, H., Shibasaki, K., Reiner, M. and Karlický, M., 2002, “Microwave Detection of Shock and Associated Electron Beam Formation”, Astrophys. J., 567, 610–621. [DOI], [ADS]. (Cited on page 22.)
Bain, H. M., Krucker, S., Glesener, L. and Lin, R. P., 2012, “Radio Imaging of Shock-accelerated Electrons Associated with an Erupting Plasmoid on 2010 November 3”, Astrophys. J., 750, 44. [DOI], [ADS]. (Cited on page 64.)
Balasubramaniam, K. S., Pevtsov, A. A. and Neidig, D. F., 2007, “Are Moreton Waves Coronal Phenomena?”, Astrophys. J., 658, 1372–1379. [DOI], [ADS]. (Cited on page 50.)
Balasubramaniam, K. S., Cliver, E. W., Pevtsov, A. et al., 2010, “On the Origin of the Solar Moreton Wave of 2006 December 6”, Astrophys. J., 723, 587–601. [DOI], [ADS]. (Cited on pages 31, 37, and 38.)
Ballai, I., 2007, “Global Coronal Seismology”, Solar Phys., 246, 177–185. [DOI], [ADS], [arXiv:0704.1398]. (Cited on pages 53, 76, and 77.)
Ballai, I. and Erdélyi, R., 2004, “Damping of Coronal EIT Waves as a Tool for Plasma Diagnostics”, in Proceedings of SOHO 13 ‘Waves, Oscillations and Small-Scale Transient Events in the Solar Atmosphere: A Joint View from SOHO and TRACE’, 29 September–3 October 2003, Palma de Mallorca, Balearic Islands, Spain, (Ed.) Lacoste, H., ESA Special Publication, SP-547, pp. 433–428, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 77.)
Ballai, I., Erdélyi, R. and Pintér, B., 2005, “On the Nature of Coronal EIT Waves”, Astrophys. J. Lett., 633, L145–L148. [DOI], [ADS]. (Cited on pages 35 and 53.)
Ballai, I., Douglas, M. and Marcu, A., 2008, “Forced oscillations of coronal loops driven by EIT waves”, Astron. Astrophys., 488, 1125–1132. [DOI], [ADS]. (Cited on page 51.)
Ballai, I., Forgács-Dajka, E. and Douglas, M., 2011a, “Magnetoacoustic surface gravity waves at a spherical interface”, Astron. Astrophys., 527, A12. [DOI], [ADS]. (Cited on page 68.)
Ballai, I., Jess, D. B. and Douglas, M., 2011b, “TRACE observations of driven loop oscillations”, Astron. Astrophys., 534, A13. [DOI], [ADS], [arXiv:1108.2593 [astro-ph.SR]]. (Cited on page 51.)
Becker, U., 1958, “Über die Fernauslösung von Eruptionen”, Z. Astrophys., 44, 243–248. [ADS]. (Cited on pages 5 and 53.)
Bemporad, A., Susino, R. and Lapenta, G., 2014, “Plasma Physical Parameters along Coronal-mass-ejection-driven Shocks. I. Ultraviolet and White-light Observations”, Astrophys. J., 784, 102. [DOI], [ADS], [arXiv:1403.0870 [astro-ph.SR]]. (Cited on page 18.)
Berkebile-Stoiser, S., Veronig, A. M., Bein, B. M. and Temmer, M., 2012, “Relation between the Coronal Mass Ejection Acceleration and the Non-thermal Flare Characteristics”, Astrophys. J., 753, 88. [DOI], [ADS]. (Cited on page 56.)
Biesecker, D. A. and Thompson, B. J., 2000, “Sympathetic flaring with BATSE, GOES, and EIT data”, J. Atmos. Sol.-Terr. Phys., 62, 1449–1455. [DOI], [ADS]. (Cited on pages 5 and 53.)
Biesecker, D. A., Myers, D. C., Thompson, B. J., Hammer, D. M. and Vourlidas, A., 2002, “Solar Phenomena Associated with ‘EIT Waves’”, Astrophys. J., 569, 1009–1015. [DOI], [ADS]. (Cited on pages 15, 25, 41, 55, and 57.)
Brosius, J. W., Davila, J. M., Thomas, R. J. and Monsignori Fossi, B. C., 1996, “Measuring Active and Quiet-Sun Coronal Plasma Properties with Extreme-Ultraviolet Spectra from SERTS”, Astrophys. J. Suppl. Ser., 106, 143–164. [DOI], [ADS]. (Cited on pages 12 and 44.)
Brueckner, G. E., Howard, R. A., Koomen, M. J. et al., 1995, “The Large Angle Spectroscopic Coronagraph (LASCO)”, Solar Phys., 162, 357–402. [DOI], [ADS]. (Cited on page 12.)
Cane, H. V., Sheeley Jr, N. R. and Howard, R. A., 1987, “Energetic interplanetary shocks, radio emission, and coronal mass ejections”, J. Geophys. Res., 92, 9869–9874. [DOI], [ADS]. (Cited on page 57.)
Carley, E. P., Long, D. M., Byrne, J. P., Zucca, P., Bloomfield, D. S., McCauley, J. and Gallagher, P. T., 2013, “Quasiperiodic acceleration of electrons by a plasmoid-driven shock in the solar atmosphere”, Nature Phys., 9, 811–816. [DOI], [ADS]. (Cited on page 26.)
Chaplin, W. J., Dumbill, A. M., Elsworth, Y., Isaak, G. R., McLeod, C. P., Miller, B. A., New, R. and Pintér, B., 2003, “Studies of the solar mean magnetic field with the Birmingham Solar-Oscillations Network (BiSON)”, Mon. Not. R. Astron. Soc., 343, 813–818. [DOI], [ADS]. (Cited on page 76.)
Chen, F., Ding, M. D. and Chen, P. F., 2010, “Spectroscopic Analysis of an EIT Wave/dimming Observed by Hinode/EIS”, Astrophys. J., 720, 1254–1261. [DOI], [ADS]. (Cited on page 46.)
Chen, F., Ding, M. D., Chen, P. F. and Harra, L. K., 2011, “Spectroscopic Analysis of Interaction between an Extreme-ultraviolet Imaging Telescope Wave and a Coronal Upflow Region”, Astrophys. J., 740, 116. [DOI], [ADS], [1107.5630]. (Cited on page 46.)
Chen, P. F., 2006, “The Relation between EIT Waves and Solar Flares”, Astrophys. J. Lett., 641, L153–L156. [DOI], [ADS]. (Cited on page 55.)
Chen, P. F., 2009, “The Relation Between EIT Waves and Coronal Mass Ejections”, Astrophys. J. Lett., 698, L112–L115. [DOI], [ADS], [arXiv:0905.3272]. (Cited on page 58.)
Chen, P. F., 2011, “Coronal Mass Ejections: Models and Their Observational Basis”, Living Rev. Solar Phys., 8, lrsp-2011-1. [DOI], [ADS]. URL (accessed 20 September 2014): http://www.livingreviews.org/lrsp-2011-1. (Cited on page 57.)
Chen, P. F. and Wu, Y., 2011, “First Evidence of Coexisting EIT Wave and Coronal Moreton Wave from SDO/AIA Observations”, Astrophys. J. Lett., 732, L20. [DOI], [ADS]. (Cited on pages 33 and 35.)
Chen, P. F., Wu, S. T., Shibata, K. and Fang, C., 2002, “Evidence of EIT and Moreton Waves in Numerical Simulations”, Astrophys. J. Lett., 572, L99–L102. [DOI], [ADS]. (Cited on pages 37, 69, 71, and 73.)
Chen, P. F., Ding, M. D. and Fang, C., 2005a, “Synthesis of CME-Associated Moreton and EIT Wave Features from MHD Simulations”, Space Sci. Rev., 121, 201–211. [DOI], [ADS]. (Cited on page 38.)
Chen, P. F., Fang, C. and Shibata, K., 2005b, “A Full View of EIT Waves”, Astrophys. J., 622, 1202–1210. [DOI], [ADS]. (Cited on pages 49, 50, 69, 71, 72, and 73.)
Cheng, X., Zhang, J., Olmedo, O., Vourlidas, A., Ding, M. D. and Liu, Y., 2012, “Investigation of the Formation and Separation of an Extreme-ultraviolet Wave from the Expansion of a Coronal Mass Ejection”, Astrophys. J. Lett., 745, L5. [DOI], [ADS]. (Cited on pages 33, 38, 60, and 66.)
Cho, K.-S., Lee, J., Moon, Y.-J., Dryer, M., Bong, S.-C., Kim, Y.-H. and Park, Y. D., 2007, “A study of CME and type II shock kinematics based on coronal density measurement”, Astron. Astrophys., 461, 1121–1125. [DOI], [ADS]. (Cited on page 27.)
Ciaravella, A., Raymond, J. C., Kahler, S. W., Vourlidas, A. and Li, J., 2005, “Detection and Diagnostics of a Coronal Shock Wave Driven by a Partial-Halo Coronal Mass Ejection on 2000 June 28”, Astrophys. J., 621, 1121–1128. [DOI], [ADS]. (Cited on page 18.)
Cliver, E. W., Webb, D. F. and Howard, R. A., 1999, “On the origin of solar metric type II bursts”, Solar Phys., 187, 89–114. [DOI], [ADS]. (Cited on page 58.)
Cliver, E. W., Laurenza, M., Storini, M. and Thompson, B. J., 2005, “On the Origins of Solar EIT Waves”, Astrophys. J., 631, 604–611. [DOI], [ADS]. (Cited on pages 55 and 58.)
Cohen, O., Attrill, G. D. R., Manchester, W. B. and Wills-Davey, M. J., 2009, “Numerical Simulation of an EUV Coronal Wave Based on the 2009 February 13 CME Event Observed by STEREO”, Astrophys. J., 705, 587–602. [DOI], [ADS], [arXiv:0909.3095]. (Cited on pages 67 and 73.)
Culhane, J. L., Harra, L. K., James, A. M. et al., 2007, “The EUV Imaging Spectrometer for Hinode”, Solar Phys., 243, 19–61. [DOI], [ADS]. (Cited on page 12.)
Dai, Y., Auchère, F., Vial, J.-C., Tang, Y. H. and Zong, W. G., 2010, “Large-scale Extreme-Ultraviolet Disturbances Associated with a Limb Coronal Mass Ejection”, Astrophys. J., 708, 913–919. [DOI], [ADS]. (Cited on pages 44 and 58.)
Dai, Y., Ding, M. D., Chen, P. F. and Zhang, J., 2012, “Quadrature Observations of Wave and Non-wave Components and their Decoupling in an Extreme-ultraviolet Wave Event”, Astrophys. J., 759, 55. [DOI], [ADS]. (Cited on page 33.)
de Toma, G., Holzer, T. E., Burkepile, J. T. and Gilbert, H. R., 2005, “Transient coronal holes as seen in the He i 1083 nm MLSO observations”, Astrophys. J., 621, 1109–1120. [DOI], [ADS]. (Cited on page 27.)
Delaboudinière, J.-P., Artzner, G. E., Brunaud, J. et al., 1995, “EIT: Extreme-Ultraviolet Imaging Telescope for the SOHO Mission”, Solar Phys., 162, 291–312. [DOI], [ADS]. (Cited on pages 5 and 12.)
Delannée, C., 2000, “Another View of the EIT Wave Phenomenon”, Astrophys. J., 545, 512–523. [DOI], [ADS]. (Cited on pages 50 and 68.)
Delannée, C., 2009, “The role of small versus large scale magnetic topologies in global waves”, Astron. Astrophys., 495, 571–575. [DOI], [ADS]. (Cited on page 71.)
Delannée, C. and Aulanier, G., 1999, “CME Associated with Transequatorial Loops and a Bald Patch Flare”, Solar Phys., 190, 107–129. [DOI], [ADS]. (Cited on pages 5, 27, 50, and 68.)
Delannée, C., Hochedez, J.-F. and Aulanier, G., 2007, “Stationary parts of an EIT and Moreton wave: a topological model”, Astron. Astrophys., 465, 603–612. [DOI], [ADS]. (Cited on page 50.)
Delannée, C., Török, T., Aulanier, G. and Hochedez, J.-F., 2008, “A New Model for Propagating Parts of EIT Waves: A Current Shell in a CME”, Solar Phys., 247, 123–150. [DOI], [ADS]. (Cited on page 70.)
Delannée, C., Artzner, G., Schmieder, B. and Parenti, S., 2014, “Time Evolution of the Altitude of an Observed Coronal Wave”, Solar Phys., 289, 2565–2585. [DOI], [ADS], [arXiv:1310.5623 [astro-ph.SR]]. (Cited on pages 12, 18, 32, and 70.)
Dodson, H. W., 1949, “Position and Development of the Solar Flares of May 8 and 10, 1949.”, Astrophys. J., 110, 382–386. [DOI], [ADS]. (Cited on page 5.)
Downs, C., Roussev, I. I., van der Holst, B., Lugaz, N. and Gombosi, T. I., 2011, “Studying extreme Ultraviolet wave transients with a digital laboratory: direct comparison of extreme ultraviolet wave observations to global magnetohydrodynamic simulations”, Astrophys. J., 728, 2. [DOI], [ADS]. (Cited on pages 65, 67, and 73.)
Downs, C., Roussev, I. I., van der Holst, B., Lugaz, N. and Sokolov, I. V., 2012, “Understanding SDO/AIA Observations of the 2010 June 13 EUV Wave Event: Direct Insight from a Global Thermodynamic MHD Simulation”, Astrophys. J., 750, 10.1088/0004-637X/750/2/134. [ADS]. (Cited on pages 33, 45, 62, 67, 73, 74, and 75.)
Dresing, N., Gómez-Herrero, R., Klassen, A., Heber, B., Kartavykh, Y. and Dröge, W., 2012, “The Large Longitudinal Spread of Solar Energetic Particles During the 17 January 2010 Solar Event”, Solar Phys., 281, 281–300. [DOI], [ADS], [arXiv:1206.1520 [astro-ph.SR]]. (Cited on page 78.)
Dulk, G. A. and Marsh, K. A., 1982, “Simplified expressions for the gyrosynchrotron radiation from mildly relativistic, nonthermal and thermal electrons”, Astrophys. J., 259, 350–358. [DOI], [ADS]. (Cited on page 21.)
Eto, S., Isobe, H., Narukage, N. et al., 2002, “Relation between a Moreton Wave and an EIT Wave Observed on 1997 November 4”, Publ. Astron. Soc. Japan, 54, 481–491. [DOI], [ADS]. (Cited on page 51.)
Fisher, R. R., Lee, R. H., MacQueen, R. M. and Poland, A. I., 1981, “New Mauna Loa coronagraph systems”, Appl. Opt., 20, 1094–1101. [DOI], [ADS]. (Cited on page 12.)
Foley, C. R., Harra, L. K., Matthews, S. A., Culhane, J. L. and Kitai, R., 2003, “Evidence for a Flux Rope driven EUV wave and CME: Comparison with the Piston Shock Model”, Astron. Astrophys., 399, 749–754. [DOI]. (Cited on page 58.)
Francile, C., Costa, A., Luoni, M. L. and Elaskar, S., 2013, “Hα Moreton waves observed on December 06, 2006. A 2D case study”, Astron. Astrophys., 552, A3. [DOI], [ADS]. (Cited on page 37.)
Gallagher, P. T. and Long, D. M., 2011, “Large-scale Bright Fronts in the Solar Corona: A Review of ‘EIT waves’”, Space Sci. Rev., 158, 365–396. [DOI], [ADS], [arXiv:1006.0140]. (Cited on page 5.)
Gilbert, H. R. and Holzer, T. E., 2004, “Chromospheric Waves Observed in the He i Spectral Line (λ = 10830 Å): A Closer Look”, Astrophys. J., 610, 572–587. [DOI], [ADS]. (Cited on pages 7, 21, 27, 35, 56, and 57.)
Gilbert, H. R., Holzer, T. E., Thompson, B. J. and Burkepile, J. T., 2004, “A Comparison of CME-Associated Atmospheric Waves Observed in Coronal (Fe XII 195 Å) and Chromospheric (He I 10830 Å) Lines”, Astrophys. J., 607, 540–553. [DOI], [ADS]. (Cited on pages 21 and 38.)
Gilbert, H. R., Daou, A. G., Young, D., Tripathi, D. and Alexander, D., 2008, “The Filament-Moreton Wave Interaction of 2006 December 6”, Astrophys. J., 685, 629–645. [DOI], [ADS]. (Cited on pages 21, 51, and 53.)
Golub, L., Deluca, E., Austin, G. et al., 2007, “The X-Ray Telescope (XRT) for the Hinode Mission”, Solar Phys., 243, 63–86. [DOI], [ADS]. (Cited on page 17.)
Gopalswamy, N., Kundu, M. R., Manoharan, P. K., Raoult, A., Nitta, N. and Zarka, P., 1997, “X-Ray and Radio Studies of a Coronal Eruption: Shock Wave, Plasmoid, and Coronal Mass Ejection”, Astrophys. J., 489, 1036–1044. [DOI], [ADS]. (Cited on page 63.)
Gopalswamy, N., Kaiser, M. L., Sato, J. and Pick, M., 2000a, “Shock Wave and EUV Transient During a Flare”, in High Energy Solar Physics: Anticipating HESSI, Proceedings of the workshop held at the University of Maryland, October 18–20, 1999, (Eds.) Ramaty, R., Mandzhavidze, N., ASP Conference Series, 206, pp. 351–354, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on pages 15 and 41.)
Gopalswamy, N., Kaiser, M. L., Thompson, B. J. et al., 2000b, “Radio-rich solar eruptive events”, Geophys. Res. Lett., 27, 1427–1430. [DOI], [ADS]. (Cited on pages 24 and 57.)
Gopalswamy, N., Lara, A., Kaiser, M. L. and Bougeret, J.-L., 2001a, “Near-Sun and near-Earth manifestations of solar eruptions”, J. Geophys. Res., 106(A11), 25 261–25 278. [DOI], [ADS]. (Cited on page 76.)
Gopalswamy, N., St Cyr, O. C., Kaiser, M. L. and Yashiro, S., 2001b, “X-ray Ejecta, White-Light CMEs and a Coronal Shock Wave”, Solar Phys., 203, 149–163. [DOI], [ADS]. (Cited on page 63.)
Gopalswamy, N., Yashiro, S., Temmer, M. et al., 2009, “EUV Wave Reflection from a Coronal Hole”, Astrophys. J. Lett., 691, L123–L127.[DOI], [ADS]. (Cited on page 48.)
Gopalswamy, N., Nitta, N., Akiyama, S., Mäkelä, P. and Yashiro, S., 2012, “Coronal Magnetic Field Measurement from EUV Images Made by the Solar Dynamics Observatory”, Astrophys. J., 744, 72–78. [DOI], [ADS], [1109.2925 [astro-ph.SR]]. (Cited on pages 76 and 77.)
Gosain, S. and Foullon, C., 2012, “Dual Trigger of Transverse Oscillations in a Prominence by EUV Fast and Slow Coronal Waves: SDO/AIA and STEREO/EUVI Observations”, Astrophys. J., 761, 103. [DOI], [ADS], [arXiv:1210.6690 [astro-ph.SR]]. (Cited on page 51.)
Grechnev, V. V., Uralov, A. M., Slemzin, V. A., Chertok, I. M., Kuzmenko, I. V. and Shibasaki, K., 2008, “Absorption Phenomena and a Probable Blast Wave in the 13 July 2004 Eruptive Event”, Solar Phys., 253, 263–290. [DOI], [ADS], [arXiv:0811.0899]. (Cited on pages 38 and 66.)
Grechnev, V. V., Afanasyev, A. N., Uralov, A. M., Chertok, I. M., Eselvich, M. V., Eselvich, V. G., Rudenko, G. V. and Kubo, Y., 2011a, “Coronal Shock Waves, EUV Waves, and Their Relation to CMEs. III. Shock-Associated CME/EUV Wave in an Event with a Two-Component EUV Transient”, Solar Phys., 273, 461–477. [DOI], [ADS], [arXiv:1104.3375 [astro-ph.SR]]. (Cited on pages 25, 26, 33, 38, 41, and 66.)
Grechnev, V. V., Uralov, A. M., Chertok, I. M., Kuzmenko, I. V., Afanasyev, A. N., Meshalkina, N. S., Kalashnikov, S. S. and Kubo, Y., 2011b, “Coronal shock waves, EUV waves, and their relation to CMEs. I. Reconciliation of ‘EIT waves’, type II radio bursts, and leading edges of CMEs”, Solar Phys., 273, 433–460. [DOI], [ADS]. (Cited on pages 25, 33, 35, 38, 65, and 66.)
Halain, J.-P., Berghmans, D., Defise, J.-M. et al., 2010, “First light of SWAP on-board PROBA2”, in Space Telescopes and Instrumentation 2010: Ultraviolet to Gamma Ray, San Diego, California, USA, June 27, 2010, (Eds.) Arnaud, M., Murray, S. S., Takahashi, T., Proc. SPIE, 7732, 77320P, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on page 15.)
Handy, B. N., Acton, L. W., Kankelborg, C. C. et al., 1999, “The Transition Region and Coronal Explorer”, Solar Phys., 187, 229–260. [DOI], [ADS]. (Cited on page 15.)
Harra, L. K. and Sterling, A. C., 2003, “Imaging and Spectroscopic Investigations of a Solar Coronal Wave: Properties of the Wave Front and Associated Erupting Material”, Astrophys. J., 587, 429–438. [DOI], [ADS]. (Cited on pages 33 and 46.)
Harra, L. K., Hara, H., Imada, S., Young, P. R., Williams, D. R., Sterling, A. C., Korendyke, C. and Attrill, G. D. R., 2007, “Coronal Dimming Observed with Hinode: Outflows Related to a Coronal Mass Ejection”, Publ. Astron. Soc. Japan, 59, S801–S806. [DOI], [ADS]. (Cited on pages 27 and 46.)
Harra, L. K., Sterling, A. C., Gömöry, P. and Veronig, A., 2011, “Spectroscopic observations of a coronal Moreton wave”, Astrophys. J. Lett., 737, L4. [DOI], [ADS]. (Cited on page 46.)
Harrison, R. A., Sawyer, E. C., Carter, M. K. et al., 1995, “The Coronal Diagnostic Spectrometer for the Solar and Heliospheric Observatory”, Solar Phys., 162, 233–290. [DOI], [ADS]. (Cited on page 12.)
Harrison, R. A., Bryans, P., Simnett, G. M. and Lyons, M., 2003, “Coronal dimming and the coronal mass ejection onset”, Astron. Astrophys., 400, 1071–1083. [DOI], [ADS]. (Cited on page 27.)
Harvey, K. L., Martin, S. F. and Riddle, A. C., 1974, “Correlation of a Flare-Wave and Type II Burst”, Solar Phys., 36, 151–155. [DOI], [ADS]. (Cited on page 25.)
Hershaw, J., Foullon, C., Nakariakov, V. M. and Verwichte, E., 2011, “Damped large amplitude transverse oscillations in an EUV solar prominence, triggered by large-scale transient coronal waves”, Astron. Astrophys., 531, A53. [DOI], [ADS]. (Cited on page 51.)
Hill, S. M., Pizzo, V. J., Balch, C. C. et al., 2005, “The NOAA Goes-12 Solar X-Ray Imager (SXI) 1. Instrument, Operations, and Data”, Solar Phys., 226, 255–281. [DOI], [ADS]. (Cited on page 16.)
Hoilijoki, S., Pomoell, J., Vainio, R., Palmroth, M. and Koskinen, H. E. J., 2003, “Interpreting Solar EUV Wave Observations from Different Viewing Angles Using an MHD Model”, Solar Phys., 586, 606–616. [DOI], [ADS]. (Cited on pages 12 and 32.)
Howard, R. A., Moses, J. D., Vourlidas, A. et al., 2008, “Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI)”, Space Sci. Rev., 136, 67–115. [DOI], [ADS]. (Cited on pages 12 and 15.)
Hudson, H. S. and Warmuth, A., 2004, “Coronal Loop Oscillations and Flare Shock Waves”, Astrophys. J. Lett., 614, L85–L88. [DOI], [ADS]. (Cited on page 51.)
Hudson, H. S., Acton, L. W. and Freeland, S. L., 1996, “A Long-Duration Solar Flare with Mass Ejection and Global Consequences”, Astrophys. J., 470, 629. [DOI], [ADS]. (Cited on page 27.)
Hudson, H. S., Khan, J. I., Lemen, J. R., Nitta, N. V. and Uchida, Y., 2003, “Soft X-ray observation of a large-scale coronal wave and its exciter”, Solar Phys., 212, 121–149. [DOI], [ADS]. (Cited on pages 16, 31, 32, 33, 36, 43, 47, 57, 63, 66, and 76.)
Innes, D. E., Genetelli, A., Attie, R. and Potts, H. E., 2009, “Quiet Sun mini-coronal mass ejections activated by supergranular flows”, Astron. Astrophys., 495, 319–323. [DOI], [ADS], [arXiv:0811.2744]. (Cited on page 5.)
Kennel, C. F., Edmiston, J. P. and Hada, T., 1985, “A quarter century of collisionless shock research”, in Collisionless Shocks in the Heliosphere: A Tutorial Review, (Eds.) Stone, R. G., Tsurutani, B. T., Geophysical Monograph, 34, pp. 1–36, American Geophysical Union, Washington, DC. [DOI], [ADS]. (Cited on page 8.)
Kerdraon, A. and Delouis, J.-M., 1997, “The Nancay Radioheliograph”, in Coronal Physics from Radio and Space Observations, CESRA Workshop, Nouan le Fuzelier, France, 3–7 June 1996, (Ed.) Trottet, G., Lecture Notes in Physics, 483, pp. 192–201, Springer Verlag, Berlin; New York. [DOI], [ADS]. (Cited on pages 21 and 26.)
Kerdraon, A., Pick, M., Hoang, S., Wang, Y.-M. and Haggerty, D., 2010, “The Coronal and Heliospheric 2007 May 19 Event: Coronal Mass Ejection, Extreme Ultraviolet Imager Wave, Radio Bursts, and Energetic Electrons”, Astrophys. J., 715, 468–476. [DOI], [ADS]. (Cited on page 79.)
Khan, J. I. and Aurass, H., 2002, “X-ray observations of a large-scale solar coronal shock wave”, Astron. Astrophys., 383, 1018–1031. [DOI], [ADS]. (Cited on pages 16, 24, 26, 31, and 38.)
Kienreich, I. W., Temmer, M. and Veronig, A. M., 2009, “STEREO Quadrature Observations of the Three-Dimensional Structure and Driver of a Global Coronal Wave”, Astrophys. J. Lett., 703, L118–L122. [DOI], [ADS], [arXiv:0908.3571 [astro-ph.SR]]. (Cited on pages 30, 32, 33, 47, 59, 60, 66, and 76.)
Kienreich, I. W., Veronig, A. M., Muhr, N., Temmer, M., Vršnak, B. and Nitta, N., 2011, “Case Study of Four Homologous Large-scale Coronal Waves Observed on 2010 April 28 and 29”, Astrophys. J. Lett., 727, L43. [DOI], [ADS]. (Cited on pages 39, 41, 42, and 43.)
Kienreich, I. W., Muhr, N., Veronig, A. M., Berghmans, D., De Groof, A., Temmer, M., Vršnak, B. and Seaton, D. B., 2013, “Solar TErrestrial Relations Observatory-A (STEREO-A) and PRoject for OnBoard Autonomy 2 (PROBA2) Quadrature Observations of Reflections of Three EUV Waves from a Coronal Hole”, Solar Phys., 286, 201–219. [DOI], [ADS]. (Cited on pages 48 and 49.)
Klassen, A., Aurass, H., Mann, G. and Thompson, B. J., 2000, “Catalogue of the 1997 SOHO-EIT coronal transient waves and associated type II radio burst spectra”, Astron. Astrophys. Suppl., 141, 357–369. [DOI], [ADS]. (Cited on pages 5, 12, 25, and 36.)
Klassen, A., Pohjolainen, S. and Klein, K.-L., 2003, “Type II radio precursor and X-ray flare emission”, Solar Phys., 218, 197–210. [DOI], [ADS]. (Cited on page 63.)
Klein, K.-L., Khan, J. I., Vilmer, N., Delouis, J.-M. and Aurass, H., 1999, “X-ray and radio evidence on the origin of a coronal shock wave”, Astron. Astrophys., 346, L53–L56. [ADS]. (Cited on page 63.)
Kocharov, L. G., Lee, J. W., Zirin, H., Kovaltsov, G. A., Usoskin, I. G., Pyle, K. R., Shea, M. A. and Smart, D. F., 1994, “Neutron and electromagnetic emissions during the 1990 May 24 solar flare”, Solar Phys., 155, 149–170. [DOI]. (Cited on page 78.)
Kohl, J. L., Esser, R., Gardner, L. D. et al., 1995, “The Ultraviolet Coronagraph Spectrometer for the Solar and Heliospheric Observatory”, Solar Phys., 162, 313–356. [DOI], [ADS]. (Cited on page 12.)
Kouloumvakos, A., Patsourakos, S., Hillaris, A. et al., 2014, “CME Expansion as the Driver of Metric Type II Shock Emission as Revealed by Self-consistent Analysis of High-Cadence EUV Images and Radio Spectrograms”, Solar Phys., 289, 2123–2139. [DOI], [ADS], [arXiv:1311.5159 [astro-ph.SR]]. (Cited on page 27.)
Kozarev, K. A., Korreck, K. E., Lobzin, V. V., Weber, M. A. and Schwadron, N. A., 2011, “Off-limb solar coronal wavefronts from SDO/AIA extreme-ultraviolet observations — implications for particle production”, Astrophys. J. Lett., 733, L25. [DOI], [ADS]. (Cited on pages 25, 27, 38, 45, 46, 60, and 79.)
Kretzschmar, M., 2011, “The Sun as a star: observations of white-light flares”, Astron. Astrophys., 530, A84. [DOI], [ADS]. (Cited on page 54.)
Krucker, S., Larson, D. E., Lin, R. P. and Thompson, B. J., 1999, “On the Origin of Impulsive Electron Events Observed at 1 AU”, Astrophys. J., 519, 864–875. [DOI], [ADS]. (Cited on page 78.)
Kumar, P. and Innes, D. E., 2013, “Multiwavelength Observations of an Eruptive Flare: Evidence for Blast Waves and Break-Out”, Solar Phys., 288, 255–268. [DOI], [ADS], [arXiv:1307.3720 [astro-ph.SR]]. (Cited on page 64.)
Kumar, P. and Manoharan, P. K., 2013, “Eruption of a plasma blob, associated M-class flare, and large-scale extreme-ultraviolet wave observed by SDO”, Astron. Astrophys., 553, A109. [DOI], [ADS], [arXiv:1304.0165 [astro-ph.SR]]. (Cited on pages 25, 63, and 64.)
Kumar, P., Cho, K.-S., Chen, P. F., Bong, S.-C. and Park, S.-H., 2013, “Multiwavelength Study of a Solar Eruption from AR NOAA 11112: II. Large-Scale Coronal Wave and Loop Oscillation”, Solar Phys., 282, 523–541. [DOI], [ADS]. (Cited on page 25.)
Kwon, R.-Y., Kramar, M., Wang, T., Ofman, L., Davila, J. M., Chae, J. and Zhang, J., 2013a, “Global Coronal Seismology in the Extended Solar Corona through Fast Magnetosonic Waves Observed by STEREO SECCHI COR1”, Astrophys. J., 776, 55. [DOI], [ADS]. (Cited on page 76.)
Kwon, R.-Y., Ofman, L., Olmedo, O., Kramar, M., Davila, J. M., Thompson, B. J. and Cho, K.-S., 2013b, “STEREO Observations of Fast Magnetosonic Waves in the Extended Solar Corona Associated with EIT/EUV Waves”, Astrophys. J., 766, 55. [DOI], [ADS]. (Cited on pages 18, 32, 50, 52, and 76.)
Landau, L. D. and Lifshitz, E. M., 1959, Fluid Mechanics, Course of Theoretical Physics, 6, Pergamon; Addison-Wesley, London; Reading, MA. [ADS]. (Cited on page 8.)
Lemen, J. R., Title, A. M., Akin, D. J. et al., 2012, “The Atmospheric Imaging Assembly (AIA) on the Solar Dynamics Observatory (SDO)”, Solar Phys., 275, 17–40. [DOI], [ADS]. (Cited on pages 15 and 44.)
Li, T., Zhang, J., Yang, S. and Liu, W., 2012, “SDO/AIA Observations of Secondary Waves Generated by Interaction of the 2011 June 7 Global EUV Wave with Solar Coronal Structures”, Astrophys. J. Lett., 746, L13. [DOI], [ADS]. (Cited on pages 33, 48, 49, and 60.)
Lin, R. P., Dennis, B. R., Hurford, G. J. et al., 2002, “The Reuven Ramaty High-Energy Solar Spectroscopic Imager (RHESSI)”, Solar Phys., 210, 3–32. [DOI], [ADS]. (Cited on page 54.)
Liu, C., Lee, J., Deng, N., Gary, D. E. and Wang, H., 2006, “Large-Scale Activities Associated with the 2003 October 29 X10 Flare”, Astrophys. J., 642, 1205–1215. [DOI], [ADS]. (Cited on page 31.)
Liu, R., Liu, C., Xu, Y., Liu, W., Kliem, B. and Wang, H., 2013, “Observation of a Moreton Wave and Wave-Filament Interactions Associated with the Renowned X9 Flare on 1990 May 24”, Astrophys. J., 773, 166. [DOI], [ADS]. (Cited on page 50.)
Liu, W. and Ofman, L., 2014, “Advances in Observing Various Coronal EUV Waves in the SDO Era and Their Seismological Applications (Invited Review)”, Solar Phys., 289, 3233–3277. [DOI], [ADS], [arXiv:1404.0670 [astro-ph.SR]]. (Cited on pages 5, 33, 35, 40, 52, and 78.)
Liu, W., Nitta, N. V., Schrijver, C. J., Title, A. M. and Tarbell, T. D., 2010, “First SDO AIA Observations of a Global Coronal EUV ‘Wave’: Multiple Components and Ripples”, Astrophys. J. Lett., 723, L53–L59. [DOI], [ADS]. (Cited on pages 5, 35, and 44.)
Liu, W., Title, A. M., Zhao, J., Ofman, L., Schrijver, C. J., Aschwanden, M. J., De Pontieu, B. and Tarbell, T. D., 2011, “Direct Imaging of Quasi-periodic Fast Propagating Waves of ∼2000 km s−1 in the Low Solar Corona by the Solar Dynamics Observatory Atmospheric Imaging Assembly”, Astrophys. J. Lett., 736, L13. [DOI], [ADS], [arXiv:1106.3150 [astro-ph.SR]]. (Cited on pages 5 and 39.)
Liu, W., Ofman, L., Nitta, N. V., Aschwanden, M. J., Schrijver, C. J., Title, A. M. and Tarbell, T. D., 2012, “Quasi-periodic Fast-mode Wave Trains within a Global EUV Wave and Sequential Transverse Oscillations Detected by SDO/AIA”, Astrophys. J. Lett., 753, L52. [DOI], [ADS]. (Cited on pages 32, 35, 38, 47, 49, 52, 53, 66, and 76.)
Long, D. M., Gallagher, P. T., McAteer, R. T. J. and Bloomfield, D. S., 2008, “The Kinematics of a Globally Propagating Disturbance in the Solar Corona”, Astrophys. J. Lett., 680, L81–L84. [DOI], [ADS], [arXiv:0805.2023]. (Cited on pages 44, 45, 48, and 59.)
Long, D. M., DeLuca, E. E. and Gallagher, P. T., 2011a, “The wave properties of coronal bright fronts observed using SDO/AIA”, Astrophys. J., 741, L21. [DOI], [ADS]. (Cited on pages 38, 44, and 45.)
Long, D. M., Gallagher, P. T., McAteer, R. T. J. and Bloomfield, D. S., 2011b, “Deceleration and dispersion of large-scale coronal bright fronts”, Astron. Astrophys., 531, A42. [DOI], [ADS]. (Cited on pages 38 and 41.)
Long, D. M., Williams, D. R., Regnier, S. and Harra, L. K., 2013, “Measuring the Magnetic-Field Strength of the Quiet Solar Corona Using ‘EIT Waves’”, Solar Phys., 288, 567–583. [DOI], [ADS]. (Cited on page 76.)
Long, D. M., Bloomfield, D. S., Gallagher, P. T. and Pérez-Suárez, D., 2014, “CorPITA: An Automated Algorithm for the Identification and Analysis of Coronal ‘EIT Waves’”, Solar Phys., 289, 3279–3295. [DOI], [ADS], [arXiv:1403.6722 [astro-ph.SR]]. (Cited on pages 28 and 36.)
Lulić, S., Vršnak, B., Žic, T., Kienreich, I. W., Muhr, N., Temmer, M. and Veronig, A. M., 2013, “Formation of Coronal Shock Wavesa”, Solar Phys., 286, 509–528. [DOI], [ADS]. (Cited on pages 9 and 62.)
Ma, S., Wills-Davey, M. J., Lin, J. et al., 2009, “A New View of Coronal Waves from STEREO”, Astrophys. J., 707, 503–509. [DOI], [ADS]. (Cited on pages 12, 32, and 39.)
Ma, S., Raymond, J. C., Golub, L., Lin, J., Chen, H., Grigis, P., Testa, P. and Long, D., 2011, “Observations and Interpretation of a Low Coronal Shock Wave Observed in the EUV by the SDO/AIA”, Astrophys. J., 738, 160. [DOI], [ADS]. (Cited on pages 25, 27, 33, 41, 45, 60, 61, and 62.)
MacQueen, R. M., Blankner, J. G., Elmore, D. F., Lecinski, A. R. and White, O. R., 1998, “Initial CHIP He i Observations of Solar Limb Activity”, Solar Phys., 182, 97–105. [DOI], [ADS]. (Cited on page 20.)
Magdalenić, J., Vršnak, B., Pohjolainen, S., Temmer, M., Aurass, H. and Lehtinen, N. J., 2008, “A Flare-Generated Shock during a Coronal Mass Ejection on 24 December 1996”, Solar Phys., 253, 305–317. [DOI], [ADS]. (Cited on pages 27 and 57.)
Maia, D., Aulanier, G., Wang, S. J., Pick, M., Malherbe, J.-M. and Delaboudinière, J.-P., 2003, “Interpretation of a complex CME event: Coupling of scales in multiple flux systems”, Astron. Astrophys., 405, 313–323. [DOI], [ADS]. (Cited on page 58.)
Mancuso, S., 2007, “Coronal transients and metric type II radio bursts. II. Accelerations at low coronal heights”, Astron. Astrophys., 463, 1137–1141. [DOI], [ADS]. (Cited on page 27.)
Mancuso, S., Raymond, J. C., Kohl, J., Ko, Y.-K., Uzzo, M. and Wu, R., 2002, “UVCS/SOHO observations of a CME-driven shock: Consequences on ion heating mechanisms behind a coronal shock”, Astron. Astrophys., 383, 267–274. [DOI], [ADS]. (Cited on page 18.)
Mandrini, C. H., Pohjolainen, S., Dasso, S., Green, L. M., Démoulin, P., van Driel-Gesztelyi, L., Copperwheat, C. and Foley, C., 2005, “Interplanetary flux rope ejected from an X-ray bright point. The smallest magnetic cloud source-region ever observed”, Astron. Astrophys., 434, 725–740. [DOI], [ADS]. (Cited on page 27.)
Mann, G., 1995, “On simple magnetohydrodynamic waves”, J. Plasma Phys., 53, 109–125. [DOI], [ADS]. (Cited on page 8.)
Mann, G. and Warmuth, A., 2011, “Budget of energetic electrons during solar flares in the framework of magnetic reconnection”, Astron. Astrophys., 528, A104. [DOI], [ADS]. (Cited on page 54.)
Mann, G., Jansen, F., MacDowall, R. J., Kaiser, M. L. and Stone, R. G., 1999a, “A heliospheric density model and type III radio bursts”, Astron. Astrophys., 348, 614–620. [ADS]. (Cited on pages 32 and 76.)
Mann, G., Klassen, A., Estel, C. and Thompson, B. J., 1999b, “Coronal Transient Waves and Coronal Shock Waves”, in Plasma Dynamics and Diagnostics in the Solar Transition Region and Corona, Proceedings of the 8th SOHO Workshop, 22–25 June 1999, Paris, France, (Eds.) Vial, J.-C., Kaldeich-Schümann, B., ESA Special Publication, SP-446, pp. 477–481, ESA Publications Division, Noordwijk. [ADS]. (Cited on pages 33, 47, 66, and 76.)
Mann, G., Klassen, A., Aurass, H. and Classen, H.-T., 2003, “Formation and development of shock waves in the solar corona and the near-Sun interplanetary space”, Astron. Astrophys., 400, 329–336. [DOI], [ADS]. (Cited on pages 25 and 76.)
Maričić, D., Vršnak, B., Stanger, A. L., Veronig, A. M., Temmer, M. and Roša, D., 2007, “Acceleration Phase of Coronal Mass Ejections: II. Synchronization of the Energy Release in the Associated Flare”, Solar Phys., 241, 99–112. [DOI], [ADS]. (Cited on page 56.)
Miteva, R. and Mann, G., 2008, “On nonlinear waves in Hall MHD plasma”, J. Plasma Phys., 74, 607–628. [DOI]. (Cited on page 68.)
Miteva, R., Klein, K.-L., Kienreich, I., Temmer, M., Veronig, A. and Malandraki, O. E., 2014, “Solar Energetic Particles and Associated EIT Disturbances in Solar Cycle 23”, Solar Phys., 289, 2601–2631. [DOI], [ADS], [1402.1676]. (Cited on page 79.)
Moon, Y.-J., Choe, G. S., Park, Y. D., Wang, H., Gallagher, P. T., Chae, J., Yun, H. S. and Goode, P. R., 2002, “Statistical Evidence for Sympathetic Flares”, Astrophys. J., 574, 434–439. [DOI], [ADS]. (Cited on page 53.)
Moreton, G. E., 1960, “Hα Observations of Flare-Initiated Disturbances with Velocities ∼1000 km/sec”, Astron. J., 65, 494–495. [DOI], [ADS]. (Cited on pages 5, 18, and 50.)
Moreton, G. E., 1964, “Hα Shock Wave and Winking Filaments with the Flare of 20 September 1963”, Astron. J., 69, 145. [DOI], [ADS]. (Cited on pages 18, 25, and 50.)
Moreton, G. E. and Ramsey, H. E., 1960, “Recent Observations of Dynamical Phenomena Associated with Solar Flares”, Publ. Astron. Soc. Pac., 72, 357–358. [DOI], [ADS]. (Cited on pages 5 and 18.)
Moses, D., Clette, F., Delaboudinière, J.-P. et al., 1997, “EIT Observations of the Extreme Ultraviolet Sun”, Solar Phys., 175, 571–599. [DOI], [ADS]. (Cited on pages 5 and 12.)
Muhr, N., Vršnak, B., Temmer, M., Veronig, A. M. and Magdalenić, J., 2010, “Analysis of a Global Moreton Wave Observed on 2003 October 28”, Astrophys. J., 708, 1639–1649. [DOI], [ADS]. (Cited on pages 26, 31, and 37.)
Muhr, N., Veronig, A. M., Kienreich, I. W., Temmer, M. and Vršnak, B., 2011, “Analysis of Characteristic Parameters of Large-scale Coronal Waves Observed by the Solar-Terrestrial Relations Observatory/Extreme Ultraviolet Imager”, Astrophys. J., 739, 89. [DOI], [ADS]. (Cited on pages 27, 41, and 42.)
Muhr, N., Veronig, A. M., Kienreich, I. W., Vršnak, B., Temmer, M. and Bein, B. M., 2014, “Statistical Analysis of Large-scale EUV Waves Observed by STEREO/EUVI”, Solar Phys., 289, 4563–4588. [DOI], [ADS], [arXiv:1408.2513]. (Cited on pages 25, 28, 36, 39, 40, 41, 56, and 57.)
Murawski, K., Nakariakov, V. M. and Pelinovsky, E. N., 2001, “Fast magnetoacoustic waves in a randomly structured solar corona”, Astron. Astrophys., 366, 306–310. [DOI], [ADS]. (Cited on page 67.)
Nakajima, H., Nishio, M., Enome, S. et al., 1994, “The Nobeyama radioheliograph”, Proc. IEEE, 82, 705–713. [DOI], [ADS]. (Cited on page 22.)
Nakariakov, V. M. and Verwichte, E., 2005, “Coronal Waves and Oscillations”, Living Rev. Solar Phys., 2, lrsp-2005-3. [DOI], [ADS]. URL (accessed 20 September 2014): http://www.livingreviews.org/lrsp-2005-3. (Cited on page 76.)
Narukage, N., Hudson, H. S., Morimoto, T., Akiyama, S., Kitai, R., Kurokawa, H. and Shibata, K., 2002, “Simultaneous Observation of a Moreton Wave on 1997 November 3 in Hα and Soft X-Rays”, Astrophys. J., 572, L109–L112. [DOI], [ADS]. (Cited on pages 16, 31, and 43.)
Narukage, N., Morimoto, T., Kadota, M., Kitai, R., Kurokawa, H. and Shibata, K., 2004, “X-Ray Expanding Features Associated with a Moreton Wave”, Publ. Astron. Soc. Japan, 56, L5–L8. [DOI], [ADS]. (Cited on pages 16, 33, 34, 41, 43, and 63.)
Narukage, N., Ishii, T. T., Nagata, S., UeNo, S., Kitai, R., Kurokawa, H., Akioka, M. and Shibata, K., 2008, “Three Successive and Interacting Shock Waves Generated by a Solar Flare”, Astrophys. J. Lett., 684, L45–L49. [DOI], [ADS]. (Cited on pages 20, 31, 35, 37, and 58.)
Nelson, G. J. and Melrose, D. B., 1985, “Type II bursts”, in Solar Radiophysics: Studies of Emission from the Sun at Metre Wavelengths, (Eds.) McLean, D. J., Labrum, N. R., pp. 333–359, Cambridge University Press, Cambridge; New York. [ADS]. (Cited on page 24.)
Neupert, W. M., 1989, “Transient coronal extreme ultraviolet emission before and during the impulsive phase of a solar flare”, Astrophys. J., 344, 504–512. [DOI], [ADS]. (Cited on page 12.)
Newkirk, G., 1961, “The Solar Corona in Active Regions and the Thermal Origin of the Slowly Varying Component of Solar Radio Radiation”, Astrophys. J., 133, 983–1013. [DOI], [ADS]. (Cited on page 76.)
Nitta, N. V., Schrijver, C. J., Title, A. M. and Liu, W., 2013, “Large-scale Coronal Propagating Fronts in Solar Eruptions as Observed by the Atmospheric Imaging Assembly on board the Solar Dynamics Observatory — an Ensemble Study”, Astrophys. J., 776, 58. [DOI], [ADS]. (Cited on pages 25, 28, 37, 39, 40, 44, 55, 56, and 57.)
Nitta, N. V., Aschwanden, M. J., Freeland, S. L., Lemen, J. R., Wülser, J.-P. and Zarro, D. M., 2014, “The Association of Solar Flares with Coronal Mass Ejections During the Extended Solar Minimum”, Solar Phys., 289, 1257–1277. [DOI], [ADS], [1308.1465]. (Cited on pages 28, 36, 37, 40, 44, and 57.)
Ofman, L. and Thompson, B. J., 2002, “Interaction of EIT Waves with Coronal Active Regions”, Astrophys. J., 574, 440–452. [DOI], [ADS]. (Cited on pages 47, 50, and 53.)
Ohyama, M. and Shibata, K., 1998, “X-Ray Plasma Ejection Associated with an Impulsive Flare on 1992 October 5: Physical Conditions of X-Ray Plasma Ejection”, Astrophys. J., 499, 934–944. [DOI], [ADS]. (Cited on page 63.)
Okamoto, T. J., Nakai, H., Keiyama, A., Narukage, N., UeNo, S., Kitai, R., Kurokawa, H. and Shibata, K., 2004, “Filament Oscillations and Moreton Waves Associated with EIT Waves”, Astrophys. J., 608, 1124–1132. [DOI], [ADS]. (Cited on page 50.)
Olmedo, O., Vourlidas, A., Zhang, J. and Cheng, X., 2012, “Secondary Waves and/or the ‘Reflection’ from and ‘Transmission’ through a Coronal Hole of an Extreme Ultraviolet Wave Associated with the 2011 February 15 X2.2 Flare Observed with SDO/AIA and STEREO/EUVIs”, Astrophys. J., 756, 143. [DOI], [ADS]. (Cited on pages 38, 48, and 49.)
Park, J., Innes, D. E., Bucik, R. and Moon, Y.-J., 2013, “The Source Regions of Solar Energetic Particles Detected by Widely Separated Spacecraft”, Astrophys. J., 779, 184. [DOI], [ADS]. (Cited on pages 78 and 79.)
Patsourakos, S. and Vourlidas, A., 2009, “‘Extreme Ultraviolet Waves’ are Waves: First Quadrature Observations of an Extreme Ultraviolet Wave from STEREO”, Astrophys. J. Lett., 700, L182–L186. [DOI], [ADS], [arXiv:0905.2164 [astro-ph.SR]]. (Cited on pages 32, 33, 39, 47, 52, 59, 60, 66, and 76.)
Patsourakos, S. and Vourlidas, A., 2012, “On the Nature and Genesis of EUV Waves: A Synthesis of Observations from SOHO, STEREO, SDO, and Hinode (Invited Review)”, Solar Phys., 281, 187–222. [DOI], [ADS]. (Cited on pages 5, 53, 54, 60, and 62.)
Patsourakos, S., Vourlidas, A., Wang, Y. M., Stenborg, G. and Thernisien, A., 2009, “What Is the Nature of EUV Waves? First STEREO 3D Observations and Comparison with Theoretical Models”, Solar Phys., 259, 49–71. [DOI], [ADS], [arXiv:0905.2189 [astro-ph.SR]]. (Cited on pages 32, 45, 59, 67, and 71.)
Patsourakos, S., Vourlidas, A. and Kliem, B., 2010a, “Toward understanding the early stages of an impulsively accelerated coronal mass ejection”, Astron. Astrophys., 522, A100. [DOI], [ADS]. (Cited on pages 60, 61, and 62.)
Patsourakos, S., Vourlidas, A. and Stenborg, G., 2010b, “The Genesis of an Impulsive Coronal Mass Ejection Observed at Ultra-high Cadence by AIA on SDO”, Astrophys. J., 724, L188–L193. [DOI], [ADS], [arXiv:1010.5234 [astro-ph.SR]]. (Cited on pages 60 and 62.)
Payne-Scott, R., Yabsley, D. E. and Bolton, J. G., 1947, “Relative Times of Arrival of Bursts of Solar Noise on Different Radio Frequencies”, Nature, 160, 256–257. [DOI], [ADS]. (Cited on pages 5 and 23.)
Pick, M., Malherbe, J.-M., Kerdraon, A. and Maia, D. J. F., 2005, “On the disk Hα and radio observations of the 2003 October 28 flare and coronal mass ejection event”, Astrophys. J. Lett., 631, L97–L100. [DOI], [ADS]. (Cited on page 31.)
Pizzo, V. J., Hill, S. M., Balch, C. C. et al., 2005, “The NOAA Goes-12 Solar X-Ray Imager (SXI) 2. Performance”, Solar Phys., 226, 283–315. [DOI], [ADS]. (Cited on page 16.)
Podladchikova, O. and Berghmans, D., 2005, “Automated Detection Of EIT Waves And Dimmings”, Solar Phys., 228, 265–284. [DOI], [ADS]. (Cited on pages 28 and 70.)
Podladchikova, O., Vourlidas, A., van der Linden, R. A. M., Wülser, J.-P. and Patsourakos, S., 2010, “Extreme Ultraviolet Observations and Analysis of Micro-Eruptions and Their Associated Coronal Waves”, Astrophys. J., 709, 369–376. [DOI], [ADS]. (Cited on pages 5 and 7.)
Podladchikova, O., Vuets, A., Leontiev, P. and van der Linden, R. A. M., 2012, “Recent Developments of NEMO: Detection of EUV Wave Characteristics”, Solar Phys., 276, 479–490. [DOI], [ADS]. (Cited on page 28.)
Pohjolainen, S., Maia, D., Pick, M. et al., 2001, “On-the-Disk Development of the Halo Coronal Mass Ejection on 1998 May 2”, Astrophys. J., 556, 421–431. [DOI], [ADS]. (Cited on page 26.)
Pohjolainen, S., Hori, K. and Sakurai, T., 2008, “Radio Bursts Associated with Flare and Ejecta in the 13 July 2004 Event”, Solar Phys., 253, 291–303. [DOI], [ADS]. (Cited on page 25.)
Pomoell, J., Vainio, R. and Kissmann, R., 2008, “MHD Modeling of Coronal Large-Amplitude Waves Related to CME Lift-off”, Solar Phys., 253, 249–261. [DOI], [ADS]. (Cited on pages 67 and 73.)
Priest, E. R, 1982, Solar Magnetohydrodynamics, Geophysics and Astrophysics Monographs, 21, Reidel, Dordrecht. [DOI], [ADS]. (Cited on pages 7 and 8.)
Ramsey, H. E. and Smith, S. F., 1966, “Flare-initiated filament oscillation”, Astron. J., 702, 197–199. [DOI], [ADS]. (Cited on pages 5 and 50.)
Raymond, J. C., Thompson, B. J., St Cyr, O. C. et al., 2000, “SOHO and radio observations of a CME shock wave”, Geophys. Res. Lett., 27, 1439–1442. [DOI], [ADS]. (Cited on page 18.)
Reames, D. V., 2013, “The Two Sources of Solar Energetic Particles”, Space Sci. Rev., 175, 53–92. [DOI], [ADS], [arXiv:1306.3608 [astro-ph.SR]]. (Cited on page 78.)
Richardson, R. S., 1951, “Characteristics of Solar Flares”, Astrophys. J., 114, 356. [DOI], [ADS]. (Cited on page 53.)
Robinson, R. D., 1985, “Velocities of type II solar radio events”, Solar Phys., 95, 343–357. [DOI], [ADS]. (Cited on page 25.)
Rouillard, A. P., Odstrcil, D., Sheeley, N. R. et al., 2011, “Interpreting the Properties of Solar Energetic Particle Events by Using Combined Imaging and Modeling of Interplanetary Shocks”, Astrophys. J., 735, 7. [DOI], [ADS]. (Cited on page 18.)
Rouillard, A. P., Sheeley, N. R., Tylka, A. et al., 2012, “The Longitudinal Properties of a Solar Energetic Particle Event Investigated Using Modern Solar Imaging”, Astrophys. J., 752, 44. [DOI], [ADS]. (Cited on page 79.)
Ryan, D. F., Milligan, R. O., Gallagher, P. T., Dennis, B. R., Tolbert, A. K., Schwartz, R. A. and Young, C. A., 2012, “The Thermal Properties of Solar Flares over Three Solar Cycles Using GOES X-Ray Observations”, Astrophys. J. Suppl. Ser., 202, 11. [DOI], [ADS]. (Cited on pages 29 and 54.)
Saint-Hilaire, P. and Benz, A. O., 2005, “Thermal and non-thermal energies of solar flares”, Astron. Astrophys., 435, 743–752. [DOI], [ADS]. (Cited on page 54.)
Schmidt, J. M. and Cairns, I. H., 2012, “Type II radio bursts: 1. New entirely analytic formalism for the electron beams, Langmuir waves, and radio emission”, J. Geophys. Res., 117, A04106. [DOI], [ADS]. (Cited on page 24.)
Schmidt, J. M. and Ofman, L., 2010, “Global Simulation of an Extreme Ultraviolet Imaging Telescope Wave”, Astrophys. J., 713, 1008–1015. [DOI], [ADS]. (Cited on pages 48 and 67.)
Schrijver, C. J., Aulanier, G., Title, A. M., Pariat, E. and Delannée, C., 2011, “The 2011 February 15 X2 flare, ribbons, coronal front, and mass ejection: interpreting the three-dimensional views from the Solar Dynamics Observatory and STEREO guided by magnetohydrodynamic flux-rope modeling”, Astrophys. J., 738, 167. [DOI], [ADS]. (Cited on pages 44, 45, 70, and 73.)
Schrijver, C. J., Title, A. M., Yeates, A. R. and DeRosa, M. L., 2013, “Pathways of Large-scale Magnetic Couplings between Solar Coronal Events”, Astrophys. J., 773, 93. [DOI], [ADS], [arXiv:1305.0801 [astro-ph.SR]]. (Cited on page 53.)
Sedov, L. I., 1959, Similarity and Dimensional Methods in Mechanics, Academic Press, New York. [ADS]. (Cited on page 38.)
Selwa, M., Poedts, S. and DeVore, C. R., 2012, “Dome-shaped EUV Waves from Rotating Active Regions”, Astrophys. J. Lett., 747, L21. [DOI], [ADS]. (Cited on page 33.)
Sheeley Jr, N. R., Howard, R. A., Michels, D. J., Koomen, M. J., Schwenn, R., Mühlhäuser, K. H. and Rosenbauer, H., 1985, “Coronal mass ejections and interplanetary shocks”, J. Geophys. Res., 90, 163–175. [DOI], [ADS]. (Cited on page 57.)
Shen, Y. and Liu, Y., 2012a, “Evidence for the Wave Nature of an Extreme Ultraviolet Wave Observed by the Atmospheric Imaging Assembly on Board the Solar Dynamics Observatory”, Astrophys. J., 754, 7. [DOI], [ADS]. (Cited on pages 39 and 48.)
Shen, Y. and Liu, Y., 2012b, “Simultaneous Observations of a Large-scale Wave Event in the Solar Atmosphere: From Photosphere to Corona”, Astrophys. J. Lett., 752, L23. [DOI], [ADS]. (Cited on pages 11, 30, 31, 38, 39, and 45.)
Shen, Y., Liu, Y., Su, J., Li, H., Zhao, R., Tian, Z., Ichimoto, K. and Shibata, K., 2013, “Diffraction, Refraction, and Reflection of an Extreme-ultraviolet Wave Observed during Its Interactions with Remote Active Regions”, Astrophys. J. Lett., 773, L33. [DOI], [ADS]. (Cited on pages 47, 48, and 49.)
Shen, Y., Ichimoto, K., Ishii, T. T., Tian, Z., Zhao, R. and Shibata, K., 2014, “A Chain of Winking (Oscillating) Filaments Triggered by an Invisible Extreme-ultraviolet Wave”, Astrophys. J., 786, 151. [DOI], [ADS], [arXiv:1403.7705 [astro-ph.SR]]. (Cited on page 50.)
Shibata, K., Ishido, Y., Acton, L. W. et al., 1992, “Observations of X-ray jets with the YOHKOH Soft X-ray Telescope”, Publ. Astron. Soc. Japan, 44, L173–L179. [ADS]. (Cited on page 63.)
Shibata, K., Masuda, S., Shimojo, M., Hara, H., Yokoyama, T., Tsuneta, S., Kosugi, T. and Ogawara, Y., 1995, “Hot-Plasma Ejections Associated with Compact-Loop Solar Flares”, Astrophys. J. Lett., 451, L83–L85. [DOI], [ADS]. (Cited on page 63.)
Smith, S. F. and Harvey, K. L., 1971, “Observational Effects of Flare-Associated Waves”, in Physics of the Solar Corona, NATO Advanced Study Institute, Athens, Greece, 6–17 September 1970, (Ed.) Macris, C. J., Astrophysics and Space Science Library, 27, pp. 156–167, Reidel, Dordrecht. [ADS]. (Cited on pages 25, 29, 30, 36, 37, 50, and 56.)
Steinegger, M., Denker, C., Goode, P. R. et al., 2001, “The new global high-resolution Hα network: preliminary results on the chromospheric differential rotation”, in Helio- and Asteroseismology at the Dawn of the Millennium, Proceedings of the SOHO 10/GONG 2000 Workshop: 2–6 October 2000, Instituto de Astrofísica de Canarias, Santa Cruz de Tenerife, Tenerife, Spain, (Eds.) Wilson, A., Pallé, P. L., ESA Special Publication, 464, pp. 315–320, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 29.)
Sterling, A. C. and Hudson, H. S., 1997, “Yohkoh SXT Observations of X-Ray ‘Dimming’ Associated with a Halo Coronal Mass Ejection”, Astrophys. J. Lett., 491, L55–L58. [DOI], [ADS]. (Cited on page 27.)
Švestka, Z., 1976, Solar Flares, Geophysics and Astrophysics Monographs, 8, Reidel, Dordrecht; Boston. [ADS]. (Cited on page 62.)
Temmer, M., Veronig, A. M., Vršnak, B., Rybák, J., Gömöry, P., Stoiser, S. and Maričić, D., 2008, “Acceleration in Fast Halo CMEs and Synchronized Flare HXR Bursts”, Astrophys. J. Lett., 673, L95–L98. [DOI], [ADS]. (Cited on page 56.)
Temmer, M., Vršnak, B., Žic, T. and Veronig, A. M., 2009, “Analytic Modeling of the Moreton Wave Kinematics”, Astrophys. J., 702, 1343–1352. [DOI], [ADS], [arXiv:0908.3746]. (Cited on pages 62 and 66.)
Temmer, M., Veronig, A. M., Gopalswamy, N. and Yashiro, S., 2011, “Relation Between the 3D-Geometry of the Coronal Waveand Associated CME During the 26 April 2008 Event”, Solar Phys., 273, 421–432. [DOI], [ADS]. (Cited on pages 31 and 59.)
Temmer, M., Vršnak, B. and Veronig, A. M., 2013, “The Wave-Driver System of the Off-Disk Coronal Wave of 17 January 2010”, Solar Phys., 287, 441–454. [DOI], [ADS]. (Cited on pages 62 and 66.)
Terradas, J. and Ofman, L., 2004, “3D MHD Simulation of the Interaction of Fast Magnetosonic Waves and a Coronal Active Region”, in Proceedings of SOHO 13 ‘Waves, Oscillations and Small-Scale Transient Events in the Solar Atmosphere: A Joint View from SOHO and TRACE’, 29 September–3 October 2003, Palma de Mallorca, Balearic Islands, Spain, (Ed.) Lacoste, H., ESA Special Publication, SP-547, p. 469, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 47.)
Thompson, B. J. and Myers, D. C., 2009, “A Catalog of Coronal ‘EIT Wave’ Transients”, Astrophys. J. Suppl. Ser., 183, 225–243. [DOI], [ADS]. (Cited on pages 15, 28, 30, 31, 36, 37, 39, 41, 55, 56, 58, and 68.)
Thompson, B. J., Plunkett, S. P., Gurman, J. B., Newmark, J. S., St Cyr, O. C. and Michels, D. J., 1998, “SOHO/EIT observations of an Earth-directed coronal mass ejection on May 12, 1997”, Geophys. Res. Lett., 25, 2465–2468. [DOI], [ADS]. (Cited on pages 5, 12, 13, 27, 30, and 36.)
Thompson, B. J., Gurman, J. B., Neupert, W. M. et al., 1999, “SOHO/EIT Observations of the 1997 April 7 Coronal Transient: Possible Evidence of Coronal Moreton Waves”, Astrophys. J. Lett., 517, L151–L154. [DOI], [ADS]. (Cited on pages 12, 30, 36, and 41.)
Thompson, B. J., Cliver, E. W., Nitta, N., Delannée, C. and Delaboudinière, J.-P., 2000a, “Coronal dimmings and energetic CMEs in April–May 1998”, Geophys. Res. Lett., 27, 1431–1434. [DOI], [ADS]. (Cited on page 27.)
Thompson, B. J., Reynolds, B., Aurass, H., Gopalswamy, N., Gurman, J. B., Hudson, H. S., Martin, S. F. and St Cyr, O. C., 2000b, “Observations of the 24 September 1997 Coronal Flare Waves”, Solar Phys., 193, 161–180. [DOI], [ADS]. (Cited on pages 15, 20, 27, 30, 36, 38, 41, and 47.)
Torsti, J., Anttila, A., Kocharov, L. et al., 1998, “Energetic (1 to 50 MeV) protons associated with Earth-directed coronal mass ejections”, Geophys. Res. Lett., 25, 2525–2528. [DOI], [ADS]. (Cited on page 78.)
Torsti, J., Kocharov, L. G., Teittinen, M. and Thompson, B. J., 1999, “Injection of 10 MeV Protons in Association with a Coronal Moreton Wave”, J. Geophys. Res., 510, 460–465. [DOI], [ADS]. (Cited on page 78.)
Tripathi, D. and Raouafi, N.-E., 2007, “On the relationship between coronal waves associated with a CME on 5 March 2000”, Astron. Astrophys., 473, 951–957. [DOI], [ADS]. (Cited on pages 18 and 52.)
Tsuneta, S., Acton, L., Bruner, M. et al., 1991, “The soft X-ray telescope for the SOLAR-A mission”, Solar Phys., 136, 37–67. [DOI], [ADS]. (Cited on page 16.)
Uchida, Y., 1960, “On the Exciters of Type II and Type III Solar Radio Bursts”, Publ. Astron. Soc. Japan, 12, 376–397. [ADS]. (Cited on pages 5 and 24.)
Uchida, Y., 1968, “Propagation of Hydromagnetic Disturbances in the Solar Corona and Moreton’s Wave Phenomenon”, Solar Phys., 4, 30–44. [DOI], [ADS]. (Cited on pages 5, 19, 33, 36, 46, 47, 50, and 65.)
Uchida, Y., 1970, “Diagnosis of Coronal Magnetic Structure by Flare-Associated Hydromagnetic Disturbances”, Publ. Astron. Soc. Japan, 22, 341–364. [ADS]. (Cited on page 65.)
Uchida, Y., 1974, “Behavior of the flare produced coronal MHD wavefront and the occurrence of type II radio bursts”, Solar Phys., 39, 431–449. [DOI], [ADS]. (Cited on page 65.)
Uchida, Y., Altschuler, M. D. and Newkirk Jr, G., 1973, “Flare-Produced Coronal MHD-Fast-Mode Wave-fronts and Moreton’s Wave Phenomenon”, Solar Phys., 28, 495–516. [DOI], [ADS]. (Cited on pages 19, 47, and 65.)
Vainio, R. and Khan, J. I., 2004, “Solar energetic particle acceleration in refracting coronal shock waves”, Astrophys. J., 600, 451–457. [DOI], [ADS]. (Cited on page 78.)
Valničnek, B, 1964, “Escape of matter from chromosphere and active regions”, Bull. Astron. Inst. Czech., 15, 207–210. [ADS]. (Cited on page 53.)
Vernazza, J. E., Avrett, E. H. and Loeser, R., 1981, “Structure of the solar chromosphere. III. Models of the EUV brightness components of the quiet-sun”, Astrophys. J. Suppl. Ser., 45, 635–725. [DOI], [ADS]. (Cited on page 54.)
Veronig, A. M., Temmer, M., Vršnak, B. and Thalmann, J. K., 2006, “Interaction of a Moreton/EIT Wave and a Coronal Hole”, Astrophys. J., 647, 1466–1471. [DOI], [ADS]. (Cited on pages 20, 31, and 49.)
Veronig, A. M., Temmer, M. and Vršnak, B., 2008, “High-Cadence Observations of a Global Coronal Wave by STEREO EUVI”, Astrophys. J. Lett., 681, L113–L116. [DOI], [ADS], [0806.0710]. (Cited on pages 31, 38, 44, 48, and 59.)
Veronig, A. M., Muhr, N., Kienreich, I. W., Temmer, M. and Vršnak, B., 2010, “First Observations of a Dome-shaped Large-scale Coronal Extreme-ultraviolet Wave”, Astrophys. J. Lett., 716, L57–L62. [DOI], [ADS], [1005.2060]. (Cited on pages 15, 33, 34, 39, 41, 42, 43, 45, 59, and 60.)
Veronig, A. M., Gömöry, P., Kienreich, I. W., Muhr, N., Vršnak, B., Temmer, M. and Warren, H. P., 2011, “Plasma diagnostics of an EIT wave observed by Hinode/EIS and SDO/AIA”, Astrophys. J. Lett., 743, L10. [DOI], [ADS]. (Cited on pages 42, 46, and 47.)
Vourlidas, A., Wu, S. T., Wang, A. H., Subramanian, P. and Howard, R. A., 2003, “Direct Detection of a Coronal Mass Ejection-Associated Shock in Large Angle and Spectrometric Coronagraph Experiment White-Light Images”, Astrophys. J., 598, 1392–1402. [DOI], [ADS], [astro-ph/0308367]. (Cited on page 18.)
Vourlidas, A., Howard, R. A., Esfandiari, E., Patsourakos, S., Yashiro, S. and Michalek, G., 2010, “Comprehensive Analysis of Coronal Mass Ejection Mass and Energy Properties Over a Full Solar Cycle”, Astrophys. J., 722, 1522. [DOI], [ADS], [arXiv:1008.3737 [astro-ph.SR]]. (Cited on page 54.)
Vršnak, B., 2001, “Dynamics of solar coronal eruptions”, J. Geophys. Res., 106, 25 249–25 260. [DOI], [ADS]. (Cited on page 63.)
Vršnak, B., 2005, “Terminology of Large-Scale Waves in the Solar Atmosphere”, Eos Trans. AGU, 86, 112–113. [DOI], [ADS]. (Cited on page 6.)
Vršnak, B. and Cliver, E. W., 2008, “Origin of Coronal Shock Waves”, Solar Phys., 253, 215–235. [DOI], [ADS]. (Cited on pages 8, 25, 55, 56, and 65.)
Vršnak, B. and Lulić, S., 2000a, “Formation Of Coronal MHD Shock Waves — I. The Basic Mechanism”, Solar Phys., 196, 157–180. [DOI], [ADS]. (Cited on pages 8 and 65.)
Vršnak, B. and Lulić, S., 2000b, “Formation of Coronal MHD Shock Waves — II. The Pressure Pulse Mechanism”, Solar Phys., 196, 181–197. [DOI], [ADS]. (Cited on pages 8 and 65.)
Vršnak, B., Aurass, H., Magdalenić, J. and Gopalswamy, N., 2001a, “Band-splitting of coronal and interplanetary type II bursts. I. Basic properties”, Astron. Astrophys., 377, 321–329. [DOI], [ADS]. (Cited on page 25.)
Vršnak, B., Magdalenić, J. and Aurass, H., 2001b, “Comparative Analysis of Type II Bursts and of Thermal and non-Thermal Flare Signatures”, Solar Phys., 202, 319–335. [DOI], [ADS]. (Cited on page 26.)
Vršnak, B., Magdalenić, J., Aurass, H. and Mann, G., 2002a, “Band-splitting of coronal and interplanetary type II bursts. II. Coronal magnetic field and Alfvén velocity”, Astron. Astrophys., 396, 673–682. [DOI], [ADS]. (Cited on pages 25 and 77.)
Vršnak, B., Warmuth, A., Brajša, R. and Hanslmeier, A., 2002b, “Flare waves observed in Helium I 10830 Å”, Astron. Astrophys., 394, 299–310. [DOI], [ADS]. (Cited on pages 20, 21, 27, 38, 50, and 66.)
Vršnak, B., Magdalenić, J., Temmer, M., Veronig, A., Warmuth, A., Mann, G., Aurass, H. and Otruba, W., 2005, “Broadband Metric-Range Radio Emission Associated with a Moreton/EIT Wave”, Astrophys. J. Lett., 625, L67–L70. [DOI], [ADS]. (Cited on pages 21, 22, 26, and 50.)
Vršnak, B., Warmuth, A., Temmer, M., Veronig, A., Magdalenić, J., Hillaris, A. and Karlický, M., 2006, “Multi-wavelength study of coronal waves associated with the CME-flare event of 3 November 2003”, Astron. Astrophys., 448, 739–752. [DOI], [ADS]. (Cited on pages 21, 25, 26, 27, 52, 56, 57, and 58.)
Wang, H., Shen, C. and Lin, J., 2009, “Numerical Experiments of Wave-like Phenomena Caused by the Disruption of an Unstable Magnetic Configuration”, Astrophys. J., 700, 1716–1731. [DOI], [ADS], [arXiv:0906.2677]. (Cited on pages 33, 65, 67, and 73.)
Wang, Y.-M., 2000, “EIT Waves and Fast-Mode Propagation in the Solar Corona”, Astrophys. J. Lett., 543, L89–L93. [DOI], [ADS]. (Cited on pages 47 and 67.)
Warmuth, A., 2007, “Large-scale Waves and Shocks in the Solar Corona”, in The High Energy Solar Corona: Waves, Eruptions, Particles, CESRA Workshop 2004, (Eds.) Klein, K.-L., MacKinnon, A. L., Lecture Notes in Physics, 725, pp. 107–138, Springer, Berlin; New York. [DOI], [ADS], [Google Books]. (Cited on pages 5, 8, and 9.)
Warmuth, A., 2010, “Large-scale waves in the solar corona: The continuing debate”, Adv. Space Res., 45, 527–536. [DOI], [ADS]. (Cited on pages 20, 21, 25, 26, 29, 37, 38, 39, 41, 56, 58, 60, and 66.)
Warmuth, A., 2011, “Globally propagating waves in the solar corona”, Plasma Phys. Control. Fusion, 53, 124023. [DOI], [ADS]. (Cited on page 5.)
Warmuth, A. and Mann, G., 2005a, “A model of the Alfvén speed in the solar corona”, Astron. Astrophys., 435, 1123–1135. [DOI], [ADS]. (Cited on pages 44, 66, 76, and 77.)
Warmuth, A. and Mann, G., 2005b, “The Application of Radio Diagnostics to the Study of the Solar Drivers of Space Weather”, in Space Weather: The Physics Behind a Slogan, 2nd AEF spring school, (Eds.) Scherer, K., Fichtner, H., Heber, B., Mall, U., Lecture Notes in Physics, 656, pp. 47–65, Springer, Berlin; New York. [DOI], [ADS]. (Cited on page 24.)
Warmuth, A. and Mann, G., 2011, “Kinematical evidence for physically different classes of large-scale coronal EUV waves”, Astron. Astrophys., 532, A151. [DOI], [ADS]. (Cited on pages 31, 36, 38, 39, 40, 42, 65, 68, and 75.)
Warmuth, A., Vršnak, B., Aurass, H. and Hanslmeier, A., 2001, “Evolution of Two EIT/Hα Moreton Waves”, Astrophys. J. Lett., 560, L105–L109. [DOI], [ADS]. (Cited on pages 36, 37, 41, and 42.)
Warmuth, A., Vršnak, B., Magdalenić, J., Hanslmeier, A. and Otruba, W., 2004a, “A multiwavelength study of solar flare waves. I. Observations and basic properties”, Astron. Astrophys., 418, 1101–1115. [DOI], [ADS]. (Cited on pages 16, 19, 20, 22, 23, 29, 30, 31, 32, 36, 37, 38, 41, and 50.)
Warmuth, A., Vršnak, B., Magdalenić, J., Hanslmeier, A. and Otruba, W., 2004b, “A multiwavelength study of solar flare waves. II. Perturbation characteristics and physical interpretation”, Astron. Astrophys., 418, 1117–1129. [DOI], [ADS]. (Cited on pages 15, 25, 26, 31, 41, 42, 44, 50, 51, 57, 65, 66, and 67.)
Warmuth, A., Mann, G. and Aurass, H., 2005, “First Soft X-Ray Observations of Global Coronal Waves with the GOES Solar X-Ray Imager”, Astrophys. J. Lett., 626, L121–L124. [DOI], [ADS]. (Cited on pages 17, 32, 38, and 56.)
Warwick, J. W., 1957, “Flare-Connected Prominences”, Astrophys. J., 125, 811. [DOI], [ADS]. (Cited on page 63.)
Webb, D. F. and Howard, T. A., 2012, “Coronal Mass Ejections: Observations”, Living Rev. Solar Phys., 9, lrsp-2012-3. [DOI], [ADS]. URL (accessed 20 September 2014): http://www.livingreviews.org/lrsp-2012-3. (Cited on page 57.)
Webb, D. F., Cliver, E. W., Crooker, N. U., Cry, O. C. S. and Thompson, B. J., 2000, “Relationship of halo coronal mass ejections, magnetic clouds, and magnetic storms”, J. Geophys. Res., 105, 7491–7508. [DOI], [ADS]. (Cited on page 27.)
West, M. J., Zhukov, A. N., Dolla, L. and Rodriguez, L., 2011, “Coronal Seismology Using EIT Waves: Estimation of the Coronal Magnetic Field Strength in the Quiet Sun”, Astrophys. J., 730, 122. [DOI], [ADS]. (Cited on page 76.)
White, S. M. and Thompson, B. J., 2005, “High-Cadence Radio Observations of an EIT Wave”, Astrophys. J. Lett., 620, L63–L66. [DOI], [ADS]. (Cited on page 23.)
Wiedenbeck, M. E., Mason, G. M., Cohen, C. M. S., Nitta, N. V., Gómez-Herrero, R. and Haggerty, D. K., 2013, “Observations of solar energetic particles from 3He-rich events over a wide range of heliographic longitude”, Astrophys. J., 762, 54. [DOI], [ADS]. (Cited on page 79.)
Wild, J. P. and McCready, L. L., 1950, “Observations of the Spectrum of High-Intensity Solar Radiation at Metre Wavelengths. I. The Apparatus and Spectral Types of Solar Burst Observed”, Aust. J. Sci. Res. A, 3, 387–398. [ADS]. (Cited on pages 5 and 23.)
Wills-Davey, M. J., 2006, “Tracking Large-Scale Propagating Coronal Wave Fronts (EIT Waves) using Automated Methods”, Astrophys. J., 645, 757–765. [DOI], [ADS]. (Cited on pages 15, 33, 41, and 68.)
Wills-Davey, M. J. and Attrill, G. D. R., 2009, “EIT Waves: A Changing Understanding over a Solar Cycle”, Space Sci. Rev., 149, 325–353. [DOI], [ADS]. (Cited on page 5.)
Wills-Davey, M. J. and Thompson, B. J., 1999, “Observations of a Propagating Disturbance in TRACE”, Solar Phys., 190, 467–483. [DOI], [ADS]. (Cited on pages 15, 27, 30, 33, 36, 44, 51, and 68.)
Wills-Davey, M. J., DeForest, C. E. and Stenflo, J. O., 2007, “Are ‘EIT Waves’ Fast-Mode MHD Waves?”, Astrophys. J., 664, 556–562. [DOI], [ADS], [arXiv:0704.2828]. (Cited on pages 15, 36, and 68.)
Wu, S. T., Zheng, H., Wang, S., Thompson, B. J., Plunkett, S. P., Zhao, X. P. and Dryer, M., 2001, “Three-dimensional numerical simulation of MHD waves observed by the Extreme Ultraviolet Imaging Telescope”, J. Geophys. Res., 106, 25 089–25 102. [DOI], [ADS]. (Cited on page 67.)
Wu, S. T., Li, B., Wang, S. and Zheng, H., 2005, “A three-dimensional analysis of global propagation of magnetohydrodynamic (MHD) waves in a structured solar atmosphere”, J. Geophys. Res., 110, A11102. [DOI], [ADS]. (Cited on pages 67 and 73.)
Wülser, J.-P., Lemen, J. R., Tarbell, T. D. et al., 2004, “EUVI: the STEREO-SECCHI Extreme Ultraviolet Imager”, in Telescopes and Instrumentation for Solar Astrophysics, San Diego, California, USA, August 3, 2003, (Eds.) Fineschi, S., Gummin, M. A., Proc. SPIE, 5171, pp. 111–122, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on page 15.)
Yang, H. Q. and Chen, P. F., 2010, “The Dependence of the EIT Wave Velocity on the Magnetic Field Strengths”, Solar Phys., 266, 59–69. [DOI]. (Cited on page 77.)
Yashiro, S., Gopalswamy, N., Michalek, G., St Cyr, O. C., Plunkett, S. P., Rich, N. B. and Howard, R. A., 2004, “A catalog of white light coronal mass ejections observed by the SOHO spacecraft”, J. Geophys. Res., 109, A07105. [DOI], [ADS]. (Cited on page 29.)
Zarro, D. M., Sterling, A. C., Thompson, B. J., Hudson, H. S. and Nitta, N., 1999, “SOHO EIT Observations of Extreme-Ultraviolet ‘Dimming’ Associated with a Halo Coronal Mass Ejection”, Astrophys. J. Lett., 520, L139–L142. [DOI], [ADS]. (Cited on page 27.)
Zhang, J., Dere, K. P., Howard, R. A., Kundu, M. R. and White, S. M., 2001, “On the Temporal Relationship between Coronal Mass Ejections and Flares”, Astrophys. J., 559, 452–462. [DOI], [ADS]. (Cited on page 56.)
Zhang, Y., Kitai, R., Narukage, N., Matsumoto, T., Ueno, S., Shibata, K. and Wang, J., 2011, “Propagation of Moreton Waves”, Publ. Astron. Soc. Japan, 63, 685–696. [ADS]. (Cited on pages 29, 30, 31, 36, 37, and 56.)
Zhao, X. H., Wu, S. T., Wang, A. H., Vourlidas, A., Feng, X. S. and Jiang, C. W., 2011, “Uncovering the Wave Nature of the EIT Wave for the 2010 January 17 Event through Its Correlation to the Background Magnetosonic Speed”, Astrophys. J., 742, 131. [DOI], [ADS]. (Cited on page 77.)
Zheng, R., Jiang, Y., Hong, J., Yang, J., Bi, Y., Yang, L. and Yang, D., 2011, “A possible detection of a fast-mode extreme ultraviolet wave associated with a mini coronal mass ejection observed by the Solar Dynamics Observatory”, Astrophys. J. Lett., 739, L39. [DOI], [ADS]. (Cited on page 64.)
Zheng, R., Jiang, Y., Yang, J., Bi, Y., Hong, J., Yang, B. and Yang, D., 2012a, “Homologous Extreme Ultraviolet Waves in the Emerging Flux Region Observed by the Solar Dynamics Observatory”, Astrophys. J., 747, 67. [DOI], [ADS]. (Cited on page 64.)
Zheng, R., Jiang, Y., Yang, J., Bi, Y., Hong, J., Yang, B. and Yang, D., 2012b, “An extreme ultraviolet wave associated with a failed eruption observed by the Solar Dynamics Observatory”, Astron. Astrophys., 541, A49. [DOI], [ADS]. (Cited on page 64.)
Zheng, R., Jiang, Y., Yang, J., Bi, Y., Hong, J., Yang, D. and Yang, B., 2012c, “A Fast Propagating Extreme-Ultraviolet Wave Associated with a Mini-filament Eruption”, Astrophys. J., 753, 112. [DOI], [ADS]. (Cited on page 64.)
Zheng, R., Jiang, Y., Yang, J., Bi, Y., Hong, J., Yang, D. and Yang, B., 2012d, “An Extreme Ultraviolet Wave Associated with a Micro-sigmoid Eruption”, Astrophys. J. Lett., 753, L29. [DOI], [ADS]. (Cited on page 64.)
Zheng, R., Jiang, Y., Yang, J., Bi, Y., Hong, J., Yang, B. and Yang, D., 2013a, “An Extreme-ultraviolet Wave Associated with a Surge”, Astrophys. J., 764, 70. [DOI], [ADS]. (Cited on page 64.)
Zheng, R.-S., Jiang, Y.-C., Yang, J.-Y., Hong, J.-C., Bi, Y., Yang, B. and Yang, D., 2013b, “Loop oscillations and an extreme ultraviolet wave associated with a micro-sigmoid eruption”, Mon. Not. R. Astron. Soc., 431, 1359–1365. [DOI], [ADS]. (Cited on page 64.)
Zhukov, A. N., 2011, “EIT wave observations and modeling in the STEREO era”, J. Atmos. Sol.-Terr. Phys., 73, 1096–1116. [DOI], [ADS]. (Cited on pages 5, 6, and 68.)
Zhukov, A. N. and Auchère, F., 2004, “On the nature of EIT waves, EUV dimmings and their link to CMEs”, Astron. Astrophys., 427, 705–716. [DOI], [ADS]. (Cited on pages 15, 33, 44, 59, and 73.)
Zhukov, A. N. and Veselovsky, I. S., 2007, “Global Coronal Mass Ejections”, Astrophys. J. Lett., 664, L131–L134. [DOI], [ADS]. (Cited on page 53.)
Zhukov, A. N., Rodriguez, L. and de Patoul, J., 2009, “STEREO/SECCHI Observations on 8 December 2007: Evidence Against the Wave Hypothesis of the EIT Wave Origin”, Solar Phys., 259, 73–85. [DOI], [ADS]. (Cited on pages 36 and 39.)
Žic, T., Vršnak, B., Temmer, M. and Jacobs, C., 2008, “Cylindrical and Spherical Pistons as Drivers of MHD Shocks”, Solar Phys., 253, 237–247. [DOI], [ADS]. (Cited on pages 9 and 62.)
Zimovets, I., Vilmer, N., Chian, A. C.-L., Sharykin, I. and Struminsky, A., 2012, “Spatially resolved observations of a split-band coronal type II radio burst”, Astron. Astrophys., 547, A6. [DOI], [ADS], [arXiv:1208.5267 [astro-ph.SR]]. (Cited on page 64.)
Zirin, H. and Russo Lackner, D., 1969, “The Solar Flares of August 28 and 30, 1966”, Solar Phys., 6, 86–103. [DOI], [ADS]. (Cited on page 62.)
Acknowledgements
I thank the editors of Living Reviews in Solar Physics, especially E. Marsch, for the invitation to write this review. The manuscript has benefited from discussion with G. Mann and H. Aurass, and from the constructive comments of two anonymous referees. Special thanks go to the organizers (S. Bloomfield and D. Long) as well as to the other participants (P. F. Chen, C. Downs, K. Vanninathan, A. Veronig, A. Vourlidas, and B. Vršnak) of the first meeting of the ISSI International Team on “The nature of coronal bright fronts”. The discussions during this meeting have helped me a lot in preparing this review. EIT data have been used courtesy of the SOHO/EIT consortium. SOHO is a project of international cooperation between ESA and NASA. STEREO/SECCHI data are produced by an international consortium of the Naval Research Lab (US), Lockheed Martin Solar Astrophysics Lab (US), NASA Goddard Space Flight Center (US), Rutherford Appleton Lab (UK), University of Birmingham (UK), Max-Planck-Institut für Sonnensystemforschung (Germany), Centre Spatiale de Liège (Belgium), Institut d’Optique Théorique et Appliqueé (France), and the Institut d’Astrophysique Spatiale (France). H-alpha data were provided by the Kanzelhoühe Observatory, University of Graz, Austria. The author acknowledges support by the German Space Agency DLR under grant No. 50 QL 0001.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Warmuth, A. Large-scale Globally Propagating Coronal Waves. Living Rev. Sol. Phys. 12, 3 (2015). https://doi.org/10.1007/lrsp-2015-3
Published:
DOI: https://doi.org/10.1007/lrsp-2015-3