Abstract
The evolution of active regions (AR) from their emergence through their long decay process is of fundamental importance in solar physics. Since large-scale flux is generated by the deep-seated dynamo, the observed characteristics of flux emergence and that of the subsequent decay provide vital clues as well as boundary conditions for dynamo models. Throughout their evolution, ARs are centres of magnetic activity, with the level and type of activity phenomena being dependent on the evolutionary stage of the AR. As new flux emerges into a pre-existing magnetic environment, its evolution leads to re-configuration of small-and large-scale magnetic connectivities. The decay process of ARs spreads the once-concentrated magnetic flux over an ever-increasing area. Though most of the flux disappears through small-scale cancellation processes, it is the remnant of large-scale AR fields that is able to reverse the polarity of the poles and build up new polar fields. In this Living Review the emphasis is put on what we have learned from observations, which is put in the context of modelling and simulation efforts when interpreting them. For another, modelling-focused Living Review on the sub-surface evolution and emergence of magnetic flux see Fan (2009). In this first version we focus on the evolution of dominantly bipolar ARs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Definition of active region
The definition of active regions (ARs) has been changing with our ability to observe them through a widening wavelength-window and with our deepening understanding of them. To illustrate this, we recall the Proceedings of the famous IAU Symposium 35 on the “Structure and Development of Solar Active Regions”, held in Budapest, Hungary in 1967, citing the Preface and Introduction by K. O. Kiepenheuer (1968):
What is an Active Region or a Center of Activity? According to D’Azambuja (1953) it is the ‘totality of all visible phenomena accompanying the birth of sunspots’.Footnote 1 Today we should extend this definition a little bit: The totality of all observable phenomena preceding, accompanying and following the birth of sunspots including radio-, X-, EUV- and particle emission.
We see here, that Kiepenheuer extended the definition of ARs well beyond the emergence phase and emphasised that ‘visible phenomena’ must be replaced by ‘observable phenomena’, in a much broader wavelength range than that of the optical. After half a century of solar research what can we add to or change in this definition? The most important change is a shift of emphasis from sunspots to magnetic fields. Sunspots appear where the most concentrated magnetic field bundles cross the photosphere, but the magnetic fields of ARs are much more extended. An example is shown in Figure 1. However, the decades-old identification of ARs with sunspots still has a strong influence: NOAA (National Oceanic and Atmospheric Administration) assigns a number to an AR when/as long as it contains at least one sunspot visible in white-light. This is not a criticism, though. One has to draw a line somewhere and the disappearance of sunspots is a practical milestone in the long gradual decay process, which has few other well-defined markers. In this review, however, we follow AR evolution beyond the presence of sunspots, therefore the term ‘active region’ is defined to include the decay phase, as Kiepenheuer suggested. The AR definition below has many similarities to the one given by Martres and Bruzek (1977), who included both magnetic fields and AR evolution in their description of how to define this “extremely complex phenomenon”.
mpg-Movie (6101.47460938 kB) Still from a movie — SOHO/MDI white-light and magnetogram images taken on 26 July 2010 show that bipolar magnetic fields (white/black = positive/negative) are more extended than the sunspots that are seen in white-light images. Sunspots correspond to the strongest magnetic field concentrations in the magnetogram. However, the active region (AR) extends as far as the distinguishable magnetic field. (For video see appendix)
Active regions are the totality of observable phenomena in a 3D volume represented by the extension of the magnetic field from the photosphere to the corona, revealed by emissions over a wide range of wavelengths from radio to X-rays and γ-rays (only during flares) accompanying and following the emergence of strong twisted magnetic flux (kG, ≥ 1020 Mx) through the photosphere into the chromosphere and corona. The simplest ARs have bipolar magnetic field configurations, but ARs may be built-up by several bipoles emerging in close succession. In the photosphere the presence of a strong magnetic field is manifested by the appearance of dark sunspots or pores and bright faculae representing concentrated and dispersed magnetic fields, respectively. In the chromosphere arch filament systems connect opposite polarity magnetic concentrations, filaments form along the magnetic inversion line and the bright regions that appear above dispersed fields are called plages. In the transition region and corona bright, hot, dense loops connect the opposite magnetic polarities. ARs are the principal source of a broad range of solar activity phenomena: ranging from small-scale brightenings and jets to the largest flares and coronal mass ejections (CMEs). The level and type of activity is dependent on the evolutionary stage of an AR, being highest at the emergence stage and decreasing after that. AR evolution from emergence through dispersion and the removal of flux through magnetic cancellation and ejection of magnetic field and helicity via CMEs are intrinsically coupled with the workings of the solar dynamo. The magnetic field of ARs is a defining factor of the interplanetary magnetic field, thus their influence extends well beyond the solar corona.
Active regions emerge into a pre-existing magnetic environment formed by previous active regions. Therefore, they do not evolve in isolation. The interaction with the surrounding magnetic fields of previous regions, new flux emergences and the open fields of coronal holes plays an important role in their evolution and is one of the determining factors of their lifetime. And, vice versa, at any given time the Sun’s large-scale field is determined by the superposed growth and subsequent diffusion of all previously occurring ARs, shaped by differential rotation and meridional circulation, while the magnetic complexity is smoothed by magnetic cancellation processes.
Throughout the last decades there have been excellent reviews and book chapters published on the evolution of active regions (e.g., Bray and Loughhead, 1964; Schrijver and Zwaan, 2000; Martres and Bruzek, 1977; Sheeley Jr, 1981), though there were relatively few reviews considering the topic in its entirety. We build on the knowledge collected in, and synthesis achieved by, these previous works, and, naturally, we also build on reviews previously written on this subject (van Driel-Gesztelyi, 1998, 2002; van Driel-Gesztelyi and Culhane, 2009). But this, like all reviews of a huge literature (and in spite of all the efforts to the contrary) is biased by personal views, preferences, and understanding.
Furthermore, the evolution of active regions includes two essential topics that have already been covered by other recent reviews: The sub-surface evolution and emergence of magnetic flux by Fan (2009), and the nature and evolution of sunspots by Solanki (2003). Instead of duplicating their work, where relevant, we refer the reader to specific parts of these insightful review articles.
This review starts with a summary of the main laws of magnetic flux emergence, followed by a concise scenario of active region evolution in which we list the most important steps from the first signs of flux emergence in the photosphere and higher atmospheric layers up to the point when the large-scale emerged flux will become an enhanced network and finally background field, including a few key references. Then we discuss the main characteristics of (bipolar) ARs in an evolutionary context from flux emergence through the decay process. Finally, a special section is dedicated to the analyses of the long-term evolution of single ARs, followed by concluding remarks. In an Appendix we describe sunspot classification schemes, pointing out how they relate to AR evolution.
1.2 Main laws and intrinsic characteristics of large-scale magnetic flux emergence
The three main observationally established rules of the emergence patterns of sunspot groups (bipoles) which persist during the 11/22-year solar cycle, namely the butterfly diagram (or Spörer’s law; Carrington, 1858), Joy’s law (Hale et al., 1919) and Hale’s law (Hale and Nicholson, 1925), are the pillars of all successful dynamo models.
-
Spörer’s law (i.e., the butterfly diagram) expresses that the latitudes of flux emergence show a dependence on the solar cycle phase. ARs emerge at high latitudes when the cycle begins and then tend to emerge at progressively lower latitudes as the cycle progresses.
-
Joy’s law recognises that there is a systematic deviation from the east-west alignment of bipolar ARs with the leading spots being closer to the equator on both solar hemispheres.
-
Hale’s law states that bipolar ARs that are aligned roughly in the east-west direction have opposite leading magnetic polarities on opposite hemispheres (leading in the sense of solar rotation). The magnetic polarities alternate between successive sunspot cycles.
These characteristics are fundamental observational constraints for dynamo models, and Hale’s and Joy’s laws are strongly suggestive of ARs being products of the emergence of Ω-loops originating in a toroidal magnetic field in the solar interior, which is thought to be located at the bottom of the convection zone in the tachocline region (for a review, see Charbonneau, 2010).
Besides these three fundamental laws there are three other intrinsic characteristics of large-scale magnetic flux emergence:
-
The leading preceding (p) and following (f) polarities of emerging flux show systematic asymmetries, e.g., in their proper motion and stability (Carrington, 1863), location of the magnetic inversion line (van Driel-Gesztelyi and Petrovay, 1990), extent of the elongation of the magnetic polarities, called magnetic “tongues” (Luoni et al., 2011), and helicity injection (Tian and Alexander, 2009).
-
Flux emerges twisted, carrying magnetic helicity and free magnetic energy from the solar interior (Leka et al., 1996).
-
Flux emergence sites are nested (Cassini, 1729).
1.3 Active region evolution: From birth to death
Based on a wide range of observational evidence and theoretical considerations, it is widely accepted that bipolar active regions are the consequence of the emergence of buoyant magnetic flux tubes through the solar photosphere into the chromosphere, corona and beyond. These magnetic flux tubes originate in the toroidal magnetic field created by the dynamo at the bottom of the convection zone in the tachocline, and during the highly organised flux emergence phase they are still rooted in it — hence their name: Ω loops (Zwaan, 1987). During their rise through the convection zone the evolution of the flux tubes is influenced by the Coriolis force, magnetic tension, drag, plasma vortices and large-scale convective motions, which all leave their mark on the emergent AR. The most important characteristics of a single major (1021–1022 Mx) bipolar flux emergence, and the sequence of events which follow, can be briefly summarised as follows:
-
Flux emergence is first seen as the appearance of a nearly horizontal, upward-moving (≈ 1 km s−1) magnetic field in the photosphere that has a strength of 200–600 G. The individual flux elements move rapidly away from the emergence site and kG field strength is reached in the photosphere only when the field has become nearly vertical. The leading polarity flux tends to converge immediately into a pore, while the following polarity is less compact (Lites et al., 1998).
-
The granulation looks fuzzy in the photosphere (anomalous granulation). Granulae between the opposite polarities become larger and more elongated before fragmenting (Guglielmino et al., 2010). Between the two opposite polarity flux concentrations (pores and spots) dark inter-granular lanes (dark alignments of channels) appear (Loughhead and Bray, 1961), along which plasma upflow (≈ 1 km s−1) is observed, while at their end(s) bright facular grains show signatures of downflow (Strous and Zwaan, 1999). These dark lanes have a lifetime of 10–30 minutes and appear where the tops of magnetic flux tubes are crossing the photosphere.
-
The compact, expanding bipolar magnetic field appears in magnetograms with corresponding compact bright plage in the chromosphere (first in the Ca K-line, Bumba and Howard, 1965 and then in Hα images Waldmeier, 1937). Recent multi-wavelength analyses show that within a few 10s of minutes after Ca II intensity starts to increase, soft X-ray (SXR) emission starts increasing and a small bright region also appears in transition region and low temperature coronal lines (He II, O VI, Mg VII, and even a faint signature is seen in the Fe XII line (Guglielmino et al., 2010). Tarr et al. (2014) found the first faint emission in 211 Å SDO/AIA images about four hours after the first detection of a rapidly-expanding, highly inclined magnetic field in the photosphere, and three hours later the first well-formed EUV loops.
-
The initially uniformly weak horizontal fields evolve into a mixture of weak magnetic fields and more vertical (kG) fields (Lites et al., 1998). At the beginning of flux emergence (first day) there is no single magnetic inversion line, but small (≈ 2 Mm) individual bipoles appear all over the AR in between the growing magnetic concentrations at the edges of the emerging flux (Wang and Zirin, 1992; Bernasconi et al., 2002). The small-scale pattern is suggestive of undulatory (serpentine) flux formed of an alternating series of small Ω and U-loops breaking through the photosphere (Strous et al., 1996; Pariat et al., 2004; Watanabe et al., 2008). These small-scale flux emergence sites may be recurrent and they may appear with a wavelike regularity (with a λ = 8 Mm) in between the two main opposite polarity concentrations (Strous and Zwaan, 1999).
-
In Hα images, dark fibrils, called an arch filament system (AFS), are seen connecting the outer edges of the plage or inner edges of spots of opposite magnetic polarity (Bruzek, 1967). These arches are rising at their tops (v ≈ 10–20 km s−1) and material is draining along their legs (v ≈ 20–25 km s−1). The rise-speed seems to be dependent on the flux of the AR, with more substantial flux rising faster (Zuccarello et al., 2009). Individual arches are short-lived (≈ 20–30 min), but the AFS exists as long as flux is emerging. Arch filaments of the order of 10″ in size are seen above the smallest-scale bipolar (serpentine) emergence sites, which through magnetic cancellation and reconnection jointly form large-scale (AFS) loops (Vargas Domínguez et al., 2012).
-
In the vicinity of growing magnetic flux concentrations strong photospheric and chromospheric downflows (≥ 1.5 km s−1; Brants, 1985) indicate that convective collapse (Parker, 1978) is taking place, increasing the magnetic field strength from a level of 500–600 G to 2000–2500 G as material drains out of the rising loops (Zwaan et al., 1985; Lites et al., 1998).
-
Hot and bright EUV and X-ray loops form right above the AFS (e.g., Kawai et al., 1992; Malherbe et al., 1998). The time-averaged expansion of ARs as observed in X-rays is less that 2 km s−1 during the very early phase of emergence (< 6–14 hrs after birth), which later decreases. This is inferior to the rise speed of AFSs by about an order of magnitude (Yashiro et al., 1998).
-
Opposite magnetic polarities become separated after about 24 hours (Wang and Zirin, 1992).
-
Opposite magnetic polarities move apart, same-polarity concentrations merge forming pores (penumbra-less dark photospheric features of ≤ 500 km diameter) which further merge, forming sunspots at the outer edges of the emerging flux region (EFR). In small (ephemeral) regions the speed of divergence can be as high as 2 km s−1 during the first 30 minutes, which decreases to 1.3–0.7 km s−1 during the next six hours (Harvey and Martin, 1973).
-
Facular motions, emergence locations, elementary flux emergence events and their foot point motions, Hα AFS, EUV and X-ray loops all line up in the same direction (Strous and Zwaan, 1999).
-
The formation of the filamentary structure of the penumbra around a sunspot is part of the flux emergence process, during which time, pores, formed by small-scale flux emergence, merge to form a spot. Penumbra starts to develop around pores with a diameter d ≥ 3.5 Mm or magnetic flux Φ ≥ (1–1.5) × 1020 Mx. Once formed, the presence of a penumbra distinguishes the sunspot from a pore. The radial elongated filaments that make up the penumbra have a width of ∼ 0.2″ to 0.3″.
-
Penumbra around a spot is partial at first, with a gap maintained towards the interior of the bipole from where new pores are moving towards the forming spot. The penumbra forms in a bursty manner, with segments forming first on the outside of the developing sunspot, that is, away from the site of the magnetic flux emergence (Bray and Loughhead, 1964; Bumba, 1965b; Schlichenmaier et al., 2010). These first penumbral segments can be co-spatial with granular regions that become ‘trapped’ between emerging and merging magnetic fragments (Yang et al., 2003; Rezaei et al., 2012). The accumulation of magnetic flux as the emergence proceeds is clearly an important factor, with some work suggesting that there may be a critical flux value, Φcrit ≤ 5 × 1020 Mx, which must be reached before the penumbra starts to form (Zwaan, 1987). The magnetic field in the penumbra is highly inclined (≥ 60°, Rezaei et al., 2012) which suggests that as the magnetic flux in the sunspot increases due to flux emergence, so too does the inclination of the magnetic field to the vertical on the periphery of the sunspot.
-
For penumbral flux that becomes nearly horizontal, an instability can set in, driven by the vigorous small-scale convection in the photosphere. The convective flows are able to drive the field lines downwards and submerge some of the penumbral flux below the photosphere (Thomas et al., 2002). This leads to a variation in inclination of the penumbral filaments and produces an interlocking comb structure (Thomas and Weiss, 1992). Once the penumbra forms, it is immediately, within an hour, followed by the Evershed flow (Evershed, 1909; Leka and Skumanich, 1998).
-
The orientation of the bipole may be arbitrary at first, but generally after 1–3 days it becomes more organised, having a latitude-dependent inclination of 1–10° with the leading polarity closer to the equator, i.e., conforming with Joy’s law (Weart, 1970).
-
A small, unstable filament starts developing in the vicinity of the main leading spot along the magnetic inversion line.
-
The divergence of bipolar flux concentrations is asymmetric, magnetic polarities leading in the sense of solar rotation move faster westward than the following magnetic polarities move eastward (Carrington, 1863; Maunder, 1919). van Driel-Gesztelyi and Petrovay (1990) showed that the magnetic inversion line is statistically closer to the centre of gravity of the following polarity than that of the leading one.
-
Magnetic flux emerges in a non-potential state (Leka et al., 1996), i.e., twisted and carrying magnetic helicity (Wang, 1996). This inherent global twist has its signatures in the longitudinal magnetic field distribution of the emerging flux: asymmetric magnetic tongues or tails, due to the azimuthal field component in the flux rope, develop. The pattern is dependent on the sign of the global twist and thus provides a simple proxy for it (López Fuentes et al., 2000; Luoni et al., 2011). For example, Figure 2b the line of sight magnetic field map shows a well-developed tongue pattern, which indicates left-handed/negative twist.
-
The low-end tail of the size- and magnetic flux-spectrum of ARs (≤ 3 × 1020 Mx), which are also the shortest-lived, are expressively called ephemeral regions (ERs: Harvey and Martin, 1973; Hagenaar et al., 2003). ERs may show most of the signatures, though typically they develop no sunspot, and go through the evolutionary steps listed above in a scaled-down manner. A statistical analysis of the emergence-state characteristics of nearly 3000 ERs observed by SDO/HMI has shown a mean ER emergence duration of ≈ 50 min, flux emergence rate of 2.6 × 105 Mx s−1, separation velocity of opposite polarities 1.1 km s−1, maximum magnetic flux 9.3 × 1018 Mx, magnetic pole separation of 4.7 Mm (Yang and Zhang, 2014).
-
The emerging flux starts reconnecting with surrounding pre-existing fields at a slow and steady rate, forming new coronal magnetic connections. Tarr et al. (2014) has measured a rate of reconnection as 0.38 × 1016 Mx s−1 over two days, starting as early as 14 hours after the first signs of magnetic flux emergence and in total releasing energy equivalent to that of an M-class flare.
-
Flares are the most numerous and intense during the flux emergence phases and when the flux reaches its maximum value; flare numbers peak when the sunspot area of the AR is at maximum (Waldmeier, 1955; Choudhary et al., 2013).
-
As soon as all the flux has crossed the photosphere, the AR starts decaying. Small magnetic flux concentrations called moving magnetic features (MMFs) stream radially out from the sunspots. Though MMFs have a mixed-polarity nature (Harvey and Harvey, 1973), and their ability to carry away flux from the sunspot has been questioned (Zhang et al., 2003), at least the mono-polar MMFs do seem to be effective in that respect. The flux shed by spots will be subjected to a random walk along the network buffeted by supergranular motions (Lawrence and Schrijver, 1993).
-
The characteristic size and stability of leading and following spots usually differ, with the leading spot being larger and significantly longer-lived than the following spots (Hale and Nicholson, 1938).
-
Sunspots start to show light bridges, regions of weaker and more horizontal magnetic field compared to the surrounding umbra (Beckers and Schröter, 1969; Leka, 1997) and a signature that the break-up of the sunspot is imminent (Bray and Loughhead, 1964). The appearance of light bridge(s) is followed by a break up of the spot, which increases the spot’s decay rate as the break-up increases the interface of the spot with surrounding turbulent granular motions. Finally, the spots gradually disappear. Bray and Loughhead (1964) give a timing of 30 to 60 days for this milestone.
-
As the fragmented magnetic field disperses, horizontal flows in supergranular cells carry small flux elements to the internal polarity inversion line. Opposite polarity fragments collide and undergo magnetic reconnection and flux cancellation (van Ballegooijen and Martens, 1989). This process builds magnetic field that is highly sheared with respect to the polarity inversion line (PIL) and within this magnetic configuration filaments form.
-
The magnetic inversion line by now hosts an increasingly stable filament, which gradually extends in length as the magnetic field becomes more dispersed and the area of the bipolar magnetic pattern as well as the length of its inversion line increases. These late-phase filaments have a greater height and are broader than their predecessors, the “active region filaments” (Tandberg-Hanssen, 1995).
-
The dispersing magnetic flux spreads over an ever-increasing area due to supergranular buffeting, establishing a surprisingly smooth large bipolar pattern, which is being sheared by differential rotation and advected by poleward meridional flow. Filaments along the magnetic inversion line are becoming increasingly parallel with the equator.
-
However, not all of the flux disperses from ARs, but, as mentioned above, a part of it cancels within the bipole, mainly along its inversion line. Flux cancellation within the AR can be as large is 10%/day of the total AR flux (Sterling et al., 2010; Baker et al., 2012; Green et al., 2011). The size of the ratio of in-AR cancellation to dispersing flux may be inversely related to the AR size (flux content) being the largest in ephemeral ARs. Yang et al. (2014) found that ≈ 6% of ephemeral regions disappear entirely owing to “self-cancellation”, suggestive of submergence.
-
While the flare activity dramatically decreases after the first rotation of an AR, the number of coronal mass ejections (CMEs) does not show a dramatic decrease, but instead levels off at a rate of a few per solar rotation (van Driel-Gesztelyi et al., 1999a), related to recurrent eruptions of the filament. These decay-phase CMEs, which occur in low magnetic flux density ARs, do not necessarily have a signature in the solar SXR flux.
-
In the magnetic field and chromospheric plage ‘holes’ develop while the magnetic field density decreases to become an “enhanced network”. At this stage, emission from chromospheric plages is still relatively bright, but the AR is already dim in the corona, except for X-ray bright points that are related to the emergence and cancellation of smaller-scale flux (Sheeley Jr, 1981; Schrijver and Zwaan, 2000; Harvey, 1993).
-
Coronal heating, a function of magnetic flux density, is strongly decreasing with the dispersing fields (van Driel-Gesztelyi et al., 2003b); (Démoulin et al., 2003). This is accompanied by a decrease of the EUV and X-ray brightness of the AR.
-
The enhanced network fades, the AR loses its identity and fades into the magnetic background.
Vector magnetic fields of an emerging bipolar AR: (a) from upper left corner clockwise: continuum intensity, azimuth angle, zenith angle, magnetic field strength. (b) Perspective view, from bottom to top: continuum intensity, magnetic flux (white is positive, black is negative), magnetic field vectors, and Doppler velocity (blue-shift is positive). Image reproduced with permission from Lites et al. (1998), copyright by ESO.
The above description of the evolution of ARs collates the essential characteristics of such a process. However, the evolution of ARs can proceed as described above only in exceptional cases, when
-
the AR emerges into a quiet-sun area, which has been free of large-scale flux emergence for several previous rotations, and
-
when no large-scale flux emergence occurs during its evolution within its boundaries.
These conditions can be satisfied mainly during and following solar minima. However, there exists a clustering tendency of magnetic activity, first noted by Cassini (1729), i.e., ARs tend to emerge in the immediate vicinity or within the boundaries of an existing AR (Bumba and Howard, 1965). Liggett and Zirin (1985) and later Harvey and Zwaan (1993) showed that there is a 10 to 22-fold higher emergence rate within existing ARs than in the quiet sun. Repeated episodes of major flux emergence within an evolving active region leads to increased
-
magnetic complexity,
-
cancellation rate, leading to
-
magnetic activity.
Therefore, each arrival of new flux will modify the above timeline. This clustering or nesting tendency of flux emergences has two major effects on the lifetime of ARs:
-
the resulting activity complex as a whole will be long-lived due to repeated injection of flux, however,
-
the lifetime of individual bipoles will be significantly shortened due to intensive flux cancellations, and their magnetic field may never leave the activity complex (Gaizauskas et al., 1983), thus the clustering tendency truncates AR evolution.
2 Active Regions: Lifetime and Magnetic Flux Distribution
2.1 Lifetime
The magnetic flux and area of ARs cover a broad range, strongly influencing their lifetime, which can be defined as the length of time an AR can be identified in magnetic field observations as a distinctly bipolar entity. This is why we avoided the inclusion of specific time indications in Section 1.3. Table 1, partially adopted from Chapter 5 of Schrijver and Zwaan (2000), illustrates very clearly that the lifetime is roughly proportional to the magnetic flux of an AR at maximum development. The lifetime of an AR can depend, however, on its interaction with surrounding magnetic fields. The lifetime of two ARs with the same flux content can be very different depending on the phase of the cycle: a large AR may be traceable for up to 10 months during solar minimum, when it can evolve undisturbed, while its identity can be lost in less than 4 months during solar maximum (Schrijver and Harvey, 1994).
The flux content also has an influence on the ratio of the length of the emergence phase to the full lifetime of the active region: for an increasing flux content and lifetime this ratio is decreasing. For a sample of 382 ARs, which emerged on the eastern hemisphere outside of pre-existing regions (Harvey, 1993, her Chapter 3, Table III) showed that for ephemeral regions, which are at the smallest end of the size-spectrum of ARs, with a lifetime of 1–3 days, the rise time is as high as 30% of the full lifetime. However, as regions become bigger, the percentage goes down to the few percent level. The last column in Table 1 is based on her results.
It is still a question whether or not ephemeral regions (ERs, Harvey and Martin, 1973; Harvey, 1993) are simply the small-scale end of a broad size-spectrum and whether their characteristics and origin are the same as larger ARs (Harvey and Martin, 1973) or if they are generated by a local dynamo process and/or are recycled flux from dispersing ARs (Nordlund et al., 1992). The latitudinal distribution of ephemeral regions extends well beyond the activity belt populated by ARs, and their tilt angle distribution is becoming increasingly random with decreasing flux content, which seems to support their origin in a local dynamo. However, as there is a smooth, continuous distribution of tilt angles, from larger towards the smaller (see Section 3.2, this strongly argues in favour of a deep-seated dynamo origin. Then, the wide distribution of ER tilt angles may result from the effect of turbulent convection. However, as in other cases when two well-argued viable scenarios for the same phenomena co-exist in science, there is a possibility that both are right, and in this specific case below a certain threshold bipoles do have a different origin from that of the large-scale AR population (Hagenaar et al., 2003). As ever-increasing spatial resolution of telescopes and magnetic field measurements are pushing the lower limit of observed ERs to the 1016 Mx range (see, e.g., Wang et al., 2012), which may well belong to the local turbulent dynamo produced population, it seems to be reasonable to draw the line for ARs at about two orders of magnitude higher than that in this review.
The flux content of an emerging flux tube has an effect on the rise speed of its top part (that forms the Hα AFS) as well as on the speed of material down-flow along its legs. Zuccarello et al. (2009), making an overview of high-resolution Doppler velocity (IPM) observations in the Hα line taken with the THEMIS telescope, report on the rising/draining speeds observed in a large, a small and an ephemeral AR. The results are summarised in Table 2, and clearly show that in larger (higher-flux, higher-B, and thus more buoyant) ARs AFS rise faster and drain with greater speeds (presumably, since the material drains from taller loops). An evolution of all these speeds was noted: both the rise speeds of the middle and the down-flow speeds along the legs on an individual strand of an AFS are highest when the strand forms and gradually decrease during the lifetime of the strand (time scale: ≈ 10 min). The characteristic up- and down-flow speeds in the AFS also gradually decrease as the emergence progresses (timescale: days). The asymmetry in the draining speeds along the legs of the ARs shown in the table is discussed in Section 3.3.
An evolution of all these speeds was noted: both the rise speeds of the middle and the down-flow speeds along the legs on an individual strand of an AFS are highest when the strand forms and gradually decrease during the lifetime of the strand (time scale: ≈ 10 min).
2.2 Flux distribution of ARs
There have been several studies of the size and magnetic flux distribution of ARs. These studies are important because they potentially provide diagnostics for the subsurface processes that flux tubes are subjected to and provide clues to the origin of magnetic features. For example, a log-normal distribution of the area/flux may be interpreted as a clue for repeated random fragmentation and coalescence, while a power-law distribution suggests that the features have the same origin or are dominated by the same processes after emergence. Another question is the area/flux range over which an empirical relation holds. For example, if the area/flux distribution of ARs significantly differs from that of the small-scale end of bipolar magnetic flux concentrations, like ephemeral regions (ERs) and even smaller bipolar features, then this can be interpreted as evidence that large- and small-scale bipoles are produced by different types of dynamo processes.
Bogdan et al. (1988), using Mt. Wilson white-light data in the period 1917–1982, made 24 000 measurements of individual sunspot umbral areas to determine the relative size distribution of sunspot umbrae. In the broad range of 1.5–141 MSH (millionth of the solar hemisphere, 3.321 Mm2 or 0.0225 heliographic square degrees or 1.84 arcsec2) they found the sunspot umbral areas to be distributed log normally. While the number of spots changes with cycle phase, and the total number of spots in a cycle difers from cycle to cycle, the distribution of umbral areas was found to be independent of the phase of the solar cycle and it also remained the same from cycle to cycle. These, they suggest, may argue for the fragmentation of magnetic flux tubes in the solar convection zone. More recent analyses also found a log-normal distribution of the flux content of magnetic elements within ARs, suggesting that repeated random bifurcation dominates fragmentation and coalescence in all active regions (Canfield and Russell, 2007) and the process of fragmentation dominates the process of flux concentration (Abramenko and Longcope, 2005).
Harvey and Zwaan (1993) used Kitt Peak magnetograms to make a careful analysis of 29 solar rotations, selected during the period 1975–1986 (cycle 21). They analysed the properties of bipolar ARs (magnetic area ≥ 2.5 square degrees, 373 Mm2, corrected for size-dependent effects) at the time of maximum development. Each AR was counted only once, even if it was recurrent. They found that the distribution n(A) of the areas A of bipolar ARs is a smooth monotonically decreasing function of their area A, i.e., an essentially fixed power-law relationship between emergence frequency and size, with a size-independent multiplicative factor that is a function of the phase of the sunspot cycle. This study was extended in Zwaan and Harvey (1994), to include a large sample of ERs defined by the size range 45 < A < 375 Mm2, who found a continuity with previous work. The close correlation between area and total magnetic flux Φ found in Schrijver and Harvey (1994) implies that the n(Φ) function has the same properties and distribution as n(A).
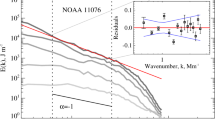
A decade later, Hagenaar et al. (2003) carried out a detailed analysis of the (directly measured) magnetic flux distribution of small-scale bipoles on the Sun using SOHO/MDI data from 1996 to 2001, and combined their distribution with that for ARs, from Harvey (1993) (which include works cited in the former paragraph). When making the composite, appropriate scaling between instruments and conversion between area and magnetic flux (Schrijver, 2001) had to be applied. The result confirmed that the emergence frequency increases smoothly and rapidly with decreasing flux (see Figure 3).
Left: Cycle-averaged area distribution (n(A)) of bipolar regions at maximum development. The numbers are corrected for incompleteness in the counts and are normalised to a number density per day and per square degree (≈ 150 Mm2). These results are based on 978 ARs (dots) and 9492 ERs (circles). The vertical bars on the latter indicate uncertainties arising from their short lifetime and low sampling rate. Error bars on AR numbers indicate uncertainties arising from statistics of small samples. Image reproduced with permission from Zwaan and Harvey (1994), copyright by CUP. Right: Hagenaar et al. (2003) combined the distribution functions of ARs (defined as regions larger than 2.5 deg2 taken from Harvey (1993), cf. left panel) with that of ephemeral regions (ERs) converting area to magnetic flux and applying flux scaling for different instruments. The plot shows flux emerging on the Sun per day, per flux interval of 1018 Mx. The distribution for active regions varies by about a factor of 8 through a typical cycle; the extremes of that variation bound the dark shaded area on the right. The much smaller variation for the smallest ephemeral regions, shown by the darkest shading is likely weakly in anti-phase with the sunspot cycle; full histograms are shown for 1997 October (black) and 2000 August (grey). The turnover below 1019 Mx likely reflects the detection threshold of SOHO/MDI. The lightly shaded area between the smallest ephemeral regions and the active regions is an approximation due to lack of proper coverage. Image reproduced with permission from Hagenaar et al. (2003), copyright by AAS.
Most recently, Parnell et al. (2009) analysed a combined set of magnetograms from SOHO/MDI (full disk and high-resolution) and Hinode/SOT to determine the flux-frequency distribution of all currently observable surface magnetic features in a range of more than 5 orders of magnitude in flux and 10 orders of magnitude in frequency. To identify features they used a ‘clumping’ algorithm, which defines a single feature as a group of contiguous, same-sign pixels, each of which exceeds an absolute flux cutoff. They found that all flux features, regardless of field strength, follow the same distribution — a power-law with slope −1.85 ± 0.14. This result implies that the processes that determine the spatial structure of surface magnetic features are scale-free. Hence, suggesting that either (i) all surface magnetic features are generated by the same mechanism (which may be a combined solar-cycle dynamo at the tachocline and a turbulent dynamo that works throughout the convection zone) that acts the same way at all scales, or that (ii) after flux emergence, the spatial structure of magnetic flux is dominated by processes in the interior or at the surface (e.g., fragmentation, coalescence and cancellation) that produce a scale-free distribution. They conclude that fragmentation produces a log-normal distribution when a single large feature is broken up, while on the Sun features come from a range of sources, and a combination of emergence, coalescence, cancellation, and fragmentation may well produce a power-law distribution. Continuing this line of research and applying the same method on Hinode/SOT data, Thornton and Parnell (2011) studied in more detail the low-flux end of the distribution extending the flux distribution study to the flux range of 1016 − 1023 Mx and nearly 18 orders of magnitude in frequency. They confirmed that there exists a single power-law distribution over all emerged fluxes, and suggested that this implies a scale-free dynamo, indicating that a turbulent dynamo may act throughout the convection zone. Moreover, from the slope of the emerging flux distribution the turbulent dynamo producing small-scale features produces considerably more flux than the active-region dynamo at the tachocline.
(a) Histograms of magnetic feature fluxes observed in the SOT data (blue), MDI high-resolution data (green), and 1998 May MDI full-disk data (red). (b) As (a), except here the lines are SOT data (blue) — for comparison — 2001 December (orange) and 2007 December (cyan) MDI full-disk data. The dashed line in both graphs is a fit to the data in (a) and has slope −1.85. These histograms show all feature fluxes between 2 × 1017 and 1023 Mx, regardless of flux amount, follow the same power-law distribution. Image reproduced with permission from Parnell et al. (2009), copyright by AAS.
2.2.1 Cycle dependence of AR distribution and characteristics
Tang et al. (1984), analysing a 15-year Mount Wilson magnetogram dataset (1967–1981), found that (i) AR size is dependent on solar cycle phase: the average area of an AR is significantly higher during cycle maximum than cycle minimum; and that (ii) “Regions of different sizes and different magnetic complexities show the same latitude variation with the phase of the solar cycle. The latitude range is smaller for larger-size regions; greater for smaller-size regions.” However, their finding (i) is in contradiction with the results shown above in Section 2.2, which show that the size/area distribution of ARs is cycle-invariant. This contradiction may be due to an underrepresentation of ARs in the low-flux end of the distribution, which is particularly likely during higher activity periods. The authors themselves admit that they may have under-estimated by as much as a factor of five the number of ARs with area inferior to 7480 Mm2, while they could detect regions as small as 450 Mm2.
In Chapter 3 of her thesis, Harvey (1993), while emphasising the cycle-invariant nature of AR area distribution, also found that there is a significant difference between the cycle-variability of ARs and ERs. The fixed spectral shape with changing activity does not hold for the ephemeral regions; while AR frequencies change by a factor of about eight from cycle minimum to maximum, the ER frequency changes by no more than a factor of two. This may point at distinct (dominant) origins for these extremes of the spectrum. She found that the first activity of a cycle is in the form of small bipoles: ERs and small ARs. Citing her:
These regions emerge 2 to 3 years before the first sunspots, at latitudes poleward of about 30°–35°. They possess preferential orientations that are reversed from the ARs at lower latitudes. (…) The size distribution of bipolar regions that belong to a given cycle varies with time, but only during the earliest years of a cycle preceding the sunspot minimum. At the time of the minimum, the size distribution of bipolar active regions has attained the characteristic size distribution of active regions, and maintains its distribution until the very end of the cycle.
For the width of the latitudinal distribution of ARs as a function of their size Harvey, 1993 (in Chapters 3 and 5) found that the spread of ARs around the average latitude of ARs (ϕ0) depends both on region size and cycle phase. We cite her summary:
At any time in the cycle, the regions larger than about 10 square degrees emerge within a confined latitude band about ϕ0. For smaller regions, the latitude distribution widens progressively with decreasing region size, most strongly on the poleward side of ϕ0. It reaches its maximum extent for ephemeral regions and (for all regions) during the maximum phase of the activity cycle. Throughout the cycle, more than half of the regions larger than 2.5 square degrees emerge within 6° of the average latitude ϕ0; half of the ephemeral regions emerge within 10 of ϕ0.
3 Fundamental Characteristics of Simple Bipoles in an Evolutionary Context
3.1 Polarity separation
Wang and Sheeley Jr (1989), analysing 2700 bipolar ARs (Bipolar Magnetic Regions or BMRs) with magnetic flux Φ ≥ 3 × 1020 Mx, corresponding to a magnetic area range of 310–11000 Mm2, i.e., excluding the smaller-flux end of the distribution, (cf. Figure 3) identified in Kitt Peak magnetogram data between 1976–1986 (cycle 21), determined the polarity separation vs. magnetic flux, shown in Figure 5. They find that the relationship between magnetic flux (in Mx) of the leading spot (which was presumed to be balanced by the following polarity field) and polarity separation (s) in heliographic degrees is Φ(s) = 4 × 1020 Mx s1.3. In this survey magnetic fluxes were determined at the region’s peak development whenever it was possible and each bipolar region was only counted once. However, magnetic fluxes were not determined by direct measurements in the magnetograms, but through proxies, using a combination of empirical rules:
-
A relation between sunspot area and magnetic flux: Φt = 0.3Ass, where Φt is the unsigned total flux expressed in 1021 Mx and Ass is the area of all the sunspots expressed in 1018 cm2, based on Sheeley Jr (1966) and Mosher (1977).
-
Or, alternatively, that the total flux in a sunspot Φspot = 0.25 × Bm × Au+p, where Bm is the central field strength of the spot and Au+p is its total umbral and penumbral area (Mattig, 1953).
Relationship (log-log) between magnetic flux (in Mx) of the leading spot in bipolar regions in the period 1976–1986 and polarity separation (s) in heliographic degrees. A least-square fit to the data (dashed line) defines a relationship as Φ(s) = 4 × 1020 Mx s1.3. Image reproduced with permission from Wang and Sheeley Jr (1989), copyright by Springer.
Tian et al. (2003), using Huairu magnetic data obtained between 1988 and 2001, analysed the magnetic flux-polarity separation relationship. Their data confirmed that the magnetic flux (Φ in 1020 Mx) is correlated with the magnetic polarity separation (d in Mm), and their best-fitting function Φ20 ∼ d1.15 is close to the result of Wang and Sheeley Jr (1989) described above.
The evolution of the polarity separation has not been deeply analysed so far in the literature. Kosovichev and Stenflo (2008) analysed 715 isolated ARs during their emergence, showed a representative example of flux, tilt angle and polarity separation evolution selected from their sample. Figure 6 shows the opposite polarities separating for four days as expected from the emergence of an Ω-loop, but then the process reverses and the polarity separation starts to decrease. Similar behaviour was shown by Waldmeier (1955), (his Figure 48) for a long-lived pair of spots (see Bray and Loughhead, 1964, their Figure 6.3). We cite Bray and Loughhead (1964): “According to Greenwich observers, the westerly motion of the preceding spot ceases when the group attains its maximum area; thereafter the motion is easterly. The following spot moves only eastward, but it comes to rest after a few days.” Wallace Hartshorn (2012) in her PhD thesis carried out the first statistical analysis of the flux and polarity separation evolution by studying 57 bipolar ARs whose full emergence phase was well observed by SOHO/MDI. The peak fluxes ranged between 1021–1022 Mx, with the average flux being 3.7 × 1021 Mx. As the spread in flux implies a spread of duration of flux emergence, a normalisation for the latter was carried out. The resulting average flux and polarity separation behaviour during the flux emergence period (on average 60 hours) is shown in Figure 6, right panel. The average behaviour shows a lag between peak flux and peak separation distance in bipoles, with the latter trailing. The latter, and a slight reversal of the flux separation at the end of the flux emergence process, confirm the generality of the behaviour demonstrated in the case study by Kosovichev and Stenflo (2008) shown in the left panel of Figure 6.
Left: Top panels show SOHO/MDI magnetograms taken at two stages of evolution of AR 8167 (a, b). The plots below show the evolution of magnetic flux, tilt angle, and separation of the centre of gravity of the two polarities as a function of time (c, d, e) and these three parameters plotted against each other (f, g, h). Image reproduced with permission from Kosovichev and Stenflo (2008), copyright by AAS. Right: Evolution of the average unsigned magnetic flux (above) and average separation distance (below), normalised to the peak values of 57 bipolar active regions that emerged on-disc in the period of 1997–2010 and observed with SOHO/MDI. Each time step is the average time for flux emergence derived from the top plot. The mean timescale was about 60 hours. The error bars are the standard errors on each averaged data point. The plot shows that polarity separation peak lags the peak flux by about 12 hours on average, and a slight reversal of the separation is seen after that, confirming the case study by Kosovichev and Stenflo (2008) in the left panel. Image reproduced with permission from Wallace Hartshorn (2012), copyright by IAU.
The polarity separation in simulations, as Fan (2009) remarks, is “so far a largely unexplored area with mostly speculations and very few quantitative calculations.” For an emerging Ω-loop (flux ring, see e.g., Caligari et al., 1995), the separation is driven by the magnetic buoyancy of the tilted flux tube legs, which is pulling the footpoints apart until the legs become vertical. Another force, acting in the opposite direction, is an attractive force between the opposite polarities (opposite electric charges ±q = Φ/2Π, where Φ is the total magnetic flux of the active region) which Fan (2009), in her Section 8.3, estimates to be (Φ/2Π)2/d62, where d is the polarity separation. However, she shows that this attractive force can only balance the magnetic tension-driven force if the polarities are very close, practically touching each other, and it falls with 1/d2, where d is the polarity separation. Thus, based on these considerations it is difficult to understand why the polarities when they are quite far apart may start to approach each other after the AR’s maximum evolution is reached. In the longer-term evolution, based on flux dispersal and a gradual disconnection of the flux tube from its toroidal roots, one may expect an ever-increasing separation trend (due to flux dispersion), unless the disconnection is owing to sub-surface magnetic reconnection between the Ω-loop’s legs (Schrijver and Title, 1999). It is surprising, however, that during the undisturbed decay of AR 7978 in 1996 Li and Welsch (2008) found no significant increase in the distance between the weighted positive and negative flux centers of the decaying AR when comparing its 3rd and 4th rotation (for more details see Section 6.1.1).
3.2 Tilt angle
A systematic tilt (a small angle to the direction of the equator) of the axis of bipolar ARs was discovered by Hale et al. (1919), see Figure 7. The result was based on a statistical study by A. H. Joy the 4th author of the paper, and this led Zirin (1988) to name this important characteristic of ARs after him as “Joy’s law”. We cite from the paper (p. 167):
A study by Joy of the sun-spot drawings of Carrington (1856–1861)Footnote 2 and Spörer (1861–1893)Footnote 3 shows that there is little change in this angle during the life of the group, but that in the mean the angle bears a definite relation to the latitude of the group. Twenty-six hundred and thirty-three bipolar and multiple groups, covering three and one-half sun-spot cycles, were examined. The following spot of the pair tends to appear farther from the equator than the preceding spot, and the higher the latitude, the greater is the inclination of the axis to the equator. This relation holds for both hemispheres.
Left: The base plot (black dots) shows the first statistical study of the latitude-dependence of the tilt angle of the axis of bipolar sunspot groups carried out by Joy on sunspot drawings of Carrington (1856–1861) and Spörer (1861–1893), as published in Hale et al. (1919). The y-axis shows the mean tilt angle and the x-axis the latitude. The study was carried out on 2633 sunspot groups over 3.5 solar cycles. Over-plotted are the results by Brunner (1930) (blue diamonds), obtained from a comparably large dataset of 8774 measurements of 1981 sunspot groups observed over three cycles (1894–1928) in Zürich. Thus, this combined plot of axial tilt angles is based on sunspot group observations of 6.5 continuous cycles. Right: Axial tilt angle of sunspot groups based on the Mt. Wilson white-light data between 1917–1985. Image reproduced with permission from McClintock and Norton (2013); copyright by Springer. Northern (diamond) and southern (triangle) hemispheres. Data were binned in 3° latitude. Error bars represent the standard error of the mean. For comparison, Joy’s law equations by Wang and Sheeley Jr (1991), dashed-dot-dot; Leighton (1969), large dash-dot; Norton and Gilman (2005), small dash-dot; Dasi-Espuig et al. (2010), solid. Linear fit for N and S hemisphere data (dash and dot, respectively) is also shown.
The weighted mean inclination results are shown in Figure 7, left panel. This result was confirmed by Brunner (1930) using 8774 measurements of 1981 sunspot groups observed between 1894–1928 in Zürich. However, Brunner’s measurements gave much higher tilt angles at high latitudes, where there are fewer spot groups.
Wang and Sheeley Jr (1989, 1991), analysing 2700 bipolar ARs (they call them BMRs) identified in Kitt Peak magnetogram data between 1976–1986 (cycle 21), found that for lower-flux bipoles the tilt angles tend to be larger in absolute value. The tilt angles of the lower-flux bipoles also have a wider scatter about their average values than the tilt angles of stronger sources. They confirmed that the average tilts of BMRs relative to the east-west line increases toward higher latitudes, and that over the analysed period the tilt angle (γ) may be expressed as a function of latitude (θ) as follows: sin γ = 0.48 cos θ + 0.03. Although this relationship is very close to that applied by Leighton (1969), namely sin γ = 0.5 cos θ, it appears incorrect, and should be replaced by the relation sin γ = 0.48 sin θ + 0.03. The latter, corrected relation, also fits the graph shown by Wang and Sheeley Jr (1991) in their Figure 1, in which sine tilt angle against sine latitude are plotted. It is noteworthy, that recently McClintock and Norton (2013) have used the corrected relation for Joy’s law when citing the relations established by Wang and Sheeley Jr (1991) and Leighton (1969). The latter was based on tilt measurements by Brunner (1930), and plotted in Figure 7, right panel.
The history of Joy’s law studies are studded with confusing and controversial results. For example, Tang et al. (1984), analysing a 15-year Mount Wilson magnetogram dataset (1967–1981), did not detect any systematic latitude-dependence of the tilt angle. Howard (1991b), using Mount Wilson white-light sunspot data for the period 1917–1985 found a strangely irregular increase of the tilt angle with latitude. Since the tilt angle analysis by Howard (1991b) was based on white-light images with no magnetic polarity information, the dataset included pseudo-bipoles (e.g., pairs of same-polarity spots) and cannot separate reversed-polarity (anti-Hale) bipoles. Later analysis by Fisher et al. (1995) is based on the same dataset used by Howard (1991a). They find that the mean tilt of sunspot groups is an increasing function of both latitude and polarity separation, which was used as a proxy for the total magnetic flux (a reasonable assumption, see Section 3.1).
More recent analyses of Joy’s law have been based on large datasets of magnetograms (SOHO/MDI and SDO/HMI data) and used automatic image-processing algorithms (Stenflo and Kosovichev, 2012; Tlatov et al., 2013). Results are shown in Figure 8. The main difference between the analyses of Stenflo and Kosovichev (2012) and Tlatov et al. (2013) is that the former folds all data into one function describing the latitude dependence of the bipole tilt angle, even that of those bipoles which very significantly deviate from Joy’s law (including those with anti-Hale orientation). Tilt angles outside the range [−90°, +90°] have been shifted by 180, and the two hemispheres have been merged by considering the tilt angle positive when the leading spot is closer to the equator than the following spot. The resulting fit function found by Stenflo and Kosovichev (2012) (γ = 32.1° sin θ) has impressively low error bars and a small deviation from the data points even at high latitudes (cf. Figure 8, left panel). It gives an easy-to-remember rule that the sine of the tilt angle is approximately half of the sine of the corresponding latitude angle. As the angles are relatively small, the relation roughly works between the tilt and latitude angles, too (γ ≈ 5° at θ = 10°, γ ≈ 10° at θ = 20°, etc.). These values are significantly higher that the tilt angles found by Howard (1991b), but fit quite well to the values found by Brunner (1930) at the same latitudes. However, the tilt angle-latitude relationship has turned out to be more complicated than the latter analysis has shown when Joy’s law for small bipoles down to the ephemeral region level was studied. Surprisingly, Tlatov et al. (2013) found that for bipoles with area < 300 MSH, Joy’s law is the opposite of that for bipoles with area above the 300 MSH limit (see Figure 8, right panel). The difference with the results of Stenflo and Kosovichev (2012) is attributed to a bias owing to inclusion of smaller bipoles in their sample. The higher the latitude, the more dominant the small bipoles and their effect on the average tilt angle becomes according to Tlatov et al. (2013).
Latitude-dependence of tilt angles determined more recently. Left: Tilt angle of 160 079 bipolar regions (bipolar active regions were identified in each magnetogram independently, so one specific bipolar region was included several times in the dataset) by Stenflo and Kosovichev (2012); image reproduced with permission, copyright by AAS. SOHO/MDI magnetograms were used for a 15 year period between May 1996–April 2011. Tilt angles outside the range [−90°, +90°] have been shifted by 180° to be brought back to this interval, to allow all regions to be described by a single relation, irrespective of hemisphere or cycle. Positive tilt angle γ means that the preceding polarity is equatorward of the following polarity. The solid curve is the fit function γ = 32.1° sin b, where b is the heliographic latitude. Right: Bipole tilt angles for small and large bipoles as well as for the north and south hemispheres determined separately using SOHO/MDI and SDO/HMI data. Image reproduced with permission from Tlatov et al. (2013), copyright by the authors. Black squares correspond to areas S > 300 MSH for MDI, green diamonds to areas S > 300 MSH for HMI. Blue points correspond to areas 50 < S < 300 MSH for MDI, red triangles to areas 20 < S < 100 MSH for HMI. Bmin = 10 G for MDI and 15 G for HMI. The tilt angles are the opposite for small bipoles than that for large ones, which conform to Joy’s law.
McClintock and Norton (2013) revisited the Mt. Wilson dataset taken in the period 1917–1985 and made a critical overview of the principle Joy’s law studies. Their main result is a revision of Joy’s law toward a weaker dependence on latitude and without forcing the tilt to zero at the equator. They also confirmed the results by Dasi-Espuig et al. (2010), i.e., that the tilt angle is cycle and hemisphere dependent. Based on data averaged for this long period they found the relations quite different for the N and S hemispheres: γN = 0.26θ + 0.58 and γS = 0.13θ + 1.38 (see Figure 7, right panel).
In summary, there is still no consensus on the latitude dependence of bipole tilt angles, as the different datasets and analysis methods lead to significantly differing results. One of the reasons behind the differing results must be data selection that combines bipoles at different stages of their evolution, as we will argue below.
To what is this systematic tilt due? Babcock (1961) proposed that the toroidal field created from a poloidal field by differential rotation would not be perfectly toroidal but spiral, retaining a small polar angle. However, he also mentioned that Coriolis forces acting on the fluid upwelling around a BMR could also cause a tilt in the observed direction. Leighton (1969) suggested kink deformation of twisted flux tubes as the origin of the tilt. Schmidt (1968) and Wang and Sheeley Jr (1991) suggested that the tilt is caused by the Coriolis force acting on the expanding plasma contained within a buoyant rising flux tube (i.e., not in the surrounding plasma), which was supported by simulations by D’Silva and Choudhuri (1993). They showed that the Coriolis force acting on plasma in the rising and expanding Ω loop will tilt the top of the fluxtube clockwise in the northern and counter-clockwise in the southern hemisphere, leading to an equatorward tilt of the bipole as observed. For more details about the simulation results and theoretical considerations see Fan (2009), Section 5.1.2. Kosovichev and Stenflo (2008) returned to Babcock’s spiral field idea based on their analysis of tilt evolution during the flux emergence process. They found that tilt did not relax to zero, as one would expect from an E-W toroidal field and tilt imparted by the Coriolis force, which should cease once the top of the flux tube has fully emerged. Most recently, McClintock and Norton (2013) argued that Joy’s law is due to a combination of both the Coriolis force acting on the rising flux as well as an initial tilt imparted to the flux rope from the toroidal geometry that it retains.
There is a large scatter in the tilt angle, which in the various studies may have contributions from the following components:
-
The age factor: (i) The orientation of the bipoles is almost random when the bipole first appears, but generally after 1–3 days it becomes more organised, attaining the final orientation (Weart, 1970; Harvey, 1993; Kosovichev and Stenflo, 2008).
-
The size factor: It was first shown by Harvey (1993) that the scatter is greatly dependent on the size (i.e., flux content) of the bipoles, being the smallest for the largest bipoles and increasing with decreasing region size (see Figure 10). However, the largest ARs again appear to statistically deviate from Joy’s law (see Tlatov et al. (2010); Figure 11).
-
Polarity separation: Fisher et al. (1995) showed that the mean tilt (α) at a given latitude increases with increasing polarity separation (d) by Δα ∼ 10° × (d/100)−3/4, where d is in Mm and Δα is in degrees.
-
Distance from the centroid of the butterfly: Harvey (1993) found that the preferential orientation of ARs and ERs is the strongest at the average latitude of ARs (ϕ0); the deviation from this orientation increases with the differential latitude Δϕ0.
-
Magnetic twist: a deformation of the flux tube axis (writhe, see Section 3.4) may introduce a scatter of the tilt angle due to an intrinsic scatter in the inherent twist (Holder et al., 2004) and the weak nature of the hemispheric helicity rule. Furthermore, during the emergence of a twisted flux tube the azimuthal field component in the flux rope shows up in the line-of-sight magnetic field, leading to elongation of the two polarities (López Fuentes et al., 2000; Luoni et al., 2011), cf. Figure 9, upper panels. When magnetograms are used for the determination of tilt angle, these magnetic tongues or tails may mask the tilt angle of the bipole. However, the magnetic tongues retract when the flux rope has crossed the photosphere and this effect disappears.
Holder et al. (2004) using a combined dataset of Mt. Wilson full-disc magnetograms and Haleakala Stokes Polarimeter (HSP) vector magnetograms analysed the tilt-twist relationship. They find no inter-dependence of tilt and twist for ARs that obey Joy’s law. These regions are the ones with a weak twist. Regions that significantly depart from Joy’s law (> 6σ) show both stronger-than-average twist and a strong inter-dependence of tilt and twist (negative correlation, since the writhe induced by twist, which obeys the hemispheric helicity rule, is of opposite sign to that required by Joy’s law for each hemisphere). They conclude that a substantial fraction of ARs in their dataset show evidence of having gone through the kink instability. Earlier, Tian et al. (2001), using Huairu vector magnetograms of 286 ARs reached an opposite conclusion: they found a positive correlation between tilt and twist (after correcting for their definition of tilt, which results in a sign opposite to that of Holder et al., 2004). As Holder et al. (2004) remark, Tian et al. (2001) did not take out the mutual latitudinal dependence between twist and tilt, and therefore any signatures of writhing could have been suppressed in their data set. Nandy (2006), further analysing the dataset used by Holder et al. (2004), as well as Yang et al. (2009), analysed the twist-tilt relationship. For further details, see Section 3.4. A different approach was taken by Wallace Hartshorn (2012), who looked for differences in tilt angle between ARs that obey and disobey the hemispheric helicity preference. In a sample of 57 bipolar ARs she found no bimodal distribution of the tilt angle in the two groups. In fact, the tilt angle dependence on latitude in these two groups was exactly the same. This negative result contradicts expectations that kinking due to internal twist may have, statistically, a significant effect on the writhe/tilt angle of ARs.
Kosovichev and Stenflo (2008), using the SOHO MDI 96-minute full-disc magnetogram dataset selected 715 isolated ARs, which were born within 30° of the central meridian, and analysed the evolution of their tilt as a function of time, polarity separation and flux content. They found that at the very start of their emergence bipoles are randomly oriented and the preferential tilt angle is only attained by mid emergence, confirming earlier results by Weart (1970) and Harvey (1993). We would like to remark that this fits well with the findings of Fisher et al. (1995), who provided evidence that in magnetic data the presence of magnetic tongues in emerging twisted flux tubes (López Fuentes et al., 2000; Luoni et al., 2011) may modify the tilt angle. Since the tongue-pattern resulting from, e.g., negative/positive twist on the northern/southern hemisphere shifts the centre of gravity of the magnetic polarities introducing an angle that is opposite to that of Joy’s law (cf. Figure 9, upper panels). Therefore, the tilt angle of bipoles that obey the hemispheric helicity rule, may be cancelled by this effect during their emergence and the bipole will only gradually assume the Coriolis-induced tilt by the time the tongues have retracted.
Upper panels: Sketches of magnetic “tongue” patterns in longitudinal magnetograms with (left) positive and (right) negative global twist in the emerging flux rope, which develop due to the presence of the transverse magnetic field component. Representative field lines of the enveloping arcade and internal (dipped) field lines are also shown. Middle and lower panels: Observations of evolving magnetic tongue pattern: SOHO/MDI magnetograms showing the emergence of AR 8171 between 26–28 February 1998. The magnetic tongue pattern indicates positive (right-handed) magnetic helicity (cf. upper left panel). Coronal loops seen in the SOHO/EIT image (taken on 1 March 1998; lowest right panel) indicates also positive shear/helicity in the corona. Image reproduced with permission from Luoni et al. (2011), copyright by Springer.
Kosovichev and Stenflo (2008) found no significant dependence of the tilt angle on the total magnetic flux of the AR. The latter is a surprising (and most disappointing) result from the point of view of interpretation of the AR tilt as the effect of the Coriolis force acting on rising and expanding flux tubes in the convection zone, since it contradicts expectations based on modelling results. Fisher et al. (1995) derived a function α ∼ Φ1/4 sin θ where α is the tilt angle, Φ is total flux (although the separation distance d was used as a proxy for it), and θ is latitude. The expectation is based on the deduction that the higher the magnetic flux, the greater the buoyancy force, and therefore the shorter the rise, i.e., the shorter the time the Coriolis force can act on the rising flux tube. From the lack of dependence of the tilt angle on magnetic flux and because after the emergence stops the Coriolis force vanishes yet the bipoles do not appear to relax to the E-W direction but (statistically) to Joy’s law, Kosovichev and Stenflo (2008) conclude that “Joy’s law reflects not the dynamics of the rising flux tubes but the spiral orientation of the toroidal magnetic field lines below the surface as suggested by Babcock (1961)”. As mentioned above, McClintock and Norton (2013) have endorsed this suggestion.
Recently, Tlatov et al. (2010) studied the latitudinal distribution and orientation of magnetic bipoles during cycles 21–23. The data set included daily observations from Kitt Peak (1975–2002) and MDI/SOHO (1996–2009). Bipole pairs were selected on the basis of proximity and flux balance of two neighbouring flux elements of opposite polarity. Based on their area, the bipoles were classified as small quiet-Sun bipoles (QSBs), ephemeral regions (ERs), and active regions (ARs). Large ERs and ARs were found to follow the Hale-Nicholson polarity rule, and the tilt of ARs follows Joy’s law. The tilt of small ERs, however, appeared to disobey Joy’s law, while QSBs were randomly oriented (Figures 10 and 11). A surprising result was that unlike ARs, ERs also show a preference in their orientation depending on the polarity of the large-scale magnetic field. The authors suggested that these orientation properties may indicate that some ERs may form at or near the photosphere via the random encounter of opposite polarity elements, while others may originate in the convection zone at about the same location as ARs.
Left: The dependence of the orientation of bipoles on their size shown in an octagonal histogram: Relative numbers in the orientation bins for six area ranges preceded by the number of regions between parentheses based on Harvey’s thesis (1993). Image reproduced with permission from Schrijver and Zwaan (2000), copyright by CUP. Right: Circular histograms of normalised number of bipoles as a function of their tilt separated for the two hemispheres (N: upper row; S: lower row) in four different area bins in MSH as indicated in each panel. The histograms were constructed by Tlatov et al. (2010) for bipoles in the ± 30° latitude range identified in SOHO/MDI data during 1998–2006. Image reproduced with permission, copyright by AAS.
Tilt (deg) of bipoles as a function of their area, S in MSH as computed by Tlatov et al. (2010) for bipoles in the ± 30° latitude range identified in SOHO/MDI data during 1998–2006. Filled squares (open circles) show an average tilt for bipoles in northern (southern) hemisphere. Error bars correspond to 1σ standard deviation. Tilts for the southern hemisphere were multiplied by −1 to allow them to be plotted over the northern hemisphere tilts. The plot shows that bipoles ≤ 300 MSH, though with a large scatter, are statistically disobeying Joy’s law. Image reproduced with permission, copyright by AAS.
However, tilt can also be caused by deep-seated large-scale vortices in the convective zone that deform the rising flux tube (López Fuentes et al., 2000, 2003). The effect of turbulent buffeting of rising flux tubes is well demonstrated by departures from Joy’s law which increase with decreasing flux content of the emerging bipole (Harvey, 1993; Longcope and Fisher, 1996). Such turbulent perturbations, if created in the topmost layer of the convection zone, should relax rapidly (Longcope and Choudhuri, 2002), which conforms with observations. For a more detailed description of the modelling efforts and theoretical background see Fan (2009). An interesting case study was carried out by González Hernández et al. (2013) of AR 11073. Its tilt angle was significantly different from that described by Joy’s law and it showed an anti-clockwise rotation for at least four days between 30 May and 2 June 2010. The authors explored the possibility of the sub-surface local dynamics being responsible for the significant rotation of this AR by applying the ring-diagram technique to infer the flows under and surrounding the AR. They found a good agreement between the direction of sub-surface vorticity and deviation from the tilt angle given by Joy’s law, which is the very first confirmation of the role of sub-surface vortices changing the tilt angle of ARs.
3.3 Asymmetric proper motion of leading and trailing sunspots
Proper motion pattern in a complicated active region may look chaotic at first glance. However, when the individual bipoles which build-up the AR are followed from their birth, a system emerges: the opposite polarity spots move apart and the ensuing divergence is rarely symmetric. As a rule, leading or preceding (p) sunspots move faster westward than their trailing or following (f) counterparts move eastward. This asymmetry in sunspot proper motions has been long known, dating back to Carrington (1863). Maunder (1919) described the phenomenon as follows:
An examination … shows that remarkable action takes place in the early history of several of the principal groups. Two chief spots become distinguishable while the group is still small, of which the one preceding in longitude — the “leader” — moves forward in longitude for several successive days, but with diminishing speed. The rear-spot, on the contrary, retrogrades, or remains stationary in longitude, so that the distance between these two spots increases, and the group lengthens out. The average length of a fully-developed group of this type is from 10° to 12°. The leader-spot increases in area and advances in longitude for a few days, the two changes, in most cases, coming to the end at the same time. The halt of the advance in longitude is, in some instances, very sudden.… After the halt of the leader the decay of the group sets in, but the process is much slower than the growth. The members of the group disappear with the exception of the leader, which generally becomes circular and strongly defined, stable in area, and with a tendency to slow retrogression in longitude.
This early asymmetry in proper motion introduces a bias in the rotation rate of young bipoles, as pointed out by, e.g., Balthasar and Wöhl (1980) and Ternullo et al. (1981). This higher-than-average rotation rate is decreasing with the age of the sunspot group (Tuominen and Virtanen, 1987). Ruždjak et al. (2004) analysed Greenwich Photoheliographic Results data for the years 1874 to 1976 to determine rotation velocity evolution for long-lived and short-lived ARs. The rotational velocities were divided into six latitude strips of 5° width and grouped according to the age of the sunspot groups. For 955 recurrent sunspot groups (groups with a lifetime of at least 20 days and reaching areas larger than 200 MSH during their evolution) they found a decrease of the rotational velocities from their emergence to the values approaching the velocities of the photospheric plasma by their 2nd and 3rd rotations. The mean velocity difference was 0.5° day−1. They also found that during their emergence phase the long-lived recurrent sunspot groups (sample size: 955) showed higher velocities than the shorter-lived non-recurrent groups (sample size: 13 169) by about 0.15° day−1. Statistical analysis of sunspot group rotation rates have their caveats, however. Petrovay (1993) pointed out that area weighting of sunspot group positions leads to fake proper motions in the decaying phase of sunspot groups, most prominently in the decay phase due to the faster decay of f spots, which will shift the weighted centre of area towards the p spots introducing a fake proper motion of the group as a whole in the direction of rotation. This can result in an overestimate of the rotational velocities by several percents.
Since sunspots appear at the intersection of strong magnetic flux tubes with the photosphere, the motion that we actually observe is merely a series of successive cross-section locations of the rising parent flux tube, therefore the geometry of the flux tube should strongly influence the proper motion pattern. Naturally, flux tubes do not emerge as rigid systems. Strong buoyancy stretches the flux tube, which also breaks up and emerges in pieces (see Section 3.5). Nevertheless, the proper motion pattern of the sunspots, which are forming at the extremes of the emerging flux tube/rope should be influenced by the geometry/inclination to the vertical of the emerging flux tube.
3.4 Magnetic helicty
The most recently recognised intrinsic characteristic of ARs, that potentially has the widest-ranging impact on the activity of ARs, was the recognition that emerging flux is inherently twisted. Leka et al. (1996) were the first to provide observational evidence for twisted flux emergence, inspiring research contributing to a revival of interest in magnetic helicity. Magnetic helicity is a measure of the shear, twist and linkage of the magnetic field. Magnetic flux emerging with inherent twist has a very important relevance for solar activity: emerging flux carries free magnetic energy ‘ready’ to be released. Photospheric shearing motions, which have been long thought to be the generators of magnetic stresses, may simply reflect the emergence of a twisted structure as successive cross-sections of a helical structure can easily be mis-interpreted as shearing flows (Démoulin and Berger, 2003). Nevertheless, plasma flows do exist on the Sun, therefore their effects on emerged fields should not be dismissed. Rather, twisted flux emergence and large-scale flows are both responsible for the free energy level of magnetic field structures we see on the Sun.
The widest-documented example of twisted flux emergence was published by Leka et al. (1996), who presented a careful analysis of flux emergence in AR 7260 utilising multi-wavelength data including Hawaii IVM vector magnetograms. They showed that:
-
the emerging bipoles were already co-spatial with significant vertical currents at a very early stage and the currents increased together with the flux;
-
Hα and X-ray morphology, proper motions and measured currents of the bipoles were all consistent, implying the same sense of twist
-
the increase of currents, as the new flux emerged, was not consistent with their generation by photospheric motions.
Wang and Abramenko (2000) used Huairou vector magnetograms to analyse the emerging AR 7321 during three days. They found that
-
the total positive (negative) electric current grew simultaneously and linearly with the increase of the total positive (negative) flux;
-
a linear extrapolation to the zero flux gave a non-vanishing total current, which may indicate that the photospheric magnetic field is not force-free;
-
the α parameter, which characterises the twist of the flux for the entire AR remained nearly constant during the emergence.
Other authors (e.g., Ishii et al., 2000; Kurokawa et al., 2002) used Hα morphology and sunspot motions to argue that flux emerged twisted.
Prior to the observational evidence by Leka et al. (1996) theoretical arguments had been raised in favour of non-potential flux emergence from considerations of energy available for flaring (McClymont and Fisher, 1989; Melrose, 1992). Furthermore, Schüssler (1979) and later Longcope et al. (1996), through MHD simulations, showed that non-twisted flux cannot even make it through the convection zone due to a strong tendency for fragmentation. However, the flux cannot be fragmented by eddies forming in its wake but can remain coherent if it is sufficiently twisted (Moreno-Insertis and Emonet, 1996). Many other simulations have been carried out since, verifying this result while probing deeper into the details of inherent twist in emerging flux tubes (see, e.g., Murray and Hood, 2008). These simulation results imply that inherent twist is a general property of flux emergence on the Sun, i.e., that all the large-scale flux that has crossed the convection zone must be twisted and therefore must possess magnetic helicity.
During the last decade, magnetic twist became one of the “buzzwords” of solar physics, igniting many observational, computational and theoretical attempts to understand its broad role in various activity phenomena, e.g., from the formation of δ active regions (Linton et al., 1999; Fan et al., 1999), sigmoids (Titov and Démoulin, 1999; Magara and Longcope, 2001) to CMEs (Low, 1996; Démoulin et al., 2002b).
Magnetic helicity is a quantitative, mathematical measure of the chiral properties of magnetic structures. Chirality patterns discovered in active regions, coronal loops, filaments, coronal arcades and interplanetary magnetic clouds (Pevtsov and Balasubramaniam, 2003, and references therein) indicate that the Sun preferentially exhibits left-handed chirality in features in the northern hemisphere and right-handed features in the south. A right-handed twist manifests itself in coronal loops that curve in a clockwise sense when viewed from above and this implies positive helicity, and vice versa for negative helicity. Exceptions to these helicity rules occur in most categories of solar activity at a significant percentage (20–35%). Nevertheless, the Sun’s preference for features adhering to these rules is suggestive of an underlying mechanism that is, evidently, global in scope. Nandy (2006), deriving the twist in a large sample of active regions from vector magnetograms, found the dispersion in the active region twist distribution is latitude-independent. The amplitude and dispersion of twist was found to decrease with increasing magnetic size of active regions, supporting the ∑-effect model, which invokes helical turbulent buffeting in the convection zone of rising flux tubes as the mechanism for twist creation (Longcope and Fisher, 1996; Longcope et al., 1998).
The exception to the hemispheric helicity rule rate depends on the evolutionary stage of the active region. It is high when active regions first emerge. Luoni et al. (2011) determined the helicity sign of 40 active regions during the emergence phase as inferred from the shape of the AR’s magnetic tongues and found that 63% of southern hemisphere active regions follow the hemispheric trend and only 57% of regions in the northern hemisphere do. Yang et al. (2009) found that 57.6% (56%) of emerging active regions in the southern (northern) hemisphere follow the helicity trend when using the method of Chae et al. (2001) to determine the helicity of the region. In a study that involved a broader spectrum of active regions (not only emerging active regions), Pevtsov et al. (1995) used the linear force-free field alpha-coefficient to determine the sign of helicity and found a stronger hemispheric helicity trend where 69% (75%) of northern (southern) regions had negative (positive) helicity. The exception to the hemispheric helicity rule rate continues to decrease as the active region flux ages, dispersing its magnetic flux and eventually disappearing, so that most quiet sun filaments fit the hemispheric rule with a very strong tendency of high-latitude filaments fitting the rule — dextral (negative helicity) in the north and sinistral (positive helicity) in the south, (Martin et al., 1992).
This is probably owing to the effect of reconnection between magnetic flux containing opposite magnetic helicity that removes equal amounts of helicity of both signs so that the once weak preference for a helicity sign becomes dominant. The slowly increasing effect of differential rotation may also play a significant role, as this injects negative helicity in the northern and positive in the southern hemisphere. However, it is noteworthy that helicity injection by differential rotation is dependent on the orientation of the bipole, and it even changes sign if the bipole has a larger than 45° tilt angle to the equator (Démoulin et al., 2002a).
3-D spherical shell anelastic MHD simulations of the buoyant rise of magnetic flux tubes through the convection zone by Fan (2008), however, indicate that the initial level of twist must be lower than previously thought. These 3-D simulations show that for tubes with the twist level that is necessary for a cohesive rise, the twist-induced tilt (deformation of the flux tube at its apex) dominates that caused by the Coriolis force, and furthermore, the twist-induced tilt is of the wrong direction (opposite to the observational Joy’s law) if the twist is left-handed (right-handed) in the northern (southern) hemisphere, following the observed hemispheric preference of the sign of the active region twist. In order for the emerging tube to show the correct tilt direction (consistent with observations), the initial twist rate of the flux tube needs to be less than half of that needed for a cohesive rise. Under such conditions, severe flux loss was found during the rise, with less than 50% of the initial flux remaining in the Ω-tube by the time it reaches the surface. This result by Fan (2008) may explain the low level twist in active regions deduced from current helicity measurements (Longcope et al., 1999).
3.5 Peculiality of flux emergence phase: serpentine flux tubes
The model of active region formation via the emergence of a coherent sub-photospheric Ω-shaped flux rope (Zwaan et al., 1985) has been further developed into a scenario where the flux rope is shredded before its passage across the photosphere; an idea driven by observations with sufficient spatial resolution that shows that the first emergence is composed of a series of very small magnetic bipoles in between the main coalescing and diverging polarities (Strous et al., 1996; Strous and Zwaan, 1999). This characteristic observation of emerging ARs suggests that the magnetic Ω-loop, which breaks through the photosphere and emerges into the chromosphere and corona, is broken into nearly parallel strands, but somewhere, not very deep under the surface, at least part of the flux bundle joins and is being held together, as indicated by the coalescence of the majority of the flux as the emergence proceeds.
The fragmentation of the Ω-loop is likely to occur just under the photosphere and indicates the difficulties that a flux tube has in crossing from the convective zone into the solar atmosphere. The rapidly changing physical conditions at the top of the convective zone, where the plasma pressure, density and temperature drop by several orders of magnitude, means that the Ω-loop rapidly loses its buoyancy. The top portion of the Ω-loop becomes denser than its surroundings as it approaches the top of the convective zone, its rise stops, and magnetic flux piles up under the photosphere. Here, the flux takes on an undulatory (serpentine) shape due to the magnetic Rayleigh-Taylor instability (Parker, 1966) and the effects of convective flows (Cheung et al., 2008, 2010).
A wave-like pattern in the emergence sites (Strous and Zwaan, 1999) indicates that the strands of the shreaded flux tube emerge at several places, like a sea-serpent, creating a mixed polarity field. Wang and Zirin (1992) remarked that in this mixed polarity field a substantial amount of flux is cancelled. If, however, we indeed witness the emergence of an undulatory flux tube, at least part of the cancellation may be due to the emergence of small U-loops, i.e., the straightening out of the wavy flux tube as it finally breaks through the photosphere. Such a scenario may show up in the evolution of arch filaments (Georgakilas et al., 1993). High temporal and spatial resolution vector magnetic, Ha and Ca i 6122.2 Å Doppler observations of the Flare Genesis balloon-borne experiment confirmed the sea-serpent topology during the early phases of emerging flux tubes (Bernasconi et al., 2002). With magnetic extrapolations, elongated flux tubes linking a series of bald patches (in which field lines are tangent to the photosphere) were found in the emerging flux region observed by Flare Genesis (Pariat et al., 2004) and also in another emerging AR (Mandrini et al., 2002), which are very suggestive of the sea-serpent topology.
However, the serpentine flux may carry a significant amount of plasma (Cheung et al., 2010) which will drain into the U-loop sections of the serpentine field and which must be unloaded from the field lines before a buoyant emergence into the solar atmosphere can resume following the sub-photospheric pile-up. A data driven 3D numerical simulation of the emergence of a serpentine field shows that electric currents build up along the separatix surface that forms along the field, and photospheric shearing motions lead to magnetic reconnection in the bald patch sections (Pariat et al., 2009). This reconnection produces the observational signature of Ellerman Bombs (Ellerman, 1917) and disconnects the U-loop sections of the field which contain the dense plasma, allowing the serpentine field to emerge (Pariat et al., 2004). Flux cancellation would also be observed in this scenario. The undulatory serpentine flux takes on the global Ω-loop shape of the active region only after successive reconnection events. This flux emergence scenario is also found in the 3D radiative numerical simulation of Cheung et al. (2010).
A study by Valori et al. (2012) brought together non-linear force-free field modelling and local correlation tracking of the photospheric flow patterns with high resolution coronal imaging and spectroscopic observations of the emergence of AR 11024. The flow patterns in this AR revealed converging motions of opposite magnetic polarities in the U-loop sections followed by flux cancellation, indicative of magnetic reconnection. The global analysis of the reconstructed magnetic field of the active region supports the transformation of the serpentine field into the global field of the active region via successive reconnection events.
Given this flux emergence scenario, there still remains the question of how the undulatory/serpentine flux influences the signed/unsigned flux of the whole active region? This must depend on the resolution of the magnetograms, but the increase of flux should be steeper at the start of the emergence phase due to the fact that the same flux tube may surface, and therefore its flux is measured, several times. Magnetic flux measurements during the full emergence-period with changing (rebinned) resolution would be very enlightening.
3.6 Clustering or nesting tendency of flux emergence
As was mentioned in Section 1.3, the first note on the clustering tendency of sunspot appearances was made by Cassini (1729). Ribes and Nesme-Ribes (1993) cited his description of the phenomena as follows: “There is some reason to believe there exist special locations in the Sun that are propitious for the formation of spots, which do not stray far from their point of origin”.
ARs tend to emerge in the immediate vicinity or within the boundaries of an existing AR (Bumba and Howard, 1969). Liggett and Zirin (1985) and later Harvey and Zwaan (1993) showed that there is a 10 to 22-fold higher emergence rate within existing ARs than in the quiet sun. Furthermore, there is a tendency for ARs to emerge in the immediate vicinity of an existing AR, or at the site of a previous AR, forming “activity nests”, which may exist as long as 6–7 months (Brouwer and Zwaan, 1990). The longest-lived activity complex of cycle 21, called the “Great Complex”, persisted for 20 solar rotations, consisted of 29 major ARs (i.e., having spots of life time ≥ 7 days with penumbrae) and spanned about 90° in longitude (Gaizauskas et al., 1983, 2001; Gaizauskas, 2008). In active nests or activity complexes there is a continuity of major flux emergence in close proximity for 3–6 months, and total magnetic flux may reach 2 × 1023 Mx, though smaller nests contain less flux. Magnetic flux is nearly balanced in nests and most of the flux is canceled within the boundary of the nest, never diffusing out of it (Gaizauskas et al., 1983). However, significant polarity separation can result from very effective cancellation processes in the interior of the nest, creating strong monopolar flux areas at/along its boundaries, which will diffuse; each will be carried by meridional flows and distorted by differential rotation, creating strong poleward “plumes” of magnetic field(s) (Gaizauskas, 2008). When a nest exhibits a local flux imbalance, the diffusing weak magnetic flux, which can be as much as that of a major AR, i.e., ≥ 1022 Mx, will be the source of a single-polarity poleward plume, which may build or erode polar fields. Opposite-polarity monopolar plumes produced by neighbouring nests form the largest (comparable to the solar radius) and longest-lived quiescent filaments (Gaizauskas, 2008).
The nested nature of flux emergence is very strong, nearly 50% of all emergent bipoles are part of an active nest or activity complex (Schrijver and Zwaan, 2000). The recurrent nature of flux emergence (called “active longitudes”, by Carrington, 1858), has been linked to longitudinal wave numbers of magnetic instabilities in a concentrated toroidal field (Gilman and Dikpati, 2000) and more recently to shallow-water instability of differential rotation and toroidal field bands in the solar tachocline (Dikpati and Gilman, 2005). They have also been linked to the non-axisymmetric nature of the solar magnetic fields (Benevolenskaya, 2005). For more details on cycle dependence, periodicities, rotation rates and multi-wavelength studies of activity complexes see Benevolenskaya (2005).
The nested nature of flux emergence is reflected in the formation of some of the large, magnetically complex ARs as several bipolar ARs emerge separated, but in close proximity and in close succession within a few days (Schrijver and Zwaan, 2000). Magnetic complexity and activity levels are closely linked.
4 Decay Phase and the Removal of Magnetic Flux from the Photosphere
4.1 Lifetime of sunspots
There is a notable asymmetry in the time spent by an active region in emergence and decay: emergence lasts for hours to days (≤ 5 days; Harvey, 1993), while the decay of spots may last from days to several weeks (e.g., Hathaway and Choudhary, 2008) and even in some cases months (van Driel-Gesztelyi et al., 1999a). Once all the magnetic flux has emerged, or possibly even before that (McIntosh, 1981; Wang et al., 1991), active regions start to decay. After sunspots reach maximum area, partially through coalescence of smaller umbrae, spots start shrinking and breaking up indicating that processes begin to occur that erode and fragment the once coherent large-scale magnetic flux concentration. See the Living Review by Rempel and Schlichenmaier (2011) for the theory of sunspots.
4.2 Moving magnetic features
Decaying sunspots that are (at least) partly surrounded by a moat can show streams of small (103 km diameter) low magnetic flux fragments (1018–1019 Mx) that move radially outwards from the spot at speeds of around 1 km s−1 (Sheeley Jr, 1969; Harvey and Harvey, 1973; Hagenaar and Shine, 2005), advected outward by the moat flow. These features have been named moving magnetic features (MMFs) by Harvey and Harvey (1973) who found in their study of 37 decaying spots that 21 showed MMFs. At the edge of the moat the MMFs disappear or merge into the network. There appear to be two types of MMF; unipolar ones, which have the same magnetic polarity as the sunspot, and bipolar ones (Zhang et al., 1992).
The bipolar MMFs are not randomly orientated, but instead are aligned so that a line connecting between the centres of each polarity is roughly parallel to the radial of the sunspot, with some MMFs’ orientation reflecting the twist in the sunspot penumbral magnetic field (Yurchyshyn and Wang, 2001). In most cases, it is the bipolar MMF fragment furthest from the sunspot that has the same magnetic polarity as the sunspot (Yurchyshyn et al., 2001; Zhang et al., 2003). Such an orientation suggests that MMFs are formed either by U-loops in a field that originates in the canopy emanating from the sunspot which has formed dips that reach down to to the photosphere (Zhang et al., 2003; Bernasconi et al., 2002), or by Ω-loop sections of flux that have detached themselves from the sub-photospheric portion of the sunspot that have subsequently risen to the photosphere to form a sea-serpent (Wilson, 1973; Spruit et al., 1987). In this case the field remains attached to the spot at the photospheric level but the flux concentration below the photosphere is being eroded. For the bipolar MMFs where the leading polarity is opposite to that of the sunspot, flux originating in the sunspot’s canopy could be dipping down into the photosphere so that the MMF dipole is formed by Ω-loops and their outward flow could be directly peeling away from the spot at the photospheric level (Harvey and Harvey, 1973) and fully detaching the field from the spot. The first appearance of MMFs can be outside of the sunspot penumbral boundary (Zhang et al., 2003) or inside the penumbra (Sainz Dalda and Martínez Pillet, 2005) and an MMF mechanism that invokes the propagation of a kink along a highly-inclined field, rather than sunspot decay, has also been proposed (Ryutova and Hagenaar, 2007).
Despite the inherent difficulties in quantitative studies of MMFs, due to their small spatial scale, short lifetimes (few hours, Vrabec, 1974) and ability to merge, the idea that MMFs transport flux away from the spot at the same rate at which flux in the spot is decreasing has been suggested (Harvey and Harvey, 1973) and accepted by many. However, conclusive evidence that all MMFs are indeed detaching flux from the periphery of the spot at the photospheric or sub-photospheric level has not yet been provided. The study by Zhang et al. (1992) shows that only the unipolar MMFs may remove flux from the spot, whereas bipolar MMFs do not. There are also cases where spots that show MMF activity remain as coherent structures over relatively long timescales. For example, the negative polarity sunspot of NOAA active region 10923 that produced MMFs (Sainz Dalda and Bellot Rubio, 2008) and which returned as a still coherent spot in NOAA active regions 10930, 10935 and 10941; lasting on the Sun for three months. The underlying mechanisms that produce MMFs and their relationship to sunspot decay are still to be fully understood.
4.3 Fragmentation of sunspots and the re-establishment of convection: umbral dots and light-bridges
The magnetic field of an active region is dominated by its sunspots. So, for the region to decay any spots that are present must be removed. Overall, the evolution of the photospheric magnetic field is described by the MHD Induction equation.
where η is the ohmic magnetic diffusivity. The first term on the right-hand side describes changes to the magnetic field as it is advected by plasma flows and the second term on the right-hand side describes changes as the magnetic field diffuses through the plasma. Which of these terms dominates is determined through the ratio known as the magnetic Reynolds number:
where ν is the velocity and ℓ is the lengthscale. If ℜm ≪ 1 then the diffusion term dominates and the plasma motions are not important. The diffusion timescale for a sunspot with a length-scale of 3000 km and η = 300 m2 s−1 is ∼ 1000 years. If ℜm ≫ 1 then advection dominates the evolution of the magnetic field. In the latter case, the magnetic energy density of the magnetic field \(({{{B^2}} \over {8\pi }})\) must be equal to, or less than, the kinetic energy density of the plasma flows in the photosphere \(({{\rho {v^2}} \over 2})\) for the flows to be able to advect the magnetic field, which, for a photospheric plasma density of 4.9 × 10−6 kg m−3 and horizontal flow velocity of 1 km s−1, means a field strength of less than ≈ 615 G. In order for active regions to decay through advection, processes that are able to break up the intense ≤ kG field of the monolithic magnetic structure of sunspots into weaker flux fragments must first become significant. In the model that describes sunspots as being composed of a closely packed collection of vertical magnetic field bundles, the weak points may lie in (relatively small) field-free regions between the bundles. In these field-free regions over-turning convection can be re-established. Indeed, the umbra of sunspots do require some level of convection to maintain their temperature of ∼ 4000 K and sub-structure in the form of umbral dots — bright spots — indicates small patches of enhanced temperature plasma where convection is thought to be occurring. For a more detailed discussion on the physical drivers of umbral dots see the Living Review by Borrero and Ichimoto (2011).
An indication that large-scale circulation patterns may be important in the break-up of spots was found by Bumba (1965a), showing evidence for an association between light-bridges within spots and the supergranulation pattern. Light bridges are bright lanes that connect from one side of the sunspot to the other and which split the sunspot into smaller sections (Figure 12). The presence of a light bridge does not necessarily mean the spot is breaking up though. Narrow light bridges that form during a spot’s intermediate stages (C to G by the Zurich classification) can disappear within a day (Vazquez, 1973). However, thicker/wider light bridges that appear when a spot is past its maximum development show a granular structure similar to the spot-free photosphere (Bray and Loughhead, 1964) and the spot decays and evolves to become type G or H (Vazquez, 1973). The exact role of light bridges in the decay of sunspots is still an open question. Indeed, Louis et al. (2012) find that although light bridges may be necessary for the break-up of spots, they are not sufficient to cause the fragmentation.
G-band image of a well-developed sunspot in NOAA Active Region 10953. The white box encloses a well-developed light bridge. Image reproduced with permission from Shimizu et al. (2009), copyright by AAS.
4.4 Asymmetry in decay of bipoles and polarity imbalance
Karachik et al. (2010) followed the evolution of four isolated bipolar ARs over two or three rotations as they decayed and measured several parameters of their magnetic fields including total flux, imbalance, and compactness. They showed that as regions decay, their leading and following polarities exhibit different dissipation rates: the less closely packed polarity tends to dissipate faster than compact polarity. As a consequence, a gradual increase in flux imbalance inside a dissipating bipolar region developed, and later a formation of a CH in place of more compact magnetic flux. The total magnetic flux within the new CH represents a significant fraction of the AR’s flux. The article’s main focus is on CH formation, which must indeed be part of active region evolution and decay process, but they also register some other aspects of the decay process.
Limb-to limb signed magnetic flux measurements of slowly-evolving decaying regions were used by Karachik et al. (2010) to determine the mean inclination γ of magnetic vector in the polarities of these bipolar ARs from the central meridian distance (CMD) where each polarity reached maximum: B∥(CMD) = B0 cos(CMD − γ), where B0 is the flux along the axis of the flux tube. The magnetic field measurements were done over a rectangular area containing the decaying ARs. There is no mention of background flux subtraction nor of the size of the box (whether it was of constant area or adjusted to the increasing dimensions of the diffusing AR), which can very well influence the measured flux decay rate, i.e., from a small box flux is diffusing out, while a box of varying size includes a varying amount of “background” field. When an AR emerges into a pre-existing monopolar area (plage field), a polarity imbalance of the bipole can develop as the emerging bipole’s polarity opposite to that of the background field will cancel with the latter. With these potential limitations, Table 3 shows two of the decaying ARs for which flux measurements, compactness on consecutive rotations were made. Compactness was characterised by
where \(S = \sum {{B_z}(x,y)}\) and \(\bar x,\bar y\) are averaged x, y coordinates of pixels of negative (positive) polarity Bz. In Table 3 a very steep flux decay is seen: Flux of both polarities shrink to 40−17% of their 1st-rotation flux value, while \(r_{{\rm{eff}}}^2\) more than doubles due to dispersion. Magnetic vector inclination does not seem to show a trend, nor does rotation rate. Measured flux imbalance, however, appears to be increasing as the ARs age.
Important remark: Though flux cancellation removes equal amounts of magnetic flux from both polarities, if we start with a flux imbalance, as the total flux is decreasing in decaying ARs, the imbalance expressed in % will always grow. Since most ARs emerge in the remnant fields of decayed ARs, most often there is a dominant polarity sign in the surrounding small-scale magnetic fields, therefore this result is expected to be generic, though it also has to be interpreted correctly.
4.4.1 Short-term observational and modelling study of AR dispersal and its energy input into the corona
Mackay et al. (2011) modelled the dispersal of a decaying AR (NOAA AR 8005 observed in December 1996) in order to quantify energy input into its coronal fields. The modelling results are discussed in Section 5, since they concern the free energy-buildup in decaying ARs by small-scale motions, which is potentially important for the radiative output in the decay phase and helicity accumulation. Here we discuss observational results relevant to the decay of ARs. Mackay et al. (2011) carried out careful magnetic field measurements over four days spanning the CMP of the AR, tracking short-term evolution of magnetic flux, flux imbalance and separation between the centre of gravity of positive and negative polarities. The latter was determined by a vector S(t) as
where Bz(i, j) is the LOS component of the magnetic field at the ith, jth pixel and Ri, j is the position vector for the ith, jth pixel from the origin (i.e., the lower-left corner of the magnetogram). Each MDI map was de-rotated to the central meridian, correcting for area-foreshortening, and measurements were taken over a fixed-area box of 181 × 126 pixels (pixel size: 1.977″ centred on the AR). The area fully covered the AR from start to end. During the four days analysed, the polarity separation increased by 18%, from 68 000 to 80 000 km. The total unsigned magnetic flux (a sum of the signed fluxes) increased during the 1st day by about 5%, reaching 1.1 × 1022 Mx, attributed to the emergence of an ER, and then was decreasing over the following days at a rate of 8% day−1. Polarity imbalance was negative, varying between 4–10%, due to dominantly negative surrounding magnetic fields. For the modelling the imbalance was removed from each magnetic map, which implied a correction of |6| G, comparable to the noise level of ±9 G. The evolution of the AR is shown in Figure 13. Note that no systematic shearing or twisting motions are present. The motions seen all appear to result from buffeting by supergranular flows. Differential rotation should also have some effect due to the large latitudinal extent (≈ 10 heliographic degrees) of the AR. The flux decay is primarily due to cancellations along the magnetic inversion line of the AR, driven by converging motions of opposite polarities resulting from the dispersal of both polarities reflected in the growing polarity separation.
Evolution of NOAA AR 8005 over four days (CMP: 18 December 1996; white: positive, black: negative polarity; SOHO MDI LOS magnetograms). Image reproduced with permission from Mackay et al. (2011), copyright by AAS.
Using the magnetic observational data (61 MDI magnetograms) as lower boundary conditions, Mackay et al. (2011) carried out a time-dependent non-linear force-free field (NLFFF) quasi-static modelling in order to study the build-up of free magnetic energy and coronal magnetic helicity resulting from the dispersal of the decaying AR 8005. The novelty of their modelling is that it is data-driven: the successive magnetograms drive the evolution of the coronal magnetic fields between successive force-free equilibria. When the initial coronal field was taken to be potential, the small-scale motions were found to inject ≈ 2.5 × 1025 erg s−1 of free magnetic energy, which was stored in the corona at low height, below 30 Mm. The initial field’s deviation from the potential did not seem to have a significant effect on the energy injection rate. Over its assumed life-time (9–10 days) a free energy injection by small-scale motions 10% of that of the potential field was found, which was consistent with energy estimates derived from Poynting flux calculations. Such an amount of energy is sufficient to balance radiative losses at million-degree coronal temperatures within the AR (≈ 1 × 1025 erg s−1). The relative magnetic helicity injected by random motions into the coronal field is nearly balanced in sign, but the converging motions toward the inversion line, the global separation of magnetic polarities as well as differential rotation acting together introduce a low net positive helicity, consistent with the hemispheric helicity pattern (being positive in the southern hemisphere). The net helicity injection rate of 1.218 × 1034 Mx2 s−1 that totals at ≈ 2.5 × 1039 Mx2 over the four days analysed. We note that supposing that a CME carries away 1042 Mx2 helicity (DeVore, 2000), this helicity injection rate would require 950 days (2.6 years) to accumulate enough helicity for a CME. However, as we discuss elsewhere, ARs do emerge in a non-potential state. The helicity injection discussed here is either building or removing that of the active region. MHD simulations based on flux cancellation leading to flux rope formation for simplicity start from a potential configuration and can only achieve an eruption when they include significant shearing or twisting of the coronal field (Amari et al., 2003; Yeates and Mackay, 2009; Yeates et al., 2010; Amari et al., 2010; Aulanier et al., 2010). With the aim to understand CMEs occurring during the decay phase of ARs, the Flux Cancellation Model (FCM) has been developed (Forbes and Isenberg, 1991; Amari et al., 2003; Yeates and Mackay, 2009; Yeates et al., 2010; Amari et al., 2010; Aulanier et al., 2010).
Most of the FCMs are computed in bipolar configuration. Amari et al. (2007) show that in a more complex (quadrupolar) configuration the model works just as well, though the field evolution and flux rope formation due to cancellation is slow. However, the presence of an X-point above the twisted flux rope facilitates eruption due to the weaker confinement near this point, i.e., the flux-cancellation and break-out (Antiochos et al., 1999) models are not exclusive, but can work in combination.
4.5 Dispersal of the active region magnetic field
Once the magnetic fields of active regions become weak enough to be susceptible to photospheric plasma flows, the fields start to be shaped by convective flows in the first instance. The advection of a magnetic field by supergranular flows carves out relatively free-field regions as it sweeps the flux to the cell edges. Differential rotation and meridional flows become significant in the longer-term. Normally the following spot (which emerges with a more dispersed nature than the leading spot) breaks apart first.
Active regions, even after the disappearance of their spots, remain distinguishable from their magnetic environment for up to seven months while their magnetic flux in a magnetically undisturbed environment during solar minimum spreads over an ever-increasing area (see, e.g., Figures 17 and 19 [upper panel] and see also van Driel-Gesztelyi, 1998) forming large bipolar regions that slowly become part of the “background field”.
4.6 Disconnection from toroidal roots
During the decay phase of active regions, observations of the motion of the photospheric magnetic field strongly suggest that it rapidly loses its original connectivity to the toroidal flux layer at the base of the convection zone. Whereas the separation and proper motion of opposite polarity sunspots during the emergence phase is indicative of the emergence of the top portion of an Ω-shaped flux tube passing through the photosphere, after a few days this motion ceases. From then on the spots (i.e., the intersection of the two vertical legs of the omega loop) stop separating from each other, fragment and advection by photospheric plasma flows passively disperses the magnetic flux over a larger and larger area as described in Section 4.5. This evolution requires that a subsurface disconnection from the toroidal belt has occurred because the (horizontal) magnetic tension from a continued connection to the toroidal flux at the base of the convection zone would drive the sunspots apart for much longer than is actually observed (van Ballegooijen, 1982; Rempel and Schlichenmaier, 2011; Schüssler and Rempel, 2005).
Schrijver and Title (1999) estimated the time necessary for the flux tube of an AR to get disconnected from its toroidal roots is tAR (days) = 15ϕ/1021 Mx, where ϕ is the total magnetic flux of the AR. This estimate gives a disconnection time of ≈ 5 months for a major AR.
The mechanism by which this disconnection occurs is still an open question, but recent work points towards the role of an ‘explosion’ of the magnetic field below the photosphere and/or an increase in plasma pressure so that the equipartition value is reached. Then, external convective motions are able to control the evolution of the sub-surface flux tube, perhaps a few Mm below the photosphere, and the upper, emerged, part loses knowledge of its connection at the base of the convective zone (Fan et al., 1994; Moreno-Insertis et al., 1995; Schüssler and Rempel, 2005). The photospheric field is then effectively disconnected from its roots. An alternative mechanism is that the photospheric field directly loses its connection to the toroidal flux as a result of magnetic reconnection that is driven as converging convective flows distort and collide (nearly) anti-parallel strands of magnetic flux (Schrijver and Title, 1999). For the active region to become disconnected, this process must be very efficient and be able to involve the majority of the flux of the active region. Such an idea may be investigated by the search for systematic and organised converging flows in the convective zone.
4.7 Flux cancellation and removal of flux from the photosphere
Once the magnetic field of an active region starts to be fragmented and advected by plasma flows, the likelihood that opposite polarity fragments will collide and undergo magnetic reconnection increases. The observational signature of this process is known as flux cancellation — small-scale opposite polarity fragments (measured in the line-of-sight magnetic field component at the photosphere) converge, collide and disappear from the line-of-sight photospheric magnetograph data (Martin et al., 1985). The mechanism that drives this phenomenon was developed by van Ballegooijen and Martens (1989). It is the result of magnetic reconnection taking place in the lower atmosphere between the converging opposite polarity fragments, each fragment being a footpoint of a sheared loop that crosses the PIL (Zwaan, 1987; van Ballegooijen and Martens, 1989). Recent results indicate that the reconnection is occurring in the photosphere (Yurchyshyn and Wang, 2001; Bellot Rubio and Beck, 2005). The post-reconnection configuration is then a very small magnetic loop that connects between the polarities that collided and a much longer loop that connects the remote footpoints. The small radius of curvature of the small loop pulls it under the photosphere via the magnetic tension force and the associated small bipole disappears from view. As flux cancellation can only remove an equal amount of flux from each polarity, in cases of unequal flux within the canceling bipole, the larger polarity survives.
Flux cancellation can occur whenever opposite polarity fragments collide. This could be along the internal polarity inversion line of the active region or around the periphery for bipolar active regions. If the active region is more magnetically complex, flux cancellation may be happening at many sites across the region and will act to reduce this complexity. Only if the active region is part of an active nest, and therefore a place of repeated large-scale flux emergence, can the magnetic complexity be maintained. In this case, however, the evolution of the individual bipoles can be significantly shortened by flux cancellation.
A significant amount of flux can be lost from the photospheric field through flux cancellation. Baker et al. (2012) and Sterling et al. (2010) studied different regions that both showed that 20% of the flux was lost over just two days and Green et al. (2011) tracked an active region from emergence to decay and found that 34% of the active region flux was cancelled along the active region’s internal polarity inversion within 3.5 days of the flux emergence ending.
We have to remark that the detection of flux disappearance from the photosphere, besides flux cancellation/submergence, can also be the result of a process that merely disperses the previously detected flux so that it becomes too small and too weak to be detected, rather than completely eliminating it. Lamb et al. (2013), analysing flux disappearance in Hinode/SOT/NFI magnetograms, concluded that dispersal of flux to smaller scales is more important for the replacement of magnetic fields in the quiet Sun than observed bipolar cancellation. This suggests that processes on spatial scales smaller than those visible to Hinode dominate the flux removal process. However, conditions in evolving active regions, especially along their magnetic inversion line, are different, and there it is most likely that their magnetic cancellation dominates on observable scales.
4.8 The build-up of magnetic flux ropes and filaments
While the decay phase is marked by a decrease of magnetic flux density accompanied by a decrease of all plasma parameters (temperature, emission measure, pressure; van Driel-Gesztelyi et al., 2003b) there is a remarkable growing feature in the AR. Filaments, which are absent, or if present, are short and variable when the AR is young, become stable and can reach a length of 105 km or more, becoming increasingly parallel to the equator. During this time the magnetic configuration of the active region slowly evolves and becomes conducive to the formation of magnetic flux ropes that can support filament material. The flare activity is fast disappearing with the decrease of magnetic flux density, but coronal mass ejections occur during the decay phase of the active region due to the repeated formation and eruption of magnetic flux ropes.
The ongoing fragmentation and dispersal of an active region by convective flows and differential rotation spreads out its magnetic field in all directions. Whilst this gradually increases the spatial extent of the active region over time and reduces its flux density, it will also bring opposite polarity fragments together along the active region’s internal PIL and PILs that separate the active region field from opposite polarity regions surrounding it. When small-scale opposite polarity fragments (measured in the line-of-sight magnetic field component at the photosphere) meet at a PIL they have been observed to undergo what has become known as ‘flux cancellation’; the fragments collide and subsequently disappear from the line-of-sight photospheric magnetograph data (Martin et al., 1985). In this way, flux cancellation removes magnetic flux from the photosphere. Although flux cancellation can occur anywhere where opposite polarity fragments collide, this section looks specifically at flux cancellation along the active region’s PIL (and assuming that the decaying region is bipolar) and the important consequences for the reconfiguration of the overlying coronal field.
The physical mechanism behind flux cancellation is resistive in nature. It is the result of magnetic reconnection taking place in the lower atmosphere between the converging opposite polarity fragments, each fragment being a footpoint of a sheared loop that crosses the PIL (Zwaan, 1987; van Ballegooijen and Martens, 1989). The weak shear that is present in the decay phase is a combination of the original non-potentiality the active region emerged with Leka et al. (1996) and the action of differential rotation on the evolving bipole, which is a slow process. Furthermore, shear originating from these two processes can be of opposite sign (Démoulin et al., 2002a). The post-reconnection configuration is a very small magnetic loop that connects between the polarities that collided and a much longer loop that connects the remote footpoints. Depending on the height at which the reconnection occurs the disappearance of the radial flux threading the photosphere can be either the submergence of the very small loop or the rise of the long loop that would contain a concave-up section. In either case a loop moves through the layer where the magnetic field is measured and the associated small bipole disappears from view.
At what height does the magnetic reconnection occur? Observations mostly support the scenario where magnetic reconnection occurs in an atmospheric layer above that where the magnetic field measurements are being made (Harvey et al., 1999; Yurchyshyn and Wang, 2001; Bellot Rubio and Beck, 2005). The small post-reconnection loop must have a sufficiently small radius of curvature for it to submerge beneath the solar surface as a result of its high magnetic tension force. What is important for the discussion here is that what remains in the solar atmosphere is a long loop that is highly sheared with respect to the PIL.
The details of how the coronal magnetic field evolves as flux cancellation proceeds in the photosphere/chromosphere have been realised in van Ballegooijen and Martens (1989). They consider what happens when the photospheric flows both shear and converge magnetic fragments toward the PIL.
Sustained flux cancellation is a mechanism by which the free magnetic energy in the coronal field is redistributed in coronal volume, becoming more concentrated above the PIL. Sheared magnetic field accumulates along the PIL and the small loops that submerge after reconnection are likely to be perpendicular to the PIL and close to a potential state. Their submergence removes nearly potential field from the corona leaving the non-potential field behind (van Ballegooijen and Martens, 1989; Welsch, 2006). In this way, flux cancellation can provide energy for the activity that takes place in decaying active regions.
More than this though, is that flux cancellation can build the specific topology of a magnetic flux rope (van Ballegooijen and Martens, 1989). This magnetic configuration is important as it can support relatively cool and dense plasma to form a filament and also provides a magnetic configuration that can evolve and become unstable, explaining the occurrence of filament eruptions and coronal mass ejections (CMEs, Hood and Priest, 1981; Kliem and Török, 2006). Figure 14 shows how flux cancellation initially leads to the accumulation of a highly-sheared field along the PIL forming axial flux of the rope, and then to a helical field that wraps itself around the axial flux and in doing so adds poloidal flux to the rope.
Flux cancellation scenario begins with converging opposite polarity magnetic flux fragments in a sheared arcade (panels a to c). Reconnection then produces a long loop (labelled AD in panel d) and a short loop (labelled CB in panel d) which then submerges. Overlying loops then converge and repeat the process (panels e to f). Image reproduced with permission from van Ballegooijen and Martens (1989), copyright by AAS.
But what observational evidence is there that the coronal field is indeed evolving in this way? Highly sheared loops are observed in the core of decaying active regions, while the more external loops are nearly potential, i.e., there is a gradient of non-potentiality within the AR away from the inversion line (Schmieder et al., 1996). However, this represents only the first phase of the scenario of van Ballegooijen and Martens (1989); the second phase being the creation of helical field lines that define the flux rope. Since we are currently unable to directly observe the coronal magnetic field in any routine and systematic way, what is the observational support for the formation of helical field lines around the accumulated sheared field via flux cancellation?
One observational approach is to study the horizontal component of the vector magnetic field data at the PIL. If it is inversely directed along a section of the PIL, it suggests the presence of a ‘bald patch’ formed by a concave-up configuration produced by the field lines at the bottom of a flux rope if the rope reaches down to the photosphere (Athay et al., 1983; Lites, 2005; Canou et al., 2009). Another approach is to study continuous S-shaped (sigmoidal) sources of X-ray and EUV emission, which follow the magnetic field lines, and which exhibit an inverse crossing of the PIL in the centre of the sigmoid — indicating that they are created by helical magnetic configurations (Green and Kliem, 2009).
Work that studies the formation of sigmoidal structures in decaying active regions indicates that the coronal field does indeed evolve as described by van Ballegooijen and Martens (1989). Whilst observations of the line-of-sight magnetic field at the photosphere comprises many cancellation events of flux fragments along the PIL, an initially weakly sheared arcade of loops, observed in soft X-rays, evolves through three phases. Phase one is a phase of increasing shear driven by the dispersal and cancellation of flux; in phase two there is an accumulation of a significant amount of flux that runs almost parallel to the PIL (axial flux) so that a remnant active region field that has not yet been involved in flux cancellation, takes on the appearance of two J’s either side of the axial flux; phase three involves further flux cancellation that produces field lines that are twisted around the axial flux (which look S-shaped) and which contribute poloidal flux and define the presence of a flux rope (Green and Kliem, 2014, see Figure 15). In light of this, sigmoids formed in decaying active regions that contain continuous S-shaped structures that have an inverse crossing of the PIL by the middle, bracketed by two regular PIL crossings by the sigmoid elbows show support for the presence of a flux rope (Green and Kliem, 2009). Such an understanding of the magnetic configuration helps explain why sigmoidal active regions have such a high tendency to produce coronal mass ejections (Canfield et al., 1999).
Sigmoidal active region structures formed in the decay phase show an evolution from acrcade (first column) to sheared arcade (second column) to double-J (third column) and then to a continuous S shape (fourth column). Four active regions are shown here NOAA AR 10930 (top row), NOAA AR 8005, an un-numbered region from February 2007 (second row from bottom) and NOAA AR 10977 (bottom row). Image reproduced with permission from Green and Kliem (2014), copyright by IAU.
Observations of sigmoidal active regions represent a subset of active regions in which flux rope formation has now been well studied. Since most sigmoidal active regions contain a filament along the same PIL as the sigmoid (91% in Pevtsov, 2002) they provide a useful way to investigate the relation between flux rope formation and filaments. In a small study by Green and Kliem (2014) the filaments were seen to start to form during the phase when the coronal arcade was becoming increasingly sheared, and before the sigmoid was observed.
4.9 Modelling magnetic flux ropes in the decay phase
Work that models the magnetic configuration in decaying active regions supports the scenario of flux rope formation discussed in Section 4.8. Savcheva et al. (2012) used the flux rope insertion method (van Ballegooijen, 2004; van Ballegooijen et al., 2007) to reconstruct the coronal magnetic field of three bipolar active regions at various stages during their decay phase. All regions exhibited flux cancellation along the PIL. The models showed that the active regions first developed a strong axial field and then, as flux cancellation proceeded, long S-shaped field lines that wrap around the axial field formed. The models allow a much deeper analysis of the magnetic configuration than can be carried out by observations alone and revealed that the dips in the S-shaped field lines were located at the sites of flux cancellation as is expected from the van Ballegooijen and Martens (1989) model.
Such models also allow the study of the evolution of the free magnetic energy and helicity in the regions. The models showed that as flux cancellation proceeded, the potential energy of the coronal field decreases. In addition, the times of CMEs from the active region were determined and a series of models were constructed in the time leading up to four CMEs. In three out of the four CMEs, the free magnetic energy and helicity show increases as expected (Welsch, 2006).
The flux cancellation process that builds the flux rope can also be used to investigate how much flux has been built into the flux rope by the time of the CME versus that in the overlying field that acts to provide a downward tension force, inhibiting the eruption of the flux rope (Green et al., 2011). Flux cancellation provides a way to investigate the onset of the loss of equilibrium/ideal instability on the real Sun.
Numerical models of flux ropes in decaying active regions have made predictions about the amount of axial and poloidal flux that a rope can contain in relation to that of the stabilising overlying active region arcade field before the rope becomes unstable and erupts as a CME. The flux rope insertion method allows a flux rope to be inserted above and along the PIL in the extrapolated potential field of an active region. The configuration then undergoes numerical relaxation. Using this technique Bobra et al. (2008), Su et al. (2009), and Savcheva and van Ballegooijen (2009) found a limit for the axial flux in a rope that can be held in a stable force-free equilibrium by the overlying flux of the active region. Most of the flux of the rope is held in the axial field component, \({{{\phi _{{\rm{poloidal}}}}} \over {{\phi _{{\rm{axial}}}}}} \ll 1\). The limit was at most 10% of the unsigned flux in the active region for the three regions studied in Bobra et al. (2008) and Su et al. (2009). The limiting axial flux given in Savcheva and van Ballegooijen (2009) for a fourth, strongly decayed and sigmoidal active region, compares with the amount of unsigned flux in the region to a limiting ratio of roughly 14%. This contrasts sharply with Green et al. (2011), who showed, using an observational study, that a flux rope formed by flux cancellation may contain as much as 60% of the unsigned flux of the active region.
Savcheva et al. (2012) carried out a study to try and reconcile the above discrepancy between the observational value of flux rope flux content and that found for a modelled flux rope. The results for four flux ropes for which it was possible to compare the rope’s axial flux to the unsigned flux of the active region just before the eruption showed the ratios 18%, 16%, 58% and 50%. The region studied in Green et al. (2011) was also modelled and there was an excellent agreement in the value found between these two approaches.
The reasons for this broad range of ratios may lie in the different specific configurations of the flux rope itself and the active-region magnetic field that then influences the profile of the magnetic field overlying the flux rope. The rope is thought to undergo the torus instability and, therefore, erupt if it rises to take on a semi-circular shape and if the overlying field falls off with height with a decay index of ∼ 1.5 (Kliem and Török, 2006). Alternatively, the broad range of ratios may highlight that there are different mechanisms that can bring the flux rope to the point of eruption. For example, runaway reconnection in a current sheet underneath the rope. There may also be the influence of photospheric line-tying in some cases due to the particular configuration of the flux rope.
The scenario outlined here, whereby flux cancellation builds flux ropes is strongly supported by a series of 3-dimensional numerical modelling approaches that complete the picture of flux rope formation and eruption in decaying active regions (Amari et al., 2003; Mackay and van Ballegooijen, 2006; Aulanier et al., 2010). Sigmoid-shaped field lines are found in Mackay and van Ballegooijen (2006) and Aulanier et al. (2010) and so show a close similarity to the observations discussed here. The latest approach to modelling the occurrence of flux ropes and their eruption in the decay phase of active regions is to conduct a data constrained simulation where the starting configuration of the numerical simulation is based on the observed magnetic field. Kliem et al. (2013) successfully bring a flux rope constructed from observations using the flux rope insertion method to a successful eruption. They find good agreement between their MHD simulation and observations of the eruption and also that the axial flux in their rope closely matched that of the criterion of the torus instability. This is promising and exciting work that will, in future, be expanded to include observations of the evolution of the photospheric field in the time leading up to the eruption and the NLFFF extrapolations.
5 Modelling the Evolution of ARs from Emergence Through Decay
The first short flux emergence phase of AR evolution has been extensively modelled and simulated, while the global evolution including the decay phase of ARs has been much less studied except for its flux transport aspect. Modelling of sub-photospheric evolution of flux tubes was reviewed by Fan (2009), including its manifestations on flux emergence as well as the main characteristics of bipolar ARs resulting from sub-photospheric effects. Here, following the brief observational scenario of a full AR evolution in Section 1.3, we describe the most relevant modelling effort of AR evolution from the fully emerged state through decay by van Ballegooijen and Mackay (2007), which describes the coupled evolution of magnetic fields in the convection zone and the corona, capturing several key observational characteristics of the AR decay process. A key question they investigate is what happens to the coronal and sub-surface magnetic fields as flux cancels along the PIL.
The numerical mean-field model by van Ballegooijen and Mackay (2007) starts with a fully emerged flux rope resulting in a bipolar AR with an initial field strength of 1 kG, left-handed (negative) twist with a twist parameter q = 2ΰH/L = −0.5 with a pitch length L ≈ 0.5 R⊙, and a magnetic flux of 1.231 × 1022 Mx in each polarity (Figure 16a). The latitude of the model emergence is +20.2°. It follows the spreading of AR magnetic flux over an increasing area, which leads to a convergence of the opposite polarities and magnetic cancellations along the PIL and the resulting submergence of flux there (Figure 16b). Shear is increasing along the magnetic inversion line in the corona due to a re-partition of shear between the short submerging and long coronal reconnected field lines: The former are perpendicular to the PIL, i.e., nearly potential, while the long reconnected field lines inherit most of the shear. In the model this is due to a nearly-radial field in the upper convection zone, which prevents the submergence of the magnetic component parallel to the PIL. While the flux is decreasing due to magnetic cancellations and ensuing flux submergence, the shear is accumulating along the PIL at low altitudes, gradually making the field-line structure sigmoidal. By day 20 of the model evolution, a loss of equilibrium and eruption (CME) ensues (see Figure 16c, d). The rate of build-up of free energy resulting from flux cancellations in a decaying AR was observationally studied by Mackay et al. (2011). They found a free energy injection rate of (2.5–3) × 1025 erg s−1, which is sufficient to balance radiative losses of the AR, but it appears to be too slow for an efficient build-up of major eruptive activity (see a more detailed discussion in Section 4.4.1).
(a) Magnetic shear on day 10 of the simulations from above and (b) viewed from latitude −60° (red = positive, green = negative polarity). The shear is strongly concentrated along the PIL and at low altitude. By day 15 of the simulations, formation of sigmoidal field lines indicate strong shear (not shown). Since the submerging flux is perpendicular to the PIL (nearly potential), shear is accumulating fast in the corona along the inversion line while the flux is decreasing due to flux cancellations. On day 20, the accumulating magnetic shear leads to a loss of equilibrium resulting in a CME-like lift-off (c) as seen from latitude −60° and (d) from latitude +20°. Images reproduced with permission from van Ballegooijen and Mackay (2007), copyright by AAS.
Since most ARs do not evolve in isolation, especially during higher-activity periods of the solar cycle, and since ARs can be closely packed together in activity complexes or active nests, the interaction of neighbouring ARs forms a very important aspect of AR evolution. Van Ballegooijen and Mackay (2007) also modelled the interaction between neighbouring flux ropes and the consequences for the sub-photospheric field. They modelled two ARs and found that on the 5th day of decay the dispersing magnetic fields have come into contact forming inter-AR magnetic inversion lines. Magnetic reconnections during cancellation events formed four connectivity systems: besides the original internal connectivities within the two ARs two sets of new connections between each pair of opposite polarities between the ARs. As a result of flux cancellations along the inter-AR inversion lines, flux retraction was taking place there. Since the retracted field along the inter-AR inversion lines represented connections between the ARs, these submerging loops represent drastically different magnetic connectivities to those of the emerging ones. Magnetic shear accumulated along the inter-AR inversion lines in the same manner and for the same reasons as along the internal inversion lines of ARs described above. Since accumulation of shear is a pre-requisite of filament formation, these inter-AR inversion lines are favourable places for filament formation. It has indeed been observed that the majority of filaments form along such inversion lines (Tang, 1987).
The retracted field lines are envisioned by the model of van Ballegooijen and Mackay (2007) to be pulled back all the way to the toroidal flux layer, to “repair the damage” caused by the flux emergence.
In the model by van Ballegooijen and Mackay (2007), the magnetic field of ARs clearly maintains their connection to their toroidal roots during the decay phase of their evolution. However, this may not be the case in the real Sun. Observations show a change in the dynamical properties of active regions from “active” to “passive”, which in the emergence phase is governed by internal large-scale dynamics, while after the emergence theoretical arguments have been raised in favour of disconnection of the emerged flux tubes from their toroidal roots. Schrijver and Title (1999) have suggested that subsurface reconnection of the two opposite polarities would lead to formation of disconnected U-loops in the upper layers.
The latest phase of AR evolution is a subject of the flux transport models that have been brilliantly described in an historical context in another Living Review by Sheeley Jr (2005). These processes are crucial for the evolution of the solar cycle. On the latter, we refer the reader to the Living Review by Hathaway (2010).
6 Long-term Evolution of Active Regions
6.1 Undisturbed long-term evolution during solar minimum: The case of AR 7978
During the activity minimum between solar cycles 22 and 23, in the second half of 1996, solar activity was dominated by a single active region (AR) on the southern hemisphere, which was identified as NOAA 7978 when it emerged in July. Due to the lack of other ARs on the Sun during its long-term evolution this region could be used as a test-case for stellar X-ray variability studies (Orlando et al., 2004). Strong and smooth rotational modulation of the X-ray and 10.7-cm radio emissions made this period ideal for testing star-spot modelling programs (Oláh et al., 1999).
The full evolution of this “last best AR” of cycle 22 as Hugh Hudson called it (Hudson et al., 1998), has been subjected to the most comprehensive analysis of any AR to date, from its five-day-long emergence throughout its six-month decay period. Using multi-wavelength and multiinstrument data there have been analyses of the long-term evolution of
-
magnetic field (van Driel-Gesztelyi et al., 1999a, 2003b,a; Ortiz et al., 2004; Li and Welsch, 2008),
-
filament evolution along its magnetic inversion line (Lionello et al., 2002),
-
flare and CME activity (van Driel-Gesztelyi et al., 1999a; Démoulin et al., 2002b),
-
magnetic non-potentiality and coronal helicity using linear force-free modelling (Démoulin et al., 2002b),
-
helicity generated by differential rotation (Démoulin et al., 2002a),
-
the magnetic helicity budget, and its relations to CME activity (Démoulin et al., 2002b),
-
coronal heating (van Driel-Gesztelyi et al., 2003b; Démoulin et al., 2003; Démoulin, 2004),
-
coronal intensity, temperature, emission measure (Orlando et al., 2000, 2004; Démoulin, 2004)
Furthermore, an extensive coordinated solar observation and analysis campaign known as the “Whole Sun Month” (10 August–08 September 1996) included the 3rd rotation of AR 7978; see e.g., Gibson et al. (1999), who carried out whole-Sun 3D magnetic modelling and linked the coronal holes (e.g., the famous “Elephant Trunk” CH, which extended from the north pole to the AR on the southern hemisphere) to fast-wind streams.
However, the literature on the long-term evolution of ARs is broader than studies of AR 7978. Therefore, although the backbone of this section is grouped by subject and based on the studies mentioned above, results from other ARs are invoked below where appropriate.
6.1.1 Evolution of the magnetic field
Like 50% of all ARs, AR 7978 emerged as part of an activity complex or activity nest (see Section 3.6). Five major ARs/flux emergence episodes formed this activity nest, and AR 7978 was the fourth AR to emerge in it. The activity nest developed on the southern hemisphere between Carrington longitudes (LC) 240–260° from 18 April 1996 (Harvey and Hudson, 2000) and included AR 7957 (S08, LC 246°) and AR 7958 (S06, LC 243°). It spanned over longitude- and latitude-ranges of 44 and 36 degrees, respectively, covering about 4% of the solar surface area. The third AR to populate this activity nest was a bipolar region, which emerged on the far side and hosted no sunspot by 1 July, when it rotated onto the visible solar disc, it was not given an AR number by NOAA. The largest, fourth, AR of the nest was AR 7978, which emerged in the dispersed negative (following) polarity remnant of AR 7958 west of the unnumbered bipolar region, which was in fact included in AR 7978 by NOAA. The new AR developed a total sunspot area exceeding 400 MSH, which was large enough to produce a detectable decrease in the total solar irradiance (Fröhlich et al., 1997; Hudson et al., 1998). Within the AR’s boundary a final, fifth, major flux emergence episode concluded the large-scale flux input into the active nest between 14–27 July 1996, while AR 7978 was on the far-side on the disc. This final flux emergence episode probably started just a few days before 27 July, as flux emergence had continued for a few days after the AR rotated onto the disk for the second time.
In AR 7978 flux emergence started at ∼ S10 E31 on 4 July 1996, in a dominantly negative polarity environment, west of the old and dispersed bipolar region mentioned above, the third member of the complex (see Figure 17). By 6 July 1996, the first well-formed sunspots of NOAA 7978 were observed, and the fast growth of the magnetic flux lasted until at least 10 July (van Driel-Gesztelyi et al., 1999a, 2003b,a). The results of the second episode of flux emergence in the AR is evidenced by the double leading (positive) polarity flux concentrations in the AR on 2 August, seen in Figure 17, which also shows that the magnetic field of the AR was clearly distinguishable from the background field for at least seven solar rotations. In summary, this active nest received large-scale flux input for over 3.5 months in five impulses. The ensuing decay phase lasted twice as long, for 7 more months. The evolution of the final (double) flux emergence episodes will be followed below, as a rare undisturbed process. In the following subsections we will identify the region as AR 7978 along all the rotations, though in fact it was denoted as NOAA 7981 and NOAA 7986 in the second and third rotations, respectively. After the spots disappeared (from the fourth rotation onward) the region did not have a NOAA number any longer, but we will still refer to it as AR 7978.
Magnetic maps of the emergence (a–d; 6–9 July 1996) and decay (f–j; July–November 1996) of AR NOAA 7978 as observed by SOHO/MDI. Contours outline the magnetic area of the AR. The rectangle around the AR has a fixed area of 1.6 × 1011 km2. Magnetic flux was measured over both sets of areas (cf. Figure 18). (a)–(d) Daily maps of the emergence phase between 6–9 July 1996. Note that the AR emerged within a dominantly negative polarity area. (e)–(j) show the evolution of NOAA AR 7978 during six solar rotations around the times of CMP. Note that although this AR emerged into an active nest resulting in a complex magnetic configuration to start with and one further major flux emergence episode took place within its boundaries before it rotated onto the disc for the 2nd time, magnetic cancellation processes efficiently wiped out the complexity, keeping the structure of the AR dominantly bipolar.
It is noteworthy that the subsurface rise of the emerging flux tube that formed AR 7978 was studied with the helioseismic method of acoustic imaging using data from the Taiwan Oscillation Network (TON) and the Michelson Doppler Imager (MDI) (Chang et al., 1999), one of the pioneering works on the subject. The average phase shifts normalised to surface values found over the active region in both datasets were attributed to upward-moving magnetic flux through the top of the convection zone during the emergence of the AR.
Van Driel-Gesztelyi et al. (2003b), using SOHO/MDI magnetograms, measured the total unsigned magnetic flux of the AR during the emergence and six more consecutive central meridian passages (CMPs). The magnetic boundary of the AR was drawn “by hand”, relying on the detection by the human eye of a steep magnetic field gradient at that location, on magnetic maps displayed in the same dynamic range (Figure 17). Based on repeated measurements the subjective errors were estimated to be ∼ 10% for the magnetic area and flux above a threshold of 9 gauss noise level (Liu and Norton, 2001). The peak total flux was reached during the third rotation (2.4 × 1022 Mx, cf. Figure 18), due to the additional episode(s) of flux emergence mentioned above. The ≈ 10% negative flux imbalance was due to the fact that the AR emerged in a dominantly negative polarity magnetic environment and as its flux dispersed and magnetic area grew, more and more of this pre-existing negative flux was included in the measurements. Another effect of the dominantly negative polarity magnetic environment is that the positive flux of the dispersing AR had a better chance to cancel than its negative polarity counterpart. Later on, the total flux decreased slowly, and even increased during the last three rotations (from October to December 1996) due to small-scale flux emergence activity and the ever-increasing area, which implied the inclusion of more quiet-sun background flux.
Evolution of magnetic flux versus time over increasing magnetic area of the AR (upper panel); and over a constant area (lower panel). Longitudinal MDI magnetograms at CMPs are used (cf. Figure 17). These flux values have not been corrected for MDI’s underestimation of magnetic flux values, as the data was not yet corrected for this at the time of these measurements, thus the flux values should be multiplied by a factor ≈ 1.45. However, this does not change the trend in the long-term evolution of the flux. The lower image reproduced with permission from van Driel-Gesztelyi et al. (2003b), copyright by AAS; see also van Driel-Gesztelyi et al. (2003a).
Choudhary et al. (2002), as part of a 137 AR sample, also measured the imbalance of AR 7978 as it evolved during five solar rotations and found 17% excess negative polarity flux, while the median of the sample was only 9.5%.
The total magnetic flux over a constant fixed area of 1.6 × 1011 km2, was found by van Driel-Gesztelyi et al. (2003b) to have returned to pre-emergence level by the sixth rotation of the AR (Figure 18, lower panel), i.e., by then magnetic cancellations had successfully removed as much magnetic flux as was injected by the emergence of AR 7978. Note also that the two diffusing polarities efficiently wiped out all the pre-existing opposite polarity concentrations over their ever-increasing area. The efficiency of this process decreased with time, which led to the appearance of more mixed polarities by the 6th rotation (Figure 17j).
A comparison of the magnetic flux curves measured using the two different methods (i.e., using the hand-drawn contours and the fixed-area box) in Figure 18 and also in Table 4, shows that the fixed-area flux peaks one month earlier than the flux measured within the contours. This puzzling discrepancy is likely to be due to the inclusion of too much remnant flux of the negative polarity into which AR 7978 had emerged. This suggests that this AR (and activity nest) had reached its highest total flux during the 2nd rotation of AR 7978.
Due to magnetic dispersal, the magnetic area of the AR increased roughly linearly at a rate of 1.28 × 104 km2 s−1(van Driel-Gesztelyi et al., 2003b). The magnetic flux density \(\bar B\) (defined as the total magnetic flux divided by the AR surface area), reached the highest level (188 Mx cm−2) by the 4th day of the AR evolution and decreased steadily after that in spite of the ensuing episodes of flux emergence (Figure 19, lower panel).
The upper panel shows the magnetic area as a function of time (enclosed by the white contours in Figure 17). The area increased nearly linearly at a rate 1.28 × 104 km2 s−1. The lower panel shows the evolution of mean magnetic flux density (i.e., total magnetic flux divided by the surface area) of the AR. Images reproduced with permission from van Driel-Gesztelyi et al. (2003b), copyright by AAS; see also van Driel-Gesztelyi et al. (2003a).
Another analysis of the magnetic field evolution of AR 7978 during its first four rotations was carried out by Li and Welsch (2008) using the same dataset (96-min cadence SOHO/MDI). Their main findings are summarised in Table 5. The magnetic flux evolution was found to have the same trend, but somewhat different relative values. They stated that AR 7978 emerged to reach 90% of the peak total magnetic flux found in the second rotation (CR 1912). The total flux decayed to 50% of the peak flux in 50 days after that. They also found an increasing flux imbalance between opposite polarities: A well-balanced emergence phase followed by increasing imbalance during the decay phase, with excess negative flux of 12% and 20% of the AR total flux in CR 1913 and CR 1914, respectively. This, on average, compares well with the average imbalance value found by Choudhary et al. (2002). Their most surprising result was that despite an area increase of 30%, the distance between weighted positive and negative magnetic flux-centres remained constant in the decay phase, in the 3rd and 4th rotations. This result might indicate an early disconnection from the toroidal roots of the AR’s magnetic field (see Section 3.1 for a discussion).
Li and Welsch (2008) measured the direction of the magnetic inversion line during the 3rd and 4th rotations of AR 7978 (CR 1913 and CR 1914) and found that it changed 26°, to become more parallel to the E-W direction, in accordance with being sheared by differential rotation (cf. Table 5). During the same CRs, Lionello et al. (2002) modelled the long filament, which formed along this magnetic inversion line by the 3rd rotation, and further extended in length by the 4th one (CR 1914). They used MDI magnetograms as the boundary condition for 3D MHD simulations. They showed that the observed magnetic flux changes are able to produce a flux rope, forming concave-up field lines/magnetic dips, which are able to support filament plasma. Their thermodynamic/hydrodynamic (TH) computations in the modelled field-line geometry indeed show condensations forming in the magnetic dips of the field lines. The pioneering magnetogram-based magnetic model of flux-rope type solar filaments was performed to reconstruct the filament in AR 7978 in the 4th rotation by Aulanier et al. (1998, 1999).
An interesting representation of the magnetic field evolution was published by Ortiz et al. (2004), who represented positive and negative magnetic field strengths as a series of histograms for six rotations (CRs 1911–1916). The histograms clearly indicate the flux evolution trends found by van Driel-Gesztelyi et al. (2003b,a), and Li and Welsch (2008), concerning the evolution of peak field strengths and asymmetries between the polarities. The narrowing spread of field strengths seen up to the 5th rotation (± 300 G in CR 1915), then was broken by small-scale flux emergence in the sixth (CR 1916; see Figure 2 in Ortiz et al., 2004).
6.2 Sun-as-a-star analyses
Hudson et al. (1998) highlighted the unique opportunity presented by the long-term evolution of AR 7978 for the use of data from whole-Sun instruments, which, during quiet solar-minimum conditions, responded primarily to this single localised source. Orlando et al. (2000) used GOES SXR data to analyse the evolution of the soft X-ray emission, emission measure (EM) and temperature of the AR during 5 solar rotations outside of flare times. Significant bremsstrahlung contamination by energetic particles in the outer radiation belt, which is strongest during solar-minimum conditions and affects mainly the hard GOES channel, made EM and T determination difficult after 20 August 1996. Orlando et al. (2000) estimated the background level when the AR was not on the solar disk, and the SXR emission (from the soft channel) temperature T and emission measure EM were derived from the background-subtracted data. They found a decrease in SXR emission from ∼ 10−7 Wm2 in July and early August (1st and 2nd rotations) to ∼ 7 × 10−8 Wm2 in October (5th rotation). Temperature data showed a great scatter between 3 and 12 MK, EM also showed significant scatter, but a trend from ∼ 9 × 10−6 1055 cm−3 in July to ∼ 9 × 10−8 1055 cm−3 in September was discernible.
6.2.1 Effects on solar irradiance
Solar irradiance was also affected by the long-term evolution of AR 7978. During its emergence phase in July a significant dip in total-irradiance data by SOHO/VIRGO (Fröhlich et al., 1997) was anti-correlated with the sunspot area (Hudson et al., 1998). Ortiz et al. (2004) used VIRGO irradiance measurements including spectral and crude imaging data from its LOI (Low-resolution Oscillations Imager) instrument, which has a 16-pixel detector, combined with MDI magnetic data to analyse the facular contribution to solar irradiance variations during six solar rotations (CRs 1910–1915). They found that the presence of sunspots over-compensated emission from faculae during the emergence phase, when the 500 nm spectral radiance dropped by ∼ 1 mW m−2 nm−1 even though the AR was at 50 W by the time it reached maximum sunspot area. The presence of large sunspots in the 2nd rotation, and a small sunspot in the 3rd, were over-compensated by facular emission when it was close to the limb (70–80°), see Figure 20. As the magnetic field of the AR dispersed and the facular area grew, the angular distribution of the observed radiance changed. As the AR became older, facular emission became less limb-bright, as its maximum shifted from ∼ 50° in the 3rd rotation to ∼ 40° in the 4th and finally ∼ 30° in the 5th rotation rotation. The changing contribution to irradiance from facular emission is shown in Figure 20 and its evolving 3D rendering is illustrated in Figure 21.
Evolution of the 500 nm spectral irradiance originating from AR 7978 as it rotated across the disc. When the AR was east of the central meridian, the measurements are plotted by crosses, when it was West of it, by circles. CMD is the date of central meridian passage. Image reproduced by permission from Ortiz (2003); see also Ortiz et al. (2004).
Three-dimensional rendering of the angular distribution of the development of the excess irradiance emitted at 500 nm by AR 7978 at two stages, in the region’s 3rd and 5th rotation. The brightening caused by the growing facular region is more uniform later in the decay phase. The magnetograms at the time of the central meridian passage of the AR are from MDI. Image reproduced by permission from Ortiz (2003); see also Ortiz et al. (2004).
6.2.2 Evolution of AR 7978 used to test photometric starspot models
Oláh et al. (1999) analysed a diagnosis of photometric starspot models through modelling active areas on the Sun using software originally written for starspot modelling. The data used were Sun-as-a-star measurements in radio (10.7 cm, DRAO) and soft X-rays (GOES). In these wavelengths the response to magnetic activity results in a similar amplitude variability on the Sun to those usually attributed to starspots in visual wavelengths of active stars. Comparing modelling results to imaging observations, Oláh et al. (1999), among others, found that: (i) knowing well the basic physical parameters of a star, the resulting total spotted area is a fairly good approximation of the reality, thus making sense of photometric starspot modelling; (ii) long-term variability coupled with the rotational modulation may result in artificially high latitude spots; (iii) in two- or multispot models a resulting small spot can account for short living spots; (iv) systematic change in spot size could be partially due to flux ratio changes.
6.2.3 The Sun as an X-ray star during the evolution of AR 7978
Analysis of the Sun as a star in soft X-rays (SXRs) using Yohkoh/SXT data during the long-term evolution of AR 7978, when it was the only sizeable AR on the Sun, provided a useful tool to disentangle various features and effects found in stellar X-ray spectra. From Yohkoh/SXT data Orlando et al. (2004) synthesized X-ray spectra of the whole solar corona, and the focal plane data as they would be collected with ROSAT/PSPC, XMM-Newton/EPIC and Chandra/ACIS (see Figure 23. The rotational modulation due to the evolution of the AR caused a significant variability of the average X-ray flux (rotational modulation), with only moderate spectral variation in the pass-bands of ROSAT/PSPC, XMM-Newton/EPIC and Chandra/ACIS. The SXT EM(T) analysis showed that the average temperature 〈T〉, reached a maximum a few days after the start of emergence, and then slowly decreased with the decay of the AR. The total emission measure EMsum reached a maximum about one month (or rotation) after the start of flux emergence, and decreased by nearly an order of magnitude during the next two rotations in decay phase. The core of the AR evolved more rapidly. It only contributes to the global corona’s EM(T) distribution during the emergence period. The AR core fades and disappears one month/rotation after that (see Figure 2 in Orlando et al., 2004).
DRAO 10.7-cm radio flux (upper panel) and GOES SXR flux (lower panel) modulation during the long-term evolution of AR 7978 during four rotations used for testing photometric starspot models. The inset legend indicates the line-style used for one-spot, two equatorial spot, and two-spot fits of the light-curves. Image reproduced with permission from Oláh et al. (1999), copyright by ESO.
Top panels: Two sample Yohkoh/SXT images showing AR 7978 during its 2nd rotation and the opposite side of the Sun, which had no major AR during the long-term evolution of AR 7978. The lower panel shows the SXT light-curve (thin Al filter) during five rotations, with a decreasing-amplitude rotational modulation and occasional flaring. Bottom panels: Stellar-like representation of the hardness ratio [HR = (H − S)/(H + S)], where S and H are the total counts in the soft and hard part of the spectrum, respectively, and X-ray surface flux in the instruments’ spectral band in the ROSAT/PSPC (0.1–3 keV), XMM-Newton/EPIC (0.1–10 keV), and Chandra/ACIS (0.5–10 keV) bands of the whole solar corona vs. time showing the evolving rotational modulation resulting from the long-term evolution of AR 7978. The grey stripes mark the times when AR 7978 was visible on the disk. Images reproduced with permission from Orlando et al. (2004), copyright by ESO.
6.2.4 Evolutionary stage of ARs and their microwave radio emission
Although the analysis described here has nothing to do with the long-term evolution of AR 7978, the results are very relevant to the long-term evolution of ARs in general, so we include them here. Microwave emission of the Sun is a widely used proxy for solar activity. Tapping and Zwaan (2001), using daily 2.8-cm microwave observations from the 46-m radio telescope at the Algonquin Radio Observatory spanning over 13 days (1–13 November 1981), Sacramento Peak Hα filtergrams and Kitt Peak magnetograms analysed contribution to the radio emission in excess of the quiet-sun level (i.e., of the slowly-varying component) by different sources. Bright compact sources (< 40″) are mainly attributed to gyroresonance emission by thermal electrons above strong sunspots (B > 1300 G), while diffuse sources (> 40″, comparable to the plage area of the source ARs) are attributed to free-free thermal emission from plasma in AR loops. In addition, magnetic complexity and flaring, which can also produce non-thermal emission, have to be taken into account. There were 31 ARs observed during the 13 days analysed. The evolutionary phase (ΦE, see below) and complexity (CP) of the ARs were determined (see Section A), and numbers were attributed to them to facilitate plotting. They also used the X-ray flare index FX = 1000 × (1 × Σ(c) + 10 × Σ(M) + 100 × Σ(X)), where C, M, and X are the importance values based on GOES X-ray data. Indices used also included sunspot area, plage area, and plage intensity.
The six evolutionary stages (ΦE), though they follow the general trend described in Section 1.3, are a compact extract of its main elements, so we find it useful to repeat them here. Below, we follow the exact description given by Tapping and Zwaan (2001) to describe the evolution of bipolar regions:
-
(1)
Emergence: the first appearance of the active region as a small, compact, bipolar plage.
-
(2)
Growth: flux emergence proceeds vigorously, with the total magnetic flux and plage area increasing rapidly.
-
(3)
Maximum development: the plage area and total magnetic flux have reached their maximum values.
-
(4)
Early decay: the plage is starting to break up. If there were sunspots, at least one is still present.
-
(5)
Late decay: all spots have disappeared, the plage has fragmented, but bipolar structure is still easily visible.
-
(6)
Remnant: widely scattered faculae/enhanced network, original bipolar structure is barely visible.
They also remarked: “In the case of an activity complex, however, more than one bipole may be present. The emergence of a new bipole, or relative motions of the constituting bipoles can cause ΦE to jump backwards.”
When these indices were plotted against the evolutionary phase, sunspot area, plage and sunspot magnetic complexity and the X-ray flare index peaked strongly at ΦE = 2, i.e., during the fast growth phase and only the plage area peaked later. The fastest fall-off with evolutionary stage was shown by the X-ray flare index and sunspot area, while the other indices declined slower.
An interesting result of this work is shown in Figure 24, where antenna temperature (Ta (K)) and flare index (FX) of the microwave sources are plotted against the evolutionary phase index from 1 to 6 defined above. Compact and diffuse sources are distinguished in the plot. Though Ta (K) is a good proxy for brightness temperature of diffuse sources, for compact sources it is at least a factor of 16 lower than that, and for obtaining the brightness temperature information on the spatial scales of the sources is required. Keeping these limitations in mind, the figure shows remarkable dominance of flaring activity during the “growth” (2) phase, when the ARs are dominantly associated with bright compact microwave sources. The fall-off with increasing evolutionary phase is steep. Compact sources characterise phase 3 (maximum evolution), while in phase 4 (early decay) both compact and diffuse sources are present. Stages 5 and 6 (late decay and remnant) are characterised by diffuse sources of decreasing brightness temperature. Flaring remains present only until phase 4, (early decay).
Microwave antenna temperature (Ta (K)), and the X-ray flare index (FX) plotted against the evolutionary phase index of the source regions. Ta (K), a measure received from a source by the radio telescope, is a proxy for brightness temperature of the source. The evolutionary phase index corresponds to: (1) emergence; (2) growth; (3) maximum development; (4) early decay; (5) late decay; (6) remnant. Symbols: ○ — compact sources; Δ — diffuse sources; x — X-ray flare index. Image reproduced with permission from Tapping and Zwaan (2001), copyright by Springer.
As expected, Tapping and Zwaan (2001) also found increasing Ta (K) and FX with increasing complexity, with a dominance of bright compact sources in the most complex γ and δ (cf. Section A) ARs. There was also a slight tendency found for diffuse sources to increase their intensity with increasing magnetic field strength. Compact sources and flares were only/mainly present in ARs in the highest two field strength categories. Total sunspot area above 500 MSH, however, showed no correlation with these indices.
In summary, Tapping and Zwaan (2001) asked the question: “How can the observed mix of mechanisms and sources produce an integrated emission having reasonably stable properties, and which correlates with other activity indices, such as sunspot area, total magnetic flux, various spectral lines and even the Sun’s irradiance?” Their answer: “Microwave sources are an evolutionary feature common to all but the smallest active regions.” Characterising microwave emission by ARs depending on evolutionary phase, they disentangled the sources and dominant emission mechanisms of the slowly varying microwave emission above the quiet-sun level, underlying the importance of active region evolution studies.
6.3 Evolution of activity
6.3.1 Evolution of AR core variability with the age of ARs
Ugarte-Urra and Warren (2012) carried out a multi-wavelength and multi-instrument (Hinode/EIS, SOHO/EIT and MDI, SDO/AIA, and STEREO/EUVI), analysis of the long-term evolution of variability of the core of two ARs observed in November–December 2009 (ARs 11029, 11032) and October 2010–January 2011 (ARs 11109, 11117, and 11127); see Figure 25 upper panel.
Top panel: Flux emitted in the 304 Å passband (SOHO/EIT and SDO/AIA data) during the multiple on-disc passages of the two ARs analysed is shown in black, with the relevant NOAA AR numbers indicated. The MDI total unsigned flux is plotted with blue diamonds below the flux curve. Hinode/EIS observing intervals are indicated by red vertical lines. Grey areas indicate intervals when the AR analysed was within ± 60° of the central meridian. Bottom panels: Variability of core pixels during the growth(black) and decay (red) phases of two ARs (top: AR 11029; middle and bottom: AR 11117). Dashed green lines indicate the 50% and 20% levels. Images reproduced with permission from Ugarte-Urra and Warren (2012), copyright by AAS.
Ugarte-Urra and Warren (2012) confirm the two-phase coronal evolution of ARs, which follows that of the magnetic field, i.e., a fast increase of T and EM during the emergence followed by a slow decay during the magnetic flux dispersion process. Their novel approach is to investigate how these evolutionary stages are reflected in the properties of different multi-thermal loop populations. Ugarte-Urra and Warren (2012) find that the core of ARs is more variable at high T (4 MK) in the early stages of the evolution. This variability is associated with low-frequency heating events, which allows the cooling of loops to 1 MK and below. During the decay phase, when the core of ARs becomes fainter, the variability also becomes smaller (see Figure 25 lower panels). In that stage there is less evidence of cooling, although weak heating events appear, which increase the EM at high T (3.5–5 MK), while there is no noticeable change in the cooler (0.6–0.9 MK) EM component, which is suggestive of high-frequency heating. They conclude that high- and low-frequency heating of AR cores co-exist, but these two processes appear to dominate at different evolutionary stages of ARs. This most interesting suggestion is worth pursuing in order to determine whether the high- and low-frequency heating represent different regimes of the same mechanism or truly different processes.
6.3.2 Evolution of flare and CME productivity
AR 7978 provided an exceptional opportunity for observing flare and CME activity as a function of evolution. The number of flares and CMEs that originated from this AR is shown in Table 6. During the emergence and the two following rotations, the AR produced numerous flares (including an X2.6 flare and CME event on 9 July, see Dryer et al. (1998), until the disappearance of the main spots after its third rotation. On the other hand, CME activity, which was at first mainly related to flare events, continued at a surprisingly high level for the next three rotations (van Driel-Gesztelyi et al., 1999a), while the magnetic helicity content of the dispersed active region remained reasonably high (Démoulin et al., 2002b), see also Section 6.4. However, none of the late CMEs were related to flare events above the GOES B1 level. Table 6 lists the number of flares in different GOES classes and of the observed CMEs. The flare data in Table 6 was taken from the GOES X-ray and optical event catalog.Footnote 4 CMEs were identified in the SOHO/EIT data (Delaboudinière et al., 1995) and SOHO/LASCO (Brueckner et al., 1995) observations by Démoulin et al. (2002b). The low level of other activity during the lifetime of AR 7978 allowed the identification of even back-side CMEs that originated from this AR when it was on the far side of the Sun. The number of CMEs has been corrected for data gaps assuming that the frequency of the CMEs was the same during the gaps as during observing times (Table 6). This doubles the sampling of CMEs relative to that of the flares which could only be observed when the AR was on the visible hemisphere. It is clear from the examples shown in Table 6 that the highest activity occurs during the emergence phase. High magnetic-flux density in an AR increases the probability of a high reconnection rate in activity events and thus the appearance of bright flare ribbons. CMEs occurring during the decay phase due to filament eruption may well have the same underlying physics, but the accompanying activity manifestation (two-ribbon flare) will be weaker and beyond a certain point into the decay phase even below detection level.
6.4 Study of the magnetic-helicity budget
An important role of CMEs is that they carry away magnetic helicity, which would otherwise accumulate incessantly in the Sun (Rust and Kumar, 1994; Low, 1996). Twisted flux tubes ejected in CMEs appear in the interplanetary space as magnetic clouds, in most of which the twisted structure is still well observable. In an attempt to trace magnetic helicity, a conserved quantity even in resistive MHD on a timescale less than the global diffusion timescale, Berger (1984), from the sub-photospheric layers to the heliosphere through an analysis of the long-term magnetic helicity budget of this isolated AR between July–Nov. 1996, Démoulin et al. (2002b) developed a method to observationally determine the evolution of the coronal helicity content of AR 7978 and relate changes in it to magnetic helicity carried away by CMEs identified to have originated from the AR (Table 6). Also included in this section is the magnetic helicity budget of AR 8100 that appeared on the southern hemisphere and was tracked between Nov. 1997 and Feb. 1998. AR 8100 exhibited a very different helicity evolution to AR 7978.
6.4.1 Magnetic energy
Li et al. (2010) analysed the build-up of energy between the three homologous flare/CME events observed on 5, 12 and 16 May 1997. The simple bipolar source region, AR 8038, was in a decay phase. Analysing how the free energy was re-introduced to the near-potential state following the eruptions, they found that prior to the flare/CME event on 12 May, the total unsigned flux of the entire AR decreased by about 18% during 66 hours. The unsigned flux evolution in the direct vicinity of the PIL first decreased by 42% in about 30 hours, then during the 30 hours prior to the eruption it started to increase again, re-gaining and surpassing its starting value by a few percents. Fourier local correlation-tracking reveals a general westward flow of 100–200 km s−1 in the following polarity towards the PIL, which may be a partial source of this flux increase, another being MMF activity around the leading sunspot. Integrating a “proxy Pointing flux” of \({S_R} = \sum {|u|\tilde B_R^2}\) defined by Welsch et al. (2009), which makes use of the computed flow field (u) and LOS MDI magnetic field (B) values, they estimated energy input to be on the order of 1.15 × 1032 erg during the 66 hours before the 12 May eruption, which appears sufficient. However, the magnetic evolution process cannot be fully explained by the flows obtained and they conclude that it may be necessary to invoke the continuing emergence of fields in a non-potential state.
Welsch et al. (2009), in an impressive article, analyse 46 ARs using MDI magnetograms to study the relationship between photospheric flow fields and flaring by computing extensive (that scale with the AR size/flux) and intensive (that are independent on AR size/flux) quantities and correlating them with flare activity above the GOES C1.0 level. The relevant part of their study to the topic of this review is that they found the above-mentioned proxy Pointing flux SR, an extensive quantity, the most strongly associated with flare flux, while all the intensive flow properties showed a poor correlation. Past flare activity was also found to be associated with future flare occurrence. In an in-depth discussion they raise the question of whether free energy propagates from below, as postulated by McClymont and Fisher (1989) and supported by Leka et al. (1996), or if it is due to photospheric flows acting on already emerged fields advocated by, e.g., Brown et al. (2003) and Antiochos et al. (1999). The lack of clear correlation with intensive flow properties as well as the repetitive nature of flare activity in certain ARs, while the lack of it in others are suggestive of the sub-photospheric origin of AR non-potentiality. However, that the correlation was found between the extensive flow property SR, which has units of energy flux, raises questions. In the decay phase of ARs, magnetic flux cancellations brought along by seemingly random flows may be building up free energy in the corona, or perhaps flaring has a systematic time delay relative to flows, involving the propagation of twist via torsional Alfvén waves (Longcope and Welsch, 2000).
6.4.2 Computation of coronal relative magnetic helicity
SOHO/MDI magnetograms taken close to the CMPs of AR 7978 at each rotation of its return were used as boundary conditions for linear force-free field (LFFF) magnetic extrapolations (\({\vec \nabla} \times {\vec B} = \alpha {\vec B}\); α = const). The extrapolated field lines were co-aligned with coronal loops observed with Yohkoh/SXT (see Figure 26). Parameters of the best general fit between the models and observations were adopted for computation of the relative coronal helicity following Berger (1985). The magnitude of the latter depends on the photospheric flux distribution and on the value of α. The two values of Hcorona given in Table 7 correspond to the minimum and maximum values of α in the best-fitting range. Even though α stays below its resonant value (which would give unrealistically high magnetic helicity) in all the extrapolations, for the helicity computations a linearised expression in α was used Green et al. (2002). A computational box of the same extension centred on the AR was taken in all the cases. The same method was followed for AR 8100 and the results can be seen in Table 8.
Yohkoh/SXT observations and linear force-free computations of the coronal field using SOHO/MDI magnetic maps. The 1st and 2nd columns correspond to Aug. 3 and 30, while 3rd and 4th columns to Sep. 25 and Oct. 23, respectively. The α value is selected to have the best global match between the computed field lines and the observed SXT loops. We have drawn with thick (thin) continuous lines the field lines computed taking the highest (lowest) value of α, and have represented them on the same figure. The abscissas and ordinates in each map are expressed in Mm. Isocontours (± 100, 500, 1000 G) of the line of sight magnetic field have been drawn with continuous/dashed lines for positive/negative values. Image reproduced with permission from Mandrini et al. (2004), copyright by Springer.
6.4.3 Computation of the helicity generated by differential rotation
For the computation of magnetic helicity generated by photospheric plasma motions, Berger (1984, 1988) derived an expression for dHr/dt that depends only on observable photospheric quantities (Bn and \({\vec v}\)). Berger (1986) showed that the helicity generation rate can be understood as the summation of the rotation rate of all the individual elementary flux pairs weighted by their magnetic flux. Démoulin et al. (2002a) noticed that photospheric plasma motions generate two different helicity terms: the rotation of each polarity introduces ‘twist’ helicity, while the relative rotation of opposite polarity flux concentrations injects ‘writhe’ helicity. Twist and writhe helicities generated by differential rotation have opposite signs, while their magnitudes are similar, thus they partially cancel. The orientation of the bipole is important to understand the helicity injection by differential rotation as twist helicity dominates when the bipole is aligned parallel to the equator, while writhe dominates when it is perpendicular. Using SOHO/MDI data the helicity injected by differential rotation was computed (Table 7, column 5 — the most accurate values in the helicity budget). Green et al. (2002) followed the same method and computed the helicity injection by differential rotation for AR 8100. The results are seen in Table 8.
6.4.4 Computation of the helicity ejected via CMEs
Démoulin et al. (2002b) identified all the CMEs that originated from AR 7978 during its entire evolution using SOHO/LASCO & EIT, and Yohkoh/SXT observations. These numbers were then corrected for LASCO data gaps (26 + 5 CMEs). Assuming a one-to-one association between CMEs and magnetic clouds, i.e., interplanetary consequences of CMEs, which have clearly twisted magnetic structures, helicity ejected in a CME was estimated. For computing relative magnetic helicity per unit length in a typical magnetic cloud a numerically integrated form of Berger’s equation (Berger, 1999) was used, and for the mean magnetic field the values B0(2 × 10−4 G) and radius R (2 × 1012 cm) of 18 magnetic clouds from the sample in Lepping et al. (1990). For the length of the flux tube in the magnetic cloud two values were used: L1 = 0.5 AU (DeVore, 2000), which yielded Hr ≈ 2 × 1042 Mx2 magnetic helicity, and L2 = 2 AU (the cloud is still connected to the Sun; e.g., Richardson, 1997), which gave four times as much helicity for one average-sized magnetic cloud, i.e., CME. These mean helicity values had to be multiplied by the number of CMEs to obtain the total magnetic helicity ejected from this AR (Table 7, column 6).
To find the magnetic helicity shed via CMEs from AR 8100 the same method was applied. The AR was observed to produce 35 CMEs during its lifetime. After correcting for data gaps and when the AR was on the far side of the Sun the total CME count rises to 65.
6.4.5 Discussion on the helicity budget
AR 7978 was a classical bipolar AR oriented E-W, distorted only by the differential rotation. It had positive relative coronal helicity, (corresponding to the hemispheric helicity trend on the South hemisphere), and the differential rotation injected positive helicity as well throughout the studied six solar rotations (Table 7, 5th column). Localised small scale photospheric surface motions, as compared to differential rotation, should also inject magnetic helicity into the coronal field. Relative motions of the AR polarities during the two main flux emergence phases were clearly evident. After this period, there was no evidence of significant shearing motions other than the differential rotation (Démoulin et al., 2002b). When looking at the changes in coronal helicity from one rotation to the next, and comparing them to the amount of helicity generated by differential rotation (4th and 5th columns in Table 7) it is obvious that differential rotation is an inefficient generator of helicity. This accentuates the importance of the helicity inflow and outflow through the boundaries of our coronal computational box. The total helicity budget of the active region may be written:
where Δ denotes the variation of the helicity, N is the number of the CMEs and HCME is the mean helicity carried away per CME event. ΔHemergence is given in the last column of Table 7. It is clear that in the helicity budget of AR 7978 the increase in coronal helicity during the first two rotations and the large amount of helicity carried away by CMEs during this period requires the largest input of helicity by the sub-photospheric layers. Indeed, major flux emergence episodes were observed then in the AR. As mentioned above, during the two episodes of flux emergence footpoint motions are thought to inject helicity in the coronal field. This helicity injection was not computed, since its contribution is included in the emergence term as defined above (Démoulin and Berger, 2003). Thus, the only surface shearing motion considered in our budget is the differential rotation. Later the emergence term in the helicity budget becomes smaller, but still not negligible. The total amount of helicity that should come from twisted flux emergence can be estimated to be between 55–241 × 1042 Mx2 in this simple bipolar region, that produced 31 CMEs. For comparison, during the same period, the differential rotation injected only 8.3 × 1042 Mx2, so it clearly was a minor contributor to the magnetic-helicity budget of AR 7978. Correction for the underestimation of the longitudinal field by MDI should bring a correction factor slightly over 2 for ΔHcorona and ΔHdiff. rot. Such correction would cause only a minor change in the total of the emergence term: ΔHemergence = 51–246 × 1042 Mx2. Though all the helicity values, especially the amount carried away in CMEs, have important uncertainties (for a discussion see Démoulin et al. (2002b); Green et al. (2002), the difference between the above mentioned total helicity numbers is significantly larger than any of the errors
AR 8100 represents an AR with a different magnetic evolution and can therefore be used to compare and contrast with that of AR 7978. The AR was born on the southern hemisphere with a bipolar configuration but within days of its first appearance secondary bipoles began to emerge and the region evolved to take on a large and complex magnetic configuration. Significant new flux continued to emerge into the region until its third rotation, after which time the flux in the AR began to decrease. The AR emerged with negative relative coronal magnetic helicity (the opposite sign to the hemispheric trend) but by its second rotation the helicity sign in the coronal field had reversed and become positive. We assign this change in helicity sign to the emergence of new flux that carried with it positive helicity as the helicity injection by differential rotation is insufficient by an order of magnitude, even though it is of the correct sign (i.e., positive).
Akin with AR 7978, columns 4 and 5 in Table 8 show that differential rotation in AR 8100 is an inefficient means of injecting helicity into the AR during rotations 1 to 4, and possibly also the 5th rotation. In contrast to AR 7978, AR 8100 displayed a strong relative motion of its main polarities throughout its lifetime. This had the consequence that, in addition to the shearing motions created by differential rotation, the polarities underwent a strong clockwise rotation of more than 150. See Figure 27. Therefore, this AR represents a case study of a region where differential rotation is not the only shear flow acting on the coronal magnetic field. The rotation of the polarities and the effect of their orientation makes this AR interesting to study. The injection of helicity by differential rotation can be split into two components — twist and writhe — which inject helicity of opposite sign. The component that dominates depends on the orientation of the bipole. See Section 6.4.3. Initially, AR 8100 is orientated in the E-W direction and the twist helicity dominates injecting postive helicity. But as the AR rotates, it becomes more aligned to the N-S direction and writhe helicity dominates, which injects negative helicity. Then, the action of differential rotation serves to deplete helicity from the corona (which is of positive sign) rather than building it.
SOHO/MDI magnetic maps showing AR 8100 during rotations two to five. The main polarities of the active region undergo a strong clockwise rotation. Image reproduced with permission from Green et al. (2002), copyright by Springer.
AR 8100 showed a high level of activity and produced 65 CMEs (corrected CME count) during 5 solar rotations — over twice that of AR 7978, which was followed for 6 solar rotations. The CME rate dropped in the second rotation but rose again in the third, probably due to the emergence of new magnetic flux, and the rate was then maintained throughout its lifetime.
AR 8100 is not alone in exhibiting a strong rotation, López Fuentes et al. (2003) found 15% of all bipoles showed significant rotation in their study of 300 regions so that for a small (but significant) sub-set of active regions, the helicity injection via differential rotation will not be constant with time.
The detailed helicity evolution of ARs 7978 and 8100 have been compared in Mandrini et al. (2004). The paper very nicely summarises that differential rotation is an ineffective source of coronal magnetic helicity in both of these very different ARs. The CMEs that are produced from the regions carry away more than 10 times the helicity injected by this mechanism, and in AR 8100 the differential rotation actually serves to deplete the coronal helicity content. What then is the source of the helicity shed by the CMEs? In the early rotations of both ARs flux emergence may provide the source. However, the flux emergence ceases in both ARs whilst the CME activity continues. The observational and theoretical considerations then point toward the helicity reservoir lying in the sub-surface portions of the AR magnetic field, which replenishes helicity into the coronal field either by a continued rise or via torsional Alfvén waves.
6.5 Evolution of coronal parameters: T, EM, ρ
The evolution of the fluxes observed in X-rays were correlated with the magnetic flux density in active region NOAA 7978 from its birth throughout its decay. Magnetic observables were derived from SOHO/MDI data while Yohkoh/SXT and Yohkoh/BCS data were used to determine the global evolution of the temperature and the emission measure of the coronal plasma at times when no significant brightenings were observed. It was shown that the mean X-ray flux and derived parameters, temperature and emission measure (together with other quantities deduced from them, such as the density and the pressure), of the plasma in the AR follow power-law relationships with the mean magnetic flux density (\(\bar B\)) (Figure 28). The exponents (b) of these power-law functions (\((a{\bar B^b})\)) were derived using two different statistical methods, a classical least-squares method in loglog plots and a non-parametric method, which takes into account the fact that errors in the data may not be normally distributed. Both methods give similar exponents, within error bars, for the mean temperature and for both instruments (SXT and BCS); in particular, b stays in the range [0.27, 0.31] and [0.24, 0.55] for SXT images and BCS data, respectively. For the emission measure the exponent b lies in the range [0.85, 1.35] and [0.45, 1.96] for SXT and BCS, respectively (see Figure 29.
Log-log curve of the flux per unit surface area observed with the Al0.1 and AlMgMn filters temperature and emission measure derived from Yohkoh/SXT versus magnetic flux density (\(\bar B\)). The solid line shows the linear least-squares fit and the two dotted lines correspond to the 3σ error in the slope of the solid curve. Only the decaying phase (points mark with ◇) are included in the least-squares fit. The same analysis has been done for Yohkoh/BCS data. Image reproduced with permission from van Driel-Gesztelyi et al. (2003b), copyright by AAS; see also van Driel-Gesztelyi et al. (2003a).
Ranges for the exponents found for the mean physical parameters in the scaling law equations: parameter ∝ \({\bar B^{\rm exponent}}\) (\(\bar B\): magnetic flux density). The temperature, T, and the emission measure, EM, are derived directly from the observations, then the plasma density, Ne, and pressure, P, are deduced. Tmax is the maximum temperature derived from the quasi-static thermal model of coronal loops. HT and HP are the heating rate derived from the observations and the thermal model. For Tmax and HP two values of a are shown (coronal radiative losses ∝ Tα). The ±3σ error range of a normally distributed statistics is light shaded. The 90% confidence interval of the non-parametric statistics is dark shaded. Image reproduced with permission from Démoulin et al. (2003), copyright by AAS.
As a next step, Démoulin et al. (2003) derived the dependence of the mean coronal heating rate on the magnetic flux density (Figure 29). They used the scaling laws of coronal loops in thermal equilibrium to derive four observational estimates of the scaling of the coronal heating with \(\bar B\) (two from SXT and two from BCS observations). These results are used to test the validity of coronal heating models. It was found that models based on the dissipation of stressed, current-carrying magnetic fields are in better agreement with the observations than models that attribute coronal heating to the dissipation of MHD waves injected at the base of the corona. This confirms, with smaller error bars, previous results obtained for individual coronal loops (Mandrini et al., 2000) as well as for the global coronal emission of the Sun and cool stars (Schrijver and Aschwanden, 2002). Taking into account that the photospheric field is concentrated in thin magnetic flux tubes, both SXT and BCS data were found to be in best agreement with models invoking a stochastic buildup of energy, current layers and MHD turbulence.
6.6 Evolution of multi-wavelength emitted fluxes
The long-term evolution of AR 7978 led to rotational modulation of the emitted fluxes with an amplitude depending on the observing wavelength range, as shown in Section 6.2.1. The evolution of the multi-wavelength emitted fluxes/flux densities from optical to X-rays as a function of the evolving magnetic field carry information about heating mechanisms acting at different atmospheric levels. Such a quantitative analysis was carried out, taking one set of data per rotation at each consecutive central meridian passage of AR 7978, outside the time of flares, obtained from SOHO (MDI, EIT, CDS, SUMER and CELIAS/SEM), Yohkoh (BCS, SXT), GOES, SOLSTICE and 10.7-cm radio data from DRAO, Canada (for a subset, see Figure 30). Preliminary results of the analysis were published in van Driel-Gesztelyi et al. (1999b) and van Driel-Gesztelyi et al. (2001), and a summary of the final results by Démoulin (2004).
Multiwavelength images of AR 7978 during four rotations (2nd–5th) showing the evolution of magnetic fields (SOHO/MDI data, upper left), 304 Å He II (SOHO/EIT, upper right), 171 Å Fe ix (SOHO/EIT, lower left), and SXRs (Yohkoh/SXT, lower right). Note that the spatial distribution of the emission in hotter lines (1–2 MK) is similar to that in 304 Å, but as the magnetic field was getting dispersed, and the loops grew, there was a re-organisation of the emission with height. At earlier times hot and dense plasma fully filled the loops, while later the EUV loops were only partially filled, as they became taller than the gravitational scale height. In SXRs (T ≈ 2–5 MK) more fully filled loops were observed besides an increasing presence of a diffuse emission.
The 19 emitted-flux datasets were obtained with different types of instruments: imager with filters (EIT), imager with spectrograph (CDS, SUMER), Sun-as-a-star spectrometer (SOLSTICE, CELIAS) and radio telescope (DRAO). From all these data, the mean radiative excess flux densities were derived ΔF = (flux − basal flux) per unit surface area for each rotation for each dataset (basal flux is attributed to heating of non-magnetic origin, e.g., acoustic wave flux). Then the dependence of the 19 ΔF values on the photospheric mean magnetic flux density \(\bar B\) was analysed. Démoulin (2004) found power-law relations between the detected excess flux density and the magnetic flux density in these different spectral domains, \(\Delta {F} \ \infty \ {\bar B}^{b}\), with the exponent b depending on the formation temperature of the spectral lines involved. For the SXRs the dependence was found to be almost quadratic (b = 1.6–2.6), while for the radiation emitted from the transition region and the chromosphere the dependence of the measured fluxes was found to be more linear (6 = 0.7–1). However, Démoulin (2004) proposed that the measured SXR fluxes are strongly affected by the instrumental response function R(T), which increases with T instead of peaking at a given T. The power-laws illustrated in Figure 31 were derived from data corrected for this instrumental effect using the observed mean T. In this corrected dataset the power-law exponents for various SXR data were found to be in the range b = 1.1–1.2, closer to the exponents found for transition-region and chromospheric emission.
Ranges for the exponents, b, found for the power-law relations between the detected excess flux density and the magnetic flux density in different spectral domains, \(\Delta F \ \infty \ {\bar B^{b}}\). The results are approximately ordered along the abscissa according to the mean temperature of the emitting plasma (except when the ranges overlap, e.g., in X-rays). Results at the extreme right, outside of the box, have such a broad wavelength (temperature) range that a mean temperature cannot be defined. The ordinate extension of the shaded regions represent the ±3σ error range. The Sun-as-a-star measurements are dark shaded, while the spatially resolved measurements are light shaded, with the lightest shading for the spectrometers (CDS, SUMER). The horizontal grey band corresponds to the range of the exponent for the coronal plasma pressure. In the X-ray range, the exponents are corrected for the temperature dependence of the instrumental response function. Image reproduced with permission from Démoulin (2004), copyright by IAU.
What is the relationship between the power laws found in this study and the power law dependence between total X-ray luminosity (Lx, total flux) of ARs and total magnetic flux \(({\Phi _{{\rm{tot}}}}):{L_x} \propto \Phi _{_{{\rm{tot}}}}^{^{1.19 \pm 0.04}}\) (Fisher et al., 1998) and for a wide range of features from X-ray bright points to red dwarfs and T Tauri stars covering over 12 magnitudes in magnetic flux: Lx ∝ Φ1.15±0 05 found by Pevtsov et al. (2003)? Obviously, the power-law exponents are very close to those found by Démoulin (2004) for X-rays, after a correction for the instrumental response functions. However, Démoulin (2004) argues that there is a natural correlation that exists between Lx and Φtot (extensive quantities) through the spatial extent of the magnetic structures involved. To make sure that the approximately linear relationship between SXR flux and magnetic field is not due to a natural proportionality of the extensive quantities with the magnetic area considered, which may dominate over the relatively smaller variations of the intensive quantities, the intrinsic physical relations between intensive quantities (ΔF and \(\bar B\)), i.e., flux densities should be analysed. In the study by Fisher et al. (1998) SXT DN was transformed into flux values by assuming a fixed T of 3 MK, therefore the T dependence of the instrumental response function was not taken into account. This may not have been important for that study, however, as the analysed ARs were approximately in the same evolutionary stage, i.e., their T was probably similar. In the analysis by Pevtsov et al. (2003) the T was estimated for most of the different magnetic structures accounting for the T dependence of the instrumental response function. As R(T) appears to be the underlying cause of discrepancy between exponents found between X-ray fluxes/flux densities and magnetic variables, accounting for this brings the relationship close to being linear both on the Sun and cool stars (see references in Démoulin, 2004).
To interpret the transition region (TR) flux densities’ relationship with \(\bar B\), Démoulin (2004) concluded that the four mechanisms previously proposed for heat transport in the TR result in scaling laws, which are compatible with those deduced from the observations shown in Figure 31. The four mechanisms are: (i) classical thermal conduction by electrons (Spitzer, 1962; Lie-Svendsen et al., 1999), (ii) enhanced conduction by turbulence (Cally, 1990), (iii) ambipolar diffusion of ions and neutral atoms (Fontenla et al., 1990), and (iv) transport by plasma flows (Chae et al., 1997).
Interpreting the power laws found for emission from the chromosphere, the best model to be compatible with the power-law exponents found was that by Solanki et al. (1991) (see Figure 32). However, the emission from the chromosphere is not simply linked to the energy deposited in the region where an emission line is formed, as radiation from the photosphere and neighbouring chromospheric layers also contribute.
Schematic representation of models of the emission of chromospheric lines outlining the main effects of a changing magnetic filling factor (longterm evolution from right to left). The emitting layer is represented by the darker gray bands. Observations are not able to resolve the flux tubes, but measure the mean excess flux, \(\Delta {\bar F}\), and the mean magnetic flux, \(\bar B\). The same atmosphere is present as \(\bar B\) decreases from right to left, while the merging height increases. This leads to a natural decrease of \(\Delta {\bar F}\) with decreasing \(\bar B\). Owing to the changing merging height with \(\bar B\), \(\Delta {\bar F}\) saturates for increasing \(\bar B\) as the magnetic flux tubes get into contact in the emission region (on the right). This is a representation of the hydromagnetic model by Solanki et al. (1991) of an expanding flux tube for the interpretation of Ca ii K line flux, and explains well the results for the evolution of chromospheric emission during the evolution of AR 7978 by Démoulin (2004), from where the image is reproduced with permission, copyright by IAU.
6.7 What did we learn from long-term evolution studies of ARs?
The results presented above on the long-term evolution of ARs confirmed that the evolution of an active region in each and every detail reflects the evolution of its magnetic field. It was found that flares mainly occur when the magnetic field of the AR has the highest complexity and magnetic flux density, and this is when the variability of AR cores are the highest, too. However, CMEs may be more closely related to the magnetic helicity content of the AR. It was also studied how much the contribution of differential rotation and twisted flux emergence contribute to building up the observed shear and helicity. Differential rotation turned out to be a very ineffective generator of magnetic helicity, thus the dominant source of coronal and interplanetary helicity is the inherent twist of the flux tubes forming the ARs. Magnetic helicity is transferred from the sub-photospheric layers to the corona by magnetic flux emergence and replenished after relaxation (CME) events either by a slow continuous emergence of the flux tube or by torsional Alfvén waves (Longcope and Welsch, 2000). It being concentrated along the magnetic inversion line by magnetic cancellations there. This process can continue for several solar rotations until the helicity reserves of the flux tube are exhausted, or the flux tube is destroyed by convective motions.
A study of how atmospheric heating is affected by the magnetic evolution was carried out by van Driel-Gesztelyi et al. (2003b) and Démoulin et al. (2003). Using Yohkoh/SXT and BCS data they studied the evolution of the coronal plasma parameters as functions of magnetic observables during five solar rotations and derived scaling laws between them (van Driel-Gesztelyi et al., 2003b). It was found that the mean X-ray flux and derived parameters, temperature and emission measure of the plasma (together with other quantities deduced from them, such as the density and the pressure), in the AR follow power-law relationships with the mean magnetic flux density. The determination of such power-law relations, when combined with scaling laws deduced from coronal heating models, can provide us with powerful tools for determining the mechanisms responsible for the existence of the high temperature corona (Démoulin et al., 2003). Through such a study it was found that models involving the dissipation of stressed, current-carrying magnetic fields as well as magnetic turbulence are in much better agreement with the scaling laws derived from the long-term evolution of AR 7978 than the ones which solely involve wave heating.
Another complex analysis involved the use of multi-instrument datasets leading to a study of the evolution of emitted flux densities in 19 different wavelength domains in correlation with magnetic flux density. Analysing the obtained power-laws and comparing them to heating mechanisms and models of different layers of the solar atmosphere, Démoulin (2004) concluded:
We have learned that the magnetic field is not only a strong structuring agent of the solar atmosphere, but also that it defines its main properties (such as pressure and temperature). There is plausibly a unique heating mechanism in the magnetised part that heats both the upper chromosphere and the corona […]. The heating rate scales approximately with the magnetic field to the second power (transforming all the parameter dependence to the magnetic one). In the intermediate layer, the TR, this heating mechanism could well be at work, but the presence of such high radiative losses makes this heating input unimportant for the TR physics. Finally, taking into account the observed universality of the flux-flux relations (power laws between fluxes from the optical to the X-ray range), this physical scenario is expected to extend to cool stars.
The latter was one of the results relevant to stellar activity studies. However, emitted flux evolution leading to evolving rotational modulation was also used to successfully test photometric starspot modelling programs (Oláh et al., 1999) and interpret stellar X-ray spectra (Orlando et al., 2004). The long-term evolution of ARs, especially during solar-minimum conditions, is an outstanding tool for creative solar and stellar physicists to decipher components of complex phenomena covered by their observations.
7 Concluding Remarks
We started this review with references to IAU Symposium 35 on the “Structure and Development of Solar Active Regions”, held in Budapest, Hungary in September 1967, and we would like to end with another reference to it. The usual welcome speech at the start of the Symposium was given by László Detre, who was then the director of Konkoly Observatory and a famous expert on variable stars, who cited a few lines from a poem published in the latest issue of the Irish Astronomical Journal which arrived to Konkoly Observatory’s library prior to the Symposium. The title of the poem was “A Solar Physicist’s Lament” and, we believe, these lines have not lost their validity (nor their charm) in nearly 50 years:
“It looks as if many a sunny day
Will pass along on its way
Before we solve it all.”
As active region evolution has relevance to most aspects of solar activity, more and even deeper analyses of AR evolution as well as studies done in an AR evolutionary context will help us to “solve it all”.
Notes
The reference given by Kiepenheuer (D’Azambuja, 1953a) was incorrect, there was no definition published there. He must have remembered verbal communication during solar physics conferences held in Italy in 1952 during and after the VIIIth General Assembly of the IAU, where both of them were present (for an account of these conferences see D’Azambuja, 1953b). A definition we have found in the literature was by his wife, Margharite D’Azambuja (1956), who wrote (in French), “The very close association between spots and faculae, which more and more appear to be consequences of a common cause, are nowadays commonly called as activity centre”.
Carrington (1863)
References
Abramenko, V. I. and Longcope, D. W., 2005, “Distribution of the Magnetic Flux in Elements of the Magnetic Field in Active Regions”, Astrophys. J., 619, 1160–1166. [DOI], [ADS]. (Cited on page 16.)
Amari, T., Luciani, J. F., Aly, J. J., Mikić, Z. and Linker, J., 2003, “Coronal Mass Ejection: Initiation, Magnetic Helicity, and Flux Ropes. II. Turbulent Diffusion-driven Evolution”, Astrophys. J., 595, 1231–1250. [DOI], [ADS]. (Cited on pages 38 and 46.)
Amari, T., Aly, J. J., Mikić, Z. and Linker, J., 2007, “Coronal Mass Ejection Initiation and Complex Topology Configurations in the Flux Cancellation and Breakout Models”, Astrophys. J., 671, L189–L192. [DOI], [ADS]. (Cited on page 38.)
Amari, T., Aly, J.-J., Mikić, Z. and Linker, J., 2010, “Coronal Mass Ejection Initiation: On the Nature of the Flux Cancellation Model”, Astrophys. J., 717, L26–L30. [DOI], [ADS], [arXiv:1005.4669]. (Cited on page 38.)
Antiochos, S. K., DeVore, C. R. and Klimchuk, J. A., 1999, “A Model for Solar Coronal Mass Ejections”, Astrophys. J., 510, 485–493. [DOI], [ADS], [arXiv:astro-ph/9807220]. (Cited on pages 38 and 67.)
Athay, R. G., Querfeld, C. W., Smartt, R. N., Landi Degl’Innocenti, E. and Bommier, V., 1983, “Vector Magnetic Fields in Prominences. III: He i D3 Stokes Profile Analysis for Quiescent and Eruptive Prominences”, Solar Phys., 89, 3–30. [DOI], [ADS]. (Cited on page 42.)
Aulanier, G., Démoulin, P., van Driel-Gesztelyi, L., Mein, P. and DeForest, C. E., 1998, “3-D magnetic configurations supporting prominences. II. The lateral feet as a perturbation of a twisted flux-tube”, Astron. Astrophys., 335, 309–322. [ADS]. (Cited on page 56.)
Aulanier, G., Démoulin, P., Mein, N., van Driel-Gesztelyi, L., Mein, P. and Schmieder, B., 1999, “3-D magnetic configurations supporting prominences. III. Evolution of fine structures observed in a filament channel”, Astron. Astrophys., 342, 867–880. [ADS]. (Cited on page 56.)
Aulanier, G., Török, T., Démoulin, P. and DeLuca, E. E., 2010, “Formation of Torus-Unstable Flux Ropes and Electric Currents in Erupting Sigmoids”, Astrophys. J., 708, 314–333. [DOI], [ADS]. (Cited on pages 38 and 46.)
Babcock, H. W., 1961, “The topology of the Sun’s magnetic field and the 22-year cycle”, Astrophys. J., 133, 527–587. [DOI], [ADS]. (Cited on pages 24 and 27.)
Baker, D., van Driel-Gesztelyi, L. and Green, L. M., 2012, “Forecasting a CME by Spectroscopic Precursor?”, Solar Phys., 276, 219–239. [DOI], [ADS]. (Cited on pages 12 and 41.)
Balthasar, H. and Wöhl, H., 1980, “Differential rotation and meridional motions of sunspots in the years 1940–1968”, Astron. Astrophys., 92, 111–116. (Cited on page 29.)
Beckers, J. M. and Schröter, E. H., 1969, “The Intensity, Velocity and Magnetic Structure of a Sunspot Region. IV: Properties of a Unipolar Sunspot”, Solar Phys., 10, 384–403. [DOI], [ADS]. (Cited on page 12.)
Bellot Rubio, L. R. and Beck, C., 2005, “Magnetic Flux Cancellation in the Moat of Sunspots: Results from Simultaneous Vector Spectropolarimetry in the Visible and the Infrared”, Astrophys. J. Lett., 626, L125–L128. [DOI], [ADS]. (Cited on pages 40 and 42.)
Benevolenskaya, E. E., 2005, “The Formation and Evolution of Complexes of Activity, Activity Nests and the Large-scale Connectivity in the Solar Corona”, in Large-scale Structures and their Role in Solar Activity, Proceedings of the Conference held 18–22 October, 2004 in Sunspot, NM, USA, (Eds.) Sankarasubramanian, K., Penn, M., Pevtsov, A., ASP Conference Series, 346, pp. 129–144, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 33.)
Berger, M. A., 1984, “Rigorous new limits on magnetic helicity dissipation in the solar corona”, Geophys. Astrophys. Fluid Dyn., 30, 79–104. [DOI], [ADS]. (Cited on pages 66 and 68.)
Berger, M. A., 1985, “Structure and stability of constant-alpha force-free fields”, Astrophys. J. Suppl. Ser., 59, 433–444. [DOI], [ADS]. (Cited on page 67.)
Berger, M. A., 1986, “Topological invariants of field lines rooted to planes”, Geophys. Astrophys. Fluid Dyn., 34, 265–281. [ADS]. (Cited on page 68.)
Berger, M. A., 1988, “An energy formula for nonlinear force-free magnetic fields”, Astron. Astrophys., 201, 355–361. [ADS]. (Cited on page 68.)
Berger, M. A., 1999, “Introduction to magnetic helicity”, Plasma Phys. Control. Fusion, 41, B167–B175. [DOI], [ADS]. (Cited on page 69.)
Bernasconi, P. N., Rust, D. M., Georgoulis, M. K. and LaBonte, B. J., 2002, “Moving Dipolar Features in an Emerging Flux Region”, Solar Phys., 209, 119–139. [DOI], [ADS]. (Cited on pages 10, 32, and 34.)
Bobra, M. G., van Ballegooijen, A. A. and DeLuca, E. E., 2008, “Modeling Nonpotential Magnetic Fields in Solar Active Regions”, Astrophys. J., 672, 1209–1220. [DOI], [ADS]. (Cited on page 45.)
Bogdan, T. J., Gilman, P. A., Lerche, I. and Howard, R., 1988, “Distribution of sunspot umbral areas: 1917–1982”, Astrophys. J., 327, 451–456. [DOI], [ADS]. (Cited on page 15.)
Borrero, J. M. and Ichimoto, K., 2011, “Magnetic Structure of Sunspots”, Living Rev. Solar Phys., 8, lrsp-2011-4. [DOI], [ADS], [arXiv:1109.4412 [astro-ph.SR]]. URL (accessed 28 April 2014): http://www.livingreviews.org/lrsp-2011-4. (Cited on page 35.)
Brants, J. J., 1985, “High-Resolution Spectroscopy of Active Regions. 2. Line-Profile Interpretation, Applied to an Emerging Flux Region”, Solar Phys., 95, 15–36. [DOI], [ADS]. (Cited on page 10.)
Bray, R. J. and Loughhead, R. E., 1964, Sunspots, The International Astrophysics Series, 7, Chapman & Hall, London. (Cited on pages 6, 11, 12, 19, and 36.)
Brouwer, M. P. and Zwaan, C., 1990, “Sunspot nests as traced by a cluster analysis”, Solar Phys., 129, 221–246. [DOI], [ADS]. (Cited on page 33.)
Brown, D. S., Nightingale, R. W., Alexander, D., Schrijver, C. J., Metcalf, T. R., Shine, R. A., Title, A. M. and Wolfson, C. J., 2003, “Observations of Rotating Sunspots from TRACE”, Solar Phys., 216, 79–108. [DOI], [ADS]. (Cited on page 67.)
Brueckner, G. E., Howard, R. A., Koomen, M. J. et al., 1995, “The Large Angle Spectroscopic Coronagraph (LASCO)”, Solar Phys., 162, 357–402. [DOI], [ADS]. (Cited on page 64.)
Brunner, W., 1930, “Gesetzmäßigkeiten in der Anordnung der Sonnenflecken zu Gruppen”, Astron. Mitt. Zurich, 13(CXXIV), 67–78. [ADS]. (Cited on pages 22 and 23.)
Bruzek, A., 1967, “On Arch-Filament Systems in Spotgroups”, Solar Phys., 2, 451–461. [DOI], [ADS]. (Cited on page 10.)
Bumba, V., 1965a, “Short note on the connections between the facular network and sunspots”, in Stellar and Solar Magnetic Fields, Proceedings from IAU Symposium 22 held in Rottach-Egern near Munich, Germany, 3–10 September 1963, (Ed.) Lust, R., IAU Symposia, 22, pp. 192–196, North-Holland, Amsterdam; New York. [ADS]. (Cited on page 35.)
Bumba, V., 1965b, “Some notes on sunspot fine structure”, in Stellar and Solar Magnetic Fields, Proceedings from IAU Symposium 22 held in Rottach-Egern near Munich, Germany, 3 – 10 September 1963, (Ed.) Lust, R., IAU Symposia, 22, pp. 305–308, North-Holland, Amsterdam; New York. [ADS]. (Cited on page 11.)
Bumba, V. and Howard, R., 1965, “A Study of the Development of Active Regions on the Sun”, Astrophys. J., 141, 1492–1501. [DOI]. (Cited on pages 9 and 13.)
Bumba, V. and Howard, R., 1969, “Solar Activity and Recurrences in Magnetic-Field Distribution”, Solar Phys., 7, 28–38. [DOI], [ADS]. (Cited on page 33.)
Caligari, P., Moreno-Insertis, F. and Schussler, M., 1995, “Emerging flux tubes in the solar convection zone. I. Asymmetry, tilt, and emergence latitude”, Astrophys. J., 441, 886–902. [DOI]. (Cited on page 19.)
Cally, P. S., 1990, “Turbulent thermal conduction in the solar transition region”, Astrophys. J., 355, 693–699. [DOI], [ADS]. (Cited on page 76.)
Canfield, R. C. and Russell, A. J. B., 2007, “Solar Active Region Flux Fragmentation, Subphotospheric Flows, and Flaring”, Astrophys. J., 662, L39–L42. [DOI], [ADS]. (Cited on page 16.)
Canfield, R. C., Hudson, H. S. and McKenzie, D. E., 1999, “Sigmoidal morphology and eruptive solar activity”, Geophys. Res. Lett., 26, 627–630. [DOI], [ADS]. (Cited on page 43.)
Canou, A., Amari, T., Bommier, V., Schmieder, B., Aulanier, G. and Li, H., 2009, “Evidence for a Pre-Eruptive Twisted Flux Rope Using the Themis Vector Magnetograph”, Astrophys. J. Lett., 693, L27–L30. [DOI], [ADS]. (Cited on page 42.)
Carrington, R. C., 1858, “On the Distribution of the Solar Spots in Latitudes since the Beginning of the Year 1854, with a map”, Mon. Not. R. Astron. Soc., 19, 1–3. [ADS]. (Cited on pages 7 and 33.)
Carrington, R. C., 1863, Observations of the Spots on the Sun: From November 9, 1853, to March 24, 1861, made at Redhill, Williams and Norgate, London. [Google Books]. (Cited on pages 7, 11, 22, and 28.)
Cassini, J. D., 1729, C. R. Acad. Sci., X, 729. (Cited on pages 7, 13, and 33.)
Chae, J., Yun, H. S. and Poland, A. I., 1997, “Effects of Non-LTE Radiative Loss and Partial Ionization on the Structure of the Transition Region”, Astrophys. J., 480, 817–824. [DOI], [ADS]. (Cited on page 76.)
Chae, J., Wang, H., Qiu, J., Goode, P. R., Strous, L. and Yun, H. S., 2001, “The Formation of a Prominence in Active Region NOAA 8668. I. SOHO/MDI Observations of Magnetic Field Evolution”, Astrophys. J., 560, 476–489. [DOI], [ADS]. (Cited on page 31.)
Chang, H.-K., Chou, D.-Y. and Sun, M.-T., 1999, “In Search of Emerging Magnetic Flux underneath the Solar Surface with Acoustic Imaging”, Astrophys. J. Lett., 526, L53–L56. [DOI], [ADS]. (Cited on page 53.)
Charbonneau, P., 2010, “Dynamo Models of the Solar Cycle”, Living Rev. Solar Phys., 7, lrsp-2010-3. [DOI], [ADS]. URL (accessed 28 April 2014): http://www.livingreviews.org/lrsp-2010-3. (Cited on page 7.)
Cheung, M. C. M., Schuössler, M., Tarbell, T. D. and Title, A. M., 2008, “Solar Surface Emerging Flux Regions: A Comparative Study of Radiative MHD Modeling and Hinode SOT Observations”, Astrophys. J., 687, 1373–1387. [DOI], [ADS], [arXiv:0810.5723]. (Cited on page 32.)
Cheung, M. C. M., Rempel, M., Title, A. M. and Schüssler, M., 2010, “Simulation of the Formation of a Solar Active Region”, Astrophys. J., 720, 233–244. [DOI], [ADS], [arXiv:1006.4117 [astro-ph.SR]]. (Cited on pages 32 and 33.)
Choudhary, D. P., Venkatakrishnan, P. and Gosain, S., 2002, “On Magnetic Flux Imbalance in Solar Active Regions”, Astrophys. J., 573, 851–856. [DOI], [ADS]. (Cited on pages 53 and 56.)
Choudhary, D. P., Gosain, S., Gopalswamy, N. et al., 2013, “Flux emergence, flux imbalance, magnetic free energy and solar flares”, Adv. Space Res., 52, 1561–1566. [DOI], [ADS]. (Cited on page 12.)
Dasi-Espuig, M., Solanki, S. K., Krivova, N. A., Cameron, R. and Peñuela, T., 2010, “Sunspot group tilt angles and the strength of the solar cycle”, Astron. Astrophys., 518, A7. [DOI], [ADS], [arXiv:1005.1774 [astro-ph.SR]]. (Cited on pages 22 and 23.)
D’Azambuja, L., 1953a, “Le colloque de Physique solaire organise a Rome par l’Academie des Lincei, en septembre 1952”, L’Astronomie, 67, 129–138. [ADS]. (Cited on page 5.)
D’Azambuja, L., 1956, “La reprise de l’Activité solaire: Méthodes nouvelles pour la mieux observer”, L’Astronomie, 70, 129–139. (Cited on page 5.)
D’Azambuja, M., 1953b, “L’Activité solaire: rotations nos 1336 et 1337”, L’Astronomie, 67, 429–430. (Cited on page 5.)
Delaboudinière, J.-P., Artzner, G. E., Brunaud, J. et al., 1995, “EIT: Extreme-Ultraviolet Imaging Telescope for the SOHO Mission”, Solar Phys., 162, 291–312. [DOI], [ADS]. (Cited on page 64.)
Démoulin, P., 2004, “The long-term evolution of active regions, multi-wavelength flux and heating studies: observations and theory”, in Multi-Wavelength Investigations of Solar Activity, Proceedings from IAU Symposium 223 held in St. Petersburg, Russian Federation, June 14–19, 2004, (Eds.) Stepanov, A. V., Benevolenskaya, E. E., Kosovichev, A. G., IAU Symposia, 223, pp. 13–22, Cambridge University Press, Cambridge; New York. [DOI], [ADS]. (Cited on pages 50, 73, 75, 76, and 77.)
Démoulin, P. and Berger, M. A., 2003, “Magnetic Energy and Helicity Fluxes at the Photospheric Level”, Solar Phys., 215, 203–215. [DOI], [ADS]. (Cited on pages 30 and 70.)
Démoulin, P., Mandrini, C. H., van Driel-Gesztelyi, L., Lopez Fuentes, M. C. and Aulanier, G., 2002a, “The Magnetic Helicity Injected by Shearing Motions”, Solar Phys., 207, 87–110. [DOI], [ADS]. (Cited on pages 31, 42, 50, and 68.)
Démoulin, P., Mandrini, C. H., van Driel-Gesztelyi, L., Thompson, B. J., Plunkett, S., Kovári, Z., Aulanier, G. and Young, A., 2002b, “What is the source of the magnetic helicity shed by CMEs? The long-term helicity budget of AR 7978”, Astron. Astrophys., 382, 650–665. [DOI], [ADS]. (Cited on pages 31, 50, 64, 66, 68, 69, and 70.)
Démoulin, P., van Driel-Gesztelyi, L., Mandrini, C. H., Klimchuk, J. A. and Harra, L., 2003, “The Long-Term Evolution of AR 7978: Testing Coronal Heating Models”, Astrophys. J., 586, 592–605. [DOI], [ADS]. (Cited on pages 13, 50, 72, 73, and 77.)
DeVore, C. R., 2000, “Magnetic Helicity Generation by Solar Differential Rotation”, Astrophys. J., 539, 944–953. [DOI], [ADS]. (Cited on pages 38 and 69.)
Dikpati, M. and Gilman, P. A., 2005, “A Shallow-Water Theory for the Sun’s Active Longitudes”, Astrophys. J., 635, L193–L196. [DOI], [ADS]. (Cited on page 33.)
Dryer, M., Andrews, M. D., Aurass, H. et al., 1998, “The Solar Minimum Active Region 7978, Its X2.6/1B Flare, CME, and Interplanetary Shock Propagation of 9 July 1996”, Solar Phys., 181, 159–183. [DOI], [ADS]. (Cited on page 64.)
D’Silva, S. and Choudhuri, A. R., 1993, “A theoretical model for tilts of bipolar magnetic regions”, Astron. Astrophys., 272, 621–633. [ADS]. (Cited on page 24.)
Ellerman, F., 1917, “Solar Hydrogen ‘Bombs’”, Astrophys. J., 46, 298. [DOI], [ADS]. (Cited on page 32.)
Evershed, J., 1909, “Radial movement in sun-spots”, Mon. Not. R. Astron. Soc., 69, 454–458. [ADS]. (Cited on page 11.)
Fan, Y., 2008, “The Three-dimensional Evolution of Buoyant Magnetic Flux Tubes in a Model Solar Convective Envelope”, Astrophys. J., 676, 680–697. [DOI], [ADS]. (Cited on pages 31 and 32.)
Fan, Y., 2009, “Magnetic Fields in the Solar Convection Zone”, Living Rev. Solar Phys., 6, lrsp-2009-4. [DOI], [ADS]. URL (accessed 28 April 2014): http://www.livingreviews.org/lrsp-2009-4. (Cited on pages 6, 19, 20, 24, 27, and 47.)
Fan, Y., Fisher, G. H. and McClymont, A. N., 1994, “Dynamics of emerging active region flux loops”, Astrophys. J., 436, 907–928. [DOI], [ADS]. (Cited on page 40.)
Fan, Y., Zweibel, E. G., Linton, M. G. and Fisher, G. H., 1999, “The Rise of Kink-unstable Magnetic Flux Tubes and the Origin of delta-Configuration Sunspots”, Astrophys. J., 521, 460–477. [DOI], [ADS]. (Cited on page 31.)
Fisher, G. H., Fan, Y. and Howard, R. F., 1995, “Comparisons between theory and observation of active region tilts”, Astrophys. J., 438, 463–471. [DOI], [ADS]. (Cited on pages 23, 25, and 27.)
Fisher, G. H., Longcope, D. W., Metcalf, T. R. and Pevtsov, A. A., 1998, “Coronal Heating in Active Regions as a Function of Global Magnetic Variables”, Astrophys. J., 508, 885–898. [DOI], [ADS]. (Cited on pages 75 and 76.)
Fontenla, J. M., Avrett, E. H. and Loeser, R., 1990, “Energy balance in the solar transition region. I. Hydrostatic thermal models with ambipolar diffusion”, Astrophys. J., 355, 700–718. [DOI], [ADS]. (Cited on page 76.)
Forbes, T. G. and Isenberg, P. A., 1991, “A catastrophe mechanism for coronal mass ejections”, Astrophys. J., 373, 294–307. [DOI], [ADS]. (Cited on page 38.)
Fröhlich, C., Andersen, B. N., Appourchaux, T. et al., 1997, “First Results from VIRGO, the Experiment for Helioseismology and Solar Irradiance Monitoring on SOHO”, Solar Phys., 170, 1–25. [ADS]. (Cited on pages 51 and 57.)
Gaizauskas, V., 2008, “Development of Flux Imbalances in Solar Activity Nests and the Evolution of Filament Channels”, Astrophys. J., 686, 1432–1446. [DOI], [ADS]. (Cited on page 33.)
Gaizauskas, V., Harvey, K. L., Harvey, J. W. and Zwaan, C., 1983, “Large-scale patterns formed by solar active regions during the ascending phase of cycle 21”, Astrophys. J., 265, 1056–1065. [DOI], [ADS]. (Cited on pages 13 and 33.)
Gaizauskas, V., Mackay, D. H. and Harvey, K. L., 2001, “Evolution of Solar Filament Channels Observed during a Major Poleward Surge of Photospheric Magnetic Flux”, Astrophys. J., 558, 888–902. [DOI], [ADS]. (Cited on page 33.)
Georgakilas, A. A., Zachariadis, T. G. and Alissandrakis, C. E., 1993, “Evolution of an active region and associated Hα arch structures”, Solar Phys., 146, 241–258. [DOI], [ADS]. (Cited on page 32.)
Gibson, S. E., Biesecker, D., Guhathakurta, M. et al., 1999, “The Three-dimensional Coronal Magnetic Field during Whole Sun Month”, Astrophys. J., 520, 871–879. [DOI], [ADS]. (Cited on page 50.)
Gilman, P. A. and Dikpati, M., 2000, “Joint Instability of Latitudinal Differential Rotation and Concentrated Toroidal Fields below the Solar Convection Zone. II. Instability of Narrow Bands at All Latitudes”, Astrophys. J., 528, 552–572. [DOI], [ADS]. (Cited on page 33.)
González Hernández, I., Komm, R., van Driel-Gesztelyi, L., Baker, D., Harra, L. and Howe, R., 2013, “Subsurface flows associated with non-Joy oriented active regions: a case study”, J. Phys.: Conf. Ser., 440, 012050. [DOI], [ADS]. (Cited on page 27.)
Green, L. M. and Kliem, B., 2009, “Flux Rope Formation Preceding Coronal Mass Ejection Onset”, Astrophys. J., 700, L83–L87. [DOI], [ADS], [arXiv:0906.4794 [astro-ph.SR]]. (Cited on pages 42 and 43.)
Green, L. M. and Kliem, B., 2014, “Observations of flux rope formation prior to coronal mass ejections”, in Nature of Prominences and their role in Space Weather, Symposium dedicated to the memory of Einar Tandberg Hanssen, June 2013, (Eds.) Schmieder, B., Malherbe, J.-M., Wu, S. T., IAU Symposium, S300, pp. 209–214, Cambridge University Press, Cambridge; New York. [DOI], [ADS], [arXiv:1312.4388]. (Cited on pages 43 and 44.)
Green, L. M., López Fuentes, M. C., Mandrini, C. H., Démoulin, P., van Driel-Gesztelyi, L. and Culhane, J. L., 2002, “The Magnetic Helicity Budget of a CME-Prolific Active Region”, Solar Phys., 208, 43–68. [DOI], [ADS]. (Cited on pages 68, 69, 70, and 71.)
Green, L. M., Kliem, B. and Wallace, A. J., 2011, “Photospheric flux cancellation and associated flux rope formation and eruption”, Astron. Astrophys., 526, A2. [DOI], [ADS], [arXiv:1011.1227 [astro-ph.SR]]. (Cited on pages 12, 41, and 45.)
Guglielmino, S. L., Bellot Rubio, L. R., Zuccarello, F., Aulanier, G., Vargas Domínguez, S. and Kamio, S., 2010, “Multiwavelength Observations of Small-scale Reconnection Events Triggered by Magnetic Flux Emergence in the Solar Atmosphere”, Astrophys. J., 724, 1083–1098. [DOI], [ADS], [arXiv:1007.4657]. (Cited on pages 8 and 9.)
Hagenaar, H. J. and Shine, R. A., 2005, “Moving Magnetic Features around Sunspots”, Astrophys. J., 635, 659–669. [DOI], [ADS]. (Cited on page 34.)
Hagenaar, H. J., Schrijver, C. J. and Title, A. M., 2003, “The Properties of Small Magnetic Regions on the Solar Surface and the Implications for the Solar Dynamo(s)”, Astrophys. J., 584, 1107–1119. [DOI], [ADS]. (Cited on pages 9, 11, 14, and 16.)
Hale, G. E. and Nicholson, S. B., 1925, “The Law of Sun-Spot Polarity”, Astrophys. J., 62, 270–300. [DOI], [ADS]. (Cited on page 7.)
Hale, G. E. and Nicholson, S. B., 1938, Magnetic Observations of Sunspots, 1917–1924, Carnegie Institution of Washington, Washington, DC. [ADS]. (Cited on page 12.)
Hale, G. E., Ellerman, F., Nicholson, S. B. and Joy, A. H., 1919, “The Magnetic Polarity of Sun-Spots”, Astrophys. J., 49, 153–178. [DOI], [ADS]. (Cited on pages 7, 22, and 80.)
Harvey, K. and Harvey, J., 1973, “Observations of Moving Magnetic Features near Sunspots”, Solar Phys., 28, 61–71. [DOI], [ADS]. (Cited on pages 12, 34, and 35.)
Harvey, K. L., 1993, Magnetic Bipoles on the Sun, Ph.D. thesis, Rijksuniversiteit Utrecht, Utrecht. [ADS]. (Cited on pages 9, 13, 14, 16, 17, 18, 25, 27, and 34.)
Harvey, K. L. and Hudson, H. S., 2000, “Solar Activity and the Formation of Coronal Holes”, Adv. Space Res., 25, 1735–1738. [DOI], [ADS]. (Cited on page 50.)
Harvey, K. L. and Martin, S. F., 1973, “Ephemeral Active Regions”, Solar Phys., 32, 389–402. [DOI], [ADS]. (Cited on pages 10, 11, and 14.)
Harvey, K. L. and Zwaan, C., 1993, “Properties and emergence of bipolar active regions”, Solar Phys., 148, 85–118. [DOI], [ADS]. (Cited on pages 13, 16, and 33.)
Harvey, K. L., Jones, H. P., Schrijver, C. J. and Penn, M. J., 1999, “Does Magnetic Flux Submerge at Flux Cancelation Sites?”, Solar Phys., 190, 35–44. [DOI], [ADS]. (Cited on page 42.)
Hathaway, D. H., 2010, “The Solar Cycle”, Living Rev. Solar Phys., 7, lrsp-2010-1. [DOI], [ADS]. URL (accessed 28 April 2014): http://www.livingreviews.org/lrsp-2010-1. (Cited on page 49.)
Hathaway, D. H. and Choudhary, D. P., 2008, “Sunspot Group Decay”, Solar Phys., 250, 269–278. [DOI], [ADS]. (Cited on page 34.)
Holder, Z. A., Canfield, R. C., McMullen, R. A., Nandy, D., Howard, R. F. and Pevtsov, A. A., 2004, “On the Tilt and Twist of Solar Active Regions”, Astrophys. J., 611, 1149–1155. [DOI], [ADS]. (Cited on page 25.)
Hood, A. W. and Priest, E. R., 1981, “Critical conditions for magnetic instabilities in force-free coronal loops”, Geophys. Astrophys. Fluid Dyn., 17, 297–318. [DOI], [ADS]. (Cited on page 42.)
Howard, R. F., 1991a, “The magnetic fields of active regions. VI. Magnetic Axis Tilt Changes”, Solar Phys., 132, 257–270. [DOI], [ADS]. (Cited on page 23.)
Howard, R. F., 1991b, “Axial tilt angles of sunspot groups”, Solar Phys., 136, 251–262. [DOI], [ADS]. (Cited on page 23.)
Hudson, H. S., LaBonte, B. J., Sterling, A. C. and Watanabe, T., 1998, “NOAA 7978: the Last best Old-Cycle Region”, in Observational Plasma Astrophysics: Five Years of YOHKOH and Beyond, Yohkoh Fifth Anniversary Symposium, Tokyo, Japan, 6–8 November 1996, (Eds.) Watanabe, T., Kosugi, T., Sterling, A. C., Astrophysics and Space Science Library, 229, pp. 237–244, Kluwer, Dordrecht. [ADS]. (Cited on pages 50, 51, and 57.)
Ishii, T. T., Kurokawa, H. and Takeuchi, T. T., 2000, “Emergence of Twisted Magnetic-Flux Bundles and Flare Activity in a Large Active Region, NOAA 4201”, Publ. Astron. Soc. Japan, 52, 337–354. [ADS]. (Cited on page 30.)
Karachik, N. V., Pevtsov, A. A. and Abramenko, V. I., 2010, “Formation of Coronal Holes on the Ashes of Active Regions”, Astrophys. J., 714, 1672–1678. [DOI], [ADS]. (Cited on pages 36 and 37.)
Kawai, G., Kurokawa, H., Tsuneta, S., Shimizu, T., Shibata, K., Acton, L. W., Strong, K. T. and Nitta, N., 1992, “Comparison between Hα and Yohkoh Soft X-Ray Images of Emerging Flux Regions”, Publ. Astron. Soc. Japan, 44, L193–L198. [ADS]. (Cited on page 10.)
Kiepenheuer, K. O., 1968, “Preface and Introduction”, in Structure and Development of Solar Active Regions, Proceedings from IAU Symposium 35 held in Budapest, Hungary, 4–8 September 1967, (Ed.) Kiepenheuer, K. O., IAU Symposia, 35, pp. 3–9, Reidel, Dordrecht. [ADS]. (Cited on page 5.)
Kliem, B. and Török, T., 2006, “Torus Instability”, Phys. Rev. Lett., 96, 255002. [DOI], [ADS], [arXiv:physics/0605217]. (Cited on pages 42 and 45.)
Kliem, B., Su, Y. N., van Ballegooijen, A. A. and DeLuca, E. E., 2013, “Magnetohydrodynamic Modeling of the Solar Eruption on 2010 April 8”, Astrophys. J., 779, 129. [DOI], [ADS], [arXiv:1304.6981 [astro-ph.SR]]. (Cited on page 46.)
Kosovichev, A. G. and Stenflo, J. O., 2008, “Tilt of Emerging Bipolar Magnetic Regions on the Sun”, Astrophys. J., 688, L115–L118. [DOI], [ADS]. (Cited on pages 19, 21, 24, 25, and 27.)
Künzel, H., 1960, “Die Flare-Höufigkeit in Fleckengruppen unterschiedlicher Klasse und magnetischer Struktur”, Astron. Nachr., 285, 271–273. [ADS]. (Cited on page 80.)
Kurokawa, H., Wang, T. and Ishii, T. T., 2002, “Emergence and Drastic Breakdown of a Twisted Flux Rope to Trigger Strong Solar Flares in NOAA Active Region 9026”, Astrophys. J., 572, 598–608. [DOI], [ADS]. (Cited on page 30.)
Lamb, D. A., Howard, T. A., DeForest, C. E., Parnell, C. E. and Welsch, B. T., 2013, “Solar Magnetic Tracking. IV. The Death of Magnetic Features”, Astrophys. J., 774, 127. [DOI], [ADS], [arXiv:1307.4019 [astro-ph.SR]]. (Cited on page 41.)
Lawrence, J. K. and Schrijver, C. J., 1993, “Anomalous diffusion of magnetic elements across the solar surface”, Astrophys. J., 411, 402–405. [DOI], [ADS]. (Cited on page 12.)
Leighton, R. B., 1969, “A magneto-kinematic model of the solar cycle”, Astrophys. J., 156, 1–26. [DOI], [ADS]. (Cited on pages 22, 23, and 24.)
Leka, K. D., 1997, “The Vector Magnetic Fields and Thermodynamics of Sunspot Light Bridges: The Case for Field-free Disruptions in Sunspots”, Astrophys. J., 484, 900–919. [DOI], [ADS]. (Cited on page 12.)
Leka, K. D. and Skumanich, A., 1998, “The Evolution of Pores and the Development of Penumbrae”, Astrophys. J., 507, 454–469. [DOI], [ADS]. (Cited on page 11.)
Leka, K. D., Canfield, R. C., McClymont, A. N. and van Driel-Gesztelyi, L., 1996, “Evidence for Current-carrying Emerging Flux”, Astrophys. J., 462, 547–560. [DOI], [ADS]. (Cited on pages 7, 11, 30, 41, and 67.)
Lepping, R. P., Burlaga, L. F. and Jones, J. A., 1990, “Magnetic field structure of interplanetary magnetic clouds at 1 AU”, J. Geophys. Res., 95, 11,957–11,965. [DOI], [ADS]. (Cited on page 69.)
Li, Y. and Welsch, B. T., 2008, “The Subsequent Decaying Regions of NOAA AR7978”, in Subsurface and Atmospheric Influences on Solar Activity, Proceedings of a workshop held at the NSO/Sac, Sunspot, New Mexico, USA, 16–20 April 2007, (Eds.) Howe, R., Komm, R. W., Balasubramaniam, K. S., Petrie, G. J. D., ASP Conference Series, 383, p. 397, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on pages 20, 50, 53, and 56.)
Li, Y., Lynch, B. J., Welsch, B. T., Stenborg, G. A., Luhmann, J. G., Fisher, G. H., Liu, Y. and Nightingale, R. W., 2010, “Sequential Coronal Mass Ejections from AR8038 in May 1997”, Solar Phys., 264, 149–164. [DOI], [ADS]. (Cited on page 66.)
Lie-Svendsen, Ø., Holzer, T. E. and Leer, E., 1999, “Electron Heat Conduction in the Solar Transition Region: Validity of the Classical Description”, Astrophys. J., 525, 1056–1065. [DOI], [ADS]. (Cited on page 76.)
Liggett, M. and Zirin, H., 1985, “Emerging flux in active regions”, Solar Phys., 97, 51–58. [DOI], [ADS]. (Cited on pages 13 and 33.)
Linton, M. G., Fisher, G. H., Dahlburg, R. B. and Fan, Y., 1999, “Relationship of the Multimode Kink Instability to δ-Spot Formation”, Astrophys. J., 522, 1190–1205. [DOI], [ADS]. (Cited on page 31.)
Lionello, R., Mikić, Z., Linker, J. A. and Amari, T., 2002, “Magnetic Field Topology in Prominences”, Astrophys. J., 581, 718–725. [DOI], [ADS]. (Cited on pages 50 and 56.)
Lites, B. W., 2005, “Magnetic Flux Ropes in the Solar Photosphere: The Vector Magnetic Field under Active Region Filaments”, Astrophys. J., 622, 1275–1291. [DOI], [ADS]. (Cited on page 42.)
Lites, B. W., Skumanich, A. and Martínez Pillet, V., 1998, “Vector magnetic fields of emerging solar flux. I. Properties at the site of emergence”, Astron. Astrophys., 333, 1053–1068. [ADS]. (Cited on pages 8 and 10.)
Liu, Y. and Norton, A. A., 2001, MDI Measurement Errors: The Magnetic Perspective, SOI Technical Notes, SOI-TN-01-144, Stanford University, Stanford. URL (accessed 28 April 2014): http://soi.stanford.edu/technotes/. (Cited on page 53.)
Longcope, D. and Choudhuri, A. R., 2002, “The Orientational Relaxation of Bipolar Active Regions”, Solar Phys., 205, 63–92. [DOI], [ADS]. (Cited on page 27.)
Longcope, D., Linton, M., Pevtsov, A., Fisher, G. and Klapper, I., 1999, “Twisted Flux Tubes and How They Get That Way”, in Magnetic Helicity in Space and Laboratory Plasmas, AGU Chapman Conference held at the HAO/NCAR, Boulder, Colorado in July 28–31, 1998, (Eds.) Brown, M. R., Canfield, R. C., Pevtsov, A. A., Geophysical Monograph Series, 111, p. 93, American Geophysical Union, Washington, DC. [ADS]. (Cited on page 32.)
Longcope, D. W. and Fisher, G. H., 1996, “The Effects of Convection Zone Turbulence on the Tilt Angles of Magnetic Bipoles”, Astrophys. J., 458, 380–390. [DOI], [ADS]. (Cited on pages 27 and 31.)
Longcope, D. W. and Welsch, B. T., 2000, “A Model for the Emergence of a Twisted Magnetic Flux Tube”, Astrophys. J., 545, 1089–1100. [DOI], [ADS]. (Cited on pages 67 and 77.)
Longcope, D. W., Fisher, G. H. and Arendt, S., 1996, “The Evolution and Fragmentation of Rising Magnetic Flux Tubes”, Astrophys. J., 464, 999–1011. [DOI], [ADS]. (Cited on page 30.)
Longcope, D. W., Fisher, G. H. and Pevtsov, A. A., 1998, “Flux-Tube Twist Resulting from Helical Turbulence: The Σ-Effect”, Astrophys. J., 507, 417–432. [DOI], [ADS]. (Cited on page 31.)
López Fuentes, M. C., Démoulin, P., Mandrini, C. H. and van Driel-Gesztelyi, L., 2000, “The Counterkink Rotation of a Non-Hale Active Region”, Astrophys. J., 544, 540–549. [DOI], [ADS]. (Cited on pages 11, 25, and 27.)
López Fuentes, M. C., Démoulin, P., Mandrini, C. H., Pevtsov, A. A. and van Driel-Gesztelyi, L., 2003, “Magnetic twist and writhe of active regions. On the origin of deformed flux tubes”, Astron. Astrophys., 397, 305–318. [DOI], [ADS]. (Cited on pages 27 and 71.)
Loughhead, R. E. and Bray, R. J., 1961, “Phenomena Accompanying the Birth of Sunspot Pores”, Aust. J. Phys., 14, 347–351. [DOI]. (Cited on page 9.)
Louis, R. E., Ravindra, B., Mathew, S. K., Bellot Rubio, L. R., Raja Bayanna, A. and Venkatakrishnan, P., 2012, “Analysis of a Fragmenting Sunspot Using Hinode Observations”, Astrophys. J., 755, 16. [DOI], [ADS], [arXiv:1205.6669 [astro-ph.SR]]. (Cited on page 36.)
Low, B. C., 1996, “Solar Activity and the Corona”, Solar Phys., 167, 217–265. [DOI], [ADS]. (Cited on pages 31 and 66.)
Luoni, M. L., Dâemoulin, P., Mandrini, C. H. and van Driel-Gesztelyi, L., 2011, “Twisted Flux Tube Emergence Evidenced in Longitudinal Magnetograms: Magnetic Tongues”, Solar Phys., 270, 45–74. [DOI], [ADS]. (Cited on pages 7, 11, 25, 26, 27, and 31.)
Mackay, D. H. and van Ballegooijen, A. A., 2006, “Models of the Large-Scale Corona. I. Formation, Evolution, and Liftoff of Magnetic Flux Ropes”, Astrophys. J., 641, 577–589. [DOI], [ADS]. (Cited on page 46.)
Mackay, D. H., Green, L. M. and van Ballegooijen, A., 2011, “Modeling the Dispersal of an Active Region: Quantifying Energy Input into the Corona”, Astrophys. J., 729, 97. [DOI], [ADS], [arXiv:1102.5296]. (Cited on pages 37, 38, 39, and 47.)
Magara, T. and Longcope, D. W., 2001, “Sigmoid Structure of an Emerging Flux Tube”, Astrophys. J. Lett., 559, L55–L59. [DOI], [ADS]. (Cited on page 31.)
Malherbe, J. M., Schmieder, B., Mein, P., Mein, N., van Driel-Gesztelyi, L. and von Uexküll, M., 1998, “Arch Filament Systems Associated with X-Ray Loops”, Solar Phys., 180, 265–284. [DOI], [ADS]. (Cited on page 10.)
Mandrini, C. H., Démoulin, P. and Klimchuk, J. A., 2000, “Magnetic Field and Plasma Scaling Laws: Their Implications for Coronal Heating Models”, Astrophys. J., 530, 999–1015. [DOI], [ADS]. (Cited on page 73.)
Mandrini, C. H., Démoulin, P., Schmieder, B., Deng, Y. Y. and Rudawy, P., 2002, “The role of magnetic bald patches in surges and arch filament systems”, Astron. Astrophys., 391, 317–329. [DOI], [ADS]. (Cited on page 32.)
Mandrini, C. H., Démoulin, P., van Driel-Gesztelyi, L. and López Fuentes, M. C., 2004, “Magnetic Helicity Budget of Solar-Active Regions from the Photosphere to Magnetic Clouds”, Astrophys. Space Sci., 290, 319–344. [DOI], [ADS]. (Cited on pages 67 and 71.)
Martin, S. F., Livi, S. H. B. and Wang, J., 1985, “The Cancellation of Magnetic Flux. II. In a Decaying Active Region”, Aust. J. Phys., 38, 929–959. [DOI], [ADS]. (Cited on pages 40 and 41.)
Martin, S. F., Marquette, W. H. and Bilimoria, R., 1992, “The Solar Cycle Pattern in the Direction of the Magnetic Field along the Long Axes of Polar Filaments”, in The Solar Cycle, Proceedings of the NSO/Sacramento Peak 12th Summer Workshop, 15–18 October 1991, (Ed.) Harvey, K. L., ASP Conference Series, 27, pp. 53–66, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 31.)
Martres, M. J. and Bruzek, A., 1977, “Active Regions”, in Illustrated Glossary for Solar and Solar-Terrestrial Physics, (Eds.) Bruzek, A., Durrant, C. J., Astrophysics and Space Science Library, 69, pp. 53–70, Reidel, Dordrecht. [ADS]. (Cited on pages 5 and 6.)
Mattig, W., 1953, “Die radiale Verteilung der magnetischen Feldstarke in normalen Sonnenflecken”, Z. Astrophys., 31, 273–281. (Cited on page 19.)
Maunder, E. W., 1919, “Notes on Some of the Sun-spots measured at the Royal Observatory, Greenwich, on Photographs of the Sun taken in the Year 1915”, Mon. Not. R. Astron. Soc., 79, 451–458. [ADS]. (Cited on pages 11 and 28.)
McClintock, B. H. and Norton, A. A., 2013, “Recovering Joy’s Law as a Function of Solar Cycle, Hemisphere, and Longitude”, Solar Phys., 287, 215–227. [DOI], [ADS], [arXiv:1305.3205 [astro-ph.SR]]. (Cited on pages 22, 23, 24, and 27.)
McClymont, A. N. and Fisher, G. H., 1989, “On the mechanical energy available to drive solar flares”, in Outstanding Problems in Solar System Plasma Physics: Theory and Instrumentation, Yosemite Conference, held at Yosemite National Park, CA, February 2–5, 1988, (Eds.) Waite Jr, J. H., Burch, J. L., Moore, R. L., Geophysical Monograph, 54, pp. 219–225, American Geophysical Union, Washington, DC. [ADS], [arXiv:1004.5318]. (Cited on pages 30 and 67.)
McIntosh, P. S., 1981, “The birth and evolution of sunspots: Observations”, in The Physics of Sunspots, Proceedings of the Conference, Sunspot, NM, July 14–17, 1981, (Eds.) Cram, L. E., Thomas, J. H., pp. 7–54, National Solar Observatory, Sunspot, NM. [ADS]. (Cited on page 34.)
McIntosh, P. S., 1990, “The classification of sunspot groups”, Solar Phys., 125, 251–267. [DOI], [ADS]. (Cited on page 79.)
Melrose, D. B., 1992, “Energy propagation into a flare kernel during a solar flare”, Astrophys. J., 387, 403–413. [DOI], [ADS]. (Cited on page 30.)
Moreno-Insertis, F. and Emonet, T., 1996, “The Rise of Twisted Magnetic Tubes in a Stratified Medium”, Astrophys. J., 472, L53–L56. [DOI], [ADS]. (Cited on page 30.)
Moreno-Insertis, F., Caligari, P. and Schüssler, M., 1995, “‘Explosion’ and Intensification of Magnetic Flux Tubes”, Astrophys. J., 452, 894–900. [DOI], [ADS]. (Cited on page 40.)
Mosher, J. M., 1977, The magnetic history of solar active regions, Ph.D. thesis, Caltech, Pasadena. [ADS]. (Cited on page 19.)
Murray, M. J. and Hood, A. W., 2008, “Emerging flux tubes from the solar interior into the atmosphere: effects of non-constant twist”, Astron. Astrophys., 479, 567–577. [DOI], [ADS]. (Cited on page 30.)
Nandy, D., 2006, “Magnetic helicity and flux tube dynamics in the solar convection zone: Comparisons between observation and theory”, J. Geophys. Res., 111, A12S01. [DOI], [ADS]. (Cited on pages 25 and 31.)
Nordlund, Å., Brandenburg, A., Jennings, R. L., Rieutord, M., Ruokolainen, J., Stein, R. F. and Tuominen, I., 1992, “Dynamo action in stratified convection with overshoot”, Astrophys. J., 392, 647–652. [DOI], [ADS]. (Cited on page 14.)
Norton, A. A. and Gilman, P. A., 2005, “Recovering Solar Toroidal Field Dynamics from Sunspot Location Patterns”, Astrophys. J., 630, 1194–1205. [DOI], [ADS], [arXiv:astro-ph/0506025]. (Cited on page 22.)
Oláh, K., van Driel-Gesztelyi, L., Kovári, Z. and Bartus, J., 1999, “Modelling the Sun as an active star. I. A diagnosis of photometric starspot models”, Astron. Astrophys., 344, 163–171. [ADS]. (Cited on pages 50, 57, 60, and 77.)
Orlando, S., Khan, J., van Driel-Gesztelyi, L., Thompson, B., Fludra, A. and Foing, B., 2000, “Large-scale evolution of the active region NOAA 7978, 7981, 7986 observed by GOES, SOHO, and Yohkoh”, Adv. Space Res., 25, 1913–1916. [DOI], [ADS]. (Cited on pages 50 and 57.)
Orlando, S., Peres, G. and Reale, F., 2004, “The Sun as an X-ray star: Active region evolution, rotational modulation, and implications for stellar X-ray variability”, Astron. Astrophys., 424, 677–689. [DOI], [ADS]. (Cited on pages 50, 59, 61, and 77.)
Ortiz, A., 2003, Solar Irradiance Variations Induced by Faculae and Small Magnetic Elements in the Photosphere, Ph.D. thesis, Universitat de Barcelona, Barcelona. [ADS]. URL (accessed 16 June 2014): http://hdl.handle.net/10803/733. (Cited on pages 58 and 59.)
Ortiz, A., Domingo, V., Sanahuja, B. and Fröhlich, C., 2004, “Excess facular emission from an isolated active region during solar minimum: the example of NOAA AR 7978”, J. Atmos. Sol.-Terr. Phys., 66, 67–75. [DOI], [ADS]. (Cited on pages 50, 56, 57, 58, and 59.)
Pariat, E., Aulanier, G., Schmieder, B., Georgoulis, M. K., Rust, D. M. and Bernasconi, P. N., 2004, “Resistive Emergence of Undulatory Flux Tubes”, Astrophys. J., 614, 1099–1112. [DOI], [ADS]. (Cited on pages 10 and 32.)
Pariat, E., Masson, S. and Aulanier, G., 2009, “Current Buildup in Emerging Serpentine Flux Tubes”, Astrophys. J., 701, 1911–1921. [DOI], [ADS]. (Cited on page 32.)
Parker, E. N., 1966, “The Dynamical State of the Interstellar Gas and Field”, Astrophys. J., 145, 811. [DOI], [ADS]. (Cited on page 32.)
Parker, E. N., 1978, “Hydraulic concentration of magnetic fields in the solar photosphere. VI. Adiabatic cooling and concentration in downdrafts”, Astrophys. J., 221, 368–377. [DOI], [ADS]. (Cited on page 10.)
Parnell, C. E., DeForest, C. E., Hagenaar, H. J., Johnston, B. A., Lamb, D. A. and Welsch, B. T., 2009, “A Power-Law Distribution of Solar Magnetic Fields Over More Than Five Decades in Flux”, Astrophys. J., 698, 75–82. [DOI], [ADS]. (Cited on pages 16 and 17.)
Petrovay, K., 1993, “Local and non-local contributions to horizontal motions in stellar convective zones”, in Inside the Stars, Proc. IAU Colloq. 137, Univ. of Vienna, Austria, Apr. 13–18, 1992, (Eds.) Weiss, W. W., Baglin, A., ASP Conference Series, 40, pp. 293–295, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 29.)
Pevtsov, A. A., 2002, “Active-Region Filaments and X-ray Sigmoids”, Solar Phys., 207, 111–123. [DOI], [ADS]. (Cited on page 43.)
Pevtsov, A. A. and Balasubramaniam, K. S., 2003, “Helicity patterns on the Sun”, Adv. Space Res., 32, 1867–1874. [DOI], [ADS]. (Cited on page 31.)
Pevtsov, A. A., Canfield, R. C. and Metcalf, T. R., 1995, “Latitudinal variation of helicity of photospheric magnetic fields”, Astrophys. J. Lett., 440, L109–L112. [DOI], [ADS]. (Cited on page 31.)
Pevtsov, A. A., Fisher, G. H., Acton, L. W., Longcope, D. W., Johns-Krull, C. M., Kankelborg, C. C. and Metcalf, T. R., 2003, “The Relationship Between X-Ray Radiance and Magnetic Flux”, Astrophys. J., 598, 1387–1391. [DOI], [ADS]. (Cited on pages 75 and 76.)
Rempel, M. and Schlichenmaier, R., 2011, “Sunspot Modeling: From Simplified Models to Radiative MHD Simulations”, Living Rev. Solar Phys., 8, lrsp-2011-3. [DOI], [ADS]. URL (accessed 28 April 2014): http://www.livingreviews.org/lrsp-2011-3. (Cited on pages 34 and 40.)
Rezaei, R., Bello González, N. and Schlichenmaier, R., 2012, “The formation of sunspot penumbra. Magnetic field properties”, Astron. Astrophys., 537, A19. [DOI], [ADS], [arXiv:1111.3189 [astro-ph.SR]]. (Cited on page 11.)
Ribes, J. C. and Nesme-Ribes, E., 1993, “The solar sunspot cycle in the Maunder minimum AD1645 to AD1715”, Astron. Astrophys., 276, 549–563. [ADS]. (Cited on page 33.)
Richardson, I. G., 1997, “Using Energetic Particles to Probe the Magnetic Topology of Ejecta, in Coronal Mass Ejections”, in Coronal Mass Ejections: Causes and Consequences, AGU Chapman Conference held at Montana State University, Bozeman, MT, USA, August 11–15, 1996, (Eds.) Crooker, N., Joselyn, J.-A., Feynman, J., Geophysical Monograph Series, 99, p. 189, American Geophysical Union, Washington, DC. [DOI]. (Cited on page 69.)
Rust, D. M. and Kumar, A., 1994, “Helicity charging and eruption of magnetic flux from the Sun”, in Solar Dynamic Phenomena and Solar Wind Consequences, Proceedings of the Third SOHO Workshop held 26–29 September, 1994 in Estes Park, Colorado, (Ed.) Hunt, J. J., ESA Special Publication, SP-373, p. 39, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 66.)
Ruždjak, D., Ruždjak, V., Brajša, R. and Wöhl, H., 2004, “Deceleration of the rotational velocities of sunspot groups during their evolution”, Solar Phys., 221, 225–236. [DOI], [ADS]. (Cited on page 29.)
Ryutova, M. and Hagenaar, H., 2007, “Magnetic Solitons: Unified Mechanism for Moving Magnetic Features”, Solar Phys., 246, 281–294. [DOI], [ADS]. (Cited on page 34.)
Sainz Dalda, A. and Bellot Rubio, L. R., 2008, “Detection of sea-serpent field lines in sunspot penumbrae”, Astron. Astrophys., 481, L21–L24. [DOI], [ADS], [arXiv:0712.2983]. (Cited on page 35.)
Sainz Dalda, A. and Martínez Pillet, V., 2005, “Moving Magnetic Features as Prolongation of Penumbral Filaments”, Astrophys. J., 632, 1176–1183. [DOI], [ADS]. (Cited on page 34.)
Savcheva, A. and van Ballegooijen, A., 2009, “Nonlinear Force-free Modeling of a Long-lasting Coronal Sigmoid”, Astrophys. J., 703, 1766–1777. [DOI], [ADS]. (Cited on page 45.)
Savcheva, A. S., Green, L. M., van Ballegooijen, A. A. and DeLuca, E. E., 2012, “Photospheric Flux Cancellation and the Build-up of Sigmoidal Flux Ropes on the Sun”, Astrophys. J., 759, 105. [DOI], [ADS]. (Cited on page 45.)
Schlichenmaier, R., Bello González, N., Rezaei, R. and Waldmann, T. A., 2010, “The role of emerging bipoles in the formation of a sunspot penumbra”, Astron. Nachr., 331, 563. [DOI], [ADS], [arXiv:1003.1313 [astro-ph.SR]]. (Cited on page 11.)
Schmidt, H. U., 1968, “Magnetohydrodynamics of an Active Region”, in Structure and Development of Solar Active Regions, Proceedings from IAU Symposium 35 held in Budapest, Hungary, 4–8 September 1967, (Ed.) Kiepenheuer, K. O., IAU Symposia, 35, pp. 95–107, Reidel, Dordrecht. [ADS]. (Cited on page 24.)
Schmieder, B., Démoulin, P., Aulanier, G. and Golub, L., 1996, “Differential Magnetic Field Shear in an Active Region”, Astrophys. J., 467, 881–886. [DOI], [ADS]. (Cited on page 42.)
Schrijver, C. J., 2001, “Simulations of the Photospheric Magnetic Activity and Outer Atmospheric Radiative Losses of Cool Stars Based on Characteristics of the Solar Magnetic Field”, Astrophys. J., 547, 475–490. [DOI], [ADS]. (Cited on page 16.)
Schrijver, C. J. and Aschwanden, M. J., 2002, “Constraining the Properties of Nonradiative Heating of the Coronae of Cool Stars and the Sun”, Astrophys. J., 566, 1147–1165. [DOI], [ADS]. (Cited on page 73.)
Schrijver, C. J. and Harvey, K. L., 1994, “The photospheric magnetic flux budget”, Solar Phys., 150, 1–18. [DOI], [ADS]. (Cited on pages 14 and 16.)
Schrijver, C. J. and Title, A. M., 1999, “Active regions losing their moorings by subsurface reconnection”, Solar Phys., 188, 331–344. [DOI], [ADS]. (Cited on pages 20, 40, and 49.)
Schrijver, C. J. and Zwaan, C., 2000, Solar and Stellar Magnetic Activity, Cambridge Astrophysics Series, 34, Cambridge University Press, Cambridge; New York. [ADS], [Google Books]. (Cited on pages 6, 13, 14, 28, 33, and 34.)
Schüssler, M., 1979, “Magnetic Buoyancy Revisited: Analytical and Numerical Results for Rising Flux Tubes”, Astron. Astrophys., 71, 79–91. [ADS]. (Cited on page 30.)
Schüssler, M. and Rempel, M., 2005, “The dynamical disconnection of sunspots from their magnetic roots”, Astron. Astrophys., 441, 337–346. [DOI], [ADS], [arXiv:astro-ph/0506654]. (Cited on page 40.)
Sheeley Jr, N. R., 1966, “Measurements of Solar Magnetic Fields”, Astrophys. J., 144, 723–732. [DOI], [ADS]. (Cited on page 19.)
Sheeley Jr, N. R., 1969, “The Evolution of the Photospheric Network”, Solar Phys., 9, 347–357. [DOI], [ADS]. (Cited on page 34.)
Sheeley Jr, N. R., 1981, “The overall structure and evolution of active regions”, in Solar Active Regions: A monograph from Skylab Solar Workshop III, Third series of workshops summarizing the results of Skylab, held in 1978–1979 in Boulder, CO, USA, (Ed.) Orrall, F. Q., pp. 17–42, Colorado Associated University Press, Boulder. [ADS]. (Cited on pages 6 and 13.)
Sheeley Jr, N. R., 2005, “Surface Evolution of the Sun’s Magnetic Field: A Historical Review of the Flux-Transport Mechanism”, Living Rev. Solar Phys., 2, lrsp-2005-5. [DOI], [ADS]. URL (accessed 28 April 2014): http://www.livingreviews.org/lrsp-2005-5. (Cited on page 49.)
Shimizu, T., Katsukawa, Y., Kubo, M. et al., 2009, “Hinode Observation of the Magnetic Fields in a Sunspot Light Bridge Accompanied by Long-Lasting Chromospheric Plasma Ejections”, Astrophys. J. Lett., 696, L66–L69. [DOI], [ADS]. (Cited on page 36.)
SIDC, “User guide from the Solar Influences Data Analysis Center”, institutional homepage, Royal Observatory of Belgium. URL (accessed 28 April 2014): http://sidc.oma.be/educational/classification.php. (Cited on page 79.)
Solanki, S. K., 2003, “Sunspots: An overview”, Astron. Astrophys. Rev., 11, 153–286. [DOI], [ADS]. (Cited on page 6.)
Solanki, S. K., Steiner, O. and Uitenbroeck, H., 1991, “Two-dimensional models of the solar chromosphere. I. The Ca II K line as a diagnostic: 1.5-D radiative transfer”, Astron. Astrophys., 250, 220–234. [ADS]. (Cited on page 76.)
Spadaro, D., Billotta, S., Contarino, L., Romano, P. and Zuccarello, F., 2004, “AFS dynamic evolution during the emergence of an active region”, Astron. Astrophys., 425, 309–319. [DOI], [ADS]. (Cited on page 15.)
Spitzer, L., 1962, Physics of Fully Ionized Gases, Interscience Tracts on Physics and Astronomy, 3, Interscience, New York, 2nd rev. edn. [ADS]. (Cited on page 76.)
Spörer, F. W. G., 1878, Publ. Astrophys. Obs. Potsdam, 1(1). (Cited on page 22.)
Spörer, F. W. G., 1880, Publ. Astrophys. Obs. Potsdam, 2(5). (Cited on page 22.)
Spörer, F. W. G., 1886, Publ. Astrophys. Obs. Potsdam, 4(17). (Cited on page 22.)
Spörer, F. W. G., 1894, Publ. Astrophys. Obs. Potsdam, 10(32). (Cited on page 22.)
Spruit, H. C., Title, A. M. and van Ballegooijen, A. A., 1987, “Is there a weak mixed polarity background field? Theoretical arguments”, Solar Phys., 110, 115–128. [DOI], [ADS]. (Cited on page 34.)
Stenflo, J. O. and Kosovichev, A. G., 2012, “Bipolar Magnetic Regions on the Sun: Global Analysis of the SOHO/MDI Data Set”, Astrophys. J., 745, 129. [DOI], [ADS], [arXiv:1112.5226 [astro-ph.SR]]. (Cited on pages 23 and 24.)
Sterling, A. C., Chifor, C., Mason, H. E., Moore, R. L. and Young, P. R., 2010, “Evidence for magnetic flux cancelation leading to an ejective solar eruption observed by Hinode, TRACE, STEREO, and SoHO/MDI”, Astron. Astrophys., 521, A49. [DOI], [ADS]. (Cited on pages 12 and 41.)
Strous, L. H. and Zwaan, C., 1999, “Phenomena in an Emerging Active Region. II. Properties of the Dynamic Small-Scale Structure”, Astrophys. J., 527, 435–444. [DOI], [ADS]. (Cited on pages 9, 10, and 32.)
Strous, L. H., Scharmer, G., Tarbell, T. D., Title, A. M. and Zwaan, C., 1996, “Phenomena in an emerging active region. I. Horizontal dynamics”, Astron. Astrophys., 306, 947–959. [ADS]. (Cited on pages 10 and 32.)
Su, Y., van Ballegooijen, A., Schmieder, B., Berlicki, A., Guo, Y., Golub, L. and Huang, G., 2009, “Flare Energy Build-up in a Decaying Active Region Near a Coronal Hole”, Astrophys. J., 704, 341–353. [DOI], [ADS]. (Cited on page 45.)
Tandberg-Hanssen, E., 1995, The Nature of Solar Prominences, Astrophysics and Space Science Library, 199, Kluwer, Dordrecht; Boston. [DOI], [ADS]. (Cited on page 12.)
Tang, F., 1987, “Quiescent prominences — Where are they formed?”, Solar Phys., 107, 233–237. [DOI], [ADS]. (Cited on page 47.)
Tang, F., Howard, R. and Adkins, J. M., 1984, “A statistical study of active regions 1967–1981”, Solar Phys., 91, 75–86. [DOI]. (Cited on pages 17 and 23.)
Tapping, K. F. and Zwaan, C., 2001, “Sources of the Slowly-Varying Component of Solar Microwave Emission and their Relationship with their Host Active Regions”, Solar Phys., 199, 317–344. [DOI], [ADS]. (Cited on pages 62 and 63.)
Tarr, L. A., Longcope, D. W., McKenzie, D. E. and Yoshimura, K., 2014, “Quiescent Reconnection Rate Between Emerging Active Regions and a Preexisting Field, with Associated Heating: NOAA AR 11112”, Solar Phys., 289, 3331–3349. [DOI], [ADS], [arXiv:1311.3705 [astro-ph.SR]]. (Cited on pages 9 and 11.)
Ternullo, M., Zappala, R. A. and Zuccarello, F., 1981, “The age dependence of photospheric tracer rotation”, Solar Phys., 74, 111–115. [DOI]. (Cited on page 29.)
Thomas, J. H. and Weiss, N. O. (Eds.), 1992, Sunspots: Theory and Observations, Proceedings of the NATO Advanced Research Workshop on the Theory of Sunspots, Cambridge, U.K., September 22–27, 1991, NATO ASI Series C, 375, Kluwer, Dordrecht; Boston. [ADS]. (Cited on page 11.)
Thomas, J. H., Weiss, N. O., Tobias, S. M. and Brummell, N. H., 2002, “Downward pumping of magnetic flux as the cause of filamentary structures in sunspot penumbrae”, Nature, 420, 390–393. [DOI], [ADS]. (Cited on page 11.)
Thornton, L. M. and Parnell, C. E., 2011, “Small-Scale Flux Emergence Observed Using Hinode/SOT”, Solar Phys., 269, 13–40. [DOI], [ADS]. (Cited on page 16.)
Tian, L. and Alexander, D., 2009, “Asymmetry of Helicity Injection Flux in Emerging Active Regions”, Astrophys. J., 695, 1012–1023. [DOI], [ADS]. (Cited on page 7.)
Tian, L., Bao, S., Zhang, H. and Wang, H., 2001, “Relationship in sign between tilt and twist in active region magnetic fields”, Astron. Astrophys., 374, 294–300. [DOI], [ADS]. (Cited on page 25.)
Tian, L., Liu, Y. and Wang, H., 2003, “Latitude and Magnetic Flux Dependence of the Tilt Angle of Bipolar Regions”, Solar Phys., 215, 281–293. [DOI], [ADS]. (Cited on page 19.)
Titov, V. S. and Démoulin, P., 1999, “Basic topology of twisted magnetic configurations in solar flares”, Astron. Astrophys., 351, 707–720. [ADS]. (Cited on page 31.)
Tlatov, A., Illarionov, E., Sokoloff, D. and Pipin, V., 2013, “A new dynamo pattern revealed by the tilt angle of bipolar sunspot groups”, Mon. Not. R. Astron. Soc., 432, 2975–2984. [DOI], [ADS], [arXiv:1302.2715 [astro-ph.SR]]. (Cited on pages 23 and 24.)
Tlatov, A. G., Vasil’eva, V. V. and Pevtsov, A. A., 2010, “Distribution of Magnetic Bipoles on the Sun over Three Solar Cycles”, Astrophys. J., 717, 357–362. [DOI], [ADS]. (Cited on pages 25, 27, 28, and 29.)
Tuominen, I. and Virtanen, H., 1987, “Solar rotation variations from sunspot group statistics”, in The Internal Solar Angular Velocity: Theory, Observations and Relationship to Solar Magnetic Fields, Proceedings of the Eighth NSO Summer Symposium, Sunspot, NM, Aug. 11–14, 1986, (Eds.) Durney, B. R., Sofia, S., Astrophysics and Space Science Library, 137, pp. 83–88, Reidel, Dordrecht; Boston. [ADS]. (Cited on page 29.)
Ugarte-Urra, I. and Warren, H. P., 2012, “Is active region variability age dependent?”, Astrophys. J., 761, 21. [DOI], [ADS]. (Cited on pages 64 and 65.)
Valori, G., Green, L. M., Démoulin, P., Vargas Domínguez, S., van Driel-Gesztelyi, L., Wallace, A., Baker, D. and Fuhrmann, M., 2012, “Nonlinear Force-Free Extrapolation of Emerging Flux with a Global Twist and Serpentine Fine Structures”, Solar Phys., 278, 73–97. [DOI], [ADS]. (Cited on page 33.)
van Ballegooijen, A. A., 1982, “The Structure of the Solar Magnetic Field Below the Photosphere. I. Adiabatic Flux Tube Models”, Astron. Astrophys., 106, 43–52. [ADS]. (Cited on page 40.)
van Ballegooijen, A. A., 2004, “Observations and Modeling of a Filament on the Sun”, Astrophys. J., 612, 519–529. [DOI], [ADS]. (Cited on page 45.)
van Ballegooijen, A. A. and Mackay, D. H., 2007, “Model for the Coupled Evolution of Subsurface and Coronal Magnetic Fields in Solar Active Regions”, Astrophys. J., 659, 1713–1725. [DOI], [ADS]. (Cited on pages 47, 48, and 49.)
van Ballegooijen, A. A. and Martens, P. C. H., 1989, “Formation and eruption of solar prominences”, Astrophys. J., 343, 971–984. [DOI], [ADS]. (Cited on pages 12, 40, 41, 42, 43, and 45.)
van Ballegooijen, A. A., Deluca, E. E., Squires, K. and Mackay, D. H., 2007, “Modeling magnetic flux ropes in the solar atmosphere”, J. Atmos. Sol.-Terr. Phys., 69, 24–31. [DOI], [ADS]. (Cited on page 45.)
van Driel-Gesztelyi, L., 1998, “Evolution and Decay of Active Regions”, in Three-Dimensional Structure of Solar Active Regions, Second Advances in Solar Physics Euroconference held in Preveza, Greece, October 7–11, 1997, (Eds.) Alissandrakis, C. E., Schmieder, B., ASP Conference Series, 155, pp. 202–223, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on pages 6 and 39.)
van Driel-Gesztelyi, L., 2002, “Emergence and loss of magnetic flux on the solar surface”, in SOLMAG 2002, Proceedings of the Magnetic Coupling of the Solar Atmosphere Euroconference and IAU Colloquium 188, Santorini, Greece, 11–15 June 2002, (Ed.) Sawaya-Lacoste, H., ESA Special Publication, SP-505, pp. 113–120, European Space Agency, Nordwijk. [ADS]. (Cited on page 6.)
van Driel-Gesztelyi, L. and Culhane, J. L., 2009, “Magnetic Flux Emergence, Activity, Eruptions and Magnetic Clouds: Following Magnetic Field from the Sun to the Heliosphere”, Space Sci. Rev., 144, 351–381. [DOI], [ADS]. (Cited on page 6.)
van Driel-Gesztelyi, L. and Petrovay, K., 1990, “Asymmetric flux loops in active regions, I”, Solar Phys., 126, 285–298. [DOI], [ADS]. (Cited on pages 7 and 11.)
van Driel-Gesztelyi, L., Mandrini, C. H., Thompson, B., Plunkett, S., Aulanier, G., Diémoulin, P., Schmieder, B. and DeForest, C. E., 1999a, “Long-Term Magnetic Evolution of an AR and its CME Activity”, in Magnetic Fields and Oscillations, Third Advances in Solar Physics Euroconference held in Caputh near Potsdam, Germany, on September 22–25, 1998, (Eds.) Schmieder, B., Hofmann, A., Staude, J., ASP Conference Series, 184, pp. 302–306, Astronomical Society of the Pacific, San Francisco. (Cited on pages 13, 34, 50, 51, and 64.)
van Driel-Gesztelyi, L., Thompson, B., Diémoulin, P. et al., 1999b, “Long-Term Evolution Of Emissivity And Heating In A Solar Active Region”, in Plasma Dynamics and Diagnostics in the Solar Transition Region and Corona, Proceedings of the 8th SOHO Workshop held 22–25 June 1999 in Paris, France, (Eds.) Vial, J.-C., Kaldeich-Schuümann, B., ESA Special Publication, SP-446, p. 663, ESA Publications Division, Noordwijk. [ADS]. (Cited on page 73.)
van Driel-Gesztelyi, L., Diemoulin, P., Ireland, J. et al., 2001, “An Observational Test for Solar Atmospheric Heating”, in Recent Insights into the Physics of the Sun and Heliosphere: Highlights from SOHO and Other Space Missions, Proceedings of the 24th General Assembly of the IAU held at Manchester, United Kingdom, 7–11 August 2000, (Eds.) Brekke, P., Fleck, B., Gurman, J. B., IAU Symposia, 203, pp. 514–516, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 73.)
van Driel-Gesztelyi, L., Diémoulin, P. and Mandrini, 2003a, “Emergence and long-term evolution of active regions”, in Understanding Active Phenomena: Progress and Perspectives, Second Franco-Chinese meeting on solar physics, August 2002, (Eds.) Hiénoux, J. C., Fang, C., Vilmer, N., pp. 37–48, International Academic Publishers/World Publishing Corporation, Beijing. (Cited on pages 50, 51, 54, 55, 56, and 72.)
van Driel-Gesztelyi, L., Diémoulin, P., Mandrini, C. H., Harra, L. and Klimchuk, J. A., 2003b, “The Long-Term Evolution of AR 7978: The Scalings of the Coronal Plasma Parameters with the Mean Photospheric Magnetic Field”, Astrophys. J., 586, 579–591. [DOI], [ADS]. (Cited on pages 13, 41, 50, 51, 53, 54, 55, 56, 72, and 77.)
Vargas Domínguez, S., van Driel-Gesztelyi, L. and Bellot Rubio, L. R., 2012, “Granular-scale elementary flux emergence episodes in a solar active region”, Solar Phys., 278, 99–120. [DOI], [ADS], [arXiv:1203.6428 [astro-ph.SR]]. (Cited on page 10.)
Vazquez, M., 1973, “A Morphological Study of the Light-Bridges in Sunspots”, Solar Phys., 31, 377–387. [DOI], [ADS]. (Cited on page 36.)
Vrabec, D., 1974, “Streaming Magnetic Features Near Sunspots”, in Chromospheric Fine Structure, Proceedings from IAU Symposium 56 held at Surfer’s Paradise, Qld., Australia, 3–7 September 1973, (Ed.) Athay, R. G., IAU Symposia, 56, pp. 201–231, Reidel, Dordrecht; Boston. [ADS]. (Cited on page 35.)
Waldmeier, M., 1937, “Chromosphärische Vorgänge bei der Entstehung von Sonnenflecken”, Z. Astrophys., 14, 91–103. [ADS]. (Cited on page 9.)
Waldmeier, M., 1955, Ergebnisse und Probleme der Sonnenforschung, Geest & Portig, Leipzig, 2nd edn. [ADS]. (Cited on pages 12, 19, and 79.)
Wallace Hartshorn, A. J., 2012, Flux emergence and its consequences in the solar atmosphere, Ph.D. thesis, University College London, London. (Cited on pages 19, 21, and 25.)
Wang, H. and Zirin, H., 1992, “Flows around sunspots and pores”, Solar Phys., 140, 41–54. [DOI], [ADS]. (Cited on pages 10 and 32.)
Wang, H., Zirin, H. and Ai, G., 1991, “Magnetic flux transport of decaying active regions and enhanced magnetic network”, Solar Phys., 131, 53–68. [DOI], [ADS]. (Cited on page 34.)
Wang, J., 1996, “A Note on the Evolution of Magnetic Helicity in Active Regions”, Solar Phys., 163, 319–325. [DOI], [ADS]. (Cited on page 11.)
Wang, J., Zhou, G., Jin, C. and Li, H., 2012, “Solar Intranetwork Magnetic Elements: Bipolar Flux Appearance”, Solar Phys., 278, 299–322. [DOI], [ADS]. (Cited on page 14.)
Wang, T. and Abramenko, V. I., 2000, “Evolution of magnetic field twist in an emerging flux region”, Astron. Astrophys., 357, 1056–1062. [ADS]. (Cited on page 30.)
Wang, Y.-M. and Sheeley Jr, N. R., 1989, “Average properties of bipolar magnetic regions during sunspot cycle 21”, Solar Phys., 124, 81–100. [DOI], [ADS]. (Cited on pages 19, 20, and 22.)
Wang, Y.-M. and Sheeley Jr, N. R., 1991, “Magnetic flux transport and the Sun’s dipole moment: New twists to the Babcock-Leighton model”, Astrophys. J., 375, 761–770. [DOI], [ADS]. (Cited on pages 22, 23, and 24.)
Watanabe, H., Kitai, R., Okamoto, K. et al., 2008, “Spectropolarimetric Observation of an Emerging Flux Region: Triggering Mechanisms of Ellerman Bombs”, Astrophys. J., 684, 736–746. [DOI], [ADS]. (Cited on page 10.)
Weart, S. R., 1970, “The Birth and Growth of Sunspot Regions”, Astrophys. J., 162, 987–992. [DOI], [ADS]. (Cited on pages 11, 25, and 27.)
Welsch, B. T., 2006, “Magnetic Flux Cancellation and Coronal Magnetic Energy”, Astrophys. J., 638, 1101–1109. [DOI], [ADS]. (Cited on pages 42 and 45.)
Welsch, B. T., Li, Y., Schuck, P. W. and Fisher, G. H., 2009, “What is the Relationship Between Photospheric Flow Fields and Solar Flares?”, Astrophys. J., 705, 821–843. [DOI], [ADS], [arXiv:0905.0529]. (Cited on pages 66 and 67.)
Wilson, P. R., 1973, “The Cooling of a Sunspot. III: Recent Observations”, Solar Phys., 32, 435–439. [DOI], [ADS]. (Cited on page 34.)
Yang, G., Xu, Y., Wang, H. and Denker, C., 2003, “High Spatial Resolution Observations of Pores and the Formation of a Rudimentary Penumbra”, Astrophys. J., 597, 1190–1199. [DOI], [ADS]. (Cited on page 11.)
Yang, S. and Zhang, J., 2014, “Properties of Solar Ephemeral Regions at the Emergence Stage”, Astrophys. J., 781, 7. [DOI], [ADS]. (Cited on page 11.)
Yang, S., Zhang, H. and Büchner, J., 2009, “Magnetic helicity accumulation and tilt angle evolution of newly emerging active regions”, Astron. Astrophys., 502, 333–340. [DOI], [ADS]. (Cited on pages 25 and 31.)
Yang, S., Zhang, J. and Liu, Y., 2014, “HMI observations of two types of ephemeral regions”, in Nature of Prominences and their Role in Space Weather, Proceedings of IAU Symposium 300, June 2013, (Eds.) Schmieder, B., Malherbe, J.-M., Wu, S. T., IAU Symposium, 300, pp. 470–472, Cambridge University Press, Cambridge; New York. [DOI], [ADS]. (Cited on page 12.)
Yashiro, S., Shibata, K. and Shimojo, M., 1998, “Early Evolution of Coronal Active Regions Observed with the YOHKOH Soft X-Ray Telescope. I. Expansion Velocity”, Astrophys. J., 493, 970–977. [DOI], [ADS]. (Cited on page 10.)
Yeates, A. R. and Mackay, D. H., 2009, “Modelling the Global Solar Corona: III. Origin of the Hemispheric Pattern of Filaments”, Solar Phys., 254, 77–88. [DOI], [ADS], [arXiv:0810.0517]. (Cited on page 38.)
Yeates, A. R., Attrill, G. D. R., Nandy, D., Mackay, D. H., Martens, P. C. H. and van Ballegooijen, A. A., 2010, “Comparison of a Global Magnetic Evolution Model with Observations of Coronal Mass Ejections”, Astrophys. J., 709, 1238–1248. [DOI], [ADS], [arXiv:0912.3347]. (Cited on page 38.)
Yurchyshyn, V. B. and Wang, H., 2001, “Magnetic Flux Cancellation Observed in the Sunspot Moat”, Solar Phys., 202, 309–318. [DOI], [ADS]. (Cited on pages 34, 40, and 42.)
Yurchyshyn, V. B., Wang, H. and Goode, P. R., 2001, “On the Correlation between the Orientation of Moving Magnetic Features and the Large-Scale Twist of Sunspots”, Astrophys. J., 550, 470–474. [DOI], [ADS]. (Cited on page 34.)
Zhang, H., Ai, G., Wang, H., Zirin, H. and Patterson, A., 1992, “Evolution of magnetic fields and mass flow in a decaying active region”, Solar Phys., 140, 307–316. [DOI], [ADS]. (Cited on pages 34 and 35.)
Zhang, J., Solanki, S. K. and Wang, J., 2003, “On the nature of moving magnetic feature pairs around sunspots”, Astron. Astrophys., 399, 755–761. [DOI], [ADS]. (Cited on pages 12 and 34.)
Zirin, H., 1988, Astrophysics of the Sun, Cambridge University Press, Cambridge; New York. [ADS]. (Cited on page 22.)
Zuccarello, F., Battiato, V., Contarino, L., Romano, P., Spadaro, D. and Vlahos, L., 2005, “AFS dynamics in a short-lived active region”, Astron. Astrophys., 442, 661–671. [DOI], [ADS]. (Cited on page 15.)
Zuccarello, F., Guglielmino, S. L., Battiato, V., Contarino, L., Spadaro, D. and Romano, P., 2009, “Emergence and evolution of active and ephemeral regions: Comparison between observations and models”, Acta Geophys., 57, 15–23. [DOI], [ADS]. (Cited on pages 10, 14, and 15.)
Zwaan, C., 1987, “Elements and patterns in the solar magnetic field”, Annu. Rev. Astron. Astrophys., 25, 83–111. [DOI], [ADS]. (Cited on pages 8, 11, 40, and 41.)
Zwaan, C. and Harvey, K. L., 1994, “Patterns in the solar magnetic field (Invited Review)”, in Solar Magnetic Fields, Proceedings of the international conference held in Freiburg, Germany, June 29–July 2, 1993, (Eds.) Schüssler, M., Schmidt, W., pp. 27–48, Cambridge University Press, Cambridge; New York. [ADS]. (Cited on pages 9 and 16.)
Zwaan, C., Brants, J. J. and Cram, L. E., 1985, “High-Resolution Spectroscopy of Active Regions. 1. Observing Procedures”, Solar Phys., 95, 3–14. [DOI], [ADS]. (Cited on pages 10 and 32.)
Acknowledgements
The authors thank Deb Baker, Pascal Démoulin and two anonymous referees for a critical reading of the manuscript and insightful comments. LvDG’s work was supported by the STFC Consolidated Grant ST/H00260/1 and the Hungarian Research grant OTKA K-109276. LMG is grateful to the Royal Society for a University Research Fellowship.
Author information
Authors and Affiliations
Corresponding author
A Appendix: Sunspot Classification Schemes
Throughout the centuries of sunspot observations there have been many attempts to classify sunspot groups. Though these classifications may appear like “zoology”, the “Zürich classification” scheme devised by Waldmeier (1955) and further developed by McIntosh (1990), is worth describing here, since it is based on the characteristic stages that a spot group may pass through during its formation and decay. There are many varieties of this scheme. Here we largely follow the scheme as summarised in the User guide from the Solar Influences Data Analysis Center (SIDC) of the Royal Observatory of Belgium.
The 3-component McIntosh classification is based on the general form ‘Zpc’, where ‘Z’ is the modified Zürich Class, ‘p’ describes the penumbra of the principal spot, and ‘c’ describes the distribution of spots in the interior of the group.
Z-values: (Modified Zürich Sunspot Classification).
-
A — A small single unipolar sunspot. Representing either the formative or final stage of evolution.
-
B — Bipolar sunspot group with no penumbra on any of the spots.
-
C — A bipolar sunspot group. One sunspot must have penumbra.
-
D — A bipolar sunspot group with penumbra on both ends of the group. Longitudinal extent does not exceeds 10°.
-
E — A bipolar sunspot group with penumbra on both ends. Longitudinal extent exceeds 10° but not 15°.
-
F — An elongated bipolar sunspot group with penumbra on both ends. Longitudinal extent of penumbra exceeds 15°.
-
H — A unipolar sunspot group with penumbra.
p-values:
-
x — No penumbra (group class is A or B)
-
r — Rudimentary penumbra partially surrounds the largest spot. This penumbra is incomplete, granular rather than filamentary, brighter than mature penumbra, and extends as little as 3 from the spot umbra. Rudimentary penumbra may be either in a stage of formation or dissolution.
-
s — Small, symmetric (like Zürich class J). Largest spot has mature, dark, filamentary penumbra of circular or elliptical shape with little irregularity to the border. The north-south diameter across the penumbra is ≤ 2.5°.
-
a — Small, asymmetric. Penumbra of the largest spot is irregular in outline and the multiple umbra within it are separated. The north-south diameter across the penumbra is ≤ 2.5°.
-
h — Large, symmetric (like Zürich class H). Same structure as type ‘s’, but north-south diameter of penumbra is ≥ 2.5°. Area, therefore, must be ≥ 250 MSH (millionths of the solar hemisphere).
-
k — Large, asymmetric. Same structure as type ‘a’, but north-south diameter of penumbra is more than ≥ 2.5°. Area, therefore, must be ≥ 250 MSH.
c-values:
-
x — Undefined for unipolar groups (class A and H)
-
o — Open. Few, if any, spots between leader and follower. Interior spots of very small size. Class E and F groups of ‘open’ category are equivalent to Zurich class G.
-
i — Intermediate. Numerous spots lie between the leading and following portions of the group, but none of them possess mature penumbra.
-
c — Compact. The area between the leading and the following ends of the spot group is populated with many strong spots, with at least one interior spot possessing mature penumbra. The extreme case of compact distribution has the entire spot group enveloped in one continuous penumbral area.
Another useful classification scheme, still widely used in the literature, devised by Hale and his colleagues at Mt. Wilson Observatory (Hale et al., 1919), refers to the magnetic complexity of sunspot groups. The scheme was widened to include the most complex class: δ-groups (Künzel, 1960).
-
α — Denotes a unipolar sunspot group.
-
β — A sunspot group having both positive and negative magnetic polarities, with a simple and distinct division between the polarities.
-
β - γ — A sunspot group that is bipolar but in which no continuous line can be drawn separating spots of opposite polarities.
-
γ — A complex active region in which the positive and negative polarities are so irregularly distributed as to prevent classification as a bipolar group.
-
δ — A complex magnetic configuration of a solar sunspot group consisting of opposite polarity umbrae within the same penumbra.
Electronic supplementary material
41116_2015_9161_MOESM1_ESM.mpg
mpg-Movie (6101.47460938 kB) Still from a movie — SOHO/MDI white-light and magnetogram images taken on 26 July 2010 show that bipolar magnetic fields (white/black = positive/negative) are more extended than the sunspots that are seen in white-light images. Sunspots correspond to the strongest magnetic field concentrations in the magnetogram. However, the active region (AR) extends as far as the distinguishable magnetic field.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
van Driel-Gesztelyi, L., Green, L.M. Evolution of Active Regions. Living Rev. Sol. Phys. 12, 1 (2015). https://doi.org/10.1007/lrsp-2015-1
Published:
DOI: https://doi.org/10.1007/lrsp-2015-1