Abstract
An overview of grid-based numerical methods used in relativistic hydrodynamics (RHD) and magnetohydrodynamics (RMHD) is presented. Special emphasis is put on a comprehensive review of the application of high-resolution shock-capturing methods. Results of a set of demanding test bench simulations obtained with different numerical methods are compared in an attempt to assess the present capabilities and limits of the various numerical strategies. Applications to three astrophysical phenomena are briefly discussed to motivate the need for and to demonstrate the success of RHD and RMHD simulations in their understanding. The review further provides FORTRAN programs to compute the exact solution of the Riemann problem in RMHD, and to simulate 1D RMHD flows in Cartesian coordinates.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Relativity is a necessary ingredient for describing astrophysical phenomena involving compact objects and flows near the speed of light. Among these phenomena are core collapse supernovae, X-ray binaries, pulsars, coalescing neutron stars, formation of black holes, active galactic nuclei (AGN) and gamma-ray bursts (GRB). The relativistic jets and outflows found in, e.g., micro-quasars, radio-loud AGN and GRB involve flows at relativistic speeds, too. Moreover, in most of these scenarios dynamically important magnetic fields are encountered.
This review summarizes the progress in grid-based methods for numerical (special) relativistic hydrodynamics (RHD) and magnetohydrodynamics (RMHD) and discusses their application to astrophysical flow. Developments in numerical RHD prior to the year 2003 are reviewed in Martí and Müller (2003) and are summarized here for completeness.
1.1 Overview of the numerical methods
Wilson (1972, 1979) and collaborators (Centrella and Wilson, 1984; Hawley et al., 1984) made the first attempt to solve the RHD equations in more than one spatial dimension using an Eulerian explicit finite-difference code with monotonic transport. The code relied on artificial viscosity techniques to handle shock waves and was widely used in numerical cosmology, studies of axisymmetric relativistic stellar collapse, and accretion onto compact objects. Almost all numerical codes developed for both special and general RHD in the 1980s (Piran, 1980; Stark and Piran, 1987; Nakamura et al., 1980; Nakamura, 1981; Nakamura and Sato, 1982; Evans, 1986) were based on Wilson’s approach. However, despite its popularity, it turned out that Wilson’s approach is unable to accurately describe highly relativistic flows, i.e., with Lorentz factors larger than 2 (see, e.g., Centrella and Wilson, 1984).
In the mid-1980s, Norman and Winkler (1986) proposed a new formulation of the difference equations of RHD with an artificial viscosity consistent with the relativistic dynamics of non-perfect fluids. They obtained accurate results in the description of strong relativistic shocks with large Lorentz factors in combination with adaptive mesh techniques. However, the strong coupling introduced in the equations by the presence of the viscous terms in the definition of relativistic momentum and total energy density required them to treat the difference equations implicitly, which has prevented the development of any multidimensional version of their formulation.
Relying on the same type of techniques (finite differencing and artificial viscosity), Wilson (1975, 1977) also pioneered the development of the first numerical code for RMHD that was used to simulate stellar collapse and the accretion of magnetized matter onto black holes.
Attempts to integrate the RHD equations without the use of artificial viscosity started in the early 1980s. Yokosawa et al. (1982) developed a 2D code based on the flux-corrected transport method (FCT) of Boris and Book (1973) to study the early phases of the interaction of a hypersonic relativistic beam with an ambient medium, in the context of extragalactic jets. The same kind of techniques were applied in the 1990s to solve the RMHD equations (Dubal, 1991; Yokosawa, 1993). Following a completely different approach, Mann (1991) presented a multidimensional code for general relativistic hydrodynamics (GRHD) based on the smoothed particle hydrodynamics (SPH) technique (Monaghan, 1992), which he applied to relativistic spherical collapse (Mann, 1993). When tested against 1D relativistic shock tubes all these codes performed similarly well as Wilson’s code.
A major break-through in the simulation of (ultra) relativistic flows was accomplished when high-resolution shock-capturing (HRSC) methods, specifically designed to solve hyperbolic systems of conservation laws were applied to integrate the RHD equations (Martí et al., 1991; Marquina et al., 1992; Eulderink, 1993; Eulderink and Mellema, 1995), and more recently the RMHD equations (Koide et al., 1996, 1999; Koide, 2003; Komissarov, 1999a; Balsara, 2001a).
1.2 Plan of the review
This review provides a comprehensive discussion of different grid-based methods used in RHD and RMHD, with special attention to HRSC methods.Footnote 1 Recent developments in finite-difference methods based on artificial-viscosity techniques are also considered. We refer to the book of Wilson and Mathews (2003) for a comprehensive review of these techniques. Despite the fact that spectral methods are able to attain very high accuracy, they have recognized limitations in the treatment of discontinuous solutions. Hence, we shall not consider them in this review and refer the reader to a recent review of spectral methods for numerical relativity by Grandclément and Novak (2009). We also do not discuss numerical methods here that are specific to general relativistic flow, but we present the underlying methods in the special relativistic limit and assess their performance. Numerical techniques for both GRHD and GRMHD are masterly reviewed by Font (2008).
In Section 2, we discuss three astrophysical phenomena (astrophysical jets, GRB, and pulsar wind nebulae) whose study has largely benefited from the development of numerical RHD and RMHD. In Section 3, we present the equations of ideal RMHD, which reduce to those of RHD in the zero field limit, and discuss their mathematical properties.
In Section 4 and 5, we review the development of grid-based methods for RHD and RMHD. We pay particular attention to HRSC methods and focus on those aspects more specific to RHD, i.e., discussing relativistic Riemann solvers and the computation of numerical fluxes. In Section 6, we present the results of several one-dimensional and multidimensional test problems simulated with different methods. In Section 7, we provide an assessment of various numerical methods together with an outlook on future developments.
Finally, in Section 8, we provide some additional information about the exact solution of the Riemann problem in both RHD and RMHD, and the corresponding spectral decompositions of the flux Jacobians. We also summarize the basics of finite difference/finite volume methods for hyperbolic systems of conservation laws in Section 8.3. In Section 8.4, we briefly discuss other approaches recently extended to numerical RHD and RMHD although not widely used yet. In this section we also summarize the method of van Putten, who first exploited the conservative nature of the RMHD equations for their numerical integration. Lastly, in Section 9, we provide source codes to compute the exact solution of the Riemann problem in RMHD and to solve numerically the equations of RMHD in one spatial dimension and Cartesian coordinates.
We presume that the reader has a basic knowledge of classical and relativistic fluid dynamics (Landau and Lifshitz, 1987; Courant and Friedrichs, 1976; Taub, 1978) and magnetohydrodynamics (Jeffrey and Taniuti, 1964; Anile, 1989), as well as of finite difference/finite volume methods for partial differential equations (Potter, 1977; Oran and Boris, 1987). A discussion of modern finite volume methods for hyperbolic systems of conservation laws can be found, e.g., in LeVeque (1992); Toro (1997); LeVeque (1998); Laney (1998). A unique monograph covering both theoretical and numerical aspects of RHD is the book by Rezzolla and Zanotti (2013). Chapters on computational MHD and RMHD can be found in the book by Goedbloed et al. (2010).
2 Astrophysical Scenarios
We note here that the following discussion of astrophysical phenomena is not thought to be a review of the respective phenomena, which would be well beyond the scope of this article on numerical methods. Instead, we present a biased view of the phenomena and of the status of the research to motivate the need for and to demonstrate the success of RHD and RMHD simulations in understanding these astrophysical phenomena.
The simulations discussed in this section were performed with RHD and RMHD codes based on the methods (mainly HRSC methods) that are reviewed in this work. The most important properties of these codes are summarized in Tables 1 and 2, respectively.
2.1 Jets from AGN
2.1.1 Observations and theoretical models
The most compelling case for a special relativistic phenomenon are the ubiquitous jets in extragalactic radio sources associated with AGN and quasars. In the commonly accepted standard model (Begelman et al., 1984), flow velocities as large as 99% (in some cases even beyond) of the speed of light are required to explain the apparent superluminal motion observed at parsec scales in many of these sources. Readers interested more deeply in the field of AGN jets may consult the recent book edited by Böttcher et al. (2012).
Models proposed to explain the origin of relativistic jets involve accretion onto a compact central object, such as a neutron star or a stellar mass black hole in the galactic microquasars (radio emitting X-ray binaries, scaled-down versions of quasars), or a rotating supermassive black hole in an AGN fed by interstellar gas and gas from tidally disrupted stars. There is a general agreement that MHD processes are responsible for the formation, collimation and acceleration up to relativistic speeds of the outflows. In the models of magnetically driven outflows (Blandford and Payne, 1982; Li et al., 1992), poloidal magnetic fields anchored at the basis of the accretion disk generate a toroidal field component and consequently a poloidal electromagnetic flux of energy (Poynting flux) that accelerates the magnetospheric plasma along the poloidal magnetic field lines, converting the Poynting flux into kinetic energy of bulk motion. Energy can also be extracted from rotating black holes with similar efficiencies (Blandford and Znajek, 1977; Hirotani et al., 1992). Several parameters are potentially important for powering the jets: the black hole mass and spin, the accretion rate, the type of ccretion disk, the properties of the magnetic field, and the nvironment of the source (Komissarov, 2012).
At parsec scales, extragalactic jets, observed via their synchrotron and inverse Compton emission at radio frequencies with VLBI imaging, appear to be highly collimated with a bright spot (the core) at one end of the jet and a series of components which separate from the core, sometimes at superluminal speeds (see, e.g., Lister et al., 2009). In the standard model of Blandford and Königl (1979), these speeds are a consequence of relativistic bulk motion in jets propagating at small angles to the line of sight with Lorentz factors up to 20 or more. Moving components in these jets, usually appearing after outbursts in emission at radio wavelengths, are interpreted in terms of traveling shock waves (Marscher and Gear, 1985). An ongoing, important debate is concerned with the nature of the radio core. Whereas in the standard Blandford and Königl’s conical jet model the core corresponds to the location near the black hole where the jet becomes optically thin, recent multi-wavelength observations of several sources [e.g., 3C 120 (Marscher et al., 2002), BL Lac (Marscher et al., 2008), and 3C 111 (Chatterjee et al., 2011)] suggest that the radio core can be a physical feature in the jet (as, e.g., a recollimation shock; Marscher, 2012) placed probably parsecs (i.e., tens of thousands of gravitational radii of the central black hole) away from the central engine.
At kiloparsec scales, the morphology and dynamics of the jets are dominated by their interaction with the surrounding extragalactic medium, the jet power being responsible for dichotomic morphologies (Fanaroff-Riley I and II classes, FR I and FR II, respectively; Fanaroff and Riley, 1974; see Bridle’s homepage). Whereas current models (Laing and Bridle, 2002a, b) interpret FR I morphologies as the result of a smooth deceleration from relativistic to non-relativistic, transonic speeds on kpc scales, flux asymmetries between jets and counter-jets in the most powerful radio galaxies (FR II) and quasars indicate that relativistic motion extends up to kpc scales in these sources (Bridle et al., 1994).
Extragalactic jets also play a very important role in the evolution of galaxies and clusters of galaxies as the most likely reheating agent to explain the low rates of cooling in the intracluster medium (McNamara and Nulsen, 2007).
Theoretical models of AGN jets have been the subject of intensive and extensive testing by relativistic numerical simulations during the past two decades. However, since jets are produced on scales of a few gravitational radii of the central black hole (≲ 10−3 pc, for a 109 M⊙ black hole) but extend to hundreds of kpcs, simulations have traditionally divided the study of the jet phenomenon into separate problems.
2.1.2 Simulations of kpc-scale jets
Although general relativistic (and MHD) effects seem to be crucial for a successful launch of the jet, purely hydrodynamic special relativistic simulations are adequate to study the morphology and dynamics of relativistic jets at distances sufficiently far from the central compact object (i.e., at parsec scales and beyond). Leaving aside the pioneering work of Yokosawa et al. (1982), the numerical simulation of relativistic jets at parsec and kiloparsec scales was triggered by the development of RHD codes based on conservative techniques as those described in Section 4.
At kiloparsec scales, the implications of relativistic flow speeds and/or relativistic internal energies for the morphology and dynamics of jets have been the subject of a number of 2D (van Putten, 1993b; Martí et al., 1994; Duncan and Hughes, 1994; Martí et al., 1995, 1997; Komissarov and Falle, 1998; Rosen et al., 1999; Mizuta et al., 2001; Scheck et al., 2002; Monceau-Baroux et al., 2012; Walg et al., 2013, 2014) and 3D (Aloy et al., 1999a; Hughes et al., 2002; Choi et al., 2007; Rossi et al., 2008) simulations. The aim of these simulations was to connect the prominence of the main structural features of the jets (internal shocks, hot spots, lobes) and their dynamical properties (hot spot advance speed and pressure, deceleration of the flow along the jet) with the basic parameters characterizing jets. They supersede former non-relativistic simulations of supersonic jets.
Recent developments concern themselves with the origin of the FR I/II dichotomy. One tries to gauge the importance of different factors contributing to the dichotomy, like the jet composition (Scheck et al., 2002), the jet propagation into an ambient medium of decreasing density (Perucho and Martí, 2007), the entrainment of ambient medium into the jet by Kelvin-Helmholtz (KH) instabilities (Rossi et al., 2008; Perucho et al., 2010), the mass load from stellar winds (Perucho et al., 2014), and the presence of density discontinuities in the jet environment (Meliani et al., 2008). Porth and Komissarov (2015) pointed to the loss of causal connectivity across jets, because of their rapid expansion in response to the fast decline of the ambient pressure with distance, as the source of the remarkable stability of FR II jets. Finally, simulations have also focused on the effects of feedback by relativistic jets on star formation in the host galaxy (Wagner and Bicknell, 2011; Wagner et al., 2012) and the heating of the intracluster medium in clusters of galaxies (Perucho et al., 2011).
As in the pure hydrodynamic case, the simulation of relativistic magnetized jets was one of the first applications of the conservative RMHD methods described in Section 5. The first simulations focused on the propagation of relativistic jets with aligned magnetic fields injected into an ambient medium with an aligned (Koide et al., 1996; Nishikawa et al., 1997) and oblique (Koide, 1997; Nishikawa et al., 1998) magnetic field to study how the fields affect the bending properties of relativistic jets. However, these early simulations covered the evolution only for a brief period of time during which the jet propagated only ∼ 20 jet radii. In addition, the Lorentz factors of the jets were small (≃ 4.56). Although these results had some impact on specific problems, like e.g., understanding the misalignment of jets between pc and kpc scales, these simulations did not address the effects of magnetic fields on the jet structure and the jet dynamics. One of these first, exploratory simulations (van Putten, 1996) dealt with the formation of ‘knots’ (i.e., bright localized features) in extragalactic jets possessing a toroidal magnetic field.
Later studies explored the dependence of morphological and dynamic properties of jets on the magnetic field configuration, and on the ratio of magnetic energy density and thermal pressure, and magnetic energy density and rest-mass energy density, respectively: Komissarov (1999b); Mignone et al. (2005a); Leismann et al. (2005) simulated jets with toroidal magnetic fields, Leismann et al. (2005) jets with poloidal magnetic fields, and Keppens et al. (2008) jets with helical magnetic fields. Mignone et al. (2010) presented the first high-resolution 3D simulations of relativistic magnetized jets (see Figure 1).
Volume renderings of the passive scalar distributions for a high-resolution 3D run (left panel) and a 2D axisymmetric case (right panel) of a relativistic magnetized jet carrying a purely toroidal magnetic field component. The picture on the right clearly shows the presence of a nose cone structure typical of 2D high Poynting flux jets, which was already noticed in Newtonian MHD simulations of e.g., Komissarov (1999b); Leismann et al. (2005). It is caused by the amplification of the toroidal field component at the terminal shock. The amplified field confines the jet matter and prevents it from freely flowing into the cocoon. In three dimensions, however, the nose cone structure is unstable leading to a very different asymmetric morphology. A poloidal magnetic field component is generated in the 3D case when the initially imposed axisymmetry is destroyed. Image reproduced with permission from Figure 1 of Mignone et al. (2010), copyright by the authors.
2.1.3 Simulations of pc-scale jets
The development of multidimensional RHD codes facilitated the simulation of parsec scale jets and of superluminal radio components (Gómez et al., 1997; Komissarov and Falle, 1997; Mioduszewski et al., 1997; Aloy et al., 2000a; Agudo et al., 2001; Aloy et al., 2003; Perucho et al., 2008). The presence of emitting flows at almost the speed of light enhances the importance of relativistic effects (relativistic Doppler boosting, light aberration, time delays) for the appearance of these sources (Gómez, 2002). This implies that one should use models which combine hydrodynamics and synchrotron radiation transfer when comparing to observations.
In these models, moving radio components are modeled as perturbations in steady relativistic jets. Reconfinement shocks are produced where pressure mismatches exist between the jet and the surrounding medium. The energy density enhancement that arises downstream from these shocks can give rise to stationary radio knots as observed in many VLBI sources (e.g., 3C 279; Wehrle et al., 2001). Superluminal components are produced by triggering small perturbations in these steady jets. The interaction between the induced traveling shocks and the underlying steady jet can account for the complex behavior observed in many sources as, e.g., the dragging of steady components in 3C 279 (Wehrle et al., 2001), the presence of trailing components in 3C 120 (Gómez et al., 1998; Gómez et al., 2001) and 3C 111 (Kadler et al., 2008), and the tangled evolution of components in 3C 111 (Perucho et al., 2008). Mimica et al. (2009a) presented numerical simulations of the spectral evolution and the emission of radio components in relativistic jets. They incorporated the time evolution of a population of non-thermal electrons which is responsible for the synchrotron emission, and included the respective radiative losses from the flow (see Figure 2).
Computed synchrotron total-intensity radio maps at 43 GHz of a steady, relativistic, overpressured jet with and without radiative losses (bottom and top panels, respectively). In the model without radiative losses, the distribution of the non-thermal electrons (responsible for the synchrotron emission) only changes by adiabatic expansion and compression during the evolution. The jet including radiative losses has brighter (darker in the figure!) standing features close to the nozzle and fades away faster than the adiabatic jet. Image reproduced with permission from Figure 8 of Mimica et al. (2009a), copyright by AAS.
The combination of hydrodynamic simulations and linear stability analysis provides a very useful tool to comprehend relativistic jets in extragalactic sources. It is commonly accepted that most of the features observed in jets (radio components, transversal structure, bends, etc.) admit an interpretation in terms of the growth of KH normal modes, hence allowing to constrain the jet properties. The main theoretical developments concerning the linear analysis of the relativistic KH instability are summarized in Section 6.7. This analysis has been successfully applied to probe the physical conditions in the jets of several sources [e.g., S5 0836+710 (Lobanov et al., 1998; Perucho and Lobanov, 2007; Perucho et al., 2012a, b), 3C273 (Lobanov and Zensus, 2001), 3C120 (Walker et al., 2001; Hardee, 2003; Hardee et al., 2005); see also the review by Hardee (2006)]. Beyond the linear regime, the analysis requires numerical (hydrodynamic or magnetohydrodynamic) simulations. Here, the main purpose is to assess the stability, collimation, and mass entrainment properties of jets at large (temporal and spatial) scales. In a series of papers, Perucho et al. studied the nonlinear phase of the KH instability in relativistic jets in two (Perucho et al., 2004b, 2005, 2007) and three spatial dimensions (Perucho et al., 2010). Motivated by the hydromagnetic nature of most jet formation mechanisms, Mizuno et al. analyzed the stability of magnetized jets under different conditions. In Mizuno et al. (2007), they focused on the stability of magnetized relativistic precessing spine-sheath jets, while they studied the growth of the current-driven kink instability in relativistic force-free jets in Mizuno et al. (2009, 2011a, 2012) (see Figure 3).
Time evolution of the current-driven kink instability in a static column of non-constant density and force-free helical magnetic field with constant pitch. The panels show density isosurfaces with transverse slices at the base of the column (left) and transverse slices at the column midplane at three different times. Colors give the logarithm of the density, and the magnetic field configuration is visualized by white lines. Displacement of the initial helical magnetic field leads to a helically twisted magnetic filament around the density isosurface. At later times the radial displacement of the high-density region (red, right panels) increases only slowly. Image reproduced with permission from Figure 4 of Mizuno et al. (2009), copyright by AAS.
2.1.4 Simulations of jet formation
The advances in the numerical methods in RMHD were soon incorporated into GRMHD codes (see, e.g., Font, 2008) allowing for the first time to explore the formation mechanism of relativistic jets. Koide et al. considered the problem of jet formation from Schwarzschild (Koide et al., 1998, 1999; Nishikawa et al., 2005) and Kerr (Koide et al., 2000) black holes surrounded by accretion disks. In the case of Schwarzschild black holes, jets are formed via Blandford-Payne’s mechanism (Blandford and Payne, 1982) with a two-layered shell structure consisting of a fast gas pressure driven jet in the inner part and a slow magnetically driven outflow in the outer part both being collimated by the global poloidal magnetic field that penetrates the disk.
In the case of counter-rotating disks around Kerr black holes (Koide et al., 2000), a powerful (although still subrelativistic, vjet < 0.5c) magnetically driven jet forms inside the gas pressure driven jet. This jet is accelerated by the magnetic field anchored in the ergospheric disk. The frame-dragging effect rapidly rotates the disk in the same direction as the black hole’s rotation, increasing the azimuthal component of the magnetic field and the magnetic tension, which in turn accelerates the plasma by the magnetic pressure and centrifugal force. This mechanism of jet production is a kind of Penrose process (Hirotani et al., 1992) that uses the magnetic field to extract rotational energy of the black hole and eject a collimated outflow from very near the horizon.
The same authors (Koide et al., 2002) also explored this jet formation mechanism in the case of a maximally rotating Kerr black hole surrounded by a uniform, magnetically dominated corona with no disk. With a similar setup, Komissarov (2005) reported significant differences in the long-term evolution of the system with respect to the short phase studied in Koide et al. (2002). The topology of magnetic field lines within the ergosphere was similar to that of the split-monopole model. It gave rise to a strong current sheet in the equatorial plane and no regions of negative hydrodynamic energy at infinity (suggestive of the MHD Penrose process) inside the ergosphere. In contrast, the rotational energy of the black hole was continuously extracted via the purely electromagnetic Blandford-Znajek mechanism (Blandford and Znajek, 1977).
None of the previously discussed simulations was able to generate strong relativistic outflows from the black hole within a few tens of gravitational radii from the central source. A couple of studies (Koide, 2004; Komissarov, 2004a) focused on the influence of the initial magnetic field configuration around the rotating black hole on the outflow characteristics considering monopole magnetospheres as in the original Blandford-Znajek mechanism. Koide (2004) obtained outflows with Lorentz factors of ∼ 2.0. In the longer simulation performed by Komissarov (2004a), the numerical solution evolved towards a stable steady-state solution very close to the corresponding force-free solution found by Blandford and Znajek. For the first time, numerical solutions showed the development of an ultrarelativistic particle wind (Lorentz factor ∼ 15) which remained Poynting-dominated all the way up to the fast critical point. The wind was poorly collimated along the equatorial plane as in the original Blandford-Znajek solution. We note here that direct numerical simulations of the Blandford-Znajek mechanism were performed by Komissarov (2001, 2004b), who solved the time-dependent equations of (force-free, degenerate) electrodynamics in a Kerr black hole magnetosphere. The equations are hyperbolic (Komissarov, 2002a) and were solved by means of a Godunov-type method. Palenzuela et al. (2010a) studied numerically the interaction of black holes with ambient magnetic fields proving the robustness of the Blandford-Znajek mechanism, by which the black hole’s rotational energy is converted into Poynting flux. In particular, they analyzed the dependence of the Poynting flux luminosity on the misalignement angle between the black hole spin and the asymptotic magnetic field. Palenzuela et al. (2010a, b) also considered the case of binary black holes and showed that the electromagnetic field extracts energy from the orbit through a kind of Blandford-Znajek’s process before merging and settling into the standard Blandford-Znajek scenario.
The first simulations of self-consistent jet production from accretion disks, i.e., without assuming a large-scale magnetic field right from the beginning, were performed by McKinney and Gammie (2004), and by De Villiers et al. (2003); Hirose et al. (2004); De Villiers et al. (2005), who performed, respectively, a series of 2D (axisymmetric) and 3D GRMHD simulations of Keplerian accretion disks orbiting Kerr black holes. In all the models considered, the outflows (formed at the edge of a funnel about 0.5 rad wide around the black hole’s rotation axis; see Figure 4) were sub-relativistic. However, tuning the floor model used to refill the evacuated funnel, McKinney (2006a) succeeded in generating long-lived, superfast magnetosonic, relativistic Poynting-flux dominated jets.
Top panels: Poloidal cuts of the initial (left) and final (right) distribution of the rest mass density (logarithmic scale) of a weakly magnetized torus around a Kerr black hole. The main regions of the black hole magnetosphere are indicated in the final state. Bottom panels: Initial (left) and final (right) distribution of the poloidal magnetic field. Magnetic field lines are shown in black, the field line density indicating the poloidal field strength. In the initial state, field lines follow iso-density lines up to some threshold density. Image adapted from Figures 1 and 3 of McKinney and Gammie (2004).
Basing on 3D simulations, McKinney and Blandford (2009) explored both the stability of the jet against the development of the non-axisymmetric helical kink (m = 1) mode that leads to rapid disruption, and the stability of the jet formation process during accretion of dipolar and quadrupolar fields. In their dipolar model, despite strong non-axisymmetric disk turbulence, the jet reaches Lorentz factors of ∼ 10 with an opening half-angle ∼ 5° at 103 gravitational radii without significant disruption (see Figure 5). Porth (2013) studied the stability of jets from rotating magnetospheres performing high-resolution adaptive mesh refinement simulations in 3D. His analysis showed that the m =1−5 modes saturate at a height of ∼ 20 inner disc radii.
Snapshot of a 3D simulation of the formation of jets from a rotating accreting black hole of mass M, at t = 4000 M (geometrized units). Left panel: inner ±100M cubical region showing the black hole, the accretion disk (pressure, yellow isosurface), the outer disk and the wind (log rest-mass density, low green, high orange, volume rendering), the relativistic jet (Lorentz factor ∼ 4, low blue, high red, volume rendering), and the magnetic field lines (green) threading the black hole. Right panel: the relativistic jet (Lorentz factor ∼ 10, orange, volume rendering; only one side shown) collimated within half-angle ∼ 5° is shown out to 103 M. Image adapted from Figures 1 and 2 of McKinney and Blandford (2009).
The strength of the magnetic field on the event horizon of the central black hole can be estimated to be of the order of thousands of gauss. How this magnetic field is built up from the disk magnetic field is another subject of current research (Tchekhovskoy et al., 2011; McKinney et al., 2012).
Following a diferent approach, Vlahakis and Königl (2003) examined the production of relativistic, large-scale jets by means of self-similar solutions of magnetically driven outflows. This semi-analytic approach was tested by Komissarov et al. (2007) using axisymmetric simulations.
2.2 Gamma-ray bursts
2.2.1 Observations and theoretical models
A phenomenon that also involves flows with velocities very close to the speed of light are gamma-ray bursts (GRB). Although known observationally since several decades their nature still is a matter of debate. They are detected with a rate of about one event per day, and come in two flavors: short-duration and long-duration bursts the emission of gamma-rays varying from milliseconds to hours. The duration of the shorter bursts and the temporal substructure of the longer bursts implies a geometrically small source (less than ∼ c · 1 ms ∼ 100 km), which in turn points towards compact objects, like neutron stars or black holes. The emitted gamma-rays have energies in the range 30 keV to 2 MeV, the spectra being non-thermal, i.e., they do not allow a direct measurement of the distance of the GRB ((for recent reviews, see the book edited by Kouveliotou et al., 2012).
Observations by the BATSE detector on board the Compton Gamma-Ray Observatory (GRO) proved that GRB are distributed isotropically over the sky (Meegan et al., 1992) indicating that they are located at cosmological distances. The detection and the rapid availability of accurate coordinates of the fading X-ray counterparts of GRB 970228 by the Italian-Dutch BeppoSAX spacecraft (Costa et al., 1997; Piro et al., 1998) allowed for subsequent successful ground based observations of faint GRB afterglows at optical, millimeter, and radio wavelength. Thereby the distances of GRB could be directly determined, which confirmed their cosmological origin (for a review see, e.g., Greiner, 2012). Updated information on GRB that have been localized to less than 1 degree can be obtained from a website maintained by Greiner.
The pure cosmological origin of GRB was challenged by the detection of the broad-lined Type Ic supernova SN 1998bw (Galama et al., 1998) at a redshift of z = 0.0085 (Tinney et al., 1998) within the error box of GRB 980425 (Soffitta et al., 1998; Pian et al., 1999). The explosion time of SN 1998bw is consistent with that of the GRB, and relativistic expansion velocities are derived from radio observations (Kulkarni et al., 1998). Modeling of the optical spectra and light curve of SN 1998bw implies an unusually energetic ((2−5) × 1052 erg) supernova explosion (Galama et al., 1998; Iwamoto et al., 1998; Woosley et al., 1999). Thus, Iwamoto et al. (1998) called SN 1998bw a hypernova, a name which was originally proposed by Paczyński (1998) for very luminous GRB/afterglow events. However, the term “hypernova” draws on a theoretical classification pertaining to energetics, and it is entirely possible to have a core collapse supernova with large expansion velocity yet typical kinetic energy (1051 erg) (Hjorth and Bloom, 2012). In addition, others (Paczyński, 1998; MacFadyen and Woosley, 1999) use hypernova as a synonym for a jet-induced supernova connected to a GRB as predicted by the collapsar model (see below).
Nowadays there exists growing observational evidence for an association between long-duration GRB and radio-bright, broad-lined Type Ic core collapse supernovae resulting from the death of a massive star with a circumburst medium which may be fed by the mass-loss wind of the progenitor (Hjorth, 2013). There still remain some open issues, however: less than ∼ 10% of Type Ic supernovae are associated with a typical GRB, while current optical data suggest that all GRB supernovae are broad-line (Soderberg et al., 2006). Hence, broad optical absorption lines do not serve as a reliable proxy for relativistic ejecta, unless quite small beaming factors are assumed. Moreover, for some long-duration bursts there is no observational evidence for an associated bright supernova (for a review, see e.g., Hjorth and Bloom, 2012). The same holds for short-duration bursts, which are thought to result from merger events (see, e.g., Paczyński, 1986; Eichler et al., 1989; Narayan et al., 1992).
Long-duration GRB associated with a supernova seem to come in two types. In low-luminosity (or sub-energetic) GRB observational evidence suggests that the radio and high-energy emission results from the breakout of a relativistic shock from the circumstellar wind of the massive progenitor, while in jet GRB (also known as normal, energetic, or cosmological GRB) the emission is thought to be produced by a relativistic jet at large distance from the progenitor star (Hjorth, 2013). The rapid temporal decay of several (long-duration) GRB afterglows provides further evidence for collimated relativistic outflows, because it is consistent with the evolution of a relativistic conical flow or jet after it slows down and spreads laterally (for a review, see e.g., Piran et al., 2012; Méeszáaros and Wijers, 2012). In addition, to find an astrophysical site isotropically releasing up to ∼ 1054 erg of gamma-ray energy within less than a second, as implied by redshift measurements, poses a severe problem unless the radiation is strongly beamed as suggested by observations (Soderberg et al., 2006).
Another problem concerns the compact nature of the GRB source. The observed fluxes and the cosmological distance taken together imply a very large photon density in the gamma-ray emitting fireball, and hence a large optical depth for pair production. This is inconsistent with the optically thin source indicated by the non-thermal gamma-ray spectrum, which extends well beyond the pair production threshold at 500 keV. Assuming an ultrarelativistic expansion of the emitting region eliminates the compactness constraint. The bulk Lorentz factors required are W > 100 (for reviews, see, e.g., Méeszáaros and Wijers, 2012; Granot and Ramirez-Ruiz, 2012). The presence of such large Lorentz factors is supported by observations of the prompt optical and gamma-ray emission from the extraordinarily bright long-duration GRB 080319B, where W ∼ 1000 can be inferred from a suitable modeling of the spectral energy distribution of the event (Racusin et al., 2008).
To explain the existence of highly relativistic outflow and the energies released in a GRB various catastrophic collapse events have been proposed (Woosley, 1993; MacFadyen and Woosley, 1999). These models all rely on a common engine, namely a stellar mass black hole which accretes several solar masses of matter from a disk (formed during a merger or by a non-spherical core collapse) at a rate of ∼ 0.01 M⊙ s−1 to ∼ 10 M⊙ s−1 (Woosley, 1993; Popham et al., 1999). A fraction of the gravitational binding energy released by accretion is converted into neutrino and anti-neutrino pairs, which in turn annihilate into electron-positron pairs. This creates a pair fireball, which will also include baryons present in the environment surrounding the black hole. Provided the baryon load of the fireball is not too large, the baryons are accelerated together with the e−/e+ pairs to ultrarelativistic speeds with Lorentz factors > 102 (Cavallo and Rees, 1978; Piran et al., 1993).
Taken as a whole current observational facts and theoretical considerations suggest that GRB involve three evolutionary stages (for reviews, see e.g., Kouveliotou et al., 2012): (i) a compact source, which is opaque to gamma-rays and cannot be observed directly, produces a relativistic energy flow; (ii) the energy is transferred by means of a highly irregular flow of relativistic particles (or by Poynting flux) from the compact source to distances larger than ∼ 1013 cm where the flow becomes optically thin; (iii) the relativistic flow is slowed down and its bulk kinetic energy is converted into internal energy of accelerated non-thermal particles, which in turn emit the observed gamma-rays via cyclotron radiation and/or inverse Compton processes. The dissipation of kinetic energy either occurs through external shocks arising due to the interaction of the flow with circumburst matter, or through internal shocks arising when faster shells overtake slower ones inside the irregular outflow (internal-external shock scenario).
2.2.2 Hydrodynamic simulations
Numerical studies of relativistic flows in GRB sources have been performed since the mid 1990s. The first simulations were one-dimensional (Piran et al., 1993; Panaitescu et al., 1997; Wen et al., 1997; Kobayashi et al., 1999; Daigne and Mochkovitch, 2000; Tan et al., 2001), i.e., restricted to simulations of spherically symmetric relativistic fireballs, which are optically thick concentrations of radiation energy with a high ratio of energy density to rest mass (for more details about these studies, see Martí and Müller, 2003). Although meanwhile superseded by 2D and 3D ones, 1D simulations are still performed to investigate certain aspects of GRB (see e.g., Kobayashi and Zhang, 2007; Mimica et al., 2009b; Mimica and Aloy, 2010; Mimica et al., 2010; Mimica and Aloy, 2012; Mimica and Giannios, 2011; Harrison and Kobayashi, 2013).
Guided by the Blandford and McKee (1976) self-similar relativistic spherical shock solution, the propagation of ultrarelativistic blast waves was simulated using AMR techniques combined with shock-capturing RHD methods. Models at high Lorentz factors (up to 75) followed the propagation of the spherically symmetric blastwave through windshaped circumburst media (Meliani and Keppens, 2007), and excluded the interpretation of optical afterglow rebrightening due to the encounter with the stellar wind termination shock (van Eerten et al., 2009). Collisions between consecutive ultrarelativistic shells were shown to produce both optical and radio variability in Vlasis et al. (2011). Extensions to 2D (ultra-)relativistic blast wave evolutions were presented in Meliani et al. (2007), while an extreme resolution AMR RHD simulation from Meliani and Keppens (2010) predicts their liability to hydrodynamic instabilities that induce fragmentation during the ultrarelativistic phase of blast wave propagation.
Multidimensional modeling of ultrarelativistic jets in the context of GRB was attempted for the first time by Aloy et al. (2000b). Using a collapsar progenitor model (MacFadyen and Woosley, 1999) they simulated the propagation of an axisymmetric jet through the envelope of a collapsing massive star that after loosing its hydrogen envelope had a mass of about 10 M⊙. The jet was instigated depositing thermal energy at rates of 1049 erg/s to 1051 erg/s within a 30 degree cone around the rotation axis of the star. At break-out, when the jet reaches the surface of the star, the maximum Lorentz factor of the jet flow is about 50, i.e., Newtonian simulations of this phenomenon (MacFadyen and Woosley, 1999) are inadequate.
Zhang et al. (2003) performed a parameter study of the propagation of axisymmetric (2D) relativistic jets through the stellar progenitor of a collapsar and beyond varying the initial Lorentz factor, opening angle, power and internal energy of the jet as well as the radius where it is injected. They find, in agreement with Aloy et al. (2000b), that relativistic jets are collimated by their passage through the stellar mantle. When they emerge from the star the jets have a moderate Lorentz factor and a very large internal energy. After the escape from the star conversion of its internal energy into kinetic energy leads to a further acceleration of the jet boosting the Lorentz factor to a terminal value of ∼ 150 for the initial conditions chosen. Zhang et al. (2004) extended this study performing 2D and 3D simulations of relativistic jet propagation and break out in massive Wolf-Rayet stars (see Figure 6 and attached movie — online version only —). Their 3D simulations showed that if the jet changes angle by more than three degrees in several seconds, it will dissipate, producing a broad beam with inadequate Lorentz factor to make a common GRB.
mpg-Movie (9419.38964844 kB) Still from a movie — Comparison of 2D (top left) and 3D simulations of GRB jets. The slices show the density distribution along the polar axis at the time of break-out from the star. The 2D model 2T and the 3D model 3A have the same jet parameters and effective zoning. Even though 3A is 3D, it retains the 2D symmetry imposed by the jet’s initial parameters. Models 3BS and 3BL are like model 3A, but with slightly asymmetric initial conditions. Image reproduced with permission from Figure 11 of Zhang et al. (2004), copyright by AAS. Animation (online version only): 3BL jet breaking out of the star (Weiqun Zhang’s webpage). Courtesy of W. Zhang. (For video see appendix)
Similar 2D studies were performed by Mizuta et al. (2006), Mizuta and Aloy (2009), Mizuta et al. (2011), and Mizuta and Ioka (2013) who investigated, in particular, the dependence of the angular energy distribution of collapsar jets on the pre-supernova stellar model (Mizuta and Aloy, 2009), and the dependence of the opening angle of the jet on the initial Lorentz factor, W0 (Mizuta and Ioka, 2013). The latter is given by Θj ∼ 1/5W0, which allows one to infer the initial Lorentz factor of the jet at the central engine from observations. They also calculated light curves and spectra of the photospheric thermal radiation of their simulated collapsar jets (Mizuta et al., 2011).
Tominaga et al. (2007); Tominaga (2009) simulated jet-induced axisymmetric explosions of 40 M⊙ Population III stars with a 2D RHD code and computed the resulting nucleosynthesis. The simulations can explain both long-duration GRB with and without a bright broad-lined Type Ic core-collapse supernovae in a unified manner. Nagakura et al. (2011) performed axisymmetric RHD simulations of a jet propagating through the envelope of a rapidly rotating collapsing massive star, and of its break-out and subsequent expansion into a stellar wind environment. They also computed the photospheric emission accompanying the event.
The first collapsar jet simulations using adaptive mesh refinement (AMR) were presented by Morsony et al. (2007), who performed their axisymmetric (2D) simulations in cylindrical coordinates with the RHD module of FLASH. In this and several related subsequent AMR studies (Lazzati et al., 2009; Morsony et al., 2010; Lazzati et al., 2012; López-Cámara et al., 2013) the authors were able to simulate the evolution of relativistic jets in collapsars after break out from the star.
They singled out three evolutionary phases: a precursor phase during which relativistic matter turbulently shed from the head of the jet first emerges from the star, a shocked-jet phase when a fully shocked jet is emerging, and an unshocked-jet phase where the jet consists of a free-streaming unshocked core surrounded by a thin boundary layer of shocked-jet material. Whether these phases can be observed depends on the angle under which one observes the GRB jet (Morsony et al., 2007).
The interaction of the relativistic matter with the progenitor star influences the outflow properties well beyond the stellar surface (Lazzati et al., 2009), and the variability imprinted by the GRB engine is preserved even if the jet is heavily shocked inside the star (Morsony et al., 2010). The latter result suggests that the broad pulses (∼ seconds) in a typical long-duration GRB are due to interaction of the jet with the progenitor, while the short-timescale (∼ msec) variability must be caused at the base of the jet (Morsony et al., 2010).
The outcome of the explosion sensitively depends on the duration of the engine activity: Only the longest-lasting engines result in successful GRB, while engines with intermediate duration produce weak GRB and those with the shortest duration give rise to explosions that lack sizable amounts of relativistic ejecta, and hence, if they exist in nature, are dynamically indistinguishable from ordinary core-collapse supernovae (Lazzati et al., 2012).
López-Cámara et al. (2013) extended these 2D studies performing 3D AMR simulations of collapsar jets, which expand inside a realistic stellar progenitor. They confirmed the result of previous 2D simulations that initially relativistic jets can propagate and break out of the progenitor while remaining relativistic. They also find that the jet’s propagation is slightly faster in 3D than in 2D models (at the same grid resolution), because the jet head can wobble around the jet axis and hence drill better when no axisymmetry is imposed. This property of 3D jets was already noticed by Aloy et al. (1999a) in the case of extragalactic jets.
Wygoda et al. (2011) studied the deceleration and expansion of highly relativistic conical jets propagating into a medium of uniform density. De Colle et al. (2012a, c, b) performed 2D AMR simulations of GRB jets, studying the influence of both uniform and, for the first time, stratified circumburst environments. Further AMR simulations in the context of GRB jets were performed by Meliani et al. (2007) and Wang et al. (2008). The former investigated various evolutionary phases in the interaction of jet-like relativistic fireballs with a surrounding interstellar medium (ISM), while the latter performed a 3D simulation of a GRB jet.
2.2.3 Magnetodynamic and magnetohydrodynamic simulations
Electromagnetic extraction of black hole spin energy by the Blandford-Znajek mechanism (Blandford and Znajek, 1977) is the most astrophysically plausible mechanism to generate a relativistic jet. Alternatively, jets in GRB may originate from rapidly rotating magnetars, the outflow being powered by the rotational energy of the strongly magnetized neutron star (for a review, see e.g., Woosley, 2012). Because the collapsar model of long-duration GRB (Woosley, 1993) relies on rapid accretion onto a black hole that forms in the center of a collapsing massive star, several groups have performed general relativistic simulations of the formation and propagation of GRB jets including the effects of magnetic fields (McKinney and Gammie, 2004; McKinney, 2006a; Mizuno et al., 2008; Tchekhovskoy et al., 2008; McKinney and Blandford, 2009; Tchekhovskoy et al., 2009; Komissarov et al., 2009, 2010; Tchekhovskoy et al., 2010; Harrison and Kobayashi, 2013).
Extending previous work to larger radii and later times, McKinney and Gammie (2004) (see also Section 2.1.4) and McKinney (2006a) studied self-consistently generated Poynting-dominated axisymmetric jets. He considered a generic black hole accretion system because the GRMHD equations scale arbitrarily with the mass of the black hole and the mass-accretion rate. He found that, unlike in some hydrodynamic simulations, the environment plays a negligible role in jet structure, acceleration, and collimation as long as the ambient pressure of the surrounding medium is small compared to the magnetic pressure in the jet. In his simulations the jet becomes marginally unstable to current-driven instabilities, beyond the Alfvién surface (located between 10 and 100 gravitational radii). These instabilities induce jet substructure with 3 ≲ W ≲ 15, whereas the jet moves at a lab-frame bulk Lorentz factor of W ∼ 10 with a maximum terminal value of W∞ ≲ 103.
Using global axisymmetric stationary solutions of magnetically dominated ultrarelativistic jets Tchekhovskoy et al. (2008) investigated whether the magnetic-driving paradigm can generate Lorentz factors and opening angles as required by the collapsar scenario. The global solutions were obtained via ideal magnetodynamic (i.e., force-free) simulations in spherical polar coordinates based on a Godunov-type scheme (McKinney, 2006b) covering the jet propagation from the central engine to beyond six orders of magnitude in radius. To ensure accuracy and to properly resolve the jet, they used a numerical grid that approximately follows the magnetic field lines in the jet solution (Narayan et al., 2007). Thereby they achieved an effective radial resolution of about 100 000 with only 256 radial grid points.
The simulations showed that the size of the progenitor star and its pressure profile determine the terminal Lorentz factor (100 ≲ W ≲ 5000) and the opening angle of the jet (0.1° ≲ Θj ≲ 10°), consistent with observations of long-duration GRB jets. In some of their solutions the Poynting flux is concentrated in a hollow cone with Θ ∼ Θj, while the maximum Lorentz factor occurs at Θ ≪ Θj, also in a hollow cone.
A similar study, but employing a MHD code, was performed by Komissarov et al. (2009) who considered, however, only special relativistic jets arguing that general relativistic effects can be neglected sufficiently far from the central engine, where most of the action takes place. They investigated the magnetic acceleration of ultrarelativistic flows within channels of prescribed geometry corresponding to power-law distributions of the confining pressure that is expected in the envelopes of GRB collapsar and magnetar progenitors.
Extending the simulations of Tchekhovskoy et al. (2008) to 3D and MHD, McKinney and Blandford (2009) explored both the stability of the jet against the development of the non-axisymmetric helical kink mode that leads to rapid disruption (see also Section 2.1.4). Tchekhovskoy et al. (2009) performed time-dependent axisymmetric RMHD simulations to find steady-state solutions for a wind from a compact object endowed with a split-monopole field geometry. For axisymmetric rapidly rotating systems, a dipolar magnetosphere is the commonly expected field configuration, which can be well modeled by a split-monopole at large radii beyond the Alfvéen surface (i.e., light cylinder). Obtaining approximate analytical solutions Tchekhovskoy et al. could extend their results to wind models with arbitrary magnetization. The simulations covered ten orders of magnitude in distance from the compact object and demonstrated that the production of ultrarelativistic jets is a quite robust process.
Tchekhovskoy et al. (2010) confirmed the work of Komissarov et al. (2009) by also exploring the effect of a finite stellar envelope on the structure of axisymmetric collapsar jets. They treated the jet-envelope interface as a collimating rigid wall, which opens up at the stellar surface to mimic loss of collimation. The onset of deconfinement causes a burst of acceleration accompanied by a slight increase in the opening angle. The results \(({W_\infty } \simeq 500,\;\Theta _j^\infty \simeq {2^ \circ })\) are consistent with observations of typical long-duration GRB and also explain the occurrence of jet breaks.
Axisymmetric RMHD simulations by Komissarov et al. (2010) support the finding of Tchekhovskoy et al. (2010) that after break out but before entering the regime of ballistic expansion (during which additional magnetic acceleration becomes ineffective), the jets experience a spurt of acceleration. Komissarov et al. attributed this acceleration to a sideways expansion of the jet, associated with a strong magnetosonic rarefaction wave that is driven into the jet when it loses pressure support. Using the equations of RMHD they demonstrated that this mechanism, which they dubbed rarefaction acceleration, can only operate in a relativistic outflow, where the total energy can still be dominated by the magnetic component even in the superfast-magnetosonic regime (Komissarov et al., 2010). This jet boosting mechanism was previously found by Aloy and Mimica (2008).
The asymptotic evolution of strongly magnetized relativistic ejecta, i.e., after they have experienced a significant deceleration and a reverse shock has formed, resembles that of hydrodynamic ejecta in the Blandford-McKee self-similar regime (Mimica et al., 2009b). Thus, the magnetization of GRB fireballs can only be determined from the early phases of the afterglow (Giannios et al., 2008; Mimica et al., 2009b, 2010; Harrison and Kobayashi, 2013) or from the prompt GRB broad spectral energy distribution (Mimica and Aloy, 2010). Giannios et al. (2008) derived the conditions for the existence of a reverse shock in arbitrarily magnetized ejecta that decelerate and interact with a circumburst medium. They concluded that the paucity of optical flashes, believed to be a distinctive signature of a reverse shock, may be explained by the existence of dynamically important magnetic fields in the ejecta.
Harrison and Kobayashi (2013) showed that with the current standard treatment, the fireball magnetization is underestimated by up to two orders of magnitude, particularly in the sub-relativistic reverse shock regime, where most optical GRB flashes are detected. For their numerical study they employed a spherical relativistic Lagrangian hydrodynamic code based on Godunov’s method with an exact Riemann solver assuming that the magnetization of the fireball is not too large (ratio of magnetic to kinetic energy flux ≲ 10%), i.e., the dynamics of the shocks is not affected by magnetic fields.
2.3 Pulsar wind nebulae
2.3.1 Fiducial Kennel-Coroniti’s model
Pulsars lose their rotational energy predominantly by generating a highly magnetized ultrarelativistic wind. The wind interacts with the ambient medium, either the supernova remnant (SNR) or the ISM, and terminates at a strong reverse shock. The shocked plasma inflates a bubble of non-thermal relativistic particles and magnetic field, known as Pulsar Wind Nebula (PWN). The Crab Nebula is the best example of a PWN (for a recent review of the Crab pulsar and its nebula, see Bühler and Blandford, 2014).
The first theoretical model of the structure and the dynamic properties of PWN was presented by Rees and Gunn (1974), further developed by Kennel and Coroniti (1984a, b), and is based on a RMHD description. In it simplest form the MHD model of PWN can be summarized as follows (see Figure 7): the ultrarelativistic pulsar wind is confined inside the slowly expanding SNR, and slowed down to non relativistic speeds in a strong termination shock. At the shock the plasma is heated, the toroidal magnetic field of the wind is compressed, and particles are accelerated to high energies. These high energy particles and magnetic field produce a post-shock flow which expands at a non-relativistic speed toward the edge of the nebula.
Schematic view of the structure of a pulsar wind nebula and its interaction with the SNR and the ISM. In young nebulae (like, e.g., Crab) the crucial role is played by the terminal shock inside the relativistic pulsar wind. In older nebulae, the evolution of the nebula is modified by the interaction with the reverse shock in the SNR shell.
Close to the pulsar, the energy is carried mostly by electromagnetic fields as Poynting flux, however the simple 1D models of PWN (Rees and Gunn, 1974; Kennel and Coroniti, 1984a, b; Begelman and Li, 1992) suggest that the magnetization parameter, here defined as the ratio of the Poynting and the kinetic energy fluxes, needs to be as small as 0.001 to 0.01 just upstream of the termination shock. If the ratio of magnetic pressure and gas pressure were larger, the amplification of the magnetic field due to compression at the shock front would cause the outer nebula to be strongly pinched and therefore highly elongated, in contradiction to observations (Rees and Gunn, 1974; Begelman and Li, 1992). This problem, known in the literature as the sigma-problem, is a long-standing puzzle in pulsar wind theory.
Despite its simplicity and limitations the model of Kennel-Coroniti has been for a long time the reference for the understanding of young PWN, with only minor theoretical developments. The presence of an underluminous region centered at the location of the pulsar is interpreted as being caused by the ultrarelativistic unshocked wind. Polarization measures — of the, e.g., Vela (Dodson et al., 2003), Boomerang (Kothes et al., 2006), and Crab (Hester, 2008) nebulae — show that the emission is highly polarized and the nebular magnetic field is mostly toroidal. Both properties are expected from the compression of the pulsar wind, and they are consistent with the inferred symmetry axis of the system. The MHD flow from the terminal shock to the edge of the nebula also explains why PWN appear bigger at smaller frequencies: high energy X-rays emitting particles are present only in the vicinity of the terminal shock. They have a shorter lifetime against synchrotron losses than radio-emitting particles which fill the entire volume.
2.3.2 The new paradigm from high resolution imaging and the role of axisymmetric numerical simulations
The high resolution optical and X-rays images from HST, Chandra, and XMM-Newton have revolutionized the field of PWN showing that the properties of their emission at high energies cannot be explained within a simplified 1D model. This refers not just to the geometrical features that are observed, but in practice to all aspects of X-ray emission.
The new data show that the inner region of young PWN is characterized by a complex axisymmetric structure, generally referred to as the jet-torus structure, first observed in the Crab Nebula (Hester et al., 1995; Weisskopf et al., 2000) (see Figure 8). This structure is characterized by an emission torus, in what is thought to be the equatorial plane of the pulsar rotation, and a series of multiple arcs or rings, together with a central knot, almost coincident with the pulsar position, and one or two opposite jets along the polar axis, which seem to originate close to the pulsar itself.
mpg-Movie (3987.49609375 kB) Still from a movie — A composite image of the inner region (1.6 arcmin) of the Crab Nebula showing the X-ray (blue), and optical (red) images superimposed. (Credit: X-ray: NASA/CXC/ASU/J. Hester et al.; Optical: NNASA/HST/ASU/J.Hester et al.). Animation (online version only): Crab time-lapse movie made from seven still images of Chandra observations taken between November 2000 and April 2001. The movie shows dynamic rings, wisps and jets in the Crab nebula (Credit: NASA/CXC/ASU/J. Hester et al.). See more Crab animations at Chandra web page. (For video see appendix)
The keys in understanding the jet-torus structure are the magnetization and energy distribution in the pulsar wind, both displaying a strong latitudinal dependence. As suggested by Bogovalov and Khangoulian (2002) and Lyubarsky (2002), the consequence of such anisotropic energy injection into the surrounding nebula would be a greatly enhanced emission in a belt around the rotational equator — the “torus” appearing in X-ray and optical images.
In addition, Lyubarsky suggested that the outflow from the torus, since it is injected into the non-relativistically expanding cavity formed by the supernova, would be deflected into a subsonic backflow at higher latitudes, where magnetic hoop stress could act to focus plasma into a magnetically compressed, outflowing, subsonic plume along the pulsar rotation axis, thus creating the appearance of a jet.
An understanding of the complexity of this scenario requires the use of efficient and robust numerical schemes for RMHD (Komissarov, 1999a; Del Zanna et al., 2003; Mizuno et al., 2006). Thanks to numerical simulations (Komissarov and Lyubarsky, 2003, 2004; Del Zanna and Bucciantini, 2004; Bogovalov et al., 2005) the qualitative picture could be extended into a quantitative model that has been successfully validated against observations (see Figure 9). The wind’s magnetization regulates the formation and the properties of the jet: for low values of the magnetization (< 0.001), equipartition is not reached inside the nebula, and no jet is formed. At higher magnetizations equipartition is reached in the close vicinity of the terminal shock, and most of the plasma ends in a jet. The simulations (Del Zanna and Bucciantini, 2004) also explain the kinematics of the post-shock flow inside the torus that requires velocities of ∼ 0.5c (Hughes et al., 2002). They contradict Kennel-Coroniti’s model which predicts significantly smaller speeds (Shibata et al., 2003) and the production of X-ray nebulae with comparable size in radio.
Left panel: Color coded velocity map and flow direction represented by arrows in the central part of the model presented in Komissarov and Lyubarsky (2003). Just above the equatorial outflow, a layer of backflow can be seen converging towards the symmetry axis. This backflow provides plasma for the two transonic jets propagating in the vertical direction. Right panel: Synchrotron X-ray image for the same model. The nebula is tilted to the plane of the sky by an angle of 30 degrees, as in the Crab nebula. The brightness distribution is shown in logarithmic scale. To create this image, synchrotron electrons and positrons with a power law energy spectrum are injected at the termination shock, which then suffer synchrotron energy losses at a constant rate determined by the typical value of magnetic field in the numerical solution. Image adapted from Figures 3 and 4 of Komissarov and Lyubarsky (2003).
One of the most recent achievements of the MHD nebular models has been the ability to reproduce the observed time variability in young PWN. Close to the supposed location of the termination shock, PWN show a short time variability mainly detected in optical and X-ray bands. Variability of the wisps in the Crab Nebula has been known for a long time (Hester et al., 2002). Recent observations have shown that the jet in Vela appears to be strongly variable (Pavlov et al., 2003; Durant et al., 2013), together with the main rings (Kargaltsev and Pavlov, 2008). Variability is also observed in MSH 15-52 (DeLaney et al., 2006), and has recently been detected in the jet of Crab (Weisskopf, 2011). In the strongly toroidal field of these nebulae, the jet variability, which usually has a time-scale of years, is likely due to a variety of MHD instabilities or pulsar spin axis precession (DeLaney et al., 2006; Durant et al., 2013). On the other hand, the wisps show variability on shorter time-scales of months having the form of an outgoing wave pattern with a possible year-long duty cycle (see movie — online version only — Figure 8). The most recent MHD simulations (Volpi et al., 2008; Camus et al., 2009; Porth et al., 2014b) are able to recover the variability, the outgoing wave pattern, its typical speed, and the luminosity variations (see the synthetic Hubble movies of the inner PWN in the online material of Porth et al., 2014b, which show several wisps emanating from the termination shock).
Finally, employing axisymmetric, highly grid-adapted, long-term RMHD simulations, Porth et al. (2014a) studied the development of Rayleigh-Taylor filaments at the decelerated contact discontinuity that separates the PWN from the SNR ejecta. These filaments resemble the filamentary structures observed in the outer regions of the Crab Nebula.
2.3.3 Towards a solution of the sigma-problem: 3D simulations
Simple 1D models of PWN fit the observations only if pulsar winds are particle-dominated, i.e., the ratio of Poynting flux to kinetic energy flux σ must be very small (10−3 − 10−2). However, theoretical models of pulsar magnetospheres and winds predict σ ≫ 1. The striped wind oblique rotator model of Coroniti (1990) offers a possible solution to this discrepancy: reconnection of stripes of toroidal magnetic field of opposite polarity close of the equatorial plane of the wind converts the initially dominant Poynting flux into thermal and kinetic energy of particles as the wind flows radially outward. However, the dissipation length-scale still significantly exceeds the radius of the wind termination shock for the Crab pulsar (Lyubarsky and Kirk, 2001).
Begelman (1998) proposed an alternative solution. Based on the axisymmetric model of Begelman and Li (1992), Begelman (1998) suggested that the sigma-problem can be alleviated if a current-driven kink instability destroys the concentric field structure in the nebula. The current-driven kink instability allows the loops to come apart and one expects that in three dimensions, the mean field strength is not amplified much by the expansion of the flow, and the hoop stress would not necessarily pinch the flow as much as would otherwise be supposed. In this case, the ratio of Poynting flux and kinetic energy flux just upstream of the termination shock might not need to be so unreasonably small as was found in axisymmetric models.
Begelman (1998) derived a dispersion relation valid for relativistic fluids in the ideal MHD limit. The dominant instabilities are kink (m = 1) and pinch (m = 0) modes. The former generally dominate, destroying the concentric field structure and driving the system toward a more chaotic state in which the mean field strength is independent of radius.
Mizuno et al. (2011b) and more recently Porth et al. (2013) have tested Begelman’s suggestion by means of 3D RMHD simulations. Mizuno et al. (2011b) investigated the relaxation of a hydrostatic hot plasma column containing toroidal magnetic field (the original cylindrical magnetostatic configuration used in Begelman and Li, 1992) by the current-driven kink instability. In their simulations, the instability is excited by a small initial velocity perturbation, which develops into a turbulent tructure inside the hot plasma column. The authors demonstrate that, as envisioned by Begelman, the hoop stress declines, the initial gas pressure excess near the axis decreases, and the ratio of the Poynting and kinetic energy flux, declines from an initial value of 0.3 to about 0.01 when the current-driven kink instability saturates.
The most important ingredient missing in the simulations by Mizuno et al. is the continuous injection of magnetic flux and energy in PWN by pulsar winds. As a result, there is no termination shock whose size is an important parameter used to test theories of PWN against observational data. Hence, the next natural step is to carry out 3D numerical simulations of PWN with setups similar to those of the previous axisymmetric simulations.
Such a study was performed by Porth et al. (2013) who showed that the kink instability (and the magnetic dissipation) inside these nebulae may be the key process allowing one to reconcile the observations with the theory of pulsar winds. In agreement with the simulations of Mizuno et al. (2011b) the highly organized coaxial configuration of the magnetic field, characteristic of previous 2D simulations of PWN, is largely destroyed in the 3D models. However, the azimuthal component still dominates in the vicinity of the termination shock, i.e., in the region roughly corresponding to Crab torus (see Figure 10), which is filled mainly with plasma that flows from the termination shock towards the center of the nebula. The hoop stress of the azimuthal field is still capable of producing a notable axial compression close to the termination shock and driving polar outflows, which are required to explain the Crab jet, and the jets of other PWN. However, these outflows are much more moderate than in the 2D models.
Left panel: 3D rendering of the magnetic field structure for a model having an initial Poynting flux and kinetic energy flux ratio of 3 about 70 yr after the start of the simulation. Magnetic field lines are integrated from sample points starting at r = 3 × 1017 cm. Colors indicate the dominating field component, blue for toroidal and red for poloidal. Right panel: azimuthally averaged poloidal magnetic field energy density over total magnetic field energy density. Image reproduced with permission from Figure 2 of Porth et al. (2013), copyright by the authors.
Simulations of PWN beyond the free expansion phase (as in, e.g., Blondin et al., 2001; Bucciantini et al., 2005; Vigelius et al., 2007) when the interaction with the SNR and the proper motion of the pulsar become important, and the interpretation of the gamma-ray emission remain two of the main challenges in the field (see, e.g., Bucciantini, 2011, 2012). Both problems are of particular importance for the study of gamma-ray binaries for which there is compelling evidence that they are driven by rotation-powered pulsars (Dubus, 2006, 2013).
3 Special Relativistic Hydrodynamics and Magnetohydrodynamics
3.1 Equations
The simplest model to describe a relativistic medium is that of a relativistic non-dissipative (perfect) fluid. When the medium is magnetized and electrically highly conducting, the simplest description is in terms of ideal MHD (the equations describing the evolution of a perfect magneto-fluid in the limit of infinite conductivity). In this review we shall refer to the equations describing such systems as the equations of relativistic hydrodynamics (RHD) and magnetohydrodynamics (RMHD). A derivation of the equations of relativistic fluid dynamics based on the analogy with Newtonian fluid dynamics with an appropriate identification of the relativistic counterparts corresponding to energy and momentum densities and fluxes can be found in Synge (1956); Landau and Lifshitz (1987); Misner et al. (1973); Taub (1978). Anile (1989) provides a justification of the RHD and RMHD equations based on the phenomenological theory of electromagnetically polarizable media. The reader is also addressed to the book of Dixon (1978). In this Section we present without derivation the equations of both RHD and RMHD. Another presentation of these equations, including a brief discussion, can also be found in Chapter 21 of Goedbloed et al. (2010).
Using the Einstein summation convention the equations describing the motion of a relativistic fluid are given by the five conservation laws
where μ,ν = 0,…, 3, and; μ denotes the covariant derivative with respect to the coordinate xμ. Furthermore, ρ is the proper rest-mass density of the fluid, uμ its 4-velocity, and Tμν is the stress-energy tensor, which for a perfect fluid can be written as
Here, gμν is the metric tensor, p the fluid pressure, and h the specific enthalpy of the fluid defined by
where ε is the specific internal energy. Finally, one requires an equation of state (EOS) that relates the thermodynamic variables, e.g., p = p(ρ, ε).
For an ideal magneto-fluid, the stress energy tensor must include the contribution of the magnetic field,
where h* = 1 + ε + p/ρ + b2/ρ is the specific enthalpy including the contribution of the magnetic field (b2 stands for bμbμ), p* = p + b2/2 is the total pressure, and bμ is the magnetic field in the fluid rest frame which satisfies the condition uμbμ = 0. In this case, the equations expressing the conservation of rest-mass, energy and momentum (1), (2) must be complemented with Maxwell’s equations that govern the evolution of the magnetic field
where * Fμν is the Maxwell dual tensor,
In the preceding equations and throughout the review, besides using units in which the speed of light is set to unity, we absorb a factor √4π in the definition of the magnetic field (see also Section 6)
The equations of RMHD can be written as a system of conservation laws. In Minkowski spacetime (gμν = ημν = diag(−1, 1, 1, 1)) and Cartesian coordinates ({i, j, k} = {x, y, z}) this system reads
where the state vector, U, and the fluxes, Fi, are the following column vectors,
and
In these equations, D, Sj, and τ are the rest-mass density, the momentum density of the magnetized fluid in j-direction, and the total energy density measured in the laboratory (i.e., Eulerian) frame, i.e.,
where vi are the components of the fluid 3-velocity measured in the laboratory frame. They are related to the components of the fluid 4-velocity by the expression uμ = W(1,vx, vy, vz) with the flow Lorentz factor
The following fundamental relations hold between the components of the magnetic field 4-vector in the comoving frame and the three vector components Bi measured in the laboratory frame:
where v and B denote the 3-vectors (vx,vy,vz) and (Bx, By, Bz), respectively. The square of the modulus of the magnetic field can be written as
with B2 = BiBi.
Subtracting the rest-mass energy D from the total energy τ, the energy equation can be written in terms of the conserved variable τ′ = τ − D. In the non-relativistic limit (i.e., v ≪ 1, ε, p ≪ 1, and B2 ≪ 1), the conserved variables D, Si and τ′ tend to their Newtonian counterparts ρ, ρvi, and ρε + ρv2/2 + B2/2, and the classical MHD equations are recovered. Setting B = 0 in the MHD or RMHD equations leads to the corresponding hydrodynamic limits.
The dynamic importance of a magnetic field can be quantified with the following two parameters: (i) β = b2/(2p), the ratio of magnetic pressure to gas pressure, and (ii) κ = b2/(ρh), which is related to the ratio of magnetic energy density to enthalpy density and coincides with the ratio of Poynting flux to kinetic energy density for flows perpendicular to the magnetic field. In a medium at rest β = B2/(2p) and κ = B2/(ρh). The parameter κ varies monotonically with the Alfvén speed given by \({c_a} = B/\sqrt {\rho h + {B^2}} \), i.e., \(\kappa = c_a^2/(1 - c_a^2)\) and κ → 0 (∞) for ca → 0 (1). Important dynamic effects due to the presence of a magnetic field are expected when β and/or κ are large. We note that our definitions of these parameters can differ from those of other authors (in particular, our β parameter is defined as the inverse of the plasma β parameter).
3.2 Mathematical aspects
3.2.1 Hyperbolicity of the RHD equations
Lichnerowicz (1967) and Anile (1989) discussed the mathematical structure of the equations of RHD and RMHD. An important property of the former set of non-linear partial differential equations is that it is hyperbolic for causal EOS (Anile, 1989). For hyperbolic systems of conservation laws, the Jacobians of the fluxes ∇Fi(U)/∇U have real eigenvalues and a complete set of eigenvectors (see Section 8.1 for the spectral decomposition of the flux Jacobians of the RHD equations). Information about the solution propagates at finite velocities given by the eigenvalues of the Jacobians, which are related to the propagation speeds of flow disturbances. In the case of a fluid, these are entropy waves and sound waves.
If the solution is known in some spatial domain at some given time, the hyperbolicity of the RHD equations can be used to advance the solution to some later time (initial value problem). In general, it is not possible, however, to derive an exact solution. Instead one has to rely on numerical methods which provide an approximate solution. Moreover, the numerical methods must be able to handle solutions with discontinuities (i.e., shocks), which are inherent to non-linear hyperbolic systems. Readers interested in the theory and numerical solution of hyperbolic systems are addressed to the monographs by LeVeque (1992) and Toro (1997).
Associated with the hyperbolicity of the system are the concepts of characteristics (integral curves of the eigenvalues of the flux Jacobians) and simple waves (solutions that are constant along characteristics). Simple waves and shocks (limiting solutions of converging simple waves) are the building blocks of the solution of Riemann problems (initial value problems with discontinuous data). They are of paramount importance from a theoretical point of view and also for the numerical solution of the hyperbolic system of equations. We present the solution of the Riemann problem in RHD in Section 8.5, as derived in Martí and Müller (1994); Pons et al. (2000). Several theoretical developments related to the theory of simple waves and shocks in RHD are discussed in Martí and Müller (1994) (and references therein), including an analysis of the jump conditions across shocks, of the shock adiabats, of self-similar solutions of relativistic blast waves, and of the process of shock formation by the steepening of simple waves.
3.2.2 Hyperbolicity of the RMHD equations and degeneracies
The hyperbolicity of the RMHD equations including the derivation of eigenvalues and the corresponding eigenvectors was studied by Anile and Pennisi (1987) and reviewed by Anile (1989). In both classical and relativistic MHD, the eigenvalues are associated with the propagation of entropy waves, Alfvén waves, and slow and fast magnetosonic waves (Jeffrey and Taniuti, 1964). Moreover, the MHD equations exhibit degeneracies in the sense that two or more eigenvalues may coincide, i.e., the set of equations is not strictly hyperbolic.
The degeneracy conditions in RMHD have been analyzed by Komissarov (1999a), and more recently by Antón et al. (2010). They coincide with those for Newtonian flows in the fluid rest frame. Degeneracies are encountered in this frame for waves propagating perpendicular (Type I) and along (Type II) the magnetic field direction. In case of the Type I degeneracy, the two Alfvén waves, the entropic wave, and the two slow magnetosonic waves propagate at the same speed, while for the Type II degeneracy, the speeds of an Alfvén wave and a magnetosonic wave (slow or fast) are the same.
Some differences between classical and relativistic MHD exist in the laboratory frame. If one encounters the Type II degeneracy in classical MHD, both Alfvén waves exhibit the degeneracy. In RMHD, due to aberration, the condition for degeneracy can be fulfilled only for one of the Alfvén waves. Only if the tangential component of the fluid velocity vanishes, one recovers the classical behavior. The degeneracies can be visualized with the help of the characteristic wave speed diagrams (Antón et al., 2010), equivalent to the phase speed diagrams for linear perturbations (Keppens and Meliani, 2008). These diagrams show the normal speed of planar wave fronts propagating in different directions, the speed given by the distance between the origin and the normal speed surface along the corresponding direction. Figure 11 displays the degeneracies for a selection of states.
Characteristic wavespeed surfaces of fast magnetosonic waves (blue), Alfvén waves (yellow), slow magnetosonic waves (red), and entropy waves (black; only bottom right panel) for a homogeneous magnetized ideal gas with γ = 4/3, ρ = 1.0, Bx = 5.0, By = 0.0, and Bz = 0.0. The gas is at rest except in the bottom right panel, where it moves along the x-axis with a speed vx = 0.9. The specific internal energy of the gas is ε = 1.0 (top left), ε = 50.0 (top right), and ε = 37.864 (bottom left), respectively. When the gas is at rest, the surface of the entropy wave degenerates in a point located at the origin and exhibits two symmetries: a rotational symmetry around the direction of the magnetic field (i.e., the x-direction), and a mirror symmetry in the y − z plane orthogonal to the magnetic field. Both types of degeneracies that may be encountered in classical and relativistic MHD can be recognized: Type I in the plane orthogonal to and Type II along the direction of the magnetic field. Moreover three sub-cases of the Type II degeneracy can be discerned: Alfvén waves propagating along the magnetic field at the same speed as the fast magnetosonic waves (top left), the slow magnetosonic waves (top right), and both the fast and slow magnetosonic waves (bottom left). When the gas moves in x-direction (i.e., along the magnetic field; bottom right) the surfaces still exhibit the rotational symmetry around the x-axis, and the Type I and II degeneracies still occur in the y − z plane and along the x-axis, respectively. Image adapted from Antón et al. (2010).
The eigenvectors derived in Anile and Pennisi (1987) and Anile (1989) do not form a complete basis for degenerate states since they become zero or linearly dependent in that case. Antón et al. (2010) obtained a new set of eigenvectors that do form such a basis both for nondegenerate and degenerate states. The new set of renormalized right eigenvectors in covariant variables as well as a short discussion of the derivation of the left and right eigenvectors in conserved variables can be found in Section 8.2.
We present the solution of the Riemann problem in RMHD in Section 8.6 as derived in Giacomazzo and Rezzolla (2006). Some interesting analytical results involving simple waves in magnetized fluids can be found in Mathews (1971); Lyutikov (2010); Lyutikov and Hadden (2012).
3.2.3 Convexity
A hyperbolic system is said to be convex when all the characteristic fields are either genuinely nonlinear or linearly degenerate (Lax, 1957; LeVeque, 1992). The solutions of a hyperbolic system are qualitatively different depending on whether the system is convex or not. In a convex system, genuinely nonlinear fields can give rise to a single shock or a single centered rarefaction wave, whereas linearly degenerate fields are associated to contact discontinuities. If the system is non-convex, the fields which have no definite character can give rise to an alternate series of shocks and rarefactions (Godlewski and Raviart, 1996) (compound waves; see below).
In a purely fluid dynamical system, the convex or non-convex character is determined by the EOS, and one speaks of convex or otherwise non-convex equations of state. An EOS is said to be convex if the isentropes are convex in the p − V plane (where V ≡ 1/ρ is the specific volume). Convexity of the isentropes is guaranteed by a positive value of the fundamental derivative (Menikoff and Plohr, 1989); see Ibáñez et al. (2013) and Ibáñez et al. (2015) for a generalization of this result to RHD and RMHD, respectively. However, whereas in unmagnetized fluids non-convexity is associated to complex equations of state, the equations of MHD are of non-convex nature because at degenerate states magnetosonic waves change from genuinely nonlinear to linearly degenerate waves (see Brio and Wu, 1988, Antón et al., 2010, for classical and relativistic MHD, respectively).
The fact that the MHD equations form a non-strictly hyperbolic, non-convex system makes them considerably more complex than the hydrodynamic ones. Shock waves in hydrodynamic flows are regular, while MHD flows admit non-regular or intermediate shocks (see Torrilhon, 2003, for the corresponding definitions). Among these intermediate shocks are the so-called overcompressive shocksFootnote 2 and switch-on/off shocks, where the magnetic field vanishes on one side of the wave.Footnote 3 Intermediate shocks are also associated with rarefactions in the so-called compound waves (Torrilhon, 2003). They are related to the question of the existence and the uniqueness of solutions of some Riemann problems. However, there is a ongoing controversy about the significance of non-regular shocks (and compound waves) in MHD (see Takahashi and Yamada, 2014, for an up-to-date overview of the problem).
3.2.4 Divergence-free constraint
The solutions of the system of classical and relativistic MHD must satisfy the divergence-free constraint for the magnetic field derived from the temporal component of Eq. (6). The evolution system guarantees the fulfillment of this constraint for an initially divergence-free magnetic field at all later times, but to satisfy the constraint in numerical simulations of MHD flows poses a challenge. We shall come back to this point later, when discussing specific numerical methods.
4 Grid-based Methods in RHD
The application of high-resolution shock-capturing (HRSC) methods caused a revolution in numerical RHD. These methods satisfy in a quite natural way the basic properties required for any acceptable numerical method: (i) high order of accuracy, (ii) stable and sharp description of discontinuities, and (iii) convergence to the physically correct solution. Moreover, HRSC methods are conservative, and because of their shock capturing property discontinuous solutions are treated both consistently and automatically whenever and wherever they appear in the flow.
HRSC methods are built following two possible strategies, namely finite volume (FV) and finite difference (FD) methods. Both strategies rely on a conservative form of the discretized equations. However, whereas FD methods are based on the differential form of the conservation equations and evolve point values of the state vectors in time, FV methods utilize the integral form of the conservation laws and cell averaged values. This difference has implications for the algorithms that have been developed following both strategies.
In FV methods, the numerical fluxes (i.e., the functions that govern the time evolution of the corresponding state vectors) are considered as an approximation to the time-averaged true fluxes. They are obtained solving in a variety of ways (e.g., Riemann solvers, flux formulas) the Riemann problems defined at each numerical interface. This restriction in the interpretation of the numerical fluxes is eased in FD methods leading to a wider set of methods.
The difference between FV and FD methods manifests itself also in the use of different spatial interpolation strategies. Although the division between both classes of methods is not strict in this respect, most RHD codes based on FV methods achieve second order spatial accuracy by employing linear interpolation and slope limiters, which leads to TVD (total variation diminishing) algorithms. The piecewise parabolic method (PPM) of Colella and Woodward (1984), using parabolas for cell reconstruction, has an accuracy higher than second order but it is not TVD. Most FD methods rely on more modern (and higher order) ENO (essentially non-oscillatory) schemes, which use adaptive stencils to reconstruct the variables at the desired grid locations from the corresponding point values. ENO schemes can be employed also in FV methods, but because they require multidimensional reconstruction they have not been employed in RHD codes.
While we present the fundamentals of HRSC methods in Section 8.3, we review specific ingredients used in modern numerical RHD codes based on HRSC methods in this section.
4.1 Relativistic Riemann solvers
4.1.1 Solvers based on the exact solution of the relativistic Riemann problem
Martí and Müller (1996) used the procedure discussed in Section 8.5 to construct an exact Riemann solver, which they then incorporated in an extension of the PPM method (Colella and Woodward, 1984) for purely 1D RHD (i.e., in the absence of transverse velocities). In their relativistic PPM method numerical fluxes are calculated according to
where UL and UR are approximations of the state vector at the left and right side of a cell interface obtained by a second-order accurate interpolation in space and time, and URP(0; UL, UR) is the solution of the Riemann problem defined by the two interpolated states at the position of the initial discontinuity.
The two-shock approximate Riemann solver is obtained from a relativistic extension of Colella’s method (Colella, 1982) for classical fluid dynamics, where it has been shown to properly handle shocks of arbitrary strength (Colella, 1982; Woodward and Colella, 1984). In order to construct Riemann solutions in the two-shock approximation one analytically continues shock waves towards the rarefaction side (if present) of the cell interface instead of using an actual rarefaction wave solution. Balsara (1994) developed an approximate relativistic Riemann solver of this kind by solving the jump conditions in the oblique shocks’ rest frames in the absence of transverse velocities, after appropriate Lorentz transformations, although it was only tested for purely 1D flows. Dai and Woodward (1997) developed a similar Riemann solver based on the jump conditions across oblique shocks that is more efficient.
Wen et al. (1997) developed a first-order code for 1D RHD combining Glimm’s random choice method (Glimm, 1965; Chorin, 1976) — using an exact Riemann solver (Martí and Müller, 1994) — with standard FD schemes. Cannizzo et al. (2008) extended the method of Wen et al. to 1D problems involving transversal flows using the exact Riemann solver in Pons et al. (2000) and Rezzolla et al. (2003). Finally, Mignone et al. (2005b) implemented and tested the two-shock relativistic Riemann solver for arbitrary initial transverse velocities and incorporated it into the RHD module of the FLASH code.
4.1.2 Roe-type relativistic solvers
Linearized Riemann solvers are based on the exact solution of Riemann problems of a modified system of conservation equations obtained by a suitable linearization of the original system. This idea was put forward by Roe (1981), who developed a linearized Riemann solver for the equations of ideal (classical) gas dynamics. Eulderink (1993) and Eulderink and Mellema (1995) extended Roe’s Riemann solver to the general relativistic system of equations in arbitrary spacetimes. Eulderink used a local linearization of the Jacobian matrices of the system fulfilling the properties demanded by Roe in his original paper. Let \(\mathcal{B} = \partial {\bf{F}}/\partial {\bf{U}}\) be the Jacobian matrix associated with one of the fluxes F of the original system, and U the vector of unknowns. Then, the locally constant matrix \(\tilde{\mathcal{B}}\), depending on UL and UR (the left and right state defining the local Riemann problem) must have the following four properties:
-
1.
It constitutes a linear mapping from the vector space U to the vector space F.
-
2.
As UL → UR → U, \(\tilde{\mathcal{B}}\left( {{{U}_{L}},{{U}_{R}}} \right)\to \mathcal{B}\left( U \right)\).
-
3.
For any UL, UR, \(\tilde{\mathcal{B}}\left( {{{U}_{L}},{{U}_{R}}} \right)\left( {{{U}_{R}},{{U}_{L}}} \right)=F\left( {{{U}_{R}}} \right)-F\left( {{{U}_{L}}} \right)\).
-
4.
The eigenvectors of \(\tilde{\mathcal{B}}\) are linearly independent.
Conditions 1 and 2 are necessary to recover smoothly the linearized algorithm from the nonlinear one. Condition 3 (supposing 4 is fulfilled) ensures that if a single discontinuity is located at the interface, then the solution of the linearized problem is the exact solution of the nonlinear Riemann problem.
Once a matrix, \(\tilde{\mathcal{B}}\), satisfying Roe’s conditions has been obtained for every cell interface, the numerical fluxes are computed by solving the locally linear system. Roe’s numerical flux is then given by
with
where \({\tilde \lambda ^{(p)}},\;{{\bf{\tilde r}}^{(p)}}\), and \({{\bf{\tilde l}}^{(p)}}\) are the eigenvalues and the right and left eigenvectors of \(\tilde{\mathcal{B}}\), respectively (m is the number of equations of the system).
Roe’s linearization for the relativistic system of equations in a general spacetime can be expressed in terms of the average state (Eulderink, 1993; Eulderink and Mellema, 1995)
with
and
where g is the determinant of the metric tensor gβν. The role played by the density ρ in case of the Cartesian non-relativistic Roe solver as a weight for averaging, is taken over in the relativistic variant by k, which apart from geometrical factors tends to ρ in the non-relativistic limit. A Riemann solver for special relativistic flows and the generalization of Roe’s solver to the Euler equations in arbitrary coordinate systems are easily deduced from Eulderink’s work. The results obtained in 1D test problems for ultrarelativistic flows in the presence of strong discontinuities and large gravitational background fields demonstrate the excellent performance of the Eulderink-Roe solver (Eulderink and Mellema, 1995).
Relaxing condition 3 above, Roe’s solver is no longer exact for shocks but still produces accurate solutions. Moreover, the remaining conditions are fulfilled by a large number of averages of the left an right states. The 1D codes described in Martí et al. (1991) (RHD, test-fluid approximation of GRHD) and Romero et al. (1996) (dynamical GRHD) use Eq. (19) with an arithmetic average of the primitive variables at both sides of the interface to compute the numerical fluxes.
Roe’s original idea has been exploited in the local characteristic approach (see, e.g., Yee, 1989a), which relies on a local linearization of the system of equations by defining at each cell a set of characteristic variables that obey a system of uncoupled scalar equations. This approach has proven to be very successful, because it allows for the extension of scalar nonlinear methods to systems in both FV and FD methods. The codes cited in the previous paragraph are examples of FV methods based on the local characteristic approach, while examples of FD methods based on this approach are those developed by Marquina et al. (1992) and Dolezal and Wong (1995), both using high-order reconstructions (PHM Marquina et al., 1992; ENO Dolezal and Wong, 1995) of the numerical characteristic fluxes.
The 2D RHD code developed by Martí (1994; 1997) and its 3D extensions GENESIS and Ratpenat can be cast as FV schemes based on the local characteristic approach. More details about the computation of the numerical fluxes in these codes will be given in Section 4.2.
Also based on a local linearization of the RHD equations are the relativistic Riemann solvers developed by Falle and Komissarov (1996) relying on previous work by Falle (1991). Instead of starting from the conservative form of the hydrodynamic equations, one can use a primitive-variable formulation in quasi-linear form
where V is any set of primitive variables. Using a local linearization of the above system one obtains a solution of the Riemann problem and from that the numerical fluxes needed to advance a conservation form of the equations in time.
Falle and Komissarov (1996) have considered two different algorithms to solve the local Riemann problems in RHD by extending the methods devised in Falle (1991). In the first algorithm, the intermediate states of the Riemann problem at both sides of the contact discontinuity, VL* and VR*, are obtained by solving the system
where \({\bf{r}}_{\rm{L}}^ - \) is the right eigenvector of \(\mathcal{A}({{\bf{V}}_{\rm{L}}})\) associated with sound waves moving upstream and \({\bf{r}}_{\rm{R}}^ + \) is the right eigenvector of \(\mathcal{A}({{\bf{V}}_{\rm{R}}})\) of sound waves moving downstream. The continuity of pressure and of the normal component of the velocity across the contact discontinuity allows one to obtain the wave strengths bL and bR from the above expressions, and hence the linear approximation to the solution of the Riemann problem, VFK(VL, VR).
In the second algorithm proposed by Falle and Komissarov (1996), a linearization of system (24) is obtained by constructing a constant matrix \(\mathcal{A}({{\bf{V}}_{\rm{L}}},{{\bf{V}}_{\rm{R}}}) = \mathcal{A}({\textstyle{1 \over 2}}({{\bf{V}}_{\rm{L}}} + {{\bf{V}}_{\rm{R}}}))\). The solution of the corresponding Riemann problem is that of a linear system with matrix \(\tilde{\mathcal{A}}\), i.e.,
or, equivalently,
with
where \({\tilde \lambda ^{(p)}},\;{{\bf{\tilde r}}^{(p)}}\), and \({{\bf{\tilde l}}^{(p)}}\) are the eigenvalues, and the right and left eigenvectors of \(\tilde{\mathcal{A}}\), respectively (p runs from 1 to the number of equations of the system).
In both algorithms, the final step involves the computation of the numerical fluxes for the conservation equations
4.1.3 Relativistic HLL and HLLC methods
Schneider et al. (1993) proposed to use the method of Harten, Lax and van Leer (HLL hereafter Harten et al., 1983) to integrate the equations of RHD. This method avoids the explicit calculation of the eigenvalues and eigenvectors of the Jacobian matrices and is based on an approximate solution of the original Riemann problems with a single intermediate state
where aL and aR are lower and upper bounds for the smallest and largest signal velocities, respectively. The intermediate state U* is determined by requiring consistency of the approximate Riemann solution with the integral form of the conservation laws in a grid cell. The resulting average of the Riemann solution between the slowest and fastest signals at some time is given by
and the numerical flux vector by
where
An essential ingredient of the HLL method are good estimates for the smallest and largest signal velocities. In the non-relativistic case, Einfeldt (1988) proposed calculating them based on the smallest and largest eigenvalues of the Jacobian matrix of the system. The HLL scheme with Einfeldt’s recipe is a very robust scheme for the Euler equations and possesses the property of being positively conservative, i.e., the scheme is conservative, and the internal energy and density remain positive during the flow’s evolution. In the relativistic case, several estimates of the limiting characteristic wavespeeds have been proposed which rely on the 1D relativistic addition of velocities. For example, Schneider et al. (1993) used in their 1D simulations the estimates
where \(\bar v\) and \({\bar c_s}\) are the fluid velocity and the sound speed, respectively. The bar denotes some average (arithmetic or Roe-like) between the corresponding left and right states. Duncan and Hughes (1994) and Hughes et al. (2002) performed multidimensional simulations with a wave speed estimate based on the 1D relativistic addition of velocities formula applied to the individual components of the velocities. Del Zanna and Bucciantini (2002) generalized the method of Schneider et al. to multidimensional RHD, the estimates of the limiting characteristic wavespeeds being based on the multidimensional relativistic addition of velocities.
Underestimating the signal velocities may introduce instabilities or entropy violating shocks, because the numerical domain of dependence does not completely cover that of the true solution. One way to prevent these undesired effects, is e.g., to define the wave speeds as
This overestimate of the signal speeds, however, gives rise to a larger numerical dissipation, and the resulting HLL scheme leads to the Lax-Friedrichs scheme (see Section 4.2.1), which is very dissipative. Finally, in the relativistic case, the speed of light is an absolute limit, i.e., one can also define the wave speeds according to
Nowadays the relativistic HLL method is one of the most popular Riemann solvers in RHD codes; see Del Zanna and Bucciantini (2002), RAM, WHAM, RENZO, and RAMSES.
The HLL method is exact for single shocks and it is very robust. However, it is also very dissipative, especially at contact discontinuities. In the HLLC method (Toro et al., 1994) the contact discontinuity in the middle of the Riemann fan is also captured in an attempt to reduce the dissipation of the HLL method across contacts. Mignone and Bodo (2005) extended the HLLC method to 1D, 2D and 3D RHD and incorporated it in the RHD module of the PLUTO code. In the HLLC approximate Riemann solver, the solution of the Riemann problem reads
where a* is the (constant) speed of the contact discontinuity separating the L* and R* intermediate states. Consistency of the approximate Riemann solution with the underlying conservation laws in a grid cell results in the relations:
and
where FL*,R* is the flux associated with the intermediate state UL*R* (note that, in general, FL*,R* = F(UL*,R*)), and
and
are the intermediate state in the original HLL method and its associated flux, respectively.
In two dimensions, the consistency relations (38) and (39) together with the continuity of pressure and normal velocity across the contact wave provide ten conditions to resolve the two intermediate states. In order to reduce the number of unknowns and to have a well-posed problem, τL*,R* and FL*,R* are defined in terms of the ten unknowns DL*,R*, \(v_{{{\rm{L}}_{\ast}},{{\rm{R}}_{\ast}}}^x,S_{{{\rm{L}}_{\ast}},{{\rm{R}}_{\ast}}}^x,S_{{{\rm{L}}_{\ast}},{{\rm{R}}_{\ast}}}^y\), pL*,R*, and the speed of the contact discontinuity a*. The latter follows from the condition \({a_\ast} = v_{{{\rm{L}}_\ast},{{\rm{R}}_\ast}}^x\), and the intercell numerical flux is given by
The HLLC solver has been implemented in the relativistic code of Matsumoto et al. (2012), and also in RENZO, AMRVAC and RAMSES.
4.2 Flux formulas
In this category we include numerical flux functions that are not obtained from the solution of specific (exact or approximate) Riemann problems, although they can be interpreted and used in that way. Given their popularity in numerical RHD, we will restrict our discussion to the Lax-Friedrichs and the Marquina flux formulas here.
4.2.1 Lax-Friedrichs flux formula
The Lax-Friedrichs scheme (Lax, 1954) is among the most known FD schemes. When applied to the linear advection equation, ∂u/∂t + a∂u/∂x = 0, the scheme reads
where a is the constant signal propagation speed. It can be cast in conservation form by defining the numerical flux
In the nonlinear case, a suitable definition of the Lax-Friedrichs (LF) numerical flux is
with
where f′(u) is the derivative of f with respect to u. A less dissipative formulation is the local Lax-Friedrichs (LLF) scheme, the numerical flux being given by
with
For systems of conservation laws, conservative schemes can be built based on the numerical fluxes defined by Eqs. (45) or (47) applied either directly to the equations in conservation form or to the characteristic equations (within the local characteristic approach, Section 4.1.2).
Lax-Friedrichs flux formulas are nowadays widely used in RHD codes. Dolezal and Wong (1995) used the LLF flux in combination with ENO-FD schemes both for the characteristic fields (following the local characteristic approach) or directly for the conserved variables. Del Zanna and Bucciantini (2002) implemented a version of the LLF flux for the conserved equations in combination with CENO (convex ENO) interpolation routines. Lucas-Serrano et al. (2004) tested the performance of the LLF flux with piecewise parabolic and piecewise hyperbolic reconstructions. RAM allows for the use of the LLF flux for both FV and FD methods (in this last case together with WENO reconstruction of the characteristic fluxes). RENZO exploits the LLF flux as an alternative for FV methods. The RHD module of AMRVAC was tested and applied to a GRB model in Meliani et al. (2007), the discretization relying on a TVDLF type method (Yee, 1989b; Tóth and Odstrčil, 1996) based on the LLF fux formula.
The Lax-Friedrichs flux is also at the heart of the NOCD (non-oscillatory central differencing) schemes (see Section 8.3) implemented in COSMOS and tested in RHD calculations (Anninos and Fragile, 2003).
4.2.2 Marquina flux formula
Godunov-type schemes are indeed very robust in most situations although they fail on occasions (Quirk, 1994). Motivated by the search for a robust and accurate approximate Riemann solver that avoids these common failures, Donat and Marquina (1996) extended to systems a numerical flux formula first proposed by Shu and Osher (1989) for scalar equations. In the scalar case and for characteristic wave speeds which do not change sign at the given numerical interface, Marquina’s flux formula is identical to Roe’s flux. Otherwise, the scheme switches to the more viscous, entropy satisfying LLF scheme (Shu and Osher, 1989).
In the case of systems, the combination of Roe and LLF solvers is carried out in each characteristic field after the local linearization and decoupling of the system of equations Donat and Marquina (1996). However, contrary to Roe’s and other linearized methods, the extension of Marquina’s method to systems is not based on any averaged intermediate state. In Marquina’s flux formula the lateral local characteristic variables and fluxes are calculated, for given left and right states, according to:
for p = 1, 2 …, m, where m is the number of equations of the system. Here l(p)(UL) and l(p)(UR), are the (normalized) left eigenvectors of the Jacobian matrix \(\mathcal{B}\) of the system of equations in conservation form, calculated for the left and right states UL and UR, respectively.
Let λ(1)(UL), …, λ(m)(UL) and λ(1)(UR), …, λ(m)(UR) be the corresponding eigenvalues. For every k = 1,…, m, one then proceeds as follows:
-
If λ(k)(U) does not change sign in [UL, UR], the scalar scheme is upwind and the numerical flux is calculated according to the relevant characteristic information:
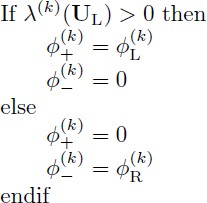
-
Otherwise, the scalar scheme is switched to the more viscous LLF scheme:
$$\matrix{ {{\alpha ^{(k)}} = \max \{ \vert{\lambda ^{(k)}}({{\bf{U}}_{\rm{L}}})\vert,\vert{\lambda ^{(k)}}({{\bf{U}}_{\rm{R}}})\vert\} } \cr {\phi _ + ^{(k)} = (\phi _{\rm{L}}^{(k)} + {\alpha ^{(k)}}\omega _{\rm{L}}^{(k)})/2} \cr {\phi _ - ^{(k)} = (\phi _{\rm{R}}^{(k)} - {\alpha ^{(k)}}\omega _{\rm{R}}^{(k)})/2} \cr } $$Marquina’s flux formula is then given by
$${{\bf{\hat F}}^{\rm{M}}} = \sum\limits_{p = 1}^m {\left({\phi _ + ^{(p)}{{\bf{r}}^{(p)}}({{\bf{U}}_{\rm{L}}}) + \phi _ - ^{(p)}{{\bf{r}}^{(p)}}({{\bf{U}}_{\rm{R}}})} \right)},$$(49)where r(p)(UL) and r(p)(UR) are the right (normalized) eigenvectors of the Jacobian matrices \(\mathcal{B}({{\bf{U}}_{\rm{L}}})\) and \(\mathcal{B}({{\bf{U}}_{\rm{R}}})\), respectively.
Marquina flux formula is nowadays widely used in RHD codes. Martí et al. (1995, 1997) implemented a version that applies the LLF flux to all characteristic fields in their 2D FV RHD code. This modified Marquina’s flux formula (MMFF) is also implemented in the 3D RHD codes GENESIS and Ratpenat, and in the code of Mizuta et al. (2001, 2004), the RAM code, and the RENZO code. In all these cases FV methods are used.
4.3 Spatial reconstruction
No special contributions from numerical RHD concern the strategies of spatial reconstruction, i.e., techniques developed for general hyperbolic systems of conservation laws are carried over to RHD.
In HRSC methods, the spatial order of accuracy is increased by interpolating the approximate solution between grid points to produce more accurate numerical fluxes. In FV schemes, this is achieved by substituting the mean values by better representations of the true flow at the left and right of cell interfaces as initial data for Riemann problems. The interpolation algorithms have to preserve the TV-stability of the algorithm. This is usually achieved by using linear interpolation and slope limiters, leading to TVD schemes. PPM (Colella and Woodward, 1984) uses parabolas for cell reconstruction and specific monotonicity constraints that keep the solution free of numerical oscillations. Experience has shown that the approach where one first recovers the primitive variables (see Section 4.6) from averaged conserved ones and then reconstructs the primitive variables is numerically more robust than the reverse approach. Hence, most of the relativistic conservative codes reconstruct primitive variables, like e.g., density, pressure, and the spatial components of the four velocity.
In FD schemes, the standard approach relies on the use of ENO schemes based on adaptive stencils to reconstruct variables (typically fluxes) at cell interfaces from point values. Contrary to TVD schemes, ENO schemes do not degenerate to first-order accuracy at extreme points but achieve the same high-resolution (third to fifth order) everywhere. We also note that there are ENO schemes adapted to FV methods.
4.3.1 Piecewise linear reconstruction and slope limiters
Within a numerical cell i a piecewise linear function of the form
with xi−1/2 < x < xi+1/2 is constructed for the quantity a from the corresponding cell averages. The quantity \(s_i^n\) is the linear slope for cell i. Note that according to the definitions of xi and xi±1/2, the linear reconstruction of a preserves its average value \(a_i^n\) within the cell. The idea to use piecewise linear slopes for cell reconstruction in combination with slope limiters is due to van Leer (1973, 1974, 1977b, a, 1979). Among the most popular slope limiters are the following:
-
$$s_i^n = {1 \over {\Delta x}}\min \bmod (a_i^n - a_{i - 1}^n,a_{i + 1}^n - a_i^n),$$(51)
where the minmod function of a set of arguments selects the one that is smaller in modulus if all of them have the same sign, or is otherwise zero.
-
MC (monotonized central-difference limiter; van Leer, 1977a)
$$s_i^n = {1 \over {\Delta x}}\text{minmod} \left({{{a_{i + 1}^n - a_{i - 1}^n} \over 2},2(a_i^n - a_{i - 1}^n),2(a_{i + 1}^n - a_i^n)} \right).$$(52) -
VAN LEER (van Leer, 1974):
$$s_i^n = {2 \over {\Delta x}}{{\max (0,(a_i^n - a_{i - 1}^n)(a_{i + 1}^n - a_i^n))} \over {a_{i + 1}^n - a_{i - 1}^n}}$$(53)
The effect of the minmod function is, on one hand, to guarantee linear slopes within cells that avoid the generation of spurious extrema at cell interfaces, and on the other, a vanishing slope at extrema (reducing the accuracy of the method to first order at these points). The MC limiter results in somehow steeper slopes than the pure MINMOD limiter, while the slopes of the VAN LEER limiter are intermediate to those obtained with the MINMOD and MC limiters.
Piecewise linear reconstructions have been widely used in RHD codes. Schneider et al. (1993) used piecewise linear reconstruction of the primitive variables (baryonic number, pressure and velocity components) together with the MINMOD slope limiter in their FV algorithm based on the relativistic HLL scheme. Duncan and Hughes (1994) and Hughes et al. (2002) employed piecewise linear reconstruction of the conserved variables within each cell. Falle and Komissarov (1996) used piecewise linear reconstruction within cells based on the gradients in the adjacent cells and applied a slope limiter different from MINMOD. The variables chosen for reconstruction were the proper rest-mass density, the pressure and the spatial components of the four-velocity. Also based on a linear interpolation within cells (and the MINMOD slope limiter) is the reconstruction procedure (applied in this case to the density, pressure and velocity components) in the code of Mizuta et al. (2004). The MUSCL-Hancock scheme (implemented in PLUTO and in the relativistic extension of RAMSES) and the PLM method implemented in the relativistic extension of RAMSES rely on piecewise linear reconstruction, too.
The RAM code utilizes a linear interpolation procedure in two of its implemented schemes, called U-PLM and F-PLM. In the first (FV) scheme, the reconstruction is performed on the primitive variables. Pressure and proper rest-mass density are reconstructed directly, whereas velocities are reconstructed using a combination of the reconstruction of the three-velocity and the Lorentz factor. For all variables, the slope limiter is a generalized MINMOD slope limiter according to which
The more diffusive usual MINMOD limiter results when θ = 1, whereas the MC limiter is recovered for θ = 2. Zhang and MacFadyen (2006) usually use θ = 1.5. In the (FD) F-PLM scheme the same reconstruction and limiter (the averaged values substituted by the corresponding point values) are used, but applied to the characteristic fluxes. The same reconstruction procedures are implemented in the HLL-PLM and F-PLM schemes in the RENZO code.
The AMRVAC code incorporates more modern limiters, like Koren and its generalizations (see Keppens et al., 2012, and references therein), which achieve third order accuracy on smooth profiles.
4.3.2 Piecewise parabolic reconstruction
The piecewise parabolic interpolation algorithm described in Colella and Woodward (1984) gives monotonic conservative parabolic profiles of variables within a cell. In the (1D) relativistic version of PPM (Martí and Müller, 1996), the original interpolation algorithm is applied to cell averaged values of the primitive variables (pressure, proper rest-mass density, 1D fluid velocity), which are obtained from cell averaged values of the conserved quantities. For each cell i, the quartic polynomial with cell averaged values ai−2, ai−1, ai, ai+1, and ai+2 (where a = ρ, p, v) is used to interpolate the structure inside the cell. In particular, the values of a at the left and right interface of the cell, aL,i and aR,i, are obtained in this way (interpolation step). Up to this point, the reconstructed values are continuous at cell interfaces, however these reconstructed values can be modified near contact discontinuities to produce narrower jumps (contact steepening), and at strong shocks to avoid spurious oscillations (flattening). Finally, the interpolated values are modified to force the parabolic profile inside each cell (uniquely determined by aL,i, aR,i and ai) to be monotonic (monotonization).
This piecewise parabolic reconstruction is used in the 2D RHD code developed by Martí et al. (1994; 1997), GENESIS and in the Ratpenat code. It is implemented also in the multidimensional version of the relativistic PPM method developed by Mignone et al. (2005b) and in the RHD module of the FLASH code. Finally, it is also used in RAM (U-PPM scheme), RENZO, and AMRVAC.
4.3.3 ENO schemes
The interpolation algorithms discussed so far use fixed stencils to reconstruct the solutions inside numerical cells. However, fixed stencil interpolation of second or higher order accuracy is necessarily oscillatory near a discontinuity. Hence the need to use slope limiters (reducing the order of the method to first order at jumps). The ENO idea proposed by Harten et al. (1987) is the first successful attempt to obtain a uniformly high order accurate, yet essentially non-oscillatory interpolation (i.e., the magnitude of the oscillations decays as O(Δxk), where k is the order of accuracy) for piecewise smooth functions. The idea behind the ENO schemes is the use of adaptive stencils for cell reconstruction, which can vary from cell to cell in order to avoid including the discontinuous cell in the stencil, if possible. To this end a kth-order accurate ENO scheme involves a stencil of k + 1 consecutive points including the cell (or interface) to be reconstructed, such that the primitive of the interpolating function is the smoothest in this stencil compared to other possible stencils.
Since the publication of the original work of Harten et al. (1987), they and many other researchers have improved the methodology and expanded the area of its application (see Shu, 1997, for a review). The original ENO schemes constructed in Harten et al. (1987) were applied to cell averages (FV schemes) obtaining left and right states of variables at cell interfaces as initial states for Riemann solvers. Hence, a reconstruction procedure is needed to recover point values from cell averages to the correct order, which can be rather complicated, especially in multidimensional problems. Shu and Osher (1988, 1989) developed ENO schemes to be carried out on numerical fluxes (FD scheme) in combination with TVD-RK methods for time advance. For stability reasons, it is important that upwinding is used in constructing the fluxes. One possibility is to use the flux splitting approach where one reconstructs separately the parts of the flux with positive and negative derivatives.
Liu et al. (1994) proposed an improved fourth-order accurate weighted ENO (WENO) scheme utilizing a weighted combination of several possible stencils instead of just one stencil. This improves the accuracy of the scheme without loosing the essentially non-oscillatory property close to discontinuities. An even more accurate scheme is the modified fifth-order WENO scheme of Jiang and Shu (1996). A more recent variant is the CENO reconstruction (Liu and Osher, 1998), which has third-order accuracy in smooth regions but reduces to linear reconstruction or even to firstorder (by using minmod-type limiters) near discontinuities. Finally, ENO schemes for hyperbolic conservation laws can be applied component-wise or characteristic-wise. In general, component by component versions of ENO schemes are simple and cost effective. They work reasonably well for many problems, especially when the order of accuracy is not high (second or sometimes third order). However, for more demanding problems, or when the order of accuracy is high, the more costly but more robust characteristic-wise schemes are preferred (Shu, 1997).
Dolezal and Wong (1995) followed the ENO strategy in their RHD code and applied the ENO reconstruction on numerical fluxes (previously splitted according to the Lax-Friedrichs splitting) both component-wise CW-ENO-LF and CW-ENO-LLF schemes) and characteristic-wise (CH-ENO-LF, CH-ENO-LLF). Del Zanna and Bucciantini (2002) developed an RHD code based on the CENO reconstruction of the point values of primitive variables in combination with approximate Riemann solvers. The RAM and RENZO codes use fifth-order WENO reconstruction of the fluxes according to a characteristic-wise flux-splitting FD scheme. The RENZO code provides CENO reconstruction of primitive variables (in a FV scheme), too. In their FV RHD code WHAM, Tchekhovskoy et al. (2007) implemented a modified WENO scheme that avoids field-by-field decomposition by adaptively reducing to 2-point stencils near discontinuities for a more accurate treatment of shocks, and the excessive reduction to low-order stencils as in standard WENO schemes.
4.4 Non-conservative finite-difference schemes
4.4.1 Flux-corrected transport method
The flux-corrected transport (FCT) algorithm of Boris and Book (1973), Boris et al. (1975), and Boris and Book (1976) was constructed to solve scalar advection equations numerically. As early as in 1982, Yokosawa et al. (1982) applied FCT techniques to describe the dynamical interaction of a hypersonic (relativistic) beam with a homogeneous ambient medium, in the context of extragalactic jets. However, it is in the context of heavy ion collisions (Martí and Müller, 2003) where relativistic extensions of FCT algorithms have been widely used. Schneider et al. (1993) compared a code based on the relativistic HLL method (see Section 4.1.3) with two FCT algorithms (SHASTA and LCPFCT). Further comparisons between these two strategies were performed by Rischke et al. (1995a, b). In the FCT algorithms, each hydrodynamic equation is treated separately as an advection equation for the corresponding conserved quantity with proper source terms. Relativistic FCT algorithms built in this way have been able to handle flows with discontinuities and large Lorentz factors although the results are in general poorer than those obtained with HLL or other Godunov-type methods.
4.4.2 Artificial viscosity methods
May and White (1966, 1967) were the first to develop a numerical code to solve the RHD equations. With their time-dependent FD Lagrangian code they simulated the adiabatic spherical collapse in general relativity. Artificial viscosity (AV) terms were included in the equations to damp the spurious numerical oscillations at shock waves. The idea of modifying the hydrodynamic equations by introducing an artificial dissipative mechanism near discontinuities mimicking a physical viscosity (AV schemes) was originally proposed by von Neumann and Richtmyer (1950) and Richtmyer and Morton (1967) in the context of the classical Euler equations. The form and strength of the AV terms are such that the shock transition becomes smooth, extending over a small number of numerical cells.
This generic recipe has been used with minor modifications in conjunction with standard FD schemes in all numerical simulations employing May and White’s approach, and particularly in Wilson’s formulation of numerical RHD. Relying on an Eulerian explicit non-conservative FD code with monotonic transport and AV terms, Wilson (1972, 1979) and collaborators (Centrella and Wilson, 1984; Hawley et al., 1984) simulated for the first time relativistic flows in more than one spatial dimension.
Wilson’s formulation was widely used in the 1980s in numerous general relativistic scenarios including cosmology, multidimensional stellar collapse, and accretion onto compact objects (see, e.g., Font, 2008, for a review). However, despite its popularity it turned out to be unable to accurately describe extremely relativistic flows (Lorentz factors larger than 2; see, e.g., Centrella and Wilson, 1984). Norman and Winkler (1986) concluded that those large errors were mainly due to the way in which the AV terms were included in the numerical scheme in Wilson’s formulation. They proposed a reformulation of the difference equations with an artificial viscosity consistent with the relativistic dynamics of non-perfect fluids (consistent AV schemes). The strong coupling introduced in the equations by the presence of the viscous terms in the definition of relativistic momentum and total energy densities required an implicit treatment of the difference equations. Accurate results across strong relativistic shocks with large Lorentz factors in 1D were obtained in combination with adaptive mesh techniques. Artificial viscosity techniques in numerical RHD are reviewed in the book of Wilson and Mathews (2003).
Anninos and Fragile (2003) and Anninos et al. (2003) compared state-of-the-art AV schemes and high-order central schemes using Wilson’s formulation for the former class of schemes and a conservative formulation for the latter (NOCD scheme). Employing the 3D Cartesian code COSMOS, they found that earlier results for AV schemes in shock tube tests are improved thanks to the consistent implementation of the AV terms (see Sections 6.3.1 and 6.3.2). This does not hold, however, for the shock reflection test that cannot be simulated accurately beyond infall velocities 0. 95 (or 0. 99 by adjusting the AV parameters). Similar results are obtained with the traditional AV schemes implemented in COSMOS++, which is a FV code designed to solve the equations of GRMHD. The results improve when applying the eAV scheme. In this scheme one solves an extra equation for the total energy, which is used to substitute the solution obtained from the internal energy equation, depending on the accuracy of the results. We note here for completeness that COSMOS and COSMOS++ incorporate five different AV recipes — three scalar (von Neumann and Richtmyer, 1950; White, 1973) and two tensor ones (Tscharnuter and Winkler, 1979; Anninos et al., 2005).
4.5 Multidimensional schemes and time advance
Many modern HRSC methods for RHD use multistep algorithms for time advance. Codes in Martí et al. (1991); Martí et al. (1994); Falle and Komissarov (1996); Choi and Wiita (2010) and the NOCD scheme in COSMOS use standard predictor-corrector algorithms to achieve second-order accuracy in time. Other codes (Marquina et al., 1992; Dolezal and Wong, 1995; Martí et al., 1997; Del Zanna and Bucciantini, 2002; Lucas-Serrano et al., 2004) and GENESIS, RAM, PLUTO, RENZO, and Ratpenat rely on second and third-order TVD-RK time discretization algorithms developed in Shu and Osher (1988, 1989). These algorithms preserve the TVD property at every substep, although standard fourth- and fifth-order Runge-Kutta methods (Lambert, 1991) have been used, too (RAM, WHAM). Radice and Rezzolla (2012) employed a third-order strong-stability-preserving Runge-Kutta scheme (Gotlieb et al., 2009).
Other RHD codes exploit single-step, second-order algorithms. Codes based on relativistic extensions of the PLM Lamberts et al. (2013) and PPM methods (Martí and Müller, 1996; Mignone et al., 2005b; FLASH; Mignone et al., 2007; Morsony et al., 2007; Lamberts et al., 2013) achieve second-order accuracy in time by incorporating information of the domain of dependence of each interface during the time step to the states used in the solution of the Riemann problems (characteristic tracing). Of special interest by its simplicity, accuracy, and robustness is the MUSCL-Hancock scheme implemented in the HRSC method of Schneider et al. (1993), the code of Mignone and Bodo (2005), and in PLUTO, and in the TVDLF scheme (Yee, 1989b; Tóth and Odstrčil, 1996) of AMRVAC.
The codes developed on the basis of Wilson’s formulation (see Section 4.4.2) all rely on explicit fully-discrete schemes. Their accuracy is sensitive to the order and frequency of the updates composing a complete time cycle, specially in the highly relativistic regime. Hence, the sequence of steps is determined by a reasonable balance between accuracy and computational cost.
Codes using operator splitting apply the differential operators separately along coordinate directions and the integration of sources in successive steps according to Strang’s (Strang, 1968) prescription to preserve second-order accuracy (Martí et al., 1994; Eulderink, 1993; Eulderink and Mellema, 1995; Mignone and Bodo, 2005; Choi and Ryu, 2005), while codes based on Runge-Kutta methods (Dolezal and Wong, 1995; Martí et al., 1997; Aloy et al., 1999b; Lucas-Serrano et al., 2004; Zhang and MacFadyen, 2006; Tchekhovskoy et al., 2007; Mignone et al., 2007; Wang et al., 2008; Perucho et al., 2010) advance the spatial operators simultaneously (unsplit schemes). The code in Mignone et al. (2005b) uses Strang splitting for the source terms and the spatially unsplit fully corner-coupled method CTU (Colella, 1990) for the evaluation of the fluxes.
4.6 Equation of state and primitive variable recovery
The equations of RHD and RMHD are closed by means of an EOS relating the thermodynamic variables. For single component fluids (like those presented in Section 3.1) only three thermodynamic quantities are involved and an EOS of the form p = p(ρ, ε) is usually needed. For multiple component fluids the EOS depends on the densities (or mass fractions) of the species, i.e., additional continuity equations (including reactive terms if necessary) for all species must be added to the evolution system.
Early on most astrophysical simulations dealt with matter whose thermodynamic properties can be described by an ideal gas equation of state with constant adiabatic index. However, present day applications concerned with astrophysical jets, GRB, accretion flows onto compact objects and the evolution of relativistic stars require a more sophisticated, microphysical EOS for a proper description of the phenomena.
In the context of relativistic jets, Falle and Komissarov (1996), Komissarov and Falle (1998), Scheck et al. (2002), and Perucho and Martí (2007) considered a mixture of ideal relativistic Boltzmann gases (Synge EOS; Synge, 1957; Chandrasekhar, 1967), hence allowing for jets with general (i.e., e, e+, p) composition. Assuming plasma neutrality, only one parameter is needed to fix the composition, e.g., the mass fraction of the leptons, Xl. Using the Synge EOS instead of a constant adiabatic index EOS requires more computation time, because an iteration of the temperature, involving modified Bessel functions, has to be performed for each cell in every time-step to recover the primitive variables from the conserved ones (see below). To avoid this extra complexity, approximate expressions for the relativistic ideal gas EOS for single (Duncan et al., 1996; Sokolov et al., 2001; Mignone et al., 2005b; Ryu et al., 2006) and multiple component (Chattopadhyay and Ryu, 2009; Choi and Wiita, 2010) flows were proposed. Of particular interest are the approximate EOS proposed by Mignone et al. (2005b) (first used by Mathews, 1971; see also Meliani et al., 2004) and Ryu et al. (2006) which are consistent with Taub’s inequalityFootnote 4 at all temperatures. They have the correct classical and ultrarelativistic limiting values and differ from the exact ideal gas EOS by only up to a few percent in the relevant thermodynamic quantities.
A comprehensive discussion of the EOS used in the astrophysical scenarios mentioned above is beyond the scope of this review. However, it is worth mentioning that a general EOS causes no special problems for HRSC methods based on Riemann solvers. If the latter are based on the exact solution, one needs to implement the proper adiabats across rarefactions and shocks (Taub’s adiabat, see Section 8.5), while if they are based on the spectral decomposition of the Jacobian matrices one has to write the eigenvalues and eigenvectors in terms of the thermodynamic quantities (i.e., enthalpy, density, sound speed, and other thermodynamic derivatives) of the EOS. Donat et al. (1998) (see also Section 8.1) provided the eigenvalues, and the left and right eigenvectors of 3D RHD for a general EOS of the form p = p(ρ, ε), and Ryu et al. (2006) for an EOS of the form h = h(ρ, p). Finally, simpler Riemann solvers like HLL or those based on the LF flux formula can be used directly.
The situation described in the previous paragraph extends to the use of any convex EOS (see Section 3.2), for which a discontinuity in the initial state gives rise to at most one (compressional) shock, one contact, and one simple centered expansion fan, i.e., one wave per conservation equation. For a real gas, however, the EOS can be nonconvex. If that is the case, the character of the solution of the Riemann problem changes resulting in anomalous wave structures. In particular, the solution may be no longer unique, i.e., an initial discontinuity may give rise to multiple shocks, multiple contacts, and multiple simple centered expansion fans (see, e.g., Laney, 1998). In these situations, Riemann solvers based on the common Riemann problem break-out or on a local linearization of the system will obviously fail.
Conservative numerical schemes in both RHD and RMHD require a method to switch between conserved variables (D, Si, τ) and primitive variables (ρ, vi, p). The transformation from primitive to conserved variables has a closed-form solution (see Eqs. (11)–(13)), but the inverse transformation (conserved to primitive) requires the solution of a set of nonlinear equations that depends explicitly on the equation of state p(ρ, ε). In the RHD case, a function of pressure, whose zero represents the pressure of the physical state, can be obtained easily from Eqs. (11)–(13), (14) and the EOS:
with \({\rho _\ast}(\bar p)\) and \({\varepsilon _\ast}(\bar p)\) given by
and
where
and
The root of Eq. (55) can be obtained by means of a nonlinear root-finder (e.g., a 1D Newton-Raphson iteration). For an ideal gas with constant adiabatic index this procedure has proven to be very successful in a large number of tests and applications (Martí et al., 1991; Martí and Müller, 1996; Martí et al., 1997; Aloy et al., 1999b; Mizuta et al., 2004). One can approximate the derivative of f with respect to \(\bar p\) by (Aloy et al., 1999b)
where cs(ρ, ε) is the sound speed which can be computed efficiently for any EOS. This approximation tends to the exact derivative as one approaches the solution, and it is used together with the algorithm described above to recover the primitive variables in the codes GENESIS and Ratpenat.
Mignone et al. (2005b) proposed a similar procedure but for an EOS of the form h = h(p, ρ). The resulting nonlinear equation is again a function of the pressure, and reads in our notation:
This procedure is implemented in the relativistic module of FLASH. It is also used in the code of Choi and Wiita (2010), and specialized for an ideal gas equation in Mignone and Bodo (2005). Radice and Rezzolla (2012) proposed a function of the enthalpy which in our notation can be written as
whose zero is the physical enthalpy.
Although the above procedures are valid for a general equation of state, in the case of the Synge EOS, it is better to define another function of the pressure:
with \({w_\ast}(\bar p) = {\rho _\ast}(\bar p)(1 + {\varepsilon _\ast}(\bar p)) + \bar p\), and \({\rho _\ast}(\bar p)\) and \({\varepsilon _\ast}(\bar p)\) being given by Eqs. (56) and (57), respectively. \({T_\ast}(\bar p) \propto \bar p/{\rho _\ast}(\bar p)\), where the constant of proportionality is a function of the effective mass of the gas particles in the mixture. Finally, w(ρ, T) is the enthalpy density according to the Synge EOS. Alternative strategies were derived for approximations of the Synge EOS (Mignone et al., 2005b; Ryu et al., 2006; Mignone et al., 2007).
Dolezal and Wong (1995) solved an implicit equation for the rest mass density and a general EOS of the form p = p(ρ, ε), and Eulderink (1993), and Eulderink and Mellema (1995) developed several procedures to calculate the primitive variables for an ideal gas EOS with constant adiabatic index. One of their procedures is based on finding the physically admissible root of a fourth-order polynomial of a function of the specific enthalpy. The quartic can be solved analytically by the exact algebraic quartic root formula, but this computation is rather expensive. The root of the quartic can be found much more efficiently using a 1D Newton-Raphson iteration. Another procedure is based on the use of a six-dimensional Newton-Kantorovich method to solve the whole set of nonlinear equations.
Also for ideal gases with constant adiabatic index, Schneider et al. (1993) and Duncan and Hughes (1994), and Hughes et al. (2002) transform the system (11)–(13) (for zero magnetic field) and (14) algebraically into a fourth-order polynomial in the modulus of the flow speed that can be solved analytically (Choi and Ryu, 2005; Ryu et al., 2006) or by means of iterative procedures (Zhang and MacFadyen, 2006). The analytic solver seems to be more robust for large (i.e.,, ≳ 100) Lorentz factor flows (Bernstein and Hughes, 2009). Del Zanna and Bucciantini (2002) solve, instead, a six-order polynomial in the Lorentz factor.
4.7 Adaptive mesh refinement (AMR)
The underlying concepts and general strategies of adaptive mesh refinement (AMR) are summarized in Section 8.3.5. Here we discuss specific implementations of AMR for RHD. For general relativistic flows, see e.g., the Whisky code which has AMR capabilities based on Carpet.
The first application of AMR in the field of RHD was presented by Duncan and Hughes (1994). Their AMR algorithm was written by Quirk (1991, 1996), which is an outgrowth of the original work of Berger and Oliger (1984), Berger and Colella (1989), and Bell et al. (1994). In order for the AMR method to sense where further refinement is needed, Duncan and Hughes used the gradient of the laboratory frame mass density. The simulations were performed using only one level of refinement by a factor of 4 in both directions. The method was extended later to 3D by Hughes et al. (2002). Wang et al. (2008) have also implemented a variant of Berger’s AMR technique in their RHD code RENZO (see Table 1) that is adaptive in time and space, can handle curvilinear coordinates (cylindrical and spherical), has load-balancing functionality, and uses the standard message passing interface (MPI).
Further AMR simulations of relativistic flows were utilizing the FLASH code, which is a general purpose simulation tool for astrophysical flow including modules for RHD and AMR. The AMR module was adapted from PARAMESH, which is a block-structured AMR-package written in Fortran 90. Contrary to the AMR implementation of Berger and Oliger (1984); Berger and Colella (1989); Bell et al. (1994) PARAMESH does not allow patches (i) rotated relative to the coordinate axes, (ii) of arbitrary shape, (iii) to overlap, and (iv) being merged with other patches at the same refinement level whenever appropriate. These four properties provide a very flexible and memory-efficient strategy, but result in a very complex code, which is difficult to parallelize. Instead, PARAMESH uses a hierarchy of nested, logically Cartesian blocks that are aligned with the coordinate axes and typically have eight cells per dimension for a total of 8 cells per block, where d = 1, 2, or 3 is the dimensionality of the flow. The refinement is by a factor of two in each direction so that each block is either at the highest level or contains 2d children blocks. Leaf blocks are defined to be those blocks with no children, i.e., they are at the bottom of the tree. The basic data structure is then an oct-tree, quad-tree and binary-tree for 3D, 2D, and 1D problems, respectively. Flux conservation at patch boundaries is imposed by replacing fluxes computed at the coarser level with appropriate sums of fluxes at the finer level. Whether to refine or coarsen the grid is determined by calculating an approximate numerical second derivative of flow variables that can be specified at run time. FLASH handles parallelization with the MPI library and uses an estimate of the work per processor for load balancing.
Using the FLASH code, López-Cámara et al. (2013) performed 3D AMR simulations of long-duration gamma-ray burst jets inside massive progenitor stars (see also Section 2.2) The AMR components of FLASH are utilized also by the RHD code RAM which is designed to handle special relativistic flows in the context of GRB, too.
A novel, hybrid block-adaptive AMR strategy for solving sets of near-conservation laws in general curvilinear (orthogonal) coordinate systems was presented by van der Holst and Keppens (2007). This was a further step in the development of the AMRVAC code (Keppens et al., 2003) which is designed to integrate the equations of hydrodynamics and magnetohydrodynamics both in their classical and special relativistic form. The hybrid block-AMR scheme is based on individual grids with a pre-fixed number of cells instead of different-sized patches, but it relaxes the full oct-tree structure where a block that needs refinement triggers 2d subblocks when the grids are refined by a factor of two. Hence, it allows for incomplete block families (also called ‘leaves’), by incorporating the idea of the patch-based strategy of an optimal adjustment of the grid structure to dynamical features of interest. However, in the patch-based strategy this was accomplished at the expense of introducing unequally sized grids per level. On the other hand, the good cache performance of the tree block-based scheme is fully utilized. In their code, van der Holst and Keppens (2007) have also eliminated the possibility that patches residing on the same level can overlap, which is a natural choice for both the hybrid and full oct-tree. The up to now latest version in this development is the code MPI-AMRVAC (Keppens et al., 2012). Currently, it works with a pure block-quadtree or block-octree (also for curvilinear grids). The block size is (N + 2G)d, where N is the number of cells in each mesh block (which can be different along each coordinate direction), and G is the number of ghost cells on each lateral side. These parameters can be adjusted by the user at compile time, i.e., MPI-AMRVAC can handle larger stencil expressions easily, and has in a sense more flexibility than the 2d block size hardcoded in RAMSES (see below).
Another AMR code for simulating classical and relativistic hydrodynamics and MHD flows is PLUTO, which was originally designed for static grids (Mignone et al., 2007, 2009, 2010), but extended to more general grids by Mignone et al. (2012) to exploit block-structured AMR based on the Chombo library. The latter is a software package providing a distributed infrastructure for serial and parallel calculations over block-structured adaptively refined grids in multiple dimensions. Chombo follows the Berger and Rigoutsos (1991) strategy to determine the most efficient patch layout to cover the cells that have been tagged for refinement. In the MPI parallelized PLUTO — Chombo code, cells are tagged for refinement whenever a prescribed function of the conserved variables and of its derivatives exceeds a prescribed threshold.
De Colle et al. (2012a) developed Mezcal-SRHD an MPI parallelized AMR code for RHD. It uses oct-tree block-structured grid refinement. Different from other AMR codes, at any given time each position on the grid is covered by only one cell, i.e., there are no pointers between ‘parent’ and ‘sibling’. Furthermore, there are no ghost cells, usually present in other tree-AMR codes (e.g., Berger and Oliger, 1984; Khokhlov, 1998), attached to any of the blocks. The code employs a global time step common to all grid levels, which may cause some important computational overhead with respect to using a local time step, but avoids an important bottleneck for parallelization. Mezcal-SRHD has been used to simulate GRB dynamics and afterglow radiation.
A relativistic extension of the AMR hydrodynamics code RAMSES was presented by Lamberts et al. (2013). RAMSES uses a Cartesian grid, where cells are related in a recursive tree structure and grouped into blocks of 2d cells (d is the number of spatial dimensions), which share the same parent cell. Grid refinement is based on the gradient of the Lorentz factor. Prolongation is performed by second-order interpolation using a minmod limiter, while restriction involves computing block averages. To avoid failures in the restriction step in the case of nearly ballistic flows, the relativistic extension of RAMSES employs reconstruction of the specific internal energy rather than of the specific total energy. This method makes the numerical scheme non-conservative, but guarantees positivity of the pressure and subluminal speeds. The code was used to perform 2D simulations of gamma-ray binaries, which are systems composed of a massive star and a rotation-powered pulsar with a highly relativistic wind. The simulated models involve winds with a Lorentz factor up to 16 (Lamberts et al., 2013).
4.8 Summary of existing codes
Table 1 lists the multidimensional codes for RHD based on HRSC methods in chronological order, which rely both on FD and FV schemes, and summarizes the basic algorithms implemented in the codes (type of spatial reconstruction, Riemann solvers and flux formulas used, time advance and multidimensional schemes). The table only includes those codes specifically developed for RHD, and those GRHD codes for fixed spacetimes that were used or tested also in RHD. We also include the GRHD code for dynamical spacetimes Whisky, because it has been widely tested in RHD. COSMOS, AMRVAC, PLUTO, and FLASH are multi-purpose codes for computational astrophysics. Special attention is paid to the algorithms implemented in their corresponding relativistic modules. COSMOS++, RAISHIN, and TESS are RMHD codes, but they have been tested in RHD, too.
The codes Whisky, AMRVAC, PLUTO, and FLASH are publicly available and provide comprehensive on-line documentation. They can be downloaded from the corresponding webpages: Whisky, AMRVAC, PLUTO, and FLASH. AMRVAC is an AMR-offspring of the Versatile Advection Code (VAC, Tóth, 1996; VAC). The website AMRVAC hosts the development version of the code and points to the former code website MPI-AMRVAC, where some further information can be found that is unfortunatley not properly updated.
5 Grid-based Methods in RMHD
The success of HRSC methods in (classical and relativistic) hydrodynamics fostered their application to MHD, and more recently, to RMHD. In MHD two additional equations must be solved, which are the induction equation
and the divergence-free condition for the magnetic field
The enlarged set of MHD equations is harder to solve than that of HD, because the MHD equations possess additional families of waves and admit additional wave structures such as switch-on/off shocks and rarefactions, and compound waves (see Section 3.2). The MHD equations involve also degeneracies, i.e., they are no longer strictly hyperbolic. Finally, satisfying the divergence-free constraint for the magnetic field poses a numerical challenge. Hence, the development of HRSC methods for numerical MHD was slower than in classical computational fluid dynamics. In Brio and Wu (1988) extended the HRSC techniques based on approximate Riemann solvers to 1D MHD. They renormalized the eigenvectors of the MHD equations in order to use them in the degenerate cases and built a Roe-type Riemann solver for the 1D MHD equations. Later this line of research was extended to Godunov-type methods for multidimensional MHD (e.g., Zachary et al., 1994; Dai and Woodward, 1994a,b; Ryu et al., 1995).
Because the induction equation and the divergence-free condition are the same in both classical and relativistic MHD, the techniques to integrate the former one and to force the magnetic field to remain divergence free carry over from classical to relativistic MHD, i.e., respective numerical schemes were developed for classical MHD in parallel with those for RMHD. The most popular approaches are reviewed in Tóth (2000), and Mignone and Bodo (2008) and summarized in this section.
In the following we discuss the development of multidimensional RMHD codes based on HRSC techniques, an activity which took place mainly during the past decade. The structure of the discussion closely follows that of the previous Section concerned with HRSC methods in RHD.
5.1 Relativistic Riemann solvers
5.1.1 Relativistic solvers based on the exact solution of the Riemann problem
The procedure described in Section 8.6 and derived by Giacomazzo and Rezzolla (2006) to obtain the exact solution of the Riemann problem in RMHD can be used to construct an exact Riemann solver. However, no numerical code based on this approach has been developed yet. As Giacomazzo and Rezzolla discussed in a more recent paper (Giacomazzo and Rezzolla, 2007), the exact solver described in Giacomazzo and Rezzolla (2006) is computationally too expensive to be used in multidimensional codes.
5.1.2 Roe-type relativistic solvers
Roe-type Riemann solvers use as a key ingredient the spectral decomposition of the flux vector Jacobians of the system of equations in conservation form. In the case of RMHD, the spectral decomposition is done in covariant variables. After removing the unphysical waves (see Section 8.2), the eigenvectors are obtained in conserved variables using the corresponding variable transformations. The treatment of degenerate states requires some extra effort.
Komissarov (1999a) developed a linearized Riemann solver based on a primitive-variable formulation of the 1D RMHD system in quasilinear form, which is similar to the RHD Riemann solverB of Falle and Komissarov (1996) (see also Section 4.1.2). The 7-component right eigenvectors in primitive variables are obtained from the 10-component right eigenvectors in the augmented system of covariant variables. Unlike the Riemann solver B of Falle and Komissarov (1996), the RMHD Riemann solver does not make use of the left eigenvectors and the wave strengths which are needed to compute the fluid state at the numerical interface are obtained from the jump conditions at the (central) contact discontinuity. Komissarov’s Riemann solver, which has been implemented successfully in a multidimensional FV scheme, treats non-degenerate and degenerate states separately.
Independently, Balsara (2001a) presented a detailed discussion of the characteristic structure of the RMHD system in covariant variables and the algebraic transformations that are needed to obtain the physical eigenvectors in primitive as well as conserved variables. The resulting eigenvectors are input for both a TVD interpolation procedure that operates on the characteristic variables, and a linearized Riemann solver. Although Balsara discussed a multidimensional extension of his code in Balsara (2001a), he described and tested only a 1D version.
Koldoba et al. (2002) also described a 1D code for the RMHD system based on a linearized Roe-type Riemann solver. They presented the left and right eigenvectors of the system in covariant variables and the transformations that are required to obtain the numerical fluxes in conservation form together with a small set of 1D tests. As far as we know, no further (multidimensional) testing of the algorithm has been done.
Antón et al. (2010) (see also Section 8.2) presented a thorough analysis of the characteristic structure of the RMHD equations and a Riemann solver based on renormalized (i.e., valid for both non-degenerate and degenerate states) sets of left and right eigenvectors of the system in conserved variables (Full Wave Decomposition Riemann solver, FWD). They provided the matrix transformations (changes of variables) from the set of eigenvectors in covariant variables to the corresponding sets in (i) the reduced system of covariant variables and (ii) the conserved variables. Running a set of 1D and 2D test calculations, they also compared the performance of their FWD Riemann solver with that of several Riemann solvers of the HLL family (HLL, HLLC, HLLD; see next Section 5.1.3).
5.1.3 Relativistic HLL, HLLC and HLLD methods
The Harten-Lax-van Leer Riemann solver (Harten et al., 1983) described in Section 4.1.3 for RHD can be used also in RMHD, if one applies proper lower and upper bounds for the smallest and largest signal velocities (fast magnetosonic wavespeeds). In the RMHD code developed by Del Zanna et al. (2003) and in the MHD version of the relativistic code GENESIS (Leismann et al., 2005), the numerical fluxes are computed according to Eq. (30), with aL (aR) equal to the speed of the slowest (fastest) left-propagating (right-propagating) wave, computed at both sides of the cell interface. The same procedure is used in the GRMHD codes HARM, RAISHIN, ECHO, WhiskyMHD, and in those of Duez et al. (2005) and Antón et al. (2006).
Relying on previous experience in RHD (Mignone and Bodo, 2005; see also Section 4.1.3), Mignone and Bodo (2006) extended the HLLC Riemann solver of Gurski (2004) and Li (2005) for classical MHD to RMHD. In the HLLC approximate Riemann solver (see Toro et al., 1994, and Section 4.1.3), the presence of a contact discontinuity in the middle of the Riemann fan is recovered. Requiring consistency of the approximate Riemann solution with the conservation laws in a cell, gives rise to fourteen conditions determining the two intermediate states in 3D RMHD.
In their discussion, Mignone and Bodo (2006) differentiated between the cases where the component of the magnetic field normal to the contact discontinuity, Bx, vanishes and where it does not. In either case, the speed of the contact discontinuity is assumed to be equal to the (constant) normal velocity in the intermediate states, i.e., \({a_\ast} = v_\ast^x\), and the normal component of the magnetic field is assumed to be continuous at the interface. Hence, \(B_\ast^x = B_{\rm{L}}^x = B_{\rm{R}}^x\) can be considered as a parameter of the solution. If Bx ≠ 0, the fourteen consistency relations together with the six continuity conditions across the contact discontinuity (for total pressure, flow velocity, and tangential magnetic field components) allow one to determine the values of 20 variables, i.e., 10 per state. Mignone and Bodo (2006) chose the relativistic density, the components of the fluid velocity, the components of the tangential magnetic field, the components of the tangential relativistic momentum, the total energy, and the total pressure as independent unknowns.
For Bx = 0, the continuity of the normal component of the fluid velocity and of the total pressure across the contact discontinuity together with the consistency relations, allows one to determine 8 unknowns per state (relativistic density, normal fluid velocity, components of the tangential magnetic field, components of the tangential relativistic momentum, total energy, and total pressure). Once the corresponding algebraic problem is solved, the remaining state variables and then the numerical fluxes can be calculated. Honkkila and Janhunen (2007) developed another HLLC scheme for RMHD using different assumptions to solve the intermediate states.
The direct application of the HLLC solver of Mignone and Bodo (2006) to genuinely 3D problems suffers from a potential pathological singularity. It arises when the component of the magnetic field normal to a cell interface is zero. Sticking to the HLL approach, Mignone et al. (2009) extended the five-wave Riemann solver HLLD originally developed by Miyoshi and Kusano (2005) for MHD to the relativistic case. In this solver, besides the central contact discontinuity, the Alfvén discontinuities are reintroduced in the Riemann fan, which then involves four intermediate states. The resulting relativistic HLLD solver is considerably more elaborate than its classical counterpart, because the velocity normal to the interface is (different from classical MHD) no longer constant across Alfvén discontinuities, and because of the higher complexity of the RMHD equations. PLUTO and ATHENA incorporate HLL, HLLC, and HLLD Riemann solvers. TESS uses HLLC, whereas Mara relies on HLLD. MPI-AMRVAC allows to switch between HLL and HLLC. The computational efficiency and the accuracy of HLL, HLLC and HLLD were tested and compared in Mignone et al. (2009), and HLL, HLLC and FWD in Antón et al. (2010).
5.2 Flux formulas
The Lax-Friedrichs flux formula (see Section 4.2.1) can be used straightforwardly to compute the numerical fluxes in conservative RMHD schemes. Most of the RMHD simulations performed by van der Holst et al. (2008) with the AMRVAC code utilized the TVDLF scheme (Yee, 1989b; Tóth and Odstrčil, 1996), which is a second-order accurate variant of the LLF flux formula. The COSMOS++ code exploits the NOCD scheme of Kurganov and Tadmor (2000), in which the numerical fluxes are calculated according to the LLF formula. None of the present-day RMHD codes uses the Marquina flux formula.
5.3 Spatial reconstruction
As in RHD, the strategies for spatial reconstruction in numerical RMHD do not differ from those developed for general hyperbolic systems of conservation laws. Again one of the preferred choices are TVD schemes (mainly used in FV methods), which rely on linear interpolation and slope limiters for cell reconstruction. The corresponding codes are limited to second-order of accuracy. Preferably, one reconstructs primitive variables, like density, pressure, the components of the tangential magnetic field, and the spatial components of the four velocity. The codes of Komissarov (1999a), Gammie and Tóth (2003), Leismann et al. (2005), Duez et al. (2005), Antón et al. (2006), Mizuno et al. (2006), Mignone and Bodo (2006), Giacomazzo and Rezzolla (2007) and Del Zanna et al. (2007) use piecewise linear reconstruction with standard slope limiters (e.g., VAN LEER, MINMOD, MC), while MPI-AMRVAC incoporates also more modern limiters, like Koren (Keppens et al., 2012). TESS employs piecewise linear reconstruction on a moving Voronoi mesh with a TVD preserving slope limiter to extrapolate the primitive variables from cell centers to face centers. Codes that also allow for piecewise parabolic reconstructions are those of Duez et al. (2005), Leismann et al. (2005) and Mizuno et al. (2006), MPI-AMRVAC and an upgraded version of HARM.
Another choice are ENO schemes (mainly used in FD methods), which are based on adaptive stencils to reconstruct variables (typically fluxes) at cell interfaces from the point values. They achieve third-order to fifth-order accuracy. The codes of Del Zanna et al. (2003) and Anderson et al. (2006) are third-order accurate using CENO reconstruction. The ECHO code includes different ENO reconstruction routines (ENO, CENO, and WENO), and also ENO-like routines, like e.g., the Monotonicity Preserving scheme (MP; Suresh and Huynh, 1997), which are up to fifth-order accurate. The MP scheme is based on interpolation using a fixed 5-point stencil and a filter that preserves monotonicity near discontinuities.
A comment is necessary here, because the above discussion concerned the spatial reconstruction of cell interface values from cell average (FV methods) or cell center (FD methods) values. However, most of the contemporary RMHD codes (i.e., those based on the constrained transport algorithm to keep the magnetic field divergence free; see Section 5.5.1) need to reconstruct the magnetic field components, defined on a staggered grid, from cell interfaces to cell centers. Special care must be taken to avoid a reduction of the spatial accuracy of the method in this additional interpolation step.
5.4 Flux-limiter methods: Davis scheme
The Lax-Wendroff scheme (Lax and Wendroff, 1960) is among the most well known finite difference schemes. When applied to the linear advection equation, the scheme reads
where a is the constant signal propagation speed. When applied to a nonlinear conservation law with flux f, the previous scheme becomes the two-step Lax-Wendroff scheme
\((f_i^{(1)} = f(u_i^{(1)}))\). In the original two-step Lax-Wendroff scheme \(u_i^{n + 1} = u_i^{(2)}\) is the solution at the new time step. However, in Davis’ approach (Davis, 1984)
where the extra terms are local, parameter-free dissipation terms that do not require any characteristic information and make the whole algorithm TVD. Koide et al. (1999) implemented the scheme of Davis in their GRMHD code.
5.5 Non-conservative finite-difference schemes
5.5.1 Flux corrected transport method
Special relativistic 2D MHD test problems with Lorentz factors up to 3 were investigated by Dubal (1991) with a code based on FCT techniques. They utilized a second-order Lax-Wendroff FD method including a fourth-order dispersion error algorithm (Weber et al., 1979). In the context of GRMHD, Yokosawa (1993) studied with a FCT technique developed for a RMHD code (Yokosawa et al., 1982) the influence of frame dragging on MHD accretion flows onto a Kerr black hole. Both Dubal (1991) and Yokosawa (1993) treated the RMHD equations as advection equations, and hence violated the conservation laws.
5.5.2 Artificial viscosity methods
Relying on a similar formulation of the equations and AV techniques as those used in the early days of numerical RHD (see Section 4.4.2), Wilson (1975, 1977) led the efforts to develop numerical codes for GRMHD. More recently, De Villiers and Hawley (2003) presented a 3D GRMHD code based on techniques (including AV) first developed for axisymmetric hydrodynamics around black holes Hawley et al. (1984). The code suffers from the known limitations of the artificial viscosity algorithm.
COSMOS++ also relies on Wilson’s formulation of the GRMHD equations, but uses consistent AV techniques (involving different AV recipes) and solves an extra equation for the total energy (see Section 4.4.2). The code seems not to suffer from the aforementioned limitations of traditional AV methods in RHD.
5.6 Multidimensional schemes and time advance
The original version of HARM uses the mid-point method for time advance. However, most RMHD codes (including the upgraded HARM) rely on Runge-Kutta methods of second and third order accuracy (whether TVD-preserving or not; Del Zanna et al., 2003; Leismann et al., 2005; Antón et al., 2006; Mizuno et al., 2006; Neilsen et al., 2006; Anderson et al., 2006; Del Zanna et al., 2007; Nagataki, 2009; Antón et al., 2010; Beckwith and Stone, 2011), and even higher order accuracy (Etienne et al., 2010), or on the MUSCL-Hancock scheme (Mignone and Bodo, 2006; van der Holst and Keppens, 2007; van der Holst et al., 2008; Beckwith and Stone, 2011; Zrake and MacFadyen, 2012). Codes like PLUTO and MPI-AMRVAC incorporate both types of schemes. TESS employs a third order TVD-RK to update the values of the conserved variables and the positions of the points generating the moving Voronoi mesh. In all these cases, the solution is advanced in time in an unsplit manner.
5.7 Divergence-free condition
In general, the divergence-free condition of the magnetic field is fulfilled during a simulation only at the truncation level, i.e., non-solenoidal components of the magnetic field may be generated. This numerical failure produces artificial forces parallel to the magnetic field and falsifies the solution (Brackbill and Barnes, 1980). Hence, different numerical strategies have been developed to keep the violation of the constraint below a reasonable value.
Mignone and Bodo (2008) gave a concise description of the respective approaches used in HRSC schemes, while Tóth (2000) provided a thorough discussion of constrained transport (CT) methods, also comparing the performance of the most popular ones. In this section, we shall closely follow the description given in these two studies. Another useful overview of numerical strategies to keep the solenoidal condition can be found in Chapter 19 of Goedbloed et al. (2010).
The approaches, which can be considered as modifications of the HRSC base scheme, comprise two categories (Balsara, 2004; Mignone and Bodo, 2008). In the first one (divergence-cleaning schemes), the magnetic field is advanced as any other variable and the fulfillment (up to truncation error) of the divergence-free condition of the magnetic field is imposed in a separate divergence-cleaning step. Such schemes use a cell centered representation of the magnetic field, which allows for an easy extension of the base scheme. Moreover, with a cell centered representation of all conserved quantities the extension to adaptive and unstructured grids is straightforward. In the second category (CT), the magnetic field is usually represented on a staggered grid, while the other variables are still allocated to cell centers. In CT schemes, the induction equation is naturally updated using Stokes theorem, i.e., the divergence-free condition is fulfilled to machine accuracy (divergence-free schemes).
5.7.1 Eight-wave method
The eight-wave formulation of the MHD equations (Powell, 1994) is based on a derivation of the equations that does not involve Maxwell’s ∇ · B = 0 equation. In this formulation, the three components of the magnetic field are evolved in an unconstrained way and source terms proportional to the divergence of the magnetic field appear in the momentum, energy, and induction equations. Powell (1994) showed that these sources terms change the character of the equations introducing an additional eighth wave which corresponds to the advection of the divergence of the magnetic field. The other seven waves are the same as in the traditional formulation.
The eight-wave formulation is more stable and robust than the original conservative formulation for any shock-capturing MHD code. However, Tóth (2000) pointed out that by virtue of the Lax-Wendroff theorem (Lax and Wendroff, 1960), the non-conservative source terms can produce incorrect jump conditions, leading to incorrect results particularly in problems involving strong shocks. Janhunen (2000) and Dellar (2001) argued to add the source terms only to the induction equation, hence restoring the momentum and energy conservation.
The eight-wave method is incorporated in PLUTO and MPI-AMRVAC as one of the algorithms for divergence cleaning in both the MHD and RMHD modules.
5.7.2 Hyperbolic/parabolic divergence cleaning
In Dedner et al. (2002) the divergence constraint for the magnetic field is coupled to the hyperbolic MHD evolution equations by introducing a new unknown scalar function. Accordingly, the induction equation is replaced by
and the solenoidal condition by
where \(\mathcal{D}\) is some differential operator. For any choice of \(\mathcal{D}\), it can be shown that the divergence of B and the function ψ satisfy the same type of equation:
One chooses \(\mathcal{D}\), and the initial and boundary conditions of ψ in such a way that a numerical approximation of Eqs. (70) and (71) also provides a good approximation of the original equations (without the ψ-terms). One possibility is to define
With this parabolic correction Eq. (73) becomes
and any nonzero values of the divergence of B are dissipated if suitable boundary conditions are imposed. In this case, ψ can be trivially eliminated from the equations and the modified induction equation reads
Defining
a hyperbolic correction is made, whereby Eq. (73) becomes
This equation implies that local divergence errors propagate off the computational grid with the speed ch.
Finally, choosing \(\mathcal{D}(\psi) = 0\) leads to an elliptic correction, since a Poisson equation has to be solved for the function ψ (Dedner et al., 2002). This approach is equivalent to the projection method of Brackbill and Barnes (1980) explained later in this section.
The hyperbolic and parabolic corrections can be combined to a mixed one offering both dissipation and propagation of the divergence errors. The MHD system augmented with either the hyperbolic or mixed corrections is hyperbolic and still possesses its original conservation properties. Moreover, divergence errors are transported by two kind of waves with speeds independent of the fluid velocity, i.e., such an approach may be considered as an extension of Powell’s eight-wave method.
COSMOS++, AMRVAC, PLUTO and TESS, as well as the codes of Neilsen et al. (2006) and Anderson et al. (2006), incorporate different implementations of this divergence cleaning algorithm.
5.7.3 Constrained transport
The CT scheme, originally developed by Evans and Hawley (1988) for artificial viscosity methods, relies on a particular discretization on a staggered grid, which maintains ∇ · B exactly in a specific discretization. If the initial magnetic field has zero divergence in this discretization, it will remain so (to the accuracy of machine round off errors) for all times.
DeVore (1991) combined the CT scheme with the FCT method, and Dai and Woodward (1998), Ryu et al. (1998), and Balsara and Spicer (1999) combined the CT discretization with schemes based on Godunov-type Riemann solvers. In their original form, the algorithms of Dai and Woodward, Ryu et al., and Balsara and Spicer require the introduction of a staggered magnetic field variable. To advance this new variable in time one has to interpolate the magnetic and velocity fields (Dai and Woodward, 1998), or the fluxes (Balsara and Spicer, 1999), or the transport fluxes (Ryu et al., 1998) of the base scheme to the cell corners. Tóth (2000) called these methods, respectively, field-CT, flux-CT, and transport-flux-CT.
The interpolations performed to obtain the required fluxes at cell edges, and the cell centered magnetic field from the staggered one reduces the accuracy of the algorithm to second order. Tóth (2000) reformulated these schemes as standard cell-centered schemes (although this requires the interpolation of the fluxes in the induction equation over a much wider stencil than in the base scheme). Following Tóth’s notation we shall call these schemes field-CD and flux-CD (from central difference as opposed to staggered one).
Before discussing more modern developments of the CT scheme, in particular, its application in RMHD, let us describe the basics of this method (staggered version). The starting point is a surface integral of the induction equation (64) across an open surface S
where Ω = v × B. Applying Stokes theorem to the integral on the right side of the equation leads to
where ∂S denotes the boundary of S.
To simplify the following discussion we restrict ourselves to a time-independent, homogeneous Cartesian grid. The cell centers of the grid have the coordinates (xi,yj, zk), and the cell interfaces are located at xi±1/2, yj±1/2, and zk±1/2, respectively (see Figure 12). Because of the homogeneity of the computational grid, the grid spacings xi+1/2 − xi−1/2, yj+1/2 − yj−1/2, and zk+1/2 − zk−1/2 in x, y and z-direction are constant, and hence simply are Δx, Δy and Δz, respectively.
Discretization of the magnetic field used in the basic staggered CT method in 2D. \(B_{i,j}^x\) and \(B_{i,j}^y\) are defined at cell centers, \(B_{i + 1/2,j}^x\) and \(B_{i + 1/2,j}^y\) at the centers of the cell interfaces in x and y direction, respectively. The fluxes for the magnetic field update, \(\Omega _{i + 1/2,j + 1/2}^z\), are defined at cell corners.
Considering now S as the face of the cubic cell (i,j,k) intersecting the x-axis at Xi+1/2, and assuming translational symmetry along the z-axis,Footnote 5 Eq. (80) can be written as
or in semidiscrete form as
where
with ΔSi+1/2, j = [yj−1/2, yj+1/2] × [zk−1/2, zk+1/2] = Δy Δz. We note that the quantities Bx, Ωz, and ΔS carry no κ-index, because of the assumed translational symmetry along the z-axis.
Repeating the above procedure for the magnetic field averaged over the cell interface at yj+1/2, we obtain
with
and ΔSi, j+1/2, = [xi−1/2, xi+1/2] × [zk−1/2, zk+1/2] = Δx Δz. Obviously, this algorithm for the time advance of the cell-interface averaged magnetic field verifies
where the integral extends over the volume of the corresponding numerical cell.
To determine the quantities Ωz, which are defined at the vertices of numerical cells, different procedures were proposed. Dai and Woodward (1998) used spatial and temporal interpolations to obtain the cell-vertex centered magnetic field \({\bf{B}}_{i + 1/2,j + 2/2}^{n + 1/2}\) and the velocity \({\bf{v}}_{i + 1/2,j + 1/2}^{n + 1/2}\), and from these
Balsara and Spicer (1999) compute \(\Omega _{i + 1/2,j + 1/2}^z\) by interpolating the cell-interface centered fluxes of the induction equation in the base Godunov-type scheme, \({\hat F^x}\) and \({\hat F^y}\), such that
where Fx = Byυx − Bxυy is the flux in x-direction in the equation for By, and Fy = Bxυy − Byυx is the flux in y-direction in the equation for Bx.
For plane-parallel grid-aligned flows the algorithm provides only half the dissipation of its 1D version, questioning the stability of the algorithm (see the discussion in Gardiner and Stone, 2005). This problem, which can be traced back to the lack of a directional bias in the averaging formula for \(\Omega _{i + 1/2,j + 1/2}^z\), was studied in a broader context by a number of researchers. To eliminate the problem, Ryu et al. (1998) considered only the transport term in the corresponding numerical flux and defined
where \(F_t^x = {B^y}{v^x}\) is the transport flux in x direction in the equation for By, and \(F_t^y = {B^x}{v^y}\) is the transport flux in y direction in the equation for Bx.
Gardiner and Stone (2005) proposed a family of staggered flux-CT algorithms that enforce consistency between volume-averaged and area-averaged magnetic fields, and between the associated numerical fluxes. These FV-consistent flux-CT schemes reduce to the 1D solver when applied to plane-parallel flows aligned with one of the coordinate axes. They combined their CT schemes with a single-step, second-order accurate Godunov scheme based on piecewise parabolic reconstruction, and the CTU method (Colella, 1990) for multidimensional integration.
In all the previous CT schemes, one first computes the magnetic field at cell interfaces, \(B_{i + 1/2,j}^x,{B_{y\;\;i,j + 1/2,j}}\), Byi,j+1/2, and then the corresponding cell-centered fields by linear interpolation, i.e.,
Focusing on the same problems as Gardiner and Stone (2005), i.e., on the construction of the upwind fluxes in the induction equation and the consistency between volume-averaged and area-averaged magnetic fields, Londrillo and Del Zanna (2000, 2004) developed the upwind constrained transport (UCT) strategy, which extends the CT method to high-order upwind schemes. UCT imposes the following conditions: (i) use the staggered magnetic field components in the computation of the numerical fluxes in the energy-momentum equations of the MHD system, (ii) avoid time-splitting techniques (the magnetic field derivatives along the two coordinate directions have to be computed at the same time), and (iii) use proper upwind expressions for the numerical fluxes in the induction equation. Finally, to go beyond second-order accuracy, the reconstruction procedure of the cell-centered magnetic fields, Eqs. (90), (91), should be changed Londrillo and Del Zanna (2000). A respective third-order ENO central-type scheme was proposed and tested against several 1D and 2D problems by Londrillo and Del Zanna (2000, 2004).
Parallel to these developments, the CT algorithm was being implemented in RMHD codes. Komissarov (1999a) used a kind of upwind field-CT scheme, the normal components of the magnetic field being defined on the staggered grid that is used to solve the Riemann problems at cell interfaces (see condition (i) above). Gammie and Tóth (2003) implemented the flux-CD scheme in their RMHD and GRMHD codes, as did Duez et al. (2005) in their GRMHD code for dynamical spacetimes, and Mizuno et al. in their GRMHD code RAISHIN (and Nagataki, 2009). The flux-CD scheme is also the option chosen in Mara. The transport-flux-CT scheme was implemented in the RMHD code of Leismann et al. (2005) and the flux-CT scheme in the codes of Antón et al. (2010) (RMHD), Antón et al. (2006) (fixed spacetime GRMHD), and WhiskyMHD (dynamical spacetime GRMHD). Mignone and Bodo (2006) and Mignone et al. (2007) combined the flux-CT scheme with the CTU method for multidimensional flows, and Del Zanna et al. (2003) and Mignone et al. (2007), and Shibata and Sekiguchi (2005), Del Zanna et al. (2007) and Etienne et al. (2010) implemented the UCT scheme in RMHD and GRMHD, respectively.
Using staggered grid involves two sets of cell-centered magnetic fields: one set consists of field values obtained from the averages of face-centered magnetic fields, while the other set derives from advancing the field directly with a Godunov method. The corresponding values from both sets usually are not much different (of the order of the discretization error of the scheme). However, in magnetically dominated flows the difference can lead to negative pressures. Hence, Komissarov (1999a) proposed to recompute the conserved variables after every time step from primitive variables that are recovered from the conserved ones advanced in time with the Godunov scheme, and cell-centered magnetic fields computed from the averages of face-centered fields. Following Balsara and Spicer (1999), Mignone and Bodo (2006) recomputed the total energy only, making a classical correction of the magnetic energy. Martí (2015) compares several correction algorithms proving the supremacy of the relativistic corrections as the one proposed by Komissarov (1999a). Redefining the conserved variables has the drawback that the whole scheme is no longer conservative. Nevertheless, the procedure was found to be useful for problems where the magnetic pressure exceeds the thermal pressure by more than two orders of magnitude.
5.7.4 Projection scheme
Brackbill and Barnes (1980) proposed the projection scheme as a correction to the magnetic field that is applied at the end of every time step. The name derives from the idea that the magnetic field B* computed with a numerical scheme in time step n + 1 is possibly not divergence-free, and hence is projected to a divergence-free field Bn+1 according to
where ϕ satisfies the Poisson equation ∇ϕ = ∇ · B*.
As noted by Tóth (2000), the correction resulting from the projection scheme is the smallest possible one to make the field divergence-free. The projection scheme does not reduce the order of accuracy of the numerical scheme, but adds the computational costs for the solution of the Poisson equation.
5.8 Equation of state and primitive variable recovery
As in RHD, the evolution of the conserved variables in HRSC RMHD codes requires one to solve a nonlinear algebraic system of equations to obtain the primitive variables. This involves the inversion of the 5 × 5 system given by Eqs. (11)–(13) in each time (sub)step. Balsara (2001a) and Gammie et al. (HARM) used a Newton-Raphson iteration for this purpose and calculated the corresponding Jacobian analytically.
The system can be manipulated, however, to reduce the number of equations that have to be solved iteratively. In Koide’s code (Koide et al., 1996, 1999; Koide, 2003), and for an ideal gas EOS, the original 5 × 5 system is reduced to two equations (with the flow Lorentz factor W and the scalar product v · B as unknowns), which are solved by means of a 2D Newton-Raphson. In the absence of a magnetic field, one of these equations becomes the one in the RHD case as derived in Schneider et al. (1993) and Duncan and Hughes (1994), whereas the other becomes a trivial equation.
Komissarov (1999a) considered a reduced system of three equations for the unknowns W, v · B, and p (thermal pressure) for a general EOS of the form ω = ω(ρ,p) (where ω and ρ are the enthalpy and the proper rest-mass densities, respectively) which is solved iteratively. Del Zanna et al. (2003) particularized Komissarov’s system to an ideal gas. Concerned with the speed and precision of the recovery procedure, Del Zanna et al. derived a single nonlinear equation to be solved iteratively (and a cubic equation which is solved analytically to get the coefficients of the other equation). The equation, a function of the square of the flow velocity, is solved by means of a Newton-Raphson iteration.
The original Komissarov’s system can be manipulated (Leismann et al., 2005) to reduce the recovery of primitive variables to the simultaneous solution of only two nonlinear equations for the unknowns Z = ρhhW2 and υ2
where \({B^2}v_ \bot ^2 = {B^2}{v^2} - {({\bf{v}} \cdot {\bf{B}})^2} = {B^2}{v^2} - {({\bf{S}} \cdot {\bf{B}})^2}/{Z^2}\).
This system is valid for general equations of state of the form p = p(ρ, h), because ρ and h can be expressed explicitly in terms of Z, υ2, and the conserved variables. For an ideal gas, Eq. (94) becomes a cubic in Z with coefficients depending on υ2 only, which can be solved analytically. Inserting the analytic solution Z (υ2) into Eq. (93), one can solve it for υ2 (Del Zanna et al., 2003).
With some modifications, the above described methodology is the basis of several procedures for the recovery of primitive variables (Leismann et al., 2005; Antón et al., 2006; Giacomazzo and Rezzolla, 2007).
Assuming an ideal gas EOS, Noble et al. (2006) analyzed the computational efficiency, accuracy and robustness of the recovery of primitive variables for six different methods, which they labeled 5D, 2D, 1DW, 1Dυ2, \(1{\rm{D}}_{{v^2}}^\ast\), and polynomial, respectively. Their survey covered a parameter space of primitive variables given by
and any relative orientation between flow velocity and magnetic field.
In the 5D method, also applicable for a general EOS, one directly solves the full set of five nonlinear equations with a Newton-Raphson scheme. In the other five methods one reduces the 5 × 5 system to either one or two nonlinear equations that are solved numerically as described in the following.
In the 2D method, applicable also for general equations of state, one solves Eqs. (93) and (94) simultaneously with a 2D Newton-Raphson method. In the 1DW method one solves Eq. (94) for Z substituting the square of the velocity υ by
The 1Dυ2 method, restricted to an ideal gas EOS, is similar to the method of Del Zanna et al. (2003). However, because the cubic equation used in the latter method can sometimes have two positive real solutions for Z, Noble et al. (2006) introduced another cubic that has only one, positive (i.e., physically admissible) solution. In the related \(1{\rm{D}}_{{v^2}}^\ast\) method, instead of the cubic, Eq. (94) is solved for using a 1D Newton-Raphson iteration and the latest value of υ2 obtained from Eq. (93). In this way the method also works for general equations of state.
Finally, in the polynomial method one solves the eight-order polynomial in that one obtains when inserting Eq. (95) into Eq. (94) and assuming an ideal gas EOS. The eight roots of the polynomial are found using a general polynomial root-finding method. The physical root is identified by requiring that it is also a solution of the original 5 × 5 system.
According to the survey of Noble et al. (2006) the 2D method is the fastest and has the smallest failure rate (≈ 9 × 10−7), whereas the polynomial method and the 5D method are the slowest and have an unacceptably high failure rate (≈ 4 × 10−2 and 4 × 10−1, respectively). Source codes of the methods discussed by Noble et al. (2006) can be downloaded from the Astrophysical Code Library of the Astrophysical Fluid Dynamics Group at the University of Illinois (AFDG’s web).
Mizuno et al. (2006) implemented both Koide’s and Noble’s et al. 2D methods for primitive variable recovery in RAISHIN. The ECHO code incorporates the 2D, 1DW, 1Dυ2 and \(1{\rm{D}}_{{v^2}}^\ast\) methods of Noble et al., and the RMHD versions of PLUTO and AMRVAC use variations of the 1DW method for an ideal gas EOS described in Mignone and Bodo (2006) and Bergmans et al. (2005), respectively. Nagataki (2009) considered Noble’s et al. 1DW and 2D methods and discussed a procedure to obtain lower and upper limits for the (physical) solution of Z, while Etienne et al. (2010) used just the 2D method. The Mara code employs the 1DW method (for an ideal gas EOS), but switches to the 2D method, if a suitable solution is not obtained with the former one. The algorithm implemented in ATHENA is the 1DW method for an ideal gas EOS, and TESS incorporates a 3D solver based on the 2D method with an additional iteration for the temperature. The codes of Neilsen et al. (2006), Anderson et al. (2006) and Giacomazzo and Rezzolla (2007) use alternative 1D algorithms for an ideal gas EOS.
For a polytropic EOS (p = KρΓ;), the integration of the total energy equation is unnecessary, because the energy density can be computed algebraically from other flow quantities, and the recovery problem reduces to the numerical solution of Eq. (93) with Z = DW + ΓKDΓW2−Γ/(Γ − 1) (Antón et al., 2006; Giacomazzo and Rezzolla, 2007). Casse et al. (2013) discuss briefly a variable switch for isothermal RMHD.
Mignone and McKinney (2007) developed an inversion procedure that allows for a general EOS and avoids problems due to loss of precision in the non-relativistic and ultrarelativistic limits. They used the total energy minus the rest-mass energy instead of the total energy density itself as one of the conserved variables, and Noble’s et al. 1DW method, but with Z′ = Z − D and u2 = W2υ2 instead of Z and υ2 as unknowns. The variable Z′, properly written as
(where χ= ρε+ p), is introduced to avoid machine accuracy problems in the non-relativistic limit. In order to perform the inversion with a Newton-Raphson iteration, one has to compute the derivative
Mignone and McKinney provided explicit expressions of the thermodynamic derivatives ∂p/∂χ∣ρ and ∂p/∂ρ∣χ that avoid catastrophic cancellation in the non-relativistic limit (χ/ρ,p/ρ → 0) for the approximate Synge EOS (Mathews, 1971; Mignone et al., 2005b; Ryu et al., 2006). The authors claim that their inversion method is accurate in the ultrarelativistic limit as long as \(W \leq \varepsilon _{{\rm{mp}}}^{ - 1/2}\) and p/(ρW2) ≥ εmp, where εmp is the machine precision. The upgraded version of HARM incorporates this inversion method as well as the 2D method of Noble et al. (2006).
In addition to the accuracy problems in the ultrarelativistic and non-relativistic (both kinematic and thermodynamic) limits, conservative RMHD codes also may encounter problems in the strong magnetization limit, when B2 ≫ ρε. In this limit relatively small truncation errors in the evolution of the conserved variables lead to large (relative) errors in the computation of the internal energy density and other primitive variables. To ease these problems, in codes based on CT schemes, at the end of every time step one recomputes the conserved variables to make them consistent with the cell-centered magnetic fields computed from the averages of the staggered fields (see Section 5.7.3). The resulting small correction of the conserved quantities has turned out to be essential in simulations of flows with a magnetization of one hundred or larger.
5.9 AMR
The application of AMR in RMHD was pioneered by Balsara (2001a,b,c). He pointed out the necessity that adaptive mesh MHD schemes should obey the divergence-free property of the magnetic field on the entire AMR hierarchy. As in hydrodynamics, he argued, it is essential for divergence-free AMR-MHD based on HRSC methods to prolong and restrict the data using the same reconstruction strategy as for the underlying HRSC schemes. He has implemented a divergence-free reconstruction strategy (of vector fields) into his RIEMANN framework, which supports multidimensional simulations of both Newtonian and relativistic MHD flows on parallel computing architectures (Balsara, 2001b). Divergence-free prolongation of magnetic fields on an AMR hierarchy requires a slight extension of the reconstruction scheme, while divergence-free restriction involves area-weighted averaging of magnetic fields over faces of fine grid patches.
Because Balsara’s work is based on an integral formulation of the MHD equations, divergence-free restriction and prolongation can be carried out on AMR grids with any integral refinement ratio. In order to efficiently evolve the MHD equations on AMR grids, the refined patches are evolved with time steps that are a fraction of their parent patch’s time step. The RIEMANN framework has been validated by performing a set of 3D AMR-MHD tests with strong discontinuities.
Adopting a local discontinuous Galerkin predictor method together with a space-time AMR based on a “cell-by-cell” approach and local time stepping, Zanotti and Dumbser (2015) obtained a high order one-step time discretization for the integration of the special relativistic hydrodynamic and magnetohydrodynamic equations, with no need for Runge-Kutta sub-steps. They explore the scheme’s ability to resolve the propagation of relativistic hydrodynamic and magnetohydrodynamic waves in different physical regime by performing a set of numerical tests in one, two and three spatial dimensions.
The GRMHD code of Anderson et al. (2006) and Neilsen et al. (2006) uses the AMR method of Berger and Colella (1989) with WENO interpolation for prolongation (see Section 8.3.5), and both hyperbolic and elliptic divergence cleaning to enforce a divergence-free magnetic field. They do not consider constrained transport, because it requires that neighboring grids align in a structured manner, precluding its application to overlapping grids with arbitrary coordinates, resolutions and/or orientation.
The (G)RMHD codes COSMOS++, WhiskyMHD, and the one developed by Etienne et al. (2010) have AMR capabilities, too. In COSMOS++ individual cells are refined rather than introducing patches of subgrids. The framework is similar to that of Khokhlov (1998), i.e., based on a fully threaded oct-tree (in 3D), but generalized to unstructured grids. The robustness of the numerical algorithms and the AMR framework implemented in COSMOS++ was demonstrated by several tests including relativistic shock tubes, shock collisions, magnetosonic shocks, and Alfvén wave propagation.
The code of Etienne et al. (2010) uses the Cactus parallelization environment and the Carpet infrastructure to implement moving-box AMR. The induction equation is recast into an evolution equation for the magnetic vector potential (Del Zanna et al., 2003) to keep the magnetic field divergence-free, in particular at AMR refinement boundaries. Prolongation and restriction are applied to the unconstrained vector potential components instead of the magnetic field components, which gives flexibility in choosing different interpolation schemes for prolongation and restriction. In simulations with uniform grids, the scheme is numerically equivalent to the constrained-transport scheme based on a staggered-mesh algorithm (Evans and Hawley, 1988). Several tests including nonlinear Alfvén waves and cylindrical explosions validated the proper working of the code (Etienne et al., 2010).
WhiskyMHD also uses the Cactus parallelization environment and the Carpet infrastructure to implement a “box-in-box” mesh refinement strategy (Schnetter et al., 2004). It adopts a Berger-Oliger prescription for the refinement of meshes on different levels (Berger and Oliger, 1984). In addition to this, a simplified form of adaptivity allows for new refined levels to be added at predefined positions during the evolution or for refinement boxes to be moved across the domain to follow, for instance, regions where higher resolution is needed.
We note that the relativistic AMR codes AMRVAC and PLUTO discussed in Section 4.7 can simulate special relativistic magnetized flows, too. The latter also holds for the code ATHENA that offers static mesh refinement.
5.10 Summary of existing codes
Table 2 lists the multidimensional codes based on HRSC methods in chronological order both for FD and FV schemes, summarizing the basic algorithms implemented in the codes (type of spatial reconstruction, Riemann solvers and flux formulas, time advance, multidimensional schemes, and ∇ · B = 0 scheme). The table includes codes specifically developed for RMHD and those GRMHD codes for fixed spacetimes that were also used or tested in RMHD. Moreover, we include several GRMHD codes for dynamical spacetimes (Duez et al., 2005; Shibata and Sekiguchi, 2005; Neilsen et al., 2006; Anderson et al., 2006; Giacomazzo and Rezzolla, 2007; Etienne et al., 2010) that were widely tested in RMHD. AMRVAC, PLUTO, and ATHENA are multipurpose codes for computational astrophysics that have RMHD modules.
The AMRVAC, PLUTO, and ATHENA codes are publicly available and provide extensive online information about their usage. They can be downloaded from the corresponding webpages (VAC; AMRVAC, PLUTO, ATHENA). The original 2D GRMHD accretion code HARM can be downloaded from the Astrophysical Code Library of the Astrophysical Fluid Dynamics Group at the University of Illinois (AFDG’s web).
6 Test Bench
This section contains a detailed discussion of most of the numerical tests presented in the literature assessing the capabilities and limits of different HRSC methods and codes in RHD and RMHD. We review the results published by different groups including one-dimensional and multidimensional tests, with and without flow discontinuities.
In most relativistic codes one sets the speed of light equal to one, and one absorbs a factor \(\sqrt {4\pi } \) in the definition of the magnetic field in RMHD codes. Hence, lengths and times have the same dimension, and this also holds for mass and energy densities, i.e., [ρ] = [p] = [ B2 ]. These are the units we use throughout the review, and particularly in this section.
In order to convert code to physical units, one has to complete the system of units with two independent units in addition to the velocity unit (uυ, the speed of light, c). A common choice is to fix the unit of density, uρ, and the unit of length, ul. In this system, the units of p or B2 (both have dimension of energy density) are uρc2. For example, with uρ = 1 g cm −3 and ul = 1 cm, the unit of p is (2.99 × 1010)2 g cm−1 s−2 or 8.94 × 1020 erg cm−3, and that of the magnetic field 1.06 × 1011 G (the square root of the pressure unit multiplied by \(\sqrt {4\pi } \))
6.1 Numerical RHD: Testing the order of convergence on smooth flows
Modern HRSC codes have been mainly developed to describe strong (relativistic) shocks properly and robustly, i.e., most tests in the literature are concerned with the shock capturing capabilities of these codes. However, it is also very important to test the accuracy of HRSC codes in handling smooth flows. This is specially relevant for codes based on high-order schemes, which are in general computationally expensive.
6.1.1 Isentropic smooth flows in one dimension
This test consists of a 1D isentropic pulse set up in a uniform reference state. The pulse is initially smooth and symmetric but steepens on one side during its propagation forming a shock in a finite time. The width and height of the pulse does not change before the shock forms (see Figure 13). Details of the initial state and the analytic solution of its evolution can be found in Zhang and MacFadyen (2006). The test is a relativistic counterpart of the convergence test performed by Colella et al. (2006) with their Newtonian hydrodynamics code.
One-dimensional isentropic pulse test simulated with the F-WENO-RK3 scheme of the RAM code. Pressure, density, and velocity are shown in the top, middle, and bottom panels, respectively, at t = 0 (plus signs) and t = 0.8 (triangles). Image reproduced with permission from Figure 6 of Zhang and MacFadyen (2006), copyright by AAS.
Zhang and MacFadyen (2006) considered this test to evaluate the accuracy of the various optional schemes that are implemented in their code RAM. In RAM one can combine any of the spatial schemes F-WENO, F-PLM, U-PPM, and U-PLM) with one of the following Runge-Kutta methods for time integration: a third-order TVD-RK method (Shu and Osher, 1988), or standard fourth- and fifth-order Runge-Kutta methods (Lambert, 1991), RK4 and RK5, respectively. The optimal order of convergence was obtained with the combination F-WENO and RK4, while combining U-PPM (formally fourth-order accurate for smooth flows) and the third-order TVD-RK or RK4 resulted only in second-order convergence.
Morsony et al. (2007) used the same test problem to determine the order of convergence of the FLASH code. The RHD module of this code utilizes PP interpolation within cells and a two-shock Riemann solver to compute the numerical fluxes. The time evolution is second-order accurate (for details, see Mignone et al., 2005b). The study showed that FLASH achieves global second-order accuracy for this test problem. Second-order convergence is also obtained with the moving grid code TESS (Duffell and MacFadyen, 2011).
6.1.2 Isentropic smooth flows in two dimensions
Several authors (Zhang and MacFadyen, 2006; Morsony et al., 2007; Duffell and MacFadyen, 2011) simulated the previous test in 2D (using Cartesian coordinates) to validate the order of accuracy of the multidimensional scheme (spatial reconstruction and time advance). The semi-discrete approach followed in RAM leads to fourth-order accuracy for the F-WENO schemes, if combined with the RK4 method, as in the 1D case. In FLASH, the second-order accurate time integration again limits the global accuracy of the code to second order (Morsony et al., 2007). Duffell and MacFadyen (2011) obtained a slightly higher than second-order accuracy in a non-relativistic limit of this test with a different shape of the isentropic pulse. The 2D test further showed that the convergence rate of TESS remains unchanged even when the nonuniform flow distorts the moving mesh (Duffell and MacFadyen, 2011).
To verify the order of convergence of WHAM in two dimensions, Tchekhovskoy et al. (2007) studied the advection of smooth oblique sound and density waves on a Cartesian mesh. A sinusoidal planar wave is set to propagate on a uniform background state at rest with an angle α = tan−1 (2) with respect to the x-axis. A polytropic EOS p = KρΓ with Γ = 5/3 is used. The amplitude of either the sound wave or the density wave is chosen so that it remains within the linear regime during the whole simulation. The results show that WHAM converges at fifth-order. For comparison, the authors also performed the test with the WENO-IFV scheme, implemented in a simplified version of WHAM, in which the averaging and de-averaging procedures of conserved variables, fluxes and sources between average and point values, are disabled. They found that the convergence rate of this scheme is only of second-order.
6.2 Numerical RHD: Relativistic shock heating in planar, cylindrical and spherical geometry
Shock heating of a cold fluid in planar, cylindrical or spherical geometry has been used since the early developments of numerical RHD as a test case for hydrodynamic codes, because it has an analytic solution (Blandford and McKee, 1976 for planar geometry; Martí et al., 1997 for cylindrical and spherical geometry), and involves the propagation of a strong relativistic shock wave.
In planar geometry, an initially homogeneous, cold (i.e., ε ≈ 0) gas with velocity υ1 and Lorentz factor W1 is supposed to hit a wall (or to collide against a similar and opposite flow), while in the case of cylindrical and spherical geometry the gas flow converges towards the symmetry axis or the center of symmetry. In all three cases the reflection causes compression and heating of the gas as kinetic energy is converted into internal energy. This occurs in a shock wave, which propagates upstream. Behind the shock the gas is at rest (see Figure 14). Due to conservation of energy across the shock the gas has a specific internal energy given by
The compression ratio of shocked to unshocked gas, σ, follows from
where γ is the adiabatic index of the EOS.
Schematic solution of the shock heating problem in spherical geometry. The initial state consists of a spherically symmetric flow of cold (p = 0) gas of unit rest mass density with a highly relativistic inflow velocity everywhere. A shock is generated at the center of the sphere, which propagates upstream with constant speed. The post-shock state is constant and at rest. The pre-shock state, where the flow is self-similar, has a density which varies as ρ = (1 + t/r)2 with time t and radius r.
In the Newtonian case the compression ratio σ of shocked to unshocked gas cannot exceed a value of σmax = (γ +1)/(γ−1) independently of the inflow velocity. This is different for relativistic flows, where σ grows linearly with the flow Lorentz factor and becomes infinite as the inflowing gas velocity approaches to speed of light.
The maximum flow Lorentz factor achievable for a hydrodynamic code with acceptable errors in the compression ratio σ is a measure of the code’s quality. Explicit finite-difference techniques based on a non-conservative formulation of the hydrodynamic equations and on non-consistent (Centrella and Wilson, 1984; Hawley et al., 1984) or consistent artificial viscosity (Anninos and Fragile, 2003) were able to handle flow Lorentz factors up to ≈ 10 with moderately large errors (σerror ≈ 1−3%) at best. Norman and Winkler (1986) obtained excellent results (σerror ≈ 0.01% for a flow Lorentz factor of 10 using consistent artificial viscosity terms and an implicit adaptive-mesh method). The performance of explicit codes improved significantly when HRSC methods both symmetric (Del Zanna and Bucciantini, 2002; Anninos and Fragile, 2003; Lucas-Serrano et al., 2004; Tchekhovskoy et al., 2007; Meliani et al., 2007) or upwind (Martí et al., 1991; Marquina et al., 1992; Eulderink, 1993; Schneider et al., 1993; Dolezal and Wong, 1995; Eulderink and Mellema, 1995; Martí and Müller, 1996; Falle and Komissarov, 1996; Wen et al., 1997; Aloy et al., 1999b; Mizuta et al., 2004; Lucas-Serrano et al., 2004; Mignone and Bodo, 2005; Choi and Ryu, 2005; Zhang and MacFadyen, 2006; Wang et al., 2008) were introduced. Meliani et al. (2007) show results for the shock heating test in Cartesian coordinates for an inflow Lorentz factor of 70710. Martí and Müller (2003) summarized the results obtained for this test by various authors until 2003. The eAV scheme (see Section 4.4.2) incorporated in COSMOS++ seems to overcome the limitations of traditional AV methods in this test and to allow for an accurate modeling of problems with highly relativistic inflow speeds (> 0.99999).
The performance of a HRSC method based on a relativistic Riemann solver is illustrated in Figure 15 (and the attached movie — online version only —) for the planar shock heating problem for an inflow velocity υ1 = −0.99999 (W1 ≈ 223). These results are obtained with the third-order relativistic code rPPM described in Martí and Müller (1996) and provided in Martí and Müller (2003). The shock wave is resolved by three cells and there are no post-shock numerical oscillations. The density increases by a factor ≈ 900 across the shock. Near x = 0 the density distribution slightly undershoots the analytic solution (by ≈ 8%) due to the numerical effect of wall heating. The profiles obtained for other inflow velocities are qualitatively similar. The mean relative error of the compression ratio is less than 10−3, and does not exhibit any significant dependence on the Lorentz factor of the inflowing gas. As in other problems involving discontinuities, the L1-norm errors converge linearly when increasing the grid resolution. The quality of the results obtained with high-order symmetric schemes is similar.
mpg-Movie (711.250976562 kB) Still from a movie — Numerical (red points) and analytic (blue line) distributions of density, velocity and pressure at t = 1.496 for the shock heating problem with an inflow velocity υ1 = −0.99999 in Cartesian coordinates. The reflecting wall is located at x = 0. The adiabatic index of the gas is 4/3. For numerical reasons, the specific internal energy of the inflowing cold gas is set to a small finite value (ε1 = 10−7 W1). The simulation was performed on an equidistant grid of 100 cells with the code rPPM (Martí and Müller, 1996). Animation (online version only): Full evolution of the numerical solution. (For video see appendix)
The wall heating phenomenon (overheating, as it is known in classical hydrodynamics; Noh, 1987) is a numerical artifact that is considerably reduced when more diffusive methods are used. For example, a third-order scheme using MFF (Donat et al., 1998) gives an overheating error of 2.5%, whereas another third-order scheme using LLF (Lucas-Serrano et al., 2004) reduces the error further down to 1%. This reduction of the error with diffusion extends to the order of the reconstruction. The errors in density at the nearest cell to the reflecting wall amount to 3.9%, 2.4%, 7.4%, and 4.3% for the schemes F-WENO (third-order), F-PLM (second-order), U-PPM (third-order), and U-PLM (second-order), respectively (Zhang and MacFadyen, 2006). Again, the more diffusive schemes F-PLM and U-PLM perform better than F-WENO and U-PPM. Let us also note that methods based on the direct reconstruction of (characteristic) fluxes lead to smaller errors than those of the same order based on the reconstruction of (primitive) variables.
Some authors considered the problem of shock heating in cylindrical or spherical geometry using adapted coordinates to test the numerical treatment of geometrical factors (Romero et al., 1996; Martí et al., 1997; Wen et al., 1997; Mizuta et al., 2004). Other authors (Aloy et al., 1999b; Mignone et al., 2005b; Wang et al., 2008) simulated the spherically symmetric shock heating problem in 3D Cartesian coordinates as a test case for the numerical treatment of multidimensions and symmetry properties. Aloy et al. (1999b) presented results of this test with the code GENESIS for an inflow Lorentz factor of 707 in a 813 cell grid with acceptable relative global errors (32% for pressure, 39% for density, and 2% for velocity). Mignone et al. (2005b) performed the test with their relativistic PPM method under the same conditions up to an inflow Lorentz factor 2236 (corresponding errors were 24%, 21%, and 1%). Wang et al. (2008) simulated the problem in spherical geometry with RENZO (LLF-PLM algorithm) for an inflow velocity of 0.9 (Lorentz factor 2.29). Keppens et al. (2012) considered this test with MPI-AMRVAC for an inflow velocity of 0.995 (Lorentz factor 10) in planar, axial, and spherical symmetry in adapted coordinates, focusing on the performance of the AMR strategy based on pure oct-tree block refinement.
Anninos et al. (2005) considered a boosted version of the shock collision test in which two boosted fluids flow toward each other, collide and form a pair of shocks with a contact discontinuity in between. Among other things, the simulation tested the Lorentz invariance of the code. In further simulations, the eAV and NOCD methods of COSMOS++ were tested for symmetric and asymmetric colliding fluids in the center-of-momentum frame, and with Lorentz factors up to 100. The agreement between the analytic and numerical solutions was very good, in general, the relative errors of the compression ratio being about 10−4. These highly relativistic, and thus very thin shocks require very fine zoning, which can be provided by AMR techniques. The latter have been extensively applied using up to 12 levels of refinement in the tests with the highest boost.
6.3 Numerical RHD: Propagation of relativistic blast waves
Riemann problems with large initial pressure jumps produce blast waves with dense shells of material propagating at relativistic speed (see Figure 16). For appropriate initial conditions, both the velocity of the leading shock front and of shell approaches the speed of light, hence producing very narrow flow structures. The accurate description of these thin, relativistic shells involving large density contrasts is a challenge for any numerical code.Footnote 6
Generation and propagation of a relativistic blast wave (schematic). The large jump in the pressure of two homogeneous fluids at rest at both sides of a discontinuity initially located at r = 0.5 gives rise to a blast wave and a shell of dense matter propagating at relativistic speeds. For appropriate initial conditions both the velocity of the leading shock front and of the shell approaches the speed of light, hence producing very narrow flow structures.
Some particular blast wave problems became standard numerical tests. Here we consider two of these tests (Problems 1 and 2 below), which were already discussed in Martí and Müller (2003). Problem 1 was a demanding problem for RHD codes in the mid-1980s (Centrella and Wilson, 1984; Hawley et al., 1984), while Problem 2 is still a challenge for state-of-the-art codes today. We will discuss two further tests involving discontinuous initial tangential speeds (Problems 3 and 4), which are very demanding for fixed-grid FD or FV methods. The initial conditions for the four tests are given in Table 3. The corresponding analytic solutions can be obtained with program RIEMANN-VT (provided in Martí and Müller, 2003).
6.3.1 Problem 1
In Problem 1, the decay of the initial discontinuity gives rise to a dense shell of matter with velocity υshell ≈ 0.72 (Wshell ≈ 1.38) propagating to the right. The shell, trailing a shock wave of speed υshock ≈ 0.83, increases its width, wshell, according to wshell ≈ 0.11t, i.e., at time t = 0.4 the shell covers about 4% of the grid (0 ≤ x ≤ 1). The test was first considered by Schneider et al. (1993).
Concerning artificial viscosity methods, the state-of-art performance on this test is still given by the (second-order accurate) code COSMOS of Anninos et al. that uses a consistent scalar artificial viscosity. With this code, it is possible to capture the constant states in a stable manner and without noticeable errors (e.g.,, the shell density is underestimated by less than 2% in a 400 cells calculation).
In Martí and Müller (2003), a MPEG movie shows the Problem 1 blast wave evolution obtained with a modern HRSC method (the third-order rPPM code described in Martí and Müller, 1996 and provided in Martí and Müller, 2003). The grid has 400 equidistant cells and, at t = 0.4, the relativistic shell is resolved by 16 cells. Because of the third-order spatial accuracy of the method in smooth regions and its small numerical diffusion (the shock is resolved by 4–5 cells, and the contact discontinuity by 5–6 cells) the density of the shell is accurately computed (error less than 0.1%). The order of accuracy of the code when increasing the grid resolution (evaluated using the L1-norm errors) is roughly 1 as expected for problems with discontinuities.
A large number of authors considered Problem 1 to test their HRSC algorithms (Schneider et al., 1993; Eulderink and Mellema, 1995; Martí and Müller, 1996; Martí et al., 1997; Wen et al., 1997; Donat et al., 1998; Del Zanna and Bucciantini, 2002; Anninos and Fragile, 2003; Mizuta et al., 2004; Lucas-Serrano et al., 2004; Mignone and Bodo, 2005; Mignone et al., 2005b; Choi and Ryu, 2005; Zhang and MacFadyen, 2006; Meliani et al., 2007; Tchekhovskoy et al., 2007; Morsony et al., 2007; Wang et al., 2008). The performance of these algorithms in terms of accuracy and dissipation is, generally speaking, similar to that of code rPPM. The results obtained with the relativistic extension of the PPM method by Mignone et al. (2005b) are the best, the contact discontinuity and the shock being spread by 2–3 cells. Given the similarities between these two PPM extensions, the differences must come from the choice of the parameters in the reconstruction procedure. The steeper contact discontinuity in Lucas-Serrano et al. (2004) could have the same origin. The TVD scheme by Choi and Ryu (2005) produces very sharp shock transitions (1–2 cells). We note that the schemes F-WENO (fifth-order in space, third-order in time; Zhang and MacFadyen, 2006), WHAM (fifth-order in space, fourth-order in time), and F-WENO5 (fifth-order in space, third-order in time; Wang et al., 2008) produce results which are similar to those obtained with rPPM (third-order in space, second-order in time). Finally, some authors also simulated multidimensional versions of this problem (Martí et al., 1997; Aloy et al., 1999b; Anninos and Fragile, 2003; Baiotti et al., 2003).
6.3.2 Problem 2
Problem 2 was proposed by Norman and Winkler (1986). The flow pattern is similar to that of Problem 1, but more extreme. Relativistic effects reduce the post-shock state to a thin dense shell with a width of only about 1% of the grid length at t = 0.4. The fluid in the shell moves with υshell = 0.960 (i.e., Wshell ∼ 3.6), while the leading shock front propagates with a velocity υshock = 0.987 (i.e., Wshcock ∼ 6.0). The density jump in the shell reaches a value of 10.4. Norman and Winkler (1986) obtained very good results with an adaptive grid of 400 cells using an implicit hydro-code with artificial viscosity. Their adaptive grid algorithm placed 140 cells of the available 400 cells within the blast wave thereby accurately capturing all features of the solution.
Later, Martí et al. (1991), Marquina et al. (1992), Martí and Müller (1996), Falle and Komissarov (1996), Wen et al. (1997), Donat et al. (1998), Del Zanna and Bucciantini (2002), Anninos and Fragile (2003), Mizuta et al. (2004), Lucas-Serrano et al. (2004), Mignone and Bodo (2005), Mignone et al. (2005b), Choi and Ryu (2005), Zhang and MacFadyen (2006), Meliani et al. (2007), Tchekhovskoy et al. (2007), Morsony et al. (2007), and Wang et al. (2008) simulated Problem 2 to test their codes based on HRSC methods. Figure 17 (and the attached movie -online version only-) shows the evolution of the blast wave simulated with rPPM (Martí and Müller, 1996; Martí and Müller, 2003) on a grid of 2000 equidistant cells. At this resolution rPPM obtains a converged solution. At lower resolution (400 cells) the relativistic PPM method gives only 69% of the theoretical shock compression ratio, which is a standard value (±3%) for third-order schemes (Marquina et al., 1992; Martí and Müller, 1996; Donat et al., 1998; Del Zanna and Bucciantini, 2002; Lucas-Serrano et al., 2004; Mignone et al., 2005b and schemes U-PPM of RAM, HLL-PPM and HLL-CENO of RENZO, and the FLASH code). Second-order schemes (Martí et al., 1991; Falle and Komissarov, 1996; Mizuta et al., 2004; Mignone and Bodo, 2005 and schemes NOCD of COSMOS and COSMOS++, F-PLM and U-PLM of RAM, HLL-PLM of RENZO) achieve 57±4% of the theoretical shock compression value. Algorithms with an order of accuracy greater than 3 (the F-WENO scheme of RAM, the WHAM code, and the F-WENO5 scheme of RENZO) get 75 ± 3% of the correct value. The most remarkable result is the one obtained with the second-order HLLC scheme of Mignone and Bodo (2005) that gives 82% of the correct shock compression ratio, because it uses a single-step MUSCL-Hancock method with fourth-order limited slopes (Colella, 1985; Miller and Colella, 2001) to construct the linear states.
mpg-Movie (1453.26757812 kB) Still from a movie — Numerical (red points) and analytic (blue line) distributions of density, velocity and pressure at t = 0.43 for the relativistic blast wave Problem 2 defined in Table 3. The simulation was performed with the code rPPM Martí and Müller (1996) on an equidistant grid of 2000 cells. Animation (online version only): Full evolution of the numerical solution. (For video see appendix)
The L1 global error of the density decreases with the formal order of accuracy of the method as expected, although the differences between second-order methods and fourth- or fifth-order methods are less than a factor of two. The order of accuracy is lower than one for third-order methods (the average order of accuracy is 0.70–0.90 when increasing the grid resolution from 400 to 1600 cells), and approaches unity for schemes with an order of accuracy larger than three (e.g., the F-WENO scheme of RAM, and WHAM). As their code is free of numerical diffusion and dispersion, Wen et al. (1997) are able to handle this problem with high accuracy.
Anninos and Fragile (2003) and Anninos et al. (2005) considered Problem 2 as a test case for their AV explicit codes. They find that the density jump across the shock wave is 24–28% (12% in the case of the eAV scheme) too low when using 800 cells. This result demonstrates the robustness and accuracy of the consistent formulation of the artificial terms in AV methods and places consistent AV methods on the same level as HRSC methods in the simulation of highly relativistic flows in 1D.
6.3.3 Problems 3 and 4
Problems 3 and 4 are variations of Problem 2 with non-zero tangential speeds in the initial state. Their analytic solutions were first computed in Pons et al. (2000) (see also Figure 34 in Section 8.5). The break-up of the initial discontinuity is similar to that of Problem 2 with a left-propagating rarefaction wave and a right-propagating shock.
In Problem 3, the initial right state has a tangential velocity of 0.99, which increases its inertia. This makes the shock stronger (shock compression ratio σshock = 23.6) and a bit slower (υshock = 0. 927). However, the post-shock state moves also slower making the dense shell wider (about six times) than in Problem 2, i.e., despite the larger density jump at the shock the analytic solution is captured more easily than in the problem without an initial tangential flow component. Lucas-Serrano et al. (2004) obtained a converged solution with 400 cells and a reasonable smearing of both contact discontinuity and shock wave (5–6 cells; see Figure 18).
Results from Lucas-Serrano et al. (2004) (piecewise parabolic reconstruction, LLF flux formula, TVD-RK method for time advance) for the relativistic blast wave Problem 3 with a non-zero tangential velocity at t = 0.4. The figure shows normalized profiles of density, pressure and normal velocity for the computed and exact (solid lines) solutions on an equally spaced grid of 400 cells. Image reproduced with permission from Figure 6 of Lucas-Serrano et al. (2004), copyright by ESO.
Similar results were produced with other HRSC schemes (Mignone et al., 2005b; Ryu et al., 2006; Zhang and MacFadyen, 2006; Tchekhovskoy et al., 2007; Morsony et al., 2007; Wang et al., 2008; Duffell and MacFadyen, 2011). The L1 global error of the density decreased in these simulations with the expected formal order of the accuracy of the method, although the differences are small. For example, using 400 cells the absolute density error was 2.77 × 10−1 and 2.31 × 10−1 for the F-PLM and F-WENO schemes, respectively (Zhang and MacFadyen, 2006). The results obtained with FLASH (1.71 × 10−1) and TESS (1.36 × 10−1) were slightly better.
The order of accuracy approaches unity (F-PLM: 0.90; F-WENO: 0.90; U-PLM: 0.85; U-PPM: 0.95; WHAM: 0.78; FLASH: 0.98; TESS: 0.97) when increasing the grid resolution from 400 to 1600 cells. We note that the two schemes using piecewise parabolic reconstruction, U-PPM and FLASH, have the highest order of accuracy.
In Problem 4, both the left and the right initial state have a tangential velocity component of 0.9, which limits the normal component of the left-propagating rarefaction to a value of υshell = 0.32 instead of 0.96 (Problem 2) or 0.77 (Problem 3). This fact, despite the increased inertia of the right tate, weakens the right-propagating shock weak (σshock =.46) and widens the dense shell (almost to the width of the shell in roblem 3). Because of a weaker shock and a similarly wide dense hell Problem 4 seems to be an easier one than Problem 3 for any ode based on finite differencing. However, this is not the case. The resence of a thin layer of gas with very large Lorentz factor ≈ 36) between the tail of the rarefaction wave and the ontact discontinuity requires extremely high resolution. The shear t the contact discontinuity, where the tangential velocity jumps from ≈ 0.95 to ≈ 0.77, tends to change the flow in the vicinity of the thin layer through the numerical dissipation of the scheme. As a result, the post-shock state is not well-captured and both contact discontinuity and right-propagating shock have a wrong velocity.
This problem was first considered by Mignone et al. (2005b). More recently, Zhang and MacFadyen (2006), and Wang et al. (2008) used it to test the AMR capabilities of RAM and RENZO, respectively. A correct solution (still with visible errors in the transverse velocity at the contact discontinuity) can be obtained with RAM (F-WENO scheme) employing 8 refinement levels, a refinement factor of 2, and 400 cells at the lowest grid level (equivalent fixed grid resolution of 51200 cells; see Figure 19), while RENZO (HLL-PLM scheme) requires 4 refinement levels, a refinement factor of 3, and also 400 cells at the lowest level (equivalent fixed grid resolution of 25 600 cells). TESS captures the position of both the contact discontinuity and the right-propagating shock (although with apparent errors in the intermediate state) with a moving mesh of an effective fixed grid resolution of roughly 10000 cells.
Results from Zhang and MacFadyen (2006) for the relativistic blast wave Problem 4 with non-zero tangential velocity at t = 0.6 obtained with the F-WENO scheme and AMR at three different resolutions equivalent to 400 (top), 3200 (middle), and 51 200 (bottom) cells. Colored lines in the different panels show density and pressure (left), normal velocity (middle), and transverse velocity (right). The black lines show the exact solutions. Image reproduced with permission from Figure 9 of Zhang and MacFadyen (2006), copyrighty by AAS.
The absolute density errors obtained with 400 cells for RAM (F-WENO scheme), WHAM, FLASH, and TESS are 5.21 × 10−1, 4.13 × 10−1, 3.25 × 10−1, and 7.12 × 10−1, respectively. The corresponding orders of accuracy when increasing the grid resolution from 400 to 1600 cells are 0.58, 0.75, and 0.64, respectively. Ryu et al. (2006) considered Problem 3 and other tests in Pons et al. (2000) for a relativistic perfect gas and obtained converged correct solutions with 217 (131 072) cells.
Meliani et al. (2007) considered the nine combinations of Problem 2 in Pons et al. (2000) with tangential speeds υt = (0,0.9, 0.99) in the left and right initial states. For small tangential velocities, the authors use a resolution of 200 cells on the base level, and four levels of AMR refinement. However, initial states with high tangential velocities could only be simulated with a higher base resolution of 400 cells and 10 levels of refinement.
Despite its known limitations in the description of smooth flows, Glimm’s random choice method (Glimm, 1965; Chorin, 1976) performs very well when simulating problems that involve shocks. It yields global errors ≈ 1–3 orders of magnitude smaller than traditional techniques. In the relativistic case, the strongest differences arise in problems with shear flows, like Problems 3 and 4 (absolute density error with 400 cells: 5.9 × 10−2 for Problem 3, and 9.6 × 10−3 for Problem 4; Cannizzo et al., 2008). The contact discontinuity and the right-propagating shock are captured at the correct position (≈ 1–2 points off) without numerical diffusion. Constant states are reproduced exactly (i.e., to within machine precision).
6.4 Numerical RMHD: Smooth flows with Alfvén waves
As in RHD, one uses various kinds of analytic smooth solutions to test the order of convergence (when increasing the grid resolution) of RMHD codes. In 1D the convergence tests probe the formal spatial and temporal order of the scheme, whereas in the multidimensional case, they provide the accuracy of the multidimensional scheme (i.e., the spatial reconstruction and time advance including the ∇ · B = 0 constraint).
The properties of classical (i.e., non-relativistic) Alfvén waves are summarized, for example, in Jeffrey and Taniuti (1964). The thermodynamic variables (e.g., pressure, density, entropy), the magnetic pressure, the normal components of the velocity and magnetic field, and the wave speed are invariant in Alfvén waves, whereas the tangential components of the magnetic field and the flow velocity rotate by an arbitrary angle.
Since only the components tangential to the wave front change across the wave, classical Alfvén waves are often referred to as transverse waves. They are linearly degenerate, because the wave speed does not change across the wave. This has two interesting implications. Firstly, one can construct smooth extended Alfvén waves of any amplitude (not necessarily small), and secondly discontinuous Alfvén waves (i.e., Alfvén shocks) cannot be produced by steepening but only by discontinuous initial conditions.
When Komissarov (1997) analyzed the properties of Alfvén waves in RMHD he found that the normal component of the fluid velocity can change across the wave (if the amplitude is large) and the tangential components of both the magnetic field and the flow velocity can rotate and change their moduli. Hence, in a relativistic Alfvén wave, there are normal vector components that can change across the wave, i.e., relativistic Alfvén waves are not transverse. The tips of the vectors representing the tangential components of the waves’ magnetic field and flow velocity are located, in general, on ellipses instead of circles. De Villiers and Hawley (2003) derived expressions for small amplitude Alfvén waves propagating in a uniform background magnetic field with constant fluid velocity.
Several groups developed various tests based on small-amplitude (De Villiers and Hawley, 2003; Del Zanna et al., 2003; Gammie and Tóth, 2003; Anninos et al., 2005; Leismann et al., 2005; Mizuno et al., 2006) and large-amplitude (Komissarov, 1999a; Koldoba et al., 2002; Duez et al., 2005; Shibata and Sekiguchi, 2005; Del Zanna et al., 2007; Mignone et al., 2009; Antón et al., 2010; Beckwith and Stone, 2011) Alfvén waves to assess the consistency and accuracy of their codes. In the following, some of these results will be discussed, in particular those devoted to testing the order of convergence of the numerical schemes.
6.4.1 Circularly-polarized Alfvén waves
Del Zanna et al. (2003) studied the evolution of small-amplitude circularly polarized Alfvén waves. As a particular case of the solutions discussed in De Villiers and Hawley (2003), they considered a homogeneous state in the fluid rest frame characterized by a magnetic field B0, pressure p0, and density ρ0. In the limit of small amplitudes, the modulus of the magnetic field is conserved, the wave speed (i.e., the Alfvén speed; see Section 3.1) is given by \({{c}_{a}}={{B}_{0}}/\sqrt{\mathcal{E}}\), where \(\mathcal{E} = {\rho _0}{h_0} + B_0^2\), and h0 is the specific enthalpy of the fluid. The relation between velocity and magnetic field perturbations reduces to \(\delta v=\pm \delta B/\sqrt{\mathcal{E}}\), similarly to classical MHD, although in the latter case \(\mathcal{E}\) contains contributions beyond the proper rest-mass density.
To generate a circularly polarized Alfvén wave, one defines in a generic Cartesian reference frame (ξ, η, ζ) an initial state with υξ = 0, Bξ = B0, and
where A is a small amplitude, and λ is the wavelength. The corresponding magnetic field component is given by
. Under these conditions, the wave takes on its initial state again after one period, T = λ/ca.
The specific initial conditions considered by Del Zanna et al. (2003) were ρ0 = 1, p0 = 0.1, A = 0. 01, and λ= 1. They performed simulations in 1D with (ξ, η, ζ) = (x, y,z) and B0 = 1, and in 2D with \((\xi,\eta,\varsigma) = ((x + y)/\sqrt 2,\;(- x + y)/\sqrt 2,\;z)\) and \({B_0} = \sqrt 2 \) studying the high resolution properties of their code. Using the L1-norm errors of the z-component of the fluid velocity calculated after one period they confirmed that both the 1D and 2D versions of their CENO3-HLL-MM scheme are third-order accurate. Leismann et al. (2005) found second-order accuracy for their 2D RMHD code utilizing both piecewise linear and piecewise parabolic reconstructions.
Applying slightly modified initial conditions (\({{\rho }_{0}}=1,\;{{p}_{0}}=1,\;A=0.01,\;\lambda =1,\;{{v}^{x}}=0,\;{{v}^{y}}=A\cos \left( {2\pi x} \right),\;{{v}^{z}}=0,\;{{B}^{x}}={{B}_{0}}=1,\;{{B}^{y}}=-\sqrt{\varepsilon }{{v}^{y}}\), and \({B^z} = 0\)) Mizuno et al. (2006) studied the convergence properties of the RAISHIN code in 1D. They tested several second-order (linear interpolation with MINMOD and MC limiters; see Section 4.3.1) and third-order (CENO, PP interpolation) reconstruction procedures. None of the tested algorithms achieved second-order accuracy, the order of accuracy becoming even worse with finer resolution, probably due to the growth of round-off errors.
Del Zanna et al. (2007) extended the above studies considering large amplitude circularly polarized Alfvén waves. Their test problem has two advantages. Firstly, an exact solution of the problem exists, while the solution of the previously studied RMHD Alfvén wave tests is exact only in the limit of no perturbation. Secondly, since the test involves large amplitude perturbations, round-off errors are insignificant. Both properties make this test well-suited to assess RMHD schemes with a very high order of accuracy.
Del Zanna et al. (2007) looked for an exact, large amplitude solution with the same properties as the linear one described above: (i) with unperturbed thermodynamic quantities, (ii) the transverse components of the magnetic field and the fluid flow velocity as the only variables, which are parallel to each other, and (iii) with vector tips describing circles in the plane normal to the unperturbed magnetic field, B0.
With Bx = B0 and υx = 0 the transverse velocity components are
and
In the previous expressions, the speed of the Alfvén wave, υa, is unknown. Its value can be obtained, however, from the transversal components of the RMHD momentum equation:
Notice that in the small amplitude limit (A ≪ 1) the expression for ca is retrieved, and that the expression for υa is different from the one in Eq. (85) of Del Zanna et al. (2007), though equivalent.
Del Zanna et al. (2007) utilized this test to assess the order of accuracy of their code ECHO, which incorporates schemes that are nominally second, third and fifth-order accurate. Using the L1-norm errors of one of the transverse quantities (υz) calculated after one period they confirmed the nominal order of the schemes for 1D and 2D test flow problems. Relying on the same test, Beckwith and Stone (2011) demonstrated the second-order accuracy of the RMHD module of ATHENA for 1D, 2D, and 3D flows.
6.4.2 Large-amplitude smooth non-periodic Alfvén waves
Komissarov included an Alfvén wave of this kind in his set of 1D tests for numerical RMHD (Komissarov, 1999a, 2002a). Figure 20 shows his results together with the analytic solution at two epochs. A detailed derivation of the latter can be found in the Appendix B of Duez et al. (2005). The numerical dissipation of Komissarov’s code (1999a) creates perturbations in the pressure distribution of the wave which are advected along with it. No converged results for the scheme were presented. Duez et al. (2005) and Shibata and Sekiguchi (2005) used the same test to demonstrate the second-order convergence of their respective codes. Koldoba et al. (2002) constructed another solution to assess the consistency of their approximate Riemann solver.
Propagation of a large-amplitude continuous Alfvén wave. The initial conditions are given by the discontinuous lines in the different panels. Also shown are the numerical solution at t = 2 (crosses) and the exact solution (continuous line) at the same time. Two characteristic properties of relativistic Alfvén waves can be noticed: the change in the normal component of the fluid velocity, and the asymmetry in the amplitude of the tangential magnetic field at the two sides of the wave. Image reproduced with permission from Figure 5 of Komissarov (1999a), copyright by RAS.
6.5 Numerical RMHD: Riemann problems
A few Riemann test problems for RMHD were constructed by Dubal (1991) and van Putten (1993a), while Komissarov (1999a) and Balsara (2001a) considered a whole series of Riemann problems that have become a test bench for RMHD codes assessing their accuracy, stability, and diffusivity. Ever since Giacomazzo and Rezzolla (2006) presented a procedure to derive analytic solution, the results on RMHD test problems were compared with their analytic solutions, allowing one to evaluate the order of accuracy of the codes for solutions involving discontinuities and to test the accuracy of Riemann solvers quantitatively.
The general RMHD Riemann problem (see Giacomazzo and Rezzolla, 2006, and Section 8.6) involves a set of seven waves: two fast waves, two slow waves, two (discontinuous) Alfvén waves, and a contact discontinuity at which only the density can be discontinuous. The fast and slow waves are nonlinear and can be either shocks or rarefactions. The remaining three waves are linear.
Two different cases can arise depending on the component of the magnetic field normal to the initial discontinuity. If this component is zero (Type I degeneracy; see Section 3.2), the structure of the solution is very similar to the hydrodynamic one. It consists of the two fast waves and a tangential discontinuity across which only the total pressure and the normal component of the velocity are continuous. Otherwise, if the magnetic field has a non-vanishing normal component, the decay of the initial discontinuity involves all seven waves, except for planar Riemann problems where the magnetic field and the flow velocity are coplanar. In the latter case the Alfvén waves are absent.
Table 4 lists the initial data of a set of tests proposed in Komissarov (1999a), Balsara (2001a) and Giacomazzo and Rezzolla (2006). In the first two tests (Ko2, GR1) the normal component of the magnetic field is zero, i.e., the solution involves only three waves. Test Ko1 is a particular case of a Type II degeneracy (see Section 3.2), for which the flow is purely hydrodynamic. This test and the next five ones (Ko3, Ba1-4) are planar Riemann problems, whereas the two last tests (Ba5, GR2) are generic ones involving all seven waves. Test Ba1 was first proposed by van Putten (1993a). It is the relativistic extension of the test by Brio and Wu (1988) in classical MHD and involves the formation of a compound wave (see Section 3.2).
In the following sections we will summarize the results of the RMHD tests listed in Table 4. We split the discussion of the tests into three groups of increasing difficulty: Riemann problems with purely tangential magnetic fields, planar Riemann problems, and generic Riemann problems.
6.5.1 Riemann problems with purely tangential magnetic fields
The second-order code of Komissarov (1999a) is unable to capture the thin, moderately relativistic (Lorentz factor about 2) shell of shocked gas of test Ko2 with 500 cells. His code also produces noticeable overshoots and undershoots in the rarefaction tails, and exhibits post-shock oscillations. These results are similar to those obtained with HARM, while the piecewise parabolic reconstruction schemes in Duez et al. (2005); Shibata and Sekiguchi (2005) give slightly better (i.e., less dissipative) results.
Van der Holst et al. (2008) simulated a couple of tests with purely tangential magnetic fields (Ko2 and GR1 in Table 4) with their multidimensional grid-adaptive code. In test Ko2, the code captures well all the details of the analytic solution including the analytic density value of the shell. The code has a small numerical diffusivity smearing the shock by only 2–3 cells. Test GR1 also involves only three waves (a left propagating shock, a tangential discontinuity, and a right propagating rarefaction), but has a more complex structure than the one in test Ko2, because the y- and z-components of the magnetic field and the flow velocity are non-zero. The code of van der Holst et al. produces overshoots at both the shock and the tangential discontinuity, which can be reduced only by increasing the grid resolution significantly. However, even then υz undershoots at the tangential discontinuity.
6.5.2 Planar Riemann problems
Test Ko1 is a particular case of planar Riemann problem, in which the magnetic field is normal to the initial discontinuity, making the flow purely hydrodynamic except for the contribution of the magnetic pressure to the total pressure. Due to the large initial pressure jump, the break-up of the initial discontinuity produces a strong blast wave (compression ratio about 9, Lorentz factor larger than 2).
As in test Ko2, the code of Komissarov (1999a) is unable to capture the thin shell of shocked gas of test Ko1 with 400 cells. Again, the scheme produces noticeable overshoots and undershoots at rarefaction tails, and post-shock oscillations. The results are similar to those obtained with code HARM. The scheme of Duez et al. (2005) again produces slightly better results than Komissarov’s code does. When Shibata and Sekiguchi (2005) performed test Ko1, they noticed a large bump in the flow velocity (linked to an overshoot of the shell density) associated with the limiter used in the piecewise parabolic interpolation.
With a four times larger resolution (1600 cells), the code of Balsara (2001a), which reconstructs the characteristic variables, captures almost all thin structures in tests Ba1 to Ba4. This holds particularly for tests Ba2 and Ba3, and the state between the right-propagating slow and fast shocks. Neither overshoots nor undershoots at rarefaction tails and also no postshock oscillations developed. The code resolves shocks, particularly fast shocks, with a few cells only.
The numerical setup used by Del Zanna et al. (2003) allows for a direct comparison with Balsara’s results. Focusing on tests Ba2 and Ba3, Del Zanna et al. found that their CENO3-HLL-MC scheme produces overshoots and undershoots at rarefaction tails. It also appears to be more diffusive at contacts and somewhat more accurate in capturing thin structures. The first two results can be attributed to the fact that primitive variables are reconstructed, whereas the increased accuracy stems from the third-order spatial accuracy of the CENO scheme. Running test Ba3, Leismann et al. (2005) obtained comparable results to those of Del Zanna et al..
Mignone and Bodo (2006) simulated several RMHD Riemann problems including tests Ba2 and Ba3 and compared the accuracy of the HLLC Riemann solver with that of the HLL one. Their results obtained with the second-order accurate MUSCL-Hancock scheme are the best in terms of accuracy (thin structures are captured with relative errors of only few percent), stability (i.e., no visible overshoots or undershoots at rarefaction tails), and with respect to the smearing of shocks or contacts (Figure 21).
Results for the planar Riemann problem Ba3 obtained on a grid of 1600 cells with the second-order scheme of Mignone and Bodo (2006), which is based on the MUSCL-HANCOCK scheme, the HLLC Riemann solver, and linear reconstruction with the van Leer limiter. The relative error is 1.2% for the density at the peak located between the slow and fast shock (propagating to the right). The corresponding peak values of υy and By are 13% and 5% less than their exact values. Image reproduced with permission from Figure 7 from Mignone and Bodo (2006), copyright by the authors.
Mizuno et al. (2006) found that 400 cells were insufficient to capture the thin structures present in test Ba2 and Ba3 with their code RAISHIN, even when using third-order reconstruction routines (piecewise parabolic, ENO). The density in the shell between the contact discontinuity and the slow magnetosonic shock was 30% too low. Moreover, both the mildly relativistic tangential flow and the strong tangential magnetic field between the fast and the slow magnetosonic shock waves were completely smeared out.
Giacomazzo and Rezzolla (2007) performed tests Ba2 and Ba3 with WhiskyMHD using 1600 cells. Their figures unfortunately do not allow one to assess the capabilities of their code in capturing thin structures, like those in test Ba3, but the numerical solution seems to be accurate and free of spurious oscillations. Two further works considered tests Ba2 and Ba3 to check the performance of AMR modules (Anderson et al., 2006; van der Holst et al., 2008). The unigrid simulations with the third-order code of Anderson et al. (2006) required 8000 cells to properly capture the dense shell of test Ba3. The results presented for tests Ba2 and Ba3 in van der Holst et al. (2008) are accurate and free of spurious oscillations, but the contact discontinuity and the fast shock are smeared out over too many points.
Tests Ko3 and Ba4 are particular cases of planar Riemann problems, where two identical slabs of magnetized plasma collide with a Lorentz factor of 5.1 (Ko3), and 22.4 (Ba4), respectively. The symmetry of the problem reduces the number of waves emanating from the collision point to four, a fast and slow shock propagating to the left and a fast and slow shock propagating to the right. Table 4 lists the works that considered these collision tests. In general, the constant states are correctly captured without any postshock oscillations, except for RAISHIN, which produces (asymmetric) pronounced oscillations behind the fast shocks.
A common problem in tests Ko3 and Ba4 is wall heating (see Section 6.2) at the collision point, which gives rise to a dip in the density profile that is less pronounced for more viscous schemes. Hence, second-order schemes with more diffusive Riemann solvers (e.g., HLL) produce shallower dips than third-order schemes with more elaborate Riemann solvers (e.g., HLLC). Some authors (Mignone et al., 2009; Antón et al., 2010) also considered tests Ko3 and Ba4 to assess the accuracy of various Riemann solvers in handling discontinuities. They found that slow shocks are better resolved when using HLLC instead of HLL, and HLLD instead of HLLC, and equally well resolved with HLLD and FWD.
Test Ba1 is one of the test introduced by Brio and Wu (1988) to proof the non-convex character of the classical MHD equations. The test, which was adapted to the relativistic case by van Putten (1993a), consists of a fast rarefaction and slow compound wave propagating to the left, a contact discontinuity, and a slow shock and fast rarefaction propagating to the right. The debate about the physical relevance of solutions of the Riemann problem involving compound waves, and the lack of an analytic solution (the compound wave consisting of a slow shock attached to a rarefaction of the same family is treated as a slow shock in Giacomazzo and Rezzolla (2006)) limits somehow the interest in this test. Apart from capturing the compound wave, the various codes perform similarly as in the previously discussed tests. Duffell and MacFadyen (2011) considered this test with TESS and found that the contact discontinuity, the shock, and the state in between both are captured much better with the moving mesh than with a fixed one.
6.5.3 Generic Riemann problems
Only two tests in Table 4 (Ba5 and GR2) are generic RMHD Riemann problems allowing all seven waves to emerge after the decay of the initial discontinuity. Test Ba5 produces a fast shock, an Alfvén discontinuity and a slow rarefaction wave propagating to the left, a contact discontinuity, and a slow shock, a Alfvén discontinuity and a fast shock propagating to the right. In the test GR2, instead, the magnetosonic waves propagating to the left are a fast rarefaction and a slow shock. Both tests produce rather thin states between the Alfvén waves and the slow waves on both sides of the initial discontinuity.
Mignone et al. (2009) and Antón et al. (2010) used tests Ba5 and GR2 to assess the accuracy of the Riemann solvers HLL, HLLC, HLLD, and FWD. Their results were similar to those obtained for tests Ko3 and Ba4 (see above), namely that HLLD and FWD are more accurate solvers than HLL and HLLC. The 800 cells used in the calculations of test GR2 were barely sufficient to detect the increase of the tangential magnetic field between the Alfvén discontinuity and the fast shock propagating to the right, but insufficient to detect the tangential flow in the same region (see Figures 22 and 23). These statements also hold for the states between the slow waves and the Alfvén discontinuities in test Ba5.
Results for the generic Riemann problem GR2 computed with the HLL, HLLC, and FWD Riemann solver. The computation were performed on a grid of 800 cells with a second-order RK method with no spatial reconstruction. Image reproduced with permission from Figure 10 of Antón et al. (2010), copyright by AAS.
Balsara (2001a) reproduced test Ba5 quite well with a grid of 1600 cells. The profiles show no numerical oscillations, the numerical diffusion is small, and all the thin states are recovered except for the profiles of υx, υy, and By between the slow rarefaction and Alfvén wave propagating to the left. Mizuno et al. (2006) used only 400 cells, which are clearly insufficient to capture the thin structures. Moreover, their results display some spurious oscillations (well visible in the results obtained with the piecewise parabolic version of RAISHIN). The same comments hold for the results obtained for test GR2.
The WhiskyMHD results for test BA5 look accurate and show no numerical oscillations judging from the profiles of the rest mass density and the y-component of the magnetic field. These are shown in Giacomazzo and Rezzolla (2007), however, only for 160 of the 1600 cells used in their calculations. The AMR results of van der Holst et al. (2008) also look accurate and stable both for tests Ba5 and GR2. Again this judgment is based on restricted information, because only the rest mass density and the z-component of the magnetic field are shown for test Ba5, and only the rest mass density and the y-component of the flow velocity for test GR2. Beckwith and Stone (2011) simulated problem Ba5 in 3D, which provides a test of the multidimensional parts of their scheme including the constrained transport algorithm to update the magnetic field. The results are accurate too, but the scales used in the figures prevent a more precise assessment of their code.
6.6 Numerical RMHD: Multidimensional tests
6.6.1 Blast waves
Despite the lack of an analytic solution, the evolution of cylindrical or spherical blast waves into a magnetically dominated medium are a standard test for multidimensional numerical schemes in RMHD. First blast wave results were presented by Dubal (1991), which indicated severe problems of his scheme with this test, and by van Putten (1995), who achieved maximum expansion speed of 0.35. Some years later, Komissarov (1999a) proposed a setup for the study of the propagation of cylindrical blast waves that became standard.
The setup consists of a square Cartesian grid of side length L with N × N cells, which is filled with a homogeneous gas at rest with a pressure pa, a density ρa, and a magnetic field Ba(aligned with the x-axis). The explosion is initiated at the grid center by setting the pressure and density of the gas inside a sphere of radius ri to values pi and ρ;i, respectively. Outside the central sphere the properties of the gas vary smoothly (linearly, exponentially) reaching those of the ambient gas at some radius ra (> ri). The important parameters of the blast wave test are the initial ambient magnetization \(({\beta _a} = B_a^2/2{p_a})\) and the Alfvén speed in the ambient medium \(({c_{a,\;{\rm{amb}}}} = {B_a}/\sqrt {{\rho _a}{h_a} + B_a^2})\).
In Komissarov’s original setup, pa = 3 × 10−5, ρa = 10−4, Ba ∈ 0.01, 0.1,1.0, pi = 1.0, and ρi = 10−2. The grid length and the number of cells per dimension were L = 12 and N = 200, respectively. The initial radius of the blast wave was ri = 0.8 ≈ 13.3Δx and the radius of the outer edge of the transition layer was ra = 1.0 ≈ 16.6Δx, where Δx = L/N was the cell size.
The homogeneous magnetic field permeating the numerical domain breaks the otherwise initial cylindrical symmetry of the problem. Along the x-axis there is no tangential magnetic field and the flow is purely hydrodynamic, while along the y-axis there is no normal magnetic field and the blast wave compresses the tangential magnetic field. The main features of the solution are three concentric discontinuities. The outermost one is a fast forward shock which is almost circular since the fast speed is very close to the speed of light in all directions. The innermost discontinuity is a strong reverse shock, which has an oblate shape, because the magnetic field is aligned with the direction of shock propagation in x-direction, but perpendicular to it in y-direction. Between the two fast shocks there is a contact discontinuity. Near the center, the expansion is almost circular, because the gas pressure dominates the magnetic pressure. Figure 24 shows contour plots of some quantities of a mildly magnetized cylindrical blast wave at time t = 4. 0.
Results for the cylindrical blast wave test with moderate magnetization (βα = 10.0; see Table 5) obtained with ECHO. Shown are contour plots (of the logarithm) of the rest-mass density (top left), pressure (top right), Lorentz factor (bottom left), and magnetic pressure (bottom right). Image reproduced with permission from Figure 4 of Del Zanna et al. (2007), copyright by ESO.
Several authors used this setup with slight modifications to simulate cylindrical blast waves in 2D planar symmetry (Komissarov, 1999a; Del Zanna et al., 2003; Shibata and Sekiguchi, 2005; Leismann et al., 2005; Mignone and Bodo, 2006; Noble et al., 2006; Neilsen et al., 2006; Del Zanna et al., 2007; Antón et al., 2010; Beckwith and Stone, 2011; Mizuno et al., 2011a) and spherical blast waves in 3D (Anderson et al., 2006; Mignone et al., 2007). Table 5 gives an overview of these simulations. Ambient magnetizations range from 1.0 to 104, and the initial Alfvén speeds cover the mildly relativistic regime \({c_{a,\;{\rm{amb}}}} = 0.56\), i.e., \(B_a^2 \approx 0.5{\rho _a}{h_a}\)) up to the strongly relativistic one (\({c_{a,\;{\rm{amb}}}} = 0.9999\), i.e., \(B_a^2 \approx 5 \times {10^3}{\rho _a}{h_a}\)).
Besides testing the proper working of multidimensional schemes and algorithms to preserve the divergence constraint, the blast wave tests also provide information about the maximum magnetization and Alfvén speed that can be handled by RMHD codes. All authors (Komissarov, 1999a; Mignone and Bodo, 2006; Antón et al., 2010), who presented results of Komissarov’s strong magnetic field case (Ba = 1.0), used the CT approach and had to redefine the magnetic contribution to the total energy (see Section 5.7.3), and hence the total energy itself, at the end of the time step. They substituted the cell-centered magnetic field obtained after the Godunov step by the average of the face-centered magnetic field obtained from the induction equation integrated (see Section 5.7.3). Mignone and Bodo (2006) claimed that the substitution is useful when βa > 102, although it violates energy conservation at the discretization level. Komissarov (1999a) estimated the violation to be smaller than 3% in all the tests. We note that this kind of energy correction is the one usually adopted in CT schemes in classical MHD (Balsara and Spicer, 1999; Tóth, 2000).
Using ECHO, Del Zanna et al. (2007) found that for magnetizations larger than 10 they had to introduce various ad hoc numerical strategies in order to avoid numerical problems. Besides the unbalance of the different terms in the energy equation, these authors argue that another cause of these problems may be the use of independent reconstruction procedures along each spatial direction, which can lead easily to incorrect fluxes and eventually unphysical states for flow or Alfvén velocities close to the speed of light.
According to Beckwith and Stone (2011), the numerical problems observed in simulations of strongly magnetized blast waves is caused by the initial conditions, and more specifically by the maximum Lorentz factor W reached by the blast wave for test problems with the same magnetization. They suggest that the recovery of the primitive variables becomes problematic for strongly magnetized blast waves with W ≳ 4. Whether this is indeed the case or whether the problem only reflects inaccuracies in the evolution of conserved variables in strongly relativistic, strongly magnetized flows still needs to be elucidated.
Duffell and MacFadyen (2011) considered a version of the blast wave test in classical MHD with TESS. Although the code resolved the explosion reasonably well at low resolution, the violation of the divergence-free constraint became unacceptably large with time. The growth of the violation was associated with a change in topology of the Voronoi mesh in TESS during the simulation, which occurred so fast that conventional techniques of divergence-cleaning were insufficient to resolve the problem.
6.6.2 The relativistic rotor
The classical MHD rotor problem (Balsara and Spicer, 1999; Tóth, 2000) was extended to RMHD by Del Zanna et al. (2003). A disc of radius rd = 0.1 and density ρd = 10 rotating at high relativistic speed with Ωd = 9.95, i.e., the rotor, is embedded in a static background with density 1. 0. Both disc and background are in pressure equilibrium with p = 1.0 and obey an ideal gas EOS with an adiabatic index Γ = 5/3. They are permeated by an homogeneous magnetic field Bx = 1.0.
The rotation of the disc makes the gas at r = 0. 1 to move at a relativistic speed with a Lorentz factor Wmax ≈ 10. The centrifugal force resulting from the rotation causes the disc to expand producing a fast shock, which propagates into the ambient medium. The radial expansion of the disc produces an oblate shell of high density and a rarefaction in the central region. The rotation also winds up the magnetic field in the disc, which slows down the rotor.
Figure 25 shows the system at t = 0. 4. The fast shock has propagated a distance of ≈ 0. 3, and the central field lines have been twisted by an angle of almost π/2. The shell density is ≈ 7 (in x-direction) and 8 (in y-direction), respectively. The central density has decreased to a value of ≈ 0. 4, and the maximum Lorentz factor is ≈ 1.79.
Snapshots of the color-coded rest-mass density distributions of the 2D rotor problem at t = 0.4 using the code described in Antón et al. (2010). The results in the upper (bottom) panels were obtained with a grid of 10242 (1282) cells. The left, middle, and right panels show the results obtained with the FWD, HLLC, and HLL solver, respectively. Image reproduced with permission from Figure 14 of Antón et al. (2010), copyright by AAS.
The relativistic rotor test, usually set up as a 2D test with slab symmetry, also exists in a 3D version, in which the disc is replaced by a sphere. When the sphere starts rotating around the z-axis, torsional Alfvén waves propagate outward transporting angular momentum into the ambient medium. The initially spherical structure gets squeezed into an equatorial disc, which generates two symmetric reflected shocks propagating into ±z-direction. Matter in the equatorial plane (z = 0) forms a thin, octagon-like shell reminiscent of the one generated in the planar 2D case. The whole configuration is embedded in a spherical fast rarefaction (along the z-axis) or shock front (in z = 0 plane) expanding almost radially.
Although there exists no analytic solution for the test, it has been widely used to gauge the performance of RMHD codes in both 2D (Del Zanna et al., 2003; Shibata and Sekiguchi, 2005; Neilsen et al., 2006; van der Holst et al., 2008; Antón et al., 2010; Etienne et al., 2010; Duffell and MacFadyen, 2011; Keppens et al., 2012) and 3D (Anderson et al., 2006; Mignone et al., 2009; Mizuno et al., 2011a). Convergence studies were hampered by the characteristics of the initial data, which produce a large gradient of the Lorentz factor near the edge of the disk. At a (typical) resolution of 500 cells (per unit length), the Lorentz factor decreases from 10 at the edge of the disc to 4.5 at the next grid point inside the disc. The situation becomes worse if non-adapted (i.e., Cartesian) coordinates are used. Whereas there were some claims of convergence (Shibata and Sekiguchi, 2005; Etienne et al., 2010), a quantitative study (Etienne et al., 2010) found none, i.e., the convergence rates were less than first order.
The results of different studies are consistent except for discrepancies that are related to the existence of small density corrugations in the shear flow at the edge of the disk. The latter were found in the 2D case by Del Zanna et al. (2003) and analyzed in detail by van der Holst et al. (2008) using AMRVAC. The latter authors simulated the rotor evolution at higher resolution (effective resolution equal to 6400 cells per unit length using seven refinement levels) for a longer time (until t = 0.8) and found no evidence of any shear induced fine structure. The same result was reported by Antón et al. (2010). In the 3D case, the differences concern the shape of the shell, octagonal in Mignone et al. (2009) and elliptical in Mizuno et al. (2011a).
A couple of works Mignone et al. (2009); Antón et al. (2010) used the rotor test to compare the performance of Riemann solvers, namely HLL, HLLC, HLLD, and FWD in 2D and 3D. For the 3D case, Mignone et al. (2009) reported that HLL needs twice the number of cells than HLLD to capture some of the features of the solution. In terms of computational cost, the HLLD solver requires approximately 1.6 times more computational time than HLL. However, it is still the more efficient solver, because the grid resolution must be doubled to reach a comparable level of accuracy with the HLL solver, which increases the computational costs by a factor ≈ 23 in 2D and ≈ 24 in 3D, respectively. The HLLC Mignone and Bodo (2005) failed to pass this test, most likely because of the flux-singularity arising in 3D computations in the zero normal field limit. The 2D rotor tests simulated by Antón et al. (2010) showed no significant differences in the performance of the HLLC and FWD solvers. We note that the simpler HLL solver was utilized in the codes in Del Zanna et al. (2003); Mizuno et al. (2011a); Duffell and MacFadyen (2011).
Anderson et al. (2006) performed three unigrid simulations with 400, 800, and 1600 cells (per unit length) to test the hyperbolic divergence cleaning. At t = 0. 4, the L2-norm error of the ∇ · B = 0 constraint is three times larger than without cleaning and decreases linearly with the grid resolution. At the highest resolution, the maximum relative pressure difference is a few percent (in the z = 0-plane) between simulations with and without divergence cleaning. The constraint violation seems to saturate already at t = 0.4 with the hyperbolic cleaning applied by Anderson et al., while it seems to continue growing linearly at t = 0.8 with the parabolic cleaning used by van der Holst et al. (2008). The analysis of van der Holst et al. also showed that the largest violations of the constraint occur at the shock fronts.
Etienne et al. (2010) presented an interesting analysis of the conservation of angular momentum in the rotor test. Different from linear momentum, angular momentum is not conserved to machine accuracy by conservative schemes in Cartesian coordinates. Etienne et al. (2010) found that the angular momentum of the system changed by 1.7%, 1.2%, and 1.0% for a resolution of 250 × 250, 400 × 400, and 500 × 500 cells, respectively. The authors attribute this slow convergence to the fact that the initial steep Lorentz factor gradient near the edge of the rotor is insufficiently resolved. The authors found that the numerically computed initial angular momentum deviates from the analytic value by 6.8%, 2.7% and 1.8% for resolutions Nx = Ny = 250,400, 500, respectively. They claim that the angular momentum conservation would improve substantially, if the thin layer near the edge of the rotor is well-resolved.
Some works also considered the rotor test to assess different aspects of AMR modules (Anderson et al., 2006; van der Holst et al., 2008; Keppens et al., 2012)
6.7 Relativistic KH instability in RHD and RMHD
6.7.1 Linear regime
The KH instability (in the simplest case a tangential velocity discontinuity at the interface of parallel flows) is one of the most important classical instabilities in fluid dynamics. Linear perturbation analyses of the KH instability have been presented for many situations including incompressible and compressible fluids, surface tension, finite shear layers, and magnetized fluids (Chandrasekhar, 1961; Gill, 1965; Gerwin, 1968).
Astrophysical applications in the context of extragalactic jets promoted studies of the KH instability in the relativistic regime. For fluids in relativistic relative motion Turland and Scheuer (1976); Blandford and Pringle (1976) developed the linear analysis of the KH instability in the infinite, single-vortex-sheet approximation. The general dispersion relation for relativistic cylindrical jets was obtained and solved for a range of parameter combinations of astrophysical interest in Ferrari et al. (1978); Hardee (1979); Hardee et al. (1998). A complete 3D analysis of the normal modes (leading to helical, elliptical and higher-order asymmetric modes) was presented in Hardee (2000). Further investigations considered the effects of magnetic fields oriented parallel to the flow (see Ferrari et al., 1980, 1981; Ray, 1981 for the analysis of the corresponding dispersion relations in the vortex-sheet approximation, and Hardee, 2007; Mizuno et al., 2007 for magnetized spine-sheath relativistic jets). The growth of the KH instability was studied by Birkinshaw (1991) for some particular class of cylindrical relativistic sheared jets. The study was limited, however, to low-order reflection modes and marginally relativistic flows. Perucho et al. considered the effects of very high-order reflection modes on sheared relativistic (both kinematic and thermodynamic) slab jets (Perucho et al., 2005, 2007) and full 3D, initially cylindrical jets (Perucho et al., 2010).
In a series of papers, Perucho et al. studied the effects of relativistic dynamics and thermodynamics on the development of KH instabilities in relativistic slab jets — both in the vortex-sheet approximation (Perucho et al., 2004a,b) and for sheared flows (Perucho et al., 2005) — covering the linear, saturation, and nonlinear phase of the evolution (see Figure 26) by means of hydrodynamic simulations with a 2D pre-release of the Ratpenat code. In both cases, vortex-sheet approximation and sheared flows, the linear growth rates of the different modes are reproduced by the numerical simulations with a relative error of a few percent (Figure 27) for the chosen grid resolutions.
Two snapshots of the evolution of the KH instability in the jet model B05 of Perucho et al. (2004a), i.e., for a pressure matched jet with a flow Lorentz factor 5.0, a specific internal energy 0.42, and a jet to ambient rest-mass density ratio 0.1. The jet flow is from left to right and initially filled the slab y ∈ [−1, 1]. The top four panels show various flow quantities at the end of the linear phase, very close to saturation. The bottom four panels display jet quantities in the nonlinear regime (only the upper half of the jet is shown). Image adapted from Perucho et al. (2004a,b).
Evolution of the relative amplitudes of pressure perturbations (pmax − p0)/p0 (dotted), longitudinal velocity perturbations in the jet reference frame 0.5 (υ∥max − υ∥min) (dashed), and perpendicular velocity perturbations in the jet reference frame 0.5 (υ⊥max − υ⊥min) (dashed-dotted). The solid line gives the prediction of a linear perturbation analysis. Arrows in the left panel mark specific stages in the evolution. The parameters of model B05 are given in the caption of Figure 26, and those of model D05 are identical to the parameters of model B05 except for the jet specific internal energy, which is 60.0. Image adapted from Perucho et al. (2004a).
Whether a code can correctly determine the linear growth rate of the KH modes depends critically on the numerical viscosity of the algorithm and the grid resolution. In the case of Ratpenat, the grid resolution was 400 cells (across) × 16 cells (along the jet) per jet radius. This is a compromise between accuracy and computational efficiency for the vortex-sheet models. In the case of the sheared jets, a resolution of 256 × 32 cells per beam radius and about 40 cells within the shear layer was used.
Zhang and MacFadyen (2006) used their code RAM with F-WENO-A and six levels of grid refinement to simulate the linear phase of the growth of KH modes in model D10 of Perucho et al. (2005). With an effective resolution of 256 × 32 cells per beam radius, RAM’s results are comparable to those obtained with Ratpenat. Duffell and MacFadyen (2011) computed the linear growth rates of the KH instability for subsonic, non-relativistic to moderately supersonic, mildly relativistic flows with TESS and compared them with the analytic solution calculated by Bodo et al. (2004). With a resolution of 128 cells per beam radius, the linear growth rates are captured within a 20% relative error.
Bucciantini and Del Zanna (2006) tested the RMHD code of Del Zanna et al. (2003) comparing the KH linear growth rates of subsonic and marginally supersonic, relativistic (unperturbed flow speeds 0.1 to 0.4) magnetized sheared flows. The numerical results obtained with the HLL solver differed from the analytic ones Ferrari et al. (1980) by less than 5% for a relativistically hot plasma (see Figure 28). Mignone et al. (2009) considered the same set-up, but studied the dependence of the growth rate on the Riemann solver (HLLD versus HLL) and the grid resolution. Simulations carried out with the HLLD solver at low, medium (the one used by Bucciantini and Del Zanna, 2006; 180 × 360 cells), and high resolution revealed similar growth rates, and saturation was reached at essentially the same time. When the HLL scheme is employed, the saturation phase and the growth rate during the linear phase change with resolution. Beckwith and Stone (2011) extended the comparison to the HLLC Riemann solver. In the linear regime, these authors find identical growth rates for both the HLLC and the HLLD solver, i.e., including the contact discontinuity in the Riemann solver leads to this behavior.
Amplitude of the perturbation \(\Delta {v^y} = 0.5(v_{\max }^y - v_{\min }^y)\) as a function of time for a sheared jet model with unperturbed flow speed 0.25 and aligned magnetic field. The solid line gives the numerical results and the dashed line the prediction of the analytic theory Ferrari et al. (1980). From top to bottom: β (σpol in the original paper) = 0.01, 0.05, 0.1, 0.2. The numerically determined growth rates are 0.21, 0.11, 0.16, and 0.08, respectively. These should be compared with the expectations of the linear theory, which are 0.205, 0.108, 0.165, and 0.075, respectively. Image reproduced with permission from Figure 1 of Bucciantini and Del Zanna (2006), copyright by ESO.
6.7.2 Beyond the linear regime: nonlinear turbulence
Bucciantini and Del Zanna (2006) presented a qualitative discussion of the effects of transverse and aligned magnetic fields on the development of the KH instability for flows of different speeds. They find that adding an even small aligned magnetic field component to a flow with purely transversal field beyond the linear phase changes qualitatively the development of the instability. Such a component strongly suppresses the KH growth and excites a turbulent cascade towards smaller scales.
Mignone et al. (2009) quantified the small-scale structure in nonlinear RMHD turbulence for the set-up of Bucciantini and Del Zanna (2006) computing the power residing at large wavenumbers in the discrete Fourier transform of the transverse component of velocity. During the statistically steady flow regime the HLL and HLLD solvers exhibit small-scale power that differs by more than one order of magnitude. The power is larger than 10−5 (at all resolutions) for HLLD and less than 10−6 for HLL (see Figure 29).
Top panel: KH growth rate as a function of time computed from \(\Delta {v^y} = (v_{\max }^y - v_{\min }^y)/2\) at low (L), medium (M), and high (H) resolution. The solid, dashed, and dotted lines show the results obtained with HLLD, whereas symbols refer to HLL. Bottom panel: corresponding small-scale power (see definition in Mignone et al. (2009)) as a function of time. Image reproduced with permission from Figure 16 of Mignone et al. (2009), copyright by the authors.
Beckwith and Stone (2011) computed the power spectra of density, Lorentz factor, and magnetic pressure for the tests of Bucciantini and Del Zanna (2006); Mignone et al. (2009) concluding that the differences between the integrated powers obtained with HLLC and HLLD are small at any resolution. The HLL results tend to match those obtained with HLLC and HLLD at sufficiently high resolution for the integrated power of density and Lorentz factor, but remain smaller by more than one order of magnitude at any resolution for the integrated power in magnetic pressure. Thus, the choice of the Riemann solver can play an important role in determining the overall spectral resolution of a given integration scheme.
In 3D simulations of the KH instability Beckwith and Stone (2011), the power spectra of density, Lorentz factor, and magnetic pressure differed at small scales (wavenumber k ≥ 100) by more than two orders of magnitude between the results obtained with HLL and HLLD, respectively. The initial set-up for this study was the same as in the 2D test discussed in the previous paragraph, but with an additional 1% Gaussian perturbation modulated by an exponential of the z-component of the 3-velocity in order to break symmetry along the z-axis.
The results of the nonlinear phase of the simulations discussed in this Section cannot be regarded as converged because of the absence of any physical dissipation (ideal RMHD). Hence, the multidimensional simulations presented here are no quantitative test of the codes. The simulations rather serve as a qualitative demonstration of the difficulties that might be encountered when using oversimplified Riemann solvers in the study of nonlinear flows.
Studies of fully-developed 3D turbulence in RHD and RMHD with the aim of determining its statistical properties were carried out by Radice and Rezzolla (2013) (with THC) and Zrake and MacFadyen (2012) (with Mara). The power spectrum of the velocity field in the inertial range was found to be in good agreement with the predictions of the classical theory of Kolmogorov, which hence seems to apply at least to subsonic and mildly supersonic, relativistic flows, too.
7 Conclusion
After the pioneering work performed in the late 1970s and 1980s, based mainly on AV and FCT techniques, the last two decades have witnessed a major breakthrough in numerical relativistic astrophysics. Conservative HRSC methods were extended to both numerical RHD and RMHD. These methods satisfy in a quite natural way the basic properties required for any acceptable numerical method: (i) high order of accuracy, (ii) stable and sharp description of discontinuities, and (iii) convergence to the physically correct solution. In this review we summarize the main developments of HRSC methods including both FD and FV strategies. We also discuss the (present) performance and limitations of these methods when simulating highly relativistic (magnetized) flows.
7.1 Finite volume and finite difference methods in numerical RHD and RMHD
Finite volume methods exploit the integral form of the partial differential conservation equations. Zone averaged values are evolved in time following a sequence of steps that involves (i) the reconstruction of the variables inside the numerical cells up to a certain order, (ii) the solution of Riemann problems at cell interfaces, which are defined by the reconstructed values, to compute the intercell numerical fluxes, and (iii) the time advance of the conserved variables from their values at the previous time step using the numerical fluxes (and sources). The interpolation inside the numerical cells is done by means of conservative, monotonic functions with slope limiters to avoid the generation of spurious oscillations in the solution (TVD property). The piecewise linear and parabolic reconstructions commonly used restrict the spatial accuracy of the methods to second or third order, respectively, or smaller since the reconstruction is usually carried out on the primitive variables, which are not exactly cell averages, because they are obtained from cell averages of the conserved quantities.
Although exact solutions of the Riemann problem exist in both RHD and RMHD, one computes the numerical fluxes by means of approximate Riemann solvers or flux formulas. Linearized Riemann solvers are based on the local linearization of the system of equations and the spectral decomposition of the Jacobian matrices of the fluxes. The flux formula of Marquina, based on lateral local linearizations of the system and the corresponding spectral decompositions, and the modified Marquina flux formula (which applies the local Lax-Friedrichs flux to all characteristic fields) have become a standard in numerical RHD. Among the Riemann solvers that avoid the computationally expensive local spectral decompositions are the HLL Riemann solver and its extensions HLLC and HLLD (in RMHD).
The equations are advanced in time using the method of lines which leads to a system of ordinary differential equations that can be integrated with high-order predictor-corrector methods. Of special interest are the second-order and third-order TVD-RK time discretization algorithms although standard fourth-order and fifth-order Runge-Kutta methods have been applied, too. The single-step MUSCL-Hancock method gives the best results at the highest computational efficiency. In multidimensional problems, the fluxes in different coordinate directions are computed and used to advance the equations simultaneously. The CTU method consists of two steps: one interpolates variables to the interfaces using information from all coordinate directions, and then one solves the Riemann problem.
In FD methods, the pointwise values of the conserved variables are advanced in time. Within this category, algorithms based on ENO reconstruction techniques (CENO, ENO, WENO) are the most successful ones. In combination with high-order Runge-Kutta methods they lead to schemes that are third-order to fifth-order accurate.
Numerical codes for RMHD should involve an additional algorithm to preserve the divergence-free character of the physical magnetic field. Among the different strategies, the constrained transport (CT) techniques are the most widely used ones. In their original form, CT techniques require the introduction of an additional staggered magnetic field variable, which is advanced in time using the induction equation and suitable interpolations to the cell edges of quantities (magnetic fields, velocities, and fluxes) of the HRSC scheme. Because of these interpolations and those needed to obtain the cell-centered magnetic field from the staggered magnetic field, the accuracy of the whole algorithms is reduced to second order. The most recent developments have focused on the construction of high-order upwind numerical fluxes in the induction equation and the use of more accurate reconstruction procedures for the cell-centered magnetic fields to surpass second-order accuracy.
7.2 Present limitations of HRSC methods for RHD and RMHD
7.2.1 Accuracy limits and the conserved-primitive variables mapping
Using conserved variables for the time advance in HRSC methods requires the recovery of the primitive variables after each time (sub)step. Whereas the mapping between conserved and primitive variables can be written in closed form in classical hydrodynamics and MHD, this mapping is defined only implicitly in the relativistic case, i.e., it involves an iterative recovery procedure. The requirement that this procedure is actually capable of obtaining the primitive variables from the conserved ones places limits on the range of flows that can be studied with the numerical code. In practice, the limits are set by the relative size of the various contributions to the total energy density of the flow, i.e., rest-mass, internal energy, kinetic energy, and (in the RMHD case) magnetic energy. As a result, the accuracy of the recovery procedure decreases in the ultrarelativistic limit where the kinetic energy dominates all other energies, in the non-relativistic limit where the kinetic energy becomes much smaller than the rest-mass and/or the internal energy, in the limit of low internal energy (pressure), and in the limit of high magnetization (i.e., large β and κ).
There are two sources of error that are responsible for the limited applicability of numerical schemes in RHD and RMHD. The first source are truncation errors resulting from the scheme as a whole which do not depend on the accuracy of the recovery procedure itself. The errors introduced by the constrained transport method (or any other method to keep the magnetic field divergence-free) belong to this class. The second source of error is the accuracy of the recovery algorithm itself which involves the solution of a set of five nonlinear equations. In the most robust and computationally fastest method one first solves the two equations for ρhW2 and υ2. The subsequent manipulation of some intermediate quantities requires that \({W_{\max }}\mathop < \limits_\sim \varepsilon _{{\rm{mp}}}^{ - 1/2}\) and \({(p/\rho {W^2})_{\min }}\mathop > \limits_\sim {\varepsilon _{{\rm{mp}}}}\), where εmp is the machine precision (i.e., Wmax ≲ 108 and pmin ≳ 10−16, ρW2 for double precision arithmetic). For magnetized flows the limit on the degree of magnetization imposes another threshold on the thermal pressure, namely pmin ≈ 10−4B2.
7.2.2 The need for high resolution
When solving hyperbolic systems high resolution is needed to describe discontinuities in the variables and in their derivatives without excessive smearing. In the case of relativistic fluid dynamics, this need is enhanced by two genuine relativistic effects. These are the Lorentz contraction and the limiting velocity of light which can give rise to very thin flow structures, good examples being the thin blast waves in Problem 2 of Section 6.3.2 and in the planar RMHD Riemann problem Ba3 of Section 6.5.2. Fixed-grid state-of-the-art HRSC codes require about 1000 to 2000 numerical cells per unit of length to obtain a converged solution in these tests. However, excessive smearing seems not to be the only consequence of poor numerical resolution. In numerical tests involving discontinuities with relativistic tangential velocities (as, e.g., Problem 4 in Section 6.3.3) the coupling of tangential and normal velocities leads to unphysical flow states and wave speeds.Footnote 7 Whereas some smearing in the representation of flow discontinuities is commonly accepted, unphysical flow states and wave speeds spoil the solution, i.e., the use of high-order methods with AMR techniques or moving grids is then necessary. Numerical studies of the growth of the (relativistic) KH instability both in the linear and nonlinear regime, and of the development of (relativistic) turbulence also foster the development of RHD codes comprising these grid features.
7.3 Current and future developments
In its early stage, the research of numerical RHD focused on the development of accurate and robust numerical methods and codes that are capable of simulating even extreme relativistic flows, i.e., flows involving large Lorentz factors and magnetic fields of relativistic strengths. Meanwhile, the research focuses on the extension of existing methods and codes to handle relativistic flows in which effects due to dissipation (viscosity, resistivity), and/or radiation are of importance. In the following sections we will briefly review these developments.
7.3.1 Viscous RHD
Classical relativistic ideal (i.e., non-viscous) hydrodynamics is well understood theoretically, and there exist well studied advanced methods to integrate the corresponding equations numerically. However, relativistic viscous hydrodynamics and relativistic quantum fluids have been explored less and only more recently, mostly in the context of the quark-gluon plasma produced in heavy-ion colliders (see, e.g., Romatschke, 2010) and for relativistic Dirac spin-1/2 quantum plasmas (Asenjo et al., 2011). The current knowledge of a relativistic theory of fluid dynamics in the presence of (mostly shear) viscosity is discussed in a comprehensive review by Romatschke (2010); see also Chapter 3 in Abramowicz and Fragile (2013), and Chapter 6 in Rezzolla and Zanotti (2013). The derivation of the corresponding fluid equations is based either on the generalized second law of thermodynamics, kinetic theory, or a complete second-order gradient expansion, the fluid equations resulting from the three derivations being consistent (Romatschke, 2010).
Particular implementations of relativistic viscous hydrodynamics were presented by Takamoto and Inutsuka (2011) who used a Riemann solver for the advection step and Strang-splitting for the source terms, and more recently by Del Zanna et al. (2013), who developed the code ECHO-QGP based on the ECHO code for simulations of the (3 + 1) spacetime evolution of the quark-gluon plasma (see also Vredevoogd and Pratt, 2012).
7.3.2 Resistive RMHD
To simulate astrophysical phenomena involving magnetic fields, the numerical methods discussed in the preceding sections are often insufficient, because the proper treatment of non-ideal effects due to magnetic dissipation and reconnection is of importance. Magnetic reconnection is a physical process in highly conducting plasmas, in which the magnetic field topology is rearranged and magnetic energy is converted into kinetic energy and thermal energy, and used to accelerate particles. Moreover, although the plasma encountered in these phenomena has a non-vanishing physical resistivity, in most cases the magnetic dissipation and reconnection observed in simulations with RMHD schemes is the result of their numerical resistivity, which depends on the resolution.
To control and properly simulate reconnection and Ohmic dissipation in a relativistic plasma there is a need for suitable numerical methods in resistive RMHD (Watanabe and Yokoyama, 2006; Komissarov, 2007). The development of such methods is challenging, because the resistivity can vary over many orders of magnitude in astrophysical phenomena, i.e., in regions of high conductivity the system will evolve on time scales which are very different from those in the low-conductivity regions.
When simulating Ohmic dissipation one has to take into account an additional term proportional to −∇ × (∇ × B) in the induction equation. Thereby, the equation becomes parabolic implying that information propagates with an infinite speed. This unphysical behavior arises because the time derivative of the electric field is neglected in the induction equation. Hence, one must evolve the electric field too, when simulating (relativistic) magnetized flows with a finite resistivity. The induction equation then becomes a telegraph equation satisfying causality (see, e.g., Komissarov, 2007). Mathematically speaking, the equations of resistive (R)MHD are either of mixed hyperbolic-parabolic type or hyperbolic with stiff source terms (if the resistivity varies strongly within the flow), and they require special numerical methods to integrate them in a stable and accurate manner (Palenzuela et al., 2009).
Watanabe and Yokoyama (2006) were the first to present a numerical study of relativistic magnetic reconnection providing, however, no details of the numerical scheme and not any test simulations. Komissarov (2007) gave the first detailed description of a numerical scheme capable of simulating RMHD flows with a finite resistivity. He employed a multidimensional HLL method in Cartesian coordinates and Strang-splitting to integrate the resistive RMHD equations for Ohm’s law with a scalar (i.e., isotropic) resistivity. The magnetic field was kept divergence-free by means of hyperbolic cleaning (see Section 5.7; Dedner et al., 2002). Because of the use of HLL, Komissarov’s method becomes very diffusive when simulating problems whose characteristic velocity is much lower than the speed of light.
A subsequent study was concerned with relativistic magnetic reconnection in an electron-positron pair plasma (Zenitani et al., 2009, 2010) using a two-fluid model with an interspecies friction force as an effective resistivity to dissipate magnetic fields. Applying a LLF approximate Riemann solver and hyperbolic cleaning (Dedner et al., 2002). Palenzuela et al. (2009) proposed an implicit-explicit (IMEX) Runge-Kutta method to integrate the equations of non-ideal RMHD for a uniform conductivity. They showed that the IMEX method, which treats stiff terms implicitly and non-stiff ones explicitly, allows for a proper treatment of both the fluid-pressure dominated and magnetic-pressure dominated flow regime.
Unstructured grids, an element-local spacetime discontinuous Galerkin approach, and hyperbolic divergence cleaning (Dedner et al., 2002) were employed by Dumbser and Zanotti (2009) and Zanotti and Dumbser (2011). This approach, which can handle properly both the resistive regime and the stiff limit of low resistivity, allowed them to simulate in 2D and 3D relativistic reconnection in a plasma giving rise to flows with Lorentz factors close to ∼ 4 (Zanotti and Dumbser, 2011).
Takamoto and Inoue (2011) proposed a method particularly suited to systems with initially weak magnetic fields and arbitrary flow speeds ranging from non-relativistic to highly relativistic ones. They employed an approximate Riemann solver to calculate the numerical flux of the fluid having a scalar resistivity and the method of characteristics to advance the electromagnetic field. They showed that their Strang-splitting method, which was used by Komissarov (2007) too, works also well when applied to discontinuous flows with low resistivity, contrary to the claim of Palenzuela et al. (2009). According to the problem encountered by Palenzuela et al. (2009) with the Strang-splitting method in that regime can be traced back to evolving the electric field during the recovery of the primitives.
The AMR version of the PLUTO code (Mignone et al., 2012) provides an option to simulate flows having a finite magnetic resistivity, which is accounted for by prescribing the resistive (diagonal) tensor. However, up to now this option is only publicly available for Newtonian MHD (see also, e.g., Keppens et al., 2013). One of the Newtonian MHD tests discussed in Mignone et al. (2012) is concerned with resistive reconnection, which was studied for various values of the magnetic resistivity in a 2D Cartesian box using PP reconstruction and a Roe Riemann solver (Roe, 1981).
7.3.3 Further developments
In order not to go beyond the scope of this review, we only mention a few further developments in the simulation of relativistic flows.
If electromagnetic fields are strong enough that hydrodynamic forces and the inertia of the plasma can be neglected, one encounters the magnetodynamic, or force-free regime, in which the Lorentz force density vanishes everywhere. Numerical studies in this ultrarelativistic limit of MHD, which is appropriate for simulating magnetically dominated GRB jets (see Section 2.2), the magnetospheres of pulsars, or pulsar wind nebulae (see Section 2.3), were performed by Contopoulos et al. (1999); Spitkovsky (2006); Tchekhovskoy et al. (2008); Parfrey et al. (2012); and Tchekhovskoy et al. (2013).
Simulating systems in relativistic astrophysics often requires besides hydrodynamics and magnetohydrodynamics also some treatment of the radiation emitted by the systems (radiative transfer) or even of the coupling between radiation and flow dynamics (radiation hydrodynamics). Numerical schemes for such simulations have been presented by Farris et al. (2008); Zanotti et al. (2011); Sadowski et al. (2013); Takahashi and Ohsuga (2013); and Takahashi et al. (2013). The first three studies were concerned with simulations of radiative flows in general dynamic spacetimes, but they also presented tests in Minkowksi spacetime for RHD (Zanotti et al., 2011; Sadowski et al., 2013) and RMHD (Farris et al., 2008). The code discussed in Zanotti et al. (2011) is an extension of the ECHO code. An explicit-implicit scheme with an approximate Riemann solver was proposed by Takahashi et al. (2013) for relativistic radiation hydrodynamics, while Takahashi and Ohsuga (2013) presented a scheme for coupling anisotropic radiation fields to relativistic resistive magnetofluids.
8 Additional Information
8.1 Spectral decomposition of the 3D RHD equations
This section, with slight variations, was already included in Martí and Müller (2003) and is maintained here for completeness.
The full spectral decomposition including the right and left eigenvectors of the Jacobian matrices associated with the RHD system in 3D was first derived by Donat et al. (1998). Martí et al.(1991) presented the spectral decomposition for 1D RHD, and Eulderink (1993) and Font et al.(1994) the eigenvalues and right eigenvectors for 3D RHD. The Jacobians of RHD are given by
where the state vector UHD and the flux vector \({\bf{F}}_{{\rm{HD}}}^i\) are the vectors defined in (9) and (10), respectively, for a vanishing magnetic field. In the following we explicitly give both the eigenvalues and the right and left eigenvectors of the Jacobi matrix ßx only (the cases i= y and i= z are easily obtained by symmetry considerations). The eigenvalues of matrix ßx are
(where cs is the sound speed and ν2 = νiνi), and
A complete set of right-eigenvectors is
where
(κ is the partial derivative of the pressure with respect to the specific internal energy at constant rest-mass density). The corresponding complete set of left-eigenvectors is
where Δ is the determinant of the matrix of right-eigenvectors, i.e.,
For an ideal gas EOS Κ = h, i.e., Κ > 1, and hence Δ ≢ 0 for \(\vert {v^x}\vert < 1\).
Finally, we note that if \({\bf{\hat l}}\) and \({\bf{\hat r}}\) are left and right eigenvectors of the system in terms of \({\tau ^{\prime}}\) (= τ − D; see Section 3.1), respectively, their components are related to those of the corresponding eigenvectors of the system in terms of τ, l, and r, according to
the remaining components being unchanged, i.e., \({\hat r_i} = {r_i}\), and \({\hat l_{i + 1}} = {l_{i + 1}}\) (i= 1, 2, 3,4).
8.2 Spectral decomposition of the 3D RMHD equations
The hyperbolicity of the equations of RMHD including the derivation of wavespeeds and the corresponding eigenvectors, and the analysis of various degeneracies was studied by Anile and Pennisi (1987) and reviewed by Anile (1989). These authors performed their analysis in a covariant framework using a set of covariant variables, in which the vector of unknowns
is extended to 10 variables, where s is the specific entropy. They cast their result in a form more suitable for numerical applications by Komissarov (1999a) (see also Balsara (2001a)), and Antón et al. (2010), which we review in the following.
In terms of variables \({\bf{\tilde U}}\), the system of RMHD equations can be written as a quasi-linear system of the form
where μ denotes the covariant derivative. The 10 × 10 matrices \({\mathcal{A}^\mu }\) are given by
with
and
The 10 covariant variables used to write down the system of equations are not independent. They are related by the constraints
and
8.2.1 Wavespeeds
If ϕ(xμ) = 0 defines a characteristic hypersurface of the system (116), the characteristic matrix, given by \({\mathcal{A}^\alpha }{\phi _\alpha }\), can be written as
where \({\phi _\mu } = {\partial _\mu }\phi,\;a = {u^\alpha }{\phi _\alpha },\;\mathcal{B} = {b^\alpha }{\phi _\alpha },\;G = {\phi ^\alpha }{\phi _\alpha },\;{l^\mu } = {l^{\mu \alpha }}{\phi _\alpha } = {\phi ^\mu } + (\rho h - {b^2}/c_s^2)a{u^\mu }/(\rho h) + \mathcal{B}{b^\mu }/(\rho h),\;{f^\mu } = {f^{\mu \alpha }}{\phi _\alpha } = (a{b^\mu }/c_s^2 - \mathcal{B}{u^\mu })/(\rho h)\) and \(m_\nu ^\mu = ({\phi ^\mu } + 2a{u^\mu }){b_\nu } - \mathcal{B}\delta _\nu ^\mu\).
Since ϕ(xμ) = 0 is a characteristic surface, the determinant of the matrix (126) must vanish, i.e.,
where
The above equations, valid for a general spacetime, can be used to obtain the wavespeeds in a flat spacetime in Cartesian coordinates. To this end, we consider a planar wave propagating along the x-axis with speed λ. The normal to the characteristic hypersurface describing this wave is given by the four-vector
Substituting Eq. (130) into Eq. (127) we obtain the characteristic polynomial, whose zeroes give the characteristic speed of the waves propagating in x-direction. There are three different kinds of waves according to which factor becomes zero in Eq. (127): for entropic waves a= 0, for Alfvén waves \(\mathcal{A} = 0\), and for magnetosonic waves \({\mathcal{N}_4} = 0\).
The characteristic speed λ of the entropic waves propagating in x-direction, given by the solution of Eq. (127) with a= 0, is
For Alfvén waves (\((\mathcal{A} = 0)\)) there exist two solutions corresponding, in general, to different wave speeds
. In the case of magnetosonic waves there are four solutions, two of them corresponding to the slow magnetosonic waves and the other two to the fast magnetosonic ones. It is however impossible, in general, to obtain simple expressions for their speeds, since these are given by the solutions of the quartic equation \({\mathcal{N}_4} = 0\) (129) with \(a,\;\mathcal{B}\), and G explicitly written in terms of λ as
As in the classical case, the seven eigenvalues corresponding to the entropic (1), Alfvén (2), slow (2) and fast (2) magnetosonic waves can be ordered as
where the subscripts e, a, s, and f denote entropic, Alfvén, slow magnetosonic, and fast magnetosonic wave, respectively, and the superscripts − or + refer to the lower or higher value of each pair. The ordering allows one to group the Alfvén and magnetosonic eigenvalues in two classes separated by the entropic eigenvalue.
In the previous discussion about the roots of the characteristic polynomial we omitted the fact that the entropy waves as well as the Alfvén waves appear as double roots. These superfluous eigenvalues are associated with unphysical waves and are the result of working with the unconstrained system of equations. We note that van Putten (1991) derived a different augmented system of RMHD equations in constrained-free form with different unphysical waves. Any attempt to develop a numerical procedure to solve the RMHD equations based on their wave structure must remove these unphysical waves (i.e., the corresponding eigenvectors) from the wave decomposition. Komissarov (1999a) and Koldoba et al. (2002) eliminate the unphysical eigenvectors by demanding the waves to preserve the values of the invariants uμuμ= −1 and uμbμ= 0 as suggested by Anile(1989). Correspondingly, Balsara (2001a) selects the physical eigenvectors by comparing with the equivalent expressions in the non-relativistic limit.
8.2.2 Degeneracies
Degeneracies are encountered for waves propagating perpendicular to (Type I) and along the direction of the magnetic field (Type II). For the Type I degeneracy, the two Alfvén waves, the entropic wave, and the two slow magnetosonic waves propagate at the same speed \((\lambda _a^ - = \lambda _s^ - = {\lambda _e} = \lambda _s^ + = \lambda _a^ +)\). For the Type II degeneracy, one of the Alfvén waves and one of the magnetosonic waves (slow or fast) belonging to the same class have the same speed \((\lambda _f^ - = \lambda _a^ -,\lambda _a^ - = \lambda _s^ -,\lambda _s^ + = \lambda _a^ +,\;{\rm{or}}\;\lambda _a^ + = \lambda _f^ +)\). Finally, in the Type II″ subcase, one of the Alfvén waves and both the slow and fast magnetosonic waves of the same class propagate at the same speed (\(\lambda _f^ - = \lambda _a^ -,\lambda _s^ -\) or \(\lambda _s^ + = \lambda _a^ + = \lambda _f^ +\)). If the Type II degeneracy is encountered in classical MHD, both Alfvén waves are of Type II″, while in RMHD this holds only for one of the Alfvén waves due to aberration effects. Only if the tangential component of the fluid velocity vanishes, one recovers the classical behavior.
Komissarov (1999a) provided a covariant characterization of the different types of degeneracy. The Type I degeneracy is encountered when \(\mathcal{B} = 0\) (see Eq. (134)) for Alfvén waves, while the Type II degeneracy arises when \({\mathcal{B}^2}/(G + {a^2}) = {b^2}\) for Alfvén waves. Antón et al. (2010) characterized both types of degeneracy in terms of the components of the magnetic field normal and tangential to the Alfvén wave front in the comoving frame, \(b_n^\alpha \) and \(b_t^\alpha \), respectively. The Type I degeneracy is encountered for \(b_n^\alpha = 0\) (magnetic field normal to the direction of propagation of the Alfvén waves), and the Type II degeneracy for \(b_t^\alpha = 0\) (magnetic field aligned with the direction of propagation of the Alfvén waves). We note that the condition \(b_n^\alpha = 0\) implies Bx= 0 for a wave propagating along the x-direction in the laboratory frame. For more details, we refer the interested reader to Antón et al. (2010).
8.2.3 Renormalized right eigenvectors
The eigenvectors given by Anile (1989) for the eigenvalue problem \(({\mathcal{A}^\mu }{\phi _\mu }){\bf{r}} = 0\) do not form a complete basis for degenerate states, because they become zero or linearly dependent. Antón et al.(2010) derived a set of eigenvectors that do not suffer from this defect, but form a complete basis both for nondegenerate and degenerate states. We omit the theoretical and technical details of their derivation here. The new ten-component renormalized right eigenvectors are given below in covariant variables. They can be transformed to the seven-component eigenvectors in conserved variables by the appropriate matrix transformations. Entropy eigenvector:
Alfvén eigenvectors:
, where
For an Alfvén wave propagating along the x-direction
and
with λ = λa±. Magnetosonic eigenvectors: The eigenvector associated with the magnetosonic eigenvalue λm± with m ϵ{s, f} reads
where λm± is the magnetosonic eigenvalue belonging to the same class as λa±, i.e.,
and
with
where Case 1 refers to the pair of magnetosonic eigenvalues (one from each class) that is closer to the Alfvén eigenvalue of the same class, and Case 2 for the remaining pair. The remaining quantities are
and
where \({\alpha _{11}} = \alpha _1^\mu {\alpha _{1\mu }},\;{\alpha _{12}} = \alpha _1^\mu {\alpha _{2\mu }},\;{\alpha _{22}} = \alpha _2^\mu {\alpha _{2\mu }}\), and f1,2 are given by Eq. (139). For a magnetosonic wave propagating along the x-direction the quantities \({\phi _\mu },a,G,\alpha _1^\nu,\alpha _2^\nu,{g_1}\), and g2 are given by Eqs. (130), (133), (135), and (140)–(143) with λ= λmα, respectively. When encountering the Type II″ degeneracy \(\mathcal{C} = 0\) for Case 1, and \(\mathcal{D} = 0\) for Case 2.
8.2.4 Right and left eigenvectors in conserved variables
To express the renormalized eigenvectors in conserved variables, one must construct the transformation matrix between the set of covariant variables, \({\bf{\tilde U}}\), and the set of the conserved ones, U, i.e., \((\partial {\bf{U}}/\partial {\bf{\tilde U}})\). Since we want to build up a Riemann solver based on the spectral decomposition of the flux vector Jacobians of the system in conservation form, and since the Riemann solver will be used to compute the numerical fluxes along the coordinate directions, we only need to consider a 1D version of system (8). We restrict our discussion here to the x-direction, along which the evolution equation for Bx reads ∂Bx/∂;t= 0, which can be removed from the system. Hence, the desired spectral decomposition will be directly worked out for the reduced 7 ×7 Jacobian of the flux vector along the x-direction, i.e., the set of conserved variables contains only seven variables and the aforementioned matrix will be of dimension 7 × 10. Its elements, the partial derivatives of the conserved variables with respect to their covariant counterparts, can be found in Antón et al.(2010)
The right eigenvectors in conserved variables, R, are computed as follows
while the calculation of the left eigenvectors is far more involved. One could obtain them by direct inversion of the matrix of right eigenvectors, but to obtain tractable expressions (Antón et al.,2010) suggested a two-step process starting from the left eigenvectors in covariant variables l. From these eigenvectors they obtain the left eigenvectors, \({\bf{\bar l}}\), in the reduced system of covariant variables, \({\bf{\tilde V}} = ({u^x},{u^y},{u^z},{b^y},{b^z},p,\rho)\), through the transformation
where \((\partial {\bf{\tilde U}}/\partial {\bf{\tilde V}})\) is the 10 ×7 matrix consisting of the partial derivatives of the covariant variables with respect to the covariant variables in the reduced system. In a second step, the left eigenvectors in conserved variables, L, are computed from those in the reduced system of covariant variables through
The comment at the end of Section 8.1) on the transformation of the fifth and first components of the right and left eigenvectors, respectively, of the RHD equations, applies also in the RMHD case.
8.3 Fundamentals of grid-based methods
We introduce the basic notation of finite differencing and summarize the fundamentals of HRSC methods for hyperbolic systems of conservation laws, i.e., the content of this Section is neither specific to RHD nor RMHD.
8.3.1 Difference schemes in conservation form, TV-stability and convergence
To simplify the notation and taking into account that the most powerful results were derived for scalar conservation laws in one spatial dimension, we will restrict ourselves to the initial value problem given by the equation
with the initial condition u(x,t= 0) = u0(x).
Hydrodynamic codes based on finite difference (FD) or finite volume (FV) methods solve Eq. (156) on a discrete numerical grid (xi,tn) with
and
where Δt and Δx are the time step and the cell size, respectively.
A difference scheme is a time-marching procedure allowing one to obtain an approximation of the solution at the new time, \(u_i^{n + 1}\), from the known approximations of previous time steps. In FDschemes, the quantity \(u_i^n\) is a pointwise approximation of the solution u(x,t) at x = xi, t= tn, namely u(xi, tn), whereas in FV schemes (consistent with the integral form of the conservation law) it is viewed as an approximation of the cell average of u(x,t) within a cell [xi-1/2, xi+1/2]at time t= tn, namely
where xi±1/2= (xi + xi±1)/2.
Convergence under grid refinement implies that the global error \(\Vert{E_{\Delta x}}\Vert\), defined as
(where \(u_{{\rm{a}},i}^{\;\;n}\) is the pointwise or volume-averaged analytic solution at cell i and time t= tn), tends to zero as Δx →. A method is said to be of order p, if the global error tends to zero under grid refinement as \(\Vert{E_{\Delta x}}\Vert\propto \Delta {x^p}\). Since the average of a linear function within the interval [xi−1/2,xi+1/2] is equal to the point-value at the center of the interval, FV and FDschemes coincide up to order p= 2. The Lax-Friedrichs (Lax, 1954) and Lax-Wendroff (Lax and Wendroff, 1960) difference schemes for linear problems are first and second-order methods, respectively.
For hyperbolic systems of conservation laws methods in conservation form are preferred as they guarantee that if the numerical solution converges, it converges to a weak solution of the original system of equations (Lax-Wendroff theorem; Lax and Wendroff, 1960). Conservation form means that the algorithm can be written as
where q and r are positive integers, and \(\hat f\) is a consistent numerical flux function, i.e., \(\hat f(u,u, \ldots,u) = f(u)\). The Lax-Friedrichs and Lax-Wendroff methods can be written in conservation form.
The Lax-Wendroff theorem does not reveal whether the method converges. To guarantee convergence, some form of stability is required, as for linear problems (Lax equivalence theorem; Richtmyer and Morton, 1967). In this context the notion of total-variation stability has proven to be very successful, although powerful results were only obtained for scalar conservation laws. The total variation of a solution at t= tn is defined as
A numerical scheme is said to be TV-stable, if TV(un)is bounded for all Δtat any time for each initial data. In that case one can prove the following convergence theorem for nonlinear, scalar conservation laws (LeVeque, 1992): For numerical schemes in conservation form with consistent numerical flux functions, TV-stability is a sufficient condition for convergence.
8.3.2 High-Resolution Shock-Capturing schemes
Modern research has focused on the development of high-order methods in conservation form that satisfy the condition of TV-stability. These methods are known as High-Resolution Shock-Capturing (HRSC) since they converge to a weak solution of the equations by construction (shock capturing property). Figure 30 summarizes the current strategies to build HRSC methods following both FD and FV approaches.
8.3.2.1 Finite-volume approach: Godunov-type methods.
Godunov-type methods (Hartenet al.,1983; Einfeldt, 1988) are an important subset of HRSC methods, which rely on the integral form of the conservation laws (FV methods). Integrating the PDE over a finite space-time domain [xi-1/2, xi+1/2] × [tn, tn+1] and comparing with Eq. (161), one recognizes that the numerical flux function fi+1/2 is an approximation of the time-averaged flux across the respective cell interface, i.e.,
Because the flux integral depends on the solution at the cell interface during the time step, one calculates u(xi+1/2, t) in Godunov-type methods by solving a Riemann problem at the cell interface, i.e.,
This approach was proposed in a seminal work by Godunov (1959), who solved the Riemann problem exactly.
In general, Godunov-type methods use different procedures (Riemann solvers) to obtain the exact or approximate solution \({u_{{\rm{RP}}}}(0;u_i^n,u_{i + 1}^n)\). Among the most popular ones is the method of Roe (1981), originally devised for the equations of (classical) ideal gas dynamics. It is based on the exact solution of Riemann problems of a modified system of conservation equations obtained by a suitable local linearization of the original system. Roe’s original idea has been exploited in the local characteristic approach (see, e.g., Yee, 1989a), which defines a set of characteristic variables at each cell that obey a system of uncoupled scalar equations. This approach has proven to be very successful, because it allows for the extension to systems of nonlinear scalar methods.
The Godunov-type methods described above are upwind, i.e., information propagates in the correct directions as dictated by the characteristic fields of the hyperbolic system. The upwind property is ensured through a local linearization and diagonalization of the system in the case of Roe-type Riemann solvers or the local characteristic approach, or by using the exact solution of the Riemann problem to compute the numerical fluxes, as in the Godunov’s original method.
Unlike Roe’s Riemann solver and the local characteristic approach, the Riemann solver of Harten, Lax and van Leer (HLL; Harten et al.,1983) avoids the explicit calculation of the eigenvalues and eigenvectors of the Jacobian matrices associated to the flux vectors. It is based on an approximate solution of the original Riemann problems involving a single intermediate state, which is determined by requiring consistency of the approximate Riemann solution with the integral form of the conservation laws within a cell.
An essential ingredient of the HLL method are good estimates for the smallest and largest signal velocities. Einfeldt (1988) proposed calculating them based on the smallest and largest eigenvalues of Roe’s matrix. This method is a very robust one for solving the Euler equations. It is exact for single shocks, but it is very dissipative, especially at contact discontinuities. In the HLLC method (Toro et al., 1994 for the Euler equations; Gurski, 2004, Li, 2005 for the MHD equations) the contact discontinuity in the middle of the Riemann fan is also captured in an attempt to reduce the dissipation of the HLL method across contacts. Being independent of the spectral decomposition of the system, these methods are symmetric in the sense that information propagates without regard of the proper directions of the characteristic speeds.
Other methods based on the use of Riemann solvers are Glimm’s random choice method (Glimm, 1965), the two-shock approximation (Colella, 1982), and the artificial wind method (Sokolov et al., 1999). A comprehensive overview of numerical methods based on Riemann solvers can be found in the book of Toro (1997).
Besides Riemann solvers, Godunov-type methods can also use flux formulas for the computation of numerical fluxes. These flux formulas can be upwind (e.g., Marquina’s flux formula; Donat and Marquina, 1996), or symmetric. To this last class belong the non-oscillatory central differencing(NOCD) methods in Nessyahu and Tadmor (1990), Jiang et al. (1998), Jiang and Tadmor (1998), Kurganov and Tadmor (2000), Kurganov et al. (2001), which are high-order extensions of the Lax-Friedrichs central (i.e., symmetric) scheme.
A priori, upwind schemes are better than symmetric ones since they are less dissipative. However, the numerical dissipation terms in modern symmetric schemes are local, free of problem-dependent parameters, and do not require any characteristic information (i.e., the knowledge of the spectral decomposition of the Jacobians, or the solution of Riemann problems). This last fact makes this kind of schemes extremely simple to program and very efficient from the computational point of view.
In FV schemes, high-order of accuracy is usually achieved by interpolating the approximate solution within cells. The idea is to produce more accurate left and right states at interfaces by substituting the mean values \(u_i^n\) (that give only first-order accuracy) by better representations of the true flow, let say \(u_{i + 1/2}^{\rm{L}}\) and \(u_{i + 1/2}^{\rm{R}}\) The interpolation algorithms have to preserve the TV-stability of the scheme. This is usually achieved by using monotonic functions and slope limiters, which decrease the total variation (TVD schemes; Harten, 1984).
High-order TVD schemes were first constructed by van Leer (MUSCL scheme; van Leer, 1973, 1974, 1977b,a, 1979), who obtained second-order accuracy using monotonic piecewise linear functions for cell reconstruction. Some of the most popular slope limiters are reviewed in, e.g., LeVeque (1992). The piecewise parabolic method (PPM) of Colella and Woodward (1984), which uses monotonized parabolas for cell reconstruction provides an accuracy higher than second order.
8.3.2.2 Finite difference approach.
As an alternative to Godunov-type methods, the numerical dissipation required to stabilize an algorithm across discontinuities can be provided also by adding local dissipation terms to standard (conservative) FD methods. The idea goes back to some of the earliest works on computational fluid dynamics, notably the paper by von Neumann and Richtmyer (1950) (see Artificial Viscosity methods below). The symmetric schemes developed by Harten (1983), Davis (1984), and Roe (1984) are extensions of the original Lax-Wendroff scheme. A general discussion and derivation of early (prior to 1987) symmetric FD TVD schemes can be found in Yee (1987).
Stable high-order FD methods can be obtained also by combining a high-order flux that works well in smooth regions and a low-order flux that behaves well near discontinuities. These algorithms are sometimes called flux-limiter methods.The modified-flux approach of Harten (1984) and the scheme of Sweby (1984) are second-order TVD flux-limiter methods (see also Yee, 1989a; LeVeque, 1992).
The TVD property implies TV-stability, but it can be too restrictive at times. In fact, TVDmethods degenerate to first-order accuracy at extreme points Osher and Chakravarthy (1984). Hence, other reconstruction alternatives were developed, which allow for some growth of the total variation. This holds for the total-variation-bounded (TVB) schemes (Shu, 1987), the essentially non-oscillatory (ENO) schemes (Harten et al.,1987), and the piecewise-hyperbolic method (PHM; Marquina, 1994).
Within the FD approach, ENO schemesFootnote 8 use adaptive stencils to reconstruct variables (typically fluxes) at cell interfaces from point values. Thus, in smooth regions symmetric stencils are used, whereas near discontinuities the stencil will shift to the left or to the right selecting the smoother part of the flow to achieve everywhere the same high resolution (typically third-order to fifth-order in the case of WENO — weighted ENO — schemes; Jiang and Shu, 1996); see Shu (1997) for a review of ENO and WENO schemes. The algorithms in Shu and Osher (1988, 1989) are ENOhigh-order extensions of the Lax-Friedrichs central scheme. The method of Liu and Osher (1998) is a third-order multidimensional (Lax-Friedrichs extension) NOCD-type scheme based on CENO (convex ENO) reconstruction. Londrillo and Del Zanna (2000) developed a high-order FD scheme based on CENO reconstruction of state variables (instead of flux components) for classical MHD.
8.3.3 Non-conservative FD schemes
To this category belong FDschemes that solve the hyperbolic system as a set of advection equations. The Flux Corrected Transport(FCT) algorithm (Boris and Book, 1973) is a member of this class. It can be viewed as a flux-limiter non-conservative method, in which high accuracy is obtained by adding an anti-diffusive flux term to the first-order numerical (transport) flux.
In the Artificial Viscosity methods (von Neumann and Richtmyer, 1950; Richtmyer and Morton, 1967), terms mimicking the role of fluid viscosity are added to the equations (written as a set of advection equations) to damp the spurious numerical oscillations caused by the development of shock waves during the flow’s evolution. The form and strength of these terms are such that the shock transition becomes smooth and covers only a small number of numerical cells.
8.3.4 Multidimensional schemes and time advance
Let us consider Eq. (156) and its explicit discretization in conservation form, i.e., Eq. (161). If the discrete spatial operator at the right-hand-side of Eq. (161) is pth-order accurate, the algorithm
with
is a fully-discrete explicit one that is 1st-order accurate in time (forward Euler algorithm) and pth-order accurate in space. The Lax-Friedrichs scheme, which uses this kind of time discretization, is hence 1st-order accurate in time.
The temporal order of the algorithm can be improved by introducing substeps in the time advance (as, e.g., in standard second-order FD methods). In the method of lines, the process of discretization proceeds in two stages. One first discretizes the equations only in space, leaving the problem continuous in time (semi-discrete methods). This leads to a system of ordinary differential equations in time (or a single ordinary differential equation in the scalar case),
In predictor-corrector methods, the quantity \({\mathcal{L}_x}({u^n})\) is an estimate of the time derivative of u at t= tn, and \(u_{i}^{n+1}\) in Eq. (165) is a prediction of u at t= tn+1, u*. This prediction is improved using a, which is an estimate of the time derivative of u at t= tn+1. The value of u at the new time step then reads, e.g.,
Of particular interest among the predictor-corrector methods are the second-order and third-order Runge-Kutta time discretization algorithms developed in Shu and Osher (1988, 1989). They preserve the TVD property of the algorithm at every substep (TVD-RK methods). Standard fourth-order and fifth-order Runge-Kutta methods (Lambert, 1991) have been used, too.
Second-order accuracy in time can also be obtained, if the input states for the Riemann problems to be solved at each numerical interface incorporate information about the domain of dependence of the interface during the time step. When eigenvalues and eigenvectors are available, upwind limiting may be used to select only those characteristics that contribute to the effective left and right states (characteristic tracing). This is the approach followed in the PLM (Colella, 1985) and PPM methods (Colella and Woodward, 1984).
In the MUSCL-Hancock method (van Leer, 1984; Toro, 1997), the input states for the Riemann solver are computed by a Taylor expansion of u at the middle of the time step
where \(u_{i,L}^n\), and \(u_{i,R}^n\) are linearly reconstructed, monotonized values of at the left and right interface of cell, respectively. The values at the new time step are obtained by
In contrast to standard predictor-corrector methods, these single-step algorithms require only one solution of the Riemann problem per cell and time step.
For explicit schemes the time step Δt is restricted by the CFL condition (Courant, Friedrichs and Lewy; Courant et al.,1928). This is a necessary condition for the method’s stability stating that the numerical domain of dependence should include the domain of dependence of the partial differential equation.
There exist several strategies to extend HRSC methods to more than one spatial dimension (for a summary see LeVeque, 1992, 1998). The simplest way is to exploit dimensional splitting, i.e., operators in the equations involving spatial derivatives are applied dimension by dimension in successive steps (fractional step methods)Footnote 9. Second-order accuracy in time can be preserved by permuting cyclically the execution of the directional operators (Strang splitting; Strang, 1968). To illustrate the method of fractional step, let us consider the 2D version of Eq. (156)
and its explicit discretization in conservation form (compare with Eq. (161))
If we define
as the pth-order accurate (p ≥2) discrete operator in x-direction, and \(\mathcal{H}_y^{\Delta t}\) as the corresponding one in y-direction, Strang splitting has the form
In the method of lines (see above), one computes the fluxes in all coordinate directions (and the potential source terms), and applies them simultaneously to advance the equations in time (unsplit methods).
Finally, there exists a special class of unsplit methods, in which second-order accuracy requires that one incorporates besides terms involving derivatives in the normal direction (as in 1D algorithms) also terms involving transverse derivatives arising from cross-derivatives in a Taylor series expansion. Examples of genuinely multidimensional upwind methods for hyperbolic conservation laws that use slightly different strategies are those described in Colella (1990); LeVeque (1997). The corner transport upwind method(CTU; Colella, 1990) proceeds in two steps. One first interpolates state variables to cell interfaces using information from all coordinate directions, and then solves the Riemann problem. This approach was implemented for classical MHD by Gardiner and Stone (2005). The algorithm proposed in LeVeque (1997) first solves Riemann problems and then propagates the information in a multidimensional manner.
8.3.5 AMR
Many, if not most, flow problems encountered in astrophysics involve vastly different length scales, and often time scales, too. Moreover, in many cases the most important flow features occupy only a small fraction of the computational domain. These structures are usually flow discontinuities like shock waves or contact surfaces. The addition of physical processes, like e.g., radiative losses or nuclear burning, may lead to the formation of qualitatively new features which, similarly to flow discontinuities, can occupy only a small fraction of the total volume. This poses a challenge to any numerical method used to integrate the hydrodynamic (or magnetohydrodynamic) equations.
A common way of dealing with the resolution challenge is to adaptively refine the computational mesh in regions where higher resolution is needed and coarsen it in regions where less resolution is sufficient to guarantee a prescribed numerical accuracy. Hence, local errors are controlled by adding or deleting cells or patches of cells from the computational grid, as and when necessary. An alternative approach that will not be discussed in this review any further, relies on moving mesh methods which adapt the grid by repositioning a fixed number of cells. However, this method has the penalty that increasing the resolution in some region implies decreasing it in some other region (see, e.g., He and Tang, 2012 for a method for 2D RMHD).
To refine the grid one can apply the cell-by-cell refinement strategy (see, e.g., Khokhlov, 1998; Teyssier, 2002; Fromang et al.,2006) where individual parent cells are refined into children cells, and the process is repeated until a predefined accuracy is obtained. This strategy is also called tree-based AMR (Teyssier, 2002), since a recursive tree structure is the natural data structure associated with it. Cell-by-cell refinement results in a high adaptivity to flow features and provides the most flexible grid structure, but it gives rise to a complicated data structure because the number of grid cells becomes time-dependent. In addition, it requires irregular memory referencing which degrades a code’s performance, particularly on computing systems with a distributed parallel architecture. When only one region of the computational domain (e.g., the center of a collapsing cloud or of an exploding star) has to be refined during the whole evolution a simpler approach with completely nested grids can be used, where the grids have a fixed structure, i.e., they all consist of an identical number of (equidistant) cells of decreasing size (see, e.g., Ruffert, 1992; Burkert and Bodenheimer, 1993; Ziegler and Yorke, 1997).
Alternatively, one adopts a patch-based or block-structured approach to grid refinement. Refined grid cells are clustered together to form larger rectangular regions, or mesh patches, overlying parent level grids. The refinement process is recursively applied to newly created fine mesh patches until the prescribed accuracy is reached. In this way, the final data structure can be seen as a hierarchy of mesh patches (Figure 31) located at different levels and integrated with individual time steps. In some implementations of this strategy one can even allow for the use of a different discretization scheme per level (as, e.g., in AMRVAC).
Hierarchy of grids in the AMR method. The base level covers the entire computational domain with mesh patches G(1,1) and G(1,2). Patches G(2,1) and G(2,2) form the second level and a single mesh patch, G(3,1), is located on the finest level. The hierarchy is fully nested, i.e., finer mesh patches are completely embedded in patches located on the next coarser level, each patch may have more than one parent or/and offspring, and siblings may overlap each other. Image reproduced with permission from Plewa and Müller (2001), copyright by Elsevier.
When each single mesh patch has a logical structure identical to the original numerical grid, the scheme is commonly called adaptive mesh refinement, AMR. It was originally proposed by Berger and her collaborators. In Berger and Oliger (1984) they presented an adaptive method for the solution of hyperbolic partial differential equations, while in Berger and Colella (1989) and Bell et al. (1994) they discussed its application to hyperbolic conservation laws in two and three space dimensions, respectively. The problems that had to be considered by them in this case are pedagogically summarized in Balsara (2001c): Solving hyperbolic conservation law with AMR requires a conservative solution strategy on the whole grid hierarchy, which is not provided if a bilinear interpolation is used for the prolongation of the solution from a coarse parent level to the finer child levels. However, when one prolongs the data with the same higher order Godunov scheme as the one used for reconstructing the hydrodynamic state variables, the prolongation can be made conservative. One also needs to develop a volume-weighted restriction strategy to transfer the more accurate solution on fine patches to the corresponding coarser parent patches that mirrors the volume-averaged representation of variables in higher order Godunov schemes. Because restriction is not conservative in general, one cures the problem by using a consistent set of fluxes at fine-coarse interfaces in a flux correction step. Berger and Colella (1989) have shown that when applying all the above steps conservation is guaranteed as long as the grid levels are properly nested, one within the other.
Berger and LeVeque (1998) extended the AMR algorithm for the Euler equations of gas dynamics further. They employed high-resolution wave-propagation algorithms in a more general framework, including hyperbolic equations not in conservation form, problems with source terms, and logically rectangular curvilinear grids. The algorithm is implemented in the AMRCLAW package, which is freely available.
8.4 Other approaches in numerical RHD and RMHD
In Sections 8.4.1–8.4.3, we briefly discuss other approaches recently extended to numerical RHDand RMHD although not widely used yet. In Section 8.4.4 we summarize the method of van Putten, who first exploited the conservative nature of the RMHD equations for their numerical integration.
8.4.1 Discontinuous Galerkin methods
Discontinuous Galerkin (DG) methods were first applied to first-order equations in the early 1970s by Reed and Hill (1973). Their widespread use followed from their application to hyperbolic problems by Cockburn and Shu (1989); Cockburn et al. (1990); Cockburn (1998).
In the DG approach, the p-th order accurate solution in a numerical cell is expanded in space using a polynomial basis whose expansion coefficients (the degrees of freedom) depend on time. Substituting the expansion in the integral form of the system of equations leads to a system of ordinary differential equations in time for the degrees of freedom, which can be solved by means of a standard Runge-Kutta discretization (RKDG scheme).
In the RKDG scheme, the values of the fluxes at the cell interfaces can be obtained by solving Riemann problems, thus incorporating the upwind property into the schemes. Moreover, the solution of the Riemann problems does not require any additional spatial interpolation since the relevant information is already incorporated in the expansion. However, if the discontinuities are strong, the scheme generates significant oscillations (which can be damped with appropriate slope limiters). The increasing success of RKDG schemes relies on their flexibility and adaptativity in handling complex geometries, and on the possibility of an efficient parallel implementation of these schemes, because the solution is advanced in time using information only from the immediate neighboring cells.
Dumbser and Zanotti (2009) presented a hybrid FV-DG approach for resistive RMHD. In their approach a local spacetime DG method provides an implicit predictor step for a high-order FV scheme to handle the stiff source term of resistive MHD. Radice and Rezzolla (2011) and Radice (2013) developed the necessary formalism for the application of fully explicit DG methods to RHD in curved spacetimes. They presented a prototype numerical code, EDGES (Extensible Discontinuous GalErkin Spectral library), which they used to test DG methods for GRHD in one spatial dimension assuming spherical symmetry. Zanotti and Dumbser (2015) present a high-order, one-step AMR FV-DG scheme for RHD and RMHD.
Zhao and Tang (2013) developed RKDG methods with WENO limiter for 1D and 2D RHD. In cells that require limiting a new polynomial solution is reconstructed locally to replace the RKDG solution by the WENO one based on the original cell average and the cell average values of the RKDG solution in the neighboring cells.
8.4.2 Kinetic beam schemes and KFVS methods
Sanders and Prendergast (1974) proposed an explicit scheme to solve the equilibrium limit of the non-relativistic Boltzmann equation, i.e., the Euler equations of Newtonian fluid dynamics. In their beam scheme, the Maxwellian velocity distribution function is approximated by several Dirac delta functions or discrete beams of particles in each computational cell, which reproduce the appropriate moments of the distribution function. The beams transport mass, momentum and energy into adjacent cells, and their motion is followed to 1st-order accuracy. The new (i.e., time advanced) macroscopic moments of the distribution function are used to determine the new local non-relativistic Maxwell distribution in each cell. The entire process is then repeated for the next time step. The CFL stability condition requires that no beam of gas travels farther than one cell in one time step. This beam scheme, although being a particle method derived from a microscopic kinetic description, has all the desirable properties of modern characteristic-based wave propagating methods based on a macroscopic continuum description.
The non-relativistic scheme of Sanders and Prendergast (1974) was extended to relativistic flows by Yang et al. (1997) replacing the Maxwellian distribution function by its relativistic analogue, i.e., by the Jüttner distribution function which involves modified Bessel functions. For 3D flows the Jüttner distribution function is approximated by seven delta functions or discrete beams of particles, which can be viewed as dividing the particles in each cell into seven distinct groups. In the local rest frame of the cell these groups represent particles at rest and particles moving in αx, αy, and α z direction, respectively. Yang et al. (1997) showed that the integration scheme for the beams can be cast in the form of an upwind conservation scheme in terms of numerical fluxes. The simplest relativistic beam scheme is only 1st-order accurate in space, but it can be extended to higher-order accuracy in a straightforward manner. They considered several high-order accurate variants generalizing their approach developed in Yang and Hsu (1992); Yang et al. (1995) for Newtonian gas dynamics, which is based on ENO reconstruction.
The same principles (microscopic kinetic approach to the Euler equations, and particles propagating to the left and right to describe the transport of mass, momentum, and energy) are exploited in the kinetic flux-vector splitting(KFVS) methods, which can be interpreted as flux-vector splitting methods Steger and Warming (1981) (hence the name) as first noted by Harten et al. (1983). Qamar (2003) reviewed the development of both kinetic schemes and KFVS schemes for the non-relativistic and the relativistic hydrodynamic equations, and Kunik et al. (2004) presented a BGK-type KFVS schemeFootnote 10 for ultrarelativistic hydrodynamics. Qamar and Warnecke (2005) extended this scheme to 1D RMHD.
8.4.3 CE/SE methods
The spacetime conservation element/solution element(CE/SE) method is a HRSC method introduced by Chang (1995) for 1D flows (see Zhang et al.,2002 and references therein for 2D and 3D extensions using structured and unstructured meshes). In contrast with conventional FV methods based on the Reynolds transport theorem, in which space and time are treated separately, the CE/SE method adopts an integral form of spacetime flux conservation as the cornerstone for the subsequent discretization. Because of its unified treatment of space and time, Chang’s flux conservation formulation allows one to choose the spacetime geometry of conservation elements such that one does not need to solve Riemann problems. In addition, considering the spatial derivatives of conserved variables as independent variables, the flux evaluation at cell interfaces can be carried out without interpolation. The method was applied to complex problems in different areas including problems related to unsteady flows, vortex dynamics in aeroacoustics, diffusion problems, viscous flows, MHD, shallow water MHD, and electrical engineering (see references in Qamar and Yousaf (2012)).
Qamar and Yousaf (2012) extended the CE/SE method to 1D and 2D RHD. In 1D they applied the original CE/SE method of Chang (1995), while they used a variant of it (Zhang et al.,2002) in 2D with a rectangular mesh. Qamar and Ahmed (2013), finally, extended the CE/SE method to 1D RMHD.
8.4.4 Van Putten’s approach
Relying on a formulation of Maxwell’s equations as a hyperbolic system in divergence form, van Putten (1991) devised a numerical method to solve the equations of ideal RMHD in flat spacetime (van Putten, 1993a). In van Putten’s approach, of which we discuss only the basic principles for 1D flows here, the state vector U and the fluxes F of the conservation laws are decomposed into a spatially constant mean (subscript 0) and a spatially dependent variational (subscript 1) part
The RMHD equations then become a system of evolution equations for the integrated variational parts \({{\bf{U}}_1}^{\ast}\), which reads
together with the conservation condition
The quantity \({{\bf{U}}_1}^{\ast}\) is defined as
Continuous and standard methods can be used to integrate the system (176). Van Putten used a leapfrog method.
The new state vector U(t,x) is obtained from \({{\bf{U}}_1}^{\ast}(t,\;x)\) by numerical differentiation. This process can lead to oscillations in the case of strong shocks, i.e., a smoothing algorithm should be applied. Details of this smoothing algorithm and of the numerical method for 1D and 2D flows can be found in van Putten (1992) together with the results of a large variety of tests.
Van Putten applied his method to simulate RHD and RMHDjets with moderate flow Lorentz factors (< 4.25) (van Putten, 1993b, 1996) and blast waves (van Putten, 1994, 1995).
8.5 Exact solution of the Riemann problem in RHD
This section was already included in Martí and Müller (2003) and is maintained here for completeness.
The simplest initial value problem with discontinuous data is called a Riemann problem, where the 1D initial state consists of two constant states separated by a discontinuity. The majority of modern numerical methods, the Godunov-type methods, are based on exact or approximate solutions of Riemann problems. Because of its theoretical and numerical importance, we discuss the solution of the special relativistic Riemann problem in this section.
Let us first consider the 1D special relativistic flow of a perfect fluid in the absence of a gravitational field. The Riemann problem then consists of computing the breakup of a discontinuity, which initially separates two arbitrary constant states L (left) and R (right) in the fluid (see Figure 32 with L = 1 and R = 5). For classical hydrodynamics the solution can be found, e.g., in Courant and Friedrichs (1976). In the case of RHD, the Riemann problem was considered by Martí and Müller (1994), who derived an exact solution for the case of pure normal flow generalizing previous results for zero initial velocities (Thompson, 1986). Pons et al. (2000) presented the general solution in the case of non-zero tangential speeds.
Schematic solution of a Riemann problem in RHD. The initial state at t = 0 (top panel) consists of two constant states (1) and (5) with p1 > p5, ρ1> ρ5, and υ1 = υ2 = 0 separated by a diaphragm at xD The evolution of the flow, once the diaphragm is removed (middle panel), is illustrated in a spacetime diagram (bottom panel) with a shock wave (solid line) and a contact discontinuity (dashed line) moving to the right. The bundle of solid lines represents a rarefaction wave propagating to the left.
The solution is self-similar, because it only depends on the two constant states defining the discontinuity vL and vR with v= (p, ρ, υx,υy,υz), and on the ratio (x − x0)/(t − t0), where x0 is the initial location of the discontinuity at the time of break up t0. Both in relativistic and classical hydrodynamics the discontinuity decays into two elementary nonlinear waves (shocks or rarefactions) which move in opposite directions towards the initial left and right states. Between these waves two new constant states vL* and vR* (note that vL*= 3 and vR*= 4 in Figure 32) appear, which are separated from each other through a contact discontinuity moving with the fluid. Accordingly, the time evolution of a Riemann problem can be represented as
where \(\mathcal{W}\) and \(\mathcal{W}\) denote a simple wave (shock or rarefaction) and a contact discontinuity, respectively. The arrows (←/→) indicate the direction (left / right) from which fluid elements enter the corresponding wave.
As in the Newtonian case, the compressive character of shock waves (density and pressure rise across the shock) allows us to discriminate between shocks (\(\mathcal{S}\)) and rarefaction waves (\(\mathcal{R}\)):
Here, p is the pressure, and subscripts a and b denote quantities ahead and behind the wave. For the Riemann problem a = L(R) and b = L*(R*) for \({{\mathcal{W}}_{\leftarrow }}\left( {{{\mathcal{W}}_{\to }}} \right)\). Thus, the possible decays of an initial discontinuity can be reduced to three types:
Across the contact discontinuity the density exhibits a jump, whereas pressure and normal velocity are continuous (see Figure 32). As in the classical case, the self-similar character of the flow through rarefaction waves and the Rankine-Hugoniot conditions across shocks provide the relations to link the intermediate states vs*(S= L,R) with the corresponding initial states vs. They also allow one to express the normal fluid flow velocity in the intermediate states for the case of an initial discontinuity normal to the x-axis) as a function of the pressure ps* in these states.
The solution of the Riemann problem consists in finding the intermediate states, L* and R*, as well as the positions of the waves separating the four states (which only depend on L, L*, R*, and R).The functions \({\mathcal{W}_{\to}}\) and \({\mathcal{W}_{\leftarrow}}\) allow one to determine the functions \(v_{{R_\ast}}^x(p)\) and \(v_{{L_\ast}}^x(p)\) (p), respectively. The pressure p* and the flow velocity \(v_\ast^x\) in the intermediate states are then given by the condition
with p* = pL* = pR*.The functions \(v_{{S_\ast}}^x(p)\) are defined by
where \({\mathcal{R}^S}(p)\) and \({\mathcal{S}^S}(p)\) denote the families of all states that can be connected through a rarefaction and a shock, respectively, with a given state vs ahead of the wave.
In RHD, the major difference with classical hydrodynamics stems from the role of tangential velocities. While for classical flows the decay of the initial discontinuity does not depend on the tangential velocity (which is constant across shock waves and rarefactions), the components of the flow velocity are coupled through the presence of the Lorentz factor in the equations for relativistic flows. In addition, the specific enthalpy also couples with the tangential velocities, which becomes important in the thermodynamically ultrarelativistic regime.
8.5.1 Solution across a rarefaction wave
The fact that one Riemann invariant is constant through any rarefaction wave provides the relation needed to derive the function \({\mathcal{R}^S}\). In differential form, the function reads
where \({v^t} = \sqrt {{{({v^y})}^2} + {{({v^x})}^2}} \) is the modulus of the tangential velocity, and
with
The + (−) sign corresponds to S= R (S= L), and cs denotes the local sound speed.
Considering that in a Riemann problem the state ahead of the rarefaction wave is known, the integration of Eq. (186) allows one to connect the states ahead (S) and behind the rarefaction wave. Using Eq. (188), the EOS, and the following relation obtained from the constraint hWυt= const in a rarefaction wave
the ODE can be integrated (along an adiabat of the EOS). The solution is only a function of p
If the tangential velocity is zero,υt = 0, the function g does not contribute. In this limiting case and for an ideal gas EOS with an adiabatic index γone finds
which is expression (30) in Martí and Müller (1994). The equation can be integrated to give (Martí and Müller, 1994)
withFootnote 11
the + (−) sign of A± corresponding to S = L (S = R).In the above equation, cs is the sound speed in state vs, and c(p) is given by
8.5.2 Solution across a shock front
The family of all states Ss(p) that can be connected through a shock with a given state vs ahead of the wave is determined by the shock jump conditions. One obtains
where the + (−) sign corresponds to S= R (S= L).The quantities V+(p) and V-(p) denote the shock velocities for shocks propagating to the right and left, respectively. They are given by
The tangential velocities present in the initial states are hidden within the flow Lorentz factor, Ws. The modulus of the mass flux across the shock front is
where the enthalpy h(p) of the post-shock state can be obtained from the Taub adiabat (Thorne, 1973)
In general, the above nonlinear equation must be solved together with the EOS to obtain the post-shock enthalpy as a function of p. For an ideal gas EOS with constant adiabatic index, the post-shock density ρ can be eliminated, and the post-shock enthalpy is the (unique) positive root of the quadratic equation Martí and Müller (1994)
Finally, the tangential velocities in the post-shock states can be obtained from Pons et al. (2000)
8.5.3 Complete solution
Figure 33 shows the solution of a particular, mildly relativistic Riemann problem for different values of the tangential velocity. The crossing point of any two lines in the upper panel gives the pressure and the normal velocity in the intermediate states. The range of possible solutions in the (p, υx)-plane is marked by the shaded region. Whereas the pressure in the intermediate state can take any value between pL and pR, the normal flow velocity can be arbitrarily close to zero in the case of an extremely relativistic tangential flow. The values of the tangential velocity in the states L* and R* are obtained from the value of the corresponding functions of υx (see lower panel of Figure 33). The influence of initial left and right tangential velocities on the solution of a Riemann problem is enhanced in highly relativistic problems.
Graphical solution in the (p, υx)-plane (top) and (υt, υx)-plane (bottom) of the relativistic Riemann problem with initial data \({p_L} = 1.0,\;{\rho _L} = 1.0,\,v_L^x = 0.0;\;{p_R} = 0.1,\;{\rho _R} = 0.125\), and \(v_R^x = 0.0\) for different values of the tangential velocity: υt = 0 (solid), υt = 0.5 (dashed), υt = 0.9 (dashed-dotted), and v* = 0.999 (dotted). An ideal gas EOS with γ = 1.4 was assumed. The crossing point of any two lines in the upper panel gives the pressure and the normal velocity in the intermediate states. The value of the tangential velocity in the states L* and R* is obtained from the value of the corresponding functions of υx in the lower panel. The curve denoted I0 gives the solution for a vanishing tangential velocity, and the shaded region in the upper panel marks the range of possible solutions. Image reproduced with permission from Figure 3 of Pons et al. (2000), copyright by CUP.
Pons et al. (2000) computed solutions for different combinations of \(v_L^t\) and \(v_R^t\). The initial data were \({p_L} = {10^3},\;{\rho _L} = 1,\;v_L^x = 0;\;{p_R} = {10^{ - 2}},\;{\rho _R} = 1,\;v_R^x = 0\), and the 9 possible combinations of \(v_{L,R}^t = 0,\;0.9,\,0.99\) (see Figure 34). The tests based on the propagation of relativistic blast waves referred to as Problems 2, 3, and 4 in Section 6.3 are based on the initial setup considered by Pons et al.
Analytic profiles of pressure, density, and flow velocity at t = 0.4 for the relativistic Riemann problem with initial data \({p_L} = {10^3},\;{\rho _L} = 1.0,\;v_L^x = 0.0;\;{p_R} = {10^{ - 2}},\;{\rho _R} = 1.0\), and \(v_R^x = 0.0\) for different values of the tangential velocity. From left to right, \(v_R^t = 0,\;0.9,\;0.99\); and from top to bottom, \(v_L^t = 0,\;0.9,\;0.99\). An ideal EOS with γ = 5/3 was assumed. Image reproduced with permission from Figure 4 of Pons et al. (2000), copyright by CUP.
The procedure to obtain the pressure in the intermediate states, p*, is valid for general (convex) EOS. Once p* is obtained, the remaining state quantities and the complete Riemann solution,
can easily be derived. Martí and Müller (2003) provide FORTRAN programs to compute the exact solution of an arbitrary special relativistic Riemann problem for an ideal gas EOS with constant adiabatic index, both with zero and non-zero tangential speeds using the algorithm discussed above.
Solving a Riemann problem involves the solution of an algebraic equation for the pressure (Eq. (184)). The functional form of this equation depends on the wave pattern under consideration (see Eqs. (181)–(183)). Rezzolla and Zanotti (2001) presented a procedure suitable for implementation into an exact Riemann solver in one dimension that removes the ambiguity arising from the wave pattern. The method exploits the fact that the expression for the relative velocity between the two initial states is a (monotonic) function of the unknown pressure, p*, which determines the wave pattern. Hence, comparing the value of the relative velocity between the initial left and right states with the values of the limiting relative velocities for the occurrence of the wave patterns (181)–(183), one can determine a priori which of the three wave patterns will actually result (see Figure 35). In Rezzolla et al. (2003) the authors extended the above procedure to multidimensional flows.
Relative velocity between the two initial states 1 and 2 as a function of the pressure at the contact discontinuity. The curve shown consists of three segments which join smoothly at the locations indicated by the filled dots. The segments describe the relative velocity corresponding to the cases of two shocks (dashed; 2S), one shock and one rarefaction wave (dotted; SR), and two rarefaction waves (solid; 2R), respectively. The inset provides a magnified view of a smaller range of p*, the filled squares giving the limiting values of the relative velocities \({({\tilde v_{12}})_{2S}},\;{({\tilde v_{12}})_{SR}}\), and \({({\tilde v_{12}})_{2R}}\). Image reproduced with permission from Figure 1 of Rezzolla and Zanotti (2001), copyright by CUP.
8.6 Exact solution of the Riemann problem in RMHD
The general Riemann problem in RMHD consists of a set of seven waves: two fast-waves, two slow-waves, two Alfvén-waves, and a contact discontinuity.The fast and slow waves are nonlinear and can be either shocks or rarefactions depending on the change of pressure and the norm of the magnetic field across the wave. The remaining three waves are linear.
Based on the experience with RHD, where the solution of the Riemann problem is found expressing all quantities behind the wave as functions of the pressure at the contact discontinuity (see Section 8.5), Giacomazzo and Rezzolla (2006) expressed all variables behind each wave as functions of the same variables ahead of the wave and of an unknown variable behind the wave. Constructing their solver, the authors assume that the Riemann problem has a unique (i.e., regular; see Section 3.2) solution. As a result, their method does not allow the formation of compound waves.
Two different cases must be distinguished when one discusses the Riemann problem in RMHD. Assuming that the initial discontinuity is oriented perpendicular to the x-axis, the initial magnetic field in x-direction can either be zero (Bx= 0) or not (Bx ≠ 0). In the first case is the structure of the solution very similar to the hydrodynamic one, consisting only of two fast waves and a tangential discontinuity at which only the total pressure and the x-component of the velocity are continuous. The spacetime structure of the Riemann problem with Bx= 0 is shown in Figure 36. Its numerical solution can be obtained with the same procedure as that implemented in RHD.Footnote 12 Giacomazzo and Rezzolla (2006) called this procedure the total-pressure approach or simply, the p-method.
Spacetime structure of the RMHD Riemann problem for a purely tangential magnetic field, i.e., Bx = 0. The “Riemann-fan” is composed of only two fast-waves (FW) and a central tangential discontinuity (TD), thus resembling the structure of the RHD Riemann problem. R1–R4 are the four regions into which the Riemann problem can be decomposed, each representing a different state. Image reproduced with permission from Figure 1 of Giacomazzo and Rezzolla (2006), copyright by CUP.
The Riemann problem for the case Bx ≠ 0 is considerably more complex, because all of the seven waves are allowed to form when the initial discontinuity is removed (Figure 37). Inspired by the procedure to obtain the exact solution of the corresponding Riemann problem in non-relativistic MHD Ryu and Jones (1995), Giacomazzo and Rezzolla (2006) implemented a hybrid approach in which the total pressure is the unknown variable (p-method) between the fast and the slow waves (i.e., in regions R2–R3 and R6–R7 in Figure 37), while the tangential components of the magnetic field, By and Bz are used between the slow waves (i.e., in regions R4–R5 in Figure 37). In this tangential magnetic field approach or Bt-method the resulting system consists of four equations for four unknowns, which can be solved numerically with root-finding techniques for nonlinear system of equations (e.g., with a Newton-Raphson method).
Spacetime structure of the general RMHD Riemann problem in which the magnetic field has also a normal component, i.e., Bx ≠ 0. The Riemann-fan is composed of two fast-waves (FW), two Alfvén waves (AW), two slow-waves (SW), and a central contact discontinuity (CD). R1–R8 are the eight regions into which the Riemann problem can be decomposed, each representing a different state. Indicated are also the different methods used to compute the solutions in the different regions (i.e., Bt-method in regions R4 and R5, and p-method in regions R2–R3 and R6–R7). Image reproduced with permission from Figure 2 of Giacomazzo and Rezzolla (2006), copyright by CUP.
In the following sections, we briefly describe both the p-method and the Bt-method applied to shocks, rarefactions, and Alfvén discontinuities. As in Section 8.5, the index a(b) denotes quantities defined ahead (behind) the corresponding wave.
8.6.1 Total-Pressure Approach: p-method
8.6.1.1 Solution across a shock front.
The solution consists of several steps. First, Giacomazzo and Rezzolla derive \(v_b^x\) as a function of \(v_b^y,\;v_b^z,\;{p_b}\), and the mass flux J across the shock (Eq. (4.25) in Giacomazzo and Rezzolla, 2006). Then they write \(v_b^y\) and \(v_b^x\) in terms of pb and J(see Appendix A in Giacomazzo and Rezzolla, 2006), and finally express J and Vs(the shock velocity) as a function of the post-shock pressure pb.Similar as in Pons et al. (2000), they write Vs in terms of J using the definition of the mass flux. Then, in a procedure that involves the post-shock density, the enthalpy, and the EOS, they solve numerically Eqs. (4.26) and (4.27) (the Lichnerowicz adiabat; Anile, 1989, the MHD counterpart of the Taub adiabat) of Giacomazzo and Rezzolla (2006) to obtain Vs as function of the post-shock pressure pb.The root is sought after in the appropriate physical interval, i.e., ∣VS∣ ϵ (∣VA∣, 1) for fast shocks, and ∣VS∣ ϵ (∣03C5x∣, ∣VA∣) for slow shocks. Here, VA is the speed of the corresponding Alfvén wave propagating to the left or right (i.e., \(\lambda _a^ \pm \) in Section 8.2).
8.6.1.2 Solution across a rarefaction wave.
Exploiting the self-similar character of rarefaction waves Giacomazzo and Rezzolla (2006) rewrote the set of partial differential RMHD equations as a set of ordinary differential equations (ODE) in the seven variables ρ,p, υ;x,υy,υz, By, and Bz as functions of the self-similar variable ξ ≡ x/t.These ODE fully determine the solution across a rarefaction wave (Eqs. (4.43)–(4.49) in Giacomazzo and Rezzolla, 2006). The system can be recast into matrix form.
Non-trivial similarity solutions exist only if the determinant of the matrix of coefficients is zero. This condition leads to a quartic equation in the self-similar variable ξ (Eq. (4.50) in Giacomazzo and Rezzolla, 2006) whose roots coincide with the eigenvalues of the original RMHD system of equations. For Bx= 0, the quartic reduces to a quadratic equation whose roots provide the velocities of the left-going and right-going fast-waves. In the general case, i.e., if Bx ≠ 0, the solution must be found numerically. The corresponding roots give the velocities of the left-going and right-going slow and fast magnetosonic rarefaction waves, respectively.
Using the appropriate root for ξ, Giacomazzo and Rezzolla rewrote the system of ODE in terms of the total pressure to obtain a reduced system of six ODE, which they then integrated over pressure across the rarefaction. Explicit expressions for these equations are given in App. B in Giacomazzo and Rezzolla (2006).
8.6.1.3 Solution across an Alfvén discontinuity
Giacomazzo and Rezzolla (2006) imposed continuity of ρ and p across the Alfvén discontinuity, and solved for the remaining jump conditions (Eqs. (4.15)–(4.17), and (4.19)–(4.20) in Giacomazzo and Rezzolla, 2006) using Vs= Va, where VA is the velocity of the corresponding Alfvén wave propagating to the left or right. Since ρ and p are continuous across the Alfvén discontinuity, they need to find a solution only for the three components of v and the tangential components of the magnetic field, By and Bz. They solved the corresponding system of equations numerically with a Newton-Raphson scheme. They reported no major difficulties in determining an accurate solution provided that the waves are all well separated and a sufficiently accurate initial guess was used.
8.6.2 Tangential Magnetic Field Approach: Bt-method
In the Bt-method, all variables in the Riemann fan are calculated using as unknowns the values of the tangential components of the magnetic field, i.e., By and Bz. The method is inspired by the corresponding approach in non-relativistic MHD developed by Ryu and Jones (1995).
8.6.2.1 Solution across a shock front.
Giacomazzo and Rezzolla (2006) solved for the jump conditions considering By and Bz as the unknown quantities. In a first step, using Eqs. (4.13), (4.19), (4.20), and the shock invariant \(\mathcal{B}\) defined in proposition 8.19 of Anile (1989), they express all quantities as a function of the post-shock values of υx, By, Bz, and the mass flux J(or the shock velocity Vs). Then they obtain the post-shock value of υx in terms of the other post-shock quantities solving numerically one of the Eqs. (4.15)–(4.17). Finally, in analogy with the p-method, they determine the value of the shock velocity solving Eq. (4.26) also numerically. They found that the numerical solution of Eq. (4.26) is at times complicated by the existence of two roots within the interval of admissible velocities of the slow shock (i.e., between υx and the corresponding Alfvén velocity). Because only one of these two roots will lead to a convergent exact solution, one needs to make a careful selection (for details see Giacomazzo and Rezzolla, 2006).
8.6.2.2 Solution across a rarefaction wave.
The solution across a rarefaction wave within the Bt-method relies again on the self-similar character of the flow. Giacomazzo and Rezzolla (2006) used Eqs. (4.29)–(4.31) and (4.35)–(4.36) with the modulus of the tangential components of the magnetic field, Bt, as the self-similar variable (i.e., substituting the derivative with respect to ξ by the one with respect to Bt). In addition to these equations, which provide a solution for variables ρ, p, υx,υy, and υz, they considered two additional ODE for the derivatives of the tangential components of the magnetic field, By and Bz, with respect to Bt(Eqs. (5.6) and (5.7) in Giacomazzo and Rezzolla, 2006). The resulting system of ODE can be solved numerically using standard techniques. In practice, the integration begins ahead of the rarefaction and proceeds toward the contact discontinuity, where Bt is given by By and Bz at the contact discontinuity.
In Eqs. (5.6) and (5.7), Giacomazzo and Rezzolla (2006) implicitly assumed that the tangential magnetic field does not rotate across the rarefaction wave. Although this condition is exact in non-relativistic MHD, it may not hold in RMHD where the tangential magnetic field can rotate across the slow rarefaction. In that case, a new strategy needs to be implemented. The simplest one consists of using the rotation angle as the self-similar variable. The integration of the system of ODE is performed starting from the value of the rotation angle given by the ratio of the tangential components of the magnetic field ahead of the rarefaction wave, up to the value given by the amplitudes of By and Bz at the contact discontinuity. Furthermore, as in the p-method, the values of the variable ξ are obtained from the quartic (Eq. (4.50) in Giacomazzo and Rezzolla, 2006) in the Bt-method, too.
In Section 9.1we provide the original code developed by Giacomazzo and Rezzolla (2006) based on the procedure described here to compute the exact solution of 1D RMHD Riemann problems with Bx ≠ 0 and Bx= 0.
9 Programs
A tar ball containing the source code of the following programs together with related information is available for download at http://www.livingreviews.org/lrca-2015-3.
9.1 riemann_rmhd
This program computes the solution of a 1D Riemann problem in RMHD with initial data UL if x < 0.5 and UR if x > 0.5 for arbitrary speeds and magnetic fields in the spatial domain [0,1]. The program was developed by Giacomazzo and Rezzolla. Users of the code should credit the source according to what is established in the README file provided in the tar ball.
9.2 rmhd_1d
This program simulates 1D RMHD flows in Cartesian coordinates using a FV method with various cell-reconstruction techniques, Riemann solvers, and time advance algorithms. Initial data and boundary conditions for several standard RMHD tests are already programmed. Readers are requested to cite this review when using this code in their own publications.
Notes
A review on SPH methods including special and general relativistic formulations of these methods can be found in Rosswog (2015).
In overcompressive shocks, the number of characteristics running into a shock is larger than that for regular shocks (p + 1, for a system of p equations).
Fast shocks and slow rarefactions can be switch-on (i.e., a zero tangential field ahead of the wave becomes non-zero behind it), whereas slow shocks and fast rarefactions can be switch-off (i.e., a non-zero tangential field ahead of the wave becomes zero behind it).
Taub’s fundamental inequality (Taub, 1948) determines the admissible region of the EOS for a relativistic gas in the enthalpy-temperature plane.
In this case, Bz does not contribute to the conservation of magnetic flux and can be advanced in time with the basic conservative scheme as a centered variable.
Anninos et al. (2005) considered the spherical ultrarelativistic blast wave of Blandford and McKee (1976) to test the performance of AMR in COSMOS++. The analytic solution depends on the initial total energy in the blast wave, the initial Lorentz factor of the shock, and the ambient density into which it expands. The relativistic blast wave is characterized by a very thin shell of matter, \(\Delta r \propto \Gamma _{{\rm{bw}}}^{ - 8/3}\), where Γbw is the initial Lorentz factor of the blast wave. The code was able to evolve a blast wave with an initial Γ,bw = 30 until it becomes non-relativistic, on a base mesh of 100 cells with initially 17 levels of refinement. Both the eAV and NOCD results agreed very well with the analytic solution. The eAV method gave a 10% error in the peak density of the blast wave. This error reduced to 1% with NOCD.
Although the origin of the failure seems to be the coupling of tangential and normal velocities, something similar (capturing unphysical flow states and wave speeds) also happens in purely normal flows in which flow variables change by many orders of magnitude across the discontinuity.
ENO schemes do not exclusively belong to the FD approach. In fact, these schemes were originally constructed for cell averages (Hartenet al.,1987).
The method of fractional step can also be applied to advance any source term, which is present in the equations (source splitting).
BGK refers to the Bhatnagar-Gross-Krook collision operator term used in the Boltzmann equation. Its inclusion in the flux function dramatically reduces the artificial dissipation in comparison with that of usual KFVSschemes based on free, i.e., non-collisional particle transport to compute the intercell fluxes. BGK-type KFVSmethods were introduced in Prendergast and Xu (1993).
For the more restrictive case of a Riemann problem with tangential magnetic fields and the additional condition v · B= 0, Romero et al.(2005) showed that the exact solution reduces to that of a purely RHD problem the contributions of the magnetic field being incorporated in the definition of a new, effective EOS.
References
Abramowicz, M. A. and Fragile, P. C., 2013, “Foundations of Black Hole Accretion Disk Theory”, Living Rev. Relativity, 16, lrr-2013-1. [DOI], [ADS], [arXiv:1104.5499 [astro-ph.HE]]. URL (accessed 14 July 2014): http://www.livingreviews.org/lrr-2013-1. (Cited on page 109.)
Astrophysical Fluid Dynamics Group, “Astrophysical Code Library”, project homepage, University of Illinois at Urbana-Champaign. URL (accessed 14 July 2014): http://rainman.astro.illinois.edu/codelib/. (Cited on pages 67, 69, and 146.)
Agudo, I., Gómez, J. L., Martí, J. M., Ibáñez, J. M., Marscher, A. P., Alberdi, A., Aloy, M. A. and Hardee, P. E., 2001, “Jet stability and the generation of superluminal and stationary components”, Astrophys. J., 549, L183–L186. [DOI], [ADS], [arXiv:astro-ph/0101188]. (Cited on page 12.)
Aloy, M. A. and Mimica, P., 2008, “Observational Effects of Anomalous Boundary Layers in Relativistic Jets”, Astrophys. J., 681, 84–95. [DOI], [ADS], [arXiv:0803.2693 [astro-ph]]. (Cited on page 22.)
Aloy, M. A., Ibáñez, J. M., Martí, J. M., Gómez, J. L. and Müller, E., 1999a, “High-resolution three-dimensional simulations of relativistic jets”, Astrophys. J. Lett., 523, L125–L128. [DOI], [ADS], [arXiv:astro-ph/9906428]. (Cited on pages 10 and 21.)
Aloy, M. A., Ibáñez, J. M., Martí, J. M. and Müller, E., 1999b, “GENESIS: A high-resolution code for three-dimensional relativistic hydrodynamics”, Astrophys. J. Suppl. Ser., 122, 151–166. [DOI], [ADS], [arXiv:astro-ph/9903352]. (Cited on pages 47, 49, 53, 75, 76, 79, and 146.)
Aloy, M. A., Gómez, J. L., Ibáñez, J. M., Martí, J. M. and Müller, E., 2000a, “Radio emission from three-dimensional relativistic hydrodynamic jets: Observational evidence of jet stratification”, Astrophys. J. Lett., 528, L85–L88. [DOI], [ADS], [arXiv:astro-ph/9911153]. (Cited on page 12.)
Aloy, M. A., Müller, E., Ibáñez, J. M., Martí, J. M. and MacFadyen, A. I., 2000b, “Relativistic Jets from Collapsars”, Astrophys. J. Lett., 531, L119–L122. [DOI], [ADS], [arXiv:astro-ph/9911098]. (Cited on page 19.)
Aloy, M. A., Martí, J. M., Gómez, J. L., Agudo, I., Müller, E. and Ibáñez, J. M., 2003, “Three-dimensional simulations of relativistic precessing jets probing the structure of superluminal sources”, Astrophys. J. Lett., 585, L109–L112. [DOI], [ADS], [arXiv:astro-ph/0302123]. (Cited on page 12.)
AMRVAC, “AMRVAC”, project homepage, Gitorius. URL (accessed 6 Nov 2014): https://gitorious.org/amrvac. (Cited on pages 52, 54, 69, 70, and 146.)
Anderson, M., Hirschmann, E. W., Liebling, S. L. and Neilsen, D., 2006, “Relativistic MHD with adaptive mesh refinement”, Class. Quantum Grav., 23, 6503–6524. [DOI], [ADS], [arXiv:gr-qc/0605102]. (Cited on pages 59, 60, 62, 67, 68, 69, 70, 89, 92, 96, 98, 99, and 100.)
Anile, A. M., 1989, Relativistic fluids and magneto-fluids: With applications in astrophysics and plasma physics, Cambridge University Press, Cambridge; New York. [Google Books]. (Cited on pages 8, 29, 31, 32, 113, 115, 116, 137, and 139.)
Anile, A. M. and Pennisi, S., 1987, “On the mathematical structure of test relativistic magnetofluiddynamics”, Ann. Inst. Henri Poincare, 46, 27–44. Online version (accessed 21 December 2015): http://www.numdam.org/item?id=AIHPA_1987__46_1_27_0. (Cited on pages 31, 32, and 113.)
Anninos, P. and Fragile, P. C., 2003, “Nonoscillatory Central Difference and Artificial Viscosity Schemes for Relativistic Hydrodynamics”, Astrophys. J. Suppl. Ser., 144, 243–257. [DOI], [ADS], [arXiv:astro-ph/0206265]. (Cited on pages 41, 46, 53, 75, 78, 79, 80, and 146.)
Anninos, P., Fragile, P. C. and Murray, S. D., 2003, “COSMOS: A radiation-chemo-hydrodynamics code for astrophysical problems”, Astrophys. J. Suppl. Ser., 147, 177–186. [DOI], [ADS], [arXiv:astro-ph/0303209]. (Cited on pages 46, 53, and 146.)
Anninos, P., Fragile, P. C. and Salmonson, J. D., 2005, “COSMOS++: Relativistic magnetohydrodynamics on unstructured grids with local adaptive refinement”, Astrophys. J., 635, 723–740. [DOI], [ADS], [arXiv:astro-ph/0509254]. (Cited on pages 46, 70, 76, 80, 83, 89, and 146.)
Antón, L., Zanotti, O., Miralles, J. A., Martí, J. M., Ibáñez, J. M., Font, J. A. and Pons, J. A., 2006, “Numerical 3+1 general relativistic magnetohydrodynamics: A local characteristic approach”, Astrophys. J., 637, 296–312. [DOI], [ADS], [arXiv:astro-ph/0506063]. (Cited on pages 57, 58, 60, 65, 66, 67, and 70.)
Antón, L., Miralles, J. A., Martí, J. M., Ibáñez, J. M., Aloy, M. A. and Mimica, P., 2010, “Relativistic magnetohydrodynamics: Renormalized eigenvectors and full wave decomposition Riemann solver”, Astrophys. J. Suppl. Ser., 188, 1–31. [DOI], [ADS], [arXiv:0912.4692 [astro-ph]]. (Cited on pages 32, 33, 57, 58, 60, 65, 70, 83, 90, 91, 92, 94, 95, 96, 98, 99, 100, 101, 113, 116, 117, and 118.)
Asenjo, F.A., Muñoz, V., Valdivia, J.A. and Mahajan, S.M., 2011, “A hydrodynamical model for relativistic spin quantum plasmas”, Phys. Plasmas, 18, 012107. [DOI]. (Cited on page 109.)
ATHENA, “The Athena MHD Code Project”, project homepage, Princeton University. URL (accessed 14 July 2014): https://trac.princeton.edu/Athena/. (Cited on pages 69, 71, and 146.)
Baiotti, L., Hawke, I., Montero, P. J. and Rezzolla, L., 2003, “A new three-dimensional general-relativistic hydrodynamics code”, Mem. Soc. Astron. Ital. Suppl., 1, 210–219. [ADS], [arXiv:1004.3849 [gr-qc]]. (Cited on pages 53, 79, and 147.)
Balsara, D. S., 1994, “Riemann Solver for Relativistic Hydrodynamics”, J. Comput. Phys., 114, 284–297. [DOI]. (Cited on page 36.)
Balsara, D. S., 2001a, “Total Variation Diminishing Scheme for Relativistic Magnetohydrodynamics”, Astrophys. J. Suppl. Ser., 132, 83–101. [DOI], [ADS]. (Cited on pages 7, 57, 66, 68, 86, 88, 89, 90, 91, 92, 94, 113, and 115.)
Balsara, D. S., 2001b, “Divergence-free adaptive mesh refinement for magnetohydrodynamics”, J. Comput. Phys., 174, 614–648. [DOI], [ADS], [arXiv:astro-ph/0112150]. (Cited on page 68.)
Balsara, D. S., 2001c, “Adaptive mesh refinement in computational astrophysics — Methods and applications”, J. Korean Astron. Soc., 34, S181–S190. [DOI], [ADS], [arXiv:astro-ph/0112148]. (Cited on pages 68 and 125.)
Balsara, D. S., 2004, “Second-order-accurate schemes for magnetohydrodynamics with divergence-free reconstruction”, Astrophys. J. Suppl. Ser., 151, 149–184. [DOI], [ADS], [arXiv:astro-ph/0308249]. (Cited on page 60.)
Balsara, D. S. and Spicer, D. S., 1999, “A staggered mesh algorithm using highorder Godunov fluxes to ensure solenoidal magnetic fields in magnetohydrodynamics simulations”, J. Comput. Phys., 149, 270–292. [DOI]. (Cited on pages 62, 64, 65, 96, and 99.)
Beckwith, K. and Stone, J. M., 2011, “A second-order Godunov method for multidimensional relativistic magnetohydrodynamics”, Astrophys. J. Suppl. Ser., 193, 6. [DOI], [ADS], [arXiv:1101.3573 [astro-ph]]. (Cited on pages 60, 71, 85, 86, 90, 95, 96, 98, 103, 105, and 146.)
Begelman, M. C., 1998, “Instability of Toroidal Magnetic Field in Jets and Plerions”, Astrophys. J., 493, 291–300. [DOI], [ADS], [arXiv:astro-ph/9708142]. (Cited on page 27.)
Begelman, M. C. and Li, Z.-Y., 1992, “An axisymmetric magnetohydrodynamic model for the Crab pulsar wind bubble”, Astrophys. J., 397, 187–195. [DOI], [ADS]. (Cited on pages 23 and 27.)
Begelman, M. C., Blandford, R. D. and Rees, M. J., 1984, “Theory of Extragalactic Radio Sources”, Rev. Mod. Phys., 56, 255–351. [DOI], [ADS]. (Cited on page 9.)
Bell, J., Berger, M.J., Saltzmann, J. and Welcome, M., 1994, “Three-dimensional adaptive mesh refinement for hyperbolic conservation laws”, SIAM J. Sci. Comput., 15, 127–138. [DOI]. (Cited on pages 50 and 125.)
Berger, M. J. and Colella, P., 1989, “Local Adaptive Mesh Refinement for Shock Hydrodynamics”, J. Comput. Phys., 82, 64–84. [DOI]. (Cited on pages 50, 68, 125, and 126.)
Berger, M. J. and Oliger, J., 1984, “Adaptive mesh refinement for hyperbolic partial differential equations”, J. Comput. Phys., 53, 484–512. [DOI]. (Cited on pages 50, 51, 69, and 125.)
Berger, M.J. and LeVeque, R. J., 1998, “Adaptive mesh refinement using wave-propagation algorithms for hyperbolic systems”, SIAM J. Numer. Anal., 35, 2298–2316. [DOI]. (Cited on page 126.)
Berger, M.J. and Rigoutsos, I., 1991, “An algorithm for point clustering and grid generation”, IEEE Trans. Syst. Man Cybern., 21, 1278–1286. [DOI]. (Cited on page 51.)
Bergmans, J., Keppens, R., van Odyck, D. E. A. and Achterberg, A., 2005, “Simulations of relativistic astrophysical flows”, in Adaptive Mesh Refinement — Theory and Applications, Proceedings of the Chicago Workshop, September 3–5, 2003, (Eds.) Plewa, T., Linde, T., Weirs, V. G., Lecture Notes in Computational Science and Engineering, 41, pp. 223–233, Springer, Berlin; New York. [DOI], [Google Books]. (Cited on page 67.)
Bernstein, J. P. and Hughes, P. A., 2009, “Refining a relativistic, hydrodynamic solver: Admitting ultrarelativistic flows”, J. Comput. Phys., 228, 6212–6230. [DOI], [ADS], [arXiv:astro-ph/0606012]. (Cited on page 50.)
Birkinshaw, M., 1991, “The stability of jets”, in Beams and Jets in Astrophysics, (Ed.) Hughes, P. A., pp. 278–341, Cambridge University Press, Cambridge, UK. [Google Books]. (Cited on page 101.)
Blandford, R. D. and Königl, A., 1979, “Relativistic Jets as Compact Radio Sources”, Astrophys. J., 232, 34–48. [DOI], [ADS]. (Cited on page 9.)
Blandford, R. D. and McKee, C. F., 1976, “Fluid Dynamics of Relativistic Blast Waves”, Phys. Fluids, 19, 1130–1138. [DOI], [ADS]. (Cited on pages 19, 74, and 76.)
Blandford, R. D. and Payne, D. G., 1982, “Hydromagnetic flows from accretion discs and the production of radio jets”, Mon. Not. R. Astron. Soc., 199, 883–903. [DOI], [ADS]. (Cited on pages 9 and 13.)
Blandford, R. D. and Pringle, J. E., 1976, “Kelvin-Helmholtz instability of relativistic beams”, Mon. Not. R. Astron. Soc., 176, 443–454. [DOI], [ADS]. (Cited on page 100.)
Blandford, R. D. and Znajek, R. L., 1977, “Electromagnetic extraction of energy from Kerr black holes”, Mon. Not. R. Astron. Soc., 179, 433–456. [DOI], [ADS]. (Cited on pages 9, 13, and 21.)
Blondin, J. M., Chevalier, R. A. and Frierson, D. M., 2001, “Pulsar wind nebulae in evolved supernova remnants”, Astrophys. J., 563, 806–815. [DOI], [ADS], [arXiv:astro-ph/0107076]. (Cited on page 28.)
Bodo, G., Mignone, A. and Rosner, R., 2004, “Kelvin-Helmholtz instability for relativistic fluids”, Phys. Rev. E, 70, 036304. [DOI], [ADS]. (Cited on page 103.)
Bogovalov, S. V. and Khangoulian, D. V., 2002, “On the origin of the torus and jet-like structures in the centre of the Crab Nebula”, Mon. Not. R. Astron. Soc., 336, L53–L55. [DOI], [ADS], [arXiv:astro-ph/0209269]. (Cited on page 26.)
Bogovalov, S. V., Chechetkin, V. M., Koldoba, A. V. and Ustyugoba, G. V., 2005, “Interaction of pulsar winds with interstellar medium: numerical simulation”, Mon. Not. R. Astron. Soc., 358, 705–715. [DOI], [ADS]. (Cited on page 26.)
Boris, J. P. and Book, D. L., 1973, “Flux corrected transport I. SHASTA, a fluid transport algorithm that works”, J. Comput. Phys., 11, 38–69. [DOI]. (Cited on pages 7, 45, and 122.)
Boris, J. P. and Book, D. L., 1976, “Flux-corrected transport III: Minimal-error FCT algorithms”, J. Comput. Phys., 20, 397–431. [DOI]. (Cited on page 45.)
Boris, J. P., Book, D. L. and Hain, K., 1975, “Flux-corrected transport II: Generalizations of the method”, J. Comput. Phys., 18, 248–283. [DOI]. (Cited on page 45.)
Böttcher, M., Harris, D.E. and Krawczynski, H. (Eds.), 2012, Relativistic Jets from Active Galactic Nuclei, Wiley-VCH, Weinheim. [Google Books]. (Cited on page 9.)
Brackbill, J. U. and Barnes, D. C., 1980, “The effect of nonzero ∇ · B on the numerical solution of the magnetohydrodynamic equations”, J. Comput. Phys., 35, 426–430. [DOI]. (Cited on pages 60, 62, and 65.)
Bridle, A., “Alan Bridle’s Image Gallery”, personal homepage, National Radio Astronomy Observatory. URL (accessed 14 July 2014): http://www.cv.nrao.edu/∼abridle/images.htm. (Cited on page 10.)
Bridle, A. H., Hough, D. H., Lonsdale, C. J., Burns, J. O. and Laing, R. A., 1994, “Deep VLA Imaging of Twelve Extended 3CR Sample”, Astron. J., 108, 766–820. [DOI], [ADS]. (Cited on page 10.)
Brio, M. and Wu, C. C., 1988, “An upwind differencing scheme for the equations of ideal magnetohydrodynamics”, J. Comput. Phys., 75, 400–422. [DOI]. (Cited on pages 32, 56, 88, and 93.)
Bucciantini, N., 2011, “MHD models of pulsar wind nebulae”, in High-Energy Emission from Pulsars and Systems, Proceedings of the First Session of the Sant Cugat Forum on Astrophysics, (Eds.) Torres, D. F., Rea, N., Astrophys. Space Sci. Proc., pp. 473–490, Springer, Berlin; New York. [DOI], [ADS], [arXiv:1005.4781 [astro-ph.HE]]. (Cited on page 28.)
Bucciantini, N., 2012, “The relativistic wind in PWNe”, Int. J. Mod. Phys.: Conf. Ser., 8, 120–131. [DOI], [ADS]. (Cited on page 28.)
Bucciantini, N. and Del Zanna, L., 2006, “Local Kelvin-Helmholtz instability and synchrotron modulation in Pulsar wind nebulae”, Astron. Astrophys., 454, 393–400. [DOI], [ADS], [arXiv:astro-ph/0603481]. (Cited on pages 103, 104, and 105.)
Bucciantini, N., Amato, E. and Del Zanna, L., 2005, “Relativistic MHD simulations of pulsar bow-shock nebulae”, Astron. Astrophys., 434, 189–199. [DOI], [ADS], [arXiv:astro-ph/0412534]. (Cited on page 28.)
Bühler, R. and Blandford, R. D., 2014, “The surprising Crab pulsar and its nebula: a review”, Rep. Prog. Phys., 77, 066901. [DOI], [ADS], [arXiv:1309.7046 [astro-ph.HE]]. (Cited on page 23.)
Burkert, A. and Bodenheimer, P., 1993, “Multiple fragmentation in collapsing protostars”, Mon. Not. R. Astron. Soc., 264, 798–806. [DOI], [ADS]. (Cited on page 125.)
Cactus, “The Cactus Code”, project homepage, Max Planck Institute for Gravitational Physics. URL (accessed 14 July 2014): http://www.cactuscode.org/. (Cited on page 146.)
Camus, N. F., Komissarov, S. S., Bucciantini, N. and Hughes, P. A., 2009, “Observations of ‘wisps’ in magnetohydrodynamic simulations of the Crab Nebula”, Mon. Not. R. Astron. Soc., 400, 1241–1246. [DOI], [ADS], [arXiv:0907.3647 [astro-ph.HE]]. (Cited on page 26.)
Cannizzo, J. K., Gehrels, N. and Vishniac, E. T., 2008, “Glimm’s method for relativistic hydrodynamics”, Astrophys. J., 680, 885–896. [DOI], [ADS], [arXiv:0802.1184 [astro-ph]]. (Cited on pages 36 and 83.)
Casse, F., Markowith, A. and Keppens, R., 2013, “Non-resonant magnetohydrodynamics streaming instability near magnetized relativistic shocks”, Mon. Not. R. Astron. Soc., 433, 940–951. [DOI], [ADS], [arXiv:1305.0847 [astro-ph.HE]]. (Cited on page 67.)
Cavallo, G. and Rees, M. J., 1978, “A qualitative study of cosmic fireballs and gamma-ray bursts”, Mon. Not. R. Astron. Soc., 183, 359–365. [DOI], [ADS]. (Cited on page 18.)
Centrella, J. M. and Wilson, J. R., 1984, “Planar numerical cosmology. II. The difference equations and numerical tests”, Astrophys. J. Suppl. Ser., 54, 229–249. [DOI], [ADS]. (Cited on pages 7, 46, 75, and 76.)
Chandra, “Crab Nebula Movie Animations”, online resource, Chandra X-Ray Observatory. URL (accessed 14 July 2014): http://chandra.harvard.edu/photo/2002/0052/animations.html. (Cited on page 25.)
Chandrasekhar, S., 1961, Hydrodynamic and Hydromagnetic Stability, International Series of Monographs on Physics, Clarendon Press, Oxford. [ADS], [Google Books]. (Cited on page 100.)
Chandrasekhar, S., 1967, An Introduction to the Study of Stellar Structure, Dover, Mineola, NY. [ADS], [Google Books]. (Cited on page 47.)
Chang, S. C., 1995, “The method of space time conservation element and solution element, a new approach for solving the Navier Stokes and Euler equations”, J. Comput. Phys., 119, 295–324. [DOI]. (Cited on pages 127 and 128.)
Chatterjee, R., Marscher, A. P., Jorstad, S. G. et al., 2011, “Connection between the accretion disk and jet in the radio galaxy 3C 111”, Astrophys. J., 734, 43. [DOI], [ADS], [arXiv:1104.0663 [astro-ph.HE]]. (Cited on page 9.)
Chattopadhyay, I. and Ryu, D., 2009, “Effects of fluid composition on spherical flows around black holes”, Astrophys. J., 694, 492–501. [DOI], [ADS], [arXiv:0812.2607 [astro-ph]]. (Cited on page 48.)
Choi, E. and Ryu, D., 2005, “Numerical relativistic hydrodynamics based on the total variation diminishing scheme”, New Astron., 11, 116–129. [DOI], [ADS], [arXiv:astro-ph/0507090]. (Cited on pages 47, 50, 53, 75, 78, and 79.)
Choi, E. and Wiita, P. J., 2010, “A multidimensional relativistic hydrodynamic code with a general equation of state”, Astrophys. J. Suppl. Ser., 191, 113–123. [DOI], [ADS], [arXiv:1009.3774 [astro-ph.HE]]. (Cited on pages 47, 48, 49, and 54.)
Choi, E., Wiita, P. J. and Ryu, D., 2007, “Hydrodynamic interactions of relativistic extragalactic jets with dense clouds”, Astrophys. J., 655, 769–780. [DOI], [ADS], [arXiv:astro-ph/0610474]. (Cited on page 10.)
Applied Numerical Algorithms Group, “Chombo: Software for Adaptive Solutions of Partial Differential Equations”, project homepage, Lawrence Berkeley National Laboratory. URL (accessed 24 July 2014): http://chombo.lbl.gov/. (Cited on page 146.)
Chorin, A. J., 1976, “Random Choice Solution of Hyperbolic Systems”, J. Comput. Phys., 22, 517–533. [DOI]. (Cited on pages 36 and 83.)
Cockburn, B., 1998, “Runge-Kutta local projection discontinuous Galerkin method for conservation laws V. Multidimensional systems”, J. Comput. Phys., 141, 199–224. [DOI]. (Cited on page 126.)
Cockburn, B. and Shu, C.-W., 1989, “Runge-Kutta local projection discontinuous Galerkin finite element method for scalar conservation laws II. General framework”, Math. Comput., 52, 411–435. [DOI]. (Cited on page 126.)
Cockburn, B., Hou, S. and Shu, C.-W., 1990, “Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws IV. The multidimensional case”, Math. Comput., 54, 545–581. [DOI]. (Cited on page 126.)
Colella, P., 1982, “Glimm’s Method for Gas Dynamics”, SIAM J. Sci. Stat. Comput., 3, 76–110. [DOI]. (Cited on pages 35 and 121.)
Colella, P., 1985, “A Direct Eulerian MUSCL Scheme for Gas Dynamics”, SIAM J. Sci. Stat. Comput., 6, 104–117. [DOI]. (Cited on pages 80 and 123.)
Colella, P., 1990, “Multidimensional Upwind Methods for Hyperbolic Conservation Laws”, J. Comput. Phys., 87, 171–200. [DOI]. (Cited on pages 47, 64, 124, and 141.)
Colella, P. and Woodward, P. R., 1984, “The piecewise parabolic method (PPM) for gas-dynamical simulations”, J. Comput. Phys., 54, 174–201. [DOI]. (Cited on pages 35, 42, 44, 121, 123, and 144.)
Colella, P., Graves, D. T., Keen, B. J. and Modiano, D., 2006, “A Cartesian grid embedded boundary method for hyperbolic conservation laws”, J. Comput. Phys., 2011, 347–366. [DOI]. (Cited on page 72.)
Contopoulos, I., Kazanas, D. and Fendt, C., 1999, “The Axisymmetric Pulsar Magnetosphere”, Astrophys. J., 511, 351–358. [DOI], [ADS], [arXiv:astro-ph/9903049]. (Cited on page 111.)
Coroniti, F. V., 1990, “Magnetically striped relativistic magnetohydrodynamic winds — The Crab Nebula revisited”, Astrophys. J., 349, 538–545. [DOI], [ADS]. (Cited on page 26.)
Costa, E., Frontera, F., Heise, J. et al., 1997, “Discovery of an X-Ray Afterglow Associated with the γ-Ray Burst of 28 February 1997”, Nature, 387, 783–785. [DOI], [ADS], [arXiv:astro-ph/9706065]. (Cited on page 17.)
Courant, R. and Friedrichs, K. O., 1976, Supersonic Flow and Shock Waves, Applied Mathematical Sciences, 21, Springer, Berlin; New York. [Google Books]. (Cited on pages 8 and 129.)
Courant, R., Friedrichs, K. O. and Lewy, H., 1928, “Über die partiellen Differenzengleichungen der mathematischen Physik”, Math. Ann., 100, 32–74. [DOI]. (Cited on page 123.)
Dai, W. and Woodward, P. R., 1994a, “An approximate Riemann solver for ideal magnetohydrodynamics”, J. Comput. Phys., 111, 354–372. [DOI]. (Cited on page 56.)
Dai, W. and Woodward, P. R., 1994b, “Extension of the piecewise parabolic method to multidimensional ideal magnetohydrodynamcis”, J. Comput. Phys., 115, 485–514. [DOI]. (Cited on page 56.)
Dai, W. and Woodward, P. R., 1997, “An Iterative Riemann Solver for Relativistic Hydrodynamics”, SIAM J. Sci. Stat. Comput., 18, 982–995. [DOI]. (Cited on page 36.)
Dai, W. and Woodward, P. R., 1998, “On the divergence-free condition and conservation laws in numerical simulations for supersonic magnetohydrodynamic flows”, Astrophys. J., 494, 317–335. [DOI], [ADS]. (Cited on pages 62 and 63.)
Daigne, F. and Mochkovitch, R., 2000, “Gamma-ray bursts from internal shocks in a relativistic wind: A hydrodynamical study”, Astron. Astrophys., 358, 1157–1166. [ADS], [arXiv:0005193 [astro-ph]]. (Cited on page 19.)
Davis, S. F., 1984, TVD Finite Difference Scheme and Artificial Viscosity, ICASE Report, No. 84-20 / NASA-CR-172373, NASA Langley Research Center, Hampton, VA. Online version (accessed 24 July 2014): http://hdl.handle.net/2060/19840021490. (Cited on pages 59, 70, and 122.)
De Colle, F., Granot, J., Líopez-Cíamara, D. and Ramirez-Ruiz, E., 2012a, “Gamma-ray burst dynamics and afterglow radiation from adaptive mesh refinement, special relativistic hydrodynamic simulations”, Astrophys. J., 746, 122. [DOI], [ADS], [arXiv:1111.6890 [astro-ph.HE]]. (Cited on pages 21, 51, 54, and 147.)
De Colle, F., Guillochon, J., Naiman, J. and Ramirez-Ruiz, E., 2012b, “The dynamics, appearance, and demographics of relativistic jets triggered by tidal disruption of stars in quiescent supermassive black holes”, Astrophys. J., 760, 103. [DOI], [ADS], [arXiv:1205.1507 [astro-ph.HE]]. (Cited on page 21.)
De Colle, F., Ramirez-Ruiz, E., Granot, J. and Lopez-Camara, D., 2012c, “Simulations of gamma-ray burst jets in a stratified external medium: dynamics, afterglow light curves, jet breaks, and radio calorimetry equations”, Astrophys. J., 751, 57. [DOI], [ADS], [arXiv:1111.6667 [astro-ph.HE]]. (Cited on page 21.)
De Villiers, J. P. and Hawley, J. F., 2003, “A numerical method for general relativistic magnetohydrodynamics”, Astrophys. J., 589, 458–480. [DOI], [ADS], [arXiv:astro-ph/0210518]. (Cited on pages 60, 83, 85, 89, and 90.)
De Villiers, J. P., Hawley, J. F. and Krolik, J. H., 2003, “Magnetically driven accretion flows in the Kerr metric. I. Models and overall structure”, Astrophys. J., 599, 1238–1253. [DOI], [ADS], [arXiv:astro-ph/0307260]. (Cited on page 16.)
De Villiers, J. P., Hawley, J. F., Krolik, J. H. and Hirose, S., 2005, “Magnetically driven accretion in the Kerr metric. III. Unbound outflows”, Astrophys. J., 620, 878–888. [DOI], [ADS], [arXiv:astro-ph/0407092]. (Cited on page 16.)
Dedner, A., Kemm, F., Kröner, D., Munz, C.-D., Schnitzer, T. and Wesenberg, M., 2002, “Hyperbolic divergence cleaning for the MHD equations”, J. Comput. Phys., 175, 645–673. [DOI]. (Cited on pages 61, 62, and 110.)
Del Zanna, L. Amato, E. and Bucciantini, N., 2004, “Axially symmetric relativistic MHD simulations of pulsar wind nebulae in supernova remnants. On the origin of torus and jet-like features”, Astron. Astrophys., 421, 1063–1073. [DOI], [ADS], [arXiv:astro-ph/0404355]. (Cited on page 26.)
Del Zanna, L. and Bucciantini, N., 2002, “An efficient shock-capturing central-type scheme for multidimensional relativistic flows. I. Hydrodynamics”, Astron. Astrophys., 390, 1177–1186. [DOI], [ADS], [arXiv:astro-ph/0205290]. (Cited on pages 39, 41, 45, 47, 50, 53, 75, 78, 79, and 80.)
Del Zanna, L., Bucciantini, N. and Londrillo, P., 2003, “An efficient shock-capturing central-type scheme for multidimensional relativistic flows. II. Magnetohydrodynamics”, Astron. Astrophys., 400, 397–413. [DOI], [ADS], [arXiv:astro-ph/0210618]. (Cited on pages 26, 57, 59, 60, 65, 66, 67, 69, 70, 83, 85, 89, 90, 92, 96, 98, 99, 100, 103, and 141.)
Del Zanna, L., Zanotti, O., Bucciantini, N. and Londrillo, P., 2007, “ECHO: an Eulerian conservative high order scheme for general relativistic magnetohydrodynamics and magnetodynamics”, Astron. Astrophys., 473, 11–30. [DOI], [ADS], [arXiv:0704.3206 [astro-ph]]. (Cited on pages 58, 60, 65, 70, 83, 85, 86, 90, 96, 97, 98, and 146.)
Del Zanna, L., Chandra, V., Inghirami, G., Rolando, V. Beraudo, A., De Pace, A., Pagliara, G., Drago, A. and Becattini, F., 2013, “Relativistic viscous hydrodynamics for heavy-ion collisions with ECHO-QGP”, Eur. Phys. J. C, 73, 8. [DOI], [ADS], [arXiv:1305.7052 [nucl-th]]. (Cited on page 109.)
DeLaney, T., Gaensler, B. M., Arons, J. and Pivovaroff, M. J., 2006, “Time variability in the X-ray nebula powered by pulsar B1509-58”, Astrophys. J., 640, 929–940. [DOI], [ADS], [arXiv:astro-ph/0512047]. (Cited on page 26.)
Dellar, P. J., 2001, “A note on magnetic monopoles and the one-dimensional MHD Riemann problem”, J. Comput. Phys., 172, 392–398. [DOI]. (Cited on page 61.)
DeVore, C. R., 1991, “Flux-corrected transport techniques for multidimensional compressible magnetohydrodynamics”, J. Comput. Phys., 92, 142–160. [DOI]. (Cited on page 62.)
Dixon, W. G., 1978, Special relativity: The foundations of macroscopic physics, Cambridge University Press, Cambridge. [Google Books]. (Cited on page 29.)
Dodson, R., Lewis, D., McConnell, D. and Deshpande, A. A., 2003, “The radio nebula surrounding the Vela pulsar”, Mon. Not. R. Astron. Soc., 343, 116–124. [DOI], [ADS], [arXiv:astro-ph/0302373]. (Cited on page 25.)
Dolezal, A. and Wong, S. S. M., 1995, “Relativistic hydrodynamics and Essentially Non-Oscillatory shock capturing schemes”, J. Comput. Phys., 120, 266–277. [DOI]. (Cited on pages 37, 41, 45, 47, 49, 53, 75, and 141.)
Donat, R. and Marquina, A., 1996, “Capturing shock reflections: An improved flux formula”, J. Comput. Phys., 125, 42–58. [DOI]. (Cited on pages 41 and 121.)
Donat, R., Font, J. A., Ibáñez, J. M. and Marquina, A., 1998, “A Flux-Split Algorithm applied to Relativistic Flows”, J. Comput. Phys., 146, 58–81. [DOI]. (Cited on pages 48, 75, 78, 79, 80, and 112.)
Dubal, M. R., 1991, “Numerical Simulations of Special Relativistic, Magnetic Gas Flows”, Comput. Phys. Commun., 64, 221–234. [DOI]. (Cited on pages 7, 59, 60, 86, and 95.)
Dubus, G., 2006, “Gamma-ray binaries: pulsars in disguise?”, Astron. Astrophys., 456, 801–817. [DOI], [ADS], [arXiv:astro-ph/0605287]. (Cited on page 28.)
Dubus, G., 2013, “Gamma-ray binaries and related systems”, Astron. Astrophys. Rev., 21, 64. [DOI], [ADS], [arXiv:1307.7083 [astro-ph.HE]]. (Cited on page 28.)
Duez, M. D., Liu, Y. T., Shapiro, S. L. and Stephens, B. C., 2005, “Relativistic magnetohydrodynamics in dynamical spacetimes: Numerical methods and tests”, Phys. Rev. D, 72, 024028. [DOI], [ADS], [arXiv:astro-ph/0503420]. (Cited on pages 57, 58, 59, 65, 69, 70, 83, 86, 89, 90, and 91.)
Duffell, P. C. and MacFadyen, A. I., 2011, “TESS: A relativistic hydrodynamic code on a moving Voronoi mesh”, Astrophys. J. Suppl. Ser., 197, 15. [DOI], [ADS], [arXiv:1104.3562 [astro-ph.HE]]. (Cited on pages 71, 72, 73, 80, 90, 93, 96, 99, 100, 101, and 147.)
Dumbser, M. and Zanotti, O., 2009, “Very high oder PNPM schemes on unstructured meshes for the resistive relativistic MHD equations”, J. Comput. Phys., 228, 6991–7006. [DOI], [ADS], [arXiv:0903.4832 [gr-qc]]. (Cited on pages 110 and 126.)
Duncan, G. C. and Hughes, P. A., 1994, “Simulations of Relativistic Extragalactic Jets”, Astrophys. J., 436, L119–L122. [DOI], [ADS]. (Cited on pages 10, 39, 43, 49, 50, 53, and 66.)
Duncan, G. C., Hughes, P. A. and Opperman, J., 1996, “Simulations of relativistic extragalactic jets: A variable equation of state”, in Energy Transport in Radio Galaxies and Quasars, Proceedings of a workshop, held in Tuscaloosa, Alabama, 19–23 September 1995, (Eds.) Hardee, P. E., Bridle, A. H., Zensus, J. A., ASP Conference Series, 100, pp. 143–148, Astronomical Society of the Pacific, San Francisco. [ADS], [Google Books]. (Cited on page 48.)
Durant, M., Kargaltsev, O. Pavlov, G. G., Kropotina, J. and Levenfish, K., 2013, “The helical jet of the Vela pulsar”, Astrophys. J., 763, 72. [DOI], [ADS], [arXiv:1211.0347 [astro-ph.HE]]. (Cited on page 26.)
Eichler, D., Livio, M., Piran, T. and Schramm, D. N., 1989, “Nucleosynthesis, neutrino bursts and gamma-rays from coalescing neutron stars”, Nature, 340, 126–128. [DOI], [ADS]. (Cited on page 18.)
Einfeldt, B., 1988, “On Godunov-type methods for gas dynamics”, SIAM J. Numer. Anal., 25, 294–318. [DOI]. (Cited on pages 39, 119, and 121.)
Etienne, Z. B., Liu, Y. T. and Shapiro, S.l., 2010, “Relativistic magnetohydrodynamics in dynamical spacetimes: A new adaptive mesh refinement implementation”, Phys. Rev. D, 82, 084 031. [DOI], [ADS], [arXiv:1007.2848 [astro-ph.HE]]. (Cited on pages 60, 65, 67, 69, 71, 99, and 100.)
Eulderink, F., 1993, Numerical relativistic hydrodynamics, Ph.D. thesis, Rijksuniversiteit Leiden, Leiden, Netherlands. [ADS]. (Cited on pages 7, 36, 37, 47, 49, 53, 75, and 112.)
Eulderink, F. and Mellema, G., 1995, “General relativistic hydrodynamics with a Roe solver”, Astron. Astrophys. Suppl., 110, 587–623. [ADS], [arXiv:astro-ph/9411056]. (Cited on pages 7, 36, 37, 47, 49, 53, 75, and 78.)
Evans, C. R., 1986, “An approach for calculating axisymmetric gravitational collapse”, in Dynamical Spacetimes and Numerical Relativity, Proceedings of the Workshop held at Drexel University, October 7–11, 1985, (Ed.) Centrella, J. M., pp. 3–39, Cambridge University Press, Cambridge; New York. [ADS], [Google Books]. (Cited on page 7.)
Evans, C. R. and Hawley, J. F., 1988, “Simulation of magnetohydrodynamic flows: a constrained transport method”, Astrophys. J., 332, 659–677. [DOI], [ADS]. (Cited on pages 62 and 69.)
Falle, S. A. E. G., 1991, “Self-Similar Jets”, Mon. Not. R. Astron. Soc., 250, 581–596. [DOI], [ADS]. (Cited on page 37.)
Falle, S. A. E. G. and Komissarov, S. S., 1996, “An upwind numerical scheme for relativistic hydrodynamics with a general equation of state”, Mon. Not. R. Astron. Soc., 278, 586–602. [DOI], [ADS]. (Cited on pages 37, 38, 43, 47, 53, 57, 75, 79, and 80.)
Fanaroff, B. L. and Riley, J. M., 1974, “The Morphology of Extragalactic Radio Sources of High and Low Luminosity”, Mon. Not. R. Astron. Soc., 167, 31–35. [DOI], [ADS]. (Cited on page 10.)
Farris, B. D., Li, T. K., Liu, Y. T. and Shapiro, S. L., 2008, “Relativistic radiation magnetohydrodynamics in dynamical spacetimes: numerical methods and tests”, Phys. Rev. D, 78, 024 023. [DOI], [ADS], [arXiv:0802.3210 [astro-ph]]. (Cited on page 111.)
Ferrari, A., Trussoni, E. and Zaninetti, L., 1978, “Relativistic Kelvin-Helmholtz instabilities in extragalactic radio sources”, Astron. Astrophys., 64, 43–52. [ADS]. (Cited on page 100.)
Ferrari, A., Trussoni, E. and Zaninetti, L., 1980, “Magnetohydrodynamic Kelvin-Helmholtz instabilities in astrophysics. I — relativistic flows — plane boundary layer in vortex sheet approximation”, Mon. Not. R. Astron. Soc., 163, 469–483. [DOI], [ADS]. (Cited on pages 100, 103, and 104.)
Ferrari, A., Trussoni, E. and Zaninetti, L., 1981, “Magnetohydrodynamic Kelvin-Helmholtz instabilities in astrophysics. II Cylindrical boundary layer in vortex sheet approximation”, Mon. Not. R. Astron. Soc., 196, 1051–1066. [DOI], [ADS]. (Cited on page 100.)
FLASH, “FLASH Center for Computational Science”, project homepage, University of Chicago. URL (accessed 14 July 2014): http://flash.uchicago.edu/site/. (Cited on pages 47, 52, 54, and 146.)
Font, J. A., 2008, “Numerical Hydrodynamics and Magnetohydrodynamics in General Relativity”, Living Rev. Relativity, 11, lrr-2008-7. [DOI], [ADS]. URL (accessed 14 July 2014): http://www.livingreviews.org/lrr-2008-7. (Cited on pages 8, 13, and 46.)
Font, J. A., Ibáñez, J. M., Martí, J. M. and Marquina, A., 1994, “Multidimensional relativistic hydrodynamics: characteristic fields and modern high-resolution shock-capturing schemes”, Astron. Astrophys., 282, 304–314. [ADS]. (Cited on page 112.)
Fromang, S., Hennebelle, P. and Teyssier, R., 2006, “A high order Godunov scheme with constrained transport and adaptive mesh refinement for astrophysical magnetohydrodynamics”, Astron. Astrophys., 457, 371–384. [DOI], [ADS], [arXiv:astro-ph/0607230]. (Cited on page 124.)
Fryxell, B., Olson, K., Ricker, P. et al., 2000, “FLASH: An adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes”, Astrophys. J. Suppl. Ser., 131, 273–334. [DOI], [ADS]. (Cited on pages 54 and 146.)
Galama, T. J., Vreeswijk, P. M., van Paradijs, J. et al., 1998, “An Unusual Supernova in the Error Box of the γ-Ray Burst of 25 April 1998”, Nature, 395, 670–672. [DOI], [ADS], [arXiv:astro-ph/9806175]. (Cited on page 17.)
Gammie, C. F. McKinney, J. C. and Tóoth, G., 2003, “HARM: A numerical scheme for general relativistic magnetohydrodynamics”, Astrophys. J., 589, 444–457. [DOI], [ADS], [arXiv:astro-ph/0301509]. (Cited on pages 58, 65, 70, 83, 89, 90, and 146.)
Gardiner, T. A. and Stone, J. M., 2005, “An unsplit Godunov method for ideal MHD via constrained transport”, J. Comput. Phys., 205, 509–539. [DOI], [ADS], [arXiv:astro-ph/0501557]. (Cited on pages 64, 65, 124, and 142.)
Gerwin, R. A., 1968, “Stability of the interface between two fluids in relative motion”, Rev. Mod. Phys., 40, 652–658. [DOI]. (Cited on page 100.)
Giacomazzo, B., “WhiskyMHD”, personal homepage, Bruno Giacomazzo. URL (accessed 14 July 2014): http://www.brunogiacomazzo.org/whiskymhd.html. (Cited on pages 70 and 147.)
Giacomazzo, B. and Rezzolla, L., 2006, “The exact solution of the Riemann problem in relativistic magnetohydrodynamics”, J. Fluid Mech., 562, 223–259. [DOI], [ADS], [arXiv:gr-qc/0507102]. (Cited on pages 32, 56, 86, 88, 89, 91, 93, 133, 136, 137, 138, and 139.)
Giacomazzo, B. and Rezzolla, L., 2007, “WhiskyMHD: a new numerical code for general relativistic magnetohydrodynamics”, Class. Quantum Grav., 24, S235–S258. [DOI], [ADS], [arXiv:gr-qc/0701109]. (Cited on pages 56, 58, 66, 67, 69, 70, 89, 90, 92, 95, and 147.)
Giannios, D., Mimica, P. and Aloy, M. A., 2008, “On the existence of a reverse shock in magnetized gamma-ray burst ejecta”, Astron. Astrophys., 478, 747–753. [DOI], [ADS], [arXiv:0711.1980 [astro-ph]]. (Cited on page 23.)
Gill, A. E., 1965, “Instabilities of ‘top-hat’jets and wakes in compressible fluids”, Phys. Fluids, 8, 14281430. [DOI]. (Cited on page 100.)
Glimm, J., 1965, “Solutions in the large for nonlinear hyperbolic systems of equations”, Commun. Pure Appl. Math., 18, 697–715. [DOI]. (Cited on pages 36, 83, and 121.)
Godlewski, E. and Raviart, P. A., 1996, Numerical approximation of hyperbolic systems of conservation laws, Springer, New York. [Google Books]. (Cited on page 32.)
Godunov, S. K., 1959, “Difference Methods for the Numerical Calculations of Discontinuous Solutions of the Equations of Fluid Dynamics”, Mat. Sb., 47, 271–306. Online version (accessed 21 December 2015): http://mi.mathnet.ru/eng/msb/v89/i3/p271. In Russian, translation in: US Joint Publ. Res. Service, JPRS, 7226 (1969). (Cited on page 120.)
Goedbloed, J. P., Keppens, R. and Poedts, S., 2010, Advanced Magnetohydrodynamics, Cambridge University Press, Cambridge; New York. [Google Books]. (Cited on pages 8, 29, and 60.)
Gómez, J. L., 2002, “Observations and simulations of relativistic jets”, in Relativistic Flows in Astrophysics, (Eds.) Guthmann, A. W., Georganopoulos, M., Marcowith, A., Manolakou, K., Lecture Notes in Physics, 589, pp. 169–196, Springer, Berlin; New York. [ADS], [arXiv:astro-ph/0109338], [Google Books]. (Cited on page 12.)
Gómez, J. L., Martí, J. M., Marscher, A. P., Ibáñez, J. M. and Alberdi, A., 1997, “Hydrodynammical Models of Superluminal Sources”, Astrophys. J., 482, L33–L36. [DOI], [ADS]. (Cited on page 12.)
Gómez, J. L., Marscher, A. P., Alberdi, A., Martí, J. M. and Ibáñez, J. M., 1998, “Subparsec Polarimetric Radio Observations of 3C 120: A Close-up Look at Superluminal Motion”, Astrophys. J., 499, 221–226. [DOI], [ADS]. (Cited on page 12.)
Gómez, J. L., Marscher, A., Alberdi, A., Jorstad, S. G. and Agudo, I., 2001, “Monthly 43 GHz polarimetric monitoring of 3C120 over 16 epochs: Evidence for trailing shocks in a relativistic jet”, Astrophys. J., 561, L16–L19. [DOI], [ADS], [arXiv:astro-ph/0110133]. (Cited on page 12.)
Gotlieb, S., Ketcheson, D. I. and Shu, C.-S., 2009, “High order strong stability preserving time discretizations”, J. Sci. Comput., 38, 251–289. [DOI]. (Cited on page 47.)
Grandclément, P. and Novak, J., 2009, “Spectral Methods for Numerical Relativity”, Living Rev. Relativity, 12, lrr-2009-1. [DOI], [ADS], [arXiv:0706.2286 [gr-qc]]. URL (accessed 14 July 2014): http://www.livingreviews.org/lrr-2009-1. (Cited on page 8.)
Granot, J. and Ramirez-Ruiz, E., 2012, “Jets and gamma-ray burst unification schemes”, in Gamma-ray Bursts, (Eds.) Kouveliotou, C., Wijers, R. A. M. J., Woosley, S., Cambridge Astrophysics Series, 51, pp. 215–250, Cambridge University Press, Cambridge; New York. [Google Books]. (Cited on page 18.)
Greiner, J., “Gamma-ray Bursts”, personal homepage, Max Planck Institute for Extraterrestrial Physics. URL (accessed 14 July 2014): http://www.mpe.mpg.de/∼jcg/grbgen.html. (Cited on page 17.)
Greiner, J., 2012, “Multiwavelength afterglow observations”, in Gamma-ray Bursts, (Eds.) Kouveliotou, C., Wijers, R. A. M. J., Woosley, S., Cambridge Astrophysics Series, 51, pp. 91–120, Cambridge University Press, Cambridge; New York. [Google Books]. (Cited on page 17.)
Gurski, K. F., 2004, “An HLLC-type approximate riemann solver for ideal magnetohydrodynamics”, SIAM J. Sci. Comput., 25, 2165–2187. [DOI]. (Cited on pages 57 and 121.)
Hardee, P. E., 1979, “On the configuration and propagation of jets in extragalactic radio sources”, Astrophys. J., 234, 47–55. [DOI], [ADS]. (Cited on page 100.)
Hardee, P. E., 2000, “On Three-Dimensional Structures in Relativistic Hydrodynamics Jets”, Astrophys. J., 533, 176–193. [DOI], [ADS]. (Cited on page 100.)
Hardee, P. E., 2003, “Modeling helical structures in relativistic jets”, Astrophys. J., 597, 798–808. [DOI], [ADS], [arXiv:astro-ph/0307400]. (Cited on page 13.)
Hardee, P. E., 2006, “AGN jets: A review of stability and structure”, in Relativistic Jets: The Common Physics of AGN, Microquasars, and Gamma-Ray Bursts, Ann Arbor, Michigan, 14–17 December 2005, (Eds.) Hughes, P. A., Bregman, J. N., AIP Conf. Proc., 856, pp. 57–77, American Institute of Physics, Melville, NY. [DOI], [ADS]. (Cited on page 13.)
Hardee, P. E., 2007, “Stability properties of strongly magnetized spine-sheath relativistic jets”, Astrophys. J., 664, 26–46. [DOI], [ADS], [arXiv:0704.1621 [astro-ph]]. (Cited on page 101.)
Hardee, P. E., Rosen, A., Hughes, P. A. and Duncan, G. C., 1998, “Time-Dependent Structure of Perturbed Relativistic Jets”, Astrophys. J., 500, 599–609. [DOI], [ADS]. (Cited on page 100.)
Hardee, P. E., Walker, R. C. and Gíomez, J. L., 2005, “Modeling the 3C 120 radio jet from 1 to 30 milliarcseconds”, Astrophys. J., 620, 646–664. [DOI], [ADS], [arXiv:astro-ph/0410720]. (Cited on page 13.)
Harrison, R. and Kobayashi, S., 2013, “Magnetization degree of gamma-ray burst fireballs: numerical study”, Astrophys. J., 772, 101. [DOI], [ADS], [arXiv:1211.1032 [astro-ph.HE]]. (Cited on pages 19, 21, and 23.)
Harten, A., 1983, “High resolution schemes for hyperbolic conservation laws”, J. Comput. Phys., 49, 357–393. [DOI]. (Cited on pages 53 and 122.)
Harten, A., 1984, “On a Class of High Resolution Total-Variation-Stable Finite-Difference Schemes”, SIAM J. Numer. Anal., 21, 1–23. [DOI]. (Cited on pages 121 and 122.)
Harten, A., Lax, P. D. and van Leer, B., 1983, “On upstream differencing and Godunov-type schemes for hyperbolic conservation laws”, SIAM Rev., 25, 35–61. [DOI]. (Cited on pages 38, 57, 119, 121, and 127.)
Harten, A., Engquist, B., Osher, S. and Chakrabarthy, S. R., 1987, “Uniformly High Order Accurate Essentially Non-oscillatory Schemes, III”, J. Comput. Phys., 71, 231–303. [DOI]. (Cited on pages 44, 45, and 122.)
Hawley, J. F., Smarr, L. L. and Wilson, J. R., 1984, “A numerical study of nonspherical black hole accretion. II. Finite differencing and code calibration”, Astrophys. J. Suppl. Ser., 55, 211–246. [DOI], [ADS]. (Cited on pages 7, 46, 60, 75, and 76.)
He, P. and Tang, H., 2012, “An adaptive moving mesh method for two-dimensional relativistic magnetohydrodynamics”, Comput. Fluids, 60, 1–20. [DOI]. (Cited on page 124.)
Hester, J. J., 2008, “The Crab Nebula: An astrophysical chimera”, Annu. Rev. Astron. Astrophys., 46, 127–155. [DOI], [ADS]. (Cited on page 25.)
Hester, J. J., Scowen, P. A. and Sankrit, R. et al., 1995, “WFPC2 studies of the Crab Nebula. I. HST and ROSA imaging of the synchrotron nebula”, Astrophys. J., 448, 240–263. [DOI], [ADS]. (Cited on page 25.)
Hester, J. J., Mori, K., Burrows, D. et al., 2002, “Hubble space telescope and Chandra monitoring of the Crab synchrotron nebula”, Astrophys. J., 577, L49–L52. [DOI], [ADS]. (Cited on page 26.)
Hirose, S., Krolik, J. H., De Villiers, J.-P. and Hawley, J. F., 2004, “Magnetically driven accretion flows in the Kerr metric. II. Structure of the magnetic field”, Astrophys. J., 606, 1083–1097. [DOI], [ADS], [arXiv:astro-ph/0311500]. (Cited on page 16.)
Hirotani, K., Takahashi, M., Nitta, S.-Y. and Tomimatsu, A., 1992, “Accretion in a Kerr black hole magnetosphere: energy and angular momentum transport between the magnetic field and the matter”, Astrophys. J., 386, 455–463. [DOI], [ADS]. (Cited on pages 9 and 13.)
Hjorth, J., 2013, “The supernova/gamma-ray burst/jet connection”, Philos. Trans. R. Soc. London, Ser. A, 371, 20120275. [DOI], [ADS], [arXiv:1304.7736 [astro-ph.HE]]. (Cited on page 18.)
Hjorth, J. and Bloom, J. S., 2012, “The GRB-supernova conncetion”, in Gamma-ray Bursts, (Eds.) Kouveliotou, C., Wijers, R. A. M. J., Woosley, S., Cambridge Astrophysics Series, 51, pp. 169–190, Cambridge University Press, Cambridge; New York.[Google Books]. (Cited on pages 17 and 18.)
Honkkila, V. and Janhunen, P., 2007, “HLLC solver for ideal relativistic RMHD”, J. Comput. Phys., 223, 643–656. [DOI]. (Cited on pages 58, 89, and 90.)
Hughes, P. A., Miller, M. A. and Duncan, G. C., 2002, “Three-dimensional hydrodynamic simulations of relativistic extragalactic jets”, Astrophys. J., 572, 713–728. [DOI], [ADS], [astro-ph/0202402]. (Cited on pages 10, 26, 39, 43, 49, 50, and 53.)
Ibáñez, J. M., Cordero-Carrión, I., Martí, J. M. and Miralles, J. A., 2013, “On the convexity of relativistic hydrodynamics”, Class. Quantum Grav., 30, 057002. [DOI], [ADS]. (Cited on page 32.)
Ibáñez, J. M., Cordero-Carrión, I., Aloy, M. Ä., Martí, J. M. and Miralles, J. A., 2015, “On the convexity of relativistic ideal magnetohydrodynamics”, Class. Quantum Grav., 32, 095007. [DOI], [ADS], [arXiv:1503.00978 [gr-qc]]. (Cited on page 32.)
Iwamoto, T. J., Mazzali, P. A., Nomoto, K. et al., 1998, “A Hypernova Model for the Supernova Associated with the γ-Ray Burst of 25 April 1998”, Nature, 395, 672–674. [DOI], [ADS], [arXiv:astro-ph/9806382]. (Cited on page 17.)
Janhunen, P., 2000, “A positive conservative method for magnetohydrodynamics based on HLL and Roe methods”, J. Comput. Phys., 160, 649–661. [DOI]. (Cited on page 61.)
Jeffrey, A. and Taniuti, T., 1964, Non-linear wave propagation, Mathematics in Science and Engineering, Academic Press, New York. [Google Books]. (Cited on pages 8, 32, and 83.)
Jiang, G. and Shu, C.-W., 1996, “Efficient implementation of weighted ENO schemes”, J. Comput. Phys., 126, 202–228. [DOI]. (Cited on pages 45 and 122.)
Jiang, G.-S. and Tadmor, E., 1998, “Nonoscillatory central schemes for multidimensional hyperbolic conservation laws”, SIAM J. Numer. Anal., 19, 1892–1917. [DOI]. (Cited on pages 53 and 121.)
Jiang, G.-S., Levy, D., Lin, C.-T., Osher, S. and Tadmor, E., 1998, “High-resolution nonoscillatory central schemes with nonstaggered grids for hyperbolic conservation laws”, SIAM J. Numer. Anal., 35, 21472168. [DOI]. (Cited on pages 53 and 121.)
Kadler, M., Ros, E., Perucho, M. et al., 2008, “The trails of superluminal jet components in 3C 111”, Astrophys. J., 680, 867–884. [DOI], [ADS], [arXiv:0801.0617 [astro-ph]]. (Cited on page 12.)
Kargaltsev, O. and Pavlov, G. G., 2008, “Pulsar Wind Nebulae in the Chandra Era”, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, Montreal, Canada, 12–17 August 2007, (Eds.) Bassa, C., Wang, Z., Cumming, A., Kaspi, V. M., AIP Conference Proceedings, 983, pp. 171–185, American Institute of Physics, Melville, NY. [DOI], [ADS], [arXiv:0801.2602 [astro-ph]]. (Cited on page 26.)
Kennel, C. F. and Coroniti, F. V., 1984a, “Confinement of the Crab pulsar’s wind by its supernova remnant”, Astrophys. J., 283, 694–709. [DOI], [ADS]. (Cited on page 23.)
Kennel, C. F. and Coroniti, F. V., 1984b, “Magnetohydrodynamic model of Crab Nebula radiation”, Astrophys. J., 283, 710–730. [DOI], [ADS]. (Cited on page 23.)
Keppens, R. and Meliani, Z., 2008, “Linear wave propagation in relativistic magnetohydrodynamics”, Phys. Plasmas, 15, 102 103. [DOI], [ADS], [arXiv:0810.2416 [astro-ph]]. (Cited on page 32.)
Keppens, R., Nool, M., Tóth, G. and Goedbloed, J. P., 2003, “Adaptive mesh refinement for conservative systems: Multidimensional efficiency evaluation”, Comput. Phys. Commun., 153, 317–339. [DOI], [ADS], [arXiv:astro-ph/0403124 [astro-ph]]. (Cited on pages 50, 54, and 146.)
Keppens, R., Meliani, Z., van der Holst, B. and Casse, F., 2008, “Extragalactic jets with helical magnetic fields: relativistic MHD simulations”, Astron. Astrophys., 486, 663–678. [DOI], [ADS], [arXiv:0802.2034 [astro-ph]]. (Cited on page 11.)
Keppens, R., Meliani, Z., van Marle, A. J., Delmont, P., Vlasis, A. and van der Holst, B., 2012, “Parallel, grid-adaptive approaches for relativistic hydro and magnetohydrodynamics”, J. Comput. Phys., 231, 718–744. [DOI]. (Cited on pages 44, 51, 54, 59, 70, 76, 99, 100, and 146.)
Keppens, R., Porth, O., Galsgaard, K., Frederiksen, J.T, Restante, A.L., Lapenta, G. and Pamell, C., 2013, “Resistive magnetohydrodynamic reconnection: Resolving long-term, chaotic dynamics”, Phys. Plasmas, 20, 092 109. [DOI]. (Cited on page 110.)
Khokhlov, A. M., 1998, “Fully Threaded Tree Algorithms for Adaptive Refinement Fluid Dynamics Simulations”, J. Comput. Phys., 143, 519–543. [DOI]. (Cited on pages 51, 69, and 124.)
Klein, Y. Y., 2010, Master’s thesis, Hebrew University, Jerusalem. (Cited on page 54.)
Kobayashi, S. and Zhang, B., 2007, “The onset of gamma-ray burst afterglow”, Astrophys. J., 655, 973979. [DOI], [ADS], [arXiv:astro-ph/0608132]. (Cited on page 19.)
Kobayashi, S., Piran, T. and Sari, R., 1999, “Hydrodynamics of a Relativistic Fireball: The Complete Evolution”, Astrophys. J., 513, 669–678. [DOI], [ADS], [arXiv:astro-ph/9803217]. (Cited on page 19.)
Koide, S., 1997, “A Two-dimensional Simulation of a Relativistic Jet bent by an Oblique Magnetic Field”, Astrophys. J., 487, 66–69. [DOI], [ADS]. (Cited on page 11.)
Koide, S., 2003, “Magnetic extraction of black hole rotational energy: Method and results of general relativistic magnetohydrodynamic simulations in Kerr space-time”, Phys. Rev. D, 67, 104 010. [DOI], [ADS]. (Cited on pages 7, 66, and 70.)
Koide, S., 2004, “Relativistic outflow magnetically driven by black hole rotation”, Astrophys. J., 606, L45–L48. [DOI], [ADS]. (Cited on page 13.)
Koide, S., Nishikawa, K.-I. and Mutel, R. L., 1996, “A Two-dimensional simulation of relativistic magnetized jet”, Astrophys. J. Lett., 463, L71–L74. [DOI], [ADS]. (Cited on pages 7, 11, 66, and 70.)
Koide, S., Shibata, K. and Kudoh, T., 1998, “General relativistic magnetohydrodynamic simulations of jets from black hole accretions disks: Two-component jets driven by nonsteady accretion of magnetized disks”, Astrophys. J. Lett., 495, L63–L66. [DOI], [ADS]. (Cited on page 13.)
Koide, S., Shibata, K. and Kudoh, T., 1999, “Relativistic jet formation from black hole magnetized accretion disks: Method, tests, and applications of a general relativistic magnetohydrodynamical numerical code”, Astrophys. J., 522, 727–752. [DOI], [ADS]. (Cited on pages 7, 13, 59, 66, and 70.)
Koide, S., Meier, D. L., Shibata, K. and Kudoh, T., 2000, “General relativistic simulations of early jet formation in a rapidly rotating black hole magnetosphere”, Astrophys. J., 536, 668–674. [DOI], [ADS], [arXiv:astro-ph/9907435]. (Cited on page 13.)
Koide, S., Shibata, K., Kudoh, T. and Meier, D. L., 2002, “Extraction of black hole rotational energy by a magnetic field and the formation of relativistic jets”, Science, 295, 1688–1691. [DOI], [ADS]. (Cited on page 13.)
Koldoba, A. V., Kuznetsov, O. A. and Ustyugova, G. V., 2002, “An approximate Riemann solver for relativistic magnetohydrodynamics”, Mon. Not. R. Astron. Soc., 333, 932–942. [DOI], [ADS]. (Cited on pages 57, 83, 86, 90, and 115.)
Komissarov, S. S., 1997, “On the properties of Alfvén waves in relativistic magnetohydrodynamics”, Phys. Lett. A, 232, 435–442. [DOI], [ADS]. (Cited on page 83.)
Komissarov, S. S., 1999a, “A Godunov-Type Scheme for Relativistic Magnetohydrodynamics”, Mon. Not. R. Astron. Soc., 303, 343–366. [DOI], [ADS]. (Cited on pages 7, 26, 32, 56, 58, 65, 66, 70, 83, 86, 87, 88, 89, 90, 91, 95, 96, 98, 113, and 115.)
Komissarov, S. S., 1999b, “Numerical simulations of relativistic magnetized jets”, Mon. Not. R. Astron. Soc., 308, 1069–1076. [DOI], [ADS]. (Cited on page 11.)
Komissarov, S. S., 2001, “Direct simulations of the Blandford-Znajek effect”, Mon. Not. R. Astron. Soc., 326, L41–44. [DOI], [ADS]. (Cited on page 16.)
Komissarov, S. S., 2002a, “Time-dependent, force-free degenerate electrodynaqmics”, Mon. Not. R. Astron. Soc., 336, 759–766. [DOI], [ADS], [arXiv:astro-ph/0202447]. (Cited on pages 16 and 86.)
Komissarov, S. S., 2002b, “Test problems for relativistic magnetohydrodynamics”, arXiv, e-print. [ADS], [arXiv:astro-ph/0209213]. (Cited on page 89.)
Komissarov, S. S., 2004a, “General relativistic magnetohydrodynamic simulations of monopole magnetospheres of black holes”, Mon. Not. R. Astron. Soc., 350, 1431–1436. [DOI], [ADS], [arXiv:astro-ph/0402430]. (Cited on page 13.)
Komissarov, S. S., 2004b, “Electrodynamics of black hole magnetospheres”, Mon. Not. R. Astron. Soc., 350, 427–448. [DOI], [ADS]. (Cited on page 16.)
Komissarov, S. S., 2005, “Observations of the Blandford-Znajek process and the magnetohydrodynamic Penrose process in computer simulations of black hole magnetospheres”, Mon. Not. R. Astron. Soc., 359, 801–808. [DOI], [ADS], [arXiv:astro-ph/0501599]. (Cited on page 13.)
Komissarov, S. S., 2007, “Multidimensional numerical scheme for resistive relativistic magnetohydrodynamics”, Mon. Not. R. Astron. Soc., 382, 995–1004. [DOI], [ADS], [arXiv:0708.0323 [astro-ph]]. (Cited on pages 109 and 110.)
Komissarov, S. S., 2012, “Central engines: Acceleration, Collimation and Confinement of Jets”, in Relativistic Jets from Active Galactic Nuclei, (Eds.) Böottcher, M., Harris, D. E., Krawczynski, H., pp. 81–114, Wiley-VCH, Weinheim. [DOI], [ADS], [Google Books]. (Cited on page 9.)
Komissarov, S. S. and Falle, S. A. E. G., 1997, “Simulations of Superluminal Sources”, Mon. Not. R. Astron. Soc., 288, 833–848. [DOI], [ADS]. (Cited on page 12.)
Komissarov, S. S. and Falle, S. A. E. G., 1998, “The Large Scale Structure of FR-II Radio Sources”, Mon. Not. R. Astron. Soc., 297, 1087–1108. [DOI], [ADS]. (Cited on pages 10 and 47.)
Komissarov, S. S. and Lyubarsky, Y. E., 2003, “The origin of peculiar jet-torus structure in the Crab Nebula”, Mon. Not. R. Astron. Soc., 344, L93–L96. [DOI], [ADS], [arXiv:astro-ph/0306162]. (Cited on pages 26 and 27.)
Komissarov, S. S. and Lyubarsky, Y. E., 2004, “Synchrotron nebulae created by anisotropic magnetized pulsar winds”, Mon. Not. R. Astron. Soc., 349, 779–792. [DOI], [ADS]. (Cited on page 26.)
Komissarov, S. S., Barkov, A. M., Königl, A. and Vlahakis, N., 2007, “Magnetic acceleration of relativistic active galactic nucleus jets”, Mon. Not. R. Astron. Soc., 380, 51–70. [DOI], [ADS], [arXiv:0703146 [astro-ph]]. (Cited on page 16.)
Komissarov, S. S., Vlahakis, N., Köonigl, A. and Barkov, M. V., 2009, “Magnetic acceleration of ultra-relativistic in gamma-ray burst sources”, Mon. Not. R. Astron. Soc., 394, 1182–1212. [DOI], [ADS], [arXiv:0811.1467 [astro-ph]]. (Cited on pages 21 and 22.)
Komissarov, S. S., Vlahakis, N. and Köonigl, A., 2010, “Rarefaction acceleration of ultrarelativistic in gamma-ray burst sources”, Mon. Not. R. Astron. Soc., 407, 17–28. [DOI], [ADS], [arXiv:0912.0845[astro-ph.HE]]. (Cited on pages 21 and 22.)
Kothes, R., Reich, W. and Uyaniker, B., 2006, “The Boomerang PWN G106.6+2.9 and the magnetic field structure in pulsar wind nebulae”, Astrophys. J., 638, 225–233. [DOI], [ADS]. (Cited on page 25.)
Kouveliotou, C., Wijers, R. A. M. J. and Woosley, S. (Eds.), 2012, Gamma-ray Bursts, Cambridge Astrophysics Series, 51, Cambridge University Press, Cambridge; New York. [Google Books]. (Cited on pages 16 and 18.)
Kulkarni, S. R., Frail, D. A., Wieringa, M. H. et al., 1998, “Radio emission from the unusual supernova 1998bw and its association with the gamma-ray burst of 25 April 1998”, Nature, 395, 663–669. [DOI], [ADS]. (Cited on page 17.)
Kunik, M., Qamar, S. and Warnecke, G., 2004, “A BGK-type kinetic flux-vector splitting schemes for the ultra-relativistic gas dynamics”, SIAM J. Sci. Comput., 26, 196–223. [DOI]. (Cited on page 127.)
Kurganov, A. and Tadmor, E., 2000, “New high-resolution central schemes for nonlinear conservation laws and convection-diffusion equations”, J. Comput. Phys., 160, 241–282. [DOI]. (Cited on pages 58 and 121.)
Kurganov, A., Noelle, S. and Petrova, G., 2001, “Semidiscrete central-upwind schemes for hyperbolic conservation laws and Hamilton-Jacobi equations”, SIAM J. Sci. Comput., 23, 707–740. [DOI]. (Cited on page 121.)
Laing, R. A. and Bridle, A. H., 2002a, “Relativistic models and the jet velocity field in the radio galaxy 3C 31”, Mon. Not. R. Astron. Soc., 336, 328–352. [DOI], [ADS], [arXiv:astro-ph/0206215]. (Cited on page 10.)
Laing, R. A. and Bridle, A. H., 2002b, “Dynamical models for jet deceleration in the radio galaxy 3C 31”, Mon. Not. R. Astron. Soc., 336, 1161–1180. [DOI], [ADS], [arXiv:astro-ph/0207427]. (Cited on page 10.)
Lambert, J. D., 1991, Numerical Methods for Ordinary Differential Systems: The initial Value Problem, Wiley, Chichester. [Google Books]. (Cited on pages 47, 72, and 123.)
Lamberts, A., Fromang, S., Dubus, G. and Teyssier, R., 2013, “Simulating gamma-ray binaries with a relativistic extension of RAMSES”, Astron. Astrophys., 560, A79. [DOI], [ADS], [arXiv:1309.7629[astro-ph.IM]]. (Cited on pages 47, 51, 55, and 147.)
Landau, L. D. and Lifshitz, E. M., 1987, Fluid Mechanics, Pergamon, New York. [Google Books]. (Cited on pages 8 and 29.)
Laney, C. B., 1998, Computational Gasdynamics, Cambridge University Press, Cambridge; New York. [Google Books]. (Cited on pages 8 and 48.)
Lax, P. D., 1954, “Weak solutions of nonlinear hyperbolic equations and their numerical computation”, Commun. Pure Appl. Math., 7, 159–193. [DOI]. (Cited on pages 40 and 119.)
Lax, P. D., 1957, “Hyperbolic systems of conservation laws, II”, Commun. Pure Appl. Math., 10, 537–566. [DOI]. (Cited on page 32.)
Lax, P. D. and Wendroff, B., 1960, “Systems of conservation laws”, Commun. Pure Appl. Math., 13, 217–237. [DOI]. (Cited on pages 59, 61, and 119.)
Lazzati, D., Morsony, B. J. and Begelman, M. C., 2009, “Very high efficiency photospheric emission in long-duration gamma-ray bursts”, Astrophys. J., 700, L47–L50. [DOI], [ADS], [arXiv:0904.2779 [astro-ph.HE]]. (Cited on pages 20 and 21.)
Lazzati, D., Morsony, B. J., Blackwell, C. H. and Begelman, M. C., 2012, “Unifying the zoo of jet-driven stellar explosions”, Astrophys. J., 750, 68. [DOI], [ADS], [arXiv:1111.0970 [astro-ph.HE]]. (Cited on pages 20 and 21.)
Leismann, T., Antón, L., Aloy, M. A., Müller, E., Martí, J. M., Miralles, J. A. and Ibáñez, J. M., 2005, “Relativistic MHD simulations of extragalactic jets”, Astron. Astrophys., 436, 503–526. [DOI], [ADS]. (Cited on pages 11, 57, 58, 59, 60, 65, 66, 70, 83, 85, 89, 90, 92, 96, and 98.)
LeVeque, R. J., 1992, Numerical Methods for Conservation Laws, Birkhäuser, Basel; Boston, 2nd edn. [Google Books]. (Cited on pages 8, 31, 32, 119, 121, 122, and 123.)
LeVeque, R. J., 1997, “Wave propagation algorithms for multi-dimensional hyperbolic systems”, J. Comput. Phys., 131, 327–353. [DOI]. (Cited on page 124.)
LeVeque, R. J., 1998, “Nonlinear Conservation Laws and Finite Volume Methods for Astrophysical Fluid Flow”, in Computational Methods for Astrophysical Fluid Flow, Lecture Notes of the Saas-Fee Advanced Course 27, Les Diablerets, Switzerland, March 3–8, 1997, (Eds.) LeVeque, R. J., Mihalas, D., Dorfi, E. A., Müller, E., Steiner, O., Gautschy, A., Saas-Fee Advanced Courses, 27, pp. 1–159, Springer, Berlin; New York. [Google Books]. (Cited on pages 8 and 123.)
LeVeque, R. J. et al., “Clawpack”, project homepage, University of Washington. URL (accessed 24 July 2014): http://depts.washington.edu/clawpack/. (Cited on page 146.)
Li, S., 2005, “An HLLC Riemann solver for magneto-hydrodynamics”, J. Comput. Phys., 203, 344–357. [DOI]. (Cited on pages 57 and 121.)
Li, Z.-Y., Chiueh, T. and Begelman, M. C., 1992, “Electromagnetically driven relativistic jets — A class of self-similar solutions”, Astrophys. J., 394, 459–471. [DOI], [ADS]. (Cited on page 9.)
Lichnerowicz, A., 1967, Relativistic hydrodynamics and magnetohydrodynamics, Benjamin, New York. [Google Books]. (Cited on page 31.)
Lister, M. L., Cohen, M. H., Homan, D. C. et al., 2009, “MOJAVE: Monitoring of jets in Active Galactic Nuclei with VLBA experiments. VI. Kinematic analysis of a complete sample of blazar jets”, Astron. J., 138, 1874–1892. [DOI], [ADS], [arXiv:0909.5100 [astro-ph.CO]]. (Cited on page 9.)
Liu, X. D. and Osher, S., 1998, “Convex ENO high order multi-dimensional schemes without field by field decomposition or staggered grids”, J. Comput. Phys., 142, 304–330. [DOI]. (Cited on pages 45 and 122.)
Liu, X.-D., Osher, S. and Chan, T., 1994, “Weighted essentially nonoscillatory schemes”, J. Comput. Phys., 115, 200–212. [DOI]. (Cited on page 45.)
Lobanov, A. P. and Zensus, J. A., 2001, “A Cosmic double helix in the archetypical Quasar 3C273”, Science, 294, 128–131. [DOI], [ADS]. (Cited on page 13.)
Lobanov, A. P., Krichbaum, T. P., Witzel, A. et al., 1998, “VSOP imaging of S5 0836+710: a close-up on plasma instabilities in the jet”, Astron. Astrophys., 340, L60–L64. [ADS], [arXiv:astro-ph/9810242]. (Cited on page 13.)
Londrillo, P. and Del Zanna, L., 2000, “High-order upwind schemes for multidimensional hydrodynamics”, Astrophys. J., 530, 508–524. [DOI], [ADS], [astro-ph/9910086]. (Cited on pages 65, 122, and 145.)
Londrillo, P. and Del Zanna, L., 2004, “On the divergence-free condition in Godunov-type schemes for ideal magnetohydrodynamics: the upwind constrained transport method”, J. Comput. Phys., 195, 17–48. [DOI], [ADS], [arXiv:astro-ph/0310183]. (Cited on pages 65 and 145.)
López-Cámara, D., Morsony, B. J., Begelman, M. C. and Lazzati, D., 2013, “Three-dimensional adaptive mesh refinement simulations of long-duration gamma-ray burst jets inside massive progenitor stars”, Astrophys. J., 767, 19. [DOI], [ADS], [arXiv:1212.0539 [astro-ph.HE]]. (Cited on pages 20, 21, and 50.)
Lucas-Serrano, A., Font, J. A., Ibáñez, J. M. and Martí, J. M., 2004, “Assesment of a high-resolution central scheme for the solution of the relativistic hydrodynamics equations”, Astron. Astrophys., 428, 703–715. [DOI], [ADS], [arXiv:astro-ph/0407541]. (Cited on pages 41, 47, 53, 75, 78, 79, 80, and 82.)
Lyubarsky, Y. and Kirk, J. G., 2001, “Reconnection in a Striped Pulsar Wind”, Astrophys. J., 547, 437–448. [DOI], [ADS], [arXiv:0009270 [astro-ph]]. (Cited on page 27.)
Lyubarsky, Y. E., 2002, “On the structure of the inner Crab Nebula”, Mon. Not. R. Astron. Soc., 329, L34–L36. [DOI], [ADS]. (Cited on page 26.)
Lyutikov, M., 2010, “Simple waves in relativistic fluids”, Phys. Rev. E, 82, 056305. [DOI], [ADS], [arXiv:1004.2428 [astro-ph.HE]]. (Cited on page 32.)
Lyutikov, M. and Hadden, S., 2012, “Relativistic magnetohydrodynamics in one dimension”, Phys. Rev. E, 85, 026401. [DOI], [ADS], [arXiv:1112.0249 [astro-ph.HE]]. (Cited on page 32.)
MacFadyen, A. I. and Woosley, S. E., 1999, “Collapsars: Gamma-Ray Bursts and Explosions in ‘Failed Supernovae’”, Astrophys. J., 524, 262–289. [DOI], [ADS], [arXiv:astro-ph/9810274]. (Cited on pages 17, 18, and 19.)
MacNeice, P. and Olson, K., 2008, “PARAMESH V4.1: Parallel Adaptative Mesh Refinement”, project homepage, Kevin Olson. URL (accessed 14 July 2014): http://www.physics.drexel.edu/∼olson/paramesh-doc/Users_manual/amr.html. (Cited on page 147.)
MacNeice, P., Olson, K. M., Mobarry, C., de Fainchtein, R. and Parker, C., 2000, “PARAMESH: A parallel adaptive mesh refinement community toolkit”, Comput. Phys. Commun., 126, 330–354. [DOI]. (Cited on page 147.)
Mann, P. J., 1991, “A relativistic smoothed particle hydrodynamics method tested with the shock tube”, Comput. Phys. Commun., 67, 245–260. [DOI]. (Cited on page 7.)
Mann, P. J., 1993, “Smoothed Particle Hydrodynamics Applied to Relativistic Spherical Collapse”, Comput. Phys. Commun., 107, 188–198. [DOI]. (Cited on page 7.)
Marquina, A., 1994, “Local Piecewise Hyperbolic Reconstruction ofNumerical Fluxes for Nonlinear Scalar Conservation Laws”, SIAM J. Sci. Stat. Comput., 15, 892–915. [DOI]. (Cited on pages 122 and 144.)
Marquina, A., Martí, J. M., Ibáñez, J. M., Miralles, J. A. and Donat, R., 1992, “Ultrarelativistic Hydrodynamics: High-Resolution Shock-Capturing Methods”, Astron. Astrophys., 258, 566–571. [ADS]. (Cited on pages 7, 37, 47, 75, 79, and 80.)
Marscher, A. P., 2012, “Structure and emission of compact blazar jets”, Int. J. Mod. Phys.: Conf. Ser., 8, 151–162. [DOI], [ADS]. (Cited on page 9.)
Marscher, A. P. and Gear, W. K., 1985, “Models for high-frequency radio outbursts in extragalactic sources, with application to the early 1983 millimeter-to-infrared flare of 3C 273”, Astrophys. J., 298, 114–127. [DOI], [ADS]. (Cited on page 9.)
Marscher, A. P., Jorstad, S. G., Gómez, J. L., Aller, M. F., Teräsranta, H., Lister, M. L. and Stirling, A. M., 2002, “Observational evidence for the accretion-disk origin for a radio jet in an active galaxy”, Nature, 417, 625–627. [DOI], [ADS]. (Cited on page 9.)
Marscher, A. P., Jorstad, S. G., D’Arcangelo, F. D. et al., 2008, “The inner jet of an active galactic nucleus as revealed by a radio-to-γ-ray outburst”, Nature, 452, 966–969. [DOI], [ADS]. (Cited on page 9.)
Martí, J. M., 2015, “On the correction of conserved variables for numerical RMHD with staggered constrained transport”, Comput. Phys. Commun., 191, 100–105. [DOI], [ADS], [arXiv:1501.02697 [astro-ph.IM]]. (Cited on page 65.)
Martí, J. M. and Müller, E., 1994, “The analytical solution of the Riemann problem in relativistic hydrodynamics”, J. Fluid Mech., 258, 317–333. [DOI], [ADS]. (Cited on pages 31, 36, 129, 130, and 132.)
Martí, J. M. and Müller, E., 1996, “Extension of the Piecewise Parabolic Method to one-dimensional relativistic hydrodynamics”, J. Comput. Phys., 123, 1–14. [DOI], [ADS]. (Cited on pages 35, 44, 47, 49, 75, 77, 78, 79, 80, 81, and 144.)
Martí, J. M. and Müller, E., 2003, “Numerical Hydrodynamics in Special Relativity”, Living Rev. Relativity, 6, lrr-2003-7. [DOI], [ADS]. URL (accessed 14 July 2014): http://www.livingreviews.org/lrr-2003-7. (Cited on pages 7, 19, 45, 75, 76, 78, 80, 112, 128, and 133.)
Martí, J. M., Ibáñez, J. M. and Miralles, J. A., 1991, “Numerical relativistic hydrodynamics: Local characteristic approach”, Phys. Rev. D, 43, 3794–3801. [DOI], [ADS]. (Cited on pages 7, 37, 47, 49, 75, 79, 80, and 112.)
Martí, J. M., Müller, E. and Ibáñez, J. M., 1994, “Hydrodynamical simulations of relativistic jets”, Astron. Astrophys., 281, L9–12. [ADS]. (Cited on pages 10, 37, 44, 47, and 53.)
Martí, J. M., Müller, E., Font, J. A. and Ibáñez, J. M., 1995, “Morphology and Dynamics oh Highly Supersonic Relativistic Jets”, Astrophys. J., 448, L105–L108. [DOI], [ADS]. (Cited on pages 10 and 42.)
Martí, J. M., Müller, E., Font, J. A., Ibáñez, J. M. and Marquina, A., 1997, “Morphology and dynamics of relativistic jets”, Astrophys. J., 479, 151–163. [DOI], [ADS]. (Cited on pages 10, 37, 42, 44, 47, 49, 53, 74, 76, 78, and 79.)
Mathews, W. G., 1971, “The hydromagnetic free expansion of a relativistic gas”, Astrophys. J., 165, 147–164. [DOI], [ADS]. (Cited on pages 32, 48, and 68.)
Matsumoto, J., Masada, Y. and Shibata, K., 2012, “Effect of interacting rarefaction waves on relativistically hot jets”, Astrophys. J., 751, 140. [DOI], [ADS], [arXiv:1204.5697 [astro-ph.HE]]. (Cited on pages 40 and 54.)
May, M. M. and White, R. H., 1966, “Hydrodynamics calculations of general-relativistic collapse”, Phys. Rev., 141, 1232–1241. [DOI], [ADS]. (Cited on page 46.)
May, M. M. and White, R. H., 1967, “Stellar dynamics and gravitational collapse”, Methods Comput. Phys., 7, 219–258. (Cited on page 46.)
McKinney, J. C., 2006a, “General relativistic magnetohydrodynamic simulations of the jet formation and large-scale propagation from black hole accretion systems”, Mon. Not. R. Astron. Soc., 368, 1561–1582. [DOI], [ADS], [arXiv:astro-ph/0603045]. (Cited on pages 16, 21, 70, and 146.)
McKinney, J. C., 2006b, “General relativistic force-free electrodynamics: a new code and applications to black hole magnetospheres”, Mon. Not. R. Astron. Soc., 367, 1797–1807. [DOI], [ADS], [arXiv:astro-ph/0601410]. (Cited on page 22.)
McKinney, J. C. and Blandford, R. D., 2009, “Stability of relativistic jets from rotating, accreting black holes via fully three-dimensional magnetohydrodynamic simulations”, Mon. Not. R. Astron. Soc., 394, L126–L130. [DOI], [ADS], [arXiv:0812.1060 [astro-ph]]. (Cited on pages 16, 17, 21, and 22.)
McKinney, J. C. and Gammie, C. F., 2004, “A measurement of the electromagnetic luminosity of a Kerr black hole”, Astrophys. J., 611, 977–995. [DOI], [ADS], [arXiv:astro-ph/0404512]. (Cited on pages 15, 16, and 21.)
McKinney, J. C., Tchekhovskoy, A. and Blandford, R. D., 2012, “General relativistic magnetohydrodynamic simulations of magnetically choked accretion flows around black holes”, Mon. Not. R. Astron. Soc., 423, 3083–3117. [DOI], [ADS], [arXiv:1201.4163 [astro-ph.HE]]. (Cited on page 16.)
McNamara, B. R. and Nulsen, P. E. J., 2007, “Heating hot atmospheres with active galactic nuclei”, Annu. Rev. Astron. Astrophys., 45, 117–175. [DOI], [ADS], [arXiv:0709.2152 [astro-ph]]. (Cited on page 10.)
Meegan, C. A., Fishman, G. J., Wilson, R. B., Horack, J. M., Brock, M. N., Paciesas, W. S., Pendleton, G. N. and Kouveliotou, C., 1992, “Spatial Distribution of γ-Ray Bursts Observed by BATSE”, Nature, 355, 143–145. [DOI], [ADS]. (Cited on page 17.)
Meliani, Z. and Keppens, R., 2007, “GRB blastwaves through wind-shaped circumburst media”, Astron. Astrophys., 467, L41–L44. [DOI], [ADS], [arXiv:0704.2461 [astro-ph]]. (Cited on page 19.)
Meliani, Z. and Keppens, R., 2010, “Dynamics and stability of relativistic gamma-ray-bursts blast waves”, Astron. Astrophys., 520, L3. [DOI], [ADS], [arXiv:1009.1224 [astro-ph.HE]]. (Cited on page 19.)
Meliani, Z., Sauty, C., Tsinganos, K. and Vlahakis, N., 2004, “Relativistic Parker winds with variable effective polytropic index”, Astron. Astrophys., 425, 773–781. [DOI], [ADS], [arXiv:astro-ph/0407100]. (Cited on page 48.)
Meliani, Z., Keppens, R. and Casse, F. and Giannios, D., 2007, “AMRVAC and relativistic hydrodynamic simulations for gamma-ray burst afterglow phases”, Mon. Not. R. Astron. Soc., 376, 1189–1200. [DOI], [ADS], [arXiv:astro-ph/0701434]. (Cited on pages 19, 21, 41, 54, 75, 78, 79, 83, and 146.)
Meliani, Z., Keppens, R. and Giacomazzo, B., 2008, “Faranoff-Riley type I jet deceleration at density discontinuities. Relativistic hydrodynamics with a realistic equation of state”, Astron. Astrophys., 491, 321–337. [DOI], [ADS], [arXiv:0808.2492 [astro-ph]]. (Cited on page 10.)
Menikoff, R. and Plohr, B. J., 1989, “The Riemann problem for fluid flow of real materials”, Rev. Mod. Phys., 61, 75–130. [DOI], [ADS]. (Cited on page 32.)
Méeszáaros, P. and Wijers, R. A. M. J., 2012, “Prompt emission from gamma-ray bursts”, in Gamma-ray Bursts, (Eds.) Kouveliotou, C., Wijers, R. A. M. J., Woosley, S., Cambridge Astrophysics Series, 51, pp. 151–167, Cambridge University Press, Cambridge; New York. [Google Books]. (Cited on page 18.)
Mignone, A. and Bodo, G., 2005, “An HLLC solver for relativistic flows — I. Hydrodynamics”, Mon. Not. R. Astron. Soc., 364, 126–136. [DOI], [ADS], [arXiv:astro-ph/0506414]. (Cited on pages 39, 47, 49, 53, 57, 75, 78, 79, 80, and 100.)
Mignone, A. and Bodo, G., 2006, “An HLLC Riemann solver for relativistic flows — II. Magnetohydrodynamics”, Mon. Not. R. Astron. Soc., 368, 1040–1054. [DOI], [ADS], [arXiv:astro-ph/0601640]. (Cited on pages 57, 58, 60, 65, 67, 70, 89, 90, 92, 93, 96, and 98.)
Mignone, A. and Bodo, G., 2008, “Shock-Capturing Schemes in Computational MHD”, in Jets From Young Stars III: Numerical MHD and Instabilities, (Eds.) Massaglia, S., Bodo, G., Mignone, A., Rossi, P., Lecture Notes in Physics, 754, pp. 71–101, Springer, Berlin; New York. [DOI], [ADS], [Google Books]. (Cited on pages 56 and 60.)
Mignone, A. and McKinney, J. C., 2007, “Equation of state in relativistic magnetohydrodynamics: variable versus constant adiabatic index”, Mon. Not. R. Astron. Soc., 378, 1118–1130. [DOI], [ADS], [arXiv:0704.1679 [astro-ph]]. (Cited on page 67.)
Mignone, A., Massaglia, S. and Bodo, G., 2005a, “Relativistic MHD simulations of jets with toroidal magnetic fields”, Space Sci. Rev., 121, 21–31. [DOI], [ADS], [arXiv:astro-ph/0511769]. (Cited on page 11.)
Mignone, A., Plewa, T. and Bodo, G., 2005b, “The Piecewise Parabolic Method for multidimensional relativistic fluid dynamics”, Astrophys. J., 160, 199–219. [DOI], [ADS], [arXiv:astro-ph/0505200]. (Cited on pages 36, 44, 47, 48, 49, 53, 54, 68, 72, 76, 78, 79, 80, 82, and 144.)
Mignone, A., Bodo, G., Massaglia, S., Matsakos, T., Tesileanu, O., Zanni, C. and Ferrari, A., 2007, “PLUTO: A numerical code for computational astrophysics”, Astrophys. J. Suppl. Ser., 170, 228–242. [DOI], [ADS], [arXiv:astro-ph/0701854]. (Cited on pages 47, 49, 51, 54, 65, 71, 96, 98, and 147.)
Mignone, A., Ugliano, M. and Bodo, G., 2009, “A five-wave Harten-Lax-van Leer Riemann solver for relativistic magnetohydrodynamics”, Mon. Not. R. Astron. Soc., 393, 1141–1156. [DOI], [ADS], [arXiv:0811.1483 [astro-ph]]. (Cited on pages 51, 58, 71, 83, 90, 91, 92, 93, 99, 100, 103, and 105.)
Mignone, A., Rossi, P., Bodo, G., Ferrari, A. and Massaglia, S., 2010, “High-resolution 3D relativistic MHD simulations of jets”, Mon. Not. R. Astron. Soc., 402, 7–12. [DOI], [ADS], [arXiv:0908.4523 [astro-ph.CO]]. (Cited on pages 11 and 51.)
Mignone, A., Zanni, C., Tzeferacos, P., van Straalen, B. Colella, P. and Bodo, G., 2012, “The PLUTO code for adaptive mesh computations in astrophysical fluid dynamics”, Astrophys. J. Suppl. Ser., 198, 7. [DOI], [ADS], [arXiv:1110.0740 [astro-ph.HE]]. (Cited on pages 51, 110, and 147.)
Miller, G. H. and Colella, P., 2001, “A high-order Eulerian Godunov method for elastic-plastic flow in solids”, J. Comput. Phys., 167, 131–176. [DOI]. (Cited on page 80.)
Mimica, P. and Aloy, M. A., 2010, “On the dynamic efficiency of internal shocks in magnetized relativistic outflows”, Mon. Not. R. Astron. Soc., 401, 525–532. [DOI], [ADS], [arXiv:0909.1328 [astro-ph.HE]]. (Cited on pages 19 and 23.)
Mimica, P. and Aloy, M. A., 2012, “Radiative signature of magnetic fields in internal shocks”, Mon. Not. R. Astron. Soc., 421, 2635–2647. [DOI], [ADS], [arXiv:1111.6108 [astro-ph.HE]]. (Cited on page 19.)
Mimica, P. and Giannios, D., 2011, “Gamma-ray burst afterglow light curves from realistic density profiles”, Mon. Not. R. Astron. Soc., 418, 583–590. [DOI], [ADS], [arXiv:1106.1903 [astro-ph.HE]]. (Cited on page 19.)
Mimica, P., Aloy, M. A., Agudo, I., Martí, J. M., Gómez, J. L. and Miralles, J. A., 2009a, “Spectral evolution of superluminal components in parsec-scale jets”, Astrophys. J., 696, 1142–1163. [DOI], [ADS], [arXiv:0811.1143 [astro-ph]]. (Cited on page 12.)
Mimica, P., Giannios, D. and Aloy, M. A., 2009b, “Deceleration of arbitrarily magnetized GRB ejecta: the complete evolution”, Astron. Astrophys., 494, 879–890. [DOI], [ADS], [arXiv:0810.2961 [astro-ph]]. (Cited on pages 19 and 23.)
Mimica, P., Giannios, D. and Aloy, M. A., 2010, “Multiwavelength afterglow light curves from magnetized gamma-ray burst flows”, Mon. Not. R. Astron. Soc., 407, 2501–2510. [DOI], [ADS], [arXiv:1004.2720 [astro-ph.HE]]. (Cited on pages 19 and 23.)
Mioduszewski, A. J., Hughes, P. A. and Duncan, G. C., 1997, “Simulated VLBI Images from Relativistic Hydrodynamic Jet Models”, Astrophys. J., 476, 649–665. [DOI], [ADS], [arXiv:astro-ph/9606004]. (Cited on page 12.)
Misner, C. W., Thorne, K. S. and Wheeler, J. A., 1973, Gravitation, W. H. Freeman, San Francisco. [ADS], [Google Books]. (Cited on page 29.)
Miyoshi, T. and Kusano, K., 2005, “A multi-state HLL approximate Riemann solver for ideal magnetohydrodynamics”, J. Comput. Phys., 208, 315–344. [DOI]. (Cited on page 58.)
Mizuno, Y., Nishikawa, K.-I., Koide, S., Hardee, P. and Fishman, G. J., 2006, “RAISHIN: A high-resolution three-dimensional general relativistic magnetohydrodynamics code”, arXiv, e-print. [arXiv:astro-ph/0609004]. (Cited on pages 26, 58, 59, 60, 67, 70, 83, 85, 89, 90, 91, 92, 94, and 147.)
Mizuno, Y., Hardee, P. E. and Nishikawa, K.-I., 2007, “Three-dimensional relativistic magnetohydrodynamic simulations of magnetized spine-sheath relativistic jets”, Astrophys. J., 662, 835–850. [DOI], [ADS], [arXiv:astro-ph/0703190]. (Cited on pages 13 and 101.)
Mizuno, Y., Hardee, P. E., Hartmann, D. H., Nishikawa, K.-I. and Zhang, B., 2008, “A magnetohydrodynamic boost for relativistic jets”, Astrophys. J., 672, 72–82. [DOI], [ADS], [arXiv:0709.1839 [astro-ph]]. (Cited on page 21.)
Mizuno, Y., Lyubarsky, Y., Nishikawa, K.-I. and Hardee, P. E., 2009, “Three-dimensional relativistic magnetohydrodynamic simulations of current-driven instability. I. Instability of a static column”, Astrophys. J., 700, 684–693. [DOI], [ADS], [arXiv:0903.5358 [astro-ph.HE]]. (Cited on pages 13 and 14.)
Mizuno, Y., Hardee, P. E. and Nishikawa, K.-I., 2011a, “Three-dimensional relativistic magnetohydrodynamic simulations of current-driven instability with a sub-Alfvénic jet: temporal properties”, Astrophys. J., 734, 19. [DOI], [ADS], [arXiv:1104.0549 [astro-ph.HE]]. (Cited on pages 13, 96, 98, 99, and 100.)
Mizuno, Y., Lyubarsky, Y., Nishikawa, K.-I. and Hardee, P. E., 2011b, “Three-dimensional relativistic magnetohydrodynamic simulations of current-driven instability. II. Relaxation of pulsar wind nebula”, Astrophys. J., 728, 90. [DOI], [ADS], [arXiv:1012.2770 [astro-ph.HE]]. (Cited on pages 27 and 28.)
Mizuno, Y., Lyubarsky, Y., Nishikawa, K.-I. and Hardee, P. E., 2012, “Three-dimensional relativistic magnetohydrodynamic simulations of current-driven instability. III. Rotating relativistic jets”, Astrophys. J., 757, 16. [DOI], [ADS], [arXiv:1207.4949 [astro-ph.HE]]. (Cited on page 13.)
Mizuta, A. and Aloy, M. A., 2009, “Angular energy distribution of collapsar-jets”, Astrophys. J., 699, 1261–1273. [DOI], [ADS], [arXiv:0812.4813 [astro-ph]]. (Cited on page 19.)
Mizuta, A. and Ioka, K., 2013, “Opening angle of collapsar jets”, Astrophys. J., 777, 162. [DOI], [ADS], [arXiv:1304.0163 [astro-ph.HE]]. (Cited on page 19.)
Mizuta, A., Yamada, S. and Takabe, H., 2001, “Numerical study of AGN jet propagation with two dimensional relativistic hydrodynamic code”, J. Korean Astron. Soc., 34, 329–331. [DOI], [ADS]. (Cited on pages 10, 42, and 53.)
Mizuta, A., Yamada, S. and Takabe, H., 2004, “Propagation and dynamics of relativistic jets”, Astrophys. J., 606, 804–818. [DOI], [ADS], [arXiv:astro-ph/0402355]. (Cited on pages 42, 43, 49, 53, 75, 76, 78, 79, and 80.)
Mizuta, A., Yamasaki, T., Nagataki, S. and Mineshige, S., 2006, “Collimated jet or expanding outflow: possible origins of gamma-ray bursts and X-ray flashes”, Astrophys. J., 651, 960–978. [DOI], [ADS], [arXiv:astro-ph/0607544]. (Cited on page 19.)
Mizuta, A., Nagataki, S. and Aoi, J., 2011, “Thermal radiation from gamma-ray bursts”, Astrophys. J., 732, 26. [DOI], [ADS], [arXiv:1006.2440 [astro-ph.HE]]. (Cited on pages 19 and 20.)
Monaghan, J. J., 1992, “Smoothed particle hydrodynamics”, Annu. Rev. Astron. Astrophys., 30, 543–574. [DOI], [ADS]. (Cited on page 7.)
Monceau-Baroux, R., Keppens, R. and Meliani, Z., 2012, “The effect of angular opening on the dynamics of relativistic hydro jets”, Astron. Astrophys., 545, A62. [DOI], [ADS], [arXiv:1211.1590 [astro-ph.HE]]. (Cited on page 10.)
Morsony, B. J., Lazzati, D. and Begelman, M. C., 2007, “Temporal and angular properties of gamma-ray burst jets emerging form massive stars”, Astrophys. J., 665, 569–598. [DOI], [ADS], [arXiv:astro-ph/0609254]. (Cited on pages 20, 21, 47, 54, 72, 73, 78, 79, 80, and 146.)
Morsony, B. J., Lazzati, D. and Begelman, M. C., 2010, “The origin and propagation of variability in the outflows of long-duration gamma-ray bursts”, Astrophys. J., 723, 267–276. [DOI], [ADS], [arXiv:1002.0361 [astro-ph.HE]]. (Cited on pages 20 and 21.)
MPI-AMRVAC, “MPI-AMRVAC”, project homepage, KU Leuven. URL (accessed 14 July 2014): http://homes.esat.kuleuven.be/∼keppens/. (Cited on page 52.)
Nagakura, H. and Yamada, S., 2008, “General relativistic hydrodynamic simulations and linear analysis of the standing accretion shock instability around a black hole”, Astrophys. J., 689, 391–406. [DOI], [ADS], [arXiv:0808.4141 [astro-ph]]. (Cited on page 54.)
Nagakura, H., Ito, H., Kiuchi, K. and Yamada, S., 2011, “Jet propagations, breakouts, and photospheric emissions in collapsing massive progenitors of long-duration gamma-ray bursts”, Astrophys. J., 731, 80. [DOI], [ADS], [arXiv:1009.2326 [astro-ph.HE]]. (Cited on pages 20 and 54.)
Nagataki, S., 2009, “Development of a general relativistic magnetohydrodynamic code and its application to the central engine of long gamma-ray bursts”, Astrophys. J., 704, 937–950. [DOI], [ADS], [arXiv:0902.1908 [astro-ph.HE]]. (Cited on pages 60, 65, 67, and 71.)
Nakamura, T., 1981, “General Relativistic Collapse of Axially Symmetric Stars Leading to the Formation of Rotating Black Holes”, Prog. Theor. Phys., 65, 1876–1890. [DOI], [ADS]. (Cited on page 7.)
Nakamura, T. and Sato, H., 1982, “General Relativistic Collapse of Non-Rotating, Axisymmetric Stars”, Prog. Theor. Phys., 67, 1396–1405. [DOI], [ADS]. (Cited on page 7.)
Nakamura, T., Maeda, K., Miyama, S. and Sasaki, M., 1980, “General relativistic collapse of an axially symmetric star. I — The Formulation and the Initial Value Equations-”, Prog. Theor. Phys., 63, 1229–1244. [DOI], [ADS]. (Cited on page 7.)
Narayan, R., Paczyński, B. and Piran, T., 1992, “Gamma-ray bursts as the death throes of massive binary stars”, Astrophys. J. Lett., 395, L83–L86. [DOI], [ADS], [arXiv:astro-ph/9204001]. (Cited on page 18.)
Narayan, R., McKinney, J. C. and Farmer, A. J., 2007, “Self-similar force-free wind from an accretion disc”, Mon. Not. R. Astron. Soc., 375, 548–566. [DOI], [ADS], [arXiv:astro-ph/0610817]. (Cited on page 22.)
Neilsen, D., Hirschmann, E. W. and Millward, R. S., 2006, “Relativistic MHD and black hole excision: formation and initial tests”, Class. Quantum Grav., 23, S505–S527. [DOI], [ADS], [arXiv:gr-qc/0512147]. (Cited on pages 60, 62, 67, 68, 69, 70, 96, 98, and 99.)
Nessyahu, H. and Tadmor, E., 1990, “Non-oscillatory central differencing for hyperbolic conservation laws”, J. Comput. Phys., 87, 408–463. [DOI]. (Cited on pages 53 and 121.)
Nishikawa, K.-I., Koide, S., Sakai, J.-I., Christodoulou, D. M., Sol, H. and Mutel, R. L., 1997, “Three-Dimensional Magnetohydrodynamic Simulations of Relativistic Jets Injected along a Magnetic Field”, A strophys. J., 483, L45–L48. [DOI], [ADS]. (Cited on page 11.)
Nishikawa, K.-I., Koide, S., Sakai, J.-I., Christodoulou, D. M., Sol, H. and Mutel, R. L., 1998, “Three-Dimensional Magnetohydrodynamic Simulations of Relativistic Jets Injected into an Oblique Magnetic Field”, Astrophys. J., 498, 166–169. [DOI], [ADS]. (Cited on page 11.)
Nishikawa, K.-I., Richardson, G., Koide, S., Shibata, K., Kudoh, T., Hardee, P. E. and Fishman, G. J., 2005, “A general relativistic magnetohydrodynamic simulation of jet formation”, Astrophys. J., 625, 60–71. [DOI], [ADS], [arXiv:astro-ph/0403032]. (Cited on page 13.)
Noble, S. C., Gammie, C. F., McKinney, J. C. and Del Zanna, L., 2006, “Primitive variable solvers for conservative, general relativistic magnetohydrodynamics”, Astrophys. J., 641, 626–637. [DOI], [ADS], [arXiv:astro-ph/0512420]. (Cited on pages 66, 67, 68, 96, and 98.)
Noh, W. F., 1987, “Errors for calculations of strong shocks using an artificial viscosity and an artificial heat flux”, J. Comput. Phys., 72, 78–120. [DOI]. (Cited on page 75.)
Norman, M. L. and Winkler, K.-H. A., 1986, “Why Ultrarelativistic Numerical Hydrodynamics is Difficult”, in Astrophysical Radiation Hydrodynamics, Proceedings of the NATO Advanced Research Workshop, Garching, Germany, August 2–13, 1982, (Eds.) Winkler, K.-H. A., Norman, M. L., NATO ASI Series C, 188, pp. 449–475, Reidel, Dordrecht; Boston. [ADS], [Google Books]. (Cited on pages 7, 46, 75, and 79.)
Oran, E. S. and Boris, J. P., 1987, Numerical Simulations of Reactive Flow, Elsevier, New York. [Google Books]. (Cited on page 8.)
Osher, S. and Chakravarthy, S., 1984, “High Resolution Schemes and the Entropy Condition”, SIAM J. Numer. Anal., 21, 955–984. [DOI]. (Cited on page 122.)
Paczyński, B., 1986, “Gamma-ray bursters at cosmological distances”, Astrophys. J. Lett., 308, L43–L46. [DOI], [ADS]. (Cited on page 18.)
Paczyński, B., 1998, “Are gamma-ray bursts in star-forming regions?”, Astrophys. J., 494, L45–48. [DOI], [ADS], [arXiv:astro-ph/9710086]. (Cited on page 17.)
Palenzuela, C., Lehner, L., Reula, O. and Rezzolla, L., 2009, “Beyond ideal MHD: towards a more realistic modelling of relativistic astrophysical plasmas”, Mon. Not. R. Astron. Soc., 394, 1727–1740. [DOI], [ADS], [arXiv:0810.1838 [astro-ph]]. (Cited on page 110.)
Palenzuela, C., Garrett, T., Lehner, L. and Liebling, S. L., 2010a, “Magnetospheres of black hole systems in force-free plasma”, Phys. Rev. D, 82, 044 045. [DOI], [ADS], [arXiv:1007.1198 [gr-qc]]. (Cited on page 16.)
Palenzuela, C., Lehner, L. and Liebling, S. L., 2010b, “Dual Jets from Binary Black Holes”, Science, 329, 927–930. [DOI], [ADS], [arXiv:1005.1067 [astro-ph.HE]]. (Cited on page 16.)
Panaitescu, A., Wen, L., Laguna, P. and Méeszáaros, P., 1997, “Impact of Relativistic Fireballs on External Matter: Numerical Models of Cosmological Gamma-Ray Bursts”, Astrophys. J., 482, 942–950. [DOI], [ADS], [arXiv:astro-ph/9610064]. (Cited on page 19.)
Parfrey, K., Belobodorov, A. M. and Hui, L., 2012, “Introducing PHAEDRA: a new spectral code for simulations of relativistics magnetospheres”, Mon. Not. R. Astron. Soc., 423, 1416–1436. [DOI], [ADS], [arXiv:1110.6669 [astro-ph.HE]]. (Cited on page 111.)
Pavlov, G. G., Teter, M. A., Kargaltsev, O. and Sanwal, D., 2003, “The variable jet of the Vela pulsar”, Astrophys. J., 591, 1157–1171. [DOI], [ADS], [arXiv:astro-ph/0305510]. (Cited on page 26.)
Perucho, M. and Lobanov, A. P., 2007, “Physical properties of the jet in 0836+710 revealed by its transversal structure”, Astron. Astrophys., 476, L23–L26. [DOI], [ADS], [arXiv:0705.0433 [astro-ph]]. (Cited on page 13.)
Perucho, M. and Martí, J. M., 2007, “A numerical simulation of the evolution and fate of a Fanaroff-Riley type I jet. The case of 3C 31”, Mon. Not. R. Astron. Soc., 382, 526–542. [DOI], [ADS], [arXiv:0709.1784 [astro-ph]]. (Cited on pages 10 and 47.)
Perucho, M., Hanasz, M., Martí, J. M. and Sol, H., 2004a, “Stability of hydrodynamical relativistic planar jets. I. Linear evolution and saturation of Kelvin-Helmholtz modes”, Astron. Astrophys., 427, 415–429. [DOI], [ADS], [arXiv:astro-ph/0407548]. (Cited on pages 101, 102, and 103.)
Perucho, M., Martí, J. M. and Hanasz, M., 2004b, “Stability of hydrodynamical relativistic planar jets. II. Long-term nonlinear evolution”, Astron. Astrophys., 427, 431–444. [DOI], [ADS], [arXiv:astro-ph/0407574]. (Cited on pages 13, 101, and 102.)
Perucho, M., Martí, J. M. and Hanasz, M., 2005, “Nonlinear stability of relativistic sheared planar jets”, Astron. Astrophys., 443, 863–881. [DOI], [ADS], [arXiv:astro-ph/0510426]. (Cited on pages 13 and 101.)
Perucho, M., Hanasz, M., Martí, J. M. and Miralles, J. A., 2007, “Resonant Kelvin-Helmholtz modes in sheared relativistic flows”, Phys. Rev. D, D75, 056 312. [DOI], [ADS], [arXiv:0705.0441 [astro-ph]]. (Cited on pages 13 and 101.)
Perucho, M., Agudo, I., Gómez, J. L., Kadler, M., Ros, E. and Kovalev, Y. Y., 2008, “On the nature of an ejection event in the jet of 3C 111”, Astron. Astrophys., 489, L29–L32. [DOI], [ADS], [arXiv:0808.3314 [astro-ph]]. (Cited on page 12.)
Perucho, M., Martí, J. M., Cela, J. M., Hanasz, M., de la Cruz, R. and Rubio, F., 2010, “Stability of three-dimensional relativistic jets: Implications for jet collimation”, Astron. Astrophys., 519, A41. [DOI], [ADS], [arXiv:1005.4332 [astro-ph.HE]]. (Cited on pages 10, 13, 47, 54, 101, and 147.)
Perucho, M., Quilis, V. and Martí, J. M., 2011, “Intracluster medium reheating by relativistic jets”, Astrophys. J., 743, 42. [DOI], [ADS], [arXiv:1107.5484 [astro-ph.CO]]. (Cited on page 10.)
Perucho, M., Kovalev, Y. Y., Lobanov, A. P., Hardee, P. E. and Agudo, I., 2012a, “Anatomy of helial extragalactic jets: The case of S5 0836+710”, Astrophys. J., 749, 55. [DOI], [ADS], [arXiv:1202.1182 [astro-ph.CO]]. (Cited on page 13.)
Perucho, M., Martí-Vidal, I., Lobanov, A. P. and Hardee, P. E., 2012b, “S5 0836+710: An FRII jet disrupted by the growth of a helical instability?”, Astron. Astrophys., 545, A65. [DOI], [ADS], [arXiv:1207.6123 [astro-ph.CO]]. (Cited on page 13.)
Perucho, M., Martí, J. M., Laing, R. A. and Hardee, P. E., 2014, “On the deceleration of FRI jets: mass loading by stellar-winds”, Mon. Not. R. Astron. Soc., 441, 1488–1503. [DOI], [ADS], [arXiv:1404.1209 [astro-ph.HE]]. (Cited on page 10.)
Pian, E., Amati, L., Antonelli, L. A. et al., 1999, “BeppoSAX detection and follow-up of GRB 980425”, Astron. Astrophys. Suppl., 138, 463–464. [DOI], [ADS], [arXiv:astro-ph/9903113]. (Cited on page 17.)
Piran, T., 1980, “Numerical Codes for Cylindrical General Relativistic Systems”, J. Comput. Phys., 35, 254–283. [DOI], [ADS]. (Cited on page 7.)
Piran, T., Shemi, A. and Narayan, R., 1993, “Hydrodynamics of Relativistic Fireballs”, Mon. Not. R. Astron. Soc., 263, 861–867. [DOI], [ADS], [arXiv:astro-ph/9301004]. (Cited on pages 18 and 19.)
Piran, T., Sari, R. and Mochkovitch, R., 2012, “Prompt emission from gamma-ray bursts”, in Gamma-ray Bursts, (Eds.) Kouveliotou, C., Wijers, R. A. M. J., Woosley, S., Cambridge Astrophysics Series, 51, pp. 121–149, Cambridge University Press, Cambridge; New York. [Google Books]. (Cited on page 18.)
Piro, L., Heise, J., Jager, R. et al., 1998, “The First X-Ray Localization of a γ-Ray Burst by BeppoSAX and its Fast Spectral Evolution”, Astron. Astrophys., 329, 906–910. [ADS], [arXiv:astro-ph/9707215]. (Cited on page 17.)
Plewa, T. and Müller, E., 2001, “AMRA: An Adaptive Mesh Refinement hydrodynamic code for astrophysics”, Comput. Phys. Commun., 138, 101–127. [DOI], [ADS], [arXiv:astro-ph/0010626]. (Cited on page 125.)
PLUTO Development Team, “PLUTO: a modular code for computational astrophysics”, project homepage, University of Turin. URL (accessed 14 July 2014): http://plutocode.ph.unito.it/. (Cited on pages 52, 54, 69, 71, and 147.)
Pons, J. A., Martí, J. M. and Müller, E., 2000, “The exact solution of the Riemann problem with nonzero tangential velocities in relativistic hydrodynamics”, J. Fluid Mech., 422, 125–139. [DOI], [ADS], [arXiv:astro-ph/0005038]. (Cited on pages 31, 36, 80, 83, 129, 132, 133, 134, 135, and 137.)
Popham, R., Woosley, S. E. and Fryer, C. L., 1999, “Hyperaccreting Black Holes and Gamma-Ray Bursts”, Astrophys. J., 518, 356–374. [DOI], [ADS], [arXiv:astro-ph/9807028]. (Cited on page 18.)
Porth, O., 2013, “Three-dimensional structure of relativistic jet formation”, Mon. Not. R. Astron. Soc., 429, 2482–2492. [DOI], [ADS], [arXiv:1212.0676 [astro-ph.HE]]. (Cited on page 16.)
Porth, O. and Komissarov, S. S., 2015, “Causality and stability of cosmic jets”, Mon. Not. R. Astron. Soc., 452, 1089–1104. [DOI], [ADS], [arXiv:1408.3318 [astro-ph.HE]]. (Cited on page 10.)
Porth, O., Komissarov, S. S. and Keppens, R., 2013, “Solution to the sigma problem of pulsar wind nebulae”, Mon. Not. R. Astron. Soc., 431, L48–L52. [DOI], [ADS], [arXiv:1212.1382 [astro-ph.HE]]. (Cited on pages 27 and 28.)
Porth, O., Komissarov, S. S. and Keppens, R., 2014a, “Rayleigh-Taylor instability in magnetohydrodynamic simulationsof the Crab nebula”, Mon. Not. R. Astron. Soc., 443, 547–558. [DOI], [ADS], [arXiv:1405.4029 [astro-ph.HE]]. (Cited on page 26.)
Porth, O., Komissarov, S. S. and Keppens, R., 2014b, “Three-dimensional magnetohydrodynamic simulations of the Crab nebula”, Mon. Not. R. Astron. Soc., 438, 278–306. [DOI], [ADS], [arXiv:1310.2531 [astro-ph.HE]]. (Cited on page 26.)
Potter, D., 1977, Computational Physics, Wiley, Chichester, UK. [Google Books]. (Cited on page 8.)
Powell, K. G., 1994, An approximate Riemann solver for magnetohydrodynamics (that works in more than one dimension), ICASE Report, No. 94-24 / NASA-CR-194902, NASA Langley Research Center, Hampton, VA. Online version (accessed 24 July 2014): http://hdl.handle.net/2060/19940028527. (Cited on page 61.)
Prendergast, K. H. and Xu, K., 1993, “Numerical Hydrodynamics from Gas-Kinetic Theory”, J. Comput. Phys., 109, 53–66. [DOI]. (Cited on page 127.)
Qamar, S., 2003, Kinetic Schemes for the Relativistic Hydrodynamics, Ph.D. thesis, Otto-von-Guericke Universität, Magdeburg. Online version (accessed 24 July 2014): http://diglib.uni-magdeburg.de/Dissertationen/2003/qamshamsul.htm. (Cited on page 127.)
Qamar, S. and Ahmed, S., 2013, “The space-time CE/SE method for solving one-dimensional special relativistic magnetohydrodynamics equations”, Comput. Phys. Commun., 184, 1094–1105. [DOI]. (Cited on page 128.)
Qamar, S. and Warnecke, G., 2005, “A high-order kinetic flux-splitting method for the relativistic magnetohydrodynamics”, J. Comput. Phys., 205, 282–204. [DOI]. (Cited on page 127.)
Qamar, S. and Yousaf, M., 2012, “The space-time CESE method for solving special relativistic hydrodynamic equations”, J. Comput. Phys., 231, 3928–3945. [DOI]. (Cited on page 128.)
Quirk, J., 1991, An adaptive grid algorithm for computational shock hydrodynamics, Ph.D. thesis, Cranfield Institute Technology, Cranfield. [ADS]. (Cited on page 50.)
Quirk, J., 1994, “A contribution to the great Riemann solver debate”, Int. J. Numer. Meth. Fluids, 18, 555–574. [DOI]. (Cited on page 41.)
Quirk, J., 1996, “A parallel adaptive grid algorithm for computational shock hydrodynamics”, Appl. Numer. Math., 20, 427–453. [DOI]. (Cited on page 50.)
Racusin, J. L., Karpov, S. V., Sokolowski, M., Granot, J. and Wu, X. F. et al., 2008, “Broadband observations of the naked-eye gamma-ray burst GRB 080319B”, Nature, 455, 183–188. [DOI], [ADS], [arXiv:0805.1557 [astro-ph]]. (Cited on page 18.)
Radice, D., 2013, Advanced numerical approaches in the dynamics of relativistic flows, Ph.D. thesis, Gottfried Wilhelm Leibniz Universitäat Hannover, Hannover. (Cited on page 126.)
Radice, D. and Rezzolla, L., 2011, “Discontinuous Galerkin methods for general-relativistic hydrodynamics: Formulation and application to spherically symmetric spacetimes”, Phys. Rev. D, 84, 024010. [DOI], [ADS], [arXiv:1103.2426 [gr-qc]]. (Cited on page 126.)
Radice, R. and Rezzolla, L., 2012, “THC, a new high-order FD HRSC code for special relativistic hydrodynamics”, Astron. Astrophys., 547, A26. [DOI], [ADS], [arXiv:1206.6502 [astro-ph.IM]]. (Cited on pages 47, 49, 55, and 147.)
Radice, R. and Rezzolla, L., 2013, “Universality and intermittency in relativistic turbulent flows of a hot plasma”, Astrophys. J. Lett., 766, L10. [DOI], [ADS], [arXiv:1209.2936 [astro-ph.HE]]. (Cited on page 106.)
Ray, T. P., 1981, “Kelvin-Helmholtz instabilities in radio jets”, Mon. Not. R. Astron. Soc., 196, 195–207. [DOI], [ADS]. (Cited on page 100.)
Reed, W. H. and Hill, T. R., 1973, Triangular mesh methods for the neutron transport equation, Los Alamos Scientific Laboratory, Los Alamos. URL (accessed 21 December 2015): http://www.osti.gov/scitech/servlets/purl/4491151. (Cited on page 126.)
Rees, M. J. and Gunn, J. E., 1974, “The origin of the magnetic field and relativistic particles in the Crab Nebula”, Mon. Not. R. Astron. Soc., 167, 1–12. [DOI], [ADS]. (Cited on page 23.)
Rezzolla, L. and Zanotti, O., 2001, “An improved exact Riemann solver for relativistic hydrodynamics”, J. Fluid Mech., 449, 395–411. [DOI], [ADS], [arXiv:gr-qc/0103005]. (Cited on pages 133 and 136.)
Rezzolla, L. and Zanotti, O., 2013, Relativistic Hydrodynamics, Oxford University Press, Oxford. [Google Books]. (Cited on pages 8 and 109.)
Rezzolla, L., Zanotti, O. and Pons, J. A., 2003, “An Improved Exact Riemann Solver for Multidimensional Relativistic Flows”, J. Fluid Mech., 479, 199–219. [DOI], [ADS], [arXiv:gr-qc/0205034]. (Cited on pages 36 and 133.)
Richtmyer, R. D. and Morton, K. W., 1967, Difference Methods for Initial-Value Problems, Interscience Tracts in Pure and Applied Mathematics, 4, Wiley-Interscience, New York, 2nd edn. [Google Books]. (Cited on pages 46, 119, and 122.)
Rischke, D. H., Bernhard, S. and Maruhn, J. A., 1995a, “Relativistic hydrodynamics for heavy-ion collisions: I. General aspects and expansion into vacuum”, Nucl. Phys. A, 595, 346–382. [DOI], [ADS], [arXiv:nucl-th/9504018]. (Cited on page 45.)
Rischke, D. H., Puürsuün, Y. and Maruhn, J. A., 1995b, “Relativistic hydrodynamics for heavy-ion collisions: II. Compression of nuclear matter and the phase transition to the quark-gluon plasma”, Nucl. Phys. A, 595, 383–408. [DOI], [ADS], [arXiv:nucl-th/9504021]. (Cited on page 46.)
Roe, P. L., 1981, “Approximate Riemann solvers, parameter vectors and difference schemes”, J. Comput. Phys., 43, 357–372. [DOI]. (Cited on pages 36, 110, and 120.)
Roe, P. L., 1984, Generalized Formulation of TVD Lax-Wendroff Schemes, ICASE Report, No. 84-53 / NASA-CR-172478, NASA Langley Research Center, Hampton, VA. Online version (accessed 24 July 2014): http://hdl.handle.net/2060/19850005219. (Cited on page 122.)
Roe, P. L., 1985, “Some contributions to the modelling of discontinuous flows”, in Large-Scale Computations in Fluid Dynamics, Proceedings of the Fifteenth Summer Seminar on Applied Mathematics, La Jolla, CA, June 27–July 8, 1983, (Eds.) Engquist, B. E., Osher, S., Somerville, R. C. J., 22, pp. 163–193, American Mathematical Society, Providence, RI. [ADS], [Goorgle Books]. (Cited on page 43.)
Roe, P. L., 1986, “Characteristic-based schemes for the Euler equations”, Annu. Rev. Fluid Mech., 18, 337–365. [DOI]. (Cited on page 43.)
Romatschke, P., 2010, “New developments in relativistic viscous hydrodynamics”, Int. J. Mod. Phys. B, 19, 1–53. [DOI]. (Cited on page 109.)
Romero, J. V., Ibáñez, J. M., Martí, J. M. and Miralles, J. A., 1996, “A new spherically symmetric general relativistic hydrodynamical code”, Astrophys. J., 462, 839–854. [DOI], [ADS], [arXiv:astro-ph/9509121]. (Cited on pages 37 and 76.)
Romero, R., Martí, J. M., Pons, J. A., Ibáñez, J. M. and Miralles, J. A., 2005, “The exact solution of the Riemann problem in relativistic MHD with tangential magnetic fields”, J. Fluid Mech., 544, 323–338. [DOI], [ADS], [arXiv:astro-ph/0506527]. (Cited on page 136.)
Rosen, A., Hughes, P. A., Duncan, G. C. and Hardee, P. E., 1999, “A comparison of the morphology and stability of relativistic and nonrelativistic jets”, Astrophys. J., 516, 729–743. [DOI], [ADS], [arXiv:astro-ph/9901046]. (Cited on page 10.)
Rossi, P., Mignone, A., Bodo, G., Massaglia, S. and Ferrari, A., 2008, “Formation of dynamical structures in relativistic jets: the FRI case”, Astron. Astrophys., 488, 795–806. [DOI], [ADS], [arXiv:0806.1648 [astro-ph]]. (Cited on page 10.)
Rosswog, S., 2015, “SPH Methods in the Modelling of Compact Objects”, Living Rev. Comput. Astrophys., 1, lrca-2015-1. [DOI], [ADS], [arXiv:1406.4224 [astro-ph.IM]]. URL (accessed 9 December 2015): http://www.livingreviews.org/lrca-2015-1. (Cited on page 8.)
Ruffert, M., 1992, “Collisions between a white dwarf and a main-sequence star. II — Simulations using multiple-nested refined grids”, Astron. Astrophys., 265, 82–105. [ADS]. (Cited on page 125.)
Ryu, D. and Jones, T. W., 1995, “Numerical magnetohydrodynamics in astrophysics: Algorithm and tests for one-dimensional flow”, Astrophys. J., 442, 228. [DOI], [ADS], [arXiv:astro-ph/9404074]. (Cited on pages 136 and 138.)
Ryu, D., Jones, T. W. and Frank, A., 1995, “Numerical magnetohydrodynamics in astrophysics: Algorithm and tests for multidimensional flow”, Astrophys. J., 452, 785–796. [DOI], [ADS], [arXiv:astro-ph/9505073]. (Cited on page 56.)
Ryu, D., Miniati, F., Jones, T. W. and Frank, A., 1998, “A divergence-free upwind code for multidimensional magnetohydrodynamic flows”, Astrophys. J., 509, 244–255. [DOI], [ADS], [arXiv:astro-ph/9807228]. (Cited on pages 62 and 64.)
Ryu, D., Chattopadhyay, I. and Choi, E., 2006, “Equation of state in numerical relativistic hydrodynamics”, Astrophys. J. Suppl. Ser., 166, 410–420. [DOI], [ADS], [arXiv:astro-ph/0605550]. (Cited on pages 48, 49, 50, 53, 68, 80, and 83.)
Sadowski, A. Narayan, R., Tchekhovskoy, A. and Zhu, Y., 2013, “Semi-implicit scheme for treating radiation under M1 closure in general relativistic conservative fluid dynamics codes”, Mon. Not. R. Astron. Soc., 429, 3533–3550. [DOI], [ADS], [arXiv:1212.5050 [astro-ph.HE]]. (Cited on page 111.)
Sanders, R. H. and Prendergast, K. H., 1974, “The Possible Relation of the 3-Kiloparsec Arm to Explosions in the Galactic Nucleus”, Astrophys. J., 188, 489–500. [DOI], [ADS]. (Cited on page 127.)
Scheck, L., Aloy, M. A., Martí, J. M., Gómez, J. L. and Müller, E., 2002, “Does the plasma composition affect the long-term evolution of relativistic jets”, Mon. Not. R. Astron. Soc., 331, 615–634. [DOI], [ADS], [arXiv:astro-ph/0111369]. (Cited on pages 10 and 47.)
Schneider, V., Katscher, U., Rischke, D. H., Waldhauser, B., Maruhn, J. A. and Munz, C.-D., 1993, “New Algorithms for Ultra-relativistic Numerical Hydrodynamics”, J. Comput. Phys., 105, 92–107. [DOI]. (Cited on pages 38, 39, 43, 45, 47, 49, 66, 75, and 78.)
Schnetter, E., “CarpetCode: A mesh refinement driver for Cactus”, project homepage, Center for Computation and Technology, Louisiana State University. URL (accessed 14 July 2014): http://www.carpetcode.org. (Cited on page 146.)
Schnetter, E., Hawley, S. H. and Hawke, I., 2004, “Evolutions inn 3D numerical relativity using fixed mesh refinement”, Class. Quantum Grav., 21, 1465–1488. [DOI], [ADS], [arXiv:gr-qc/0310042]. (Cited on page 69.)
Shibata, M. and Sekiguchi, Y., 2005, “Magnetohydrodynamics in full general relativity: Formulation and tests”, Phys. Rev. D, 72, 044014. [DOI], [ADS], [arXiv:astro-ph/0507383]. (Cited on pages 65, 69, 70, 83, 86, 89, 90, 91, 96, 98, and 99.)
Shibata, S., Tomatsuri, H., Shimanuki, M., Saito, K. and Mori, K., 2003, “On the X-ray image of the Crab Nebula: comparison with Chandra observations”, Mon. Not. R. Astron. Soc., 346, 841–845. [DOI], [ADS], [arXiv:astro-ph/0308422]. (Cited on page 26.)
Shu, C. W., 1987, “TVB uniformly high-order schemes for conservationlaws”, Math. Comput., 49, 105–121. [DOI]. (Cited on page 122.)
Shu, C. W., 1997, Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws, ICASE Report, No. 97-65 / NASA CR-97-206253, NASA Langley Research Center, Hampton, VA. Online version (accessed 24 July 2014): http://hdl.handle.net/2060/19980007543. (Cited on pages 45, 122, and 141.)
Shu, C. W. and Osher, S., 1988, “Efficient implementation of essentially non-oscillatory shock-capturing schemes”, J. Comput. Phys., 77, 439–471. [DOI]. (Cited on pages 45, 47, 72, 122, and 123.)
Shu, C. W. and Osher, S., 1989, “Efficient Implementation of Essentially Non-Oscillatory Shock-Capturing Schemes, II”, J. Comput. Phys., 83, 32–78. [DOI]. (Cited on pages 41, 45, 47, 122, and 123.)
Soderberg, A. M., Nakar, E., Berger, E. and Kulkarni, S. R., 2006, “Late-time radio observations of 68 type Ibc supernovae: strong constraints on off-axis gamma-ray bursts”, Astrophys. J., 638, 930–937. [DOI], [ADS], [arXiv:astro-ph/0507147]. (Cited on page 18.)
Soffitta, P., Feroci, M., Pior, L. et al., 1998, GRB 980425, IAU Circular, 6884, Central Bureau for Astronomical Telegrams, Cambridge, MA. [ADS]. (Cited on page 17.)
Sokolov, I. V., Timofeev, E., Sakai, J.-I. and Takayama, K., 1999, “Development and applications of artificial wind schemes for hydrodynamics, MHD and relativistic hydrodynamics”, in Proceedings of the 13th National CFD Symposium, Chuo University, Tokyo, Japan, December 21–23, 1999 (CD-ROM), (Cited on page 121.)
Sokolov, I. V., Zhang, H.-M. and Sakai, J.-I., 2001, “Simple and efficient Godunov Scheme for Computational Relativistic Gas Dynamics”, J. Comput. Phys., 172, 209–234. [DOI]. (Cited on page 48.)
Spitkovsky, A., 2006, “Time-dependent Force-free Pulsar Magnetospheres: Axisymmetric and Oblique Rotators”, Astrophys. J. Lett., 648, L51–L54. [DOI], [ADS], [arXiv:astro-ph/0603147]. (Cited on page 111.)
Stark, R. F. and Piran, T., 1987, “A general relativistic code for rotating axisymmetric configurations and gravitational radiation: Numerical methods and tests”, Comput. Phys. Rep., 5, 221–264. [DOI]. (Cited on page 7.)
Steger, J. L. and Warming, R. F., 1981, “Flux-vector splitting of the inviscid gas dynamic equations with applications to finite-difference methods”, J. Comput. Phys., 40, 263–293. [DOI]. (Cited on page 127.)
Strang, G., 1968, “On the construction and comparison of difference schemes”, SIAM J. Numer. Anal., 5, 506–517. [DOI]. (Cited on pages 47 and 123.)
Suresh, A. and Huynh, H. T., 1997, “Accurate monotonicity-preserving schemes with Runge-Kutta time stepping”, J. Comput. Phys., 136, 83–99. [DOI]. (Cited on page 59.)
Sweby, P. K., 1984, “High resolution schemes using flux limiters for hyperbolic conservation laws”, SIAM J. Numer. Anal., 21, 995–1011. [DOI]. (Cited on page 122.)
Synge, J. L., 1956, Relativity: The special theory, North-Holland; Interscience, Amsterdam; New York. [Google Books]. (Cited on page 29.)
Synge, J. L., 1957, The Relativistic Gas, North-Holland; Interscience, Amsterdam; New York. [Google Books]. (Cited on page 47.)
Takahashi, H. R. and Ohsuga, K., 2013, “A numerical treatment of anisotropic radiation fields coupled with relativistic resistive magnetofluids”, Astrophys. J., 772, 127. [DOI], [ADS], [arXiv:1306.0049 [astro-ph.HE]]. (Cited on page 111.)
Takahashi, H. R., Ohsuga, K., Sekiguchi, Y., Inoue, T. and Tomida, K., 2013, “Explicit-implicit scheme for relativistic radiation hydrodynamics”, Astrophys. J., 764, 122. [DOI], [ADS], [arXiv:1212.4910 [astro-ph.HE]]. (Cited on page 111.)
Takahashi, K. and Yamada, S., 2014, “Exact Riemann solver for ideal magnetohydrodynamics that can handle all types of intermediate shocks and switch-on/off waves”, J. Plasma Phys., 80, 255–287. [DOI], [ADS], [arXiv:1310.2330 [astro-ph.HE]]. (Cited on page 34.)
Takamoto, M. and Inoue, T., 2011, “A new numerical scheme for resistive relativistic magnetohydrodynamics using method of characteristics”, Astrophys. J., 735, 113. [DOI], [ADS], [arXiv:1105.5683 [astro-ph.HE]]. (Cited on page 110.)
Takamoto, M. and Inutsuka, S., 2011, “A fast numerical scheme for causal relativistic hydrodynamics with dissipation”, J. Comput. Phys., 230, 7002–7017. [DOI], [ADS], [arXiv:1106.1732 [astro-ph.HE]]. (Cited on page 109.)
Tan, J. C., Matzner, C. D. and McKee, C. F., 2001, “Trans-relativistic blast waves in supernovae as gamma-ray burst progenitors”, Astrophys. J., 551, 946–972. [DOI], [ADS], [arXiv:astro-ph/0012003]. (Cited on page 19.)
Taub, A. H., 1948, “Relativistic Rankine-Hugoniot equations”, Phys. Rev., 74, 328–334. [DOI]. (Cited on page 48.)
Taub, A. H., 1978, “Relativistic Fluid Mechnaics”, Annu. Rev. Fluid Mech., 10, 301–332. [DOI]. (Cited on pages 8 and 29.)
Tchekhovskoy, A., McKinney, J. C. and Narayan, R., 2007, “WHAM: A WENO-based general relativistic numerical scheme I: hydrodynamics”, Mon. Not. R. Astron. Soc., 379, 469–497. [DOI], [ADS], [arXiv:0704.2608 [astro-ph]]. (Cited on pages 45, 47, 54, 73, 75, 78, 79, 80, and 147.)
Tchekhovskoy, A., McKinney, J. C. and Narayan, R., 2008, “Simulations of ultrarelativistics magnetodynamic jets from gamma-ray burst engines”, Mon. Not. R. Astron. Soc., 388, 551–572. [DOI], [ADS], [arXiv:0803.3807 [astro-ph]]. (Cited on pages 21, 22, and 111.)
Tchekhovskoy, A., Narayan, R. and McKinney, J. C., 2009, “Efficiency of magnetic to kinetic energy conversion in a monoploe magnetosphere”, Astrophys. J., 699, 1789–1808. [DOI], [ADS], [arXiv:0901.4776 [astro-ph.HE]]. (Cited on pages 21 and 22.)
Tchekhovskoy, A., Narayan, R. and McKinney, J. C., 2010, “Magnetohydrodynamic simulations of gamma-ray burst jets: beyond the progenitor star”, New Astron., 15, 749–754. [DOI], [ADS], [arXiv:0909.0011 [astro-ph.HE]]. (Cited on pages 21 and 22.)
Tchekhovskoy, A., Narayan, R. and McKinney, J. C., 2011, “Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole”, Mon. Not. R. Astron. Soc., 418, L79–L83. [DOI], [ADS], [arXiv:1108.0412 [astro-ph.HE]]. (Cited on page 16.)
Tchekhovskoy, A., Spitkovsky, A. and Li, J. G., 2013, “Time-dependent 3D magnetohydrodynamic pulsar magnetospheres: oblique rotators”, Mon. Not. R. Astron. Soc., 435, L1–L5. [DOI], [ADS], [arXiv:1211.2803 [astro-ph.HE]]. (Cited on page 111.)
Teyssier, R., 2002, “Cosmological hydrodynamics with adaptive mesh refinement. A new high resolution code called RAMSES”, Astron. Astrophys., 385, 337–364. [DOI], [ADS], [arXiv:astro-ph/0111367]. (Cited on pages 124 and 147.)
Thompson, K. W., 1986, “The Special Relativistic Shock Tube”, J. Fluid Mech., 171, 365–375. [DOI]. (Cited on page 129.)
Thorne, K. S., 1973, “Relativistic shocks: the Taub adiabat”, Astrophys. J., 179, 897–908. [DOI], [ADS]. (Cited on page 132.)
Tinney, C., Stathakis, R., Cannon, R. et al., 1998, GRB 980425, IAU Circular, 6896, Central Bureau for Astronomical Telegrams, Cambridge, MA. [ADS]. (Cited on page 17.)
Tominaga, N., 2009, “Aspherical properties of hydrodynamics and nucleosynthesis in jet-induced supernovae”, Astrophys. J., 690, 526–536. [DOI], [ADS], [arXiv:0711.4815 [astro-ph]]. (Cited on pages 20 and 54.)
Tominaga, N., Maeda, K., Umeda, H., Nomoto, K., Tanaka, M., Iwamoto, N., Suzuki, T. and Mazzali, P. A., 2007, “The connection between gamma-ray bursts and extremely metal-poor stars: black hole-forming supernovae with relativistic Jets”, Astrophys. J., 657, L77–L80. [DOI], [ADS], [arXiv:astro-ph/0702471]. (Cited on page 20.)
Toro, E. F., 1997, Riemann Solvers and Numerical Methods for Fluid Dynamics, Springer, Berlin. [Google Books]. (Cited on pages 8, 31, 121, and 123.)
Toro, E. F., Spruce, M. and Speares, W., 1994, “Restoration of the Contact Surface in the Harten-Lax-van Leer Riemann Solver”, Shock Waves, 4, 25–34. [DOI]. (Cited on pages 39, 57, and 121.)
Torrilhon, M., 2003, “Uniqueness conditions for Riemann problems of ideal magnetohydrodynamics”, J. Plasma Phys., 69, 253–276. [DOI]. (Cited on page 34.)
Tóth, G., 1996, “A general code for modeling MHD flows on parallel computers: versatile advection code”, Astrophys. Lett. Commun., 34, 245–250. [ADS]. (Cited on pages 52 and 146.)
Tóth,^G., 2000, “The \(\nabla \cdot \bar{B}=0\) Constraint in Shock-Capturing Magnetohydrodynamics Codes”, J. Comput. Phys., 161, 605–652. [DOI], [ADS]. (Cited on pages 56, 60, 61, 62, 66, 96, 99, 142, and 144.)
Tóth, G. and Odstrčil, D., 1996, “Comparison of some flux corrected transport and total variation diminishing numerical schemes for hydrodynamic and magnetohydrodynamic problems”, J. Comput. Phys., 128, 82–100. [DOI]. (Cited on pages 41, 47, and 58.)
Tscharnuter, W. M. and Winkler, K. H., 1979, “A method for computing selfgravitating gas flows with radiation”, Comput. Phys. Commun., 18, 171–199. [DOI], [ADS]. (Cited on page 46.)
Turland, B. D. and Scheuer, P. A. G., 1976, “Instabilities of Kelvin-Helmholtz type for relativistic streaming”, Mon. Not. R. Astron. Soc., 176, 421–441. [DOI], [ADS]. (Cited on page 100.)
VAC, “Versatile Advection Code (VAC)”, project homepage, Gabor Tioth. URL (accessed 14 July 2014): http://grid.engin.umich.edu/∼gtoth/VAC/. (Cited on pages 52, 69, and 146.)
van der Holst, B. and Keppens, R., 2007, “Hybrid block-AMR in Cartesian and curvilinear coordinates: MHD applications”, J. Comput. Phys., 226, 925–946. [DOI]. (Cited on pages 50, 51, 60, 70, and 146.)
van der Holst, B., Keppens, R. and Meliani, Z., 2008, “A multidimensional grid-adaptive relativistic magnetofluid code”, Comput. Phys. Commun., 179, 617–627. [DOI], [ADS], [arXiv:0807.0713 [astro-ph]]. (Cited on pages 58, 60, 70, 89, 90, 91, 92, 95, 99, 100, and 146.)
van Eerten, H. J., Meliani, Z., Wijers, R. A. M. J. and Keppens, R., 2009, “No visible optical variability from a relativistic blast wave encountering a wind termination shock”, Mon. Not. R. Astron. Soc., 398, L63–L67. [DOI], [ADS], [arXiv:0906.3629 [astro-ph.HE]]. (Cited on page 19.)
van Leer, B., 1973, “Towards the ultimate conservative difference scheme. I. The quest of monotonicity”, in Proceedings of the Third International Conference on Numerical Methods in Fluid Mechanics, Vol. I: General Lectures. Fundamental Numerical Techniques, Paris, July 3–7, 1972, (Eds.) Cabannes, H., Temam, R., Lecture Notes in Physics, 18, pp. 163–168, Springer, Berlin; New York. [DOI], [Google Books]. (Cited on pages 43 and 121.)
van Leer, B., 1974, “Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme”, J. Comput. Phys., 14, 361–370. [DOI]. (Cited on pages 43 and 121.)
van Leer, B., 1977a, “Towards the ultimate conservative difference scheme. IV. A new approach to numerical convection”, J. Comput. Phys., 23, 276–299. [DOI], [ADS]. (Cited on pages 43 and 121.)
van Leer, B., 1977b, “Towards the ultimate conservative difference scheme. III. Upstream-centered finite-difference schemes for ideal compressible flow”, J. Comput. Phys., 23, 263–275. [DOI]. (Cited on pages 43 and 121.)
van Leer, B., 1984, “On the relation between the upwind-differencing schemes of Godunov, Engquist-Osher and Roe”, SIAM J. Sci. Comput., 5, 1–20. [DOI]. (Cited on page 123.)
van Leer, B. J., 1979, “Towards the ultimate conservative difference scheme. V. A second order sequel to Godunov’s method”, J. Comput. Phys., 32, 101–136. [DOI]. (Cited on pages 43 and 121.)
van Putten, M. H. P. M., 1991, “Maxwell’s equations in divergence form for general media with applications to MHD”, Commun. Math. Phys., 141, 63–77. [DOI]. (Cited on pages 115 and 128.)
van Putten, M. H. P. M., 1992, MHD in Divergence Form: A Computational Method for Astrophysical Flow, Ph.D. thesis, California Institute of Technology, Pasadena, CA. [ADS]. (Cited on page 128.)
van Putten, M. H. P. M., 1993a, “A Numerical Implementation of MHD in Divergence Form”, J. Comput. Phys., 105, 339–353. [DOI], [ADS]. (Cited on pages 86, 88, 90, 93, and 128.)
van Putten, M. H. P. M., 1993b, “A Two-Dimensional Relativistic (Γ = 3.25) Jet Simulation”, Astrophys. J., 408, L21–L24. [DOI], [ADS]. (Cited on pages 10 and 128.)
van Putten, M. H. P. M., 1994, “A 2–Dimensional Blast Wave in Relativistic Magnetohydrodynamics”, Int. J. Bifurcat. Chaos, 4, 57–69. [DOI]. (Cited on page 128.)
van Putten, M. H. P. M., 1995, “A two-dimensional numerical implementation of magnetohydrodynamics in divergence form”, SIAM J. Numer. Anal., 32, 1504–1518. [DOI]. (Cited on pages 95 and 128.)
van Putten, M. H. P. M., 1996, “Knots in Simulations of Magnetized Relativistic Jets”, Astrophys. J., 467, L57–L60. [DOI], [ADS]. (Cited on pages 11 and 128.)
Vigelius, M., Melatos, A., Chatterjee, S., Gaensler, B. M. and Ghavamian, P., 2007, “Three-dimensional hydrodynamic simulations of asymmetric pulsar wind bow shocks”, Mon. Not. R. Astron. Soc., 374, 793–808. [DOI], [ADS], [arXiv:astro-ph/0610454]. (Cited on page 28.)
Vlahakis, N. and Königl, A., 2003, “Relativistic magnetohydrodynamics with application to gamma-ray burst outflows. I. Theory and semianalytic trans-Alfvénic solutions”, Astrophys. J., 596, 1080–1103. [DOI], [ADS], [arXiv:astro-ph/0303482]. (Cited on page 16.)
Vlasis, A., van Eerten, H. J., Meliani, Z. and Keppens, R., 2011, “Two-shell collisions in the gamma-ray burst afterglow phase”, Mon. Not. R. Astron. Soc., 415, 279–291. [DOI], [ADS]. (Cited on page 19.)
Volpi, D., Del Zanna, L., Amato, E. and Bucciantini, N., 2008, “Non-thermal emission from relativistic MHD simulations of pulsar wind nebulae: from synchrotron to inverse Compton”, Astron. Astrophys., 485, 337–349. [DOI], [ADS], [arXiv:0804.1323 [astro-ph]]. (Cited on page 26.)
von Neumann, J. and Richtmyer, R. D., 1950, “A method for the numerical calculation of hydrodynamic shocks”, J. Appl. Phys., 21, 232–247. [DOI]. (Cited on pages 46, 121, and 122.)
Vredevoogd, J. and Pratt, S., 2012, “Viscous hydrodynamics and relativistic heavy ion collions”, Phys. Rev. C, 85, 044 908. [DOI], [ADS], [arXiv:1202.1509 [nucl-th]]. (Cited on page 109.)
Wagner, A. Y. and Bicknell, G. V., 2011, “Relativistic jet feedback in evolving galaxies”, Astrophys. J., 728, 29. [ADS], [arXiv:1012.1092 [astro-ph.CO]]. (Cited on page 10.)
Wagner, A. Y., Bicknell, G. V. and Umemura, M., 2012, “Driving outflows with relativistic jets and the dependence of active galactic nucleus feedback efficiency on interstellar medium inhomogeneity”, Astrophys. J., 757, 136. [DOI], [ADS], [arXiv:1205.0542 [astro-ph.CO]]. (Cited on page 10.)
Walg, S., Achterberg, A., Markoff, S., Keppens, R. and Meliani, Z., 2013, “Relativistic AGN jets I. The delicate interplay between jet structure, cocoon morphology and jet-head propagation”, Mon. Not. R. Astron. Soc., 433, 1453–1478. [DOI], [ADS], [arXiv:1305.2157 [astro-ph.HE]]. (Cited on page 10.)
Walg, S., Achterberg, A., Markoff, S., Keppens, R. and Porth, O., 2014, “Relativistic AGN jets II. Jet properties and mixing effects for episodic jet activity”, Mon. Not. R. Astron. Soc., 439, 3969–3985. [DOI], [ADS], [arXiv:1311.4234 [astro-ph.GA]]. (Cited on page 10.)
Walker, R. C., Benson, J. M., Unwin, S. C., Lystrup, M. B., Hunter, T. R., Pilbratt, G. and Hardee, P. E., 2001, “The Structure and Motions of the 3C 120 Radio Jet on Scales of 0.6 to 300 parsecs”, Astrophys. J., 556, 756–772. [DOI], [ADS], [arXiv:astro-ph/0103379]. (Cited on page 13.)
Wang, P., Abel, T. and Zhang, W., 2008, “Relativistic hydrodynamic flows using spatial and temporal adaptive structured mesh refinement”, Astrophys. J., 176, 467–483. [DOI], [ADS], [arXiv:astro-ph/0703742]. (Cited on pages 21, 47, 50, 54, 75, 76, 78, 79, 80, 82, and 147.)
Watanabe, N. and Yokoyama, T., 2006, “Two-dimensional magnetohydrodynamic simulations of relativistic magnetic reconnection”, Astrophys. J., 647, L123–L126. [DOI], [ADS], [arXiv:astro-ph/0607285]. (Cited on pages 109 and 110.)
Weber, W. J., Boris, J. P. and Gardner, J. H., 1979, “Alfvén: A two-dimensional code based on SHASTA, solving the radiative, diffusive MHD equations”, Comput. Phys. Commun., 16, 243–265. [DOI]. (Cited on page 60.)
Wehrle, A. E., Piner, B. G., Unwin, S. C., Zook, A. C., Xu, W., Marscher, A. P., Teräsranta, H. and Valtaoja, E., 2001, “Kinematics of the parsec-scale relativistic jet in quasar 3C 279: 1991–1997”, Astrophys. J. Suppl. Ser., 133, 297–320. [DOI], [ADS], [arXiv:astro-ph/0008458]. (Cited on page 12.)
Weisskopf, M., 2011, “New results about an old friend: the Crab Nebula and its pulsar”, in The Extreme and Variable High Energy Sky (Extremesky 2011), Chia Laguna (Cagliari), Italy, September 19–23, 2011, Proceedings of Science, PoS(Extremesky 2011)002, SISSA, Trieste. URL (accessed 14 July 2014): http://pos.sissa.it/cgi-bin/reader/conf.cgi?confid=147. (Cited on page 26.)
Weisskopf, M. C., Hester, J. J. and Tennant, A. F. et al., 2000, “Discovery of spatial and spectral structure in the X-ray emission from the Crab Nebula”, Astrophys. J. Lett., 536, L81–L84. [DOI], [ADS], [arXiv:astro-ph/0003216]. (Cited on page 25.)
Wen, L., Panaitescu, A. and Laguna, P., 1997, “A shock-patching code for ultrarelativistic fluid flows”, Astrophys. J., 486, 919–927. [DOI], [ADS], [arXiv:astro-ph/9612045]. (Cited on pages 19, 36, 75, 76, 78, 79, and 80.)
Whisky, “Whisky — the EU Network GR Hydrodynamics code”, project homepage, Max Planck Institute for Gravitational Physics. URL (accessed 14 July 2014): http://www.whiskycode.org/. (Cited on pages 52, 53, and 147.)
White, J. W., 1973, “A new form of artificial viscosity”, J. Comput. Phys., 11, 573–590. [DOI]. (Cited on page 46.)
Wilson, J. R., 1972, “Numerical study of fluid flow in a Kerr space”, Astrophys. J., 173, 431–438. [DOI], [ADS]. (Cited on pages 7 and 46.)
Wilson, J. R., 1975, “Some magnetic effects in stellar collapse and accretion”, in Seventh Texas Symposium on Relativistic Astrophysics, (Eds.) Bergmann, P. G., Fenyves, E. J., Motz, L., Ann. N.Y. Acad. Sci., 262, pp. 123–132, New York Academy of Sciences, New York. [DOI], [ADS], [Google Books]. (Cited on pages 7 and 60.)
Wilson, J. R., 1977, “Magnetohydrodynamics near a black hole”, in First Marcel Grossmann Meeting on General Relativity, Proceedings of the meeting held at the International Centre for Theoretical Physics, Trieste and Istituto di fisica, University of Trieste, 7–12 July 1975, (Ed.) Ruffini, R., pp. 393–413, North-Holland, Amsterdam. [ADS]. (Cited on pages 7 and 60.)
Wilson, J. R., 1979, “A Numerical Method for Relativistic Hydrodynamics”, in Sources of Gravitational Radiation, Proceedings of the Battelle Seattle Workshop, July 24–August 4, 1978, (Ed.) Smarr, L. L., pp. 423–445, Cambridge University Press, Cambridge; New York.[ADS], [Google Books]. (Cited on pages 7 and 46.)
Wilson, J. R. and Mathews, G. J., 2003, Relativistic numerical hydrodynamics, Cambridge University Press, Cambridge, UK. [Google Books]. (Cited on pages 8 and 46.)
Woodward, P. R. and Colella, P., 1984, “The numerical simulation of two-dimensional fluid flow with strong shocks”, J. Comput. Phys., 54, 115–173. [DOI]. (Cited on page 35.)
Woosley, S., 2012, “Models for gamma-ray burst progenitors and central engines”, in Gamma-ray Bursts, (Eds.) Kouveliotou, C., Wijers, R. A. M. J., Woosley, S., Cambridge Astrophysucs Series, 51, pp. 191–213, Cambridge University Press, Cambridge, New York. [Google Books]. (Cited on page 21.)
Woosley, S. E., 1993, “Gamma-ray bursts from stellar mass accretion disks around black holes”, Astrophys. J., 405, 273–277. [DOI], [ADS]. (Cited on pages 18 and 21.)
Woosley, S. E., Eastman, R. G. and Schmidt, B. P., 1999, “Gamma-Ray Bursts and Type Ic Supernova SN 1998bw”, Astrophys. J., 516, 788–796. [DOI], [ADS], [arXiv:astro-ph/9806299]. (Cited on page 17.)
Wygoda, N., Waxman, E. and Frail, D. A., 2011, “Relativistic jet dynamics and calorimetry of gamma-ray bursts”, Astrophys. J., 738, L23. [DOI], [ADS], [arXiv:1102.5618 [astro-ph.HE]]. (Cited on pages 21 and 54.)
Yang, J. Y. and Hsu, C. A., 1992, “High-resolution, Non-oscillatory Schemes for Unsteady Compressible Flows”, AIAA J., 30, 1570–1575. [DOI]. (Cited on page 127.)
Yang, J. Y., Huang, J. C. and Tsuei, L., 1995, “Numerical solutions of the nonlinear model Boltzmann equations”, Proc. R. Soc. London, Ser. A, 448, 55–80. [DOI]. (Cited on page 127.)
Yang, J. Y., Chen, M. H., Tsai, I.-N. and Chang, J. W., 1997, “A Kinetic Beam Scheme for Relativistic Gas Dynamics”, J. Comput. Phys., 136, 19–40. [DOI]. (Cited on page 127.)
Yee, H. C., 1987, “Construction of explicit and implicit symmetric TVD schemes and their applications”, J. Comput. Phys., 68, 151–179. [DOI]. (Cited on page 122.)
Yee, H. C., 1989a, “A class of high-resolution explicit and implicit shock-capturing methods”, in Computational Fluid Dynamics, VKI Lecture Series, 04, von Karman Institute for Fluid Dynamics, Rhode-Saint-Genèse, Belgium. [Google Books]. (Cited on pages 37, 120, and 122.)
Yee, H. C., 1989b, A Class of High-Resolution Explicit and Implicit Shock-Capturing Methods, NASA Technical Memorandum, NASA-TM-101088, NASA Ames Research Center, Moffett Field, CA. Online version (accessed 24 July 2014): http://hdl.handle.net/2060/19890016281. (Cited on pages 41, 47, and 58.)
Yokosawa, M., 1993, “Energy and angular momentum transport in magnetohydrodynamical accretion onto a rotating black hole”, Publ. Astron. Soc. Japan, 45, 207–218. [ADS]. (Cited on pages 7 and 60.)
Yokosawa, M., Ikeuchi, S. and Sakashita, S., 1982, “Structure and expansion law of a hypersonic beam”, Publ. Astron. Soc. Japan, 34, 461–481. [ADS]. (Cited on pages 7, 10, 45, and 60.)
Zachary, A., Malagoli, A. and Colella, P., 1994, “A higher-order godunov method for multidimensional ideal magnetohydrodynamics”, SIAM J. Sci. Comput., 15, 263–284. [DOI]. (Cited on page 56.)
Zanotti, O. and Dumbser, M., 2011, “Numerical simulations of high Lundquist number relativistic magnetic reconnection”, Mon. Not. R. Astron. Soc., 418, 1004–1011. [DOI], [ADS], [arXiv:1103.5924 [astro-ph.HE]]. (Cited on page 110.)
Zanotti, O. and Dumbser, M., 2015, “A high order special relativistic hydrodynamic and magnetohydrodynamic code with space-time adaptive mesh refinement”, Comput. Phys. Commun., 188, 110–127. [DOI]. (Cited on pages 68 and 126.)
Zanotti, O., Roedig, C., Rezzolla, L. and Del Zanna, L., 2011, “General relativistic radiation hydrodynamics of accretion flows — I. Bondi-Hoyle accretion”, Mon. Not. R. Astron. Soc., 417, 2899–2915. [DOI], [ADS], [arXiv:1105.5615 [astro-ph.HE]]. (Cited on page 111.)
Zenitani, S., Hesse, M. and Klimas, A., 2009, “Two-fluid magnetohydrodynamic simulations of relativistic magnetic reconnection”, Astrophys. J., 696, 1385–1401. [DOI], [ADS], [arXiv:0902.2074 [astro-ph.HE]]. (Cited on page 110.)
Zenitani, S., Hesse, M. and Klimas, A., 2010, “Resistive magnetohydrodynamic simulations of relativistic magnetic reconnection”, Astrophys. J., 716, L214–L218. [DOI], [ADS], [arXiv:1005.4485 [astro-ph.HE]]. (Cited on page 110.)
Zhang, W., “Weiqun Zhang’s Homepage”, personal homepage, New York University. URL (accessed 14 July 2014): http://cosmo.nyu.edu/∼wqzhang/. (Cited on page 20.)
Zhang, W. and MacFadyen, A. I., 2006, “RAM: A Relativistic adaptive mesh refinement hydrodynamics code”, Astrophys. J. Suppl. Ser., 164, 255–279. [DOI], [ADS], [arXiv:astro-ph/0505481]. (Cited on pages 44, 47, 50, 54, 72, 73, 75, 78, 79, 80, 82, 84, 101, 142, and 147.)
Zhang, W., Woosley, S. E. and MacFadyen, A. I., 2003, “Relativistic jets in collapsars”, Astrophys. J., 586, 356–371. [DOI], [ADS], [arXiv:astro-ph/0207436]. (Cited on page 19.)
Zhang, W., Woosley, S. E. and Heger, A., 2004, “The propagation and eruption of relativistic jets from stellar progenitors of gamma-ray bursts”, Astrophys. J., 608, 365–377. [DOI], [ADS], [arXiv:astro-ph/0308389]. (Cited on pages 19 and 20.)
Zhang, Z.-C., Yu, S. T. J. and Chang, S. C., 2002, “A Space-Time Conservation Element and Solution Element Method for Solving the Two- and Three-Dimensional Unsteady Euler Equations Using Quadrilateral and Hexahedral Meshes”, J. Comput. Phys., 175, 168–199. [DOI]. (Cited on pages 127 and 128.)
Zhao, J. and Tang, H., 2013, “Runge-Kutta discontinuous Galerkin methods with WENO limiter for the special relativistic hydrodynamics”, J. Comput. Phys., 242, 138–168. [DOI]. (Cited on page 126.)
Ziegler, U. and Yorke, H. W., 1997, “A nested grid refinement technique for magnetohydrodynamical flows”, Comput. Phys. Commun., 101, 54–74. [DOI]. (Cited on page 125.)
Zrake, J. and MacFadyen, A. I., 2012, “Numerical simulations of driven relativistic magnetohydrodynamic turbulence”, Astrophys. J., 744, 32. [DOI], [ADS], [arXiv:1108.1991 [astro-ph.HE]]. (Cited on pages 60, 71, 106, and 146.)
Acknowledgements
J.-M.M. acknowledges financial support from the Spanish Ministerio de Economía y Competitividad (grants AYA2013-40979-P, and AYA2013-48226-C3-2-P) and from the local Autonomous Government (Generalitat Valenciana, grant Prometeo-II/2014/069). The authors thank Profs. M.A. Aloy and A. Marquina for a careful reading of parts of the original manuscript.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
41115_2016_3_MOESM1_ESM.mpg
Movie of Fig. 6 (mpg 9419.38964844 kB) 3BL jet breaking out of the star (Weiqun Zhang’s webpage). Courtesy of W. Zhang.
41115_2016_3_MOESM2_ESM.mpg
Movie of Fig. 8 (mpg 3987.49609375 kB) Crab time-lapse movie made from seven still images of Chandra observations taken between November 2000 and April 2001. The movie shows dynamic rings, wisps and jets in the Crab nebula (Credit: NASA/CXC/ASU/J. Hester et al.). See more Crab animations at Chandra web page.
41115_2016_3_MOESM3_ESM.mpg
Movie of Fig. 1 (mpg 711.250976562 kB) Full evolution of the numerical solution.
41115_2016_3_MOESM4_ESM.mpg
Movie of Fig. 17 (mpg 1453.26757812 kB) Full evolution of the numerical solution.
Glossary
- AGN
-
Active Galactic Nuclei. 7, 9, 10
- AMR
-
Adaptive Mesh Refinement. 20, 21, 50, 51, 53–55, 68–71, 76, 82–84, 92, 95, 100, 109, 110, 124–126
- AV
-
Artificial Viscosity schemes. Sometimes refers to the extra terms added to the equations in these schemes. 46, 60, 75, 80, 107
- CE/SE
-
Conservation element / solution element methods. 127, 128
- CENO
-
Convex, Essentially Non-Oscillatory, third-order, interpolation scheme. 41, 45, 53, 54, 59, 70, 85, 92, 107, 122
- CENO3-HLL-MC
-
Finite-difference scheme based on the CENO reconstruction with MC slope limiter, and HLL Riemann solver (Del Zanna et al., 2003). 92
- CENO3-HLL-MM
-
Finite-difference scheme based on the CENO reconstruction with MINMOD slope limiter, and HLL Riemann solver (Del Zanna et al., 2003). 85
- CH-ENO-LF
-
Finite-difference scheme based on the ENO reconstruction of the characteristic fluxes splitted according to the Lax-Friedrichs splitting (Dolezal and Wong, 1995). 45, 53
- CH-ENO-LLF
-
Finite-difference scheme based on the ENO reconstruction of the characteristic fluxes splitted according to the local Lax-Friedrichs splitting (Dolezal and Wong, 1995). 45, 53
- CT
-
Constrained Transport scheme for magnetic field advance. 60–62, 64, 65, 68, 96, 108
- CTU
-
Corner Transport Upwind method (Colella, 1990). 47, 53, 54, 64, 65, 70, 71, 107, 124
- CW-ENO-LF
-
Finite-difference scheme based on the ENO reconstruction of the component-wise fluxes splitted according to the Lax-Friedrichs splitting (Dolezal and Wong, 1995). 45, 53
- CW-ENO-LLF
-
Finite-difference scheme based on the ENO reconstruction of the componentwise fluxes splitted according to the local Lax-Friedrichs splitting (Dolezal and Wong, 1995). 45, 53
- DG
-
Discontinuous Galerkin methods. 126
- eAV
-
Artificial-viscosity finite-volume scheme that solves an extra equation for the total energy used to overwrite the solution computed from the internal energy evolution equation, depending on the accuracy of the results. One of the schemes in COSMOS++. 46, 75, 76, 80
- ENO
-
Essentially Non-Oscillatory, third-order to fifth-order, interpolation schemes (see Shu (1997) for a review). 35, 37, 41, 43–45, 53, 59, 65, 70, 92, 107, 122, 127
- EOS
-
Equation of state. 29, 31, 32, 47–49, 66–68, 73, 75, 99, 113
- F-PLM
-
Finite-difference scheme based on the piecewise linear reconstruction of the characteristic fluxes splitted according to the Lax-Friedrichs splitting. One of the schemes in RAM and RENZO codes (Zhang and MacFadyen, 2006). 44, 54, 72, 75, 80
- F-WENO
-
Finite-difference scheme based on the WENO fifth-order reconstruction of the characteristic fluxes splitted according to the Lax-Friedrichs splitting. One of the schemes in RAM code. 54, 72, 73, 75, 79, 80, 82, 84
- F-WENO-A
-
F-WENO scheme of RAM with adaptive mesh refinement. 101
- F-WENO5
-
Finite-difference scheme based on the WENO fifth-order reconstruction of the characteristic fluxes splitted according to the Lax-Friedrichs splitting. One of the schemes in RENZO code and similar to F-WENO scheme in RAM. 79, 80
- FCT
-
Flux-Corrected-Transport method. 7, 45, 46, 59, 60, 62, 107, 122
- FD
-
Finite-Difference methods. 35–37, 40, 41, 43–46, 51, 53–55, 59, 69, 70, 76, 107, 118, 119, 121–123
- field-CD
-
Cell-centered (i.e., non-staggered) CT scheme. Notation introduced in Tóth (2000). 62
- field-CT
-
Field-interpolated CT scheme. The staggered magnetic field is advanced in time from spatial and temporal interpolations to the cell corners of the magnetic and velocity fields. Notation introduced in Tóth (2000). 62, 65, 70
- flux-CD
-
Cell-centered (i.e., non-staggered) CT scheme. Notation introduced in Tóth (2000). 62, 65, 70, 71
- flux-CT
-
Flux-interpolated CT scheme. The staggered magnetic field is advanced in time from spatial and temporal interpolations to the cell corners of the fluxes of the base scheme. Notation introduced in Tóth (2000). 62, 64, 65, 70, 71
- FV
-
Finite-Volume methods. 35, 37, 41–46, 51, 53–55, 57–59, 69–71, 76, 107, 118, 119, 121, 126, 127, 140
- FV-consistent flux-CT
-
Staggered CT algorithms forcing the consistency between volume-and area-averaged magnetic fields and their associated numerical fluxes (Gardiner and Stone, 2005). 64, 71
- FWD
-
Full-Wave Decomposition Riemann solver. 57, 58, 92, 94, 100
- GRB
-
Gamma-Ray Burst. 7, 8, 16–23, 41, 47, 50, 51, 111
- GRHD
-
General Relativistic Hydrodynamics. 7, 8, 37, 51, 52, 126
- GRMHD
-
General Relativistic Magnetohydrodynamics. 8, 13, 16, 21, 46, 57, 59, 60, 65, 68, 69
- HLL
-
Harten-Lax-van Leer Riemann solver. 38–40, 43, 45, 46, 48, 53–55, 57, 58, 70, 71, 92, 94, 100, 103, 105, 107, 110, 121
- HLL-CENO
-
Finite-volume scheme based on the CENO reconstruction of the primitive variables and the HLL Riemann solver. One of the schemes in RENZO. 80
- HLL-PLM
-
Finite-volume scheme based on the piecewise linear reconstruction of the primitive variables and the HLL Riemann solver. One of the schemes in RENZO. 44, 80, 82
- HLL-PPM
-
Finite-volume scheme based on the piecewise parabolic reconstruction of the primitive variables and the HLL Riemann solver. One of the schemes in RENZO. 80
- HLLC
-
HLL Riemann solver with contact discontinuity. 39, 40, 53–55, 57, 58, 70, 71, 80, 92, 94, 100, 103, 105, 107, 121
- HLLD
-
HLLC Riemann solver with Alfvén discontinuities. 57, 58, 71, 92, 94, 100, 103, 105, 107
- HRSC
-
High-Resolution Shock-Capturing methods. 7–9, 35, 42, 47, 48, 51, 56, 60, 66, 68, 69, 72, 75, 78–80, 107, 108, 118, 119, 123, 127
- ISM
-
Interstellar Medium. 21, 23, 24
- KFVS
-
Kinetic flux-vector splitting methods. 127
- KH
-
Kelvin-Helmholtz instability. 10, 12, 13, 100, 101, 103, 105, 109
- LF
-
Lax-Friedrichs flux formula. 40, 48, 70
- LLF
-
Local Lax-Friedrichs flux formula. 41, 42, 53, 54, 58, 70, 71, 75, 82, 110
- LLF-PLM
-
Finite-volume scheme based on the piecewise linear reconstruction of the primitive variables and the local Lax-Friedrichs flux formula. One of the schemes in RENZO. 76
- MFF
-
Marquina flux formula. 54, 75
- MHD
-
Magnetohydrodynamics. 8–11, 13, 22, 23, 25–27, 29, 31–34, 51, 56–62, 65, 68, 85, 88, 93, 96, 99, 108, 110, 111, 115, 121, 122, 124, 126, 128, 136–139
- MMFF
-
Modified Marquina flux formula. 42, 53, 54
- MP
-
Monotonicity Preserving interpolation scheme (fifth order). 55, 59, 70
- MUSCL
-
Monotonic Upstream-centered Schemes for Conservation Laws. 121
- MUSCL-Hancock
-
MUSCL-Hancock scheme. Global second-order, single-step, scheme based on the solution of Riemann problems from second-order, monotonized states computed by Taylor expansions at the middle of the time step. 43, 47, 53–55, 60, 70, 71, 80, 92, 107, 123
- NOCD
-
Non-Oscillatory Central-Differencing schemes. Also one of the schemes in COSMOS and COSMOS++ based on this kind of techniques. 41, 46, 47, 53, 58, 70, 76, 80, 121, 122
- PH
-
Local piecewise hyperbolic interpolation. Originally developed as the reconstruction step in the PHM method. 53, 54
- PHM
-
Local Piecewise-Hyperbolic Method (Marquina, 1994). 37, 122
- PL
-
Piecewise linear interpolation scheme with slope limiting. 53–55, 70, 71
- PLM
-
Piecewise-Linear Method. 44, 47, 123
- PP
-
Piecewise interpolation scheme with monotonic parabolae, including limiting at shocks and steepening at contact discontinuities. Originally developed as the reconstruction step in the PPM method. 53, 54, 70–72, 85, 110
- PPM
-
Piecewise-Parabolic Method. Refers to the original scheme developed in Colella and Woodward (1984) or its relativistic extensions (Martí and Müller, 1996; Mignone et al., 2005b). 35, 42, 44, 47, 76, 79, 80, 121, 123
- PWN
-
Pulsar Wind Nebula. 23, 25, 26, 28
- RHD
-
Relativistic Hydrodynamics. 7–10, 12, 20, 29, 31, 32, 35–48, 50–53, 56–58, 60, 66, 72, 74, 76, 83, 105, 107–109, 111, 112, 118, 126, 128–130, 133, 136, 137
- RK
-
Runge-Kutta time discretization algorithms. Third to fifth order of accuracy. 53–55, 70, 71
- RKDG
-
Runge-Kutta Discontinuous Galerkin methods. 126, 127
- RMHD
-
Relativistic Magnetohydrodynamics. 7–10, 13, 22, 23, 26, 27, 29–32, 47, 48, 52, 56–62, 65–69, 72, 83, 85, 86, 91–93, 95, 96, 99, 103, 105, 107–111, 113, 115, 118, 124, 126–128, 133, 137–140
- SMR
-
Static Mesh Refinement. 71
- SNR
-
Supernova Remnant. 23, 24, 26, 28
- transport-flux-CT
-
Transport-flux-interpolated CT scheme. The staggered magnetic field is advanced in time from spatial and temporal interpolations to the cell corners of the transport fluxes of the base scheme. Notation introduced in Tóth (2000). 62, 65, 70
- TV
-
Total Variation. 42, 119, 121, 122
- TVD
-
Total-Variation-Diminishing schemes. Refers to the schemes satisfying the property of ensuring the decrease of the total variation of the solution with time, or refers to the property itself. 35, 42, 43, 47, 53, 57–60, 79, 107, 121–123
- TVD-RK
-
Runge-Kutta time discretization algorithms that preserve the TVD properties of the algorithm at every substep. Second and third order of accuracy. 45, 47, 53, 54, 60, 70–72, 82, 107, 123
- TVDLF
-
Second-order TVD scheme relying on the local Lax-Friedrichs flux formula. The scheme used in AMRVAC for relativistic simulations. 41, 47, 58
- U-PLM
-
Finite-volume scheme based on the piecewise linear reconstruction of the primitive variables. One of the schemes in RAM code. 44, 54, 72, 75, 80
- U-PPM
-
Finite-volume scheme based on the piecewise parabolic reconstruction of the primitive variables. One of the schemes in RAM code. 44, 54, 72, 75, 80, 82
- UCT
-
Upwind CT scheme. The staggered magnetic field is advanced in time from spatial and temporal interpolations to the cell corners of the upwind fluxes of the base scheme. Described in Londrillo and Del Zanna (2000, 2004). 65, 70, 71
- WENO
-
Weighted, Essentially Non-Oscillatory, third-order to seventh-order, interpolation schemes. 41, 45, 54, 55, 59, 68, 70, 71, 107, 122, 126, 127
- AMRCLAW
-
AMRCLAW package. Web page: LeVeque’s web. 126
- AMRVAC
-
AMRVAC code (see Tables 1 and 2). Outgrowth of the VAC, Versatile Advection Code (VAC; Tóth, 1996). (MPI-) AMRVAC web page: AMRVAC’s web. Current version of the code: Keppens et al. (2012). The following references refer to previous variants of the code and contain relevant information partly applicable to the current MPI version Keppens et al. (2003); Meliani et al. (2007); van der Holst and Keppens (2007); van der Holst et al. (2008). 40, 41, 44, 47, 50–52, 58–62, 67, 69, 76, 99, 125
- ATHENA
-
ATHENA code. For the relativistic extension, see Table 2 and Beckwith and Stone (2011). Web page: ATHENA’s web. 58, 67, 69, 86
- Cactus
-
Cactus code. Cactus is an open source problem solving environment designed for scientists and engineers. The Cactus Framework and Computational Toolkit provides the framework for the Einstein Toolkit, that addresses computational relativistic astrophysics, supporting simulations of black holes, neutron stars, and related systems. Cactus code web page: Cactus’ web. 69
- Carpet
-
AMR driver for the Cactus code. Web page: Schnetter’s web. 50, 69
- Chombo
-
Chombo (software for adaptive solutions of partial differential equations). Web page: Chombo’s web. 51
- COSMOS
-
COSMOS code. See Table 1 and Anninos and Fragile (2003); Anninos et al. (2003). 41, 46, 47, 52, 78, 80
- COSMOS++
-
COSMOS++ code. See Table 2 and Anninos et al. (2005). 46, 52, 58, 60, 62, 69, 75, 76, 80
- ECHO
-
ECHO code. See Table 2 and Del Zanna et al. (2007). 57, 59, 67, 86, 96, 98, 109, 111
- FLASH
-
FLASH code. See Table 1 and Fryxell et al. (2000); Morsony et al. (2007). Web page: FLASH’ web. 20, 36, 44, 49, 50, 52, 72, 73, 80, 82, 83
- GENESIS
-
GENESIS code. See Table 1 and Aloy et al. (1999b). 37, 42, 44, 47, 49, 57, 76
- HARM
-
HARM code (see Table 2). Original version in Gammie and Tóth (2003). Upgraded version in McKinney (2006a). The original version can be downloaded from the Astrophysical Code Library of the Astrophysical Fluid Dynamics Group at the University of Illinois (AFDG’s web). 57, 59, 60, 66, 68, 69, 91, 98
- Mara
-
Mara code. See Table 2 and Zrake and MacFadyen (2012). 58, 65, 67, 106
- Mezcal-SRHD
-
Relativistic extension of Mezcal code. See Table 1 and De Colle et al. (2012a). 51
- PARAMESH
-
PARAMESH software (MacNeice et al., 2000). Web page: MacNeice and Olson (2008)’ web. 50
- PLUTO
-
PLUTO code (see Tables 1 and 2) Mignone et al. (2007). AMR version: Mignone et al. (2012). Web page: PLUTO’ web. 39, 43, 47, 51, 52, 58, 60–62, 67, 69, 98, 110
- RAISHIN
-
RAISHIN code. See Table 2 and Mizuno et al. (2006). 52, 57, 65, 67, 85, 92, 95, 98 RAM
- RAMSES
-
RAMSES code. See Teyssier (2002) for the original RAMSES code and Table 1 and Lamberts et al. (2013) for its relativistic extension. 39, 40, 44, 51
- Ratpenat
-
Ratpenat code. See Table 1 and Perucho et al. (2010). 37, 42, 44, 47, 49, 101
- RENZO
-
RENZO code. See Table 1 and Wang et al. (2008). 39–42, 44, 45, 47, 50, 76, 80, 82
- TESS
-
TESS code. See Table 2 and Duffell and MacFadyen (2011). 52, 58–60, 62, 67, 72, 73, 80, 82, 83, 93, 96, 99, 103
- THC
- WHAM
-
WHAM code. See Table 1 and Tchekhovskoy et al. (2007). 39, 45, 47, 73, 74, 79, 80, 82
- Whisky
-
Whisky code. See Table 1 and Baiotti et al. (2003). Web page: Whisky’s web. 50, 52
- WhiskyMHD
-
WhiskyMHD code. See Table 2 and Giacomazzo and Rezzolla (2007). Web page: Giacomazzo’s web. 57, 65, 69, 92, 95
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Martí, J.M., Müller, E. Grid-based Methods in Relativistic Hydrodynamics and Magnetohydrodynamics. Living Rev Comput Astrophys 1, 3 (2015). https://doi.org/10.1007/lrca-2015-3
Accepted:
Published:
DOI: https://doi.org/10.1007/lrca-2015-3