1 Introduction

With additive manufacturing (AM) it is possible to produce parts of complex shapes and with improved functionality, and the industrial interests and commercial implementations of the metal AM technologies are increasing drastically each year.[1] Within the automotive industry, AM offers innovations in the product development by shortening of design time (through rapid prototyping and testing) and allows for building of complex structure parts[2,3] as well as efficient replacement of rare spare parts.[4,5] Examples are fasteners and parts for catalytic convertors whose geometrical complexity can be easily achieved via AM. In addition, in hot gas exhaust systems, the heat transfer efficiency can be improved by optimizing complicated shapes of heat exchangers, and hence, applying AM can be beneficial. Furthermore, AM is potentially applicable in solid oxide fuel cells (SOFC) systems for, e.g., interconnects or other parts where freedom of geometry is an advantage. The ferritic stainless steel AISI 441 is an appropriate material for all these applications, and hence, research concerning the AM processing of this grade is needed.

AISI 441 has good oxidation, corrosion, and creep resistance and is a suitable material for applications at elevated temperatures.[6] Besides, AISI 441 has good thermal and electrical conductivity, and can easily be fabricated.[7,8,9] Other than that, AISI 441. is a solid-solution strengthened steel with some alloying additions of Ti and Nb for stabilization and improved high-temperature strength.[8,9] Previous work has shown that AM of AISI 441 by laser-powder bed fusion (L-PBF) lead to excellent mechanical properties compared to the conventional material produced by casting and hot rolling, attributed to the finer structure with small grain size in the printed material.[12] Conventionally manufactured AISI 441 is usually used in the hot or cold rolled and heat-treated state. The extremely high cooling rates and thermal gradients of L-PBF process conditions are significantly different from the conventional manufacturing conditions resulting in different as-manufactured microstructures, and the response to post-heat treatments may differ. Hence, conventional post-heat treatment procedures may not be transferable to the L-PBF-processed material without modification.[11,12]

In this work, the microstructure response of L-PBF-processed AISI 441 during post-heat treatments is studied in detail for the temperature range 850 °C to 1150 °C. Focus is on the precipitation kinetics as well as the grain structure evolution. The evolution of the precipitates is characterized using scanning and transmission electron microscopy (SEM and TEM) and the experimental results are used to calibrate the settings of precipitation kinetics simulations using the precipitation module (TC-PRISMA) within the Thermo-Calc Software package.[15] A calibrated precipitation model will allow for post-heat treatment optimization of AM components and can be used as creator tool for process and structure linkages in an integrated computational materials engineering (ICME) framework for alloy and process development of AM for ferritic steels. Finally, the microstructure response of the L-PBF-processed material to the post-heat treatments is discussed in relation to the post-heat treatment response of conventionally produced AISI 441.

2 Experimental and Computational Methods

2.1 Experimental Methods

Samples of the AISI SS441 alloy investigated in this study were based on the Sandvik’s Osprey® SS441 IGA powders produced via inert nitrogen gas atomization. The used powder particle size distribution was 10 to 45 µm. The studied samples were built using an EOS M100, equipped with a 200 W laser with a spot size of approximately 40 µm, in a flowing argon gas atmosphere, see previous work by Karlsson et al.[12] The cylindrical samples were vertically built (0 deg) with a laser power of 130 W, a scanning speed of 1000 mm/s, a hatch distance of 0.07 mm and layer thickness of 0.02 mm, resulting in a laser energy density of 92.6 J/mm3. The scanning strategy of each layer was based on bidirectional scan vectors with 5 mm wide stripes overlapping 0.1 mm, and between each layer there was a 67 deg rotation. More details of the L-PBF process to produce the current samples can be found in.[12] The composition of the as-built material was measured by X-ray fluorescence (XRF) using a XRF PANalytical Magic Fast analyzer according to ASTM E572. A combustion analyzer Leco-CS600 was used to analyze C and S content, while for O and N a Leco-TC600 analyzer was used according to ASTM E1019. The Al content was analyzed by an ARL iSpeak 8860 Optical Emission Spectrometry (OES) analyzer according to ASTM E1086. The as-built material composition is summarized in Table I.

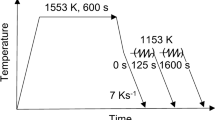
Table I Composition of the Ferritic Stainless Steel AISI SS441 in Wt Pct From the As-Built L-PBF Sample
Full size table

The as-built samples were heat treated at 850 °C to 1150 °C for 2 h in a tube furnace with flowing argon gas, followed by quenching in brine. In addition, one sample was heat treated for 10 h at 900 °C. The results for a heat treatment at 900 °C for 20 minutes are available from previous work.[12] As will be shown later, experimentally, the main precipitates after heat treatment are the Laves phase (Fe2Nb) and a Nb-rich cubic carbo-nitride, hereafter denoted Laves and NbC, respectively.

The microstructure after heat treatment was studied using a JEOL JSM-7800F field emission gun (FEG) SEM. A Bruker analytical system Energy-Dispersive X-ray Spectroscopy (EDS) detector was used to measure the phase composition. The elemental information from the EDS measurements coupled with equilibrium calculation results were used for phase identification. Different microstructural features were evaluated from micrographs using the image processing program ImageJ. Under the FEG microscope, the fine Laves and NbC precipitates showed very similar morphologies and contrast and were difficult to distinguish. Furthermore, due to the large number of fine precipitates included in the study, it was not feasible to characterize them one-by-one by EDS composition mapping method. Hence, two different methods were applied. The first method was to combine micrographs of the sample surfaces under two imaging modes: the Secondary Electron (SE) mode and Back Scattering Electron (BSE) mode. A relatively long time (8 minutes) of polishing was performed in the final step using 0.02 µm Silica colloidal suspension. Due to the different wear resistance of the phases, the sample surfaces were selectively polished. Under the SE mode, where topographical difference was revealed, the higher wear-resistant NbC, protruded above the matrix surface and showed a shadow around the particles in contrast to the Laves phase which was polished flat and not revealed completely in this mode. The BSE mode micrographs, however, showed also the Laves phase and by comparing the SE mode and BSE mode micrographs it was possible to separate between the Laves and NbC phases to quantify the phase fractions and sizes. The quantified values from this method may involve some uncertainty from the polishing, and thus a second method was introduced to lower the experimental uncertainty. The second method was to correlate the BSE-coefficient values to the experimental gray level of the observed precipitates. In the second method, an acceleration voltage of 5 kV and a working distance (WD) of 5 mm were used in the SEM. Samples were ground using SiC-paper, followed by diamond suspension polishing to 1 µm and final polishing using a 0.02 µm colloidal silica solution. Due to different values of BSE-coefficients of the precipitates, they could be distinguished by the different gray level under the BSE mode. The details of this method can be referred to Supplementary Material.

The precipitates were further studied by TEM using a FEI Titan Themis 200 Scanning transmission electron microscope (STEM) equipped with a SuperX EDS operating at an acceleration voltage of 200 kV. Prior to the TEM analysis, the specimen was prepared by the in-situ lift-out technique in a Zeiss Crossbeam 550 focused ion beam (FIB). Pt was deposited on the region of interest prior to preparation and a final polishing step using a low-energy ion beam of 5 kV was employed to minimize beam damage on the lamella.

Vickers micro-hardness tests were performed in a Matsuzawa MXT-α1micro-hardness tester. The tests were applied with 300 g load and holding time of 10 sec. Seven indents were done on sample cross-sections, both parallel and perpendicular to the building direction.

2.2 Computational Methods

In this work, the Thermo-Calc Software Package[16] and its precipitation module (TC-PRISMA)[15] have been used for simulating the precipitation kinetics of the NbC and the Laves phase during post-heat treatments. TC-PRISMA is based on the Langer–Schwartz–Kampmann–Wagner numerical approach[15,16] and can be used to simulate the simultaneous nucleation, growth, and coarsening of precipitates in multi-component systems. The settings used in TC-PRISMA are shown in Table II. The selection of nucleation site types for the Laves phase and NbC was guided by experimental observations and set to grain edges (three-grain junctions) and dislocations or grain boundaries (two-grain junctions) in the BCC matrix, respectively. The available number of nucleation sites depends on the shape and the size of the grains in the precipitation module TC-PRISMA. Assuming that all the grains are equally large tetrakaidecahedra, the boundary area density or edge length density can be calculated. Details of how this density is obtained in TC-PRISMA can be found in Reference 15. By further assuming that the boundary thickness is one atomic layer, the number of nucleation sites, \({N}_{i}\), can then be calculated by

Table II Settings for the TC-PRISMA Simulations
Full size table
$${N}_{i}= {\rho }_{i }{\left(\frac{{N}_{A}}{{V}_{m}^{\alpha }}\right)}^{{i}/{3}} i=2, 1, 0$$
(1)

where \({\rho }_{2}\), \({\rho }_{1}\) , and \({\rho }_{0}\) are grain boundary area density, grain edge length density, and grain corner number density, respectively. \({V}_{m}^{\alpha }\) is the molar volume of the matrix phase and \({N}_{A}\) is the Avogadro number. The number of available nucleation sites at dislocations, \({N}_{d}\), can be calculated by the same expression as in Eq. [1] with the dislocation density, \({\rho }_{d}\).

A grain size of 1.76 µm, with aspect ratio 1, in line with experimental observations of precipitates in regions of equiaxed grains reported by Karlsson et al.,[12] was used. The dislocation density used as input for the calculations of the number of nucleation sites for NbC was taken as 1 × 1014 m−2, in accordance with measurements on an austenitic stainless steel manufactured using L-PBF by Bertsch et al.[19] The interfacial energy plays a crucial role in many areas of materials science, and precipitation reactions including nucleation, growth, and coarsening are no exceptions. In TC-PRISMA, a constant value of the interfacial energy is used for these three steps. In the present work, the interfacial energies for BCC/Laves phase and BCC/NbC were used as fitting parameters, see Table II.

The simulations in TC-PRISMA were performed using the thermodynamic database TCFE10 Steels/Fe-alloys[20] and the mobility database MOBFE5 Steels/Fe-alloys mobility databases.[21]

3 Results and Discussion

3.1 Thermodynamic Calculations

For all simulations in this work, a reduced composition Fe-18.8Cr-0.8Mn-0.9Si-0.02C-0.8Nb (wt. pct) was used to avoid numerical issues in the TC-PRISMA simulations. The calculated equilibrium phase fractions as a function of temperature are shown in Figure 1 for the full composition excluding negligible trace elements (Table I) (Figure 1(a)) and the reduced composition (Figure 1(b)), respectively. From the calculations in Figure 1, it can be confirmed that the phase fraction and temperature stability ranges for the Laves phase and NbC are only marginally affected by the reduction of the composition. However, the driving force for precipitation of NbC increases when using the reduced composition, while the change in driving force for precipitating Laves phase is relatively small. This can be understood from the fact that both Ti and N dissolve in NbC, but not in Laves by a significant amount.

Fig. 1
figure 1

Calculated equilibrium phase fractions as function of temperature for (a) the full composition excluding negligible trace elements (Table I) and (b) the reduced composition (Fe-18.8Cr-0.8Mn-0.9Si-0.02C-0.8Nb) using the thermodynamic database TCFE10[20]

Full size image

3.2 Experimental Characterizations After Heat Treatment

The gas-atomized powder and the as-built microstructure of the L-PBF-processed SS441 were thoroughly characterized in the previous work.[12] It was found that Nb has segregated to grain boundaries in both the as-atomized polycrystalline powder particles and in the as-built microstructure produced by L-PBF-processed material. The as-built microstructure also showed a fine-scaled cellular sub-structure indicative of strong segregation during solidification, in particular of Nb, in accordance with Scheil–Gulliver solidification calculations. The as-built microstructure was fine-grained and consisted of regions with equiaxed and columnar grains with an average grain size calculated from Electron Back Scatter Diffraction (EBSD) data to 1.76 µm. Furthermore, precipitates containing Al, Ti, N, and O were identified. It is suggested that these O-rich particles act as nucleation sites during solidification and provide an effective grain refinement effect for SS441 produced by L-PBF.[12]

After heat treatment for 2 h at the temperatures 850 °C, 900 °C, and 950 °C, the microstructure is still fine-grained see Figure 2(a). Note also that the regions with equiaxed and columnar grains from the as-built microstructure are still observed. Only the microstructure for the 950 °C heat treatment is shown since it is representative also for the microstructures after heat treatment at the temperatures 850 °C and 900 °C. Similar to the heat-treated microstructure characterized in the previous work,[12] Nb-rich precipitates exist at the grain boundaries, especially in the grain junctions, after the heat treatments, see Figure 2(b). These particles were identified by XRD as Laves phase in the case of the heat treatment for 20 minutes at 900 °C.[12] The formation of the Laves phase is further supported by the EDS measurements of the phase compositions and the equilibrium calculations shown in Figure 1(a). Inside the grains as well as at grain boundaries, a large number of fine-sized precipitates are also observed, see Figure 2(c). These are shown in higher magnification in the HAADF-TEM image and EDS maps in Figure 3(a) and are identified as the Nb-rich cubic carbo-nitride (NbC). Although there is some solubility of both Ti and N in NbC, it is still denoted as NbC in the following sections.

Fig. 2
figure 2

SEM images of the microstructure after heat treatment for 2 h at 950 °C; (a) overview of a fine grain structure, (b) Laves phase (Fe2Nb) located at grain edges, and (c) fine-scaled NbC carbides (yellow arrows) inside the ferrite grains and at grain boundaries. Dark spherical particles in micrographs are oxides. All images are taken parallel to the build direction (BD) (Color figure online)

Full size image
Fig. 3
figure 3

STEM images and EDS maps showing (a) the NbC and (b) TiN/oxides and oxides after heat treatment for 2 h at 950 °C. In (a) the precipitates are denoted as NbC for naming consistency even though there is some solubility of Ti and N in NbC

Full size image

The spherical dark particles in Figures 2(b) and (c) were recognized as oxides in the previous work[12] in the as-built and heat-treated microstructures. These spherical particles are here identified as TiN/oxide complexes in the HAADF-STEM image and EDS maps in Figure 3(b). The identification of the TiN/oxide complexes in Figure 3(b) is also supported by the calculation in Figure 1(a), where at higher temperature corundum and TiN are stable together with the liquid phase. The TiN/oxide complexes are expected to form during printing where TiN seems to nucleate on the fine oxides stable in the liquid phase.[22] In the current work, sizes and distribution of these oxide particles do not vary notably in the studied microstructures. Although the TiN particles should be present in all heat-treated microstructures, due to their low fraction they are only occasionally found. Therefore, TiN is not included in the representative heat-treated microstructures in Figures 2, 3, 4, and 5.

Besides precipitation, heat treatment at temperatures above 950 °C resulted in a change in grain size. Larger grains together with regions of fine grains are observed after the heat treatments at 1000 °C, 1050 °C, 1100 °C, and 1150 °C, see Figures 4(a) through (d). The large grains seem related to the interior part of melt-pools, while the regions of columnar grains are still fine-grained (see Figure 4(a)). With increasing temperature, the area fraction of larger grains increases, but few areas of fine grains remains after heat treatment at 1150 °C. A sudden increase in grain size for higher heat treatment temperatures has also been observed in hot rolled AISI SS441.[23] In this case, however, it seems like certain regions of the microstructure are less sensitive to grain coarsening (the originally columnar regions). This could be related to a difference in the precipitation behavior.

Fig. 4
figure 4

SEM images showing the increased area fraction of larger grains (yellow arrows) with increasing temperature after heat treatment for 2 h at (a) 1000 °C, (b) 1050 °C, (c) 1100 °C, and (d) 1150 °C (Color figure online)

Full size image

In Figure 5, SEM images are shown in higher magnification for the heat treatments at 1000 °C and 1100 °C. For all four heat treatment temperatures (1000 °C, 1050 °C, 1100 °C, and 1150 °C), precipitates of Laves and NbC are found. The average size of the Laves phase has increased up to 1000 °C. At higher temperatures, when the solvus temperature of the Laves phase is approached, the phase appears smaller and the area fraction lower, see Figure 5(b). This is in agreement with the calculation in Figure 1(a), where the calculated solvus temperature of the Laves phase is about 1050 °C and the calculated equilibrium fraction of the phase decreases with temperature. It is believed that the grain growth at 1000 °C-1050 °C in Figure 4(a) and (b) does not affect the precipitate nucleation sites. The precipitates (Laves phase, NbC, and oxides) particles distribution at larger grain region at 1000 °C in Figure 5(b) are similar to the ones observed in the grain junctions in fine grain region in Figure 5(a). After heat treatment at 1100 °C, fine elongated Nb/Si-rich precipitates identified as Laves phase precipitates can be observed along the grain boundaries, see Figures 5(c) and (d). The Laves phase shown as particles are scarce after heat treatment at 1100 °C and can only be occasionally detected by SEM in lower magnification. It is possible that the difference in grain growth behavior (see Figures 4(a) through (d)) is related to a difference in Laves phase precipitation in the different parts of the microstructure. It is clear that Laves phase preferably nucleates at grain junctions (see Figures 2(b) and 5(a) and (b) in the initially equiaxed grain regions; in the columnar regions there are less junctions, and the Laves is instead found as fine elongated precipitates along the grain boundaries. It is likely that fine elongated precipitates along the grain boundaries are more effective in hindering grain growth compared to larger ones in the grain junctions. This could lead to the fact that the equiaxed grain regions are more susceptible to grain growth compared to the columnar regions. Furthermore, the decreasing areas of fine-grained regions with heat treatment increasing temperature could be related to the Laves solvus temperature.

Fig. 5
figure 5

SEM images under BSE mode showing the location of the Laves phase, the NbC, and the oxides as dark spherical particles (a) in fine-grained regions at 1000 °C, (b) in larger grain regions at 1000 °C, (c) in fine-grained regions at 1100 °C, and (d) in larger grain regions at 1100 °C

Full size image

The NbC carbides are stable at higher temperatures on the other hand, see Figure 1. The carbides located at the grain boundaries grow larger on behalf of the smaller ones within the grains seen at lower temperature which leads to a larger average NbC radius at higher temperature compared to at temperatures < 950 °C. However, in addition to the Laves phase and NbC discussed above, very fine Nb-rich nano-sized particles are detected within the larger grains after heat treatment at 1100 °C, see Figure 5 (d). These Nb-rich nano-sized particles observed at temperature >1100 °C in Figure 5(d) are likely to be NbC according to the calculation in Figure 1. It is possible that the Laves phase solvus temperature can vary locally due to the chemical segregation in the L-PBF samples. In fact, the Laves solvus temperature is expected to increase up to 1390 °C for a Nb concentration of 2 wt. pct according to equilibrium calculation and may therefore form in the grain boundaries of the ferrite. Furthermore, TiN is occasionally found in all heat-treated microstructures. In addition, in the temperature interval 1100 °C to 1150 °C, MnS is also found occasionally in the heat-treated microstructures. However, due to low amount of the element S (0.006 wt. pct) in the as-built composition, S is not included in the calculation in Figure 1. Excluding S does not have noticeable effect on the equilibrium calculation in Figure 1(a). All measured grain sizes, area phase fractions, precipitate mean radii, area fraction, and grain sizes of the larger grain region are listed in Table III.

Table III Measured Laves Phase and NbC Sizes for the Different Heat Treatments
Full size table

In Figure 6, the micro-hardness values are shown for the material heat treated for 2 h at different temperatures. Overall, the hardness decreases with increasing temperature, regardless whether the measurement was done in parallel or perpendicular to the building direction. The decreasing hardness with temperature is likely an effect of the depletion of Nb in the matrix material due to the formation of Nb-containing precipitates, resulting in a loss of solid-solution strengthening, as well as the increase in grain size. At the same time, a precipitation hardening effect should be present.

Fig. 6
figure 6

Micro-hardness of the as-built and heat treated for 2h materials, parallel and perpendicular to the building direction (BD)

Full size image

3.3 Simulations of the Precipitation Kinetics

The results of the TC-PRISMA simulations using the settings listed in Table II and the reduced composition are presented and discussed in this section. Two sets of input parameters for the TC-PRISMA simulations were applied to study the effect of different nucleation sites at each temperature. In the first set, the NbC precipitates were set to nucleate at grain boundaries and in the second set, they were set to nucleate on dislocations. In Figure 7, the mean radius for the evolution of Laves phase during heat treatment at 900 °C calculated with TC-PRISMA is shown and compared with the experimental sizes determined after heat treatments for 20 min,[12] 2 h, and 10 h. The calculated size of the Laves phase is in fair agreement with the experimentally measured sizes, see Figure 7 . The calculated fraction of Laves phase reaches the equilibrium volume fraction 0.85 pct at 900 °C within a short time. The experimentally measured Laves area fraction also shows a rather constant value over time at 900 °C, see Table III. The measured Laves area fraction is 1.3 pct at 900 °C after 10 h which suggests that the calculated Laves phase fraction is somewhat underestimated in comparison with the experimental measurements. The deviation between experiments and calculations is attributed to experimental errors associated with the challenges of estimating volume phase fractions from two-dimensional area fraction data from micrographs and the uncertainty in selecting a sufficiently large region for the measurements.

Fig. 7
figure 7

Calculated precipitation kinetics for the Laves phase at 900 °C showing the average mean radius of the Laves phase. The results are compared with the measurements of this work as well as with the previous work[12]

Full size image

The calculated mean radii for the Laves and NbC precipitates, and amount of Laves phase, as a function of temperature can be seen in Figure 8. The calculated and experimental radii show good agreement at all temperatures for the Laves phase except at 1050 °C, see Figure 8(a), where the radius is somewhat overestimated by the calculations. The same trend is seen for NbC, see Figure 8(b), where the calculations in the case of nucleation at grain boundaries at 1150 °C, considerably overestimates the measured radius. The other set of calculations, where NbC nucleates at dislocations, on the other hand, underestimates the radii at 1150 °C. The experimentally observed bimodal size distribution of the NbC particles is inherent from the as-built microstructure, where in previous work,[12] Nb-rich precipitates are shown to form at grain boundaries and inside the grains at the cellular structure during the AM process. The calculated radius of the lager-sized grain boundary NbC capture the trends of experimentally observed NbC from 1000 °C to 1150 °C (see Figure 8(b) open symbols) but underestimates experimentally observed NbC radii. The reason can be that during heat treatment at temperatures of 1000 °C to 1050 °C, many of the smaller-sized dislocation NbC precipitates inside the grains (see Figure 3(a) 950 °C NbC by TEM) are too small to be characterized with the current approach. Not until heat treated at higher temperatures, 1100 °C to 1150 °C, do enough of the smaller-sized dislocation NbC precipitates coarsen to a size sufficiently large to be captured with the current approach. The experimental NbC radii become more representative at 1100 °C to 1150 °C and can then be well described by the calculations. The very fine elongated grain boundary Laves phase and the fine Nb-rich particles at 1100 °C to 1150 °C in Figures 5(c) and (d) are neglected in the simulations since their fraction is very small. In addition, Nb-rich precipitates at grain boundaries in the as-built microstructure[12] are not considered in current work, due to limitations in the software on defining the initial state of precipitates particle size distribution in the simulations.

Fig. 8
figure 8

Calculated mean radius for (a) the Laves phase and (b) the NbC carbide, and (c) amount of the Laves phase after heat treatment for 2 h at different temperatures in comparison with the experimental measurements of the mean radii and the area phase fraction

Full size image

The reasons for deviation between experimental data and simulations in Figures 8(a) through (c) may be temperature dependencies on input parameters for the simulations such as interfacial energies which are currently not accounted for or uncertainties in the applied thermodynamic descriptions in the Calphad database. In addition, the increase in driving force for precipitation of NbC when using the reduced composition could play a role. Besides, the deviation in Figure 8(a) at 1050 °C can also be attributed to the fact that the Laves phase has already dissolved at a temperature lower than the Laves solvus temperature (1094 °C) when using the reduced composition for TC-PRISMA in Figure 1(b). In addition, the predicted amount of the Laves phase is somewhat underestimated by the calculations, although the trend with decreasing values with increasing temperatures are captured, see Figure 8(c). This deviation, as mentioned, can also be attributed to the fact that estimating calculated volume fractions from the measured Laves area fractions.

Compared to cast and hot rolled AISI 441, the as-built grain size is much finer.[12] This affects the number of nucleation sites for the Laves phase and the NbC carbides significantly. Furthermore, oxides forming during AM processing[24] may act as heterogeneous nucleation sites and affect the precipitation kinetics during AM processing and post-heat treatments. Consequently, subsequent growth and coarsening of the precipitates are expected, as fewer precipitates will nucleate in a cast and hot rolled AISI 441. The local enrichment of Nb seen in the as-built microstructure[12] due to the micro-segregation during solidification with high cooling rates is expected to accelerate the precipitation kinetics further[14] with respect to the kinetics in the cast and hot rolled material. Comparing the precipitation kinetics of the Laves phase in the L-PBF-processed material with the study by Sello et al.[25] on a hot rolled AISI SS441, an accelerated precipitation kinetic can be concluded. In the present study, a large fraction of the Laves phase has precipitated already after 20 minutes at 900 °C, see Table III, according to experiments. Calculations at 900 °C using the calibrated settings also suggests a rapid increase in Laves phase fraction for the L-PBF-processed material similar to the 900 °C behavior observed experimentally. The precipitation kinetics of the Laves phase in the work by Sello et al.[25] on the other hand is much slower, where at 800 °C, it takes over 1 h to reach a considerable Laves phase fraction. The formation of precipitates in the L-PBF-produced ferritic stainless steel SS441 is expected to influence the mechanical properties, and a complex interplay of the precipitation strengthening, solid-solution strengthening, and the grain growth occurs during the heat-treated conditions. A careful control of the post-heat treatments is therefore of great importance to design high strength materials.

4 Conclusions

The microstructure response of L-PBF-processed AISI 441 during post-heat treatments was studied in detail for the temperature range 850 °C to 1150 °C. The focus was on the precipitation kinetics of the Nb-rich Laves (Fe2Nb) phase and the Nb-rich cubic carbo-nitride (NbC). Based on the precipitates observed in the as-built and heat-treated microstructures, two sets of calculations were performed at each heat-treated temperature to study the effect of different nucleation sites in the TC-PRISMA simulations. The precipitation kinetics was characterized using SEM and TEM and the experimental results were used to calibrate precipitation kinetics simulations using the precipitation module TC-PRISMA. The experimental results show that the Laves phase is still present in the microstructure after heat treatment at 1150 °C which suggests that the solvus temperature in the L-PBF-processed AISI 441 has higher solvus temperature than calculated using the commercial thermodynamic database. Larger grains resulting from grain growth were also observed at heat treatments at temperatures above 1000 °C and the fraction of these larger grains increased with the increase in heat treatment temperature. On the whole, simulation results from the calibrated TC-PRISMA model reproduce the trend of the time evolution of the precipitate mean radii and phase fraction, even though the Laves phase fractions are slightly underestimated by the calculations. In conclusion, the calibrated model reproduces the trends observed experimentally and can thus be used for selecting heat treatment conditions for post-heat treatment of AM ferritic stainless steels. Finally, it is observed that the precipitation kinetics of the Laves phase is enhanced in the L-PBF-processed steel compared to conventionally manufactured ferritic stainless steel. According to micro-hardness at different heat-treated temperatures, a complex interplay of different strengthening mechanisms (precipitation strengthening, solid-solution strengthening, and grain boundary strengthening) is involved during the post-heat treatments. This should be accounted for when optimizing post-heat treatments for the AM materials.