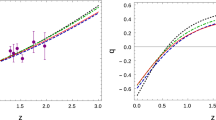
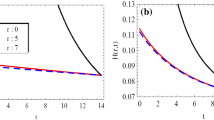
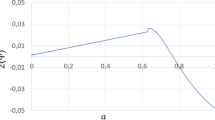
Abstract
This paper is devoted to the canonical analysis of inhomogeneous Dark Energy Model and the model of limiting curvature that were proposed recently by Chamseddine and V. Mukhanov. We argue these models are well defined and have similar properties as a system consisting from general gravity action and action for incoherent dust.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
A.H. Chamseddine and V. Mukhanov, Mimetic Dark Matter, JHEP 11 (2013) 135 [arXiv:1308.5410] [INSPIRE].
A.O. Barvinsky, Dark matter as a ghost free conformal extension of Einstein theory, JCAP 01 (2014) 014 [arXiv:1311.3111] [INSPIRE].
A.H. Chamseddine, V. Mukhanov and A. Vikman, Cosmology with Mimetic Matter, JCAP 06 (2014) 017 [arXiv:1403.3961] [INSPIRE].
L. Sebastiani, S. Vagnozzi and R. Myrzakulov, Mimetic gravity: a review of recent developments and applications to cosmology and astrophysics, arXiv:1612.08661 [INSPIRE].
A.H. Chamseddine and V. Mukhanov, Inhomogeneous Dark Energy, JCAP 02 (2016) 040 [arXiv:1601.04941] [INSPIRE].
M. Chaichian, J. Kluson, M. Oksanen and A. Tureanu, Mimetic dark matter, ghost instability and a mimetic tensor-vector-scalar gravity, JHEP 12 (2014) 102 [arXiv:1404.4008] [INSPIRE].
O. Malaeb, Hamiltonian Formulation of Mimetic Gravity, Phys. Rev. D 91 (2015) 103526 [arXiv:1404.4195] [INSPIRE].
A.H. Chamseddine and V. Mukhanov, Resolving Cosmological Singularities, arXiv:1612.05860 [INSPIRE].
A.H. Chamseddine and V. Mukhanov, Nonsingular Black Hole, arXiv:1612.05861 [INSPIRE].
R.L. Arnowitt, S. Deser and C.W. Misner, The Dynamics of general relativity, in Gravitation: An Introduction to Current Research, L. Witten ed., John Wiley & Sons Inc., New York U.S.A. and London U.K. (1962), pp. 227-265, reprinted as R.L. Arnowitt, S. Deser and C.W. Misner, Republication of: The dynamics of general relativity, Gen. Rel. Grav. 40 (2008) 1997 [gr-qc/0405109] [INSPIRE].
E. Gourgoulhon, 3 + 1 formalism and bases of numerical relativity, gr-qc/0703035 [INSPIRE].
T. Thiemann, Solving the Problem of Time in General Relativity and Cosmology with Phantoms and k-Essence, astro-ph/0607380 [INSPIRE].
J.D. Brown and K.V. Kuchar, Dust as a standard of space and time in canonical quantum gravity, Phys. Rev. D 51 (1995) 5600 [gr-qc/9409001] [INSPIRE].
S. Ramazanov, F. Arroja, M. Celoria, S. Matarrese and L. Pilo, Living with ghosts in Hořava-Lifshitz gravity, JHEP 06 (2016) 020 [arXiv:1601.05405] [INSPIRE].
R.P. Woodard, Ostrogradsky’s theorem on Hamiltonian instability, Scholarpedia 10 (2015) 32243 [arXiv:1506.02210] [INSPIRE].
Open Access
This article is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
ArXiv ePrint: 1701.08523
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Klusoň, J. Canonical analysis of inhomogeneous Dark Energy Model and theory of limiting curvature. J. High Energ. Phys. 2017, 31 (2017). https://doi.org/10.1007/JHEP03(2017)031
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/JHEP03(2017)031