1 Introduction

The evidences of dark matter are of many kinds. We can roughly divide the “dark matter phenomena” in two categories: global dark matter effects, which consist in unexpected values of some cosmological parameters (the deceleration parameter [1, 2], the deuterium abundance, the power spectrum of CMB anisotropies, etc.), and local dark matter effects, appearing in observations of astronomical objects (the galaxies rotation curves [3], the virial of galaxy clusters [4], gravitational lensing [5], etc.). In both cases are exclusively gravitational phenomena, anomalies of gravitation with respect to what we expect: some of them derive directly from the study of a gravitationally interacting system, as a galaxy, or from the space-time dynamics, as the deceleration parameter; for some others the derivation is indirect, like for the deuterium abundance, which, anyway, depends on “dark matter contributions”, i.e. on gravitation effects that cannot be associated to a distribution of baryonic matter. Several followed hypotheses on dark matter assume that it could also interact weakly, at least, but such “weakly dark matter effects” have not been observed up to now [6, 7].

The evidences of dark energy are restricted to more specific phenomena. There are only global dark energy effects, which consist in unexpected values of some cosmological parameters, due to a negative deceleration parameter [1, 2]. Again, it is a purely gravitational phenomenon, consisting in an unexpected distortion of the space-time metric. Dark energy is often described as an exotic kind of energy having a negative pressure, or as a “vacuum energy”; these assume some non gravitational interaction. However, none of such new non gravitational interactions have been observed yet, and as for the dark matter, all our knowledge about the dark energy comes just from gravitational phenomena.

In the last 20 years, several lines of research have been opened that seek to study some essentially relativistic effects in cosmology. MOND theories are an attempt in this direction, but they actually didn’t give rise to a good matching with data [8,9,10]. Rather, we will consider rather the attempts to obtain unusual effects from the usual General Relativity.

A general relativistic explanation of the unexpected distortion of the space-time tensor, even without the presence of real energy-matter, would provide the justification of at least a part of dark matter and/or dark energy effects. A point is that the formalism usually used to show these effects is not truly general relativistic. Especially for local effects, it is adopted the Newtonian approximation, while for global ones, one assumes a Friedmannian model for the expansion, with matter and curvature assumed to be homogeneous, which could be an oversimplification. By now, we will refer to the Newtonian approximation, for galaxies, and the homogeneous Friedmannian model, for the universe expansion, as “the standard calculations”.

There are three principal lines of research that try to explain (at least a fraction of) dark matter and/or dark energy as a difference between the standard calculations and a more precise general relativistic model. One of them started form a deep analysis of the coordinate systems adopted in observational general relativity [11,12,13,14,15,16,17]. Recently it had some confirmations by observations on the rotation curves of our galaxy [18, 19]. Another line of research explores the backreaction effects, which means the discrepancy between the spatial curvature due to an averaged quantity of matter, and the averaged spatial curvature due to an inhomogeneous quantity of matter [20, 21]; it doesn’t vanish in general since the Einstein Equations are not linear. This effects needs averaging on large dominions, and arise the standard deviation of the spatial curvature.

The third line considers two main ingredients: the inhomogeneity of the matter distribution, and the delay of the space-time distortions that it generates. In the universe, the matter is inhomogeneous and anisotropic, so that the Birkhoff Theorem cannot be applied in general; the distortions due to the inhomogeneity do not cancel out. The influence of the external objects on the dynamic of galaxies was recently confirmed in [22], which allows also a quantitative comparison. The Cosmological Principle states that, at large scale, the matter distribution is near to a homogeneous one, so that we must remember that globally the matter inhomogeneities are quite small. However, the second ingredient, the retarded distortions, provides a magnification effect, for which the resulting space-time distortion is not negligible even if its source is small. This magnification is due to the fact that the distortions we feel nowadays were generated by matter sources in the past, when the matter density was greater, because of universe expansion. The actual distortion is a superposition of all retarded distortions from all past times, which predictably have a singularity at the Big Bang time. However, there is also a decrease with the distance. It needs a precise calculation to see if it prevails the magnification or the reduction, and [23, 24] highlighted that the magnification dominates.

These ideas were presented in nuce in the article [23], which however had several lacks. It doesn’t work in a general relativistic context. The authors adopted a linearized gravity model on a Minkowskian background, where the simulated expansion of the universe is forced by hand, and an effective FLRW metric is imposed with a “compatibility condition”. In [24] we firstly developed a truly general relativistic framework apt for this line of investigation. Since the matter inhomogeneity is small according to the Cosmological Principle, we considered it as a first order perturbation on a homogeneous FLRW background metric. We derived the linearized Einstein Equations, which returns the metric distortion, at the first order. Choosing the suitable gauge, these result to be wave equations, so that the metric distortion is retarded, traveling at the speed of light. This framework was then tested on a specific universe, which was not a realistic one, but a model chosen such that the linearized Einstein Equations have constant coefficients, with the only aim to make them easier to be solved. We obtained an explicit formula for the retarded gravitational potentials. Averaging the resulting metric, we got an evaluation of the global effects of such perturbative correction, which manifested the magnification effect we hoped, and was able to explain a non negligible fraction of the dark matter and the dark energy.

In the present article, we will push forward such treatment in a substantial way, by applying the method to a general realistic background universe, with any possible combination of matter and energy components. The main consequence is that the linearized Einstein Equations will not have constant coefficients, in general. From those, we will obtain an averaged metric, which can be compared with the metric assumed by the Cosmological Standard Model. We will obtain a set of consistency conditions, which reduce the acceptability of the possible universe. For acceptable universes, the gap between our averaged metric and the standard calculation provides some quantity of “fictitious” matter and dark energy. We will apply these formulas to the case of the real universe, which depends in general on three parameters: the real quantity of radiation, of matter, and of dark energy (where the last one can eventually be zero, if all the dark energy can be explained as fictitious). Substituting the most recent cosmological data, two parameters will be fixed. The last one will leave a range of possible solutions, some of which looks of particular interest.

The paper is structured as follows. In Sect. 2 we outline the perturbative method, defining the background universe and the perturbed universe, and showing the fictitious matter and dark energy from the gap between them. In Sect. 3 we recall the linearized Einstein Equations from [24]. In Sect. 4 we average the metric perturbations, ignoring temporarily their precise development, and we get a formula for the fictitious matter and dark energy. We reduce the PDEs for the evolution of the metric perturbations to ODEs, with an averaging procedure. In Sect. 5 we solve such ODEs with a single-component approximation, finding also some “Selfconsistency Conditions” for the components that can fill the universe. In Sect. 6 we apply all the previous formulas to our universe, getting an explicit model, which will result to leave a free parameter. The model is numerically solved in Sect. 7, finding a set of solutions depending on the free parameter.

2 Framework and notations

We will adopt the following terminology. With “radiation” we mean any component of the universe with a pressure \(p=w\rho \) with \(w=\frac{1}{3}\). We call “matter” any component with \(w=0\); and “dark energy” any one with \(w=-1\). A component with \(w<0\) will be called “exotic”.

Moreover, we call “total matter” the quantity of matter \(\Omega _{M0}\), which is required in the Cosmological Standard Model in order to explain the observed deceleration parameter; analogous for the “total dark energy” \(\Omega _{\Lambda 0}\). We call “dark matter” \(\Omega _{DM0}\) the part of total matter that is not observed, unless indirectly via gravitational phenomena. The observed part is essentially the “baryonic matter” \(\Omega _{BM0}\cong \Omega _{M0}-\Omega _{DM0}\).

2.1 Perturbative method

Let us consider a universe filled with any choice of components, each one characterized by its constant w. \(\rho =\sum _w\rho _w\) is the true matter-energy density. Only the matter component \(\rho _M({\underline{x}};\tau )\) can be inhomogeneous. Let us call its homogeneous partFootnote 1

$$\begin{aligned} {\bar{\rho }}(\tau ):=\min _{{\underline{x}}}\rho ({\underline{x}};\tau ). \end{aligned}$$
(2.1)

Let now consider a background universe, approximating our true universe at zero order, so assuming it filled with a perfectly homogeneous \({\bar{\rho }}\). We assume this universe to be spatially flat, in order to keep all calculations as simple as possible. For the same reason, we assume irrotational matter. Then, for a more realistic description of the universe, we perform a first order perturbative. The perturbation of the energy-matter, which in fact consists only on matter, is

$$\begin{aligned} {\tilde{\rho }}({\underline{x}};\tau ):=\rho ({\underline{x}};\tau ) -{\bar{\rho }}(\tau )=\rho _M({\underline{x}};\tau )-{\bar{\rho }}_M(\tau ). \end{aligned}$$
(2.2)

Notice that this inhomogeneity is always non negative. In a symmetric way, we could also define

$$\begin{aligned} {\bar{\rho }}(\tau ):=\max _{{\underline{x}}}\rho ({\underline{x}};\tau ); \end{aligned}$$
(2.3)

in such a case, \({\tilde{\rho }}\) would be non positive. It is a matter of convenience to fix the choice with always positive or negative \({\tilde{\rho }}\).

2.2 Background evolution

We adopt the most minus signature and natural units, so that \(c=1\). The background metric is

$$\begin{aligned} {\bar{g}}_{\mu \nu }(\tau )dx^{\mu }\otimes dx^{\nu }=a(\tau )^2(d\tau \otimes d\tau -\delta _{ij}dx^i\otimes dx^j). \end{aligned}$$
(2.4)

Any quantity has associated an “unperturbed” (or “averaged”) version \({\bar{Q}}\), computed using the background metric \({\bar{g}}_{\mu \nu }\), and a “perturbed” (or “true”) version Q computed using the real metric \(g_{\mu \nu }\). Its “perturbation” is the difference \({\tilde{Q}}:=Q-{\bar{Q}}\), which we consider negligible beyond the first order.

\(\tau \) is the conformal time for the unperturbed metric. The dot will always denote derivation with respect to the conformal time: \({\dot{Q}}:=\partial _{\tau }Q\). \(a(\tau )\) is the unperturbed expansion parameter, so that \({\bar{t}}=\int a(\tau )d\tau \) is the usual (unperturbed) time. \(H(\tau ):=\frac{{\dot{a}}}{a}\) is the Hubble parameter for the unperturbed model. \(\tau \), a and H are written without the overline, with abuse of notation, for better readability. Their perturbed versions will be \(\mathbf{a }\) and \(\mathbf{H }\).

\(\tau _0\) is the actual instant for the unperturbed universe, s.t. \(a(\tau _0)=1\). \(t_0\) is the present for the true model, s.t. \(\mathbf{a }(t_0)=1\). The “0” label means evaluation in the present time, both for unperturbed and perturbed quantities. Notice that in general \(t_0\ne t(\tau _0)\), again with a little abuse of notation.

\(a(\tau )\) solves the Friedmann Equations

$$\begin{aligned} {\left\{ \begin{array}{ll} 3H^2=8\pi Ga^2{\bar{\rho }} \\ \dot{{\bar{\rho }}}=-3H({\bar{\rho }}+p), \end{array}\right. } \end{aligned}$$

with \(p(\tau )=\sum _wp_w(\tau )=\sum _ww{\bar{\rho }}_w(\tau )\). From the second Friedmann Equation we know

$$\begin{aligned} {\bar{\rho }}_w(\tau )={\bar{\rho }}_{w0}a(\tau )^{-3(1+w)}. \end{aligned}$$

We can describe the background components as

$$\begin{aligned} {\bar{\Omega }}_w(\tau ):=a(\tau )^2\frac{{\bar{\rho }}_w(\tau )}{{\bar{\rho }}_0}={\bar{\Omega }}_{w0}a(\tau )^{-1-3w} \end{aligned}$$
(2.5)

s.t. \({\bar{\rho }}_0=\frac{3H_0^2}{8\pi G}\), so \(\sum _w{\bar{\Omega }}_{w0}=1\). The first Friedmann Equation says now that \(H(\tau )^2=H_0^2\sum {\bar{\Omega }}_w(\tau )\), from which we get a ODE for the evolution of a

$$\begin{aligned} \left( \frac{{\dot{a}}}{H_0}\right) ^2=\sum _w{\bar{\Omega }}_{w0}a^{1-3w}. \end{aligned}$$
(2.6)

We define \(a(\tau )\) as a maximal solution of this ODE, with maximal domain \((\tau _I; \tau _F)\), eventually unbounded. The initial condition for a is provided by the request that \(\lim _{\tau \rightarrow \tau _I}a(\tau )=0\). The radius of the visible universe results to be \(R(\tau )=\tau -\tau _I\); notice that it is always infinite if \(\tau _I=-\infty \).

2.3 Comparison with the cosmological standard model

Averaging it \({\tilde{\rho }}\) on the whole space, we get \(\langle {\tilde{\rho }}\rangle (\tau )\). The average of a certain \({\mathcal {S}}\) on the whole \({\underline{x}}\in {\mathbb {R}}^3\) is defined as the average on some increasing sequence of compact domains \({\mathcal {D}}\subset {\mathbb {R}}^3\) filling the whole space in the limit

$$\begin{aligned} \langle {\mathcal {S}}\rangle :=\lim _{{\mathcal {D}} \rightarrow {\mathbb {R}}^3}\langle {\mathcal {S}}\rangle _{\mathcal {D}}. \end{aligned}$$

The exact process of averaging is described in [25]. Since we need the average on the whole space, we perform the averaging prescription called \(J({\mathcal {S}}, \rho , V_0, A, B_s, \Delta B_s)\) with the thickness \(\Delta B_s\) tending to infinity, and with trivial weight \(\rho \equiv 1\). The choice of B and \(B_s\) are hence irrelevant, and we take \(V:=A:=\tau \). Indeed, we do not need a lightlike gradient for V, as it is prescribed in [25] for averaging cosmological observables: a set of measures suffers from the delay of information, due to the speed of light, but the quantities \(\rho \) or \(g_{\mu \nu }\) we need to average are not measures, but rather inhomogeneous fields that we want to consider as they were homogeneous, at a certain instant of the time foliation. Moreover, the relativistic delay of information is already accomplished by the study of the retarded potentials, as in Sect. 3. For these reasons, we choose a time section for V.

As we will see in Sect. 4, the space-time metric will have form \(g_{\mu \nu }=a^2[(1+2\Psi )d\tau \otimes d\tau +(-1+2\Psi )\delta _{ij}dx_i\otimes dx_j]\). Its determinant is \(g=-a^8(1-4\Psi )+o(\Omega _{IM0})\), and we can rewrite the factors in \(J({\mathcal {S}}, 1, \tau _0, \tau , B_s, \Delta B_s\rightarrow \infty )\) as \(n^{\mu }\nabla _{\mu }\Theta (V_0-V)=\delta (V_0-V)\frac{\partial ^{\mu }A\partial _{\mu }V}{\sqrt{|\partial _{\nu }A\partial ^{\nu }A|}}=\delta (V_0-V)\sqrt{|g^{\mu \nu }\partial _{\mu }V\partial _{\nu }V|}\), where \(\partial _{\mu }V=\delta _{\mu \tau }\) and \(g^{\tau \tau }=\frac{1}{a^2(1+2\Psi )}\). Thus we have

$$\begin{aligned}&J({\mathcal {S}}, \rho \equiv 1, V_0:={\bar{t}}_0, A:={\bar{t}}, B_s, \Delta B_s\rightarrow \infty )\\&\quad =\int d^4x\sqrt{-g}{\mathcal {S}}\overbrace{\rho }^{1}n^{\mu }\nabla _{\mu }\Theta (V_0-V)\\&\quad \overbrace{\Theta (B_s+\Delta B_s-B)\Theta (B-B_s)}^{1}\\&\quad =\int d^4x a^4\sqrt{1-4\Psi +o(\Omega _{IM0})}{\mathcal {S}}\frac{\delta (\tau _0-\tau )}{a\sqrt{1+2\Psi }}\\&\quad =a(\tau )^3\int {\mathcal {S}}({\underline{x}}; \tau )[1-3\Psi ({\underline{x}}; \tau )]d^3{\underline{x}}|_{\tau =\tau _0}+o(\Omega _{IM0}). \end{aligned}$$

The \(a^3\) factor is simplified dividing by the volume \(J(1, \rho , V_0, A, B_s, \Delta B_s)\). Thus, for a first order calculation, this cosmological average is equal to the average of \({\mathcal {S}}-3\Psi {\mathcal {S}}\) on a usual Euclidean metric. Notice that the second term vanishes whenever \({\mathcal {S}}\) is a first order quantity, as it will be throughout this article.

We can define the “inhomogeneous matter” as a part of the total matter component

$$\begin{aligned} \Omega _{IM}(\tau ):=\frac{\langle {\tilde{\rho }}\rangle (\tau )}{\rho _0}=\frac{8\pi G}{3\mathbf{H }_0^2}\langle {\tilde{\rho }}\rangle (\tau ). \end{aligned}$$
(2.7)

The Cosmological Standard Model measures the cosmic components via the observed deceleration parameter

$$\begin{aligned} {\left\{ \begin{array}{ll} {\sum }_w\Omega _{w0}=1 \\ \frac{1}{2}{\sum }_w(1+3w)\Omega _{w0}=q_0:=-\frac{\partial _t^2\mathbf{a }_0}{\mathbf{H }_0^2}, \end{array}\right. } \end{aligned}$$
(2.8)

but it assumes a homogeneous \(\rho \). Since it is not our case, \(\mathbf{a }\) will be obtained by just an adaptation of the true space-time metric to a FLRW one

$$\begin{aligned} \langle g_{\mu \nu }\rangle dx^{\mu }\otimes dx^{\nu }:=dt\otimes dt-\mathbf{a }(t)\delta _{ij}dx^i\otimes dx^j. \end{aligned}$$
(2.9)

This provides a distortion of the expansion law, so that in general \(\mathbf{a }(t)\ne a({\bar{t}})\), \(q_0\ne -\frac{\ddot{a}}{H_0^2}\), and \(\Omega _{w0}\ne {\bar{\Omega }}_{w0}\). To fit the two conditions (2.8), two more parameters are needed. Interpreting the distortion as the unexpected presence of matter and dark energy, we will see an effect of “fictitious matter and dark energy”. We evaluate them as \(\Omega _{FM0}\), \(\Omega _{F\Lambda 0}\).

Remark 1

Since they come from a global evaluation and we used a first order approximation, these fictitious components will result to be proportional to the total perturbation \(\Omega _{IM0}\). Thus, these global effects do not depend on the spatial distribution of the matter inhomogeneities, but only on their total amount.

The matter and the dark energy components used in the CSM have a “true” and a fictitious part

$$\begin{aligned} \Omega _{M0}:=\Omega _{TM0}+\Omega _{FM0},\quad \Omega _{\Lambda 0}:=\Omega _{T\Lambda 0}+\Omega _{F\Lambda 0}. \end{aligned}$$
(2.10)

The other components are all “true”. The “true” parts must be proportional to the same components of the background universe

$$\begin{aligned} \Omega _{Tw0}:=\frac{{\bar{\Omega }}_{w0}}{\sum _{w'}\Omega _{Tw'0}}= \frac{{\bar{\Omega }}_{w0}}{1-\Omega _{FM0}-\Omega _{F\Lambda 0}}, \end{aligned}$$
(2.11)

with the exception of matter, for which we have to add again the inhomogeneous part

$$\begin{aligned}&\Omega _{TM0}=\frac{{\bar{\Omega }}_{M0}}{1-\Omega _{FM0}- \Omega _{F\Lambda 0}}+\Omega _{IM0}\nonumber \\&\quad :=\Omega _{HM0}+\Omega _{IM0}:=\Omega _{BM0}+\Omega _{TDM0}. \end{aligned}$$
(2.12)

Remember \(\Omega _{IM0}\) can be considered as positive or negative. In the second case, the homogeneous approximation \({\bar{\rho }}\) is a rounding up, so that \(\Omega _{HM0}>\Omega _{TM0}\).

Some of the true matter must be the baryonic matter we know to exists. If there is still some part left, it is “true dark matter” \(\Omega _{TDM0}\). It is some kind of matter that actually exists, which gravitational action is not just a relativistic effect, but that is not a directly observable matter, like primordial black holes, neutron stars, and so on and so forth.

2.4 Classifying possible results

We can apply this framework to a universe filled by any choice of components \(\{w\}\).

Definition 1

We will call “selfconsistent” a choice for which

  • all calculations return a finite result;

  • the linearized Einstein Equations give a unique solution;

  • the perturbative method is justified by small enough perturbations.

We can write the last condition as

$$\begin{aligned} {\left\{ \begin{array}{ll} |{\tilde{g}}_{\mu \nu }|\ll |g_{\mu \nu }| \\ |\Omega _{IM0}|\ll \Omega _{TM0}, \end{array}\right. } \end{aligned}$$

where the second condition means that the Cosmological Principle holds.

Definition 2

We will call “acceptable” a choice for which

$$\begin{aligned} {\left\{ \begin{array}{ll} \forall w: 0\le \Omega _{Tw0}\le 1 \\ \Omega _{TDM0}\le 0. \end{array}\right. } \end{aligned}$$

The second part states that all the baryonic matter we see is really existing, so it is included in the model.

Remark 2

Notice that the fictitious components can be negative, and such a case means that the dark matter and/or the dark energy is not explained at all, but rather its quantity is more than what is predicted by the CSM.

Definition 3

We will call “good” the choices for which both the dark matter and the dark energy are explained, at least for some fraction, i.e.

$$\begin{aligned} {\left\{ \begin{array}{ll} \Omega _{TDM0}<\Omega _{DM0} \\ \Omega _{T\Lambda 0}<\Omega _{\Lambda 0}. \end{array}\right. } \end{aligned}$$

Even better choices are whose which fully explain the dark matter and/or the dark energy, i.e. \(\Omega _{TDM0}=0\), \(\Omega _{T\Lambda 0}=0\).

3 Linearized Einstein equations

Let us summarize one of the main results of [24].

Theorem 3.1

The linearized Einstein Equations admit at first order a solution

$$\begin{aligned} g_{\mu \nu }({\underline{x}};\tau )=a(\tau )^2\left( \begin{matrix} 2A+1 &{} -\vec {\nabla }B \\ -\vec {\nabla }B &{} (2C-1)\delta _{ij} \end{matrix}\right) , \end{aligned}$$
(3.1)

in the harmonic gauge

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{A}}+4HA+\nabla ^2B+3{\dot{C}}=0 \\ A+{\dot{B}}+2HB=C, \end{array}\right. } \end{aligned}$$
(3.2)

where the “metric perturbations” A, B, C follow the PDEs

$$\begin{aligned} {\left\{ \begin{array}{ll} \Box A -2H{\dot{A}}+2({\dot{H}}-2H^2)A=4\pi Ga^2{\tilde{\rho }} \\ \Box B -2H{\dot{B}}+2({\dot{H}}-2H^2)B=16\pi Ga^2q \\ \Box C -2H{\dot{C}}-2{\dot{H}}A=4\pi Ga^2{\tilde{\rho }}. \end{array}\right. } \end{aligned}$$
(3.3)

The box operator denotes the flat d’Alembertian

$$\begin{aligned} \Box :=\delta _{ij}\partial _i\partial _j-\partial _{\tau }^2. \end{aligned}$$

The source \(q({\underline{x}};\tau )\) has nothing to do with the deceleration parameter \(q_0\), but it is an expression for the (irrotational) velocity field

$$\begin{aligned} \vec {\nabla }q:=\vec {q}:=({\bar{\rho }}+p)\vec {v}. \end{aligned}$$

A general solution of the linearized Einstein Equations has also a wave term

$$\begin{aligned} \Box {\tilde{g}}_{\mu \nu }-2H\dot{{\tilde{g}}}_{\mu \nu } +2({\dot{H}}-2H^2){\tilde{g}}_{\mu \nu }=0; \end{aligned}$$

but we will not consider it, since we are seeking for selfconsistent choices, so we want that the linearized Einstein Equations have a unique solution. From now on, we will call as “the linearized Einstein Equations” the system (3.3).

Near \(\tau _I\), the matter inhomogeneities cannot have yet generated the metric perturbations A, B, C. For this reason, as initial conditions for (3.3) we ask that A, B, C are zero at \(\tau _I\).

4 Newtonian gauge

4.1 Gauge-invariant quantities

In order to get effective parameters \(\Omega _{FM0}, \Omega _{F\Lambda 0}\) with a physical meaning, we must show their gauge independence. In perturbative cosmology, the gauge represents a map which identifies points of the background manifold with those of the physical manifold, so that the metric perturbation \({\tilde{g}}_{\mu \nu }:=g_{\mu \nu }-{\bar{g}}_{\mu \nu }\) is well defined (see [26, §4]). Hence, the gauge is a different matter from the coordinates choice in GR; in particular, a gauge change \(x^{\mu \prime }:=x^{\mu }+\xi ^{\mu }(x)\) has \(\xi ^{\mu }\) of a first order in perturbation.

Since we want to use only gauge-invariant fields, we consider the Bardeen’s potentials, that for a metric as (3.1) have the form

$$\begin{aligned} \Psi&=A+{\dot{B}}+HB \nonumber \\ \Phi&=C-HB. \end{aligned}$$
(4.1)

Notice that the second gauge condition (3.2) guarantees that

$$\begin{aligned} \Psi \equiv \Phi . \end{aligned}$$
(4.2)

A crucial observation is that the Bardeen’s potentials result to be the components of metric perturbation once it is expressed in Newtonian gauge.

Lemma 4.1

Via the transformation \(\tau '=\tau -B({\underline{x}};\tau ),\) the metric \(g_{\mu \nu }\) is expressed in the Newtonian gauge as

$$\begin{aligned} g_{\mu '\nu '}=a(\tau ')^2\left( \begin{matrix} 2\Psi +1 &{} \vec {0} \\ \vec {0} &{} (2\Psi -1)\delta _{ij} \end{matrix}\right) , \end{aligned}$$
(4.3)

where the gravitational potential \(\Psi \) coincides to both the Bardeen’s potentials.

Hence, from now on we will use this gauge, without writing the primes. The gauge-invariance of its components guarantees the gauge-independence of the following calculations.

Notice that the newtonian gauge has some nice properties, for our purposes: it is already diagonal, while we want to compare its average to a FLRW metric, hence a diagonal one. With another gauge choice, e.g. the harmonic one, the off-diagonal terms would vanish just for the averaging procedure, which would be acceptable but less elegant. The framework of “fake dark matter from GR” finds dark matter effects from the comparison between a “usual” model, i.e. a Newtonian one for local DM and a Friedmannian one for global DM, and a “true” inhomogeneous model; such comparison result to be more natural if the true model has a diagonalized metric, since both the Newtonian approximation of GR and the FLRW metric are diagonal.

4.2 Averaging the metric

What we will compare with the CSM is just the average of the metric, since the metric itself is not homogeneous and never allow for an exact equivalence. Such an average depends only on time

$$\begin{aligned} \langle g_{\mu \nu }\rangle =a^2\left( \begin{matrix} 2\langle \Psi \rangle +1 &{} \vec {0} \\ \vec {0} &{} (2\langle \Psi \rangle -1)\delta _{ij} \end{matrix}\right) , \end{aligned}$$
(4.4)

where we know

$$\begin{aligned} \langle \Psi \rangle&=\langle A\rangle +\langle {\dot{B}}\rangle +H\langle B\rangle =\langle C\rangle -H\langle B\rangle . \end{aligned}$$
(4.5)

Now we recall another result from [24]. Let us consider the Green functions for (3.3)

$$\begin{aligned} {\mathcal {L}}G_{\tau '}({\underline{x}};\tau )&= \delta ^{(3)}({\underline{x}})\delta (\tau -\tau ') \nonumber \\ {\mathcal {L}}^CG^C_{\tau '}({\underline{x}};\tau )&= \delta ^{(3)}({\underline{x}})\delta (\tau -\tau '), \end{aligned}$$
(4.6)

where the second-order operators for gravitational waves are defined:

$$\begin{aligned} {\mathcal {L}}(\tau )&:=\Box -2H(\tau )\partial _{\tau }+2 \left( {\dot{H}}(\tau )-2H(\tau )^2\right) \nonumber \\ {\mathcal {L}}^C(\tau )&:=\Box -2H(\tau )\partial _{\tau }. \end{aligned}$$
(4.7)

Notice that, for such homogeneous operators, the Green functions are completely described by the dependence on \({\underline{x}}\). E.g. \(G_{\tau '}({\underline{x}};\tau )\) represents the retarded potentials for \(A({\underline{x}}; \tau )\) generated by a delta source localized at the point \({\underline{0}}\) and at the instant \(\tau '\).

Lemma 4.2

Let us assume the separation of variables for the matter inhomogeneity

$$\begin{aligned} {\tilde{\rho }}({\underline{x}};\tau ):={\tilde{\rho }}_0({\underline{x}})T(\tau ). \end{aligned}$$
(4.8)

Then we can express the average of metric distortions as follows

$$\begin{aligned} \langle A\rangle (\tau )=4\pi G\langle {\tilde{\rho }}_0 \rangle u_A(\tau )=\frac{3}{2}\Omega _{IM0}H_0^2u_A(\tau ), \end{aligned}$$
(4.9)

s.t.

$$\begin{aligned} u_A(\tau ):=\int _{|{\underline{r}}|<R(\tau )} \int _{\tau _I}^{\tau }G_{\tau '}({\underline{r}};\tau ) a(\tau ')^2T(\tau ')d\tau 'd^3{\underline{r}}. \end{aligned}$$
(4.10)

Proof

\({\mathcal {L}}\) is a linear operator, hence the field generated by a source \(4\pi G{\tilde{\rho }}\) can be expressed as the superposition of all Green functions, generated from any point \({\underline{x}}\in {\mathbb {R}}^3\) of the space and at any times \(\tau \) after \(\tau _I\).

$$\begin{aligned} A({\underline{x}}; \tau )&=\int _{\tau _I}^{\tau }d\tau '\int _{{\mathbb {R}}^3}d^3{\underline{x}}' G_{\tau '}({\underline{x}}-{\underline{x}}'; \tau )4\pi Ga(\tau ')^2{\tilde{\rho }}({\underline{x}}'; \tau ') \\&=4\pi G\int _{|{\underline{x}}-{\underline{x}}'|\le \tau -\tau _I}{\tilde{\rho }}_0({\underline{x}}')\\&\quad \times \left[ \int _{\tau _I}^{\tau }G_{\tau '}({\underline{x}}-{\underline{x}}'; \tau )a(\tau ')^2T(\tau ')d\tau '\right] d^3{\underline{x}}' \\&=4\pi G\int _{|{\underline{r}}|\le R(\tau )}{\tilde{\rho }}_0({\underline{r}}+{\underline{x}})\\&\quad \times \left[ \int _{\tau _I}^{\tau }G_{\tau '}({\underline{r}}; \tau )a(\tau ')^2T(\tau ')d\tau '\right] d^3{\underline{r}}; \end{aligned}$$

where we exploited the causality of wave equations in the second passage, and the isotropy of G w.r.t. \({\underline{r}}\) in the third passage.

Now we average A on a region \({\mathcal {D}}\). As we saw in Sect. 2.3, since it is a first order quantity its average can we written at the first order as

$$\begin{aligned} \langle A\rangle _{{\mathcal {D}}}(\tau )&=\frac{1}{|{\mathcal {D}}|}\int _{{\mathcal {D}}}A({\underline{x}}; \tau )d^3{\underline{x}} \\&=4\pi G\int _{|{\underline{r}}|<R(\tau )}\left[ \frac{1}{|{\mathcal {D}}|} \int _{{\mathcal {D}}}{\tilde{\rho }}_0({\underline{r}}+{\underline{x}})d^3{\underline{x}}\right] \\&\quad \times \left[ \int _{\tau _I}^{\tau }G_{\tau '}({\underline{r}}; \tau )a(\tau ')^2T(\tau ')d\tau '\right] d^3{\underline{r}}; \end{aligned}$$

where we exchanged the integrals in \({\underline{r}}\) and \({\underline{x}}\).

For \({\mathcal {D}}\rightarrow {\mathbb {R}}^3\), the integral in \({\tilde{\rho }}_0\) becomes \(\langle {\tilde{\rho }}_0\rangle \) and is pulled out, so that the remaining integral coincides with the definition of \(u_A\). \(\square \)

Corollary 4.3

The separation of variables does not hold exactly for A,  but let we can approximate

$$\begin{aligned} A({\underline{x}};\tau )\propto u_A(\tau ). \end{aligned}$$
(4.11)

Then,  in the same way

$$\begin{aligned} \langle C\rangle (\tau )=\frac{3}{2}\Omega _{IM0}H_0^2(2u_{AC}(\tau )+u_C(\tau )), \end{aligned}$$
(4.12)

s.t.

$$\begin{aligned} u_{AC}(\tau ):\cong \int _{|{\underline{r}}|<R(\tau )}\int _{\tau _I}^{\tau }G^C_{\tau '}({\underline{r}};\tau ){\dot{H}}(\tau ')u_A(\tau ')d\tau 'd^3{\underline{r}} \end{aligned}$$
(4.13)

and

$$\begin{aligned} u_C(\tau ):=\int _{|{\underline{r}}|<R(\tau )}\int _{\tau _I}^{\tau }G^C_{\tau '}({\underline{r}};\tau )a(\tau ')^2T(\tau ')d\tau 'd^3{\underline{r}}. \end{aligned}$$
(4.14)

Another calculation of \(\langle C\rangle \) will be shown in Sect. 5.2.

Here we use the u functions to describe the time evolution of the perturbations.

The separation of variables for \({\tilde{\rho }}\) holds when there is a single component dominating. We can express it with the density contrast

$$\begin{aligned} {\tilde{\rho }}_0T(\tau )={\tilde{\rho }}:=\delta _M{\bar{\rho }}_M\propto \delta _Ma(\tau )^{-3}. \end{aligned}$$

E.g. when the matter dominates, it is

$$\begin{aligned} \delta _M\propto a \Rightarrow T(\tau )=a(\tau )^{-2}, \end{aligned}$$

as we know from [26,27,28].

When to dominate is dark energy, the matter structures are ripped apart with the same expansion rate of the universe

$$\begin{aligned} \delta _M=cost. \Rightarrow T(\tau )=a(\tau )^{-3}. \end{aligned}$$

When to dominate is radiation, the density contrast is well described by

$$\begin{aligned} \delta _M\propto \ln \left( \frac{4}{y}\right) ,\quad s.t.\ y:=\frac{a(\tau )}{a_{RM}}, \end{aligned}$$

as [26,27,28] say again, and \(a_{RM}\) is the value of a for which the matter starts to dominate on the radiation; thus the T function is

$$\begin{aligned} T(\tau )=a(\tau )^{-3}\ln \left( \frac{4a_{RM}}{a(\tau )}\right) =a(\tau )^{-3}[\ln (4a_{RM})-\ln a(\tau )]. \end{aligned}$$

Since we are in the Newtonian gauge, we need also the average of B. We can obtain it averaging the second gauge condition (3.2).

Lemma 4.4

$$\begin{aligned} \langle B\rangle (\tau )=\frac{3}{2}\Omega _{IM0}H_0^2u_B(\tau ), \end{aligned}$$
(4.15)

s.t.

$$\begin{aligned} u_B(\tau ):=a(\tau )^{-2}\int _{\tau _I}^{\tau }a(\tau ')^2(2u_{AC}(\tau ')+u_C(\tau ')-u_A(\tau '))d\tau '. \end{aligned}$$
(4.16)

Proof

We know that \(\langle {\dot{B}}\rangle +2\frac{{\dot{a}}}{a}\langle B\rangle =\langle C\rangle -\langle A\rangle \). After expressing \(\langle B\rangle (\tau ):=a(\tau )^{-2}b(\tau )\), we obtain

$$\begin{aligned}&a(\tau )^{-2}{\dot{b}}(\tau )=\langle C\rangle -\langle A\rangle =\frac{3}{2}\Omega _{IM0}H_0^2(2u_{AC}(\tau ) +u_C(\tau )-u_A(\tau )) \Rightarrow \\&b(\tau )=\frac{3}{2}\Omega _{IM0}H_0^2\int _{\tau _I}^{\tau }a(\tau ')^2(2u_{AC}(\tau ')+u_C(\tau ')-u_A(\tau '))d\tau ', \end{aligned}$$

which proves the assertion. \(\square \)

4.3 Formulas for the fictitious components

The fictitious components are determined by (2.8). We can rewrite it using the auxiliary variables ract and sum, defined as in [24].

$$\begin{aligned} {\left\{ \begin{array}{ll} s_{um}\Omega _{IM0}+o(\Omega _{IM0}):=\Omega _{FM0}+\Omega _{F\Lambda 0}=1-{\sum }_w\Omega _{Tw0} \\ r_{act}\Omega _{IM0}+o(\Omega _{IM0}):=\Omega _{FM0}-2\Omega _{F\Lambda 0}=2q_0-{\sum }_w(1+3w)\Omega _{Tw0}. \end{array}\right. } \end{aligned}$$
(4.17)

For an evaluation of these, we need to know the perturbations of on \(q_0\) and \(\Omega _{Tw0}\). The magnitude of the perturbations is determined by the comparison with the CSM metric

$$\begin{aligned}&a^2[(2\langle \Psi \rangle +1)d\tau ^2+(2\langle \Psi \rangle -1)\delta _{ij}dx_idx_j]\nonumber \\&\quad =\langle g_{\mu \nu }\rangle :=dt^2-\mathbf{a }^2\delta _{ij}dx_idx_j \Rightarrow \nonumber \\&dt={\tilde{t}}a d\tau :=\sqrt{1+2\langle \Psi \rangle }a d\tau ,\quad \mathbf{a }={\tilde{a}}a:=\sqrt{1-2\langle \Psi \rangle }a. \end{aligned}$$
(4.18)

The conditions at the present time are

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf{a }(t_0):=1 \\ \mathbf{H }_0=\partial _t\mathbf{a }|_{t_0} \\ q_0=-\frac{\partial _t^2\mathbf{a }}{\mathbf{H }^2}|_{t_0}. \end{array}\right. } \end{aligned}$$
(4.19)

From the first of these, we obtain the value of \(a_0:=a(t_0)\ne a(\tau _0)=1\), since

$$\begin{aligned} \frac{1}{a_0}&={\tilde{a}}_0=\sqrt{1-2\langle C\rangle _0-2H_0\langle B\rangle _0} \Rightarrow \\ a_0&=1+\langle C\rangle _0+H_0\langle B\rangle _0+o(\Omega _{IM0}). \end{aligned}$$

Now, we can consider a as the time variable. By now, we denote with a prime the derivatives with respect to a. From (4.18)

$$\begin{aligned} dt={\tilde{t}}a d\tau ={\tilde{t}}\frac{a}{\partial _{\tau }a}\partial _{\tau }a=\frac{{\tilde{t}}}{H}da \end{aligned}$$

so that for any given quantity Q depending on the time, we have

$$\begin{aligned} Q':=\frac{dQ}{da}=\frac{H}{{\tilde{t}}}\frac{dQ}{d\tau }=\frac{H}{{\tilde{t}}}{\dot{Q}}. \end{aligned}$$

Using the relation in (4.19), we can find firstly the perturbations of \(\Omega _{Tw0}\). Indeed, from definition (2.5)

$$\begin{aligned} \Omega _{Hw}=\frac{8\pi G}{3\mathbf{H }_0^2}\mathbf{a }^2{\bar{\rho }}_{w0}=\left( \frac{H_0}{\mathbf{H }_0}\right) ^2{\tilde{a}}^2{\bar{\Omega }}_w. \end{aligned}$$
(4.20)

From the second equation in (4.19), we can compute

$$\begin{aligned} \left( \frac{H_0}{\mathbf{H }_0}\right) ^2{\tilde{a}}_0^2= & {} 1+2[\langle A\rangle _0 +H_0\langle B\rangle _0-H'_0\langle B\rangle _0+\langle C\rangle '_0]\nonumber \\&+o(\Omega _{IM0}). \end{aligned}$$
(4.21)

For any w it’s \(\Omega _{Tw0}=\Omega _{Hw0}\), with the exception of \(\Omega _{TM0}=\Omega _{HM0}+\Omega _{IM0}\). Thus

$$\begin{aligned} s_{um}\Omega _{IM0}+o(\Omega _{IM0})&=1-\sum _w\Omega _{Tw0}=1-\Omega _{IM0}\\&\quad -\left( \frac{H_0}{\mathbf{H }_0}\right) ^2{\tilde{a}}_0^2\sum _w{\bar{\Omega }}_w \Rightarrow \\ (s_{um}+1)\Omega _{IM0}+o(\Omega _{IM0})&=1-[1+2(\langle A\rangle _0+H_0\langle B\rangle _0 -H'_0\langle B\rangle _0 \\&\quad +\langle C\rangle '_0)+o(\Omega _{IM0})]1 -2[\langle A\rangle _0+H_0\langle B\rangle _0\\&\quad -H'_0\langle B\rangle _0 +\langle C\rangle '_0]+o(\Omega _{IM0}). \end{aligned}$$

As for the perturbation of \(q_0\), we must remember that its zeroth order part is not zero, in general, but the background has a deceleration

$$\begin{aligned} {\bar{q}}_0=\frac{1}{2}\sum _w(1+3w){\bar{\Omega }}_{w0}. \end{aligned}$$
(4.22)

It is distorted by the perturbation, then at first order we expect to have

$$\begin{aligned} q_0:={\bar{q}}_0+q_{\Omega }\Omega _{IM0}+o(\Omega _{IM0}) \end{aligned}$$
(4.23)

for some coefficient \(q_{\Omega }\). We can compute each of these from the third of (4.19), obtaining

$$\begin{aligned} q_0= & {} -\frac{H'_0}{H_0}+\left[ \langle A\rangle '_0+2\langle C\rangle '_0\right. +\langle C\rangle ''_0-\frac{H'_0}{H_0}(\langle C\rangle _0+\langle C\rangle '_0\nonumber \\&\left. -H'_0\langle B\rangle _0)-H''_0\langle B\rangle _0\right] +o(\Omega _{IM0}). \end{aligned}$$
(4.24)

In particular, this means that

$$\begin{aligned} \frac{1}{2}\sum _w(1+3w){\bar{\Omega }}_{w0}={\bar{q}}_0=-\frac{H'_0}{H_0}. \end{aligned}$$
(4.25)

Together with (4.20), this gives

$$\begin{aligned}&\frac{1}{2}r_{act}\Omega _{IM0}+o(\Omega _{IM0})=q_0-\frac{1}{2}\sum _w(1+3w)\Omega _{Tw0} \\&\quad =[{\bar{q}}_0+q_{\Omega }\Omega _{IM0}+o(\Omega _{IM0})] -\frac{1}{2}(1+3w)|_{w=0}\Omega _{IM0}\\&\quad -[1-(s_{um}+1)\Omega _{IM0}+o(\Omega _{IM0})]\frac{1}{2}\sum _w(1+3w){\bar{\Omega }}_{w0} \Rightarrow \\&\frac{1}{2}(r_{act}+1)\Omega _{IM0}+o(\Omega _{IM0}) =(s_{um}+1)\Omega _{IM0}{\bar{q}}_0+q_{\Omega }\Omega _{IM0}+o(\Omega _{IM0}). \end{aligned}$$

Theorem 4.5

At first order, the effects of the matter inhomogeneities can be interpreted in terms of total fictitious components

$$\begin{aligned} {\left\{ \begin{array}{ll} \Omega _{FM0}=\frac{2s_{um}+r_{act}}{3}\Omega _{IM0}+o(\Omega _{IM0}) \\ \Omega _{F\Lambda 0}=\frac{s_{um}-r_{act}}{3}\Omega _{IM0}+o(\Omega _{IM0}), \end{array}\right. } \end{aligned}$$
(4.26)

where the auxiliary quantities are

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\frac{1}{2}(s_{um}+1)\Omega _{IM0}=-\langle A\rangle _0-H_0\langle B\rangle _0+H'_0\langle B\rangle _0-\langle C\rangle '_0 \\ &{}\frac{1}{2}(r_{act}+1)\Omega _{IM0}=\langle A\rangle '_0+2\langle C\rangle '_0+\langle C\rangle ''_0-H''_0\langle B\rangle _0 \\ &{}\quad +\frac{H'_0}{H_0}(2\langle A\rangle _0+2H_0\langle B\rangle _0-H'_0\langle B\rangle _0+\langle C\rangle '_0-\langle C\rangle _0) \end{array}\right. }. \end{aligned}$$
(4.27)

4.4 ODEs for the metric perturbations

Now we should solve (3.3), replacing the resultant A, B, C inside (4.27). The general PDEs (3.3) are a formidable mathematical task. We obtained in [24] an exact solution for the case with constant coefficients, but it seems to be impossible an analytical solution when the coefficients depend on \(\tau \). However, here we are investigating only the global effects, which depend only on the average of A, B, C, as (B.11) shows.

Let us notice again that \({\mathcal {L}}, {\mathcal {L}}^C\) are linear differential operators, depending on time but homogeneous in space. Hence, the average of the solution of (3.3) is equal to the solution of the average of (3.3); in other words, (3.3) are transparent to the spatial average, without backreaction terms, because all the non-linearity appears in the time dependence of the coefficients.

Performing a spatial averaging procedure on the PDEs (3.3), these are replaced by simpler ODEs, depending on the time only, for \(\langle A\rangle , \langle B\rangle , \langle C\rangle \). Such ODEs admit analytical solutions.

From Lemmas 4.2 and 4.4 we have

$$\begin{aligned}&\langle A\rangle =\frac{3}{2}\Omega _{IM0}H_0^2u_A(\tau ),\quad \langle B\rangle =\frac{3}{2}\Omega _{IM0}H_0^2u_B(\tau ),\\&\quad \langle C\rangle \cong \frac{3}{2}\Omega _{IM0}H_0^2(2u_{AC}(\tau )+u_C(\tau )); \end{aligned}$$

where the u functions are studied in Appendix A. From those results, we get

Theorem 4.6

If \(\tau _I>-\infty \) and \(a(\tau )^2T(\tau )\in L^1_{loc}([\tau _I;\tau _F)),\) then

$$\begin{aligned}&\ddot{u}_A(\tau )+2H{\dot{u}}_A(\tau )+2(2H^2-{\dot{H}})u_A(\tau )=-a(\tau )^2T(\tau ) \nonumber \\&\ddot{u}_{AC}(\tau )+2H{\dot{u}}_{AC}(\tau )=-{\dot{H}}(\tau )u_A(\tau ) \nonumber \\&\ddot{u}_C(\tau )+2H{\dot{u}}_C(\tau )=-a(\tau )^2T(\tau ). \end{aligned}$$
(4.28)

Otherwise,  \(\langle A\rangle ,\) \(\langle B\rangle ,\) \(\langle C\rangle \) always diverge.

Proof

From Lemmas A.2, A.3 and A.4, all the us are

$$\begin{aligned} u(\tau )=\int _{-R(\tau )}^{R(\tau )}v(r;\tau )dr={\hat{v}}(\omega ;\tau )|_{\omega =0}. \end{aligned}$$

The \({\hat{v}}\)s obey equations like (A.6). Writing them for the \(u\hbox {s}\) we have the assertion. \(\square \)

5 Single component cases

It is still impossible to solve analytically the evolution (2.6) for a and the ODEs (4.28) for a general choice of components \(\{{\bar{\Omega }}_{w0}\}_w\). Moreover, for such a general choice it’s quite difficult to determine the form of the source \({\tilde{\rho }}\propto T(\tau )\). However, we are able to solve exactly the equations when a single component \({\bar{\Omega }}_{w}\) dominates. We can approximate the general evolution as a succession of “epochs”; during each epoch, we consider just the dominant component

$$\begin{aligned} \forall \tau | {\bar{\Omega }}_{w}(\tau )=\max _{w'}{\bar{\Omega }}_{w'}(\tau ) : {\bar{\Omega }}_{w0}\cong 1, \end{aligned}$$

so that each epoch has a single-component evolution. The full evolution is obtained sticking the partial functions, imposing that \(a(\tau )\in C^0(\tau _I;\tau _F)\), since (2.6) is first order, \(\langle A\rangle , \langle C\rangle \in C^1(\tau _I;\tau _F)\), since (4.28) are second order; and \(\langle B\rangle \in C^0(\tau _I;\tau _F)\), because \(u_B\) is obtained by an integral in (4.16).

5.1 The first selfconsistency condition

Let’s start solving (2.6) for a general epoch with \({\bar{\Omega }}_{w'0}\cong \delta _{w',w}\).

$$\begin{aligned}&\left( \frac{{\dot{a}}}{H_0}\right) ^2=a^{1-3w} \Rightarrow \nonumber \\&a(\tau )={\left\{ \begin{array}{ll} \left( \frac{1}{\alpha }H_0(\tau -c)\right) ^{\alpha }\quad w\ne -\frac{1}{3} \\ e^{H_0(\tau -c)} \quad w=-\frac{1}{3} \end{array}\right. } \quad s.t. \quad \alpha (w):=\frac{2}{1+3w};\nonumber \\ \end{aligned}$$
(5.1)

where c is an integration constant. We get immediately the coefficients of (4.28)

$$\begin{aligned}&H(\tau )={\left\{ \begin{array}{ll} \frac{\alpha }{\tau -c} \quad w&{}\ne -\frac{1}{3} \\ H_0 \quad w&{}=-\frac{1}{3} \end{array}\right. }, \end{aligned}$$
(5.2)
$$\begin{aligned}&2H={\left\{ \begin{array}{ll} 2\frac{\alpha }{\tau -c} \quad w&{}\ne -\frac{1}{3} \\ 2H_0 \quad w&{}=-\frac{1}{3} \end{array}\right. }, \end{aligned}$$
(5.3)
$$\begin{aligned}&2(2H^2-{\dot{H}})={\left\{ \begin{array}{ll} 2\frac{2\alpha ^2+\alpha }{(\tau -c)^2} \quad w&{}\ne -\frac{1}{3} \\ 4H_0^2 \quad w&{}=-\frac{1}{3}. \end{array}\right. } \end{aligned}$$
(5.4)

Recalling (2.5) and that \(a(\tau )\) is increasing (at least) near \(\tau _I\), we see that the epochs must be in order of decreasing w. In particular, during the first epoch it dominates \(w_M:=\max \{w\}\). Setting the initial condition

$$\begin{aligned}&\lim _{\tau \rightarrow \tau _I}a(\tau )=0 \Rightarrow \nonumber \\&\tau _I={\left\{ \begin{array}{ll} -\infty \quad \alpha (w_M)&{}<0 \vee w=-\frac{1}{3} \\ c \quad \alpha (w_M)&{}>0 \end{array}\right. }. \end{aligned}$$
(5.5)

By definition it is always \(\alpha \ne 0\) for definition. From the previous Theorem, we get immediately

Corollary 5.1

(First Selfconsistency Condition) A selfconsistent choice of components must be such that \(w_M>-\frac{1}{3}\).

In particular, a selfconsistent universe must develop the metric perturbations as described by (4.28), with non constant coefficients.

Remark 3

In [24] we studied the constant coefficient case, filling the universe with an exotic component s.t. \(w=-\frac{1}{3}\). This breaks the First Selfconsistency Condition, which explains the divergences we found in [24, §4.3]: it is the contribution of \(rv(r;\tau )|_{r=R(\tau )}\equiv \infty \). It is possible to extract finite results even when the I SC is broken, as we did with a renormalization via analytic continuation. A general renormalization method could be to always neglect the term \(rv(r;\tau )|_{r=R(\tau )}\equiv \infty \), using (4.28) for any \(w_M\).

As long as the I SC holds, we can fix \(\tau _I:=0\) without lost of generality.

5.2 Decoupling

As we say in Lemma 4.2, for general coefficients of (3.3) we have just an approximated solution of \(\langle C\rangle \). This is due to the coupling between C and A. Another advantage of the single component evolution is to allow the decoupling the PDEs of A and C

$$\begin{aligned} {\left\{ \begin{array}{ll} \Box A-2\alpha \frac{{\dot{A}}}{\tau -c}-2\alpha (2\alpha +1)\frac{A}{(\tau -c)^2}=4\pi Ga^2{\tilde{\rho }} \\ \Box C-2\alpha \frac{{\dot{C}}}{\tau -c}+2\alpha \frac{A}{(\tau -c)^2}=4\pi Ga^2{\tilde{\rho }}. \end{array}\right. } \end{aligned}$$

Let \(\alpha \ne -\frac{1}{2}\).Footnote 2 Then it is convenient to define the auxiliary field

$$\begin{aligned} D:=A+(2\alpha +1)C, \end{aligned}$$
(5.6)

which must satisfy the PDE

$$\begin{aligned} \Box D-2\frac{\alpha }{\tau -c}{\dot{D}}=8(\alpha +1)\pi Ga^2{\tilde{\rho }}. \end{aligned}$$
(5.7)

All the results in Sect. 5 hold true for D, so that

$$\begin{aligned}&\langle D\rangle =3\Omega _{IM0}H_0^2u_D(\tau ) \quad s.t. \nonumber \\&\ddot{u}_D+2\frac{\alpha }{\tau -c}{\dot{u}}_D=-(\alpha +1)a(\tau )^2T(\tau ). \end{aligned}$$
(5.8)

From these we get an exact formula for \(\langle C\rangle \)

$$\begin{aligned} \langle C\rangle =\frac{\langle D\rangle -\langle A\rangle }{2\alpha +1}=\frac{3}{2}\Omega _{IM0}H_0^2\frac{2u_D(\tau )-u_A(\tau )}{2\alpha +1}. \end{aligned}$$
(5.9)

Remark 4

Notice that in the dark energy epoch \(\alpha =-1\) and the ODE for \(u_D\) is free of source. However, this doesn’t imply that \(u_D\) is zero, thus in general \(\langle C\rangle \ne \langle A\rangle \).

5.3 Solving the ODEs

To solve (4.28) for a general w, we need the form of \(T(\tau )\). We will assume

$$\begin{aligned} \delta _M\propto a(\tau )^n, \end{aligned}$$
(5.10)

with n(w) a regular function, of which we know \(n(0)=1\) and \(n(-1)=0\). This assumption does not certainly hold for the radiation epoch (\(w=\frac{1}{3}\)), when

$$\begin{aligned} \delta _M\propto \ln (4a_R)-\ln a(\tau )\quad s.t.\ a_R= & {} \max \{a(\tau )|{\bar{\Omega }}_{R}(\tau )\nonumber \\= & {} \max {\bar{\Omega }}_w(\tau )\}. \end{aligned}$$
(5.11)

Let us start by solving for \(u_A\). In general, it has a term \(u_{IA}\) generated by the source \(-a(\tau )^2T(\tau )=-a(\tau )^{n-1}\), and a term \(u_{HA}\) without sources. They result to be

$$\begin{aligned}&u_{IA}(\tau )=H_0^{-2}u_{A0}(H_0\tau )^{n_A} \quad s.t. \quad n_A=(n-1)\alpha +2 \nonumber \\&\quad and \quad u_{A0}=-\frac{\alpha ^{(1-n)\alpha }}{(n\alpha -\alpha +2)(n\alpha +\alpha +1)+2\alpha (2\alpha +1)}, \end{aligned}$$
(5.12)
$$\begin{aligned}&u_{HA}(\tau )\propto (H_0\tau )^{n_H} \quad s.t. \ n_H^2+(2\alpha -1)n_H\!+\!(4\alpha ^2\!+\!2\alpha )\!=\!0. \end{aligned}$$
(5.13)

The exponent of \(u_{HA}\) is

$$\begin{aligned} n_H=\left( \frac{1}{2}-\alpha \right) \pm \sqrt{\frac{1}{4}-3\alpha -3\alpha ^2}. \end{aligned}$$
(5.14)

It has an imaginary part if and only if

$$\begin{aligned}&\alpha \in \left( -\infty ; \alpha (w_+):=-\frac{1}{\sqrt{3}}-\frac{1}{2}\right) \sqcup \left( \alpha (w_-):=\frac{1}{\sqrt{3}}-\frac{1}{2};+\infty \right) \\&\quad \Leftrightarrow w\in (w_-\cong -0.9521;w_+\cong 8.2855). \end{aligned}$$

Because of the arbitrariness of the integration constants \(c_1\) and \(c_2\), we can write in general

$$\begin{aligned}&H_0^2u_A(\tau )=u_{A0}(H_0\tau )^{(n-1)\alpha +2}\nonumber \\&\quad +{\left\{ \begin{array}{ll} \left[ c_{A1}\sin (\sqrt{\xi }\ln H_0\tau )+c_{A2}\cos (\sqrt{\xi }\ln H_0\tau )\right] (H_0\tau )^{\frac{1}{2}-\alpha } &{} w\in (w_;w_+) \\ \left[ c_{A1}(H_0\tau )^{\sqrt{-\xi }}+c_{A2}(H_0\tau )^{-\sqrt{-\xi }}\right] (H_0\tau )^{\frac{1}{2}-\alpha } &{} w\not \in (w_;w_+) \end{array}\right. }, \end{aligned}$$
(5.15)

where \(\xi :=3\alpha ^2+3\alpha -\frac{1}{4}\). The solution for D is simpler.

$$\begin{aligned}&H_0u_D(\tau )=u_{D0}(H_0\tau )^{(n-1)\alpha +2}+c_{D1}(H_0\tau )^{1-2\alpha }+c_{D2} \nonumber \\&\quad s.t. \ u_{D0}=-\frac{\alpha ^{(1-n)\alpha }}{(n\alpha -\alpha +2)(n\alpha +\alpha +1)}. \end{aligned}$$
(5.16)

Using this, we get for C

$$\begin{aligned} H_0^2&u_C(\tau )=u_{C0}(H_0\tau )^{(n-1)\alpha +2}+c_{D1}(H_0\tau )^{1-2\alpha }+c_{D2} \nonumber \\&+{\left\{ \begin{array}{ll} -\frac{1}{2\alpha +1}\left[ c_{A1}\sin (\sqrt{\xi }\ln H_0\tau )+c_{A2}\cos (\sqrt{\xi }\ln H_0\tau )\right] (H_0\tau )^{\frac{1}{2}-\alpha } &{} w\in (w_;w_+) \\ -\frac{1}{2\alpha +1}\left[ c_{A1}(H_0\tau )^{\sqrt{-\xi }}+c_{A2}(H_0\tau )^{-\sqrt{-\xi }}\right] (H_0\tau )^{\frac{1}{2}-\alpha } &{} w\not \in (w_;w_+) \end{array}\right. } \end{aligned}$$
(5.17)
$$\begin{aligned} s.t. \quad u_{C0}:=\frac{2(\alpha +1)u_{D0}-u_{A0}}{2\alpha +1}. \end{aligned}$$
(5.18)

The evolution of B is determined by Lemma 4.4.

$$\begin{aligned}&u_B(\tau )=H_0^{-3}\frac{u_{C0}-u_{A0}}{(n+1)\alpha +3}(H_0\tau )^{(n-1)\alpha +3}+u_{HB}(\tau ) \nonumber \\&s.t. \quad u_{HB}(\tau )=a(\tau )^{-2} \int a(\tau ')^2\left( \frac{2u_{HD}(\tau ') -u_{HA}(\tau ')}{2\alpha +1}-u_{HA}(\tau ')\right) d\tau '. \end{aligned}$$
(5.19)

5.4 Particular components

In the following sections, we will need the single-component solutions for some particular components. The dark energy has \(w=-1<w_-\). The perturbations evolve as

$$\begin{aligned} H_0^2u_A(\tau )&=u_{A0}|_{w=-1}(H_0\tau -H_0c_{\Lambda })^3+c_{A1\Lambda } (H_0\tau -H_0c_{\Lambda })^2\nonumber \\&\quad +c_{A2\Lambda }(H_0\tau -H_0c_{\Lambda }); \nonumber \\ H_0^2u_C(\tau )&=u_{C0}|_{w=-1}(H_0\tau -H_0c_{\Lambda })^3-c_{A1\Lambda }(H_0\tau -H_0c_{\Lambda })^2\nonumber \\&\quad -c_{A2\Lambda }(H_0\tau -H_0c_{\Lambda }) \nonumber \\&\quad +c_{D1\Lambda }(H_0\tau -H_0c_{\Lambda })^5+c_{D2\Lambda }; \nonumber \\ H_0^3u_B(\tau )&=-2c_{A1\Lambda }(H_0\tau -H_0c_{\Lambda })^3\nonumber \\&\quad -2c_{A2\Lambda }(H_0\tau -H_0c_{\Lambda })^2\ln |H_0\tau -H_0c_{\Lambda }| \nonumber \\&\quad +\frac{1}{4}c_{D1\Lambda }(H_0\tau -H_0c_{\Lambda })^6-c_{D2\Lambda }(H_0\tau -H_0c_{\Lambda })\nonumber \\&\quad +c_{B\Lambda }(H_0\tau -H_0c_{\Lambda })^2. \end{aligned}$$
(5.20)

Indeed, \(\alpha (-1)=-1\Rightarrow \sqrt{\xi }=\frac{1}{2}\) and \(n(-1)=0\), thus

$$\begin{aligned} u_{A0}|_{w=-1}=u_{C0}|_{w=-1}=\frac{1}{2}, \Rightarrow u_{C0}-u_{A0}|_{w=-1}=0. \end{aligned}$$
(5.21)

The matter has \(w=0\in (w_-;w_+)\). The perturbations evolve as

$$\begin{aligned} H_0^2u_A(\tau )&=u_{A0}|_{w=0}(H_0\tau -H_0c_M)^2 +(H_0\tau -H_0c_M)^{-\frac{3}{2}}[c_{A1M}\nonumber \\&\quad \times \sin \left( \frac{\sqrt{71}}{2}\ln (H_0\tau -H_0c_M)\right) \nonumber \\&\quad +c_{A2M}\cos \left( \frac{\sqrt{71}}{2}\ln (H_0\tau -H_0c_M)\right) ]; \nonumber \\ H_0^2u_C(\tau )&=u_{C0}|_{w=0}(H_0\tau -H_0c_M)^2\nonumber \\&\quad +c_{D1M}(H_0\tau -H_0c_M)^{-3}+c_{D2M}\nonumber \\&\quad +\frac{1}{5}(H_0\tau -H_0c_M)^{-\frac{3}{2}}\cdot \nonumber \\&\quad \cdot \left[ c_{A1M}\sin \left( \frac{\sqrt{71}}{2}\ln (H_0\tau -H_0c_M)\right) \right. \nonumber \\&\quad \left. +c_{A2M}\cos \left( \frac{\sqrt{71}}{2}\ln (H_0\tau -H_0c_M)\right) \right] ; \nonumber \\ H_0^3u_B(\tau )&=\frac{u_{C0}-u_{A0}}{7}|_{w=0}(H_0\tau -H_0c_M)^3\nonumber \\&\quad +\frac{1}{2}c_{D1M}(H_0\tau -H_0c_M)^{-2}+\frac{1}{5}c_{D2M}(H_0\tau -H_0c_M) \nonumber \\&\quad -\frac{1}{50}(H_0\tau -H_0c_M)^{-\frac{1}{2}}[(3c_{A1M}\nonumber \\&\quad +\frac{\sqrt{71}}{2}c_{A2M})\sin \left( \frac{\sqrt{71}}{2}\ln (H_0\tau -H_0c_M)\right) \nonumber \\&\quad +(3c_{A2M}-\sqrt{71}c_{A1M})\cos \left( \frac{\sqrt{71}}{2}\ln (H_0\tau -H_0c_M)\right) ]\nonumber \\&\quad +c_{BM}(H_0\tau -H_0c_M)^{-4}. \end{aligned}$$
(5.22)

Indeed, \(\alpha (0)=2\Rightarrow \sqrt{-\xi }=\frac{\sqrt{71}}{2}\) and \(n(0)=1\), thus

$$\begin{aligned} u_{A0}|_{w=0}= & {} -\frac{1}{30}, \nonumber \\ u_{C0}|_{w=0}= & {} -\frac{17}{150} \Rightarrow \frac{u_{C0}-u_{A0}}{7}|_{w=0}=-\frac{2}{175}. \end{aligned}$$
(5.23)

For the peculiar evolution during the radiation epoch, we don’t use \(T=a^n\). The perturbations evolve as

$$\begin{aligned} H_0^2u_A(\tau )&=\frac{1}{8}(H_0\tau )\left[ \ln \left( \frac{H_0\tau }{4a_R}-\frac{3}{8}\right) \right] +u_{HA}(\tau ); \nonumber \\ H_0^2u_C(\tau )&=\frac{1}{8}(H_0\tau )\left[ 5\ln \left( \frac{H_0\tau }{4a_R}-\frac{63}{8}\right) \right] +u_{HC}(\tau ); \nonumber \\ H_0^3u_B(\tau )&=\frac{1}{8}(H_0\tau )^2\left[ \ln \left( \frac{H_0\tau }{4a_R}-\frac{17}{8}\right) \right] +u_{HB}(\tau ). \end{aligned}$$
(5.24)

5.5 Other selfconsistency conditions

Recalling our definition of a “selfconsistent”universe, the First Selfconsistency Condition ensures that there exist finite solutions for \(\langle A\rangle \), \(\langle B\rangle \), \(\langle C\rangle \). We must require also that these solutions are unique and that they describe small enough perturbations. The initial conditions for (3.3) were

$$\begin{aligned} \lim _{\tau \rightarrow 0}\langle A\rangle (\tau ), \langle B\rangle (\tau ), \langle C\rangle (\tau )=0. \end{aligned}$$
(5.25)

These functions are described by (5.15), (5.19) and (5.17) accordingly to the dominating w near \(\tau =0\), i.e. \(w_M\). The initial conditions put some restraints on \(w_M\) and on the integration constants: we can satisfy (5.25) if all \(u_{HA}, u_{HB}, u_{HC}\equiv 0\), and also

$$\begin{aligned} 0=&\lim _{\tau \rightarrow 0}(H_0\tau )^{(n(w_M)-1)\alpha (w_M)+2}\propto \lim _{\tau \rightarrow 0} a(\tau )^{n(w_M)+3w_M}\\&\Leftrightarrow n(w_M)+3w_M>0 \\ 0=&\lim _{\tau \rightarrow 0}(H_0\tau )^{(n(w_M)-1)\alpha (w_M)+3}\propto \lim _{\tau \rightarrow 0} a(\tau )^{n(w_M)+3w_M+\frac{1}{\alpha (w_M)}} \\&\Leftrightarrow n(w_M)+3w_M+\frac{1}{\alpha (w_M)}>0. \end{aligned}$$

For the I SC one has \(\alpha (w_M)>0\), so that the first limit implies the second one.

Theorem 5.2

(Second Selfconsistency Condition) A selfconsistent choice of components must be such that \(n(w_M)+3w_M>0\).

Remark 5

For a monotonically increasing n(w), the II SC is equivalent to

$$\begin{aligned} w_M>w_0 \end{aligned}$$
(5.26)

for some limit value \(w_0\). We can estimate it with a linear interpolation \(n(w)\cong 1+w\), that gives \(w_0\cong -\frac{1}{4}\). With more generality, remembering from [24] thatFootnote 3\(n(-\frac{1}{3})\in (\phi ;1)\) and that \(n(0)=1\), we have

$$\begin{aligned} -\frac{1}{3}<w_0<0. \end{aligned}$$
(5.27)

The II SC is not necessary if \(w_M=\frac{1}{3}\), for which always

$$\begin{aligned} \lim _{\tau \rightarrow 0}(H_0\tau )\left[ \ln \left( \frac{H_0\tau }{4a_R}-\frac{3}{8}\right) \right] =0; \end{aligned}$$
(5.28)

and the same for B and C.

Corollary 5.3

The II SC ensures that the perturbations are small near the Big Bang.

Proof

$$\begin{aligned} \frac{|\langle {\tilde{g}}_{\mu \nu }\rangle |}{|{\bar{g}}_{\mu \nu }|}\propto |\langle \Psi \rangle |=|\langle C\rangle -H\langle B\rangle |\rightarrow ^{\tau \rightarrow 0}0\ll 1; \end{aligned}$$
(5.29)

where the second term is \(H\langle B\rangle \propto \frac{1}{\tau }(H_0\tau )^{(n(w_M)-1)\alpha (w_M)+3}\propto a^{n(w_M)+3w_M}\rightarrow ^{\tau \rightarrow 0}0\) for the II SC again. \(\square \)

Do the initial conditions (5.25) fix uniquely \(\langle A\rangle \), \(\langle B\rangle \), \(\langle C\rangle \)? Not always. There are values of w for which \(u_{HA}, u_{HB}, u_{HC}\) go to zero even if the integration constants are not fixed to zero. Such cases are not selfconsistent, because the solutions are not unique. This is forbidden by

Theorem 5.4

(Third Selfconsistency Condition) A selfconsistent choice of components must be such that \(w_-<w_M\le 1\).

Proof

Let us try any non zero choice for the integration constant, and check if nevertheless \(u_{HA}\) tends to zero; if it is the case, the corresponding value of w will not be selfconsistent. First, let us consider the case \(w_M\in (w_-;w_+)\). Remembering (5.15)

$$\begin{aligned}&\lim _{\tau \rightarrow 0}u_{HA}(\tau )=0 \Leftrightarrow \lim _{\tau \rightarrow 0}(H_0\tau )^{\frac{1}{2}-\alpha (w_M)}=0 \Leftrightarrow \alpha (w_M)\\&\quad <\frac{1}{2} \Leftrightarrow w_M>1, \end{aligned}$$

otherwise the limit does not exist because of oscillations. This forbids the values \(w_M\in (1;w_+)\). Considering now the case \(w_M\not \in (w_-;w_+)\), it means \(\alpha (w_M)\in \left[ -\frac{1}{\sqrt{3}}-\frac{1}{2};\frac{1}{\sqrt{3}}-\frac{1}{2}\right] \), and in particular \(\alpha <\frac{1}{2}\). Recalling (5.15), for a choice \(c_{A1}\ne 0\), \(c_{A2}=0\)

$$\begin{aligned}&\sqrt{\frac{1}{4}-3\alpha -3\alpha ^2}+\frac{1}{2}-\alpha |_{w_M}>\frac{1}{2}-\alpha (w_M)>0 \\&\quad \Rightarrow \lim _{\tau \rightarrow 0}(H_0\tau )^{\sqrt{\frac{1}{4}-3\alpha -3\alpha ^2}+\frac{1}{2}-\alpha }|_{w_M}=0 \\&\quad \Rightarrow \lim _{\tau \rightarrow 0}u_{HA}(\tau )=0, \end{aligned}$$

and this is enough to forbid all the values \(w_M\not \in (w_-;w_+)\). For the allowed values \(w_M\in (w_-;1]\), the integration constants for \(u_C\) are fixed to zero as well, since (5.17) has the same functional form of (5.15). From (5.19) and (5.25) we see that also \(u_{HB}\) is fixed to zero, so that the metric perturbations are unique. \(\square \)

The Three Selfconsistency Conditions we proved allow only a “selfconsistency interval” for the component dominating near the Big Bang:

$$\begin{aligned} w_M\in (w_0;1]. \end{aligned}$$
(5.30)

Remark 6

Our universe contains certainly radiation and matter as homogeneous components, and probably dark energy. The biggest w is that of radiation, and \(w_M=\frac{1}{3}\) is included in the selfconsistency interval. This is not obvious. Some universes, as the “constant coefficient universe” studied in [24], break the Three Selfconsistency Conditions. The selfconsistency of our universe provides some empirical reinforcement to our model.

When I and III SC hold, the requirement of selfconsistency is reduced to asking that the perturbations are small enough to neglect orders higher than the first. This constitutes a last Condition.

Lemma 5.5

(Fourth Selfconsistency Condition) A selfconsistent choice of components must have an inhomogeneous matter such that \(\Omega _{IM0}\ll \Omega _{TM0}\), and such that \(\forall t\in [0;t_0]:|\langle \Psi \rangle |\ll \frac{1}{2}\).

Proof

The first requirement on \(\Omega _{IM0}\) is the same we asked in Sect. 2.4. The other requirement is evident from (4.4), where \(2\langle \Psi \rangle \) is the perturbation of the metric, and must be smaller than 1. \(\square \)

This is no more a Condition on w, but on \(\Omega _{IM0}\), so that the selfconsistency interval remains the same. Indeed, \(\langle A\rangle \), \(\langle B\rangle \), \(\langle C\rangle \) are proportional to \(\Omega _{IM0}\), and so is \(\langle \Psi \rangle \): the IV SC defines a maximum value \(\Omega ^M_{IM0}\) for the inhomogeneity.

Remark 7

Notice that the IV SC does not imply the II SC, since in the limit case \(w_M=w_0\), \(\langle \Psi \rangle \) doesn’t tend to zero, but, nevertheless, it could be small.

6 A model for the real universe

6.1 The 1-manifold of possible universes

Until now, our computations concerned a general choice of components \(\{{\bar{\Omega }}_{w0}\}_w\), for which we found the Selfconsistency Conditions. Now we will apply this general method to our universe.

It contains just three components: radiation \(\Omega _{R0}\), matter \(\Omega _{M0}\) and dark energy \(\Omega _{\Lambda 0}\). These are fixed by the measures of \(\Omega _{R0}\), of \(q_0=\Omega _{R0}+\frac{1}{2}\Omega _{M0}-\Omega _{\Lambda 0}\) and of the space flatness [29] \(1=1-\Omega _{k0}=\Omega _{R0}+\Omega _{M0}+\Omega _{\Lambda 0}\). The background components are as well \({\bar{\Omega }}_{R0}\), \({\bar{\Omega }}_{M0}\) and \({\bar{\Lambda 0}}\), on which the model puts the restraints

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( \frac{H_0}{\mathbf{H }_0}{\tilde{a}}_0\right) ^2{\bar{\Omega }}_{R0}=\Omega _{R0} \\ \Omega _{FM0}+\left( \frac{H_0}{\mathbf{H }_0}{\tilde{a}}_0\right) ^2{\bar{\Omega }}_{M0}+\Omega _{IM0}=\Omega _{M0} \\ \Omega _{F\Lambda 0}+\left( \frac{H_0}{\mathbf{H }_0}{\tilde{a}}_0\right) ^2{\bar{\Omega }}_{\Lambda 0}=\Omega _{\Lambda 0}. \end{array}\right. } \end{aligned}$$
(6.1)

Notice that these are not independent, since \({\bar{\Omega }}_{R0}+{\bar{\Omega }}_{M0}+{\bar{\Omega }}_{\Lambda 0}:=1\). We have only two independent constraints from

$$\begin{aligned} {\left\{ \begin{array}{ll} [1-(s_{um}+1)\Omega _{IM0}]{\bar{\Omega }}_{R0}=\Omega _{R0} \\ \frac{2s_{um}+r_{act}}{3}\Omega _{IM0}+[1-(s_{um}+1)\Omega _{IM0}]{\bar{\Omega }}_{M0}+\Omega _{IM0}=\Omega _{M0} \\ \frac{s_{um}-r_{act}}{3}\Omega _{IM0}+[1-(s_{um}+1)\Omega _{IM0}]{\bar{\Omega }}_{\Lambda 0}=\Omega _{\Lambda 0}=1-\Omega _{R0}-\Omega _{M0}. \end{array}\right. } \end{aligned}$$
(6.2)

However, we have three unknown parameters: the inhomogeneity \(\Omega _{IM0}\) and other two among \({\bar{\Omega }}_{R0}\), \({\bar{\Omega }}_{M0}\) and \({\bar{\Omega }}_{\Lambda 0}\). This means that the components of our universe are not completely determined by (6.2), but we will find more possible solutions, when a parameter changes. We choose \({\bar{\Omega }}_{M0}\in [0;1]\) as parameter, with \(\Omega _{\Lambda 0}(\Omega _{R0}; \Omega _{M0})=1-\Omega _{R0}-\Omega _{M0}\),

$$\begin{aligned} \Omega _{IM0}(\Omega _{R0}; \Omega _{M0})=\frac{1}{1+s_{um}(\Omega _{R0}; \Omega _{M0})}\left( 1-\frac{\Omega _{R0}}{{\bar{\Omega }}_{R0}}\right) \end{aligned}$$
(6.3)

and \({\bar{\Omega }}_{R0}={\bar{\Omega }}_{R0}({\bar{\Omega }}_{M0})\) is determined by the last independent constraint of (6.2).

We will have to check which of these values of \({\bar{\Omega }}_{M0}\) gives selfconsistent (i.e., if for them hold the IV SC and that \(\Omega _{IM0}\ll \Omega _{TM0}\)), acceptable and eventually good solutions.

6.2 Epochs of evolution

Applying (2.5),

$$\begin{aligned} {\bar{\Omega }}_R={\bar{\Omega }}_{R0}a^{-4}, \quad {\bar{\Omega }}_M={\bar{\Omega }}_{R0}a^{-3}, \quad {\bar{\Omega }}_{\Lambda }\equiv {\bar{\Omega }}_{\Lambda 0}. \end{aligned}$$

So we can get the values of a for which the matter starts to be more than the radiation, and the same for other couples

$$\begin{aligned} {\bar{\Omega }}_R\ge {\bar{\Omega }}_M&\Leftrightarrow a\le a_{RM}:=a(\tau _{RM})=\frac{{\bar{\Omega }}_{R0}}{{\bar{\Omega }}_{M0}} \nonumber \\ {\bar{\Omega }}_M\ge {\bar{\Omega }}_{\Lambda }&\Leftrightarrow a\le a_{M\Lambda }:=a(\tau _{M\Lambda })=\root 3 \of {\frac{{\bar{\Omega }}_{M0}}{{\bar{\Omega }}_{\Lambda 0}}} \nonumber \\ {\bar{\Omega }}_R\ge {\bar{\Omega }}_{\Lambda }&\Leftrightarrow a\le a_{R\Lambda }:=a(\tau _{R\Lambda })=\root 4 \of {\frac{{\bar{\Omega }}_{R0}}{{\bar{\Omega }}_{\Lambda 0}}}. \end{aligned}$$
(6.4)

The evolution of the universe until now is for \(0\le a\le a_0\cong 1\). During this time, there may have been three or two epochs, depending on the values \({\bar{\Omega }}_{R0}\), \({\bar{\Omega }}_{M0}\) and \({\bar{\Omega }}_{\Lambda 0}\).

Lemma 6.1

A selfconsistent background evolution can be divided in epochs in the following ways.

  • If \(a_{RM}<a_{M\Lambda }<a_0,\) then there are three epochs :  for radiation \([0;\tau _{RM}],\) matter \([\tau _{RM};\tau _{M\Lambda }],\) and dark energy \([\tau _{M\Lambda };\tau (t_0)]\).

  • If the first inequality does not hold,  then there are just two epochs :  radiation \([0;\tau _{R\Lambda }]\) and dark energy \([\tau _{R\Lambda };\tau (t_0)]\).

  • If the second inequality does not hold,  then there are just two epochs :  radiation \([0;\tau _{RM}]\) and matter \([\tau _{RM};\tau (t_0)]\).

Proof

Since the radiation exists, we know \({\bar{\Omega }}_{R0}>0\), so that \(a_{RM}>0\) and \(a_{R\Lambda }>0\) for any values of \({\bar{\Omega }}_{M0}\), \({\bar{\Omega }}_{\Lambda 0}\). Thus, we have always a radiation epoch, which is the first one after the Big Bang. The presence of other epochs depends on our parameter: the quantity of homogeneous matter \({\bar{\Omega }}_{M0}\).

We will not consider the case with only the radiation epoch, because it would mean that \(a_{RM}, a_{R\Lambda }\ge a_0\cong 1\), which happens for high values of \({\bar{\Omega }}_{R0}\); but we know from the measures [29] that the radiation is far more less than the matter. Moreover, if the homogeneous matter would be so little, it would mean that \(\Omega _{IM0}\cong \Omega _{TM0}\), that is not selfconsistent. \(\square \)

Let us consider the two cases with a matter epoch. From (5.1) we get the background evolution

$$\begin{aligned} a(\tau )={\left\{ \begin{array}{ll} H_0\tau &{} \tau \in [0;\tau _{RM}] \\ \frac{H_0^2}{4}(\tau -c_M)^2 &{} \tau \in [\tau _{RM};\tau _{M\Lambda }] \\ \frac{1}{H_0(c_{\Lambda }-\tau )} &{} \tau \in [\tau _{M\Lambda };\tau _F] \end{array}\right. }, \end{aligned}$$
(6.5)

where the continuity determines

$$\begin{aligned}&H_0\tau _{RM}=a_{RM} \Rightarrow H_0c_M=a_{RM}-2\sqrt{a_{RM}}, \nonumber \\&H_0\tau _{M\Lambda }=2\sqrt{a_{M\Lambda }}+H_0c_M, \nonumber \\&H_0c_{\Lambda }=H_0\tau _{M\Lambda }+4(H_0\tau _{M\Lambda }-H_0c_M)^{-2}. \end{aligned}$$
(6.6)

On the other hand, in the case such that there is no matter epoch, the evolution is

$$\begin{aligned} a(\tau )={\left\{ \begin{array}{ll} H_0\tau &{} \tau \in [0;\tau _{R\Lambda }] \\ \frac{1}{H_0(c_R-\tau )} &{} \tau \in [\tau _{R\Lambda };\tau _F], \end{array}\right. } \end{aligned}$$
(6.7)

where the continuity determines

$$\begin{aligned} H_0\tau _{R\Lambda }=a_{R\Lambda } \Rightarrow H_0c_R=a_{R\Lambda }+\frac{1}{a_{R\Lambda }}. \end{aligned}$$
(6.8)

7 Evaluations of dark matter and dark energy

Now we employ the most recent measures of the cosmological parameters. The space flatness is confirmed by [29]

$$\begin{aligned} \Omega _{tot}=1-\Omega _{k0}=1.02\pm 0.02. \end{aligned}$$
(7.1)

Thus we can assume \(\Omega _{R0}+\Omega _{M0}+\Omega _{\Lambda 0}=\Omega _{tot}:=1\). We have also

$$\begin{aligned} \Omega _{R0}=8.24\times 10^{-5}\pm 10^{-7}\, [29], \quad \Omega _{M0}=0.315\pm 0.007\, [30]. \end{aligned}$$
(7.2)

These are coherent with

$$\begin{aligned} \Omega _{\Lambda 0}=0.685\pm 0.007, q_0=-0.527\pm 0.0105. \end{aligned}$$
(7.3)

Moreover,

$$\begin{aligned} \Omega _{BM0}=0.0486\pm 0.0010\, [30]\, \Rightarrow \Omega _{DM0}=0.266\pm 0.008. \end{aligned}$$
(7.4)

The fraction of matter unexplained by the CSM is \(84.57\%\).

7.1 Searching for good solutions

For any value of the free parameter \({\bar{\Omega }}_{M0}\), we can get a numerical solution of \({\bar{\Omega }}_{R0}\). Following Sect. 6.2 we have, for any chosen value, the evolution of \(a(\tau )\), and from the formulas of Appendix B the quantities ract and sum, and thus \(\Omega _{IM0}\), \(\Omega _{FM0}\) and \(\Omega _{F\Lambda 0}\).

Imposing (6.2), there could be one or more solutions for \({\bar{\Omega }}_{R0}\), or no one, depending on \({\bar{\Omega }}_{M0}\). For any solution, we have to check if it is acceptable. The selfconsistency checking will require to compute the evolution of \(\langle \Psi \rangle \), since we have to find that its maximum is less than \(\frac{1}{2}\). Getting a set of selfconsistent and acceptable solutions, we will seek if some of them are also good.

Applying this planwork with a numerical algorithm, we find that for a generic \({\bar{\Omega }}_{M0}\) there are up to two acceptable values of \({\bar{\Omega }}_{R0}\). E.g. we can find

$$\begin{aligned} {\bar{\Omega }}_{R0}|_{{\bar{\Omega }}_{M0}=0.5}\cong {\left\{ \begin{array}{ll} 10.97\times 10^{-5} \\ 0.2216. \end{array}\right. } \end{aligned}$$
(7.5)

The set of solutions with \({\bar{\Omega }}_{R0}\sim 10^{-4}\) have a radiation density quite near to the value of the CSM. We can call them the “principal” solutions, and “secondary” solutions the others. Indeed, following these solutions with continuity, for \({\bar{\Omega }}_{M0}=0.315\cong \Omega _{M0}\) we find trivially

$$\begin{aligned} \Omega _{IM0}=0 \Rightarrow \Omega _{FM0}=\Omega _{F\Lambda 0}=0,\quad {\bar{\Omega }}_{w0}\equiv \Omega _{w0}. \end{aligned}$$
(7.6)

The secondary solutions are not selfconsistent, since all of them have \(\Omega _{IM0}>99\%\cdot \Omega _{TM0}\), so that they break the Cosmological Principle. Moreover, the secondary solutions have quite big perturbations \(2\max \langle \Psi \rangle >0.5\): they are smaller than 1 anyway, but not small enough.

On the other hand, the principal solutions are selfconsistent. \(\frac{\Omega _{IM0}}{\Omega _{TM0}}\) becomes greater as \({\bar{\Omega }}_{M0}\) runs away from \(\Omega _{M0}\), but it is always less than \(45\%\). It is the same for \(2\max \langle \Psi \rangle \), which is always smaller than \(0.28\ll 1\).

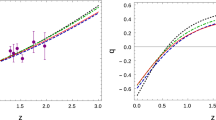
However, most of the principal solutions are not good. We find just a little interval around \({\bar{\Omega }}_{M0}\cong 0.2\) for which are explained some fraction of both dark matter and dark energy (Fig. 1). For the values \({\bar{\Omega }}_{M0}=0.2, {\bar{\Omega }}_{R0}\cong 10.03\times 10^{-5}, {\bar{\Omega }}_{\Lambda 0}\cong 0.8\) it is

$$\begin{aligned}&\Omega _{IM0}\cong -0.0316, \quad \Omega _{TM0}\cong 0.1327 \nonumber \\&\quad \Rightarrow |\Omega _{IM0}|\cong 23.8\%\cdot \Omega _{TM0}\ll \Omega _{TM0}, \nonumber \\&2\max \langle \Psi \rangle \cong 0.0485\ll 1, \nonumber \\&\Omega _{FM}\cong 0.1823 \Rightarrow \Omega _{TDM0}\cong 0.0841\cong 63.39\%\cdot \Omega _{TM0}, \nonumber \\&\Omega _{F\Lambda }\cong 0.0276 \Rightarrow \Omega _{T\Lambda 0}\cong 0.6572\cong 95.96\%\cdot \Omega _{\Lambda 0}. \end{aligned}$$
(7.7)
Fig. 1
figure 1

The evolution of the metric perturbation \(2\langle \Psi \rangle (a)\), for the case \({\bar{\Omega }}_{M0}=0.2\)

Full size image

For \({\bar{\Omega }}_{M0}>0.2\) we start soon to have \(\Omega _{FM0}<0\), so that the solutions are no more good. For \({\bar{\Omega }}_{M0}<0.2\) it starts vice versa to be \(\Omega _{F\Lambda 0}<0\), and the solutions are no more good as well.

7.2 Searching for solutions without dark energy or dark matter

We can seek if there is a selfconsistent and acceptable solution which fully explains the dark energy as fictitious. From the last paragraph, we know it would require an high \({\bar{\Omega }}_{M0}\), for which \(\Omega _{FM0}<0\) and the dark matter is more than in the CSM.

The condition of nonexistence of dark energy is \({\bar{\Omega }}_{\Lambda 0}:=0\), to that it is automatically fixed \({\bar{\Omega }}_{R0}=1-{\bar{\Omega }}_{M0}\) (Fig. 2). The (6.2) are solved by

$$\begin{aligned} {\bar{\Omega }}_{R0}\cong 26.31\times 10^{-5}, \quad {\bar{\Omega }}_{M0}\cong 0.9997, \quad {\bar{\Omega }}_{\Lambda 0}=0. \end{aligned}$$
(7.8)

In such a case we find

$$\begin{aligned}&\Omega _{IM0}\cong 0.2516, \quad \Omega _{TM0}\cong 0.5647 \nonumber \\&\quad \Rightarrow |\Omega _{IM0}|\cong 44.56\%\cdot \Omega _{TM0}\ll \Omega _{TM0}, \nonumber \\&2\max \langle \Psi \rangle \cong 0.2792\ll 1, \nonumber \\&\Omega _{FM}\cong -0.2507 \Rightarrow \Omega _{TDM0}\cong 0.5161\cong 91.39\%\cdot \Omega _{TM0}, \nonumber \\&\Omega _{F\Lambda }\cong 0.685 \Rightarrow \Omega _{T\Lambda 0}\cong 0. \end{aligned}$$
(7.9)
Fig. 2
figure 2

The evolution of the metric perturbation \(2\langle \Psi \rangle (a)\), for the case fully explaining the dark energy

Full size image

On the opposite, we can seek if there is a selfconsistent and acceptable solution that fully explains the dark matter as fictitious. From the last paragraph, we know it would require a small \({\bar{\Omega }}_{M0}\), for which \(\Omega _{F\Lambda 0}<0\) and the dark energy is more than in the CSM.

The condition of nonexistence of dark matter is \({\bar{\Omega }}_{TM0}:=\Omega _{MB0}\) (Fig. 3). The corresponding value of \({\bar{\Omega }}_{R0}\) is fixed by (6.2), which we solve numerically

$$\begin{aligned} {\bar{\Omega }}_{R0}\cong 9.59\times 10^{-5}, \quad {\bar{\Omega }}_{M0}\cong 0.0819, \quad {\bar{\Omega }}_{\Lambda 0}\cong 0.9170. \end{aligned}$$
(7.10)

In such a case we find

$$\begin{aligned}&\Omega _{IM0}\cong -0.0218, \quad \Omega _{TM0}=\Omega _{MB0}\cong 0.0486 \nonumber \\&\quad \Rightarrow |\Omega _{IM0}|\cong 44.84\%\cdot \Omega _{TM0}\ll \Omega _{TM0}, \nonumber \\&2\max \langle \Psi \rangle \cong 0.1608\ll 1, \nonumber \\&\Omega _{FM}=\Omega _{DM0}\cong 0.266 \Rightarrow \Omega _{TDM0}=0, \nonumber \\&\Omega _{F\Lambda }\cong -0.1039 \Rightarrow \Omega _{T\Lambda 0}\cong 0.7888\cong 115.17\%\Omega _{\Lambda 0}. \end{aligned}$$
(7.11)
Fig. 3
figure 3

The evolution of the metric perturbation \(2\langle \Psi \rangle (a)\), for the case fully explaining the dark matter

Full size image

7.3 The principal solutions

For values \({\bar{\Omega }}_{M0}>0.9997\) we would find \(\Omega _{T\Lambda 0}<0\), which is not acceptable. For values \({\bar{\Omega }}_{M0}<0.0819\) we would find \(\Omega _{TM0}<\Omega _{BM0}\), which is not acceptable. This mean that the acceptable principal solutions range in the interval \({\bar{\Omega }}_{M0}\in [0.0819; 0.9997]\).

We summarize with the following graphics the numerical results about the principal solutions (Figs. 4, 5, 6, 7, 8).

Fig. 4
figure 4

Background radiation density \({\bar{\Omega }}_{R0}\), depending on the parameter \({\bar{\Omega }}_{M0}\)

Full size image
Fig. 5
figure 5

Inhomogeneous matter \(\Omega _{IM0}\) (blue line) and homogeneous matter \(\Omega _{HM0}\) (red line), depending on the parameter \({\bar{\Omega }}_{M0}\)

Full size image
Fig. 6
figure 6

Maximum of the metric perturbation \(2\max \langle \Psi \rangle \), depending on the parameter \({\bar{\Omega }}_{M0}\)

Full size image
Fig. 7
figure 7

Fictitious matter \(\Omega _{FM0}\) (blue line), true matter \(\Omega _{TM0}\) (red line) and true dark matter \(\Omega _{TDM0}\) (grey line), depending on the parameter \({\bar{\Omega }}_{M0}\)

Full size image
Fig. 8
figure 8

Fictitious dark energy \(\Omega _{F\Lambda 0}\) (blue line) and true dark energy \(\Omega _{T\Lambda 0}\) (red line), depending on the parameter \({\bar{\Omega }}_{M0}\)

Full size image

8 Conclusions and future perspective

In this paper we developed the framework of [24], managing to apply it to a model of our universe, complete with all the components. The large number of variables leaves a free parameter, depending on which we found a one-dimensional set of possible solutions. Within this interval, more dark matter is explained less as less dark energy is, and vice versa. At an end of the range, dark matter is fully explained as a relativistic effect, but the same effect caused an underestimation of dark energy in the Cosmological Standard Model. At the other end the numbers are analogous, with dark matter and dark energy exchanged. For a particular value, both dark matter and dark energy found a partial explanation. An additional measure would determine which is the right solution, but anyway a correction of the parameters of the CSM is required.

Better measures of the density parameters will improve our estimations of \(\Omega _{FM0}\) and \(\Omega _{F\Lambda 0}\), but they can’t fix the right parameter \({\bar{\Omega }}_{M0}\). The difference between \({\bar{\Omega }}_{R0}\) and the measured \(\Omega _{R0}\), e.g., is not matter of measure precision, but of the factor \(\left( \frac{H_0}{\mathbf{H }_0}{\tilde{a}}_0\right) ^2\), which concerns the background universe and is not measurable. Rather, a measure of the actual gravitational force \(\vec {\nabla }\Psi ({\underline{x}};t_0)\) could put the restraint we need. Another possible measure could be the estimation of the matter inhomogeneity at large scale \(\Omega _{IM0}\), i.e. the deviation from the exact Cosmological Principle.

We approximated our calculations in many points. To overcome them would be an improvement of the framework. Solving numerically the evolution \(a(\tau )\) it would not be necessary any sticking, which presumably would return more regular graphics than in Sect. 8.3; but recall that this would require the form of \(T(\tau )\) for the multi-component case. Even if we found \(2\max \langle \Psi \rangle \) always far smaller than 1, it could not be considered fully negligible, so that an higher order calculation could provide some relevant corrections. Moreover, we assumed a spatially flat background metric and an irrotational matter, which is not the most general framework.

In the present article we considered the global dark matter effects only. Our cosmological model requires also the calculation of the local effects, to be empirically verified. This needs to overcome the averaging of \(g_{\mu \nu }\), and the distribution of fictitious dark matter would depend on the spatial distribution of inhomogeneities \({\tilde{\rho }}({\underline{x}};t_0)\). A study of such distribution could start from the fractal properties of the matter structures at large scales [31, 32]. The fluctuations of the resultant potential \(\Psi ({\underline{x}};t_0)\) should be compared to the dark matter halo of the galaxies.

The study of local dark matter effects would provide corrections to the standard Newtonian approximations for the dynamic of galaxies and clusters. For such calculations, we cannot assume an irrotational matter as we did here. The rotation of galaxies could provide a rotational term for the non diagonal components of the metric \(\vec {B}\), which contributes to fictitious gravitational effects [18, 19]. Finally, the total amount of the local fictitious effects could be compared to the global fictitious effect \(\Omega _{FM0}\) we found here, and the equivalence between them could be the additional restraint we need to fix uniquely the parameter \({\bar{\Omega }}_{M0}\).