Abstract
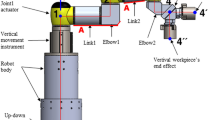
This paper presents a motion control method and its simulation results of a mobile robot for a lattice type welding. Its dynamic equation and motion control methods for welding speed and seam tracking are described. The motion control is realized in the view of keeping constant welding speed and precise target line even though the robot is driven for following straight line or curve. The mobile robot is modeled based on Lagrange equation under nonholonomic constraints and the model is represented in state space form. The motion control of the mobile robot is separated into three driving motions of straight locomotion, turning locomotion and torch slider control. For the torch slider control, the proportional-integral-derivative (PID) control method is used. For the straight locomotion, a concept of decoupling method between input and output is adopted and for the turning locomotion, the turning speed is controlled according to the angular velocity value at each point of the corner with range of 90° constrained to the welding speed. The proposed control methods are proved through simulation results and these results have proved that the mobile robot has enough ability to apply the lattice type welding line.
Similar content being viewed by others
Abbreviations
- b :
-
Distance between driving wheel and symmetry axis
- d :
-
Distance fromP 0 to mass center of mobile robot
- D :
-
Viscous friction
- I c :
-
Inertia moment of mobile robot excluding driving wheels and rotors of motors on a vertical axis through intersection between symmetry axis and driving wheel axis
- I m :
-
Inertia moment of wheel and motor rotor on wheel diameter
- I w :
-
Inertia moment of wheel and motor rotor on driving wheel axis
- J :
-
Inertia moment of rotor
- K Dp :
-
Derivative gain for the mobile robot
- K Ds :
-
Derivative gain for the torch slider
- K Is :
-
Integral gain for the torch slider
- K Pp :
-
Proportional gain for the mobile robot
- K Ps :
-
Proportional gain for the torch slider
- l s :
-
Maximum distance of the seam tracking sensor
- l ts :
-
Maximum distance of the torch slider
- m c :
-
Mass of mobile robot excluding masses for driving wheels and rotors of DC motors
- m w :
-
Mass of driving wheel including rotor of motor
- P c :
-
Mass center of the mobile robot with coordinates (x c ,y c )
- P o :
-
Geometric center with coordinates (x o ,y o ), that is the intersection between symmetry and the driving wheel axis
- Y p :
-
Radius of pinion
- Y w :
-
Radius of driving wheel
- V weld :
-
Welding speed
- X s :
-
Distance of the seam tracking sensor
- X ts :
-
Distance of the torch slider
- X tss :
-
Distance of the end of torch
- X-Y :
-
World coordinate system
- x-y :
-
Coordinate system fixed on the mobile robot
- θ sm :
-
Motor shaft angle
- τ p :
-
Torque acting on the left and right wheel
- τ s :
-
Torque acting on the torch slider
References
Campion, G., Bastine, G., and dAndrea-Novel, B., 1996, “Structural Properties and Classification of Kinematic and Dynamic Models of Wheeled Mobile Robots,”IEEE Transactions on Robotics and Automation, Vol. 12, No. 1, pp. 47–62.
Chung, J. H. and Velinsky, S. A., 1999, “Robust Control of a Mobile Manipulator Dynamic Modeling Approach,”Proceedings of the 1999 American Control Conference, pp. 2435–2439.
dAndrea-Novel, B., Bastine, G., and Campion, G., 1991, “Modelling and Control of Nonholonomic Wheeled Mobile Robots,”Proceedings of the 1991 IEEE International Conference on Robotics and Automation, pp. 1130–1135.
Fierro, R. and Lewis, F. L., 1995, “Control of a Nonholonomic Mobile Robot: Backstepping Kinematics into Dynamics,”Proceedings of the 34th Conference on Decision & Control, pp. 3805–3810.
Kang, C. J., Jeon, Y. B., Kam, B. O., and Kim, S. B., 2000, “Development of Continuous/Intermittent Welding Mobile Robot,”Proceedings of the National Meeting of Autumn, The Korean Welding Society, Vol. 36, pp. 31–33.
Sarkar, N., Yun, X. and Kumar, V., 1994, “Control of Mechanical Systems With Rolling Constraints: Application to Dynamic Control of Mobile Robots,”The International Journal of Robotics Research, Vol. 13, No. 1, pp. 55–69.
Sastry Shankar, 1999,Nonlinear Systems Analysis, Stability, and Control, Springer-Verlag, New York, pp. 384–448.
Yamamoto, Y. and Yun, X., 1999, “Unified Analysis on Mobility and Manipulability of Mobile Manipulators,”Proceedings of the 1999 IEEE International Conference on Robotics and Automation, Vol. 2, pp. 1200–1206.
Yamamoto, Y. and Yun, X., 1994, “Coordinating Locomotion and Manipulation of a Mobile Manipulator,”IEEE Transactions on Automatic Control, Vol. 39, No. 6, pp. 1326–1332.
Yun, X. and Yamamoto, Y., 1993, “Internal Dynamics of a Wheeled Mobile Robot,”Proceedings of the 1993 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 1288–1294.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Jeon, Y.B., Kim, S.B. Modeling and motion control of mobile robot for lattice type welding. KSME International Journal 16, 83–93 (2002). https://doi.org/10.1007/BF03185158
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF03185158