Abstract
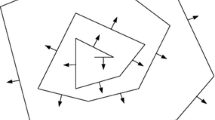
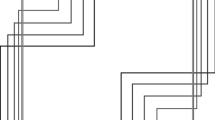
We introduce a three-dimensional crystalline motion whose Wulff shape is a convex polyhedron (Wk). We prove that this crystalline motion converges to the motion by Gauss curvature in ℝ3 under the assumptions that the polyhedra (Wk) converge to the unit ball B3 and are symmetric with respect to the origin.
K. Ishii and H. M. Soner showed the convergence of the two-dimensional crystalline motion to the curve shortening flow by a kind of perturbed test function methods. We employ their method to prove our result under aid from the theory of Minkowski problem.
Similar content being viewed by others
References
B. Andrews, Gauss curvature flow: the fate of the rolling stones. Inventione Mathematicae,138 (1999), 151–161.
B. Andrews, Motion of hypersurfaces by Gauss curvature. Pacific J. Math.,195 (2000), 1–34.
B. Andrews, Singularities in crystalline curvature flows. Asian J. Math.,6 (2002), 101–121.
S. Angenent and M.E. Gurtin, Multiphase thermomechanics with interfacial structure 2. Evolution of an isothermal interface. Arch. Rational Mech. Anal.,108 (1989), 323–391.
G. Bellettini, M. Novaga and M. Paolini, Facet-breaking for three-dimensional crystals evolving by mean curvature. Interfaces Free Bound.,1 (1999), 39–55.
G. Bellettini, M. Novaga and M. Paolini, Characterization of facet breaking for nonsmooth mean curvature flow in the convex case. Interfaces Free Bound.,3 (2001), 415–446.
B. Chow, Deforming convex hypersurfaces by then th root of the Gaussian curvature. J. Differential Geometry,22 (1985), 117–138.
L.C. Evans, The perturbed test function method for viscosity solutions of nonlinear PDE. Proc. Royal Soc. Edinburgh,111 (1989), 359–375.
W.J. Firey, Shapes of worn stones. Mathematika, 21 (1974), 1–11.
T. Fukui and Y. Giga, Motion of a graph by nonsmooth weighted curvature. World Congress of Nonlinear Analysis ’92 (ed. V. Lakshmikantham), Walter de Gruyter, 1996, 47–56.
M.-H. Giga and Y. Giga, Stability for evolving graphs by nonlocal weighted curvature. Comm. in PDE,24 (1999), 109–184.
M.-H. Giga and Y. Giga, Generalized motion by nonlocal curvature in the plane. Arch. Rational Mech. Anal.,159 (2001), 295–333.
P.M. Girão, Convergence of a crystalline algorithm for the motion of a simple closed convex curve by weighted curvature. SIAM J. Numer. Anal.,32 (1995), 886–899.
P.M. Girão and R.V. Kohn, Convergence of a crystalline algorithm for the heat equation in one dimension and for the motion of a graph by weighted curvature. Numer. Math.,67 (1994), 41–70.
H. Ishii, Gauss curvature flow and its approximation. Free Boundary Problems: Theory and Applications, II (Chiba, 1999), 198–206, GAKUTO Internat. Ser. Math. Sci. Appl.,14, Gakkotosho, Tokyo, 2000.
H. Ishii and T. Mikami, A two-dimensional random crystalline algorithm for Gauss curvature flow. Adv. Appl. Prob.,34 (2002), 491–504.
H. Ishii and T. Mikami, Convexified Gauss curvature flow of sets: a stochastic approximation. SIAM J. Math. Anal.,36 (2004), 552–579.
K. Ishii and H.M. Soner, Regularity and convergence of crystalline motion. SIAM J. Math. Anal.,30 (1998), 19–37.
R. Schneider, Convex Bodies: the Brunn-Minkowski Theory. Cambridge University Press, 1993.
H.M. Soner, Motion of a set by the curvature of its boundary. J. Differential Equations,101 (1993), 313–372.
J.E. Taylor, Constructions and conjectures in crystalline nondifferential geometry. Differential Geometry (eds. B. Lawson and K. Tanenblat), Pitman, 1991, 321–336.
J.E. Taylor, Motion of curves by crystalline curvature. including triple junctions and boundary points, Differential Geometry (eds. R. Greene and S. T. Yau), AMS, 1993, 417–438.
K. Tso, Deforming a hypersurface by its Gauss-Kronecker curvature. Comm. Pure Appl. Math.,38 (1985), 867–882.
T.K. Ushijima and S. Yazaki, Convergence of a crystalline algorithm for the motion of a closed convex curve by a power of curvatureV = Kα. SIAM J. Numer. Anal.,37 (2000), 500–522.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors are partially supported by Grant-in-Aid for Encouragement of Young Scientists (Ushijima: No. 16740061, Yagisita: No. 16740099).
About this article
Cite this article
Ushijima, T.K., Yagisita, H. Convergence of a three-dimensional crystalline motion to Gauss curvature flow. Japan J. Indust. Appl. Math. 22, 443–459 (2005). https://doi.org/10.1007/BF03167494
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF03167494