Distribution of stars perpendicular to the plane of the galaxy

Abstract

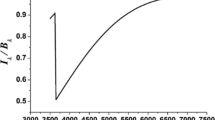
We present here rigorous analytical solutions for the Boltzmann-Poisson equation concerning the distribution of stars above the galactic plane. The number density of stars is considered to follow a behaviour n(m,0) ∼H(m - m₀)m^−x, wherem is the mass of a star andx an arbitrary exponent greater than 2 and also the velocity dispersion of the stars is assumed to behave as < v²(m)> ∼ m^−θ the exponent θ being arbitrary and positive. It is shown that an analytic expression can be found for the gravitational field K_z, in terms of confluent hypergeometric functions, the limiting trends being K_z∼z for z →0, while K_z → constant for z → infinity. We also study the behaviour of < |z(m)|²>,i.e. the dispersion of the distance from the galactic disc for the stars of massm. It is seen that the quantity < |z(m)|²>∼ m^t-θ, for m→ þ, while it departs significantly from this harmonic oscillator behaviour for stars of lighter masses. It is suggested that observation of < |z(m)|²> can be used as a probe to findx and hence obtain information about the mass spectrum.