Abstract
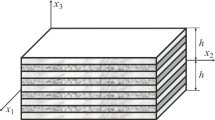
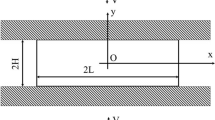
A phenomenological yield condition for quasi-brittle and plastic orthotropic materials with initial stresses is suggested. All components of the yield tensor are determined from experiments on uniaxial loading. The reliability estimates of the criterion suggested is discussed. For a plastic material without initial stresses, the given condition transforms into the Marin—Hu criterion. The defining equations of the deformation theory of plasticity with isotropic and “anisotropic” hardening, associated with the yield condition suggested, are obtained. These equations are used as the basis for a highly accurate nonclassical continuous model for nonlinear deformation of thick sandwich plates. The approximations with respect to the transverse coordinate take into account the flexural and nonflexural deformations in transverse shear and compression. The high-order approximations allow us to model the occurrence of layer delamination cracks by introducing thin nonrigid interlayers without violating the continuity concept of the theory.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. G. Piskunov and V. E. Verizhenko, Linear and Nonlinear Problems of Calculation of Laminate Structures [in Russian], Budivel’nik, Kiev (1986).
V. G. Piskunov, V. E. Verizhenko, V. K. Prisyazhnyuk, V. S. Sipetov, and V. S. Karpilovskii, Calculation of Inhomogeneous Shallow Shells and Plates by the Finite Element Method [in Russian], Vishcha Shkola, Kiev (1987).
V. E. Verizhenko, “Nonclassical models of the mechanics of layered orthotropic structures under nonlinear deformation,” Ph. D. Thesis [in Russian], Kiev (1987).
B. E. Pobedrya, Mechanics of Composite Materials [in Russian], Izd. Moskovsk. Universiteta, Moscow (1981).
A. A. Il’yushin, Theory of Plasticity [in Russian], Gostekhizdat, Moscow (1948).
A. G. Gurtovyi, “High-precision modeling of deformation of laminated structures,” Mech. Compos. Mater.,35, No. 1, 7–18 (1999).
V. V. Kosarchuk and S. A. Mel’nikov, “Deformation theory of plasticity of initially anisotropic media,” Probl. Prochn., No. 9, 3–15 (1995).
G. S. Pisarenko and A. A. Lebedev, Deformation and Strength of Materials under a Complex Stress State [in Russian], Naukova Dumka, Kiev (1976).
A. A. Lebedev, B. I. Koval’chuk, F. F. Giginyak, and V. P. Lamashevskii, Mechanical Characteristics of Constructional Materials under a Complex Stress State [in Russian], Naukova Dumka, Kiev (1983).
V. N. Bastun, M. I. Kolyakov, and Yu. N. Semko, “Strength condition of materials with different resistance to tension and compression,” Probl. Prochn., No. 5, 31–37 (1996).
A. B. Golyshev, V. Ya. Bachinskii, V. P. Polishchuk, A. V. Kharchenko, and I. V. Rudenko, Design of Reinforced Concrete Constructions [in Russian], Budivel’nik, Kiev (1990).
R. Hill, The Mathematical Theory of Plasticity, Clarendon Press, Oxford (1950).
V. G. Piskunov, V. S. Sipetov, and Sh. Sh. Tuymetov, “Solution of the problems of statics for laminated orthotropic plates in the three-dimensional statement,” Prikl. Mekh.,26, No. 2, 41–49 (1990).
A. V. Marchuk, “Three-dimensional analytical solution for laminated plates with regard to friction of layers,” Prikl. Mekh.,33, No. 9, 10–14 (1997).
Author information
Authors and Affiliations
Additional information
Submitted to the 11th International Conference on Mechanics of Composite Materials (Riga, June 11–15, 2000).
Translated from Mekhanika Kompozitnykh Materialov, Vol. 36, No. pp. 329–340, May–June, 2000.
Rights and permissions
About this article
Cite this article
Gurtovyi, O.G. A continuous model for investigation of physically nonlinear deformation of orthotropic sandwich plates. Mech Compos Mater 36, 193–198 (2000). https://doi.org/10.1007/BF02681870
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02681870