Abstract
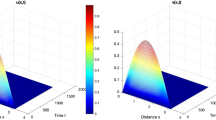
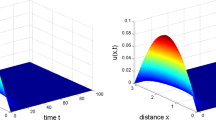
In this paper, a mathematical model of competition between plasmid-bearing and plasmid-free organisms in a chemostat with an inhibitor is investigated. The model is in the form of a system of nonlinear differential equations. By using qualitative methods, the conditions for the existence and local stability of the equilibria are obtained. The existence and stability of periodic solutions of the Hopf type are studied. Numerical simulations about the Hopf bifurcation value and Hopf limit cycle are also given.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
H.L. Smith, P. Waltman. The Theory of the Chemostat: Dynamics of Microbial Competions. Cambridge University Press, Cambridge, 1995
P. Waltman. Coexistence in Chemostat-like Models.Rockey Mountain Journal of mathematics, 1990, 20: 777–807.
P. Waltman. Competition Models in Population Biology. Philadelphia: Society for Industrial and Applied Mathematics, 1983
E.B. Pike, C.R. Curds. The Microbial Ecology Ecology of Activated Sludge Process. Microbial Aspects of Pollution, G. Skykes and F. A. Skinner, eds., Academic Press, New York, 1971
G. D'ans, P.V. Kokotovic, D. Gottlieb. A Nonlinear Regulator Problem for a Model of Biological Wastewater Treatment.IEEE Transactions Automatic Control, 1971, AC-16:341–347
G. Stephanopoulis, G. Lapidus. Chemostat Dynamics of Plasmid-bearing Plasmid-free Mixed Recombinant Cultures.Chem. Engr. Science, 1988, 43: 49–57
S.B. Hsu, P. Waltman, G.S.K. Wolcowicz. Global Analysis of a Model of Plasmid-bearing, Plasmid-free Competition in a Chemostat.J. Math. Biol., 1994, 32: 731–742
T.K. Luo, S.B. Hsu. Global Analysis of a Model of Plasmid-bearing, Plasmid-free Competition in a Chemostat with Inhibitions.J. Math. Biol., 1995, 34: 41–76
C.A. Macken, S.A. Levin, R. Waltstätter. The Dynamics of Bacteria-plasmid Systems.J. Math. Biol., 1994, 32: 123–145
R.E. Lenski, S. Hattingh. Coexistence of Two Competitors on One Resource and One Inhibitor: A Chemostat Model Based on Bacteria Antibiotics.J. Theor. Bio., 1986, 122: 83–93
S.B. Hsu, P. Waltman. Analysis of a Model of Two Competitors in a Chemostat with an External Inhibitor.SIAM Journal of Applied Mathematics, 1991, 52: 528–540
S.B. Hsu, T.K. Luo, P. Waltman. Competition Between Plasmid-bearing and Plasmid-free Organisms in a Chemostat with an Inhibitor.J. Math. Biol., 1995, 34(2): 225–235
H.R. Thieme. Convergence Results and a Poincare'-Bendixson Trichotomy for Asymptotically Autonomous Differential Equations.J. Math. Biol., 1992, 30: 755–763
P. Lancaster. Theory of Matrices. Academic, New York, 1969
I. Hsu, N.D. Kazarinoff. Existence and Stability of Periodic Solutions of a Third-order Nonlinear Autonomous System Simulating Response in Animals.Proc. Roy. Soc. Edin. (Series A), 1977, 77: 163–175
B.D. Hassard, N.D. Kazarinoff, Y.H. Wan. Theory and Applications of Hopf Bifurcation. London Mathematical Society Lecture Notes Series, No. 41, 1981
Z. Liu, Z. Jing. Qualitative Analysis for a Third-order Differential Equation in a Model of Chemical Systems.Systems Science and Mathematical Sciences, 1992, 5(4): 299–311
J.E. Marsden, M. McCracken. The Hopf Bifurcation and Its Applications. Springer-Verlag, New York, 1976
D.F. Ryder, D. DiBiaso. An Operational Strategy for Unstable Recombinant DNA Cultures.Biotech. and Bioeng, 1984, 26: 952–947
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Almocera, L.S., Zhujun, J. & Sy, P.W. Hopf bifurcation and analysis of equilibrium for a third-order differential equation in a model of competition. Acta Mathematicae Applicatae Sinica 17, 68–80 (2001). https://doi.org/10.1007/BF02669686
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02669686