Skip to main content
SpringerLink
Log in

Turing Instability and Turing–Hopf Bifurcation in Diffusive Schnakenberg Systems with Gene Expression Time Delay

  • Published:
Journal of Dynamics and Differential Equations Aims and scope Submit manuscript

Abstract

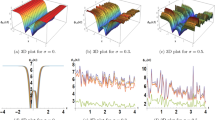
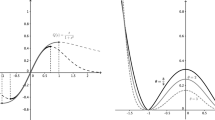
In this paper, we study the delayed reaction–diffusion Schnakenberg systems with Neumann boundary conditions. Sufficient and necessary conditions for the occurrence of Turing instability are obtained, and the existence of Turing, Hopf and Turing–Hopf bifurcation for the model are also established. Furthermore, for Turing–Hopf bifurcation, the explicit formula of the truncated normal form up to third order is derived. With the aid of these formulas, we determine the regions on two parameters plane, on which a pair of stable spatially inhomogeneous steady states and a pair of stable spatially inhomogeneous periodic solutions exist, respectively. The theoretical results not only reveals the joint effect of diffusion and delay on the patterns that the model can exhibit, but also explain the phenomenon that time delay may induce a failure of Turing instability, found by Gaffney and Monk (Bull Math Biol 68(1):99–130, 2006).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. An, Q., Jiang, W.: Spatiotemporal attractors generated by the Turing-Hopf bifurcation in a time-delayed reaction-diffusion system. Discrete Contin. Dyn. Syst. Ser. B (2018). https://doi.org/10.3934/dcdsb.2018183

    Article  MATH  Google Scholar 

  2. Baurmann, M., Gross, T., Feudel, U.: Instabilities in spatially extended predator-prey systems: Spatio-temporal patterns in the neighborhood of Turing-Hopf bifurcations. J. Theret. Biol. 245, 220–229 (2007)

    Article  MathSciNet  Google Scholar 

  3. Chen, S., Yu, J.: Stability analysis of a reaction–diffusion equation with spatiotemporal delay and Dirichlet boundary condition. J. Dynam. Differ. Equ. 28(3–4), 857–866 (2016)

    Article  MathSciNet  Google Scholar 

  4. Faria, T., Magalhaes, L.: Normal forms for retarded functional differential equations and applications to Bogdanov–Takens singularity. J. Differ. Equ. 122(2), 201–224 (1995)

    Article  MathSciNet  Google Scholar 

  5. Faria, T., Magalhaes, L.: Normal forms for retarded functional differential equations with parameters and applications to Hopf bifurcation. J. Differ. Equ. 122(2), 181–200 (1995)

    Article  MathSciNet  Google Scholar 

  6. Gaffney, E., Monk, N.: Gene expression time delays and Turing pattern formation systems. Bull. Math. Biol. 68(1), 99–130 (2006)

    Article  MathSciNet  Google Scholar 

  7. Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer-Verlag, Berlin (1983)

    Book  Google Scholar 

  8. Guo, S.: Stability and bifurcation in a reaction–diffusion model with nonlocal delay effect. J. Differ. Equ. 259(4), 1409–1448 (2015)

    Article  MathSciNet  Google Scholar 

  9. Guo, S., Ma, L.: Stability and bifurcation in a delayed reaction–diffusion equation with Dirichlet boundary condition. J. Nonlinear Sci. 26(2), 545–580 (2016)

    Article  MathSciNet  Google Scholar 

  10. Gurdon, J., Bourillot, P.: Morphogen gradient interpretation. Nature 413(6858), 797–803 (2001)

    Article  Google Scholar 

  11. Hadeler, K., Ruan, S.: Interaction of diffusion and delay. Discrete Contin. Dyn. Syst. Ser. B 8(1), 95–105 (2012)

    MathSciNet  MATH  Google Scholar 

  12. Jang, J., Ni, W., Tang, M.: Global bifurcation and structure of Turing patterns in the 1-d Lengyel–Epstein model. J. Dynam. Differ. Equ. 16(2), 297–320 (2004)

    Article  MathSciNet  Google Scholar 

  13. Jiang, W., Anm Q., Shi, J.: Formulation of the normal forms of Turing-Hopf bifurcation in reaction–diffusion systems with time delay. arXiv:1802.10286 (2018)

  14. Just, W., Bose, M., Bose, S., Engel, H., Schöll, E.: Spatiotemporal dynamics near a supercritical Turing–Hopf bifurcation in a two-dimensional reaction-diffusion system. Phys. Rev. E 64(2), 026219 (2001)

    Article  Google Scholar 

  15. Kidachi, H.: On mode interactions in reaction diffusion equation with nearly degenerate bifurcations. Prog. Theor. Phys. 63(4), 1152–1169 (1980)

    Article  MathSciNet  Google Scholar 

  16. Kuznetsov, Y.A.: Elements of Applied Bifurcation Theory. Springer-Verlag, Berlin (1995)

    Book  Google Scholar 

  17. Lee, S., Gaffaney, E., Baker, R.: The dynamics of Turing patterns for morphogen-regulated growing domains with cellular response delays. Bull. Math. Biol. 73, 2527–2551 (2011)

    Article  MathSciNet  Google Scholar 

  18. Li, X., Jiang, W., Shi, J.: Hopf bifurcation and Turing instability in the reaction-diffusion Holling–Tanner predator–prey model. IMA J. Appl. Math. 78(2), 287–306 (2013)

    Article  MathSciNet  Google Scholar 

  19. Liu, P., Shi, J., Wang, Y., Feng, X.: Bifurcation analysis of reaction–diffusion Schnakenberg model. J. Math. Chem. 51(8), 2001–2019 (2013)

    Article  MathSciNet  Google Scholar 

  20. Maini, P., Painter, K., Chau, H.: Spatial pattern formation in chemical and biological systems. J. Chem. Soc. Faraday Trans. 93(20), 3601–3610 (1997)

    Article  Google Scholar 

  21. Meixner, M., Dewit, A., Bose, S., Scholl, E.: Generic spatiotemporal dynamics near codimension-two Turing–Hopf bifurcations. Phy. Rev. E 55(6), 6690–6697 (1997)

    Article  MathSciNet  Google Scholar 

  22. Murray, J.: Mathematical Biology. Springer, New York (2003)

    Book  Google Scholar 

  23. Ni, W., Tang, M.: Turing patterns in the Lengyel–Epstein system for the CIMA reaction. Trans. Am. Math. Soc. 357(10), 3953–3969 (2005)

    Article  MathSciNet  Google Scholar 

  24. Peng, R., Yi, F., Zhao, X.: Spatiotemporal patterns in a reaction–diffusion model with the Degn–Harrison reaction scheme. J. Differ. Equ. 254(6), 2465–2498 (2013)

    Article  MathSciNet  Google Scholar 

  25. Ricard, M., Mischler, S.: Turing instabilities at Hopf bifurcation. J. Nonlinear Sci. 19(5), 467–496 (2009)

    Article  MathSciNet  Google Scholar 

  26. Schnakenberg, J.: Simple chemical reaction systems with limit cycle behaviour. J. Theor. Biol. 81(3), 389 (1979)

    Article  MathSciNet  Google Scholar 

  27. Shi, H., Ruan, S.: Spatial, temporal and spatiotemporal patterns of diffusive predator–prey models with mutual interference. IMA J. Appl. Math. 80(5), 1534–1568 (2015)

    Article  MathSciNet  Google Scholar 

  28. Song, Y., Jiang, H., Liu, Q., Yuan, Y.: Spatiotemporal dynamics of the diffusive Mussel–Algae model near Turing–Hopf bifurcation. SIAM J, Appl Dyn. Syst. 16(4), 2030–2062 (2017)

    Article  MathSciNet  Google Scholar 

  29. Su, Y., Wei, J., Shi, J.: Hopf bifurcations in a reaction-diffusion population model with delay effect. J. Differ. Equ. 247(4), 1156–1184 (2009)

    Article  MathSciNet  Google Scholar 

  30. Turing, A.: The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. Ser. B 237(641), 37–72 (1952)

    Article  MathSciNet  Google Scholar 

  31. Wang, J.: Spatiotemporal patterns of a homogeneous diffusive predator–prey system with Holling type III functional response. J. Dyn. Differ. Equ. 29, 1–27 (2016)

    MathSciNet  Google Scholar 

  32. Ward, M., Wei, J.: The existence and stability of asymmetric spike patterns for the Schnakenberg model. Stud. Appl. Math. 109(3), 229–264 (2002)

    Article  MathSciNet  Google Scholar 

  33. Wittenberg, R., Holmes, P.: The limited effectiveness of normal forms: a critical review and extension of local bifurcation studies of the Brusselator PDE. Physica D 100(1–2), 1–40 (1997)

    Article  MathSciNet  Google Scholar 

  34. Xu, C., Wei, J.: Hopf bifurcation analaysis in a one-dimensional Schnakenberg reaction–diffusion model. Nonlinear Anal. RWA 13, 1961–1977 (2012)

    Article  Google Scholar 

  35. Yan, X., Li, W.: Stability of bifurcating periodic solutions in a delayed reaction-diffusion population model. Nonlinearity 23(6), 1413 (2010)

    Article  MathSciNet  Google Scholar 

  36. Yi, F., Gaffney, E., Seirin, L.: The bifurcation analysis of Turing pattern formation induced by delay and diffusion in the Schnakenberg system. Discrete Contin. Dyn. Syst. Ser. B 22(2), 647–668 (2017)

    MathSciNet  MATH  Google Scholar 

  37. Yi, F., Wei, J., Shi, J.: Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator–prey system. J. Differ. Equ. 246(5), 1944–1977 (2009)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The work was supported in part by the National Natural Science Foundation of China (Nos. 11871176, 11671110).

Author information

Authors and Affiliations

  1. Department of Mathematics, Harbin Institute of Technology, Harbin, 150001, China

    Weihua Jiang, Hongbin Wang & Xun Cao

Authors
  1. Weihua Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hongbin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xun Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Weihua Jiang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiang, W., Wang, H. & Cao, X. Turing Instability and Turing–Hopf Bifurcation in Diffusive Schnakenberg Systems with Gene Expression Time Delay. J Dyn Diff Equat 31, 2223–2247 (2019). https://doi.org/10.1007/s10884-018-9702-y

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10884-018-9702-y

Keywords

Search

Navigation