Skip to main content
SpringerLink
Log in

Bifurcation in a parametrically excited two-degree-of-freedom nonlinear oscillating system with 1∶2 internal resonance

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

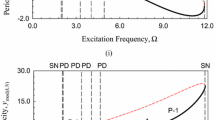
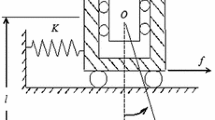
The nonlinear response of a two-degree-of-freedom nonlinear oscillating system to parametric excitation is examined for the case of 1∶2 internal resonance and, principal parametric resonance with respect to the lower mode. The method of multiple scales is used to derive four first-order autonomous ordinary differential equations for the modulation of the amplitudes and phases. The steadystate solutions of the modulated equations and their stability are investigated. The trivial solutions lose their stability through pitchfork bifurcation giving rise to coupled mode solutions. The Melnikov method is used to study the global bifurcation behavior, the critical parameter is determined at which the dynamical system possesses a Smale horseshoe type of chaos.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Chen Yushu.Bifurcation and Chaos Theory of Nonlinear Vibration Systems [M]. Beijing: High Education Press, 1993 (in Chinese)

    Google Scholar 

  2. Nayfeh A H, Nayfeh J F. Surface waves in closed basins under principal and autoparametric resonances [J].Phys. Fluids, 1990, A2(9):1635–1648

    Article  MATH  MathSciNet  Google Scholar 

  3. Feng Z C, Sethna P R. Global bifurcation and chaos in parametrically forced systems with one-one resonance[J].Dynamics and Stability of Systems, 1990,5(4):210–225

    MathSciNet  Google Scholar 

  4. Feng Z C, Wiggins S. On the existence of chaos in a class of two-degree-of-freedom, damped, strongly parametrically forced mechanical systems with brokenO(2) symmetry [J].Z Angew Math Phys, 1993,44(2):201–248

    Article  MATH  MathSciNet  Google Scholar 

  5. Nayfeh A H.Perturbation Methods[M]. New York: Wiley-Interscience, 1973

    Google Scholar 

  6. Wiggins S.Global Bifurcations and Chaos—Analytical Methods [M]. New York: Springer-Verlag, 1990

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanics, Tianjin University, 300072, Tianjin, P R China

    Ji Jinchen & Chen Yushu

Authors
  1. Ji Jinchen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chen Yushu
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Project supported by the National Natural Science Foundation of China (19472046)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jinchen, J., Yushu, C. Bifurcation in a parametrically excited two-degree-of-freedom nonlinear oscillating system with 1∶2 internal resonance. Appl Math Mech 20, 350–359 (1999). https://doi.org/10.1007/BF02458560

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02458560

Key words

Search

Navigation