Skip to main content
SpringerLink
Log in

On one of Graffiti's conjecture (583)

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

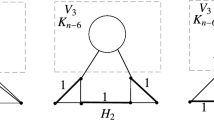
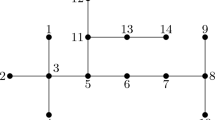
In the paper, a counterexample of the Graffiti's conjecture (583) is given out which proves the conjecture is false. And the best bounds of I(T)+a′(T) are got, where T denotes a tree, I(T) denotes the inverse degree of T and a′(T) is the matching of T.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. F. R. K. Chung. The average distance and the independence number,J. of Graph Theory,12 (1988), 229–235.

    MATH  Google Scholar 

  2. I. A. Bondy and U. S. R. Murty,Graph Theory with Applications, The MacMillan Press Ltd. (1976).

Download references

Author information

Authors and Affiliations

  1. Heilongjiang Hydraulic Engineering College, 150086, Harbin, P. R. China

    Wang Liuxing

Authors
  1. Wang Liuxing
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by Liu Renhuai

Project supported by the NSF of Gansu Province and Railway Ministry

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liuxing, W. On one of Graffiti's conjecture (583). Appl Math Mech 18, 381–383 (1997). https://doi.org/10.1007/BF02457552

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02457552

Key words

Search

Navigation