Skip to main content
SpringerLink
Log in

An approximate method of response analysis of vibrations for cracked beams

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

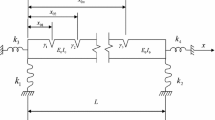
In this paper a method based on a line-spring model was proposed to analyze approximately vibration responses of cracked beams. The method in conjunction with the Euler-Bernoulli beam theory, modal analysis and fracture mechanics principle was applied to derive a characteristic equation for the cracked beam vibration. As application examples, natural frequency responses for a cracked hinged-hinged beam and a cracked cantilever beam were examined. It was shown that the present solutions obtained are quite in agreement with the solutions or experimental results in available references.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. G. Chondros and A. D. Dimarogonas, Identification of cracks in welded joints of complex structures,J. Sound & Vib.,69 (1980), 531–538.

    Article  Google Scholar 

  2. Y. P. Shen, and Z. Q. Tang, The effects of cracks on the spectra of cantilever beam,Acta, Mechanica Solida Sinica,3 (1982), 247–251. (in Chinese)

    Google Scholar 

  3. P. F. Rizos, N. Aspragathos and A. D. Dimarogonas, Identification of crack location and magnitude in a cantilever beam from the vibration mode,J. Sound & Vib.,138 (1990), 381–388.

    Article  Google Scholar 

  4. G. E. Nash, Bending deflections and moments in notched beam,Engng. Fract. Mech.,3 (1971), 139–150.

    Article  Google Scholar 

  5. P. Gudmundson, Eigenfrequency changes of structures due to cracks, notches or other geometrical changes,J. Mech. Phys. Solids,30 (1982), 339–353.

    Article  Google Scholar 

  6. J. R. Rice and N. Levy, The part-through surface crack in an elastic plate,J. Appl. Mech.,39 (1972), 185–194.

    MATH  Google Scholar 

  7. H. Tada, P. C. Paris and G. R. Irwin,The Stress Analysis of Crack Handbook, Del Research Corp, Hellerton, PA (1973).

    Google Scholar 

  8. T. M. Tharp, A finite element for edge-crack beam columns,Int. J. Numer. Methods Engng.,24 (1987), 1941–1950.

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, Shanghai Jiaotong University, 200030, Shanghai, PR China

    Chen Mengcheng & Tang Renji

Authors
  1. Chen Mengcheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tang Renji
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mengcheng, C., Renji, T. An approximate method of response analysis of vibrations for cracked beams. Appl Math Mech 18, 221–228 (1997). https://doi.org/10.1007/BF02453364

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02453364

Key words

Search

Navigation