Skip to main content
SpringerLink
Log in

A more comprehensive method for yield locus construction for metallic alloys and composites

  • Published:
Experimental Mechanics Aims and scope Submit manuscript

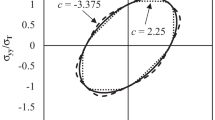
Abstract

Conventional methods for constructing yield loci rely on the assumption that nonlinear strains are permanent strains, which is not always the case. A nickel-base alloy, SiC fiber-reinforced titanium, an aluminum alloy, and particlereinforced aluminum have been observed to violate this assumption. We present a method for constructing yield loci using a proof strain criterion for the permanent strain that relies on cyclic, proportional, probes of the yield surface. Two criteria are implemented: one for stress reversal and one for yielding. The method is demonstrated by the construction of initial and subsequent yield loci in the axial-shear stress plane using thin-walled tubular specimens. Results are presented for 6061-T6 aluminum as well as for 6092/SiC/17.5p-T6, which is 6092 aluminum reinforced with 17.5 volume percent silicon carbide particulate. The centers of the initial yield loci for the composite are eccentric to the origin of the stress plane most likely because of the residual stresses induced during processing. Material hardening due to multiaxial stress states can be described by tracking evolution of the subsequent yield surfaces and here hardening of the particulate composite was primarily kinematic

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

D o, Di :

outer and inner diameters

P :

axial force

T :

torque

ɛ-45, ɛ0, ɛ45 :

normal strains measured by rosette

E 1, Eu :

Young's modulus

G l, Gu :

shear modulus

σ l, σu :

axial stress axis intercept

τ l, τu :

shear stress axis intercept

σ c, τc,a,b:

post-processed ellipse parameters

etv :

target value equivalent strain (proof strain)

e th :

threshold equivalent strain

Δσe :

equivalent stress increment

Θ:

probe angle

στ:

axial and shear stress

εγ:

axial and shear strain components

ɛ off,γ off,e off,ɛ off,γ off,e p :

offset and plastic strain components

⁛ cor :

axial offset strain correction; for compression only

σ max :

maximum equivalent stress in a cycle of a probe

σ0,τ0 :

center of yield surface probe pattern

s ij :

deviatoric stress tensor

ɛ pij :

plastic strain tensor

References

  1. Sun, L.Z. Ju, J.W. andLiu, H.T., “Elastoplastic Modeling of Metal Matrix Composites with Evolutionary Particle Debonding,”Mechanics of Materials,35,559–569 (2003).

    Article  Google Scholar 

  2. Ahmad, J., Newaz, G.M. andNicholas, T., “Analysis of Characterization Methods for Inelastic Composite Material Deformation under Multiaxial Stress,” Multiaxial Fatigue and Deformation: Testing and Prediction, ASTM-STP 1387, S. Kalluri andP.J. Bonacuse, editors, American Society for Testing and Materials, West Conshohocken, PA, 41–53 (2000).

    Google Scholar 

  3. Li, M., Ghosh, S. andRichmond, O., “An Experimental-Computational Approach to the Investigation of Evolution in Discontinuously Reinforced Aluminum Matrix Composites,”Acta Materialia,47,3515–3532 (1999).

    Article  Google Scholar 

  4. Lissenden, C.J., Arnold, S.M. andIyer, S.K., “Flow/Damage Surfaces for Fiber-Reinforced Metals Having Different Periodic Microstructures,”International Journal of Plasticity,16,1049–1074 (2000).

    Article  MATH  Google Scholar 

  5. Lissenden, C.J. andArnold, S.M., “Theoretical and Experimental Considerations in Representing Macroscale Flow/Damage Surfaces for Metal Matrix Composities”International Journal of Plasticity,13,327–358 (1997).

    Article  Google Scholar 

  6. Lode, W., “Versuche über den Einfluss der mittleren Hauptspannung auf das Fliessen der Metalle, Eisen, Kupfer, und Nickel,”Zeitscrift für Physik,36,913–939 (1926).

    Article  Google Scholar 

  7. Taylor, G.I. andQuinney, H., “The Plastic Distortion of Metals,”Philosophical Transactions of the Royal Society (London) Series A,230,323–362 (1937).

    Google Scholar 

  8. Tresca, H.E., “Sur l'écoulement des corps solides soumis á de fortes pressions,”Comptes Rendus de l'Académie des Sciences (Paris),59,754 (1864).

    Google Scholar 

  9. von Mises, R., “Mechanik der festen Körper im plastisch deformablen Zustand,” Nachrichten der Gesellschaft der Wissenschaften in Göttingen, Mathematisch Physikalische Klasse, 582–592 (1913).

  10. Hill, R., The Mathematical Theory of Plasticity, Oxford University Press, London (1950).

    MATH  Google Scholar 

  11. Hecker, S.S., “Experimental Studies of Yield Phenomena in Biaxially Loaded Metals,”Constitutive Equations in Viscoplasticity: Computational and Engineering Aspects, AMD-Vol. 20, J.A. Stricklin andK.J. Saczalski, editors,ASME, New York, 1–33 (1976).

    Google Scholar 

  12. Michno, M.J. andFindley, W.N., “An Historical Perspective of Yield Surface Investigations For Metals,”International Journal of Nonlinear Mechanics,11,59–82 (1976).

    Article  MATH  Google Scholar 

  13. Liu, K.C. andGreenstreet, W.L., “Experimental Studies to Examine Elastic-Plastic Behavior of Metal Alloys Used in Nuclear Structures,”Constitutive Equations in Viscoplasticity: Computational and Engineering Aspects, AMD-Vol. 20, J.A. Stricklin andK.J. Saczalski, editors ASME, New York, 35–56 (1976).

    Google Scholar 

  14. Phillips, A., “A Review of Quasi-Static Experimental Plasticity and Viscoplasticity,”International Journal of Plasticity,2,315–328 (1986).

    Article  Google Scholar 

  15. Helling, D.E., Miller, A.K. andStout, M.G., “An Experimental Investigation of the Yield Loci of 1100-0 Aluminum, 70:30 Brass, and an Overaged 2024 Aluminum Alloy After Various Prestrains,”Journal of Engineering Technology,108,313–320 (1986).

    Article  Google Scholar 

  16. Dvorak, G.J., Bahei-El-Din, Y.A., Macheret, Y. andLiu, C.H., “An Experimental Study of Elastic-Plastic Behavior of a Fibrous Boron-Aluminum Composite,”Journal of the Mechanics and Physics of Solids,36,655–687 (1988).

    Article  Google Scholar 

  17. Wu, H.C. andYeh, W.C., “On the Experimental Determination of Yield Surfaces and Some Results of Annealed 304 Stainless Steel,”International Journal of Plasticity,7,803–826 (1991).

    Article  Google Scholar 

  18. Khan, A. andWang, X., “An Experimental Study on Subsequent Yield Surface After Finite Shear Prestraining,”International Journal of Plasticity,9,889–905 (1993).

    Article  Google Scholar 

  19. Gil, C.M., Lissenden, C.J. andLerch, B.A., “Yield of Inconel 718 by Axial-Torsional Loading at Temperatures up to 649°C,”Journal of Testing and Evaluation,27,327–336 (1999).

    Article  Google Scholar 

  20. Lissenden, C.J., Lerch, B.A., Ellis, J.R. andRobinson, D.N., “Experimental Determination of Yield and Flow Surfaces Under Axial-Torsional Loading,”Multiaxial Fatigue and Deformation Testing Techniques, ASTM STP 1280, S. Kalluri andP.J. Bonacuse, editors American Society for Testing and Materials, West conshohocken, PA, 92–112 (1997).

    Google Scholar 

  21. Gil, C.M., Lissenden, C.J. andLerch, B.A., “Unusual Response of Some Metallic Materials,”Mechanics of Materials,31,565–577 (1999).

    Article  Google Scholar 

  22. Hirth, J.P. andCohen, M., “On the Strength-Differential Phenomenon in Hardened Steel,”Metallurgical Transactions,1,3–8 (1970).

    Google Scholar 

  23. Arsenault, R.J. andTaya, M., “Thermal Residual Stress in Metal Matrix Composite,”Acta Metallurgica,35,651–659 (1987).

    Article  Google Scholar 

  24. Arsenault, R.J. andWu, S.B., “The Strength Differential and Bauschinger Effects in SiC−Al Composites,”Material Science and Engineering A,96,77–88 (1987).

    Article  Google Scholar 

  25. Lubliner, J., Plasticity Theory, Macmillan, New York (1990).

    MATH  Google Scholar 

  26. Shen, H. andLissenden, C.J., “3D Finite Element Analysis of Particle-Reinforced Aluminum,”Material Science and Engineering A,338,271–281 (2002).

    Article  Google Scholar 

  27. Lei, X. andLissenden, C.J., “Tensile, Compressive, and Shear Response of a Particulate Reinforced Aluminum Composite,”composite Materials: Testing and Design Fourteenth Volume, ASTM STP 1436, American Society for Testing and Materials, C.E. Bakis, editor West Conshohoken, PA, 255–272 (2003).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering Science and Mechanics, Penn State University, 16802, University Park, PA, USA

    C. J. Lissenden (Associate Professor) & X. Lei (Research Assistant)

Authors
  1. C. J. Lissenden
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. X. Lei
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lissenden, C.J., Lei, X. A more comprehensive method for yield locus construction for metallic alloys and composites. Experimental Mechanics 44, 10–20 (2004). https://doi.org/10.1007/BF02427970

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02427970

Key words

Search

Navigation