Abstract
The RockwellC hardness,RC, was measured as a function of position on steel rings with different residual-stress profiles through the thickness. An experimental correlation between residual stress andRC was obtained. A relationship between the average pressurep of a spherical indenter, the yield strengthS y and the residual stress of the material was conceived and used in fitting the experimental data.
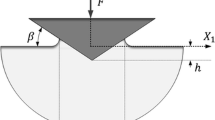
In order to model the effects of residual stresses on the measured hardness, the von Mises-Hencky (power) yield criterion was utilized, together with an adaptation for residual stresses of the expression for the stress state under a spherical indenter, given in Shaw, Hoshi and Henry. A parameter α was introduced in our calculations to account for the effect of the nonperpendicularity of the residual stresses to the pressurep of the spherical indenter.
The proposed model in large measure fits experimental hardness versus residual stress data, and results are consistent with different samples. This model can be used as a basis for the measurement of residual stresses in steel or other materials.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Abbreviations
- A :
-
acoustoelastic constant
- b 1 :
-
constant of conversion betweenR C andp, i=1…5
- BHN :
-
Brinell hardness number
- c 1, c2 :
-
constants of conversion betweenR C andBHN
- d :
-
diameter of the ball indentation
- D :
-
diameter of the ball indenter
- h :
-
depth of the indentation
- MHN :
-
Meyer hardness number
- p :
-
average pressure under spherical indenter
- R C :
-
RockwellC hardness
- R C0 :
-
RockwellC hardness at zero residual stress
- S y :
-
yield strength
- W :
-
load applied to the indenter
- ν:
-
sound wave velocity
- ν 0 :
-
sound wave velocity for zero residual stresses
- α:
-
stress scaling factor
- σ:
-
Residual stress
- σ R :
-
radial residual stress
- σ H :
-
hoop residual stress
- τ max :
-
maximum shear stress
References
Shaw, M.C., Hoshi, T. andHenry, P., “Reverse Plastic Flow Associated with Plastic Indentation,”Trans. ASME,101,104–108, (1979).
Holm, E., Holm, R. andShobert, II, E.I., “Theory of Hardness and Measurements Applicable to Contact Problems,”J. Appl. Physics,20,319–320, (1949).
Blain, P.A., “Influence of Residual Stress on Hardness,”Metal Progress,71 99–100 (1957).
Oppel, G.U., “Biaxial Elasto-Plastic Analysis of Load and Residual Stresses,”Experimental Mechanics,4,135–140 (1964).
Sines, T.R., Mellor, S.G. andHills, P.A., “A Note on the Influence of Residual Stress on Measured Hardness,”J. of Strain Analysis,19 (2),135–137 (1984).
Brown, B.B., “Measurement of Extent of Autofrettage in Tube Sections,” Technical Rep. ARLCB-TR-83042 (1983).
Frankel J., Scholz W., Capsimalis G. and Korman W., “Residual Stress Measurement in Circular Steel Cylinders,” Proc. IEEE Ultrasonic Symp. 1009–1012 (1983).
Scholz, W., Frankel J., “Acoustoelastic Effects in Autofrettaged Steel Cylinders,” Proc. Conf. Ultrasonics International, 441–446, Butterworth & Co. Publ. Ltd. (1985).
Hughes, P.S. andKelly, J.L., “Second Order Elastoic Deformation of Solids,”Phys. Rev.,92,1145–1149 (1953).
Murnaghan, F.P., Finite Deformation of an Elastic Solid, John Wiley, New York (1951).
Timoshenko, S.P. andGoodier, J.N., Theory of Elasticity, 3rd Ed., McGraw-Hill, New York, 72 (1970).
Kapp, J.A. andPflegl, G.A., “Stress Analysis of O.D. Notched Thick-Walled Cylinders Subjected to Internal Pressure or Thermal Loads,”J. Press. Vessel Tech.,103,76–81 (1981).
Harvey, J.F., Theory and Design of Modern Pressure Vessels, 2nd Ed., Van Nostrand Reinhold, 61–67, New York (1974).
Tabor, T., The Hardness of Metals, Oxford at the Clarendon Press (1951).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Frankel, J., Abbate, A. & Scholz, W. The effect of residual stresses on hardness measurements. Experimental Mechanics 33, 164–168 (1993). https://doi.org/10.1007/BF02322494
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02322494