Abstract
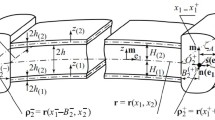
Displacements and transverse normal stresses in sandwich plates and masses have been approximated by the Ambartsumyan iterative approach to constructing mathematical models of the stress-strain state of sandwich structures. A linear distribution of the displacements in the sandwich structure is set up as the first step of the iterative process, while in the subsequent steps the displacement approximations with higher-order polynomials are obtained. The approximation of the compression stresses is based on Hooke's law using the expression of the tangential displacements in the second step and the normal displacements in the third step of the iterative process. Two shear functions are introduced. The finite element is rectangular and has four nodes. The number of degrees of freedom of finite elements is independent of the quantity of the layers that may be orthotropic. The finite element allows us to simulate delamination by a thin low-modulus interlayer. In doing so, the quantity of the layers increases, while the order of the resolving set of equations does not grow. A number of numerical experiments were carried out. It has been shown that the delamination can greatly increase the level of the stresses in the structure. This effect is especially significant for thin structures. The stresses are somewhat lower when taking into account the interlaminar friction.
Similar content being viewed by others
References
A. A. Dudchenko, S. A. Lur'e, and S. A. Obraztsov, “Anisotropic multilayer plates and shells,” Itogi Nauki i Tekhniki. Mekhanika Deformiruemogo Tverdogo Tela,15, 3–68 (1983).
J. N. Reddy, “A review of the literature on finite-element modeling of laminated composite plates,” Shock Vibr. Digest,17, 3–8 (1985).
R. K. Kapania and S. Richiti, “Recent achievements in studies on beams and plates. Part 1: Effect of shear and stability,” Aerokosm. Tekhn., No. 5, 43–57 (1990).
R. L. Spilker, S. C. Chou, and O. Orringer, “Alternate hybrid-stress elements for analysis of multilayer composite plates,” J. Compos. Mater.,11, 51–70 (1977).
R. L. Hinrichsen and A. N. Palazotto, “Nonlinear finite-element analysis of thick composite plates using cubic spline functions,” AIAA J.,24, 1836–1842 (1986).
J. Argiros and D. Sharpf, “Calculation theory for plates and shells with account of transverse shear strains based on the finite element method,” in: Computer Calculation of Elastic Structures, Vol. 1 [in Russian], Sudostroenie, Leningrad (1974), pp. 179–210.
R. B. Rikards and A. K. Chate, “Isoparametric triangular finite element of a multilayered shell after Timoshenko's shear model. 1. Stiffness, mass, and geometric-element-stiffness matrices,” Mech. Compos. Mater.,17, No. 3, 302–309 (1981).
R. B. Rikards and A. K. Chate, “Isoparametric triangular finite element of a multilayer shell according to the Timoshenko shear model. 2. Numerical examples,” Mech. Compos. Mater.17, No. 5, 547–551 (1981).
J. N. Reddy, “Finite-element modeling of layered, anisotropic composite plates and shells: A review of recent research,” Shock Vibr. Digest,13, 3–12 (1981).
A. O. Rasskazov, “Calculation of multilayer orthotropic shells by the finite element method,” Prikl. Mekh.,14, No. 8, 51–57 (1978).
N. D. Phan and J. N. Reddy, “Analysis of laminated composite plates using a higher-order shear-deformation theory,” Int. J. Numer. Meth. Eng.,21, 2201–2219 (1985).
J. G. Ren and E. Hinton, “The finite-element analysis of homogeneous and laminated composite plates using a simple higher-order theory,” Commun. Appl. Numer. Meth.,2, 217–228 (1986).
A. O. Rasskazov, I. I. Sokolovskaya, and N. A. Shul'ga, Theory and Calculation of Laminated Orthotropic Plates and Shells [in Russian], Vishcha Shkola, Kiev (1986).
S. A. Ambartsumyan, Theory of Anisotropic Plates [in Russian], Nauka, Moscow (1987).
J. N. Reddy, “A simple higher-order theory for laminated composites” J. Appl. Mech.,51, 745–752 (1984).
V. G. Piskunov, “Construction of a discrete-continuum scheme for calculating inhomogeneous plates using the finite element method,” Soprot. Mater. Teor. Sooruzh.,33, 78–81 (1978).
A. V. Marchuk, “Generalization of discrete and continuous structural approaches to elaboration of a mathematical model of laminated plates and masses,” Mech. Compos. Mater.,32, No. 3, 261–269 (1996).
N. J. Pagano, “Exact solutions for rectangular bidirectional composites and sandwich plates,” J. Compos. Mater.,4, 20–34 (1970).
A. V. Marchuk, “Three-dimensional analytical solution for laminated plates with regard to friction of layers,” Prikl. Mekh.,33, No. 9, 10–14 (1997).
V. G. Piskunov et al., Calculation of Inhomogeneous Shallow Shells and Plates Using the Finite Element Method [in Russian], Vishcha Shkola, Kiev (1987).
V. A. Bazhenov et al., A Semianalytic Finite Element Method in the Mechanics of Deformable Bodies [in Russian], NII SM, Kiev (1993).
Additional information
Submitted to the 10th International Conference on Mechanics of Composite Materials (Riga, April 20–23, 1998).
Ukrainian Transport University, Kiev, Ukraine. Translated from Mekhanika Kompozitnykh Materialov, Vol. 34, No. 2, pp. 251–263, March–April, 1998.
Rights and permissions
About this article
Cite this article
Marchuk, A.V. Finite element construction for simulating delamination of sandwich composite plates and masses. Mech Compos Mater 34, 184–193 (1998). https://doi.org/10.1007/BF02256037
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02256037