Skip to main content
SpringerLink
Log in

Refined stability theory for sandwich shells with transversally stiff core. 1. Nonlinear equilibrium equations

  • Published:
Mechanics of Composite Materials Aims and scope

Abstract

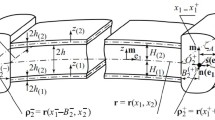
A refined version of geometrically nonlinear relationships is proposed for the static thermoelastic response of sandwich shells with face sheets made of composite or homogeneous materials and a transversally stiff core. This theory has primary importance for studying mixed forms of buckling of the bearing sheets, which are mainly realized in the zones of a momentary stress-deformed state of the shell on the whole. An iteration procedure was developed for construction of the model. In the first step, assuming that the core is transversally soft, expressions are derived for the components of the displacement vector after integration of the three-dimensional equilibrium equations. In the second step, the tangential stresses are determined assuming a transversally stiff core to obtain the in-plane stresses and highly accurate transverse normal stresses. The proposed model admits a formal changeover to the model of a shell with a transversely soft core.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. N. Paimushin and S. N. Bobrov, “Buckling forms of sandwich plates and shells with face sheets made of homogeneous and reinforced materials” Mekhan. Kompozitn. Mater., No. 1, 79–86 (1985).

    Google Scholar 

  2. V. V. Bolotin and Yu. N. Novichkov, Mechanics of Multilayered Objects [in Russian], Mashinostroenie, Moscow (1980).

    Google Scholar 

  3. V. A. Ivanov and V. N. Paimushin, “Refined theory of the stability of sandwich structures (nonlinear equations of the precritical equilibrium of shells with transversally soft cores)”, Izv. Vyssh. Uchebn. Zaved., Matem, No. 11, 29–42 (1994).

    Google Scholar 

  4. Yu. V. Orlov, V. N. Paimushin, and T. V. Polyakova, “Refined postulation of problems of the stability of momentary equilibrium of sandwich rotational shells with transversally soft cores”, in: Proceedings of the Sixteenth International Conference on the Theory of Shells and Plates [in Russian], Vol. 2, Izd. Nizhegorodsk. Univ., Nizhnii Novgorod (1994), pp. 167–176.

    Google Scholar 

  5. V. A. Ivanov, V. N. Paimushin and T. V. Polyakova, “Refined theory of the stability of sandwich structures (linearized neutral equilibrium equations and simple one-dimensional problems)”, Izv. Vyssh. Uchebn. Zaved., No. 3, 15–24 (1995).

    Google Scholar 

  6. V. A. Ivanov and V. N. Paimushin, “Refined postulation of dynamic problems of sandwich shells with transversally soft cores and numeroanalytical method for their solution”, Prikl. Mekhan. Tekhn. Fiz.,36, No. 4, 137–151 (1995).

    Google Scholar 

  7. A. I. Golovanov, V. A. Ivanov, and V. N. Paimushin, “Numeroanalytical method for studying local buckling forms of bearing layers of sandwich shells using mixed forms,” Mekhan. Kompozitn. Mater.,31, No. 1, 88–100 (1995).

    Google Scholar 

  8. V. N. Paimushin, “Refined theory of the stability of multilayered structures (nonlinear equations for the precritical equilibrium of multilayered shells with transversally soft cores)”, in: Fundamental and Applied Problems in the Mechanics of Strained Media and Structures [in Russian], No. 1, Izd. Nizhegorodsk. Univ., Nizhnii Novgorod(1993), pp. 44–56.

    Google Scholar 

  9. V. A. Ivanov and V. N. Paimushin, “Stability of flat multilayered shells with transversally soft cores”, Mekhan. Kompozitn. Mater., No. 3, 372–390 (1994).

    Google Scholar 

  10. M. K. Galimov, V. A. Ivanov, and V. N. Paimushin, “Problem of stability of momentary equilibrium of sandwich panels and shells and modeling of a core in a perturbed state,” in: Proceedings of the Seventeenth International Conference on the Shell and Panel Theory [in Russian], Kazan (1995).

  11. V. G. Piskunov and V. E. Verizhenko, Linear and Nonlinear Problems for the Calculation of Layered Structures [in Russian], Budivel'nik, Kiev (1986).

    Google Scholar 

  12. A. K. Noor, W. S. Burton, and J. M. Peters, “Hierarchical adaptive modeling of structural sandwiches and multilayered composite panels”, Appl. Num. Math., No. 14, 69–90 (1994).

    Article  Google Scholar 

  13. K. Z. Galimov, Fundamentals of the Nonlinear Theory of Thin Shells [in Russian], Izd. Kazan'sk. Univ., Kazan (1975).

    Google Scholar 

  14. V. N. Paimushin, “Variational methods for solving nonlinear spatial problems of the conjugation of strained objects”, Dokl. Akad. Nauk SSSR,273, No. 5, 1083–1086 (1983).

    Google Scholar 

  15. V. N. Paimushin, “Iteration variant of the refined nonlinear theory of fine elastic sandwich shells”, Prikl. Matem. Mekhan.,54, No. 1, 86–92 (1990).

    Google Scholar 

Download references

Authors
  1. V. N. Paimushin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. I. Mushtari
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Center for the Study of Dynamics and Stability. A. N. Tupolev Kazan State Technical University, Kazan, Tatarstan, Russia. Translated from Mekhanika Kompozitnykh Materialov, Vol. 32, No. 4, pp. 513–524, July–August, 1996.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Paimushin, V.N., Mushtari, A.I. Refined stability theory for sandwich shells with transversally stiff core. 1. Nonlinear equilibrium equations. Mech Compos Mater 32, 355–363 (1996). https://doi.org/10.1007/BF02254748

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02254748

Keywords

Search

Navigation