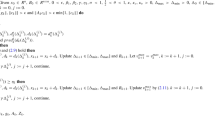Abstract
In this note, we derive a geometric formulation of an ideal penalty function for equality constrained problems. This differentiable penalty function requires no parameter estimation or adjustment, has numerical conditioning similar to that of the target function from which it is constructed, and also has the desirable property that the strict second-order constrained minima of the target function are precisely those strict second-order unconstrained minima of the penalty function which satisfy the constraints. Such a penalty function can be used to establish termination properties for algorithms which avoid ill-conditioned steps. Numerical values for the penalty function and its derivatives can be calculated efficiently using automatic differentiation techniques.
Similar content being viewed by others
References
Fletcher, R.,A Class of Methods for Nonlinear Programming with Termination and Convergence Properties, Integer and Nonlinear Programming, Edited by J. Abadie, North-Holland, Amsterdam, Holland, pp. 157–175, 1970.
Fletcher, R., andLill, S.,A Class of Methods for Nonlinear Programming, II: Computational Experience, Nonlinear Programming, Edited by J. B. Rosen et al., Academic Press, New York, New York, pp. 67–92, 1970.
Fletcher, R.,A Class of Methods for Nonlinear Programming, III: Rates of Convergence, Numerical Methods for Nonlinear Optimization, Edited by F. A. Lootsma, Academic Press, New York, New York, pp. 371–393, 1973.
Di Pillo, G., andGrippo, L.,A New Class of Augmented Lagrangians in Nonlinear Programming, SIAM Journal on Control and Optimization, Vol. 17, pp. 618–628, 1979.
Di Pillo, G., et al.,An RQP Algorithm Using a Differentiable Exact Penalty Function for Inequality Constrained Problems, Mathematical Programming, Vol. 55, pp. 49–68, 1992.
Bertsekas, D. P.,Enlarging the Region of Convergence of Newton's Method for Constrained Optimization, Journal of Optimization Theory and Applications, Vol. 36, pp. 221–252, 1982.
Biggs, M. C.,On the Convergence of Some Constrained Minimization Algorithms Based on Recursive Quadratic Programming, Journal of the IMA, Vol. 21, pp. 67–81, 1978.
Powell, M. J. D., andYuan, Y.,A Recursive Quadratic Programming Algorithm That Uses Differentiable Exact Penalty Functions, Mathematical Programming, Vol. 35, pp. 265–278, 1984.
Griewank, A.,On Automatic Differentiation, Mathematical Programming: Recent Developments and Applications, Edited by M. Iri and K. Tanabe, Kluwer Academic Publishers, Tokyo, Japan, pp. 83–108, 1989.
Griewank, A., andCorliss, G., Editors,Automatic Differentiation of Algorithms, Society for Industrial and Applied Mathematics, Philadelphia, Pennsylvania, 1991.
Christianson, B.,Automatic Hessians by Reverse Accumulation, IMA Journal of Numerical Analysis, Vol. 12, pp. 135–150, 1992.
Dixon, L. C. W., andPrice, R. C.,Truncated Newton Algorithms for Large-Scale Unconstrained Optimization Using Automatic Differentiation, Journal of Optimization Theory and Applications, Vol. 60, pp. 261–275, 1989.
Christianson, B.,Reverse Accumulation of Functions Containing Gradients, Technical Report No. 278, Numerical Optimisation Centre, University of Hertfordshire, Hatfield, England, 1993.
Kubota, K.,An Implementation of Fast Automatic Differentiation with C++, Abstracts of the Spring 1989 Meeting of the Operations Research Society of Japan, pp. 175–176, 1989 (in Japanese).
Bischof, C. et al.,Structured Second- and Higher-Order Derivatives through Univariate Taylor Series, Optimization Methods and Software, Vol. 2, pp. 211–232, 1993.
Pearlmutter, B.,Fast Exact Multiplication by the Hessian, Neural Computing, Vol. 6, pp. 147–160, 1994.
Yoshida, T.,Rapid Learning Method for Multilayered Neural Networks Using Two-Dimensional Conjugate Gradient Search, Journal of Information Processing, Vol. 15, pp. 79–86, 1992.
Gilbert, J. C.,Automatic Differentiation and Iterative Processes, Optimization Methods and Software, Vol. 1, pp. 13–21, 1992.
Christianson, B.,Reverse Accumulation and Attractive Fixed Points, Optimization Methods and Software, Vol. 3, pp. 311–326, 1994.
Griewank, A., et al.,Derivative Convergence for Iterative Equation Solvers, Optimization Methods and Softwave, Vol. 2, pp. 321–355, 1993.
Fletcher, R.,An Exact Penalty Function for Nonlinear Programming with Inequalities, Mathematical Programming, Vol. 5, pp. 129–150, 1973.
Author information
Authors and Affiliations
Additional information
Communicated by L. C. W. Dixon
Rights and permissions
About this article
Cite this article
Christianson, B. Geometric approach to Fletcher's ideal penalty function. J Optim Theory Appl 84, 433–441 (1995). https://doi.org/10.1007/BF02192124
Issue Date:
DOI: https://doi.org/10.1007/BF02192124