Abstract
We study representations of the central extension of the Lie algebra of differential operators on the circle, the

algebra. We obtain complete and specialized character formulas for a large class of representations, which we call primitive; these include all quasi-finite irreducible unitary representations. We show that any primitive representation with central chargeN has a canonical structure of an irreducible representation of the

with the same central charge and that all irreducible representations of

with central chargeN arise in this way. We also establish a duality between “integral” modules of

and finite-dimensional irreducible modules ofgl N , and conjecture their fusion rules.
Similar content being viewed by others
References
[ASvM] Adler, M., Shiota, T., van Moerbeke, P.: From thew ∞ algebra to its central extension: A τ-function approach. Preprint
[AFOQ] Awata, H., Fukuma, M., Odake, S., Quano, Y.-H.: Eigensystem and full character formula of the
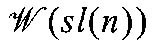 algebra withc=1. Preprint YITP/K-1049, Dec 1993, hep-th/9312208
algebra withc=1. Preprint YITP/K-1049, Dec 1993, hep-th/9312208[AFMO] Awata, H., Fukuma, M., Matsuo, Y., Odake, S.: Determinant formulae of quasi-finite representation of
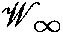 algebra at lower levels. Preprint YITP/K-1054, Jan 1994, hep-th/9402001
algebra at lower levels. Preprint YITP/K-1054, Jan 1994, hep-th/9402001[BBSS] Bais, F.A., Bouwknegt, P., Schoutens, K., Surridge, M.: Extensions of the Virasoro algebra constructed from Kac-Moody algebras using higher order Casimir invariants. Nucl. Phys.B304, 348–370 (1988)
[BK] Bakas, I., Kiritsis, E.: Bosonic realization of a universal
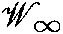 and Z∞ parafermions. Nucl. Phys.B343, 185–204 (1990)
and Z∞ parafermions. Nucl. Phys.B343, 185–204 (1990)[B] Borcherds, R.: Vertex algebras, Kač-Moody algebras, and the Monster. Proc. Natl. Acad. Sci. USA83, 3068–3071 (1986)
[Bo] Bouwknegt, P.: “Extended conformal algebras from Kac-Moody algebras.” In: Infinitedimensional Lie algebras and groups, ed. V. Kac, Adv. Ser. in Math. Phys.7, Singapore: World Scientific, 1989, pp. 527–555
[BMP] Bouwknegt, P., McCarthy, J., Pilch, K.: Semi-infinite cohomology of
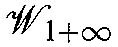 . Preprint USC, Feb 1993, hep-th/9302086
. Preprint USC, Feb 1993, hep-th/9302086[BS] Bouwknegt, P., Schoutens, K.: W-symmetry in conformal field theory. Phys. Rep.223, 183–276 (1993)
[CTZ] Capelli, A., Trugenberger, C.A., Zemba, G.R.: Infinite symmetry in the quantum Hall effect. Nucl. Phys.B396, 465–490 (1993) and Classification of quantum Hall universality classes by
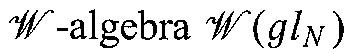 symmetry. Phys. Rev. Lett.72, 1902–1905 (1994)
symmetry. Phys. Rev. Lett.72, 1902–1905 (1994)[FL] Fateev, V., Lukyanov, S.: Conformally invariant models of two-dimensional quantum field theory with ℤ n -symmetry. Sov. Phys. JETP67, 447–462 (1988)
[FF1] Feigin, B., Frenkel, E.: Affine Kac-Moody algebras at the critical level and Gelfand-Dikii algebras. Int. J. Mod. Phys. A Suppl.1A, 197–215 (1992)
[FF2] Feigin, B., Frenkel, E.: Integrals of motion and quantum groups. Yukawa Institute preprint YUTP/K-1036, Sep 1993, hep-th/9310022. To appear in Proceedings of the Summer School Integrable Systems and Quantum Groups, Montecatini Terme, Italy, June 1993, Lect. Notes in Math., Springer Verlag
[FFu] Feigin, B.L., Fuchs, D.B.: Cohomology of some nilpotent subalgebras of Virasoro algebra and affine Kac-Moody Lie algebras. J. Geom. Phys.5, 209–235 (1988)
[F1] Frenkel, I.B.: Representations of affine Lie algebras, Hecke modular forms and Kortewegde Vries type equations. Lect. Notes in Math.933, 71–110 (1982)
[F2] Frenkel, I.B.: Representations of Kac-Moody algebras and dual resonance models. In: Applications of Group Theory in Physics and Mathematical Physics, eds. M. Flato, P. Sally, G. Zuckerman, Lect. in Appl. Math.21, Providence, RI: AMS, 1985, pp. 325–353
[FHL] Frenkel, I.B., Huang, Y.-Z., Lepowsky, J.: On axiomatic approaches to vertex operator algebras and modules. Mem. Am. Math. Soc.104, No. 494 (1993)
[FK] Frenkel, I.B., Kac, V.G.: Basic representations of affine Lie algebras and dual resonance models. Invent. Math.62, 23–66 (1980)
[FLM] Frenkel, I.B., Lepowsky, J., Meurman, A.: Vertex Operator Algebras and the Monster. New York: Academic Press, 1988
[FKN] Fukuma, M., Kawai, H., Nakayama, R.: Infinite Dimensional Grassmannian Structure of Two-Dimensional Quantum Gravity. Commun. Math. Phys.143, 371–403 (1992)
[G] Goddard, P.: Meromorphic conformal field theory. In: Infinite-dimensional Lie algebras and groups. ed. V. Kac, Adv. Ser. in Math. Phys.7, Singapore: World Scientific, 1989, pp. 556–587
[IKS] Iso, S., Karabali, D., Sakita, B.: Fermions in the lowest Landau level bosonization,w ∞ algebra, droplets, chiral bosons. Phys. Lett.B296, 143–150 (1992)
[K] Kac, V.G.: Contravariant form for infinite-dimensional Lie algebras and superalgebras. Lect. Notes in Phys.94, 441–445 (1979)
[K1] Kac, V.G.: An elucidation of “Infinite-dimensional algebras ... and the very strange formula.E (1)8 and the cube root of the modular invariant j”. Adv. Math.35, 264–273 (1980)
[K2] Kac, V.G.: Infinite-dimensional Lie algebras. Third edition, Cambridge: Cambridge University Press, 1990
[KP1] Kac, V.G., Peterson, D.H.: Spin and wedge representations of infinite-dimensional Lie algebras and groups. Proc. Natl. Acad. Sci. USA78, 3308–3312 (1981)
[KP2] Kac, V.G., Peterson, D.H.: Lectures on the infinite wedge representation and the MKP hierarchy. Seminaire de Math. Superieures, Les Presses de L'Universite de Montreal102, 141–186 (1986)
[KR] Kac, V.G., Radul, A.: Quasi-finite highest weight modules over the Lie algebra of differential operators on the circle. Commun. Math. Phys.157, 429–457 (1993), hep-th/9308153
[L] Li, H.: Local systems of vertex operators, vertex superalgebras and modules. Preprint
[M] Macdonald, I.: Symmetric functions and Hall polynomials. Oxford: Clarendon Press, 1979
[Mat] Matsuo, Y.: Free fields and quasi-finite representations of
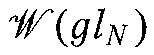 . Phys. Lett.B326, 95–100 (1994), hep-th/9312192
. Phys. Lett.B326, 95–100 (1994), hep-th/9312192[N] Niedermaier, M.: Irrational free field resolutions for
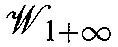 and extended Sugawara construction. Commun. Math. Phys.148, 249–281 (1992)
and extended Sugawara construction. Commun. Math. Phys.148, 249–281 (1992)[PRS] Pope, C.N., Romans, L.J., Shen, X.:
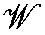 and the Racah-Wigner algebra. Nucl. Phys.339B, 191–221 (1990)
and the Racah-Wigner algebra. Nucl. Phys.339B, 191–221 (1990)[R] Radul, A.: Lie algebras of differential operators, their central extensions, and W-algebras. Funct. Anal. and Appl.25, 86–91 (1991)
[W] Wang, W.: Rationality of Virasoro vertex operator algebras. Duke Math. J., IMRN,71, 197–211 (1993)
[Z] Zamolodchikov, A.: Infinite additional symmetries in two dimensional conformal quantum field theory. Theor. Math. Phys.65, 1205–1213 (1986)
[Zh] Zhu, Y.: Vertex operator algebras, elliptic functions and modular forms. Ph.D. thesis, Yale Univ. (1990)
Author information
Authors and Affiliations
Additional information
Communicated by M. Jimbo
Supported by a Junior Fellowship from Harvard Society of Fellows and in part by NSF grant DMS-9205303.
Supported in part by NSF grant DMS-9103792.
Rights and permissions
About this article
Cite this article
Frenkel, E., Kac, V., Radul, A. et al.  with central chargeN
.
Commun.Math. Phys. 170, 337–357 (1995). https://doi.org/10.1007/BF02108332
with central chargeN
.
Commun.Math. Phys. 170, 337–357 (1995). https://doi.org/10.1007/BF02108332
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02108332



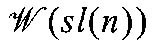 algebra withc=1. Preprint YITP/K-1049, Dec 1993, hep-th/9312208
algebra withc=1. Preprint YITP/K-1049, Dec 1993, hep-th/9312208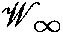 algebra at lower levels. Preprint YITP/K-1054, Jan 1994, hep-th/9402001
algebra at lower levels. Preprint YITP/K-1054, Jan 1994, hep-th/9402001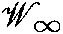 and Z∞ parafermions. Nucl. Phys.B343, 185–204 (1990)
and Z∞ parafermions. Nucl. Phys.B343, 185–204 (1990)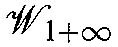 . Preprint USC, Feb 1993, hep-th/9302086
. Preprint USC, Feb 1993, hep-th/9302086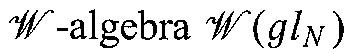 symmetry. Phys. Rev. Lett.72, 1902–1905 (1994)
symmetry. Phys. Rev. Lett.72, 1902–1905 (1994)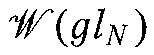 . Phys. Lett.B326, 95–100 (1994), hep-th/9312192
. Phys. Lett.B326, 95–100 (1994), hep-th/9312192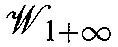 and extended Sugawara construction. Commun. Math. Phys.148, 249–281 (1992)
and extended Sugawara construction. Commun. Math. Phys.148, 249–281 (1992)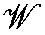 and the Racah-Wigner algebra. Nucl. Phys.339B, 191–221 (1990)
and the Racah-Wigner algebra. Nucl. Phys.339B, 191–221 (1990)