Viscosity of saturated R152a measured with a vibrating wire viscometer

Abstract

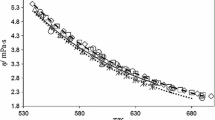
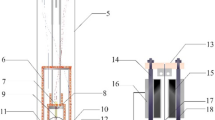
Earlier reported values of the viscosity coefficient of the refrigerant R152a (1,1-difluoroethane) have been recalculated with an improved value for the mechanical damping of the vibrating wire viscometer. The measurements were taken along the saturation line both in the saturated liquid and in the saturated vapor every 10 K from 243 up to 393 K by means of a vibrating wire viscometer The damping of the vibration of the wire is a measure for the viscosity provided that the mechanical damping is subtracted. The latter is usually measured in vacuum. It turns out that the damping value measured in this way depends on the vacuum pressure and on the way the wire has been handled before. It appeared that the damping applied previously, measured after 6 days of pumping, is too small, resulting in values of the viscosity coefficient which are too large. The effect on the data for the saturated-liquid viscosity is small, but the new saturated-vapor viscosity data agree much better with the unsaturated-vapor data reported by Takahashi et al.