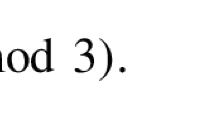Abstract
A formula expressing the Chebyshevψ function in terms of the characteristic values of the Laplace-Beltrami operator on the fundamental domain of a modular group and the hyperbolic classes of conjugate elements of this group is derived.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Literature cited
A. Selberg, “Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series,” J. Indian Math. Soc.,20, 47–87 (1956).
D. A. Hejhal, “The Selberg trace formula and the Riemann zeta function,” Duke Math. J.,43, 441–482 (1976).
E. T. Whittaker and G. N. Watson, A Course of Modern Analysis, Cambridge Univ. Press, Cambridge (1927).
Author information
Authors and Affiliations
Additional information
Translated from Matematicheskie Zametki, Vol. 23, No. 4, pp. 497–503, April, 1978.
Rights and permissions
About this article
Cite this article
Venkov, A.B. A formula for the Chebyshev PSI function. Mathematical Notes of the Academy of Sciences of the USSR 23, 271–274 (1978). https://doi.org/10.1007/BF01786954
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01786954