Numerical modeling studies of lee mesolows, mesovortices and mesocyclones with application to the formation of Taiwan mesolows

Summary

Numerical experiments are performed for inviscid flow past an idealized topography to investigate the formation and development of lee mesolows, mesovortices and mesocyclones. For a nonrotating, low-Froude number flow over a bell-shaped moutain, a pair of mesovortices form on the lee slope move downstream and weaken at later times. The advection speed of the lee vortices is found to be about two-thirds of the basic wind velocity, which is due to the existence of a reversed pressure gradient just upstream of the vortices. The lee vortices do not concur with the upstream stagnation point in time, but rather form at a later time. It is found that a pair of lee vortices form for a flow withFr=0.66, but take a longer time to form than in lower-Froude number flows. Since the lee vortices are formed rather progressively, their formation may be explained by the baroclinically-induced vorticity tilting as the mountain waves become more and more nonlinear.

A stationary mesohigh and mesolow pressure couplet forms across the mountain and is produced in both high and low-Froude number flows. The results of the high Froude number simulations agree well with the classical results predicted by linear, hydrostatic mountain wave theory. It is found that the lee mesolow is not necessarily colocated with the lee vortices. The mesolow is formed by the downslope wind associated with the orographically forced gravity waves through adiabatic warming. The earth's rotation acts to strengthen (weaken) the cyclonic (anticyclonic) vortex and shifts the lee mesolow to the right for an observer facing downstream. The cyclonic vortex then develops into a mesocyclone with the addition of planetary vorticity at later times. For a flow over a steeper mountain, the disturbance is stronger even though the Froude number is kept the same.

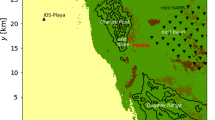
For a southwesterly flow past the real topography of Taiwan, there is no stagnation point or lee vortices formed because the impinging angle of the flow is small. A major mesoscale low forms to the southeast of the Central Mountain Range (CMR), while a mesohigh forms upstream. For a westerly flow past Taiwan, a stagnation point forms upstream of the mountain and a pair of vortices form on the lee and move downstream at later times. The cyclonic vortex then develops into a mesocyclone. A mesolow also forms to the southeast of Taiwan. For a northeasterly flow past Taiwan, the mesolow forms to the northwest of the mountain. Similar to flows over idealized topographies, the Taiwan mesolow is formed by the downslope wind associated with mountain waves through adiabatic warming. A conceptual model of the Taiwan southeast mesolow and mesocyclone is proposed.