Orographic effects on a 3-D barotropic lee wave across a meso-scale mountain corner

Abstract

An attempt has been made to study 3-D lee waves associated with an adiabatic, non-viscous, Bousisnesq, non-rotating, stationary dry mean flow across a meso-scale Mountain Corner hills (MCH). For simplicity, the far upstream undisturbed basic flow is assumed to have horizontal components of wind (U,V) and Brunt Vaisala frequency (N) to be independent of height. MCH is synthesized by the intersection of two semi-infinite ridges, parallel to the horizontal axes of co-ordinates. The primitive equations are used in z-coordinate. The nonlinear governing equations are linearized by using perturbation technique. The linearized equations are then subjected to two-dimensional Fourier transform. The 2nd order ordinary differential equation in the Fourier transform ŵ of perturbation vertical velocity w′ is obtained by some algebraic simplification. This equation has been solved by using the radiational upper boundary condition and the lower boundary condition imposed by the profile of the hill at surface. The vertical velocity (w′) is represented by double integral, which is very complicated. This double integral is evaluated by using asymptotic technique.

Introduction

Weather and climate of a place is substantially influenced by the presence of orographic barriers at that place. Influence of orographic barriers on airflow depends on the scale of the barrier as well as scale of flow.

When a stably stratified air parcel flows an orographic barrier, gravity waves are excited to propagate upward direction under certain conditions of thermal stability and airflow stratification. It is also known as internal gravity waves (IGW). The IGW can propagate horizontally and vertically to a great distance carrying energy and momentum to higher levels in the atmosphere. Sometimes, they are associated with the formation of clear air turbulence (CAT). The information about standing waves, which under favorable meteorological conditions form on the lee side of the mountain barrier, is very important for the safety of aviation. Many aircraft accidents reported in mountainous areas are often attributed to the vertical velocities of large magnitude associated with the lee waves. Hence the studies on lee waves associated with air flow across an orographic barrier have an important bearing on the safety of aviation.

Theoretical investigation in this field can broadly be divided into two types. In one type, the orographic barrier has been assumed to have an infinite extension in the cross mean flow direction, which constrains the perturbation to be 2-dimensional. Such studies may be traced back to the works of Lyra (1943), Queney (1947, 1948), Scorer (1949), Sawyer (1960), Sarker (1965, 1966, 1967), De (1973), Sinha Ray (1988), Kumar et al. (1998), etc. In another type of theoretical studies, the orographic barrier has been assumed to have finite extension in both directions, viz., along and across the basic flow, due to which the perturbations are essentially of 3-dimensional. Such studies may be traced back to the work of Scorer and Wilkinson (1956), Wurtele (1957), Crapper (1959), Sawyar (1962), Das (1964), Onishi (1969), Smith (1979, 1980), Dutta et al. (2002), Dutta (2003, 2005), Kumar (2007), Das et al. (2013, 2016), etc.

In some of the above studies, wind and stability were assumed to be either invariant with height or assumed to have some analytical behavior with height. Solutions for such studies were essentially obtained by analytical method. In other studies, realistic vertical variation of wind and stability were considered and the solution obtained using quasi numerical or numerical method.

In India studies on the effect of an orographic barrier on airflow have been addressed by Das (1964), Sarker (1965, 1966, 1967), Sarker et al. (1978), De (1971, 1973), Sinha Ray (1988), Dutta et al. (2002), Dutta (2005), Dutta et al. (2006), Kumar et al. (2005), Das et al. (2016), etc. In all the studies the barrier (2-D) or the major ridge axis (3-D) of the barrier has been assumed to be extended broadly either in the East–West (EW) direction or in North–South (NS) direction.

In India in the northeast region, the Khasi–Jayantia (KJ) hill is broadly EW oriented whereas the Assam–Burma (AB) hill is broadly NS oriented and they meet at almost right angle forming a mountain corner to the northeast. It is believed that weather and climate in that region are neither controlled by KJ hill alone nor it is controlled by AB hill alone, rather they are controlled by their combined effect. To address the problem of this combined effect, one has to investigate the effect of the above mountain corner on airflow and rainfall in that region.

From the foregoing discussion it appears that the corner mountain wave problem has not been addressed so far. The objective of the present study is to develop a 3-D meso scale lee wave model for air flow across an idealized mountain corner and apply it for the corner effect of KJ hills and AB hills.

Database

Guwahati (26.19°N latitude and 91.73°E longitude) is the only radio sonde station to the upstream of both KJ hills and AB hills. Accordingly for the present study we have used the RS/RW data of Guahati for those dates, which corresponds to the observed lee waves across ABH, as reported by De (1970, 1971) and Farooqui and De (1974) and has been obtained from Archive of India Meteorological Department, Pune.

Methodology

In this paper, we shall develop a three dimensional meso-scale lee wave model considering the basic flow consist of both zonal component (U) and meridional component (V). To develop this model we have considered the flow is an adiabatic, steady state, non-rotating, non-viscous, Bousisnesq. Also we assume two components (U, V) of basic flow and Brunt–vaisala frequency (N) are invariant with height. Under these assumptions the linearized governing equations are:

$$U\frac{{\partial u^{\prime}}}{\partial x} + V\frac{{\partial u^{\prime}}}{\partial x} = - \frac{1}{{\rho_{0} }}\frac{{\partial p^{\prime}}}{\partial x}$$

(1)

$$U\frac{{\partial v^{\prime}}}{\partial x} + V\frac{{\partial v^{\prime}}}{\partial x} = - \frac{1}{{\rho_{0} }}\frac{{\partial p^{\prime}}}{\partial y}$$

(2)

$$U\frac{{\partial w^{\prime}}}{\partial x} + V\frac{{\partial w^{\prime}}}{\partial x} = - \frac{1}{{\rho_{0} }}\frac{{\partial p^{\prime}}}{\partial z} + g\frac{{\theta^{\prime}}}{{\theta_{0} }}$$

(3)

$$\frac{{\partial u^{\prime}}}{\partial x} + \frac{{\partial v^{\prime}}}{\partial y} + \frac{{\partial w^{\prime}}}{\partial z} = 0$$

(4)

$$U\frac{{\partial \theta^{\prime}}}{\partial x} + V\frac{{\partial \theta^{\prime}}}{\partial y} + w^{\prime}\frac{{d\theta_{0} }}{dz} = 0$$

(5)

where $U,V,\rho_{0} ,\theta_{0}$ are, respectively, zonal state wind, meridional wind, density and potential temperature and $u^{\prime},v^{\prime},w^{\prime},p^{\prime},\rho^{\prime},\theta^{\prime}$ are, respectively, the perturbation zonal wind, meridional wind, vertical wind, pressure, density, and potential temperature. Since the perturbation quantities, $u^{\prime},v^{\prime},w^{\prime},p^{\prime},\rho^{\prime},\theta^{\prime}$, etc., are all continuous functions of x,y,z hence their horizontal variation may be represented by a double Fourier integral, such as,

$$u^{\prime}\left( {x,y,z} \right) = \frac{1}{{4\pi^{2} }}\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {\hat{u}\left( {k,l,z} \right)e^{{i\left( {kx + ly} \right)}} } } {\text{d}}k{\text{d}}l$$

where $\hat{u}\left( {k,l,z} \right) = \int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {u^{\prime}\left( {x,y,z} \right)e^{{ - i\left( {kx + ly} \right)}} {\text{d}}x{\text{d}}y} }$ is the double Fourier transform of $u^{\prime}\left( {x,y,z} \right)$.

Perform double Fourier transform to (1)–(5) we get

$$i\left( {kU + lV} \right)\hat{u} = - ik\frac{{\hat{p}}}{{\rho_{0} }}$$

(6)

$$i\left( {kU + lV} \right)\hat{v} = - il\frac{{\hat{p}}}{{\rho_{0} }}$$

(7)

$$i\left( {kU + lV} \right)\hat{w} = - \frac{1}{{\rho_{0} }}\frac{{\partial \hat{p}}}{\partial z} + g\frac{{\hat{\theta }}}{{\theta_{0} }}$$

(8)

$$ik\hat{u} + il\hat{v} + \frac{{\partial \hat{w}}}{\partial z} = 0$$

(9)

$$i\left( {kU + lV} \right)\hat{\theta } + \hat{w}\frac{{{\text{d}}\theta_{0} }}{{{\text{d}}z}} = 0$$

(10)

Eliminating $\hat{u},\hat{v}$ from the Eqs. (6)–(10) we get

$$\frac{{\partial^{2} \hat{w}}}{{\partial z^{2} }} + \frac{1}{{\rho_{0} }}\frac{{{\text{d}}\rho_{0} }}{{{\text{d}}z}}\frac{{\partial \hat{w}}}{\partial z} + \left( {k^{2} + l^{2} } \right)\left[ {\frac{{N^{2} }}{{\left( {kU + lV} \right)^{2} }} - 1} \right]\hat{w} = 0$$

(11)

where, $N = \sqrt {\frac{g}{{\theta_{0} }}\frac{{{\text{d}}\theta_{0} }}{{{\text{d}}z}}}$ is the Brunt–Vaisala frequency.

Now, putting $\hat{w}\left( {k,l,z} \right) = \sqrt {\frac{{\rho_{0} \left( o \right)}}{{\rho_{0} \left( z \right)}}} \hat{w}_{1} (k,l,z)$ in Eq. (11), we get

$$\frac{{\partial^{2} \hat{w}_{1} }}{{\partial z^{2} }} + \left[ {\frac{{N^{2} }}{{\left( {kU + lV} \right)^{2} }} - 1} \right]\left( {k^{2} + l^{2} } \right)\hat{w}_{1} = 0$$

$$\frac{{\partial^{2} \hat{w}_{1} }}{{\partial z^{2} }} + m^{2} \hat{w}_{1} = 0$$

(12)

where,

$$m^{2} = \left[ {\frac{{N^{2} }}{{\left( {kU + lV} \right)^{2} }} - 1} \right]\left( {k^{2} + l^{2} } \right)$$

(13)

For vertically propagating wave, the solution of (12) can be taken as

$$\hat{w}_{1} (k,l,z) = \hat{w}_{1} (k,l,0)e^{imz}$$

(14)

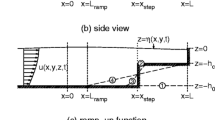
Now, at the surface the airflow follows the contour of the mountain, the profile is given by

$$h\left( {x,y} \right) = \frac{H}{2}\left[ {\frac{{a^{2} }}{{a^{2} + \left( {x - x_{0} } \right)^{2} }} + \frac{{b^{2} }}{{b^{2} + \left( {y - y_{0} } \right)^{2} }}} \right]$$

(15)

Where ‘H’ be height of MCH and the profile of (15) is given by Fig. 1. The Gray and Sky color of this figure is the Corner Montain which we are interested to study.

Fig. 1

Profile of Mountain Corner hills

Now the double Fourier transform of (15) is given by

$$\hat{h}\left( {k,l} \right) = - \frac{iH}{2}\left[ {\frac{a}{l}e^{{ - ak - kix_{0} }} + \frac{b}{k}e^{{ - bl - liy_{0} }} } \right]$$

(16)

Thus at the ground surface (at z = 0) the streamline displacement η′(x,y,z=0) follows the ground contour

$$\eta^{\prime}\left( {x,y,z = 0} \right) = \frac{H}{2}\left[ {\frac{{a^{2} }}{{a^{2} + \left( {x - x_{0} } \right)^{2} }} + \frac{{b^{2} }}{{b^{2} + \left( {y - y_{0} } \right)^{2} }}} \right] = h\left( {x,y} \right)$$

Hence

$$\hat{\eta }\left( {k,l,0} \right) = \hat{h}\left( {k,l} \right) = - \frac{iH}{2}\left[ {\frac{a}{l}e^{{ - ak - ikx_{0} }} + \frac{b}{k}e^{{ - bl - ily_{0} }} } \right]$$

(17)

Now the linearized lower boundary condition for $w^{\prime}_{1}$ is given by

$$w^{\prime}_{1} \left( {x,y,0} \right) = w^{\prime}\left( {x,y,0} \right) = U\frac{{\partial \eta^{\prime}\left( {x,y,0} \right)}}{\partial x} + V\frac{{\partial \eta^{\prime}\left( {x,y,0} \right)}}{\partial y}$$

Hence

$$\hat{w}_{1} \left( {k,l,0} \right) = i\left( {kU + lV} \right)\hat{\eta }(k,l,0)$$

(18)

Then from (14) and (18) we get

$$\hat{w}_{1} (k,l,z) = i\left( {kU + lV} \right)\hat{\eta }(k,l,0)e^{imz}$$

(19)

Hence

$$w^{\prime}_{1} \left( {x,y,z} \right) = \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\hat{w}_{1} (k,l,z)} } e^{i(kx + ly)} {\text{d}}k{\text{d}}l$$

(20)

Therefore

$$w^{\prime}\left( {x,y,z} \right) = \frac{H}{{8\pi^{2} }}\sqrt {\frac{{\rho_{0} \left( o \right)}}{{\rho_{0} \left( z \right)}}} Re\mathop \int \limits_{0}^{\infty } \mathop \int \limits_{0}^{\infty } \left( {kU + lV} \right)\left[ {\frac{a}{l}e^{{ - ak - ikx_{0} }} + \frac{b}{k}e^{{ - bl - ily_{0} }} } \right]e^{i(kx + ly + mz)} {\text{d}}k{\text{d}}l$$

(21)

To evaluate (21) we make following substation:$k = \frac{\lambda N}{{\sqrt {U^{2} + V^{2} } \cos \alpha }}$, $l = \frac{\mu N}{{\sqrt {U^{2} + V^{2} } \cos \alpha }}$ and $x = X\frac{{\sqrt {U^{2} + V^{2} } \cos \alpha }}{N}$, $y = Y\frac{{\sqrt {U^{2} + V^{2} } \cos \alpha }}{N}$, $z = Z\frac{{\sqrt {U^{2} + V^{2} } \cos \alpha }}{N}$ where α be the angle between the basic flow vector $\vec{V} = U\vec{i} + V\vec{j}$ and the wave number vector $\vec{K} = k\vec{i} + l\vec{j}$.

Now

$$\vec{V}.\vec{K} = \left| {\vec{V}} \right|\left| {\vec{K}} \right|\cos \alpha$$

(22)

Now

$$m^{2} = \left[ {\frac{{N^{2} }}{{\left( {kU + lV} \right)^{2} }} - 1} \right]\left( {k^{2} + l^{2} } \right)$$

$$= \left[ {\frac{{N^{2} }}{{\left( {U^{2} + V^{2} } \right)\cos^{2} \alpha }} - \frac{{\left( {\lambda^{2} + \mu^{2} } \right)N^{2} }}{{\left( {U^{2} + V^{2} } \right)\cos^{2} \alpha }}} \right]$$

$$= \frac{{N^{2} }}{{\left( {U^{2} + V^{2} } \right)\cos^{2} \alpha }}\left[ {1 - \lambda^{2} - \mu^{2} } \right]$$

Therefore,

$$m = \frac{N}{{\sqrt {\left( {U^{2} + V^{2} } \right)} \cos \alpha }}\sqrt {1 - \lambda^{2} - \mu^{2} }$$

(23)

Using the above substitutions, the integral in (21) has been approximated using asymptotic method, following Hsu (1948).

$$w^{\prime}\left( {x,y,z} \right) = \exp \left( {\frac{g - R^{*}\gamma }{2R^{*}T}z} \right)\frac{{N HZr_{1} }}{{16R_{1}^{2} }}\left[ \begin{aligned} \frac{a}{y}\exp \left( {\frac{{ - axNr_{1} }}{{R_{1} R_{4} }}} \right)\cos \left( {\frac{{NR_{1} r_{1} }}{{R_{4} }} - \frac{{Nxx_{0} r_{1} }}{{R_{1} R_{4} }}} \right) + \hfill \\ \frac{b}{x}\exp \left( {\frac{{ - byNr_{1} }}{{R_{1} R_{4} }}} \right)\cos \left( {\frac{{NR_{1} r_{1} }}{{R_{4} }} - \frac{{Nyy_{0} r_{1} }}{{R_{1} R_{4} }}} \right) \hfill \\ \end{aligned} \right]$$

(24)

Details of the above derivation is given in “Appendix”, where $r_{1} = \sqrt {x^{2} + y^{2} }$, $R_{1} = \sqrt {x^{2} + y^{2} + z^{2} }$ and $R_{4} = Ux + Vy$

Result and discussion

Now the Eq. (24), it is clearly shown that at the ground surface (i.e., z = 0) w′ vanishes. This should be so for lee wave (Dutta et al. 2002). Using the Eq. (24), the perturbation vertical velocity (w′) is computed at different levels for the typical lee wave case across the corner mountain hill, the order of magnitude ‘U’, ‘V’ and ‘N’ are 1 m/sec, 1 m/sec and 0.01/s, respectively. We computed w′ at four levels only, viz., at 1.5, 3, 6 and 10  km above mean see level, which approximately resemble to 850, 700, 500 and 300hPa, respectively. The downstream variation of w′ along the line ‘Uy−Vx = −50’ at the levels 1.5, 3, 6 and 10 km above the mean see level are shown in the Fig. 2a–d. From these figures we see that the downstream decay at above mentioned levels in the amplitude of w′ about the line ‘Uy−Vx = −50’.

Fig. 2

a–d Downstream variation of w′ along the line ‘Uy−Vx = −50’ at the levels 1.5, 3, 6 and  10 km, respectively

The contours of perturbation vertical velocity (w′) at the levels 1.5, 3, 6 and  10 km above the mean see level, which approximately resemble to 850, 700, 500 and 300hPa, respectively, are shown in Fig. 3a–d. These figures show that the maximum updraft regions are ‘crescent shaped’ and symmetric about the line line ‘Uy−Vx = 0’. Wurtele (1957) showed crescent shaped updraft region, symmetric about x-axis, taking constant basic flow, with only component (only U component) across the barrier. Dutta et al. (2002) and Das et al. (2013) they obtained horseshoes shaped updraft region symmetric about the line ‘y = 0’ and taking constant basic flow (U) with only U-component. In the present study, due to the presence of V-component, there is a meridional forcing acting at all level, causing the symmetric(about the line y = 0) crescent shaped updraft region to rotate through an angle $\tan^{ - 1} \left( {\frac{V}{U}} \right)$.

Fig. 3

a–d Contours of w′ across the corner mountain barrier at the levels 1.5, 3, 6 and  10 km, respectively

The vertical profile of perturbation vertical velocity (w′) along the line ‘Uy−Vx = −50’ at different heights, at different downstream locations is shown in Fig. 4. It is seen that the perturbation vertical velocity (w′) at every point of downstream location does not form alternatively positive and negative, i.e., cellular structure.

Fig. 4

Vertical profile of w′ along the line ‘Uy−Vx = −50’ at different heights and at different downstream locations

Conclusions

In this investigation, we have presented the orographic effects on a 3-D barotropic lee wave across a meso-scale mountain corner following the asymptotic approach. In the sequel, we have made some interesting observation. Moreover,

• 1. The asymptotic solution for perturbation vertical velocity (w′), along the line Uy−Vx = −50, the downstream decay at the mentioned levels.

• 2. The contours of the perturbation vertical velocity (w′) at the above mentioned levels are symmetric about the central plane along the line Uy−Vx = 0 and maximum updraft regions are crescent shaped which are inclined at an angle $\tan^{ - 1} \left( {\frac{V}{U}} \right)$.

• 3. The vertical profile of w′ along the line Uy−Vx = −50, is obtained by asymptotic method and does not form the cellular structure.

Appendix

Hsu’s (1948) theorem: In the theorem, he has shown that if $\varPhi \left( {x,y} \right),h\left( {x.y} \right)$ and $f\left( {x,y} \right) = e^{h(x,y)}$are continuous functions defined on a region S such that,

• (1) $\varPhi \left( {x,y} \right),[f\left( {x,y} \right)]^{n}$ are absolutely integrable over S for n=0,1,2.

• (2) $\frac{\partial f}{\partial x},\frac{{\partial^{2} f}}{{\partial x^{2} }},\frac{\partial f}{\partial y},\frac{{\partial^{2} f}}{{\partial y^{2} }}$ exist and continuous over S.

• (3) $h(x,y)$has an absolute maximum value at an interior pt (x ₀, y ₀)such that

$$ {\text{At}}\;(x_{0} ,y_{0} )\;\frac{\partial h}{\partial x} = \frac{\partial h}{\partial y} = 0,\frac{{\partial^{2} h}}{{\partial x^{2} }}\frac{{\partial^{2} h}}{{\partial y^{2} }} - (\frac{{\partial^{2} h}}{\partial x\partial y})^{2} > 0 $$

• (4) $\varPhi \left( {x,y} \right)$ is continuous at (x ₀, y ₀)and $\varPhi (x_{0} ,y_{0} ) \ne 0.$ Now if C be an analytic curve passing through the point (x ₀, y ₀), such that the region S is divided into two sub regions S ₁ and S ₂. Then the integral

• (5) $\mathop {\iint }\nolimits \varPhi \left( {x,y} \right)[f\left( {x,y} \right)]^{n} ds$ taken over either of S ₁ and S ₂ asymptotic to

$$ \frac{{\pi \varPhi (x_{0} ,y_{0} )[f\left( {x_{0} ,y_{0} } \right)]^{n} }}{{\sqrt[n]{{\left[ {\frac{{\partial^{2} h}}{{\partial x^{2} }}\frac{{\partial^{2} h}}{{\partial y^{2} }} - \left( {\frac{{\partial^{2} h}}{\partial x\partial y}} \right)^{2} } \right]_{{(x_{0} ,y_{0} )}} }}}} $$

Using $\sqrt {\frac{{\rho_{0} (0)}}{{\rho_{0} (z)}}} \approx \exp \left( {\frac{{g - R^{*} \gamma }}{{2R^{*} T}}z} \right)$ (Dutta 2003) in the integral (21), has been transformed to $\frac{H}{{8\pi^{2} }}\exp \left[ {\frac{{z(g - R^{*} \gamma )}}{{2R^{*} T}}} \right]I_{1}$, where, R ^* is the gas constant and γ is the ratio of two specific heat of gas.

$$ \begin{aligned} I_{1} = \mathop {\iint }\limits_{0}^{\infty } \left( {kU + lV} \right)\left[ {\frac{a}{l}e^{{ - \left( {a + ix_{0} } \right)k}} + \frac{b}{k}e^{{ - \left( {b + iy_{0} } \right)l}} } \right]\exp \left[ {i\left( {kx + ly + mz} \right)} \right]dkdl \hfill \\ = \mathop {\iint }\limits_{0}^{\infty } p(\lambda U + \mu V)\left[ {\frac{a}{\mu p}e^{{ - \left( {a + ix_{0} } \right)\lambda p}} + \frac{b}{\lambda p}e^{{ - \left( {b + iy_{0} } \right)\mu p}} } \right]\exp \left[ {i\left( {\lambda X + \mu Y + \nu Z} \right)} \right]p^{2} d\lambda d\mu = I_{11} + I_{12} \hfill \\ \end{aligned} $$

Where,

$$ \begin{aligned} I_{11} = \mathop {\iint }\limits_{0}^{\infty } \left( {\lambda U + \mu V} \right)\left[ {\frac{a}{\mu }e^{{ - (a + ix_{0} )\lambda p}} \exp \left[ {i(\lambda X + \mu Y + \nu Z)} \right]} \right]p^{2} d\lambda d\mu \hfill \\ I_{12} = \mathop {\iint }\limits_{0}^{\infty } \left( {\lambda U + \mu V} \right)\left[ {\frac{b}{\lambda }e^{{ - (b + iy_{0} )\mu p}} \exp \left[ {i(\lambda X_{1} + \mu Y_{1} + \nu Z_{1} )} \right]} \right]p^{2} d\lambda d\mu \hfill \\ \end{aligned} $$

Now to evaluate the double integrals I ₁₁ and I ₁₂ following substitutes are made:

$$ \lambda = \tau cos\beta ,\mu = \tau sin\beta ,X = Rcos\theta { ,}Y = RSin\theta . $$

Therefore, $\lambda X + \mu Y + \nu Z = \tau R\cos \left( {\beta - \theta } \right) + Z\sqrt {1 - \tau^{2} } = \sigma$ (say)

Hence, $I_{11} = \mathop \smallint \limits_{0}^{\infty } \mathop \smallint \limits_{{ - {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \frac{{\tau ap^{2} \left( {Ucos\beta + Vsin\beta } \right)}}{sin\beta }e^{{ - a\tau pcos\beta - ix_{0} p\tau cos\beta }} e^{i\sigma } d\tau d\beta$. This double integral is difficult to evaluate analytically. So they are amenable to the method of stationary phase, following Hsu’s (1948). According to this method, first those points (τ, β) in the wave number domain are found out, where the phase σ is stationary. Those points are termed as saddle points. Then the entire integrand is expanded in Taylor’s series about the saddle point and the first term of the expansion is retained as the asymptotic approximation of the integrals, which is valid at far down wind location of the mountain. Details of the theorem, given by Hsu’s (1948). Following Hsu’s (1948),

Let $\phi \left( {\tau ,\beta } \right) = \frac{{\tau ap^{2} \left( {Ucos\beta + Vsin\beta } \right)}}{sin\beta }e^{{ - a\tau pcos\beta - ix_{0} p\tau cos\beta }}$ and $h\left( {\tau ,\beta } \right) = i\tau R\cos \left( {\beta - \theta } \right) + Z_{1} \sqrt {1 - \tau^{2} }$ and $f\left( {\tau ,\beta } \right) = e^{h(\tau ,\beta )}$. $\frac{\partial h}{\partial \tau } = 0 \,and\, \frac{\partial h}{\partial \tau } = 0$ Gives the stationary point $\left( {\tau_{0,} \beta_{0} } \right)$ as

$$ \tau_{0} = \frac{{R_{1} }}{{\sqrt {Z^{2} + R_{1}^{2} } }} = \sqrt {\frac{{X^{2} + Y^{2} }}{{X^{2} + Y^{2} + Z^{2} }}} = \sqrt {\frac{{x^{2} + y^{2} }}{{x^{2} + y^{2} + z^{2} }}} = \frac{{r_{1} }}{{R_{1} }} \,and \,\beta_{0} = \theta, $$

Where $r_{1}^{2} = x^{2} + y^{2} \,and \,R_{1}^{2} = x^{2} + y^{2} + z^{2}$. It can be shown that at stationary point$\left( {\tau_{0,} \beta_{0} } \right)$.

$p = \frac{{Nr_{1} }}{{R_{4} }}, \,\sigma = \frac{{Nr_{1} R_{1} }}{{R_{4} }},\,\tau pcos\beta = \frac{{Nxr_{1} }}{{R_{1} R_{4} }},\,\frac{Ucos\beta + Vsin\beta }{sin\beta } = \frac{{R_{4} }}{y},\,$ Where $R_{4} = Ux + Vy.$

$$ \phi \left( {\tau_{0} ,\beta_{0} } \right) = \frac{{\tau ap^{2} \left( {Ucos\beta + Vsin\beta } \right)}}{sin\beta }e^{{ - a\tau pcos\beta - ix_{0} p\tau cos\beta }} = \frac{{N^{2} r_{1}^{3} }}{{R_{1} R_{4} }}\frac{a}{y}\exp \left( {\frac{{ - {\text{aNr}}_{1} x}}{{{\text{R}}_{1} {\text{R}}_{4} }}} \right)\exp \left( {\frac{{ - {\text{ix}}_{0} {\text{Nr}}_{1} x}}{{{\text{R}}_{1} {\text{R}}_{4} }}} \right) $$

Now$\left( {\frac{{\partial^{2} h}}{{\partial \tau^{2} }}} \right)_{{(\tau_{0,} \beta_{0} )}} = - \frac{{Z_{1} }}{{\left( {1 - \tau^{2} } \right)^{{\frac{3}{2}}} }},\left( {\frac{{\partial^{2} h}}{{\partial \tau^{2} }}} \right)_{{(\tau_{0,} \beta_{0} )}} = - \frac{{Z_{1} }}{{\left( {1 - \tau^{2} } \right)^{{\frac{3}{2}}} }},\left( {\frac{{\partial^{2} h}}{{\partial \beta^{2} }}} \right)_{{(\tau_{0,} \beta_{0} )}} = - \tau R_{1} \cos (\beta - \theta )$ and $\left( {\frac{{\partial^{2} h}}{\partial \tau \partial \beta }} \right)_{{(\tau_{0,} \beta_{0} )}} = - R_{1} \sin (\beta - \theta )$.

Hence, $\left[ {\left( {\frac{{\partial^{2} h}}{{\partial \tau^{2} }}} \right)\left( {\frac{{\partial^{2} h}}{{\partial \beta^{2} }}} \right) - \left( {\frac{{\partial^{2} h}}{{\partial \tau^{2} }}} \right)^{2} } \right]_{{\left( {\tau_{0,} \beta_{0} } \right)}} = \frac{{\tau_{0} R_{1} Z_{1} }}{{\left( {1 - \tau^{2} } \right)^{{\frac{3}{2}}} }} = \frac{{R^{2} \left( {R^{2} + Z_{1}^{2} } \right)}}{{Z_{1}^{2} }} = \frac{{Nr_{1}^{2} R_{1} }}{{R_{4} z}} > 0$. Let us consider a path ‘C’, in the region passing through the stationary point $\left( {\tau_{0,} \beta_{0} } \right)$,which has divided the region into two parts, viz., the upstream side and downstream side of the mountain. Hence following, Hsu (1948), the contribution of the integral $I_{11}$ to the downstream side can be approximated as

$$ \frac{{\pi \varphi \left( {\tau_{0} ,\beta_{0} } \right)[f\left( {\tau_{0} ,\beta_{0} } \right)]}}{{2\sqrt {\left[ {\frac{{\partial^{2} h}}{{\partial \tau^{2} }}\frac{{\partial^{2} h}}{{\partial \beta^{2} }} - \left( {\frac{{\partial^{2} h}}{\partial \tau \partial \beta }} \right)^{2} } \right]_{{\left( {\tau_{0} ,\beta_{0} } \right)}} } }} = \frac{\pi }{2}\frac{{Nr_{1} \,z}}{{R_{1}^{2} }}\frac{a}{y}\;\exp \left( {\frac{{ - aNr_{1} x}}{{R_{1} R_{4} }}} \right)\,\exp \left( {i\left[ {\frac{{Nr_{1} R_{1} }}{{R_{4} }} - \frac{{Nr_{1} x_{0} x}}{{R_{1} R_{4} }}} \right]} \right) $$

Following similar argument, it can be seen that the contribution of the integral $I_{12}$ to the downstream side can be approximated as $\frac{\pi }{2}\frac{{Nr_{1} \,z}}{{R_{1}^{2} }}\frac{b}{x}\;\exp \left( {\frac{{ - bNr_{1} y}}{{R_{1} R_{4} }}} \right)\,\exp \left( {i\left[ {\frac{{Nr_{1} R_{1} }}{{R_{4} }} - \frac{{Nr_{1} y_{0} y}}{{R_{1} R_{4} }}} \right]} \right)$.

Hence

$$ \begin{aligned} w^{\prime}\left( {x,y,z} \right) = \frac{H}{{8\pi^{2} }}\exp \left( {\frac{{g - R^{*} \gamma }}{{2R^{*} T}}z} \right)\left[ {RealpartofI_{11} + RealpartofI_{12} } \right] \hfill \\ w'(x,y,z) = \exp \left( {\frac{{g - R^{*} \gamma }}{{2R^{*} T}}z} \right)\frac{{NHr_{1} z}}{{16R_{1}^{2} }}\left[ \begin{aligned} \frac{a}{y}\exp \left( {\frac{{ - aNr_{1} x}}{{R_{1} R_{4} }}} \right)\cos \left( {\frac{{Nr_{1} R_{1} }}{{R_{4} }} - \frac{{Nr_{1} x_{0} x}}{{R_{1} R_{4} }}} \right) + \hfill \\ \frac{b}{x}\exp \left( {\frac{{ - bNr_{1} y}}{{R_{1} R_{4} }}} \right)\cos \left( {\frac{{Nr_{1} R_{1} }}{{R_{4} }} - \frac{{Nr_{1} y_{0} y}}{{R_{1} R_{4} }}} \right) \hfill \\ \end{aligned} \right] \hfill \\ \end{aligned} $$