Mass transfer from a pulsating drop

Abstract

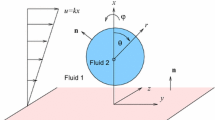
The primary difficulty in solving the problem of mass transport through an isolated drop (or bubble) moving in a fluid medium at high Reynolds numbers lies in the extreme complexity of the hydrodynamic pattern of the phenomenon. For sufficiently high velocities a separation of the external flow will occur in the rear portion of the drops and bubbles, which leads to the appearance of a turbulent wake and a sharp increase of the hydrodynamic resistance. Beginning with those dimensions for which the resistance force acting per unit surface of the drop or bubble from the external medium becomes greater than the capillary pressure, the surface of the drops and bubbles begins to deform and pulsate. The local variations of the surface tension, resulting either from the process of convective diffusion or from adsorption of surface-active substances, have a large effect on the hydrodynamics of drops and bubbles (particularly on the deformation of their surface) [1, 2], The presence of vortical, and possibly even turbulent, motion within the drops and bubbles may, under certain conditions [1], lead to their fractionation.

Naturally, at the present time such complex hydrodynamics cannot be described by exact quantitative relations. Several authors have attempted to solve this problem approximately within the framework of certain assumptions. In particular [3–6], a theory was developed for the boundary layer on the surface of spherical and ellipsoidal gaseous bubbles moving in a liquid, studies were made [7, 8] of the hydrodynamics of drops located in a gas flow and the conditions were found for which fractionation of such drops takes place. Of considerable practical interest is the development of the theory of mass transfer in pulsating drops and bubbles and finding in explicit form the dependence of the mass transfer coefficients on the hydrodynamic characteristics of these systems. Until this relationship is established, every theory which ignores the effect of hydrodynamics on the mass transfer rate from an individual drop or bubble cannot be considered in any way well-founded. This relates particularly to the theories [9, 10] which consider mass transfer in systems with concentrated streams of drops and bubbles. The present paper is devoted to the study of mass transport through the surface of an isolated drop in an irrotational gas or liquid stream for large Peclet numbers P.