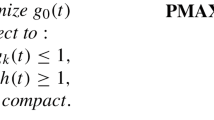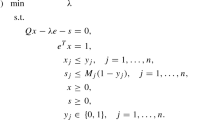Abstract
When the terms in a convex primal geometric programming (GP) problem are multiplied by slack variables whose values must be at least unity, the invariance conditions may be solved as constraints in a linear programming (LP) problem in logarithmically transformed variables. The number of transformed slack variables included in the optimal LP basis equals the degree of difficulty of the GP problem, and complementary slackness conditions indicate required changes in associated GP dual variables. A simple, efficient search procedure is used to generate a sequence of improving primal feasible solutions without requiring the use of the GP dual objective function. The solution procedure appears particularly advantageous when solving very large geometric programming problems, because only the right-hand constants in a system of linear equations change at each iteration.
Similar content being viewed by others
References
Dembo, R. S.,Current State of the Art of Algorithms and Computer Software for Geometric Programming, Journal of Optimization Theory and Applications, Vol. 26, pp. 149–183, 1978.
Fattler, J. E. et al.,On the Computational Utility of Posynomial Geometric Programming Solution Methods, Mathematical Programming, Vol. 22, pp. 163–201, 1982.
Ecker, J. G., Kupferschmid, M., andSacher, R. S.,Comparison of a Special-Purpose Algorithm with General-Purpose Algorithms for Solving Geometric Programming Problems, Journal of Optimization Theory and Applications, Vol. 43, pp. 237–262, 1984.
Cole, F., Gochet, W., andSmeers, Y.,Comparison between a Primal and a Dual Cutting Plane Algorithm for Posynomial Geometric Programming Problems, Journal of Optimization Theory and Applications, Vol. 47, pp. 159–180, 1985.
Gonen, A., andAvriel, M.,A Primal-Dual Newton-Type Algorithm for Geometric Programs with Equality Constraints, Journal of Optimization Theory and Applications, Vol. 49, pp. 239–268, 1986.
Duffin, R. J.,Linearizing Geometric Programs, SIAM Review, Vol. 12, pp. 211–227, 1970.
Sposito, V. A.,Linear and Nonlinear Programming, Iowa University Press, Ames, Iowa, 1975.
Everett, H.,Generalized Lagrange Multipliers Method for Solving Problems of Optimal Allocation of Resources, Operations Research, Vol. 11, pp. 399–471, 1963.
Wilde, D. J., andBeightler, C.,Foundations of Optimization, Prentice-Hall, Englewood Cliffs, New Jersey, 1967.
McNamara, J. R.,Geometric Programming with Multiplicative Slack Variables, Naval Research Logistics Quarterly, Vol. 33, pp. 501–533, 1986.
Wilde, D. J.,Globally Optimal Design, Wiley, New York, New York, 1978.
Best, M. J., andCaron, R. J.,The Simplex Method and Unrestricted Variables, Journal of Optimization Theory and Applications, Vol. 45, pp. 33–39, 1985.
Brooks, R., andGeoffrion, A.,Finding Everett's Multipliers by Linear Programming, Operations Research, Vol. 14, pp. 1149–1153, 1966.
Author information
Authors and Affiliations
Additional information
Communicated by M. Avriel
The influence of J. G. Ecker, the writer's teacher, is present throughout this paper. Two anonymous referees and the Associate Editor made very helpful suggestions. Dean Richard W. Barsness provided generous support for this work.
Rights and permissions
About this article
Cite this article
McNamara, J.R. On geometric programming and complementary slackness. J Optim Theory Appl 74, 305–316 (1992). https://doi.org/10.1007/BF00940896
Issue Date:
DOI: https://doi.org/10.1007/BF00940896