Abstract
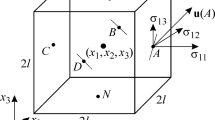
A discrete model of a deformable elastic body in the form of an oriented graph is examined. The graph can be used as a nontraditional means of deriving resolvent equations, involving the transformation of systems of generalized coordinates describing elements of the sectioned body to a coordinate system that describes the body as a whole. It is shown that graphing (vertex and loop) laws can be interpreted as equilibrium and strain compatibility conditions that in the limit become the corresponding differential equations. With the use of a unit cell having eight degrees of freedom, the strain field is approximated by linear polynomials (which corresponds to approximation of the displacement fields by quadratic polynomials). The standard finite-element method requires 16 degrees of freedom (elements with eight nodes) for the same purpose. The proposed graphical approach thus reduces the number of equations that describe the model and the time and amount of memory needed to obtain a solution.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Literature cited
G. Kron, Tensor Analysis of Networks [Russian translation], Sov. Radio, Moscow (1978).
G. Kron, Investigation of Complex Systems by Parts – Diacoptics [Russian translation], Nauka, Moscow (1972).
G. Kron, “Equivalent circuits of the elastic field,” J. Appl. Mech., Sept., A149–A161 (1944).
H. Trent, “Isomorphisms between oriented linear graphs and lumped physical systems,” J. Acoust. Soc. Am.,27, No. 3, 500–527 (1955).
E. G. Kuzovkov, “Graph model of an elastic body. Calculation of the stress-strain space,” Preprint, Inst. Probl. Prochn., AN Ukr. SSR, Kiev (1985).
E. G. Kuzovkov, “Configuration and parameters of a graph model of an elastic body,” Probl. Prochn., No. 5, 98–103 (1986).
E. G. Kuzovkov, “Equations of state of a graph model of an elastic body,” ibid., No. 5, 112–117 (1986).
E. G. Kuzovkov, “Graph model of an elastic body in mixed variables,” ibid., No. 6, 88–92 (1986).
R. Gallagher, Finite Elements Method. Principles [Russian translation], Mir, Moscow (1984).
M. Svami and K. Tkhulasiraman, Graphs, Networks, and Algorithms [Russian translation], Mir, Moscow (1984).
A. E. Petrov, Tensor Methods in Systems Theory [in Russian], Radio i Svyaz', Moscow (1985).
S. A. Brebbia et al., “Critical comparison of boundary element and finite element methods for stress analysis” BETECH'85. Proc. 1. Boundary Elem. Technol. Conf., Adelaide, Nov. 1985, pp. 225–256.
Author information
Authors and Affiliations
Additional information
Translated from Problemy Prochnosti, No. 12, pp. 60–70, December, 1993.
Rights and permissions
About this article
Cite this article
Kuzovkov, E.G. Graphical model of an elastic medium in a cartesian coordinate system. Strength Mater 25, 906–914 (1993). https://doi.org/10.1007/BF00774638
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00774638