Skip to main content
SpringerLink
Log in

Upper critical field of Nb and Nb+1 at % Ta determined by calorimetric and magnetic methods

  • Published:
Journal of Low Temperature Physics Aims and scope Submit manuscript

Abstract

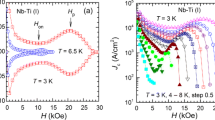
The upper critical fieldH c2 of single-crystal Nb and arc-melted Nb+1 at % Ta near the critical temperatureT c has been measured using both calorimetric and magnetic methods. In contrast with theH c2 curve determined by the magnetic measurement, which shows a clear upward curvature, the calorimetric measurement gives a nearly straight line nearT c. The data disagree with available models. A possible explanation is given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. L. Fetter and P. C. Hohenberg, inSuperconductivity, R. D. Parks, ed. (Marcel Dekker, New York, 1969), Vol. 2, p. 817.

    Google Scholar 

  2. H. Devantay, J. L. Jorda, M. Decroux, J. Muller, and R. Flukiger,J. Mat. Sci. 16, 2145 (1981).

    Google Scholar 

  3. T. P. Orlando, E. J. McNiff, S. Foner, and M. R. Beasley,Phys. Rev. B 19, 4545 (1979).

    Google Scholar 

  4. B. J. Dalyrimple and D. E. Prober,Bull. Am. Phys. Soc. 23, 230 (1978).

    Google Scholar 

  5. N. Toyota, H. Natasujii, K. Nota, A. Hoshi, N. Kobayashi, and Y. Muto,J. Low Temp. Phys. 25, 483 (1976).

    Google Scholar 

  6. R. E. Somekh, C.-G. Cui, and J. E. Evetts,J. Low Temp. Phys. 50, 33 (1983).

    Google Scholar 

  7. W. H Butler,Phys. Rev. Lett. 44, 1516 (1980).

    Google Scholar 

  8. G. Deutscher, O. Entin-Wohlman, M. Rappaport, and Y. Shapira, inInhomogeneous Superconductors (AIP, New York, 1978), Vol. 79, p. 23.

    Google Scholar 

  9. V. Novotny and P. P. M. Meincke,J. Low Temp. Phys. 18, 147 (1975).

    Google Scholar 

  10. J. M. Daams and J. P. Carbotte,J. Low Temp. Phys. 43, 263 (1981).

    Google Scholar 

  11. T. Ohtsuka and Y. Kimura,Physica 55, 562 (1971).

    Google Scholar 

  12. H. A. Leupold and H. A. Boorse,Phys. Rev. 134, A1322 (1964).

    Google Scholar 

  13. F. J. Morin and J. P. Maita,Phys. Rev. 129, 1115 (1963).

    Google Scholar 

  14. T. McConville and B. Serin,Phys. Rev. 140A, 1169 (1965).

    Google Scholar 

  15. E. Helfand and N. R. Werthamer,Phys. Rev. 147, 288 (1966).

    Google Scholar 

  16. D. K. Finnemore, T. F. Stromberg, and C. A. Swenson,Phys. Rev. 149, 231 (1966).

    Google Scholar 

  17. G. Eilenberger,Phys. Rev. 153, 584 (1967).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Physics, Chinese Academy of Sciences, Beijing, China

    Zhang Dianlin, Lin Shuyuan & C. -G. Cui

  2. University of Science and Technology of China, Hefei, China

    Chen Zhaojia

Authors
  1. Zhang Dianlin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lin Shuyuan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. C. -G. Cui
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Chen Zhaojia
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhang, D., Lin, S., Cui, C.G. et al. Upper critical field of Nb and Nb+1 at % Ta determined by calorimetric and magnetic methods. J Low Temp Phys 55, 303–308 (1984). https://doi.org/10.1007/BF00683449

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00683449

Keywords

Search

Navigation