An effective solver for absolute variable formulation of multibody dynamics

Abstract

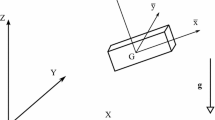
This paper presents an effective and general method for converting the equations of motion of multibody systems expressed in terms of absolute variables and Lagrange multipliers into a convenient set of equations in a canonical form (constraint reaction-free and minimal-order equations). The method is applicable to open-loop and closed-loop multibody systems, and to systems subject to holonomic and/or nonholonomic constraints. Being aware of the system configuration space is a metric space, the Gram-Schmidt ortogonalization process is adopted to generate a genuine orthonormal basis of the tangent (null, free) subspace with respect to the constrained subspace. The minimal-order equations of motion expressed in terms of the corresponding tangent speeds have the virtue of being obtained directly in a “resolved” form, i.e. the related mass matrix is the identity matrix. It is also proved that, in the case of absolute variable formulation, the orthonormal basis is constant, which leads to additional simplifications in the motion equations and fits them perfectly for numerical formulation and integration. Other useful peculiarities of the orthonormal basis method are shown, too. A simple example is provided to illustrate the convertion steps.